Simulated annealing reveals the kinetic activity of SGLT1, a member of the LeuT structural family

Abstract

The Na⁺/glucose cotransporter (SGLT1) is the archetype of membrane proteins that use the electrochemical Na⁺ gradient to drive uphill transport of a substrate. The crystal structure recently obtained for vSGLT strongly suggests that SGLT1 adopts the inverted repeat fold of the LeuT structural family for which several crystal structures are now available. What is largely missing is an accurate view of the rates at which SGLT1 transits between its different conformational states. In the present study, we used simulated annealing to analyze a large set of steady-state and pre–steady-state currents measured for human SGLT1 at different membrane potentials, and in the presence of different Na⁺ and α-methyl-d-glucose (αMG) concentrations. The simplest kinetic model that could accurately reproduce the time course of the measured currents (down to the 2 ms time range) is a seven-state model (C₁ to C₇) where the binding of the two Na⁺ ions (C₄→C₅) is highly cooperative. In the forward direction (Na⁺/glucose influx), the model is characterized by two slow, electroneutral conformational changes (59 and 100 s⁻¹) which represent reorientation of the free and of the fully loaded carrier between inside-facing and outside-facing conformations. From the inward-facing (C₁) to the outward-facing Na-bound configuration (C₅), 1.3 negative elementary charges are moved outward. Although extracellular glucose binding (C₅→C₆) is electroneutral, the next step (C₆→C₇) carries 0.7 positive charges inside the cell. Alignment of the seven-state model with a generalized model suggested by the structural data of the LeuT fold family suggests that electrogenic steps are associated with the movement of the so-called thin gates on each side of the substrate binding site. To our knowledge, this is the first model that can quantitatively describe the behavior of SGLT1 down to the 2 ms time domain. The model is highly symmetrical and in good agreement with the structural information obtained from the LeuT structural family.

INTRODUCTION

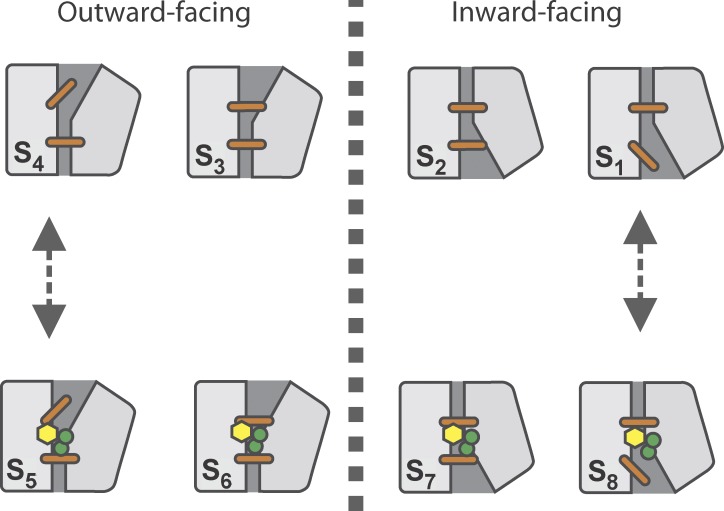
The Na⁺/glucose cotransporter (SGLT1) is the archetypical member of a class of membrane proteins that couple the energy stored in the downhill electrochemical gradient of an ion to the translocation of a substrate across the membrane. SGLT1 is expressed at the apical surfaces of epithelial cells of the small intestine and the renal proximal tubule, where it absorbs glucose. It is also expressed in the heart (Zhou et al., 2003) where its role remains to be defined. SGLT1 is believed to function according to the alternating access mechanism. This model, proposed by Jardetzky (1966), states that the transporter protein exists in two distinct states where the substrate binding sites are alternatively exposed to each side of the membrane. In 2008, the 3D structure of vSGLT, a prokaryote homologue of SGLT1, was determined in a substrate-bound, inward-facing occluded configuration (Faham et al., 2008). It was immediately realized that vSGLT belonged to the LeuT family of structurally homologous transporters built around a functional core of two inverted repeats of five transmembrane segments each. Members of this family have been found in different configurations including outward facing (LeuT [Yamashita et al., 2005; Singh et al., 2008], Mhp1 [Weyand et al., 2008], and AdiC [Fang et al., 2009; Gao et al., 2009, 2010]) and inward facing (LeuT [Krishnamurthy and Gouaux, 2012], vSGLT [Faham et al., 2008; Watanabe et al., 2010], Mhp1 [Shimamura et al., 2010], BetP [Ressl et al., 2009; Perez et al., 2011], ApcT [Shaffer et al., 2009], CaiT [Schulze et al., 2010], and GadC [Ma et al., 2012]) conformations. In each of these configurations, the ion and substrate binding sites may be freely accessible or blocked by so-called thin gates that are present on each side of the binding sites. This is shown in Fig. 1 where the simple displacement of the thin gates may represent a more complex rearrangement of the access vestibule on each side of the membrane (Krishnamurthy and Gouaux, 2012). Although computational studies at the molecular level are beginning to unravel the way vSGLT reorients itself in the membrane to cotransport glucose (Watanabe et al., 2010), the rate at which these conformational changes occur is still unsettled.

Figure 1.

Cotransport mechanism of SGLT1 suggested by the structural data of the LeuT fold family. In state S₁, the cotransporter is in its inward open conformation. The transition from S₁ to S₂ closes the intracellular thin gate (orange stick), thus occluding the binding sites. A major conformational change (S₂→S₃) then reorients SGLT1 to its outward facing state. The subsequent opening of the extracellular thin gate (S₃→S₄) makes it possible for SGLT1 to bind Na⁺ ions (green circles) and glucose (yellow hexagon; S₄→S₅). The extracellular thin gate is then free to close (S₅→S₆), which provokes a structural rearrangement of the fully loaded transporter leading to the intracellular facing occluded state S₇. This is followed by the opening of the intracellular thin gate (S₇→S₈), allowing intracellular release of the substrates (S₈→S₁).

The cloning of SGLT1 cDNA (Hediger et al., 1987) and its expression in Xenopus laevis oocytes has allowed extensive functional characterization using electrophysiology (Umbach et al., 1990; Parent et al., 1992a) and voltage-clamp fluorometry (Loo et al., 1998; Meinild et al., 2002). In addition to the steady-state Na⁺/glucose cotransport currents, expression of SGLT1 in oocytes (and, more recently, in mammalian cells) generates strong phlorizin (Pz)-sensitive transient currents in the absence of glucose (Loo et al., 1993; Hazama et al., 1997; Hummel et al., 2011). These transient currents are thought to reflect electrogenic transitions experienced by the cotransporter when it goes through the glucose-independent steps of the cotransport mechanism, and the time course of these currents can be measured with great accuracy as a function of membrane potential and [Na⁺]_o. These currents are reminiscent of the gating currents observed in voltage-dependent ionic channels and can be used to estimate values of the parameters describing the cotransport mechanism. The first kinetic model developed for SGLT1 by using detailed two-electrode voltage clamp data were an ordered six-state mirror symmetry model (Parent et al., 1992b). In this oversimplified model, the mobile binding site was assumed to carry two negative charges which were neutralized by the binding of two Na⁺ ions. Because of this simplifying hypothesis, the binding of glucose, the translocation of the fully loaded cotransporter and the intracellular unbinding of Na⁺ and glucose were all assumed to be voltage independent. The basis of this initial model was kept and slightly modified in several subsequent studies (Loo et al., 1993; Hirayama et al., 1996; Hazama et al., 1997; Eskandari et al., 2005). More recently, using a larger set of electrophysiological and fluorescence measurements, an eight-state model was proposed for SGLT1. The set of rate constants suggested in that study (Loo et al., 2006) was primarily qualitative and failed to reproduce the time courses of the transient currents. To our knowledge, none of the kinetic models previously proposed have been able to account quantitatively for the pre–steady-state and steady-state kinetics of SGLT1 over a range of Na⁺ concentrations and membrane potentials.

In an effort to find a robust kinetic model, the present work uses a novel approach based on a simulated annealing (SA) algorithm to fit an extended set of electrophysiological data. SA offers the possibility of exploring a large field of rate constants and their voltage dependence. Also, we chose to rely on a direct fitting approach, i.e., to find parameters that can reproduce the current traces themselves instead of fitting a set of parameters derived from previous multiexponential fitting of the data. The structure of the kinetic model found is a seven-state model whose connectivity is similar to the model proposed in Loo et al. (2006) but with distinct voltage sensitivities and rate-limiting steps. Interestingly, the model reveals a high degree of symmetry as the two slowest steps are the voltage-independent conformational changes of the free and fully loaded carrier. Voltage-dependent steps come immediately before and after these slow conformational changes.

MATERIALS AND METHODS

Oocyte preparation and injection

After surgical removal from X. laevis frogs, oocytes were individually isolated before enzymatic defolliculation as described previously (Bissonnette et al., 1999). 1 or 2 d after the procedure, healthy oocytes were injected with 4.6 ng mRNA coding for human myc-SGLT1 at a concentration of 0.1 µg/µl in water. This N-terminal myc-tagged version of human SGLT1 was previously shown to be functionally indistinguishable from the untagged form (Bissonnette et al., 1999). Oocytes were kept in Barth’s solution (in mM: 90 NaCl, 3 KCl, 0.82 MgSO₄, 0.41 CaCl₂, 0.33 Ca(NO₃)₂, and 5 Hepes, pH 7.6) supplemented with 5% horse serum, 2.5 mM Na⁺ pyruvate, 100 units/ml penicillin, and 0.1 mg/ml streptomycin for 4–5 d before performing electrophysiological experiments.

Solutions

To stimulate the cotransport activity of SGLT1, 5 or 0.1 mM α-methyl-d-glucose (αMG) was added to the normal saline solution used for electrophysiology (in mM: 90 NaCl, 3 KCl, 0.82 MgCl₂, 0.74 CaCl₂, and 10 HEPES, and adjusted to pH 7.5 with Tris). In cases where a lower extracellular Na⁺ concentration ([Na⁺]_o) was needed, the removed quantity of NaCl was isotonically replaced by N-methyl-d-glucamine/HCl. To inhibit the cotransporter, 0.2 mM Pz was added. Unless otherwise mentioned, all chemicals were obtained from Sigma-Aldrich.

Electrophysiology

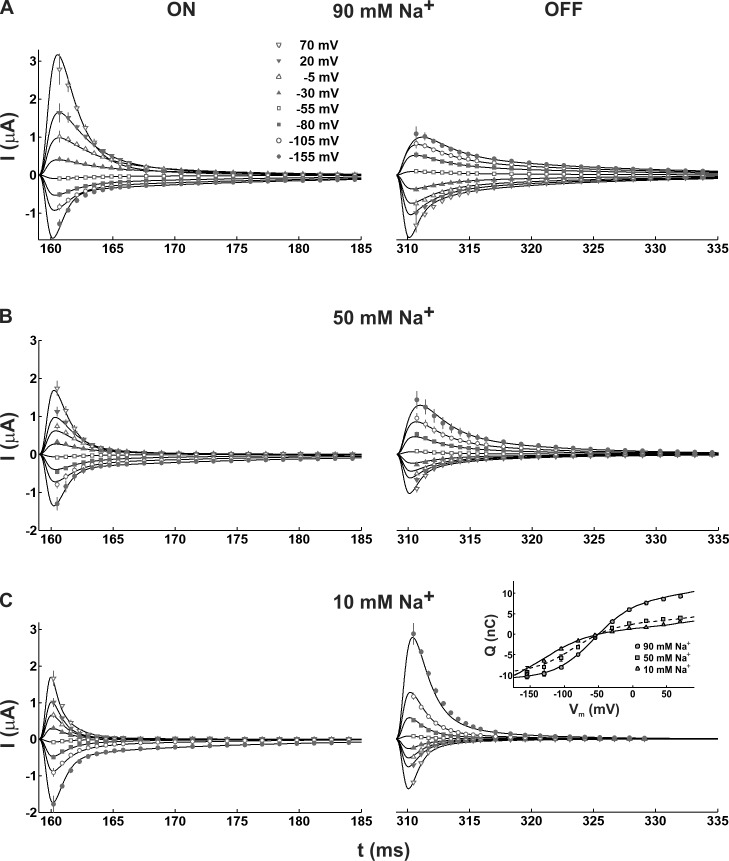
Two-microelectrode voltage-clamp experiments and current filtering (1 kHz) were done using an OC-725C Oocyte Clamp (Warner Instrument Corp.). Data recording was achieved using a Digidata 1322A acquisition system and pClamp 8.2 software (Axon Instruments Inc.). Voltage and current microelectrodes were filled with 1 M KCl and exhibited resistances of 1–3 MΩ. The bath current electrode was an Ag-AgCl pellet and the reference voltage electrode was a 1 M KCl agar bridge. To perform electrophysiological measurements, oocytes were clamped to a holding potential (V_m) of −50 mV and three sequential repetitions of a series of 150 ms voltage steps, ranging from +70 mV to −155 mV (in increments of 25 mV), were applied with an interval of 418 ms between each step. Data were recorded with a sampling rate of 10 points/ms. In the absence of substrate, SGLT1 pre–steady-state currents were isolated by subtracting the current in 0.2 mM Pz from the corresponding current measured when 90, 50, or 10 mM Na⁺ was present in the saline solution. Time integration of these Pz-sensitive currents was used to compute the transported charge as a function of the membrane potential (Q(V_m) curves) as explained previously (Gagnon et al., 2007).

Kinetic modeling of SGLT1 through the direct fitting approach

The currents were simulated using a program written in MATLAB 7.9.0 R2009b (MathWorks) representing different multistate kinetic models (source code available upon request). To mimic more closely the experimental conditions, the time course of the membrane potential used in the current simulation was constructed by integrating the membrane capacitive current in response to a voltage step. The mean current measured in the presence of 0.2 mM Pz was used as a good approximation of the membrane capacitive currents because the integration of these currents (Q) yielded a linear Q(V_m) relationship. The simulations were done with a time resolution of 20 points/ms, except for 12 ms after each voltage change (ON and OFF) when it was set to 100 points/ms. Occupational probabilities for the different states (C₁, C₂, etc.) were calculated using a set of differential equations, which is presented in Eq. 1, for an n-state model.

The voltage-dependent rate constants (k_ij) are expressed using Eyring rate theory as follows:

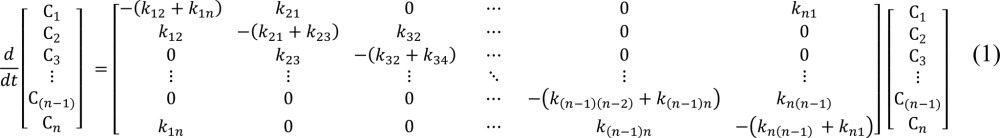$$k_{\mathit{ij}}=k_{\mathit{ij}0}\text{exp}\left(z{\delta }_{\mathit{ij}}{\alpha }_i\frac{{\mathit{FV}}_m}{\mathit{RT}}\right),$$ (2a)

$$k_{\mathit{ji}}=k_{\mathit{ji}0}\text{exp}\left[-z{\delta }_{\mathit{ij}}(1-{\alpha }_i)\frac{{\mathit{FV}}_m}{\mathit{RT}}\right],$$ (2b)

where zδ_ij is the valence of the equivalent moveable charge (a charge z moving across a fraction δ of the membrane electric field during a transition from state i to state j, a negative zδ_ij representing a negative charge moving toward the extracellular side of the membrane), α_i represents the asymmetry of the energy barrier, F is the Faraday constant, R is the gas constant, and T is the temperature. The description of each step of a given model requires four parameters (k_ij0, k_ji0, zδ_ij, and α_i). In the n-state cyclic model, this represents 4n-1 parameters (as one rate constant is adjusted to respect microreversibility). To this set of kinetic parameters, we need to add N, the total number of transporters expressed at the membrane of an oocyte. Moreover, as the measurement of the Pz-sensitive transient currents requires application of the inhibitor in each condition studied (3 [Na⁺]_o and 2 [αMG]_o), we realized that a variable N needed to be used in each case because a fraction of the cotransporters could remain inhibited as a result of imperfect Pz removal.

The parameters of the n-state model that can satisfactorily reproduce SGLT1 activity were obtained by directly fitting the currents using an SA algorithm. The determination of the numerous parameters involved was undertaken in two parts. First, both ON (going from −50 mV to different V_m) and OFF (going from different V_m to −50 mV) pre–steady-state currents were recorded in the presence of 90, 50, and 10 mM [Na⁺]_o (0 mM αMG in all cases) and were simultaneously fitted with a reduced model that did not include states representing substrate-bound configurations. The current pulses were baseline corrected to subtract the leak current of SGLT1 based on the recent finding that this current represents a permeation pathway that is independent of the conformational changes associated with Na⁺/glucose cotransport (Longpré et al., 2010). The experimental currents were compared with the simulated currents by taking the squared difference between corresponding points in two time windows beginning 2 ms after V_m was stepped and spanning 42 ms (ON) and 34 ms (OFF) when 90 or 50 mM Na⁺ was present. When 10 mM Na⁺ was present, the fitting windows began 1.5 ms after V_m was stepped and lasted only 35 ms (ON) and 19 ms (OFF) because the current decays were significantly faster than for the other [Na⁺]_o. To take into account the different lengths of the windows so that each [Na⁺]_o contributes equally to the fitting process, the sum of the squared differences calculated from each [Na⁺]_o were added together using a weighted linear combination. This linear combination, corresponding to the global error, was used as a cost function to find the optimal parameter set which could simultaneously reproduce the ON and OFF transient currents of SGLT1 at the three [Na⁺]_o, using the SA algorithm.

Although the parameters found in the absence of αMG were maintained constant, the complete n-state model was then used to simulate cotransport currents and find the values of the remaining parameters needed to reproduce the experimental currents obtained when 0.1 and 5 mM αMG were added to the normal saline solution. These two conditions were fitted simultaneously using the same strategy as in the first part but with different time windows to take into account the steady-state cotransport currents as well as the transient currents. In the case of 5 mM αMG currents, the time windows began 2 ms after V_m was stepped and lasted 145 ms (to measure both the ON transient current and the steady-state cotransport current) and 9 ms (OFF). Two windows were also used when 0.1 mM αMG was present, but the length of the window used for comparison of the OFF transients currents was increased to 24 ms to account for the slower decay observed.

A simulated annealing algorithm

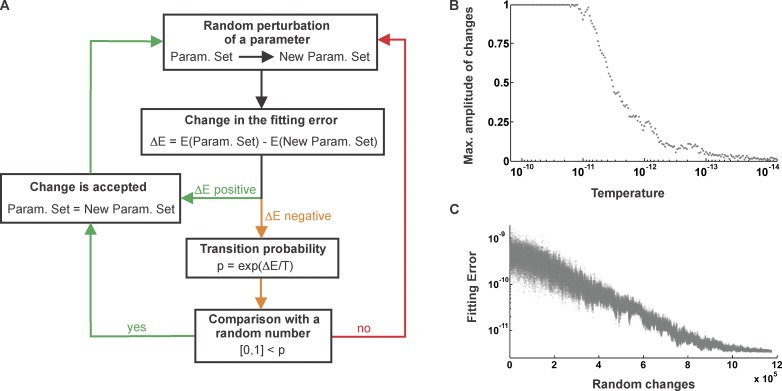
SA algorithms were introduced in the field of iterative processes in 1983 (Kirkpatrick et al., 1983) to improve convergence toward the global minimum of a cost function and to eliminate reliability issues observed when searches became stuck in local minima. The technique is based on an analogy with the relaxation experienced by misplaced atoms in a metal when it is heated up and slowly cooled down. To implement the SA algorithm, a temperature term is added to the problem. The system is first used at an initial temperature, where the Metropolis algorithm (see Fig. 2 A) is run until the system reaches thermal equilibrium. For our SGLT1 kinetic model, thermal equilibrium is represented by a situation where there are as many accepted random changes of the parameters (according to Fig. 2 A) that lower the fitting error as there are that make it larger. The temperature is subsequently decreased slowly, ensuring that thermal equilibrium is reached at each cooling step. As the limit of sufficiently low temperature is approached, the global minimum of the optimization problem is likely to be found. The logical scheme of the Metropolis algorithm was originally developed in 1952 to accurately simulate a group of atoms in equilibrium at a given temperature (Metropolis et al., 1953).

Figure 2.

The Metropolis algorithm and the principal parameters characterizing a SA run. (A) A random modification of one of the parameters is made and the resulting fitting error is compared with the error obtained with the original parameter set. If the new error is smaller than the previous one, the new parameter value is accepted. In contrast, if the new error is larger, it is not necessarily rejected. Instead, a temperature-dependent transition probability is calculated, and if its value is greater than a random number between 0 and 1, the change is accepted. Then, the loop starts again and a new parameter to be modified is randomly chosen. (B) Dynamic adjustment of the maximal amplitude of random changes applied to the kinetic parameters of the model. The amplitude decreases when the system is cooled down to keep an acceptance ratio of ∼50%. (C) Evolution of the fitting error throughout a simulation.

There are several important points that need to be stressed when considering the SA algorithm. In the case of our SGLT1 kinetic model, one of the parameters (zδ_ij, k_ij0, and k_ji0) is altered randomly at each iteration of the search (the α_i’s are initially set to 0.5). The available domain for each of these parameters is dynamically adjusted throughout a simulation (Fig. 2 B) so that the acceptance ratio of the trials stays ∼50% to adequately sample the parameter space. In simulations where the complete cotransport cycle was considered, we added a Lagrange multiplier to the change in the computed error (“E” is presented in Fig. 2 C). This object tends to reject a trial zδ_ij value that compromises the quality of

$${\displaystyle \sum _{i=1}^{n-1}z{\delta }_{i(i+1)}}+z{\delta }_{n1}=-2,$$

even if the new zδ_ij value implies a lower error. In the end, this ensures that the zδ_ij values are consistent with the stoichiometry of two Na⁺ transported per cycle. The initial temperature of the SA must be chosen so that it is neither too high, leading to unnecessary long simulation times, nor too low, which could eventually trap the system in a local minimum from which it cannot escape. This quantity is problem dependent and is usually determined by trial and error. In our case, the initial temperature was set to 2 × 10⁻¹⁰ (no units to be consistent with ΔE of Fig. 2 A). Moreover, the cooling schedule must be smooth enough to ensure the convergence to the global minimum. It has been shown that this is guaranteed if the temperature decreases according to a logarithmic scheme (Geman and Geman, 1984). In this scheme, the temperature decreases by a fixed ratio at each step (in the present case, we used $T_{i+1}=0.95T_i$). The simulation ends when 200 cooling steps have occurred.

The SA algorithm was written in the MATLAB language, compiled and executed on the computing server Cottos provided by the Réseau québécois de calcul haute performance. Finding a satisfactory parameter set for a five-state model while simultaneously considering three [Na⁺]_o required ∼3 d of computation on a single 3 GHz CPU, where around a million different parameter combinations are tested. Taking advantage of the computing server, several independent simulations were executed at the same time to confirm that the parameter set that minimizes the fitting error can be repeatedly found.

Statistics

Experimental data are presented as mean ± SEM over the number of oocytes used (one experiment per oocyte). In the figures, error bars are not shown when smaller than symbols. Kinetic parameters found by SA are presented as a rounded mean ± SD over several representative independent simulations.

Online supplemental material

The online supplemental material contains Fig. S1, which shows the simulated transient currents resulting from a four-state model (see Fig. S2) as compared with experimental data for 90, 50, and 10 mM [Na⁺]_o. Systematic discrepancies can be observed between the simulated and the experimental OFF currents when the membrane potential is going from +20 and +70 mV to −50 mV. Fig. S2 depicts a four-state model where the step C₃→C₄ represents the cooperative binding of two Na⁺ ions. The online supplemental material also contains a brief video (Video 1) depicting the cotransport mechanism of SGLT1 in the presence of 0.5 mM αMG $(\sim K_m^{\alpha \mathit{MG}})$, 90 mM [Na⁺]_o, and a membrane potential of −50 mV. The cartoon represents a true simulation of 210 ms made with the seven-state model and the parameters given in Table 1. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201210822/DC1.

Table 1.

Rate constants and parameters of the seven-state kinetic model

Parameter	Value	SD
k120 (s−1)	1,500	110
k230 (s−1)	59	2
k340 (s−1)	200	10
k450 (M−2s−1)	600,000	140,000
k560 (M−1s−1)	111,000	4,300
k670 (s−1)	300	25
k710 (s−1)	100	5
zδ12	-0.41	0.01
zδ23	0.00	0.001
zδ34	−0.70	0.02
zδ45	−0.19	0.02
zδ56	−0.01	0.01
zδ67	−0.66	0.02
zδ71	−0.02	0.01
k210 (s−1)	200	35
k320 (s−1)	200	10
k430 (s−1)	1,900	55
k540 (s−1)	1,000	160
k650 (s−1)	82	5
k760 (s−1)	700	50
k170 (M−3 s−1)	6,700,000	220,000
N90Na	1.35 × 1011	3.6 × 109
N50Na	8.94 × 1010	2.5 × 109
N10Na	1.24 × 1011	5.5 × 109
N0.1αMG	7.34 × 1010	2.1 × 108
N5αMG	7.93 × 1010	6.3 × 108

The seven-state model refers to the scheme presented in Fig. 3. The parameters highlighted in bold were obtained using the five-state model (absence of αMG) before expansion to the seven-state cotransport model. The α_i’s (representing the energy barrier asymmetries) are fixed at 0.5. The rate constant k₁₇₀ is adjusted to respect microreversibility. In the case of the five-state model, the SD was computed using 11 parameter sets reproducing satisfactorily the current traces averaged from four oocytes, whereas 8 parameter sets were used for the three additional transitions taking place in the seven-state model.

RESULTS

The first part of this study sought to identify the simplest kinetic model able to describe SGLT1 pre–steady-state ON and OFF currents, in the absence of αMG, as a function of [Na⁺]_o and V_m. The first issue was to determine how many states were required to correctly model the ON and OFF transients at each of the [Na⁺]_o considered separately (90, 50, and 10 mM), without any assumptions regarding the specific nature of each transition. The current traces to be fitted were averaged from four oocytes after having normalized the amplitudes using steady-state cotransport currents measured at −155 mV in the presence of 5 mM αMG. Using the SA algorithm to directly fit the averaged experimental currents, we reached the conclusion that a four-state model with symmetrical energy barriers (α_i = 0.5) was the minimal structure capable of perfectly reproducing the transient currents and their V_m dependence at any given [Na⁺]_o. However, when comparing the parameter sets obtained for each of the three [Na⁺]_o, only the parameters associated with the C₂↔C₃ transition (k_230, k₃₂₀, and zδ₂₃) were similar at each [Na⁺]_o, and it was difficult to identify the Na-dependent reaction rate as neither of the two remaining reactions appeared to have rate constants proportional to either [Na⁺]_o or [Na⁺]_o². Assuming that the slow and voltage-independent transition (C₂↔C₃) might represent the reorientation of the cotransporter binding sites, we modeled the transition from C₃ to C₄ as the cooperative binding of two Na⁺ ions. SA was then used to optimize simultaneously the transient currents at 90, 50, and 10 mM [Na⁺]_o in the framework of this more explicit four-state model (Fig. S2). Out of eight attempts, the best parameter set could simulate the ON transient currents, but there was a small but clear discrepancy in the way the OFF transients settled when returning to −50 mV from a positive V_m (Fig. S1). This discrepancy was already present at 90 mM [Na⁺]_o but could be better observed at 50 and 10 mM [Na⁺]_o.

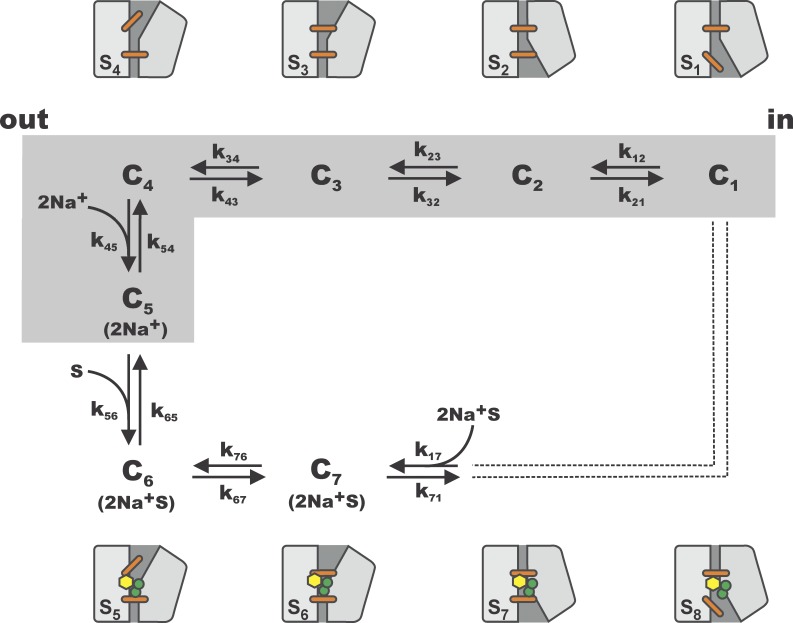
In light of these findings, we decided to incorporate one more state to our scheme and to simultaneously fit the ON and OFF transient currents at 90, 50, and 10 mM [Na⁺]_o in the framework of a five-state model. Because it is not known whether one or two Na⁺ ions participate in the pre–steady-state kinetics, we considered three different ways of assigning [Na⁺]_o dependence to the model. In the first case, the binding of a single Na⁺ ion was assigned to the transition C₄→C₅. In the second case, two Na⁺ ions were assumed to bind sequentially in the steps C₃→C₄ and C₄→C₅. Finally, in a third scenario, the binding of the two Na⁺ ions occurred simultaneously (high cooperativity) in the transition from C₄ to C₅ (Fig. 3). Of those three models, the one exhibiting a cooperative Na⁺ binding event led to the most accurate and convincing fit of the experimental ON and OFF currents (Fig. 4), yielding a fitting error approximately two times smaller than the two other models. To be sure that we were not missing any possible improvements in our models, we considered the effect of asymmetric voltage dependencies. Letting the α_i parameters free to vary between 0 and 1, the results of simulations done for the five-state models did not generate a significant improvement of the fits that could justify the incorporation of asymmetric barriers. Our results thus suggested that the conformational change in which SGLT1 is empty and reorients itself in the membrane should occur in three distinct steps. Moreover, the parameter set describing our data (Table 1) suggested that the transient currents were associated with the movement of −1.3 equivalent charges across the membrane, and that the only voltage-independent transition was the second free carrier reorientation step (C₂↔C₃). It is interesting to note that the rate constants k₂₃₀ and k₃₂₀, as well as the voltage dependencies parameterized by zδ₁₂, zδ₂₃, and zδ₃₄, were similar to those found while performing the individual fits at each [Na⁺]_o using the four-state model, thus reinforcing our conclusion that the presence of an intermediary, slow and voltage-independent step among the empty carrier movements seemed to be mandatory. We then integrated both the simulated and experimental OFF current relaxations to analyze the charge transfer occurring as a consequence of V_m steps. The resulting Q(V_m) curves are depicted in Fig. 4, where we observe that the five-state model reproduced within experimental error the [Na⁺]_o dependence of the charge movements.

Figure 3.

Complete seven-state model used to simulate SGLT1 transient and steady-state currents. Intracellular binding of Na⁺ and αMG have been lumped into a single transition (k₁₇). The scheme includes a five-state model (gray box) which is the simplest structure leading to an accurate fit of the transient currents in the absence of αMG. The different states suggested by the LeuT structural family are labeled S₁ to S₈ and are presented above and below the kinetic model.

Figure 4.

Simulation of the pre–steady-state ON and OFF currents (solid lines) using the five-state model. The simulation is generated in the presence of (A) 90 mM, (B) 50 mM, and (C) 10 mM external Na⁺ concentrations ([Na⁺]_o). Symbols represent the mean experimental data ± SEM (inset) The Q(V_m) curves corresponding to the integrals of the simulated and experimental OFF transient currents are compared at 90, 50, and 10 mM [Na⁺]_o.

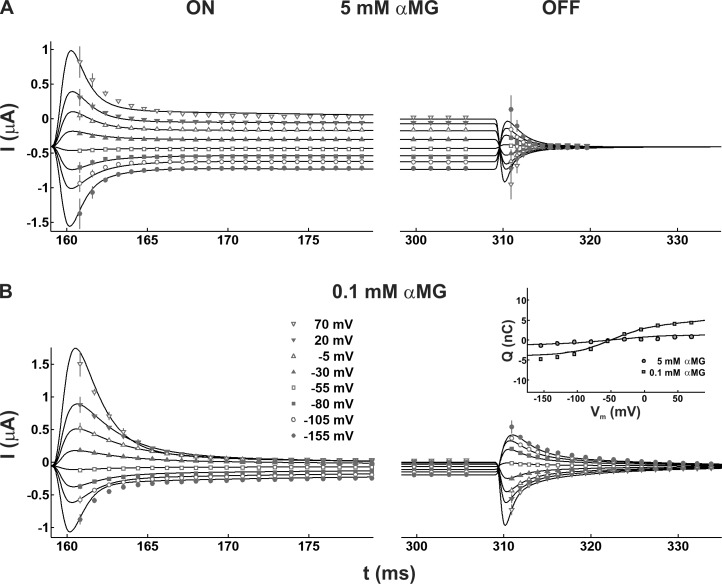
Having established a model describing the kinetics of SGLT1 in the absence of substrate, we next addressed simulation of steady-state and pre–steady-state currents in the presence of αMG. The straightforward way of doing that was to incorporate a single new state (C₆) into our current scheme to represent the binding of glucose (C₅→C₆). To keep the model as simple as possible, the states where the cotransporter is facing the intracellular side were all lumped together. This seems to be a reasonable assumption because the experimental conditions mimic the zero-trans conditions, where intracellular Na⁺ and glucose concentrations are not sufficient to generate a measurable reverse mode of cotransport. This is supported by the previously reported low affinity for intracellular Na⁺ (Quick et al., 2003; Eskandari et al., 2005) and the fact that intracellular [Na⁺] has to be raised to ∼30 mM to measure an outward Na⁺/glucose cotransport current upon intracellular glucose injection (Charron et al., 2006). Furthermore, the size of the Pz-sensitive outward current after intracellular αMG injection in the presence of elevated intracellular [Na⁺] is consistent with a starting intracellular glucose concentration much smaller than 1 mM (we set [αMG]_i to 10 µM in our simulations). An intracellular [Na⁺] of 7 mM was used in our simulations in accordance with the estimate of 5–8 mM previously established using intracellular Na-selective electrodes (Charron et al., 2006). Then, keeping constant the parameters obtained in the absence of glucose (five-state model), we used SA to simultaneously fit the currents (transient + steady-state) measured at 0.1 and 5 mM [αMG]_o, in the presence of 90 mM [Na⁺]_o, and to deduce the remaining unknown parameters of the full six-state scheme. Although the simulated currents adequately reproduced the steady-state currents at 5 mM [αMG]_o, the six-state model failed to fit the steady-state kinetics at 0.1 mM [αMG]_o. In view of these limitations, we added one more state (C₇) to the scheme after the glucose binding step resulting in a seven-state model (Fig. 3). This time, the model adequately described the voltage dependence and amplitude of the steady-state cotransport currents for both [αMG]_o’s, as can be observed in Fig. 5, where the simulated currents resulting from the best parameter set (Table 1) are compared with the experimental data. The fit of the ON and OFF transient currents were generally satisfactory, despite slight discrepancies at larger V_m steps in the case of the OFF relaxation at 5 mM [αMG]_o. However, this relaxation is a fast event of low amplitude, which represents an experimental challenge to measure. Nevertheless, the presence of 5 mM [αMG]_o produced a massive reduction of the transient currents that was very well reproduced by the kinetic model. The corresponding Q(V_m) curves calculated from the OFF transients at both [αMG]_o’s are plotted in Fig. 5 and are in agreement with experiments within 1 nC for all V_m. This means that our simulations correctly predict the loss of transferred charge associated with the presence of increasing [αMG]_o, which is a well documented feature of SGLT1 (Parent et al., 1992a; Loo et al., 2006; Gagnon et al., 2007). It is also important to state that, in terms of Q(V_m) and time constants, the experimental currents from which our model parameters were established (Fig. 4 and Fig. 5) are representative of typical SGLT1 data measured by us (Gagnon et al., 2007) as well as other laboratories (Wright et al., 2011).

Figure 5.

The simulated steady-state and pre–steady-state ON and OFF currents in the presence of 90 mM [Na⁺]_o and αMG. Simulated currents obtained with (A) 5 mM or (B) 0.1 mM [αMG]_o are compared with experimental data. (Inset) Q(V_m) curves obtained from integration of the OFF transient currents in the presence of 90 mM [Na⁺]_o and 5 mM or 0.1 mM [αMG]_o.

Looking at the parameter set of the proposed seven-state model, it should be noted that the outwardly oriented, fully loaded cotransporter experiences a multistep reorientation (C₆ to C₁) which bears certain similarities to the conformational changes experienced by the empty carrier (C₁ to C₄). As was the case for the empty cotransporter, the fully loaded carrier goes through a voltage-dependent conformational change (C₆→C₇, zδ₆₇ = −0.66) which is followed by a slow, voltage-independent step (k₇₁₀ = 100 s⁻¹). This is in sharp contrast with the conclusions of previous models, where all reaction rate constants after Na⁺ binding were assumed to be voltage independent (Parent et al., 1992b; Loo et al., 2006).

DISCUSSION

The main goal of this study was to find the simplest kinetic model capable of reproducing the pre–steady-state and steady-state currents of SGLT1 as a function of [Na⁺]_o and [αMG]_o. In the past, partial models with three (Loo et al., 1993; Hazama et al., 1997) or four (Krofchick and Silverman, 2003) states were proposed together with complete models consisting of six to eight states (Parent et al., 1992b; Eskandari et al., 2005; Loo et al., 2006). As the number of parameters increases (up to 32 parameters for an eight-state model), a systematic method becomes necessary to estimate the values of these parameters and to assess the quality of any given model. The SA algorithm used in the present study has proven to be reliable in solving complicated problems such as this.

Model structure and rate-limiting steps

We first established that the minimal scheme leading to a satisfactory reproduction of the measured currents in the absence of αMG was a five-state model. The choice to have four empty carrier states (C₁↔C₄) and to group the binding of the two Na⁺ ions into a single, cooperative transition (C₄→C₅) was based on the fact that this model produced the smallest fitting error as compared with any other modeling of the binding events, including where the binding of a single Na⁺ ion was considered. It was surprising to find that lumping the binding of two Na⁺ ions together could produce such a good result, as it has previously been argued that this maneuver would introduce an artifactual Na⁺ dependence in the rate constants of the transition preceding the Na-binding event, making them pseudo–rate constants (Falk et al., 1998). This phenomenon has often been stated as the source of the inability to find a unique parameter set that could reproduce experimental data as a function of [Na⁺]_o (Loo et al., 1993, 2005, 2006; Hazama et al., 1997; Krofchick and Silverman, 2003). It is possible that the problems reported in these studies stem either from the use of an insufficient number of states (Loo et al., 1993; Hazama et al., 1997; Krofchick and Silverman, 2003) or from the difficulty of assessing the values of the numerous parameters when five or more states are considered (Loo et al., 2005, 2006).

In the presence of αMG, we found that two more states were necessary to account for the way in which the presence of a substrate produces steady-state cotransport currents and reduces the transient current amplitudes. The parameters shown in Table 1 present an interesting element of symmetry which was not found in any of the previous models proposed for SGLT1. In the forward transport cycle (leading to Na⁺/glucose uptake), the two slowest reactions are voltage independent, with k₂₃₀ and k₇₁₀ at 59 and 100 s⁻¹, respectively (corresponding to activation energies >14.5 kcal/mol). These are likely to represent the major conformational changes that occur when the empty cotransporter goes from the inward-facing to the outward-facing configuration (k₂₃) and when the fully loaded cotransporter goes from the outward-facing to the inward-facing configuration (k₇₁).

Interestingly, these two slow and rate-limiting steps are surrounded by voltage-dependent steps (C₁↔C₂ and C₃↔C₄ for the empty carrier and C₆↔C₇ for the fully loaded carrier). These transitions are faster and must represent local rearrangements that are necessary to allow the major conformational changes to occur. Comparing the proposed model to the general cotransport scheme of Fig. 1, these voltage-sensitive steps could include the displacement of the so-called thin gates on each side of the membrane (Krishnamurthy et al., 2009; Shimamura et al., 2010). In the case of the fully loaded carrier, only one voltage-dependent step could be identified because of the quasi zero-trans experimental condition. Future studies using increased intracellular Na⁺ and αMG concentrations will be necessary to explore the nature and sequence of intracellular Na⁺ and substrate binding steps.

Voltage-sensitive steps

An interesting consequence of using SA to find the parameters of the proposed kinetic scheme is the new insight that it provides regarding the charge movements taking place during cotransport. It should be reiterated that in the search process, no assumption was made in selecting which transitions would involve a charge movement, the only restriction being that the sum of their apparent valences must correspond to the net movement of two positive charges across the whole membrane to mimic the entry of two Na⁺ ions into the cell. The two most extreme cases are: (1) two negative charges moving outside from C₁ to C₄ and no charge movement for the Na-bound conformational changes (C₄ to C₁); or (2) no charge movement from C₁ to C₄ and two positive charges (the two Na⁺ ions) are moving in between C₄ and C₁. The situation that we have found is an intermediate between these two cases. Our model establishes that the empty carrier translocation (from C₁ to C₄) is associated with an overall movement of 1.1 equivalent charges (0.4 charge is associated with the C₁↔C₂ transition and 0.7 charge is involved with the C₃↔C₄ transition) across the membrane. This is consistent with the possibility that a negatively charged segment is moving outside.

It was also found that the binding of the two Na⁺ ions (C₄↔C₅) was associated with the displacement of ∼0.2 charge. This could be interpreted as 0.2 positive charges moving inward, which would be consistent with an ion-well effect (i.e., Na⁺ ions crossing a part of the membrane electric field on their way to their binding site). An alternative interpretation could also be proposed where Na-dependent charge movements would be the result of an electrogenic conformational change that would be allowed by the binding of the two Na⁺ ions. Finally, as the Na-loaded transporter is moving from C₅ to C₁ (through C₆ and C₇), a 0.69 positive charge is moving in. For the complete cycle, the sum of our zδ_ij values is 1.99 charges, in good agreement with the cotransport stoichiometry. Again, comparing the proposed kinetic model with the general cotransport mechanism depicted in Fig. 1, transition from C₃ to C₄ could possibly represent a group of reactions associated with the opening of the extracellular thin gate, whereas the transition from C₆ to C₇ would represent the closing of that same gate. It is interesting to see that the charge movements associated with these two reactions are very similar (zδ₃₄ = 0.7 for C₃↔C₄ and zδ₆₇ = 0.66 for C₆↔C₇).

Additional elements supporting the quality of the proposed model

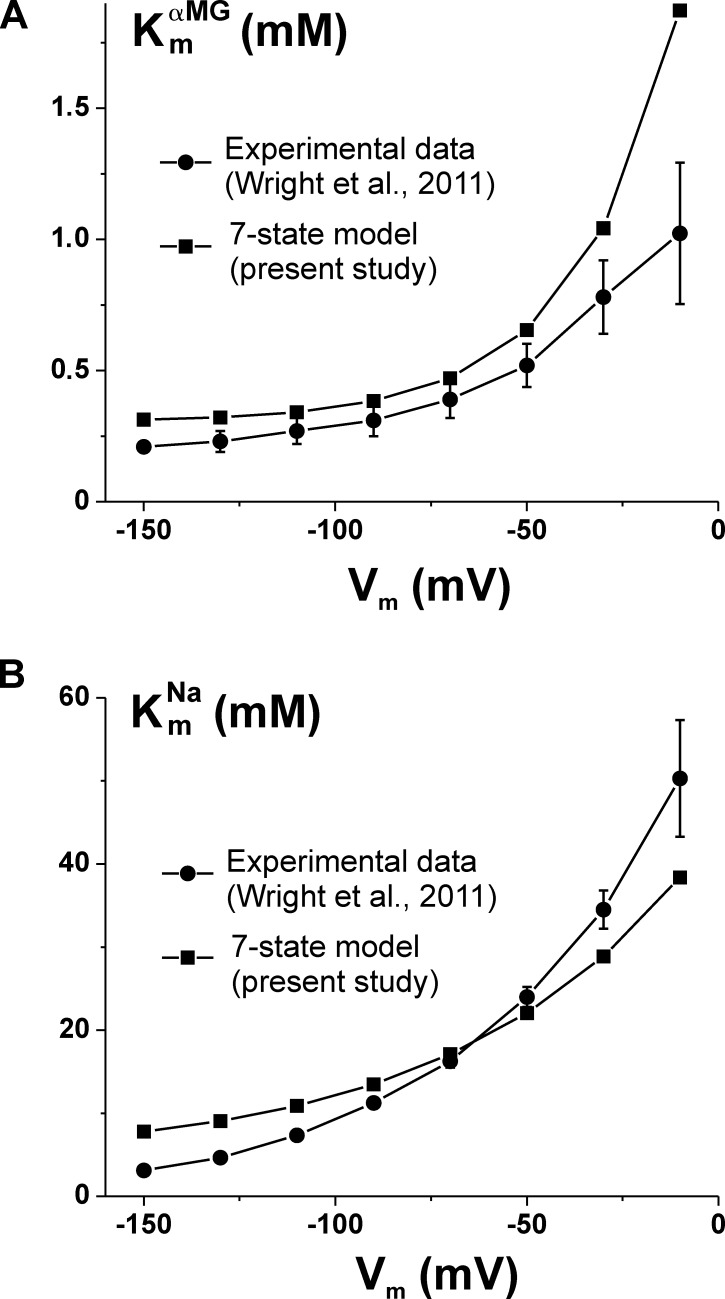
The seven-state model proposed in the present study is based on the analysis of the transient currents observed in the absence of substrate at three different [Na⁺]_o and on the transient and stationary currents observed at two [αMG]_o’s in the presence of 90 mM [Na⁺]_o. As the cotransport currents at 0.1 and 5 mM [αMG]_o are well reproduced by the model (see Fig. 5), its ability to correctly predict the αMG affinity constant $\left(K_m^{\alpha \mathit{MG}}\right)$ is not surprising. This is shown in Fig. 6 A, where the $\left(K_m^{\alpha \mathit{MG}}\right)$‘s measured as a function of membrane potential (Wright et al., 2011) are compared with the affinities simulated using our seven-state model. A more challenging test is to compare the Na⁺ affinity constant $\left(K_m^{\mathit{Na}}\right)$ with the model prediction, as this experimental information was not considered in the determination of the model parameters. This is depicted in Fig. 6 B, where the Na⁺ affinity constants measured in the presence of 25 mM [αMG]_o (Wright et al., 2011) are shown along with the seven-state model predictions. It can be seen that the absolute values around −70 mV and the strong voltage dependency are correctly predicted by the model.

Figure 6.

Comparison of αMG and Na⁺ affinity constants predicted by the seven-state model with experimental data from a published study. (A) $K_m^{\alpha \mathit{MG}}$, in the presence of 100 mM [Na⁺]_o, and (B) $K_m^{\mathit{Na}},$ in the presence of 25 mM [αMG]_o, are calculated as a function of membrane potential using the seven-state model and the parameters given in Table 1 (filled squares without error bars). These values are compared with the data published by Wright et al. (2011) for a typical hSGLT1-expressing oocyte (filled circle with error bars representing the fitting uncertainty).

A film of the cotransport mechanism

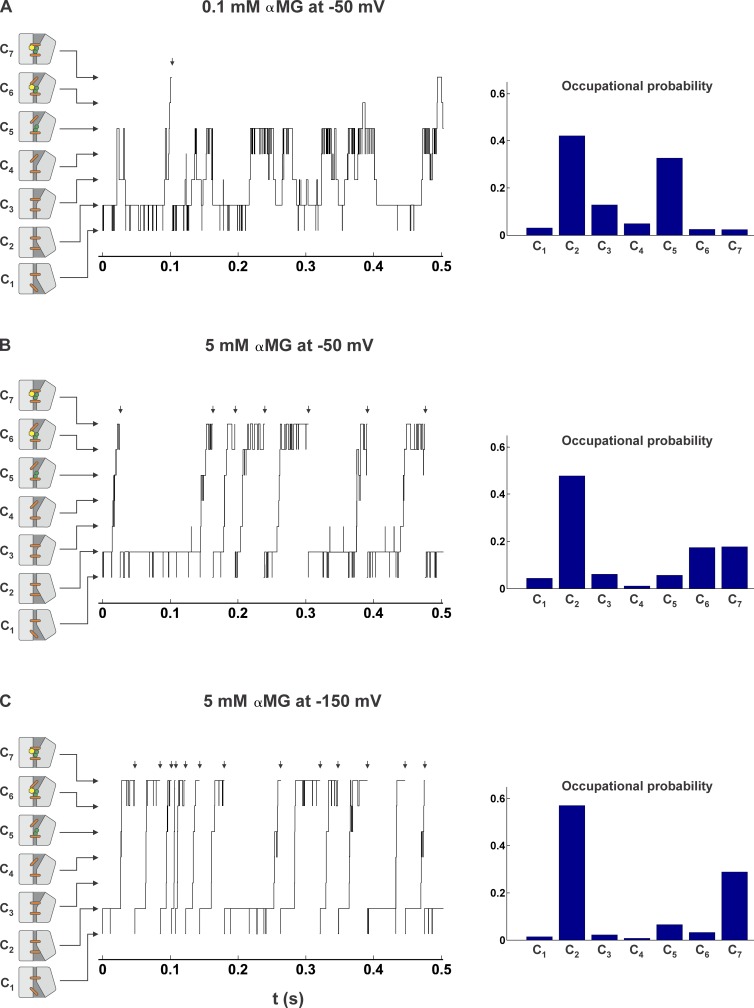
Having obtained a set of kinetic parameters that can account for the transient and steady-state currents of SGLT1, we can present a credible visualization of the cotransporter activity under different conditions. To do so, we first considered a single cotransporter molecule whose conformation corresponds to a state j of our model. The probabilities that it changes conformation to the states j + 1 or j − 1 within a short time increment dt are given by k_j(j+1)dt and k_j(j−1)dt, respectively. Using a time increment of 0.1 µs, we simulated the conformational behavior of that single cotransporter molecule for a period of 10 s, in the presence of a low [αMG]_o of 0.1 mM (∼1/10 of the $K_m^{\alpha \mathit{MG}}$) with V_m set to −50 mV (the first 0.5 s are shown in Fig. 7 A). The course of the fluctuations performed by SGLT1 between the different states of the model reveals that the cotransporter spends ∼40 and 35% of the time in states C₂ and C₅, respectively. Furthermore, the cotransporter is shown to flicker between Na-bound (C₅) and Na-free (C₄) conformations, adopting the C₅ state six times more often than C₄. This illustrates that numerous Na⁺ binding and unbinding events take place as the cotransport activity is severely limited by the low [αMG]_o. Flickering between states C₁ and C₂ also happens, but to a lesser extent.

Figure 7.

The conformational time course of SGLT1 in different conditions. The time courses were simulated for 10 s (events occurring during the first 0.5 s are depicted) in the presence of 90 mM [Na⁺]_o and (A) 0.1 mM [αMG]_o at −50 mV, (B) 5 mM [αMG]_o at −50 mV, and (C) 5 mM [αMG]_o at −150 mV. Short arrows above each panel indicate the completion of a cotransport cycle and conformational change from C₇ to C₁. The occupational probabilities of the seven states during the 10 s period are shown on the right side of each panel. In addition, conformations suggested by the structural data of the LeuT fold family have been assigned to states C₁ through C₇ to illustrate the behavior of SGLT1. The so-called thin gates are represented by orange sticks, and the green circles and yellow hexagons represent Na⁺ ions and glucose molecules.

When [αMG]_o reaches an almost saturating concentration of 5 mM (Fig. 7 B), very few oscillations between the Na-bound and Na-free configurations are observed, as the cotransporter now flickers between its two fully loaded states, spending approximately the same amount of time (∼20%) in C₆ (open to the extracellular side) as in C₇ (open to the extracellular side, but occluded). Moreover, SGLT1 is found ∼50% of the time in the C₂ configuration waiting for the rate-limiting conformational change (k₂₃) to occur. Doing so, it oscillates between the C₁ and C₂ conformations in a manner similar to what was seen in the presence of 0.1 mM [αMG]_o.

When the membrane potential is brought to −150 mV (Fig. 7 C), the electrogenic transitions C₁→C₂, C₃→C₄, and C₆→C₇ are accelerated, which makes the probability of finding SGLT1 in the states C₁, C₃, and C₆ practically nil. Under these conditions, the course of conformations adopted by the fully activated cotransporter clearly indicates that it functions in a pseudo two-state mode (namely C₂ and C₇ states). Its turnover rate (TOR) is mainly limited by the slow conformational changes of the free carrier (transition k₂₃) and of the fully loaded carrier (k₇₁), which are both voltage-independent steps. For a video of the cotransport mechanism based on the rate constants presented in Table 1, please see the Supplemental material associated with this article (Video 1).

It is tempting to argue that events related by some functional symmetry occur during the cotransport cycle. Indeed, when the cotransporter has just released Na⁺ ions and glucose to the intracellular milieu (C₇→C₁), it undertakes a voltage-sensitive step (C₁→C₂) resulting in the conformation C₂, where it faces a voltage-independent and rate-limiting step (k₂₃). Similarly, after the binding of extracellular Na⁺ and glucose, a voltage-sensitive step (C₆→C₇) takes place which brings SGLT1 in state C₇ where it awaits for a slow voltage-independent rate constant (k₇₁). As k₇₁ represents lumped transitions including the intracellular release of substrates, it is difficult to identify the specific event responsible for this relatively slow rate constant (100 s⁻¹).

TOR

Knowing that at −150 mV, in the presence of a saturating [αMG]_o, 60% of the cotransporters occupy the state C₂ (Fig. 7 C), and that the transition C₂→C₃ occurs at a rate of ∼59 s⁻¹ (Table 1), we can estimate the TOR of cotransport at −150 mV to be ∼35 s⁻¹ (considering a small backward transition rate from C₃ to C₂ under these conditions). This TOR is about twice the TOR that we recently evaluated using the ion-trap technique (Longpré and Lapointe, 2011). One of the crucial points in using the ion-trap technique to obtain the TOR is to correctly evaluate a rapid change (a step) of ∼0.5 mV in the potential of an ion selective electrode. It is possible that the true value of the step is somewhat smaller than was initially estimated.

Differences and similarities with previously suggested models of SGLT1

In the model of SGLT1 originally proposed by Parent et al. (1992b), it was assumed for simplification purposes that the empty carrier possessed a −2e charge which was completely neutralized after the binding of two Na⁺ ions. As a consequence, all the steps after Na⁺ binding were considered to be electroneutral. Furthermore, the parameter set proposed to describe the model predicted that the intracellular release of Na⁺, taking place at a very slow rate of 10 s⁻¹ (Parent et al., 1992b), was the rate-limiting step of forward Na⁺/glucose cotransport. These assumptions were kept in all subsequent models proposed over the years by the same laboratory (Loo et al., 1993, 2005, 2006; Hazama et al., 1997; Eskandari et al., 2005). Accordingly, the eight-state model proposed in 2006 (Loo et al., 2006) was characterized by a rate-limiting step representing the intracellular release of Na⁺, which was proposed to occur at a rate of 5 s⁻¹. Interestingly, the connectivity of the aforementioned model (see Loo et al., 2006, Fig. 9) is similar to the kinetic scheme presented in the present study. However, the position of the electrogenic steps and the rate-limiting conformational changes in the transport cycle are completely different in the two models. Moreover, it can be argued that, in contrast to the present model, the parameter set proposed in Loo et al. (2006) fails to quantitatively reproduce the time course of the transient current and, therefore, cannot account for the diminution of these currents in the presence of increasing [αMG]_o (in Loo et al., 2006, compare Fig. 11 to Fig. 4).

In previous work from our laboratory (Chen et al., 1996), a four-state model was used to recreate the pre–steady-state kinetics of SGLT1. In that scheme, the empty carrier reorientation occurred in two steps C₁↔C₂↔C₃, and the binding of a single Na⁺ ion was taken into account in the reaction C₃→C₄. Despite the fact that this four-state scheme differs from the one used in the present study, it is interesting to note that the charge movements taking place between the states C₁ and C₄ were characterized by a cumulative valence of −1.35, in close agreement with the valence of −1.3 found in the present study. Also, the four-state model included a high degree of asymmetry in the transition C₂↔C₃, as k₂₃ was 100 s⁻¹ and voltage independent and k₃₂ was 280 $\text{exp}\left(0.35\frac{{\mathit{FV}}_m}{\mathit{RT}}\right){\text{s}}^{-1}$. In the present model, this asymmetric transition was replaced by an electroneutral transition C₂↔C₃ (with k₂₃ = 59 s⁻¹) followed by an electrogenic transition C₃↔C₄ (with k₄₃ = 1,900 $\text{exp}\left(0.35\frac{{\mathit{FV}}_m}{\mathit{RT}}\right){\text{s}}^{-1}$). It appears that the presence of an asymmetric transition was a result of lumping together voltage-dependent and voltage-independent transitions. More recently, a five-state model was proposed by our laboratory to rationalize Na⁺/glucose cotransport (Gagnon et al., 2007). In the absence of substrate, a four-state scheme where the binding of two Na⁺ ions is modeled in the step C₃→C₄ was used, and all the voltage dependence of the model (−2 equivalent mobile charges) was comprised in the transitions between C₁ and C₄. Furthermore, glucose binding occurred in the transition C₄→C₅, and subsequent reactions were lumped. Although that five-state model and the present model differ on some major conceptual points, the rate-limiting step of cotransport at −150 mV was suggested to be k₂₃, in accordance with our current results.

Conclusion

In this study, we have used an SA algorithm to establish that a seven-state kinetic model was the simplest scheme describing the activity of SGLT1 up to a 2 ms time resolution as a function of V_m, [Na⁺]_o and [αMG]_o. The resulting simulated currents were in direct quantitative agreement with the experimental ON and OFF transient currents, as well as the steady-state Na⁺/glucose cotransport currents. It was established that the free and fully loaded carrier reorientations are voltage-independent slow steps and that faster voltage-sensitive structural rearrangements are necessary for these major conformational changes to occur. At −150 mV, in the presence of a saturating [αMG]_o, the rate-limiting conformational change of cotransport is the voltage-independent free carrier reorientation step k₂₃, which sets the TOR of SGLT1 at 35 s⁻¹.