Abstract
Neanderthals have been shown to share more genetic variants with present-day non-Africans than Africans. Recent admixture between Neanderthals and modern humans outside of Africa was proposed as the most parsimonious explanation for this observation. However, the hypothesis of ancient population structure within Africa could not be ruled out as an alternative explanation. We use simulations to test whether the site frequency spectrum, conditioned on a derived Neanderthal and an ancestral Yoruba (African) nucleotide (the doubly conditioned site frequency spectrum [dcfs]), can distinguish between models that assume recent admixture or ancient population structure. We compare the simulations to the dcfs calculated from data taken from populations of European, Chinese, and Japanese descent in the Complete Genomics Diversity Panel. Simulations under a variety of plausible demographic parameters were used to examine the shape of the dcfs for both models. The observed shape of the dcfs cannot be explained by any set of parameter values used in the simulations of the ancient structure model. The dcfs simulations for the recent admixture model provide a good fit to the observed dcfs for non-Africans, thereby supporting the hypothesis that recent admixture with Neanderthals accounts for the greater similarity of Neanderthals to non-Africans than Africans.
Keywords: admixture, ancient structure, Neanderthal, frequency spectrum
Introduction
The interaction between Neanderthals and early modern humans has been a long-standing question in human evolutionary studies. Specimens with morphological traits typical of Neanderthals have been found across Eurasia, from southwest Spain in Europe to southern Siberia in Asia. The first appearance of these traits is as early as 400 thousand years ago (kya), and they persist until about 30 kya (Krause et al. 2007). Some paleoanthropologists have argued for interbreeding between Neanderthals and early modern humans, using finds such as the child found in Lagar Velho, Portugal, that shows a mixture of Neanderthal and early modern human skeletal characteristics (Duarte et al. 1999). Critics, however, have been skeptical that these finds really suggest potential admixture (Tattersall and Schwartz 1999). Genetic evidence using Neanderthal mitochondrial DNA has consistently shown Neanderthals falling outside the range of modern human variation (Krings et al. 1997; Serre et al. 2004; Green et al. 2008). This result was taken by many to mean no interbreeding occurred between Neanderthals and early modern humans, although Nordborg (1998) showed that low levels of admixture could not be excluded by the mitochondrial DNA data.
Green et al. (2010) sequenced the first draft of the Neanderthal genome and presented evidence from genomic data that present-day non-African human populations share more genetic variants with Neanderthals than did modern African human populations represented by Yorubans. Part of their evidence was based on a four-taxon statistic, called the D statistic (Green et al. 2010; Reich et al. 2010; Durand et al. 2011). The D statistic quantifies the excess sharing of derived sites between the Neanderthal and any two modern human populations. A nonzero value of D indicates that one of the modern human populations is more similar to the Neanderthal than is the other. Green et al. found that D statistics indicated greater similarity between Neanderthals and non-African populations than between Neanderthals and African populations.
Green et al. (2010) proposed a model in which 1–4% of non-African genomes result from admixture from Neanderthals into the ancestors of non-African populations after the separation of Africans from non-Africans. These results imply that Neanderthals and early modern humans did interbreed. However, recent admixture is not the only hypothesis consistent with the observations. Substructure in early hominin populations in Africa could produce the same patterns (Slatkin and Pollack 2008; Durand et al. 2011).
The ancient substructure in Africa model posits that there were two or more subpopulations of hominins in Africa with limited gene flow. Then, ancestors of Neanderthals emigrated from the same subpopulation from which the ancestors of present-day non-Africans later emigrated. As a consequence, non-Africans would be slightly more genetically similar to Neanderthals than would Africans because of their more recent common ancestry. After the ancestors of Neanderthals emigrated, the gene flow between the ancestors of present-day Africans and non-Africans would be sufficiently high until the out-of-Africa event, thus making the Africans and non-Africans more genetically similar to one another than either is to Neanderthals. In this model, no later interbreeding between Neanderthals and early modern humans occurred. Durand et al. (2011) showed that both models could account for the greater similarity of non-Africans than Africans to Neanderthals.
The model of ancient substructure is consistent with other recent studies. Plagnol and Wall (2006), Barreiro et al. (2005), and Hayakawa et al. (2006) have all suggested the possibility of ancient structure in Africa. Plagnol and Wall (2006) showed that non-Africans may have arisen from a Western African subpopulation, whereas Barreiro et al. (2005) and Hayakawa et al. (2006) observed deep lineages in some genes that seem best explained by ancestral structure in Africa. It is important to be able to distinguish whether the genetic similarity observed by Green et al. (2010) is due to recent admixture or ancient structure in Africa.
To distinguish between these two models, we develop here a new approach that relies on the site frequency spectrum (sfs). Durand et al. (2011) suggested that the ancient structure model results in more variation in gene tree depth than the recent admixture model. Greater variance in tree depth would alter the frequency spectrum but not the D statistic. Here, we show that the sfs appropriately conditioned can distinguish between recent admixture and ancient structure because it is particularly sensitive to episodes of recent admixture. We construct the sfs for non-Africans, conditioning on sites that have the derived allele in the Neanderthal draft genome and the ancestral allele in one randomly sampled African chromosome. This doubly conditioned frequency spectrum (dcfs) is enriched for sites in non-African sequences that are Neanderthal specific. Similarly to the D statistic, the sites explored are shared derived sites between Neanderthals and non-African humans and are likely to be informative about a recent admixture event.
We derive the analytical expression of the dcfs in non-Africans for a null model with no gene flow and compare a series of simulated dcfs for demographic models of both recent admixture and ancient structure. In the simulations, we allow for a variety of demographic histories, including bottlenecks in population size, ongoing gene flow between present-day human populations, population growth in early humans, varying admixture rates, and different rates of ancient gene flow. The shape of the dcfs are observed for each parameter set and compared with the observed non-African dcfs.
The observed dcfs are computed using four modern human populations from the Complete Genomics Diversity Panel (CGDP) and the draft sequence of the Neanderthal genome (Green et al. 2010). Following Green et al. (2010), we chose the Yoruba population (YRI), the Utah residents with European ancestry (CEU), the Japanese (JPT), and the Han Chinese (CHB) from the CGDP to represent the African, the European, and the Asian populations. The Yoruba population is not representative of all the African populations as current African populations are very diverse (Campbell and Tishkoff 2008; Tishkoff et al. 2009). However, the CGDP has several individuals of Yoruba ancestry and like most Africans, the Yoruba population probably had no interactions with Neanderthals. Using these populations, we assess whether the dcfs better supports a demographic history of recent admixture or ancient structure.
Materials and Methods
CGDP and Data Processing
The CGDP data we used consists of 46 individuals from nine populations whose genomes were sequenced to an average 45-fold coverage (Drmanac et al. 2010). We used five CEU, four CHB, four JPT, and seven YRI individuals downloaded from the Complete Genomics, Inc., ftp site (ftp://ftp2.completegenomics.com/) in May 2011. The individuals are listed in supplementary table S1 (Supplementary Material online). Each individual genome was aligned with the reference human genome, hg18. We used the release of the data set version 1.2 (Software version 1.10, File Format version 1.5).
The Neanderthal sequence was obtained by pooling reads from the three Vindija bones (SLVi33.16, SLVi33.25, and SLVi33.26) that were aligned to hg18 (Green et al. 2010). The Neanderthal data were downloaded from the UCSC genome browser (http://genome.ucsc.edu/Neandertal/) in May 2011. Following Green et al. (2010), we used only sites with a mapping quality score of at least 90, a sequence quality higher than 40, and a coverage of at most two since the average coverage of the draft genome was 1.3.
We assumed that the ancestral state at each of the sites is the reconstructed common ancestor as given in the 1,000 Genomes project. This reconstruction is based on an alignment of four species: Homo sapiens (human), Pan troglodytes (chimp), Pongo pygmaeus (orangutan), and Macaca mulatta (rhesus macaque). The reconstructed common ancestor was downloaded from the 1,000 Genomes ftp site (ftp://ftp-trace.ncbi.nih.gov/1000genomes) in May 2011. Only sites where the human–chimp ancestral sequence, the chimp sequence, and the human–chimp–orangutan ancestral sequence agree were kept. From the merged set of data, we filtered out transition substitutions to reduce the number of sites that are the result of ancient DNA damage (Briggs et al. 2007) and removed all sites that had three or more alleles.
Recent Admixture Model
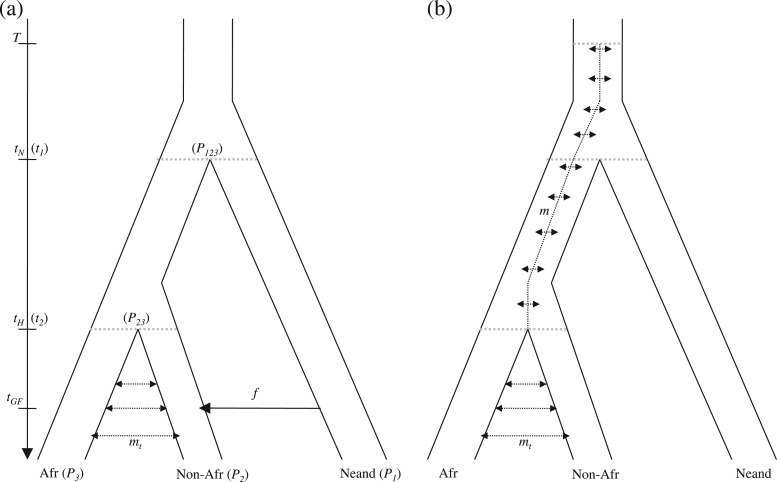
In this model, we assume that there was a single episode of admixture at time tGF in the past (t = 0 being the present) from Neanderthals to non-Africans after the migration of humans out of Africa (fig. 1a). With probability f, a non-African lineage was derived from a Neanderthal lineage. The parameter f represents the fraction of the non-African genomes of Neanderthal origin. We define the divergence time of non-African and African populations as tH > tGF. We denote by tN > tH the divergence time of Neanderthals and the population ancestral to modern humans. All the populations are assumed to be panmictic. Green et al. (2010) proposed this model as the most parsimonious explanation for why Neanderthals share more genetic variants with non-Africans than with Africans.
FIG. 1.
Demographic models relating Neanderthals and modern humans. At time tH in the past (t = 0 being the present), non-African humans (Non-Afr) split from African humans (Afr). After they split, Non-Afr and Afr may exchange migrants at rate mt. At time tN, Neanderthals (Neand) split from the ancestors of modern humans. (a) Recent admixture model. At time tGF < tH, Neand admixed with non-Afr at rate f. The variables used in the derivation of the dcfs are shown in parantheses. (b) Ancient structure model. The ancestral population of modern humans is structured in two subpopulations exchanging migrants at rate m. The substructure continues in the ancestral population of Neanderthals and modern humans.
Ancient Structure Model
We assume in this model that the population ancestral to modern humans and Neanderthals was divided into two randomly mating subpopulations (fig. 1b). We assume that subpopulations exchanged migrants symmetrically at rate m per generation. At time T in the past, subpopulations merged into one panmictic population. A similar model was proposed in Slatkin and Pollack (2008). Green et al. (2010) noted that this model could explain the extra similarity of Neanderthals with non-Africans, and Durand et al. (2011) showed that D statistics could not distinguish between ancient structure and recent admixture for plausible demographic parameter ranges.
Analytical Expression for the dcfs
We detail the coalescent derivation of the dcfs under a three-population tree model with no gene flow. We denote P1, P2, and P3, three closely related populations, which correspond to Neanderthals, non-Africans, and Africans, respectively (fig. 1a). Going backward in time, populations P2 and P3 split at time t2 from ancestral population P23. Population P1 splits from population P23 at time t1. We denote P123 the population ancestral to P1 and P23. Using an infinite sites model, we assume we have sampled one chromosome from P1 and P3 and n chromosomes from P2. Using diffusion theory, Chen et al. (2007) showed that the frequency spectrum in P2 conditioned on a chromosome from P1 carrying the derived allele was uniform. For completeness, we re-derive this result using coalescent theory (Appendix A).
We generalize the method described in Appendix A to derive the frequency spectrum in P2 given that a chromosome in P1 carries the derived allele and a chromosome in P3 carries the ancestral allele. This is the doubly conditioned frequency spectrum (dcfs).
Assume we have sampled n chromosomes in P2, one in P1, and one in P3, P2 and P3 split at time t2 and P1 splits from P23 at time t1. At time t2, there are k lineages from P2 and one from P3. As shown in Appendix A, the probability that m of these k + 1 lineages and the lineage in P1 carry the derived allele is uniform on m:
where θ′ is a constant that depends on t1, t2, n, and the effective ancestral population sizes. The probability that j = m derived lineages are among the k lineages from P2 and that the lineage from P3 has the ancestral state is
Then, the probability that i chromosomes in P2 and the chromosome in P1 carry the derived allele and the chromosome in P3 carries the ancestral allele is
where H (n, i, k) is the hypergeometric distribution with parameters (n, i, k). Summing over j, we obtain
The exact dcfs is obtained by averaging over k. It can be written as
| (1) |
where α′ and β′ are positive constants that depend on t1, t2, n, and effective population sizes in P23 and P123.
Another dcfs of interest is the one obtained when conditioning on a chromosome from P1 carrying the ancestral allele and a chromosome from P3 carrying the derived allele, therefore changing the order of conditioning in the previous derivation. At time t2, the probability that m out of k lineages carry the derived allele and that one chromosome from P1 carries the ancestral allele is
Thus, the probability that j = m – 1 lineages from P2 and the lineage from P3 carry the derived allele and the lineage from P1 carries the ancestral allele is
Using the same derivation as before, we find again that
| (2) |
where α″ and β″ are positive constants that depend on t1, t2, n, and effective population sizes in P23 and P123. It is important to note that equations (1) and (2) are valid regardless of the population size histories (bottlenecks, growth, etc.) of P1, P2, P3, P23, and P123.
We assume we have a sample of n chromosomes from a non-African population and one chromosome each from a Neanderthal and an African population. Assuming the chimp has the ancestral allele, we are concerned with the frequency of the derived allele in non-Africans. In particular, we denote dcfs(x) the expected frequency the derived allele appears x number of times in the non-African population, conditioned on the Neanderthal chromosome carrying the derived allele and the African chromosome carrying the ancestral allele. We showed in equation (1) that under a model with no recent admixture or ancient structure, the dcfs(x) is given by
| (3) |
where α and β are positive constants that depend on the effective population sizes and population divergence times. This result is also valid for the ancient structure model with no ancestral gene flow (m = 0). Such a model is equivalent to a model with no gene flow but in which the African population is the outgroup to Neanderthals and non-Africans. Equation (3) is also valid for the ancient structure model with large m because such a model is equivalent to the null model of no gene flow between Neanderthals and modern humans.
Calculating the dcfs from the CGDP Data
In order to build the dcfs, at each site, we sampled one read at random for the Neanderthal and called it ancestral if it matched the reconstructed ancestor or derived if it did not. Similarly for the Yoruba, at each position, we sampled one chromosome at random and compared it to the reconstructed ancestor. We then counted the number of derived alleles in the ten CEU chromosomes, the eight CHB chromosomes, and the eight JPT chromosomes for sites at which the Neanderthal draft genome carried the derived allele and the Yoruba chromosome carried the ancestral allele.
Simulations
To simulate models of recent admixture and ancient structure (fig. 1), samples were generated in the coalescent simulator ms (Hudson 2002). Unless otherwise specified, we assumed an effective population size of N = 10,000 for all populations and a generation time of 25 years per generation. In each replicate of both models, the simulated sample consisted of one Neanderthal chromosome, one YRI chromosome, and either eight (CHB or JPT), or ten (CEU) chromosomes of non-African origin.
In the recent admixture model, tH was set to 4,500 generations ago (112.5 kya, Li and Durbin 2011), and tN was set to 12,000 generations ago (300 kya, Green et al. 2010). The tGF parameter was set to 2,000 generations (50 kya), and f was chosen to be 0.05.
In the ancient structure model, T was varied between 12,000 and 32,000 generations ago, in steps of 2,000 generations. The intensity of ancient migration m was set to 4Nm = {0, 1, …, 10}. The non-African and Neanderthal populations split 12,000 generations ago (tN), and tH, the population split time between YRI and the non-African populations, was 4,500 generations ago. The parameter values for the ancient structure model were chosen so that the D statistic did not differ significantly from the observed D statistics (Durand et al. 2011).
For each model, a bottleneck reducing the effective size of the non-African populations by a factor of 100 (b) for 100 generations was set to (tb) 1,200 generations (30 kya) and 4,000 generations ago (100 kya). The two times of the bottleneck allowed it to be either before or after the time of admixture. We also considered ongoing symmetric gene flow between YRI and the non-African populations with rates 4Nmt = 1 and 4Nmt = 5. We simulated population growth in humans 100 generations before the YRI and non-African split, increasing the population size 100-fold in humans. We simulated the dcfs for other admixture rates of 2%, 3%, and 10% admixture with no bottleneck and a bottleneck younger or older than the time of admixture. The parameter values for ms are shown in table 1. The ms commands used to generate the simulated sequences can be found in Appendix B.
Table 1.
Parameters Used in ms (Hudson 2002) for the Recent Admixture and Ancient Structure Models.
| Parameter | Recent Admixture | Ancient Structure |
|---|---|---|
| θ (4Nμ) | 20 | 20 |
| Admixture rate (f) | {0.02, 0.03, 0.05, 0.1} | NA |
| Admixture time (tGF) | 0.05 | NA |
| African/Non-African coalescence time (tH) | 0.1125 | 0.1125 |
| Neanderthal/human coalescence time (tN) | 0.3 | 0.3 |
| Ancient migration time (T) | NA | {0.3, 0.35, … , 0.8} |
| Ancient migration rate (4Nm) | NA | {0,1, … ,10} |
| Bottleneck time (tb) | {0.03, 0.1} | {0.03, 0.1} |
| Bottleneck effect (b) | 0.01 | 0.01 |
| Ongoing gene flow (4Nmt) | {0, 1, 5} | {0, 1, 5} |
| Time of population growth (tg) | 0.1150 | 0.1150 |
| Amount of population growth (g) | 100 | 100 |
NOTE.—“μ” refers to the neutral mutation rate for the entire locus.
For each set of parameters, 1 million replicates were run and the non-African dcfs were estimated averaging over all the replicates. To allow comparison between different sets of parameters, the dcfs were normalized by the number of segregating sites in each simulation. Finally, the shapes of the dcfs were characterized for each model for each set of parameters.
To test the effect of misassignment of the ancestral allele on the dcfs, we simulated a model with no bottleneck, population growth, or present-day gene flow and incorrectly assigned the ancestral allele for 0.5%, 1%, 5%, and 25% of the analyzed sites.
Results
Distinguishing Recent Admixture and Ancient Structure
To be consistent with observed D statistics, we chose our parameters so that our simulations yield D statistics between 1% and 10% (table 2). Three main shapes characterized the dcfs for the simulated data: linear (eq. 2), L-shaped (an excess of singletons compared with the null hypothesis of no gene flow), or U shaped (excess of both rare and common alleles). The exact forms depended on the parameter values.
Table 2.
The Average D Statistic for Each Simulated Demographic History in Figure 2.
|
D Statistic |
|||
|---|---|---|---|
| Changing Demographic Parameters | Recent Admixture, f = 0.05 | Ancient Structure, 4Nm = 4, T = 0.6 | |
| No ongoing gene flow | No bottleneck | 0.0531 | 0.0489 |
| Bottleneck later than admixture, tGF = 0.03 | 0.0533 | 0.0496 | |
| Bottleneck earlier than admixture, tGF = 0.1 | 0.0521 | 0.0500 | |
| Ongoing gene flow, 4Nm = 1 | No bottleneck | 0.0528 | 0.0375 |
| Bottleneck later than admixture, tGF = 0.03 | 0.0463 | 0.0401 | |
| Bottleneck earlier than admixture, tGF = 0.1 | 0.0487 | 0.0413 | |
| Ongoing gene flow, 4Nm = 5 | No bottleneck | 0.0318 | 0.0185 |
| Bottleneck later than admixture, tGF = 0.03 | 0.0365 | 0.0172 | |
| Bottleneck earlier than admixture, tGF = 0.1 | 0.0342 | 0.0224 | |
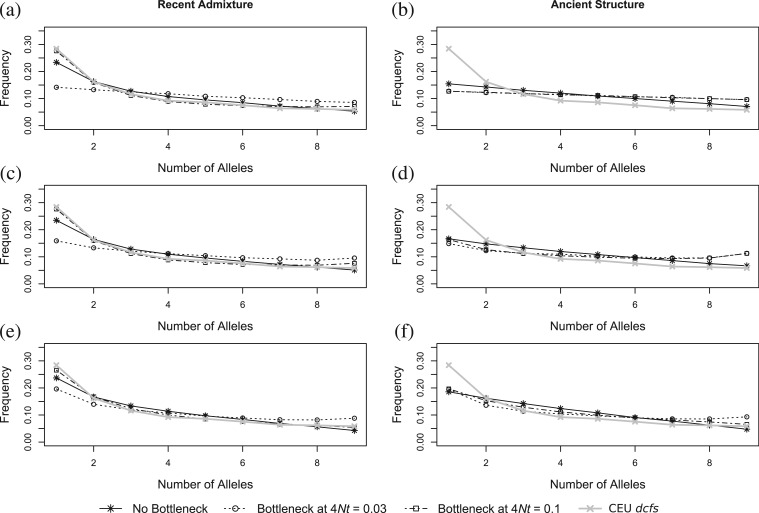
In the simplest case of no bottleneck or ongoing gene flow between modern humans, the dcfs had an L-shape for the recent admixture model simulations with f = 0.05 (fig. 2a and supplementary figs. S1a and S2a, Supplementary Material online). The dcfs for the ancient structure model decreased linearly, regardless of the values of m and T (fig. 2b and supplementary fig. S3b, Supplementary Material online). Adding a bottleneck in the ancient structure model reduced the slope of the line, but the dcfs was still linear (fig. 2b and supplementary fig. S3b, Supplementary Material online). Note that this result is the theoretical result for the ancient structure model with very low or very high values of m, and this results holds independently of population size fluctuations (eq. 2). For the recent admixture model, the placement of the bottleneck before or after the admixture event had an effect. When tb > tGF, the dcfs was still L-shaped, whereas when tb < tGF, the shape was linear for the dcfs (fig. 2a).
FIG. 2.
The dcfs for recent admixture (a, c, e) and ancient structure (b, d, f) for parameters shown in table 1, including no ongoing gene flow (a, b), ongoing gene flow of 4Nmt = 1 (c, d), and ongoing gene flow of 4Nmt = 5 (e, f). The time of admixture in the recent admixture model was 4NtGF = 0.05. The admixture rate simulated was 0.05.
Including ongoing gene flow between the non-African populations and the YRI population without a bottleneck resulted in a steeper linear dcfs for the model of ancient structure and a slightly more pronounced L-shape for a model of recent admixture, with little difference from a model containing no ongoing gene flow (fig. 2c–f and supplementary figs. S1b and S2b, Supplementary Material online). Including a bottleneck before or after admixture and ongoing gene flow of 4Nmt = 1 gave a U-shaped dcfs in both models, though when tb > tGF, there was a slightly greater excess of rare alleles (fig. 2c and d). Increasing the level of ongoing gene flow to 4Nmt = 5 makes each observed shape steeper, but in both models, when 4Ntb = 0.1, the U-shape was lost (fig. 2e and f and supplementary figs. S1b and S2b, Supplementary Material online). The inclusion of population growth in humans still retained the L-shape in the recent admixture model and the linear shape in the ancient structure model. Population growth made little difference in the shape of the curve for the different bottleneck times without increasing the severity of the bottleneck (supplementary figs. S4 and S5, Supplementary Material online).
Misassignment of the ancestral allele did not change the shape of the dcfs for the ancient structure model. As the error rate increased from 0.5% to 25%, the slope was steeper but the ancient structure dcfs remained linear (supplementary fig. S6, Supplementary Material online).
The observed dcfs for the 10 CEU haplotypes from the CGDP had an L-shape (fig. 2, gray curve), showing an excess of rare alleles but not higher frequency of sites carrying nearly fixed derived alleles. The shape did not fit any of the simulations for the ancient structure model (fig. 2b, d, and f) for all m and T (supplementary fig. S3, Supplementary Material online). The dcfs for the eight Han Chinese and eight Japanese chromosomes from the CGDP were also L-shaped and thus were also a better fit for the recent admixture model than the ancient structure model (supplementary figs. S1 and S2, Supplementary Material online).
Using an admixture rate of about 5% provided a much better fit to the observed data when combined with an older bottleneck (supplementary fig. S7, Supplementary Material online) than any model containing ancient structure only. Because many parameters can affect the fit of the simulated results to the observed data, this does not imply that the true admixture rate is 5%. Rather, the results suggest that scenarios with recent admixture are plausible. Various versions of the recent admixture model gave very good fits to the observed data, which was not the case for the ancient structure model for any set of parameter values we used.
Discussion and Conclusion
Support for the Recent Admixture Hypothesis
The sfs for the derived European (CEU), Chinese (CHB), and Japanese (JPT) alleles, conditioned on the ancestral YRI allele and the derived Neanderthal allele (dcfs), did not have the shape predicted by the ancient structure model for any set of parameters explored. The actual dcfs showed a noticeable excess of rare alleles that was not observed in any of the simulations for ancient structure but was observed in most of the simulations for recent admixture. An excess of rare alleles has been a characteristic feature that many past studies have described. The excess of rare alleles in the dcfs is unlikely to be due to errors in sequencing (Johnson and Slatkin 2008). Singletons are not biased toward any particular individual, chromosome, or region of a chromosome (supplementary material S1, Supplementary Material online). Misassignment of the ancestral allele under a model of ancient structure was simulated and does not alter our conclusions. The high coverage of the genomic data from the CGDP makes it highly unlikely that sequencing error in those genomes is large enough to affect our conclusions.
In the unconditional sfs, an excess of rare alleles can also be due to recurrent selective sweeps (Kim 2006) and logistic population growth (Fu 1997). However, these explanations for an excess of rare alleles is observed when no conditioning is used and do not account for an excess of rare alleles specifically at sites derived in the Neanderthal draft genome and ancestral in the YRI chromosomes. We have shown that population size fluctuations do not affect linearity in the dcfs in the absence of gene flow. Thus, the excess of rare alleles in the actual dcfs is due to recent admixture and not ancient structure, recent population growth, or recurrent sweeps.
To further understand the recent admixture model, we compared the effect of a bottleneck in non-Africans before or after the admixture occurred. We found that a bottleneck before admixture provides a better fit than a bottleneck after admixture. Although we did not attempt to estimate parameters, we found that in all simulations, the shape of dcfs when the bottleneck was before admixture was more similar to the dcfs calculated from the data than the shape of the dcfs for a younger bottleneck. For the parameters we kept constant, an admixture rate of about 5% provided a good fit, but this is unlikely to be true for other plausible demographic parameters. For instance, population growth before the divergence between the Yoruba and the non-African populations may make it difficult to distinguish between younger and older bottlenecks. However, we can be confident that the shape of the dcfs is unlikely to change dramatically if parameters remain within a plausible range. The lack of an excess of common alleles in the actual dcfs seem to suggest little, if any, ongoing gene flow between the Yoruba and non-African populations, but this effect may be more difficult to observe, as the excess seen in the simulation is small and is lost with higher rates of ongoing gene flow.
The simulations showed clear trends in the dcfs indicating that although the D statistic cannot distinguish between different demographic models, the dcfs can. The differences in the dcfs show that the greater variation in gene tree depth in the ancient structure model compared with the recent admixture model can be used to distinguish between these two models. The data from the Neanderthal genome and the CGDP showed a markedly different dcfs compared with any of the dcfs simulated for the ancient structure model, suggesting that the model of ancient structure does not accurately approximate the history of humans and Neanderthals. The results, however, do support the hypothesis of recent admixture. Interbreeding between Neanderthals and early modern humans is currently the most parsimonious and plausible explanation for the observed excess of genetic similarity between Neanderthals and non-Africans.
Supplementary Material
Supplementary table 1, figures S1–S7, and supplementary material S1 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Acknowledgments
We thank David Reich, Nick Patterson, Svante Pääbo, and the rest of the Neanderthal Consortium for their advice and suggestions that helped in the development of this study. This work was supported in part by a National Institutes of Health NRSA Trainee appointment grant (T32 HG 00047 to M.A.Y.), in part by a National Institutes of Health grant (R01-GM40282 to M.S.), and in part by the Ernst and Lucie Schmidheiny foundation (fellowship to A.S.M.).
Appendix A
The conditional derived sfs in two closely related populations was derived by Chen et al. (2007) and shown to be uniform using diffusion theory. Below, we derive this result again using coalescent theory.
Joint Site Frequency Spectrum in Two Closely Related Populations
Assume we have sampled n chromosomes from P2 and one from P1. Here we derive the conditional derived sfs in P2, which is the sfs in P2 given that the chromosome in P1 carries the derived allele (Chen et al. 2007). The two populations are assumed to split at time t1, and there is no gene flow between them after they split. At time t1, there are k lineages from P2 and one from P1. The probability distribution of k is given by Tavaré (1984):
We further assume that the ancestral population of P1 and P2 was at mutation-drift equilibrium. Let m denote the number of ancestral lineages that carry the derived allele. We have
the equilibrium neutral spectrum. Thus, the joint probability that j = m – 1 lineages from P2 and the lineage from P1 carry the derived allele is
We denote H the hypergeometric distribution. H(N, M, T)(K) is the probability to obtain K white balls when drawing T balls from an urn containing N balls, M of them being white. The probability that i lineages in P2 today carry the derived allele, given j, k, and n is given by (Slatkin 1996). Therefore, the joint probability that i lineages in P2 and one lineage in P1 carry the derived allele today is
Averaging over j, we obtain
Therefore, the conditional derived spectrum is uniform on i. The exact density is obtained by averaging over the distribution of k.
Appendix B
The two main demographic models considered are a model of recent admixture and a model of ancient structure. The ms command for a model of recent admixture is of the form:
ms 12 1000000 −t θ −I 3 1 1 10 –n 2 g –n 3 g −m 3 2 4Nm −m 2 3 4Nm −es tGF 3 1−f −ej tGF 4 1 −en tb 3 bg −en tb+0.025 3 g −ej tH 3 2 –en tg 2 1 −ej tN 2 1 (bottleneck older than time of admixture)
ms 12 1000000 −t θ −I 3 1 1 10 –n 2 g –n 3 g −m 3 2 4Nm −m 2 3 4Nm −en tb 3 bg −en tb+0.025 3 g −es tGF 3 1−f −ej tGF 4 1 −ej tH 3 2 –en tg 2 1 −ej tN 2 1 (bottleneck younger than time of admixture)
For example, ms 12 1000000 −t 20 −I 3 1 1 10 –n 2 100 –n 3 100 −m 3 2 5 −m 2 3 5 −es 0.05 3 0.9 −ej 0.05 4 1 −en 0.1 3 1 −en 0.1025 3 100 −ej 0.1125 3 2 –en 0.1150 2 1 −ej 0.3 2 1 means three populations were sampled, with recent symmetric gene flow of 4Nm = 5 between populations 2 and 3. Populations 2 and 3 are 100 times the effective population size. A 10% admixture event occurred at time 0.05 from population 1 to population 3. A bottleneck older than the time of admixture occurred at time 0.1, reducing the population 100-fold. Populations 3 and 2 coalesce at time 0.1125, and a sudden expansion in the ancestral population occurred at time 0.1150 from the original effective population size. They and population 1 coalesce at time 0.3.
The ms command for a model of ancient structure is of the form: ms 12 1000000 −t θ −I 3 1 1 10 –n 2 g –n 3 g −m 3 2 4Nm −m 2 3 4Nm −en tb 3 bg −en tb+0.025 3 g −em tH 3 2 4Nma −em tH 2 3 4Nma –en tg 2 1 –en tg 3 1 −ej tN 1 3 −ej ts 3 2.
For example, ms 12 1000000 −t 20 −I 3 1 1 10 –n 2 1 –n 3 1 −m 3 2 0 −m 2 3 0 −en 0.03 3 0.01 −en 0.0325 3 1 −em 0.1125 3 2 6 −em 0.1125 2 3 6 –en 0.1150 2 1 –en 0.1150 3 1 −ej 0.3 1 3 −ej 0.8 3 2 means three populations were sampled, with no recent gene flow and a population bottleneck occurring at time 0.03 reducing the population 100-fold. Ancient symmetric migration between Africans and Europeans occurred in the past starting at 0.1125, with a high gene flow of 4Nma = 6, and Europeans and Neanderthals coalesce at time 0.3. Ancient gene flow ends at time 0.8. No population growth occurred.
For no admixture, f = 0. For no gene flow, 4Nm = 0, and for no bottleneck, b = 1. For no population growth, g = 1. The full range of parameters explored for each model can be found in table 1.
References
- Barreiro LB, Patin E, Neyrolles O, Cann HM, Gicquel B, Quintana-Murci L. The heritage of pathogen pressures and ancient demography in the human innate-immunity CD209/209L region. Am J Hum Genet. 2005;77:869–886. doi: 10.1086/497613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs AW, Stenzel U, Johnson PLF, et al. (11 co-authors). 2007. Patterns of damage in genomic DNA sequences from a Neandertal. Proc Nat Acad Sci. 104:14616–14621. doi: 10.1073/pnas.0704665104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell MC, Tishkoff SA. African genetic diversity: implications for human demographic history, modern human origins, and complex disease mapping. Annu Rev Genomics Hum Genet. 2008;9:403–433. doi: 10.1146/annurev.genom.9.081307.164258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H, Green RE, Pääbo S, Slatkin M. The joint allele-frequency spectrum in closely related species. Genetics. 2007;177:387–398. doi: 10.1534/genetics.107.070730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drmanac R, Sparks AB, Callow MJ, et al. (65 co-authors) Human genome sequencing using unchained base reads on self-assembling DNA nanoarrays. Science. 2010;327:78–81. doi: 10.1126/science.1181498. [DOI] [PubMed] [Google Scholar]
- Duarte C, Maurício J, Pettitt PB, Souto P, Trinkaus E, vans der Plicht H, Zilhão J. The early Upper Paleolithic human skeleton from the Abrigo do Lagar Velho (Portugal) and modern human emergence in Iberia. Proc Natl Acad Sci U S A. 1999;96:7604–7609. doi: 10.1073/pnas.96.13.7604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- doi: 10.1093/molbev/msr048. Durand EY, Patterson N, Reich D, Slatkin M. 2011. Testing for ancient admixture between closely related populations. Mol Biol Evol. 28:2239–2252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu YX. Statistical tests of neutrality of mutations against population growth, hitchhiking, and background selection. Genetics. 1997;147:915–925. doi: 10.1093/genetics/147.2.915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green RE, Krause J, Briggs AW, et al. (56 co-authors) A draft sequence of the Neanderthal genome. Science. 2010;328:710–722. doi: 10.1126/science.1188021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green RE, Malaspinas A, Krause J, et al. (25 co-authors) A complete Neanderthal mitochondrial genome sequence determined by high-throughput sequencing. Cell. 2008;134:416–426. doi: 10.1016/j.cell.2008.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayakawa T, Aki I, Varki A, Satta Y, Takahata N. Fixation of the human-specific CMP-N-acetylneuraminic acid hydroxylase pseudogene and implications of haplotype diversity for human evolution. Genetics. 2006;172:1139–1146. doi: 10.1534/genetics.105.046995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- doi: 10.1093/bioinformatics/18.2.337. Hudson RR. 2002. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18:337–338. [DOI] [PubMed] [Google Scholar]
- Johnson PLF, Slatkin M. Accounting for bias from sequencing error in population genetic estimates. Mol Biol Evol. 2008;25:199–206. doi: 10.1093/molbev/msm239. [DOI] [PubMed] [Google Scholar]
- Kim Y. Allele frequency distribution under recurrent selective sweeps. Genetics. 2006;173:1967–1978. doi: 10.1534/genetics.105.048447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krause J, Orlando L, Serre D, Viola B, Prüfer K, Richards MP, Hublin J, Hänni C, Derevianko AP, Pääbo S. Neanderthals in central Asia and Siberia. Nature. 2007;449:902–904. doi: 10.1038/nature06193. [DOI] [PubMed] [Google Scholar]
- Krings M, Stone A, Schmitz RW, Krainitzki H, Stoneking M, Pääbo S. Neanderthal DNA sequences and the origin of modern humans. Cell. 1997;90:19–30. doi: 10.1016/s0092-8674(00)80310-4. [DOI] [PubMed] [Google Scholar]
- Li H, Durbin R. Inference of human population history from individual whole-genome sequences. Nature. 2011;475:493–496. doi: 10.1038/nature10231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg M. On the probability of Neanderthal ancestry. Am J Hum Genet. 1998;63:1237–1240. doi: 10.1086/302052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plagnol V, Wall JD. Possible ancestral structure in human populations. PLoS Genet. 2006;2:e105. doi: 10.1371/journal.pgen.0020105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich D, Green RE, Kircher M, et al. (28 co-authors) Genetic history of an archaic hominin group from Denisova Cave in Siberia. Nature. 2010;468:1053–1060. doi: 10.1038/nature09710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- doi: 10.1371/journal.pbio.0020057. Serre D, Langaney A, Chech M, Teschler-Nicola M, Paunovic M, Mennecier P, Hofreiter M, Possnert G, Pa ¨a ¨bo S. 2004. No evidence of Neandertal mtDNA contribution to early modern humans. PloS Biol. 2:e57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M. Gene genealogies within mutant allelic classes. Genetics. 1996;143:579–587. doi: 10.1093/genetics/143.1.579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M, Pollack J. Subdivision in an ancestral species creates asymmetry in gene trees. Mol Biol Evol. 2008;25:2241–2246. doi: 10.1093/molbev/msn172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tattersall I, Schwartz JH. Hominids and hybrids: the place of Neanderthals in human evolution. Proc Nat Acad Sci U S A. 1999;96:7117–7119. doi: 10.1073/pnas.96.13.7117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavaré S. Line-of-descent and genealogical processes, and their applications in population genetics models. Theo Popul Biol. 1984;26:119–164. doi: 10.1016/0040-5809(84)90027-3. [DOI] [PubMed] [Google Scholar]
- Tishkoff SA, Reed FA, Friedlaender FR, et al. (25 co-authors) The genetic structure and history of Africans and African Americans. Science. 2009;324:1035–1044. doi: 10.1126/science.1172257. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.