Equilibrium at the edge and atomistic mechanisms of graphene growth

Abstract

The morphology of graphene is crucial for its applications, yet an adequate theory of its growth is lacking: It is either simplified to a phenomenological-continuum level or is overly detailed in atomistic simulations, which are often intractable. Here we put forward a comprehensive picture dubbed nanoreactor, which draws from ideas of step-flow crystal growth augmented by detailed first-principles calculations. As the carbon atoms migrate from the feedstock to catalyst to final graphene lattice, they go through a sequence of states whose energy levels can be computed and arranged into a step-by-step map. Analysis begins with the structure and energies of arbitrary edges to yield equilibrium island shapes. Then, it elucidates how the atoms dock at the edges and how they avoid forming defects. The sequence of atomic row assembly determines the kinetic anisotropy of growth, and consequently, graphene island morphology, explaining a number of experimental facts and suggesting how the growth product can further be improved. Finally, this analysis adds a useful perspective on the synthesis of carbon nanotubes and its essential distinction from graphene.

Recent years have seen development of ever simpler and cheaper methods to produce graphene on metal substrates (1, 2). Yet the quality of as-produced material suffers from defects and polycrystallinity (3–9), with electronic transport orders of magnitude inferior to mechanically exfoliated graphene (10, 11). Understanding the atomistic mechanisms governing the sp² carbon growth remains a scientific challenge, critical for production of quality graphene, as well as controllable growth of nanotubes. Experimentally, graphene grows at very different conditions, on many different substrates, and from various precursors (12). In principle, this ubiquity is not surprising because graphene is a deep global minimum in the phase diagram of carbon. Overall carbon flow is often pictured as a VLS (vapor–liquid–solid, or vapor–solid–solid) model for nanowires (13, 14) or tubes (15). Yet this flow from the higher chemical potential gas-feedstock (μ) into its product (μ₀) is mediated by various states of carbon atoms, first bound to the substrate-catalyst and then to the nanotube or graphene edge. The detailed atom-by-atom sequence of carbon accretion to the sp² lattice remains essentially unknown. How are these states ordered in space and in energy scale? Accordingly, which are populated or empty, and what serves as the bottleneck controlling the growth rates of different crystallographic faces? The answers to these questions determine how the equilibrium shape is replaced by its kinetic alternative, and how the excess nonequilibrium, Δμ ≡ μ - μ₀ > 0, might impose defects into the generally highly periodic lattice.

These questions compel one to step from the VLS paradigm (13–15) up to a more detailed and quantitative view, by assigning specific energies to different locations of C-atoms, migrating toward the edge of graphene lattice, across the metal-carbon interface zone, a nanoreactor. To this end, here we combine crystal growth theory and first-principles atomistic computations. First, the edge energy γ(χ), definitive for the equilibrium shapes, is calculated for all edge orientations (angle χ, measured from the zigzag lattice direction) on different catalyst substrates. Then we turn to nonequilibrium to investigate how the energy changes upon addition of C-atoms, and focus on the nucleation of consecutive atomic rows. Computed energy levels at different sites (on the catalyst or at the edge, including possible imperfections) dictate their occupancies, resembling a form of Fermi-statistics, with each site occupied by no more than one atom. Further, the step flow growth ideas (16) combined with computed nucleation barriers allow one to evaluate the growth rates v(χ) for different directions. Notably, the similar growth kinetics manifests itself in strikingly different ways for carbon nanotubes (CNT) and graphene. For graphene, as a simple corollary of kinetic Wulff construction (17), the perimeter type is selected and the island shape is defined. This kinetic shape selection contrasts with nanotubes whose edge chirality is locked by their cylindrical topology and thus each individual tube just keeps growing with its own chirality-controlled speed (18, 19). For the substrate, we used trigonal surfaces of four metals: Ni, Fe, Co, and Cu, catalysts often used for CVD growth of both graphene (Ni, Cu, Co) and CNT (Ni, Fe, Co); the main focus is on Ni, used frequently for the synthesis of both CNT and graphene (20).

In equilibrium, an obvious initial concern is the structure and the lowest ground-state energy of the edge. Given the edge free energy per unit length γ(χ), the Wulff construction readily yields the thermodynamically optimal shape. In ref. 21, the shapes for free standing graphene flakes were studied based on direct first-principles computations for edges of a few orientations, between armchair (A) and zigzag (Z). For most orientations, excessive system size makes this direct approach impractical, especially if a substrate metal is included. Instead, a more efficient way is to make use of the analytical expression, γ(χ) = 2γ_A sin(χ) + 2γ_Z cos(30°-χ) (22), which reduces the direct computations to just the energies of two principal directions, A and Z. From this equation alone it is straightforward to show that the Wulff construction for graphene contains both A and Z (and intermediate) edges only when 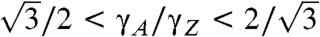; i.e., when the edge energies along the A and Z crystallographic directions differ by no more than approximately 15%; outside of this range, either A or Z fully dominates, resulting in a hexagonal island.

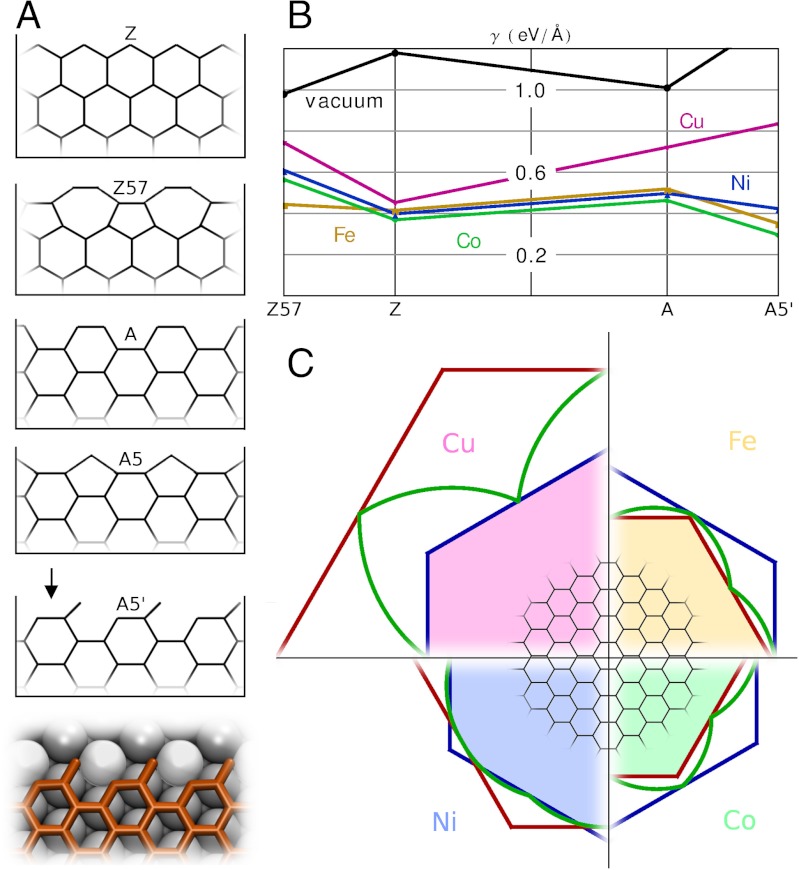
Using density functional theory (DFT), we computed edge energies for graphene on metals (SI Text), including not only generic A and Z edges, but also their self-passivating reconstructions (23) that reduce dangling bond density at the expense of lattice strain, A5 and Z57 (Fig. 1A). Unexpectedly, the A5 structure turned out to be unstable on all the metals: Geometry optimization led to another structure, which we refer to as A5’ for open-pentagon armchair. Moreover, for Fe, Co, and Ni this structure has lower energy than the unreconstructed A edge, making it the ground state for A-orientation. Because the surface atoms that bridge twofold- and single-coordinated carbon atoms are pulled slightly (approximately 0.3 Å) out of the metal surface plane, the open pentagons can alternatively be viewed as buckled heterohexagons with one carbon substituted by metal, Fig. 1A, Bottom. Fig. 1B summarizes the edge energies on all four metals and in vacuum, revealing interesting trends. First, the Z57 is energetically unfavorable (in contrast to vacuum, where it happens to be the lowest energy edge known). Second, the unreconstructed A edge has higher energy than unreconstructed Z—again, in a marked contrast to vacuum environment. Finally, the A5’ edge energy is lower than that of Z edges on Fe and Co, and the two are almost equal on Ni. All these trends are explicable: Whereas in vacuum it pays off energetically to saturate dangling bonds at the expense of lattice strain by forming nonhexagonal polygons, on a substrate metal atoms provide some saturation without straining the lattice, making reconstruction unnecessary (moreover, the high edge energy on Cu correlates with the low solubility).

Fig. 1.

Equilibrium shapes of graphene. (A) Graphene edge structures and notations. (B) DFT edge energies on different metals and in vacuum, for comparison. (C) Wulff constructions for graphene on metals; blue lines denote Z edge, red represent A edge (on Cu) or A5’-edge (on Ni, Fe, Co), green curve is a polar plot of the edge energy γ(χ).

With full γ(χ) at hand, the Wulff construction plots (24) can be readily obtained (Fig. 1C). We only show one quadrant for each metal, but full shapes can be recovered by reflection symmetry. Red and blue lines denote A and Z edge directions, and the green is the polar plot of γ(χ). The variety of shapes covers the full spectrum of possibilities. On Ni, the small difference of Z and A5’ edge energies leads to a smooth rounded equilibrium shape. On Fe and Co, the energy of A5’ edge is so low that it dominates the hexagonal shape completely. Finally, on Cu, the equilibrium shape of a graphene isle is a hexagon having only Z edges. Thus, the thermodynamically optimal shapes of graphene islands are diverse and vary from metal to metal.

Near the equilibrium, slow growth cannot invalidate Wulff construction abruptly. At very low rate of carbon accretion v = v_→ - v_←, an island of size L still tends to preserve its thermodynamic shape, maintained by the diffusion (D) around its perimeter, if the redistribution time t_diffusion ∝ L²/D is much shorter than the size-change time t_growth ∝ L/v. This condition vL ≪ D holds for small islands and slow growth. One concludes that in this quasiequilibrium regime the island simply scales up with the apparent propagation speed of each facet proportional to its energy, v_qe(χ) ∝ γ(χ).

Further away from equilibrium, more relevant for the actual growth conditions, the growth rate v(χ) ≈ v_→(χ) of each facet does not depend on others and is determined by the process of atoms attachment. To unravel its details, here we invoke the ideas of step-flow growth of crystals in the canonical Burton–Cabrera–Frank (16) representation (Fig. S1). The growing edge of graphene assumes the role of the surface step. It moves forward by incorporating to its active sites the carbon atoms arriving through the substrate. We first consider the docking of atoms to the two fundamental graphene edge directions (A and Z) on the Ni catalyst. We then discuss arbitrary edge orientations on Ni and other metal catalysts.

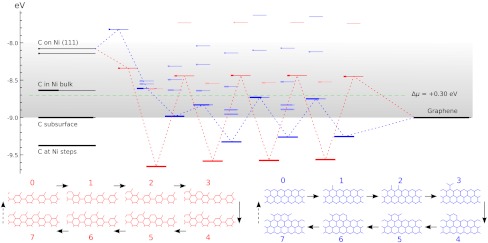
Starting from perfect A5’ or Z edges we sequentially add atoms, and for each such addition screen multiple metastable configurations. Covering both lowest-energy structures and possible defects such as pentagons, heptagons, or dangling linear chains, we compute the energies using DFT (SI Text and Fig. S2), to assess their formation probability. The results are summarized in Fig. 2, in a form we used recently for catalytic spillover (25). C-atoms from feedstock (chemical potential μ set by horizontal dashed line) are first adsorbed on the metal substrate. Fig. 2, Left, shows the computed energies of available sites marked as lines, with thicker segments representing their probability-occupancy by incoming atom, evaluated at kT = 0.1 eV by the Fermi function p(ϵ) = 1/[1 + e^(ϵ-μ)/kT], accounting for the exclusion principle of no more than one atom per site. In spite of its limited applicability to a nonequilibrium high gradient process, it serves best to assess the likelihood of different configurations. The rightmost line represents the binding energy μ₀ of graphene, on Ni. The multiple lines/levels in between represent binding energies ε_n for each successive carbon atom addition, n = 1,2,3…, and are filled sequentially. Red and blue correspond to the A and Z edges.

Fig. 2.

The nanoreactor diagram for A5’ and Z edges growth on Ni substrate. Carbon atoms migrate from the source (metal substrate, leftmost levels) to the product (graphene, rightmost) by sequentially populating energy levels in the middle that represent energies of n^th carbon atom at the extending row already containing n - 1 atoms. (The occupancies at kT = 0.1 eV are marked by thicker segments.) Lowest-energy atomic configurations are shown in the bottom. The green line sets the chemical potential μ of carbon atoms (established by the feedstock gas). An animated version of Figs. 2–4 is provided as Movie S1.

This quantitative diagram is a significant advance from the VLS model. It could be detailed further by including other possibilities on/in the metal (Left), considering additional specific configurations at the graphene edges (Center), or considering other substrates. Yet already in present form it captures main behaviors and reveals a number of important aspects. Overall, it shows the substrate’s key roles in the sp² lattice assembly: Not only (i) does it serve as a planar template, but (ii) it also prevents formation of defects at the very front of growth, thus making their posterior annealing unnecessary. Indeed, the lowest-energy states sequence in the bottom of Fig. 2, defining the lattice-building path, never includes defects. Notably, the states containing pentagons or heptagons, a 5/7, or dangling carbon chains are all higher in energy and consequently are suppressed. This suppression would not happen in vacuum, with no substrate: Pentagon and heptagon formations are relatively low in energy and therefore probable, causing reconstruction of sp² edges with 5s and/or 7s, which are responsible for closure of nanotubes or fullerene cages (26). Further, (iii) the nanoreactor scheme of Fig. 2 also explains the highly defective outcome of essentially all molecular dynamics or Monte Carlo simulations of growth [regardless the choice of interatomic force field (27, 28)]. The exceedingly high rate of carbon deposition in MD studies corresponds to the excessive chemical potential which populates the defect states—higher levels in Fig. 2—so they do form frequently and corrupt the lattice. Besides explaining the prevention of topological defects, (iv) the diagram also shows that protruding fingers are higher in energy and unlikely to happen, which prevents branching into dendrites—unless again μ is raised high enough to allow their formation. This observation can explain the dendrite flakes often forming on Cu, which indeed has higher energies for C sites in the left of Fig. 2. In spite of the diagram’s complexity (a detailed account of all the configurations is given in Figs. S3–S5), there are notable regularities. (v) After just a few initial atoms, a periodic up-down alternating level sequence is established. The energy variation amplitudes |ϵ_n - ϵ_n+1| differ for A and Z edges, but the average value 1/2(ϵ_n + ϵ_n+1) for either edge is the same, and equals the binding energy of graphene (the rightmost level). Interestingly, (vi) this diagram shows clearly how beneficial it might be to have carbon provided in the form of C₂ (dimers). If the substrate favors them rather than monomers, the dimers’ subsequence skips the heights, permitting faster and perhaps better quality growth (yet less chance for defects). (vii) The initial atomic levels are crucial and show a fundamental distinction between A and Z edges: For Z, the first atom addition is strongly endoergic, and it is likely to fall back onto the substrate, whereas the subsequent Z levels all lie below the high-energy states for the A edge sequence.

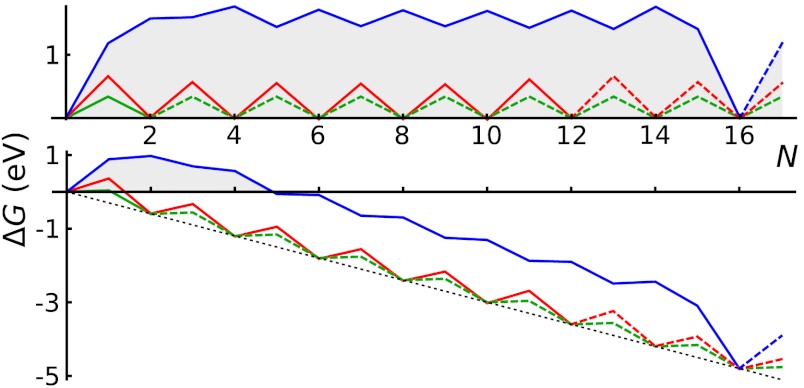
This row-nucleation stage is convenient to analyze using the total free energy evolution in Fig. 3, obtained as the partial sums over lowest-energy states in Fig. 2, 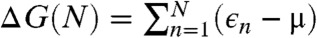. More telling is the lower plot of Fig. 3, showing free energy variation at a moderate value of Δμ = 0.3 eV. For Z edge, a substantial barrier has to be overcome to nucleate a new row, after which growth proceeds with a monotonous decrease of energy. For A edge, the nucleation barrier is much smaller, but remains present at every other atom addition (a somewhat larger Δμ≥0.7 eV is needed for A edge to grow unobstructed downhill). It is evident that growth of Z edge comprises two stages. The first is nucleation of a new atomic row, and then the sequential addition of atoms to the kink sites at its ends (Fig. 2), or kink flow. The first stage is slow, and the second is very fast. At intermediate orientations, edges contain both Z terraces and kink sites, and concentration of kinks becomes the dominant factor for the overall growth rate. The green line in Fig. 3 shows calculations for the (6,1) edge, with the same oscillation amplitude as in the kink-propagation stage in Z plot, but with no nucleation/termination of kinks, so that the overall growth of the skewed edge ends up being faster than both A and Z edges.

Fig. 3.

Free energy evolution during growth, Δμ = 0 (Top) and Δμ = 0.3 eV (Bottom, with characteristic nucleation barrier). Green lines represent kink-flow growth of skewed (6, 1) edge. Dashed lines show periodic repetitions due to finite size of supercells used in calculations, which corresponds to the growth of a next atomic row upon the completion of the previous.

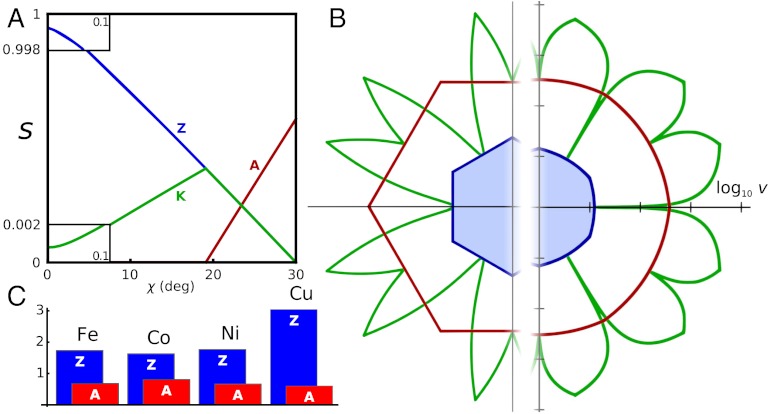
We are now ready to formulate an expression for direction-dependent growth velocity, v(χ). The details are explained in SI Text. We obtain closed-form expressions for the concentrations s_K, s_A, and s_Z of the active sites at kinks, armchair, and zigzag edge-segments, and they are plotted in Fig. 4A. Then, the carbon precipitation rate, i.e., growth velocity, is proportional to the sum of site concentrations times the respective probability factors (exponential at not too high μ; see SI Text for the full expression, and Fig. S6 and Movie S1 for illustration of the effect of μ on v(χ)):

Fig. 4.

Anisotropy of growth velocity. (A) Concentrations of different active sites (per lattice parameter) with respect to edge orientation χ. Red, blue, and green lines represent A, Z, and kink sites. (B) Kinetic Wulff construction for graphene on Ni. Green line is a polar plot of v(χ), red and blue lines show envelope velocities of pure A and Z edges. The left half uses artificially raised kT = 0.3 eV, and the right uses a realistic kT = 0.1 eV but a log ₁₀ scale. Fig. S6 shows the dependence of shape on Δμ. (C) DFT-computed free energy nucleation barriers for edge propagation on different metals, for Δμ = 0.

Here, E represents the free energy barriers and N^∗ is the critical Z nucleus size, and so plugging our computed above DFT values we obtain the speed of propagation as a function of arbitrary edge direction v(χ), plotted in Fig. 4B. For graphene, a simple immediate corollary obtained with kinetic Wulff construction [with the velocity v(χ) replacing the energy γ(χ) (17)—an intuitive consequence of shape self-similarity], is that a growing island is a hexagon with entirely Z perimeter. Same holds for the other metals, and Fig. 4C compares the growth barriers for A and Z propagation, the shape-defining minima of v(χ). The barrier difference E_Z - E_A is invariably large, from 0.8 eV (the smallest, on Co) and up to as much as 2.4 eV, on Cu. Therefore, A sides advance much faster, and the overall shape must always be limited by the lagging Z edges, a conclusion being universal independent of the substrate metal, in contrast with the thermodynamic equilibrium shapes on Fe, Co, and Ni (while on Cu, graphene grows in the equilibrium shape).

These results suggest a simple morphological evolution scenario for a graphene flake of arbitrary initial shape. At nearly equilibrium conditions, the lateral transport ensures that it grows with the thermodynamic shape being maintained. [Note that in this regime, v(χ) ∝ γ(χ), and thus both equilibrium and kinetic Wulff’s recipes concur.] Away from equilibrium, when the transport around the entire perimeter is relatively slow, the individual edges/facets establish their own propagation speeds v(χ), with sharp minima for the basic A and Z facets (χ = 0 or 30°). Consequently, all skewed edges advance quickly via kink flow, are weeded out into Z and A segments, and finally to the slowest all-Z perimeter hexagon—the asymptotic steady state result of kinetic Wulff construction. Such selection changes any initial flakes into Z-edged hexagons, growing further via nucleation of new atomic rows and kink flow. This convergent evolution is in striking contrast with growth of tubes, whose cylindrical topology forbids edge chiral angle from changing, leading to different kinetic behavior. For a nanotube, the atomic dynamics in the nanoreactor zone near the edge is essentially the same as for graphene (18). However, its chirality prescribes the edge orientation, and cylindrical topology makes kink propagation perpetual [barring formation of 5/7 defects that change chirality, as observed in simulations (29)]. Consequently, there is no simple kinetic selection of the edge type (like for flat graphene), but instead each tube maintains its own stationary chiral edge structure and its own growth speed, v(χ) ∝ s_K(χ) ∝ sin(χ) (18, 19).

Beside the several behaviors derivable directly from the nanoreactor diagram (defectless growth, nucleation of edge-additions, speed vs. direction, edge energies and shapes, either equilibrium or kinetic), additional interesting aspects can be related and further explored separately. Our results can offer an interpretation of nonlinear, high power concentration dependence of graphene growth rate (30, 31). As described above, the late-stage growth rate is limited by formation of kinks upon nucleation of new atomic rows on Z edges, with some critical nucleus size causing the power dependence (see Fig. 3). A power-law dependence on concentration of C feedstock can be a natural consequence of the nucleation–kink-flow scenario. Moreover, factors such as carrier gas (32), presence of water vapor (33), or molecular hydrogen (34) are seen to play important but poorly understood roles in the growth of carbon nanomaterials. They may deplete specific sites in the nanoreactor, thus improving the transport and avoiding defects or even growth termination. Experiments with graphene show a broad variety of flake shapes, from hexagons with almost exclusively Z edges (6, 34–38) to continuous shapes with smooth or rough sides (39) to dendrites (40). The latter are undesirable for applications and typically result from diffusion-limited aggregation, when carbon sticks to most positions—which in Fig. 2 happens if chemical potential excess Δμ is greater than the edge energy (per atom), and protruding hexagons can form uninhibited. The diagram suggests a window 0 < Δμ < 1 eV (gray band in Fig. 2) to avoid dendrites while maintaining growth (as opposed to etching/dissolution). Notably, calculated levels on Cu are rather high, and this placement correlates with often observed dendritic shapes.

Whereas the analysis above is focused on the growing front of an individual island, an important question is how different flakes fuse to form a continuous sheet. One then needs to consider not a single but a pair of edges, generally askew, where the arriving atoms can dock. The simulated lowest energy atom addition sequence would then yield a grain boundary between the tilted domains. To fully apply the nanoreactor approach, all energy states in Figs. 2 and 3 should be recomputed, which goes far beyond the scope of the present work. Moreover, the boundary conditions may be extremely different for different experimental protocols. Growth on Cu foils typically yields grain misorientation angle distributions that cover the entire 0–30° range, with peaks around certain values(3–5). On Ni, a shift resulting from coexistence of two energetically near-degenerate stackings causes a unique zero-misorientation grain boundary structure (41). Finally, when synthesis is carried out above the melting point of Cu (36, 37), individual graphene islands may be able to drift and reorient on the liquefied metal surface, suggesting that capillary forces may also affect the boundary conditions. On the other hand, recently shown capability to synthesize individual flakes as large as 0.1–1 mm (38) suggests that the problem of polycrystalline film formation may eventually be completely circumvented.

In summary, we recast a complicated nonequilibrium dynamics near the border of a growing graphene lattice into the detailed yet tractable diagram (Fig. 2) of energy levels available to C atoms as they move from substrate to the carbon phase. As a key to growth mechanisms of graphene (and, with some modification, nanotubes), this nanoreactor scheme represents an advance from a qualitative VLS paradigm, canonical in nanotubes and wires growth research (13–15). It invokes the seminal concepts of crystal growth theory (16), enriched with a bulk of important quantitative details of carbon-metal interactions computed with first principles methods. In the equilibrium case, we determine the edge structures and energies, and accordingly, plot the Wulff construction shapes, varying among the substrates (Co, Cu, Fe, or Ni). Through the nanoreactor diagram, we find that metal substrates prevent formation of nonhexagonal edge reconstructions and any defective configurations during growth (and also explain the excessive disorder in the bulk of MD simulations). Further, it shows exact steps of carbon accretion: Kink propagation has a small energy barrier (which might even fully vanish if the feedstock and catalyst provide carbon in the dimer form, C₂), but for creation of kinks, considerable nucleation barriers must be overcome—especially on the zigzag edge. Together, these data allow one to calculate the general growth speed dependence on the facet direction v(χ), and to easily establish—by virtue of kinetic Wulff construct—the nonequilibrium shape. Because the zigzag edge is decidedly the slowest, an effect that is especially pronounced if Cu is used as the substrate, the growing graphene isles are universally hexagonal with zigzag perimeter, as observed in a large body of experimental evidence. This behavior notably contrasts with nanotubes, where similar interface dynamics is at play, but because of their cylindrical topology, it leads to entirely different conclusions. First, tube chirality is invariant, precluding changes of edge type. Then, common kinetic effects favor nanotubes with near-armchair edges, whereas in graphene growth, zigzag edge seems to dominate universally.

Supporting Information Available

In the SI we provide (i) details of DFT calculations; (ii) derivation of analytical expression for v(χ); (iii) illustrations explaining the analogy between graphene edge growth and step-flow lateral growth of crystals; (iv) supercells used for modeling edge and kink growth; (v–vii) possible atomistic structures (with energies) during A, Z, and kink growth; (viii) kinetic Wulff construction for graphene on Ni as a function of chemical potential; and (ix) animation illustrating the changes in the nanoreactor diagram and the kinetic Wulff construction as μ is varied.

Note Added in Proof.

Recent analysis (42) of defect healing in CNT growth is applicable to the case of graphene as well, and further enforces the defect inhibition, mentioned above. The healing transformations would correspond to vertical-down transitions in the nanoreactor diagram of Fig. 2.