Mode-Locking Dynamics of Hair Cells of the Inner Ear

Abstract

We explore mode-locking of spontaneous oscillations of saccular hair cell bundles to periodic mechanical deflections. A simple dynamic systems framework is presented that captures the main features of the experimentally observed behavior in the form of an Arnold Tongue. We propose that the phase-locking transition can proceed via different bifurcations. At low stimulus amplitudes F, the transition to mode-locking as a function of the stimulus frequency ω has the character of a saddle-node bifurcation on an invariant circle. At higher stimulus amplitudes, the mode-locking transition has the character of a supercritical Andronov-Hopf bifurcation.

INTRODUCTION

Auditory organs of the inner ear provide exquisitely sensitive detection of sound [1]. The human cochlea, for example, can detect over six orders of magnitude in sound intensity, with a frequency selectivity that can be as high as Δω/ω ≃ 0.2% [2]. In the 1940s, Gold [3] pointed out that hearing must involve active non-linear amplification to overcome viscous damping by the fluid environment within the cochlea. Numerous experimental studies have since verified that active amplification mechanisms reside in hair cells [4? ?, 5], mechano-sensory cells embedded in the supporting tissue, and also that nonlinearity is crucial to the acuity of hearing [6]. Mechanical detection by a hair cell is performed via an array of stereocilia protruding from its surface that contain mechanically sensitive ion channels. Motor proteins are believed to maintain tension in the tip links that interconnect these stereocilia [4, 5]. When the tension exceeds a threshold value, mechano-sensitive ion channels open, allowing an inflow of ionic current, a small fraction of which is carried by Ca²⁺. Entry of calcium ions into the cell causes the motor proteins to slip, releasing the tension and allowing the channels to close and the process to repeat. In non-mammalian systems, active motility by the stereociliary bundle has been proposed to provide amplification of incoming signals. In the mammalian cochlea, with higher frequencies represented, somatic electromotility has also shown to be crucial to the active amplification [? ? ].

Studies performed in vitro on the mechanical properties of individual hair cells obtained from the bullfrog sacculus showed that stereociliary bundles exhibit spontaneous oscillations [7–9] with amplitudes of 20–100 nm and frequencies in the 10–80 Hz range. These innate movements significantly exceed thermal fluctuations and have been shown to require an energy-consuming amplification process [7]. They frequently occur in irregular bursts, with oscillatory behavior interspersed with quiescent intervals.

The role of spontaneous bundle oscillation in auditory detection is uncertain since it is not known if they occur under in vivo conditions, or at higher frequencies. Hearing organs have been shown to produce spontaneous otoacoustic emissions [10], which may indicate that spontaneous oscillations do arise in vivo. Current theories of frequency-selective hearing assume that hair cells self-tune to the onset point of the spontaneous oscillations, since at that point hair cells should exhibit pronounced, frequency-selective sensitivity to mechanical stimulation [11–17].

Nonlinear biological oscillators, including neuronal, cardiac, and circadian pacemaker circuits are known to respond sensitively to external signals through phase-locking, also known as entrainment [18, 19]. Phase-locking of hair bundles to periodic mechanical perturbations has likewise been reported in the literature [7]. This raises the possibility that hair cells performing large-amplitude spontaneous oscillations might be able to detect weak, periodic signals by phase-locking. In this paper we explore the phase-locking of spontaneously oscillating hair bundles subjected to external stimuli over the full physiological range of frequencies and amplitudes. We demonstrate that the amplitude of the phase-locked component of the spontaneous oscillations exhibits a narrow, frequency-selective response, which broadens with increasing drive amplitude. By comparison between our experimental results with an analysis of the driven Normal Form Equation, we relate stereociliary bundle phase-locking to the well-known Arnold Tongue of the theory of dynamical systems [18]. For lower drive amplitude, phase-locking proceeds via an infinite-period bifurcation and at higher amplitudes via a super-critical Hopf bifurcation [20].

MODE-LOCKING OF STEREOCILIARY BUNDLES

We imaged bundle movement in an optical microscope, recording images at 1000 frames per second [21]. We used a customized pipette puller to fabricate elastic glass fibers of ~0.5–1 μm tip diameter. The probe was mounted on a piezoelectric stimulator and attached to a stereociliary bundle (see the left part of Figure 1). Lateral sinusoidal displacements were applied to the stereocilia, mimicking the mechanical stimulation evoked by sound in vivo. The applied frequency (ω) was varied in 1 Hz increments, spanning the range of 5–50 Hz, with 10 cycles sent at each frequency. The full sweep was applied at stimulus amplitudes from 4–120 nm. A 10 nm probe displacement corresponds to, approximately, a 1 pN force on the bundle. A set of traces showing the response of a hair bundle to an evenly spaced subset of the complete 2D scan is provided in the Supplementary Material.

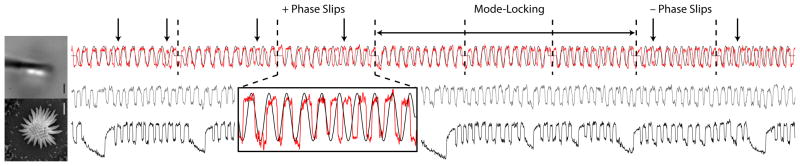
FIG. 1.

Left panel: Bottom image: scanning electron microscope image of a stereociliary bundle, in a top-down view. Top image: optical image of a glass fiber attached to the row of tallest stereocilia. The space bars in both images denote 1 μm. Right panel: Mode-locking at a drive amplitude of 20 nm. Bottom trace: spontaneous oscillations of a free stereociliary bundle. Middle trace: spontaneous oscillations of a stereociliary bundle with an elastic glass probe attached to its tip with a stiffness of 100 μN/m with no imposed deflection. Top trace: sinusoidal deflections are imposed on the bundle with a 20 nm amplitude and with increasing frequency from 17 to 23 Hz (red trace). The displacement of the base of the probe is shown overlaid in black, which has been arbitrarily scaled for visibility. Frequency increases by 1 Hz every ten cycles. Decades of drive cycles are indicated by vertical dashed lines. Events of phase slip between bundle and probe are indicated by arrows. The magnified portion shows a “phase-slip” event.

Figure 1 illustrates the entrainment dynamics of the hair bundle at a low amplitude of stimulation. The bottom trace shows the innate dynamics of free stereociliary bundles. The oscillations are highly anharmonic, noisy, and occur in bursts. The middle trace shows the spontaneous oscillations with a probe attached to the tip of the bundle, but with no applied force. Bursting is largely suppressed, and the spontaneous oscillations are more regular. The top trace shows the oscillations in the presence of a weak stimulus of increasing frequency applied to the base of the probe. Decades of drive cycles are indicated by vertical dashed lines. Complete mode-locking is observed over an interval of three decades. In this interval, the frequency is in the vicinity of the characteristic frequency of the cell (between 20 and 25 Hz). This region is flanked by intervals where the number of bundle cycles is either 11 or 9. The loss or gain of the 2π phase difference happens regularly, over one to several cycles. These “phase-slip” events are indicated in the figure by arrows. The rate of phase-slip production increases with distance between the stimulus frequency and the characteristic frequency of the cell. Note that the system does not appear to exhibit resonance: the amplitudes of oscillation are the same inside and outside of the mode-locked region. Due to the production of phase slips, however, the phase-locked component of the large-amplitude spontaneous oscillation decreases away from the characteristic frequency, with modest frequency resolution.

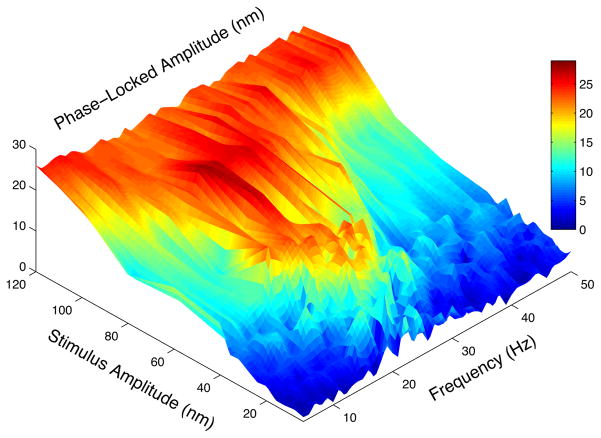
To quantify this mode-locking, we plotted the phase-locked component of the response across the physiological range of frequencies and amplitudes (see Figure 2). At low amplitudes of stimulation, the system exhibits mode-locking around its characteristic frequency, as discussed above. The phase-locked frequency interval of Fig. 1 increases with stimulus amplitude. In the vicinity of the characteristic frequency, the phase-locked amplitude rises quite steeply as a function of the applied force, past some threshold. Away from the natural frequency, the rise in the phase-locked amplitude with the drive becomes increasingly gradual.

FIG. 2.

Phase-locked component of the response (in nm) of a stereociliary bundle subject to sinusoidal deflection, over a range of drive frequencies (5–50 Hz in 1 Hz increments). Each stimulus frequency is presented for ten periods. The corresponding bundle motion trace is split into ten segments and then averaged. A single sine wave of fixed frequency is fit to the averaged response and its amplitude is extracted to obtain the phase-locked component. Linear interpolation was applied along the stimulus amplitude direction. Stimulus was applied at 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 60, 80, 100 and 120 nm (amplitudes refer to the base of the probe).

Figure 3 shows that as the force amplitude is increased, the nature of the mode locking process changes qualitatively. At drive frequencies below the characteristic frequency, the oscillation pattern shows variation from cycle to cycle. The top trace displays the bundle’s oscillation entrained near the low-frequency boundary of the mode-locking interval, from 5–8 Hz. In the frequency intervals on the left, extra spike-like excursions can be seen, an example of which is indicated by an arrow, that does not amount to a phase slip. In this region, a complex and incommensurate secondary spike pattern develops, superimposed on a carrier wave that follows the drive. As one approaches the characteristic frequency, this secondary pattern is diminished (full traces are shown in Supplementary Material). The bottom trace shows the mode-locking of spontaneous oscillations to the stimulus. The anharmonic oscillation pattern is repeated rather precisely from cycle to cycle.

FIG. 3.

Mode-locking at a drive amplitude of 120 nm. The drive frequency of the top trace is near the low-frequency boundary of the mode-locking interval (from 5 to 8 Hz). The arrow indicates a spike-like event. The bottom trace displays the progression of the mode-locking, with a reduction of the secondary pattern. The scale bar to the left indicates excursion of the hair bundle; the overlaid stimulus trace (black) has been arbitrarily scaled for visibility.

BIFURCATION DIAGRAM

The triangular shape of the 1:1 mode-locking plot in Fig. 2 is a characteristic feature observed in a variety of non-linear dynamical systems, and is known as an Arnold Tongue [22]. The simplest description of bundle motion based on dynamical systems theory is the “Normal Form Equation” (NFE) for the supercritical Andronov-Hopf bifurcation. It has been extensively used to model the dynamics of hair bundle response at the critical point, corresponding to the onset of spontaneous oscillation [12, 13]. Here, we examine whether the NFE captures the mode-locking dynamics of hair bundle oscillations by an external drive, away from the critical point.

The NFE for an Andronov-Hopf bifurcation in the presence of an external stimulus is defined as:

$$\stackrel{.}{z}=(\mu +i{\omega }_0)z-{\mid z\mid }^{2}z+{Fe}^{i\omega t}$$ (1)

where z is the generalized complex displacement variable, ω₀ the natural frequency, μ the control parameter, F the stimulus amplitude, and ω the stimulus frequency. We will briefly summarize the different mode-locking bifurcations that are encountered.

We look for solutions of the form z = r(t)e^iωt+iφ(t), with r(t) denoting the amplitude and φ(t) the phase difference between drive and displacement. Mode-locking corresponds to the case when both are time-independent. Substituting into Eq. 1 leads to two coupled first order differential equations:

$$\stackrel{.}{r}=r(\mu -r^2)+Fcos\phi$$ (2)

$$\stackrel{.}{\phi }=-(\omega -{\omega }_0)-\frac{F}{r}sin\phi .$$ (3)

At zero forcing (F = 0) and for positive μ, the solution yields harmonic oscillation with amplitude r = μ^1/2 and with a constant rate of change of the phase φ̇ = −(ω−ω₀), with oscillation frequency ω₀. For weak external drives, with stimulus amplitude F small compared to μ^3/2, retaining r ≈ μ^1/2 yields a good approximation. The remaining equation for the phase

$$\stackrel{.}{\phi }=({\omega }_0-\omega )-(F/{\mu }^{1/2})sin\phi$$ (4)

is familiar both from the driven pendulum and the theory of Josephson Junctions [20, 23]. If the dimensionless stimulus amplitude F/μ^1/2 exceeds the detuning parameter |ω − ω₀|, then the phase equation admits a static solution:

$$sin\phi =({\omega }_0-\omega )/(F/{\mu }^{1/2})$$ (5)

which corresponds to mode-locking. If F/μ^1/2 is less than |ω − ω₀|, there is no static solution. The phase angle remains most of the time near π/2, but periodically, the phase sweeps rapidly over 2π. The time-averaged rate of change of the phase

$$<\stackrel{.}{\phi }>={[{({\omega }_0-\omega )}^2-(F^2/\mu )]}^{1/2}$$ (6)

can be viewed as the production rate of 2π phase-slips. The phase-slip production rate goes to zero when the detuning parameter |ω − ω₀| equals F/μ^1/2 at the onset of mode-locking. This form of mode locking is known either as an “infinite-period bifurcation”, since the period of precession diverges at the critical point, or as a Saddle-Node on an Invariant Circle (“SNIC”) bifurcation, because two fixed points, a saddle and a node, coalesce and annihilate on a limit-cycle [20].

To analyze mode-locking at higher levels of the stimulus amplitude, one must locate all the fixed points of the system. Define

$$g(r,\phi )=r(\mu -r^2)+Fcos\phi$$ (7)

and

$$h(r,\phi )=-(\omega -{\omega }_0)-\frac{F}{r}sin\phi .$$ (8)

Fixed points are determined by the conditions g(r^*, φ^*) = h(r^*, φ^*) = 0. These two conditions combine to yield a cubic equation for r^*2 that has either three real roots, with at least one of them a saddle point, or one real root and two complex conjugate roots. Mode-locking corresponds to a stable fixed point, hence the real root of the equation. The stability of the fixed points is determined by the Jacobian matrix:

$$A={\left(\begin{array}{cc}\frac{\partial g}{\partial r}& \frac{\partial g}{\partial \phi }\\ \frac{\partial h}{\partial r}& \frac{\partial h}{\partial \phi }\end{array}\right)}_{(r^{\ast },{\phi }^{\ast })}$$ (9)

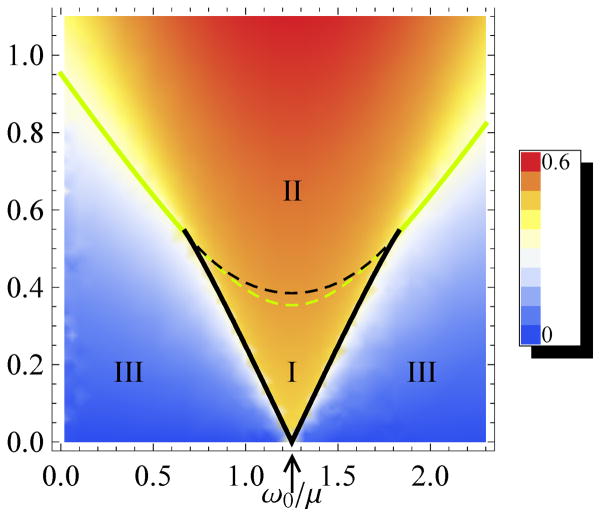
The nature of the bifurcation depends on the eigenvalues of this matrix. For a mode-locking transition occurring via a SNIC bifurcation, Det[A] must change sign at the critical point. If, on the other hand, the transition occurs via a supercritical Andronov-Hopf bifurcation, then Tr[A] must change sign at the critical point, while Det[A] remains positive. It should be noted that these are necessary but not sufficient conditions for SNIC and Andronov-Hopf bifurcations; we follow conventions established for the forced Kuramoto model [24]. Figure 4 shows the locus of the SNIC bifurcations in the (F-ω) plane as a black border and that of the Andronov-Hopf bifurcations as a yellow border, both computed in the above manner. The computed amplitude of the phase-locked component, in response to sinusoidal forcing, is displayed in a color-coded manner.

FIG. 4.

Phase-locked amplitude as computed from Eq. 1, using scaled variables F/μ^3/2 and ω/μ. The black lines indicate Saddle Node on an Invariant Circle (“SNIC”) bifurcations and the yellow lines Andronov-Hopf bifurcations. They meet at a Bogdanov-Takens (BT) bifurcation. The intersection of the phase-locked region with the horizontal axis at the tip of the triangle is ω₀/μ. Tr[A]=0 along the yellow dashed line, and Det[A]=0 along the black dashed line. These additional bifurcations are not detected experimentally as the system remains mode-locked in both regions I an II.

The enclosed region marked I contains three fixed points: a stable node and a saddle point occurring on an invariant circle, as well as an unstable fixed point. The stable node corresponds to mode-locking. The stable node merges with the saddle point along the SNIC border. The region marked II contains only a single real fixed point, a stable node. Region III encloses an unstable fixed point at the center of a limit cycle.

Figure 4 is a simplified bifurcation diagram of the driven Normal Form Equation. The full bifurcation diagram is more complex. It contains additional bifurcations, such as the co-dimension 2 Bogdanov-Takens bifurcation that separates the SNIC and supercritical Hopf bifurcations and a line of so-called “crisis” bifurcations.

NUMERICAL FITS

We now compare the results of this analysis to the experimentally measured phase-locked response. The dimensionless theoretical mode-locked amplitude was scaled to match the data, and the characteristic frequency was chosen to correspond to that of the hair cell in Fig. 2. The Bogdanov-Takens points were selected to match the points of inflection seen in the experimental plot (F = 40 nm, f = 12 Hz, and f₀ = 21 Hz). Apart from this scaling, the only fitting parameter used was the control parameter μ. The specific choice of the Bogdanov-Takens point is rendered somewhat ambiguous by the noise inherent in a biological system. We tested the sensitivity of the fits to the specific choice of the Bogdanov-Takens point, as the noise inherent in a biological system broadens the inflection region. The quality of the fits was not substantively affected by small variation in the location of this multi-critical point (see Supplementary material)

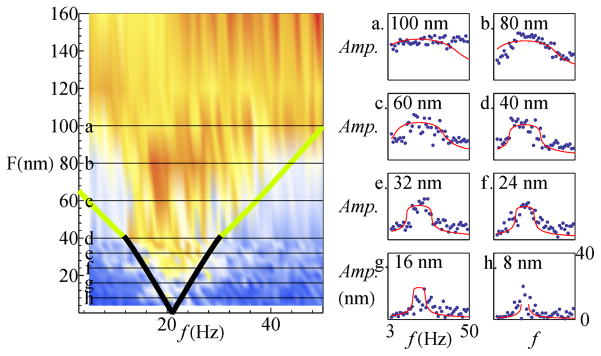
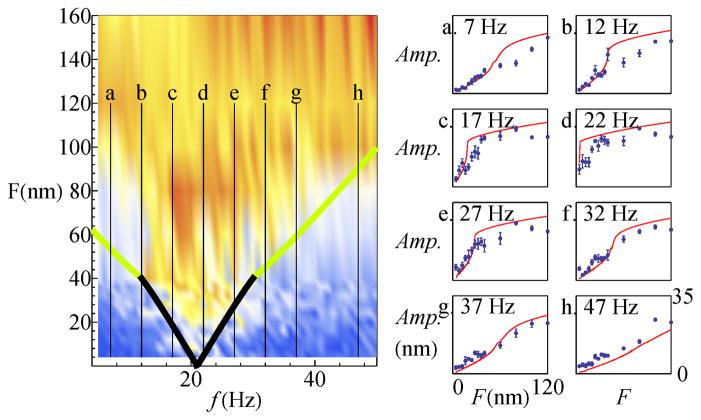
In Fig. 5, we compare the measured (blue dots) and computed (red lines) responses at selected slices in the horizontal direction, corresponding to frequency sweeps at specific stimulus amplitudes. The best choice for the ratio of ω₀ and μ was found to be 1.3, which produced the optimal fit over the whole phase space. This method thus provides us with a route to estimate the control parameter μ for hair cells. At low stimulus levels (bottom panel), the phase-locked amplitude has a well-defined maximum around the natural frequency. This resembles a resonant response, but it should be recalled that the plot displays only the component mode-locked to the stimulus frequency. The degree of broadening of the frequency selectivity under increasing amplitude of stimulation is well reproduced by the simulation.

FIG. 5.

Data and numerical fits to slices through the Arnold Tongue, taken along the horizontal axis. The data are indicated with blue dots, and the red lines show the numerical fits. The Bogdanov-Takens boundary point was selected to correspond to the point of inflection seen in the experimental plot, and the characteristic frequency ω₀ to match the peak in the response (F_bt = 40 nm and f_bt = 12 Hz, with characteristic frequency f₀ = 21 Hz). The scaling factor μ for the overall response was varied to optimize the fits; no additional free parameters were introduced. (F_scale = 24.09 = F_bt/(0.53 μ^3/2), f_scale = 7.52 = (f₀ − f_bt)/(0.56 μ), μ = 2.14 ω₀/μ = f₀/f_scale/μ = 1.3) Note: We fixed the intersection between the two curves, trace = 0 and det = 0, to be at the above points. This falls in the close vicinity rather than exactly at the Bogdanov-Takens point [24]. As these are indistinguishable experimentally, we refer to this as the BT point for conciseness.

Figure 6 compares the experimental and theoretical phase-locked response along vertical slices, corresponding to stimuli of increasing amplitudes at fixed selected frequencies. The ratio of ω₀ and μ was kept the same as in Fig. 5. The slope of the curves shown in the panels can be viewed as a measure of the susceptibility of the system to mechanical perturbation. Slices that correspond to transitions through the supercritical Andronov-Hopf bifurcation (a, g, and h in the Figure) show a more gradual increase in the mode-locked amplitude than those that transition through a SNIC bifurcation (c, d, e), which exhibit a sudden onset of phase-locking. The traces b and f pass through the vicinity of the Bogdanov-Takens point, and hence show intermediate characteristics.

FIG. 6.

Data and numerical fits to slices through the Arnold Tongue, taken along the vertical axis. The data were binned into 5 Hz intervals, with blue dots (indicating the average of five neighboring frequencies), and the error bars showing the standard deviation of the phase-locked amplitude. The red lines show the numerical fits. (Scaling an fitting parameters are the same as for figure 5.)

We note that some features apparent in the data are not fully reproduced by the model: the computed curve overestimates the phase-locked amplitude at low frequencies and the sharpness of the onset of mode-locking. Further, the exact oscillation profiles are not reproduced by the numerical simulation. Inside a phase-slip, the computational model predicts a decrease in amplitude, that is not seen in the data. Near the supercritical Hopf bifurcation, the measured secondary pattern is considerably more spiky than the theoretical prediction.

DISCUSSION AND CONCLUSION

The NFE captures the main features of the mode-locking dynamics of hair bundles poised in the spontaneously oscillatory regime. With only one fitting parameter, the numerical model yields remarkable agreement with the measured data, across frequencies and amplitudes that span the physiological range of amphibian saccular hair cells.

We explored the question of how hair bundles that exhibit large-amplitude spontaneous oscillations detect weak external signals. The innate oscillations mode-lock, in a frequency-selective manner, to periodic external deflection in the pN range. A general conclusion of this study is that mode-locking to a low-amplitude external drive proceeds via a SNIC bifurcation. As the spontaneous oscillations phase-lock to the applied signal, phase-slip events are observed that are reminiscent of similar events in condensed-matter systems, such as Josephson Junctions. At the center of a phase-slip event, the applied signal and the bundle response are out of phase by π. The out-of-phase condition could lead to an increase or decrease in the tension of the tip link that connects the stereocilia and thus rapidly modulate the opening probability of the mechano-sensitive ion channels.

We note that the NFE is a simplified model equation. More complex biological phenomena, including myosin-mediated adaptation and other calcium-dependent mechanisms, are not described by this formalism. However, it does capture the generic features associated with mode-locking, including the experimentally observed Arnold Tongue. Other model equations that describe mode-locking, such as the driven van der Pol oscillator, the Chirikov Map, the Circle Map, and the forced Kuramoto model, all have similar mode-locking bifurcation diagrams [22].

The parameter μ determines the location of the bundle in the Arnold Tongue phase diagram, and hence controls the dynamics of its mode locking to external signals. A biological hair cell could have a feedback mechanism whereby it modulates this internal parameter and thus self-tunes to the vicinities of different bifurcations. As the various transitions in the phase-locking diagram display different characteristics, the hair bundle could thus adjust its susceptibility, frequency selectivity, and/or mode-locking dynamics.

In summary, we explored both experimentally and theoretically the dynamics of mode-locking exhibited by hair bundles subjected to a periodic stimulus. The mode-locked region in the (F-ω) plane is well described by the driven Normal Form Equation, yielding the Arnold Tongue bifurcation diagram that captures the main features of the dynamic response. We found that hair-bundles performing large-amplitude spontaneous oscillations are capable of rapidly mode-locking to external signals, with signatures of different bifurcations apparent at increasing amplitudes.