A rapid method for the differentiation of yeast cells grown under carbon and nitrogen-limited conditions by means of partial least squares discriminant analysis employing infrared micro-spectroscopic data of entire yeast cells

Abstract

This paper shows the ease of application and usefulness of mid-IR measurements for the investigation of orthogonal cell states on the example of the analysis of Pichia pastoris cells. A rapid method for the discrimination of entire yeast cells grown under carbon and nitrogen-limited conditions based on the direct acquisition of mid-IR spectra and partial least squares discriminant analysis (PLS-DA) is described. The obtained PLS-DA model was extensively validated employing two different validation strategies: (i) statistical validation employing a method based on permutation testing and (ii) external validation splitting the available data into two independent sub-sets. The Variable Importance in Projection scores of the PLS-DA model provided deeper insight into the differences between the two investigated states. Hence, we demonstrate the feasibility of a method which uses IR spectra from intact cells that may be employed in a second step as an in-line tool in process development and process control along Quality by Design principles.

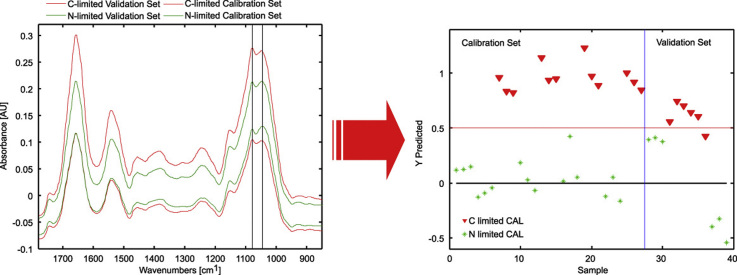
Graphical abstract

Using mid IR transmission spectra and Partial Least Squares Discriminant analysis, yeast cells (Pichia pastoris) grown under C-limited and N-limited conditions could be distinguished.

Highlights

► Direct spectra acquisition of entire yeast cells employing an FTIR microscope. ► PLS-DA for differentiating cells grown under carbon and nitrogen-limited conditions. ► Model validation based on permutation testing and an external validation set. ► Variable Importance in Projection (VIP) scores for detecting relevant variables. ► Feasibility study for the development of an IR-based in-line process control tool.

1. Introduction

In the last decades, infrared (IR) spectroscopy has demonstrated to be a useful tool for the analysis of microbiological samples [1,2] as well as for biomedical diagnostics [3]. A vast amount of molecules present in prokaryotic and eukaryotic cells show typical spectral features in the mid-IR range. Concerning yeast, FTIR spectroscopy has been used for the analysis of genetically modified yeast strains [4], for the identification of different strains by comparison of the FTIR spectra to library data [5] and for the monitoring or investigation of yeast metabolism [6–10]. Furthermore, FTIR spectroscopy was used for the monitoring of a baker´s yeast fermentation process [11].

Due to the complexity of biological samples, spectra suffer from a high grade of band-overlapping, especially in the fingerprint region, that complicates an exact band assignment and consequently the signal interpretation. To enhance exploitation of those information rich spectroscopic data, in many cases multivariate chemometric tools like for example principal component analysis (PCA), cluster analysis (CA) and partial least squares (PLS) regressions were used [1,3,12]. This leads to a broad field of applications including the characterization of particular cell compounds, the differentiation, classification and identification of species and strains [1] as well as the detection of biomedical relevant constituents such as DNA, RNA, proteins, carbohydrates and lipids or even diseases [3]. As mentioned before, chemometric tools are frequently used as an aid in interpreting the complexity of the IR spectra of biological samples. Partial least squares-discriminant analysis (PLS-DA) is a supervised classification method based on the use of a vector containing the class label for predicting the class membership of objects [13]. In comparison to PCA, which is frequently used as unsupervised classification method, PLS-DA is still effective when the within group variation is greater than the between group variation [14]. In the field of IR spectroscopy applied to biological samples, PLS-DA has been used for the differentiation of bacterial strains [15,16].

Several issues are of utmost importance when developing and operating biotechnological fermentation processes. In the early quantitative screening, strain performance needs to be differentiated. Further on, limitations in nutrients are the main intended design element in quantitative bioprocess development in order to target a certain product for industrial biotechnology or biopharmaceutical use. Hence, the media has to be designed to suit the metabolic needs also in high density fermentations [17,18]. Finally the developed process needs to be controlled by using easy and rapid analytical methods. All elements fit into the initiative of Quality by Design (QbD), a system approach to design a quality product based on scientific process understanding [19]. One suitable approach is to rapidly identify different physiological states, such as how cells react to different fermentation conditions to control the accumulation of the desired product or to achieve optimum growth rates. Already in 1972 Künzi and Fiechter investigated the carbohydrate composition of Saccharomyces cerevisiae under growth limitation [20]. Under glucose limitation the synthesis of the storage carbohydrates glycogen and trehalose increases when there is a surplus of nitrogen and all other compounds in the medium. In the same way, cells accumulate glycogen and trehalose in presence of exogenous carbon and energy source when there is a lack of nitrogen in the medium. The authors found out that under carbon-limitation almost the same amount of storage carbohydrates is achieved as under nitrogen-limiting conditions, whereas in the presence of an excess of all substrates, the accumulation of reserve carbohydrates is low. In any case the content of structural carbohydrates mannan and glucan shows little change. FTIR spectroscopy was already used for the investigation of nutrient stress on cyanobacteria and bacillariophyceae [21] as well as on rhizobacterium [22] by analyzing changes in IR spectral bands representing typical components of biological samples in relation with the growth conditions.

For the identification of physiological states, such as C-limitation, N-limitation or C and N excess, mainly off-line methods were employed which quantified primary metabolites using primarily liquid chromatography, enzymatic or immunological test methods [23]. In certain situations also on-line gas chromatography [24] as well as in-line fiber optic [25] sensors were used to quantify target analytes present in the fermentation broth. Up to now, also the response of yeast cells to stress has been deduced from the measurement of a set of metabolites [26], which, while feasible, is inappropriate for the rapid detection of the physiological state of cells. A different route for assessing physiological states of cells and hence for stress detection would be direct analysis of the biomass of cells. Using conventional analysis techniques, this is usually a time consuming process, as reproducible cell disruption is required prior to the analysis and so, it is not convenient for an effective control of a production process.

The long term objective of our research efforts is the development of an easy IR based technique for the rapid identification of physiological states in entire yeast (Pichia pastoris) cells, to monitor the growth conditions of fermentation processes in-line in order to achieve efficient production conditions avoiding stress. In the work reported here, we aim to demonstrate the feasibility for a rapid identification of two well defined orthogonal physiological states using mid-IR spectra of whole cells, hence no cell disruption is required. Simply, yeast was sampled, washed with distilled water and dried on an IR transparent carrier prior to the measurement by mid-IR transmission spectroscopy. A multivariate PLS-DA model was developed to differentiate cells obtained under carbon-limited and nitrogen-limited growth conditions. Special emphasis was put on the validation of the PLS-DA model to assure the accuracy of the obtained results, although only a limited number of samples was available. The presented results are a first step toward the development of an IR based non invasive in-line sensor for process analytical applications along QbD principles [27]. In turn, as a demonstration of feasibility, it is not the aim of the contribution to physiologically interpret or compare the results from the different samples.

2. Experimental

2.1. Fermentation process and sample preparation

In this study, yeast cells (Pichia Pastoris X-33, wild type strain) withdrawn from a fermentation process were investigated. Cells were grown at 30 °C during 24 h in a 100 mL Erlenmeyer flask containing 20 mL of complex YPG (yeast extract, peptone and glycerol) medium on a shaker at 250 rpm. The medium contained 20 g L⁻¹ glycerol (Fluka, Buchs, Switzerland), 6 g L⁻¹ yeast extract (Merck, Darmstadt, Germany) and 5 g L⁻¹ Bacto Peptone (DIFCO, Lawrence, USA) and was autoclaved during 20 min at 120 °C. Subsequently, 50 mL of this preculture were inoculated in an autoclavable 1 L Applikon fermenter containing 1 L of medium prepared according to the Egli recipe [28] with minor modifications. All components are listed in Table 1. During the fermentation, pH was maintained constant at 5.0 by the addition of 1 M KOH and the reactor was thermo-stated at 28 °C. To homogenize the culture broth, it was agitated at a constant agitation speed of 1200 rpm and the aeration was kept constant at 1.25 L min⁻¹ using a Mass Flow Controller (AALBORG, Orangeburg, USA). The dissolved oxygen level (dO₂) was monitored with a dO₂ probe (Hamilton, Bonaduz, Switzerland) and was maintained always higher than 30% in order to avoid oxygen limitation in the liquid phase. The fermenter was run in batch mode. The media was designed in such a way, that the batch culture during its exponential growth phase ran into a nitrogen limitation, before the carbon source was depleted. Hence, during the latter phase 4 N-limited samples were withdrawn. Subsequently the culture was switched to continuous mode performed at a constant dilution rate of 0.15 h⁻¹. This chemostat culture was set up with two identical feeds according to Table 1, except that one feed did not contain any nitrogen. The ratio between the two feeds was adjusted in such a way that the culture could be driven on purpose into carbon as well as nitrogen limitation. During this culture, 6 carbon-limited (C-limited) and 3 nitrogen-limited (N-limited) samples from different steady states were obtained.

Table 1.

List of the medium components, suppliers and concentrations.

Component (supplier)	Concentration
Glycerol (Fluka)	30 g L−1
NH4Cl (Merck)	10 g L−1
KH2PO4 (Merck)	5.62 g L−1
MgSO4 ·7H2O (Merck)	1.18 g L−1
EDTA ·2H2O (Merck)	900 mg L−1
CaCl2 ·2H2O (Merck)	110 mg L−1
FeCl3 ·6H2O (Fluka)	75 mg L−1
MnSO4 ·2H2O (Fluka)	28 mg L−1
ZnSO4 ·7H2O (Fluka)	44 mg L−1
CuSO4 ·5H2O (Loba)	8 mg L−1
CoCl2 ·6H2O (Riedel de Haen)	8 mg L−1
Na2MoO4 ·H2O (Merck)	5.2 mg L−1
H3BO3 (Merck)	8 mg L−1
KI (Loba)	1.2 mg L−1
Biotin (Sigma)	3.48 mg L−1
Antifoam Struktol J650	800 μl L−1

Samples of a volume of 2 mL were taken in different time steps as described. Prior to the IR measurements, yeast cells were washed three times with 500 μL of de-ionized water centrifuging for 5 min at 7500 rpm. After the washing step, the cell suspension was conveniently diluted with de-ionized water to subsequently achieve appropriate sample thicknesses for IR measurements. As no quantification was carried out, the sample thickness is not critical in this procedure.

2.2. FTIR measurements

Absorbance spectra of the yeast cells were obtained using the 20x microscope objective fitted to a Hyperion 3000 interfaced with a Tensor 37 FTIR spectrometer, from Bruker Optics (Ettlingen, Germany), in transmission mode. For spectra acquisition, the microscope was operated in single point mode using a liquid N₂ cooled mercury cadmium telluride detector. Spectra were recorded between 4000 and 600 cm⁻¹ by co-adding 32 scans with an optical resolution of 4 cm⁻¹ and a zero filling factor of 2 operating the scanner of the interferometer at a HeNe laser modulation frequency of 20 kHz. OPUS software (version 6.5) was used for instrument control and data acquisition.

From each sample, three spots of 2 μL of cell suspension were pipetted onto a ZnSe window (53×38 mm) and placed in the dry air purged sample compartment of the microscope. The measurement was started when the water content in the spectra had reached a constant level. Spectra were collected at multiple positions from each sample spot. A background spectrum was recorded at a clean spot of the ZnSe window. Spectra of each spot were averaged in order to obtain one mean spectrum per sample spot. In total, 18 C-limited and 21 N-limited sample spots, corresponding to 6 C-limited and 7 N-limited samples, were analyzed.

2.3. Data analysis

Data analysis was carried out using Matlab 7.7.0 (Mathworks Inc., Natick, MA, USA). PCA and PLS-DA model calculations, cross validation and predictions were performed using Matlab functions included in PLS Toolbox 6.2.1 (Eigenvector Research Inc., Wenatchee, WA, USA) as well as in-house written functions.

For the calculation of PCA and PLS-DA models, the wavenumber region between 1778 and 847 cm⁻¹ was used, corresponding to 484 variables employing an optical resolution of 4 cm⁻¹ and a zero-filling factor of 2. The data set was split into two sub-sets, a calibration data set consisting of 9 samples (4 C-limited and 5 N-limited samples) and an external validation set containing 4 samples (2 C-limited and 2 N-limited samples) with three replicates each, resulting in a total of 27 and 12 spectra, respectively. Initially the calculation of second derivative row vectors resulting from a 9 point cubic Savitzky–Golay function was performed as pre-processing step for the calculation of PCA and PLS-DA models followed by normalization to the sum of the absolute value of all variables in the considered region for a given sample (i.e., spectrum), returning a vector with unit area (area=1) under the curve. This normalization step is necessary to compensate differences in the absorbance intensity due to variations in sample thickness. Normalization was followed by mean centering.

For the assessment of the predictive capabilities of the calibration model, two types of model validation were carried out: (i) double cross validation (2CV) and (ii) external validation. 2CV of the PLS-DA model was carried out using the calibration data set. Permutation testing was used to evaluate the statistical significance of selected predictive quality parameters. In the outer loop of the 2CV approach, the 9 samples included in the dataset were split into a ‘calibration’ subset and a ‘test’ sample. The split was done on biological sample basis, i.e., all three replicates of each biological sample were included either in the calibration or in the test set. In the inner loop of the 2CV for each ‘calibration’ subset a leave-one sample-out CV was used to obtain the optimal number of PLS latent variables (LVs) corresponding to the maximum predicted squared correlation coefficient (Q²) value with a maximum number of LV=5. Again, all three replicates of each biological sample were included or removed from the data subset. A PLS model using the ‘calibration’ set and the determined number of LVs was calculated and applied for class prediction of the ‘test’ sample. The whole procedure was repeated until all samples had been included once in the ‘test’ set. The statistical significance of the obtained class separations was assessed comparing quality parameters (number of misclassifications, the Q² and area under the receiver operating characteristic curve (AUROC) values) calculated using real class assignments to the distributions of the quality parameters obtained from re-estimations after class randomization repeated 5000 times. The Q² statistic is defined as one minus the ratio of the prediction error sum of squares over the total sum of squares of the response vector. It is used as a measure for class prediction ability frequently employed to validate discrimination models [29] and shows ideally a value close to 1. The AUROC is 1 for perfect class separations and close to 0.5 if there is no separation [29,30].

Furthermore, an external validation dataset was used for testing the performance of PLS-DA models. Cross validation was carried out on biological sample basis employing contiguous sub-sets with 8 data splits. The optimum number of latent variables to be included in the PLS-DA model was chosen based on the misclassification rate of the calibration dataset. For a straightforward interpretation of the PLS-DA model, Variable Importance in Projection (VIP) scores were used. Their calculation is based on estimating the importance of each variable in the projection used in a PLS model: a variable with a VIP score higher than one can be considered important in a given model. The advantage of the use of VIP scores over the use of the regression vector is that spectral regions with a high contribution to the model are easily identified even though derivatives were calculated in the pre-processing step.

For PCA model calculation the calibration set was used consisting of 9 samples. Again, cross validation was carried out employing contiguous sub-sets with 8 data splits. The Hotelling T² statistic and the Q residuals are frequently used to detect outliers in data sets. The Hotelling T² statistic is the sum of normalized squared scores and is therefore a measure of the variation in each sample within the PCA model, or, in other words, it is a measure of the distance from the multivariate mean to the projection of the sample onto the k principal components. The Q residual is the sum of squares of each sample in the error matrix and therefore it is a measure of the difference, or residual, between a sample and its projection into the k principal components used to build up the model. It indicates how well each sample conforms to the PCA model [31]. The optimum values of the Hotelling T² value and the Q residuals are 100 and 0%, respectively.

3. Results and discussion

3.1. Mid-IR spectra of entire yeast cells

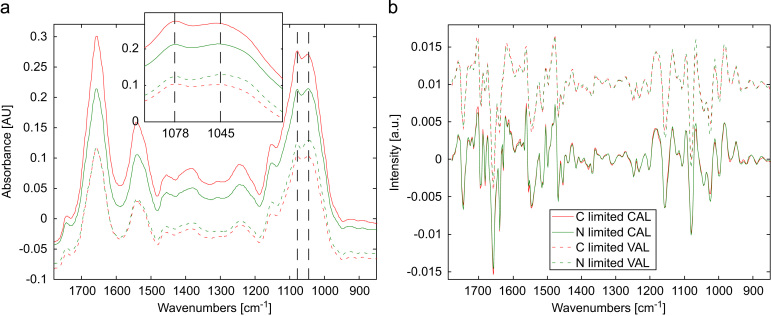
Fig. 1a shows mean mid-IR absorbance spectra of C-limited and N-limited samples of the calibration and validation set in the region between 1800 and 850 cm⁻¹. Fig. 1b shows 2nd derivative spectra from the spectra depicted in Fig. 1a after normalization.

Fig. 1.

Mean spectra of different data sets (raw data) and close-up view of the region between 1000 and 1100 cm⁻¹ (a) and mean spectra of different data sets after derivative (2nd derivative, points: 9, polynomial order: 3) and normalization (b). Note: CAL stands for calibration set and VAL stands for validation set (for details about the normalization see Experimental section).

Basically, in the depicted region the main spectral contributions are derived from proteins, showing the very intense and broad Amide I band around 1660 cm⁻¹ and the Amide II band around 1540 cm⁻¹. The region between 1250 and 950 cm⁻¹ is dominated by the intense absorption of carbohydrates with a minor contribution of phosphate bands from DNA, RNA and phospholipids. Additionally, proteins, lipids and storage carbohydrates show strongly overlapping, but less intense bands in the region from 1500 to 1250 cm⁻¹. For a detailed description of the observed bands the reader is referred to Table 2 [4,7,32].

Table 2.

Positions an assignment of the main absorption bands observed in the region between 1800 and 850 cm⁻¹.

IR band position [cm−1]		Assignments
N limited	C limited
1743	1743	C=O stretching vibrations in lipid esters [7]
1657	1657	Amide I: mainly C=O stretching vibrations and contributions of N–H bending vibrations [4]
1539	1541	Amide II: mainly C–N stretching vibrations and N–H bending vibrations [4]
1454	1454	Various CH2/CH3 bending vibrations in lipids and proteins [7]
1379	1383	C=O of COO− symmetric stretching vibrations in proteins, CH2 wagging vibrations in lipids and β(1–3) glucans [7]
1308	1306	Amide III: C–N and C–O stretching vibrations, N–H and O=C–N bending vibrations [7]
1246	1246	PO2− asymmetric stretching vibrations in DNA, RNA and phospholipids [7]
1151	1151	β(1–3) glucans [4], C–O, C–OH carbohydrates, various contributions [7]
1078	1078	β(1–3) glucans [4], nucleic acids and glycogen [33], PO2− symmetric stretching vibrations mainly from RNA [7]
1045	1047	Glycogen and mannans [33]

Note: Refs. [4,7]: ATR-FTIR spectra obtained from the measurement of Saccharomyces cerevisiae; Ref. [33]: FTIR transmission spectra of Candida albicans.

From Fig. 1a and b it can be appreciated that spectra of N-limited and C-limited samples show a very high similarity and no significant band shifts were observed. A slight change in the absorbance ratio at 1078 and 1045 cm⁻¹ between the mean spectra of both classes could be identified. It is also remarkable, that the calibration and validation sets, which were subsequently employed for external validation of the calculated PLS-DA model, show similar spectral features.

3.2. Data exploration using PCA

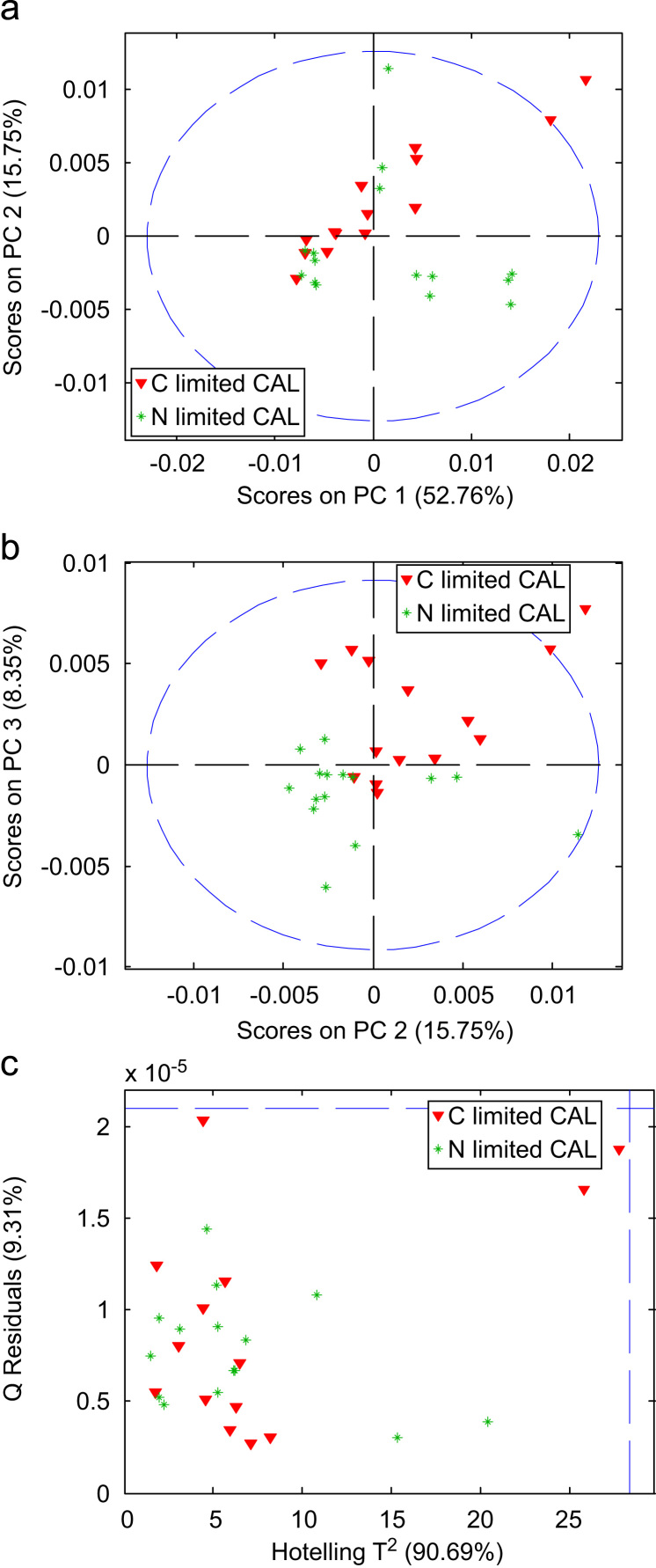
A PCA model was built from the calibration set using 6 PCs explaining together 90.69% of the variance in the data after applying the pre-processing described in the experimental section (2nd derivative, normalization, and mean centering). In Fig. 2a and b, two obtained scores plots are depicted. It can be appreciated that the PC1 vs. PC2 scores plot, although representing the main part of the data variance (52.76 and 15.75%, respectively), does not show class separation between the two groups. On the contrary, the PC2 vs. PC3 scores plot (explaining 8.35 of the variance) is useful for differentiation between cells grown under C and N-limiting conditions. However, these PCs do not contain sufficient information to achieve complete class separation. Employing even higher PCs (data not shown), explaining only a minor part of the variance in the studied data, class separation between yeast samples grown under N and C-limiting conditions could not be achieved.

Fig. 2.

Scores plots of PC1 vs. PC2 (a), scores plots of PC2 vs. PC3 (b) Hotelling T² vs. Q residuals (c) obtained from PCA.

The data obtained in this study contains complex IR spectral information with several different sources of variation (e.g., growth rate, availability of nutrients (N-limited and C-limited growth), batch mode and continuous mode etc.). Due to this, PCA, which is frequently used as unsupervised classification method, might not be powerful enough to achieve class separation, as it is not effective anymore when the within group variation is greater than the between group variation [14]. In situations like this, the use of supervised classification methods, such as PLS-DA has to be considered.

PCA is frequently used to explore data sets in order to detect outliers prior to the calculation of PLS models or the application of other chemometric techniques. From the scores plot in Fig. 2a and b, it can be observed that none of the samples falls outside the 99% confidence limit (blue dashed line). In Fig. 2c the Hotelling T² values are plotted versus the Q residuals. For the present data set, it can be observed that all the samples fall within the 99% confidence limits and no outliers were identified.

3.3. Classification employing PLS-DA

As no significant changes in band positions or shape extracted from the mean spectra of cells grown under C and N limiting conditions were observed, a classification using the information on a single band shift resulted in high classification errors (data not shown). Therefore, the use of a multivariate approach as PLS-DA was necessary.

To quantify the predictive abilities of a PLS-DA model, the Q², the AUROC and the number of misclassifications are usually employed. Whereas these parameters vary between standardized ranges there are no threshold values which can be used to define a classification between two groups as ‘good’ or ‘acceptable’ [29]. Additionally, PLS-DA is known to tend to overfit data, being able to achieve clear class separations in the score plots even from unstructured data. This aspect is of special relevance when the number of samples is limited, as sample size affects the stability of the obtained quality parameters [33]. Nevertheless, the required size depends on a series of factors such as for example the within- and between-class variance, instrument stability and sample treatment. Therefore a rigorous validation of the results is of great importance. External validation can be seen as the ‘gold standard’, provided that the validation set spans the whole calibration space [34], and 2CV is an approximation to an external validation [35,36]. It is relevant that 2CV figures of merit can be considered as external, as samples used for test the model are not used during model calculation, scaling or LV selection steps, and therefore, model over-fitting is avoided [37,38].

To assess the lack of model over-fit, the obtained PLS model has been validated following two strategies: (i) permutation testing for the assessment of 2CV results; and (ii) the use of an external validation set. Prior to the calculation of all PLS-DA models, the pre-processing described in the experimental section (2nd derivative, normalization and mean centering) was applied to the spectra.

3.3.1. Double cross validation and permutation testing

Westerhuis et al. [29] developed a strategy based on repeatedly permuting the class labels to enable efficient assessment of cross-validation results. In order to avoid overoptimistic results, this approach was applied to assess the validity of a PLS-DA classification model of C- and N-limited samples. The aforementioned PLS-DA model performance parameters obtained using real class labels were compared to a reference distribution of the same parameters corresponding to random class assignments which was built under the H₀ hypothesis that no difference exists between the two classes, as described in the experimental section. The non-parametric permutation test for the calculation of the statistical significance of the three 2CV PLS-DA figures of merit (i.e., Q², AUROC and the number of misclassifications) assess the lack of model over-fitting as shown in [35].

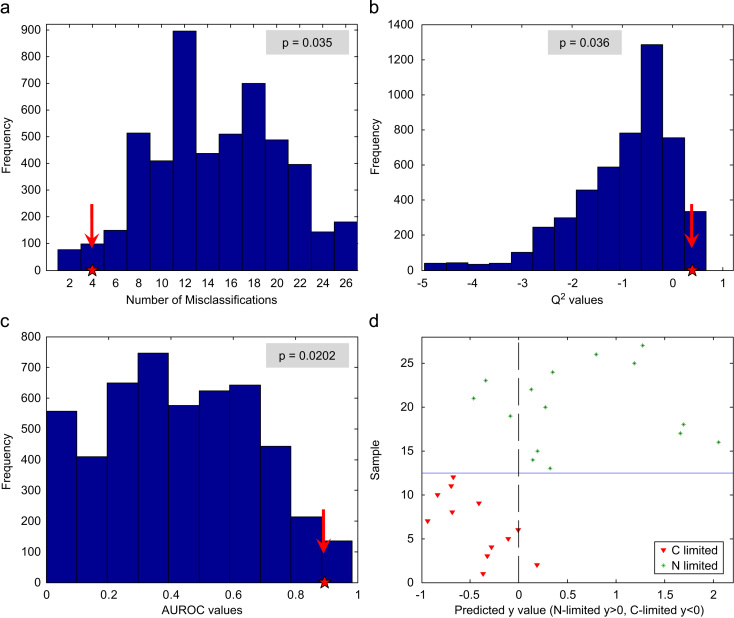
Fig. 3a shows the histograms of the obtained mean number of misclassifications (blue bars) using permutated class labels and the value obtained using the correct class assignments (red asterisk). As it can be seen, considering the number of samples included in the calibration set (n=9, with three replicates each, 27 data points), the number of misclassifications using real class labels is low (4 objects) compared to the mode of misclassifications obtained from the permutation test (15 objects). A p-value of 0.035 was obtained, indicating an acceptable separation between the distribution obtained from the permuted class labels and the number of misclassifications obtained from real class labels. Fig. 3b shows the Q² values. Whereas the Q² value obtained for real class labels is 0.396, most of the permutated data provided negative Q² values with a median of −0.664. In this case, the obtained p-value was 0.036. Finally, the AUROC value obtained for real class labels is 0.896, being close to the optimum value of 1. In addition, the median of the AUROC values obtained using random class memberships was 0.422 and a p-value of 0.0202 indicated an acceptable difference between the AUROC values obtained from real and permuted class labels (see Fig. 3c).

Fig. 3.

Results of the PLS-DA permutation test using the calibration dataset (9 samples with 3 replicates each): number of misclassifications (a), Q² values (b), AUROC values (c) and sample predictions using the real class labels (d).

Fig. 3d shows the predicted class values obtained during double cross-validation in which, as aforementioned, four data points were assigned to the wrong class. This leads to the conclusion that the PLS-DA model is adequate for the classification of N-limited and C-limited yeasts using their mid-IR spectra.

3.3.2. External validation

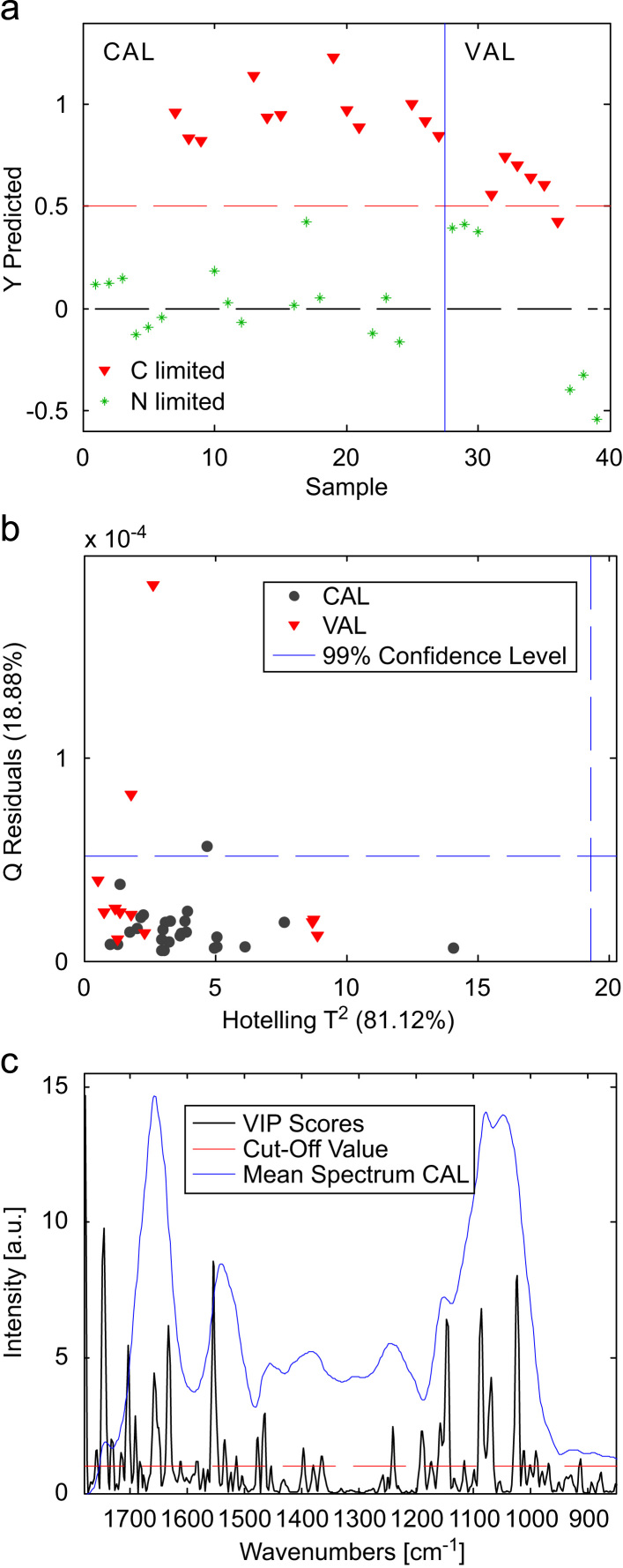
Using the calibration (n=9, 27 data points) and validation (n=4, 12 data points) sets described in the experimental section, a PLS-DA model was calculated and validated. Fig. 4a shows the class prediction obtained for all data points included in the calibration and validation sets. On the left side of the graph results obtained for the calibration set are shown whereas samples depicted on the right side pertain to the independent validation set. The model was calculated using 4 latent variables. The selection was based on the misclassification rate of the data points included in the calibration set. It can be seen that the class prediction is satisfactory not only for the calibration data, but also for data from the external validation set as C-limited and N-limited samples can be classified correctly (only one sample of the external validation set was assigned to the wrong class). Fig. 4b shows the Hotelling T² values versus the Q residuals, obtained for the PLS-DA model. It can be seen that only three objects (i.e., sample replicates) are located slightly outside the 99% confidence limit.

Fig. 4.

Score plot of the class prediction of samples included in calibration (first 27 data points) and validation set (last 12 data points (a), Q Residuals vs. Hotelling T² values for calibration (CAL) and validation data (VAL) (b) and PLS-DA VIP Scores (c); Note: mean spectrum (×50) of the calibration data set has been included in (c) for an easier interpretation; for a better visibility it has been shifted in the y direction.

The VIP scores are depicted in Fig. 4c. The magnitudes of the VIP scores can be employed to detect variables that influence mostly on the model [13]. Accordingly, the most relevant variables were observed around 1745 and 1554 cm⁻¹, corresponding to the C=O stretching vibrations in lipid esters and the amide II region, respectively. In addition, also variables around 1022, from 1086 to 1068 and around 1146 cm⁻¹ corresponding mainly to storage carbohydrates (glucans, glycogen and mannan) as well as to the PO²⁻ symmetric stretching vibrations (mainly from RNA) have a strong impact on the model. This is in good agreement with the change in absorbance ratio observed in the mean class spectra as described before. Furthermore variables located around 1632, 1703 and 1657 cm⁻¹ contribute strongly to the model, corresponding to changes in the amide I band. Several other regions also show minor contributions to the VIP scores. In summary it can be said that many different variables in different spectral regions affect the model which reinforces the use of a multivariate model for the classification of spectra of entire yeast cells between cells grown under N and C-limiting conditions.

4. Conclusions

The experiments carried out in this study demonstrate that the information contained in mid-IR spectra of entire P. pastoris cells is suitable for the differentiation between cells grown under nitrogen and carbon limiting conditions. The measurement procedure is fast as the cells only have to be rinsed with water prior to their analysis thus avoiding problems resulting from irreproducible and labor-intense cell disruption.

Due to the complexity of the investigated system which is reflected in a high amount of overlapping mid-IR bands, it is not possible to differentiate between the two groups without the use of multivariate chemometric tools. To overcome this problem and to establish an automatic process, a PLS-DA model that enables the classification of samples according to the two investigated states (C-limited and N-limited growth) has been developed. Having a closer look on the VIP scores enhances the understanding of the compositional differences between samples from both classes. In order to ensure the accuracy of the obtained results and to prevent wrong conclusions due to over-fitting, the obtained model has been deeply validated.

The results presented in this paper demonstrate the feasibility of the method as a first step towards an IR based non-invasive in-line sensor for the monitoring of the physiological state of yeast cells in fermentation processes as a central element in early quantitative screening of strains, media development and development of a control strategy along QbD principles.