Thermodynamic Cycle Without Turning Off Self-Interactions: Formal Discussion and a Numerical Example

Abstract

The efficiency and accuracy of thermodynamic cycle calculations are considered. It is rigorously shown that the energy of the mutated part (MP) need not be scaled in a thermodynamic cycle computed with dual topology. Hence, there is no need to scale to zero any of the self-interactions (i.e. the interactions involving only particles of the same MP) regardless of whether the MP is bound or not to the main system. This observation carries a promise to lower computational resources and increase accuracy. A numerical test of a complete thermodynamic cycle illustrates cost and accuracy considerations.

Introduction

Free energy calculations make it possible to directly compare simulations to experiments, a necessary step in the validation of atomically detailed models. They also guide future experiments, by (for example) suggesting candidates for drug design¹.

While the comparison between computed and measured free energy is direct, frequently the computational scheme does not “mimic” the experimental process. Indeed, experimental phenomena often occur at time scales inaccessible for direct Molecular Dynamics (MD) simulations. For example, it is costly to evaluate the dissociation constant of a ligand-enzyme complex by simulating binding and unbinding events. It is also challenging to compute the stability of the structure of a protein by letting the protein explore configurations that are accessible on long time scales. Specific reaction coordinates² or a set of sparsely sampled conformations (anchors)^3,4 can be used to compute the thermodynamics of large scale conformational transitions, however, they are typically very expensive and not always possible to converge.

A more efficient method to compute such free energy differences makes use of alchemical changes⁵. In alchemical changes a molecule, or a small part of it, is mutated into another by modifying its external and self-interactions. We denote the mutated part by MP. By external interactions we mean interactions between the MP and its environment, while self-interactions are within the MP. Such a mutation is usually performed according to two protocols⁶: a single topology protocol, in which the geometry of the native molecule/moiety is progressively changed into the geometry of the mutant, and a dual topology, in which the two molecules/moieties coexist. Along the substitution pathway the interactions of the native part are gradually annihilated while those of the mutant are growing to their full strength. To connect the initial and final state, we often use multiple alchemical processes, presented on a Thermodynamic Cycle (TC)⁷ (see Fig. 1). The experimental free energy difference is then obtained as a sum of the free energies of the computed alchemical steps. The sum can be used to compute “absolute”^8,9 or relative^10–15 free energy differences.

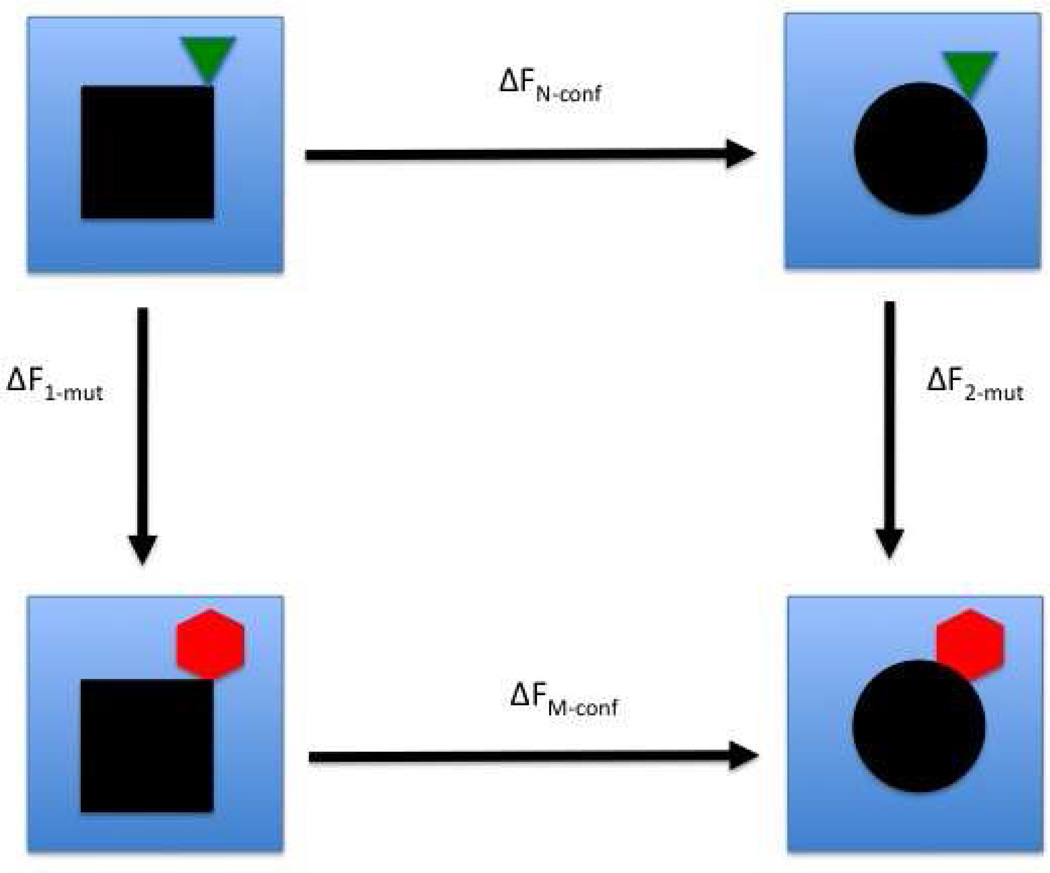
Fig. 1.

An example of a thermodynamic cycle for a conformational transition in a protein and a protein mutant. The black shapes represent the protein in two conformations (the square and the circle). The green triangle and the red hexagon represent native and mutant residues, respectively. The blue background represents solution. The horizontal arrows indicate conformational transitions. The vertical arrows indicate mutations. This cycle compares experimentally measured free energy differences (those that are related to the conformation transitions ΔF_N-conf and ΔF_M-conf) to computed free energy differences (the mutations, ΔF_1-mut − ΔF_2-mut).

In the present paper we examine the possibility of retaining the interaction of a MP throughout a mutation performed according to the dual topology protocol. Keeping the self-interactions is equivalent to a change in the end-state of the alchemical process from atomic to molecular ideal gas^16,17. It was suggested that retaining the bonded self-interactions does not affect relative free energy differences^16,17 and a proof of this assertion followed¹⁸. In¹⁹ a more general proof was reported, in which no distinction was made between bonded and non-bonded interactions. However the proof given is less direct than the simple argument provided here.

We propose a dual topology alchemical pathway in which the self-interactions of the MP, bonded and non-bonded, are retained. We then prove that, in the context of a TC, the relative free energy difference computed according to this pathway is exact.

We also discuss the retention of some of the interactions between the decoupled fragment and the larger scaffold. The annihilation/creation of the external non-bonded interactions is required to compute the proper free energy difference. However, it is not necessary to annihilate/create all the external bonded interactions connecting a fragment to a scaffold. It is possible to fix its six external degrees of freedom retaining six bonded interactions with the scaffold without affecting the internal degrees of freedom of the scaffold or of the fragment. All the other external bonded interactions are annihilated/created in the MD simulation. This concept was introduced as the Virtual Bond Algorithm (VBA)²⁰, which was proposed in the context of protein-ligand binding, and is exact. Six bonded interactions between the protein and the ligand are added to restrain the overall motions of the ligand. The same VBA interactions may be retained in the process of substituting a fragment bonded to a scaffold. The idea of retaining external bonded interactions was examined also in^18,19. However, VBA makes it clearer which interactions can be safely retained in an alchemical substitution, and how to account for their contribution to the free energy.

The proof that we hereby propose and the use of VBA in the context of the alchemical substitution of a molecular fragment lead to an algorithm in which the number of interactions created/annihilated along a TC is reduced to the minimum. This is likely to benefit computations. Indeed, retaining the bonded self-interactions has improved convergence of the results since the overlap of distributions along the reaction coordinate increases, making the standard deviations smaller. It is likely that also retaining the non-bonded self-interactions will improve the convergence further.

This manuscript is organized as follows. We review the thermodynamic cycle and prove that the relative free energy difference computed along a thermodynamic path of our own design is in agreement with the formula for experimental free energy difference. We then review VBA and illustrate that in the context of a TC the restraining of the external degrees of freedom of the mutated part gives no contribution to the relative free energy difference. Finally, a numerical illustration of the theory is described in which the free energy of solvation of two amino acid side chain analogs is computed. In the numerical illustration, and in Supplementary Information, we discuss technical issues presented by the annihilation/creation of bonded terms in the force field and by the selective annihilation/creation of a subset of the non-bonded, long-range interactions.

Free energy differences

We consider the free energy difference between a physical system “P,N”, which consists of “Protein” and “Native” parts, and a system “P,M”, that consists of “Protein” and “Mutant” parts. “P” refers to all atoms that are not alchemically substituted. “N” and “M” are the two sets of atoms that are mutated to each other.

The two Hamiltonians are:

$$\begin{array}{c}{H}_N=K(P,N)+U(P)+U(P,N)+U(N)\hfill \\ H_M=K(P,M)+U(P)+U(P,M)+U(M)\hfill \end{array}$$ (1)

Here K is the kinetic energy and U the potential. The term U(X) includes interactions within “X” (self-interactions) and U(X,Y) only interactions between “X” and “Y” (external interactions). The phase space volume element is dΓ (e.g. dΓ_P,N = dΠ_PdQ_PdΠ_NdQ_N were Π_X denotes momentum and Q_X coordinate vectors of atoms of species “X”). The volume element of coordinate space is dΓ’ (e.g. dΓ'_P,N = dQ_PdQ_N). Finally, we denote the number of “X” particles as N_X, where “X” can be any combination of “P”, “M” and “N”. The desired free energy difference, ΔF_M,N is given by

$$\begin{array}{c}\mathrm{\Delta }{F}_{M,N}=F_{P,M}-F_{P,N}=\hfill \\ =-{\beta }^{-1}\text{ln}\left(\frac{\frac{1}{C_{\mathit{\text{PM}}}{h}^{3N_{\mathit{\text{PM}}}}}}{\frac{1}{C_{\mathit{\text{PN}}}{h}^{3N_{\mathit{\text{PN}}}}}}\frac{{\displaystyle \int }d{\mathrm{\Gamma }}_{P,M}\text{exp}\{-\beta [K(P,M)+U(P)+U(P,M)+U(M)]\}}{{\displaystyle \int }d{\mathrm{\Gamma }}_{P,N}\text{exp}\{-\beta [K(P,N)+U(P)+U(P,N)+U(N)]\}}\right)\hfill \end{array}$$ (2)

The coefficients C_PM and C_PN are corrections for permutation of identical particles²¹ and h is the Planck constant. Note that the number of particles of the two states can be different. The free energies are functions of the temperature, the volume and the total number of particles (e.g. N_P+N_N or N_P+N_M).

In the dual topology approach of the alchemical methods we mix the two Hamiltonians of equation (1) to a single Hamiltonian, which is a function of an order parameter λ:

$$\begin{array}{c}H(P,M,N,\lambda )=K(P,M,N)+U(P)+\hfill \\ +(1-\lambda )[U(P,N)+U(N)]+\lambda [U(P,M)+U(M)]\hfill \end{array}$$ (3)

The order parameter λ varies between 0 and 1. To ensure stability of MD simulations the kinetic energy is not scaled to zero, so the end state presents a gas of non-interacting particles. The free energies of non-interacting particles (ideal gas) are estimated analytically as explained in textbooks²¹ and removed from the total. At λ=0, the alchemical Hamiltonian includes interacting particles “P,N” and ideal gas of particles “M”. At λ=1, the alchemical Hamiltonian describes interacting particles “P,M” and ideal gas particles “N”. This straightforward dual topology approach helps us illustrate the properties of a TC. On the other hand, it presents numerical difficulties that will be discussed later.

The free energy difference between the initial and final state according to the alchemical Hamiltonian is:

$$\begin{array}{c}f(\lambda =1)-f(\lambda =0)=\mathrm{\Delta }f=\hfill \\ =-{\beta }^{-1}\text{ln}\frac{{\displaystyle \int }d{\mathrm{\Gamma }}_{P,N,M}\text{exp}\{-\beta [K(P,M,N)+U(P)+U(P,M)+U(M)]\}}{{\displaystyle \int }d{\mathrm{\Gamma }}_{P,N,M}\text{exp}\{-\beta [K(P,M,N)+U(P)+U(P,N)+U(N)]\}}\hfill \end{array}$$ (4)

The integration over the momenta yields the same free energy contribution in the initial and final states, and cancels out. In the initial (final) state the “M” (“N”) particles do not interact with any other particle, so each of their configuration integrals is the volume V. Therefore, the integration over the N_N decoupled atoms at the numerator and the N_M decoupled atoms at the denominator contributes to the logarithm of rhs of Eq (4) with V^N_N /V^N_M. We have:

$$\mathrm{\Delta }f=-{\beta }^{-1}\text{ln}\frac{V^{N_N}}{V^{N_M}}-{\beta }^{-1}\text{ln}\frac{{\displaystyle \int }d{\mathrm{\Gamma }\text{'}}_{P,M}\text{exp}[-\beta (U(P)+U(P,M)+U(M))]}{{\displaystyle \int }d{\mathrm{\Gamma }\text{'}}_{P,N}\text{exp}[-\beta (U(P)+U(P,N)+U(N))]}$$ (5)

The alchemical Hamiltonian preserves the number of particles of the reactant and the product. Particles that are missing from the physical system are made into ideal gas atoms that bring a textbook contribution to the free energy²¹. The difference between the alchemical difference and the free energy of mutations (in which the number of particles changes) is summarized in the formula below

$$\mathrm{\Delta }{F}_{M,N}=\mathrm{\Delta }f-{\beta }^{-1}\text{ln}\left[\frac{C_{\mathit{\text{PN}}}}{C_{\mathit{\text{PM}}}}{\left(\frac{{\displaystyle \prod _{i\in M}}\frac{2\pi m_i}{h^2\beta }{V}^{\frac{2}{3}}}{{\displaystyle \prod _{i\in N}}\frac{2\pi m_i}{h^2\beta }{V}^{\frac{2}{3}}}\right)}^{\frac{3}{2}}\right]=\mathrm{\Delta }f-\mathrm{\Delta }{F}_{\mathit{\text{corr}}}$$ (6)

Computing a single free energy difference between the native and the mutant using alchemical pathway requires the calculation of ΔF_corr.

Thermodynamic cycle (TC)

Alchemical methods are often used in thermodynamic cycles (TC)²² to compare an experimental measurement to an equivalent quantity that can be computed but is not accessible to direct experimental measurements. As an example, we refer to Fig. 1

The two different black shapes correspond to two different conformations of the protein, “P1” and “P2”. The green triangle is a native residue, “N”, and the red hexagon represents a mutated residue “M”. The free energy differences associated with transitions between the four states of the system are of conformational transitions (horizontal arrows), and of mutations of one residue (vertical arrows). We are interested in the relative stability of the two conformational states (“P1” and “P2”) for the two mutants (“PN” and “PM”), i.e.:

$$\mathrm{\Delta }\mathrm{\Delta }{F}_{\text{exp}}=\mathrm{\Delta }{F}_{N-\mathit{\text{conf}}}-\mathrm{\Delta }{F}_{M-\mathit{\text{conf}}}$$ (7)

which is measured experimentally. The computation of the transition between the two conformations and the convergence of free energy differences may be difficult to obtain and/or expensive. For a complete TC the free energy change is zero, i.e. ΔF_N−conf + ΔF_2−mut − ΔF_M−conf − ΔF_1−mut = 0, which we exploit to write

$$\mathrm{\Delta }\mathrm{\Delta }{F}_{\text{exp}}\equiv \mathrm{\Delta }{F}_{N-\mathit{\text{conf}}}-\mathrm{\Delta }{F}_{M-\mathit{\text{conf}}}=\mathrm{\Delta }{F}_{1-\mathit{\text{mut}}}-\mathrm{\Delta }{F}_{2-\mathit{\text{mut}}}\equiv \mathrm{\Delta }\mathrm{\Delta }{F}_{\mathit{\text{mut}}}$$ (8)

We can therefore compute ΔΔF_mut instead of ΔΔF_exp, which is less costly.

The free energy differences of mutation computed by alchemical methods (see Eq. 5) are:

$$\begin{array}{c}\mathrm{\Delta }{f}_{1-\mathit{\text{mut}}}=-{\beta }^{-1}\text{ln}\frac{V^{N_N}}{V^{N_M}}-{\beta }^{-1}\text{ln}\frac{{\displaystyle \int }d{\mathrm{\Gamma }\text{'}}_{P,M}{\mathrm{\Theta }}_{P1}\text{exp}[-\beta (U(P)+U(P,M)+U(M))]}{{\displaystyle \int }d{\mathrm{\Gamma }\text{'}}_{P,N}{\mathrm{\Theta }}_{P1}\text{exp}[-\beta (U(P)+U(P,N)+U(N))]}\hfill \\ \mathrm{\Delta }{f}_{2-\mathit{\text{mut}}}=-{\beta }^{-1}\text{ln}\frac{V^{N_N}}{V^{N_M}}-{\beta }^{-1}\text{ln}\frac{{\displaystyle \int }d{\mathrm{\Gamma }\text{'}}_{P,M}{\mathrm{\Theta }}_{P2}\text{exp}[-\beta (U(P)+U(P,M)+U(M))]}{{\displaystyle \int }d{\mathrm{\Gamma }\text{'}}_{P,N}{\mathrm{\Theta }}_{P2}\text{exp}[-\beta (U(P)+U(P,N)+U(N))]}\hfill \end{array}$$ (9)

where Θ_X is a Heaviside function which is equal to one if the coordinate vector belongs to conformation X and is zero otherwise. To adjust the free energy differences of the dual topology to the free energy of mutation the correction must be added to each of these terms (Eq. 6). We have

$$\begin{array}{c}\mathrm{\Delta }{F}_{1-\mathit{\text{mut}}}=\mathrm{\Delta }{f}_{1-\mathit{\text{mut}}}-\mathrm{\Delta }{F}_{\mathit{\text{corr}}}\hfill \\ \mathrm{\Delta }{F}_{2-\mathit{\text{mut}}}=\mathrm{\Delta }{f}_{2-\mathit{\text{mut}}}-\mathrm{\Delta }{F}_{\mathit{\text{corr}}}\hfill \end{array}$$ (10)

The correction to the free energy differences is independent of the protein conformation (Eq. 6). Therefore, the relative free energy difference computed by alchemical methods (ΔΔf_mut) is the same as the actual relative free energy (ΔΔF_mut):

$$\mathrm{\Delta }\mathrm{\Delta }{F}_{\mathit{\text{mut}}}=\mathrm{\Delta }{F}_{1-\mathit{\text{mut}}}-\mathrm{\Delta }{F}_{2-\mathit{\text{mut}}}=\mathrm{\Delta }{f}_{1-\mathit{\text{mut}}}-\mathrm{\Delta }{F}_{\mathit{\text{corr}}}-\mathrm{\Delta }{f}_{2-\mathit{\text{mut}}}+\mathrm{\Delta }{F}_{\mathit{\text{corr}}}=\mathrm{\Delta }\mathrm{\Delta }{f}_{\mathit{\text{mut}}}$$ (11)

The elimination of the correction terms suggests that the end points of the calculations can be manipulated to our advantage (as first suggested in¹⁶) to minimize the cost of the calculations. As long as they cancel out the correct relative free energy difference is obtained.

Retaining all the self-interactions

We illustrate an alchemical pathway that retains the self-interactions of the substituted fragment and provides the correct relative free energy difference. This pathway avoids the scaling of the self-interactions by the order parameter λ in the interpolating Hamiltonian:

$$\begin{array}{c}H\text{'}(P,M,N,\lambda )=K(P,M,N)+U(P)+(1-\lambda )U(P,N)+\hfill \\ +\lambda U(P,M)+U(N)+U(M)\hfill \end{array}$$ (12)

If λ =0 the system described by the Hamiltonian is composed by particles “P” and “N” and by a molecule “M” in the gas phase. When λ=1, the “P” and “M” particles make the mutant protein, while “N” is a molecule in gas phase.

The free energy difference between the initial and final state computed using this Hamiltonian is:

$$\mathrm{\Delta }f\text{'}=-{\beta }^{-1}\text{ln}\frac{{\displaystyle \int }d{\mathrm{\Gamma }\text{'}}_{P,M,N}\text{exp}\{-\beta [U(P)+U(P,M)+U(M)+U(N)]\}}{{\displaystyle \int }d{\mathrm{\Gamma }\text{'}}_{P,M,N}\text{exp}\{-\beta [U(P)+U(P,N)+U(M)+U(N)]\}}$$ (13)

The key observation is that the “N” particles in the numerator and “M” particles in the denominator do not interact with the protein or the solution; therefore their contribution to the free energy difference can be isolated:

$$\begin{array}{c}\mathrm{\Delta }f\text{'}=-{\beta }^{-1}\text{ln}\frac{{\displaystyle \int }d{\mathrm{\Gamma }\text{'}}_{P,M}\text{exp}\{-\beta [U(P)+U(P,M)+U(M)]\}}{{\displaystyle \int }d{\mathrm{\Gamma }\text{'}}_{P,N}\text{exp}\{-\beta [U(P)+U(P,N)+U(M)]\}}+\hfill \\ -{\beta }^{-1}\text{ln}\frac{{\displaystyle \int }{\mathit{\text{dQ}}}_N\text{exp}[-\beta U(N)]}{{\displaystyle \int }{\mathit{\text{dQ}}}_M\text{exp}[-\beta U(M)]}\hfill \end{array}$$ (14)

The deviation of this free energy difference and the one obtained with alchemical methods that scale the self-interactions (Eq. 5) is:

$$\mathrm{\Delta }f=\mathrm{\Delta }f\text{'}+{\beta }^{-1}\text{ln}\frac{V^{N_M}{\displaystyle \int }{\mathit{\text{dQ}}}_N\text{exp}(-\beta U(N))}{V^{N_N}{\displaystyle \int }{\mathit{\text{dQ}}}_M\text{exp}(-\beta U(M))}$$ (15)

Similar to our previous argument about the difference between ΔF and Δf, the difference in Eq 15 is independent of the protein conformations and we therefore have

$$\mathrm{\Delta }\mathrm{\Delta }{f}_{\mathit{\text{mut}}}=\mathrm{\Delta }{f}_{1-\mathit{\text{mut}}}-\mathrm{\Delta }{f}_{2-\mathit{\text{mut}}}=\mathrm{\Delta }{f}_{1-\mathit{\text{mut}}}^{\text{'}}-\mathrm{\Delta }{f}_{2-\mathit{\text{mut}}}^{\text{'}}=\mathrm{\Delta }\mathrm{\Delta }{f\text{'}}_{\mathit{\text{mut}}}$$ (16)

This proves that the ΔΔF computed along this pathway that avoids the annihilation/creation of self-interactions of the substituted fragment is exact. This proof is similar to the one reported in¹⁸, where only the non-bonded interactions are scaled. Our argument is more general: all the interactions involving only “M” or “N” particles are left “as are”. The gas phase molecule with non-bonded interactions on will have more restricted conformational space to explore.

Scaling of “P”-“M”(“N”) bonded interactions

The path discussed in the previous section requires that all the external interactions (e.g. interactions involving “P” and “N” particles) are annihilated/created to bring the system to the correct end-states. If the annihilated chemical group is decoupled from the rest of the environment, it explores the whole simulation box, which makes statistical convergence difficult¹⁶. A solution is to restrain the overall relative translations and rotations of the fragment with respect to the scaffold. An algorithm to that effect was presented for free energy calculation of binding of a ligand to an enzyme, and is called Virtual Bond Algorithm (VBA)^19,20.

According to VBA, it is possible to retain a few bonded “P”-“M”(“N”) interactions by “cross linking” the six external degrees of freedom of the annihilated particles to the “P” atoms. If there are no interactions between the annihilated particles (say “M”) and the “P” atoms, the partition function of the overall system is:

$$Z(P,M)=Z(P)Z(M)=Z(P)Z_{\text{int}}(M)8{\pi }^{2}V$$ (17)

In the right hand side of Eq. 17 we separated the partition function of the “M” molecule/fragment Z(M) into the partition function of its internal degrees of freedom Z_int(M) and the partition function of its external degrees of freedom, which is 8π²V²⁰.

The VBA algorithm makes it possible to find a transformation of coordinates such that we can isolate the six external degrees of freedom of the “M” species and restrain them to the “P” particles. This yields:

$$Z\text{'}(P,M)=Z(P)Z_{\text{int}}(M)Z_{P-M}$$ (18)

Here, Z_P-M is the “cross linking” partition function, i.e. the partition function of the six restraints on the external degrees of freedom of the “M” molecule/fragment that restrain its relative distance and orientation with respect to the “P” molecule/scaffold. It is important to highlight that Z_P-M does not depend on the coordinates of the “P” molecule/scaffold. The free energies of the system with the free “M” molecule/fragment (Eq. 17) and the one with the “cross linked” “M” molecule/fragment (Eq. 18) are different. Their difference is:

$$\mathrm{\Delta }{F}_{P-M}=-{\beta }^{-1}\text{ln }Z\text{'}(P,M)+{\beta }^{-1}\text{ln }Z(P,M)={\beta }^{-1}\text{ln}\frac{Z_{P-M}}{8{\pi }^{2}V}$$ (19)

Since the six restraints in Z_P-M are independent, Z_P-M can be written as the product of six one-dimensional integrals. These integrals may be solved analytically or numerically, but no further MD simulations are required.

According to VBA, it is possible to retain one bond, two angles and three torsions, chosen in such a way that they involve 3 “P” particles and 3 “M” or “N” particles^19,20. Since we often have more bonded interactions between “P” and “M” or “N” particles, we still have to deal with the alchemical annihilation/creation of a few bonded interactions. In the Methods section and in the Supplementary Information we propose a route to remove such interactions avoiding problems in angles, torsions, and improper torsions due to removal of bond angles.

In a thermodynamic cycle these cross-linking restraints do not affect the relative free energy difference, i.e. ΔΔF computed with a cross-linked system is identical to ΔΔF computed without the cross-linking interactions. To illustrate this, let us refer to Fig. 1. The restraining potential appears only in the two mutations (vertical arrows). In the first mutation (right vertical arrow), the simulation is run with the cross-links “on” for both the mutant and the native fragments. To correct for this bias we need to add the free energy contribution of restraining the mutant to the protein (ΔF_P-M) and remove the free energy difference of restraining the native (−ΔF_P-N). In the second mutation (left vertical arrow), the simulations are run again with the cross-links “on” for both the mutant and the native. However, in this case we remove the free energy contribution of restraining the mutant (−ΔF_P-M) and add the free energy difference of restraining the native (ΔF_P-N). The restraining partition function is decoupled from the “P” partition function (see Eq. 18), therefore it is not affected by the conformation of the protein. The contribution to the relative free energy difference due to the cross-linking ΔΔF_CL is:

$$\mathrm{\Delta }\mathrm{\Delta }{F}_{\mathit{\text{CL}}}=\mathrm{\Delta }{F}_{P-M}-\mathrm{\Delta }{F}_{P-N}+\mathrm{\Delta }{F}_{P-N}-\mathrm{\Delta }{F}_{P-M}=0$$ (20)

The possibility of retaining the external bonded interactions was discussed in¹⁸, where the authors did not use VBA, but consider examples to explain which bonded interactions between “P”-“M”(“N”) may be retained without introducing “spurious correlations” within the protein. In¹⁹ it was highlighted that the contribution of dummy atoms (i.e. atoms that do not interact with the environment) cancels out exactly only if the set of bond-angles and dihedrals between dummy atoms and the environment is non-redundant.

With respect to the arguments reported elsewhere^18,19, the use of VBA theory clarifies how to choose “non-redundant” interactions between “P”-“M”(“N”), and so how to avoid “spurious correlations”.

A direct application of VBA is not possible if the created/annihilated fragment has more than one chemical bond with the scaffold. In this case it is necessary to perform two simulations. First, all the bonded interactions in excess of those required by VBA are removed. Since the fragment is still bound to the scaffold, the computational cost of this removal should not be too expensive. Then, the regular VBA can be applied.

Numerical example

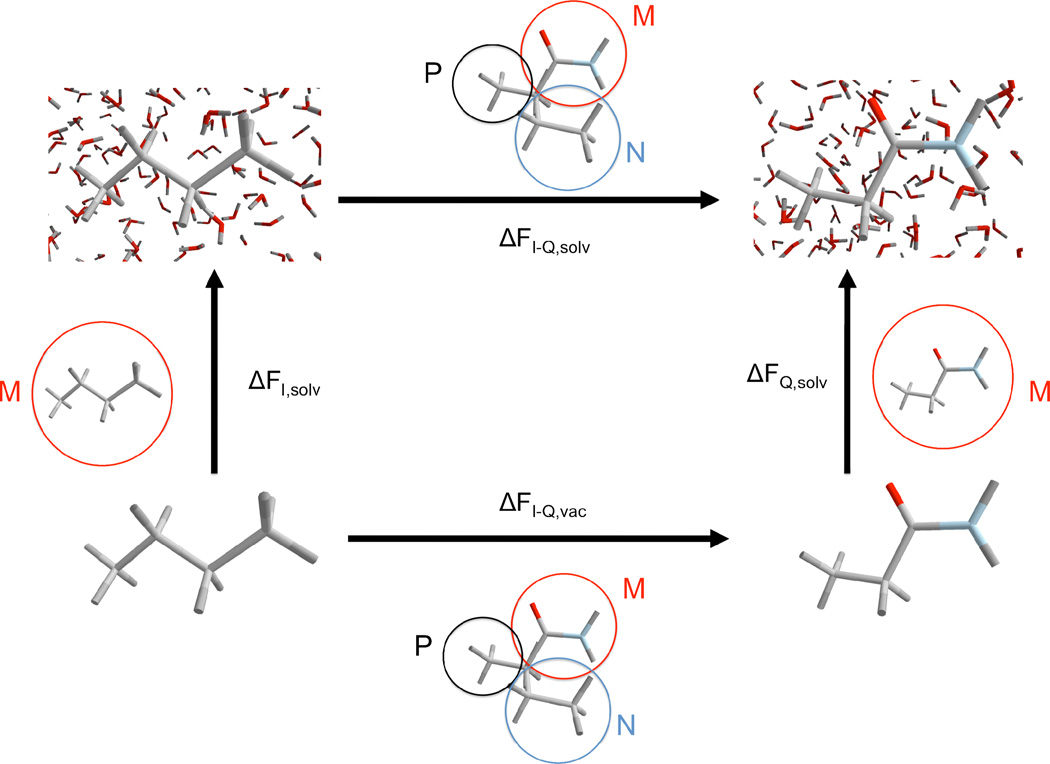
To illustrate the theory, we study an alchemical substitution that retains all the self-interactions. The difference in hydration free energies of ILE and GLN side chain analogs is computed. The cycle that we consider is presented in Fig. 2.

Fig. 2.

The thermodynamic cycle that we used in our calculations. The horizontal arrows represent free energy differences upon mutation of the solute (ILE side chain analog and GLN side chain analog). The vertical arrows represent the solvation process, i.e. the solute is brought from vacuum into solution. For each free energy calculation the colored circles highlight which atoms are considered “P” (black), “N” (blue) or “M” (red).

ΔF_I-Q,solv is the free energy difference of mutating ILE to GLN side chain analog in solution, while ΔF_I-Q,vac is the same quantity computed in vacuum (gas phase). ΔF_I,solv and ΔF_Q,solv are the free energy differences of inserting ILE and GLN side chain analogs into water from gas phase, respectively.

The free energy difference of the complete cycle is (the q-s are the partition functions):

$$\begin{array}{c}{\displaystyle \int }\mathit{\text{dF}}=\mathrm{\Delta }{F}_{I-Q,\mathit{\text{solv}}}-\mathrm{\Delta }{F}_{Q,\mathit{\text{solv}}}-\mathrm{\Delta }{F}_{I-Q}+\mathrm{\Delta }{F}_{I,\mathit{\text{solv}}}=\hfill \\ =-{\beta }^{-1}\text{ln}\left[\frac{q_{\mathit{\text{solv}},Q}}{q_{\mathit{\text{solv}},I}}\frac{q_{\mathit{\text{solv}}}{q}_Q}{q_{\mathit{\text{solv}},Q}}\frac{q_I}{q_Q}\frac{q_{\mathit{\text{solv}},I}}{q_{\mathit{\text{solv}}}{q}_I}\right]=0\hfill \end{array}$$ (21)

as it should be. The numerical task and test is to reproduce the zero in simulations.

Mutations

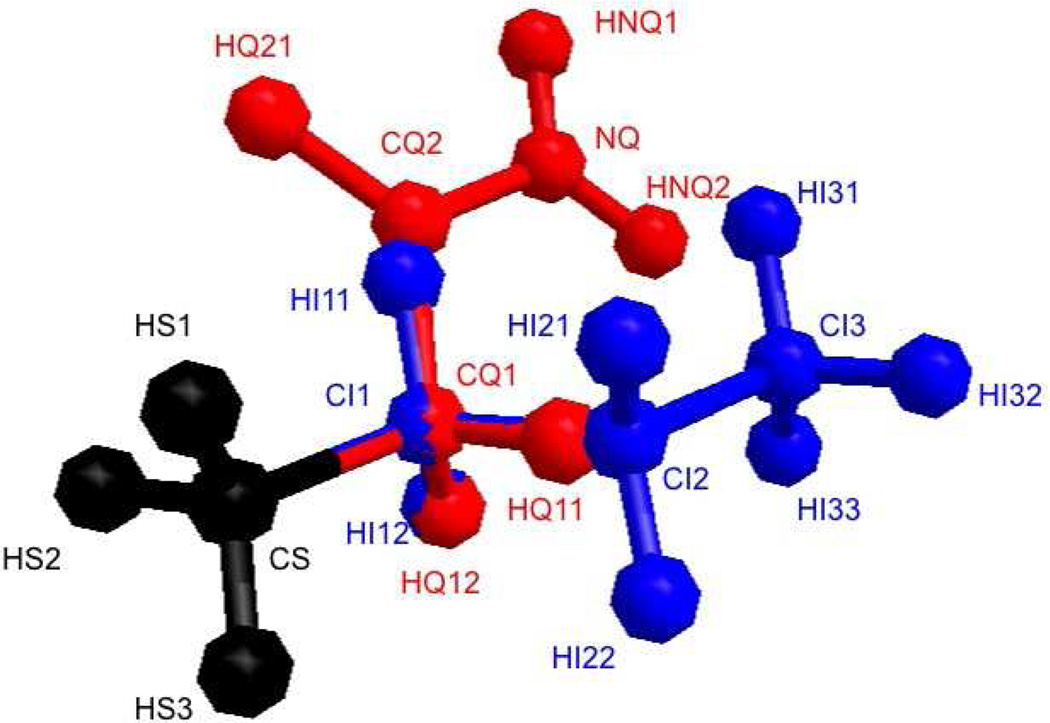
To compute the free energy differences ΔF_I-Q,solv and ΔF_I-Q we used the system shown in Fig. 3

Fig. 3.

The alchemical intermediate that we use. The black methyl group is shared between the two side chain analogs. The blue atoms are the rest of the ILE side chain analog. The red atoms are the remaining of the GLN side chain analog. While the black atoms interact with all the other atoms, blue and red particles do not interact with each other.

The black methyl group is considered the “P” part of the system, i.e. the part that interacts with both mutants during TI. The blue atoms are the native “N”, i.e. the ILE side chain without its methyl group that is considered “P”. The red atoms are the mutant “M”, i.e. the GLN side chain analog without the methyl group which is part of “P”. To illustrate our procedure, the simulations are performed while retaining the full strength of the self-interactions. More details about the simulations follow.

Solvation

To compute the free energy difference of the two side chains in solution and in gas phase the non-bonded interactions between the side chain analog and the solvent around it are turned off²³. Following the nomenclature introduced in the previous sections, we consider water as “P” molecules, the side chain analog (ILE or GLN) as “M” particles. No “N” particles are involved in these simulations.

Alchemical pathway

In the previous sections, we described a Hamiltonian for the alchemical substitution that depends linearly on λ (see Eq. 3 and Eq. 12). This is the most straightforward choice, but not necessarily the best one from a numerical perspective. Indeed, the creation and the annihilation of particles with a finite Van der Waals radius present (integrable) singularities²⁴. Such singularities are removed if the Van der Waals interactions are created/annihilated with scaling parameter λ^α, with α≥4²⁴. Moreover, the use of a soft core Lennard Jones potential avoids hard clashes during the creation/annihilation of interactions between particles²⁴. The potential used is then:

$${\lambda }^{4}U(r)=4\epsilon {\lambda }^4\left\{\frac{{\sigma }^{12}}{{[r^6+{\alpha }_{\mathit{\text{LJ}}}{(1-\lambda )}^2{\sigma }^6]}^2}-\frac{{\sigma }^6}{[r^6+{\alpha }_{\mathit{\text{LJ}}}{(1-\lambda )}^2{\sigma }^6]}\right\}$$ (22)

It is clear that for λ=0 this potential disappears, for λ=1 we recover the usual Lennard Jones potential (in this way the correct end-state is recovered), for 0<λ<1 the hard core is softened, i.e. there is no divergence at r=0. The larger the value of α_LJ, the softer is the potential. In our simulations we used α_LJ=0.3.

To avoid the collapse of particles with opposite charges to the same point in space, while the Van der Waals repulsion is reduced, the free energy calculation is conducted in two steps: in the first step the electrostatic interactions of the “N” particles are turned off, and in the second step the Van der Waals interactions are removed²⁵. The opposite is done for “M” particles (first the Van der Waals interactions are created, and then the electrostatic interactions are turned on).

While we retain (of course) all the internal covalent interactions in “N” and “M”, some of the external covalent interactions need to be annihilated/created. Indeed, as we discussed in the section Scaling of “P”-“M”(“N”) bonded interactions, there is a maximal number of external bonded interactions that can be retained throughout the calculation. All the other interactions have to be removed to properly decouple the partition function into separated terms. In Supplementary Information (SI) the computational implementation of this annihilation/creation is discussed. In particular, Urey-Bradley (UB) terms, instead of the angular harmonic potential, are used for the angles to be created/annihilated. UB terms are regular bonds in Cartesian space that are placed between two atoms sharing an angle but not directly bonded. The reason for the use of the UB terms is of numerical stability: the removal/creation of a bond-angle is problematic, as explained in SI. In the solvation simulations there are no angle terms annihilated/created, therefore only the regular bond-angle potential is used. This inconsistency introduces a correction to the free energy (the difference between the UB and the usual harmonic angular terms) that we need to compute explicitly. Such calculation is described in SI. It turns out that the resulting correction is negligible in this numerical illustration.

In what follows, given the small size of the “P” part of the solute (it is just the black methyl group in Fig. 3), we decided to retain only the external bond between the CS and CI1/CQ1 (see Fig. 3). This avoids the drift of the decoupled fragment in the simulation box. All the other external bonded interactions were treated in the same way and alchemically removed/created.

We further use an order parameter λ^β with β≥2 for the scaling of the bond angles (see SI).

Finally, we suggest that the torsion and improper torsion interactions should be removed before the bond angles (see SI).

A summary of all these considerations is in Table 1 and Table 2. We break the free energy calculation into two parts: MutationPHase1 (MPH1) and MutationPHase2 (MPH2). In MPH1 we remove electrostatic interactions, torsions and improper torsions between “P” and “N” particles and create Van der Waals interactions and angles between “P” and “M” particles. In MPH2 we do the opposite: we remove Van der Waals interactions and angles between “P” and “N” particles and create electrostatic interactions, torsions and improper torsions between “P” and “M” particles. Note that we do not create or remove the bond between particles “P” and “M” or the bond between “P” and “N”. Note also that all the self-interactions, bonded and non-bonded, are never created nor annihilated.

Table 1.

The alchemical pathway for the first phase of the mutation. The angular and Van der Waals interactions between “P” and “M” particles are created, while torsions, improper torsions and electrostatic interactions between “P” and “N” are progressively switched off. The right hand side of the table reports the corrections to the regular OPLS-AAL²⁶ potential that were used. Notice that the self-interactions, as well as the bonds, are never scaled (see details in the text).

	MPH1
	scaling					correction
	P-P	P-M	P-N	M-M	N-N	P-P	P-M	P-N	M-M	N-N
Vdw	1	λ4	1	1	1		Soft core
Ele	1	0	(1−λ)	1	1
Bond	1	1	1	1	1
Angle	1	λ2	1	1	1		Urey-Bradley
Tors	1	0	(1−λ)2	1	1
ImpT	1	0	(1−λ)2	1	1

Table 2.

The alchemical pathway for the second phase of the mutation. The torsions, improper torsions and electrostatic interactions between “P” and “M” particles are created, while angular and Van der Waals interactions between “P” and “N” are progressively switched off. The right hand side of the table reports the corrections to the regular OPLS-AAL²⁶ potential that were used. Notice that the self-interactions, as well as the bonds, are never scaled (see details in the text).

	MPH2
	scaling					correction
	P-P	P-M	P-N	M-M	N-N	P-P	P-M	P-N	M-M	N-N
Vdw	1	1	(1−λ)4	1	1			Soft core
Ele	1	λ	0	1	1
Bond	1	1	1	1	1
Angle	1	1	(1−λ)2	1	1			Urey-Bradley
Tors	1	λ2	0	1	1
ImpT	1	λ2	0	1	1

To ensure accurate estimates of the electrostatic interaction we use Particle Mesh Ewald²⁷. The drawback of this method with respect to the alchemical substitution is that the reciprocal space contribution to the energy cannot be separated into the specific contributions of each pair of interacting particles. Therefore, it is not obvious how to selectively annihilate/create only the interactions between “P” and “M” or “N” particles.

Recall the PME theory²⁷. We define n as the lattice vectors, and C(i,j) are interaction parameters for pair of particles. The potential energy is a sum of the interactions of all the pair of particles with the exception of self. The exception is denoted by the prime in the summation symbol below

$$E(\stackrel{𝗋}{r_1},\dots ,\stackrel{𝗋}{r_N})=\frac{1}{2}{\displaystyle \sum _{\stackrel{𝗋}{n}}}\text{'}{\displaystyle \sum _i}{\displaystyle \sum _j}\frac{C(i,j)}{|\stackrel{𝗋}{r_i}-\stackrel{𝗋}{r_j}+\stackrel{𝗋}{n}|}$$ (23)

the PME methodology is applicable if we can write (see Appendix of²⁷):

$$C(i,j)=\pm C(i)C(j).$$ (24)

If we want to retain the “self” electrostatic interactions, we cannot use Eq. 24. Indeed, let us suppose that particle i is a “M” particle, then we have:

$$C(i,j)=\{\begin{array}{cc}\hfill \lambda \frac{q_i{q}_j}{4\pi {\epsilon }_0}\hfill & \hfill j\in P\hfill \\ \hfill 0\hfill & \hfill j\in N\hfill \\ \hfill \frac{q_i{q}_j}{4\pi {\epsilon }_0}\hfill & \hfill j\in M\hfill \end{array}$$ (25)

where q are charges and ε₀ is the electric constant. Since the “P” particles interact according to the usual Coulomb law (q_iq_j/4πε₀, without λ) and the “N” particles may carry a charge different from zero, we cannot write Eq. 25 as Eq. 24.

To solve this problem we compute the reciprocal space energy term between selected types of particles and scale the interactions with the proper switching parameter. A sum of these terms gives us an overall electrostatic potential energy in which the self-interactions are not scaled.

The recipe is summarized in the two following tables that explain how to carry out the Ewald sums for MPH1 and MPH2.

This solution has two major disadvantages. First, using PME four times per time step is an expensive procedure. Second, the formulation is not exact. Indeed, we are neglecting a term in the Ewald summation that is proportional to the square of the dipole of the unit cell²⁷. While this term is routinely neglected in solvated simulations, it is hard to argue that this term is zero in a vacuum calculation or when we use PME to evaluate U(M) or U(N). From this perspective, further developments of the PME theory are needed to extend its applicability to the type of problem hereby described.

The use of PME in the context of calculation of solvation free energy was debated²⁸. The periodicity of the system adds some interactions between the solute in the unit cell and its periodic images. The solvation of an isolated molecule in liquid requires that all interactions between the solute in the unit cell and its periodic copies are removed. The advantage of PME is that the energy is conserved providing well defined statistical mechanic properties throughout the cycle. We use PME also in the simulations carried out in vacuum to ensure consistency. The differences of free energies computed with and without PME in vacuum were small (~0.02 kcal/mol).

Thermodynamic integration

To compute numerically the free energy differences defined in Eq. 21 we use thermodynamic integration (TI)²⁹:

$$\mathrm{\Delta }f\text{'}={\displaystyle \underset{0}{\overset{1}{\int }}}d\lambda \frac{\mathit{\text{dF}}}{d\lambda }={\displaystyle \underset{0}{\overset{1}{\int }}}d\lambda {\langle \frac{\partial H\text{'}}{\partial \lambda }\rangle }_{\lambda }$$ (26)

where H '(λ) is the sum of kinetic and potential energies and its dependence on the order parameter λ is defined in Table 1 and Table 2.

The brackets in Eq. 26 denote an ensemble average performed at a fixed value of λ.

The simulations are performed at a finite set of λ states. The numerical integrations are performed according to the trapezoidal rule, i.e. the integral is approximated by:

$$\mathrm{\Delta }f\text{'}\approx {\langle \frac{\partial H\text{'}}{\partial \lambda }\rangle }_{{\lambda }_1}{\lambda }_1+\frac{1}{2}{\displaystyle \sum _{i=2}^{N_{\lambda }}}\left[{\langle \frac{\partial H\text{'}}{\partial \lambda }\rangle }_{{\lambda }_i}+{\langle \frac{\partial H\text{'}}{\partial \lambda }\rangle }_{{\lambda }_{i-1}}\right]({\lambda }_i-{\lambda }_{i-1})+{\langle \frac{\partial H\text{'}}{\partial \lambda }\rangle }_{{\lambda }_{N_{\lambda }}}(1-{\lambda }_{N_{\lambda }})$$ (27)

where N_λ is the number of λ states used.

The configurations are sampled with a MD simulation using a variant of the program MOIL³⁰ with the MUTA option https://wiki.ices.utexas.edu/clsb/wiki/GetSubversionMoil.

Simulation details

We used the OPLS-AAL force field²⁶ with a modification on the charges of the Cβ of the residue analogs²³. Also, the Lennard-Jones parameters for polar hydrogens belonging to the solutes were set to σ=0.3Å and ε=0.0498kcal/mol. All the systems were solvated in a periodic cubic box of volume 34.45ų with 1355 TIP3P water molecules³¹ at 300K. The size of the water box was chosen in such a way to have an average water density at corners of the box near 0.998g/cm³ with the ILE side chain analog solvated in the center of the water box. The rationale of this choice is that at the corners of the box we are far enough from the solute to be in “bulk”.

The cutoff distance was 10Å for Van der Waals interactions and 14Å for electrostatic forces. These real space cutoff distances gave very good energy conservation throughout the simulation on a 2ns test case conducted in the NVE ensemble. Particle Meshed Ewald (PME)²⁷ was used in all simulations with a grid of 64×64×64. To be consistent with the solvated simulations, PME was used also in the simulations carried out in vacuum.

The contributions of Van der Waals interactions between particles that are beyond the cutoff distance are (of course) not considered explicitly in this simulation. Other authors have used an analytical correction for the free energy of solvation of small molecules²³. The solvent distribution around each of the alchemically substituted particles of the solute is assumed homogeneous and isotropic. The cutoff is set large enough so there are no correlations between the particle at the origin and the particles beyond the cutoff. In this case, the pair correlation function between the alchemically substituted solute and the solvent particles is independent of λ and is equal to 1. The final correction formula is^23,32:

$$\mathrm{\Delta }{F}_{\mathit{\text{LRC}}}=4\pi {\displaystyle \sum _{i\in M}}{\rho }_O{\displaystyle \underset{r_c}{\overset{\mathrm{\infty }}{\int }}}{\mathit{\text{dr}}}_{i,O}{r}_{i,O}^2{U}_{\mathit{\text{VdW}}}(r_{i,O})-4\pi {\displaystyle \sum _{i\in N}}{\rho }_O{\displaystyle \underset{r_c}{\overset{\mathrm{\infty }}{\int }}}{\mathit{\text{dr}}}_{i,O}{r}_{i,O}^2{U}_{\mathit{\text{VdW}}}(r_{i,O})$$ (28)

Here, the density ρ_O is the number density of oxygen in water molecules. The Van der Waals interactions considered are only between solute and oxygen, according to the TIP3P water model.

The results for this correction are reported in Table 6, together with all the other results. This correction is not affecting the overall free energy cycle. In Fig. 2, we notice that each correction is added (at the end of the solvation simulation for ILE, and at the end of the mutation for GLN) and then removed (at the beginning of the mutation simulation for ILE and the end of the solvation simulation for GLN) per each solute. The net effect is zero.

Table 6.

Free energy differences and statistical errors (all the values are in kcal/mol). (a) Current simulations. The second column reports the total, the third the free energy difference in MPH1, the fourth the free energy difference in MPH2 and the fifth the long-range correction (LRC). (b) Solvation free energies of the ILE and GLN side chain analogs as reported in²³. The second column is total, the third the free energy difference while creating Van der Waals interactions between the solute and the solvent with the electrostatic interactions off (analogous to MPH1), the fourth column reports the free energy of creating electrostatic interactions when the Van der Waals are already ”on” (analogous to MPH2). The last column is the long-range correction (LRC). The protocol used to carry out these calculations in²³ is significantly different from ours. The authors in²³ carried out NPT simulations and their cutoff scheme is different (no Ewald summation for electrostatics, they used instead group-based and tapered interactions). This is reflected mostly in the LRC term, which depends on the scheme used for the Van der Waals cutoff. (c) Experimental results for the solvation free energies of the two side chain analogs³⁵. These results were used as a comparison with the simulations in²³.

a
	TOTAL	MPH1	MPH2	LRC
ΔFI-Q,solv	−14.073±0.066	−16.218±0.050	2.199±0.043	−0.051
ΔFI-Q,vac	−2.847±0.068	−10.931±0.047	8.084±0.049
ΔFI,solv	2.891±0.050	3.379±0.050	−0.0075±0.0019	−0.481
ΔFQ,solv	−8.354±0.054	1.858±0.047	−9.680±0.027	−0.532

b
	Total23	Vdw23	Ele23	LRC23
ΔFI,solv	2.73±0.03	3.10±0.03	−0.01±0.001	−0.37
ΔFQ,solv	−8.40±0.04	1.80±0.03	−9.79±0.02	−0.41

c
	Experiment23,35
ΔFI,solv	2.15
ΔFQ,solv	−9.38

In the two mutations, the geometric center of the “P” particles was restrained to the center of the box by a harmonic potential with spring constant k=1kcal/mol. In the two calculations in solvent, the geometric center of the analog was restrained to the center of the box by a harmonic potential with the same spring constant k. In both of the cases, the free energy contribution from this harmonic potential restrains an external degree of freedom, so it is separable. Since the two spring constants are the same, the free energy of the system is not affected by the choice of the subset of particles to restrain. Therefore, there is no overall contribution from this restraint to the total free energy difference.

The solvated simulations were performed in the NVT ensemble by rescaling the velocities at every time step to maintain the temperature of the thermal bath. The vacuum simulations were performed in the NVT ensemble using a Langevin thermostat³² to enhance coupling between different degrees of freedom and ergodicity.

The TI was performed following the “multiconfiguration” approach³³. The number of intermediates λ states at which the free energy differences were sampled and computed are listed in the following table. They were chosen to allow a good description of the regions in dF/dλ characterized by a large curvature.

For the solvated simulations, at each λ state two equilibrations of 100ps were performed: one with the solute frozen and the other with the solute free to move. Then a 2ns long sampling of configurations was carried out for each λ state. For the simulations carried out in vacuum, we sampled configurations for 2ns using Langevin dynamics with friction coefficient γ=60ps⁻¹. One configuration per picosecond was used to compute the average and the variance of dH/dλ. The configurations sampled in this way may be correlated. To account for this correlation we computed the variance of dH/dλ using the following formula^32,34:

$${\sigma }^2\left({\langle \frac{\mathit{\text{dH}}}{d\lambda }\rangle }_T\right)=\frac{2}{T}{\displaystyle \underset{0}{\overset{T}{\int }}}d\tau (1-\frac{\tau }{T}){\langle (\frac{\mathit{\text{dH}}}{d\lambda }(\tau )-{\langle \frac{\mathit{\text{dH}}}{d\lambda }\rangle }_T)(\frac{\mathit{\text{dH}}}{d\lambda }(0)-{\langle \frac{\mathit{\text{dH}}}{d\lambda }\rangle }_T)\rangle }_T$$ (29)

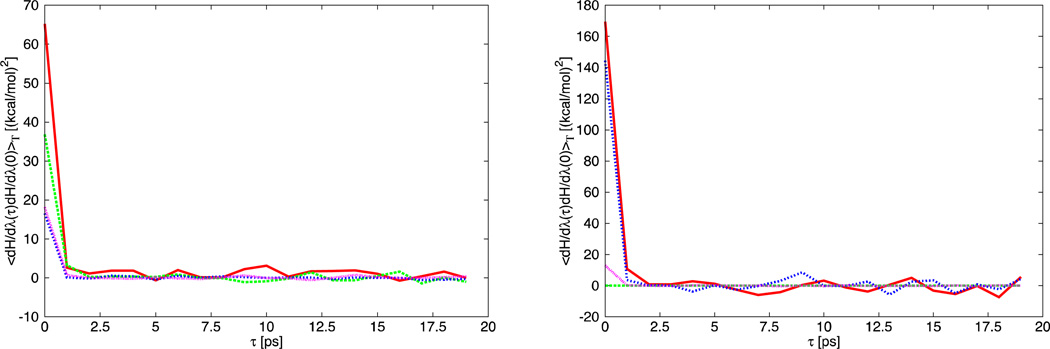
In this equation, the symbol “<…>_T” refers to a time average over the sampled configurations carried out for the length of simulation T. The argument of the integral contains the correlation function of dH/dλ. The correlation function decays to 0 within the first few picoseconds (see Fig. 4). Therefore, it was computed for 19ps and then set to 0 to avoid integration over a noisy tail that may introduce unphysical contributions to the integral. The integral in Eq. 29 was evaluated using the trapezoidal rule. Examples of correlation functions are reported in Fig. 4.

Fig. 4.

Correlation function of dH/dλ as a function of time (in ps). The left figure reports calculations at λ=0.5 of the MPH1 (red) and MPH2 (green) phases of the mutation from ILE side chain analog to GLN sidechain analog in solution. In the same figure the MPH1 (blue) and MPH2 (pink) phases of the same mutations in vacuum are reported. The right figure shows the calculations at λ=0.5 of the MPH1 (red) and MPH2 (green) of the solvation of ILE side chain. In the same figure the MPH1 (blue) and the MPH2 (pink) phases of the solvation of GLN side chain analog are also reported.

The variance of the integral was estimated from the variances of 〈∂H '/ ∂λ〉_λi using the error propagation formula.

Results

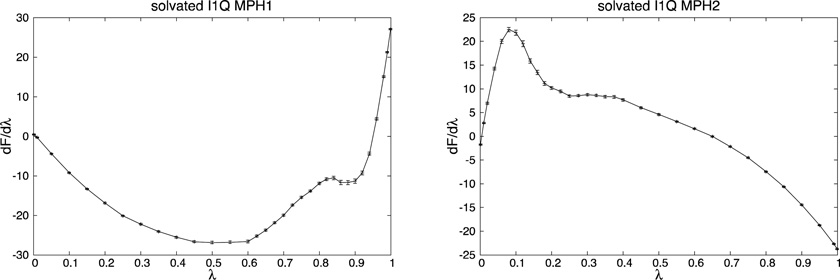
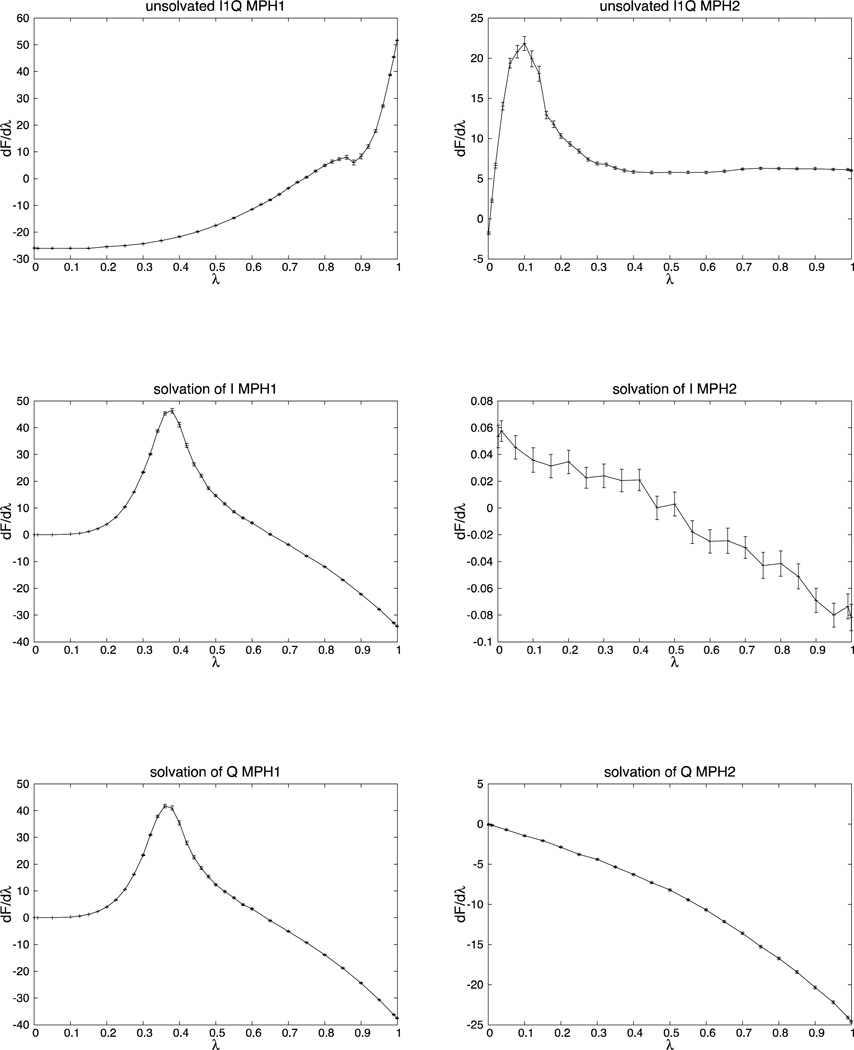
The profiles for dF/dλ as a function of λ are reported in Fig. 5.

Fig. 5.

dF/dλ profiles (in kcal/mol) as a function of λ of the phases MPH1 and MPH2 of the free energy differences of each part of the cycle of Fig. 2. On the left the MPH1 phase is reported, and on the right the MPH2. From top to bottom we have: mutation from ILE to GLN in solution, mutation from ILE to GLN in vacuum, solvation of ILE and solvation of GLN. The error bars are shown in all figures.

In Table 6a the results are reported for each part of the calculation.

In the second column of Table 6a we report the total of the free energy calculation. The total is broken into three parts: the result for the first phase (MPH1, third column), the result for second phase (MPH2, fourth column) and the Long Range Correction (LRC, fifth column) approximately accounting for the finite Van der Waals cutoff used in the simulations.

In²³, the authors computed the solvation free energies of these two side chain analogs. The free energy calculation was performed following an alchemical pathway similar to ours: i.e. splitting the decoupling in two steps. First the Van der Waals interactions are turned on, while the electrostatic interactions are kept off. Second, the electrostatic interactions are created, while keeping the Van der Waals interactions at their full strength. The first step is analogous to MPH1, and it is reported in the third column of Table 6b. The second step is analogous to MPH2, and it is reported in the fourth column of Table 6b. Our results are close to²³. This is particularly interesting since we used a significantly different sampling protocol. First, they sampled from the NPT ensemble, while we sampled configurations from the NVT ensemble. Second, they did not use Ewald sum to compute long-range electrostatics. They adopt a neutral group based, tapered, finite cutoff distance for both electrostatics and Van der Waals interactions. The different cutoff scheme for Van der Waals interactions results in a significant difference between our longrange Van der Waals corrections (fifth column in Table 6a) and theirs (fifth column in Table 6b). Overall, our agreement with the simulations previously reported (second column of Table 6b)²³ and the experimental results to which they compare with^23,35 (Table 6c) are in a reasonable range.

The expected result for the free energy difference over the complete cycle is, of course, 0kcal/mol. The free energy computed numerically over the complete cycle is:

$$\mathrm{\Delta }{F}_{I-Q,\mathit{\text{solv}}}-\mathrm{\Delta }{F}_{Q,\mathit{\text{solv}}}-\mathrm{\Delta }{F}_{I-Q,\mathit{\text{vac}}}+\mathrm{\Delta }{F}_{I,\mathit{\text{solv}}}=(0.02\pm 0.12)\mathit{\text{kcal}}/\mathit{\text{mol}}$$ (30)

The correction for the use of Urey-Bradley term for angles over the cycle is negligible (see SI), and our final result is therefore:

$${\displaystyle \int }\mathit{\text{dF}}=(0.02\pm 0.12)\mathit{\text{kcal}}/\mathit{\text{mol}}$$ (31)

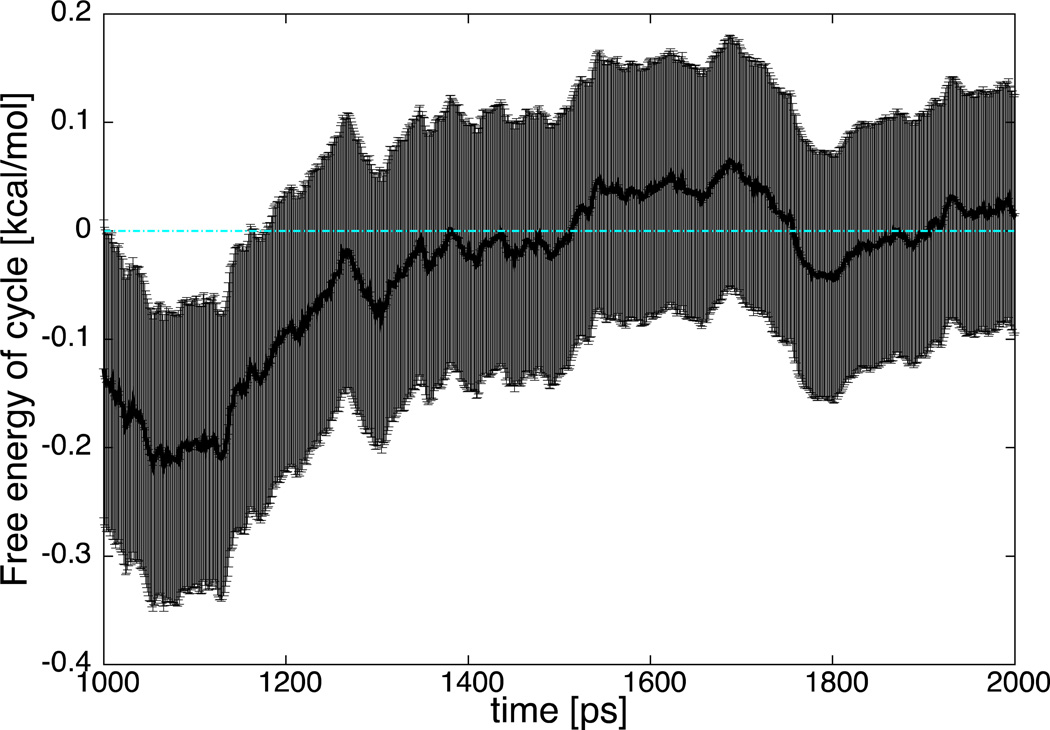
To further illustrate that the result is converged we report the free energy of the complete cycle for the last 1ns of simulation in Fig. 6.

Fig. 6.

Free energy of the complete cycle as a function of time of the last 1ns of simulation. The thickness of the black line provides the error bars. The light blue the exact value.

The numerical result is consistent with the analytical prediction of zero and is well within the statistical error bars. This calculation illustrates numerically the use of a thermodynamic cycle that retains the full strength of all the self-interactions.

Influence of the size of the system

A possible dependence of the accuracy on the size of the periodic system was discovered while running the simulations in a smaller water box. The result of the cycle in this smaller box (29.35Å size) turned out to be different from zero and of 0.24±0.1kCal/mol. Inaccuracy in the treatment of long range electrostatic interactions may be responsible for this anomalous behavior. Indeed, as we discussed in the section Alchemical pathway, there is a term proportional to the dipole of the primitive cell that is neglected in the formulation of Ewald²⁷. The error neglecting this term is inversely proportional to the volume of the system²⁷. It is possible that such a term influences the accuracy of the calculation when the box is small. Further analysis is required to account for this term in free energy calculations.

BAR vs TI

We require a relatively large number of λ states to accurately follow dF/dλ at domains of high curvature. A large number of intermediates reduces efficiency. As pointed out in³⁶, the method of Bennett Acceptance Ratio (BAR)³⁷ does not require as many intermediate states as TI. The equations for BAR are derived as a minimization of the variance of the estimate of the free energy difference in the limit of a large sample³⁷. The free energy difference between two states defined by the values of the switching parameter λ_i and λ_i+1 is computed according to the following formula:

$$\mathrm{\Delta }f({\lambda }_i\to {\lambda }_{i+1})=-k_{B}T\text{ ln}\frac{{\langle \frac{1}{1+\text{exp}\{\beta [U({\lambda }_{i+1})-U({\lambda }_i)-C]\}}\rangle }_{{\lambda }_i}}{{\langle \frac{1}{1+\text{exp}\{-\beta [U({\lambda }_{i+1})-U({\lambda }_i)-C]\}}\rangle }_{{\lambda }_{i+1}}}+C$$ (32)

The constant C is defined as

$$C=\mathrm{\Delta }f({\lambda }_i\to {\lambda }_{i+1})+k_{B}T\text{ ln}\frac{n_{i+1}}{n_i}$$ (33)

where n_i and n_i+1 are the number of configurations sampled with λ_i and λ_i+1, respectively. Using iteratively Eq. 32 and Eq. 33, we obtain the free energy difference between the two states. The overall free energy difference is then:

$$\mathrm{\Delta }f\text{'}={\displaystyle \sum _{i=1}^{N_{\lambda }-1}}\mathrm{\Delta }f({\lambda }_i\to {\lambda }_{i+1}).$$ (34)

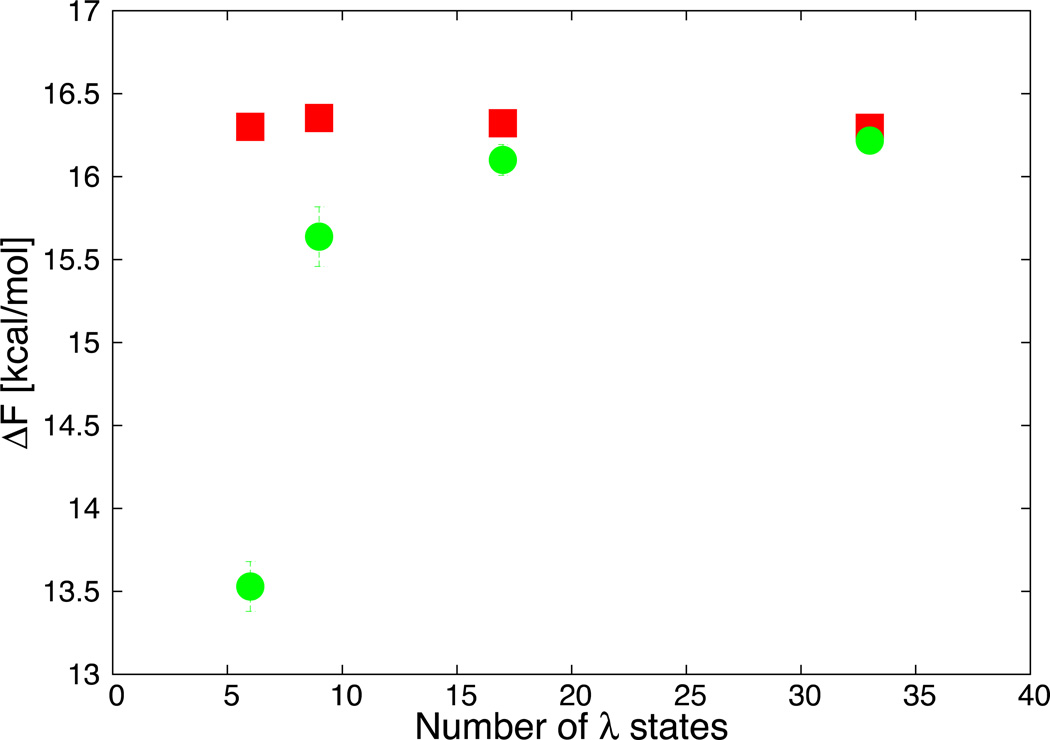
To test if BAR is more efficient than TI in our example, we performed the calculation of the MPH1 phase of the mutation in solution from the ILE side chain analog to GLN using a series of sets of λ states decreasing in size. The largest set is the one used for the calculations reported in the results. The second one has been obtained by keeping the first and last λ states and removing every other λ state. Removal of every other state was used to create other sets with a smaller number of states. The result is reported in Fig. 7.

Fig. 7.

The value of the free energy difference obtained with BAR (red) and TI (green) is reported as a function of the number of λ states used. Missing error bars imply error smaller than the size of symbol.

Even when only seven λ states were used, BAR is within half a kcal/mol from the result obtained with all the λ states, while the systematic error in TI grows much faster.

We repeated the cycle calculation with BAR for both the large and the smaller box and the same values for the free energy (as in TI) were obtained.

CONCLUSION

We examined and illustrated numerically a concrete dual topology pathway for a thermodynamic cycle that retains the self-interactions of the alchemical parts. We demonstrate that this path is exact, using straightforward argument based on statistical mechanics. No approximations are required. No distinction between bonded and non-bonded interactions was made. Numerical calculations illustrate high accuracy with a few nanosecond sampling at each λ using thermodynamic integration or BAR.

It is worth highlighting the following point: we are not proving that the self-interactions do not contribute to the free energy difference in a thermodynamic cycle. Different paths^12,14,38 show different contributions of the self-interactions to the relative free energy difference. This is due to the fact that the free energy difference is a state function, but the single contributions of the different interactions to the free energy are not. So it is possible to engineer pathways in which the specific contribution of bonded interactions to the relative free energy difference are not the same. Instead we propose an alchemical pathway that avoids their annihilation/creation. Avoiding their creation/annihilation reduces the terms that need to be turned on/off along the pathway, making, at least in principle, the calculation easier. The removal of interactions increases, in principle, the accessible space of conformations and is likely to require longer trajectories starting from a state with the full interactions on. This concept is intuitively clear when the bonded interactions are scaled down: in that case all the atoms of the annihilated compound close to the end-state are (almost) free to sample the whole simulation box^16,17 and the overlap between the distributions at different λ values significantly diminish. Therefore, retaining their covalent geometry reduces significantly the space to sample and increase the overlap of the intermediate distributions. The non-bonded interactions are likely to be similar. Indeed, hydrogen bonds and 1–4 interactions may help retaining the conformation of a compound close to a certain structure enhancing useful overlap between distributions of sequential λ.

Table 3.

Computing the reciprocal space electrostatic interactions by Ewald sums in MPH1. The reciprocal space is computed four times. In each of these calculations only a subset of charges is kept on, while the others are set to zero. The resulting potential and forces are then scaled by the switching parameter. In the first calculation only the electrostatic interactions between the “P” particles are kept on and the energy and forces are scaled by λ. Secondly, the electrostatic interactions of “P” and “N” particles are turned on and the resulting energy and forces are scaled by 1−λ. Third only the “M” particles have their charges on and the result is not scaled. Finally, only the charges of the “N” particles are kept on, and the result is scaled by λ. The sum of these four contributions is shown at the bottom of the table. The self-interactions are not scaled, and the external interactions are scaled by 1−λ.

MPH1
#	Type of particle interacting	Scaling	Result
1	P	λ	λU(P)
2	P N	(1−λ)	(1−λ)[U(P)+U(P,N)+U(N)]
3	M	1	U(M)
4	N	λ	λU(N)
OVERALL: U(P) + (1−λ)U(P,N) + U(N) + U(M)

Table 4.

Computing the reciprocal space electrostatic interactions by Ewald sums in MPH2. The reciprocal space is computed four times. In each of these calculations only a subset of charges is kept on, while the others are set to zero. The resulting potential and forces are then scaled by the switching parameter. In the first calculation only the electrostatic interactions between the “P” particles are kept on and the energy and forces are scaled by 1−λ. Secondly, the electrostatic interactions of “P” and “M” particles are turned on and the resulting energy and forces are scaled by λ. Third only the “M” particles have their charges on and the result is scaled by 1−λ. Finally, only the charges of the “N” particles are kept on, and the result is not scaled. The sum of these four contributions is shown at the bottom of the table. The self-interactions are not scaled, and the external interactions are scaled by λ.

MPH2
#	Type of particle interacting	Scaling	Result
1	P	(1−λ)	(1−λ)U(P)
2	P M	λ	λ[U(P)+U(P,M)+U(M)]
3	M	(1−λ)	(1−λ)U(M)
4	N	1	U(N)
OVERALL: U(P) + λU(P,M) + U(M) + U(N)

Table 5.

The number of λ states used in the evaluation of the free energy differences of Fig. 2 for each of the mutation phases MPH1 and MPH2. More details on MPH1 and MPH2 are available in Table 1 and Table 2. The last column shows the total simulation time for each stage in the cycle.

	MPH1	MPH2	Total simulation time
ΔFI-Q,solv	33	33	132ns
ΔFI-Q,vac	33	33	132ns
ΔFI,solv	35	23	116ns
ΔFQ,solv	35	23	116ns