Thermodynamic Analysis of Protegrin-1 Insertion and Permeation through a Lipid Bilayer

Abstract

Molecular dynamics (MD) simulations are used to study the pathway for the insertion of the cationic antimicrobial peptide protegrin-1 (PG1) into mixed anionic lipid bilayers composed of palmitoyl-oleoyl-phosphatidylglycerol (POPG) and palmitoyl-oleoyl-phosphatidylethanolamine (POPE) in a 1:3 ratio (POPG:POPE). We calculate the potential of mean force (PMF) during the transfer of the peptide from the bulk aqueous phase to the transmembrane (TM) configuration using the adaptive biasing force (ABF) method. We find that the PMF has two energy minima separated by an energy barrier. One minimum corresponds to the fully transmembrane inserted state, with a free energy of −20.1 kcal/mol. The second PMF minimum, which corresponds to adsorption to the membrane surface, has a value of −2.5 kcal/mol. The PMF also shows the existence of a free energy barrier of +6.3 kcal/mol for the insertion process.

Using the Kramers theory Langevin equation and the Grote-Hynes theory generalized Langevin equation, we calculated the transmission coefficient for PG1 diffusion through the potential barrier. We focus on the use of the PMF and the time correlation function of the fluctuation of the instantaneous force to calculate the rate constants for insertion/deinsertion of PG1 from the mixed POPG:POPE membrane. The influence of the activation free energy barrier on the dynamics of the insertion and permeation of peptides through the membrane are discussed.

Introduction

The thermodynamics and kinetics of cationic peptides interacting with different types of membranes have been the subject of considerable experimental, theoretical and computational interest in recent years. Much of this interest results from the important role that membrane insertion of cationic peptides and permeation through the lipid bilayer plays in antimicrobial defense.

Protegrin-1 (PG1) is a potent β-hairpin cationic antimicrobial peptide.^1,2 A simple model that explains how PG1 kills bacteria involves insertion of peptides into the membrane and oligomerization to form pores. Cytosolic potassium is released through these pores, and sodium enters the cell, causing a significant transmembrane potential decay, a subsequent cell volume expansion and lethal membrane rupture.^3,4 Importantly, octameric pores have been observed inside anionic lipid bilayers determined by NMR⁵ and simulated by molecular dynamics.⁶

In order to develop mechanistic explanations of the antimicrobial activity of PG1, substantial efforts have been expended on determining how protegrin peptides interact with model membranes.^6–16 For example, in,¹⁵ the energetics of protegrin binding to model membranes were determined. The preferred orientations and conformations of PG1 were also established in model membranes.¹⁶ Recently an interested study suggested that PG-1 forms fibrils in solution but only small oligomers on the surface of lipid bilayer membrane.¹⁷ Less attention has been paid to the phenomenon of membrane insertion. In this work, we attempt to address this gap by investigating the insertion and permeation of PG1 through a mixed anionic lipid bilayer composed of a 1:3 ratio of palmitoyl-oleoyl-phosphatidylglycerol (POPG) to palmitoyl-oleoyl-phosphatidylethanolamine (POPE) (1:3 POPG:POPE) at 310 K, using fully atomistic molecular dynamics (MD) simulations. We calculate the potential of mean force (PMF) along a single reaction coordinate corresponding to the separation distance between the centers of mass of the PG1 peptide and the POPG:POPE membrane. We present a methodology based on the adaptive biasing force method (ABF)^18,19 method which is implemented as a part of the Collective Variables module of NAMD²⁰ to probe membrane insertion profiles.

Recently, an implementation of the ABF method was described to cases involving conformational changes in model peptides, and translocation of ions and small molecules across a lipid membranes.²¹ Gorfe et. all,²² also presented computational results on the free energy profile for the transfer of the H-ras membrane anchor from water to a bilayer of DMPC lipids. Ulmshnaider et al.²³ used replica exchange simulations and showed that insertion for the termostable tryptophanflanked WALP peptides is highly favorable, with transmembrane states preferred over interfacial state.

Herein, we calculate the simulated potential of mean force for the PG1 insertion across a mixed POPG:POPE membrane. We find that the PMF has two minima in the energy profile and one potential barrier. We focus on the use of the PMF and the time correlation function of the instantaneous force fluctuations from the mean to calculate the rate constants for insertion/deinsertion of PG1 from the mixed POPG:POPE membrane. The transmission factor for PG1 peptide insertion/deinsertion is calculated using a simplified stochastic model based on the Langevin and generalized Langevin equations, which represent dynamical solvent effects on the rate constant. We then present and discuss the results and also speculate on the kinetic pathways for PG1 insertion and permeation.

Theory

We use MD simulations to extract the PMF,W(z), and the diffusion coefficient profile, D(z), along the relevant reaction coordinate for the calculation of both equilibrium and dynamic properties. The diffusion over an energy barrier in a biological membrane is an important example of a kinetic process involving a jump over a barrier. The combination of MD simulations and transition state theory offers the possibility to evaluate the insertion and permeation of a PG1 peptide through a lipid bilayer.

The membrane permeability

Membrane permeation studies are important for drug design and for predicting the permeability of peptides. The permeation resistance of the membrane, R to any solute is defined as the inverse of the permeability coefficient P, and can be expressed²⁴ as the integral over the local resistance L(z) across the membrane (see Appendix for detailed derivation)

$$R=\frac{1}{P}={\displaystyle {\int }_{-l}^l}\mathit{\text{dzL}}(z)\equiv {\displaystyle {\int }_{-l}^l}\mathit{\text{dz}}\frac{1}{K(z)D(z)},$$ (1)

where z is the reaction coordinate of the peptide’s center of mass with the origin z = 0 chosen to coincide with the center of the membrane, (see Figure 1). The distance l divides the free and bound volumes. Peptides are considered to be bound if |z| ≤ l and free if |z| > l, where the choice of l is discussed below. In this study, the reaction pathway for the peptide is explored for z > 0. We can safely assume that the result for the lipid bilayer leaflet considered is valid for the opposing leaflet due to the symmetry of the lipid bilayer.

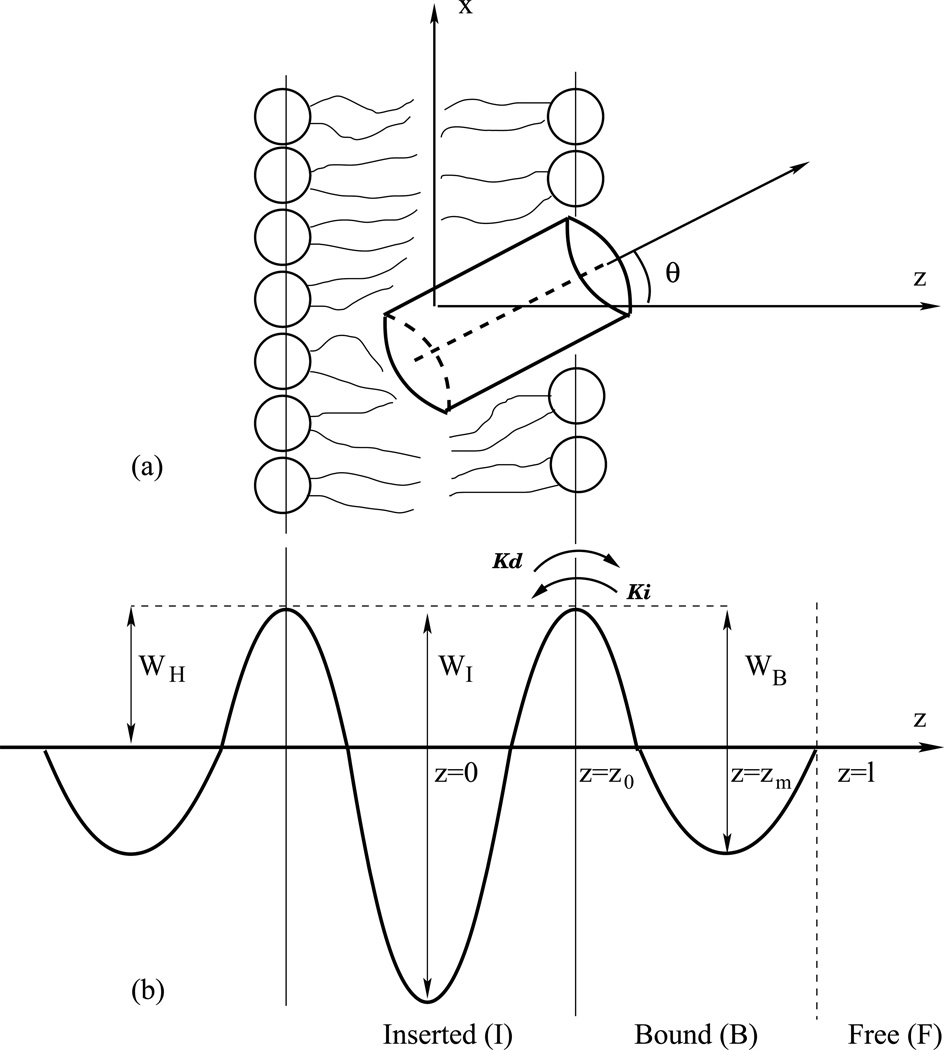
Figure 1.

(a) Schematic illustration of a cylindrical protein in a lipid bilayer. The peptide center of mass is displaced a distance z from the bilayer midplane, and its long axis is oriented at angle θwith respect to the membrane normal. (b) Illustration of barrier crossing with activation free energy barrier W_H with the rate constant K_I from the bound state B to the inserted state I. z is the reaction coordinate, z₀ the location of the barrier top (transition state), and W_B and W_I the bound and insertion energy wells, respectively. z = l divides the free (F) and bound (B) volumes.

K(z) and D(z) are the depth-dependent partition coefficient and diffusion coefficient of PG1, respectively. The partition coefficient K(z) is related to the difference in the free energy, or the value of the PMF, W(z), between the bulk aqueous phase (outside the membrane) and the value at a particular depth z

$$K(z)=\text{exp}(-\beta W(z))$$ (2)

where β = 1/k_BT with k_B being Boltzmann’s constant. In particular, the PMF, W(z), is calculated as explained in²⁵ with the following equation:

$$W(z)=-{\displaystyle {\int }_l^z}\mathrm{F̅}(z\prime )\mathit{\text{dz}}\prime ,$$ (3)

where F̅(z) is the simulation time-averaged force acting on the peptide center of mass at a particular depth z.

To find the diffusion coefficient D(z) from MD simulations, it is useful to determine the fluctuation of the instantaneous forces F(z, t) acting on the peptide, expressed as deviations from the mean force F̅(z)

$$\mathrm{\Delta }F(z,t)=F(z,t)-\mathrm{F̅}(z)$$ (4)

and the related local time-dependent friction coefficient ξ(z, t) of the diffusing peptide, which is defined by the time autocorrelation function²⁶ C_ΔF (z, t) of the fluctuations of the instantaneous forces ΔF(z, t) as

$$\xi (z,t)=\beta C_{\mathrm{\Delta }F}(z,t)=\beta \langle \mathrm{\Delta }F(z,t)\mathrm{\Delta }F(z,0)\rangle$$ (5)

Here 〈…〉 is an equilibrium ensemble average (or a time-average over a trajectory in a simulation). Using the fluctuation-dissipation theorem, the local diffusion coefficient D(z) is related to the static friction coefficient ξ̃(z), as follows

$$D(z)=\frac{1}{\beta \xi ̃(z)}$$ (6)

where the static friction coefficient ξ̃(z) is given by

$$\xi ̃(z)={\displaystyle {\int }_0^{\mathrm{\infty }}}\mathit{\text{dt}}\xi (z,t)=\beta {\displaystyle {\int }_0^{\mathrm{\infty }}}{\mathit{\text{dtC}}}_{\mathrm{\Delta }F}(z,t)$$ (7)

From (2) and (6), the resistance (1) R can be evaluated as

$$R={\displaystyle {\int }_{-l}^l}\mathit{\text{dz}}\beta \xi ̃(z)\text{exp}(\beta W(z))\equiv {\displaystyle {\int }_{-l}^l}L(z)\mathit{\text{dz}}.$$ (8)

with the local resistance L(z) given by

$$L(z)=\beta \mathrm{\xi ̃}(z)\text{ exp}(\beta W(z)).$$ (9)

The permeation resistance can thus be found by MD simulations.

Insertion rate constant

The transfer of the peptide between the free state F, the bound (adsorbed) state B and then the inserted (absorbed) state I can be described as the spatial diffusion-controlled regime of reactions F ⇄ B ⇄ I, viewed as a series of potential barrier crossing events (Figure 1). In this work we will be interested only in the B ⇄ I reaction. The equilibrium partition coefficient, K, between the bound state B and the inserted state I can be determined by the ratio of the insertion rate constant k_i from state B to state I, and the deinsertion rate constant k_d from state I to state B. Equivalently, K can also be computed from the change in free energy between the two states:

$$K=\frac{k_i}{k_d}=\text{exp}(-\beta (W_I-W_B))$$ (10)

Below, we use this estimate of the partition coefficient to calculate the rate constant k_i for the insertion of PG1 from knowledge of the deinsertion rate constant k_d.²⁷ The exact kinetic constants k_d and k_i can be calculated using rare-event methods^28–30 by sampling trajectories from the equilibrium distribution at a dividing surface using MD simulations. However, these computational methods are inordinately time-consuming, leading us to the use of the present stochastic approximation. The motion of a particle over a potential barrier located between reactant and product potential wells is now described by the Langevin equation (LE) of motion:

$$m\mathrm{z̈}(t)=-\frac{\mathit{\text{dW}}(z)}{\mathit{\text{dz}}}-\mathrm{\xi ̃}(z)ż(t)+F(z,t)$$ (11)

Here, F(z, t) is a random force resulting from the solvent molecules colliding with the solute. Using the LE equation (11), Kramers^31,32 analyzed the steady-state Fokker-Plank equation which is based on the concept of a Markov process for the position and velocity of a particle. For thermally activated processes, it is possible to show that the expression for the rate constant $k_d^{\mathit{\text{KR}}}$ for deinsertion from the inserted state (I) to the bound state (B) is:

$$k_d^{\mathit{\text{KR}}}=k^{\mathit{\text{TST}}}{\kappa }_{\mathit{\text{KR}}}$$ (12)

where k^TST is the transition state theory (TST) rate constant and κ_KR is the transmission coefficient. The former is an equilibrium quantity, and can be obtained from the free energy profile, or the potential of mean force W(z) for the reaction coordinate z along the reaction path (Figure 1). The transmission coefficient κ_KR is a dynamical quantity, which could be obtained using the autocorrelation function of fluctuations in the instantaneous forces between the peptide and the solvent. TST assumes the peptide never recrosses the barrier once it has passed over it. However, interactions of the peptide with the solvent can cause a recrossing of the free energy barrier, leading to lower values of the kinetic rate constant. Thus, the error in the TST approximation is corrected by a transmission coefficient κ_KR ≤ 1. A transition rate process of deinsertion is based on the determination of the barrier. That is why the first step in our evaluation of the deinsertion rate constant for PG1 is the calculation of the PMF for PG1 inside and outside the membrane. For a PMF W(z), with a single barrier at z₀, (see Figure 1), k^TST is given by^33,34

$$k^{\mathit{\text{TST}}}={(2\pi m\beta )}^{-1/2}\frac{\text{exp}(-\beta (W(z_0)-W(0)))}{{\displaystyle {\int }_0^{z_0}}\mathit{\text{dz}}\text{exp}(-\beta (W(z)-W(0)))}$$ (13)

where m is the effective mass of the peptide. Equation (13) has three terms with physical interpretations. The first term is independent of the PMF and is a measure of the average magnitude of the velocity of the molecule. The next two terms that contain exponential functions are dependent on the shape of the PMF. The TST equation (13) calculates the equilibrium probability of finding the molecule at the maximum of the free energy barrier relative to the probability of finding the molecule in the adsorbed state, multiplied by the mean velocity, using a half-Maxwellian for probability velocity averaging. Note that k^TST is an equilibrium property. The dynamics are accounted for by the transmission factor κ_KR, given by

$${\kappa }_{\mathit{\text{KR}}}=\sqrt{1+{(\gamma /2{\omega }_b)}^2}-\gamma /(2{\omega }_b)$$ (14)

where γ= ξ̃ (z₀)/m and ω_b is the barrier frequency which is related to the external potential near the transition state defined by ω_b = (−Ẅ (z₀)/m). With a parabolic shape approximation for the PMF, we find the barrier frequency from

$$W(z)=-\frac{1}{2}m{\omega }_b^2{z}^2$$ (15)

We should note that Kramers theory is valid in the high-viscosity regime. The LE equation with a constant friction coefficient is only valid in the limit of long times, where an equilibrium is established. Grote and Hynes^35,36 analyzed the system dynamics based on the concept of a non-Markov process with memory friction, when the friction coefficient at a given time γ(t) depends on previous velocities along the trajectory, described by the generalized Langevin equation (GLE)

$$m\mathrm{z̈}(t)=-\frac{\mathit{\text{dW}}(z)}{\mathit{\text{dz}}}-{\displaystyle {\int }_0^t}\mathit{\text{dt}}\prime \xi (z,t\prime )ż(t-t\prime )+F(z,t)$$ (16)

Using this equation, the rate constant $k_d^{\mathit{\text{GH}}}$ ³⁵ has the form

$$k_d^{\mathit{\text{GH}}}=k^{\mathit{\text{TST}}}{\kappa }_{\mathit{\text{GH}}}$$ (17)

where κ_GH is the transmission factor which is related to MD simulations through the time correlation function ξ(z₀, t) of the fluctuations of the instantaneous forces in the intermediate, or “barrier” region located between two stable states.

$${\kappa }_{\mathit{\text{GH}}}=\frac{1}{{\kappa }_{\mathit{\text{GH}}}}-\frac{1}{{\omega }_b}{\displaystyle {\int }_0^{\mathrm{\infty }}}\mathit{\text{ dt}}\text{exp}(-{\kappa }_{\mathit{\text{GH}}}{\omega }_{b}t)\xi (z_0,t)$$ (18)

This equation is obtained with the assumption of a parabolic barrier (see Appendix) and is an implicit equation for κ_GH that in general must be solved by iteration. In,³⁷ Tolokh and co-workers found that the Grote-Hynes estimate for the transmission coefficient κ_GH is in excellent agreement with MD results based on rare-event methods, while the Kramers estimate for the transmission coefficient κ_KR is about 40%too small for ionmotion across the energy barrier. For our system, we will estimate and compare the transmission coefficients κ_GH and κ_KR, since we expect the process of PG-1 crossing the insertion barrier to exhibit significantly different properties as compared to ion transport.

Methods

Microscopic models for a PG1 peptide inside a POPG:POPE membrane

Our system contains a single PG1 peptide inside a mixed membrane of 112 lipids (i.e., 56 lipids in each leaflet) containing 84 POPE lipids and 28 POPG lipids. The system is solvated with nearly 10,000 TIP3P water molecules, 53 chlorine ions, and 74 sodium ions. Chlorine and sodium ions are added to create a 0.15 M physiological salt solution and to neutralize the charge of the peptide and POPG head groups. PG1 is an 18-residue cationic β-hairpin antimicrobial peptide (RGGRL CYCRR RFCVC VGR-NH2).¹ The monomeric solution structure of the β-hairpin PG1 was obtained from the protein data bank (PDB code 1PG1). To build a transmembrane complex for molecular dynamics (MD) simulations of PG1 inside POPG:POPE membrane, we used the CHARMM-GUI membrane builder with the replacement method.³⁸ The peptide was placed with its principal axis parallel to the bilayer normal and the peptide center of mass was located at the bilayer center of mass (Figure 1). The lateral area occupied by the peptide and used in the membrane builder is approximately 160 Ų.¹²

Molecular Dynamics Protocol

Our goal is to use molecular dynamics simulations to calculate a potential of mean force (PMF) for the deinsertion of PG1. In this section, we discuss the molecular dynamics simulation protocol; the details of the PMF calculation are deferred to the next section. Seventeen different simulations were conducted with different values of the separation distance between the centers of mass of the peptide and bilayer. The system was constructed in a rectangular cell using the CHARMM.³⁹ The CHARMM-27 force field⁴⁰ with CMAP corrections⁴¹ was employed. The structure of the β-hairpin PG1 was generated with two disulfide bonds, amidated C-termini, and six positively charged arginines, reflecting the typical protonation state of arginine. An assumption that may be of limited accuracy is that the protonation state of PG1 does not change when PG1 is embedded inside the lipid bilayer. We used the NAMD software package version 2.7b1,²⁰ and employed the Nose-Hoover-Langevin temperature and pressure controller^42,43 for all simulations. The pressure was set to 1 atmosphere with a piston period set to 200 fs and a piston decay of 100 fs. The system was heated to 310 K (above the gel-liquid crystal phase transition of the mixed membrane⁴⁴) in increments of 30 K, running for 5000 steps at each temperature. After minimization and heating, each simulation box was equilibrated for 8 ns in the NPT ensemble. The water molecules were simulated using the TIP3P water model.⁴⁵ The van derWaals interactions were smoothly switched off over a distance of 4 Å, between 8 and 12 Å. The electrostatic interactions were simulated using the particle mesh Ewald summation with a grid of approximately 1 point per 1Å in each direction.⁴⁶ Use of the SHAKE algorithm to constrain bonds involving hydrogens enable an integration time steps of 2 fs to be used. During equilibration, the area per lipid remained constant for the mixed (1:3) POPG:POPE system, with an average value of 62.3 ± 1.4 Ų. The average dimensions of the equilibrated simulation box were 60.4 × 60.4 × 120.1 Å.

Construction of the potential of mean force (PMF) with the adaptive-biasing-force (ABF) method

The PMF was computed using the ABF method.^18,19 ABF is implemented as a part of the Collective Variables module of NAMD, version 2.7b1.²⁰ We calculate the potential of mean force,W(z), along a single reaction coordinate corresponding to the separation distance, z, between the centers of mass of the peptide and the membrane. The path depicted in (Figure 2) is used to describe the insertion process. The main idea is that the electrostatic interaction^7,8,12,16 drives the spontaneous insertion of the highly polar peptide from the binding state B to the transmembrane state I inside the hydrophobic core. We should note, however, that the charged N- and C- termini and the β-hairpin turn are all outside of the lipid hydrophobic core and in contact with lipid headgroups.

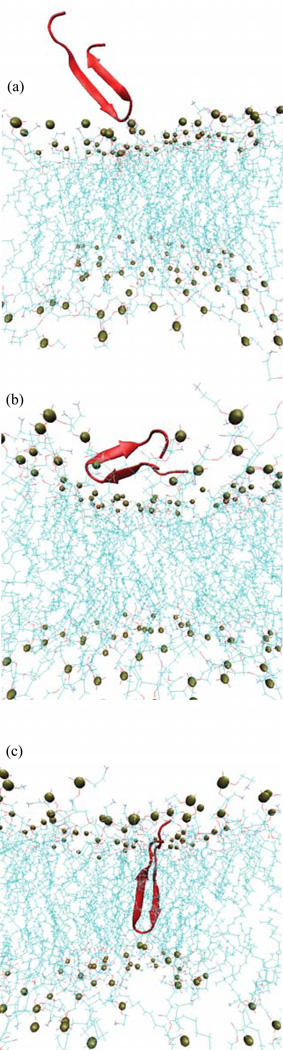
Figure 2.

Insertion path of the PG-1 peptide. The peptide is shown from the free state (a) to the adsorbed state (b), followed by subsequent insertion (c). The snapshots illustrate peptide localization in three of the seventeen independent ABF runs. For (b) and (c) average peptide distance z = 22 Å and z = 14 Å above the membrane mid-plane, respectively.

In the ABF method, the derivative of the PMF, dW(z)/dz, with respect to the reaction coordinate and the forces exerted along the reaction coordinate during MD simulation can be evaluated in a scheme similar to thermodynamic integration as follows

$$\frac{\mathit{\text{dW}}(z)}{\mathit{\text{dz}}}={\langle \frac{\partial U(r)}{\partial z}-\frac{1}{\beta }\frac{\partial \text{log }|J|}{\partial z}\rangle }_z\equiv -{\langle F_z\rangle }_z,$$ (19)

where U(r) is the potential energy function of the system with Cartesian coordinates r and |J| is the determinant of the Jacobian for the transformation from generalized to Cartesian coordinates. 〈F_z〉_z is the mean force for the reaction coordinates z along the reaction pathway. ABF is based on the computation of the mean force along z, which is then canceled out by an equal and opposite biasing force, allowing the system to overcome barriers and escape from minima in the free energy landscape. To overcome free energy barriers so that the system diffuses on a flat energy surface during unconstrained dynamics, an iterative biasing force, F^ABF, is defined by:

$$F^{\mathit{\text{ABF}}}={\nabla }_r\mathrm{W̃}={\langle F_z\rangle }_z{\nabla }_{r}z,$$ (20)

where W̃ denotes the current estimate of the PMF, 〈F_z〉_z, the current average of F_z, and ∇_rz is a gradient of reaction coordinate⁴⁷ Because the estimation of W̃ is progressively improved during the simulation, uniform sampling is achieved as a biasing force adapts to precisely match the free energy barrier.

The reaction pathway z for PG1 is explored between 0 and 34 Å along the membrane normal. The peptide was initially placed in a transmembrane configuration in the centre of the membrane, i.e. at z = 0, in which the peptide backbone is perpendicular to the surface of the membrane. To increase the efficiency of the calculation and to minimize statistical errors, the reaction pathway was divided into 17 sections of 2 Å each, and boundary potentials with a force constant of 100 kcal/mol/Ų were applied in each window. In the ABF calculation, force samples were accumulated in bins 0.01 Å wide and the canceling adaptive-biasing-force force was applied after sampling for 500 steps in each bin. The duration of the simulated trajectory for the free energy profile in each section was 20 ns, as the total sampling time must be long enough to ensure the collection of uncorrelated configurations. We found from a numerical test that 500 samples in each bin of size 0.01Å are enough to minimize systematical error and to obtain a reasonable estimate of average force. Comparable ABF parameters have been used in⁴⁸ during investigation free energy landscape for shot peptides.

Results and discussion

Insertion Affinity of PG1 Peptides

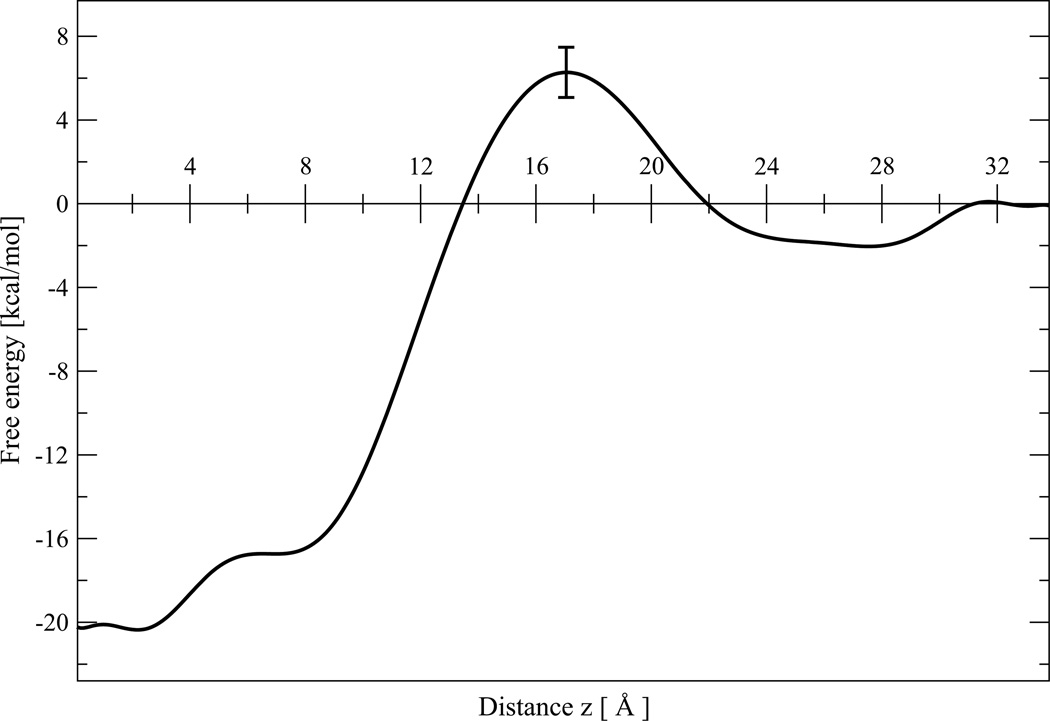
Figure 3 shows the one-dimensional PMF, W(z), for the PG1-POPG:POPE system, as a function of the reaction coordinate z. Apparently the PMF has two minima of the energy profile and one potential energy barrier. One minimum corresponds to full insertion or transmembrane (TM) peptide topology at z = 0 with a plateau which extends to z=3Å. Another minimum which has a wider plateau in the region from z=23 to z = 27Å corresponds to the surface-bound or adsorbed state of PG1. As displayed in Figure 3, the first PMF minimum is relatively deep, with a value of −20.1 ± 1.1 kcal/mol. The second PMF minimum, which corresponds to adsorption, is relatively shallow, with a value of −2.5 ± 0.6 kcal/mol. This last value is in good agreement with a PMF minimum of −2.4 ± 0.8 kcal/mol which was obtained using a variant of constrained MD and thermodynamic integration for PG1 on a POPG:POPE membrane.¹⁵ The potential barrier is about 6.3 ± 1.2 kcal/mol at z = 17 Å. Because the system is nonuniform in the z direction, it is useful to consider three regions of the PMF separately. The dividing lines between the regions are somewhat arbitrary; for 0.0 < z < 13.8Å and z > 22.0 Å we obtain that W(z) < 0, whereas for 13.8<z < 22 Å,W(z) > 0.

1. Adsorption region (22 < z < 34 Å). This is the region of the PG1 interaction with the membrane due to indirect peptide-membrane electrostatic interaction, and due to the asymmetrical distributions of water and ions around the peptide. This region can be characterized as a region with low headgroup density.

2. Transition state or barrier-crossing bilayer water interface region (13.8 < z < 22.0 Å), the region with high lipid headgroup density. This is the region where the direct peptide-membrane electrostatic interactions and van der Waals forces between headgroups of the upper lipid leaflet and peptide play a dominant role.

3. Insertion region (0.0 < z < 13.8 Å), the region with high lipid tail density. From one side there are strong electrostatic interactions between the peptide’s positively charged residues and negatively charged lipid headgroups, and from another side there are strong hydrophobic interactions between the peptide backbone and lipid tails inside the hydrophobic core.

Figure 3.

One-dimensional PMF W(z) for PG1-POPG:POPE system, as a function of reaction coordinate z. Each data point represents the mean of the last four 5 ns simulation of W(z), and the error bar represents the dispersion among the four.

All these interactions drive the spontaneous transfer of the highly charged peptide from the adsorbed region to an intermediate one (transition state or barrier-crossing bilayer-water interface), and subsequently to the inserted region.

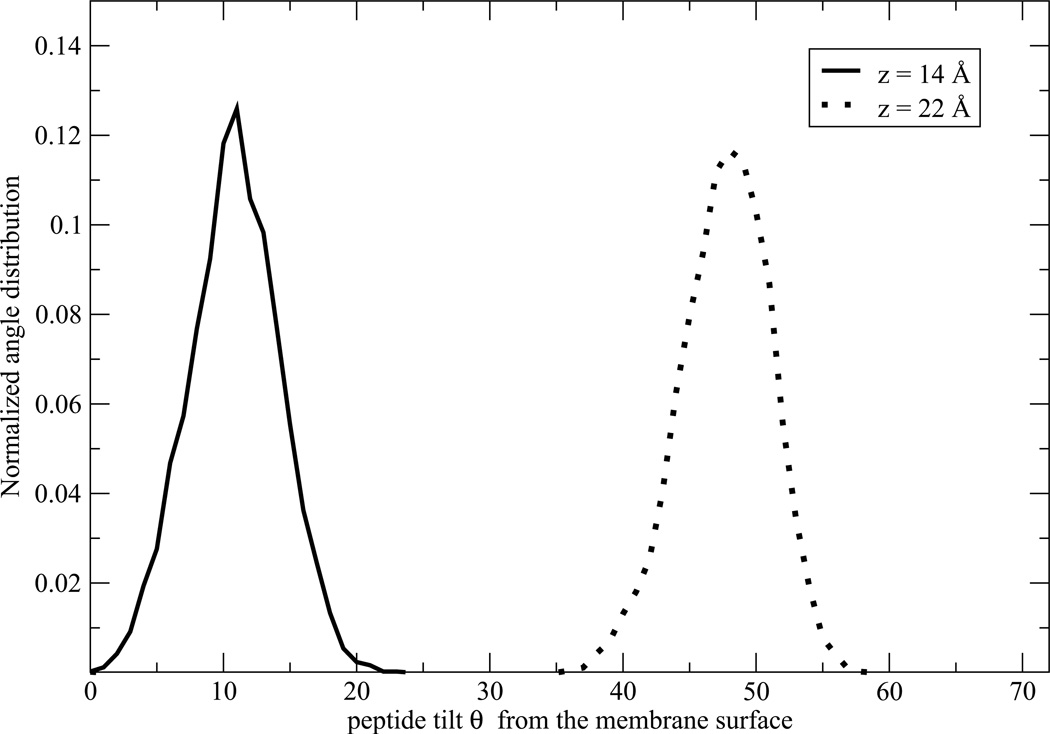
The peptide insertion mechanism can be visualized by the schematic illustration of the insertion of the PG1 peptide at 310 K (Figure 2), and by plotting the distribution of the angle between its long axis and the membrane normal (Figure 4). In the last figure, we show only two angle distributions θ for the most important distances z: for z = 14.0 Å from the bilayer center, the peptide is located near the end of the insertion region and for z = 22.0 Å, PG1 is located near the beginning of the adsorbed region. In the adsorbed and binding regions, MD simulations indicate that there is not a significant time effect on the peptide orientation. The average angle between the peptide long axis and the membrane normal is θ ≈ 48° ± 12° for the adsorption region. In the second region, for 13.8 < z < 22.0 Å, the barrier crossing process involves fast orientational reorganization. In the inserted region, the peptide is almost perpendicular to the membrane surface, with an average of θ ≈ 11° ± 4° (see Figure 2 and Figure 4). For clarity, data are shown only for z = 14 Å.

Figure 4.

The peptide insertion mechanism can be visualized by plotting its long axis angle distribution θ with respect to the membrane normal as shown in Figure 1 (a).

Diffusion Coefficient and Force Fluctuation Autocorrelation Function

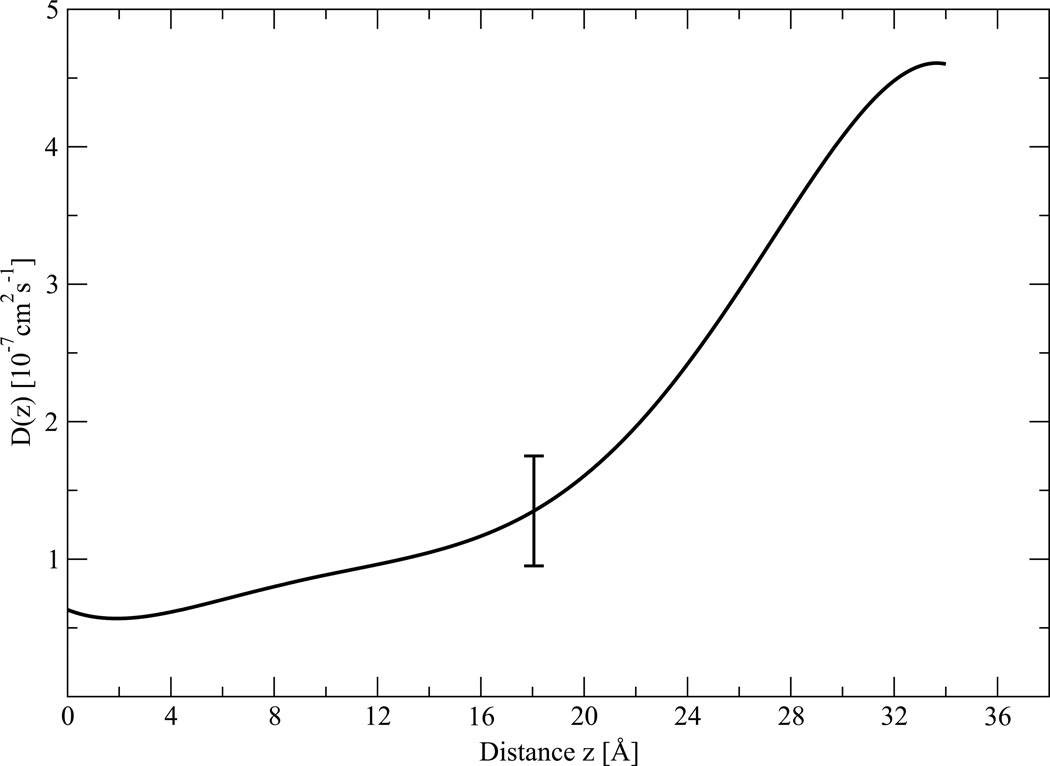
According to eq. 10, the diffusion coefficient can be obtained from the time correlation function of the instantaneous force fluctuation from the mean. The diffusion coefficient profile D(z) as calculated with eq. 6 is plotted in Figure 5. We calculate the diffusion coefficient separately inside each of the seventeen windows from the ABF calculation. Each data point represents the mean of the last four 5 ns simulations of D(z), and the error bars represent the variation among the four at each depth. The diffusion curve was interpolated with six degree polynomial constructed on these seventeen data points. Here we made an assumption that the diffusion coefficient does not change significantly inside each 2 Å window, as the size of the window is relatively small compared to the size of the peptide. As we see from Figure 5, D(z) decreases entering the membrane, especially in region II, then becomes relatively uniform in region III. Diffusion coefficients inside the membrane are lower than in the bulk water phase because of the higher viscosity of the lipid environment.

Figure 5.

Diffusion coefficient D(z) profile calculated with eq. (6). Each data point represents the mean of the last four 5 ns simulation of D(z), and the error bars represents the dispersion among the four at each depth.

Local Resistance and Permeability Coefficient

In order to calculate the resistance and permeability coefficient, we need to define the binding geometry parameter, l. Thus, when analyzing the PMF above the membrane, we find that W(z) decreases monotonically with the peptide-membrane separation distance. In particular, the PMF for l = 34 Å, calculated using the ABF method, is less than k_BT for our system. We can therefore surmise that above 34 Å, where the PMF has relatively low values, interactions between the peptide and membranei are relatively weak compared to thermal forces. Therefore, the peptide is considered to be bound within z < 34 Å.

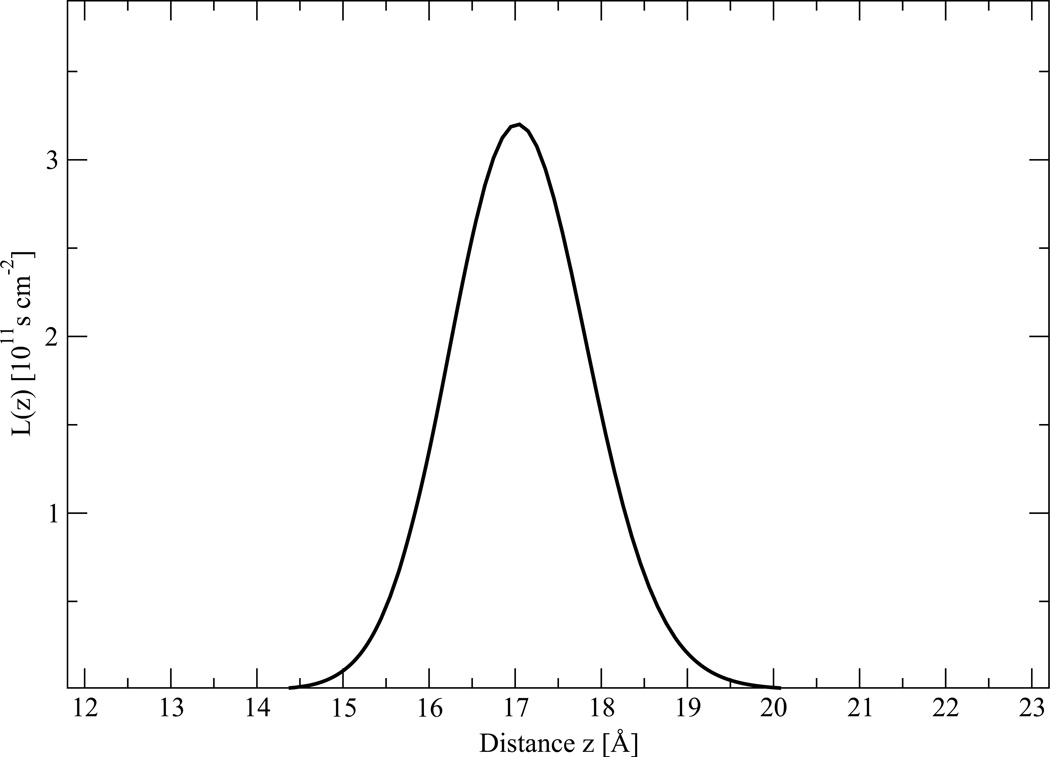
Local resistance values L(z) for PG1, calculated with equation (9), are plotted in Figure 6. Despite the fact that no experimental data are available for PG1, some discussion is possible. Based on local resistance L(z), using equation (8), the value for the permeability P for PG1 through POPG:POPE membranes is 6.2 × 10⁻⁵ cm s⁻¹. For comparison, water and methanol have permeability coefficients of 1.3 × 10⁻² cm s⁻¹ and 1.9 × 10⁻² cm s⁻¹ through PC bilayers, as measured from MD simulations.^24,49 The resistance is largely determined by the free energy profile, as L(z) is proportional to exp(βW(z)). The contribution of the diffusion coefficient is relatively small. The main contribution to L(z) is offered by the headgroup region, which is highly charged and where βW(z) > 0. The hydrophobic hydrocarbon core of the membrane corresponding to the insertion region (III) and the adsorption region (I) do not offer significant contributions to resistance, as L(z) is essentially determined by the PMF barrier.

Figure 6.

Local resistace profile L(z) for the PG1 peptide, obtained from eq. (9) along the z axis from one side of the bilayer.

It is possible to estimate an error in the permeability from the propagation of PMF and diffusivity uncertainties. The fairly sizeable error for the free energy in Figure 3 gives the relatively large uncertainty in permeability, which may be as large 200% of the absolute value. For example, this uncertainty in permeability, near the peak of the barrier, has an average of L₀ = 3.2 ± 6.5 × 10¹¹ s cm⁻². Similarly this error for the PMF would propagate a large uncertainty to the insertion and de-insertion rate constants. Therefore we caution that our permeability results are only a rough estimate, suitable merely for qualitatively analysis only. In principle, in order to reduce uncertainties by a factor of two in free energy an increase is required in the simulation times by a factor of four. Furthermore, the reaction coordinate pathway of interest should be divided into small sections in a such way that changing of energy in each section should not exceed 1 k_BT. The computational cost to reduce the uncertainty levels can then be prohibitive.

Calculation of the rate constants for insertion/deinsertion of PG1

We now focus on the use of the PMF and the time correlation function of the instantaneous force fluctuation from the mean to calculate the rate constants for insertion/deinsertion of PG1 from the mixed POPG:POPE membrane. By using the PMF presented in Figure 3 and the TST equation (13), we have calculated the deinsertion rate constant (k^TST) to be 3.3 × 10⁻⁹ s⁻¹ at 310K.

We have combined our estimates of the TST rate constant to calculate an apparent rate constant for desorption of PG1 using Kramers (14) and Grote-Hynes (18) transmission coefficients, which were calculated to be 0.11 and 0.12, respectively. That is, for each PG-1 peptide that reaches the peak of the free energy barrier (from the inserted state), only about 11–12 % transfer to the adsorbed state.

We calculate the values for the rate constants $k_d^{\mathit{\text{KR}}}\text{ and }{k}_d^{\mathit{\text{GC}}}$ for deinsertion from the insertetd state (I) to the bound state (B) to be 3.5 × 10⁻¹⁰ s⁻¹ and 4.0 × 10⁻¹⁰ s⁻¹, respectively. At the same time, the value of the rate constants $k_i^{\mathit{\text{KR}}}\text{ and }{k}_i^{\mathit{\text{GC}}}$ for insertion, using equation (10), were found to be 6.6 × 10³ s⁻¹ and 7.6 × 10³ s⁻¹ at 310K, respectively.

Conclusion

We calculate the potential of mean force along a single reaction coordinate corresponding to the separation distance between the centers of mass of a PG1 peptide and a 1:3 POPG:POPE membrane using the ABF method. We find that the PMF has two minima and one potential barrier. One minimum corresponds to full insertion or TM peptide topology, with a free energy of −20.1 ± 1.1 kcal/mol. The TM state is characterized by a stable orientation, in which PG1 is almost perpendicular to the membrane surface, with an average angle between the membrane normal and the peptide principal axis of θ ≈ 11° ± 4°. The second PMF minimum, which corresponds to adsorption to the membrane surface, is −2.5 ± 0.6 kcal/mol. This minimum is located in the adsorbed region. The peptide here is no longer in a TM orientation, but is located on the membrane/water interface, with an average angle θ ≈ 49° ± 7° with respect to the membrane normal. The potential barrier is about 6.3 ± 1.2 kcal/mol at z = 16. Our simulation results for the TM orientation are in qualitative agreement with experimentally observed orientations derived from solid-state NMR data for PG1 in a TM configuration and for PG1 with dimethylated arginine groups, which is bound to the POPG:POPE membrane/water interface.⁴⁴ In addition, our predictions of the TM configuration are in good agreement with the theoretical predictions for PG1 orientation in DLPC lipid bilayers derived from an implicit membrane model¹⁶ The influence of the activation free energy barrier plays an important role in determining the dynamics of the insertion of peptides into the membrane. Using the time correlation function of the instantaneous force fluctuation from the mean, we calculated the diffusion coefficient profile. As expected, we found that diffusion coefficients inside the membrane are lower than in the bulk water phase because of the higher density of the lipid environment. We focus on the use of the PMF and the time correlation function of the instantaneous force fluctuation from the mean to calculate the rate constants for insertion/deinsertion of PG1 from the mixed POPG:POPE membrane. We found that for crossing the barrier in our system, the Kramers estimate for the transmission coefficient κ_KR is about 10 % lower than the Grote-Hynes transmission coefficient κ_GH, which is generally in better agreement with MD results based on rare-event methods.³⁷ It will be interesting to compare dynamic properties of other systems, such as PG1 interacting with zwitterionc, neutral membranes. In a separate publication,⁵⁰ we will report the PMF for PG1 insertion into neutral membranes. This will give some insight into the mechanism leading to membrane-peptide selectivity, and peptide-induced membrane disruption, features necessary to understand in order to rationally design novel antimicrobial peptides.

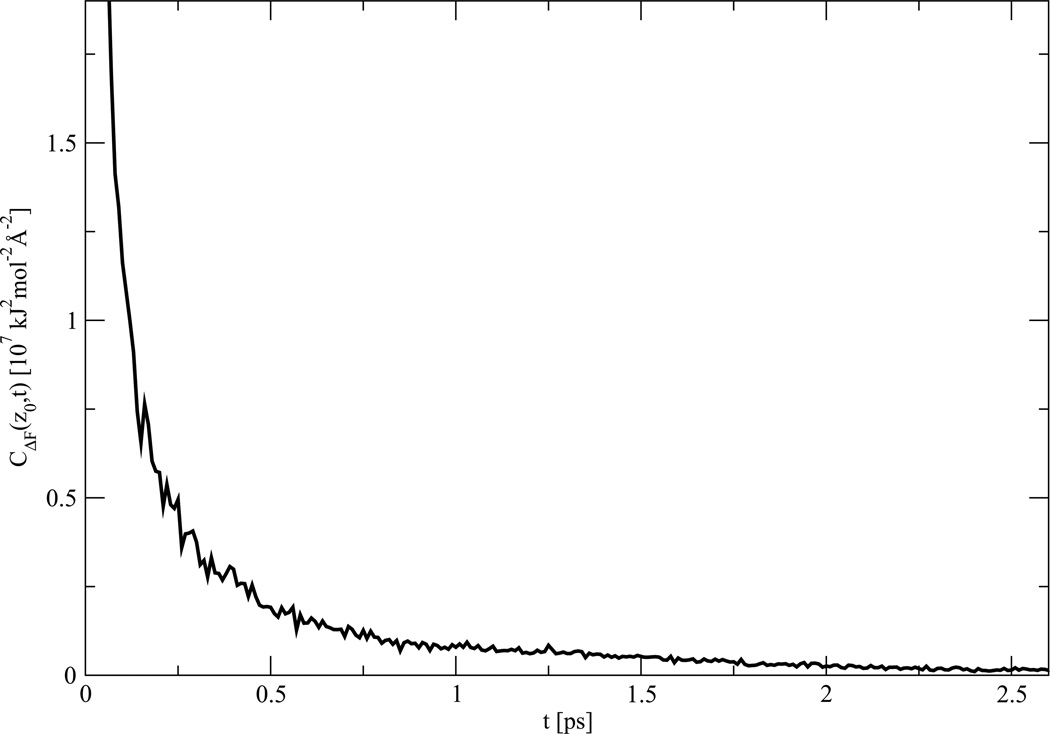
Figure 7.

Autocorrelation function C_ΔF (z₀, t), determined using eq. (5). The data correspond to the MD trajectory of the system with the PG1 peptide restrained in a 2 Å window centered at the barrier top, z₀.

Appendix

The permeation resistance

Here we will give a simple derivation of the membrane resistance to solute permeation based on general diffusion theory. In the diffusional limit the average velocity, ν_α of particles of the α species is proportional to the thermodynamic driving force, F_α as

$$F_{\alpha }=-{\mathrm{\xi ̃}}_{\alpha }{\nu }_{\alpha }\equiv \nabla {\mu }_{\alpha }$$ (21)

where ξ̃_α is the static friction coefficient of the particle and μ_α is the chemical potential of the solute α. From equation (21), the average velocity ν_α is

$${\nu }_{\alpha }=-\frac{1}{{\mathrm{\xi ̃}}_{\alpha }}\nabla {\mu }_{\alpha }$$ (22)

Using equation(21), the flux J_α of particles with given velocity ν_α is

$$J_{\alpha }={\rho }_{\alpha }{\nu }_{\alpha }=-\frac{{\rho }_{\alpha }}{{\mathrm{\xi ̃}}_{\alpha }}\nabla {\mu }_{\alpha }$$ (23)

In one dimension, the linear flux relation Eq.(23) can be written as an Onsager relation:

$$J_{\alpha }(z)=-\beta {\rho }_{\alpha }(z)D_{\alpha }(z)\frac{d{\mu }_{\alpha }(z)}{\mathit{\text{dz}}}$$ (24)

where we used EinsteinâǍŹs relation for the diffusion constant D_α = 1/βξ̃_α. We are interested in the steady-state solution of the flux, when J_α is not a function of z. Integration Eq.(24) from a depth of −l to l, where the distance ±l divides the free and bound volumes, gives

$$J_{\alpha }{\displaystyle {\int }_{-l}^l}\mathit{\text{dz}}\frac{1}{{\rho }_{\alpha }(z)D_{\alpha }(z)}=\beta \mathrm{\Delta }{\mu }_{\alpha }$$ (25)

This equation can be rearranged as

$$J_{\alpha }=-\frac{\beta {\rho }_{\alpha }^0\mathrm{\Delta }{\mu }_{\alpha }}{R_{\alpha }}$$ (26)

where permeation resistance R_α is defined as

$$R_{\alpha }(d)={\displaystyle {\int }_{-l}^l}\mathit{\text{dz}}\frac{1}{K_{\alpha }(z)D_{\alpha }(z)}$$ (27)

where $K_{\alpha }(z)={\rho }_{\alpha }(z)/{\rho }_{\alpha }^0$ is the depth-dependent partition coefficient and ${\rho }_{\alpha }^0$ is the concentration in the bulk solutions. This represents the resistance of the membrane near the adsorption region of thickness 2l. The overall resistance R can be expressed as the integral through the entire membrane, including the binding region above the membrane.

The Grote - Hynes equation

If we fit our PMF at the peak of the energy barrier with a parabola (15) and take into account that the average of the random force exerted by the solvent on the solute for an ensemble of trajectories over the barrier < F(z, t) >= 0, Eq.(16) takes the form

$$m\mathrm{z̈}(t)=m{\omega }_b^{2}z(t)-{\displaystyle {\int }_0^t}\mathit{\text{dt}}\prime \xi (z_0,t\prime )ż(t-t\prime )$$ (28)

The solution of the GLE equation (28) can be introduced as

$$z(t)=C\text{exp}(\omega t)$$ (29)

where w > 0 is the effective barrier top frequency which we will find here. Substituting (29) into (28), we find

$$m{\omega }^{2}C\text{ exp}(\omega t)=m{\omega }_b^{2}C\text{ exp}(\omega t)-C\omega {\displaystyle {\int }_0^t}\mathit{\text{dt}}\prime \xi (z_0,t\prime )\text{ exp}(-\omega (t-t\prime ))$$ (30)

Dividing Eq. (30) by mCexp(ωt) we obtain the Grote-Hynes equation for the frequency ω

$${\omega }^2={\omega }_b^2-\frac{1}{m}\omega {\displaystyle {\int }_0^t}\mathit{\text{dt}}\prime \xi (z_0,t\prime )\text{ exp}(-\omega t)$$ (31)

In the absence of friction, we see that ω = ω_b. The transmission coefficient can be defined as the ratio between the frequencies with and without friction:

$${\kappa }_{\mathit{\text{GH}}}=\frac{\omega }{{\omega }_b}$$ (32)

Dividing Eq.(31) by ${\omega }_b^2$ gives the desired relation (17) for the κ_GH.