Urea–Water Solvation Forces on Prion Structures

Abstract

Solvation forces are crucial determinants in the equilibrium between the folded and unfolded state of proteins. Particularly interesting are the solvent forces of denaturing solvent mixtures on folded and misfolded states of proteins involved in neurodegeneration. The C-terminal globular domain of the ovine prion protein (1UW3) and its analogue H2H3 in the α-rich and β-rich conformation were used as model structures to study the solvation forces in 4 M aqueous urea using molecular dynamics. The model structures display very different secondary structures and solvent exposures. Most protein atoms favor interactions with urea over interactions with water. The force difference between protein–urea and protein–water interactions correlates with hydrophobicity; i.e., urea interacts preferentially with hydrophobic atoms, in agreement with results from solvent transfer experiments. Solvent Shannon entropy maps illustrate the mobility gradient of the urea–water mixture from the first solvation shell to the bulk. Single urea molecules replace water in the first solvation shell preferably at locations of relatively high solvent entropy.

Introduction

Protein solvation determines to a large extent the physicochemical behavior of proteins, and it is therefore an essential part of their exerted function. In particular, complex formation, which is involved in almost all protein functions, depends on the detailed balance between solvent–solute and solute–solute forces. Too strong solvent–solute forces would impair protein function, while too strong solute–solute forces would lead to unspecific protein aggregation. This balance has shaped protein surfaces and their folded state over evolutionary times. Protein folds are generally stable under physiological conditions, but changes in the environment can induce unfolding and denaturation. Urea is among the most frequently used denaturants in studies of protein folding and stability. The effect of cosolvents on proteins has been studied experimentally and theoretically (for reviews, see refs (1−3)), but to date the molecular mechanisms and particularly the driving forces of urea-induced protein denaturation are not yet fully understood.

Several theoretical studies using molecular dynamics (MD) on single amino acids, peptides, and proteins have been performed to elucidate the atomic details of the interactions between urea and amino acids, peptides, or proteins.⁴⁻¹⁷ Most simulation studies focused on the energetic components governing the interaction between the proteic solute and the water–urea solvent mixture. Different interaction mechanisms have been suggested, debating whether urea-induced denaturation is driven by polar interactions or by hydrophobic interactions and if these are induced by direct or indirect interactions with the solute atoms,¹⁸ but in the meantime there is sufficient experimental evidence to exclude a urea-induced structural change of water.¹⁹ A recent experimental study expands thermodynamic data to the spectrum of atoms occurring in proteins²⁰ with the conclusion that urea interacts favorably, compared to water, with most atom types. A general consensus attributes a dominant role to van der Waals interactions between urea and protein atoms over pure electrostatic contributions. This was proposed earlier on the basis of thermodynamic studies.²¹ The hydration shell model explained the solvation terms of small aliphatic hydrocarbons in urea–water mixtures. An essential term of this model is an enthalpic contribution arising from the van der Waals forces between the solute and the cosolvent urea. However, the model neglected the cavity formation, an integral element of solvent transfer models. Urea does not reduce the free energy of cavity formation; on the contrary, the strong interaction between urea and water increases the surface tension. Therefore, the replacement of water from the solvation shell around the hydrophobic solute seems not to contribute to the transfer free energy.²² Also, the hydrogen bond reorganization in the first solvation shell has only a compensatory energetic effect; i.e., enthalpic interaction of water with the protein surface is replaced by a gain of entropy in the bulk solvent.¹⁹ An alternative thermodynamic approach is the solvent exchange model that considers the solute surface as a collection of small interaction sites.^2,18 This model is closer in spirit to molecular simulations, because (i) system trajectories provide direct information about the urea–protein interactions and (ii) the model allows for the existence of heterogeneous sites; i.e., the heterogeneity of the protein surface may be accounted for by the formalism.

A strong interest in protein unfolding and the principles underlying conformational transitions comes from observations that denatured cellular proteins tend to aggregate, a phenomenon that is often associated with a diseased cellular state.²³ A prominent example of a potentially fatal condition caused by protein misfolding and aggregation is the prion disease that is associated with the formation of aggregates of the prion protein (PrP). While the native structure of the globular C-terminus of the cellular prion protein (PrP^C) is mostly helical, its amyloid fibrillar aggregates contain β-rich conformers (PrP^Sc). The details of the conformational transition as well as the structure of the fibrillar aggregates are still elusive. In a quest to determine a minimal set of structural elements that retain the aggregation propensity of the prion protein, the 36-residue fragment H2H3, comprising the helices H2 and H3, has been designed. As demonstrated by our previous studies,²⁴ H2H3 shows fibrillation, GPI anchoring, and insoluble PK-resistant aggregate formation analogous to PrP.

We evaluate here the forces acting at the initial stage of urea-induced denaturation on three PrP constructs, a stable structure and two H2H3 intermediates isolated from misfolding simulations of H2H3 in water.²⁵ These two intermediates of H2H3 represent an α-rich state H2H3^α as an analogue of PrP^C and a β-rich state H2H3^β as an analogue of PrP^Sc. These two conformers have been previously extensively characterized by MD simulations, and their role in the assembly of misfolded states has been evaluated.²⁵ Besides being very different in their secondary structure content, they differ remarkably in their solvent exposure, with the H2H3^β state exposing considerably more hydrophobic surface. H2H3^α and H2H3^β are therefore ideal systems to study the solvation effects.

The solvent forces on H2H3^α and H2H3^β in pure water and in ∼4 M aqueous urea solution were analyzed. The urea solution matches the condition under which fibril formation is induced experimentally. We have previously introduced Shannon entropy maps and analyzed the hydration properties of water at the surface of PrP, identifying particular loci with different entropies.²⁶ By studying the effect of urea on folded and intermediate structures, we (i) isolate the urea effect on defined conformers from the unfolding process itself and by restraining the protein structure (ii) observe the competition of urea and water for protein interaction in the absence of protein dynamics.

It is clear that urea denaturation is induced spontaneously, because protein surface atoms interact stronger with urea than with water. To our knowledge, no study has yet been directed to the role of solvent forces in the initiation of urea-induced unfolding. Here, the preference of the proteic solute to interact with either urea or water was computed on the basis of atomic force distributions. Shannon entropies of the solvent were computed to illustrate the replacement of water from the solvation shell. We compare our results of atomic solvation forces to thermodynamic data and observe good correlations, as well as general trends in hydrophobicity scales extracted from molecular dynamics simulations and based on energetical considerations.

Methods

Selected Model Systems

Three starting structures were used in this study: α-rich H2H3 (H2H3^α), β-rich H2H3 (H2H3^β), and the crystal structure of the C-terminal globular domain of PrP (PDB: 1UW3).

H2H3 is a truncated form of the prion protein comprising mainly helices H2 and H3 (residues 183–218). It is cyclysed by an intramolecular cystine bridge Cys183–Cys218. H2H3 has been shown previously to undergo a conformational transition from an α-rich (H2H3^α) to a β-rich (H2H3^β) conformation.²⁴ These two conformations were used here to compare forces on the same sequence in two different folds. The C-terminal globular domain of PrP is used as a native reference protein for the analyses.

Simulations

MD simulations were performed using the GROMOS biomolecular simulation software.^27,28 The employed force field was GROMOS 53A6. The urea model of Smith et al.²⁹ was used in its implementation as molecular building block 'UREA' in this force field.

The integration time step was set to 2 fs. The temperature was set to 300 K and controlled by weak coupling to a temperature bath³⁰ with a coupling constant τ_T = 0.1 ps. Bond lengths were constrained by the SHAKE algorithm.³¹ The non-bonded pair list was updated every time step for pairs within 0.8 nm and every fifth time step for the range 0.8–1.4 nm. Twin-range cutoff radii of 0.8/1.4 nm were used to compute non-bonded interactions. Long-range electrostatic interactions were approximated by a reaction-field force, using a dielectric constant of 54. Simulations were kept at 0.061020 kJ mol^–1 nm^–3 (1 atm) with a coupling time of τ_P = 0.5 ps and an isothermal compressibility of 5.575 × 10^–4 (kJ mol^–1 nm^–3)⁻¹. Bond lengths were constrained by the SHAKE algorithm.³¹

Initial protein structures H2H3^α, H2H3^β, and 1UW3 were energy minimized using 100 steps of steepest descent. Energy minimized protein conformations were solvated in a periodic box of 5.2 Å edge length. The minimum solute–wall distance was set to 0.8 Å. Systems were electrostatically neutralized by replacing water molecules with sodium ions to compensate the net charge (H2H3, −1; 1UW3, −2) of the protein at a neutral pH value.

The neutralized systems were energy minimized using 100 steps of steepest descent, while the protein was harmonically positionally restrained using a force constant of 2.5 × 10⁴ kJ mol^–1 nm^–2. The systems were run for 5 × 10⁵ steps (1000 ps) of MD while keeping the solute positionally constrained. Configurations, energies and forces were saved at intervals of 250 steps (0.5 ps), yielding 2000 conformations per trajectory. The final urea concentrations were c_urea(H2H3^α) = 3.8 M, c_urea(H2H3^β) = 4.5 M, and c_urea(1UW3) = 4.2 M. Forces between the following groups of atoms were recorded: protein, ion, water, and urea. Two sets of simulations were performed, (i) in pure water (ii) and in a urea/water mixture. Since water equilibration around solutes occurs on the time scale of 10–20 ps, explicit solvent simulations of 1000 ps are sufficiently long for the pure water simulations to sample representative force distributions. The urea/water systems equilibrated after about 5 ns, as shown by the radial distribution functions of urea and water in Supporting Information Figure S1. Simulations of these systems were run for 10 ns, and the last 3 ns were used for the analysis. Given that we estimate the equilibration to occur at approximately 5 ns, we considered 10 ns as sufficiently long to obtain accurate equilibrium solvent properties.

Data Analysis

The first 300 ps of the trajectories were excluded from analysis to remove potential equilibration effects. Atom contacts were attributed to atom pairs within a distance of 0.35 nm. The contact coefficient is the contact ratio, the fraction of protein–urea contacts, normalized by the mole ratio of urea:¹⁰

1

where N is the number of contacts, M is the number of molecules, p:u are protein–urea interactions, and p:s are protein–(co)solvent (urea and water) interactions.

Normalized force differences Δf̂^uw were computed for protein atoms with at least one contact to urea via

2

where ⟨f⟩ denotes the mean force over a specified interval of the trajectory.

Rescaled forces were computed for protein atoms with at least one contact to urea via

3

Statistical values were computed over the last 700 ps of the trajectories using the statistics functions of the GNU Scientific Library³² and plotted using the R-project software.³³

Atom exposure was computed with the tools of the Gromacs simulation package.³⁴ Molecular images were generated with VMD³⁵ and PyMol.³⁶

Results

The ability of PrP to form fibrils is well recognized, but only recently has the neurotoxic activity been correlated with the formation of soluble oligomeric species.³⁷⁻³⁹ We have shown that oligomers from the H2H3 subdomain have very similar physicochemical charateristics to those of the entire ovine PrP protein. The formation of these oligomeric species is accompanied by an increase in β-sheet (H2H3^β) content.²⁴ We have studied in detail this conformational transition in water by molecular dynamics simulations and have characterized the process of interconversion from an all α-helical to a β-rich conformer in water. After only 90 ns, a β-sheet seed forms close to the disulfide bridge (nucleating at residues V183–N184); later the elongation of this sheet resulted in the refolding of the entire structure to what we call a double-β-hairpin (first hairpin, V183–T191/I208–M216; second hairpin, V192–T196/Q199–Q203) (Figure 1A,B). This conformer was very stable in solution and has been repetitively observed in simulations of oligomer-forming mutants. We therefore suspect that this is one of the β-rich species in solution leading to oligomer formation.

Figure 1.

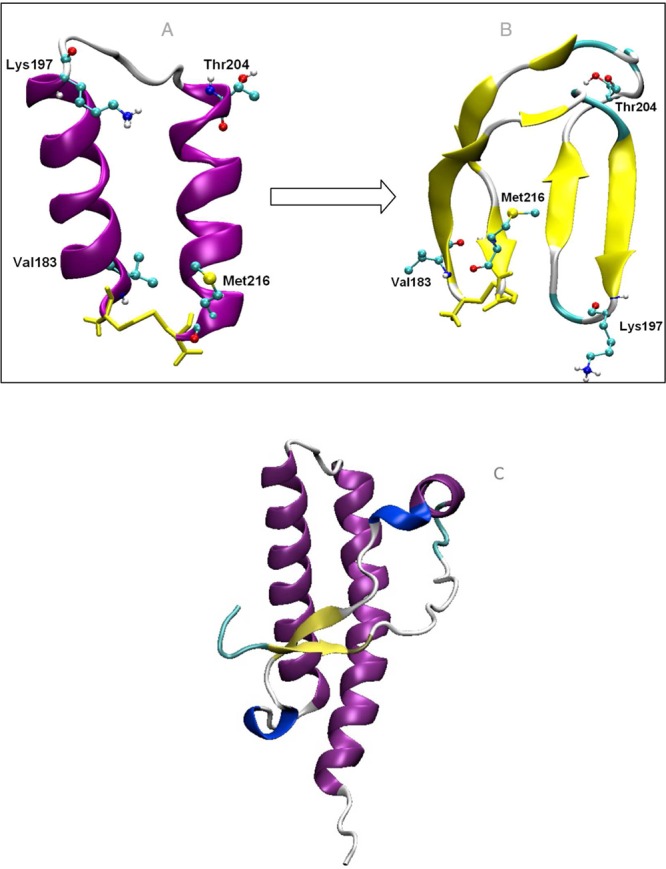
Transition from (A) the α-rich H2H3^α to (B) the β-rich H2H3^β conformation. (C) C-terminal globular domain of ovine PrP (1UW3).

The model systems illustrated in Figure 1 were selected, because we assume that they are among the species present in the oligomerization pathway. The comparison of the organization of the urea mixture around these structures can reveal the tendency of denaturants to favor the species that is more prone to forming oligomers.

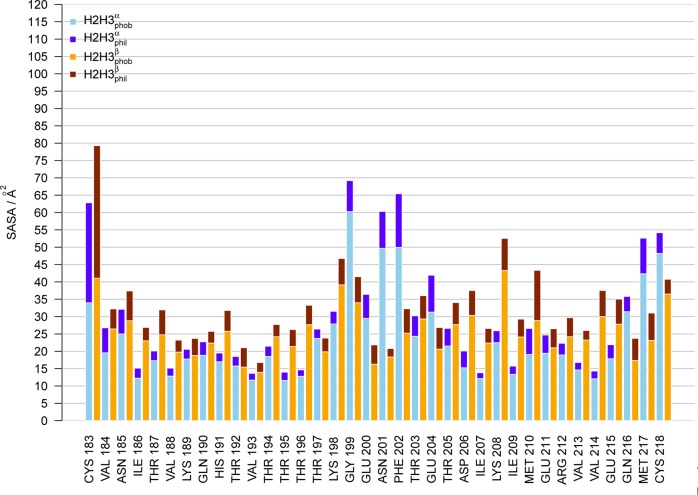
By computing the solvent accessible surface area (SASA) calculated by POPS⁴⁰ and divided into hydrophilic and hydrophobic contributions (Figure 2), one observes the exposure of backbone atoms in the transition from the α-rich to the β-rich conformer observed in pure water solution (hydrophobic SASA in yellow, hydrophilic SASA in red). This is intriguing for the study of solvation forces, because one of the postulated effects of urea-induced denaturation is strong interactions with backbone atoms that become exposed. The only region in which the α-rich conformer exposes more hydrophobic surface is observed in the stretch 198–204, which corresponds to the loop connecting the two helices. This loop becomes quite buried in the β-rich conformer, forming a minimal core between the two aforementioned hairpins.

Figure 2.

Solvent-accessible surface areas (in Ų) of the prion protein conformers H2H3^α (blue) and H2H3^β (red). The bars are divided into hydrophobic (light colors) and hydrophilic (dark colors) contributions.

Solvation Preferences of Protein Atoms

In denaturant-induced unfolding experiments, the number of denaturant molecules bound to the protein can be derived from the depression of the transition temperature, and thermodynamic parameters can broken down into increments per contact.¹⁸ In computational studies, this type of information is directly accessible if one defines a contact distance threshold (here 3.5 Å) between protein atoms and (co)solvent atoms. The relative preference of protein surface atoms to bind to either the cosolvent (urea) or the solvent (water) can be expressed by the contact coefficient,¹⁰ which is the fraction of contacts to a given cosolvent normalized by the mole fraction of the cosolvent in the mixture. A contact coefficient above 1 indicates a favored contact to the cosolvent and below 1, a disfavored contact. In Figure 3, the normalized force difference between the protein–urea contacts and the protein–water contacts is plotted for several atom types against the contact coefficient. There is a clear correlation between the force difference and the contact coefficient. Hydrophobic C atoms show the strongest preference for urea, and their force difference is positive; i.e., protein–urea forces are stronger than protein–water forces for hydrophobic atoms. The polar amide atoms N and O have a preference for urea contacts, but the interaction forces with urea are on average lower than those with water. Polar OH and charged O^– and N⁺ atoms show the highest preference and force differences for water. The normalized force differences between protein–urea and protein–water interactions in Figure 3 follow a hydrophobicity scale. A corresponding trend was found for force field energies of amino acid analogues.¹⁰

Figure 3.

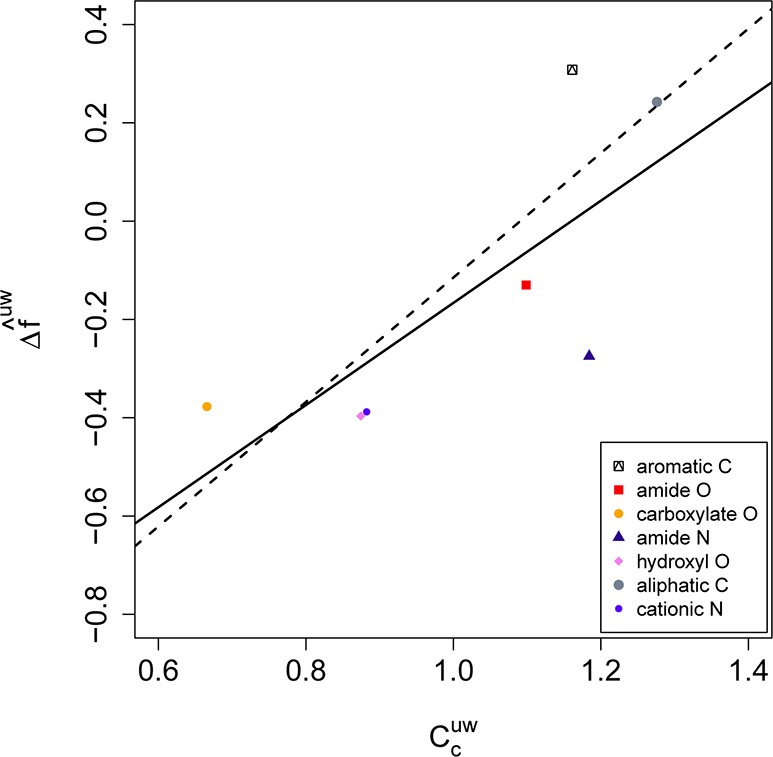
Normalized mean force difference f̂^uw between protein–urea and protein–water interactions per atom type as a function of the contact coefficient. Atom types are increasingly apolar from low to high contact coefficients. Values were averaged over the three prion structures H2H3^α, H2H3^β, and 1UW3. The linear fit through all data points (solid line) has a regression coefficient of r² = 0.6, exclusion of the outlier ‘amide N’ yields a fit (dashed line) with r² = 0.8.

Comparison between Urea and Water Forces on Protein Atoms

Solvent forces on individual protein atoms are cumulative; i.e., the recorded forces originate from interactions with one to several (co)solvent atoms and molecules. The effect of denaturants is concentration dependent, because the number of interactions and therefore the cumulative solvation forces increase with the mole ratio. The concentration effect can be compensated computationally by a scaling of the solvation forces with the contact ratio (eq 3). This creates a useful theoretical scenario, in which solvent and cosolvent form an equal number of contacts with the protein, and therefore the forces are represented on a symmetric basis.

A detailed picture of this scenario is obtained from a plot of the force distributions. The quantile–quantile (Q–Q) plots in Figure 4 provide a graphical summary of the differences between the force distributions. Identical distributions yield a diagonal line in Q–Q plots, while increased frequencies in one distribution ‘bend’ the curve toward that dimension. The axes show the scaled forces f_c of protein–urea versus protein–water interactions of the prion conformers in urea–water mixtures for seven atom types. It is apparent that almost all atom types favor urea interactions compared to water interactions, with the exception of ‘hydroxyl O’ and partially ‘cationic N’. The atom types ‘carboxylate O’ and ‘amide N’ establish particularly strong forces with urea, while forces on ‘amide O’ are moderate. The increased backbone exposure of H2H3^β compared to H2H3^α is notable in the relatively large forces on the backbone atoms ‘amide N’ and ‘amide O’. The surface interaction potentials (in units 10⁴ m^–1 Å^–2) determined by Guinn et al.²⁰ follow a similar order: ‘carboxylate O’ −4.0, ‘amide N’ −3.2, ‘hydroxyl O’ −2.5, ‘aliphatic C’ −1.1, and ‘cationic N’ 1.8. However, the potentials ‘aromatic C’ −8.9 and ‘amide O’ −8.7 were not reproduced by our simulations, possibly because the exposure of these atoms was significantly higher in the model compounds of the thermodynamic study than in the protein folds used here. The mean forces (not scaled), contacts, and contact ratios are tabulated in Table 1.

Figure 4.

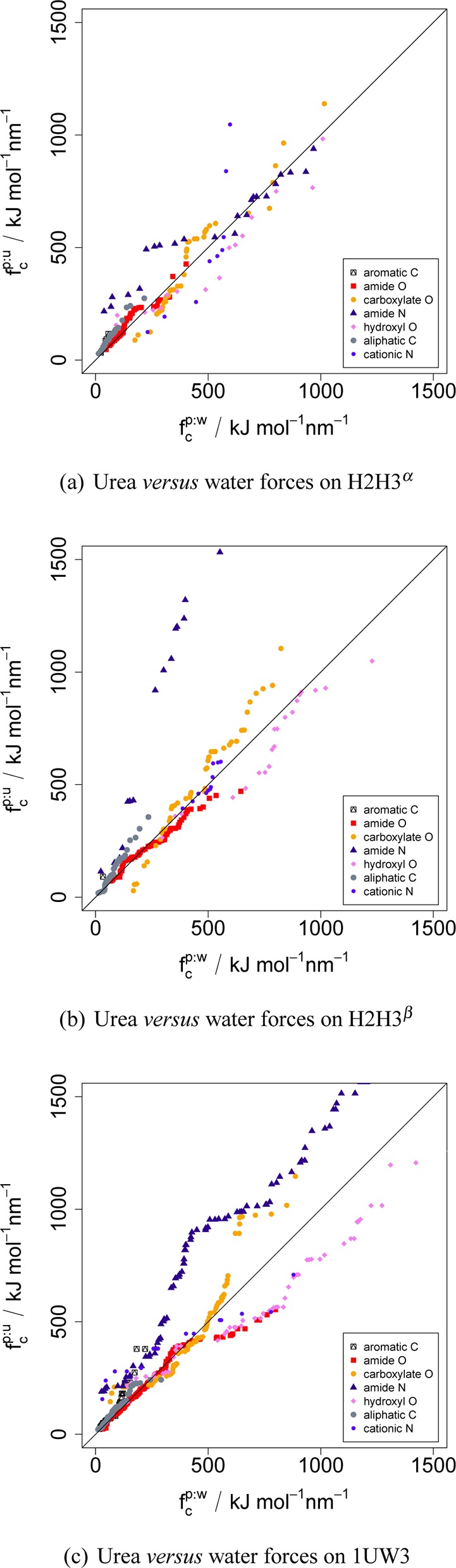
Comparison between force distributions of urea and water around prion molecules. Interaction forces normalized by the contact ratio between H2H3 and urea (f_c^p:u) compared to H2H3 and water (f_c). Shown are the force distributions of selected types of atoms as Q–Q plot. (a) H2H3^α, (b) H2H3^β, and (c) 1UW3. Data points above the diagonal line indicate a preferred interaction with urea, below a preferred interaction with water.

Table 1. Interactions between Protein Atoms and Urea or Water Atoms for Selected Types of Atoms^a.

atom type	⟨fcp,u⟩	cont.p,u	⟨fcp,w⟩	cont.p,w
H2H3α
aromatic C	27 ± 13	1.6 (0.35)	36 ± 15	3.0 (0.78)
amide O	59 ± 35	2.3 (0.38)	124 ± 50	4.2 (0.82)
carboxylate O	101 ± 65	2.9 (0.25)	329 ± 146	8.4 (0.78)
amide N	176 ± 70	2.0 (0.34)	445 ± 256	4.5 (0.89)
hydroxyl O	149 ± 148	1.9 (0.31)	447 ± 252	5.1 (0.91)
aliphatic C	42 ± 23	1.4 (0.42)	54 ± 31	2.2 (0.81)
cationic N	150 ± 98	1.8 (0.31)	399 ± 147	4.8 (0.79)
H2H3β
aromatic C	26 ± 15	1.5 (0.28)	31 ± 10	3.1 (0.72)
amide O	102 ± 41	2.6 (0.50)	173 ± 75	4.1 (0.81)
carboxylate O	157 ± 85	3.6 (0.35)	303 ± 139	8.3 (0.80)
amide N	427 ± 308	2.1 (0.45)	317 ± 262	2.7 (0.89)
hydroxyl O	253 ± 107	3.4 (0.39)	610 ± 249	5.7 (0.71)
aliphatic C	60 ± 47	1.7 (0.56)	64 ± 39	2.2 (0.81)
cationic N	106 ± 28	1.9 (0.22)	416 ± 79	6.3 (0.80)
1UW3
aromatic C	47 ± 37	2.0 (0.49)	66 ± 46	2.8 (0.85)
amide O	95 ± 56	2.9 (0.48)	160 ± 84	4.2 (0.82)
carboxylate O	155 ± 61	4.0 (0.37)	351 ± 129	8.7 (0.86)
amide N	305 ± 148	2.2 (0.43)	466 ± 313	3.5 (0.89)
hydroxyl O	184 ± 91	2.4 (0.34)	572 ± 331	5.6 (0.83)
aliphatic C	46 ± 32	1.5 (0.48)	64 ± 42	2.2 (0.87)
cationic N	149 ± 56	2.1 (0.40)	291 ± 213	3.9 (0.87)

^a⟨f_c⟩: mean force per contact ± standard deviation in units kJ mol^–1 nm^–1. cont.: mean number of contacts and contact ratio in parentheses. p,u: protein–urea interactions. p,w: protein–water interactions.

Solvent Shannon Entropies

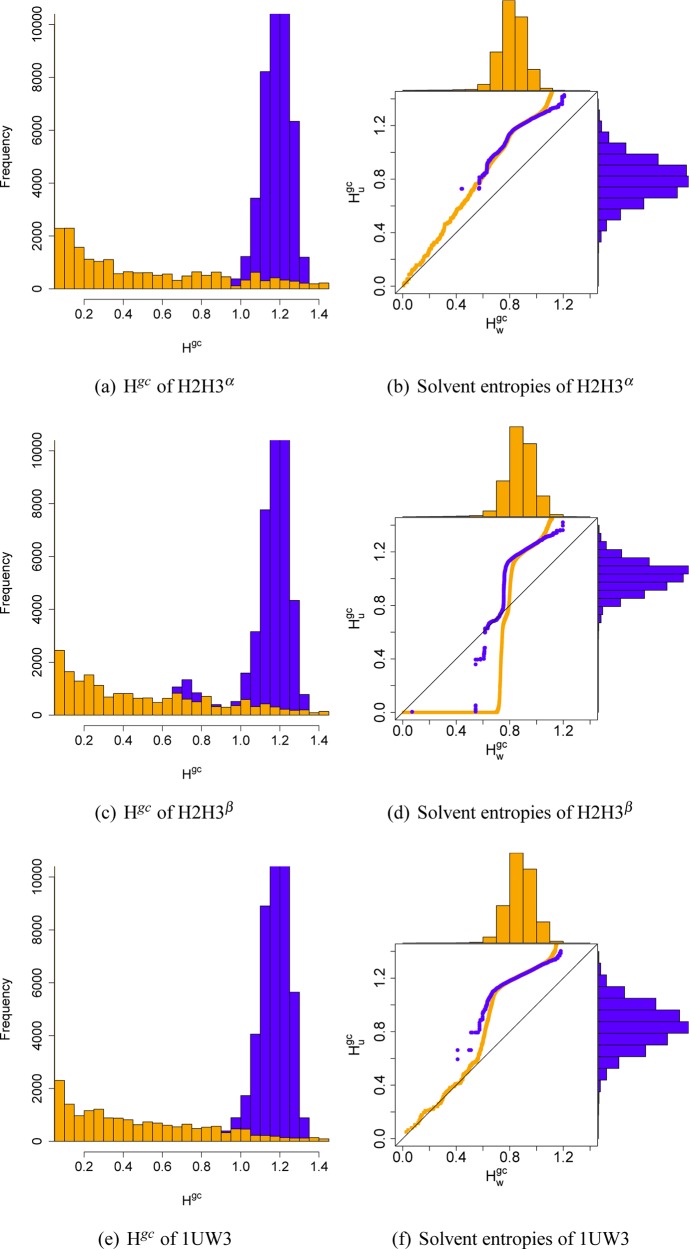
Entropic solvation effects are as important as the enthalpic force contributions discussed in the previous section. As urea replaces water in the first solvation shell, water gains entropy, but the reorganization of hydrogen bonds is an endothermic process. Therefore, the water replacement has been refuted as a driving force (Gibbs energy change) of denaturation.¹⁹ The solvent entropy in simulated systems can be approximated by the Shannon entropy H of the solvent.²⁶ The atom occupancy within cells of a virtual grid were recorded along the simulation and transformed into an entropy H^gcper grid cell (for details, see the Methods). The H^gc distributions of the prion conformers in urea–water mixtures were plotted in the left column of Figure 5. The orange distributions show the values of grid cells close to the protein surface (0–0.25 Å distance); the blue distributions show the values of the second solvation shell (0.5–0.75 Å distance). The differences between the orange and blue distributions illustrate that the H^gc values are a sensitive measure of local atom fluctuations, although the resolution of the grid cells is limited (here 2.0 Å) to provide a sufficiently diverse cell occupancy, because each additional atom contributes to the Shannon term. A comparison of the Shannon entropy distributions of water in urea–water mixtures (H_u^gc) and pure water (H_w) are given as Q–Q plots in the right column of Figure 5, the color code representing the same distance ranges as in the left column. The entropy distributions of the bulk are about the same for protein–urea mixtures and pure water, with the exception of the lower entropy range of the H2H3^β system. Entropic differences arise, as one might expect, in the solvation shell. H2H3^β shows a reduction, compared to the pure water system, of the number of water molecules in the urea/water mixture in the entropy range of 0.4–0.7, which indicates a loss of low entropy water molecules in the solvation shell of the protein. H2H3^β exposes the largest fraction of hydrophobic surface area among the three prion conformers, and this entropic effect is most likely due to the replacement of water by urea at the protein surface. This effect is not detectable in the urea/water mixture systems of the helical proteins H2H3^α and 1UW3. However, all urea/water systems show an increase, compared to the pure water system, in the number of water molecules in the entropy range 0.7–1.2, which is caused by the presence of urea in the solvation shell and the concurring reduction of solvent mobility.

Figure 5.

Shannon entropy distributions of the solvent around prion conformers H2H3^α (a,b), H2H3^β (c,d), and 1UW3 (e,f). Distributions are divided into grid cells close to (0–0.25 Å, orange) and far from (0.5–0.75 Å, blue) the protein surface. Left: Distributions of the Shannon entropy of all grid cells. Right: Q–Q plots of the Shannon entropy distributions of the solvent environment of water (H_w^gc) and urea (H_c) atoms. Histograms of the H_w^gc distributions are plotted over the axes.

This coincides with direct observations of urea molecules in the simulation trajectories. Urea does not replace water molecules that are tightly bound to the protein surface and therefore create a low entropy environment. Urea replaces water molecules at protein surface locations where the bound solvent water fluctuates. The water–urea Shannon entropy maps are shown as isosurfaces in Figure 6 for both H2H3^α and H2H3^β. These maps highlight the structural and dynamical properties of the solvent mixture around the molecules. High entropy solvents close to the protein surface are visible as locations where the contour map touches the protein. These are sites that are prone to (water) desolvation by exchange with cosolvents like urea that form stronger interactions with these sites. For the H2H3 α-rich conformer, the loop between the two helices shows a high entropy environment, and urea molecules interact closely with the backbone. For both conformers, one can observe clustering of urea molecules at exposed amide N atoms (blue space-filling spheres), in agreement with observations in the atomic force analysis, where amide N atoms gave rise to the largest scaled forces in water urea mixtures.

Figure 6.

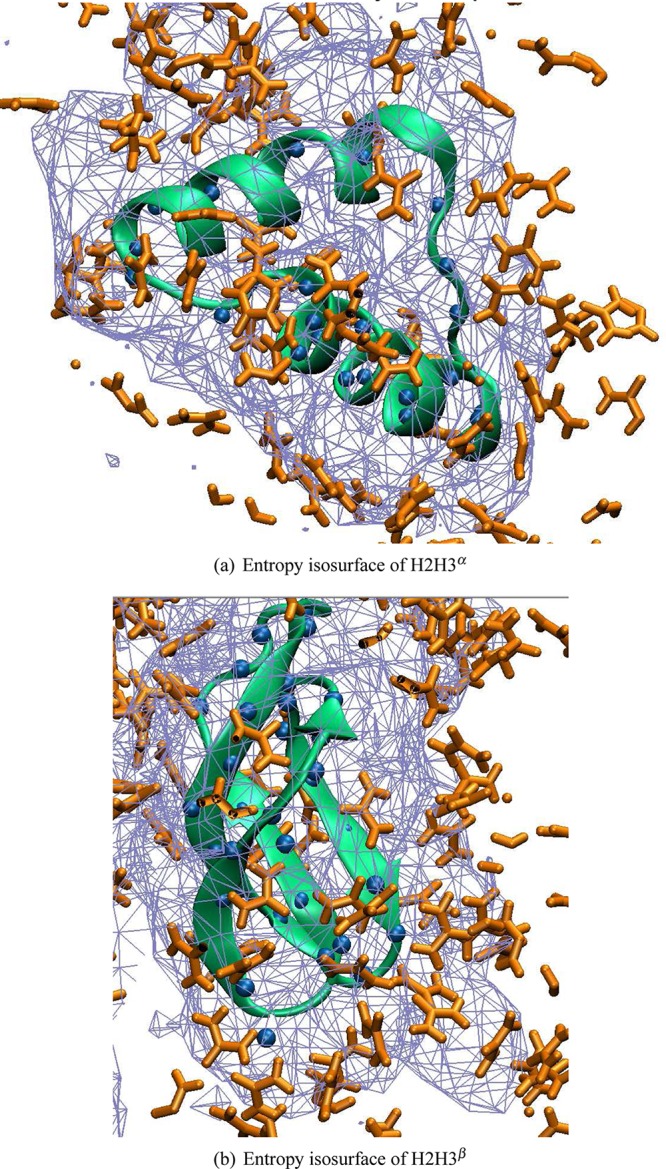
Shannon entropy of the solvent surrounding (a) H2H3^α and (b) H2H3^β illustrated as isosurface in wire mesh rendering. Blue spheres indicate amide N atoms of the backbone. Urea molecules are shown in orange stick rendering.

Discussion

Solvation forces are a sensitive measure to gauge the solution properties of protein atoms in urea–water mixtures. The individual preferences to interact with urea or water follow a hydrophobicity scale in a similar trend as force field energies of amino acid analogues.¹⁰ The comparison of the scaled forces showed largely agreement with data of surface interaction potentials.²⁰ Particularly strong force differences were observed for ‘carboxylate O’ and ‘amide N’ atoms. The direct comparison of urea and water forces on the protein was performed on rescaled forces to compensate for the dependence of the solvation forces on the urea concentration. It has been pointed out by Shellman² that “solvent species appear in two forms: occupying a site and as a solution component.” This has implications for the relative weights of the contributions to the solvation force of the (co)solvent components. In the direct comparison of the force distributions of the protein–urea and protein–water interactions (Figure 4), the forces were scaled by the inverse of the contact ratio, but not additionally by the mole fraction as in the contact coefficient. Therefore the interacting solvent components were viewed as ‘occupying a site’, which reflects the fact that the relative concentrations of urea and water are different close to the protein surface compared to in solution, as has been shown by radial distribution functions here and in previous studies.^13,41

The urea molecules close to the protein surface remained largely outside the first water solvation shell, except at locations where the solvent entropy is relatively high. It was noted earlier for the 1UW3 molecule in pure water that surface sites surrounded by high entropy water molecules are likely to be structural defects or interaction sites, because of the low energetic cost of desolvation.²⁶ One of these sites, the loop between the two helices, is also an apparent interaction site in the H2H3 α-rich conformer: it is surrounded by high entropy solvent, and urea molecules bind to the backbone amide N atoms.

The use of other cosolvents like fluorinated derivatives in the stabilization of folded and unfolded species of PrPc has been explored in experimental and theoretical approaches.⁴²⁻⁴⁴ Generally, a stabilization of helical structure is observed in these solvents. Hexafluoro-2-propanol has been shown to affect the ultrastructure of PrP amyloid and to decrease the β-sheet content as well as prion infectivity. In contrast, 1,1,1-trifluoro-2-propanol does not inactivate prion infectivity but alters the morphology of the rods and abolishes Congo red binding.

Protein simulations in urea–water mixtures provide a rich source of information about solvation effects that can be used to detect potential structural defects and interaction sites.⁴⁵ The solvent interaction forces of individual atom types could be converted to solvation parameters and embedded in an implicit solvation model for urea–water mixtures. Another, more challenging, perspective is the combination of the observed surface site interactions in MD simulations with a thermodynamic site model.⁴⁶

Supporting Information Available

Radial distribution function (RDF) of urea (a,c,e) and water (b,d,f) in the systems H2H3^α (a,b), H2H3^β (c,d), and 1UW3 (e,f) (Figure S1). This information is available free of charge via the Internet at http://pubs.acs.org/.

The authors declare no competing financial interest.

Dedication

This contribution is dedicated to Wilfred van Gunsteren on the occasion of his 65th birthday, who has been a role model with outstanding enthusiasm and dedication to science.