Abstract
A novel ab initio parameter-tuning-free system to identify transcriptional factor (TF) binding motifs (TFBMs) in genome DNA sequences was developed. It is based on the comparison of two types of frequency distributions with respect to the TFBM candidates in the target DNA sequences and the non-candidates in the background sequence, with the latter generated by utilizing the intergenic sequences. For benchmark tests, we used DNA sequence datasets extracted by ChIP-on-chip and ChIP-seq techniques and identified 65 yeast and four mammalian TFBMs, with the latter including gaps. The accuracy of our system was compared with those of other available programs (i.e. MEME, Weeder, BioProspector, MDscan and DME) and was the best among them, even without tuning of the parameter set for each TFBM and pre-treatment/editing of the target DNA sequences. Moreover, with respect to some TFs for which the identified motifs are inconsistent with those in the references, our results were revealed to be correct, by comparing them with other existing experimental data. Thus, our identification system does not need any other biological information except for gene positions, and is also expected to be applicable to genome DNA sequences to identify unknown TFBMs as well as known ones.
INTRODUCTION
On the basis of experimental exploration data of transcriptional factor (TF) binding sites combined with genome DNA sequences, the detailed constitution of transcriptional networks is a crucial issue for understanding the regulatory mechanisms of cellular responses, such as gene expression, cell differentiation, proliferation, reprogramming, etc. (1–5).
For instance, ChIP-on-chip (6,7) and ChIP-Seq (8–11) are experimental techniques for systematical genome-wide mapping of the positions where specific TFs are bound. The ChIP-on-chip technique is a combination of chromatin immunoprecipitation (ChIP) and cDNA microarray hybridization (6,7). ChIP-Seq is a combination of ChIP and the next-generation high-throughput sequencing method (8–11). However, the length of the detected DNA sequence fragments is, in principle, 1∼2 kb (ChIP-on-chip) or 100∼200 bp (ChIP-Seq), and so the fragments include various types of noise, such as simple sequence repeats (SSRs) and other biological signals (e.g. translation signals), as well as the target TFBMs. In contrast, the lengths of the actual TFBMs are as small as 5∼30 bp. Thus, computational methodologies are required to identify the specific motifs from the experimentally extracted DNA sequence fragments.
Various programs for identifying TFBMs are currently available (12–17), with some employed for analyses of experimental data obtained by protein binding microarray (PBM) (18–20) and high-throughput SELEX (HT-SELEX) (21) techniques (22–26). Evaluations of the accuracy of such motif identification systems were previously reported (27,28), revealing some issues that remained to be solved. For instance, Hu et al. indicated that the conventional systems suffer from three serious limitations (29). First, the accuracy of the identification decreases with longer target DNA fragments, since the amount of the background noise involved in the target sequences increases. Second, it is difficult to capture TFBMs when random sequences (i.e. gaps) are involved. Third, to remove the false-positives, such as SSRs, pre-processing is required to obtain highly accurate identification. Furthermore, this report also mentioned that some TFBMs exhibiting significant score values are not corresponding to the correct ones.
Moreover, with respect to some existing algorithms, the accuracy depends on the use of biological knowledge, such as the TF-binding intensities (i.e. P-values) and the peak distributions of those intensities (30,31). On the other hand, recently developed experimental techniques can simultaneously identify various, distinct TFs associated with the specific TFBMs. The cap analysis of gene expression (CAGE) is such a technique to quantitatively identify genes regulated by TFs relevant to particular biological functions (32). In fact, CAGE can identify mRNA sequences that exist in cells for a certain moment, without using a microarray.
Accordingly, our goal is to develop a computational methodology to identify various unknown TFBMs, as well as known ones, as an ‘ab initio’ discovery technique of characteristic base sequence patterns in genome DNA sequences. This means that the system should identify such TFBMs, without using other experimental data and biological knowledge and optimizing the parameters involved in the system with respect to each TFBM (the gene positions in the genome DNA sequences should only be used in the algorithm as external information). Thus, in this study we developed a highly accurate motif identification system with the use of only genome DNA sequences, by exploiting a direct comparison scheme of signal/noise distributions, and introducing a novel scoring function for identifying the plausible TFBMs.
To evaluate the algorithm, we applied our system to the datasets extracted by the ChIP-on-chip and ChIP-seq techniques. The identification of TFBMs in ChIP-on-chip data is, in principle, more difficult than that in ChIP-Seq data, because of the different lengths of the DNA fragments extracted by the two types of experiments. In this study, we used 65 ChIP-on-chip datasets of yeast TFBMs, obtained from the website reported by Harbison et al. (33). We compared the accuracy of our algorithm with those of the existing ones, i.e. MEME (12), Weeder (13), BioProspector (14), MDscan (15) and DME (16). Moreover, to apply our algorithm to higher eukaryote data, we examined whether four mammalian TFBMs could be identified in ChIP-on-chip and ChIP-seq datasets. We compared the accuracy of our system with those of the above-mentioned five existing algorithms.
The benchmark tests revealed that our algorithm accurately identified various yeast TFBMs and mammalian TFBMs using the same set of parameter values, which means that parameter tuning is not needed for our system. Moreover, our algorithm does not require pre-treatment/editing of the input data, such as the removal of SSRs prior to the adaptation. Nevertheless, the accuracy of the present system is higher than those of the tested existing algorithms, for which the accuracy is dependent on pre-treatments and/or parameter tuning for each TFBM. Thus, the present benchmark tests revealed that our algorithm can identify various TFBMs without using any other biological information, except for the gene positions on the genome DNA sequences. This is an advantage for identifying unknown TFBMs, which lack experimental evidence, as well as the known motifs.
MATERIALS AND METHODS
Experimental data used in this study
To evaluate the accuracy of our algorithm, we used datasets of yeast genome DNA sequences, each identified by ChIP-on-chip techniques with a treatment to induce the specific TFs. Each DNA fragment is P < 10−3 (P represents P-value), which was calculated using experimentally measured TF-binding intensities. The datasets are archived in the web site of Harbison et al. (33). In the previous study, the 65 datasets, exploited for the benchmark test in this study, had been identified to involve TFBMs with high confidence (33). Here, each dataset includes 17–195 DNA sequence fragments (see Supplementary Material and Supplementary Table S1). For the noise reduction phase (the third stage) in our algorithm, all of the DNA sequences found in the intergenic regions in the Saccharomyces cerevisiae genome were used. This dataset is archived in the Saccharomyces Genome Database (SGD) (34).
For the test of the identification of mammalian TFBMs, we used genome DNA fragments extracted by ChIP-on-chip and ChIP-seq techniques, and identified the binding motifs of human estrogen receptor (hER), mouse Tcfcp2l1 (mTcfcp2l1), human androgen receptor (hAR) and human vitamin D receptor (hVDR). All these four TFBMs include gaps to evaluate our gap identification (GI) algorithm. Since time-consuming methods are involved in the systems used for the test (for example, the computational cost of MEME is O(N2), where N represents the size of the target DNA sequence), the DNA fragments employed were restricted to those of chromosomes 1 and 2 in this study. The detailed conditions of the four datasets are described in Table S2. For the noise reduction phase, the base sequences found in the upstream region within 0–2000 bp from the transcription starting site (TSSs) of each gene in the human and mouse genome DNA sequences were employed as the background sequences.
Overall scheme of the present system
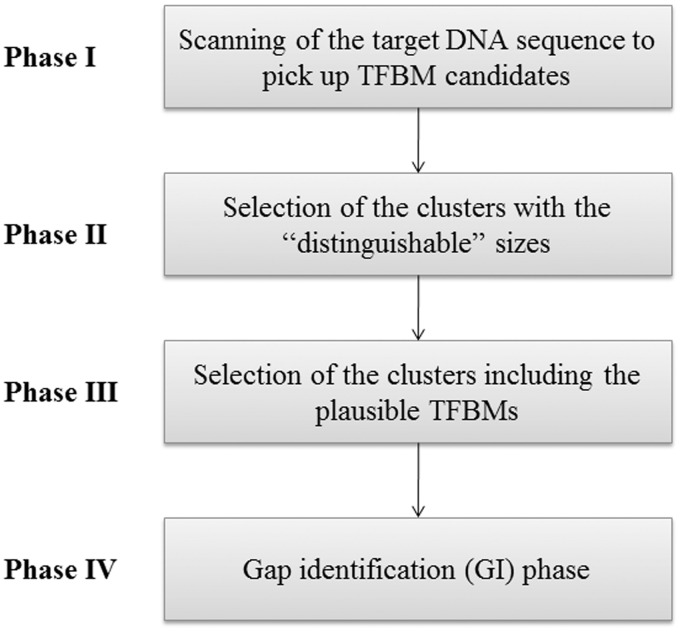
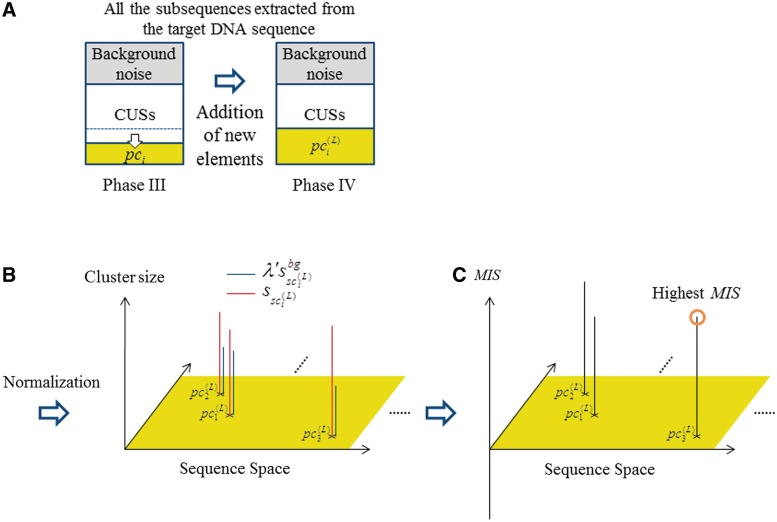
Our identification system is schematically depicted in Figure 1, and consists of four phases for identifying the TFBMs. In the first phase, the subsequences, each involving identical sequence pieces with a length defined by the window size (i.e. sequence redundancy is allowed for a subsequence), are generated by scanning the target DNA sequence, and the obtained sets of the subsequences are used for the probes in the next stages). With respect to each point (i.e. a subsequence) in the sequence space, which is defined by the window size (e.g. the default number of points that should be considered in the sequence space is 48), its ‘neighboring’ points (i.e. the ‘similar’ subsequences to that employed as the probe) are unified into a ‘cluster’. Then, the frequency of each subsequence (i.e. the number of the elements included in the subsequence) in the cluster is summed up to calculate the size of the cluster. This is done for all of the points in the sequence space. In the second phase, the clusters, each possessing a ‘distinguishable’ frequency, are selected as the plausible candidates of the TFBMs. In the third phase, the clusters involving the plausible candidates of TFBMs are selected, by comparing the distribution functions obtained using the target and background sequences. In the fourth phase, to identify the gaps that were not detected in the previous stages, new elements are added to the plausible candidates, and then a procedure similar to the third phase is performed for the final selection of the plausible TFBMs. Our algorithm is referred to here as MODIC (MOtif identification algorithm through DIrect Comparison of signal/noise distributions based on maximum entropy method).
Figure 1.
Schematic representation of the workflow of the present algorithm for the identification of TFBMs in genome DNA sequences.
Scanning of TFBM candidates on the target DNA sequence (phase I)
For scanning the genome DNA sequences, a set of probe sequences is created, as follows. First, a subsequence is extracted from the target DNA sequence by using a search window, for which the length is given as a parameter wprobe (the default value is set to eight). Note here that a subsequence involves sequence pieces with the identical sequence, since sequence redundancy is allowed for a subsequence, as described in ‘Overall scheme of the present system’ subsection.
As the window size (wprobe), 4 × n (n = 1, 2, 3, …) is used in our system (see further). For the identification of longer TFBMs, larger search windows are available to extract the full-length elements. In this study, the binding elements of the mammalian TFs were examined by using sixteen as wprobe (i.e. the default window size × 2). The search window is then shifted on the target sequence by one base, and the second subsequence with the length of wprobe is extracted there. This process is repeated on the target sequence, and thereby a set of all subsequences, representing the initial candidates of TFBMs for use as probes, is extracted from the target sequence. This reduces the number of probe sequences, as compared with the case where all of the sequence variations with wprobe sites are considered. The latter scheme is computationally intensive when long TFBMs are considered.
Using each probe, the target DNA sequence is scanned, and the subsequences that are ‘similar’ to each probe are identified. Here, the similarity is defined by using the Hamming distance. When wprobe is used as the window size (which is identical to the length of the probe sequence), the Hamming distance h(wprobe) is determined as follows:
| (1) |
For example, when the wprobe value is eight, the criterion (i.e. the threshold) of the similarity between the probes and the chosen subsequences corresponds to one Hamming distance; i.e. when the Hamming distance is larger than two, the two subsequences are not defined as being mutually similar. This criterion was determined through tests in which various values of the above-mentioned threshold and wprobe were examined (the definition of this threshold is similar to that employed by Pavesi et al. (13), but the involvement of the gap-identification stage as phase 4 was also considered for the determination of the threshold in our system).
In this scanning phase of the target DNA sequence using the probes, the number of elements (identical sequence pieces) of each subsequence included in each cluster is counted (note that the cluster cp is specified by the probe p); i.e. the same subsequences are also repeatedly counted in the other clusters. Here, 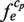 represents the frequency of an extracted subsequence e. When sequence e is found repeatedly, by scanning cluster cp with the probe p,
represents the frequency of an extracted subsequence e. When sequence e is found repeatedly, by scanning cluster cp with the probe p, 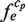 is incremented every time, where the primitive duplications of e, such as NN … N (here, the number of the same continuous nucleotide residue N is larger than wprobe), are hindered when counting
is incremented every time, where the primitive duplications of e, such as NN … N (here, the number of the same continuous nucleotide residue N is larger than wprobe), are hindered when counting 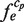 . Thus, the size of each cluster,
. Thus, the size of each cluster, 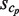 , is defined as
, is defined as 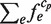 . The distance between the two clusters is defined as the Hamming distance between the probes that were originally involved in the two clusters (Figure 2).
. The distance between the two clusters is defined as the Hamming distance between the probes that were originally involved in the two clusters (Figure 2).
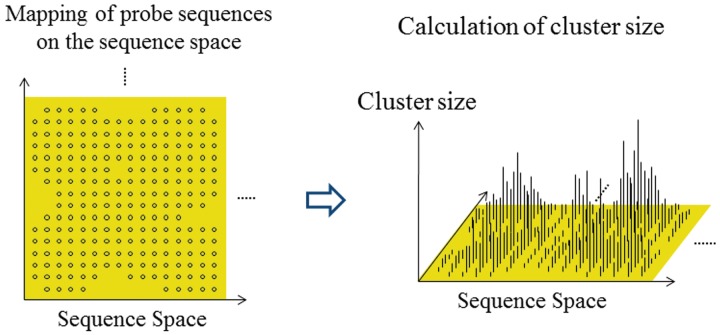
Figure 2.
Schematic diagram of a ‘cluster’. The frequency of each ‘set’ (i.e. cluster), in which similar subsequences (see ‘Overall scheme of the present system’ and ‘Scanning of TFBM candidates on the target DNA sequence (phase I)’ subsections) are extracted by scanning of the target DNA sequence, is mapped on the sequence space of the probes used for the scanning. The cluster size is then calculated with respect to each subsequence, by summing up the frequencies of the ‘neighboring’ subsequences (see ‘Overall scheme of the present system’ and ‘Scanning of TFBM candidates on the target DNA sequence (phase I)’ subsections).
Selection of ‘distinguishable’ clusters (phase II)
To select the plausible clusters of TFBMs efficiently, we search for the clusters with sizes that exhibit peaks on the local sequence space, as follows.
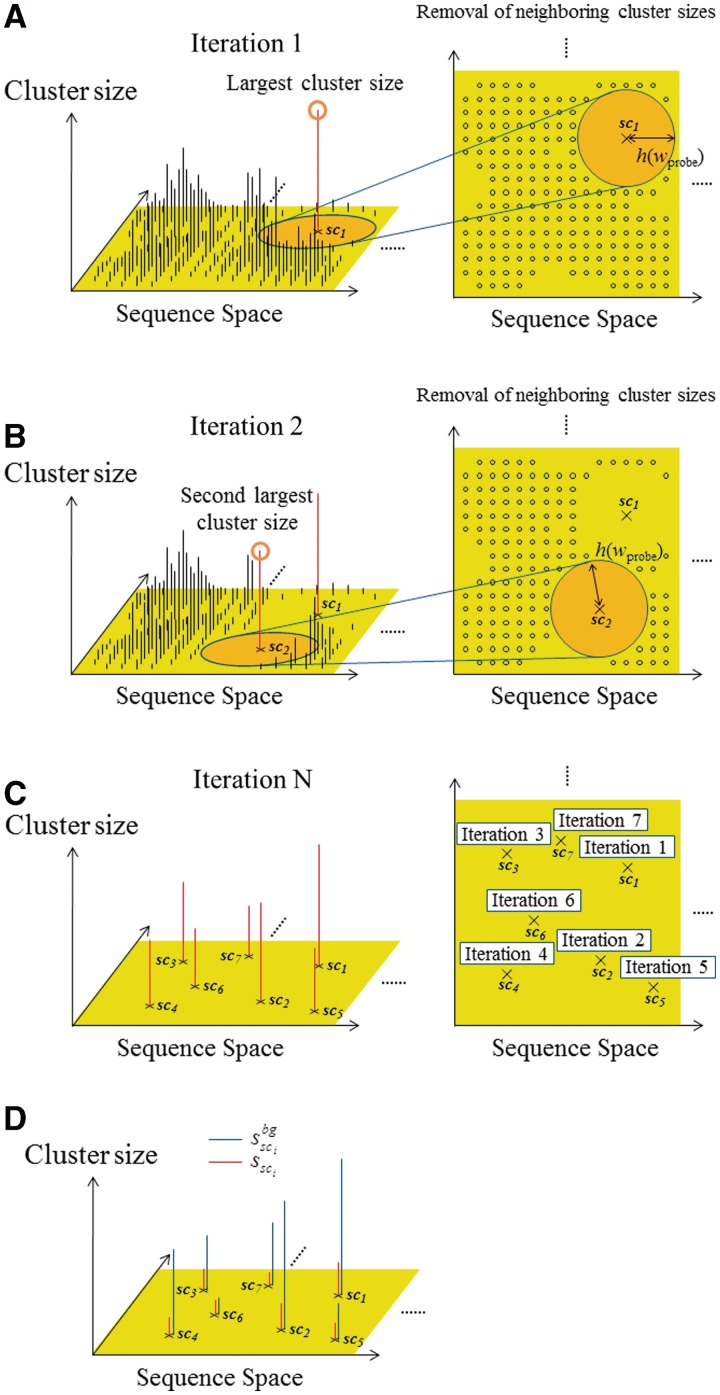
First, the cluster for which the 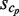 is the largest among all of the clusters is selected and saved as the first ‘selected cluster’; this is referred to as sc1, and its size is represented by
is the largest among all of the clusters is selected and saved as the first ‘selected cluster’; this is referred to as sc1, and its size is represented by 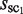 . Its neighboring clusters, which are within the Hamming distance h(wprobe) obtained by equation (1) in the sequence space, are removed in the following selections (Figure 3A). Second, the cluster with the second largest cluster size, among those remaining after the above-mentioned first selection, is selected and saved as the second selected cluster; this is referred to as sc2, and its size is represented by
. Its neighboring clusters, which are within the Hamming distance h(wprobe) obtained by equation (1) in the sequence space, are removed in the following selections (Figure 3A). Second, the cluster with the second largest cluster size, among those remaining after the above-mentioned first selection, is selected and saved as the second selected cluster; this is referred to as sc2, and its size is represented by 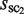 . Its neighboring clusters, which are within the Hamming distance h(wprobe) in the sequence space, are removed in the subsequent selections (Figure 3B). Similarly, the following selections are repeated for all of the clusters, except for those with a cluster size of one (Figure 3C). Here, the number of selected clusters is represented by N. This procedure is referred to as the ‘selection of distinguishable clusters’ (SDCs).
. Its neighboring clusters, which are within the Hamming distance h(wprobe) in the sequence space, are removed in the subsequent selections (Figure 3B). Similarly, the following selections are repeated for all of the clusters, except for those with a cluster size of one (Figure 3C). Here, the number of selected clusters is represented by N. This procedure is referred to as the ‘selection of distinguishable clusters’ (SDCs).
Figure 3.
Schematic diagram of the selection scheme of the ‘distinguishable’ clusters. (A) In the first iteration, the cluster with the largest size is selected, and then the neighboring sets closed to the largest cluster are removed in the subsequent iteration for the selection. (B) In the second iteration, the cluster with the second largest size is selected, and the neighboring sets closed to the second largest one are removed. Similar iterations are repeated for all of the clusters. (C) Finally, the distinguishable clusters are only left. (D) With respect to each extracted cluster (red), the cluster size calculated from the background data (blue) is also mapped.
Next, instead of the target DNA sequence and the probes used in the previous scanning procedure, the intergenic region sequences of the yeast genome and human chromosome 1 (also see the ‘Experimental data used in this study’ subsection) are scanned as the background data, by exploiting each probe of the cluster sci (i = 1, … , N), which is selected in the SDC procedure, as the probe sequence. In this manner, the size of each cluster with respect to the background data (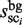 ) is obtained (Figure 3D).
) is obtained (Figure 3D).
Selection of clusters including plausible TFBMs (phase III)
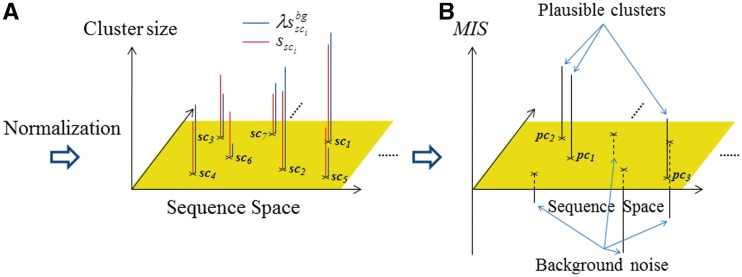
To identify the plausible candidates of TFBMs, the following score function, which is referred to as the motif identity score (MIS), is calculated using 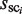 ,
, 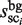 , and a scaling factor λ (this factor normalizes the cluster sizes in the background sequence (i.e.
, and a scaling factor λ (this factor normalizes the cluster sizes in the background sequence (i.e. 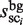 ), and enables the direct comparison of two cluster sizes in the target and background sequences).
), and enables the direct comparison of two cluster sizes in the target and background sequences).
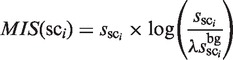 |
(2) |
Here, to compare the two distributions concerning the cluster sizes, i.e. 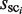 and
and 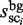 (i = 1, … , N), λ is introduced to normalize the two distribution functions (Figure 4A). With respect to each selected cluster, the plausible TFBM candidates are identified in the cluster by comparing the normalized distribution functions, as mentioned later. It should be noted here that the TFBM sequences are expected to be rare in the background data, but ‘distinguishable’ in the target DNA sequence. Based on this fundamental principle, the selection of TFBMs is performed by comparing the two distribution functions, as mentioned below. This is referred to as the direct comparison scheme of the signal/noise distributions.
(i = 1, … , N), λ is introduced to normalize the two distribution functions (Figure 4A). With respect to each selected cluster, the plausible TFBM candidates are identified in the cluster by comparing the normalized distribution functions, as mentioned later. It should be noted here that the TFBM sequences are expected to be rare in the background data, but ‘distinguishable’ in the target DNA sequence. Based on this fundamental principle, the selection of TFBMs is performed by comparing the two distribution functions, as mentioned below. This is referred to as the direct comparison scheme of the signal/noise distributions.
Figure 4.
Schematic diagram of the selection scheme for plausible clusters. (A) With respect to each selected cluster (red), the cluster sizes calculated from the background data are normalized, and then are mapped (blue). (B) MISs calculated for the selected clusters. The selected clusters with positively high and negatively low MISs are identified as the plausible clusters of the TFBMs and background noise, respectively.
First, the λ value is determined such that the following R is ∼0.7.
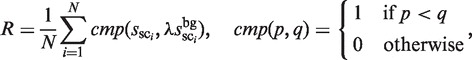 |
(3) |
where R represents the ratio of the ‘noise’ in all of the distinguishable clusters. This means that the λ value is determined such that the number of selected clusters (sci) for which 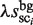 is higher than
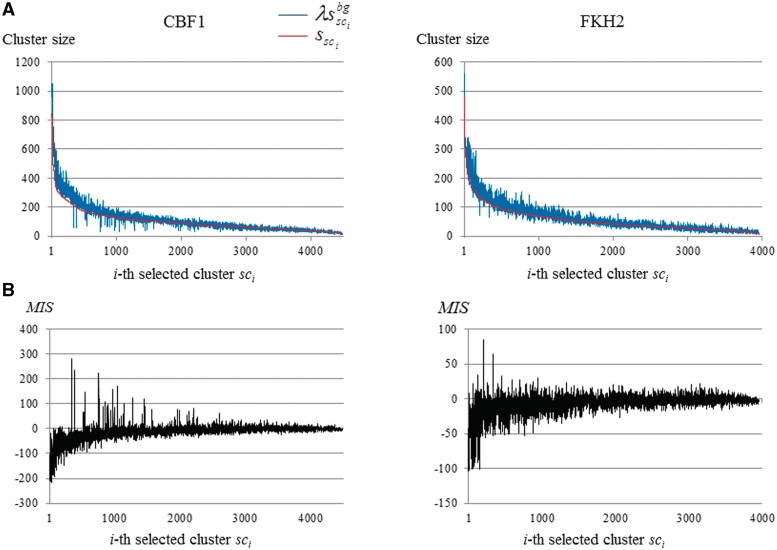
is higher than 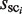 is ∼0.7N (the actual MIS values are shown in Figure 5 for two TFs). Thus, the R and λ values are determined in a self-consistent manner. This calibration procedure also reduces the bias that might be induced in the selection of the distinguishable clusters (phase 2).
is ∼0.7N (the actual MIS values are shown in Figure 5 for two TFs). Thus, the R and λ values are determined in a self-consistent manner. This calibration procedure also reduces the bias that might be induced in the selection of the distinguishable clusters (phase 2).
Figure 5.
Frequency distributions in the clusters and MISs with respect to CBF1 and FHK2. (A) The clusters sizes calculated from the target DNA sequence are plotted in ascending order (red). For each cluster selected, the corresponding cluster size is calculated by using the background data (blue). (B) The MISs of the selected clusters are plotted.
Next, the five sci clusters are selected such that their MIS(sci) values are higher than the top five. These five clusters are selected as ‘plausible clusters’ of TFBMs (here, five is the default value), and are referred to as pcj, where the suffix j ( j = 1, … , 5) is assigned in the ascending order of the 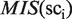 values. Thus, the clusters involving the plausible TFBMs are identified.
values. Thus, the clusters involving the plausible TFBMs are identified.
Then, in the target sequence, the currently unselected regions are identified for use in the next stage. To extract the ‘noise’ sequences and to prevent them from being included in the ‘signal’ sequences, the clusters for which the MISs exhibit negative values are picked up among the clusters that are selected through the SDC procedure in the second phase (as a result, the noise sequences are selected among the subsequences). The number of resultant clusters is ∼0.7N, due to the above-mentioned scheme for the determination of the λ value. Here, the false negatives are minimized through the optimization of R, since the actual noise ratio involved in the distinguishable clusters is approximately greater than 0.9 (i.e. the R value is selected to be sufficiently smaller than the noise ratio, which is dominant in the clusters. As a consequence, R was set to 0.7 in our identification system) (see Supplementary Figure S1).
Thus, these clusters are exploited as ‘noise’ clusters. The noise clusters involve the subsequences that frequently and commonly appear in the target DNA sequence as well as the background data. Here, in the target DNA sequence, the subsequences, except for those involved in the plausible and noise clusters, are referred to as the currently unselected subsequences (CUSs), which are defined for each plausible cluster. The CUSs are exploited to add new subsequences to each plausible cluster in the fourth phase. This means that the MIS classifies all of the subsequences in the target DNA sequence into the plausible clusters of TFBMs, the background noise or the CUSs (Figure 4B).
GI phase (phase IV)
To identify the large gaps in the plausible TFBMs, the following score function, which is combined with the PSSM (a wprobe × 4 matrix), is exploited. For each plausible cluster (pci) of TFBMs identified in the third phase, the elements of the PSSM, 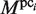 , are calculated as follows:
, are calculated as follows:
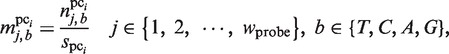 |
(4) |
in which 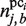 represents the number of elements in the plausible cluster pci, for which the base of position j is b. Next, by exploiting this PSSM, the following motif similarity score (MSS), which was proposed by Kel et al. (35), is calculated for a subsequence s (its length is equal to the window size wprobe) in the CUSs, in which the sequences included in each plausible cluster are excluded, as mentioned.
represents the number of elements in the plausible cluster pci, for which the base of position j is b. Next, by exploiting this PSSM, the following motif similarity score (MSS), which was proposed by Kel et al. (35), is calculated for a subsequence s (its length is equal to the window size wprobe) in the CUSs, in which the sequences included in each plausible cluster are excluded, as mentioned.
| (5) |
Here, Current(M, s), I(M, j ), Min(M ) and Max(M ) are defined as follows:
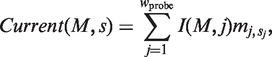 |
(6) |
| (7) |
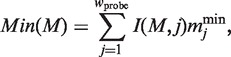 |
(8) |
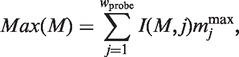 |
(9) |
where 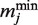 and
and 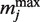 represent the minimum and maximum values of the matrix elements at the column j in the PSSM, respectively. Each MSS value ranges from 0.0 to 1.0 (1.0 represents the best match score of MSS). I(M, j) is the information vector, which represents the identity of position j.
represent the minimum and maximum values of the matrix elements at the column j in the PSSM, respectively. Each MSS value ranges from 0.0 to 1.0 (1.0 represents the best match score of MSS). I(M, j) is the information vector, which represents the identity of position j.
The MSS is used to identify the larger gaps in the GI phase, which is performed for each pci (i = 1, … , 5), as follows (Figure 6A). First, a subsequence s is extracted from the CUSs. When the 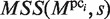 value is larger than the threshold value MINMSSk, the subsequence is saved as a new element of pci, which is now referred to as
value is larger than the threshold value MINMSSk, the subsequence is saved as a new element of pci, which is now referred to as 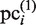 (here, ‘(1)‘ represents the number of updates, and
(here, ‘(1)‘ represents the number of updates, and 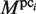 is not modified at this stage). Here, MINMSSk is calculated as follows:
is not modified at this stage). Here, MINMSSk is calculated as follows:
| (10) |
where k represents the k-th cycle of the subsequence search in the CUSs. In each k-th cycle, this procedure is conducted for every s in the CUSs. Here, MINMSSk increases from 0.8 to 0.9 for the conversion of the search, depending on the cycle number. According to Kel et al. (35), when the cutoff value, 0.75 (fixed in their report), was used for the identification, the obtained TFBM candidates were found to involve some false positives. Therefore, in this study, to minimize the false positives, the lower limit of MINMSSk was set to 0.8, through the optimization using the 65 yeast datasets. This value (i.e. 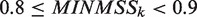 ) was also used for the identification of the four mammalian datasets employed for the present benchmark test, and thus was determined in our system.
) was also used for the identification of the four mammalian datasets employed for the present benchmark test, and thus was determined in our system.
Figure 6.
Schematic diagram of the GI algorithm implemented in the present program. (A) The new subsequences are extracted from the CUSs, and are added to the plausible clusters. (B) With respect to each updated cluster (red), the normalized cluster sizes calculated from the background data are also mapped (blue). (C) The MISs of the updated clusters are plotted. By employing the MISs for the updated clusters, the most plausible cluster is selected.
After the first cycle (k = 1) of the search, the updated plausible clusters 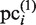 are used to generate the new PSSMs. The updated PSSMs are then utilized for the calculation of
are used to generate the new PSSMs. The updated PSSMs are then utilized for the calculation of 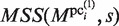 , when this scanning procedure is repeated for the CUSs. Thereby, each
, when this scanning procedure is repeated for the CUSs. Thereby, each 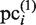 is further updated as a new element of the PSSM, which is referred to here as
is further updated as a new element of the PSSM, which is referred to here as 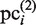 . In our present calculation, this iteration is repeated until the new subsequences in the CUSs are not added to the plausible cluster, as judged on the basis of the above-mentioned criteria. Thus,
. In our present calculation, this iteration is repeated until the new subsequences in the CUSs are not added to the plausible cluster, as judged on the basis of the above-mentioned criteria. Thus, 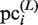 (here, ‘L’ represents the last iteration) is obtained.
(here, ‘L’ represents the last iteration) is obtained.
Finally, to evaluate the plausible clusters obtained in the final iteration of the GI phase, 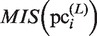 is calculated for each
is calculated for each 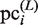 (i = 1, … , N) by using equation (2). The variables,
(i = 1, … , N) by using equation (2). The variables, 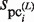 ,
, 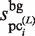 and
and 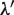 , are then calculated as follows: For the
, are then calculated as follows: For the 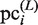 , which is updated using
, which is updated using 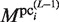 , the variables,
, the variables, 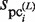 and
and 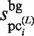 , represent the size of
, represent the size of 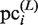 and the number of elements (i.e. identical sequence pieces; see ‘Scanning of TFBM candidates on the target DNA sequence (phase I)’ section) in each subsequence that is chosen from the background data such that their MSS values are higher than 0.8 (this threshold is equal to the value of MINMSS1), respectively. As mentioned earlier, the original
and the number of elements (i.e. identical sequence pieces; see ‘Scanning of TFBM candidates on the target DNA sequence (phase I)’ section) in each subsequence that is chosen from the background data such that their MSS values are higher than 0.8 (this threshold is equal to the value of MINMSS1), respectively. As mentioned earlier, the original 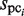 and
and 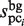 values are obtained by counting the number of elements in each subsequence that are located within the value obtained by the equation (1) from each probe sequence in the first and third stages, respectively; i.e. the similarity of the subsequences is primarily emphasized for the selection. In contrast, in the GI stage, the
values are obtained by counting the number of elements in each subsequence that are located within the value obtained by the equation (1) from each probe sequence in the first and third stages, respectively; i.e. the similarity of the subsequences is primarily emphasized for the selection. In contrast, in the GI stage, the 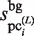 values tend to be much larger than the original
values tend to be much larger than the original 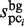 values, since
values, since 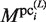 is obtained by involving gap information, through the addition of new subsequences. Here, the
is obtained by involving gap information, through the addition of new subsequences. Here, the 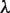 value (which is determined in the third phase to normalize
value (which is determined in the third phase to normalize 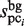 ) is not suitable to normalize
) is not suitable to normalize 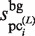 ; i.e.
; i.e. 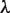 does not lead to the correct results, since the elements of the two types of clusters, which correspond to those of the TFBM candidates and noise sequences, are distinct from those obtained in the GI phase. Accordingly, we determine the
does not lead to the correct results, since the elements of the two types of clusters, which correspond to those of the TFBM candidates and noise sequences, are distinct from those obtained in the GI phase. Accordingly, we determine the 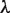 value again in the GI phase (the new value is referred to as
value again in the GI phase (the new value is referred to as 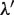 ).
).
For the normalization of the 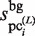 values,
values, 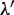 is calculated as follows:
is calculated as follows:
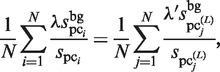 |
(11) |
where the 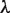 and
and 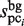 values are equal to those obtained in the third phase. The value of
values are equal to those obtained in the third phase. The value of 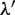 is determined such that the average value of the ratio of
is determined such that the average value of the ratio of 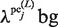 and
and 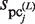 corresponds to that of
corresponds to that of 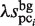 and
and 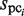 . Thus,
. Thus, 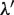 is determined as follows:
is determined as follows:
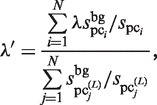 |
(12) |
Using this value, we calculate the MIS for the updated clusters (Figure 6B). In this manner, the most plausible motif is selected, based on the MIS values (Figure 6C).
Existing algorithms and their parameter settings
To compare the accuracy of our algorithm with those of the existing ones, we performed motif identification using MEME (12), Weeder (13), BioProspector (14), MDscan (15) and DME (16), which are frequently used and are accessible at their websites. Here, MEME, Weeder, BioProspector, MDscan and DME use an expectation-maximization (EM) algorithm, a consensus-based algorithm that exhaustively enumerates all the subsequences, a Gibbs sampling technique, an enumerative deterministic greedy algorithm and a noise/signal discriminating algorithm, respectively. In this study, the best five plausible motifs (and their PSSMs) were obtained for each identification system, and were compared with the PSSMs deposited in the website of Harbison et al., each of which exhibits the highest Z-score values among the candidates identified using the six types of conventional tools. These TFBMs in this database are referred to as the ‘reference TFBMs’.
When the i-th plausible motif among the five candidates ‘corresponds’ to a reference TFBM, the ‘rank’ is assigned as i; this ranking is judged for each of the outputs of the above-mentioned five existing programs and our algorithm. Here, the similarity between the obtained and reference PSSMs is defined by employing the following correlation coefficients: the obtained and reference PSSMs are wprobe × 4 and wRef × 4 matrices, respectively. Since the wprobe and wRef values are generally different, many combinations for determining the corresponding elements are present. For all such combinations, the correlation coefficients are calculated: here, when the elements of the obtained PSSM do not correspond to any elements in the PSSM deposited in the reference database, those elements of the reference PSSM are considered to be ‘random’. Both PSSMs are defined as being equivalent, when the maximum value of the correlation coefficients is more than 0.8. If the five candidates obtained from each of the six programs including the present system are different from the reference PSSMs, the rank is assigned as ‘disagreement (DA)’.
With respect to the following programs, i.e. MEME, BioProspector and MDscan, the default parameter value for a Markov model, which calculates the probability of each candidate motif observed in the background data, was used (the third-order Markov chain was imposed as the default). Since for BioProspector, the trial results are different, due to the stochastic optimization scheme (the Gibbs sampling technique is exploited). Accordingly, to evaluate the BioProspector results, five trials were performed for each of the 65 yeast datasets. In each trial, the candidate motif with the highest score was chosen, and thus five candidates were obtained through the five trials. Then, with respect to each dataset, either a Rank or a DA was assigned to the five candidate motifs, in a similar manner to the other cases.
For MDscan, the P-value associated with the binding intensities between each TF and its target DNA is required, to generate the initial candidates of the TFBMs as the initial guesses for the search (MDscan was specifically designed for ChIP-on-chip data). Thus, for the calculation using MDscan, the accuracy depends on the data sorting of the target DNA fragments, prior to the program application. Therefore, the sequence fragments retrieved from the web site of Harbison et al. were sorted in the descending order of the P-values. In the present tests, both the descending and unsorted orders of the sequences were utilized, to evaluate the effect of the data sorting on the MDscan (here, the unsorted order of the DNA fragments is corresponding to the order that is found in the raw experimental data).
RESULTS
Identification of yeast TFBMs
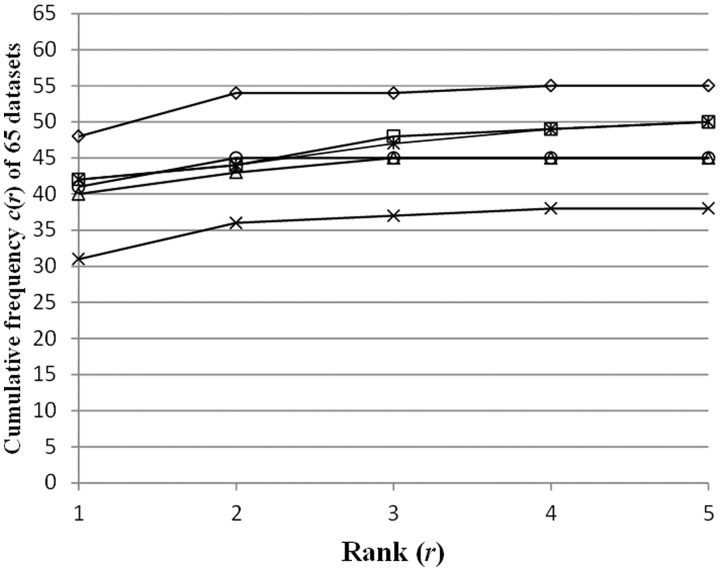
We evaluated the accuracy of the six programs, i.e. the five existing systems and the present algorithm, by employing 65 datasets, which were experimentally extracted from the yeast genome DNA sequences by using the ChIP-on-chip technique in the previous study (33). Some conditions were modified in the identification: for the six programs, we obtained the results coupled/uncoupled to the reduction of SSRs using RepeatMasker (http://www.repeatmasker.org/). For MDscan, we obtained the results coupled/uncoupled to the rearrangement of the target DNA fragments, in the descending order of the P-values (in the latter case, the unsorted order of the DNA fragments was used, as described in ‘Existing algorithms and their parameter settings’ subsection). In Figure 7, the following cumulative frequency c(r) (r represents ‘Rank’, i.e. r = 1, … , 5) is plotted with respect to the six programs, each performed using the best conditions for the program (i.e. minimal DA) (see the legend of Figure 7)
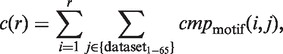 |
(13) |
where 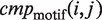 is either one, when the i-th candidate corresponds to the reference TFBM of the dataset j, or zero, when it does not correspond to it. For example, c(1) is equal to the number of ‘Rank 1’ among the 65 datasets. The detailed results of the TFBM identification using the six programs are shown in Supplementary Tables S3–S16, and those generated by the various other conditions are shown in Supplementary Figures S2–S7.
is either one, when the i-th candidate corresponds to the reference TFBM of the dataset j, or zero, when it does not correspond to it. For example, c(1) is equal to the number of ‘Rank 1’ among the 65 datasets. The detailed results of the TFBM identification using the six programs are shown in Supplementary Tables S3–S16, and those generated by the various other conditions are shown in Supplementary Figures S2–S7.
Figure 7.
The cumulative frequency c(r) (r represents ‘Rank’, i.e. r = 1, … , 5) in equation (13) is plotted with respect to the six programs. MDscan (squares) was performed with pre-treatments of each dataset (i.e. the SSR reduction and the rearrangement of the target DNA fragments). DME (asterisks) and Weeder (circles) were performed with the SSR reduction. Our system (rhombuses), BioProspector (triangles) and MEME (crosses) were performed without any pre-treatments. See Supplementary Figures S1–S4, concerning the results performed under other various conditions.
When the reduction of SSRs and the rearrangement of the DNA fragments were not performed (i.e. the most ‘difficult’ case for identification), the number of TFBMs in ‘Rank 1’ identified using our program (i.e. 48) was larger than those of the five existing systems, each performed under the best conditions for the system (Figure 7). Moreover, for all cases specified by c(r) (r = 1, … , 5), our system exhibited the best accuracy, as compared with the other five programs. As shown in Figure 7, our system identified the correct TFBMs in higher ranks (i.e. ‘Rank 1’ or ‘Rank 2’). In fact, the c(r) of our system is converged for r = 2, and the c(2) value obtained using our system (∼83% in all of the datasets) is larger than those obtained using the other five programs, by 15–28%. The accuracy of our program is higher than the second best ones (i.e. DME together with the SSR reduction and MDscan together with the SSR reduction and the rearrangement of the DNA fragments), by ∼15%.
The accuracy of MDscan, DME and Weeder was slightly improved by performing the reduction of SSRs. Moreover, the combination of the reduction of SSRs and the sorting of the DNA fragments in the descending order of P-value (i.e. the ‘easiest’ case) remarkably improved the accuracy of MDscan (Supplementary Figure S3).
In contrast, for our program, BioProspector and MEME, the accuracy did not depend on such pre-treatments. Furthermore, the results of our program without performing any pre-treatments were better than those of MDscan with the full pre-treatments. More specifically, when the reduction of SSRs was performed, the accuracy of our program was actually slightly worse. This means that the pre-treatment may reduce the signals of the TFBMs as well as the noisy sequences.
Identification of the mammalian TFBMs
To apply our algorithm to higher eukaryote data and to test the GI of the TFBMs, we performed a test using ChIP-on-chip/ChIP-seq data inducing mammalian TFs (i.e. hER, mTcfcp2l1, hAR and hVDR), for which the binding motif involves a gap composed of 2–6 bases (see Supplementary Table S2). In a similar manner to the case of the yeast TFBMs, we compared the accuracy of our system with those of the existing ones.
To identify these mammalian TFBMs, we commonly used a larger window size (sixteen) in the five programs tested. Here, for Weeder, 12 is used for the large window size, due to the limitation of the available program. Since MDscan requires the descending order of the P-values of the DNA sequence fragments, we tested two cases, i.e. the unsorted order and the descending order of the P-values. To examine whether the existing programs are sensitive to the presence/absence of SSRs, we further examined two cases with/without the use of the pre-reduction of SSRs. Thus, with respect to these mammalian datasets, we examined the responses of the six identification systems with various combinations of the above-mentioned conditions (Table 1).
Table 1.
Summary of the results obtained using the six identification systems with respect to the four mammalian TFBMs (i.e. hER, mTcfcp2l1, hAR and hVDR) ‘DA’ represents disagreement (see ‘Existing algorithms and their parameter settings’ subsection). The detailed results that were identified by the six programs are shown in Table S17
| TF | SSR reductiona | MDscanb |
MEME |
BioProspector |
Weeder |
DME |
MODIC |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rank (Correlation coefficient) | Frequency | Rank (Correlation coefficient) | Frequency | Rank (Correlation coefficient) | Frequency | Rank (Correlation coefficient) | Frequency | Rank (Correlation coefficient) | Frequency | Rank (Correlation coefficient) | Frequency | ||
| hER | × | DA | – | DA | – | DA | – | 1 (0.8687) | 23 | DA | – | 1 (0.9835) | 247 |
| ○ | 2 (0.8691) | 584 | DA | – | DA | – | 1 (0.8687) | 23 | DA | – | 1 (0.9837) | 224 | |
| mTcfcp2l1 | × | 5 (0.8842) | 1100 | 1 (0.9182) | 3811 | 1 (0.9506) | 2622 | 1 (0.8741) | 125 | DA | – | 1 (0.9767) | 1322 |
| ○ | 1 (0.8951) | 917 | 1 (0.9184) | 2683 | 1 (0.9506) | 2297 | 1 (0.8819) | 103 | 1 (0.8034) | 242 | 1 (0.9712) | 1100 | |
| hAR | × | DA | – | DA | – | DA | – | DA | – | DA | – | 2 (0.8980) | 242 |
| ○ | 1 (0.8882) | 228 | DA | – | 5 (0.9157) | 440 | 1 (0.8158) | 12 | DA | – | 1 (0.8951) | 159 | |
| hVDR | × | DA | – | DA | – | DA | – | 1 (0.8613) | 16 | DA | – | 1 (0.8891) | 60 |
| ○ | DA | – | DA | – | DA | – | DA | – | DA | – | 5 (0.8244) | 31 | |
aSSR reduction was performed by using RepeatMasker.
bWith MDscan, the DNA fragments in the datasets were sorted in terms of the P-values.
When the order of the DNA sequence fragments was unsorted without the pre-reduction of SSRs (the most ‘difficult’ case in the present test of the mammalian TFBMs), only our system identified all four mammalian TFBMs (Table 1). When the SSRs were reduced, BioProspector and Weeder identified the hAR binding motif as ‘Rank 5’ and ‘Rank 1’, respectively, and DME identified the mTcfcp2l1 motif as ‘Rank 1’. On the other hand, for the hVDR binding motif, Weeder failed to identify it when the SSRs were reduced. These results mean that, with respect to BioProspector and DME, the reduction of SSRs is effective to identify these mammalian TFBMs. Furthermore, MDscan failed in the identification, for all the datasets, in both the absence and presence of the SSRs, when the DNA fragments were not sorted (data not shown). In contrast, with our identification system, all four of the mammalian TFBMs were found in both the absence and presence of the SSRs, as shown in Table 1. More specifically, the hVDR binding motif was identified as Rank 5 in the absence of the SSRs, and as Rank 1 in the presence of the SSRs. This suggests that the SSR reduction decreased the accuracy of our system, indicating that RepeatMasker reduces the signals as well as the noise from the target DNA sequences.
When the two datasets lacking SSRs were rearranged in descending order, MDscan identified the three mammalian TFBMs (i.e. the binding motifs of hER, mTcfcp2l1 and hAR) as ‘Rank 1’ or ‘Rank 2’. However, for datasets involving SSRs, MDscan failed, except for the case of mTcfcp2l1. Thus, for MDscan, the two conditions, i.e. the descending order of the DNA sequences and the lack of SSRs, are important to correctly identify the motif.
In this manner, only our identification system successfully identified the four mammalian TFBMs without editing the target DNA sequences and using any additional combinations of information, such as the P-values of the sequence data obtained from experiments. Moreover, the other sets of background data that involved more distal regions from TSS were tested, and we found that the calculated results of our system are not sensitive to such differences of background data (data not shown).
DISCUSSION
TFBMs that are not included in the database identified using our program
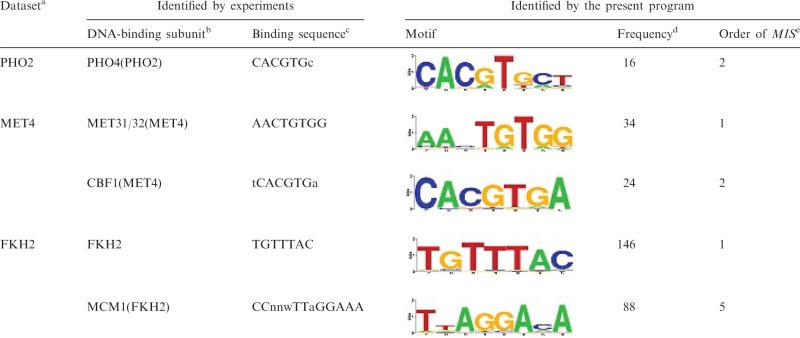
We found the four reference TFBMs that were not identified by each of the six programs (‘DA’ is assigned in Supplementary Tables S3–S16). For example, with respect to PHO2, which regulates genes involved in phosphate metabolism, we found that all of the TFBMs identified with the top five score values, using our program, are different from the reference described in the database built by Harbison et al. To the best of our knowledge, the PHO2 binding motif has not yet been elucidated experimentally (only MEME_c (33) exclusively predicted the TFBM candidate deposited in Harbison’s web site, among the six programs employed to build their database). However, it should be noted here that previous experimental studies revealed that PHO2 forms a complex with Pho4, which binds to the (Pho4-binding) consensus sequence, 5′-CACGTGc-3′ (36). In fact, our system identified the candidate motif (5′-CACGTGct-3′) (Table 2), which is equivalent to the above-mentioned Pho4-binding sequence, as the second best score; however, this TFBM was not identified by the other five existing systems. Thus, for PHO2, the reference may be incorrect, on the basis of the previous and present results. For the other three cases, we could not obtain the relevant literature, and thus did not compare the references.
Table 2.
Results of our identification system, with respect to FKH2, MET4 and PHO2 ‘logo’ representing information contents of the identified PSSMs is generated by STAMP (41)
 |
aDataset deposited in the database involving the target DNA sequence.
bSubunit that binds to DNA in the complex.
cExperimentally identified DNA-binding consensus sequence.
dThe plausible cluster size (see ‘TFBMs that are not included in the database identified using our program’ subsection).
eThe order of the MIS value, where the corresponding plausible cluster was experimentally identified in previous studies.
With respect to MET4, the TFBM (5′-AAnTGTGg-3′) was identified as ‘Rank 1’ by using our system (Table 2). In addition to the reference, we noticed that another motif, 5′-CACGTGAn-3′, which is equivalent to the reference of CBF1, was also found as the TFBM candidate of MET4 with our system (Table 2). It should be noted here that Met4 itself does not bind to the DNA, but does so in the complex with Met28 and either Met31 or Met32, or in the complex with Met28 and Cbf1. In previous biochemical experiments, the former complex was revealed to bind to the sequence 5′-AACTGTGg-3′ (which is equivalent to the reference of MET4) in the upstream regions of the MET3 and MET28 genes, and the latter complex bound to the sequence 5′-tCACGTGa-3′ (this is equivalent to the above-mentioned TFBM, identified by our system as the second best score) in the upstream region of the MET16 gene (37,38). Thus, our system correctly identified the two TFBMs corresponding to both complexes involving MET4. In contrast, the five existing systems identified only one of the two TFBMs, which is the one distinct from the reference deposited in the database.
Similarly, Fkh2, which regulates the G2/M phase genes, forms a complex with Mcm1, and this complex binds to both 5′-TGTTTAC-3′ (which is bound by the Fkh2 subunit) and 5′-CCnnwTTaGGAAA-3′ (which is bound by the Mcm1 subunit) (39,40). In fact, our system identified both TFBMs of FKH2; i.e. 5′-TGTTTAC-3′ (the reference), and 5′-TtAGGAcA-3 (see Table 2). In contrast, the latter TFBM was not identified by the five other programs.
Scoring function of our identification system
The fundamental idea for the identification of the correct TFBMs in target genome DNA sequences is based on the direct comparison of the frequencies of each TFBM candidate in the target and background sequences, as follows. The signal is defined as the subsequences that exhibit higher and lower frequencies in the target and background sequences, respectively. The noise is defined as the subsequences that exhibit high frequency in the background sequence. For example, when the frequency of a subsequence is high in the background sequence, this candidate is usually defined as noise, although it also actually depends on the frequency in the target sequence through the MIS value. This is the concept of our scoring function.
In this manner, the scoring function (equation (2)) evaluates the identity of each distinguishable cluster, which is classified to a TFBM candidate, the background noise or a CUS, by comparing the frequencies (sizes) of the two distinguishable clusters, each possessing the common probe sequence in the target or background sequences. For example, with respect to the clusters involving SSRs, which are quite frequent among both the target and background sequences, the values of the scoring function are negative and their absolute values are very large. Such sequence clusters are considered to be noise (e.g. SSRs), and can be removed as background noise by our scoring function, without any pre-treatments of the target DNA sequences.
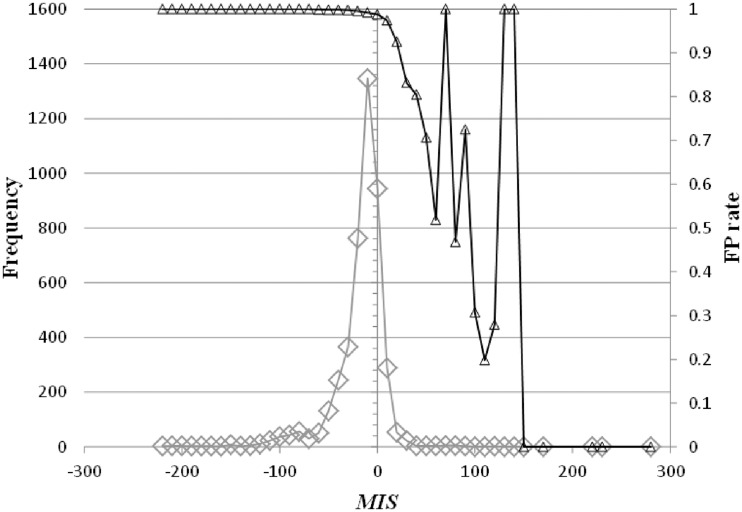
In the sequence space, we define a ‘similar’ region as a space that includes the properties of a TFBM candidate; i.e. a ‘similar’ region in the sequence space, referred to here, does not include the properties of more than two TFBM candidates. Where a cluster, as defined by equation (1), covers a region, it should be small, such that the cluster does not involve more than two TFBM properties or involves only noise properties. Conversely, the properties for one TFBM are, in general, divided into more than two clusters; therefore, to reproduce the consensus sequence of the TFBM, one should unify a cluster with the others that possess ‘similar’ properties. In fact, as shown in Figure 8, the candidate motifs that exhibit the higher MIS values include few false positives (FPs), where the FP rate (rFP) is defined, together with the true positive (TP) rate (rTP), by the following equations:
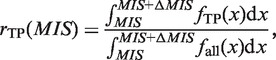 |
(14) |
| (15) |
Here, 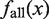 represents the summation of the cluster size (cf. ‘Scanning of TFBM candidates on the target DNA sequence (phase I)’ subsection) of each distinguishable cluster for which the MIS value is equal to x. Similarly, with respect to the same distinguishable clusters (i.e. their MIS values are equal to x),
represents the summation of the cluster size (cf. ‘Scanning of TFBM candidates on the target DNA sequence (phase I)’ subsection) of each distinguishable cluster for which the MIS value is equal to x. Similarly, with respect to the same distinguishable clusters (i.e. their MIS values are equal to x), 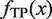 represents the summation of the numbers of subsequences (cf. ‘Overall scheme of the present system’ subsection) that are ‘corresponding to’ the reference TFBM (as described in ‘GI phase (phase IV)’ subsection, ‘corresponding’ means that the MSS value of the element is more than 0.8 with respect to the PSSM of the reference). ΔMIS represents the step width to obtain the distributions.
represents the summation of the numbers of subsequences (cf. ‘Overall scheme of the present system’ subsection) that are ‘corresponding to’ the reference TFBM (as described in ‘GI phase (phase IV)’ subsection, ‘corresponding’ means that the MSS value of the element is more than 0.8 with respect to the PSSM of the reference). ΔMIS represents the step width to obtain the distributions.
Figure 8.
The distributions of our score function (i.e. MIS) (rhombuses) and the FP rate (i.e. rFP(MIS)) (triangles) are plotted. 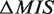 (see ‘Scoring function of our identification system’ subsection) is set to 10.
(see ‘Scoring function of our identification system’ subsection) is set to 10.
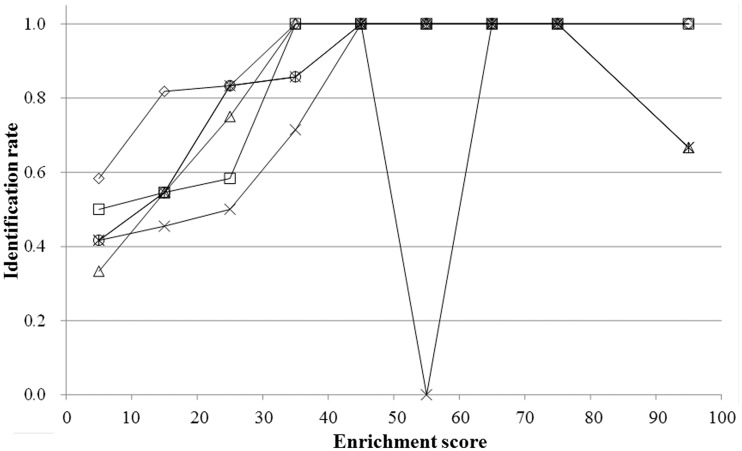
Thus, our scoring function was found to decrease the ratio of false positives in the candidates, which may be critical for the discrimination of the correct/incorrect ones. Moreover, we conducted another examination by calculating the ratio of the correctly identified TFBMs (the identification rates) as a function of the enrichment score, which exhibits the degree of difficulty for the correct identification of each TFBM (33). As a result of the analysis, our system also exhibited the best identification rates with respect to the TFBMs with lower enrichment scores (Figure 9). More specifically, for the TFBMs with enrichment scores as small as 10–20, the identification rates of the existing systems are less than 55%, whereas that of our system is more than 80%. This indicates that our system can identify the correct TFBMs with better accuracy than the other programs that were tested here, even when the datasets are noisy.
Figure 9.
For the 65 yeast datasets, the rates of successful identification, defined as Ranks 1 and 2, are shown with the respect to the enrichment scores employing the results obtained by our system (rhombuses), BioProspector (triangles), MEME (crosses), MDscan (squares), DME (asterisks) and Weeder (circles). Note that in the datasets, there is one sample in the 50–60 enrichment score range.
Characteristic features of our identification system
In the conventional programs, the number of distinct TFBMs considered in the algorithms should initially be assumed; for example, the default values are one type in MEME, 40 in BioProspector, and 5 in MDscan. In contrast, in our system, this assumption is not required, and thus the number of TFBMs that can be identified by our system is restricted by the length of the search window used in the first phase (in this sense, the number of TFBMs that can be identified is limitless in our algorithm). Thus, due to its exploration capability, based on the simultaneous comparison of various TFBMs, our system can explore a much wider sampling space than the other conventional programs. Nevertheless, the number of FPs is less than those of the conventional algorithms, as shown in Figure 7. This advantage is established by the direct comparison scheme of the signal/noise distributions. Despite the enhanced exploration capability, the execution time is comparable to those of BioProspector and DME.
It should be noted that the cluster size, i.e. the frequency of a TFBM observed in genome DNA, is not substantial for the biological functions. In general, some clusters with small/large sizes (i.e. low/high frequencies) are crucial in their biology. In fact, in the second phase, the maximum peak of the cluster sizes is chosen in each iteration, and thereby even the smaller ‘distinguishable’ clusters can be identified in the later iterations. Thus, our system can find the characteristic clusters in the target DNA sequence without neglecting the small, but biologically significant, clusters. The combination of this iterative scheme and our scoring function (equation (2)) is the most crucial implement to identify the TFBMs correctly even in noisy datasets, without depending on their frequencies (Figure 9).
The accuracy of the five existing algorithms significantly depends on the pre-treatments for the identification, i.e. the removal of the background noise and other biological signals, which are well-conserved in the target base sequences (e.g. SSRs) (Table 1). However, the reduction of SSRs via RepeatMasker (and other similar programs) does not always effectively improve the accuracy of the motif identification. In fact, such programs sometimes remove signal sequences as well as noise. Accordingly, in this study, we developed a novel scoring function (i.e. MIS), which identifies the plausible TFBMs, without pre-treatments, in the third phase. Furthermore, as mentioned earlier, our algorithm also discriminates the SSRs and the other biological signals from TFBMs, by comparing the frequencies of the subsequences that are extracted from the target DNA sequence and the background data (i.e. the intergenic sequences) in the third phase. Thereby, in the fourth phase (i.e. the GI stage), we can minimize the addition of noise and such other signals as the updating sequences into the plausible TFBM clusters, by using another scoring function (i.e. MSS) to evaluate the agreement between the selected subsequences and the PSSM for each plausible TFBM cluster (i.e. this means the comparison between a string and a matrix, which MSS can perform).
In summary, our system identifies the plausible TFBMs without pre-treatments of the target DNA sequences and tuning of the parameter set involved in the system. The accuracy of our system is not sensitive to the S/N ratios of the experimental data, as compared with some conventional programs. Although eight sites are used as the default length of its search window, the PSSMs of the reference yeast TFBMs, which are longer/shorter than eight, were precisely identified. Even if the gap regions are included in the TFBMs, our system exactly identified them without tuning the parameter set; this is an important advantage of our system, as compared with the conventional programs. Thus, the present system is also applicable to genome DNA sequences as well as experimental data extracted by using ChIP-on-chip/Chip-Seq techniques.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online: Supplementary Tables 1–17, Supplementary Figures 1–7 and Supplementary Reference [42].
FUNDING
Grants-in-Aid from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), under contract No. 21340108 (in part). Funding for open access charge: Hyogo prefecture, Japan.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
Computations were performed using computer facilities under the ‘Interdisciplinary Computational Science Program’ at the Center for Computational Sciences, University of Tsukuba; the Computer Center for Agriculture, Forestry, and Fisheries Research, MAFF, Japan,; and the Supercomputer Center, Institute for Solid State Physics, University of Tokyo.
REFERENCES
- 1.Wyrick JJ, Young RA. Deciphering gene expression regulatory networks. Curr. Opin. Genet. Dev. 2002;12:130–136. doi: 10.1016/s0959-437x(02)00277-0. [DOI] [PubMed] [Google Scholar]
- 2.Ben-Tabou de-Leon S, Davidson EH. Deciphering the underlying mechanism of specification and differentiation: the sea urchin gene regulatory network. Sci. STKE. 2006;2006:pe47. doi: 10.1126/stke.3612006pe47. [DOI] [PubMed] [Google Scholar]
- 3.Pan G, Thomson JA. Nanog and transcriptional networks in embryonic stem cell pluripotency. Cell Res. 2007;17:42–49. doi: 10.1038/sj.cr.7310125. [DOI] [PubMed] [Google Scholar]
- 4.Suzuki H, Forrest AR, van Nimwegen E, Daub CO, Balwierz PJ, Irvine KM, Lassmann T, Ravasi T, Hasegawa Y, de Hoon MJ, et al. The transcriptional network that controls growth arrest and differentiation in a human myeloid leukemia cell line. Nat. Genet. 2009;41:553–562. doi: 10.1038/ng.375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Macquarrie KL, Fong AP, Morse RH, Tapscott SJ. Genome-wide transcription factor binding: beyond direct target regulation. Trends Genet. 2011;27:141–148. doi: 10.1016/j.tig.2011.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ren B, Robert F, Wyrick JJ, Aparicio O, Jennings EG, Simon I, Zeitlinger J, Schreiber J, Hannett N, Kanin E, et al. Genome-wide location and function of DNA binding proteins. Science. 2000;290:2306–2309. doi: 10.1126/science.290.5500.2306. [DOI] [PubMed] [Google Scholar]
- 7.Iyer VR, Horak CE, Scafe CS, Botstein D, Snyder M, Brown PO. Genomic binding sites of the yeast cell-cycle transcription factors SBF and MBF. Nature. 2001;409:533–538. doi: 10.1038/35054095. [DOI] [PubMed] [Google Scholar]
- 8.Barski A, Cuddapah S, Cui K, Roh TY, Schones DE, Wang Z, Wei G, Chepelev I, Zhao K. High-resolution profiling of histone methylations in the human genome. Cell. 2007;129:823–837. doi: 10.1016/j.cell.2007.05.009. [DOI] [PubMed] [Google Scholar]
- 9.Johnson DS, Mortazavi A, Myers RM, Wold B. Genome-wide mapping of in vivo protein-DNA interactions. Science. 2007;316:1497–1502. doi: 10.1126/science.1141319. [DOI] [PubMed] [Google Scholar]
- 10.Robertson G, Hirst M, Bainbridge M, Bilenky M, Zhao Y, Zeng T, Euskirchen G, Bernier B, Varhol R, Delaney A, et al. Genome-wide profiles of STAT1 DNA association using chromatin immunoprecipitation and massively parallel sequencing. Nat. Methods. 2007;4:651–657. doi: 10.1038/nmeth1068. [DOI] [PubMed] [Google Scholar]
- 11.Mikkelsen TS, Ku M, Jaffe DB, Issac B, Lieberman E, Giannoukos G, Alvarez P, Brockman W, Kim TK, Koche RP, et al. Genome-wide maps of chromatin state in pluripotent and lineage-committed cells. Nature. 2007;448:553–560. doi: 10.1038/nature06008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bailey TL, Elkan C. The value of prior knowledge in discovering motifs with MEME. Proc. Int. Conf. Intell. Syst. Mol. Biol. 1995;3:21–29. [PubMed] [Google Scholar]
- 13.Pavesi G, Mauri G, Pesole G. An algorithm for finding signals of unknown length in DNA sequences. Bioinformatics. 2001;17(Suppl. 1):S207–S214. doi: 10.1093/bioinformatics/17.suppl_1.s207. [DOI] [PubMed] [Google Scholar]
- 14.Liu X, Brutlag DL, Liu JS. BioProspector: discovering conserved DNA motifs in upstream regulatory regions of co-expressed genes. Pac. Symp. Biocomput. 2001;6:127–138. [PubMed] [Google Scholar]
- 15.Liu XS, Brutlag DL, Liu JS. An algorithm for finding protein-DNA binding sites with applications to chromatin-immunoprecipitation microarray experiments. Nat. Biotechnol. 2002;20:835–839. doi: 10.1038/nbt717. [DOI] [PubMed] [Google Scholar]
- 16.Smith AD, Sumazin P, Zhang MQ. Identifying tissue-selective transcription factor binding sites in vertebrate promoters. Proc. Natl Acad. Sci. USA. 2005;102:1560–1565. doi: 10.1073/pnas.0406123102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mason MJ, Plath K, Zhou Q. Identification of context-dependent motifs by contrasting ChIP binding data. Bioinformatics. 2010;26:2826–2832. doi: 10.1093/bioinformatics/btq546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Berger MF, Bulyk ML. Universal protein-binding microarrays for the comprehensive characterization of the DNA-binding specificities of transcription factors. Nat. Protoc. 2009;4:393–411. doi: 10.1038/nprot.2008.195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mukherjee S, Berger MF, Jona G, Wang XS, Muzzey D, Snyder M, Young RA, Bulyk ML. Rapid analysis of the DNA-binding specificities of transcription factors with DNA microarrays. Nat. Genet. 2004;36:1331–1339. doi: 10.1038/ng1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bulyk ML, Huang X, Choo Y, Church GM. Exploring the DNA-binding specificities of zinc fingers with DNA microarrays. Proc. Natl Acad. Sci. USA. 2001;98:7158–7163. doi: 10.1073/pnas.111163698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhao Y, Granas D, Stormo GD. Inferring binding energies from selected binding sites. PLoS Comput. Biol. 2009;5:e1000590. doi: 10.1371/journal.pcbi.1000590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stormo GD, Zhao Y. Determining the specificity of protein-DNA interactions. Nat. Rev. Genet. 2010;11:751–760. doi: 10.1038/nrg2845. [DOI] [PubMed] [Google Scholar]
- 23.Agius P, Arvey A, Chang W, Noble WS, Leslie C. High resolution models of transcription factor-DNA affinities improve in vitro and in vivo binding predictions. PLoS Comput. Biol. 2010;6:e1000916. doi: 10.1371/journal.pcbi.1000916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhao Y, Stormo GD. Quantitative analysis demonstrates most transcription factors require only simple models of specificity. Nat. Biotechnol. 2011;29:480–483. doi: 10.1038/nbt.1893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chua G, Morris QD, Sopko R, Robinson MD, Ryan O, Chan ET, Frey BJ, Andrews BJ, Boone C, Hughes TR. Identifying transcription factor functions and targets by phenotypic activation. Proc. Natl Acad. Sci. USA. 2006;103:12045–12050. doi: 10.1073/pnas.0605140103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Georgiev S, Boyle AP, Jayasurya K, Ding X, Mukherjee S, Ohler U. Evidence-ranked motif identification. Genome Biol. 2010;11:R19. doi: 10.1186/gb-2010-11-2-r19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tompa M, Li N, Bailey TL, Church GM, De Moor B, Eskin E, Favorov AV, Frith MC, Fu Y, Kent WJ, et al. Assessing computational tools for the discovery of transcription factor binding sites. Nat. Biotechnol. 2005;23:137–144. doi: 10.1038/nbt1053. [DOI] [PubMed] [Google Scholar]
- 28.Sandve GK, Abul O, Walseng V, Drablos F. Improved benchmarks for computational motif discovery. BMC Bioinformatics. 2007;8:193. doi: 10.1186/1471-2105-8-193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hu J, Li B, Kihara D. Limitations and potentials of current motif discovery algorithms. Nucleic Acids Res. 2005;33:4899–4913. doi: 10.1093/nar/gki791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hu M, Yu J, Taylor JM, Chinnaiyan AM, Qin ZS. On the detection and refinement of transcription factor binding sites using ChIP-Seq data. Nucleic Acids Res. 2010;38:2154–2167. doi: 10.1093/nar/gkp1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Boeva V, Surdez D, Guillon N, Tirode F, Fejes AP, Delattre O, Barillot E. De novo motif identification improves the accuracy of predicting transcription factor binding sites in ChIP-Seq data analysis. Nucleic Acids Res. 2010;38:e126. doi: 10.1093/nar/gkq217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kodzius R, Kojima M, Nishiyori H, Nakamura M, Fukuda S, Tagami M, Sasaki D, Imamura K, Kai C, Harbers M, et al. CAGE: cap analysis of gene expression. Nat. Methods. 2006;3:211–222. doi: 10.1038/nmeth0306-211. [DOI] [PubMed] [Google Scholar]
- 33.Harbison CT, Gordon DB, Lee TI, Rinaldi NJ, Macisaac KD, Danford TW, Hannett NM, Tagne JB, Reynolds DB, Yoo J, et al. Transcriptional regulatory code of a eukaryotic genome. Nature. 2004;431:99–104. doi: 10.1038/nature02800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Cherry JM, Adler C, Ball C, Chervitz SA, Dwight SS, Hester ET, Jia Y, Juvik G, Roe T, Schroeder M, et al. SGD: Saccharomyces Genome Database. Nucleic Acids Res. 1998;26:73–79. doi: 10.1093/nar/26.1.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kel AE, Gossling E, Reuter I, Cheremushkin E, Kel-Margoulis OV, Wingender E. MATCH: a tool for searching transcription factor binding sites in DNA sequences. Nucleic Acids Res. 2003;31:3576–3579. doi: 10.1093/nar/gkg585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Vogel K, Horz W, Hinnen A. The two positively acting regulatory proteins PHO2 and PHO4 physically interact with PHO5 upstream activation regions. Mol. Cell Biol. 1989;9:2050–2057. doi: 10.1128/mcb.9.5.2050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Blaiseau PL, Thomas D. Multiple transcriptional activation complexes tether the yeast activator Met4 to DNA. EMBO J. 1998;17:6327–6336. doi: 10.1093/emboj/17.21.6327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lee TA, Jorgensen P, Bognar AL, Peyraud C, Thomas D, Tyers M. Dissection of combinatorial control by the Met4 transcriptional complex. Mol. Biol. Cell. 2010;21:456–469. doi: 10.1091/mbc.E09-05-0420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pic A, Lim FL, Ross SJ, Veal EA, Johnson AL, Sultan MR, West AG, Johnston LH, Sharrocks AD, Morgan BA. The forkhead protein Fkh2 is a component of the yeast cell cycle transcription factor SFF. EMBO J. 2000;19:3750–3761. doi: 10.1093/emboj/19.14.3750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Boros J, Lim FL, Darieva Z, Pic-Taylor A, Harman R, Morgan BA, Sharrocks AD. Molecular determinants of the cell-cycle regulated Mcm1p-Fkh2p transcription factor complex. Nucleic Acids Res. 2003;31:2279–2288. doi: 10.1093/nar/gkg347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mahony S, Benos PV. STAMP: a web tool for exploring DNA-binding motif similarities. Nucleic Acids Res. 2007;35:W253–W258. doi: 10.1093/nar/gkm272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Crooks GE, Hon G, Chandonia JM, Brenner SE. WebLogo: a sequence logo generator. Genome Res. 2004;14:1188–1190. doi: 10.1101/gr.849004. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.