Abstract
Heart failure research suggests that multiple biomarkers could be combined with relevant clinical information to more accurately quantify individual risk and to guide patient-specific treatment strategies. Therefore, statistical methodology is required to determine multi-marker risk scores that yield improved prognostic performance. Development of a prognostic score that combines biomarkers with clinical variables requires specification of an appropriate statistical model and is most frequently achieved using standard regression methods such as Cox regression. We demonstrate that care is needed in model specification and that maximal use of marker information requires consideration of potential non-linear effects and interactions. The derived multi-marker score can be evaluated using time-dependent ROC methods, or risk reclassification methods adapted for survival outcomes. We compare the performance of alternative model accuracy methods using simulations, both to evaluate power and to quantify the potential loss in accuracy associated with use of a sub-optimal regression model to develop the multi-marker score. We illustrate development and evaluation strategies using data from the Penn Heart Failure Study. Based on our results, we recommend that analysts carefully examine the functional form for component markers and consider plausible forms for effect modification to maximize the prognostic potential of a model-derived multi-marker score.
Keywords: Cox regression, predictive accuracy, ROC curve, risk reclassification, survival analysis
1 Introduction
Chronic heart failure is a multi-factorial, progressive disorder in which structural damage to the heart impairs its ability to provide adequate blood-flow to the body. In the United States, heart failure accounts for more than one million hospitalizations and approximately 60 000 deaths per year.1 Among heart-failure patients, substantial heterogeneity exists in the risk of adverse outcomes, even after accounting for key factors that are known to impact risk.2 Clinical research suggests that one or more biomarkers—proteins in the blood whose concentration reflects the presence or severity of an underlying disease condition—could be combined with relevant clinical information to more accurately quantify risk heterogeneity among all patients and to inform more beneficial treatment strategies for individual patients by focusing attention on patients at high risk and providing reassurance to patients at low risk.3,4 Therefore, statistical methodology is required to address relevant scientific questions regarding which biomarkers, or which combinations thereof, provide improved prognostic metrics to predict adverse outcomes. The primary statistical challenges are: development of a multi-marker risk score that maximizes use of all available information; and evaluation of the predictive accuracy of the multi-marker score for a censored survival outcome.
Modern statistical methods for prediction, or classification, are based on the fundamental epidemiologic concepts of sensitivity and specificity for a binary disease outcome.5 Sensitivity is measured by the proportion of diseased individuals who are correctly classified as diseased; specificity is measured by the proportion of non-diseased individuals who are correctly classified as non-diseased. For a diagnostic marker defined on a continuous scale, a receiver operating characteristic (ROC) curve is a standard method to summarize predictive accuracy. The ROC curve is a graphical plot of the sensitivity (or, the true-positive fraction) versus 1 – specificity (or, the false-positive fraction) across all possible dichotomizations of the continuous diagnostic marker. The predictive accuracy of the diagnostic marker is quantified by the area under the ROC curve (AUC), which measures the probability that the diagnostic marker will rank a randomly chosen diseased individual higher than a randomly chosen non-diseased individual. An AUC of 0.5 indicates that the diagnostic marker is uninformative; an increase in the AUC indicates an improvement in predictive accuracy; an AUC of 1.0 indicates a perfect diagnostic marker. Recent advances have allowed adjustment for covariates associated with the marker of interest.6
Standard measures of predictive accuracy based on ROC curves and their corresponding AUC are limited to a diagnostic marker and a binary disease outcome collected at a single time-point. However, in a typical prospective study, interest lies in quantifying the ability of a marker measured on non-diseased individuals at baseline to classify accurately diseased and non-diseased individuals after a fixed follow-up time. In our motivating example, interest lies in predicting the combined outcome of all-cause mortality or cardiac transplantation after one year of follow-up. However, individuals may be lost to follow-up, so that their time of disease onset is unknown, or censored. It is well known that analyses based solely on the uncensored outcomes may provide biased point estimates. Recent advances in statistical methodology have extended ROC analyses for a single binary disease outcome to time-dependent binary disease outcomes (or, survival outcomes), which may be subject to censoring.7,8 Time-dependent ROC methodology has also been extended to accommodate censored survival outcomes in the presence of competing risks.9
Methods recently developed for censored survival outcomes have focused on a single diagnostic maker, but there are situations in which interest lies the predictive accuracy of a set of diagnostic markers. In our motivating example, interest lies in determining the added value of a novel biomarker, ST2, when used in combination with two established risk predictors: brain natriuretic peptide level (NT-proBNP), a diagnostic and prognostic measure of heart failure severity; and the Seattle Heart Failure Model (SHFM), a validated risk score for mortality based on readily available clinical and laboratory variables.10 We illustrate the use of a standard Cox regression model11 to derive a multi-marker risk score, hereafter referred to as a `composite marker,' as a weighted combination of biomarkers and clinical variables, in which the weights are determined by the estimated regression coefficients. Alternative regression methods include proportional odds models and additive failure time models, which have been shown to be as accurate as Cox regression models for developing a composite marker from time-independent component markers.12 Specialized methods, such as non-parametric transformation models13 and extended generalized linear models14, are also available to derive the composite marker. The composite marker can then be supplied as the input to a time-dependent ROC analysis.
ROC-based methods have been criticized for their relative insensitivity to detect clinically important risk differences15 and for their lack of direct clinical relevance.16 For a binary disease outcome, a marker strongly associated with the odds of disease may be a poor classification marker. For example, if a marker has a 10% false-positive rate and an association odds ratio of 3.0, then its true-positive rate is only 25%.15 Methods based on risk reclassification were recently proposed to offer an alternative approach to compare risk-prediction models.17,18 Reclassification methods are based on the stratification of estimated absolute risk into categories defined by clinically relevant risk thresholds, and the degree to which a model of interest more accurately classifies individuals into higher or lower risk categories relative to a comparison model. For censored survival outcomes, the Kaplan-Meier estimator can be used to estimate the number of cases and controls within cross-classified risk strata.19,20
We focus on prospective studies of a censored survival outcome, in which multiple biomarkers and clinical variables are collected at baseline. Our goals are to compare analytic strategies to develop a composite marker that maximizes use of all available biomarker and clinical information, and to compare statistical methods to evaluate the accuracy of the composite marker in predicting a censored survival outcome. In Section 2, we detail the use of a standard Cox regression model to combine multiple biomarkers and clinical variables and review methods to quantify the predictive accuracy of the composite marker using time-dependent ROC curves.7 In addition, we contrast ROC-based methods with recently developed methods based on risk reclassification.17,19,20 In Section 3, we apply the methods to our motivating example, based on the Penn Heart Failure Study.21 In Section 4, we discuss key model assumptions and provide results from a simulation study evaluating the impact of a sub-optimal marker combination on estimation of the AUC and the net reclassification improvement. We provide concluding discussion in Section 5.
2 Statistical Methods
2.1 Notation
Let Xj, j = 1, …, p denote biomarkers and Zk, k = 1, …, q denote clinical variables collected at baseline. Let T denote the subsequent failure time, such as the time to all-cause mortality or cardiac transplantation, which may or may not be observed due to censoring. Then let D(t) denote the occurrence of an event prior to time t such that if T ≤ t, then D(t) = 1 indicates a `case' and if T > t, then D(t) = 0 indicates a `control.'
2.2 Development of a Composite Marker
A standard Cox regression model can be used to derive a composite marker as a weighted combination of biomarkers and clinical variables, in which the weights are determined by the estimated regression coefficients. Recall that a Cox regression model is specified by the hazard function, which is defined as the instantaneous rate at which failures occur for individuals that are surviving at time t:
| (1) |
The Cox regression model employs a log function to relate the hazard function to a linear combination of biomarkers and clinical variables:
| (2) |
where: λ0(t) is an unspecified baseline hazard function; βj are regression parameters that correspond to biomarkers Xj; and γk are regression parameters that correspond to clinical variables Zk. Because biomarkers and clinical variables are only measured at baseline and are constant over time, λ(t) is often referred to as a `proportional hazards' model. Censoring can be accommodated in likelihood-based estimation of the regression parameters, but censoring must be assumed to be independent of survival, i.e. non-informative censoring. The estimated regression coefficients can then be used to derive a composite marker M as a weighted combination of biomarkers and clinical variables:
| (3) |
To quantify the predictive accuracy of the composite marker, M can be supplied as the input to a time-dependent ROC analysis, which we review in the following section.
2.3 Evaluation of Time-Dependent Predictive Accuracy
2.3.1 Time-Dependent ROC Analysis
Recall that a standard ROC curve is a graphical plot of the sensitivity, or the true-positive fraction, versus 1 – specificity, or the false-positive fraction, across all possible dichotomizations of a continuous diagnostic marker. For censored survival outcomes, sensitivity and specificity can be defined as a time-dependent function across all possible dichotomizations c of the composite marker M:
| (4) |
| (5) |
where: S(t) is the survival function at time t, i.e. S(t) = P[T > t]; S(t | M > c) is the conditional survival function for the subset defined by M > c; and S(t | M ≤ c) is the conditional survival function for the subset defined by M ≤ c. A time-dependent ROC curve at time t is simply a plot of the time-dependent false-positive fraction (or, 1 – specificity) versus the time-dependent true-positive fraction (or, sensitivity). Estimation of time-dependent sensitivity and specificity based on censored survival outcomes may proceed via either a simple Kaplan-Meier estimator or nearest neighbor estimation.7 Nearest neighbor estimation is preferable because it guarantees monotone sensitivity and specificity, and allows the censoring process to depend on the composite marker. The area under the time-dependent ROC curve can be calculated to quantify the predictive accuracy of the composite marker at time t; the difference between two AUCs can be used to quantify the difference in predicative accuracy between two markers. Standard error estimation is discussed in Section 2.4.
2.3.2 Risk Reclassification for Censored Survival Outcomes
Risk reclassification methods are based on the stratification of estimated absolute risk into categories defined by clinically relevant risk thresholds, and the degree to which a model of interest more accurately classifies individuals into higher or lower risk categories relative to a comparison model.17,18 Proposed reclassification metrics include the net reclassification improvement (NRI). The NRI quantifies the predictive accuracy of a marker or set of markers by examining the difference in the proportions `moving up' into a higher risk category and `moving down' into a lower risk category among cases and controls between models with and without the marker(s) of interest:
| (6) |
By considering reclassification improvement separately among cases and controls, the NRI facilitates evaluation of a marker's ability to more accurately classify high-risk and low-risk individuals. For survival outcomes, risk at time t can be quantified by estimated survival probabilities obtained from a Cox regression model. Because individuals may be censored before time t, their true `case' or `control' status is unknown at t. Within cross-classified risk strata, the Kaplan-Meier estimator can be used to estimate the number of cases and controls at time t so that all individuals contribute information to the analysis.19,20 Thus for censored survival outcomes, NRI(t) can be calculated for the estimated number of cases and controls `moving up' or `moving down' risk categories. Alternatively, a general `prospective form' of the NRI may be obtained by exploiting Bayes' rule.20 Standard error estimation is discussed in the following section.
2.4 Standard Error Estimation
In Section 2.3.1, we described a simple procedure to quantify the predictive accuracy of a multiple biomarkers and clinical variables for censored survival outcomes, in which estimated Cox regression coefficients are used to derive a composite marker, which is then supplied as the input to a time-dependent ROC analysis. A confidence interval for the corresponding AUC can be used to quantify uncertainty in the predictive accuracy of the composite marker. In addition, a Wald test based on the difference between two AUCs can be used to test for a statistically significant difference in predictive accuracy between two markers. Standard error estimates for confidence intervals and Wald tests must account for both the uncertainty due to the estimation of the Cox regression parameters and the uncertainty due to estimation of the time-dependent sensitivity and specificity. Assuming that the sample is from an independent and identically distributed population, a bootstrap can be used to obtain standard error estimates.22 Bootstrap procedures involve constructing resamples of the original dataset (of equal size), each of which is obtained by sampling with replacement from the original dataset. Estimates of the AUC and of the difference between two AUCs are obtained for each resampled dataset, and the standard deviation of the estimates across resampled datasets can be used as the standard error. There are options for model-based standard error estimation.14
In Section 2.3.2, we discussed the NRI, which evaluates the degree to which a model with marker(s) of interest more accurately classifies individuals into higher or lower risk categories relative to a comparison model without marker(s) of interest. A confidence interval for the corresponding NRI can be used to quantify uncertainly in the improvement in predictive accuracy associated with the marker(s) of interest. In addition, a Wald test of the hypothesis that the NRI is equal to 0 can be used to formally test whether the improvement in predictive accuracy is statistically significant. Standard error estimates must account for both the uncertainty due to Kaplan-Meier estimation of the number of cases and controls and the uncertainty due to estimation of the NRI. A bootstrap can be used to obtain standard error estimates, in which estimates of the NRI are obtained from each resampled dataset, and the standard deviation of the estimated NRI across resampled datasets can be used as the standard error. In the following section, we apply ROC-based methods and methods based on risk reclassification to our motivating example.
3 Case Study
3.1 Background
The Penn Heart Failure Study is a prospective cohort study of outpatients with primarily chronic systolic heart failure recruited from referral centers at the University of Pennsylvania (Philadelphia, Pennsylvania), Case Western Reserve University (Cleveland, Ohio), and the University of Wisconsin (Madison, Wisconsin).21 Biomarker levels were measured from plasma samples collected at enrollment. Subsequent adverse events, including all-cause mortality and cardiac transplantation, were prospectively ascertained every six months via direct contact with participants or through death certificates, medical records, and contact with family members. All participants provided written, informed consent; the study protocol was approved by participating Institutional Review Boards.
The analysis goal was to determine the added prognostic value of a novel biomarker, ST2, when used in combination with two established risk predictors: brain natriuretic peptide level (NT-proBNP), a diagnostic and prognostic measure of heart failure severity; and the Seattle Heart Failure Model (SHFM), a validated risk score for mortality based on readily available clinical and laboratory variables.10 The SHFM was based on age, gender, New York Heart Association functional classification, heart failure etiology, left ventricular ejection fraction, medications (angiotensin converting enzyme inhibitor/angiotensin receptor blocker use, beta-blocker use, carvedilol use, statin use, furosemide equivalent daily dose, digoxin use), and laboratory values (serum sodium and creatinine). We limited our analysis to the combined outcome of all-cause mortality or cardiac transplantation, or transplant-free survival, to focus on the most serious outcomes associated with heart failure.
3.2 Methods
ST2 and NT-proBNP were positively skewed and were transformed using a log2 transformation to avoid the undue influence of participants with an abnormally high ST2 or NT-proBNP. Estimates of the baseline hazard function were used to recalibrate SHFM, which was derived from an external cohort. Transformed biomarkers, as well as SHFM, exhibited a symmetric distribution. To aide in the comparison of estimated regression coefficients, log2-transformed biomarkers and SHFM were scaled by their standard deviation (on the log2 scale).
Time-dependent ROC analyses were used to determine the predictive ability of ST2 in combination with NT-proBNP and SHFM. First, Cox regression models for transplant-free survival were used to derive a composite marker M1 as a weighted combination of NT-proBNP and SHFM, and to derive a composite marker M2 as a weighted combination of ST2, NT-proBNP, and SHFM. Weights were determined by the estimated Cox regression coefficients. Next, ST2 and the composite markers M1 and M2 were supplied as inputs to a time-dependent ROC analysis to estimate the AUC at one year. Confidence intervals for the AUC and p-values for the difference between two AUCs were computed from 1000 bootstrap samples.
Net reclassification improvement was used to determine the added predictive value of ST2 above that of NT-proBNP and SHFM. Cox regression models with NT-proBNP and SHFM, but with and without ST2, were used to predict one-year risk of all-cause mortality or cardiac transplantation. All participants were cross-classified according to their estimated risk across clinically meaningful risk thresholds of 10%, 20%, and 50%. Within each cross-classified risk stratum, the Kaplan-Meier estimate of one-year risk was used to estimate the number of cases and controls. The NRI at one year was calculated for the estimated number of cases and controls `moving up' or `moving down' risk categories. Confidence intervals and p values were computed from 1000 bootstrap samples.
3.3 Results
Complete information was available on 1125 participants, of which 107 participants were censored before one year. Of the remaining 1018 participants, 147 (14%) died or received a cardiac transplantation within one year.
According to the estimated Cox regression coefficients, the composite markers M1 and M2 were:
| (7) |
| (8) |
These results indicated that the composite marker for NT-proBNP and SHFM (M1) was more heavily weighted by SHFM compared to NT-proBNP. Similarly, the composite marker for ST2, NT-proBNP, and SHFM (M2) was most heavily weighted by SHFM compared to ST2 and NT-proBNP; ST2 was weighted more heavily compared to NT-proBNP.
Figure 1 displays estimated time-dependent ROC curves for transplant-free survival at one year for ST2 and both composite markers. The AUC for ST2 was 0.746, 95% CI: (0.697, 0.794), which indicated that ST2 accurately discriminated between high- and low-risk individuals at one year. The AUC for M1—the composite marker for NT-proBNP and SHFM—was 0.828, 95% CI: (0.791, 0.865), which when compared to the AUC for ST2 indicated that the predictive accuracy of NT-proBNP and SHFM was significantly greater than that of ST2 (p < 0.01). The AUC for M2—the composite marker for ST2, NT-proBNP, and SHFM—was 0.825, 95% CI: (0.786, 0.864). Because the AUC for M2 was not significantly different from that for M1 (p = 0.69), there was no evidence to suggest that ST2 had added predictive ability when used in combination with NT-proBNP and SHFM.
Figure 1.
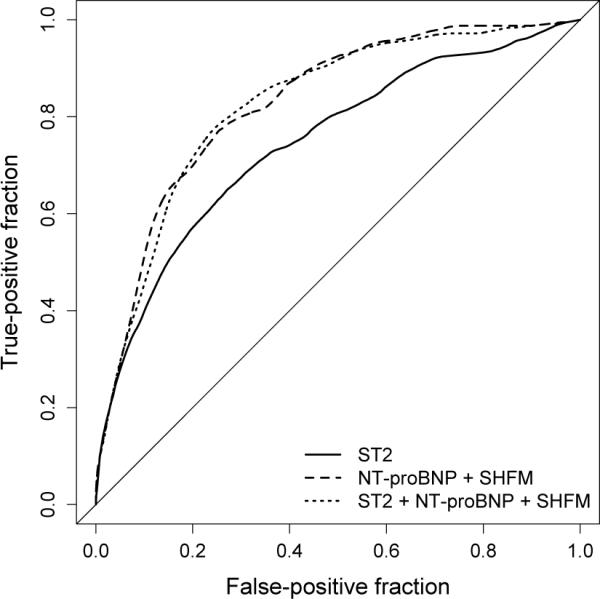
Estimated time-dependent ROC curves for transplant-free survival at one year: ST2 (` ') the composite marker for NT-proBNP and SHFM (`
') the composite marker for NT-proBNP and SHFM (` '); and the composite marker for ST2, NT-proBNP, and SHFM (`
'); and the composite marker for ST2, NT-proBNP, and SHFM (` ').
').
Table 1 provides a risk reclassification table comparing one-year risk of all-cause mortality or cardiac transplantation from Cox regression models with NT-proBNP and SHFM, but with and without ST2. The model without ST2 classified 56% of participants into the <10% risk category, 23% into the 10% to <20% risk category, 18% into the 20% to <50% risk category, and 3% into the ≥50% risk category. Similar marginal proportions were observed for the model with ST2. Reclassification rates can be calculated from the estimated number of cases and controls `moving up' or `moving down' risk categories in Table 1. For example, the number of cases at one year was estimated from the Kaplan-Meier risk estimate: 1125 × 0.132 = 148.6. Of the 148.6 estimated cases, 3.0 + 6.2 + 9.0 = 18.2 `moved up' in risk category when ST2 was added to the model with NT-proBNP and SHFM, whereas 1.0 + 10.4 + 2.0 = 13.4 `moved down' in risk category. Thus the reclassification rate among cases was 3.2% (18.2 – 13.4 of 148.6), 95% CI: (−5.6%, 12.0%), although the improvement was not statistically significant (p = 0.48). The reclassification rate among controls was 3.3% (77.6 – 45.8 of 976.4), 95% CI: (−0.3%, 6.8%), which represented a marginally significant improvement in classification accuracy (p = 0.07). Overall, the net reclassification improvement with the addition of ST2 was 6.4%, 95% CI: −4.2%, 17.1%), although the improvement was not statistically significant (p = 0.23).
Table 1.
Risk reclassification table comparing one-year risk of all-cause mortality or cardiac transplantation from Cox regression models with NT-proBNP and SHFM, but with and without ST2. Cases and controls estimated from Kaplan-Meier risk at one year; Cases = All × Observed risk / 100; Controls = All × (1 – Observed risk / 100).
| Model with ST2 | Reclassified, % | |||||||
|---|---|---|---|---|---|---|---|---|
| Model without ST2 | 0% to <10% | 10% to <20% | 20% to <50% | 50% to 100% | Total, n (%) | Lower | Higher | Total |
| 0% to <10% | ||||||||
| All, n (%) | 613 (97) | 20 (3) | 0 (0) | 0 (0) | 633 (56) | – | 3 | 3 |
| Cases, n (%) | 19.2 (85) | 3.0 (13) | 0 (0) | 0 (0) | 22.2 (15) | – | 13 | 13 |
| Controls, n (%) | 593.8 (95) | 17.0 (3) | 0 (0) | 0 (0) | 610.8 (54) | – | 3 | 3 |
| Observed risk, % | 3.1 | 15.0 | 3.5 | |||||
| 10% to <20% | ||||||||
| All, n (%) | 49 (19) | 183 (71) | 27 (10) | 0 (0) | 259 (23) | 19 | 10 | 29 |
| Cases, n (%) | 0.0 (0) | 23.1 (77) | 6.2 (21) | 0 (0) | 29.3 (20) | 0 | 21 | 21 |
| Controls, n (%) | 49.0 (21) | 159.9 (68) | 20.8 (9) | 0 (0) | 229.7 (24) | 21 | 9 | 30 |
| Observed risk, % | 0.0 | 12.6 | 22.8 | 11.3 | ||||
| 20% to <50% | ||||||||
| All, n (%) | 3 (2) | 34 (17) | 143 (73) | 17 (9) | 197 (18) | 19 | 9 | 28 |
| Cases, n (%) | 1.0 (2) | 10.4 (21) | 52.2 (80) | 9.0 (7) | 72.4 (49) | 23 | 7 | 30 |
| Controls, n (%) | 2.0 (2) | 23.6 (21) | 90.8 (80) | 8.0 (7) | 124.6 (13) | 23 | 7 | 30 |
| Observed risk, % | 33.3 | 30.7 | 36.5 | 52.9 | 36.8 | |||
| 50% to 100% | ||||||||
| All, n (%) | 0 (0) | 0 (0) | 5 (14) | 31 (86) | 36 (3) | 14 | – | 14 |
| Cases, n (%) | 0 (0) | 0 (0) | 2.0 (8) | 22.0 (93) | 24.3 (16) | 8 | – | 8 |
| Controls, n (%) | 0 (0) | 0 (0) | 3.0 (26) | 9.0 (79) | 11.7(1) | 26 | – | 26 |
| Observed risk, % | 40.0 | 71.0 | 67.4 | |||||
| Total | ||||||||
| All, n (%) | 665 (59) | 237 (21) | 175 (16) | 48 (4) | 1125 (100) | – | – | – |
| Cases, n (%) | 20.3 (14) | 36.4 (24) | 60.5 (41) | 31.0 (21) | 148.6 (100) | – | – | – |
| Controls, n (%) | 644.7 (66) | 200.6 (21) | 114.5 (12) | 17.0 (2) | 976.4 (100) | – | – | – |
| Observed risk, % | 3.1 | 15.4 | 34.5 | 64.6 | 13.2 | |||
3.4 Summary
The goal of this analysis was to determine the added prognostic value of ST2 when used in combination with two established risk predictors: NT-proBNP and SHFM. Time-dependent ROC analyses indicated that, although ST2 exhibited an ability to predict risk, the predictive ability of a combination of ST2, NT-proBNP, and SHFM was similar to that of a combination of NT-proBNP and SHFM. Risk reclassification analyses indicated that, although the addition of ST2 improved discrimination of low-risk individuals, there was no overall improvement in discrimination for defined risk thresholds. Therefore, although ST2 was a potent predictor of risk, it offered limited predictive accuracy beyond that of an established biomarker (NT-proBNP) and a clinical risk score (SHFM).
4 Model Assumptions
In our case study, we illustrated the use of methods based on time-dependent ROC curves and risk reclassification to evaluate the ability of multiple biomarkers and clinical variables measured at baseline to predict a subsequent survival outcome that may be subject to censoring. Both approaches relied on a semi-parametric Cox regression model to form a simple linear combination of the component markers based on their estimated regression coefficients. However, there are two typical situations in which a simple linear combination of the component markers may not optimally capture their true association with the outcome of interest. First, there may be a non-linear association between a marker and the outcome. Second, there may be an interaction between two or more markers. In these situations, a simple linear combination of the component markers can be viewed as a sub-optimal marker combination, whereas a combination that more closely approximates the true functional form between the markers and the outcome can be viewed as an optimal combination. In a simulation study and our case study, we evaluated the impact of a sub-optimal linear marker combination on estimation and inference regarding the improvement in predictive accuracy associated with a marker of interest.
4.1 Simulation Study
We performed a simulation study to evaluate the impact of a sub-optimal linear marker combination on estimation of the time-dependent AUC and NRI. We considered two settings: first, when the optimal marker combination includes a quadratic term for the biomarker; and second, when the optimal marker combination includes an interaction between the biomarker and the clinical variable.
4.1.1 Parameters
At each of 1000 iterations, we simulated a biomarker X and a clinical variable Z for a sample of n = 300 individuals from a bivariate Normal distribution:
| (9) |
for which ρ = 0.3. We specified the following optimal marker combinations: one that included a quadratic term for the biomarker [Setting (1)]; and one that included an interaction between the biomarker and the clinical variable [Setting (2)]:
| (10) |
| (11) |
In each setting, we generated a failure time T for each individual from an Exponential distribution with rate exp(M). We introduced an independent censoring process and in each setting selected the rate such that approximately 20% of individuals were censored before their failure time. In each setting, we estimated time-dependent ROC curves for Z alone, for the sub-optimal linear combination of X and Z, and for the optimal combination of X and Z at t = 0.25. We also estimated the NRI for the sub-optimal linear combination of X and Z versus Z alone and for the optimal combination of X and Z versus Z alone at t = 0.25. Standard error estimation was based on 200 bootstrap samples at each iteration.
4.1.2 Results
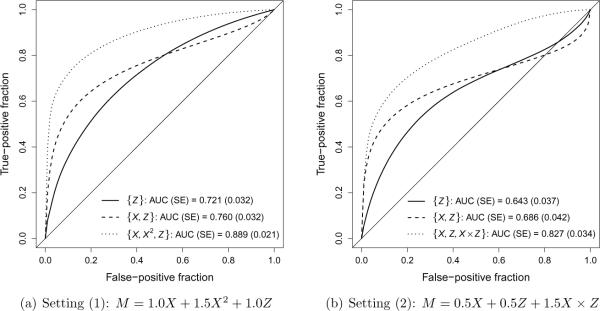
Figure 2 presents time-dependent ROC curves for Z alone (` '), for the sub-optimal linear combination of X and Z (`
'), for the sub-optimal linear combination of X and Z (` '), and for the optimal combination of X and Z (`
'), and for the optimal combination of X and Z (` ') in settings (1) and (2). Table 2 provides the difference in AUC and the NRI to quantify the improvement in predictive accuracy associated with a biomarker X for the sub-optimal linear combination of X and Z and for the optimal combination of X and Z in settings (1) and (2). In Figure 2 and Table 2, summaries are presented as the average estimate across 1000 iterations and the average standard error obtained as the average standard deviation of estimates from 200 bootstrap samples. In both settings, the sub-optimal linear marker combination provides a modest improvement in predictive accuracy compared to the clinical covariate alone, as exhibited by the increase in AUC and the positive NRI. However, in both settings the optimal marker combination provides a substantial improvement in predictive accuracy.
') in settings (1) and (2). Table 2 provides the difference in AUC and the NRI to quantify the improvement in predictive accuracy associated with a biomarker X for the sub-optimal linear combination of X and Z and for the optimal combination of X and Z in settings (1) and (2). In Figure 2 and Table 2, summaries are presented as the average estimate across 1000 iterations and the average standard error obtained as the average standard deviation of estimates from 200 bootstrap samples. In both settings, the sub-optimal linear marker combination provides a modest improvement in predictive accuracy compared to the clinical covariate alone, as exhibited by the increase in AUC and the positive NRI. However, in both settings the optimal marker combination provides a substantial improvement in predictive accuracy.
Figure 2.
Simulation results for time-dependent ROC curves for Z alone (` '), for the sub-optimal linear combination of X and Z (`
'), for the sub-optimal linear combination of X and Z (` '), and for the optimal combination of X and Z (`
'), and for the optimal combination of X and Z (` ') in settings (1) and (2). Summaries presented as the average estimated AUC across 1000 iterations (`AUC') and the average standard error obtained as the average standard deviation of estimates from 200 bootstrap samples (`SE').
') in settings (1) and (2). Summaries presented as the average estimated AUC across 1000 iterations (`AUC') and the average standard error obtained as the average standard deviation of estimates from 200 bootstrap samples (`SE').
Table 2.
Simulation results for the improvement in predictive accuracy associated with a biomarker X for the sub-optimal linear combination of X and Z and for the optimal combination of X and Z in settings (1) and (2). Summaries presented as the average estimate across 1000 iterations (`Mean') and the average standard error obtained as the average standard deviation of estimates from 200 bootstrap samples (`SE'); p value obtained from a hypothetical two-sided, one-sample z test based on average estimate and average standard error.
| Mean (SE) | p | |
|---|---|---|
| Setting (1): M = 1.0X + 1.5X2 + 1.0Z | ||
| Difference in AUC | ||
| {X, Z} versus {Z} | 0.038 (0.028) | 0.18 |
| {X,X2,Z} versus {Z} | 0.168 (0.030) | < 0.01 |
| NRI | ||
| {X, Z} versus {Z} | 7.3% (13.5%) | 0.59 |
| {X,X2,Z} versus {Z} | 37.7% (8.3%) | < 0.01 |
| Setting (2): M = 0.5X + 0.5Z + 1.5X × Z | ||
| Difference in AUC | ||
| {X, Z} versus {Z} | 0.043 (0.030) | 0.16 |
| {X,Z,X × Z} versus {Z} | 0.183 (0.043) | < 0.01 |
| NRI | ||
| {X, Z} versus {Z} | 19.3% (28.9%) | 0.50 |
| {X,Z,X × Z} versus {Z} | 41.3% (10.7%) | < 0.01 |
For the purpose of illustration, assume that the point estimates for the difference in AUC and the NRI provided in Table 2, along with their associated estimated standard errors, were obtained from a single dataset. These estimates could be used to formally test for an improvement in predictive accuracy based on a two-sided, one-sample z test. The p values from such a test are provided in Table 2. Of note, in neither setting would the sub-optimal linear marker combination provide evidence for a statistically significant improvement in predictive accuracy associated with the biomarker X (all p > 0.05). However, in both settings the optimal marker combination would provide evidence for a highly significant improvement in predictive accuracy (all p < 0.01).
4.2 Case Study
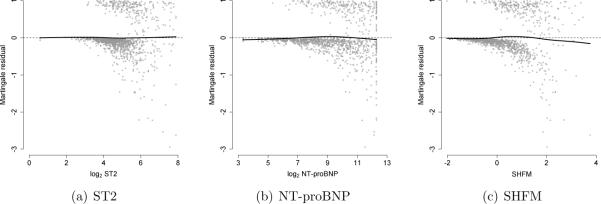
The results of our simulation study suggest that in applications it is critical to verify assumptions regarding the functional form for component markers and to consider plausible forms for effect modification to determine whether the composite marker is correctly specified. Otherwise, the improvement in predictive accuracy associated with the marker(s) of interest may be incorrectly estimated. To evaluate the assumption of linearity, Martingale residuals can be plotted against each component marker.23
Figure 3 presents Martingale residuals versus (a) log2 ST2, (b) log2 NT-proBNP, and (c) SHFM with a flexible smoothing spline with 4 degrees of freedom (` '). If the linearity assumption was satisfied, then the smoothing spline would appear as a flat line at 0. For each component marker, this appears to be the case. To evaluate plausible forms for effect modification, a model-based Wald test could be used to evaluate the statistical significance of the interaction term. In our case study, there was no evidence of effect modification.
'). If the linearity assumption was satisfied, then the smoothing spline would appear as a flat line at 0. For each component marker, this appears to be the case. To evaluate plausible forms for effect modification, a model-based Wald test could be used to evaluate the statistical significance of the interaction term. In our case study, there was no evidence of effect modification.
Figure 3.
Diagnostics to evaluate linearity for the Cox regression model used to derive the composite marker for ST2, NT-proBNP, and SHFM: Smoothing spline with 4 degrees of freedom (` ').
').
5 Discussion
In this article, we illustrated analytic strategies to develop a composite marker that maximizes use of all available biomarker and clinical information, and compared alternative statistical methods to evaluate the accuracy of the composite marker in predicting a censored survival outcome. We considered a standard Cox regression model to derive a composite marker as a weighted combination of biomarkers and clinical variables, in which the weights were determined by the estimated regression coeffcients; the composite marker was supplied as the input to a time-dependent ROC analysis. Alternatively, we considered risk reclassification methods based on the stratification of absolute risk estimated from a Cox regression model into categories defined by clinically relevant risk thresholds, and the degree to which a model of interest more accurately classified individuals into higher or lower risk categories relative to a comparison model. Our research adds to the growing body of literature on statistical methods for evaluating the predictive accuracy of a survival model.24,25 To our knowledge, our simulation study is the first to directly compare the statistical properties of AUC-based and reclassification-based approaches in the context of a censored survival outcome. In our simulation study, we showed that a sub-optimal marker combination may provide an incorrect estimate of the improvement in predictive accuracy associated with the marker(s) of interest, as quantified by the difference in AUC and the NRI. Therefore, in applications we recommend that analysts carefully examine the functional form for component markers and consider plausible forms for effect modification to maximize the prognostic potential of the composite marker.
In part, methods based on risk reclassification have been popularized because ROC-based methods may be insensitive to clinically important differences in risk.17,18,26 Our results provided examples in which these methods were similarly able (or, unable) to detect risk differences. First, in our case study neither the difference in AUC nor the NRI suggested that ST2 significantly improved predictive accuracy when used in combination with NT-proBNP and SHFM. Second, in our simulation study the difference in AUC and the NRI exhibited a similar ability to detect an improvement in predictive accuracy. Table 3 provides a comparison of p values from each simulated dataset for the optimal and sub-optimal combination of X and Z in settings (1) and (2). Note that p values were obtained at each iteration from a two-sided, one-sample z test based on the estimated NRI, the estimated difference in AUC, and their corresponding bootstrap standard errors. In each setting, the difference in AUC was slightly more sensitive to an improvement in predictive accuracy than the NRI. For example, Table 3(a) compares p values evaluating the improvement in predictive accuracy for the sub-optimal linear combination in setting (1), at a threshold of α = 0.05. There was limited evidence of an improvement in this setting, such that the power level—the rate at which the null hypothesis of no improvement was rejected—was 10% for the NRI and 20% for the difference in AUC. Table 3(d) compares p values evaluating the improvement in predictive accuracy for the optimal combination in setting (2), at a threshold of α = 0.01. In this setting, there was strong evidence of an improvement, such that the power level for the NRI and the difference in AUC was 90% and 95%, respectively.
Table 3.
Comparison of p values from each simulated dataset for the optimal and sub-optimal combination of X and Z in settings (1) and (2); p values were obtained at each iteration from a two-sided, one-sample z test based on the estimated NRI, the estimated difference in AUC, and their corresponding bootstrap standard errors.
| (a) Setting (1), {X, Z} versus {Z} | |||
|---|---|---|---|
| NRI | |||
| AUC | p ≥ 0.05 | p < 0.05 | Total |
| p ≥ 0.05 | 769 | 31 | 800 |
| p < 0.05 | 130 | 70 | 200 |
|
| |||
| Total | 899 | 101 | 1000 |
| (b) Setting (1), {X,X2,Z} versus {Z} | |||
|---|---|---|---|
| NRI | |||
| AUC | p ≥ 0.01 | p < 0.01 | Total |
| p ≥ 0.01 | 0 | 0 | 0 |
| p < 0.01 | 20 | 980 | 1000 |
|
| |||
| Total | 20 | 980 | 1000 |
| (c) Setting (2), {X, Z} versus {Z} | |||
|---|---|---|---|
| NRI | |||
| AUC | p ≥ 0.05 | p < 0.05 | Total |
| p ≥ 0.05 | 615 | 141 | 756 |
| p < 0.05 | 148 | 96 | 244 |
|
| |||
| Total | 763 | 237 | 1000 |
| (d) Setting (2), {X,Z,X × Z} versus {Z} | |||
|---|---|---|---|
| NRI | |||
| AUC | p ≥ 0.01 | p < 0.01 | Total |
| p ≥ 0.01 | 11 | 27 | 38 |
| p < 0.01 | 85 | 877 | 962 |
|
| |||
| Total | 96 | 904 | 1000 |
In our simulation study, we focused on two typical situations in which a simple linear combination of the component markers based on their estimated Cox regression coefficients may not optimally capture their true association with the outcome of interest: the presence of a non-linear association; and the presence of effect modification. In the context of censored survival outcomes, regression coefficients may also depend on time, i.e. the hazard may not be proportional. In this situation, a simple linear combination that ignores time-dependent effects may lead to a composite marker that does not accurately quantify predictive accuracy. There are standard methods to evaluate the proportional hazards assumption based on graphical representations and statistical tests.27 In our case study, there was no evidence to suggest that the proportional hazards assumption was violated for ST2, NT-proBNP, or SHFM. If the proportional hazards assumption was violated, then a time-dependent marker should be included in the model by interacting the marker with an appropriate function of time. The composite marker can be calculated as a weighted average of the time-independent and time-dependent component markers.
An important consideration when exploring effect modification in the analysis of censored survival outcomes is the scale of interaction. Interactions on one scale (e.g., multiplicative hazards) may not be present on another scale (e.g., additive hazards). Therefore, it may be important to explore alternative model structures when developing the composite marker. We performed additional simulation studies in which failure times were generated according to both multiplicative and additive interaction models with M = 1.0X + 0.5Z + 2.0X × Z. For the true multiplicative model, failure times were generated from an Exponential distribution with rate exp(M), so that the true AUC for the optimal combination of X and Z at t = 0.25 was 0.881. For the true additive model, failure times were generated according to , with U ~ Uniform(0, 1), so that the true AUC for the optimal combination at t = 0.42 was 0.762. We implemented both multiplicative and additive models to develop the composite marker. Because we focused on time-independent markers, we fit additive models using a partly parametric additive risk model, which accommodates time-independent effects.28 In the scenarios we considered, we found that incorrectly specifying the scale of interaction did not have a substantial impact on estimation of predictive accuracy. For example, under a true multiplicative model, the AUC for the optimal combination of X and Z based on the fitted multiplicative model was 0.871, wheres that based on the fitted additive model was 0.851. Under a true additive model, the AUC for the optimal combination of X and Z based on the fitted additive model was 0.729, wheres that based on the fitted multiplicative model was 0.738. Additional research is required to fully explore the use of alternative models to develop multi-marker risk scores.
Our case study considered the clinically relevant combined outcome of all-cause mortality or cardiac transplantation, or transplant-free survival, to focus on the most serious outcomes associated with heart failure. However, the occurrence of a cardiac transplantation may precede the occurrence of death, and if a transplantation occurs, then it may fundamentally alter the risk of death. Therefore, death and transplantation exist as competing risk events. A major goal in such a setting may be to accurately predict only those individuals who would require transplantation, and in this case the competing events must be considered in the choice of an inferential target. Simply censoring the competing risk events, such as all-cause mortality, leads to incorrect inference. Appropriate time-dependent ROC methods and risk reclassification methods were recently proposed to account for such competing risk events.9,20 If the goal is to identify individuals who are at risk for a particular event type (e.g., patients who require transplantation) rather than a combined outcome (e.g., cardiac transplantation and all-cause mortality), then these approaches may be adopted.
In our case study, we used all observed data to derive the composite marker and subsequently to evaluate its accuracy in predicting censored survival outcomes based on a time-dependent ROC curve, which may provide an overly optimistic estimate of predictive accuracy. For example, in the context of binary outcomes, estimation of a composite marker based on a logistic regression model followed by estimation of the corresponding ROC curve from the same dataset may lead to bias in the predictive accuracy of the composite marker, but the bias vanishes at a rate proportional to the sample size.29 In our case study, the sample size was sufficiently large (n = 1125). Alternatively, analysts could consider a jackknife approach in which the composite marker and its corresponding time-dependent ROC curve are computed across datasets, each of which is formed by leaving out one or more observations from the original dataset. For large datasets, computational approaches based on cross-validation are also available to ameliorate the potential for bias.30 Of course, external validation is only available when the prediction rule or classifier is applied to an independent dataset.
We used R (R Development Core Team, Vienna, Austria) and various extension packages to analyze the data in our case study and to perform the simulation study. We fit Cox regression models using the survival31 package, fit (partly parametric) additive survival models using the timereg32,33 package, and estimated time-dependent ROC curves using the survivalROC34,35 package. Limited software is available to implement risk reclassification methods. Therefore, in the Supplementary Material we provide R code to estimate the NRI in the context of censored survival outcomes using simulated data.
Supplementary Material
Acknowledgements
We gratefully acknowledge the University of Pennsylvania for supporting this research and the Penn Heart Failure Study for providing the data.
Funding This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors. The Penn Heart Failure Study is supported by the National Institutes of Health [grant number R01 HL088577].
Footnotes
Declaration of Competing Interests Dr. Cappola reports receiving research support from Abbott Diagnostics.
References
- 1.Roger VL, Go AS, Lloyd-Jones DM, Adams RJ, Berry JD, Brown TM, et al. Heart disease and stroke statistics—2011 update: A report from the American Heart Association. Circulation. 2011;123:e18–e209. doi: 10.1161/CIR.0b013e3182009701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Neubauer S. The failing heart—an engine out of fuel. New England Journal of Medicine. 2007;356:1140–51. doi: 10.1056/NEJMra063052. [DOI] [PubMed] [Google Scholar]
- 3.Vasan RS. Biomarkers of cardiovascular disease. Circulation. 2006;113:2335–62. doi: 10.1161/CIRCULATIONAHA.104.482570. [DOI] [PubMed] [Google Scholar]
- 4.Braunwald E. Biomarkers in heart failure. New England Journal of Medicine. 2008;358:2148–59. doi: 10.1056/NEJMra0800239. [DOI] [PubMed] [Google Scholar]
- 5.Koepsell T, Weiss NS. Epidemiologic Methods: Studying the Occurrence of Disease. Oxford University Press; New York: 2003. [Google Scholar]
- 6.Janes H, Pepe MS. Adjusting for covariate effects on classification accuracy using the covariate-adjusted receiver operating characteristic curve. Biometrika. 2009;96:371–82. doi: 10.1093/biomet/asp002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Heagerty PJ, Lumley T, Pepe MS. Time-dependent ROC curves for censored survival data and a diagnostic marker. Biometrics. 2000;56:337–44. doi: 10.1111/j.0006-341x.2000.00337.x. [DOI] [PubMed] [Google Scholar]
- 8.Heagerty PJ, Zheng Y. Survival model predictive accuracy and ROC curves. Biometrics. 2005;61:92–105. doi: 10.1111/j.0006-341X.2005.030814.x. [DOI] [PubMed] [Google Scholar]
- 9.Saha P, Heagerty PJ. Time-dependent predictive accuracy in the presence of competing risks. Biometrics. 2010;66:999–1011. doi: 10.1111/j.1541-0420.2009.01375.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Levy WC, Mozaffarian D, Linker DT, Sutradhar SC, Anker SD, Cropp AB, et al. The Seattle Heart Failure Model: Prediction of survival in heart failure. Circulation. 2006;113:1424–33. doi: 10.1161/CIRCULATIONAHA.105.584102. [DOI] [PubMed] [Google Scholar]
- 11.Cox D. Regression models and life tables (with discussion) Journal of the Royal Statistical Society, Series B. 1972;34:187–220. [Google Scholar]
- 12.Zheng Y, Cai T, Feng Z. Application of the time-dependent ROC curves for prognostic accuracy with multiple biomarkers. Biometrics. 2006;62:279–87. doi: 10.1111/j.1541-0420.2005.00441.x. [DOI] [PubMed] [Google Scholar]
- 13.Cai T, Cheng S. Robust combination of multiple diagnostic tests for classifying censored event times. Biostatistics. 2008;9:216–33. doi: 10.1093/biostatistics/kxm037. [DOI] [PubMed] [Google Scholar]
- 14.Hung H, Chiang C-T. Optimal composite markers for time-dependent receiver operating characteristic curves with censored survival data. Scandinavian Journal of Statistics. 2010;37:664–79. [Google Scholar]
- 15.Pepe MS, Janes H, Longton G, Leisenring W, Newcomb P. Limitations of the odds ratio in gauging the performance of a diagnostic, prognostic, or screening marker. American Journal of Epidemiology. 2004;159:882–90. doi: 10.1093/aje/kwh101. [DOI] [PubMed] [Google Scholar]
- 16.Janes H, Pepe MS, Gu W. Assessing the value of risk predictions by using risk stratification tables. Annals of Internal Medicine. 2008;149:751–60. doi: 10.7326/0003-4819-149-10-200811180-00009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pencina MJ, D'Agostino RB, Sr, D'Agostino RB, Jr, Vasan RS. Evaluating the added predictive ability of a new marker: From area under the ROC curve to reclassification and beyond. Statistics in Medicine. 2008;27:157–72. doi: 10.1002/sim.2929. [DOI] [PubMed] [Google Scholar]
- 18.Cook NR, Ridker PM. Advances in measuring the effect of individual predictors of cardiovascular risk: The role of reclassification measures. Annals of Internal Medicine. 2009;150:795–802. doi: 10.7326/0003-4819-150-11-200906020-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Viallon V, Ragusa S, Clavel-Chapelon F, Bénichou J. How to evaluate the calibration of a disease risk prediction tool. Statistics in Medicine. 2009;28:901–16. doi: 10.1002/sim.3517. [DOI] [PubMed] [Google Scholar]
- 20.Pencina MJ, D'Agostino RB, Sr, Steyerberg EW. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Statistics in Medicine. 2011;30:11–21. doi: 10.1002/sim.4085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ky B, French B, McCloskey K, Rame JE, McIntosh E, Shahi P, et al. High-sensitivity ST2 for prediction of adverse outcomes in chronic heart failure. Circulation Heart Failure. 2011;4:180–7. doi: 10.1161/CIRCHEARTFAILURE.110.958223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Efron B, Tibshirani RJ. An Introduction to the Bootstrap. Chapman and Hall; New York: 1993. [Google Scholar]
- 23.Therneau TM, Grambsch PM, Fleming TR. Martingale-based residuals for survival models. Biometrika. 1990;77:147–60. [Google Scholar]
- 24.Cook NR, Paynter NP. Performance of reclassification statistics in comparing risk prediction models. Biometrical Journal. 2011;53:237–58. doi: 10.1002/bimj.201000078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pepe MS. Problems with risk reclassification methods for evaluating prediction models. American Journal of Epidemiology. 2011;173:1327–35. doi: 10.1093/aje/kwr013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Vickers AJ, Cronin AM, Begg CB. One statistical test is sufficient for assessing new predictive markers. BMC Medical Research Methodology. 2011;11:13. doi: 10.1186/1471-2288-11-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Grambsch P, Therneau T. Proportional hazards tests and diagnostics based on weighted residuals. Biometrika. 1994;81:515–26. [Google Scholar]
- 28.McKeague IW, Sasieni PD. A partly parametric additive risk model. Biometrika. 1994;81:501–14. [Google Scholar]
- 29.Copas JP, Corbett P. Overestimation of the receiver operating characteristic curve for logistic regression. Biometrika. 2002;89:315–31. [Google Scholar]
- 30.Simon RM, Subramanian J, Li M-C, Menezes S. Using cross-validation to evaluate predictive accuracy of survival risk classifiers based on high-dimensional data. Briefings in Bioinformatics. 2011;12:203–14. doi: 10.1093/bib/bbr001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Therneau T, Lumley T. survival: Survival analysis, including penalized likelihood. R package version 2.36–9. Available at: http://CRAN.R-project.org/package=survival.
- 32.Scheike TH. timereg: timereg package for flexible regression models for survival data. R package version 1.6–3. Available at: http://CRAN.R-project.org/package=timereg.
- 33.Scheike TH, Martinussen T. Dynamic Regression Models for Survival Data. Springer; New York: 2006. [Google Scholar]
- 34.Heagerty PJ, Saha P. survivalROC: Time-dependent ROC curve estimation from censored survival data. R package version 1.0.0. Available at: http://CRAN.R-project.org/package=survivalROC.
- 35.Saha P, Heagerty PJ. Introduction to survivalROC: An R package for survival-ROC method. Available at: http://faculty.washington.edu/heagerty/Software/SurvROC/
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.