A ROAD to Classification in High Dimensional Space

Summary

For high-dimensional classification, it is well known that naively performing the Fisher discriminant rule leads to poor results due to diverging spectra and noise accumulation. Therefore, researchers proposed independence rules to circumvent the diverging spectra, and sparse independence rules to mitigate the issue of noise accumulation. However, in biological applications, there are often a group of correlated genes responsible for clinical outcomes, and the use of the covariance information can significantly reduce misclassification rates. In theory the extent of such error rate reductions is unveiled by comparing the misclassification rates of the Fisher discriminant rule and the independence rule. To materialize the gain based on finite samples, a Regularized Optimal Affine Discriminant (ROAD) is proposed. ROAD selects an increasing number of features as the regularization relaxes. Further benefits can be achieved when a screening method is employed to narrow the feature pool before hitting the ROAD. An efficient Constrained Coordinate Descent algorithm (CCD) is also developed to solve the associated optimization problems. Sampling properties of oracle type are established. Simulation studies and real data analysis support our theoretical results and demonstrate the advantages of the new classification procedure under a variety of correlation structures. A delicate result on continuous piecewise linear solution path for the ROAD optimization problem at the population level justifies the linear interpolation of the CCD algorithm.

1. Introduction

Technological innovations have had deep impact on society and on various areas of scientific research. High-throughput data from microarray and proteomics technologies are frequently used in many contemporary statistical studies. In the case of microarray data, the dimensionality is frequently in thousands or beyond, while the sample size is typically in the order of tens. The large-p-small-n scenario poses challenges for the classification problems. We refer to Fan and Lv (2010) for an overview of statistical challenges associated with high dimensionality.

When the feature space dimension p is very high compared to the sample size n, the Fisher discriminant rule performs poorly due to diverging spectra as demonstrated by Bickel and Levina (2004). These authors showed that the independence rule in which the covariance structure is ignored performs better than the naive Fisher rule (NFR) in the high dimensional setting. Fan and Fan (2008) demonstrated further that even for the independence rules, a procedure using all the features can be as poor as random guessing due to noise accumulation in estimating population centroids in high-dimensional feature space. As a result, Fan and Fan (2008) proposed the Features Annealed Independence Rule (FAIR) that selects a subset of important features for classification. Dudoit et al. (2002) reported that for microarray data, ignoring correlations between genes leads to better classification results. Tibshirani et al. (2002) proposed the Nearest Shrunken Centroid (NSC) which likewise employs the working independence structure. Similar problems are also studied in the machine learning community such as Domingos and Pazzani (1997) and Lewis (1998).

In microarray studies, correlation among different genes is an essential characteristic of the data and usually not negligible. Other examples include proteomics, and metabolomics data where correlation among biomarkers is commonplace. More details can be found in Ackermann and Strimmer (2009). Intuitively, the independence assumption among genes leads to loss of critical information and hence is suboptimal. We believe that in many cases, the crucial point is not whether to consider correlations, but how we can incorporate the covariance structure into the analysis with a bullet proof vest against diverging spectra and significant noise accumulation effect.

The setup of the objective classification problem is now introduced. We assume in the following that the variability of data under consideration can be described reasonably well by the means and variances. To be more precise, suppose that random variables representing two classes 𝒞₁ and 𝒞₂ follow p-variate normal distributions: X|Y = 1 ~ 𝒩_p(μ₁,Σ) and X|Y = 2 ~ 𝒩_p(μ₂,Σ) respectively. Moreover, assume ℙ(Y = 1) = 1/2. This Gaussian discriminant analysis setup is known for its good performance despite its rigid model structure. For any linear discriminant rule

$${\delta }_{\mathbf{w}}(\mathbf{X})=𝕀\{{\mathbf{w}}^T(\mathbf{X}-{\mathit{\mu }}_a)>0\},$$ (1)

where μ_a = (μ₂ + μ₁)/2, and 𝕀 denotes the indicator function with value 1 corresponds to assigning X to class 𝒞₂ and 0 class 𝒞₁, the misclassification rate of the (pseudo) classifier δ_w is

$$W({\delta }_{\mathbf{w}})=\frac{1}{2}{P}_2({\delta }_{\mathbf{w}}(\mathbf{X})=0)+\frac{1}{2}{P}_1({\delta }_{\mathbf{w}}(\mathbf{X})=1)=1-\mathrm{\Phi }({\mathbf{w}}^T{\mathit{\mu }}_d/{({\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w})}^{1/2}),$$ (2)

where μ_d = (μ₂ − μ₁)/2, and P_i is the conditional distribution of X given its class label i. We will focus on such linear classifier δ_w(·), and the mission is to find a good data projection direction w. Note that the Fisher discriminant

$${\delta }_F(\mathbf{X})=𝕀\{{({\mathbf{\Sigma }}^{-1}{\mathit{\mu }}_d)}^T(\mathbf{X}-{\mathit{\mu }}_a)>0\}$$ (3)

is the Bayes rule. There is an equivalent derivation of the Fisher discriminant, which does not involve Gaussian assumptions. We would skip it for now, and come back to this point when we extend our method to multi-class learning scenarios. There are two fundamental difficulties in applying the Fisher discriminant whose missclassification rate is

$$1-\mathrm{\Phi }\left({({\mathit{\mu }}_d^T{\mathbf{\Sigma }}^{-1}{\mathit{\mu }}_d)}^{1/2}\right).$$ (4)

The first difficulty arises from the noise accumulation effect in estimating the population centroids (Fan and Fan, 2008) when p is large. The second challenge is more severe: estimating the inverse of covariance matrix Σ when p > n (Bickel and Levina, 2004). As a result, much previous researches focus on the independence rules, which act as if Σ is diagonal. However, correlation matters!

To illustrate this point, consider a case when p = 2. These two features can be selected from the original thousands of features, and we can estimate the correlation between two variables with reasonable accuracy. Let

$$\mathbf{\Sigma }=\left(\begin{array}{cc}\hfill 1\hfill & \hfill \rho \hfill \\ \hfill \rho \hfill & \hfill 1\hfill \end{array}\right),$$

where ρ ∈ [0, 1) and μ_d = (μ₁, μ₂)^T. Without loss of generality, assume |μ₁| ≥ |μ₂| > 0. The misclassification rate of Fisher discriminant depends on

$${\mathrm{\Delta }}_p(\rho )={\mathit{\mu }}_d^T{\mathbf{\Sigma }}^{-1}{\mathit{\mu }}_d=\frac{1}{1-{\rho }^2}({\mu }_1^2+{\mu }_2^2-2\rho {\mu }_1{\mu }_2).$$ (5)

Note that

$${\mathrm{\Delta }}_{\rho }^{\prime }(\rho )>0\iff {\mu }_1{\mu }_2{\rho }^2-({\mu }_1^2+{\mu }_2^2)\rho +{\mu }_1{\mu }_2<0.$$

Therefore, when μ₁μ₂ < 0, ${\mathrm{\Delta }}_p^{\prime }(\rho )>0$ for all ρ ∈ [0, 1). On the other hand, when μ₁μ₂ > 0, Δ_p(ρ) decreases on $\rho \in (0,\frac{{\mu }_2}{{\mu }_1})$, and increases on $(\frac{{\mu }_2}{{\mu }_1},1)$. Notice that when ρ → 1, Δ_p → ∞ regardless of signs for μ₁μ₂, which in turn leads to vanishing classification error. On the other hand, if we use independence rule (also called naive Bayes rule), the optimal misclassification rate

$$1-\mathrm{\Phi }\left(\frac{{\Vert {\mathit{\mu }}_d\Vert }_2^2}{{({\mathit{\mu }}_d^T\mathbf{\Sigma }{\mathit{\mu }}_d)}^{1/2}}\right)$$ (6)

depends on $\mathrm{\Gamma }(\rho )={\Vert {\mathit{\mu }}_d\Vert }_2^4/{\mathit{\mu }}_d^T\mathbf{\Sigma }{\mathit{\mu }}_d$, which is monotonically decreasing for ρ ∈ [0, 1), with the limit ${({\mu }_1^2+{\mu }_2^2)}^2/{({\mu }_1+{\mu }_2)}^4$ that is smaller than unity when μ₁ and μ₂ have the same sign. Hence, the optimal classification error using the independence rule actually increases as correlation among features increases.

The above simple example shows that by incorporating correlation information, the gain in terms of classification error can be substantial. Elaboration on this point in more realistic scenarios is provided in Section 2. Now it seems wise to use at least a part of covariance structure to improve the performance of a classifier. So there is a need to estimate the covariance matrix Σ. Without structural assumptions on Σ, the pooled sample covariance Σ̂ is one natural estimate. But for p > n, it is not considered as a good estimate of Σ in general. We are lucky here because our mission is not constructing a good estimate of the covariance matrix, but finding a good direction w that leads to a good classifier. To mimic the optimal data projection direction Σ⁻¹μ_d, we do not adopt a direct plug-in approach, simply because it is unlikely that a product is a good estimate when at least one of its components is not. Instead, we find the data projection direction w by directly minimizing the classification error subject to a capacity constraint on w. From a broad spectrum of simulated and real data analysis, we are convinced that this approach leads to a robust and efficient sparse linear classifier.

Admittedly, our work is far from the first to use covariance for classification; support vector machines (Vapnik, 1995), for example, implicitly utilize covariance between covariates. Another notable work is “shrunken centroids regularized discriminant analysis” (SCRDA) (Guo et al., 2005), which calls for a version of regularized sample covariance matrix Σ̂_reg, and soft-thresholds on ${\widehat{\mathbf{\Sigma }}}_{\text{reg}}^{-1}{\widehat{\mathbf{x}}}_i$. Shao et al. (2011) consider a sparse linear discriminant analysis, assuming the sparsity on both the covariance matrix and the mean difference vector so that they can be regularized. They show that such a regularized estimator is asymptotically optimal under some conditions. However, to the best of our knowledge, this work is the first to select features by directly optimizing the misclassification rates, to explicitly use un-regularized sample covariance information, and to establish the oracle inequality and risk approximation theory.

There is a huge literature on high dimensional classification. Examples include principal component analysis in Bair et al. (2006) and Zou et al. (2006), partial least squares in Nguyen and Rocke (2002), Huang (2003) and Boulesteix (2004), and sliced inverse regression in Li (1991) and Antoniadis et al. (2003).

The rest of our paper is organized as follows. Section 2 provides some insights on the performances of naive Bayes, Fisher discriminant and restricted Fisher discriminants. In Section 3, we propose the Regularized Optimal Affine Discriminant (ROAD) and variants of ROAD. An efficient algorithm Constrained Coordinate Descent (CCD) is constructed in Section 4. Main risk approximation results and continuous piecewise linear property of the solution path are established in Section 5. We conduct simulation and empirical studies in Section 6. A short discussion is given in Section 7, and all proofs are relegated to the appendix.

2. Naive Bayes and Fisher Discriminant

To compare the naive Bayes and Fisher discriminant at the population level, we assume without loss of generality that variables have been marginally standardized so that Σ is a correlation matrix. Recall that the naive Bayes discriminant has error rate (6) and the Fisher discriminant has error rate (4). Let ${\mathrm{\Gamma }}_p={\Vert {\mathit{\mu }}_d\Vert }_2^4/{\mathit{\mu }}_d^T\mathbf{\Sigma }{\mathit{\mu }}_d\text{ and }{\mathrm{\Delta }}_p={\mathit{\mu }}_d^T{\mathbf{\Sigma }}^{-1}{\mathit{\mu }}_d$. Denote by ${\{{\lambda }_i\}}_{i=1}^p$ the eigenvalues and ${\{{\mathit{\xi }}_i\}}_{i=1}^p$ eigenvectors of the matrix Σ. Decompose

$${\mathit{\mu }}_d=a_1{\mathit{\xi }}_1+\cdots +a_p{\mathit{\xi }}_p,$$ (7)

where ${\{a_i\}}_{i=1}^p$ are the coefficients of μ_d in this new orthonormal basis ${\{{\mathit{\xi }}_i\}}_{i=1}^p$. Using the decomposition (7), we have

$${\mathrm{\Delta }}_p={\displaystyle \sum _{j=1}^p}{a}_j^2/{\lambda }_j,{\mathrm{\Gamma }}_p={\left({\displaystyle \sum _{j=1}^p}{a}_j^2\right)}^2/{\displaystyle \sum _{j=1}^p}{\lambda }_j{a}_j^2.$$ (8)

The relative efficiency of Fisher discriminant over naive Bayes is characterized by Δ_p/Γ_p. By the Cauchy-Schwartz inequality,

$${\mathrm{\Delta }}_p/{\mathrm{\Gamma }}_p\ge 1.$$

The naive Bayes method performs as well as the Fisher discriminant only when μ_d is an eigenvector of Σ.

In general, Δ_p/Γ_p can be much larger than unity. Since Σ is the correlation matrix, ${\displaystyle {\sum }_{j=1}^p}{\lambda }_j=\text{tr}(\mathbf{\Sigma })=p$. If μ_d is equally loaded on ξ_j, then the ratio

$${\mathrm{\Delta }}_p/{\mathrm{\Gamma }}_p=p^{-2}{\displaystyle \sum _{j=1}^p}{\lambda }_j{\displaystyle \sum _{j=1}^p}{\lambda }_j^{-1}=p^{-1}{\displaystyle \sum _{j=1}^p}{\lambda }_j^{-1}.$$ (9)

More generally, if ${\{a_j\}}_{j=1}^p$ are realizations from a distribution with the second moment σ², then by the law of large numbers,

$${\displaystyle \sum _{j=1}^p}{a}_j^2{\lambda }_j^{-1}\approx {\sigma }^2{\displaystyle \sum _{j=1}^p}1/{\lambda }_j,p^{-1}{\displaystyle \sum _{j=1}^p}{a}_j^2\approx {\sigma }^2,{\displaystyle \sum _{j=1}^p}{\lambda }_j{a}_j^2\approx {\sigma }^2{\displaystyle \sum _{j=1}^p}{\lambda }_j.$$

Hence, (9) holds approximately in this case. In other words, the right hand side of (9) is approximately the relative efficiency of the Fisher discriminant over the naive Bayes. Now suppose further that half of the eigenvalues of Σ are c and the other half are 2−c. Then, the right hand side of (9) is (c⁻¹+(2−c)⁻¹)/2. For example when the condition number is 10, this ratio is about 3. A high ratio translates into a large difference in error rates: $1-\mathrm{\Phi }({\mathrm{\Gamma }}_p^{1/2})$ for independence rule is much larger than $1-\mathrm{\Phi }(3{\mathrm{\Gamma }}_p^{1/2})$ for Fisher discriminant. For example, when ${\mathrm{\Gamma }}_p^{1/2}=0.5$, we have 30.9% and 6.7% error rates respectively for the naive Bayes and Fisher discriminant.

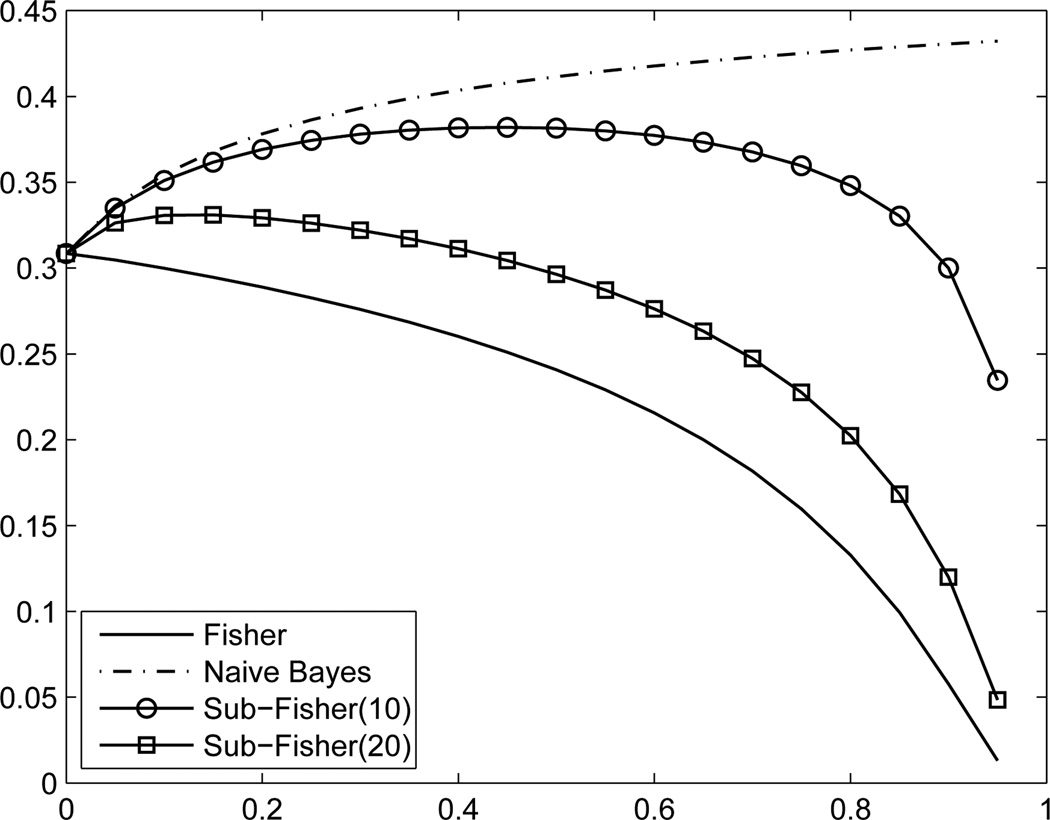
To put the above arguments under a visual inspection, consider a case in which p = 1000, ${\mathit{\mu }}_d={({\mathit{\mu }}_s^T,{\mathbf{0}}^T)}^T$ with μ_s = (1, 1, 1, 1, 1, 2, 2, 2, 2, 2)^T and Σ equals the equi-correlation matrix with pairwise correlation ρ. The vector μ_d simulates the case in which 10 genes out of 1000 express mean differences. Figure 1 depicts the theoretical error rates of the Fisher discriminant and the naive Bayes rule as functions of ρ.

Fig. 1.

Misclassification rates of Fisher discriminant, naive Bayes and restricted Fisher rules (10 and 20 features, respectively) against ρ.

It is not surprising that the Fisher discriminant rule performs significantly better than the naive Bayes as ρ deviates away from zero. The error rate of the naive Bayes actually increases with ρ, whereas the error rate of the Fisher discriminant tends to zero as ρ approaches 1. This phenomenon is the same as what was shown analytically through the toy example in Section 1. To mimic Fisher discriminant by a plug-in estimator, we need to estimate Σ⁻¹μ_d with reasonable accuracy. This mission is difficult if not impossible. On the other hand, imitating a weaker oracle is more manageable. For example, when the samples are of reasonable size, we can select the 10 variables with differences in means by applying a two-sample t-test. Restricting to the best linear classifiers based on these s = 10 variables, we have the optimal error rate

$$1-\mathrm{\Phi }({({\mathit{\mu }}_s^T{\mathbf{\Sigma }}_s^{-1}{\mathit{\mu }}_s)}^{1/2}),$$

where the classification rule is δ_w^R and ${\mathbf{w}}^R={({({\mathbf{\Sigma }}_s^{-1}{\mathit{\mu }}_s)}^T,{\mathbf{0}}^T)}^T$. The performance of this oracle classifier is depicted by the sub-Fisher (10 features) in Figure 1. It performs much better than the naive Bayes method. One can also employ the naive Bayes rule to the restricted feature space, but this method has exactly the same performance as the naive Bayes method in the whole space. Thus, the restricted Fisher discriminant outperforms both the naive Bayes method with restricted features and the naive Bayes method using all features.

Mimicking the performance of the restricted Fisher discriminant is feasible. Instead of estimating a 1000 × 1000 covariance matrix, we only need to gauge a 10 × 10 submatrix. However, this restricted Fisher rule is not powerful enough, as shown in Figure 1. We can improve its performance by including 10 most correlated variables to each of those selected features to further account for the correlation effect, giving rise to a 20-dimensional feature space. Since the variables are equally correlated in this example, we are free to choose any 10 variables among the other 990. The performance of such an enlarged restricted Fisher discriminant is represented by sub-Fisher (20 features) in Figure 1. It performs closely to the Fisher discriminant which uses the whole feature space, and it is feasible to implement with finite samples.

3. Regularized Optimal Affine Discriminant

The misclassification rate of Fisher discriminant is $1-\mathrm{\Phi }({\mathrm{\Delta }}_p^{1/2})$, where ${\mathrm{\Delta }}_p={\mathit{\mu }}_d^T{\mathbf{\Sigma }}^{-1}{\mathit{\mu }}_d$. However, for high dimensional data, it is impossible to achieve such a performance empirically. Among other reasons, the estimated covariance matrix Σ̂ is ill-conditioned or not invertible. One solution is to focus only on the s(≪ p) most important features for classification. Ideally, the best s features should be the ones with the largest Δ_s among all $\left(\begin{array}{c}\hfill p\hfill \\ \hfill s\hfill \end{array}\right)$ possibilities, where Δ_s is the counterpart of Δ_p when only s variables are considered. Naive search for the best subset of size s is NP-hard. Thus, we develop a regularized method to circumvent these two problems.

3.1. ROAD

Recall that by (2), minimizing the classification error W(δ_w) is the same as maximizing w^Tμ_d/(w^TΣw)^1/2, which is equivalent to minimizing w^TΣw subject to w^Tμ_d = 1. We would like to add a penalty function for capacity control. There are many ways to do regularization; for the literature on penalized methods, refer to LASSO (Tibshirani, 1996), SCAD (Fan and Li, 2001), Elastic net (Zou and Hastie, 2005), MCP (Zhang, 2010) and related methods (Zou, 2006; Zou and Li, 2008). As our primary interest is classification error (the risk of the procedure), an L₁ constraint ‖w‖₁ ≤ c is added for regularization, so the problem can be recast as

$${\mathbf{w}}_c=\underset{{\Vert \mathbf{w}\Vert }_1\le c,{\mathbf{w}}^T{\mathit{\mu }}_d=1}{\text{argmin}}{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}.$$ (10)

We name the classifier δ_wc (·) the Regularized Optimal Affine Discriminant(ROAD). The existence of a feasible solution in (10) dictates

$$c\ge 1/\underset{1\le i\le p}{\text{max}}|{\mu }_{d,i}|.$$ (11)

When c is small, we obtain a sparse solution and achieve feature selection using covariance information. When $c\ge {\Vert {\mathbf{\Sigma }}^{-1}{\mathit{\mu }}_d\Vert }_1/{\mathit{\mu }}_d^T{\mathbf{\Sigma }}^{-1}{\mathit{\mu }}_d$, the L₁ constraint is no longer binding and δ_wc reduces to the Fisher discriminant, which can be denoted by δ_w∞ (= δ_F). Therefore we have provided a family of linear discriminants, indexed by c, using from only one feature to all features. In some applications such as portfolio selection, the choice of c reflects the investor’s tolerance upper bound on gross exposure. In other applications, when the user does not have a such a preference, the choice of c can be data-driven. To accommodate both application scenarios, we propose a coordinate descent algorithm (Section 4) to implement our ROAD proposal.

3.2. Variants of ROAD

At the sample level, NSC (Tibshirani et al., 2002) and FAIR (Fan and Fan, 2008) both use shrunken versions of standardized mean difference to find the s features. In the same spirit, we consider the following Diagonal Regularized Optimal Affine Discriminant(D-ROAD) ${\delta }_{{\mathbf{w}}_c^I}$, where

$${\mathbf{w}}_c^I=\underset{{\Vert \mathbf{w}\Vert }_1\le c,{\mathbf{w}}^T{\mathit{\mu }}_d=1}{\text{argmin}}{\mathbf{w}}^T\text{diag}(\mathbf{\Sigma })\mathbf{w}.$$ (12)

The D-ROAD will be compared with NSC (Tibshirani et al., 2002) and FAIR (Fan and Fan, 2008) in the simulation studies, and all these independence based rules will be compared with ROAD and its two variants defined below.

A screening-based variant (to be proposed) of ROAD aims at mimicking the performance of sub-Fisher (10 features) in Figure 1. A fast way to select features is the independence screening, which uses the marginal information such as the two-sample t-test. We can also enlarge the selected feature subspace by incorporating the features which are most correlated to what have been chosen. This additional variant of ROAD tracks the performance of sub-Fisher (20 features) in Figure 1. We will refer to the two variants of ROAD as S-ROAD1 and S-ROAD2. More description of these procedures, along with their theoretical properties and numerical investigations, will be detailed in Sections 5 and 6.

A hint of the rationale behind including correlated features that do not show a difference in means between the two classes, is revealed through the two-feature example in the introduction. Suppose μ₂ = 0. Then, by (5), the power of the discriminant using two features is $1-\mathrm{\Phi }({\mathrm{\Delta }}_2^{1/2})\text{ where }{\mathrm{\Delta }}_2={\mu }_1^2/(1-{\rho }^2)$, whereas with the first feature alone the misclassification rate is $1-\mathrm{\Phi }({\mathrm{\Delta }}_1^{1/2})\text{ where }{\mathrm{\Delta }}_1={\mu }_1^2$. Therefore when the correlation |ρ| is large, using two correlated features is far more powerful than employing only one feature, even though the second feature has no marginal discrimination power. More intuition is granted by this observation: at the population level, the best s features are not necessarily those with largest standardized mean differences. In other words, with the two class Gaussian model in mind, when Σ is the correlation matrix, the most powerful s features for classification are not necessarily the coordinates of μ_d with largest absolute values. This is illustrated by the next stylized example.

Let X|Y = 0 ~ 𝒩 (μ₁,Σ) and X|Y = 1 ~ 𝒩 (μ₂,Σ), where μ₁ = (0, 0, 0)^T, μ₂ = (4, 0.5, 1)^T, and

$$\mathbf{\Sigma }=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill -0.25\hfill & \hfill 0\hfill \\ \hfill -0.25\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).$$

Suppose the objective is to choose 2 out of 3 variables for classification. If we rank features by marginal information, for example by the absolute value of standardized mean differences, then we would choose the 1st and 3rd features. On the other hand, denote μ_d,ij the mean difference vector for features i and j, Σ_ij the covariance matrix of features i and j, then the classification power using features i and j depends on ${\mathrm{\Gamma }}_{\mathit{\text{ij}}}={\mathit{\mu }}_{d,\mathit{\text{ij }}}^T{\mathbf{\Sigma }}_{\mathit{\text{ij}}}^{-1}{\mathit{\mu }}_{d,\mathit{\text{ij}}}$. Simple calculation leads to

$${\mathrm{\Gamma }}_{12}=18.4>17={\mathrm{\Gamma }}_{13}.$$

Hence the most powerful two features for classification are not the 1st and 3rd.

3.3. Extension to Multi-Class

In this section, we outline an extension of ROAD to multi-class classification problems. Suppose that there are K classes, and for j = 1,⋯, K, the jth class has mean μ_j and common covariance Σ. Denote the overall mean of features by ${\mathit{\mu }}_a=K^{-1}{\displaystyle {\sum }_{j=1}^K}{\mathit{\mu }}_j$. Fisher’s reduced rank approach to multi-class classification is a minimum distance classifier in some lower dimensional projection space. The first step is to find s ≤ K−1 discriminant coordinates $({\mathbf{w}}_1^{*},\cdots ,{\mathbf{w}}_s^{*})$ that separate the population centroids ${\{{\mathit{\mu }}_j\}}_{j=1}^K$ the most in the projected space $𝒮=\text{span}\{{\mathbf{w}}_1^{*},\cdots ,{\mathbf{w}}_s^{*}\}$. Then the population centroids μ_j ’s and new observation X are both projected onto 𝒮. The observation X will be assigned to the class whose projected centroid is closest to the projection of X onto 𝒮. Note that it is usually not necessary to compute all K −1 discriminant coordinates whose span is that of all K population centroids; the process can stop as long as the projected population centroids are well spread out in 𝒮.

We adopt the above procedure for multi-class classification. However, the large-p-small-n scenario demands regularization in selecting discriminant coordinates. Indeed, in the Fisher’s proposal the first discriminant coordinate ${\mathbf{w}}_1^{*}$ is the solution of

$$\underset{\mathbf{w}}{\text{max}}\frac{{\mathbf{w}}^T\mathbf{\text{Bw}}}{{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}},$$ (13)

where B = Ψ^TΨ, and the jth column of Ψ^T is (μ_j − μ_a). Note that a multiple of B is the between-class variance matrix. The second discriminant coordinate ${\mathbf{w}}_2^{*}$ is the maximizer of w^TBw/(w^TΣw) with constraint ${\mathbf{w}}_1^{*T}\mathbf{\Sigma }\mathbf{w}=0$, and the subsequent discriminant coordinates are determined analogously.

Since solving (13) is the same as looking for the eigenvector of Σ^−1/2BΣ^−1/2 corresponding to the largest eigenvalue, diverging spectrum and noise accumulation have to be considered when we work on the sample. To address these issues, we regularize w as in the binary case,

$$\underset{{\Vert \mathbf{w}\Vert }_1\le c,{\mathbf{w}}^T\mathbf{\text{Bw}}=1}{\text{min}}{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w},$$ (14)

whose solution is the first regularized discriminant coordinate ${\overline{\mathbf{w}}}_1^{*}$. The second regularized discriminant coordinate is obtained by solving (14) with additional constraint ${\overline{\mathbf{w}}}_1^{*T}\mathbf{\Sigma }\mathbf{w}=0$. Other regularized discriminant coordinates can be found similarly. With these s (≤ K − 1) regularized discriminant coordinates, the classifier is now based on the minimum distance to the projected centroids in the s-dimensional space spanned by ${\{{\overline{\mathbf{w}}}_j^{*}\}}_{j=1}^s$.

4. Constrained Coordinate Descent

With a Lagrangian argument, we reformulate problem (10) as

$${\overline{\mathbf{w}}}_{\lambda }=\underset{{\mathbf{w}}^T{\mathit{\mu }}_d=1}{\text{argmin}}\frac{1}{2}{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}+\lambda {\Vert \mathbf{w}\Vert }_1.$$ (15)

In this section, we propose a Constrained Coordinate Descent (CCD) algorithm that is tailored for solving our minimization problem with linear constraints. Optimization (15) is a constrained quadratic programming problem and can be solved by existing softwares such as MOSEK. Although these softwares are well regarded in practice, they are slow for our application. The structure of (15) could be exploited in order to obtain a more efficient algorithm. In line with the LARS algorithm, we will exploit the fact that the solution path has a piecewise-linear property.

In the compressed sensing literature, it is common to replace an affine constraint by a quadratic penalty. We borrow this idea and consider the following approximation to (15):

$${\tilde{\mathbf{w}}}_{\lambda ,\gamma }=\text{argmin}\frac{1}{2}{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}+\lambda {\Vert \mathbf{w}\Vert }_1+\frac{1}{2}\gamma {({\mathbf{w}}^T{\mathit{\mu }}_d-1)}^2.$$ (16)

In practice, we replace Σ by the pooled sample covariance Σ̂ and μ by the sample mean difference vector μ̂_d. By Theorem 6.7 in Ruszczynski (2006), we have

$${\tilde{\mathbf{w}}}_{\lambda ,\gamma }\to {\overline{\mathbf{w}}}_{\lambda }\text{ when }\gamma \to \mathrm{\infty }.$$

Note that we do not have to enforce the affine constraint strictly, because it only serves to normalize our problem. In the optimization problem (16), when λ = 0, the solution w̃_0,γ is always in the direction of Σ⁻¹μ_d, the Fisher discriminant, regardless of the value of γ. In addition, this observation is confirmed in the data analysis (Section 6.2) by the insensitivity of choice for γ. Therefore we hold γ as a constant in practice.

We solve (16) by coordinate descent. Non-gradient algorithms seem to be less popular for convex optimization. For instance, the popular textbook Convex Optimization by Boyd and Vandenberghe (2004) does not even have a section on these methods. Coordinate descent method is an algorithm, in which the p search directions are just unit vectors e₁, ⋯, e_p, where e_i denotes the ith element in the standard basis of ℝ^p. These unit vectors are used as search directions in each search cycle until some convergence criterion is met. If the objective function is convex but non-differentiable, the coordinate descent algorithm might gets trapped in a nonstationary point. However, this is not a problem in our case. Although the objective function is not strictly convex, it is strictly convex in each of the coordinates. Combining with the fact that the non-differentiable part of the objective function is separable, either Theorem 4.1 or Theorem 5.1 of Tseng (2001) guarantees that coordinate descent algorithms converge to local minima. Moreover, since since all directional derivatives exist, every coordinate-wise minimum is also a local minimum. A similar study on the convergence of the coordinate descent algorithm can be found in Breheny and Huang (2011).

What makes the coordinate-descent algorithmparticularly attractive for (16) is that there is an explicit formula for each coordinate update. For a given γ, fix τ and K, then do the optimization on a grid (of log-scale) of λ values: τλ_max = λ_K < λ_K−1 < ⋯ < λ₁ = λ_max. The λ_max is the minimum λ value such that no variables enter the model; this is analogous to the minimum requirement on c in (11). In our implementation, we take τ = 0.001 and K = 100. The problem is solved backwards from λ_max. When λ = λ_i+1, we use the solution from λ = λ_i as the initial value. This kind of “warm start” is very effective in improving computational efficiency.

Consider a coordinate descent step to solve (16). Without loss of generality, suppose that w̃_j for all j ≥ 2 are given, and we need to optimize with respect to w₁. The objective function now becomes

$$g(w_1)=\frac{1}{2}\left(\begin{array}{cc}{w}_1^T\hfill & {\tilde{\mathbf{w}}}_2^T\hfill \end{array}\right)\left(\begin{array}{cc}{\mathrm{\Sigma }}_{11}\hfill & {\mathbf{\Sigma }}_{12}\hfill \\ {\mathbf{\Sigma }}_{21}\hfill & {\mathbf{\Sigma }}_{22}\hfill \end{array}\right)\left(\begin{array}{c}{w}_1\hfill \\ {\tilde{\mathbf{w}}}_2\hfill \end{array}\right)+\lambda |w_1|+\lambda {|{\tilde{\mathbf{w}}}_2|}_1+\frac{1}{2}\gamma {({\mathbf{w}}^T{\mathit{\mu }}_d-1)}^2.$$

When w₁ ≠ 0, we have

$$\begin{array}{cc}g\prime (w_1)\hfill & ={\mathrm{\Sigma }}_{11}{w}_1+{\mathbf{\Sigma }}_{12}{\tilde{\mathbf{w}}}_2+\lambda \text{ sign}(w_1)+\gamma ({\mathbf{w}}^T{\mathit{\mu }}_d-1){\mu }_{d1}\hfill \\ \hfill & =({\mathrm{\Sigma }}_{11}+\gamma {\mu }_{d1}^2)w_1+({\mathbf{\Sigma }}_{12}+\gamma {\mu }_{d1}{\mathit{\mu }}_{d2}^T){\tilde{\mathbf{w}}}_2+\lambda \text{ sign}(w_1)-\gamma {\mu }_{d1}.\hfill \end{array}$$

By simple calculation (Donoho and Johnstone, 1994), the coordinate-wise update has the form

$${\tilde{w}}_1=\frac{S(\gamma {\mu }_{d1}-({\mathbf{\Sigma }}_{12}+\gamma {\mu }_{d1}{\mathit{\mu }}_{d2}^T){\tilde{\mathbf{w}}}_2,\lambda )}{{\mathrm{\Sigma }}_{11}+\gamma {\mu }_{d1}^2},$$

where S(z, λ) = sign(z)(|z| − λ)⁺ is the soft-thresholding operator.

In each coordinate update, the computational complexity is 𝒪(p). A complete cycle through all p variables costs 𝒪(p²) operations. From our experience, CCD converges quickly after a few cycles if “warm start” is used for the initial solution. Let C denote the average number of cycles until convergence for each λ. Then our algorithm CCD enjoys computational complexity 𝒪(CKp²). This is compared with the Fisher discriminant, where matrix inversion alone costs at least 𝒪(p^2.376) operations (the Coppersmith-Winograd algorithm), though we should emphasize here that our algorithm has no ambition to fully recover the Fisher discriminant (this task is infeasible anyway). The D-ROAD can be similarly implemented by replacing the covariance matrix with its diagonal.

5. Asymptotic Property

5.1. Risk Approximation

Let ŵ_c be a sample version of w_c in (10),

$${\widehat{\mathbf{w}}}_c\in \underset{{\Vert \mathbf{w}\Vert }_1\le c,{\mathbf{w}}^T{\widehat{\mathit{\mu }}}_d=1}{\text{argmin}}{\mathbf{w}}^T\widehat{\mathbf{\Sigma }}\mathbf{w}.$$ (17)

The fact that Σ̂ is only positive semi-definite leads to potential non-uniqueness of ŵ_c. Now, we have three different classifiers: ${\delta }_{{\mathbf{w}}_{\mathrm{\infty }}}=𝕀\{{\mathbf{w}}_{\mathrm{\infty }}^T(\mathbf{X}-{\mathit{\mu }}_a)>0\},{\delta }_{{\mathbf{w}}_c}=𝕀\{{\mathbf{w}}_c^T(\mathbf{X}-{\mathit{\mu }}_a)>0\}\text{ and }{\widehat{\delta }}_{{\mathbf{w}}_c}=𝕀\{{\widehat{\mathbf{w}}}_c^T(\mathbf{X}-{\widehat{\mathit{\mu }}}_a)>0\}$. The first two are oracle classifiers, requiring the knowledge of unknown parameters μ₁, μ₂ and Σ, while the third one is the feasible classifier, ROAD, based on the sample. Their classification errors are given by (2). Explicitly, the error rates are respectively W(δ_w∞) [see (4)], W(δ_wc), and W(δ̂_wc). By (2), an obvious estimator of the misclassification rate of δ̂_wc is

$$W_n({\widehat{\delta }}_{{\mathbf{w}}_c})=1-\mathrm{\Phi }\left(\frac{{\widehat{\mathbf{w}}}_c^T{\widehat{\mathit{\mu }}}_d}{{({\widehat{\mathbf{w}}}_c^T\widehat{\mathbf{\Sigma }}{\widehat{\mathbf{w}}}_c)}^{1/2}}\right).$$ (18)

Two questions arise naturally:

1. how close is W(δ̂_wc), the misclassification error of δ̂_wc, to that of its oracle W(δ_wc)?

2. does W_n(δ̂_wc) estimate W(δ̂_wc) well?

Theorem 1 addresses these two questions. We introduce an intermediate optimization problem for convenience:

$${\mathbf{w}}_c^{(1)}=\underset{{\Vert \mathbf{w}\Vert }_1\le c,{\mathbf{w}}^T{\widehat{\mathit{\mu }}}_d=1}{\text{argmin}}{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}.$$

Theorem 1. Let s_c = ‖w_c‖₀, $s_c^{(1)}={\Vert {\mathbf{w}}_c^{(1)}\Vert }_0$, and ŝ_c = ‖ŵ_c‖₀. Assume that ${\lambda }_{\text{min}}(\mathbf{\Sigma })\ge {\sigma }_0^2>0$, ‖Σ̂ − Σ‖_∞ = O_p(a_n) and ‖μ̂_d − μ_d‖_∞ = O_p(a_n) for a given sequence a_n → 0. Then, we have

$$W({\widehat{\delta }}_{{\mathbf{w}}_c})-W({\delta }_{{\mathbf{w}}_c})=O_p(d_n),$$

and

$$W_n({\widehat{\delta }}_{{\mathbf{w}}_c})-W({\widehat{\delta }}_{{\mathbf{w}}_c})=O_p(b_n),$$

where $b_n=(c^2\vee s_c\vee s_c^{(1)})a_n$ and d_n = b_n ∨ (ŝ_ca_n).

Remark 1. In Theorem 1, ‖·‖_∞ is the element wise super-norm. When Σ̂ is the sample covariance, by Bickel and Levina (2004), ${\Vert \widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\mathrm{\infty }}=O_p(\sqrt{(\text{log }p)/n})$; hence we can take $a_n=\sqrt{(\text{log }p)/n}$. The first result in Theorem 1 shows the difference between the misclassification rate of δ̂_wc and its oracle version δ_wc; the second result says about the error in estimating the true misclassification rate of ROAD.

Remark 2. In view of (2), one intends to choose a w that makes w^TΣw small and w^Tμ_d large. A compromise of these dual objectives leads to a utility function

$$U(\mathbf{w})=-{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}+\xi {\mathit{\mu }}_d^T\mathbf{w},$$

as a proxy of the objective function (2) for a fixed ξ. For any ξ > 0, the optimal choice w* ∈ argmin U(w) leads to the Fisher discriminant rule. Consider also the regularized versions

$${\mathbf{w}}_c^{*}={\text{argmin}}_{{\Vert \mathbf{w}\Vert }_1\le c}U(\mathbf{w}),\mathit{\text{ and }}{\widehat{\mathbf{w}}}_c^{*}={\text{argmin}}_{{\Vert \mathbf{w}\Vert }_1\le c}\widehat{U}(\mathbf{w}),$$

where Û (w) is the utility function with Σ and μ_d estimated by Σ̂ and μ̂_d. Then, it is easy to see the following utility approximation: for any ‖w‖₁ ≤ c

$$|U(\mathbf{w})-\widehat{U}(\mathbf{w})|\le {\Vert \widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\mathrm{\infty }}{c}^2+\xi c{\Vert {\widehat{\mathit{\mu }}}_d-{\mathit{\mu }}_d\Vert }_{\mathrm{\infty }}$$

and

$$|U({\widehat{\mathbf{w}}}_c^{*})-U({\mathbf{w}}_c^{*})|\le 2({\Vert \widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\mathrm{\infty }}{c}^2+\xi c{\Vert {\widehat{\mathit{\mu }}}_d-{\mathit{\mu }}_d\Vert }_{\mathrm{\infty }}).$$

Remark 3. The most prominent technical challenge of our original problem (10) is due to different dualities of penalization problems. For the population version (10), it can be reduced, by the Lagrange multiplier method, to the utility U(w) optimization problem in Remark 2 with a given ξ > 0, while for the sample version (17), it can be reduced to the utility Û (w) optimization problem with a different ξ̂. Therefore, the problem is not the same as the utility optimization problem in Remark 2: ξ̂ is hard to bound. In fact, it is much harder and yields more complicated results.

We now show how different the data projection direction in the regularized oracle can be from that in the Fisher discriminant. To gain better insight, we reformulate the L₁ constraint problem as the following penalized version:

$${\mathbf{w}}^{\lambda }=\underset{\mathbf{w}:{\mathit{\mu }}_d^T\mathbf{w}=1}{\text{argmin}}{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w}+\lambda {\Vert \mathbf{w}\Vert }_1.$$ (19)

The following characterizes its convergence to the Fisher discriminant weight w_∞ as λ → 0.

Theorem 2. Let s be the size of the set {k : (Σ⁻¹μ_d)_k ≠ 0}. Then, we have

$${\Vert {\mathbf{w}}^{\lambda }-{\mathbf{w}}_{\mathrm{\infty }}\Vert }_2\le \frac{\lambda \sqrt{s}}{{\lambda }_{\text{min}}(\mathbf{\Sigma })},$$

where ${\mathbf{w}}_{\mathrm{\infty }}={\mathbf{\Sigma }}^{-1}{\mathit{\mu }}_d/({\mathit{\mu }}_d^T{\mathbf{\Sigma }}^{-1}{\mathit{\mu }}_d)$ is the normalized Fisher discriminant, optimizing (19) with λ = 0.

5.2. Screening-based ROAD (S-ROAD)

Following the idea of Sure Independence Screening in Fan and Lv (2008), we pre-screen all the features before hitting the ROAD. The advantage of this two-step procedure is that we have a control on the total number of features used in the final classification rule. A popular method for independent feature selection is the two-sample t-test (Tibshirani et al., 2002; Fan and Fan, 2008), which is a specific case of marginal screening in Fan and Lv (2008). The sure screening property of such a method was demonstrated in Fan and Fan (2008), which selects consistently the features with different means in the same settings as ours.

Once the features are selected, we can hit the ROAD, producing the vanilla Screening-based Regularized Optimal Affine Discriminant (S-ROAD1):

1. Employ a screening method to get k features.

2. Apply ROAD to the k selected features.

In the first step, we use the t-statistics as the screening criteria and determine a data-driven threshold. This idea is motivated by a FDR criterion for choosing marginal screening threshold in Zhao and Li (2010). A random permutation π of {1, ⋯, n} is used to decouple X_i and Y_i so that the resulting data (X_π(i), Y_i) follow a null model, by which we mean that features have no prediction power for the class label. More specifically, the screening step is carried out as follows:

1. Calculate the t-statistic t_j for each feature j, where j = 1, ⋯, p.

2. For the permuted data pairs (X_π(i), Y_i), recalculate the t-statistic $t_j^{*}$, for j = 1, ⋯, p. (Intuitively, if j is the index of an important feature, |t_j | should be larger than most of $|t_j^{*}|$, because the random permutation is meant to eliminate the prediction power of features.)

3. For q ∈ [0, 1], let ω_(q) be the q^th quantile of $\{|t_j^{*}|,j=1,2,\cdots ,p\}$. Then, the selected set 𝒜 is defined as

   $$𝒜=\{j||t_j|\ge {\omega }_{(q)}\}.$$

The choice of threshold is made to retain the features whose t-statistics are significant in the two sample t-test. Alternatively, if the user knows his k, (due to budget constraints, etc.), then he can just rank |t_j|’s and choose the threshold accordingly.

The S-ROAD1 tracks the performance of oracle procedures like sub-Fisher (10 features) in Figure 1. The feature space gotten by step (1) can be expanded by including those features which are most correlated with what have already been selected. This additional variant, S-ROAD2, aims at achieving the performance of sub-Fisher (20 features) type of procedure in Figure 1.

To elaborate on the theoretical properties of S-ROAD1, assume with no loss of generality that the first k variables are selected in the screening step. Denote by Σ_k the upper left k × k block of Σ and μ_k the first k coordinates of μ_d. Let

$${\mathit{\beta }}_c=\underset{{\Vert \mathit{\beta }\Vert }_1\le c,{\mathit{\beta }}^T{\mathit{\mu }}_k=1}{\text{argmin}}{\mathit{\beta }}^T{\mathbf{\Sigma }}_k\mathit{\beta }.$$

The quantities β̂_c and ${\mathit{\beta }}_c^{(1)}$ are defined similarly to ŵ_c and ${\mathbf{w}}_c^{(1)}$ (defined right before Theorem 1). Then denote by ${\mathit{y}}_c={({\mathit{\beta }}_c^T,{\mathbf{0}}^T)}^T,{\widehat{\mathit{y}}}_c={({\widehat{\mathit{\beta }}}_c^T,{\mathbf{0}}^T)}^T\text{ and }{\mathit{y}}_c^{(1)}={({\mathbf{w}}_c^{(1)},{\mathbf{0}}^T)}^T$. The next two theorems can be verified along lines similar to Theorems 1 and 2. Hence, the proofs are omitted.

Theorem 3. If ${\Vert {\widehat{\mathbf{\Sigma }}}_k-{\mathbf{\Sigma }}_k\Vert }_{\mathrm{\infty }}=O_p(\sqrt{\text{log }k/n}),{\Vert {\widehat{\mathit{\mu }}}_k-{\mathit{\mu }}_k\Vert }_{\mathrm{\infty }}=O_p(\sqrt{\text{log }k/n})$, and λ_min(Σ_k) ≥ δ₀ > 0, then we have

$$W({\widehat{\delta }}_{{\mathit{y}}_c})-W({\delta }_{{\mathit{y}}_c})=O_p(e_n),$$

and

$$W_n({\widehat{\delta }}_{{\mathit{y}}_c})-W({\delta }_{{\mathit{y}}_c})=O_p(e_n),$$

where $e_n=(c^2\vee k)\sqrt{\frac{\text{log }k}{n}}$.

This result is cleaner than Theorem 1, as the rate does not involve s_c and ŝ_c: they are simply replaced by the upper bound k. Accurate bounds for s_c and ŝ_c are of interest for future exploration, but they are beyond the scope of this paper.

Theorem 4. Let ${\mathit{y}}_k^{\lambda }={\text{argmin}}_{\mathit{y}:{\mathit{\mu }}_d^T\mathit{y}=1,\mathit{y}\in M_k}R(\mathit{y})+\lambda {\Vert \mathit{y}\Vert }_1$ where M_k is the subspace in R^p with the last p − k components being zero, and ${\mathit{y}}^0={({({\mathbf{\Sigma }}_k^{-1}{\mathit{\mu }}_k)}^T/({\mathit{\mu }}_k^T{\mathbf{\Sigma }}_k^{-1}{\mathit{\mu }}_k),{\mathbf{0}}^T)}^T$. Then we have

$${\Vert {\mathit{y}}_k^{\lambda }-{\mathit{y}}^0\Vert }_2\le \frac{\lambda \sqrt{k}}{{\lambda }_{\text{min}}({\mathbf{\Sigma }}_k)}.$$

5.3. Continuous Piecewise Linear Solution Path

We use the word “linear” when referring to “affine”, in line with the status quo in the statistical community. Continuous piecewise linear paths are of much interest to statisticians, as the property reduces the computational complexity of solutions and justifies the linear interpolations of solutions at discrete points. Previous well known investigations include Efron et al. (2004) and Rosset and Zhu (2007). Our setup differs from others mainly in that in addition to a complexity penalty, there is also an affine constraint. Our proof calls in point set topology, and is purely geometrical, in a spirit very different from the existing ones. In particular, we stress that the continuity property is intuitively correct, but it is far from a trivial consequence of the assumptions. The authors also believe that the claim holds true even if the p−1 dimensional affine subspace constraint is replaced by more generic ones, though the technicality of the proof must be more involved.

Theorem 5. Let μ_d ∈ ℝ^p be a constant, and Σ be a positive definite matrix of dimension p × p. Let

$${\mathbf{w}}_c=\underset{{\Vert \mathbf{w}\Vert }_1\le c,{\mathbf{w}}^T{\mathit{\mu }}_d=1}{\text{argmin}}{\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w},$$

then w_c is a continuous piecewise linear function in c.

Proposition 1. W(δ_wc) is a Lipschitz function in c.

Proof. Recall that

$$W({\delta }_{{\mathbf{w}}_c})=1-\mathrm{\Phi }(1/{(R({\mathbf{w}}_c))}^{1/2}).$$

By Theorem 5 and the fact that composition of Lipschitz functions is again Lipschitz, the conclusion holds.

6. Numerical Investigation

In this section, several simulation and real data studies are conducted. We compare ROAD and its variants S-ROAD1 (Screening-based ROAD version 1), S-ROAD2 (Screening-based ROAD version 2) and D-ROAD (Diagonal ROAD) with NSC (Nearest Shrunken Centroid), SCRDA (Shrunken Centroids Regularized Discriminant Analysis), FAIR (Feature Annealed Independence Rule), NB (Naive Bayes), NFR (Naive Fisher Rule, which uses the generalized inverse of the sample covariance matrix), as well as the Oracle.

In all simulation studies, the number of variables is p = 1000, and the sample size of the training and testing data is n = 300 for each class. Each simulation is repeated 100 times to test the stability of the method. Without loss of generality, the mean vector of the first class μ₁ is set to be 0. We use five-fold cross-validation to choose the penalty parameter λ.

6.1. Equal Correlation Setting, Sparse Fixed Signal

In this subsection, we consider the setting where Σ_i,i = 1 for all i = 1, ⋯, p and Σ_i,j = ρ for all i, j = 1, ⋯, p and i ≠ j, and take μ₂ to be a sparse vector: ${\mathit{\mu }}_2={({\mathbf{1}}_{10}^T,{\mathbf{0}}_{990}^T)}^T$, where 1_d is a length d vector with all entries 1, 0_d is a length d vector with all entries 0, where the sparsity size is s₀ = 10. Also, we fix γ = 10 in (16) for this simulation. Sensitivity of the performance due to the choice of γ will be investigated in the next subsection.

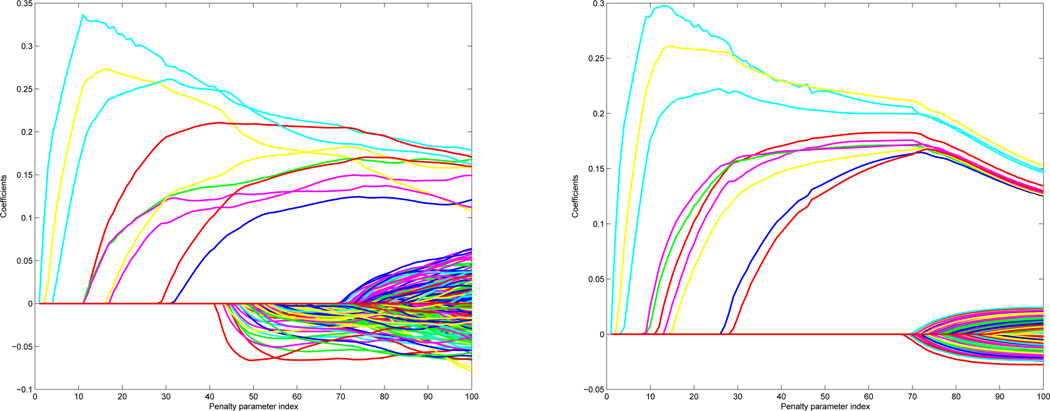
The solution paths for ROAD and D-ROAD of one realization are rendered in Figure 2. It is clear from the figure that, as the penalty parameter decreases (index increases), both ROAD and D-ROAD use more features. Also, the cutoff point for D-ROAD, where the number of features starts to increase dramatically, tends to come later than that for ROAD.

Fig. 2.

Solution Path for ROAD (left panel) and D-ROAD (right panel). Equal correlation setting (ρ = 0.5), Sparse Signal (s₀ = 10) as in Section 6.1.

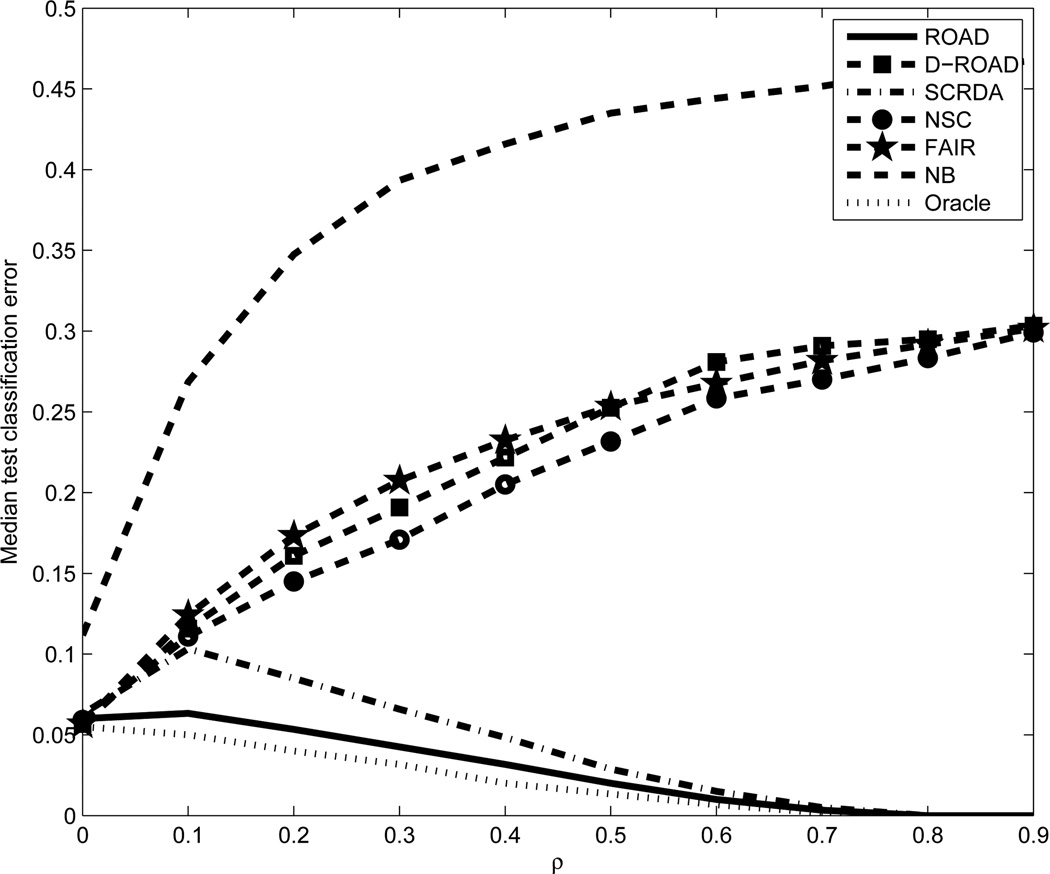
The simulation results for the pairwise correlations ranging from 0 to 0.9 are shown in Tables 1 and 2. We would like to mention that the results for NFR (Naive Fisher Rule) are not included in these (and the subsequent) tables because the test classification error is always around 50%, i.e., it is about the same as random guess. Also in the tables are the screening-based versions of the ROAD. S-ROAD1 refers to the vanilla version where we first apply the two-sample t-test to select any features with the corresponding t-test statistic with absolute value larger than the maximum absolute t-test statistic value calculated on the permuted data. S-ROAD2 does the same except for each variable in S-ROAD1’s pre-screened set, it adds an additional variable which is most correlated with that variable. Figure 3, a graphical summary of Table 1, presents the median test errors for different methods. We can see from Table 1 and Figure 3 that the oracle classification error decreases as ρ increases. This phenomenon is due to a similar reason to the two-dimensional showcase in the introduction. When ρ goes to 1, all the variables contribute in the same way to boost the classification power. ROAD performs reasonably close to the Oracle, while working independence based method such as D-ROAD, NSC, FAIR and NB fail when ρ is large. The huge discrepancy shows the advantage of employing the correlation structure. Since SCRDA also employ the correlation structure, it does not fail when ρ is large. However, ROAD still outperforms SCRDA in all the correlation settings. S-ROAD1 and S-ROAD2 both have misclassification rates similar to that of ROAD. It is worth to emphasize that the merits of the screening based ROADs mainly lie in the computation cost, which is reduced significantly by the pre-screening step.

Table 1.

Equal correlation setting, fixed signal: Median of the percentage for testing classification error and standard deviations (in parentheses). Signal all equal to 1. s₀ = 10.

ρ	ROAD	S-ROAD1	S-ROAD2	D-ROAD	SCRDA	NSC	FAIR	NB	Oracle
0	6.0(1.2)	6.0(1.1)	6.0(1.2)	5.7(1.1)	6.3(1.0)	5.9(1.0)	5.7(1.0)	11.2(1.4)	5.5(1.1)
0.1	6.3(2.5)	12.2(5.0)	8.8(2.4)	11.6(5.1)	10.3(1.4)	11.1(3.0)	12.4(1.4)	26.8(10.1)	5.0(0.9)
0.2	5.3(1.0)	16.0(6.3)	8.7(2.5)	16.1(7.5)	8.5(1.2)	14.5(4.3)	17.3(1.7)	34.8(11.6)	4.0(0.8)
0.3	4.2(0.9)	19.1(7.9)	7.8(2.6)	19.1(9.4)	6.6(1.1)	17.1(5.5)	20.8(1.7)	39.3(12.3)	3.2(0.7)
0.4	3.2(0.8)	22.8(9.4)	6.5(2.6)	22.2(9.9)	4.8(1.0)	20.5(6.1)	23.2(1.8)	41.6(11.3)	2.0(0.6)
0.5	2.0(0.6)	25.8(11.0)	4.8(1.4)	25.2(10.2)	2.9(0.7)	23.2(6.0)	25.3(1.6)	43.5(11.1)	1.3(0.5)
0.6	1.0(0.4)	18.3(12.4)	3.3(1.3)	28.1(10.3)	1.5(0.5)	25.8(5.7)	26.8(1.8)	44.4(12.1)	0.7(0.3)
0.7	0.3(0.2)	15.5(13.6)	1.7(1.0)	29.1(10.1)	0.5(0.3)	27.0(8.2)	28.2(2.0)	45.2(12.3)	0.2(0.2)
0.8	0.0(0.1)	5.0(14.0)	0.3(0.4)	29.5(9.9)	0.0(0.1)	28.3(8.7)	29.2(2.0)	46.2(10.3)	0.0(0.1)
0.9	0.0(0.0)	0.6(14.8)	0.0(0.1)	30.3(7.6)	0.0(0.2)	29.9(8.0)	30.2(1.9)	46.8(8.8)	0.0(0.0)

Table 2.

Equal correlation setting, fixed signal: Median of number of nonzero coefficients and standard deviations (in parentheses). Signal all equal to 1. s₀ = 10.

ρ	ROAD	S-ROAD1	S-ROAD2	D-ROAD	SCRDA	NSC	FAIR
0	16.00(24.16)	10.00(1.31)	17.00(4.31)	29.50(58.54)	10.00(13.25)	10.00(44.86)	11.00(1.62)
0.1	117.50(30.50)	11.00(3.32)	21.00(4.15)	14.00(122.02)	1000.00(345.48)	35.50(117.32)	10.00(0.27)
0.2	130.50(33.33)	11.00(6.99)	22.00(8.98)	15.50(111.42)	1000.00(0.00)	95.00(120.17)	10.00(0.69)
0.3	136.50(36.16)	11.00(11.56)	22.00(10.38)	17.50(106.16)	1000.00(0.00)	103.50(117.52)	9.00(1.19)
0.4	135.00(34.43)	10.00(14.21)	22.00(17.07)	10.00(98.10)	1000.00(0.00)	70.00(131.65)	8.00(1.33)
0.5	138.50(38.17)	9.00(21.71)	22.00(21.56)	10.00(105.33)	1000.00(0.00)	65.00(137.97)	7.00(1.30)
0.6	148.00(49.74)	10.50(27.92)	22.00(31.88)	10.00(110.23)	1000.00(0.00)	38.00(141.91)	6.00(1.30)
0.7	170.50(52.29)	11.00(37.37)	22.00(41.76)	1.00(118.43)	1000.00(0.00)	27.50(140.10)	5.00(1.20)
0.8	203.00(27.72)	12.00(50.36)	24.00(59.23)	1.00(143.83)	1000.00(10.92)	15.00(157.98)	5.00(1.29)
0.9	151.50(8.02)	14.00(55.32)	28.00(50.45)	1.00(153.27)	1000.00(56.30)	14.00(225.38)	3.00(1.08)

Fig. 3.

Median classification error as a function of ρ in the equi-correlation matrix. Sparse μ_d as in Section 6.1.

The ROAD is a very robust estimator. It performs well even when all the variables are independent, in which case there could be a lot of noise for fitting the covariance matrix. Table 1 indicates that ROAD has almost the same performance as D-ROAD, NSC and FAIR under the independence assumption, i.e. ρ = 0. As ρ increases, the edge of ROAD becomes more substantial. In general, the ROAD is recommended on the grounds that even with pairwise correlation of about 0.1 (which is quite common in microarray data as well as financial data), the gain is substantial.

Another interesting observation is that the D-ROAD performs similarly to NSC and FAIR in terms of classification error. An intuitive explanation is that they are all “sparse” independence rules. NSC uses soft-thresholding on the standardized sample mean difference, and its equivalent LASSO derivation can be found in Wang and Zhu (2007). FAIR selects features with large marginal t-statistics in absolute values, while D-ROAD is another L1 penalized independence rule, whose implementation is different from NSC.

Table 2 summarizes the number of features selected by different classifiers. Note that ROAD mimics Fisher discriminant coordinate Σ⁻¹μ_d, which has p = 1000 nonzero entries under our simulated model. Therefore, the large number of features selected by ROAD is not out of expectation.

6.2. The Effect of γ

Under the settings of the previous subsection, we look into the variation of the ROAD performance as γ changes. In Table 3, the number of active variables varies; however, the median classification error remains about the same for a broad range of γ values. The reason is that the cross validation step chooses the “best” λ according to a specific γ. Therefore, the final performance remains almost unchanged. Since our primary concern is the classification error, we fix γ = 10 for simplicity in the subsequent simulations and in the real data analysis.

Table 3.

Equal correlation setting; signals all equal to 1; s₀ = 10. Results for different γ.

		ρ = 0	ρ = 0.5	ρ = 0.9
Median classification error (in percentage)	ROADγ=0.01	5.8(1.2)	2.7(0.6)	0.2(0.2)
	ROADγ=0.1	6.0(1.2)	2.0(0.6)	0.2(0.1)
	ROADγ=1	6.0(1.3)	2.0(0.6)	0.0(0.1)
	ROADγ=10	6.0(1.2)	2.0(0.6)	0.0(0.0)
	ROADγ=100	6.2(1.2)	2.3(0.6)	0.0(0.1)
		ρ = 0	ρ = 0.5	ρ = 0.9
Median number of nonzeros	ROADγ=0.01	14.0(19.2)	129.5(42.5)	657.0(179.6)
	ROADγ=0.1	14.0(19.6)	137.0(37.6)	773.5(103.2)
	ROADγ=1	16.5(22.9)	139.0(37.9)	514.0(39.7)
	ROADγ=10	16.0(24.2)	138.5(38.2)	151.5(8.0)
	ROADγ=100	22.0(16.1)	114.5(9.4)	94.0(9.6)

6.3. Block Diagonal Correlation Setting, Sparse Fixed Signal

In this subsection, we follow the same setup as in Section 6.1 except that the covariance matrix Σ is taken to be block diagonal. The first block is a 20 × 20 equi-correlated matrix and the second block is a (p − 20) × (p − 20) equi-correlated matrix, both with pairwise correlation ρ. In other words, Σ_i,i = 1 for all i = 1, ⋯, p, Σ_i,j = ρ for all i, j = 1, ⋯, 20 and i ≠ j, Σ_i,j = ρ for all i, j = 21, ⋯, p and i ≠ j, and the rest elements are zeros. As before, we examine the performances of various estimators when ρ varies. The percentage for testing error and the number of selected features in the estimators are shown in Tables 4 and 5, respectively.

Table 4.

Block diagonal correlation setting, sparse fixed signal: Median of the percentage for testing classification error and standard deviations (in parentheses). Signal all equal to 1. s₀ = 10.

ρ	ROAD	S-ROAD1	S-ROAD2	D-ROAD	SCRDA	NSC	FAIR	NB	Oracle
0	6.0(1.2)	6.0(1.1)	6.0(1.2)	5.7(1.1)	6.0(0.1)	5.5(0.3)	5.7(1.0)	11.2(1.4)	5.5(1.1)
0.1	10.8(3.6)	13.0(4.8)	10.3(3.0)	12.8(4.4)	13.0(0.3)	12.5(0.8)	12.7(1.5)	25.7(7.6)	8.8(1.2)
0.2	10.7(4.1)	18.0(5.7)	9.7(3.6)	17.7(5.9)	14.2(1.1)	17.2(0.4)	17.7(1.6)	34.4(7.9)	8.8(1.2)
0.3	9.5(3.8)	23.2(5.5)	8.8(4.0)	23.2(5.6)	12.7(0.9)	20.0(0.8)	20.4(1.6)	38.3(7.5)	7.7(1.0)
0.4	8.0(3.3)	29.7(4.2)	7.5(4.2)	29.3(4.1)	11.0(1.2)	23.8(1.3)	23.2(1.8)	41.0(6.9)	6.6(1.1)
0.5	6.2(2.6)	30.1(3.9)	5.7(0.9)	30.0(3.1)	8.7(0.4)	26.2(1.7)	25.1(1.7)	42.2(6.6)	5.0(1.0)
0.6	4.2(0.9)	30.3(4.2)	4.0(0.8)	30.3(2.2)	6.4(0.1)	26.5(1.2)	26.8(1.8)	43.6(7.0)	3.5(0.7)
0.7	2.3(0.7)	30.0(6.4)	2.2(0.7)	30.6(2.1)	2.5(0.7)	28.1(3.2)	28.2(2.0)	44.2(6.5)	1.8(0.6)
0.8	0.8(0.4)	29.8(9.8)	0.7(0.4)	30.6(2.1)	0.6(0.4)	29.2(1.6)	29.2(2.0)	44.8(5.7)	0.7(0.3)
0.9	0.0(0.1)	29.8(12.8)	0.0(0.1)	30.6(1.9)	0.2(0.2)	29.2(1.2)	30.2(1.9)	45.2(4.9)	0.0(0.1)

Table 5.

Block diagonal correlation setting, fixed signal: Median of number of nonzero coefficients and standard deviations (in parentheses). Signal all equal to 1. s₀ = 10.

ρ	ROAD	S-ROAD1	S-ROAD2	D-ROAD	SCRDA	NSC	FAIR
0	16.00(24.16)	10.00(1.31)	17.00(4.31)	29.50(58.54)	10.00(1.15)	10.00(1.73)	11.00(1.62)
0.1	48.50(35.99)	10.00(2.73)	20.00(3.77)	14.00(26.73)	33.00(17.79)	65.00(38.84)	18.00(2.67)
0.2	48.00(31.48)	10.00(4.59)	20.00(5.84)	10.00(18.23)	38.00(117.54)	10.00(16.17)	18.00(2.77)
0.3	47.50(42.75)	9.00(5.28)	20.00(6.03)	10.00(11.80)	208.00(103.94)	10.00(13.58)	18.00(3.91)
0.4	40.50(32.42)	1.00(4.82)	20.00(10.08)	1.00(9.25)	27.00(90.95)	33.00(14.22)	17.00(5.43)
0.5	40.50(33.23)	1.00(4.88)	20.00(10.10)	1.00(8.51)	24.00(76.79)	10.00(1.15)	7.00(5.98)
0.6	39.50(30.03)	1.00(3.74)	20.00(14.53)	1.00(5.92)	127.50(6.36)	6.50(2.12)	6.00(5.98)
0.7	40.00(41.35)	1.00(4.71)	20.00(8.07)	1.00(2.49)	94.50(2.12)	9.50(0.71)	5.00(5.52)
0.8	55.00(58.67)	1.00(6.20)	20.00(18.32)	1.00(0.93)	58.00(2.83)	6.00(5.66)	5.00(4.84)
0.9	120.00(30.66)	1.00(21.29)	20.00(30.46)	1.00(0.35)	20.00(0.00)	8.00(2.83)	3.00(3.81)

In this block-diagonal setting, we have observed similar results to those in Section 6.1: ROAD and S-ROAD2 perform significantly better than the other methods. One interesting phenomenon is that S-ROAD1 does not perform well when ρ is large. The reason is that the current true model has 20 important features, and by looking only at marginal contribution, S-ROAD1 misses some important variables, as shown in Table 4. Indeed, because those features have no expressed mean differences, it does not fully take advantage of highly correlated features. In contrast, S-ROAD2 is able to pick up all the important variables, takes advantage of correlation structure, and leads to a sparser model than the vanilla ROAD. In view of the results from this simulation setting and the previous one, we recommend S-ROAD2 over S-ROAD1.

6.4. Block-Diagonal Negative Correlation Setting, Sparse Fixed Signal

In this subsection, we again follow a similar setup as in Section 6.1. Here, the covariance matrix Σ is taken to be block diagonal with each block size equals to 10. Each block is an equi-correlated matrix with pairwise correlation ρ = −0.1. In other words, Σ = diag(Σ₀, ⋯, Σ₀), where Σ₀ is a 10 × 10 equi-correlated matrix with correlation −0.1. Here, ${\mathit{\mu }}_2=0.5\times {({\mathbf{1}}_5^T,{\mathbf{0}}_5^T,{\mathbf{1}}_5^T,{\mathbf{0}}_{985}^T)}^T$ and the sparsity size is s₀ = 10. As before, we examine the performances of various estimators when ρ varies. The percentage for testing error and the number of selected features in the estimators are shown in Table 6.

Table 6.

Block-Diagonal Negative Correlation Setting, Sparse Fixed Signal: Median error (in percentage) and number of nonzero coefficients with standard deviations in parentheses.

	ROAD	S-ROAD1	S-ROAD2	D-ROAD	SCRDA	NSC	FAIR	NB	Oracle
error	7.3(3.4)	16.0(5.2)	12.7(3.4)	17.8(8.0)	18.5(1.1)	20.8(0.6)	24.8(2.1)	33.5(2.1)	3.2(0.7)
nonzero	168.00(47.59)	10.00(2.40)	20.00(3.58)	15.50(15.32)	24.00(0.58)	41.00(17.90)	59.00(4.27)	–	–

6.5. Random Correlation Setting, Double Exponential Signal

To evaluate the stability of the ROAD, we take a random matrix Σ as the correlation structure, and use a signal μ whose nonzero entries come from a double exponential distribution. A random covariance matrix Σ is generated as follows:

1. For a given integer m (here we take m = 10), generate a p × matrix Ω where Ω_i,j ~ Unif(−1, 1). Then the matrix ΩΩ^T is positive semi-definite.

2. Denote c_Ω = min_i(ΩΩ^T)_ii. Let Ξ = ΩΩ^T + c_ΩI, where I is the identity matrix. It is clear that Ξ is positive definite.

3. Normalize the matrix Ξ to get Σ whose diagonal elements are unity.

For the signal, we take μ to be a sparse vector with sparsity size s = 10, and the nonzero elements are generated from the double exponential distribution with density function

$$f(x)=\text{exp}(-2|x|).$$

Table 7 summaries the results. It shows that even under random correlation setting and random signals, our procedure ROAD still outperforms other competing classification rules such as SCRDA, NSC and FAIR in terms of the classification error.

Table 7.

Random correlation setting, double exponential signal: Median error (in percentage) and number of nonzero coefficients with standard deviations in parentheses.

	ROAD	S-ROAD1	S-ROAD2	D-ROAD	SCRDA	NSC	FAIR	NB	Oracle
error	2.0(0.6)	11.0(5.2)	5.8(3.9)	17.0(2.2)	5.2(1.1)	16.2(1.3)	17.0(1.6)	46.2(2.4)	1.3(0.5)
nonzero	83.00(39.54)	4.00(8.13)	9.00(10.69)	1.00(3.89)	1000.00(0.00)	4.00(0.58)	1.00(0.17)	–	–

6.6. Real Data

Though the ROAD seems to perform best in a broad spectrum of idealized experiments, it has to be tested against reality. We now evaluate the performance of our newly proposed estimator on three popular gene expression data sets: “Leukemia” (Golub et al., 1999), “Lung Cancer” (Gordon et al., 2002), and “Neuroblastoma data set” (Oberthuer et al., 2006). The first two data sets come with predetermined, separate training and test sets of data vectors. The Leukemia data set contains p = 7, 129 genes for n₁ = 27 acute lymphoblastic leukemia (ALL) and n₂ = 11 acute myeloid leukemia (AML) vectors in the training set. The test set includes 20 ALL and 14 AML vectors. The Lung Cancer data set contains p = 12, 533 genes for n₁ = 16 adenocarcinoma (ADCA) and n₂ = 16 mesothelioma training vectors, along with 134 ADCA and 15 mesothelioma test vectors. The Neuroblastoma data set, obtained via the MicroArray Quality Control phase-II (MAQC-II) project, consists of gene expression profiles for p = 10, 707 genes from 251 patients of the German Neuroblastoma Trials NB90–NB2004, diagnosed between 1989 and 2004. We analyzed the gene expression data with the 3-year event-free survival (3-year EFS), which indicates whether a patient survived 3 years after the diagnosis of neuroblastoma. There are 239 subjects with the 3-year EFS information available (49 positives and 190 negatives). We randomly select 83 subjects (19 positives and 64 negatives, which are about one third of the total subjects) as the training set and the rest as the test set. The readers can find more details about the data sets in the original papers.

Following Dudoit et al. (2002) and Fan and Fan (2008), we standardized each sample to zero mean and unit variance. The classification results for ROAD, S-ROAD1, S-ROAD2, SCRDA, FAIR, NSC and NB are shown in Tables 8, 9 and 10. For the leukemia and lung cancer data, ROAD performs the best in terms of classification error. For the neuroblastoma data, NB performs best, however, it makes use of all 10,707 genes, which is not very desirable. In contrast, ROAD has a competitive performance in terms of classification error and it only selects 33 genes. Although SCRDA has a close performance, the number of selected variables varies a lot for the three data set (264, 2410, 1). Overall, ROAD is a robust classification tool for high-dimensional data.

Table 8.

Classification error and number of selected genes by various methods of leukemia data. Training and testing samples are of sizes 38 and 34, respectively.

	ROAD	S-ROAD1	S-ROAD2	SCRDA	FAIR	NSC	NB
Training Error	0	0	0	1	1	1	0
Testing Error	1	3	1	2	1	3	5
No. of selected genes	40	49	66	264	11	24	7129

Table 9.

Classification error and number of selected genes by various methods of lung cancer data. Training and testing samples are of sizes 32 and 149, respectively.

	ROAD	S-ROAD1	S-ROAD2	SCRDA	FAIR	NSC	NB
Training Error	1	1	1	0	0	0	6
Testing Error	1	4	1	3	7	10	36
No. of selected genes	52	56	54	2410	31	38	12533

Table 10.

Classification error and number of selected genes by various methods of neuroblastoma data. Training and testing samples are of sizes 83 and 163, respectively.

	ROAD	S-ROAD1	S-ROAD2	SCRDA	FAIR	NSC	NB
Training Error	3	22	14	16	15	16	14
Testing Error	33	47	37	37	44	35	32
No. of selected genes	33	1	9	1	18	41	10707

7. Discussion

With a simple two-class gaussian model, we explored the bright side of using correlation structure for high dimensional classification. Targeting directly on the classification error, ROAD employs un-regularized pooled sample covariance matrix and sample mean difference vector without suffering from curse of dimensionality and noise accumulation. The sparsity of chosen features is evident in simulations and real data analysis; however, we have not discovered intuitively good conditions on Σ and μ_d, such that a certain desirable sparsity pattern of ŵ_c follows. We resolve a part of the problem by introducing screening-based variants of ROAD, but the precise control of the sparsity size is worth for further investigation. Furthermore, we can explore the conditions for the model selection consistency.

In this paper, we have restricted ourselves to the linear rules. They can be easily extended to nonlinear discriminants via transformations such as low order polynomials or spline basis functions. One may also use the popular “kernel tricks” in the machine learning community. See, for example, Hastie et al. (2009) for more details. After the features are transformed, we can hit the ROAD. One essential technical challenge of the current paper is rooted in a stochastic linear constraint. The precise role of this constraint has not been completely pinned down. Extension of the theoretical properties from binary case to multi-class is also interesting for future research.

A. Proofs

A.1. Proof of Theorem 1

We now show first part of the theorem. Let f₀(w) = w^Tμ_d/(w^TΣw)^1/2, f₁(w) = w^T μ̂_d/(w^TΣw)^1/2, and f₂(w) = w^T μ̂_d/(w^T Σ̂w)^1/2. Then, it follows easily that

$$|f_0({\mathbf{w}}_c)-f_2({\widehat{\mathbf{w}}}_c)|\le {\mathrm{\Lambda }}_1+{\mathrm{\Lambda }}_2,$$

where ${\mathrm{\Lambda }}_1=|f_0({\mathbf{w}}_c)-f_1({\mathbf{w}}_c^{(1)})|\text{ and }{\mathrm{\Lambda }}_2=|f_1({\mathbf{w}}_c^{(1)})-f_2({\widehat{\mathbf{w}}}_c)|$. We now bound both terms separately in the following two steps.

Step 1(bound Λ₁): For any w, we have

$$|f_0(\mathbf{w})-f_1(\mathbf{w})|\le |\frac{{\mathbf{w}}^T{\mu }_d}{{({\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w})}^{1/2}}-\frac{{\mathbf{w}}^T{\widehat{\mathit{\mu }}}_d}{{({\mathbf{w}}^T\mathbf{\Sigma }\mathbf{w})}^{1/2}}|\le \frac{{\Vert \mathbf{w}\Vert }_1{\Vert {\widehat{\mathit{\mu }}}_d-{\mathit{\mu }}_d\Vert }_{\mathrm{\infty }}}{{\Vert \mathbf{w}\Vert }_2{\lambda }_{\text{min}}^{1/2}(\mathbf{\Sigma })}\le \sqrt{{\Vert \mathbf{w}\Vert }_0}\frac{{\Vert {\widehat{\mathit{\mu }}}_d-{\mathit{\mu }}_d\Vert }_{\mathrm{\infty }}}{{\sigma }_0}=\sqrt{{\Vert \mathbf{w}\Vert }_0}{O}_p(a_n).$$ (20)

Since ${\mathbf{w}}_c^{(1)}$ maximizes f₁(·), it follows that

$$f_0({\mathbf{w}}_c)-f_1({\mathbf{w}}_c^{(1)})=f_0({\mathbf{w}}_c)-f_1({\mathbf{w}}_c)+[f_1({\mathbf{w}}_c)-f_1({\mathbf{w}}_c^{(1)})]\le f_0({\mathbf{w}}_c)-f_1({\mathbf{w}}_c),$$ (21)

and similarly noticing w_c maximizing f₀(·), we have

$$f_1({\mathbf{w}}_c^{(1)})-f_0({\mathbf{w}}_c)=f_1({\mathbf{w}}_c^{(1)})-f_0({\mathbf{w}}_c^{(1)})+[f_0({\mathbf{w}}_c^{(1)})-f_0({\mathbf{w}}_c)]\le f_1({\mathbf{w}}_c^{(1)})-f_0({\mathbf{w}}_c^{(1)}).$$ (22)

Combining the results of (21) and (22) and using (20), we conclude that

$${\mathrm{\Lambda }}_1=|f_0({\mathbf{w}}_c)-f_1({\mathbf{w}}_c^{(1)})|=O_p((s_c\vee s_c^{(1)})a_n).$$

By the Lipschitz property of Φ,

$$|\mathrm{\Phi }(f_1({\mathbf{w}}_c^{(1)}))-\mathrm{\Phi }(f_0({\mathbf{w}}_c))|=O_p((s_c\vee s_c^{(1)})a_n).$$

Step 2(bound Λ₂): Note that ${\mathbf{w}}_c^{(1)}$ and ŵ_c both are in the set {w : w^Tμ_d = 1, ‖w‖₁ ≤ 1}. Therefore, by definition of minimizers, we have

$${{\mathbf{w}}_c^{(1)}}^T\mathbf{\Sigma }{\mathbf{w}}_c^{(1)}-{\widehat{\mathbf{w}}}_c^T\mathbf{\Sigma }{\widehat{\mathbf{w}}}_c\le 0,\text{ and }{\widehat{\mathbf{w}}}_c^T\widehat{\mathbf{\Sigma }}{\widehat{\mathbf{w}}}_c-{{\mathbf{w}}_c^{(1)}}^T\widehat{\mathbf{\Sigma }}{\mathbf{w}}_c^{(1)}\le 0.$$

Consequently,

$${{\mathbf{w}}_c^{(1)}}^T\mathbf{\Sigma }{\mathbf{w}}_c^{(1)}-{\widehat{\mathbf{w}}}_c^T\widehat{\mathbf{\Sigma }}{\widehat{\mathbf{w}}}_c=[{{\mathbf{w}}_c^{(1)}}^T\mathbf{\Sigma }{\mathbf{w}}_c^{(1)}-{\widehat{\mathbf{w}}}_c^T\mathbf{\Sigma }{\widehat{\mathbf{w}}}_c]+{\widehat{\mathbf{w}}}_c^T\mathbf{\Sigma }{\widehat{\mathbf{w}}}_c-{\widehat{\mathbf{w}}}_c^T\widehat{\mathbf{\Sigma }}{\widehat{\mathbf{w}}}_c\le {\widehat{\mathbf{w}}}_c^T(\mathbf{\Sigma }-\widehat{\mathbf{\Sigma }}){\widehat{\mathbf{w}}}_c\le {\Vert \mathbf{\Sigma }-\widehat{\mathbf{\Sigma }}\Vert }_{\mathrm{\infty }}{\Vert {\widehat{\mathbf{w}}}_c\Vert }_1^2\le c^2{\Vert \mathbf{\Sigma }-\widehat{\mathbf{\Sigma }}\Vert }_{\mathrm{\infty }}=O_p(a_n{c}^2).$$ (23)

By the same argument, we also have

$${\widehat{\mathbf{w}}}_c^T\widehat{\mathbf{\Sigma }}{\widehat{\mathbf{w}}}_c-{{\mathbf{w}}_c^{(1)}}^T\mathbf{\Sigma }{\mathbf{w}}_c^{(1)}=[{\widehat{\mathbf{w}}}_c^T\widehat{\mathbf{\Sigma }}{\widehat{\mathbf{w}}}_c-{{\mathbf{w}}_c^{(1)}}^T\widehat{\mathbf{\Sigma }}{\mathbf{w}}_c^{(1)}]+{{\mathbf{w}}_c^{(1)}}^T\widehat{\mathbf{\Sigma }}{\mathbf{w}}_c^{(1)}-{{\mathbf{w}}_c^{(1)}}^T\mathbf{\Sigma }{\mathbf{w}}_c^{(1)}\le {{\mathbf{w}}_c^{(1)}}^T(\widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }){\mathbf{w}}_c^{(1)}\le c^2{\Vert \mathbf{\Sigma }-\widehat{\mathbf{\Sigma }}\Vert }_{\mathrm{\infty }}=O_p(a_n{c}^2).$$ (24)

Combination of (23) and (24) leads to

$$|{\widehat{\mathbf{w}}}_c^T\widehat{\mathbf{\Sigma }}{\widehat{\mathbf{w}}}_c-{{\mathbf{w}}_c^{(1)}}^T\mathbf{\Sigma }{\mathbf{w}}_c^{(1)}|=O_p(a_n{c}^2).$$

Let g(x) = Φ(x^−1/2). The function g is Lipschitz on (0,∞), as g′(x) is bounded on (0,∞). Hence, $|\mathrm{\Phi }(f_2({\widehat{\mathbf{w}}}_c))-\mathrm{\Phi }(f_0({\mathbf{w}}_c^{(1)}))|=O_p(a_n{c}^2)$. Thus,

$$|W_n({\widehat{\delta }}_{{\mathbf{w}}_c},\mathit{\theta })-W({\delta }_{{\mathbf{w}}_c},\mathit{\theta })|\le |\mathrm{\Phi }(f_2({\widehat{\mathbf{w}}}_c))-\mathrm{\Phi }(f_0({\mathbf{w}}_c^{(1)}))|+|\mathrm{\Phi }(f_1({\widehat{\mathbf{w}}}_c^{(1)}))-\mathrm{\Phi }(f_0({\mathbf{w}}_c))|=O_p((s_c\vee s_c^{(1)})a_n)+O_p(a_n{c}^2)=O_p(b_n).$$

We now prove the second result of the Theorem. Since $|{\widehat{\mathbf{w}}}_c^T\mathbf{\Sigma }{\widehat{\mathbf{w}}}_c-{\widehat{\mathbf{w}}}_c^T\widehat{\mathbf{\Sigma }}{\widehat{\mathbf{w}}}_c|=O_p(a_n{c}^2)$, we have

$$|\mathrm{\Phi }(f_1({\widehat{\mathbf{w}}}_c))-\mathrm{\Phi }(f_2({\widehat{\mathbf{w}}}_c))|=O_p(a_n{c}^2).$$ (25)

By (20), (25), and the first part of the Theorem, we have

$$|W({\widehat{\delta }}_{{\mathbf{w}}_c},\mathit{\theta })-W({\delta }_{{\mathbf{w}}_c},\mathit{\theta })|=|\mathrm{\Phi }(f_0({\widehat{\mathbf{w}}}_c))-\mathrm{\Phi }(f_0({\mathbf{w}}_c))|\le |\mathrm{\Phi }(f_0({\widehat{\mathbf{w}}}_c))-\mathrm{\Phi }(f_1({\widehat{\mathbf{w}}}_c))|+|\mathrm{\Phi }(f_1({\widehat{\mathbf{w}}}_c))-\mathrm{\Phi }(f_2({\widehat{\mathbf{w}}}_c))|+|\mathrm{\Phi }(f_2({\widehat{\mathbf{w}}}_c))-\mathrm{\Phi }(f_0({\mathbf{w}}_c))|=O_p({\widehat{s}}_c{a}_n)+O_p(a_n{c}^2)+O_p(b_n)=O_p(d_n).$$

This completes the proof of Theorem.

A.2. Proof of Theorem 2

Let w^λ = w_∞ + γ^λ. Then, from the definition of w^λ, we have

$${\mathit{\gamma }}^{\lambda }=\underset{{\mathit{\mu }}_d^T{\mathbf{w}}_{\mathrm{\infty }}+{\mathit{\mu }}_d^T\mathit{\gamma }=1}{\text{argmin}}R({\mathbf{w}}_{\mathrm{\infty }}+\mathit{\gamma })+\lambda {\Vert {\mathbf{w}}_{\mathrm{\infty }}+\mathit{\gamma }\Vert }_1=\underset{{\mathit{\mu }}_d^T\mathit{\gamma }=0}{\text{argmin}}f(\mathit{\gamma }),$$ (26)

where $f(\mathit{\gamma })=R(\mathit{\gamma })+\lambda {\Sigma }_{k\in K^c}|{\mathit{\gamma }}_k|+\lambda {\Sigma }_{k\in K}(|{\mathbf{w}}_{\mathrm{\infty }}^k+{\mathit{\gamma }}_k|-|{\mathbf{w}}_{\mathrm{\infty }}^k|)$. In the last statement, we used the fact that

$${\mathbf{w}}_{\mathrm{\infty }}^T\mathbf{\Sigma }\mathit{\gamma }={\mathit{\mu }}_d^T\mathit{\gamma }/({\mathit{\mu }}_d^T{\mathbf{\Sigma }}^{-1}{\mathit{\mu }}_d)=0.$$

We write γ for γ^λ for short in what follows.

By (26), we have f(γ) ≤ f(0) = 0. This implies that

$$R(\mathit{\gamma })\le \lambda {\mathrm{\Sigma }}_{k\in K}(|{\mathbf{w}}_{\mathrm{\infty }}^k|-|{\mathbf{w}}_{\mathrm{\infty }}^k+{\mathit{\gamma }}_k|)\le \lambda {\mathrm{\Sigma }}_{k\in K}|{\mathit{\gamma }}_k|\le \lambda \sqrt{s}{\Vert \mathit{\gamma }\Vert }_2.$$

On the other hand, $R(\mathit{\gamma })\ge {\lambda }_{\text{min}}(\mathbf{\Sigma }){\Vert \mathit{\gamma }\Vert }_2^2$. Bringing the upper and lower bound of R(γ) together, we conclude that

$${\Vert \mathit{\gamma }\Vert }_2\le \frac{\lambda \sqrt{s}}{{\lambda }_{\text{min}}(\mathbf{\Sigma })}.$$

The proof is now complete.

A.3. Proof of Theorem 5

By the positive definiteness of Σ, Σ⁻¹ and ${\mathbf{\Sigma }}^{-\frac{1}{2}}$ are also positive definite. Let υ = Σ^1/2w, then the transformation v ↦ w is linear. Define

$${\mathit{v}}_c=\underset{{\Vert {\mathbf{\Sigma }}^{-1/2}\mathit{v}\Vert }_1\le c,{\mathit{v}}^T{\overline{\mathit{\mu }}}_d=1}{\text{argmin}}{\mathit{v}}^T\mathit{v},$$

where μ̄_d = Σ^−1/2μ_d. It is enough to show that v_c is piecewise linear in c.

Let Ω_c = {v : ‖Σ^−1/2v‖₁ ≤ c} and S = {v : v^T μ̄_d = 1}. When c is small, the solution set is ∅ when c is large, the constraint Ω_c is inactive. Denote by “a” the smallest “c” such that Ω_c ⋂ S ≠ ∅, and by “b” the smallest such that v_c are the same for all c ≥ b. Hence we are interested in c ∈ [a, b], when changes in c actually affects the solution.

Let P be the projection of the origin O onto the hyperplane S in the p dimensional space. Let

$${ℱ}_c=\{S_{1,c}^0,\cdots ,S_{j_0,c}^0;S_{1,c}^1,\cdots ,S_{j_1,c}^1;\cdots ;S_{1,c}^{p-1},\cdots S_{j_{p-1},c}^{p-1}\},$$

where $S_{j,c}^i$ denotes an i-dimensional face of Ω_c, i.e., $S_{j,c}^0$ represents a vertex, $S_{j,c}^1$ an edge, and $S_{j,c}^{p-1}$ a facet. It is clear that ℱ_c is a finite set.

Define a mapping φ : [a, b] → ℤ × ℤ, where φ(c) = (i, j) such that i) ${\mathit{v}}_c\in S_{j,c}^i$ and ii) i is minimal. By definition, this mapping is single valued.

For any c₀ ∈ (a, b], denote D_c0 = {(i, j)|∀ε > 0, ∃c ∈ [c₀ − ε, c₀) s.t. φ(c) = (i, j)}. The set D_c0 is non-empty because the collection $\{(i,j)\in \mathbb{Z}\times \mathbb{Z}|S_{j,c}^i\in {ℱ}_c\}$ is finite. Then the theorem follows from compactness of [a, b] and Lemma 2, Remark 4 and Lemma 3.

Lemma 1. ∀c₀ ∈ (a, b], ∃ε > 0 such that ∀(i, j) ∈ D_c0 and ∀c ∈ (c₀ − ε, c₀), $P_{j,c}^i\in S_{j,c}^{i◦}\cap S$, where $P_{j,c}^i$ is the projection of P onto $S\cap \stackrel{～}{S_{j,c}^i}$, and $\stackrel{～}{S_{j,c}^i}$ denotes the i-dimensional affine space in which $S_{j,c}^i$ embeds, and $S_{j,c}^{i◦}$ is the interior of $S_{j,c}^i$, where the topology is the natural subspace topology restricted to $\stackrel{～}{S_{j,c}^i}$.

Proof. Fix c₀ ∈ (a, b]. For any (i, j) ∈ D_c0 and ε̄ > 0, by the definition of D_c0, there exists c′ ∈ [c₀ − ε̄, c₀) such that φ(c′) = (i, j). The minimality of i in the definition for φ implies that ${\mathit{v}}_{c\prime }=P_{j,c\prime }^i\in S_{j,c\prime }^{i◦}$, which in the interior of $S_{j,c\prime }^i$. Therefore, $P_{j,c\prime }^i\in S_{j,c\prime }^{i◦}\cap S$. By arbitrariness of ε̄, ∃(c_n) ↗ c₀ such that $P_{j,c_n}^i\in S_{j,c_n}^{i\circ }\cap S$ for all n.

It can also be shown that $\{c|P_{j,c}^i\in S_{j,c}^{i◦}\cap S\}$ is connected: let $P_{j,c_1^{\prime }}^i\in S_{j,c_1^{\prime }}^{i◦}\cap S,P_{j,c_2^{\prime }}^i\in S_{j,c_2^{\prime }}^{i◦}\cap S,c_1^{\prime }<c_2^{\prime }$. For any $c_3^{\prime }\in (c_1^{\prime },c_2^{\prime }),P_{j,c_3^{\prime }}^i$ is on the line segment with endpoints $P_{j,c_1^{\prime }}^i\text{ and }{P}_{j,c_2^{\prime }}^i$ because $\stackrel{～}{S_{j,c}^i}$ are parallel affine subspace in ℝ^p. Let $S_{j,\mathit{\text{cone}}}^i≔{\cup }_{c\ge 0}{S}_{j,c}^{i◦}$, then it is a cone. Since $P_{j,c_1^{\prime }}^i\in S_{j,\mathit{\text{cone}}}^i\text{ and }{P}_{j,c_2^{\prime }}^i\in S_{j,\mathit{\text{cone}}}^i$, we have $P_{j,c_3^{\prime }}^i\in S_{j,\mathit{\text{cone}}}^i$. Then, $P_{j,c_3^{\prime }}^i\in S_{j,\mathit{\text{cone}}}^i\cap S\cap \stackrel{～}{S_{j,c_3^{\prime }}^i}=S_{j,c_3^{\prime }}^{i◦}\cap S$. Hence, ∃ε_ij > 0 such that for all c ∈ [c₀ − ε_ij, c₀), $P_{j,c}^i\in S_{j,c}^{i◦}$. Take ε = min_(i,j)∈Dc0 ε_ij, the claim follows.

Lemma 2. ∀c₀ ∈ (a, b], D_c0 is a singleton, and ∃ε′ > 0 such that v_c is linear in c on (c₀ − ε′, c₀).

Proof. Fix c₀ ∈ (a, b]. We claim that for some (i, j) ∈ D_c0, there exists positive ε′(≤ ε that validates Lemma 1) such that for any c ∈ (c₀ − ε′, c₀), ${\mathit{v}}_c=P_{j,c}^i$. Assume that the claim is not correct, then pick any (i, j) ∈ D_c0, there exists a sequence {c_k} (c_k ≠ c_k′ if k ≠ k′) converging to c₀ from the left s.t. ${\mathit{v}}_{c_k}\ne P_{j,c_k}^i$. Without loss of generality, take {c_k} ⊂ (c₀ − ε, c₀). Lemma 1 implies that $P_{j,c_k}^i\in S_{j,c_k}^{i◦}\cap S$. If ${\mathit{v}}_{c_k}\in S_{j,c_k}^i$, we would have ${\mathit{v}}_{c_k}=P_{j,c_k}^i$. Hence ${\mathit{v}}_{c_k}\notin S_{j,c_k}^i$. By finiteness of the index pairs in ℱ_c, there exists (i′, j′) ≠ (i, j) such that φ(c) = (i′, j′) for c ∈ {c_kl}, where {c_kl} is some subsequence of {c_k}. This implies (i′, j′) ∈ D_c0, which together with Lemma 1 implies ${\mathit{v}}_c=P_{j\prime ,c}^{i\prime }$ for c ∈ {c_kl}. Therefore

$${\Vert P_{j\prime ,c}^{i\prime }-P\Vert }_2<{\Vert P_{j,c}^i-P\Vert }_2$$

for c ∈ {c_kl}.

On the other hand, because (i, j) ∈ D_c0, there exist infinitely many c′ ∈ (c₀ − ε, c₀) such that ${\Vert P_{j\prime ,c\prime }^{i\prime }-P\Vert }_2\ge {\Vert P_{j,c\prime }^i-P\Vert }_2$. Therefore,

$$g(c)={\Vert P-P_{j,c}^i\Vert }_2^2-{\Vert P-P_{j\prime ,c}^{i\prime }\Vert }_2^2$$

changes signs infinitely many times on (c₀ − ε, c₀). This leads to a contradiction because $P_{j,c}^i\text{ and }{P}_{j\prime ,c}^{i\prime }$ are both linear functions of c. Hence, the conclusion holds.

To show that D_c0 is a singleton, suppose it has two distinct elements (i, j) and (i′, j′). We have shown that ${\mathit{v}}_c=P_{j,c}^i\text{ and }{\mathit{v}}_c=P_{j\prime ,c}^{i\prime }$ for all c in a left neighborhood of c₀ (not including c₀). Also we have $P_{j,c}^i\in S_{j,c}^{i◦}\text{ and }{P}_{j\prime ,c}^{i\prime }\in S_{j\prime ,c}^{i\prime ◦}$ by Lemma 1. This can be true only when $S_{j,c}^{i◦}\subset S_{j\prime ,c}^{i\prime ◦}$ (or vice versa), but then i < i′, contradicting with minimality in definition of D_c0.

Remark 4. Similarly, ∀c₀ ∈ [a, b), ∃ε′ > 0 such that v_c is linear in c on (c₀, c₀ + ε′).

Lemma 3. v_c is a continuous function of c on [a, b].

Proof. The continuity follows from two parts i) and ii).

1. ∀c₀ ∈ [a, b), ∃ε > 0 such that v_c is continuous on [c₀, c₀ + ε). Indeed, let

   $$h(c)=\underset{{\Vert {\mathbf{\Sigma }}^{-\frac{1}{2}}\mathit{v}\Vert }_1\le c,{\mathit{v}}^T{\overline{\mathit{\mu }}}_d=1}{\text{min}}{\mathit{v}}^T\mathit{v}.$$

   We know that the mapping $c\mapsto {\mathit{v}}_c(=P_{j,c}^i)$ is linear and hence continuous on (c₀, c₀ + ε) for some small ε > 0. It only remains to show that the mapping is right continuous at c₀. Notice here $h(c)={\Vert P_{j,c}^i\Vert }_2^2$ for c ∈ (c₀, c₀ + ε). Let $L={\text{lim}}_{c\downarrow c_0}{P}_{j,c}^i$. It is clear that $L\in S_{j,c_0}^i$. Because L ∈ Ω_c0 ∩ S, $h(c_0)\le {\Vert L\Vert }_2^2$. This inequality has to take the equal sign because h(·) is monotone decreasing, and $h(c)={\Vert P_{j,c}^i\Vert }_2^2\to {\Vert L\Vert }_2^2$ as c approaches c₀ from the right. Because v_c0 is unique, ${\mathit{v}}_{c_0}=L={\text{lim}}_{c\downarrow c_0}{P}_{j,c}^i={\text{lim}}_{c\downarrow c_0}{\mathit{v}}_c$.

2. ∀c₀ ∈ (a, b], ∃ε > 0 such that v_c is continuous on (c₀ − ε, c₀]. Again, it remains to show that there is no jump at c₀. Let (i_c0, j_c0) = φ(c₀). Clearly $P_{j_{c_0},c_0}^{i_{c_0}}\in S_{j_{c_0},c_0}^{i_{c_0}\circ }$. Introduce a notion of parallelism of affine subspaces in ℝ^p. We denote $\stackrel{～}{S_{j_{c_0},c}^{i_{c_0}}}\Vert S$, if only by translation, $\stackrel{～}{S_{j_{c_0},c}^{i_{c_0}}}$ becomes a subset of S (or vice versa in other situations); use the notation $\stackrel{～}{S_{j_{c_0},c}^{i_{c_0}}}\nparallel S$ otherwise.

   If $\stackrel{～}{S_{j_{c_0},c}^{i_{c_0}}}\nparallel S$, for c in some left neighborhood of c₀, $P_{j_{c_0},c}^{i_{c_0}}$ exists and $P_{j_{c_0},c}^{i_{c_0}}\in S_{j_{c_0},c}^{i_{c_0}\circ }$. Note $P_{j_{c_0},c}^{i_{c_0}}\in {\mathrm{\Omega }}_c\cap S$, and ${\Vert P_{j_{c_0},c}^{i_{c_0}}\Vert }_2\to {\Vert P_{j_{c_0,}{c}_0}^{i_{c_0}}\Vert }_2$ as c approaches c₀ from the left. Since h(·) is monotone decreasing, obviously $h(c)\to {\Vert P_{j_{c_0},c_0}^{i_{c_0}}\Vert }_2^2=h(c_0)$. This shows the left continuity of h at c₀. Suppose D_c0 = {(i, j)}, then we know on a left neighborhood of c₀ (not including c₀), ${\mathit{v}}_c=P_{j,c}^i$. Let $E={\text{lim}}_{c\uparrow c_0}{P}_{j,c}^i$, then E ∈ Ω_c0 ∩ S. Note that ${\Vert P_{j_{c_0},c}^{i_{c_0}}\Vert }_2\ge {\Vert P_{j,c}^i\Vert }_2$ for all c in c₀’s left neighborhood, so we have ${\Vert P_{j_{c_0},c_0}^{i_{c_0}}\Vert }_2\ge {\Vert E\Vert }_2$. On the other hand, ${\Vert P_{j_{c_0},c_0}^{i_{c_0}}\Vert }_2\le {\Vert E\Vert }_2$ by the definition of $P_{j_{c_0},c_0}^{i_{c_0}}$. Also, consider the uniqueness of distance minimizing point in Ω_c0 ∩ S to origin $E=P_{j_{c_0},c_0}^{i_{c_0}}$, and hence v_c has left continuity at c₀.

   If $\stackrel{～}{S_{j_{c_0},c}^{i_{c_0}}}\Vert S$, ∃Q ∈ Ω_c0−ε/2 ∩ S such that $Q\ne P_{j_{c_0},c_0}^{i_{c_0}}$. When c goes from c₀ − ε/2 to c₀, there exists a point Q_c ∈ Ω_c ∩ S moving on the line segment from Q to $P_{j_{c_0},c_0}^{i_{c_0}}$. Therefore, h(·) is left continuous at c₀. Replace $P_{j_{c_0},c}^{i_{c_0}}$ by Q_c in the previous paragraph, the left continuity of v_c at c₀ follows from the same argument.