Why GPCRs behave differently in cubic and lamellar lipidic mesophases

Abstract

Recent successes in the crystallographic determination of structures of transmembrane proteins in the G protein-coupled receptor (GPCR) family have established the lipidic cubic phase (LCP) environment as the medium of choice for growing structure-grade crystals by the method termed “in meso”. The understanding of in meso crystallogenesis is currently at a descriptive level. To enable an eventual quantitative, energy-based description of the nucleation and crystallization mechanism, we have examined the properties of the lipidic cubic phase system and the dynamics of the GPCR rhodopsin reconstituted into the LCP with coarse-grained molecular dynamics simulations with the Martini force-field. Quantifying the differences in the hydrophobic/hydrophilic exposure of the GPCR to lipids in the cubic and lamellar phases, we found that the highly curved geometry of the cubic phase provides more efficient shielding of the protein from unfavorable hydrophobic exposure, which leads to a lesser hydrophobic mismatch and less unfavorable hydrophobic–hydrophilic interactions between the protein and lipid–water interface in the LCP, compared to the lamellar phase. Since hydrophobic mismatch is considered a driving force for oligomerization, the differences in exposure mismatch energies between the LCP and the lamellar structures suggest that the latter provide a more favorable setting in which GPCRs can oligomerize as a prelude to nucleation and crystal growth. These new findings lay the foundation for future investigations of in meso crystallization mechanisms related to the transition from the LCP to the lamellar phase and studies aimed at an improved rational approach for generating structure-quality crystals of membrane proteins.

Introduction

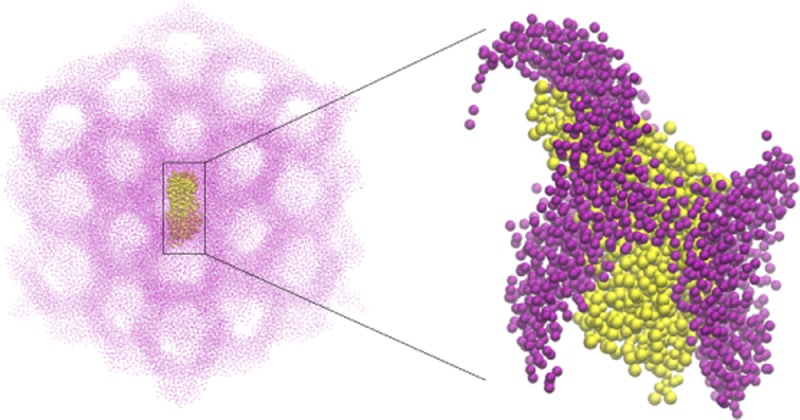
Rapid advances in the crystallographic determination of transmembrane (TM) protein structures, and especially of G-protein coupled receptors (GPCRs), have established the lipidic cubic phase (LCP) as a suitable medium for growing high quality crystals of these proteins (see ref (1,2) and citations therein). The LCP consists of a highly curved lipid bilayer structure (see Figure 1B–C) that is continuous in three dimensions (3D) and separates in space two nonintersecting intertwined aqueous channels.³⁻⁵ Because of the continuous nature of both the lipid and the water compartments, LCP has been described as a bicontinuous mesophase with its bilayer midplane tracing a triply periodic minimal surface (TPMS, characterized by zero mean curvature) (see refs (6−8) and citations therein). The particular kind of LCP utilized during in meso crystallization trials is of Pn3m symmetry type, where each aqueous network of the LCP assumes a tetrahedral geometry (see Figure 2D–E).⁵

Figure 1.

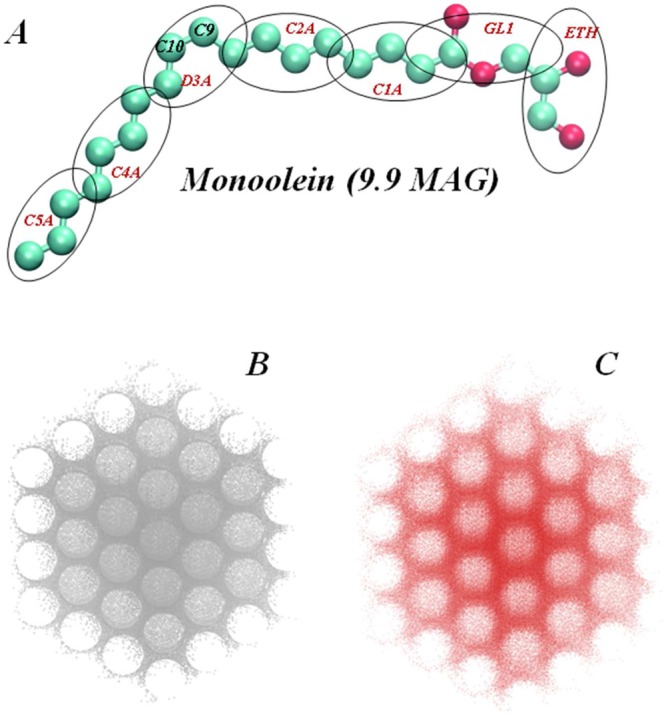
(A) Ball-and-stick representation of the Monoolein (9.9 MAG) lipid. Oxygen atoms are shown in red, carbon atoms are in cyan. Double bonded carbon atoms (C9 and C10) in the hydrocarbon chain of 9.9 MAG are highlighted. Hydrogens are omitted. The grouping of atoms in Martini coarse-grained beads (ETH, GL1, C1A, C2A, D3A, C4A, and C5A) is highlighted by ellipsoids. (B, C) Comparison of the triply periodic minimal surface (TPMS) of Pn3m symmetry calculated from the improved nodal approximation given in eqs 1–3 (B), to a snapshot after 6 μs-long coarse-grained MD simulations of spontaneous self-assembly of 9.9 MAG/water complex at 40% (w/w) water concentration and at 20 °C temperature (C). The figure in C (see also Figures 2 and 3) shows the location of the C5A coarse-grained beads from the 9.9 MAG lipid (see A); note the cubic phase structure. The similarity evident in B and C underscores the close relation between the organization of the C5A beads (representing the density of terminal methylene and methyl groups in 9.9 MAG lipids) and the TPMS of the Pn3m cubic phase.

Figure 2.

(A, B) Views of the unit simulation cell containing 9.9 MAG/water complex at 40% (w/w) water concentration and at 20 °C temperature, after 6 μs of self-assembly simulation. (A) Entire system where different components are colored as following: 9.9 MAG lipid headgroup beads, blue; 9.9 MAG lipid hydrocarbon tail beads, red; and water beads, cyan. (B) Separately 9.9 MAG hydrocarbon chain beads from the same perspective as in A. (C) View of the tetrahedral arrangement of the water channel from A. The four arms of the tetrahedral geometry are visible. (D) Snapshot of two nonintersecting continuous intertwined water channels (in gold and cyan, respectively). The representations are for the “expanded” system obtained by replicating the simulated system 9 times (in positive x, y, and z directions). Note the tetrahedral geometry formed by each of the aqueous networks.

The rapid pace of new structural data acquisition⁹ using the features of the in meso method underscores the usefulness and success of the technology. Thus, structural information obtained in this manner for several rhodopsin-like GPCRs (reviewed in ref (6)) and a GPCR-G protein complex,¹⁰ provided breakthrough insights about the structural basis for signal transduction through these 7-TM helical proteins. However, the present lack of a mechanistic understanding, at the molecular level, of the events that lead to in meso crystallization of membrane proteins, makes the success of the method somewhat enigmatic and results in the need for extensive trials to identify specific conditions, that is, the host and additive lipid, precipitant etc., that would yield high quality samples for crystallographic analysis.^5,11−18

Such in meso trials begin with the target protein being reconstituted into the LCP, and a hypothetical descriptive mechanism based on the membrane curvature and hydrophobic mismatch has been proposed^13,19,20 to address the crucial step during in meso crystallization—the preferential partitioning of proteins from the LCP to the lamellar phase. In the original trials, the lipid used to form the LCP was monoolein (9.9 MAG, see Figure 1A), however recent experiments have utilized shorter chain analogs of monoolein as well as mixtures of monoolein with cholesterol (see refs (12, 18,21)and citations therein). The reconstituted proteins appear to be well-accommodated, functional, and mobile inside the LCP where they are believed to reside largely in a monomeric state.

The addition of a precipitant of suitable composition, which is the next step in the in meso trial, is proposed to result in local structural and compositional changes in the mesophase and likely in protein conformation as well,^8,13,19 which alter the interactions between the proteins and the cubic phase lipid bilayer; ultimately this drives the preferential partitioning of the proteins into the lamellar phase that presumably appears within the LCP.¹⁹ The critical aspect of the nucleation and subsequent crystal growth process that is triggered in this manner, and ultimately determines the quality of the grown crystals, is that once they have diffused from the LCP to the lamellar phase the proteins form tight 3D oligomeric arrays.¹⁹

The oligomerization of TM proteins in lipid bilayers has generally been suggested to involve the hydrophobic mismatch effects originating from the difference in the lengths of the hydrophobic core of the protein and the surrounding lipid hydrocarbon region.²²⁻²⁶ Such mismatch effects have been shown from experiments to play a role not only in the spatial organization but also in the function of TM proteins, such as the GPCR Rhodopsin.^27,28 The hydrophobic mismatch is considered to drive the membrane to deform in order to alleviate the energetically unfavorable hydrophilic/hydrophobic exposure this mismatch entails. When such membrane deformation cannot achieve a complete hydrophobic adaptation, the “residual exposure” (or “residual mismatch”) to unfavorable interactions gives rise to an unfavorable contribution to the free energy of protein/membrane interaction.²⁹ The mitigation of this energy term through oligomerization has been suggested as an important mechanistic contribution to membrane-driven oligomerization of multihelical TM proteins, such as GPCRs, in lipid bilayers.^28,30 Therefore, we investigated the potential role of differential hydrophobic exposure of such proteins in lipid bilayers of the cubic and lamellar phases as a possible determinant of the favorable outcome of in meso crystallization trials.

Here we present the results of a molecular dynamics-based study of a GPCR reconstituted into an LCP environment that reveal differences in the hydrophobic/hydrophilic exposure of the GPCR to lipid–water interface in the cubic and lamellar phases. The quantitative results reflect the drive for differential oligomerization behavior of these proteins in the two lipid environments that essentially define the end points along the in meso crystallization pathway. With the ability to connect quantitatively the difference in GPCR oligomerization behavior in the two different media, to the curvature and mismatch alleviation capabilities of the two environments, we are able to predict lipid types that would enhance/diminish the difference in the residual exposure for a GPCR in the cubic and lamellar phases.

Given the recognized importance of protein–membrane interaction for the functional properties of GPCRs, molecular dynamics simulation studies using all-atom^31,32 and coarse-grained representations²⁶ have been carried out for the prototypical GPCR, Rhodopsin, in lamellar membranes. To our knowledge the present work is the first molecular dynamics-based study of a GPCR reconstituted into the LCP. The results enable quantitative inferences about the energetically unfavorable hydrophobic–hydrophilic interactions that differentiate the behaviors of GPCRs in the two different lipid environments, LCP and lamellar membranes. We attain these insights from comparative microsecond time-scale coarse-grained simulations with the Martini force-field^33,34 of rhodopsin in monoolein-based cubic and lamellar lipid bilayers. Using our recently reported computational framework for quantifying residual mismatch energies from MD trajectories,³⁰ we evaluated the protein-dependent membrane deformations and their attendant energy cost, and identified specific TM regions and residues of rhodopsin that exhibit differential hydrophobic exposure in the LCP and lamellar bilayers. We show that the bilayer of the LCP more efficiently shields the protein from unfavorable interactions, and that the reduced level of hydrophobic mismatch in the LCP is attributable to the specific, highly curved geometry of the cubic phase. Better protection from unfavorable hydrophobic exposure of rhodopsin in the LCP phase is especially evident for residues in TM helix 1 (TMH1) and TMH5. The differences suggest that compared to the “protective” LCP environment, the planar bilayer of the lamellar phase provides a more favorable setting for GPCR oligomerization as a prelude to nucleation and crystal growth. Thus, our findings provide novel energy-based insights into driving elements of in meso crystallization mechanisms and lay the foundation for future quantitative exploration of rational approaches for the generation of structure-quality crystals of membrane proteins.

Theory and Methods

Molecular Constructs and Coarse-grained Molecular Dynamics (MD) Simulations

Coarse-grained (CG) MD simulations of the lipid cubic phases (LCP) with or without rhodopsin were done with the Martini force field,^33,34 grouping atoms into coarse-grained beads (see Figure 1A), and the Gromacs 3.3.1 package³⁵ as listed for the various molecular constructs in Table 1. As a host lipid for the LCP, we used monoolein (9.9 MAG) which consists of an 18 carbon fatty acid with a cis double bond between carbons 9 and 10 in ester linkage to the primary hydroxyl of glycerol (Figure 1A).

Table 1. Simulations Performed in Lipid Cubic phase (LCP).

number of monoolein lipids	water content (w/w %)	number of rhodopsin molecules	temperature,°C	number of simulations	duration of simulationsa	simulation type
500	40	0	20	3	6 μs	self-assembly
13374	40	1b	20	1	4.8 μs	preformed LCPc

^aSimulation times reported are effective times, taking into consideration typical for Martini force-field based coarse-grained simulations factor of 4.

^bSimulations with protein also included counterions to ensure electroneutrality of the system.

^cSimulations with protein were initiated from self-assembled lipid diamond cubic phase of 500 lipids by replicating the Monoolein/water system 27 times (3 times in positive and negative x, y, z directions) and inserting rhodopsin randomly into the expanded LCP phase.

Self-assembly Simulations of a Lipidic Diamond Cubic Phase

In the first phase of the study, we conducted extensive self-assembly simulations of randomly mixed CG 9.9 MAG lipids and water molecules into a lipidic diamond cubic phase. As listed in Table 1 and detailed in the Results, the diamond lipid phase was successfully achieved in multiple simulations conducted at 20 °C temperature and 40% (w/w) water weight percent.

All the self-assembly simulations (see Table 1) were initiated from a random placement of 500 CG 9.9 MAGs (a number that is within the experimentally determined range of 9.9 MAG molecules in the unit cell of the diamond cubic phase), and a corresponding number (determined by the desired percentage) of CG water beads in a cubic box. Each system was first equilibrated for a short period of time with the isotropic pressure coupling scheme and the Lennard-Jones (LJ) parameters of all the atoms set to those of the beads representing water molecules in the Martini force-field. This setup, implemented as well in earlier CG self-assembly simulations of the LCP,³⁶ allowed efficient adaptation of the volume of the simulation box to the number of CG molecules in the system, and ensured complete mixing of lipids and waters prior to self-assembly simulation.

After this initial equilibration phase, the LJ parameters for 9.9 MAG lipids were reset to their proper values (see details of force-field parametrization, below), and 6 μs-long self-assembly MD simulations were performed (the simulation times reported throughout are effective times,³⁴ taking into consideration the factor of 4 typical for Martini force-field-based coarse-grained simulations), and using isotropic pressure coupling (with 3.0 ps and 3e^–5 bar^–1 time constant and compressibility, respectively), and a 30 fs time step.

Simulations of Rhodopsin in Lipid Diamond Cubic Phase

To simulate rhodopsin in the diamond phase, we constructed the system by replicating 27 times (along positive and negative x, y, z directions) one of the cubic phase structures obtained from the self-assembly simulations conducted at 20 °C and at 40% (w/w) water. The diamond cubic phase in this enlarged construct remained stable in a microsecond-long CG MD simulation (data not shown). A rhodopsin molecule was inserted at a random position in this large cubic phase (at ∼122:1 9.9MAG/rhodopsin molar ratio, corresponding to 4 mg/mL concentration, see Figure S1 in the Supporting Information). After removing overlapping waters and 9.9 MAG molecules and adding counterions for electroneutrality, a 4.8 μs-long CG MD simulation was carried out at 20 °C. The total number of CG beads in this large construct was 139 979, which corresponds to ∼1 400 000 actual atoms. The simulation utilized the isotropic pressure coupling scheme as above, and a 30 fs time step.

Simulations of Rhodopsin in Lamellar Bilayers

Rhodopsin was simulated in 9.9 MAG lipid lamellar bilayers with the CG Martini force-field. The CG model of rhodopsin (see below) was inserted into a pre-equilibrated CG 9.9 MAG lipid membrane containing 1772 lipids, and after solvation and ionization steps, a 3.2 μs-long MD simulation was carried out at 20 °C temperature using a 40 fs integration time step and the semi-isotropic pressure coupling scheme.

Force-field Parameters

The details of the Martini CG force fields and the parametrization scheme employed for 9.9 MAG lipid and Rhodopsin can be found in the Supporting Methods section of Supporting Information.

Quantification of the Residual Exposure of Rhodopsin Residues in Lipid Bilayers

The residual exposure energy is the energy cost of the hydrophobic mismatch that persists in the equilibrium state of the membrane-protein interaction, even after membrane remodeling around multi-TM proteins has taken place to reduce the hydrophobic mismatch.^27,29,30 This result of the anisotropy of the protein–membrane boundary when multi-TM proteins are inserted in the bilayer has been discussed in detail.^29,30 For rhodopsin, the residual exposure of residues in the TM segments was quantified with the computational protocol described in ref (30) in both the lipid cubic and lamellar phases, using solvent accessible surface area (SASA) calculations with the NACCESS software³⁷ and a probe radius of 1.4 Å. As described previously,³⁰ SASA values were obtained either with the solute comprising the protein only (SA_prot), or with the solute containing the protein and the hydrophobic core of the lipid bilayer (SA_mem)—the latter being defined as the 9.9 MAG bilayer region consisting of the GL1-C1A-C2A-D3A-C4A-C5A CG beads (see above for the CG bead definition, depicted in Figure 1A). The residual exposure SA_res was then calculated as SA_res = SA_prot – SA_mem for polar residues and as SA_res = SA_mem for hydrophobic residues (see ref (30) for details).

These accessible surface values were used to obtain the residual mismatch energy penalty ΔG_res associated with a particular residue as ΔG_res = σ_resSA_res, where σ_res = 0.028 kcal/(mol·Å²) is a constant of proportionality related to the free energy of transfer of amino acids between aqueous and lipid environments.^38,39 According to a well-accepted protocol,³⁰ interfacial Trp, Arg, and Lys residues were not penalized for residual mismatch due to their ability to adapt favorably to hydrophobic/hydrophilic interfaces.

Quantifying Lipid Bilayer Shapes in Computationally Derived Bicontinuous Structures

Evaluation of the Lipid Bilayer Shape in Protein-free LCP

For a quantitative assessment of the spatial organization of the bicontinuous lipid/water structures assembled computationally, we utilized an analytical fit of the data obtained from the simulations. To obtain this fit we represented the location of the lipid bilayer midplane of the bicontinuous cubic phase by the triply periodic minimal surface (TPMS, surface with zero mean curvature):

1

where f(x, y, z, λ) is the improved nodal approximation given by:

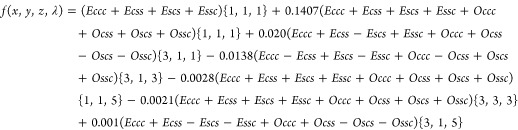2

with

3

and X = λπx, Y = λπy, Z = λπz, and p,q,r = c,s (c and s stand for Cosine and Sine, respectively). The {h,k,l} in the above equations are the crystallographic Miller indices, and λ is a fitting parameter such that 1/λ represents the linear size of the primitive unit cell. This surface was shown to provide an accurate representation of the surface in the Pn3m symmetry group (see, for example, ref (3) and citations therein).

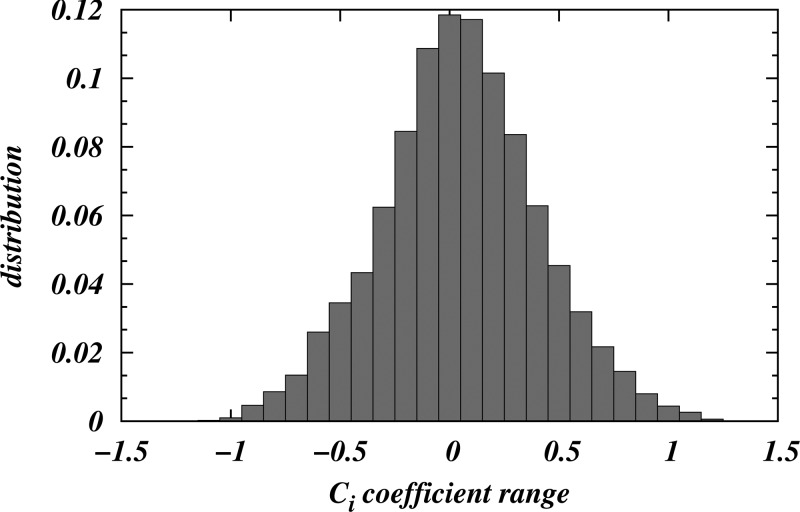
For each 9.9MAG/water trajectory listed in Table 1, a fit to the analytical solution was performed on 20 separate frames spaced 350 ns apart. To this end we extracted the coordinates {x⃗_i} of N C5A coarse-grained beads representing the location of the terminal methylene and methyl groups in the hydrocarbon tail of 9.9 MAG lipids for each frame, and the fit was done by optimizing f(x⃗_i, λ) = C_i through a search for the translational and rotational transformations that minimized σ² = (1/N)∑_i=1^NC_i². The quality of the fit was assessed from the distribution of {C_i} values obtained from the minimization procedure; this distribution is centered around the theoretical mean, zero (i.e., the analytical solution of eq 1). Such a distribution was collected for each MD trajectory by merging the {C_i} coefficients obtained from fitting all 20 separate frames, and the quality was assessed as described above (see distribution plots and captions in Figure 4 and in Figure S3 in the Supporting Information).

Figure 4.

Distribution of {C_i} coefficients from the fitting of the C5A bead positions from the simulations to the analytical TPMS approximation (see Methods). The standard deviation of the distribution is ∼0.4. The χ² test established the significance of the fit with probability p < 0.05.

Quantification of the Lipid Bilayer Shape in Protein-containing LCP

To compare quantitatively the structural arrangement of the LCP bilayer near the protein, to that in the bulk cubic phase, we employed two complementary approaches. In the first, we obtained an analytical solution for the lipid bilayer midplane around the protein by fitting the simulation data (coordinates of C5A beads) to f(x, y, z, λ) = C_i, as described above in the TPMS representation, except that for this purpose the {C_i} coefficients were also considered as variable parameters that must be self-consistently minimized (see above). In this manner, the extent of the deviation of the mean value of the {C_i} distribution obtained from the solution for the Pn3m phase (⟨C_i⟩ ≥ 0, see above), measures the distortion of the diamond cubic phase due to the protein.

The alternative approach we developed for quantifying the perturbation of lipid bilayer shape induced by the GPCR departs from the symmetry group definition and focuses on the lipid–water boundary. In this approach, different trajectory frames from the simulation of rhodopsin in LCP are aligned onto snapshots from the simulations of the large protein-depleted 9.9 MAG/water system. Using a locally defined scoring function (see below), we assess how well the lipid bilayers of the protein-containing and protein-free systems align (the large protein-free system was constructed by replicating 27 times the equilibrated system composed of 500 9.9 MAG lipids/6800 water molecules, and subjecting it to microsecond long CG MD simulation during which the Pn3m phase was maintained; data not shown).

To align the protein-free and protein-containing structures, we used water densities to first align 10 frames from the last 100 ns of the protein-free simulation, which served as a reference on which we aligned 10 frames from the last 100 ns of the protein-containing trajectory. Only water beads at least 50 Å away from the protein were considered, in order to avoid degradation of the alignment quality due to deformations of the lipid cubic phase near the protein.

The alignments utilized the electron density ρ(y⃗) at any point y of a set of beads with coordinates r⃗_i; the density function was constructed as a superposition of Gaussians, so that for a particular trajectory frame

4

where C and k are the amplitude and width of the Gaussians, respectively, chosen to produce a 10 Å resolution density map.⁴⁰

The quality of the superposition of two frames was estimated by measuring the overlap of the water-containing and water-free regions using:

5

where X = {x⃗_j} (j = 1,2,...,M₁, M₁+1,...,N) are coordinates of beads in the fitted frame which contains M₁ water beads and N – M₁ lipid beads; ρ_w is the density of water in the reference frame obtained using eq 5; s_j = 1 for j ≤ M₁, and s_j = −1 for j > M₁. The best alignment was calculated by maximizing S with respect to the rotational and translational transformations applied to X.

The local quality of the alignment was assessed by a normalized scoring function defined as:

6

where ρ(x⃗_j) represents the electron density of the beads in the reference frame.

Results

Self-Assembly of a 9.9 MAG/Water System into a Lipidic Diamond Cubic Phase

The self-assembly of the 9.9 MAG/water complex with 40% (w/w) water composition was probed at 20 °C, which are conditions similar to those used in the original in meso crystallization trials of GPCR proteins (see ref (14) and citations therein). Figures 2 and 3 show several views of 9.9 MAG/water complexes obtained under these conditions produced by the 6 μs-long self-assembly simulation of 500 9.9 MAG lipids. In Figure 2, panels A–C offer views of the unit simulation cell, whereas Figure 3 depicts various snapshots of the same system replicated 27 times (3 times in each orthogonal direction). Typically, in our simulations the initially randomly mixed 9.9 MAG/water system became organized as illustrated in Figures 2–3 within the first 350 ns of simulation, and remained stable for the remainder of the 6 μs trajectory.

Figure 3.

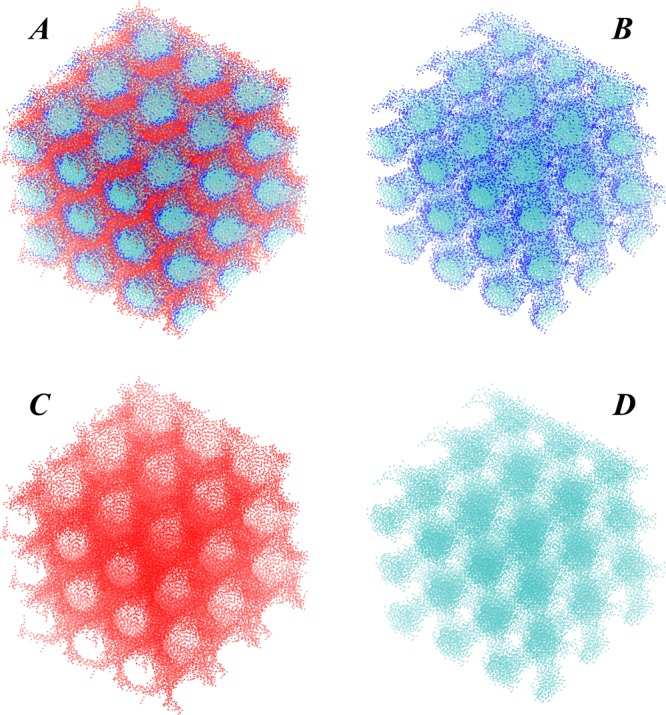
Views of the 9.9 MAG/water complex from Figure 2 replicated 27 times (3 times in positive and negative x, y, and z directions) reveal bicontinuous diamond cubic phase nature of the self-assembled structure. Different panels show: the entire system (A), 9.9 MAG headgroup and water CG beads (B), 9.9 MAG hydrocarbon chain beads (C), only water beads (D). Color code is from Figure 2A.

The bicontinuous cubic phase nature of the self-assembled structure is apparent from inspection of the spatial organization of both lipid and water components. Indeed, the hydrophobic core of the 9.9 MAG lipids (shown in red in Figures 2–3) traces a single highly curved continuous surface in 3D, surrounded by 9.9 MAG headgroups (dark blue shades in Figures 2–3) adjacent to aqueous compartments (cyan colors in Figures 2A,C and 3). The aqueous part of the system consists of two nonintersecting three-dimensional continuous networks of water channels (Figure 2D), which makes the assembled structure a bicontinuous cubic phase.

Figure 2C shows that in each of the water compartments four aqueous channels meet in a tetrahedral arrangement. A similar arrangement can be observed as well for the surface traced by the hydrocarbon chains of 9.9 MAG lipids (see Figures 2B and 3C). Thus, the assembled structure resembles closely the doubly bicontinuous lipidic diamond cubic phase. One general feature of such mesophases is that the surface traced by the midplane of the lipid bilayer, which separates the two aqueous compartments, can be approximated by the triply periodic minimal surface (TPMS) that has a special property: it is characterized at every point by zero mean curvature. Consequently, the TPMS is saddle-shaped (Figure S2, Supporting Information). This saddle-shaped geometry of the 9.9 MAG/water assembly resulting from our calculations can be appreciated, for example, by tracing the surface formed by the 9.9 MAG hydrophobic core (see Figures 2–3).

For a quantitative assessment of the adherence of the bicontinuous structure from our simulations to the organization of the Pn3m diamond cubic phase, we performed a fit of the simulation data to the analytical solution, as described in Methods. The quality of the fit was assessed quantitatively from the distribution of the fitting coefficients {C_i} (see Methods) shown in Figure 4. Clearly, the distribution is centered around zero mean, and is relatively narrow (with a standard deviation of ∼0.4), suggesting that the surface traced by the C5A beads is consistent with the TPMS of the Pn3m cubic phase (see eqs 1–3).

As indicated in Table 1, the self-assembly of 9.9 MAG/water mixture was investigated in two additional simulations performed at T = 20 °C and 40% (w/w) water content. In all cases 9.9 MAG and water molecules aggregated in doubly bicontinuous diamond lipid cubic phases, similar to that described in Figures 2–3 (see Figure S3 in the Supporting Information).

Different Residual Exposure Patterns for Rhodopsin in Bilayers of the Cubic and Lamellar Phases

To explore the organization of a GPCR inside the cubic mesophase we simulated the prototypical class-A GPCR, rhodopsin, in 9.9 MAG-containing lipidic cubic phase in a large system constructed as described in Methods. The simulation results were used as described below to compare quantitatively the interactions of rhodopsin with bilayers of the cubic and lamellar phases, as a basis for interpreting the mechanistic role of the hydrophobic mismatch in triggering the nucleation process during the in-meso crystallization.¹⁹

Residues in the rhodopsin TM bundle that participate in unfavorable interfacial hydrophobic/hydrophilic interactions with the lipid bilayers of the cubic and lamellar phase were identified, as described in Methods, with a SASA-based approach.³⁰ The last 1.5 μs intervals from the respective CG MD trajectories for rhodopsin in the 9.9 MAG LCP (4.8 μs), and in the 9.9 MAG lipid lamellar phase (for 3.2 μs) were used for the residual exposure analysis (see Methods for definitions), and the corresponding residual exposure energies were evaluated as described.³⁰ Table 2 lists rhodopsin TM residues that were found to exhibit different hydrophobic exposures in the LCP and lamellar phase simulations, alongside their respective residual exposure energy penalties (ΔG_res). All other residues in the TM bundle experienced a residual penalty of <1 k_BT (k_B denoting the Boltzmann constant) in both LPC and lamellar phases.

Table 2. Residual Exposure Penalties (in k_BT)^a for Rhodopsin TM Residues That Exhibit Different Hydrophobic Mismatch in the Lipid Bilayers of the Cubic (ΔG_LCP) Compared to the Lamellar (ΔG_LAMELLAR) Phases.

rhodopsin residueb	ΔGLCP	ΔGLAMELLAR	ΔGLCP – ΔGLAMELLAR
Pro 34 (1.29)	0	4.7	–4.7
Gln 36 (1.31)	3.4	1.4	2.0
Phe 228 (5.63)	0	1.8	–1.8

^aAnalysis was carried out on the last 1.5 μs time interval of the respective trajectories where SASA values and corresponding residual exposure energies remained, within fluctuations, unchanged.

^bNumbering shown in parentheses corresponds to the generic residue numbering scheme for GPCRs defined by Ballesteros and Weinstein.⁴¹

Different residual exposure in the two lipid environments became evident for residues in the extracellular (EC) end of TMH1, and the intracellular side (IC) of TMH5 (Table 2). Specifically, the Pro34^1.29/Gln36^1.31 pair on TMH1 (superscript numbers identify the residues by the Ballesteros and Weinstein generic residue numbering scheme for GPCRs⁴¹), and Phe228^5.63 in TMH5 were found to generate a lower residual exposure energy penalty in the LCP than in the lamellar phase. Especially remarkable is the difference in ΔG_res for the hydrophobic Pro34^1.29 residue, that is, 4.7 k_BT in the lamellar bilayers, but <1 k_BT in the cubic phase. This difference results from Pro34^1.29 being largely exposed to the lipid polar headgroups and/or water environment in the planar membrane, but shielded from such unfavorable interactions in the LCP.

The large residual exposure predicted for Pro34^1.29 in the lamellar 9.9 MAG bilayers is consistent with findings from our earlier all-atom MD simulations of rhodopsin in planar membranes composed of diC_n:1PC (n = 14, 16, 18, 20) lipids; the largest residual exposure for Pro34^1.29 was found in the bilayers with the thinnest hydrophobic core, that is, diC_14:1PC and diC_16:1PC membranes. Due to the substantial difference between the hydrophobic length of TMH1 in rhodopsin (∼37 Å, measured along the membrane normal) and the bulk hydrophobic thickness of the thinner bilayers (∼27.2 and 30.5 Å, respectively for diC_14:1PC and diC_16:1PC membranes), the mismatch was not alleviated by membrane deformations around the protein (see ref (30)). Here, the hydrophobic thickness of the 9.9 MAG lamellar bilayers, calculated from the average distance between the lipid GL1 backbone beads on the two leaflets, is 31.5 Å, so that the hydrophobic mismatch between TMH1 and the bilayer is again substantial, and can be alleviated only partially by membrane deformation, as shown below.

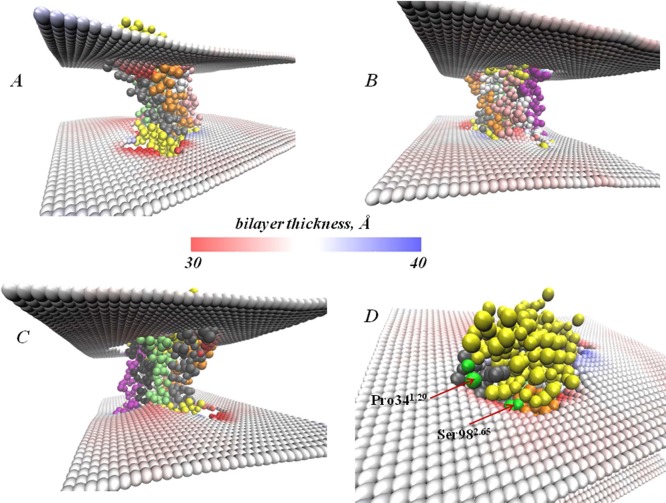
The average thickness of the 9.9 MAG lamellar bilayer around rhodopsin, calculated from the last 1.5 μs of the MD trajectory and the membrane thinning around TMH2—the helix adjacent to TMH1—is evident in Figure 5. Interestingly, we find that the bilayer deforms near the polar Ser98^2.65 residue (see Figure 5D), which is apparently shielded from the unfavorable exposure to the hydrophobic lipid core by the local thinning of the lipid membrane. Usually, the membrane-facing −OH of Ser residues in a TM bundle can avoid hydrophobic contact by forming hydrogen bonds with the helix backbone. When this is not feasible energetically, the bilayer thins around this residue. In our simulations we find that in order to shield Ser98^2.65 from unfavorable hydrophobic exposure, the thinning at TMH2 also constrains the lipids at the adjacent TMH1 (see ref (30) for a discussion of this type of constraint), so that the membrane cannot deform significantly and thus leaves the Pro34^1.29 residue highly exposed (see Figure 5D and Table 2).

Figure 5.

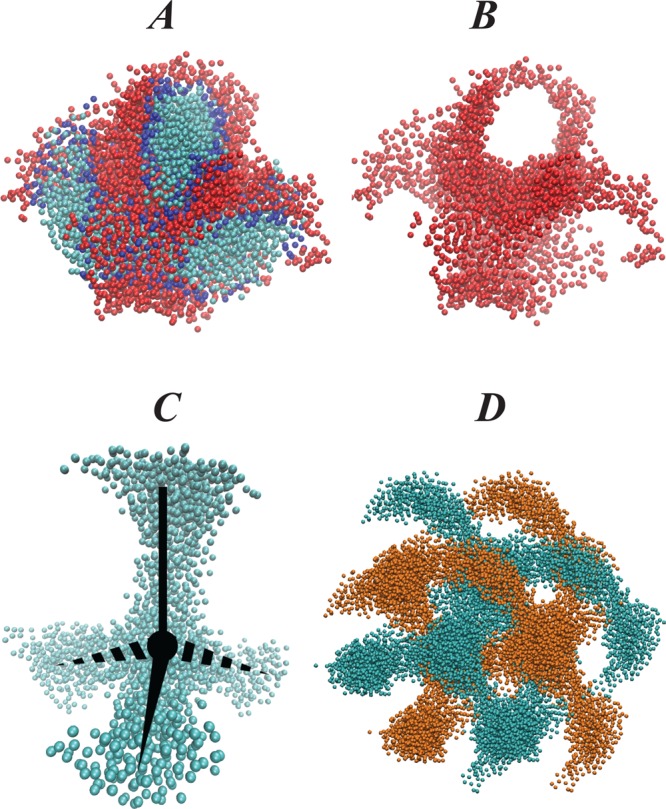
(A–C) Views of membrane deformation patterns around the rhodopsin immersed into 9.9 MAG lamellar bilayers. The average positioning of membrane leaflets is identified by the two surfaces colored according to the local thickness of the bilayer (see the bar for color definition). The GPCR is shown in van der Waals representation with the TM helices colored as follows: TM1 in gray, TM2 in orange, TM3 in white, TM4 in pink, TM5 in purple, TM6 in black, and TM7 in lime The rest of the protein (loops, etc.) is rendered in yellow. The membrane representation is focused on the region near the protein. (D) Magnified view of the region containing residues Pro34^1.29 and Ser98^2.65 (both rendered in green) showing the membrane deformations in their vicinity.

Figure 5 shows that the 9.9 MAG planar bilayer deforms around other TM helices as well. Specifically, the membrane thins around TMH4, alleviating the residual mismatch for this helix, and around TMH7 where the deformation efficiently accommodates the juxtaposed amphipathic helix 8 at the hydrophobic/hydrophilic interface. Overall, the heterogeneous pattern of membrane deformations we observe around rhodopsin in the current simulations agrees with earlier findings from all-atom MD simulations showing the pattern of membrane remodeling around rhodopsin and the homologous serotonin 5-HT_2A GPCR.^30,31,42 Consistent with those studies, we find here that the deformations of the lamellar 9.9 MAG bilayer do not completely alleviate the hydrophobic mismatch with the receptor (Table 2). The different organization of the two lipid phases around the GPCR, as presented below, explains why the residual exposure was larger for rhodopsin in the lamellar 9.9 MAG bilayer than in the 9.9 MAG LCP.

The Intrinsically Curved Geometry of the Lipidic Cubic Phase Is Key to the Low Residual Exposure Experienced by Rhodopsin in the Cubic Mesophase

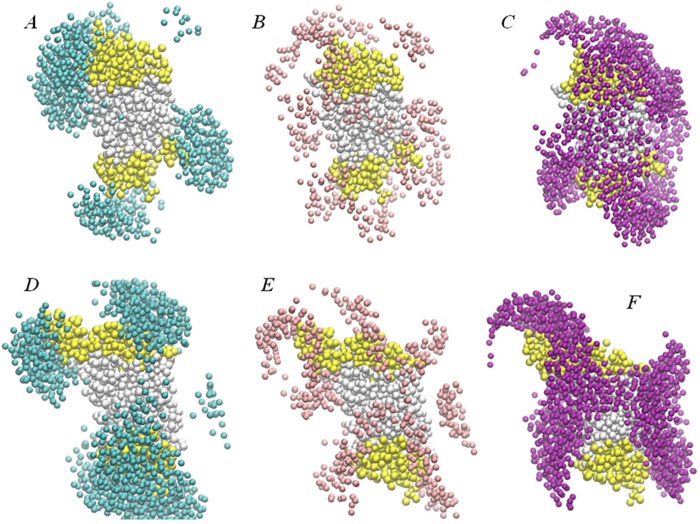
Figure 6 shows the organization of the lipid cubic phase around rhodopsin in the initial configuration where the protein was randomly inserted in the LCP (see also Figure S1 in the Supporting Information), compared to the organization after 4.8 μs of CG MD simulations. Thus, comparison of A–C with D–F in Figure 6 shows the substantial rearrangement of the lipids and solvent around rhodopsin during the long MD trajectory. Specifically, it appears that the LCP tends to minimize hydrophobic/hydrophilic contacts with the GPCR as the water and lipid headgroup beads organize around polar regions of the protein (yellow colors in Figure 6), whereas the lipid hydrocarbon chain beads surround the hydrophobic core of the protein (see caption of Figure 6 for TM definitions).

Figure 6.

Snapshots illustrating initial (A–C), and final (after 4.8 μs simulations) positioning (D–F) of rhodopsin (in yellow/white) inside the cubic phase. A and D show the organization of water beads (in cyan), B and E illustrate the organization of 9.9 MAG lipid headgroup beads (in pink), and C and F show the organization of 9.9 MAG lipid hydrophobic core beads (in purple). In all panels rhodopsin transmembrane (TM) helices are colored in white and the rest of the protein in yellow. Shown are only water and 9.9 MAG lipids that are within 20 Å of rhodopsin; rhodopsin is oriented so that its intracellular and extracellular ends (as defined in the lipid bilayer) point toward the bottom and top of the panels, respectively.

The snapshots in Figure 6 also show that rhodopsin equilibrates, as expected, around the saddle-point inside the LCP⁵ so that the TM bundle perpendicularly traverses a narrow but relatively flattened region of the LCP bilayer, much like the GPCR protein does in the lamellar bilayers. However, due to continuous and intrinsically saddle-shaped geometry of the diamond cubic phase, the LCP bilayer is dramatically curved near TMH1 and TMH5, which effectively confines the protein to a small region of the LCP. This special arrangement of the cubic mesophase around rhodopsin shields the GPCR in the LCP from the kind of unfavorable hydrophobic/hydrophilic interactions with the lipid bilayer seen in the lamellar membranes. Thus, as illustrated in Figure S4 (in the Supporting Information) and reflected in the residual energy penalties (in Table 2), residues Pro34^1.29 and Phe228^5.63 are in contact with the hydrophobic core of the LCP bilayer and therefore do not incur a residual mismatch penalty, although Gln36^1.31 experiences somewhat higher residual exposure in the LCP compared to the lamellar phase (see Figure S4 and Table 2). Overall, we find the difference in energy ΔG_LCP – ΔG_LAMELLAR to be −2.7 k_BT for the Pro34^1.29/Gln36^1.31 pair, and −1.8 k_BT for Phe228^5.63 (Table 2). Notably, the shielding of Ser98^2.65 that faced the 9.9 MAG lipid bilayer in the lamellar phase simulations, occurs in the LCP simulations through interaction with the protein backbone.

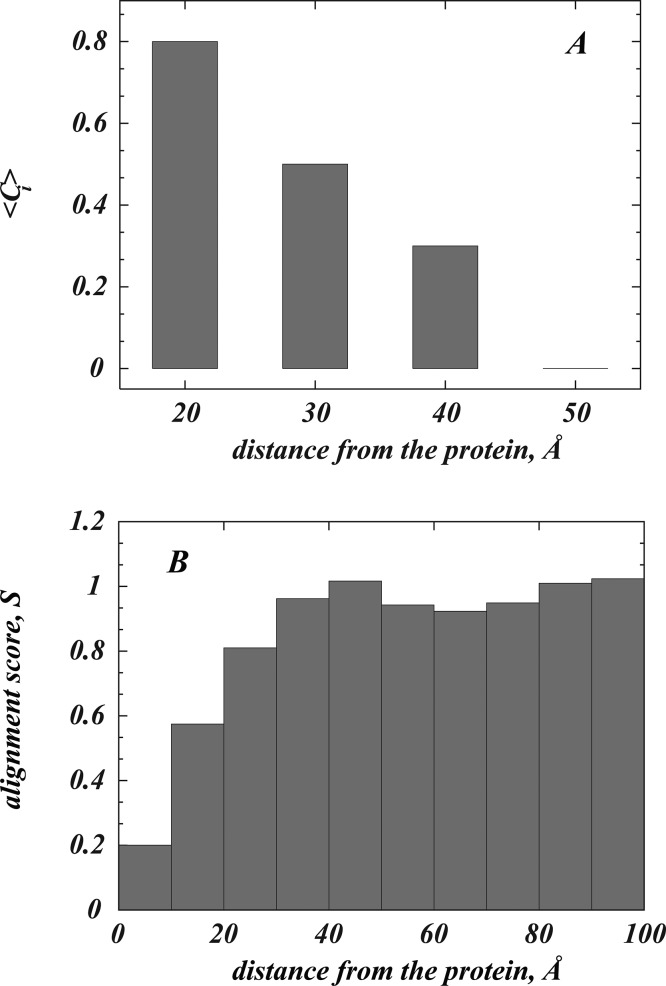
To relate the calculated residual mismatch energies to the organization of the lipidic cubic mesophase around the GPCR, we quantitatively compared the structural arrangement of the LCP bilayer near the protein, to that in the bulk cubic phase. As described in Methods, two different approaches were used: In the first, we obtained an analytical fit of the lipid bilayer midplane shape around the protein by fitting the coordinates of 9.9 MAG lipid C5A methyl terminus beads (Figure 1A) from the simulations to f(x, y, z, λ) = C_i, considering {C_i} coefficients as variable parameters that must be minimized during the fitting (see Methods). The application of this procedure to spherical lipid shells situated at different distances from rhodopsin (see Figure 7A) revealed that the organization of the LCP close to the GPCR is different from that expected for the Pn3m lipid bilayer (⟨C_i⟩ ≠ 0 in Figure 7A). However, already at distances ∼50 Å from the center of rhodopsin (compare to ∼35–40 Å linear dimension of a rhodopsin-like GPCR in bilayer x–y plane directions), the simulated structure relaxes to the organization of the diamond cubic phase (⟨C_i⟩ = 0, Figure 7A). The second approach confirms that the distorted LCP bilayer near the protein tends to relax toward the Pn3m phase arrangement at larger distances (Figure 7B). In this alternative approach we locally quantify the shape of the lipid bilayer around the GPCR by aligning trajectory frames from the simulation of rhodopsin in LCP onto snapshots from the simulations of the pure LCP system, so as to optimize the overlap of the water-containing and water-free regions (see Methods). A scoring function defined locally (see eq 5) is used to assess the quality of the alignment. As seen from Figure 7B, this procedure revealed that the fit between the densities of C5A lipid beads in protein-containing and protein-free systems progressively improves with the radial distance from the GPCR (increasing S in Figure 7B). Indeed, consistent with the result in Figure 7A, the scoring function reaches its plateau ∼50 Å away from the protein, indicating that at these distances the LCP arrangement becomes similar to that expected for the Pn3m phase.

Figure 7.

Distance dependence of the relaxation of membrane deformation near rhodopsin in the cubic phase. (A) Analytical fit of the density of C5A 9.9 MAG lipid beads from CG MD simulation of rhodopsin in the LCP phase to the surface defined by the f(x, y, z, λ) = C_i equation (see Methods). The mean values of the {C_i} fitting coefficient distribution as a function of r, are shown for 10 Å spherical lipid shells located at r = 20, 30, 40, and 50 Å away the protein center-of-mass. (B) Reasults from the same measurements performed with an alternative approach based on the alignment of the lipid bilayer midplane in protein-containing and protein-free cubic phases (see Methods). The quality of the fit upon alignment was determined for 10 Å spherical lipid shells located at distances r from the protein center-of-mass, and the panel shows the dependence of the scoring function S on r. Note that the deformed cubic phase near rhodopsin relaxes to the arrangement that is characteristic of the Pn3m phase ∼50 Å away from the protein.

Taken together, our results establish a quantitative link between the residual mismatch penalty and the lipid bilayer deformations around the GPCR in the cubic phase. Thus, the areas where the largest perturbations from the diamond cubic phase were observed included residues Pro34^1.29 and Phe228^5.63 (see Figure S5 in the Supporting Material), which are also the residues with the largest value of ΔG_LCP – ΔG_LAMELLAR (Table 2).

Discussion

The main findings from this study offer unprecedented insight into molecular level processes related to in meso crystallization, which are likely leading to protein nucleation and eventually to crystal growth. Thus, we found that the difference in the hydrophobic/hydrophilic exposure of the protein to the lipid bilayers of 9.9 MAG LCP and lamellar phases is responsible for a lower residual mismatch (and its corresponding energy penalty) in the cubic mesophase compared to the lamellar membranes. This indicates why GPCRs reconstituted into the LCP in the initial stages of the in meso trial are well accommodated inside the cubic phase, where they are believed to reside mostly in the monomeric form. Indeed, from our findings there is insignificant drive toward rhodopsin oligomerization in the LCP. We showed, however, why this drive is increased in the planar bilayer environment of the lamellar phase where there are several critical mechanistic factors that determine the probability for proteins to oligomerize. One important energy component that has been established from both experiments^28,29 and computations,^26,30 involves the hydrophobic mismatch. In particular, a plausible mechanism to relieve the energy penalty due to residual exposure is protein oligomerization, whereby the TM segments incurring the highest energy penalty from the residual exposure come together in the lipid bilayer.^29,30

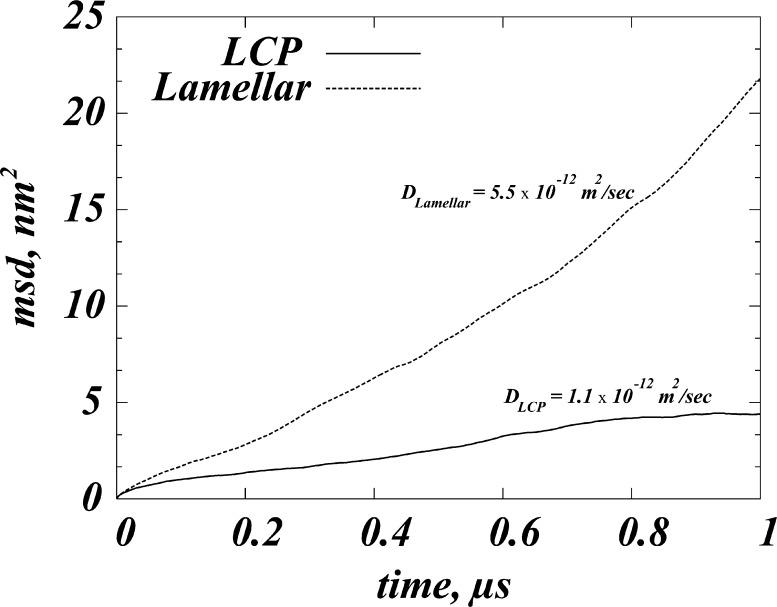
For such hydrophobic-mismatch driven association to occur, the residual exposure penalty alleviated by the protein association must counteract other critical factors that could favor proteins in the monomeric state. One such important consideration is the mobility of proteins, because constrained diffusion reduces the chance for protein–protein encounter. As shown in Figure 8, the spatial restriction encountered by the GPCR inside the LCP (see Figure 6) significantly affects protein mobility, with the diffusion coefficient of the GPCR in the cubic phase being smaller (D_LCP = 1.1 × 10^–12 m²/sec) than that in the lamellar bilayers (D_LAMELLAR = 5.5 × 10^–12 m²/sec). The restricted diffusion mode for rhodopsin in the LCP environment is consistent with the suggested high energy cost in the LCP for GPCR-sized proteins to cross between different regions of the mesophase.⁸ This energy penalty was quantified from phenomenological principles to be as high as ∼12–20 k_BT in the Pn3m phase with lattice parameter values in the 75–110 Å range.⁸ This estimated energy cost of protein diffusion in the LCP is significantly higher than the residual mismatch penalty we calculated for rhodopsin in the cubic phase (Table 2). When considered together, the relatively low residual exposure energy for the GPCR in the LCP is not likely to be sufficient to compensate for the high energy barrier for protein mobility in the LCP and drive protein association. The prediction is, therefore, that in the cubic mesophase GPCR proteins will remain largely in the monomeric state.

Figure 8.

Mean-square-displacement (msd) as a function of time calculated for rhodopsin in the 9.9 MAG lipidic cubic phase (LCP) and in the 9.9 MAG lamellar membrane (Lamellar). Corresponding diffusion coefficient values, calculated from the linear fit performed in [0 μs;1 μs] time interval, are D_LCP = 1.1 × 10^–12 m²/sec and D_LAMELLAR = 5.5 × 10^–12 m²/sec.

In contrast to the LCP, the lamellar membrane environment is more favorable for GPCR oligomerization: The residual energy penalty for the rhodopsin TM bundle in the lamellar bilayers is ∼8 k_BT (Table 2) and is significantly higher compared to that in the LCP, indicating a stronger drive for GPCR oligomerization in the lamellar membranes. A higher propensity for association in the planar bilayers is also supported by our calculations of the protein mobility in the two lipid environments, whereby we find a 5-fold larger diffusion coefficient for the GPCR in the lamellar bilayers (Figure 8).

Taken together, results from our simulations suggest that planar 9.9 MAG lipid membranes provide a more suitable setting for oligomerization of the GPCR proteins. Notably, this prediction is based on results for oligomerization in a plane of the lipid bilayer. This 2D nucleation process together with the formation of protein-enriched lamellar stacks in 3D¹⁹ should ultimately drive the emergence of a bulk crystal.

The question remains regarding the mechanism that drives the proteins from the LCP to the lamellar membranes and the potential role of the differential residual interactions between the protein and the bilayers of the two lipidic phases in the nucleation process. We note that the nucleation is triggered by the addition of the precipitant which is known to cause transient water depletion from the LCP interior,¹⁹ resulting in structural changes in the cubic phase bilayer. Our current study has not attempted to quantify the effects of the precipitant, but it is reasonable to speculate that dehydration of the cubic phase will only increase the unfavorable residual interactions between the GPCR and the LCP bilayer.¹⁹ This is likely to increase the drive for protein oligomerization inside the LCP upon precipitant addition, which could lead to the formation of locally flattened lamellar bilayers as a prelude to protein crystallization. In order to address quantitatively the structural perturbations due to precipitant, such as changes in curvature of the LCP bilayer, it is critical to calculate the corresponding deformation energies in the presence of the protein. However, the representation of the complex geometry of the LCP around the insertion (Figures 6–7) in the numerical approach developed in the current work for quantifying the LCP shape (i.e., fitting the MD data to the analytical solution) is not sufficiently refined to serve in the calculation of reliable energies. We will be addressing these numerical challenges in future work.

We note, however, that recent experimental studies^12,18,21 showed that, compared to 9.9 MAG, in meso trials conducted on the GPCR-Gs protein complex with a shorter chain MAG analog, 7.7 MAG (acyl chain 14 carbon atoms long with the cis double bond between carbon atoms 7 and 8) resulted in better quality crystals. These results support the mechanism we describe based on the residual mismatch. Thus, results from our current studies as well as from recently reported all-atom simulations of GPCRs in membranes of different thicknesses,³⁰ explain why 7.7 MAG would provide a better platform in which GPCRs can aggregate more extensively: based on our findings we can predict that, due to the expected ∼7–8 Å difference in the hydrophobic thickness of planar 9.9 MAG and 7.7 MAG membranes, the residual exposure of the GPCR will be substantially higher in the thinner 7.7 MAG lamellar bilayers. As an example, we recently reported that the rhodopsin TM bundle will exhibit a 12 k_BT higher residual energy penalty in diC_14:1PC than in diC_18:1PC bilayers.³⁰ A more complete quantitative elucidation of the GPCR nucleation process in relation to the residual mismatch energy component requires further studies that would take into consideration the effect of the different precipitants on various lipids.

The structurally specific predictions of the regions where the residual mismatch with lipid bilayers of cubic and lamellar phases differed for the rhodopsin TM bundle made it possible to probe the resulting predictions and general character of the findings by examining crystallographic data. In particular, we showed here that the intracellular (IC) end of TMH1 (Pro34^1.29), and the extracellular (EC) part of the TMH5 including Phe228^5.63 have higher residual exposure in lamellar membranes, which leads to the prediction (e.g., see Shan et al.⁴²) that in the planar bilayers rhodopsin will exhibit strong hydrophobic-mismatch driven tendency for oligomerization through TMH1 and TMH5. To assess this hypothesis in the context of structural information available for GPCRs, we examined crystallographic contact interfaces for 12 different structures of rhodopsin-like GPCRs obtained by means of the in meso technology (β₂ receptor – PBD codes: 2RH1, 3PDS, 3SN6; A2A receptor – PDB codes: 3EML, 3QAK; Chemokine CXCR4 receptor – PDB codes: 3ODU, 3OE0, 3OE6, 3OE8, 3OE9; Dopamine D3 receptor – PDB code: 3PBL, and Histamine H1 receptor – PDB code: 3RZE). For all these GPCR structures, we analyzed the content of the unit crystallographic cell and quantified for each TM helix (1) the frequency of its occurrence at the crystallographic contact interface and (2) the number of residue interactions each TM helix forms at the contact interface. In this analysis only “canonical” interfaces were considered, where the crystallographic contacts were formed exclusively through TM–TM interactions between monomers in parallel orientations.

Remarkably, we found that TMH1 and TMH5, the two helices implicated in the largest residual mismatch in our simulations of rhodopsin with 9.9 MAG lamellar bilayers, contribute to the most common contact interfaces in the crystallographic structures of the homologous GPCRs. More specifically, as illustrated in Figure S6A (see Supporting Information), all but 4 of the 14 distinct intermolecular TM–TM interfaces identified in this analysis, involve TMH1 and/or TMH5. Furthermore, examining the residues involved in the interactions at the contact interfaces revealed that the TMH1 stretch of residues in positions 1.29–1.34 (that would include Pro34^1.29 in the homologous rhodopsin GPCR) contribute significantly to the formation of the crystallographic interface.

During the final preparation of this manuscript, two new crystal structures of rhodopsin-like GPCRs, the κ-opioid receptor (KOR) and the μ-opioid receptor (MOR) were reported to be obtained by means of in meso crystallization.^43,44 Consistent with the data presented above, the crystallographic interface of KOR consists of TM1, TM2 and H8, with the N-terminal end of TM1 (region harboring the residue homologous to Pro34^1.29 in rhodopsin) forming extensive dimeric contacts.⁴³ For MOR,⁴⁴ two crystallographic interfaces were reported: the more prominent interface consisted of TM5/TM6 helices with the I256^5.62 residue (aligning with the residue next to Phe228^5.63 in rhodopsin) residing at the dimer interface, and more limited contacts formed by TM1, TM2 and H8.

Taken together, our findings support the mechanistic inferences that (1) the reduced level of hydrophobic mismatch in the LCP is attributable to the specific highly curved geometry of the cubic phase that provides for more coverage from unfavorable hydrophobic exposure; (2) compared to the LCP, lamellar structures provide a more favorable setting in which GPCRs can oligomerize as a prelude to nucleation and crystal growth; and (3) the extent of the residual mismatch penalty is likely one of the critical mechanistic factors that determines not only the drive for GPCR proteins to oligomerize during in meso crystallization, but also the structural elements that are likely to participate in contact interfaces.

These findings provide novel energy-based insights into in meso crystallization mechanisms and lay a foundation for future computational explorations involving other class-A GPCRs toward designing rational approaches for generation of structure-quality crystals of membrane proteins.

Supporting Information Available

Supporting methods and six figures describing organization of rhodopsin in the lipid cubic and lamellar mesophases. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States