Visual grading regression: analysing data from visual grading experiments with regression models

Abstract

For visual grading experiments, which are an easy and increasingly popular way of studying image quality, hitherto used data analysis methods are often inadequate. Visual grading analysis makes assumptions that are not statistically appropriate for ordinal data, and visual grading characteristic curves are difficult to apply in more complex experimental designs. The approach proposed in this paper, visual grading regression (VGR), consists of an established statistical technique, ordinal logistic regression, applied to data from single-image and image-pair experiments with visual grading scores selected on an ordinal scale. The approach is applicable for situations in which, for example, the effects of the choice of imaging equipment and post-processing method are to be studied simultaneously, while controlling for potentially confounding variables such as patient and observer identity. The analysis can be performed with standard statistical software packages using straightforward coding of the data. We conclude that the proposed statistical technique is useful in a wide range of visual grading studies.

Visual grading experiments have recently increased in popularity for studying image quality in medical imaging systems [1–10]. With a limited amount of work, requiring access only to images from the routine workflow, the rating by a number of experienced observers may result in information that is highly relevant for evaluating the diagnostic quality of an imaging procedure to be used in clinical practice and for comparisons between alternative techniques.

In a typical experiment, each image is graded in one or more respects by a number of observers who select a score reflecting the general quality of the image or the fulfilment of a specific criterion such as the visibility of a certain anatomical structure. Well-defined criteria, such as the EU criteria [11–13], are often used, and the score is typically set on a scale with a limited number of steps where, for example, 0 denotes the lowest and 4 the highest category. Although the values on the scale have a natural ordering, there is no guarantee that the difference between 0 and 1 is equivalent to that between 1 and 2 or between 3 and 4. In statistical terms, the score is defined on an ordinal scale.

A variant of the method, intended to increase the sensitivity to small differences in image quality, involves simultaneous viewing of two images, where the score is meant to express a comparison of the two images, such as −2 for “certainly better in left image than in right image”, −1 for “probably better in left image than in right image”, 0 for “equivalent”, +1 for “probably better in right image than in left image” and +2 for “certainly better in right image than in left image”. Again, this judgement may refer to a general concept of image quality or to a single well-defined criterion.

Both of these experimental set-ups present the observers with a simple and easily understood task. When it comes to analysing the data, e.g. to compare two imaging methods with each other, however, the task is less straightforward. Applying common statistical methods relying on least-squares estimation, such as t-tests or analysis of variance (ANOVA), might be tempting, but these techniques, which seek to minimise the sum of squared distances between predicted and observed values, assume that the dependent variable is defined on an interval scale, so that a certain difference in score always has the same meaning. From a statistical point of view, it is not acceptable to use these methods on ordinal-type data.

A way to overcome this problem has been suggested by Båth and Månsson [14], who use a mathematical formalism similar to that of receiver operating characteristic (ROC) curves to create a visual grading characteristic (VGC) curve. Assuming normal distributions of two underlying (unobserved) variables, their method treats the ordinal-scale data in an irreproachable manner and is easy to apply in situations in which two procedures are to be compared. However, in many situations, researchers may want to assess simultaneously the effect of several factors potentially influencing the grading and their interaction, e.g. to compare the relative importance of the choice of imaging equipment and the choice of post-processing method. In such situations, application of the VGC approach is not straightforward.

A different statistical technique, designed to handle situations with dependent variables defined on an ordinal scale, is ordinal logistic regression [15, 16]. Ordinal logistic regression models easily handle situations involving several factors potentially influencing the outcome variable, and the technique now belongs to the standard statistical armamentarium. We have, however, been able to find only two publications in which it was applied to visual grading studies of image quality [17, 18]. Occasionally, researchers have applied dichotomisation of ordinal visual grading data prior to analysis with binary logistic regression, i.e. recoding the scores into two categories such as good and poor, and thus part of the information has been discarded [19].

The purpose of this article, therefore, is to point out how established statistical methods involving ordinal logistic regression models may be applied to the analysis of visual grading experiments. It is not, however, meant to replace standard statistical textbooks.

Suggested approach

Consider a visual grading experiment in which a number of patients (P) are examined with one of several types of imaging equipment (Im) and the results are processed with one of several post-processing methods (PP) before being presented to a number of observers (O). Methods for organising and analysing the data will differ slightly between situations in which one image is assessed at a time and those in which two images are compared, and we will therefore treat the two cases separately, using hypothetical data for illustration. (The reader not interested in the technical details of the method may prefer to skip the two subsections entitled Analysis.)

Single-image rating

Data organisation

The most straightforward way to tabulate the collected data from a single-image rating experiment is probably to assign one column for each independent variable and use suitable category labels for the different values that the variable may assume, as illustrated with hypothetical data in Table 1. This data set of 144 fictional observations thus contains the results of visual grading by 4 observers of 36 images (2 types of imaging equipment (Im1, Im2) combined with 3 post-processing methods (PP1, PP2, PP3) and 6 patients). An alternative way is to let each variable to be studied correspond to several columns in the table, one for each possible category, where the values are restricted to take the value 1 in the column for the actual category and 0 in the other columns (Table 2). The resulting numerical variables are called dummy variables and are closer to the internal representation in the computer needed for the calculations. Most modern software packages, however, make this conversion automatically, and the choice between the two types of coding is at the discretion of the researcher as they yield identical analysis results.

Table 1. Data from a hypothetical single-image rating experiment with category label coding. Combining 2 types of imaging equipment (lm), 3 post-processing methods (PP), 6 patients (P) and 4 observers (O) yields a data set with 2×3×6×4 = 144 observations.

Observation no.	Im	PP	P	O	Score
1	Im1	PP1	P1	O1	1
2	Im1	PP2	P1	O1	2
3	Im1	PP3	P1	O1	1
4	Im2	PP1	P1	O1	0
5	Im2	PP2	P1	O1	3
6	Im2	PP3	P1	O1	2
7	Im1	PP1	P1	O2	1
8	Im1	PP2	P1	O2	3
...	...	...	...	...	...
144	Im2	PP3	P6	O4	3

The score is defined on a scale ranging from 0 (worst) to 4 (best).

Table 2. Data from the same single-image rating experiment as in Table 1 with dummy variable coding of factors Im and PP.

Observation no.	Im1	Im2	PP1	PP2	PP3	P	O	Score
1	1	0	1	0	0	P1	O1	1
2	1	0	0	1	0	P1	O1	2
3	1	0	0	0	1	P1	O1	1
4	0	1	1	0	0	P1	O1	0
5	0	1	0	1	0	P1	O1	3
6	0	1	0	0	1	P1	O1	2
7	1	0	1	0	0	P1	O2	1
8	1	0	0	1	0	P1	O2	3
...	...	...	...	...	...	...	...	...
144	0	1	0	0	1	P6	O4	3

Analysis

The basic assumption underlying logistic regression in its simplest form (binary logistic regression) is that the ratio of the probability of an event occurring to the probability of the same event not occurring is multiplied by a certain numerical constant if a risk factor is present, and that the effect of several simultaneous risk factors is obtained by multiplying sequentially by the corresponding constants. The ratio between the two probabilities is called the odds for the event. Transforming probability with the logistic function (the logarithm of the odds)

(log here denotes the natural logarithm) results in a linear equation, which in the simplest case, with one continuous independent variable, takes the form

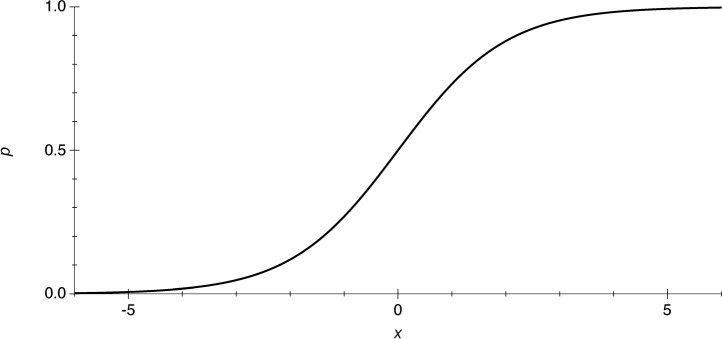
where a = −1 and b = 0. The explicit dependence of the probability p on the independent variable x is given by

where exp denotes the exponential function (see Figure 1).

Figure 1.

Probability (p) as a function of a single independent variable (x) according to a simple logistic regression model (Equation (3).

In the case of several independent variables, we will instead need a linear combination of the independent variables, and the probability predicted by the model is given by

where z is a weighted sum of independent numerical variables (continuous or dummy variables). If all independent variables are categorical, as is the case when a limited number of components are compared, every independent variable is represented by a term that takes a separate value for each category. If the model includes the two variables PP and Im, these will correspond to two terms A_Im and B_PP, where, for example, A₁ characterises equipment Im1 and A₂ equipment Im2. In most situations, the researcher is not interested in differences between specific patients or observers, but the corresponding variables P and O should be introduced in the model nonetheless, in order to handle the variation that arises due to differences between patients and observers.

When the dependent variable y is defined on an ordinal scale, as in our example, the probability of obtaining a value not greater than n is given by

where D_P, E_O and C_n have values specific for each patient, observer and quality level, respectively. In most modern software for ordinal logistic regression, such a model is easily specified by declaring Im, PP, P and O as independent nominal variables and y as the dependent variable.

Using dummy variables for PP and Im, as in Table 2, the same equation will take the form

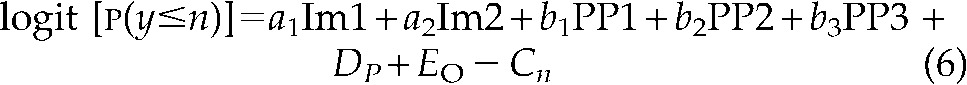where Im1, Im2, PP1, PP2 and PP3 are dummy variables that can only have the values 0 or 1, and a₁, a₂, b₁ and b₂ are parameters to be estimated. This formulation makes the similarity to linear regression more obvious.

A model of this type can also easily be specified in current software. However, as the algorithm requires that the independent variables of the model not be linearly dependent on each other, one cannot include both Im1 and Im2 as independents (since Im1 + Im2 = 1 always). Thus, one has to select one category as the “reference category” against which the other values are compared. In our example, if we should consider the imaging method Im1 and the post-processing technique PP1 as reference categories, we would specify Im2, PP2, PP3, P and O as independent variables, and the program would test Im2 against Im1, and each of PP2 and PP3 against PP1.

Image-pair rating

Data organisation

Data from a hypothetical image-pair rating experiment are presented in Table 3. In this example, the first three rows of the data set represent a comparison between imaging methods, whereas rows 4–9 represent comparisons of post-processing methods. In total, this data set contains 216 comparisons; 72 comparisons between imaging methods and 144 comparisons between post-processing methods (still with 6 patients and 4 observers). Although not included in this simple example, it is also possible to compare image pairs that differ in both independent variables simultaneously. Image pairs, though, never represent comparisons between patients or between observers as these are not of interest to the researcher.

Table 3. Data from a hypothetical image-pair rating experiment with category label coding.

Observation no.	Im-L	Im-R	PP-L	PP-R	P	O	Score
1	Im1	Im2	PP1	PP1	P1	O1	0
2	Im1	Im2	PP2	PP2	P1	O1	1
3	Im1	Im2	PP3	PP3	P1	O1	1
4	Im1	Im1	PP1	PP2	P1	O1	−2
5	Im1	Im1	PP2	PP3	P1	O1	0
6	Im1	Im1	PP3	PP1	P1	O1	1
7	Im2	Im2	PP1	PP2	P1	O1	−2
8	Im2	Im2	PP2	PP3	P1	O1	1
9	Im2	Im2	PP3	PP1	P1	O1	1
10	Im2	Im1	PP1	PP1	P1	O2	1
11	Im2	Im1	PP2	PP2	P1	O2	0
12	Im2	Im1	PP3	PP3	P1	O2	1
13	Im1	Im1	PP2	PP1	P1	O2	1
...	...	...	...	...	...	...	...
216	Im2	Im2	PP1	PP3	P6	O4	−1

Variable names ending in -L refer to the left image in each image pair, and those in -R to the right one. The first 3 observations in the data set represent comparisons between imaging methods, whereas observations 4–9 represent comparisons of post-processing methods (PP).

Im, imaging equipment; P, patient; O, observer.

In situations with image-pair rating, it turns out that the alternative type of coding, with dummy variables, will facilitate the analysis. We therefore recommend organising the data in the style of Table 4. The difference compared with Table 2 is that the values of the numerical variables corresponding to dummy variables are no longer restricted to 0 and 1, but take the value 1 when a feature is present in only the left image, −1 when the same feature is present in only the right image and 0 when the two images do not differ with respect to the independent variable in question. For example, for observation 1, only the left image was produced with imaging equipment Im1 and only the right image with Im2; hence the variable Im1 is given the value 1 and the variable Im2 the value −1 with the dummy-style coding. Variables not occurring in the comparisons, however (in this example P and O), may still be coded with category labels.

Table 4. Data from the same image-pair rating experiment as in Table 3 with dummy-variable-like coding of factors Im and PP.

Observation no.	Im1	Im2	PP1	PP2	PP3	P	O	Score
1	1	−1	0	0	0	P1	O1	0
2	1	−1	0	0	0	P1	O1	1
3	1	−1	0	0	0	P1	O1	1
4	0	0	1	−1	0	P1	O1	−2
5	0	0	0	1	−1	P1	O1	0
6	0	0	−1	0	1	P1	O1	1
7	0	0	1	−1	0	P1	O1	−2
8	0	0	0	1	−1	P1	O1	1
9	0	0	−1	0	1	P1	O1	1
10	−1	1	0	0	0	P1	O2	1
11	−1	1	0	0	0	P1	O2	0
12	−1	1	0	0	0	P1	O2	1
...
216	0	0	1	0	−1	P6	O4	−1

Analysis

With category label coding, the equation corresponding to Equation (5) would be

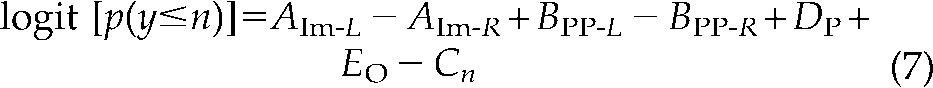Although mathematically correct, this equation is not suitable for estimating the quality of images regardless of their position (left or right). Thus, a different formalism must be sought in order to make the problem solvable with standard software.

If we instead use variables analogous to the dummy variables above, we can again apply the familiar regression given in Equation (6), the only difference being that the “dummy variables” now take the values 1, 0 and −1. This equation is easy to use with most software for ordinal logistic regression. Again, one must consider the requirement that the independent variables not be linearly dependent on each other and, after selecting reference categories, include “dummy variables” only for the other categories of each factor in the model. With the data in Table 4, we might thus specify Im2, PP2, PP3, P and O as independent variables.

For numerical reasons, the accuracy of the estimated parameter values (and thus of the significance levels obtained) may depend on the appearance of the columns containing the numerical dummy variables (in Table 4, columns 2–6), which describe the design of the experiment. How to optimally design an experiment is, however, beyond the scope of this paper. For a pedagogical introduction to that subject, see Pocock [20].

Results

Different statistical programs provide the user with varying amounts of numerical results of an ordinal logistic regression analysis. To assess the value of a logistic regression model applied to one's data, the researcher should both answer questions concerning the effect of each independent variable on the dependent variable and give some information on how well the model fits the data. Table 5 shows the result of applying the ordinal logistic regression model described by Equation (5) to the data in Table 1. In the lower part of the table, significant results of the likelihood ratio χ² test are displayed for the independent variables PP and P, but not for Im or O, i.e. in the hypothetical visual grading experiment the perceived image quality was affected by the choice of post-processing method, but not by the choice of imaging equipment.

Table 5. Result of applying the logistic regression model described by Equation (5) to the data in Table 1.

Ordinal logistic fit for score
Model	−Log Likelihood	DF	χ2	Prob>χ2
Whole model test
Difference	77.995	11	155.99	<0.0001
Full	146.207
Reduced	224.202
R2 (U)	0.3479
Observations (or sum Wgts)	144

In the upper part of the table, information is given on how well the model explains the studied data. The software chosen for this example (JMP 7.0.1; SAS, Cary, NC) gives a value of R², analogous to the result of a linear regression analysis. This measure, however, is not the only possible choice. As explained by Long and Freese in [21], a plethora of different parameters describing goodness of fit are available.

The middle part of the table contains the estimated values of the parameters included in the model, i.e. the coefficients in Equation (5). The degree of uncertainty in these estimates is indicated by the standard errors and the confidence limits in the last two columns. For each parameter, a significance test is carried out to test if the parameter differs from 0 or not. The parameter estimates can be used for interpretation of the results if one is interested in just one particular type of imaging equipment or post-processing method. In this example, the confidence intervals indicate that both PP1 and PP2 differ significantly from PP3 (the reference category), but in different directions. Most statistical software also includes methods for performing post hoc tests, i.e. tests to calculate the probability of whether the difference between the estimates is likely to be caused by chance.

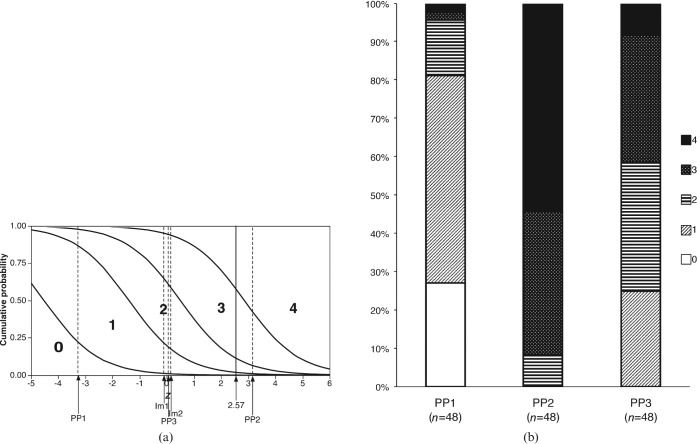
For a graphical presentation of the results, the cumulative probabilities of different outcomes, P(y≤n), predicted by the ordinal logistic model can be plotted against the linear combination of independent variables, z, which is used in the model (Figure 2a). The horizontal axis of this diagram can be thought of as a “risk score” obtained by summing “risk scores” for every factor potentially affecting the visual grading score. With the numerical example from Table 1, the imaging method Im1 was given a risk score of −0.12*, the post-processing method PP2 a risk score of 3.15, and patient P1 and observer O3 risk scores of −0.98 and 0.52, respectively. For the combination of Im1, PP2, P1 and O3, the combined risk score will thus be (−0.12 + 3.15) + (−0.98 + 0.52) = 2.57. The vertical axis represents the probability of obtaining at least a certain visual grading score, and the horizontal locations of the curves correspond to the values of the parameters C_n in Equation (5). For each value of z, i.e. for each combination of factor values, the predicted probability for a given outcome corresponds to the height between two of the curves in the graph. For the combination mentioned above, the model predicts a probability close to 0% for a visual grading score of 0, and probabilities of approximately 2%, 9%, 46% and 43% for visual scores of 1, 2, 3 and 4, respectively, as can be seen by following a vertical line above the value 2.57 on the horizontal axis. For a certain subpopulation defined by the value of some independent variable, the heights seen in the logistic regression plot can easily be compared with the empirical frequencies displayed in the bar graph in Figure 2b. For example, for the 48 observations representing the post-processing method PP1, the model predicts probabilities of approximately 26%, 56%, 14%, 3% and 0% for the visual grading scores 0, 1, 2, 3 and 4, respectively, not differing too much from the observed frequencies of 27%, 54%, 15%, 2% and 2% (see Figure 2b).

Figure 2.

(a) Graph of predicted cumulative probabilities (P(y≤n)) according to an ordinal logistic regression model applied to the single-image grading experiment in Tables 1 and 2. The dashed vertical lines represent the predictions for each of the two types of imaging equipment (Im) and the three post-processing techniques (PP), and the solid vertical line refers to a numerical example in the text. The length of every vertical line segment between two curves corresponds to the predicted probability for a particular score. (b) Observed relative frequencies of scores 0–4 for each of the three post-processing techniques.

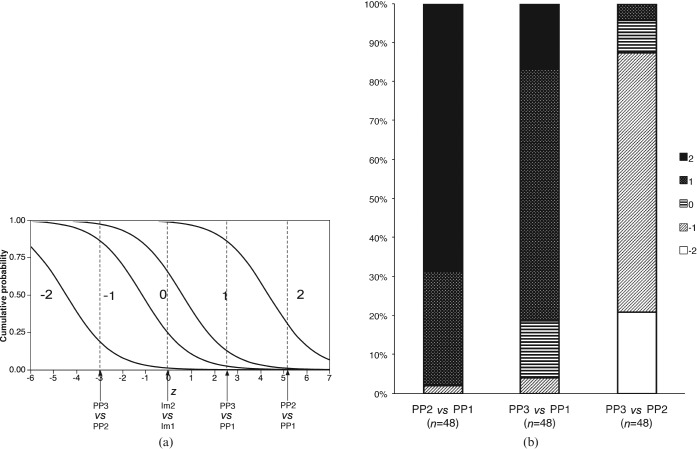
Analogous results for the image-pair data in Table 4, analysed with the model described by Equation (6), are shown in Figure 3a,b. In this case, strongly significant differences were found between all pairs of post-processing methods, but not between Im1 and Im2, and the R² for the model was 0.388.

Figure 3.

(a) Graph of predicted cumulative probabilities according to an ordinal logistic regression model applied to the image-pair grading experiment in Tables 3 and 4. The dashed vertical lines represent the predictions for each pair of imaging equipment (Im) and post-processing techniques (PP). The length of each vertical line segment between two curves corresponds to the predicted probabilities for a particular score. (b) Observed relative frequencies of scores for each pair of post-processing techniques. In cases with opposite order of the two images within the pair (left and right exchanged), the sign of the score has been inverted to ensure consistent meaning of each score.

A different way of presenting the results of a logistic regression analysis that is sometimes used is illustrated by Table 6. It indicates how each observation was actually scored, as well as what would have been the most probable scoring according to the model. It should be noted that the uncertainty inherent in the statistical model (see Figure 2a) is not reflected in this type of table.

Table 6. Observed scores vs most likely scores according to the logistic regression model applied to the data in Table 1.

	Observed score
Most likely score	0	1	2	3	4	Sum
0	2	1	0	0	0	3
1	11	26	9	0	1	47
2	0	10	9	9	0	28
3	0	1	7	18	12	38
4	0	0	2	8	18	28
Sum	13	38	27	35	31	144

The predicted score coincided with the observed score in 2 + 26 + 9 + 18 + 18 = 73 cases out of 144 (51%).

Finally, it should be noted that binary logistic regression can also be used with ordinal outcomes. The usual approach is then to create several binary variables from the ordinal variable, studying, for example, Score 0 vs 1–4 in the first analysis, Score 0–1 vs 2–4 in the second run, and so on. An example of this approach can be found in Bing et al [22].

Discussion

Although studies with an independent reference (gold standard), often using ROC methodology, are generally accepted as the most reliable way of evaluating the diagnostic value of medical imaging techniques [23], the practical difficulties associated with such studies make complementary ways of evaluating image quality indispensable. Visual grading studies are an alternative solution, simple to carry out with clinically available images and not requiring any external ground truth. But in order for these studies to gain general acceptance, the data analysis methods must be appropriate.

For analysing data from visual grading experiments, the visual grading regression (VGR) approach proposed in this paper has certain advantages. First, the ordinal nature of the grading data is correctly handled with ordinal logistic regression. This is in contrast to visual grading analysis methods treating the dependent variable as an interval variable and employing t-tests or analysis of variance. The potential bias arising from differences between individuals (patients or observers) is also taken into account in an appropriate way. Second, the models can simultaneously include several factors that might influence the perceived image quality. In addition to the choice of imaging equipment and post-processing method, a medical imaging researcher may be interested in interactions between these two factors: for images from a certain apparatus, but not for other image types, a certain type of post-processing may be most appropriate. Including interaction terms in the statistical model may solve this problem, analogous to what has been done in areas other than visual grading [24, 25]. More complete information from experiments with complex design can be obtained by expanding the model further.

The dummy variable-like coding introduced in Table 4 also makes ordinal logistic regression applicable in situations where pairs of images are compared and graded on an ordinal scale. To our knowledge, this approach has not been used before.

The regression model framework also allows for continuous independent variables. In order to study the effect of, for example, the kVp and mAs settings in radiography and CT, or of various image acquisition parameters in MRI, one can vary the relevant parameter systematically across a certain interval and then include the corresponding variable in the VGR model. To find an optimal setting, it might be advantageous to use a quadratic term rather than a linear one.

The most important assumption of the ordinal logistic model is the proportional odds assumption (or parallel regression assumption), which states that the odds predicted by the model of obtaining at most a given outcome n, i.e. P(y≤n)/(1 − P(y≤n)), is proportional to the corresponding odds for a different outcome m for all combinations of independent variables. This means, for example, that exchanging one type of imaging equipment for another will always affect the odds by multiplication with the same factor. Another way of stating this assumption is to require that the different curves in the logistic regression plot be identical except for a translation in the horizontal direction. This is in contrast to the VGC analysis [14], which assumes that there exist two underlying variables that are normally distributed. However, for our approach, the validity of the assumption can readily be tested formally [21] or illustrated graphically by comparing theoretical logistic regression plots (Figure 2a) with empirical distributions (Figure 2b). This is considerably more difficult for the unobserved variables underlying VGC.

If the main purpose of the investigation is to discriminate between, for example, some post-processing methods, the easiest way is to look at the parameter estimates. The coefficients can also easily be interpreted as odds ratios (ORs) by applying the exponential function to the parameter values. As many researchers are familiar with ORs, these might be easier to understand. For example, for PP1 vs PP3 in Table 5, an OR of exp(3.23) = 25.3 means that on the average over the 5 values of the score (the dependent variable) the OR is 25.3 for PP1 vs PP3. In this case, this indicates a dramatic difference between PP1 and PP3.

A situation that might cause a problem, however, is when the number of parameters (degrees of freedom) in the model is too great in relation to the number of observations. There is a certain risk that the flexibility of such a model will make it fit the data “too well” (overfitting), resulting in parameter estimates that will be strongly dependent on the observed data, so that minor changes to the data can result in large changes to the estimates. Statisticians usually advise against using logistic regression models when the number of parameters approaches the number of observations in the data set divided by 10 [26]. This should be borne in mind when visual grading experiments are designed. In image-pair rating experiments, the number of observations can be increased without increasing the number of parameters in the model if the same images are compared in more combinations. In studies with few observations, or where one of the score values is attained in a small number of cases, it might also be desirable to replace the standard ordinal logistic regression algorithm, which includes certain large-sample assumptions in the maximum likelihood estimation, with exact logistic regression [27].

There are also a number of methods that should be used to check problems other than overfitting regarding the validity of the model. These can be found in the manual of the statistical software used.

An alternative, non-parametric approach that has been suggested involves calculating the measure relative position (RP) based on the change of a categorical or continuous variable between two measurements [28]. The RP can have a value between −1 and 1, and it is also possible to calculate a confidence interval. This method is used in Geijer et al [10], which, however, also includes results from a linear regression model. The advantage of the RP method is that it gives a measure that is as easy to interpret as the Pearson or Spearman correlation coefficient. The method involves several computational steps, and most of them are not available in standard statistical software. The RP also shares a problem of interpretation with the correlation coefficient — whether a certain value of the estimate should be considered to be good or not is a somewhat arbitrary decision.

Practical suggestions when using the VGR approach include the following. Different software packages capable of performing ordinal logistic regression should be equally useful, including current versions of JMP (SAS), SAS (SAS), SPSS (SPSS, Chicago, IL), Stata (Stata Corp LP, College Station, TX), and Statistica (StatSoft, Tulsa, OK). For image-pair studies, the data should be organised with dummy variable-like coding of the variables for which comparisons are made (as in Table 4). When reporting the results, both results of the significance tests and information on the goodness of fit should be included. Stacked bar graphs such as Figures 2b and 3b can serve both to illustrate the fit of the theoretical model to the empirical data and to give an intuitive presentation of the strength of the relationship. This, however, presupposes a balanced experimental design, such that all subpopulations defined by one factor have the same composition in terms of the other factors included in the model. The use of agreement between predicted and observed values (see Table 6) as a measure of fit is not encouraged, as it fails to take into account the degree of uncertainty incorporated in the predicting model.

In ordinary linear least-squares regression, the most common measure of the goodness of fit is R², which is usually interpreted as the percentage of variance explained by the model, thus varying between 0 and 1. There are, however, a number of alternative interpretations, since R² can be calculated in a number of ways, all yielding the same numerical result for linear regression. The R² measure has counterparts for other generalised linear models, sometimes called “pseudo-R²”, but their interpretation is less straightforward, as various formulas for R² result in different numerical results [29]. Thus, the interpretation will depend on which formula was used, which must be specified; in some cases the result is more like a deviance measure or a squared correlation measure between the dependent and the independent variables. Despite these drawbacks, the pseudo-R² can be used as a measure when the purpose is to compare different models, e.g. when deciding whether or not to include a new variable in the model.

The model should always be reported with the relevant variables included, i.e. the variables that were the reason for carrying out the analysis; in our example, imaging equipment and post-processing method. Confounding variables, such as those identifying observers and patients, also need to be included since the model is based on repeated measures on the same observer and patient. The ideal solution would be to perform an analysis conditional on observer and patient, as can be done in binomial logistic regression [30]. Unfortunately, this option is not available for ordinal logistic regression. It is not clear whether the recently proposed technique of composite logistic regression may change this situation [31].

A general problem when fitting statistical models to data is the recommendation that the model should be created with one set of data and then tested with another data set. The data used to create the model usually give better predictions than any other data set. In the case of visual grading experiments, researchers rarely have the possibility of using more than one data set, but it should be borne in mind that the goodness-of-fit measures may give deceptively high values.

Conclusion

We have presented a framework for analysing visual grading data with ordinal logistic regression that takes into account the ordinal character of data and allows for studying several factors at once. It should be useful for a wide range of visual grading studies of image quality.