Abstract
The control of pathogen density during infections is typically assumed to be the result of a combination of resource limitation (loss of target cells that the pathogen can infect), innate immunity, and specific immunity. The contributions of these factors have been considered in acute infections, which are characterized by having a short duration. What controls the pathogen during persistent infections is less clear, and is complicated by two factors. First, specific immune responses become exhausted if they are subject to chronic stimulation. Exhaustion has been best characterized for CD8 T cell responses, and occurs through a combination of cell death and loss of functionality of surviving cells. Second, new nonexhausted T cells can immigrate from the thymus during the infection, and may play a role in the control of the infection. In this article, we formulate a partial-differential-equation model to describe the interaction between these processes, and use this model to explore how thymic influx and exhaustion might affect the ability of CD8 T cell responses to control persistent infections. We find that although thymic influx can play a critical role in the maintenance of a limited CD8 T cell response during persistent infections, this response is not sufficiently large to play a significant role in controlling the infection. In doing so, our results highlight the importance of resource limitation and innate immunity in the control of persistent infections.
Introduction
The control of pathogen within an infected host is typically assumed to be the result of a combination of resource limitation, innate immunity, and antigen-specific immunity. In the case of infections with intracellular pathogens such as viruses, resource limitation arises from the loss of cells that the pathogen is able to infect. Innate immunity arises from the rapid activation of macrophages, NK cells, and other factors in a manner that is not dependent on the specific antigens displayed by the pathogen (1,2). Antigen-specific immune responses are generated by the clonal expansion of a few pathogen-specific cells to generate a large population of cells specific for the pathogen (3).
The contributions of these mechanisms to the control of infections are a key problem that has been the focus of a number of modeling and experimental studies. Most studies have focused on the role of these factors in the control of acute infections such as influenza (which are characterized by the rapid growth of the pathogen followed by its elimination in the course of a few weeks), or the initial acute phase of persistent infections such as HIV and malaria. Although the role of all three of these factors has been widely debated in the case of influenza infections (4–6), the evidence suggests that innate immunity plays a dominant role. Both resource limitation and innate immunity have been suggested to play a key role in the initial control of murine malaria infections as this occurs before the generation of specific immunity (7–9). The initial control of HIV infections was suggested to be due to resource limitation (10), but joint experimental and modeling studies on Simian immunodeficiency virus have shown that the initial decline in virus, taking place a few weeks after infection, is due to specific immunity (11). The role of these factors for the control of persistent infections (e.g., lymphocytic choriomeningitis virus [LCMV], hepatitis C virus, and polyomavirus [PyV]), though of central importance, is largely unexplored.
What happens after the initial clonal expansion of pathogen-specific cells depends largely on whether the pathogen is cleared or not (i.e., whether the infection is acute or persistent). In the case of an acute infection, the pathogen is rapidly cleared, and is followed by the maintenance of a stable population of antigen-specific cells that characterizes immunological memory. In contrast, if the infection persists, the cells that have undergone expansion become habituated to constant stimulation by the persisting antigen in a phenomenon called immune exhaustion. Exhausted cells have deficiencies in proliferation and reduced functionality (12–14). Exhaustion has been shown to occur in the context of both CD4 and CD8 T cell as well as antibody responses (12,15–19), and has been suggested to play a key role in regulating immune responses during persistent infections and cancer (20,21). Because exhaustion has been best characterized in the context of CD8 T cell responses, we focus on the dynamics of these responses in this article.
An additional difference between acute and chronic infections is that pathogen-specific naive T cells (new cells that have not previously encountered antigen and are nonexhausted) can immigrate from the thymus during persistent infections, and these cells may play a role in the control of the infection. (The influx of new cells from the thymus does not play an important role during acute infections because the duration of these infections is short.) Recent experiments have examined the role of thymic influx during persistent infections. Vezys et al. (14) have shown that in polyoma virus infections of mice, thymic influx is necessary to maintain CD8 T cell numbers in the long-term. These authors have shown that in both PyV and LCMV during the persistent stage of infection, an influx of pathogen-specific CD8 T cells from the thymus is observed. This thymic influx of pathogen-specific naive T cells generates diversity in the CD8 population during persistent PyV infection, as the new cells are relatively functional whereas the older cells are exhausted. There is an additional feedback between pathogen density and the influx of new pathogen-specific cells. This influx from the thymus is inversely dependent on the pathogen density, because at high pathogen densities, pathogen-specific T cells will undergo deletion in the thymus.
The combination of thymic influx, antigen-dependent proliferation, and exhaustion gives rise to a complex interaction where increases in pathogen density limit thymic influx, increase T cell proliferation, and also enhance progression toward a state of exhaustion. We develop mathematical models, which incorporate these interactions and use the models to explore the dynamics of pathogen and immune cells during persistent infections. These models include clonal expansion, exhaustion, thymic influx, and thymic deletion. We show below that these factors alone result in an unstable state where fluctuations result in either clearance or decay of the T cell population. We find that pathogen-resource limitations and innate immunity, when included, provide stabilizing mechanisms for controlling pathogen density during persistent infections, and that in this situation, specific T cell responses play a minor role in controlling the pathogen.
We note that exhaustion is one of the multiple mechanisms to protect against autoimmunity as well as limiting immune pathology (22,23). Other mechanisms by which the immune system prevents the generation of T cell responses against both self and nonself-antigens include clonal deletion and clonal anergy. Clonal deletion describes the process of central tolerance in which T cells specific for antigens present on cells in the thymus are deleted during maturation (24). Anergy is a mechanism of peripheral tolerance whereby T cells that encounter specific antigen in the absence of costimulation (an indication of infection) are rendered nonfunctional (25). Exhaustion is another mechanism of peripheral tolerance that limits immune-system-mediated pathology that would occur during persistent infections.
Model
The model presented below utilizes a structured population dynamics approach with continuous structuring variable (26) to study the diversity of exhaustion levels in the population of CD8 T cells. Similar structured population models of diverse T cell populations have been used to study the effect of the Hayflick limit in persistent infections (27), the dynamics of programmed T cell responses, and differentiation between CD4 subtypes (28).
In this article, the lymphocytes we consider are cytotoxic CD8 T cells, which for brevity we refer to simply as T cells. The model used here considers T cell exhaustion as a continuous spectra. Cells have an internal variable a, which describes their exhaustion level, ranging from a = 0 for nonexhausted, to a = 1 for complete exhaustion. A similar model utilizing an internal variable for T cell exhaustion without thymic influx, was presented in Johnson et al. (29). Without thymic influx, the entire population was considered homogeneous, with all T cells having identical exhaustion level.
Because we are considering the effects of thymic influx, we must incorporate diversity in the level of exhaustion of different T cells in the model. The diversity arises from the continual influx of nonexhausted naive T cells (a = 0) from the thymus during the course of the infection, and the gradual exhaustion of these cells over time. Diversity is incorporated using a partial differential equation (PDE) with a boundary condition describing the thymic influx. Rather than have a total number of T cells described by an ordinary differential equation, the PDE describes the evolution of a density of T cells U(a,t). The density is the abundance of cells at each value of exhaustion a. The integral of this density over the range of exhaustion levels is the total number of T cells X.
The extension to a PDE (via the structured population approach (26)) consists of constructing a nonconservative advection equation. These tools give a straightforward result for our system:
| (1) |
| (2) |
A derivation of these equations, based on mechanistic considerations of PD-1 expression (a protein shown to drive T cell exhaustion), and antigen-presenting cells interacting with pathogen and CD8 T cells, is presented in the Supporting Material.
This PDE can be understood by viewing the two terms on the right-hand side of Eq. 1 separately. The term under the derivative with respect to a is the flux, describing cells changing in a, either progressing to exhaustion or recovering from it. The flow rate of the flux varies with a, and is given by
| (3) |
The second term in Eq. 1 models the birth and death of cells at a particular value of exhaustion. The effect of exhaustion in the model is the reduction of CD8 T cell proliferation rate.
The boundary condition (Eq. 2) is the flux at a = 0 that is set to equal the influx of cells from the thymus. We have included thymic deletion in this term, taking thymic influx to be a monotonically decreasing function of pathogen density P. We have used an m-order Hill function to describe this reduction in influx. This function for influx transitions from a gradual decrease with low m value, to a more threshold like function at high m.
We describe the change in the pathogen density using two terms. Because this article focuses on the role of specific immune responses on the control of persistent infections, we use a simple logistic function to describe pathogen growth. The logistic function has a carrying capacity C representing a combination of resource limitations on pathogen growth rates, and limitations due to innate immunity. See the Supporting Material for derivation and details. Clearance of pathogen by the T cell response is described by a mass-action term in which clearance is proportional to both pathogen and lymphocyte density. Taken together, we have
| (4) |
where X is the total number of T cells.
We have limited our analysis to persistent infections. These pathogens are neither latent nor sequestered in contrast to infections like Herpes virus or mycobacteria, which utilize other mechanisms to subvert the immune response. Additionally, we do not consider antigenic variation, another subversion mechanism.
Trajectories
A numerical simulation of the development of a persistent infection from the model (Eqs. 1, 2, and 4) is shown in Fig. 1 A. The numerical values of parameters used in the simulation are found in Table 1.
Figure 1.
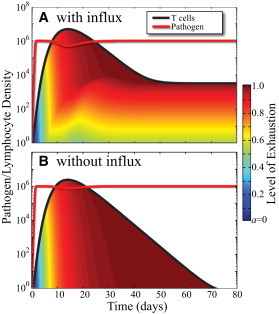
(Color online) Time series simulations of persistent infections using the model defined in Eqs. 1, 2, and 4. (Red) Pathogen P; (black) T cells X(t). The fill under the T cell curve shows the fraction of cells with a given exhaustion level, similar to a stacked bar chart. The distribution for the case with thymic influx (A) converges to the distribution shown in Fig. 2. Without thymic influx (B) the T cell population decays to zero and has very little heterogeneity at any given time. Numerical values of the model parameters used in the simulation can be found in Table 1.
Table 1.
Definition of model parameters and numerical values of the parameters used in simulations
| Parameter | Symbol | Value | Units |
|---|---|---|---|
| Pathogen growth | r | 10 | Day−1 |
| Pathogen threshold | C | 106 | Cells/μL |
| Killing | k | 10−6 | Cell/μL/cell/day |
| Stimulation coefficient | φ | 103 | Cell/μL |
| Progression rate | δ | 0.2 | Day−1 |
| T cell growth | s | 4 | Day−1 |
| T cell decay | d | 0.3 | Day−1 |
| T cell influx | α | 1 | Cells/μL/day |
| Influx coefficient | K | 104 | Cell/μL |
| Influx Hill coefficient | m | 2 | |
| Initial pathogen density | P(0) | 1 | Cell/μL |
| Initial T cells | X(0) | 1 | Cell/μL |
In Fig. 1 A, the red curve is the pathogen density P and the black curve, the T cell density X. The fill under the T cell curve shows the stacked fractions of cells with indicated exhaustion levels, blue for nonexhausted (a = 0) to red for completely exhausted (a = 1).
The simulation in Fig. 1 A shows the pathogen rapidly proliferating from the inoculating dose to the carrying capacity C. The high level of pathogen causes the T cells to rapidly progress to an exhausted phenotype (red fill) by around day 10. The system then converges to a stable, persistent infection.
The effect of thymic influx can be seen in the persisting small numbers of T cells with moderate levels of exhaustion (yellow, and orange fill). Thymic deletion reduces the influx (Eq. 2) from 1 cell/μL/day before the infection, to 1 × 10−4 cells/μL/day during the persistent phase.
Equilibrium distributions
Here we look at stationary distributions Ueq(a) for U(a,t) when P is held constant. These can be found by setting the time derivative in Eq. 1 to zero:
| (5) |
| (6) |
Solving these differential equations is aided by first solving for the flux Y(a) at equilibrium,
| (7) |
| (8) |
| (9) |
which has the solution
| (10) |
Because the only source of new cells is at a = 0, we know that above any point where Y(a) = 0, the density Ueq(a) = 0. We can see from Eq. 10 that for a > P/(ϕ + P), Ueq(a) = 0. This gives us an upper limit on exhaustion level when P remains constant:
| (11) |
This value also determines the existence of a stationary distribution. We see that if the proliferation term in Eq. 1 has a positive value at am, then cells will proliferate indefinitely and the number of T cells is not bounded. The condition for existence of a stationary distribution for Eq. 5 is therefore given by
| (12) |
This sets a discontinuous range on values of P, where a stationary solution Ueq(a) exists as
| (13) |
| (14) |
and
| (15) |
| (16) |
where the approximations are valid as s ≫ d. The interpretation of the two discontinuous regions is: for small P satisfying Eq. 13, the pathogen is not stimulating T cells to a large-enough extent to overcome the natural decay; for large P satisfying Eq. 15, the cells become so exhausted that they can no longer proliferate efficiently. In the intermediate range of pathogen values, T cells never become exhausted enough to halt proliferation and there is no bound on T cell density.
Calculating the equilibrium solution Ueq(a) from Y(a), we have
| (17) |
| (18) |
valid for P values specified by Eqs. 13 and 15 and for a ≤ P/(ϕ + P). For a > P/(ϕ + P), Ueq(a) = 0. The T Cell population in Fig. 1 A is converging to the density in Fig. 2.
Figure 2.
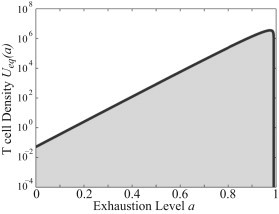
Stationary solution of Eq. 1 when P is held constant. The T cell population in Fig. 1A is converging to the density pictured here. For a > P/(ϕ + P), the density equals zero.
For some choices of parameter values, Ueq(a) can have a singularity at am (not shown). In these cases, the integral of the distribution will still remain finite. The distribution in those cases therefore remains bounded and biologically meaningful.
The total number of cells at equilibrium is also of interest to us, as it governs the pathogen killing in Eq. 4. This is found by integrating the stable distribution over the range of exhaustion levels,
| (19) |
| (20) |
where γ(…) denotes the lower incomplete gamma function defined by
| (21) |
In Fig. 3, we have plotted X (Eq. 20) as a function of P when P is held constant. Here we see that the solution only exists for P values specified by the ranges in Eqs. 13 and 15.
Figure 3.
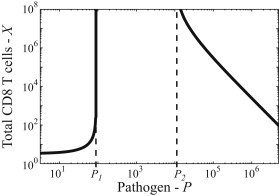
Equilibrium number of T cells given by Eq. 20 as a function of the pathogen density P, when P is held constant. For intermediate levels of pathogen, there is no equilibrium distribution as the T cells do not reach a high enough level of exhaustion and thus can proliferate without limit. High pathogen densities in the model reduce the thymic influx resulting in a decreasing number of T cells at high pathogen density.
Results
In the following subsections, we examine the consequences of this model. The model suggests that persistent infections require both T cell exhaustion and restrictions to pathogen growth (from resource limitations or innate immunity), that a stable population of T cells requires thymic influx, and that T cells do little to control the infection.
Fixed points
A persistent infection corresponds to a stable fixed point of the model described by Eqs. 1, 2, and 4. The existence of the fixed points, their values, and their dependence on the model parameters can be visualized by looking at intersections between X values given by Eq. 20 (X curve) and the nullclines (dP/dt = 0 isoclines) of Eq. 4 (P curve). The P curve is given by
| (22) |
| (23) |
To visualize the importance of factors such as T cell exhaustion and thymic influx, we have taken the α = 0 and δ = 0 limits of the model system (Eqs. 1, 2, and 4) and compared it with the full-model. The α = 0 limit describes the system with no influx while the δ = 0 limit describes T cells with no exhaustion.
In Fig. 4 we plot the P curves (dashed) and the X curves (solid) for four models: without influx or exhaustion (top left), with exhaustion but no influx (top right), with influx but no exhaustion (bottom left), and the full-model (bottom right). Stationary points of the models exist where the solid and dashed curves intersect. Stable stationary points are annotated with circles (both solid and open). The unstable stationary points (no circles) are discussed under Control of Infection, below.
Figure 4.
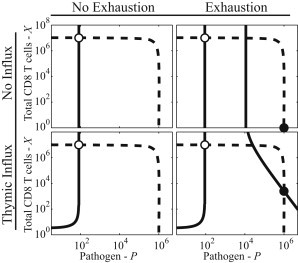
Comparison of four limits of the model: no influx and no exhaustion (top left), exhaustion but no influx (top right), influx but no exhaustion (bottom left), and the full model (bottom right). Each subplot shows the nullcline for Eq. 4 (dashed) and the total T cells at equilibrium given by Eq. 20 (solid). Stationary points exist at the intersections of the curves and stable fixed points are annotated (circle). The systems without exhaustion have no persistent state, only a stable fixed point that acute infections orbit around (open circles). The orbits of acute infections drop to values corresponding to pathogen clearance and do not typically converge to these points. The plots illustrate the requirement of exhaustion and constraints on pathogen growth (resource limitations and innate immunity) in the existence of the second stable point (solid circles). We also see the requirement of thymic influx in maintaining a population of T cells during the infection. Without resource limitations or innate immune mechanisms, the dashed curve would be a horizontal line with no persistent state.
The plots in Fig. 4 are very similar to phase-plane plots but are constructed assuming that the T cell population is at an equilibrium density for exhaustion. In reality the phase-space has a high dimensionality and this plot is presented as a reduced representation of the phase-space to visualize the requirements for fixed points.
Acute infections and the first stable point
All of the models in Fig. 4 have a stable fixed point at X ≈ r/h, P ≈ ϕd/s (see open circles). This point is characterized by high T cell density, low-exhaustion, and low-pathogen density.
This stable point is a focal point for acute infections. The trajectories of acute infections orbit around this point but are cleared when the orbits reach pathogen densities less than a single pathogen per host. Because of clearance, acute infections do not converge to this stable point.
Experimentally, it is also unlikely that this stable fixed point could be reached for typical infections. The models in this article neglect two factors known to contribute to pathogen clearance: programmed responses and stimulation by killed pathogen. These factors effectively raise s, forcing the fixed point to lower values of pathogen density that may not be biologically reasonable. We neglect these factors in our model, as they are not relevant to the dynamics of persistent infections where the programmed response is complete and live pathogen is abundant.
Recent models of HIV dynamics suggest that this stationary point may correspond to the persistent stage of HIV infection, where there is low viral load, high T cell density, and T cells play a key role in the control of the virus (30). In HIV infection the virus uses many mechanisms to subvert the immune system including downregulation of MHC molecules. This effect, combined with other feedbacks unique to HIV, may make trajectories converging to this point possible but outside the scope of this article.
Requirement of exhaustion
Models without exhaustion (Fig. 4, left column) have only acute infections, as there is no limit on T cell proliferation. When exhaustion is included in the model (Fig. 4, right column) we see that above P2 (Eq. 16), T cells are driven to a level of exhaustion where they can no longer proliferate indefinitely.
For C < P2, the carrying capacity (set by resource limitations and innate immunity) prevents pathogen from reaching a density that restricts T cell proliferation. The result of this scenario is pathogen clearance, as T cells will continue to proliferate until they clear the infection. Density-dependent effects, though unobserved, would eventually constrain T cell numbers from proliferating indefinitely. For these effects to interfere with pathogen clearance, they must act below a density of X = r/k, an unlikely scenario that we do not consider.
The value of the X curve in the case of exhaustion with no influx, is zero above P2. The consequence is that if C > P2 in the no-influx scenario, there is an additional stable fixed point at P = C, X = 0 (see Fig. 4, solid circle). This second stable fixed point in models with exhaustion (Fig. 4, right column) corresponds to a persistent infection. The time-series plots in Fig. 1 show trajectories converging toward the persistent states in Fig. 4 (note that Fig. 1 A shows the case with influx corresponding to Fig. 4, bottom right, and Fig. 1 B corresponds to the case without influx corresponding to Fig. 4, top right). Trajectories converging to this persistent state are characterized by high levels of exhaustion.
Control of infection
In Fig. 4, right column, we see that the models with exhaustion have two additional intersections between the P curves and the X curves. The first of these intersections is unstable and corresponds to a delicate balance between pathogen density and T cell number, where fluctuations cause the system to cascade toward either pathogen clearance or the elimination of the T cell population. This unstable point (in both Fig. 4, top right and bottom right) therefore does not correspond to persistent infections.
Without pathogen-resource limitations or innate immunity, the P curves in Fig. 4 would be horizontal lines. In this case, the only stationary points would be the focal points of the acute trajectories, and the unstable points. The model therefore suggests that either resource limitations or innate immunity are essential in establishment of persistent infections.
For P > P2, the X curve is monotonically decreasing. For the persistent state to exist, the P curve must converge to zero more rapidly than the X curve. This is satisfied by the logistic equation used in this article. The logistic term is derived from both a standard “target cell, infected cell, free pathogen” model and an innate immunity model in the Supporting Material. Substituting a Hill function instead of a logistic equation could also yield a persistent state if the Hill function exponent is larger than m.
The requirement of non-antigen-specific limitations on pathogen growth suggests that T cell killing alone cannot be responsible for controlling the infection. We can see from the location of the persistent states in Fig. 4, right column, that the presence of ∼500 T cell/μL is doing very little to control the infection, as the P value is not reduced by any observable amount from top right to bottom right.
T cell affinity for pathogen
Here we model the likely effects of changing the affinity of the antigen-specific immune response. In our model, we consider the stimulation coefficient φ, the killing rate k, and the influx coefficient K to be affinity-dependent, with φ decreasing with increased affinity, k increasing with increased affinity, and K decreasing with increased affinity. In Fig. 5 A, we plot the P curves and the X curves for the typical parameters and for a scenario with reduced affinity where we have increased both φ and K by a factor of 10 and reduced k by a factor of 10. These changes have essentially no effect on the value of P at equilibrium, as either innate immunity or resource limitations are controlling the pathogen at just below the carrying capacity C. Reducing the affinity results in an increase in the number of T cells at the chronic state (Fig. 5 A). It can be shown that this arises predominantly due to the increase in thymic output arising from an increase in the influx coefficient K.
Figure 5.
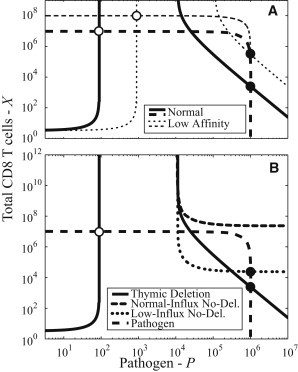
(A and B) Comparison of fixed points for different levels of immune affinity and thymic influx, respectively. (A) Reduction in the affinity of the cells of the antigen-specific immune response results in little change in pathogen load but an increase in the numbers of immune cells at the chronic state (solid circles). (B) Three cases for thymic influx: thymic deletion (solid), where thymic influx is reduced by pathogen, normal-influx no-deletion (rounded dash) where thymic influx is unaffected by pathogen, and low-influx no-deletion where thymic influx is reduced by other effects but unaffected by pathogen (dotted). The thymic deletion curve represents the result from the full model (Eqs. 1, 2, and 4). The normal-influx no-deletion has the full influx α (equivalent to setting K ≫ C). In this case, the number of T cells is great enough to clear the pathogen and there is no possibility of a persistent state. The low-influx no-deletion case shows the effect of thymic influx reduced by an effect other than the presence of pathogen such as the reduced thymic capacity associated with old age. In this case, a persistent state is possible.
Thymic influx
In comparison to the scenario with thymic influx (Fig. 1 A), the scenario without influx (Fig. 1 B) is characterized by both a decaying population and by minimal heterogeneity.To maintain a stable population, there must be an influx of new T cells replacing the ones that are decaying. This lifts the persistent state from zero T cells (Fig. 4, top right), to nonzero T cell number (Fig. 4, bottom right).
In our model we have included thymic deletion (Eq. 2), where thymic influx is reduced by the presence of pathogen. The large P asymptotic behavior of the total T cell number X in a persistent state is approximately described by
| (24) |
a power-law function. Without thymic deletion, this is reduced to a horizontal asymptote at
Fig. 5 B shows X curves for three different models of thymic influx: thymic deletion, normal-influx no-deletion, and low-influx no-deletion. The thymic deletion curve is the full-model shown in Fig. 3 that has the previously described persistent state.
The normal-influx no-deletion curve in Fig. 5 B uses the same α-value as the thymic deletion model. Here the combination of the full influx and the proliferation provides enough T cells that there can be no persistent state, and pathogen will be cleared.
The low-influx no-deletion curve in Fig. 5 B describes the case where there is no thymic deletion but the naive influx α is reduced by a factor of 1000. Here the low-influx reduces T cell numbers preventing pathogen clearance. This low-influx case is relevant to the reduced thymic capacity associated with old age and is one way that elderly are more susceptible to persistent infections.
Discussion
We have used a PDE model to explore the role of immune responses in the control of persistent infections—focusing on the CD8 T cell response. The model incorporates two key features of the T cell response during persistent infections—immune exhaustion and the continual influx of cells from the thymus. We find that although T cells may be present and capable of killing infected cells, it is unlikely that their presence does much to control the pathogen. In doing so our results highlight the importance of resource limitation and innate immunity in the control of persistent infections.
Our model prediction that the T cell response does relatively little to control the pathogen during a persistent infection corresponds well with a number of experimental observations. First, mice that are β2-microglobulin-deficient have no CD8 T cell response and have high LCMV virus density (31). Second, congenital LCMV infection also results in the lack of a T cell response to the virus and high viral loads (32,33). In both of these situations, the control of virus density despite the lack of a T cell response indicates the importance of resource limitations or innate immunity. We propose that our models could be further tested by accurate quantification of virus densities in mice with and without CD8 T cells. CD8 T cell responses can be removed in a number of ways including depletion of these cells through killing by CD8-specific antibodies, by congenital infection, and by using β2-microglobulin-deficient mice. Our model predicts that viral load will be very similar in mice with and without responding T cells.
Our model suggests that although the level of pathogen is largely independent of the T cell response, the level of immunity depends on the influx of T cells and how fast they get exhausted. We show that the number of T cells specific to the pathogen declines with increasing sensitivity—and this occurs predominantly because of increased thymic deletion. This too could be tested by comparing the numbers of T cells with different affinity for pathogen during the course of infection. We would also expect that the control of the pathogen by resource limitation or innate immunity reduces competition between the responses to different epitopes (and consequently competitive exclusion), and facilitates the maintenance of multiple responses during persistent infections.
Although we have attempted to capture the basic features of exhaustion during persistent infections, there are many details that are still poorly understood. The model should be refined as these are better understood. For example, we have used a model where exhaustion limits T cell proliferation but not T cell killing. This is based on recent results showing that exhausted T cells kill at roughly half the rate of nonexhausted T cells (34,35), a relatively small reduction compared to the logarithmic scales of T cells and pathogen. Including a reduction of killing rate k with exhaustion further reduces the already small effect of T cell control and shifts the P curves in Fig. 4 up by less than a factor of two. Thus, our conclusion that the pathogen is controlled largely by resource limitations or innate immunity is robust to this assumption.
One complication, which we have not included in this model, is the change in pattern of production of cytokines in exhausted CD8 T cells (13) as the effects are still unknown. Cytokines such as interferons secreted by CD8 T cells can alter viral dynamics. The cytokine production likely reduces the pathogen replication rate r and carrying capacity C. Including reduced cytokine secretion by exhausted cells in our model would therefore increase C and r. This would shift P curves in Fig. 5 up and to the right, increasing the range of parameters where a persistent state is possible. However, as before, our conclusion that the pathogen is controlled largely by resource limitations or innate immunity is robust to this assumption.
Models are used to reevaluate the roles of resource limitations, innate immunity, and antigen-specific immune mechanisms in the control of pathogen. The science of T cell exhaustion is still evolving and as future experimental results are obtained we expect that this model will be further fine-tuned to make additional predictions.
Acknowledgments
The authors thank the editor and reviewers for their time and careful attention, which has led to a number of improvements to the manuscript.
This work was funded by National Institutes of Health grant No. R01-AI049334 to R.A.
Footnotes
Sean Stromberg's current address is Department of Physics, University of California, Santa Barbara.
Supporting Material
References
- 1.Medzhitov R., Janeway C., Jr. Innate immunity. N. Engl. J. Med. 2000;343:338–344. doi: 10.1056/NEJM200008033430506. [DOI] [PubMed] [Google Scholar]
- 2.Antia R., Koella J.C. A model of non-specific immunity. J. Theor. Biol. 1994;168:141–150. doi: 10.1006/jtbi.1994.1094. [DOI] [PubMed] [Google Scholar]
- 3.Murphy K. Janeway’s Immunobiology. 8th Ed. Garland Science; New York: 2011. Immunobiology: the immune system. [Google Scholar]
- 4.Saenz R.A., Quinlivan M., Gog J.R. Dynamics of influenza virus infection and pathology. J. Virol. 2010;84:3974–3983. doi: 10.1128/JVI.02078-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Baccam P., Beauchemin C., Perelson A.S. Kinetics of influenza A virus infection in humans. J. Virol. 2006;80:7590–7599. doi: 10.1128/JVI.01623-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Handel A., Longini I.M., Jr., Antia R. Towards a quantitative understanding of the within-host dynamics of influenza A infections. J. R. Soc. Interface. 2010;7:35–47. doi: 10.1098/rsif.2009.0067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Barclay V.C., Råberg L., Read A.F. CD4+ T cells do not mediate within-host competition between genetically diverse malaria parasites. Proc. Biol. Sci. 2008;275:1171–1179. doi: 10.1098/rspb.2007.1713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Antia R., Yates A., de Roode J.C. The dynamics of acute malaria infections. I. Effect of the parasite’s red blood cell preference. Proc. Biol. Sci. 2008;275:1449–1458. doi: 10.1098/rspb.2008.0198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kochin B.F., Yates A.J., Antia R. On the control of acute rodent malaria infections by innate immunity. PLoS ONE. 2010;5:e10444. doi: 10.1371/journal.pone.0010444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Phillips A.N. Reduction of HIV concentration during acute infection: independence from a specific immune response. Science. 1996;271:497–499. doi: 10.1126/science.271.5248.497. [DOI] [PubMed] [Google Scholar]
- 11.Regoes R.R., Antia R., Staprans S.I. Roles of target cells and virus-specific cellular immunity in primary simian immunodeficiency virus infection. J. Virol. 2004;78:4866–4875. doi: 10.1128/JVI.78.9.4866-4875.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zajac A.J., Blattman J.N., Ahmed R. Viral immune evasion due to persistence of activated T cells without effector function. J. Exp. Med. 1998;188:2205–2213. doi: 10.1084/jem.188.12.2205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wherry E.J., Ha S.J., Ahmed R. Molecular signature of CD8+ T cell exhaustion during chronic viral infection. Immunity. 2007;27:670–684. doi: 10.1016/j.immuni.2007.09.006. [DOI] [PubMed] [Google Scholar]
- 14.Vezys V., Masopust D., Lukacher A.E. Continuous recruitment of naive T cells contributes to heterogeneity of antiviral CD8 T cells during persistent infection. J. Exp. Med. 2006;203:2263–2269. doi: 10.1084/jem.20060995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mueller S.N., Ahmed R. High antigen levels are the cause of T cell exhaustion during chronic viral infection. Proc. Natl. Acad. Sci. USA. 2009;106:8623–8628. doi: 10.1073/pnas.0809818106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Day C.L., Walker B.D. Progress in defining CD4 helper cell responses in chronic viral infections. J. Exp. Med. 2003;198:1773–1777. doi: 10.1084/jem.20031947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Day C.L., Kaufmann D.E., Walker B.D. PD-1 expression on HIV-specific T cells is associated with T-cell exhaustion and disease progression. Nature. 2006;443:350–354. doi: 10.1038/nature05115. [DOI] [PubMed] [Google Scholar]
- 18.Moir S., Ho J., Fauci A.S. Evidence for HIV-associated B cell exhaustion in a dysfunctional memory B cell compartment in HIV-infected viremic individuals. J. Exp. Med. 2008;205:1797–1805. doi: 10.1084/jem.20072683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Moir S., Fauci A.S. B cells in HIV infection and disease. Nat. Rev. Immunol. 2009;9:235–245. doi: 10.1038/nri2524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kim P.S., Ahmed R. Features of responding T cells in cancer and chronic infection. Curr. Opin. Immunol. 2010;22:223–230. doi: 10.1016/j.coi.2010.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Campbell C., Zhang R., Thakar J. Why do CD8+ T cells become indifferent to tumors: a dynamic modeling approach. Frontiers Physiol. 2011;2:32. doi: 10.3389/fphys.2011.00032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bergstrom C.T., Antia R. How do adaptive immune systems control pathogens while avoiding autoimmunity? Trends Ecol. Evol. (Amst.) 2006;21:22–28. doi: 10.1016/j.tree.2005.11.008. [DOI] [PubMed] [Google Scholar]
- 23.Sharpe A.H., Wherry E.J., Freeman G.J. The function of programmed cell death 1 and its ligands in regulating autoimmunity and infection. Nat. Immunol. 2007;8:239–245. doi: 10.1038/ni1443. [DOI] [PubMed] [Google Scholar]
- 24.Stritesky G.L., Jameson S.C., Hogquist K.A. Selection of self-reactive T cells in the thymus. Annu. Rev. Immunol. 2012;30:95–114. doi: 10.1146/annurev-immunol-020711-075035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Schwartz R.H. T cell anergy. Annu. Rev. Immunol. 2003;21:305–334. doi: 10.1146/annurev.immunol.21.120601.141110. [DOI] [PubMed] [Google Scholar]
- 26.Metz J.A.J., Diekmann O. Number 68 in Lecture Notes in Biomathematics. 1st Ed. Springer; New York: 1986. The dynamics of physiologically structured populations. [Google Scholar]
- 27.Pilyugin S., Mittler J., Antia R. Modeling T-cell proliferation: an investigation of the consequences of the Hayflick limit. J. Theor. Biol. 1997;186:117–129. doi: 10.1006/jtbi.1996.0319. [DOI] [PubMed] [Google Scholar]
- 28.Yates A., Callard R., Stark J. Combining cytokine signaling with T-β and GATA-3 regulation in Th1 and Th2 differentiation: a model for cellular decision-making. J. Theor. Biol. 2004;231:181–196. doi: 10.1016/j.jtbi.2004.06.013. [DOI] [PubMed] [Google Scholar]
- 29.Johnson P.L.F., Kochin B.F., Antia R. Vaccination alters the balance between protective immunity, exhaustion, escape, and death in chronic infections. J. Virol. 2011;85:5565–5570. doi: 10.1128/JVI.00166-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Althaus C.L., De Boer R.J. Implications of CTL-mediated killing of HIV-infected cells during the non-productive stage of infection. PLoS ONE. 2011;6:e16468. doi: 10.1371/journal.pone.0016468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Matloubian M., Concepcion R.J., Ahmed R. CD4+ T cells are required to sustain CD8+ cytotoxic T-cell responses during chronic viral infection. J. Virol. 1994;68:8056–8063. doi: 10.1128/jvi.68.12.8056-8063.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Traub E. Persistence of lymphocytic choriomeningitis virus in immune animals and its relation to immunity. J. Exp. Med. 1936;63:847–861. doi: 10.1084/jem.63.6.847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.King C.C., Jamieson B.D., Ahmed R. Viral infection of the thymus. J. Virol. 1992;66:3155–3160. doi: 10.1128/jvi.66.5.3155-3160.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ganusov V.V., Lukacher A.E., Byers A.M. Persistence of viral infection despite similar killing efficacy of antiviral CD8+ T cells during acute and chronic phases of infection. Virology. 2010;405:193–200. doi: 10.1016/j.virol.2010.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Graw F., Richter K., Regoes R.R. Comparison of cytotoxic T lymphocyte efficacy in acute and persistent lymphocytic choriomeningitis virus infection. Proc. Biol. Sci. 2011;278:3395–3402. doi: 10.1098/rspb.2011.0453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Thakar J., Poss M., Zhang R. Dynamic models of immune responses: what is the ideal level of detail? Theor. Biol. Med. Model. 2010;7:35–37. doi: 10.1186/1742-4682-7-35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.De Boer R.J., Oprea M., Perelson A.S. Recruitment times, proliferation, and apoptosis rates during the CD8+ T-cell response to lymphocytic choriomeningitis virus. J. Virol. 2001;75:10663–10669. doi: 10.1128/JVI.75.22.10663-10669.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Perelson A.S. Modeling viral and immune system dynamics. Nat. Rev. Immunol. 2002;2:28–36. doi: 10.1038/nri700. [DOI] [PubMed] [Google Scholar]
- 39.Stafford M.A., Corey L., Perelson A.S. Modeling plasma virus concentration during primary HIV infection. J. Theor. Biol. 2000;203:285–301. doi: 10.1006/jtbi.2000.1076. [DOI] [PubMed] [Google Scholar]
- 40.Nowak M.A., Bangham C.R. Population dynamics of immune responses to persistent viruses. Science. 1996;272:74–79. doi: 10.1126/science.272.5258.74. [DOI] [PubMed] [Google Scholar]
- 41.Nowak M.A., Lloyd A.L., Lifson J.D. Viral dynamics of primary viremia and antiretroviral therapy in simian immunodeficiency virus infection. J. Virol. 1997;71:7518–7525. doi: 10.1128/jvi.71.10.7518-7525.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bonhoeffer S., May R.M., Nowak M.A. Virus dynamics and drug therapy. Proc. Natl. Acad. Sci. USA. 1997;94:6971–6976. doi: 10.1073/pnas.94.13.6971. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


