Molecular Dynamics of Class A β-lactamases—Effects of Substrate Binding

Abstract

The effects of substrate binding on class A β-lactamase dynamics were studied using molecular dynamics simulations of two model enzymes; 40 100-ns trajectories of the free and substrate-bound forms of TEM-1 (with benzylpenicillin) and PSE-4 (with carbenicillin) were recorded (totaling 4.0 μs). Substrates were parameterized with the CHARMM General Force Field. In both enzymes, the Ω loop exhibits a marked flexibility increase upon substrate binding, supporting the hypothesis of substrate gating. However, specific interactions that are formed or broken in the Ω loop upon binding differ between the two enzymes: dynamics are conserved, but not specific interactions. Substrate binding also has a global structuring effect on TEM-1, but not on PSE-4. Changes in TEM-1’s normal modes show long-range effects of substrate binding on enzyme dynamics. Hydrogen bonds observed in the active site are mostly preserved upon substrate binding, and new, transient interactions are also formed. Agreement between NMR relaxation parameters and our theoretical results highlights the dynamic duality of class A β-lactamases: enzymes that are highly structured on the ps-ns timescale, with important flexibility on the μs-ms timescale in regions such as the Ω loop.

Introduction

β-lactam resistance in bacteria is realized through a variety of strategies, the most prevalent of which is the synthesis of the antibiotics-hydrolyzing β-lactamase proteins (reviewed in (1,2)). Class A β-lactamases are an extremely varied group of enzymes that includes extended-spectrum β-lactamases (3). TEM-1 and PSE-4 (Fig. 1) are two model class A β-lactamases and the focus of this work. TEM-1 is a penicillin-cleaving enzyme originating from Escherichia coli (4,5), whereas PSE-4 was discovered in opportunistic pathogen Pseudomonas aeruginosa (6) and preferentially hydrolyzes carbenicillin (CBC) (Fig. 2 A). Class A β-lactamases all share a similar structure made of two domains (one α/β and one all α, see Fig. 1) at the interface of which lies the active site (7–10) (see Fig. 3). Two conserved loops (SDN and Ω) border this site and are involved in catalysis. Five residues, S70, K73, S130, E166, and K243 (R243 in PSE-4) are involved in the two-step acylation-deacylation reaction by which the amide bond in the β-lactam ring of the antibiotics is broken. β-lactam compounds are reviewed in (11,12).

Figure 1.

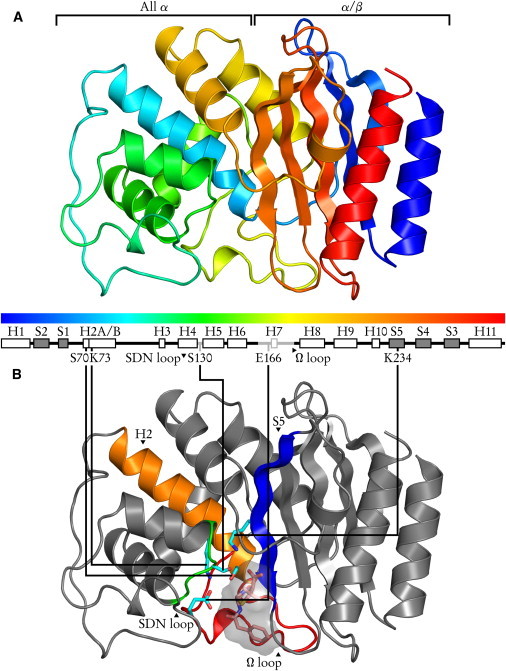
General structure of class A β-lactamases, illustrated by the TEM-1/BZP complex. (A) The N- and C-terminal sequences form the α/β domain, a five-stranded antiparallel sheet bordered by two helices. The all α domain is a bundle of six helices. (B) The active site is at the domain junction. Catalytic residues and substrate are shown as sticks, with CPK-colored atoms: cyan carbons (pink for BZP), red oxygens, blue nitrogens, yellow sulphurs. Substrate volumetric surface is shown in translucent gray. Protein elements forming the catalytic site are colored: blue for the S5 strand bearing catalytic K/R234; orange for H2 providing S70 and K73; green for the SDN loop bearing S130; red for the Ω loop with catalytic E166.

Figure 2.

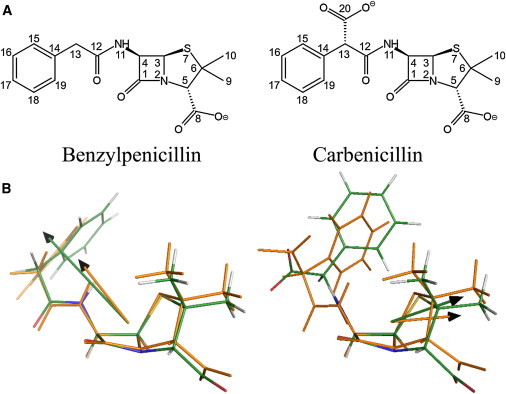
(A) BZP and CBC structures. The atom numbering used in this work is shown. (B) Comparison of BZP and CBC QM- and MM-optimized structures and dipoles after parameterization. QM-optimized structure is in orange. Atoms in MM-optimized structure are CPK-colored: green carbons, red oxygens, blue nitrogens, white hydrogens, yellow sulfurs. Arrows show dipole orientation, in orange and green for QM and MM, respectively.

Figure 3.

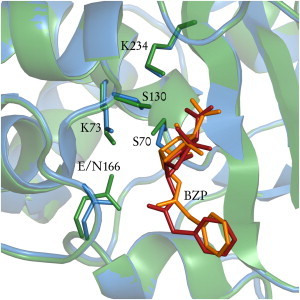
TEM-1 active site of the crystallographic structure of E166N mutant (13) and the TEM-1/BZP computational model used in this study. Catalytic side chains and substrate are shown as sticks. Carbons in the crystal structures are green; those in the theoretical model are cyan. BZP in the crystal structure is in orange; BZP theoretical model is in red.

X-ray (8–10,13–17), NMR (18,19), and theoretical (20–34) studies of the catalytic properties of TEM-1 and its variants have shaped our understanding of its serine protease-like reaction mechanism. However, all these studies assume conformations that are near those of x-ray structures. Crystal constraints and protein dynamics are therefore mostly neglected. The first molecular dynamics (MD) simulations of TEM-1 reported no flexibility on the nanosecond timescale (21,22,24) but as trajectory length increased to 5 ns, a motion bringing the E166-bearing Ω loop in contact with the protein core was first observed (23). NMR relaxation studies from our laboratory showed that both TEM-1 and PSE-4 are highly structured on the ps-ns timescale, with slower motions near the active site and in the Ω loop (18,19). Our relaxation NMR studies of PSE-4 are consistent with a flap-like motion in the Ω loop that could promote substrate gating. Complete loop desolvation was observed in another MD study where 10 5-ns trajectories were recorded (30). A more recent MD study from our laboratory characterized TEM-1 dynamics and motions in the Ω loop in more detail, using three 20-ns trajectories (31). However, none of these studies considered the effects of substrate binding, and none compared the dynamics of TEM-1 and PSE-4 except our previous NMR investigation (19). Enzyme dynamics in the bound form could extend our understanding of β-lactamase specificity and catalysis, and help the rational design of novel β-lactam antibiotics (35).

Here, we present results from a simulation study of model β-lactamases TEM-1 and PSE-4 and their preferred substrates, respectively benzylpenicillin (BZP) and CBC that were parameterized to be used with the CHARMM force field. Forty 100-ns MD trajectories were used to compare the bound and free forms of each enzyme, showing that substrate binding affects TEM-1 and PSE-4 in different ways, even though they present 41.5% sequence identity and are highly similar from a structural standpoint (1.3 Å backbone root mean-square deviation (RMSD) between the two enzymes). We highlight the structuring effect of BZP binding on TEM-1, and the increased flexibility of the Ω loop in both enzymes in the bound form. Simulation validation using NMR relaxation order parameters (S²) shows improved reproduction of protein dynamics compared to previous work (31), and particularly good agreement between experiment and simulation for PSE-4 main chain dynamics. We discuss long-timescale enzyme motions that confirm our hypothesis of dynamical duality (19) in class A β-lactamases: highly structured enzymes on the ps-ns timescale, with flexibility on the μs-ms timescale. We hypothesize that rigidity on the faster timescale allows the precise positioning of the catalytic side chains for catalysis, whereas motions on the slower timescale would facilitate substrate entry and product release, one such motion being the flap of the Ω loop associated with substrate gating.

Methods

β-lactam parameterization

BZP and CBC (Fig. 2 A) were parameterized within the context of CGenFF (CHARMM General Force Field for organic molecules) (36), version 2b5. Because β-lactam antibiotics are mimetic dipeptides, a first attempt was made at parameterizing a minimal β-lactam by analogy with existing amino acid parameters, chiefly proline (due to the disubstituted amide in the lactam cycle). However, molecular mechanics (MM)- and quantum mechanics (QM)-optimized geometries differed significantly (see Fig. S2 in the Supporting Material). We therefore introduced new atom types in CGenFF for the unique chemistry of the β-lactam ring. Subsequent parameter refinement was performed according to the suggested CGenFF protocol and philosophy to obtain transferable parameters that could be used to construct a wide variety of penicillin-like β-lactams.

The sulfur to tertiary carbon bond present in both compounds was not available in CGenFF, and had to be parameterized, using existing parameters and partial charges for carbon-sulfur bonds as reference. The two rings forming the penicillin scaffold were then fused, summing hydrogen charges into neighboring heavy atoms. Finally, benzyl and methyl substituents were added to the scaffold to make the final compounds. A comparison of MM and QM geometries and dipoles is presented in Fig. 2 B. All QM calculations were performed with Gaussian 03 (37). Detailed protocol, parameters, and force field files in CHARMM format are given in the Supporting Material.

System generation

The CHARMM (Chemistry at HARvard Molecular Mechanics) program (38), version c35, was used to build all systems. Initial coordinates were taken from crystallographic structures 1XPB (9) and 1G68 (10) for TEM-1 and PSE-4, respectively. Crystallographic waters and ions were removed. Hydrogens were added using CHARMM’s hbuild function. Initial protonation states were as in previous simulations (31), i.e., all residues have standard protonation states at pH 7.0 except the aspartic acid dyad D214 and D233 that share a proton; D214 was protonated. For PSE-4, five residues are missing from the 1G68 structure: SS at the N-terminus and QSR at the C-terminus. These were added using the internal coordinates method and then relaxed by Langevin dynamics for 5 ns, keeping the rest of the protein fixed.

For the free form, protein was then immersed in a cubic preequilibrated Ewald-compatible TIP3P (39) water box of 78 Å side. Water molecules overlapping with protein (within a distance of 2.8 Å) were removed. Three randomly chosen water molecules were replaced by sodium ions to yield neutral systems of ∼47,000 atoms.

The substrate-bound form of both TEM-1 and PSE-4 were generated using the free forms as starting points, before these systems were solvated. Substrate coordinates were taken from crystallographic structure 1FQG (13), which is the BZP acyl-enzyme intermediate in deacylation-defective TEM-1 variant E166N. This 1FQG structure was superposed on the models prepared from 1XPB and 1G68 using RMSD minimization. The resulting substrate coordinates were retained to add the β-lactam to the systems, and the internal coordinates method was used to fill in missing atom positions. The substrate and all atoms within 5 Å of it were then energy minimized for 5000 iterations of the steepest descent algorithm. All other atoms were fixed. Solvation was afterward performed as described for the free enzyme systems.

The resulting active site, for TEM-1 in complex with BZP, is shown in Fig. 3. All catalytic side chains have similar conformations in the crystallographic structure and the computational model; RMSD computed for catalytic residues and substrate (heavy atoms) is 0.15 Å, and there was no steric clash with noncatalytic residues. We used this system generation method, rather than mutating N166 back to E in the 1FQG structure, because such a protocol would have been impossible for PSE-4, for which no acyl-enzyme structure is available. The quality of the resulting TEM-1/BZP system (minimal RMSD to 1FQG and identical side-chain and substrate conformations) argue strongly for the protocol applicability to the similar PSE-4 enzyme. Another substrate-bound PSE-4 computational model Lim2001 (10) suggests an active site conformation that is identical to ours.

Molecular dynamics

NAMD (Not (just) Another Molecular Dynamics program) (40) was used for all simulations. In the first step, water energy was minimized for 5000 steps while keeping solute fixed. Initial velocities were assigned at 100 K. For each trajectory, a different seed was used when initiating the random number generator, yielding different velocity distributions. Water was relaxed for 1 ns while still keeping the solute fixed. Full system was then relaxed for another ns. Heating to 30°C (303 K) was afterward performed over 1 ns. This temperature was chosen to facilitate comparison with NMR observables recorded at that temperature (18). For each system (TEM-1, PSE-4, TEM-1/BZP, PSE-4/CBC), 10 trajectories were then recorded. The first 10 ns are considered equilibration time, followed by 100 ns production dynamics. Several trajectories were recorded, as opposed to a single longer one, both for feasibility reasons and to avoid known problems with current force fields and very long trajectories (41).

In all simulations, the CHARMM22 force field (42) with CMAP (43) was used. Simulations were performed in the NPT (constant pressure and temperature) ensemble with periodic boundary conditions. The r-RESPA integrator was used with a timestep of 2 fs for electrostatics and 1 fs for all other potentials. Electrostatics was computed by the particle mesh Ewald method, with center of mass drift removal. Van der Waals interactions were smoothed between 10 Å and the cutoff distance of 12 Å using a switching algorithm. Pair lists were computed up to 14 Å and updated at least every 10 timesteps. Langevin damping (1.0 γ coefficient) was used to maintain a constant 30°C temperature. The system was coupled to a Nosé-Hoover Langevin piston to maintain a constant one atmosphere pressure. The length of bonds between hydrogens and heavy atoms were constrained using SETTLE for bonds in water molecules, and SHAKE/RATTLE for all other bonds. No other constraint was applied to the systems, e.g., substrates remained in the active sites only because of protein/substrate interactions. Coordinates were recorded every ps.

Principal component analysis

Principal component analysis (PCA) was performed using the covariance method with the ptraj program from the Amber tools (44) package. Only heavy main-chain atoms were considered, and floppy residues were ignored: W at TEM-1 C-terminus; SSK at PSE-4 N-terminus; SQSR at PSE-4 C-terminus. All 10 production trajectories for each system (TEM-1, PSE-4, TEM-1/BZP, and PSE-4/CBC) were used for filling the covariance matrix before diagonalization.

Order parameters

The method used to obtain the S² estimates was described in detail and validated in previous work by Fisette et al. (31). Generalized squared order parameters (S²) for main peptide chain amide (NH) bonds were extracted from their local autocorrelation functions. Global tumbling was removed by a root mean-square minimizing superposition of the C_α of residues involved in α-helix and β-strand secondary structures. By doing so, a fixed reference frame was obtained where only local motions take place. The autocorrelation function $C_I\left(t\right)$ is computed for each trajectory (approximating the ensemble using the 100 ns production dynamics) for t < 10 ns, which is the order of magnitude of global tumbling in this system:

$$C_I\left(t\right)=\langle P_2\left[\mu \left(\tau \right)·\mu \left(\tau +t\right)\right]\rangle ,$$ (1)

where P₂ is the second Legendre polynomial: $P_2\left(x\right)=\left(3x^2-1\right)/2$ ; $\mu \left(\tau \right)$ and $\mu \left(\tau +t\right)$ are unit vectors describing the chemical bond orientation at times τ and $\tau +t$ in a fixed reference frame. Angle brackets $\langle \dots \rangle$ denote ensemble averaging. The generalized squared order parameter S² is the plateau value of the autocorrelation function:

$$S^2=\underset{t\to \infty }{\text{lim}}{C}_I\left(t\right).$$ (2)

See the Supporting Material in (31) for a more detailed analysis. Here, S² is estimated as C_I at $t=10\text{ns}$ for each trajectory, and then averaged over the 10 simulations; error is estimated by standard deviation. It should be noted that the time dimension here refers to correlation time, not trajectory time; the full 100 ns of each trajectory is used to compute the autocorrelation function. The choice of $t=10\text{ns}$ (comparable to the protein global tumbling) is necessary to recouple global and local slow dynamics, yielding synthetic S² that can be validated against their experimental counterparts; in NMR relaxation, motions slower than the global tumbling cannot be decoupled from the global tumbling itself, and therefore do not contribute to S².

Results and Discussion

Comparison with NMR observables

Generalized squared order parameters (S²) were computed from the trajectories presented herein and compared to previous NMR relaxation experiments on TEM-1 (18) and PSE-4 (19) and simulations of TEM-1 (31) from our group, as shown in Fig. 4 and Table 1. (Experimental values are available only for the free form.) As expected from the increased conformational space exploration realized with the present simulations, a better agreement between experimental (18) and theoretical results is observed for TEM-1 compared to previous work (31). For PSE-4, an excellent agreement between NMR (19) and simulation results is observed. The most pronounced disagreements are still located in the less ordered regions, and in the Ω loop, where many residues are associated to R_ex parameters in NMR studies, suggesting motions on the μs-ms timescale. The only other theoretical study of TEM-1 where S² were computed (from 10 5-ns trajectories) (30) exhibited a less precise agreement, although general features were similar: a highly structured enzyme with limited flexibility in the Ω loop on the ps-ns timescale.

Figure 4.

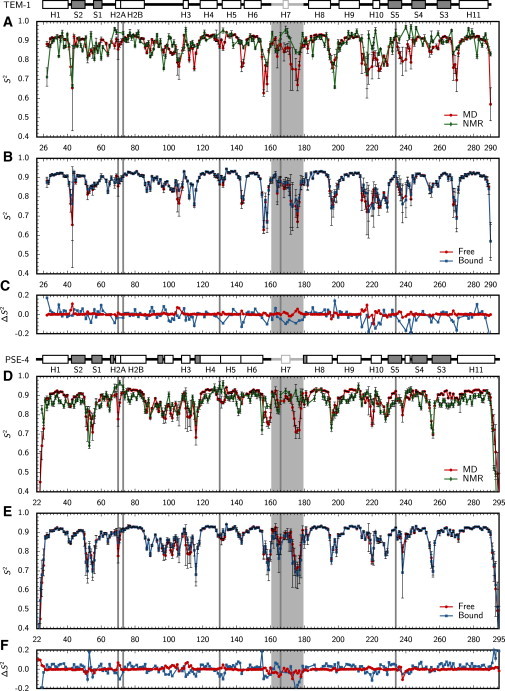
Generalized squared order parameters (S²) along sequence for amide NH bonds in peptide planes. MD-derived (red circles) and NMR relaxation (green diamonds) S² are compared for TEM-1 (A) and PSE-4 (D). Free (red circles) and substrate-bound (blue squares) S² are compared for TEM-1 (B) and PSE-4 (E). Difference between MD and NMR S² for the free form (blue squares), and for the free and bound forms (red circles) are given for TEM-1 (C) and PSE-4 (F). Catalytic residues (S70, K73, S130, E166, and K/R234) are indicated with gray lines, the Ω loop with a light gray box. Indicated above panels are TEM-1 and PSE-4 sequences: α-helices are white boxes; β-strands gray boxes; the Ω loop is in light gray; a vertical bar in H2 indicates the bend between H2A and H2B. NMR data were taken from (18) (TEM-1) and (19) (PSE-4).

Table 1.

Average S² from MD and NMR

	TEM-1			PSE-4		TEM-1/BZP	PSE-4/CBC
	MD1∗	MD2†	NMR‡	MD2†	NMR§	MD2†	MD2†
All residues¶	0.853	0.873	0.886	0.868	0.861	0.876	0.868
α-Helices	0.896	0.907	0.904	0.897	0.881	0.908	0.900
β-Strands	0.876	0.889	0.877	0.878	0.855	0.894	0.877
All loops	0.797	0.829	0.869	0.805	0.824	0.835	0.799
Ω Loop||	0.748	0.834	0.899	0.849	0.885	0.843	0.813

^∗Previous simulations from our group (31).

^†Present work.

^‡NMR relaxation from our group (18) and its reanalysis (31).

^§NMR relaxation from our group (19).

^¶Except N-terminus and prolines.

^||The Ω loop spans residues 161–179.

Substrate binding affects S² of residues in the Ω loop region of both enzymes (Fig. 4, red circles versus blue squares, and $\Delta S^2$ in panels B and D, and Table 1), an expected result given our hypothesis of substrate gating and the necessity to position E166 in a catalytically relevant position. Localized differences in S² are observed at or nearby other catalytic residues, notably S70, S130, and R234 in PSE-4. Increased R234 flexibility in the bound form is of particular interest, as the catalytic arginine has been shown to be important for the carbenicillinase activity of PSE-4 by relieving a steric clash between S130 side chain and the CBC carboxyl moiety (10). Increased flexibility in the bound form is not seen in TEM-1.

Backbone dynamics

Global RMSD for backbone atoms in all 40 trajectories remain under 2.0 Å at all times, showing simulation stability and the absence of large-scale motions such as partial unfolding (Fig. S9). Average RMSD along sequence is shown for the four different systems (TEM-1, TEM-1/BZP, PSE-4, and PSE-4/CBC) in Fig. 5. Substrate binding affects the two enzymes in different ways. TEM-1 becomes globally more rigid (1.02 Å vs. 1.16 Å), except for the C-terminal region of the Ω loop, which becomes more flexible (1.55 Å vs. 1.33 Å for residues 167–179). PSE-4 shows no global change in flexibility (1.04 Å vs. 0.99 Å), but rather an important increase in the motions of the Ω loop and nearby H6-Ω region (1.80 Å vs. 1.05 Å for the Ω loop spanning residues 161–179; 1.18 Å vs. 0.95 Å for the H6-Ω region spanning residues 143–160).

Figure 5.

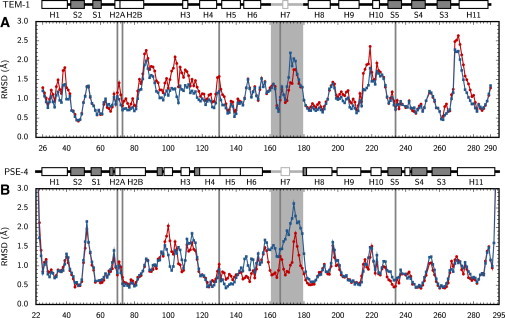
RMSD along sequence for the free (red circles and lines) and substrate-bound (blue squares and lines) forms of TEM-1 (A) and PSE-4 (B). Catalytic residues (S70, K73, S130, E166, and K/R234) are indicated with gray lines, the Ω loop with a light gray box. Above panels are TEM-1 and PSE-4 sequences: α-helices are white boxes; β-strands gray boxes; the Ω loop is in light gray; a vertical bar in H2 indicates the bend between H2A and H2B.

These differences are consistent with those seen for S² parameters (Fig. 4). However, the relative amplitude of the changes observed upon substrate binding differ depending on whether RMSD or S² are considered. This is particularly the case for the vicinity of the Ω loop, indicating that motions in this region have an important translational component. This is confirmed by observation of PCA normal modes, as discussed in the next paragraph. The translational motions that bring the Ω loop in contact with the protein core are further analyzed in the next section.

Normal modes resulting from PCA analysis of TEM-1 trajectories are shown in Movies S1 and S2. The first five principal components for free form TEM-1 (Movie S1) show the α/β and all α domains rotating and undergoing concerted deformations. The sixth eigenvector shows an independent rocking motion where the Ω loop moves back and forth between solvent and protein core. With the antibiotics in the active site, only the first principal component shows substantial concerted domain rotation/deformation, and motion amplitude is reduced compared to the free form (Movie S2). The second eigenvector in the bound form shows motions essentially limited to the Ω loop. Long-range effects on the dynamics of TEM-1 were also observed in other studies (45,46), but caused by the mutation of Y150 (near the active site) rather than by substrate binding. Substrate binding affects TEM-1 dynamics by filling the space at the domain interface, making the concerted domain rotation and deformation observed in the free form more difficult.

The case of PSE-4 is different, as illustrated in Fig. 6, which shows the first PCA normal modes for the free and bound forms of that enzyme, animated in Movies S3 and S4. Substrate binding is correlated to an increase in flexibility in the whole H6-Ω loop region, and a decrease in the H2-H3 interregion. However, there is no global rigidification in PSE-4 as in TEM-1 because the higher flexibility in the region spanning H6 to the C-terminal portion of the Ω loop (inclusively) compensates for the structuring effect of substrate binding at the domain interface. PCA results show that motions in the Ω loop are independent from those in the rest of the structure, and make up most of the observed protein dynamics, driving eigenvectors 1, 3, and 4 in the bound form; concerted domain rotation and deformation appear in later normal modes. By contrast, in the free form, the Ω loop is not involved at all in the first eigenvector. Rather, the most important motions are to be found in the H2-H3 loop. (Motions in the solvent-exposed S1-S2 linker, eigenvector 2, are observed in both the free and bound forms. These will not be discussed because that region is not relevant for catalysis.)

Figure 6.

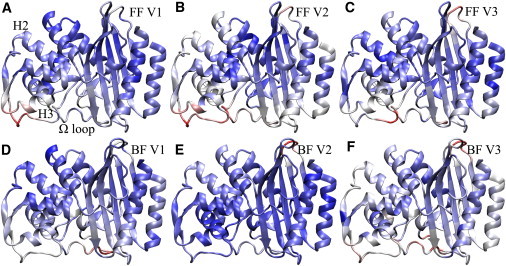
Residues involved in the first three PSE-4 normal modes in the free and ligand-bound enzyme. FF: free form; BF: bound form; V: eigenvector number. Residues are colored on a scale from blue to red according to their amplitude of motion within the eigenvector; blue means little amplitude and red high amplitude. The Ω loop and helices H2 and H3 are indicated in the first panel.

The first, nanosecond-length simulations of TEM-1 (21,22,24) suggested a rigid enzyme with little motion in the vicinity of the Ω loop. This was contradicted shortly afterward by a 5 ns simulation (23), that suggested a rapid motion in the Ω loop, which made contact with the protein core after only 1 ns. Longer simulations (50 ns total) studying desolvation of the Ω loop (30) did not reproduce these results; although an open-close motion was seen in the Ω loop, its timescale was slower than the nanosecond. No significant tethering of the Ω loop to the protein core was observed in 60 ns in a previous work by our group (31), although the Ω loop was shown to be mobile. As the available simulations lengthen and conformational space sampling increases (21,23,30,31), it became apparent that class A β-lactamase residues are highly structured on the ps-ns timescale, but that Ω loop motions happen on the μs-ms timescale, as indicated by the presence of R_ex parameters in NMR relaxation. Dynamic duality was first proposed in an NMR study of PSE-4 from our group (19), and is consistent both with the current work and our previous NMR observations of TEM-1 dynamics (18).

It should be noted that equilibrium on the μs-ms timescale cannot be assessed from the current simulations that total 1 μs for each system. Equilibrium on the ps-ns timescale is evident from stable RMSD (see Fig. S9), however, and because the TEM-1/BZP starting structure is similar to that of the acyl-enzyme intermediate, it is unlikely that system equilibration would be responsible for the increased flexibility.

Ω loop flexibility

The Ω loop is stabilized by a number of hydrogen bonds and salt bridges established both between residues inside the loop and between residues inside and outside of it. Most of these were first described from crystallographic structures (8,10), whereas others were seen only in simulation studies (23,31). These polar interactions are indexed in Table 2. Fig. 7 presents timeseries of key interactions whose prevalence change in the substrate-bound form for at least one of the two enzymes.

Table 2.

Polar contacts stabilizing the Ω loop

TEM-1∗				PSE-4†
R43	Nη	N175	Oδ (31)	No homologous interaction
R65	Nη	N175	OC‡	R65	Nη	G175	OC‡
R65	Nη	N175	Oδ	No homologous interaction
F66	NH	T181	OC	F66	NH	T181	OC
R161	NH	T180	OC	R161	NH	T180	OC‡
R161	Nε	H158	OC	R161	Nε	K158	OC
R161	Nε	D163	Oδ	R161	Nε	D163	Oδ
R164	Nε	D179	Oδ‡	R164	Nε	D179	Oδ
R164	Nη	E171	Oε‡	R164	Nη	E171	Oε‡
N175	NH	R65	OC‡ (23)	G175	NH	R65	OC‡ (23)
R178	Nε	D176	Oδ	R178	Nε	D176	Oδ‡
T181	NH	F66	OC	T181	NH	F66	OC

^∗First seen in TEM-1 structure (8) unless noted otherwise.

^†First seen in PSE-4 structure (10) unless noted otherwise.

^‡Impacted by substrate binding (see main text).

Figure 7.

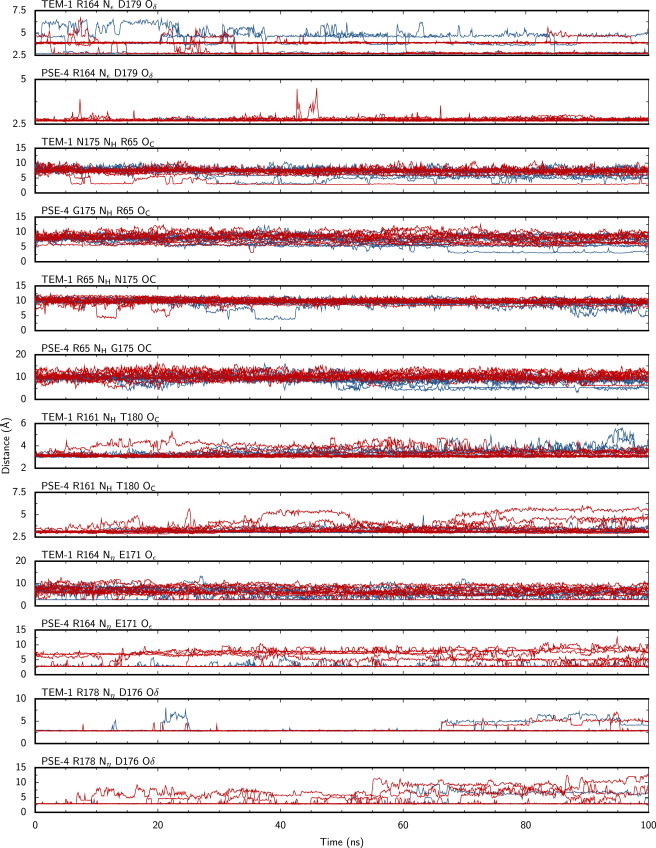
Timeseries of key interactions stabilizing the Ω loop in TEM-1 and PSE-4. Each graph shows all 10 simulations of the free enzyme (red lines) and the substrate-bound form (blue lines). Data points are 10 ps apart and averaged over that time period (10 values).

The intra-Ω loop R164 N_ε–D179 O_δ salt bridge is present in both free TEM-1 (8) and E166Q acyl-enzyme (13) structures. We observe here that substrate binding favors its disruption for TEM-1, but not PSE-4. In free TEM-1, the bridge interconverts between two conformations, where interacting atoms are separated by either 2.5 Å or 3.7 Å. In the bound form, these two conformations are still visited, but larger distances are also observed, where the salt bridge is no longer present. Because these residues are at the extremities of the 161–179 spanning Ω loop, disrupting this salt bridge makes the hinge of the loop more flexible. The homolog interaction in PSE-4 is not affected by substrate binding. It might be that it is not required in PSE-4 due to the aforementioned increased flexibility of the H6-Ω loop region that compensates by making the Ω loop even more flexible in PSE-4 than in TEM-1.

The N/G175 N_H–R65 O_C H-bond has been of particular interest in many dynamics studies of TEM-1. In previous simulations, we did not observe this interaction (31). Here, we observe it in three trajectories, where the Ω loop becomes tethered to the protein core. Two are for the substrate-bound form, one for the free enzyme; the interaction is observed in TEM-1 and PSE-4. Once formed, the H-bond is extremely stable: in two cases, it lasts for the remainder of the trajectory (73 and 34 ns); in the third simulation, the bonds last 16 ns before the loop moves back toward the solvent. Because this is a rare event, the current simulations do not allow a statistically accurate assessment of the timescale of the motion. However, we can rule out the hypotheses of an Ω loop that is either rigid or flexible on the tens of ns timescale. Our current view of the Ω loop, in the light of this work and our previous NMR investigations, is that large-scale motions (loop translation) happen on a timescale exceeding 100 ns (NMR R_ex parameters suggest the μs-ms). This is consistent with substrate gating, possibly by a flap-like behavior. These motions are also critical in positioning catalytic E166.

In contrast, some interactions are stabilized by substrate binding. This is the case of R164 N_η–E171 O_ε in both enzymes, and R178 N_η–D176 O_δ and R161 N_H–T180 O_C in PSE-4. The increased occupancy of these salt bridges augments the internal rigidity of the Ω loop when the substrate is bound to the β-lactamase. This is consistent with our PCA analysis of the Ω loop presented in the next two paragraphs: upon substrate binding, the Ω loop not only exhibits increased motions, but these motions are more focused, less random.

A precise description of Ω loop motions is difficult from PCA of complete TEM-1 and PSE-4 proteins, because the eigenvectors resulting from this analysis show correlated motions for the whole backbone. A separate PCA focusing only on the Ω loop (residues 161–179) was therefore performed. Normal modes 1 to 3 are shown for both enzymes in Fig. 8. TEM-1 Ω loop first eigenvector shows a sweeping, left-to-right motion (considering a reference frame where the observer faces the Ω loop as in Fig. 1). The second normal mode is an up-and-down motion mainly affecting the C-terminal portion of the loop, and allowing the tethering of the loop to the protein core as described previously. In the third normal mode, the Ω loop moves horizontally; the N-terminal portion is again less affected. PSE-4 shows similar normal modes, but their order of importance is different. In PSE-4, the first eigenvector is similar to TEM-1’s second. The second vector is similar to TEM-1’s first, but with an important difference: the motion also affects the N-terminal portion of the loop. This is consistent with the previously discussed S² parameters. PSE-4 third normal mode is identical to the corresponding mode in TEM-1.

Figure 8.

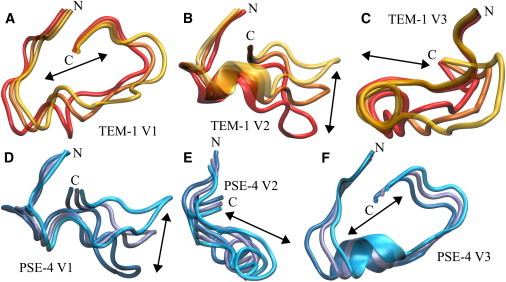
Normal modes of the Ω loop (residues 161–179). In each normal mode, the average and extremum structures are shown in different colors. Arrow indicates average direction of motion. A, B, and C are the three first eigenvector for TEM-1 Ω loop. D, E, and F are the three first eigenvectors for PSE-4. In this figure, vectors for enzyme free forms are illustrated; normal modes for bound forms are similar (refer to discussion in main text). The relative amounts of motion represented by the eigenvectors are: TEM-1 free form: 26%, 17%, 12%; TEM-1-bound form: 33%, 28%, 19%; PSE-4 free form: 24%, 14%, 8%; PSE-4 bound form: 39%, 30%, 15%.

Interestingly, normal modes for the bound and free forms are similar, for both TEM-1 and PSE-4. The increase in flexibility observed on substrate binding rather results in the relative importance of the first normal modes. In TEM-1 free enzyme, modes 1 to 3 account for 55% of the Ω loop motions; in the bound form, they represent 80% of motions. A similar tendency is observed in PSE-4, where normal modes 1 to 3 encompass only 47% of all motions in the free form, but 84% in the enzyme-substrate complex. The increase in flexibility shown in S², and caused by the destabilization of certain hydrogen bonds in the loop, manifests itself as an increase in the amplitude and relative importance of motions that translate and, to a lesser extent, distort the loop. For both enzymes, eigenvectors 4 and later comprise smaller scale motions. There is more motion in the Ω loop upon substrate binding, but that motion is less random, more focused in the first eigenvectors.

RMSD, S², and PCA analysis show that motions in the Ω loop are similar in TEM-1 and PSE-4: the loop is subjected to a translation along three axes, and substrate binding further focuses motions along those axes. This increased loop flexibility is tied to the destabilization of some interactions, and the establishment of new, transient ones. However, Fig. 7 clearly shows that different salt bridges and H-bonds are affected by substrate binding in TEM-1 and PSE-4; protein dynamics are conserved, even though specific interactions are not.

Side-chain dynamics in the active site

β-Lactam substrates BZP and CBC exhibit similar dynamics in the active site of TEM-1 and PSE-4 (respectively). Both molecules are very rigid, with no angle or dihedral angle having an accessible range of >20°, with the exception of an unconstrained rotation around the C₁₂–C₁₃ bond, present only in BZP/TEM-1 (see Fig. 2 for substrate structure and atom numbering). In PSE-4, this rotation is absent because the CBC-specific carboxyl moeity establishes an intramolecular salt bridge with nearby amide hydrogen H₁₁. This strong interaction makes CBC less flexible than BZP, and brings it away from the Ω loop. This partially explains the difference in Ω loop flexibility between TEM-1 and PSE-4.

In the free enzyme, the active site maintains its high rigidity through a network of hydrogen bonds involving the catalytic residue side chains. This was previously observed in free TEM-1 simulations (31), and sampled exhaustively for both TEM-1 and PSE-4 in this work. Key polar interactions, along with their average occupancy in the trajectories, are indexed in Table 3.

Table 3.

Key side-chain interactions in the active site

Donor		Acceptor		Occupancy (%)∗
				TEM-1		PSE-4
				Free	Bound	Free	Bound
S70	Oγ	BZP/CBC	O1	–	6 (10)	–	50 (22)
S70	Oγ	BZP/CBC	O8	–	43 (31)	–	3 (6)
S70	Oγ	S130	Oγ	8 (4)	6 (6)	1 (1)	0
S70	Oγ	E166	Oε	3 (9)	18 (30)	23 (34)	5 (13)
K73	Nζ	S70	Oγ	69 (30)	63 (39)	55 (27)	86 (16)
K/R234	Nζ/η	S70	Oγ	12 (15)	15 (20)	35 (16)	0
K73	Nζ	S130	Oγ	1 (6)	14 (18)	23 (33)	0
K73	Nζ	N132	Oδ	55 (30)	86 (14)	47 (37)	87 (21)
K73	Nζ	E166	Oε	98 (4)	97 (3)	96 (3)	99 (2)
S130	Oγ	BZP/CBC	O8	–	63 (27)	–	73 (17)
K/R234	Nζ/η	S130	Oγ	84 (18)	51 (33)	77 (33)	Â 98 (21)
N170	Nδ	E166	Oε	60 (25)	75 (23)	88 (11)	82 (30)
K/R234	Nζ/η	BZP/CBC	O8	–	51 (34)	–	39 (11)
K/R234	Nζ/η	S70	OC	27 (20)	43 (14)	54 (26)	30 (19)
K/R234	Nζ/η	I/M127	OC	38 (25)	10 (15)	35 (14)	48 (10)
K/R234	Nζ/η	D/N214	Oδ	23 (17)	8 (10)	93 (13)	90 (5)
K/R234	Nζ/η	S235	OC	38 (25)	82 (14)	13 (9)	69 (19)

Standard deviation between trajectories given in parentheses.

^∗Given a 3.0 Å cutoff distance.

Substrate insertion in the active site allows the formation of new interactions. These are also listed in Table 3 and described here. Fig. 9 shows the active site with bound substrate for both TEM-1 and PSE-4, illustrating these interactions. The amide oxygen in the β-lactam ring (O₁) is stabilized in PSE-4 by transient H-bonding with a catalytic S70 side chain. Interactions with the carboxyl oxygens substituted to the five-membered ring (O_8,1/2) are key to substrate stabilization. Three catalytic residues in TEM-1, and two in PSE-4, are linked through strong salt bridges to one of these oxygens. In both enzymes, S130 and K/R234 establish salt bridges. S70, on the other hand, only makes contact with the carboxyl in TEM-1, as it is already involved in O₁ stabilization in PSE-4 (discussed previously). These new interactions are consistent with the observed dynamics in the vicinity of active site residues: an increase in S² parameters accompanies substrate binding for S70, S130, and K/R234 in both enzymes.

Figure 9.

Substrate-bound active site for TEM-1/BZP (A) and PSE-4/CBC (B). Heavy substrate and catalytic side-chain atoms are shown as sticks and CPK-colored, with cyan (substrate) or pink (residues) carbons. Protein elements forming the catalytic site are colored: blue for S5 strand (K/R234); orange for H2 (S70, K73); green for the SDN loop (S130); red for the Ω loop (E166). H-bonds between catalytic residues and substrate are shown as white lines, as is the intrasubstrate H-bond in CBC. Stereo figure: left pairs are wall-eyed; right pairs cross-eyed.

Interestingly, substrate binding does not break the hydrogen bond network observed in the free enzymes. On the contrary, some interactions have increased occupancy in the bound forms (see Table 3). This effect is particularly important for K/R234 N_ζ/η binding to S235 O_C. Substrate binding therefore has a structuring effect on the active site, as it allows the establishment of new interactions without impacting existing ones. Of particular interest is S70 side-chain dynamics. In PSE-4, the catalytic serine mostly interacts with the carbonyl moeity in the active site, as expected. However, for TEM-1, the side chain can flip, and spends 43% of its time in a position where it interacts with BZP O_8,1/2 rather than the carbonyl. This conformation may be important for serine activation. Involvement of the carboxyl oxygen (and S130) in S70 deprotonation has been suggested before (20), although it is not the prevalent hypothesis in recent QM/MM studies (25,29).

High standard deviations in Table 3 indicate important variability between trajectories for some interactions. This is an expected result given our hypothesis of dynamic duality in β-lactamases on the μs-ms timescale in and near the active site. Because the current trajectories total 1 μs per system, insufficient statistical sampling on that timescale leads to the observed variability. It can be hypothesized that most of these interactions can be divided into two categories: those associated with small trajectory variability form and break on the ns timescale, while those associated with high standard deviations are involved in motions on the slower, μ-ms timescale.

Some class A β-lactamases (including TEM-1) have been shown to operate at the diffusion limit for their preferred substrates (47). Dynamic duality may be an important strategy for an enzyme to achieve diffusion-limited speeds. It is a reasonable assumption that the chemistry leading to substrate cleaving makes up only a small part of the catalytic cycle of these β-lactamases; most of the time is spent for substrate diffusion toward the active site, substrate recognition, and product ejection from the active site. With this in mind, rigidity on the ps-ns timescale where chemistry takes place allows a precise, optimal positioning of the catalytic residues. On the other hand, μs-ms motions correspond to the recognition part of the catalytic cycle, accelerating substrate entry and product ejection thanks to the flap-like motion of the Ω loop. Although the present simulations do not allow determining if the Ω loop is involved in both substrate entry and product release, involving gating in both events does seem like an optimal strategy. A certain plasticity in the active site on the μs-ms timescale would favor the recognition of a broad variety of substrates.

Conclusion

Using extensive MD simulations, we have shown that substrate binding has long-range effects on the dynamics of class A β-lactamases, and that these effects are different for TEM-1 and PSE-4. TEM-1 becomes globally more rigid, whereas PSE-4 shows increased flexibility in the H6-Ω loop region. In both enzyme-substrate complexes, the Ω loop shows increased translational motions along well-defined axes, and less random motion than in the free form. This reinforces the hypothesis of substrate gating. Because different Ω-loop-stabilizing polar interactions are influenced by substrate binding in TEM-1 and PSE-4, we conclude that the particular dynamical behavior of the Ω loop is possibly a conserved feature of class A β-lactamases, even though specific interactions are not. Stable contacts between the Ω loop and the protein core are shown to happen on the μs-ms timescale, and observed here in only three of the 40 trajectories that total 4.0 μs of simulation. This is consistent with the hypothesis of a dynamical duality in class A β-lactamases: catalysis-related motions on the fast, ps-ns timescale; substrate recognition, and gating motions on the slow, μs-ms timescale. Accelerated MD techniques are a possible venue for characterizing the timescale of these motions and the free energy profile of the Ω loop flap more precisely.

Comparison with NMR observables shows that 1.0 μs of simulation time is adequate to accurately reproduce protein dynamics, except for the Ω loop region. Unfortunately, no NMR S² is available in the literature for a substrate-bound class A β-lactamase. This is partially due to experimental difficulties, as it is impossible to saturate diffusion-limited enzymes such as TEM-1 with their preferred substrate for the duration of the relaxation experiments. Nevertheless, NMR measurements with β-lactamase inhibitor-complexed enzymes would further our understanding of these enzyme’s dynamics. With simulations now routinely exceeding 100 ns, and the possibility of using accelerated MD techniques for further exploring the role of the Ω loop, residual dipolar coupling order parameters or relaxation dispersion experiments, in particular, would provide additional insights into μs-ms dynamics, with the caveat that using inhibitors may influence dynamics differently than the conventional substrate.

The differing behavior of the catalytic serine in TEM-1 and PSE-4 shows that active site dynamics vary between the penicillin- and CBC-cleaving enzymes. The important conformational space sampling achieved here provides interesting starting points for QM/MM studies that would take into account important dynamic events, such as Ω loop position. Finally, parameterization of the penicillin scaffold makes a variety of antibiotics amenable to simulation, facilitating the study of substrate specificity in class A β-lactamases.