Bayesian Inference of Signaling Network Topology in a Cancer Cell Line

Abstract

Motivation: Protein signaling networks play a key role in cellular function, and their dysregulation is central to many diseases, including cancer. To shed light on signaling network topology in specific contexts, such as cancer, requires interrogation of multiple proteins through time and statistical approaches to make inferences regarding network structure.

Results: In this study, we use dynamic Bayesian networks to make inferences regarding network structure and thereby generate testable hypotheses. We incorporate existing biology using informative network priors, weighted objectively by an empirical Bayes approach, and exploit a connection between variable selection and network inference to enable exact calculation of posterior probabilities of interest. The approach is computationally efficient and essentially free of user-set tuning parameters. Results on data where the true, underlying network is known place the approach favorably relative to existing approaches. We apply these methods to reverse-phase protein array time-course data from a breast cancer cell line (MDA-MB-468) to predict signaling links that we independently validate using targeted inhibition. The methods proposed offer a general approach by which to elucidate molecular networks specific to biological context, including, but not limited to, human cancers.

Availability: http://mukherjeelab.nki.nl/DBN (code and data).

Contact: s.hill@nki.nl; gmills@mdanderson.org; s.mukherjee@nki.nl

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Protein signaling plays a central role in diverse cellular functions, and aberrations in signaling are implicated in almost every aspect of cancer biology. Indeed, an emerging literature suggests that signaling networks may be ‘rewired’ in specific contexts, including cancer (Lee et al., 2012; Pawson and Warner, 2007). That is, the network may differ in a cancer cell compared with a normal cell, for example due to genetic alterations. Yet the manner in which genomic alterations in specific cancers are manifested at the level of signaling networks is not currently well understood.

Elucidating signaling networks in a data-driven manner, specific to a context of interest (such as a cell line or tissue type), requires the ability to probe post-translational modification states in multiple proteins through time and across samples. However, proteomic analyses on this scale remain challenging.

At the same time, the modeling of signaling connectivity poses statistical challenges. Noise, both intrinsic and experimental, is ubiquitous in this setting and network components may interact in a complex, non-linear manner. Candidate networks may differ with respect to model dimension, which in turn means that analyses that do not account for this run the risk of preferring networks that are over-complex, yet not predictive. This makes the trade-off between fit-to-data and model parsimony a crucial one in network modeling.

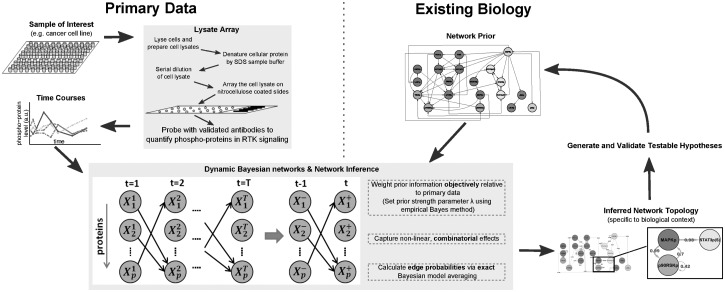
In this article, we present a data-driven approach to the characterization of context-specific signaling networks (Fig. 1). We exploit reverse-phase protein array technology (Tibes et al., 2006) to interrogate dynamic signaling responses in a defined set of 20 phospho-proteins. We use directed graphical models known as dynamic Bayesian networks (DBNs) (Friedman et al., 1998; Murphy, 2002), to probabilistically describe relationships between variables. DBNs have previously been applied to gene expression data for inference of gene regulatory networks (Husmeier, 2003; Rau et al., 2010), but to the best of our knowledge have not been applied to inference of protein signaling networks. Static Bayesian networks (BNs) have previously been employed to infer both protein signaling networks (Ciaccio et al., 2010; Mukherjee and Speed, 2008; Sachs et al., 2005) and gene regulatory networks (Friedman et al., 2000), but unlike DBNs, do not incorporate an explicit time element.

Fig. 1.

Data-driven characterization of signaling networks. Reverse-phase protein arrays interrogate signaling dynamics in samples of interest. Network structure is inferred using DBNs, with primary phospho-proteomic data integrated with existing biology, using informative priors objectively weighted by an empirical Bayes approach. Edge probabilities then allow the generation and prioritization of hypotheses for experimental validation

We perform inference regarding network topology within a Bayesian framework, with existing signaling biology incorporated through an informative prior distribution on networks (following Werhli and Husmeier (2007); Mukherjee and Speed (2008), see Fig. 1). Model averaging over network structures is used to score network features (Madigan et al., 1995), highlighting those links that are common to many, relatively high-scoring topologies. The calculations required for model averaging are performed exactly. This is done by exploiting a connection between variable selection and network inference (Murphy, 2002), echoing work in undirected graphical models (Meinshausen and Bühlmann, 2006).

An empirical Bayes approach is used to objectively weight the contribution of the prior relative to proteomic data. This is related to the approach proposed by Werhli and Husmeier (2007) in which full Bayesian inference for the prior weighting is performed using Markov chain Monte Carlo (MCMC). We perform a simpler maximum marginal likelihood empirical Bayes analysis, but do so within an exact framework that is computationally fast at the moderate data dimensions that are typical of phospho-proteomic data.

We follow recent work (Grzegorczyk and Husmeier, 2011; Rau et al., 2010) in using a continuous formulation, thereby avoiding lossy thresholding of data. We use a variant of the Bayesian prior known as the ‘g-prior’ (Zellner, 1986) to obtain a closed-form score (marginal likelihood) for the networks; in contrast to the widely used ‘BGe’ score (Geiger and Heckerman, 1994) this gives an analysis that is essentially free of user-set parameters and invariant to data rescaling. Further, we permit interactions between parents through product terms.

A number of authors, including Sachs et al. (2005) and Bender et al. (2010) , have used statistical approaches to explore signaling network topology; this article is in this vein. However, we note that statistical network inference approaches typically use linear models that are a coarse approximation to the underlying chemical kinetics. When network topology is known, ordinary differential equations (ODEs) offer a powerful framework for modeling signaling. Our work complements ODE-based approaches by providing a tractable way to explore large spaces of candidate network topologies in a data-driven manner. In principle, statistical network inference can be explicitly based on biochemically plausible ODE models. However, due to severe computational constraints such approaches are currently limited to investigating only a handful of hypothesized networks (Xu et al., 2010) and not the large number of possible networks considered here. A recent study (Bender et al., 2010) also proposes a method for inference of cancer signaling networks from reverse-phase protein array time-series data after external perturbation of network components. This work is similar in spirit, but differs methodologically in that it uses DBNs, Bayesian model averaging, and network priors to incorporate existing biological knowledge.

Thus, we combine protein array technology with dynamic network inference to shed light on signaling networks in samples of interest. We apply these approaches to the breast cancer cell line MDA-MB-468. MDA-MB-468 is an adenocarcinoma, originally from a 51-year-old patient, belonging to the well-characterized basal breast cancer subtype (Neve et al., 2006); the line is EGFR amplified and PTEN, RB1, SMAD4 and p53 mutant. We learn a network model that is specific to this line; focusing on an individual cell line allows us to generate hypotheses that are coupled to a specific well-defined genomic context and are readily testable. We predict a number of known and unexpected signaling links which we validate using independent inhibition experiments.

2 METHODS

We use DBNs to model signaling networks (Fig. 1). In this section, we describe the models and inferential approach used. A full technical description is presented in Supplementary Text; further details can be found in Hill (2012) , while related regression methodology is discussed in Hill et al. (2012). All computations were performed in MATLAB R2009a.

2.1 Dynamic Bayesian networks

DBNs (Murphy, 2002) are a type of statistical model for time-varying data, in which dependence between variables is described by a directed graph. The nodes of the graph represent variables under study and the edges represent probabilistic relationships between the variables. DBNs can be regarded as static BNs ‘unrolled’ through time, with each variable now represented at multiple time points (Fig. 1 and Supplementary Fig. S1). DBNs are capable of modeling feedback loops whereas, since the graphs must be acyclic, BNs are unable to do so (Supplementary Fig. S1). Further, when edges are restricted to be forwards in time only, the network structure of a DBN is fully identifiable. This is in contrast to BNs, for which graph structures are identifiable only up to certain equivalence classes.

In the present setting, the graph represents a signaling network and its topology is the object of inference. Let p denote number of proteins under study and T denote number of time points sampled. DBNs associate a random variable with each of the p components at each time point. Let these pT variables be denoted by 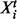. To facilitate inference over large spaces of candidate network structures, we make several simplifying assumptions. Following Friedman et al. (1998) and Husmeier (2003) , we make (first-order) Markov and stationarity assumptions: each variable at a given time is conditioned only on variables at the previous time point, with the conditional probability distribution being time independent. Moreover, this first-order dependence may be sparse, with each component at time t depending on only a subset of components at time t–1. The sparsity pattern is described by the edge structure of the network and the above assumptions result in this structure being fixed in time. This results in a relatively simple, parsimonious model in which a graph G, with two vertices for each protein, representing adjacent time points, is sufficient to describe the pattern of dependence (Fig. 1). Following related work in gene regulatory networks (Husmeier, 2003; Rau et al., 2010), we permit only edges forward in time. This guarantees acyclicity of G, removing the need for computationally expensive acyclicity checks during inference and facilitating exact inference as described below.

The DBN graph G permits factorization of the ‘global’ joint probability distribution over all variables (the likelihood) into a product of ‘local’ conditional distributions,

(1)

where X denotes the complete data, 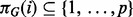is the set of parents of protein i in graph G, 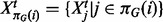is a corresponding data vector including only those variables in 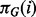and 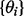are parameters that fully define the conditional distributions. (We note that the marginal distributions 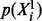are suppressed in Equation (1) because they do not depend on G.)

2.2 Network learning

We take a Bayesian approach to inference regarding graph G, focusing on the posterior distribution over graphs 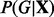. From Bayes’ rule, we have 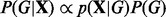. The term 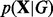is the marginal likelihood and the term P(G) is a prior distribution over graphs that allows for the incorporation of existing signaling biology into inference (‘network prior’).

2.2.1 Marginal likelihood

The marginal likelihood is obtained by integrating out model parameters 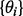from the likelihood (Equation (1)). This has the effect of accounting for model complexity by penalizing complex models with many parameters and thereby helps to avoid over-fitting of the model to the data (Denison et al., 2002). The conditionals 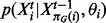constituting the likelihood are taken to be Gaussian. These describe the dependence of child nodes on their parents and can be thought of as regression models, with parents and child corresponding to covariates and response, respectively. We take these ‘local’ models to be linear-in-the-parameters, but allow interactions through products of parents; that is, we allow dependence on products of parents as well as parents themselves. The models are fully saturated, including products of distinct parents up to all parents. For example, if 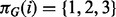then the mean for variable 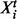is a linear combination of the three parents 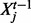, the three possible pairwise products of parents 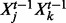and the product of all parents 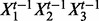. For each protein i, let 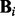denote a design matrix, with columns corresponding to each parent of i, and products of distinct parents up to and including the product over all parents.

The regression coefficients, forming a vector 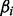, and variance 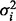, constitute parameters 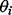. Following Kohn et al. (2001) , we use the reference prior 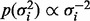for variances and a 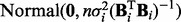prior for regression coefficients, where n is sample size. For the model above, if we have m time courses each consisting of T time points, then n = m(T – 1). Following Geiger and Heckerman (1994) , we assume prior parameter independence. Then, integrating out parameters yields the following closed-form marginal likelihood:

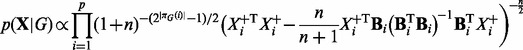(2)

where .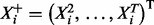

This formulation has attractive invariance properties under rescaling of the data (for details, see Kohn et al. 2001) and, in contrast to the widely used ‘BGe’ score (Geiger and Heckerman, 1994), has no free, user-set parameters. However, we note that it requires inversion of matrix 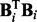, which is not guaranteed to be invertible or well-conditioned, especially when graph in-degree 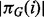is large and n relatively small. In this work, a restriction on in-degree (see below) helps to avoid these numerical issues. However, if necessary, conditioning of 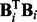is improved by ridge regularization. In our experiments below, regularization is invoked only for the combination of interaction terms with larger parent set sizes; see Supplementary Text for further details.

2.2.2 Network prior and empirical Bayes

We follow Mukherjee and Speed (2008) and use a prior of the form 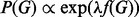, where 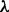is a strength parameter, weighting the contribution of the prior, and f(G) is a real-valued function over graphs, scoring the degree to which graphs concord with our prior beliefs. We use available signaling maps, obtained from online resources and the literature, to define a set of a priori expected edges E* and let 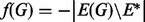, where E(G) is the set of edges contained in G. That is, f(G) is the number of edges in G that are not included in our expected edge set E*. Therefore, our prior does not actively promote any particular edge, but rather penalizes unusual edges (see also Section 4). We set the prior strength parameter 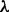using an objective, empirical Bayes approach. Specifically, this is done by empirically maximizing the quantity 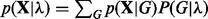, which can be done efficiently within the exact inference framework used here (see below and Supplementary Text for further details).

2.2.3 Exact inference by variable selection

We are interested in calculating posterior probabilities of edges e = (a, b) in the graph G. The posterior probability of the edge is an average over the space of all possible graphs G (Madigan et al., 1995),

(3)

where 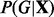is the posterior distribution over graphs.

For DBNs with p vertices in each time slice, the size of the graph space is 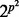, hence growing super-exponentially with p. This precludes explicit enumeration of the sum in Equation (3) for even small-to-moderate p. However, since the DBNs used here have only edges forward in time and are therefore guaranteed to be acyclic, we can exploit a connection between network inference and variable selection (Murphy, 2002) for efficient and exact calculation of posterior edge probabilities. In brief (full details appear in Supplementary Text), instead of averaging over full graphs G as in Equation (3), we consider the simpler problem of variable selection for each protein. That is, for each protein i, we score subsets of potential parents 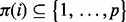. Model averaging is then performed in the variable selection sense, i.e. by averaging over subsets of parents rather than over full graphs. If the network prior P(G) factorizes into a product of local priors over parents sets 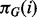for each variable, then posterior edge probabilities calculated by averaging over parent sets equal those calculated by averaging over the (much larger) space of graphs. (We note that, while this equivalence holds for edge probabilities, it does not hold for arbitrary graph features.)

Motivated by the fact that typically only a small number of key upstream regulators are likely to be critical for any given signaling component, and following related work in gene regulation (Husmeier, 2003), we enforce a maximum in-degree constraint and only consider up to 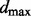proteins jointly influencing a target. The size of the space of parent sets then becomes polynomial in p, enabling exact calculation of posterior edge probabilities. For the experiments reported below, we set 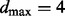. Results reported below agreed closely with both an increased maximum in-degree of 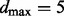and the results of MCMC-based inference with no restriction on in-degree (Supplementary Fig. S2), showing that results did not depend on the in-degree restriction.

3 RESULTS

3.1 Simulation study

A simulation study was performed using 20 proteins, 8 time points and 4 complete time courses per protein (this mimicked the biological study reported below). Data-generating graphs were created using a random, Erdös-Renyi-like approach configured to ensure that the graphs differed substantially from the prior graph used (for each graph 10 out of total 30 edges were not in the prior graph, while the prior graph had 54 edges not in the data-generating graph). Data were generated from a given graph by ancestral sampling (through time), using a Gaussian model with interaction terms. Full details appear in Supplementary Text.

Knowledge of the true data-generating graph allowed us to construct average receiver-operating characteristic (ROC) curves from inferred posterior edge probabilities (Fig. 2). Along with network inference for DBNs, as described above (‘DBN, network prior, +int’ in Fig. 2), we also show results using DBNs without interaction terms (‘−int’) and/or with a flat prior over graphs (‘flat prior’); baseline correlational analysis (thresholded absolute correlation coefficients between variables at adjacent time points; ‘correlations’); variable selection through 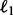-penalized regression (‘Lasso’; Tibshirani, 1996); and several previously proposed network inference approaches for time-course data [including Gaussian graphical models (‘GGMs’; Opgen-Rhein and Strimmer, 2006], a non-Bayesian DBN approach [‘DBN (non-Bayesian)’; Lèbre, 2009] and a non-parametric Bayesian approach using Gaussian processes (‘Gaussian processes’; Äijö and Lähdesmäki, 2009); see Supplementary Text for full details]. Average area under the ROC curve (AUCSD) for DBN inference with informative and flat priors were 0.930.03 and 0.840.05, respectively (Supplementary Fig. S4). The network prior provides gains in sensitivity and specificity, even though by design of the simulation experiment there is non-trivial disagreement between the data-generating and prior graphs.

Fig. 2.

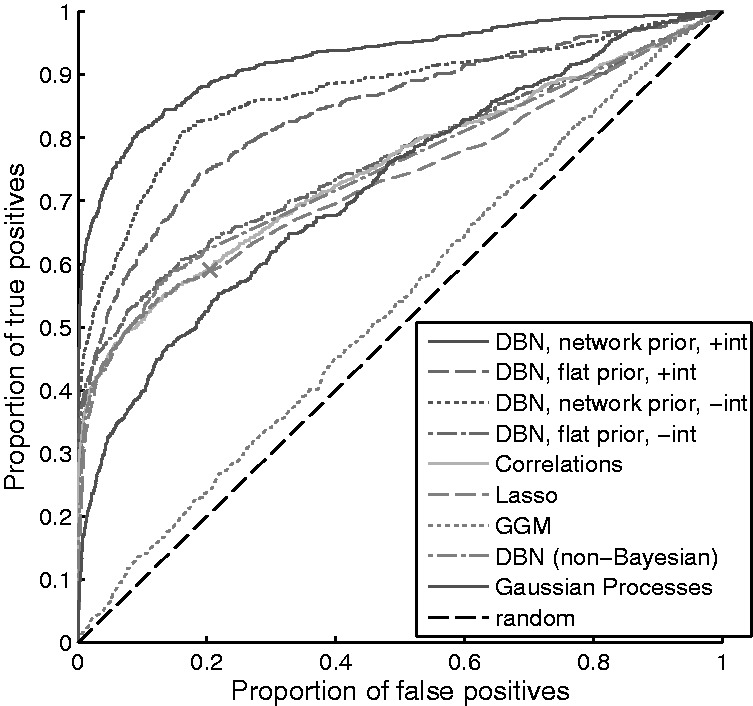
Simulation study. Average ROC curves. True-positive rate (for network edges) plotted against false-positive rate across a range of edge probability thresholds. Simulated data were generated from known graph structures by ancestral sampling. Graph structures were created to be in only partial agreement with the network prior (Supplementary Fig. S3). Results shown are averages obtained from 25 iterations. See text for full details of simulation and for description of methods shown. (For ‘Lasso’, curve produced by thresholding absolute regression coefficients, while marker ‘X’ is single graph obtained by taking non-zero coefficients to be edges)

3.2 Synthetic yeast network study

Ancestral sampling above can be viewed as simulating from a discretized system of linear ODEs. However, linear ODEs are a crude approximation to real biological systems, motivating further validation using either non-linear ODE simulations or, ideally, real data. We took the latter approach, using a recent biological system due to Cantone et al. (2009). Cantone et al. constructed a gene regulatory network in yeast, comprising five genes and six regulatory interactions, and obtained time-course expression data from the synthetic system. Since the true network is known by design, network inference performance can be directly assessed; we applied this approach here. In order to investigate the effect of including prior information, we formed prior graphs that only partially agreed with the true network (see Supplementary Text for full details).

Table 1 shows AUC scores obtained for the same methods appearing in Figure 2. The network prior leads to gains despite differing substantially from the true network. We also see that inclusion of interaction terms yields improved performance. Only the Gaussian processes method performs comparably to the proposed DBN approach, but it is more computationally intensive (DBN: 1.5 s; Gaussian processes: 160 s).

Table 1.

Synthetic yeast network study. Inference methods assessed on time-series gene expression data generated from a synthetically constructed gene regulatory network in yeast (Cantone et al., 2009). Results shown are area under the ROC curve (AUC). See text for description of methods shown. [The regimes using a network prior are mean AUCSD over 25 prior network structures. Prior networks were generated to be in partial agreement with the true, underlying network structure (see text for details).]

Method	AUC
DBN, network prior, +int	0.82 ± 0.04
DBN, flat prior, +int	0.75
DBN, network prior, −int	0.74 ± 0.04
DBN, flat prior, −int	0.67
Correlations	0.39
Lasso	0.50
GGM	0.44
DBN (non-Bayesian)	0.43
Gaussian processes	0.75

3.3 Network model for breast cancer cell line MDA-MB-468

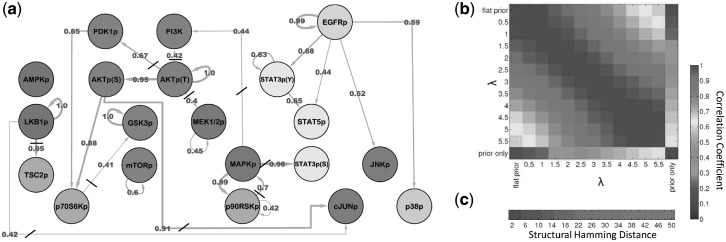
We used DBNs to model network topology using a combination of proteomic data, from cell line MDA-MB-468, and existing knowledge of signaling topology, incorporated using an informative prior distribution over network structures. Time courses were performed at eight time points, under four growth conditions, for 20 phospho-proteins. The network prior is shown in Supplementary Figure S3 (see Supplementary Text for full details of experimental protocol and biological information encoded in the prior). Empirical Bayes selection of the prior strength resulted in a value of 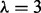(Supplementary Fig. S5). Figure 3a shows the inferred network.

Fig. 3.

Data-driven signaling topology in the breast cancer cell line MDA-MB-468. Reverse-phase protein arrays were used to interrogate the phospho-proteins shown in (a), including key components of AKT, MAPK and STAT pathways, through time. DBNs were used to integrate the data with a network prior, derived from existing biology (Supplementary Fig. S3). Prior strength 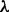was set objectively using an empirical Bayes approach, resulting in 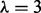(see text and Supplementary Fig. S5). (a) Edges represent probabilistic relationships between proteins, through time. Edge labels indicate corresponding (posterior) probabilities (calculated exactly; edge thickness proportional to probability; all edges with probability 0.4 shown; strikethroughs ‘/’ indicate edges not expected under the network prior; Supplementary Figure S6 shows heatmap of all 400 posterior edge probabilities; list of proteins (and antibodies) given in Supplementary Table S1). (b) Sensitivity to prior strength. Results were compared over a range of values of 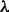plus the flat prior (i.e. 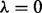) and prior only. Heatmap shows Pearson correlations between edge probabilities for pairs of prior regimes. Results were not sensitive to precise value of 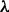and differed markedly from prior alone. (c) Sensitivity to prior graph. The prior graph was perturbed and results obtained compared with those reported (see Supplementary Text for details). Correlation (as in (b)) is shown as a function of number of edge changes in the prior graph (‘Structural Hamming Distance’, see Supplementary Fig. S7 for error bars)

3.3.1 Robustness analysis

We investigated the robustness of results reported to specification of the network prior (Fig. 3b and c). We investigated changes to prior strength 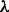by comparing results over various 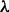values, plus prior alone (i.e. no data; with 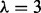) and data alone (i.e. flat prior). Results using various values of 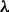differed somewhat from data alone and markedly from prior alone suggesting that inference did not simply recapitulate the prior but rather integrated prior and data. Robustness to specification of the prior graph was investigated by perturbing the prior graph and comparing inferred posterior edge probabilities to those reported above (see Supplementary Text for details). Results were robust to changes in the prior graph: e.g. changing one-third of the edges (25 out of 74 edges; ‘Structural Hamming Distance’ equal to 50) gave edge probabilities that showed a correlation of 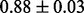with those reported (mean Pearson correlation SD; calculated from 25 perturbed prior graphs). We also found that results were not overly sensitive to data perturbation and that the sparse models learned satisfied predictive checks; see Supplementary Text and Figure S8.

3.3.2 Experimental validation

Many of the edges inferred recapitulate previously described (direct and indirect) links (including MAPK 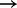p90RSKp and AKT 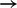p70S6Kp). A number of other edges were unexpected. We experimentally tested some of these predictions by inhibitor approaches. Edges were selected on the basis of posterior probability, biological interest and availability of selective inhibitors by which to perform validation experiments.

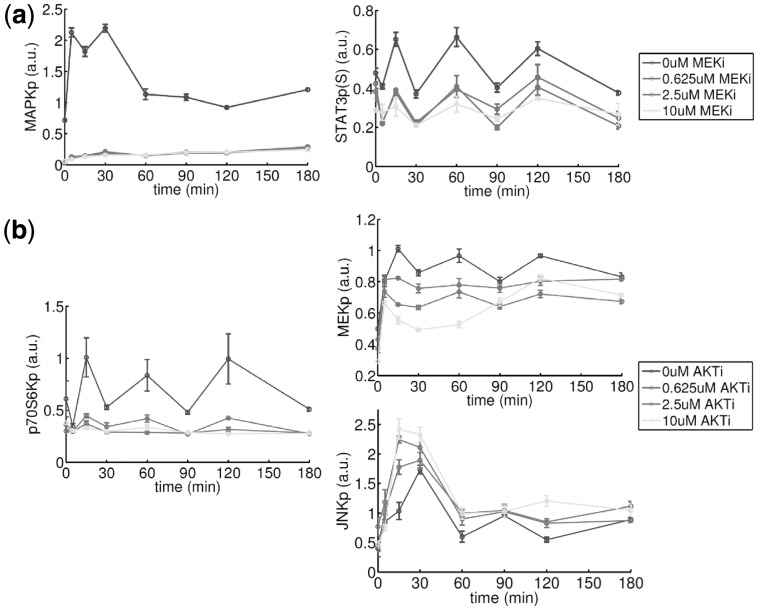
The edge MAPKp 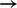STAT3p(S727) appears with a high posterior probability of 0.98. This suggests the possibility of crosstalk between the MAPK and JAK/STAT pathways. To investigate this link, we used a MEK inhibitor (MEKi) and monitored the response of MAPKp and STAT3p(S727) (Fig. 4a). Inhibition successfully reduced MAPK phosphorylation (paired t-test comparing the average difference between the 0 uM and 10 uM time courses gave P-value 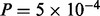; all P-values reported below were calculated in an analogous manner): since MAPK is directly downstream of MEK, this showed that the inhibitor was effective. Moreover, in line with model predictions, we observed a corresponding decrease in STAT3p(S727) (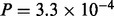). We note that the MEK to MAPK link does not appear in the inferred model; the MEKi data reported here suggest this is a false negative.

Fig. 4.

Validation of predictions by targeted inhibition in breast cancer cell line MDA-MB-468. (a) MAPK-STAT3 crosstalk. Network inference (Fig. 3a) predicted an unexpected link between phospho-MAPK (MAPKp) and STAT3p(S727) in the breast cancer cell line MDA-MB-468. The hypothesis of MAPK-STAT3 crosstalk was tested by MEK inhibition: this successfully reduced MAPK phosphorylation and resulted in a corresponding decrease in STAT3p(S727). (b) AKTp 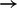p70S6Kp, AKT-MAPK crosstalk and AKT-JNK/JUN crosstalk. AKTp is linked to p70S6kp, MEKp and cJUNp. In line with these model predictions, use of an AKT inhibitor reduced both p70S6K and MEK phosphorylation and increased JNK phosphorylation. (RPPA data; MEK inhibitor GSK1120212 and AKT inhibitor GSK690693B at 0 uM, 0.625 uM, 2.5 uM and 10 uM; measurements taken 0, 5, 15, 30, 60, 90, 120 and 180 min after EGF stimulation; average values over 3 replicates shown, error bars indicate SEM)

The network model predicts a previously described edge AKTp 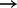p70S6Kp and, of greater interest, two unexpected links AKTp 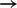MEKp and AKTp 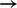cJUNp. The former suggests possible crosstalk between the AKT and MAPK pathways, and the latter suggests crosstalk between the AKT and JNK/JUN pathways. We tested these links using an AKT inhibitor (AKTi; Fig. 4b). Phosphorylation of p70S6K was reduced by AKTi (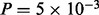), validating the edge predicted (and verifying the effect of the inhibitor). We also observe a clear decrease in MEKp levels P = 1.8 × 10⁻³) and an increase in JNKp levels (P = 0.047). Furthermore, we see dose dependence, with the effects changing monotonically with dose of the inhibitor. This provides independent evidence in favor of the existence of crosstalk in both cases (JNK is known to be directly upstream of cJUN).

4 DISCUSSION

Network inference in general, and model averaging in particular, are often viewed as computationally burdensome. Certainly, this can often be the case (e.g. for static BNs with many nodes). However, for the DBNs employed here, using the approaches described above, network inference is relatively efficient and, for datasets of moderate dimensionality, arguably fast enough for routine exploratory use. For example, empirical Bayes analysis and inference of posterior edge probabilities for the 20 variables in our cancer study took under 20 s (on a standard single-core personal computer).

We took account of known signaling biology by means of a prior distribution on networks, weighted objectively using empirical Bayes. The use of a prior incorporates existing knowledge in a ‘soft’ probabilistic manner that can be over-ridden by data. In contrast to hard constraints, this does not preclude discovery of unexpected edges. This is an important feature in the cancer setting since cancer-specific networks may be rewired and therefore differ from the general biology upon which the prior is built. Indeed, the network model yielded unexpected links that were validated by targeted inhibition. We verified empirically that results reported were not overly sensitive to prior specification or data perturbation.

The network prior employed here is asymmetric in the sense that it only penalizes edges that are not in the prior network (‘unexpected edges’). This is motivated by the observation that for context-specific networks and data obtained under specific growth conditions (as is the case here) some edges in a prior network based on canonical signaling may not be relevant, e.g. some pathways may simply be inactive due to experimental conditions or rewiring. In contrast, due to structural specificity, entirely novel kinase–substrate pairs are arguably less likely to arise. Werhli and Husmeier (2008) propose a more general prior with two hyperparameters controlling penalization of unexpected edges and non-edges, respectively. Applying this prior to the cancer data, using empirical Bayes to set both hyperparameters, we found that the hyperparameter for unexpected non-edges was set to zero, reducing the prior to the asymmetric form used in this work (and hence giving identical results).

Approximate inference methods such as MCMC are often used for inference in BNs and DBNs (Husmeier, 2003; Madigan et al., 1995). In contrast, we used a variable selection approach and sparsity constraints to calculate posterior edge probabilities exactly, thereby removing Monte Carlo uncertainty (and the need for associated diagnostics). The exact approach also facilitates the empirical Bayes analysis. In high dimensions, where the exact approach becomes intractable, the fully Bayesian MCMC approach proposed in Werhli and Husmeier (2007) can be used to sample from the joint posterior over networks and hyperparameters. The variable selection approach we describe also provides benefits for model averaging with MCMC-based inference since it factorizes the problem and also allows computations to be trivially run in parallel.

Prior specification for Bayesian variable selection remains an active research area (Casella et al., 2009; Forte Deltell, 2011). The parameter prior employed here (a form of the g-prior) has benefits but can suffer from matrix ill-conditioning. This issue was not prominent in this work due to the use of in-degree constraints. Alternative priors that do not suffer from ill-conditioning, such as standard shrinkage priors or the ‘BGe’ prior, could also be used within our formulation.

The DBN model in this work makes a widely used assumption of homogeneity of parameters and network structure through time. However, these assumptions are likely to be unrealistic for cellular protein signaling. The softening of these homogeneity assumptions can lead to a rapid increase in numbers of parameters and/or the size of graph space, resulting in statistical (and computational) challenges. Recently, non-homogeneous DBN methods have been proposed in the literature that aim to ameliorate these effects (Grzegorczyk and Husmeier, 2011; Robinson and Hartemink, 2010).

We predicted and validated unexpected links, suggesting existence of crosstalk between signaling pathways, as well as links that have been previously well documented. These results suggest that statistical approaches can usefully integrate proteomic data with existing knowledge to infer signaling networks that are context-specific; here, specific to an individual breast cancer cell line. Our results are a first step toward characterization of signaling network topologies in individual cancers. By applying these approaches to many individual cancers, we could probe signaling heterogeneity across, and even within, cancer subtypes, and thereby shed light on therapeutic heterogeneity.

At present it is not possible to assay any more than a (usually small) subset of proteins involved in signaling. Therefore, data-driven studies of signaling confront a severe missing variable problem. This necessarily limits causal or mechanistic interpretation of results. For example, an inferred edge from one protein to another may operate through one or more unmeasured intermediates, and the same caveat applies also to validation by inhibition. Statistical models that permit the inclusion of unobserved, latent variables may help, but network inference with latent variables remains challenging (Knowles and Ghahramani, 2011). Thus, unexpected links uncovered by network modeling require further biochemical work to clarify the mechanisms involved.

The sheer complexity of cancer signaling is daunting and this work is only a first step in the direction of network models that are context-specific. In addition to the points raised above, important directions for future work include, among others: experimental design, including adaptive selection of treatments that are informative with respect to network topology; improved, systematic high-throughput validation and incorporation of explicit chemical kinetics into large-scale network inference.