Recoupling of chemical shift anisotropy by R-symmetry sequences in magic angle spinning NMR spectroscopy

Abstract

¹³C and ¹⁵N chemical shift (CS) interaction is a sensitive probe of structure and dynamics in a wide variety of biological and inorganic systems, and in the recent years several magic angle spinning NMR approaches have emerged for residue-specific measurements of chemical shift anisotropy (CSA) tensors in uniformly and sparsely enriched proteins. All of the currently existing methods are applicable to slow and moderate magic angle spinning (MAS) regime, i.e., MAS frequencies below 20 kHz. With the advent of fast and ultrafast MAS probes capable of spinning frequencies of 40–100 kHz, and with the superior resolution and sensitivity attained at such high frequencies, development of CSA recoupling techniques working under such conditions is necessary. In this work, we present a family of R-symmetry based pulse sequences for recoupling of ¹³C/¹⁵N CSA interactions that work well in both natural abundance and isotopically enriched systems. We demonstrate that efficient recoupling of either first-rank (σ₁) or second-rank (σ₂) spatial components of CSA interaction is attained with appropriately chosen γ-encoded RN_n^v symmetry sequences. The advantage of these γ-encoded RN_n^v-symmetry based CSA (RNCSA) recoupling schemes is that they are suitable for CSA recoupling under a wide range of MAS frequencies, including fast MAS regime. Comprehensive analysis of the recoupling properties of these RN_n^v symmetry sequences reveals that the σ₁-CSA recoupling symmetry sequences exhibit large scaling factors; however, the partial homonuclear dipolar Hamiltonian components are symmetry allowed, which makes this family of sequences suitable for CSA measurements in systems with weak homonuclear dipolar interactions. On the other hand, the γ-encoded symmetry sequences for σ₂-CSA recoupling have smaller scaling factors but they efficiently suppress the homonuclear dipole-dipole interactions. Therefore, the latter family of sequences is applicable for measurements of CSA parameters in systems with strong homonuclear dipolar couplings, such as uniformly-¹³C labeled biological solids. We demonstrate RNCSA NMR experiments and numerical simulations establishing the utility of this approach to the measurements of ¹³C and ¹⁵N CSA parameters in model compounds, [¹⁵N]-N-acetyl-valine (NAV), [U-¹³C, ¹⁵N]-alanine, [U-¹³C,¹⁵N]-histidine, and present the application of this approach to [U-¹³C/¹⁵N]-Tyr labeled C-terminal domain of HIV-1 CA protein.

INTRODUCTION

Orientation-dependent spin interactions in nuclear magnetic resonance (NMR), such as chemical shift anisotropy (CSA), bear a wealth of information about molecular structure and dynamics.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13} Even though select non-isotropic properties of chemical shift tensors can be obtained through solution-state NMR approaches, solid-state NMR spectroscopy is far more suitable for deriving the anisotropic information.¹⁴ In solids, CSA can be directly measured by recording powder patterns in static powder samples, but these experiments suffer from poor sensitivity, spectral overlap when multiple chemical sites are present, and from broadening and distortion to the CSA line shapes introduced by homonuclear dipolar couplings. Under magic angle spinning (MAS), the CSA interactions are averaged out provided sufficiently high spinning frequencies, giving rise to highly resolved isotropic spectra. Numerous methods have been developed to reintroduce the anisotropic chemical shift interactions in the indirect dimensions under MAS conditions.^{15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32} For most of these recoupling methods, determination of the CSA parameters requires analysis of the spinning sideband patterns^{16, 21, 23, 26, 27, 28, 29, 31, 32} or powder patterns,^{15, 17, 18, 19, 20, 22, 24, 25, 30} and usually periodic radio frequency (rf) field irradiation is applied in synchrony with the MAS sample rotation during the evolution period. In these recoupling techniques, the required rf field strengths are generally so high that, in practice, these sequences are only applicable under low or moderate MAS conditions. In addition, since homonuclear dipole-dipole interactions cannot be suppressed efficiently, most of the existing recoupling methods are not suitable for CSA measurements in strongly coupled systems, i.e., uniformly ¹³C enriched samples.

In this work, we demonstrate that R-type symmetry pulse sequences^{33, 34, 35, 36} are well suited for recoupling of CSA interactions under MAS. Two classes of γ-encoded RN_n^v symmetry sequences are discussed, which are designed for recoupling of either the first-rank (σ₁) or the second-rank (σ₂) spatial CSA components. We have recently explored a subset of these sequences for the measurement of the relative orientations of the CSA and dipolar tensors under moderate MAS conditions.³⁷ In this work, we analyze the general properties of these sequences and show that they are suitable for CSA recoupling under a wide range of MAS frequencies, including fast-MAS conditions with rotation frequencies of 25 kHz and above. We demonstrate that a specific combination of symmetry numbers (N, n, v) can be tailored to the MAS frequency range of interest within the practically attainable rf field strength. Furthermore, these R-symmetry sequences are not very sensitive to the rf field inhomogeneities, permitting accurate measurements of CSA tensors in samples with inherently low sensitivity or in hydrated samples, such as microcrystalline proteins and protein assemblies. As we demonstrate in this report, these sequences are suitable for CSA measurements in both isotopically enriched and natural abundance systems.

Our results indicate that the R-symmetry sequences for σ₁-CSA recoupling generally have larger scaling factors than those for the σ₂-CSA recoupling. At the same time, the first-order average homonuclear dipolar Hamiltonian terms are not fully suppressed to zero in the σ₁-CSA sequences, which makes them suitable only for CSA measurements in systems with weak homonuclear dipolar interactions. In contrast, the γ-encoded symmetry sequences for σ₂-CSA recoupling have smaller scaling factors but they suppress efficiently the homonuclear dipole-dipole interactions. Therefore, the latter family of sequences is well suited for the measurements of CSA parameters in systems with strong homonuclear dipolar couplings, such as uniformly-¹³C labeled biological solids. We present RNCSA experiments and simulations establishing the utility of this approach to the measurements of ¹³C and ¹⁵N CSA parameters in model compounds, [¹⁵N]-N-acetyl-valine (NAV), [U-¹³C, ¹⁵N]-alanine (Ala), [U-¹³C,¹⁵N]-histidine, and present the application of this approach to [U-¹³C/¹⁵N]-Tyr labeled C-terminal domain of HIV-1 CA protein.

EXPERIMENTS AND METHODS

Materials

[U-¹⁵N] NAV, [U-¹³C, ¹⁵N]-L-histidine (L-His), [U-¹³C, ¹⁵N]-Ala and natural abundance L-alanine were purchased from Cambridge Isotope Laboratories. Powder samples of NAV and Ala were used in the subsequent NMR experiments without any further purification or recrystallization. L-His was doped with 0.1 mol. % CuCl₂ and recrystallized before solid-state NMR experiments. The conical assemblies of U-¹³C,¹⁵N-Tyr-labeled C-terminal domain (CTD) of HIV-1 CA protein were prepared by controlled precipitation from 50% w/v solution of PEG-4000 at the ratio of 1:1 (v/v) with the final protein concentration of 16 mg/mL, as reported previously.^{38, 39}

Solid-state NMR spectroscopy

All NMR experiments were carried out on a 14.1 T Varian InfinityPlus narrow bore solid-state NMR spectrometer, operating at a Larmor frequency of 599.8 MHz for ¹H, 150.8 MHz for ¹³C, and 60.8 MHz for ¹⁵N. A 3.2 mm Varian MAS triple-resonance T3 probe, a 1.6 mm Varian fast-MAS triple-resonance probe, and a 1.8 mm fast-MAS triple-resonance probe developed in the Ago Samoson Laboratory were used. The model compounds [U-¹⁵N]-NAV and [U-¹³C, ¹⁵N]-Ala were packed into 3.2 mm rotors, and all spectra were recorded at MAS frequencies of 10 and 20 kHz, controlled to within ±0.005 kHz. The n.a. alanine was packed into 1.6 mm rotor, and all spectra were recorded at MAS frequency of 10 kHz. The HIV-1 CTD CA protein and Cu(II)-doped L-His were packed into 1.8 mm rotors, and their spectra were recorded at MAS frequencies of 10 and 25 kHz. To reduce the sample heating during MAS, nitrogen gas was used for cooling, resulting in a final sample temperature of 20 °C for the three model samples, and of −25 °C for U-¹³C, ¹⁵N-Tyr labeled CTD CA protein. The temperature was calibrated for different MAS frequencies using a PbNO₃ temperature sensor,⁴⁰ and the actual temperature at the sample was maintained to within ±0.5 °C throughout the experiments using the Varian temperature controller.

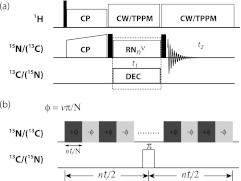
For NMR experiments, a 2D RNCSA pulse sequence shown in Figure 1a was used. A series of 2D NMR spectra were recorded by applying different RN_n^v symmetry pulse irradiation during t₁. The basic R element was a π pulse; the rf field strength (N/2n·ω_R) and the phase (±v/N · 180°) are determined by the symmetry properties for each of the symmetry sequences used.^{34, 35, 36, 39, 41, 42, 43} During the RN_n^v symmetry pulse irradiation on nucleus X (X = ¹³C or ¹⁵N), a π pulse was applied at the center of each R cycle (nτ_r) on nucleus Y to decouple the X-Y heteronuclear dipolar interactions (X, Y = ¹³C or ¹⁵N), as shown in Figure 1b. High continuous-wave (CW) or two-pulse phase-modulated (TPPM) proton decoupling with rf field of 90–110 kHz was applied during the RN CSA recoupling period, and the actual ¹H decoupling rf field was chosen so as to avoid ¹H–¹³C/¹⁵N Hartmann-Hahn matching conditions (ω_1H – ω_1X > 3ω_R or ω_1H – ω_1X ≠ nω_R). Sixteen transients were added for each t₁ increment (dw = nτ_r), and a total of 32 t₁ increments were used to record the spectra for NAV, Ala, and His. For 2D RNCSA experiments on U-¹³C,¹⁵N-Tyr-CTD CA protein, 4096 and 3072 transients were accumulated for each t₁ increment in the R8₁³-based ¹⁵N σ₁-CSA and R12₁⁴-based ¹³C^′σ₂-CSA measurements, respectively, and the same transients were used in the corresponding 2D recoupling of chemical shift anisotropy (ROCSA) experiments. The pulse delay was 2 s.

Figure 1.

(a) General pulse scheme for recoupling of CSA interactions by R-type symmetry sequences. Solid black squares denote 90° pulses. (b) Rotor synchronized RN_n^v symmetry rf pulses are applied on heteronuclei during t₁ evolution time to reintroduce CSA interactions under MAS conditions.

Numerical simulations

Numerical simulations of ¹³C/¹⁵N σ₁- and σ₂-CSA powder spectra were performed using the SIMPSON software package.⁴⁴ To produce a powder average, 986 pairs of {α, β} angles generated according to the ZCW algorithm⁴⁵ and 16 γ angles were used for all simulations, resulting in a total of 15 776 angle triplets. For extracting the best-fit CSA parameters (δ_σ, η_σ), all of the experimental and processing parameters (i.e., Larmor frequency, MAS frequency, rf field strength, number of t₁ points, finite pulse lengths, zero-filling, line broadening, etc.) were taken into account in the simulations for each experiment. Haeberlen-Mehring-Spiess convention was followed to define the CSA parameters, where the isotropic value δ_iso, the reduced anisotropy δ_σ, the anisotropy Ω, and the asymmetry parameter η, are related to the principal elements of the chemical shift tensor according to |δ_zz − δ_iso| ⩾ |δ_xx − δ_iso| ⩾ |δ_yy − δ_iso|, δ_iso = 1/3(δ_xx + δ_yy + δ_zz), δ_σ = δ_zz − δ_iso = 2/3Ω, and η = (δ_yy − δ_xx) / (δ_yy − δ_iso).

RESULTS AND DISCUSSION

γ-encoded σ₁- and σ₂-CSA recoupling by RN_n^v symmetry sequences

The rotational properties of anisotropic spin interactions under MAS conditions allow us to reintroduce the MAS-averaged anisotropic couplings by synchronization of nuclear spin degrees of freedom with rf field irradiation and MAS rotor frequency, in an appropriately designed sequence. The symmetry-based theory^{33, 34, 36, 41, 42} introduced and developed by Levitt and co-workers provides a general principle for designing rotor-synchronized rf pulse sequences to selectively recouple and/or decouple various anisotropic spin interactions in MAS NMR spectroscopy. The symmetry-based approaches are classified as CN_n^v and RN_n^v schemes, depending on whether a “Cycle” or “Reverse” operation is applied on the irradiated spins by a basic pulse element. The symbols N, n, and v are small integers and are referred to as the symmetry numbers of the pulse sequence. When the rf field irradiation is composed of the periodic RN_n^v symmetry pulses, the selection rules for the first-order average Hamiltonian are expressed as

$${\overline{H}}_{lm\lambda \mu }^{\Lambda }=0\mathrm{if}mn-\mu v=Z_{\lambda }N/2$$ (1)

where Z_λ is an integer with the same parity as λ, which is defined according to the rotational properties of the spin interactions.^{33, 34, 35, 36} The first-order average Hamiltonian term in Equation 1 can be expressed with the Magnus expansion of the effective Hamiltonian in the interaction frame,

$$H^{\Lambda }=K_{m\lambda \mu }{A}_{lm}^{\Lambda }\left({\Omega }_{PR}\right)d_{m0}^l\left({\beta }_{RL}\right)T_{\lambda \mu }^{\Lambda },$$ (2)

where K_mλμ, $A_{lm}^{\Lambda }$, and $T_{\lambda \mu }^{\Lambda }$ denote the scaling factor, the component of the spatial tensor and the component of the spin tensor, respectively. Each single Hamiltonian component is γ-encoded with its magnitude independent of the Euler angle γ. With specially designed symmetry sequences, a given single or multiple types of interactions can be recoupled selectively. The average CSA Hamiltonian interaction can be separated into three terms according to the spatial rank m = 0, ±1, ±2,³⁷

$$\begin{array}{ccc}\hfill {\overline{H}}^{CSA}& =& {\overline{H}}_{\left(0\right)}^{CSA}+{\overline{H}}_{\left(1\right)}^{CSA}+{\overline{H}}_{\left(2\right)}^{CSA}\hfill \\ & =& \sum _{m=0,\lambda ,\mu }{K}_{m\lambda \mu }{A}_{lm}^{\Lambda }\left({\Omega }_{PR}\right)d_{m0}^l\left({\beta }_{RL}\right)T_{\lambda \mu }^{\Lambda }\hfill \\ & & +\sum _{m=\pm 1,\lambda ,\mu }{K}_{m\lambda \mu }{A}_{lm}^{\Lambda }\left({\Omega }_{PR}\right)d_{m0}^l\left({\beta }_{RL}\right)T_{\lambda \mu }^{\Lambda }\hfill \\ & & +\sum _{m=\pm 2,\lambda ,\mu }{K}_{m\lambda \mu }{A}_{lm}^{\Lambda }\left({\Omega }_{PR}\right)d_{m0}^l\left({\beta }_{RL}\right)T_{\lambda \mu }^{\Lambda }\hfill \\ & =& \gamma B_0{\sigma }_0{I}_z+\gamma B_0{\sigma }_1\cos ({\gamma }_{PR}+{\omega }_{r}t+{\delta }_1)I_z\hfill \\ & & +\gamma B_0{\sigma }_2\cos 2({\gamma }_{PR}+{\omega }_{r}t+{\delta }_2)I_z,\hfill \end{array}$$ (3)

where σ₀, σ₁, and σ₂ coefficients are dependent on the three principal components of the CSA tensor and on the crystallite orientations, and the recoupled CSA pattern of each spatial Hamiltonian term reveals all the properties of the CSA interactions.

The explicit expressions for σ₀, σ₁, and σ₂ coefficients are

$$\begin{array}{ccc}\hfill {\sigma }_0& =& {\sigma }^{iso}+P_2\left(\cos {\beta }_{RL}\right)[P_2\left(\cos {\beta }_{PR}\right)\left({\sigma }_{zz}^{PAS}-{\sigma }^{iso}\right)\hfill \\ & & +\frac{1}{2}\sin {\beta }_{PR}\cos 2{\alpha }_{PR}\left({\sigma }_{xx}^{PAS}-{\sigma }_{yy}^{PAS}\right)],\hfill \end{array}$$ (4)

$$\begin{array}{ccc}\hfill {\sigma }_1& =& \sqrt{{\sigma }_{\cos 1}^2+{\sigma }_{\sin 1}^2}\hfill \\ & =& \sin {\beta }_{RL}\cos {\beta }_{RL}\sin {\beta }_{PR}\left\{\cos {\beta }_{PR}\right[-3\left({\sigma }_{zz}^{PAS}-{\sigma }^{iso}\right)\hfill \\ & & {+\cos 2{\alpha }_{PR}\left({\sigma }_{xx}^{PAS}-{\sigma }_{yy}^{PAS}\right)\left]\right\}}^2\hfill \\ & & {+{\left[\sin 2{\alpha }_{PR}\left({\sigma }_{xx}^{PAS}-{\sigma }_{yy}^{PAS}\right)\right]}^2\}}^{1/2},\hfill \end{array}$$ (5)

$$\begin{array}{ccc}\hfill {\sigma }_2& =& \sqrt{{\sigma }_{\cos 2}^2+{\sigma }_{\sin 2}^2}\hfill \\ & =& \frac{1}{2}{\sin }^2{\beta }_{RL}\left\{\right[\frac{3}{2}{\sin }^2{\beta }_{PR}\left({\sigma }_{zz}^{PAS}-{\sigma }^{iso}\right)\hfill \\ & & {+\frac{1}{2}(1+\cos 2{\beta }_{PR})\cos 2{\alpha }_{PR}\left({\sigma }_{xx}^{PAS}-{\sigma }_{yy}^{PAS}\right)]}^2\hfill \\ & & {+{\left[\cos {\beta }_{PR}\sin 2{\alpha }_{PR}\left({\sigma }_{xx}^{PAS}-{\sigma }_{yy}^{PAS}\right)\right]}^2\}}^{1/2},\hfill \end{array}$$ (6)

where σ_cosi and σ_sini (i = 1 and 2) are the projected elements of the spatial ith-rank CSA Hamiltonian term (σ_i) in the x^′y^′ plane of the rotor fixed frame (RFF), δ_i denotes the projection angle of CSA Hamiltonian σ_i relative to the x^′ axis of the RFF.³⁷

Depending on the spatial rank number l and spin rank number λ of the tensorial interaction of interest, it is possible, using a suitable symmetry sequence, to reintroduce selectively the Hamiltonian components characterized by quantum numbers {l, m, λ, μ}. For the γ-encoded recoupling of CSA interaction with spatial rank number l = 2, either the first spatial component σ₁-CSA or the second spatial component σ₂-CSA can be reintroduced under the MAS conditions; these components correspond to the Hamiltonian terms {2, ±1, 1, ∓1} and {2, ±2, 1, ∓1}, respectively. It can be immediately seen that, in the regime of double-quantum homonuclear dipolar recoupling, when the first-rank spatial components (σ₁-CSA) are recoupled by the RN_n^v schemes, the homonuclear dipole-dipole Hamiltonian components with quantum numbers {2, ±2, 2, ∓2} are recoupled as well. These recoupled σ₁-CSA interactions and homonuclear dipolar couplings interfere with each other, which would result in inaccuracy or uncertainty of the derived CSA determinations. Therefore, γ-encoded σ₁-CSA recoupling symmetry schemes are only suitable for systems that have either no or weak homonuclear dipolar interactions, such as ³¹P and ¹⁵N in dilute environments or naturally abundant ¹³C spins.

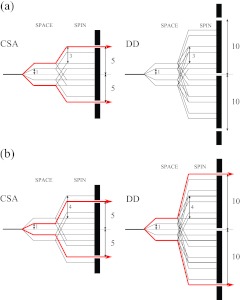
Figure 2 illustrates an example of the selection properties of anisotropic Hamiltonian interactions by R-type symmetry sequences R10₁³ (a) and R10₁⁴ (b). It can be seen that both of these sequences are suitable for γ-encoded single-quantum CSA recoupling, and the symmetry-allowed Hamiltonian components retained by R10₁³ and R10₁⁴ are {l, m, λ, μ} = {2, ±2, 1, ∓1} and {2, ±1, 1, ∓1}, respectively. R10₁⁴ symmetry sequence recouples σ₁-CSA interactions (the first spatial rank), while σ₂-CSA (the second spatial rank) is recoupled by R10₁³. As discussed above, usually the homonuclear dipolar interaction would be recoupled partially by the σ₁-CSA recoupling symmetry sequence. In the case of the R10₁⁴ symmetry sequence, the components of the dipolar Hamiltonian with quantum numbers {2, ±2, 2, ∓2} are symmetry-allowed, as shown in the spin-space selection (SSS) diagram in Figure 2. Additionally, it should be noted that these γ-encoded σ₁- and σ₂-CSA symmetry sequences also reintroduce heteronuclear dipolar interactions since CSA and heteronucear dipolar interactions exhibit the same rotational properties under MAS. Heteronuclear decoupling, by CW, TPPM, or XiX (X inverse-X) irradiation or any other suitable sequence, is therefore required during the CSA evolution period. Alternatively, the reintroduced heteronuclear dipolar couplings can be refocussed easily with a series of π pulses located at the center of each R cycle, as shown in Figure 1b, and such π pulse-based refocusing is advantageous as it avoids the sample heating by rf field irradiation.

Figure 2.

Space-spin selection diagrams for selecting the first order Hamiltonian terms corresponding to CSA (left) and homonuclear dipolar interactions (right) by symmetry sequences R10₁³ (a) and R10₁⁴ (b). (a) R10₁³ selects the components of CSA interactions characterized by quantum numbers {2, 2, 1, −1} and {2, −2, 1, 1} while suppressing all the components of homonuclear dipolar interactions. (b) R10₁⁴ selects the components of CSA interactions with quantum numbers {2, 1, 1, −1} and {2, −1, 1, 1} while recoupling two components of homonuclear dipolar interactions with quantum numbers {2, 2, 2, −2} and {2, −2, 2, 2}.

Scaling factors for σ₁- and σ₂-CSA recoupling

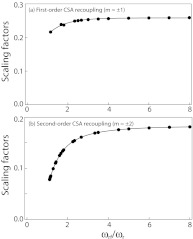
The R-type symmetry sequences suitable for σ₁- and σ₂-CSA recoupling under MAS are summarized in the supplementary material (see Table S1).⁴⁶ The symmetry numbers of the sequences listed in Table S1 are limited to the range of 6 ≤ N ≤ 20, and the ratios of the symmetry numbers are limited to 1.0 < N/2n ≤ 8.0, to yield rf powers compatible with the available modern hardware. If the basic R element is a π pulse, the rf field strength required for the RN_n^v symmetry sequences is Nω_R/2n, and the different sequences exhibit different scaling factors for recoupling of σ₁- or σ₂- CSA interactions and for decoupling of homonuclear dipole-dipole interactions. All the σ₂-CSA recoupling R-type symmetry sequences except for R6₁¹ and R8₁² can suppress the first-order homonuclear dipolar Hamiltonian to zero; however, there are always partial homonuclear dipolar Hamiltonian components reintroduced simultaneously while the σ₁-CSA interactions are recoupled by γ-encoded RN_n^v symmetry sequences. In Figure 3, the effective scaling factors for the σ₁- and σ₂-CSA recoupling by RN_n^v symmetry sequences are plotted as a function of the symmetry number ratio, Nω_R/2n. As illustrated in this figure, the symmetry sequences with higher N/n ratio have larger scaling factors for both σ₁- and σ₂-CSA recoupling, and the scaling factors are reduced greatly when the ratio N/2n is lower than 2.0. Notably, the σ₁-CSA recoupling schemes have at least 1.4-fold higher scaling factors than the σ₂-CSA recoupling schemes with the same symmetry number ratio N/n. This higher scaling factor in σ₁-CSA recoupling might be advantageous, especially at low magnetic fields, as it enables accurate measurements of small CSA values, even though these experiments are restricted to the spin systems with weak homonuclear dipolar couplings. Another advantage of the σ₁-CSA recoupling schemes is that they are less sensitive to the required rf field strength. On the other hand, for the measurement of large CSA interactions (e.g., in ¹³C carbonyl atoms or in heavy nuclei, such as ²⁰⁷Pb), σ₂-CSA recoupling sequences with smaller scaling factors would be more suitable, especially at high magnetic fields. For a given MAS frequency, it is generally the best to employ RN_n^v symmetry sequences with higher N/2n ratio for accurately determining CSA interactions, as long as the required rf field strength (Nω_R/2n) can be attained in the MAS NMR probes available to the experimentalist.

Figure 3.

The scaling factors for recoupling σ₁-CSA (a) and σ₂-CSA (b) by RN_n^v symmetry sequences plotted as a function of the ratio, ω_rf/ω_r (N/2n).

¹⁵N CSA recoupling by γ-encoded RN_n^v sequences

To understand the performance of the RNCSA recoupling with the RN-based pulse scheme shown in Figure 1, we simulated ¹⁵N σ₁- and σ₂-CSA line shape patterns for the R10₁⁴ and R10₁³ symmetry sequences, at the MAS frequency of 10 kHz. The resulting line shapes are shown in Figure S1 of the supplementary material.⁴⁶ It can be seen that the CSA parameters can be accurately captured by both σ₁- and σ₂-CSA recoupled line shape patterns, and the line shapes are very similar in appearance except for the size of the scaling factors. These simulated spectra suggest that R-type symmetry sequences should work well for CSA recoupling under MAS conditions, that both the anisotropy and asymmetry parameters of the CSA tensor are available from each individual experiment. In practice, a single measurement is sufficient for extracting accurate CSA parameters. As shown below, the choice of a recoupling sequence for each measurement of interest is dictated by the system under study and by the available experimental settings (spectrometer hardware).

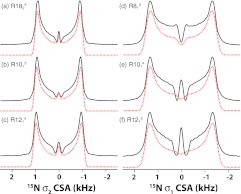
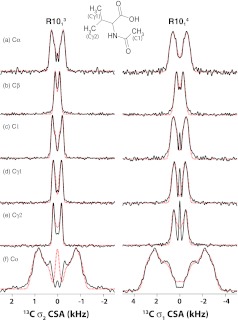
Following the results of the numerical simulations, we performed ¹⁵N σ₁- and σ₂-CSA measurements on [¹⁵N]-NAV spun at the MAS frequency of 10 kHz. Figure 4 shows the ¹⁵N RNCSA line shapes recorded by the various symmetry sequences designed for σ₂-CSA recoupling (R18₂⁵ (a), R10₁³ (b), and R12₁⁴ (c)) and for σ₁-CSA recoupling (R8₁³ (d), R10₁⁴ (e), and R12₁⁵ (f)). The rf field strengths applied on ¹⁵N during the RNCSA recoupling period at this MAS frequency are 5N/n kHz. All these RN_n^v symmetry sequences produce similar ¹⁵N CSA line shapes, and the σ₁-CSA recoupled line shapes (right) show much larger scaling factors than the σ₂-CSA line shapes (left), in accord with the theory and simulations. For both σ₁-CSA and σ₂-CSA recoupling measurements, the symmetry sequences with higher symmetry number ratio of N/n give rise to higher scaling factors, i.e., R12₁⁵ > R10₁⁴ > R8₁³, as expected. The ¹⁵N CSA parameters were extracted from numerical simulations of each line shape, and the simulated line shapes are displayed as dotted lines in Figure 4.

Figure 4.

Experimental (black solid lines) and simulated (red dotted lines) ¹⁵N σ₁- (right) and σ₂- (left) CSA line shapes of [¹⁵N]-N-acetyl-valine generated by the various R-symmetry sequences: R18₂⁵ (a), R10₁³ (b), R12₁⁴ (c), R8₁³ (d), R10₁⁴ (e), and R12₁⁵ (f). The sample was spun at an MAS frequency of 10 kHz. The rf field strength applied during the recoupling period was 45, 50, 60, 40, 50, and 60 kHz for (a)–(f), respectively. The best-fit ¹⁵N CSA parameters measured by each symmetry sequence are listed in Table 2.

Since the ¹⁵N CSA tensor components, reduced anisotropy δ_σ and asymmetry parameter η, are the primary parameters determining the features of CSA line shape patterns recoupled by R-symmetry sequences, the best-fit line shape can be readily derived, using the minimal least square error criterion, χ². It should be noted that the central part (usually the entire center peak) is excluded from the curve fitting when minimizing χ², due to its complex dependence on rf field inhomogeneity, multiple relaxation processes and the recoupled second-order Hamiltonian terms. The exclusion of the center peak from the simulations does not affect the accuracy of the derived CSA parameters to any significant extent. The fit parameters as well as the uncertainty errors are derived using the SIMPLEX method, as shown in Figure S2 of the supplementary material.⁴⁶ In Figure S2a, a χ² contour plot is depicted for the fitting result of the ¹⁵N σ₁-CSA line shape recorded by R10₁⁴ symmetry sequence, from which the best-fit values are determined to be δ_σ = 105.8 ± 0.5 ppm and η = 0.19 ± 0.04. These results are consistent with our previous report.³⁷ Table 1 lists the ¹⁵N CSA parameters extracted from the σ₁- and σ₂-CSA measurements performed with various RN_n^v symmetry sequences. It can be seen that the ¹⁵N CSA parameters derived from all RNCSA experiments are in excellent agreement. The average values for the reduced anisotropy and asymmetry parameters recorded with the rest of the sequences are δ_σ = 105.9 ± 0.5 ppm and η = 0.20 ± 0.05.

Table 1.

The best-fit ¹⁵N CSA parameters for [¹⁵N]-N-acetyl-valine (NAV) extracted from the σ₁- and σ₂-CSA measurements performed with various RN_n^v symmetry sequences.

N	n	v	δσ (ppm)	ησ
6	1	2	105.1	0.23
8	1	3	105.7	0.21
10	1	3	106.2	0.18
10	1	4	105.8	0.19
12	1	4	108.9	0.18
12	1	5	106.5	0.17
14	2	3	104.9	0.21
14	2	5	105.4	0.20
18	2	5	105.3	0.19
Static NMR			107.2	0.19

¹Note: The MAS frequency was 10 kHz, and the rf field strength was 5N/n kHz for each RN_n^v symmetry sequence.

To verify the accuracy of CSA parameters determined by the R-symmetry sequences, static ¹⁵N CP NMR experiment was performed on ¹⁵N-NAV sample to record the ¹⁵N CSA powder pattern. The results are shown in Figure S2b of the supplementary material.⁴⁶ The best-fit simulation yielded the following ¹⁵N CSA parameters: δ_σ = 107.2 ppm and η = 0.19, which agrees well with the corresponding values derived from the R-symmetry based experiments conducted under MAS conditions. Since the intermolecular homonuclear ¹⁵N–¹⁵N dipolar interactions are weak enough to be negligible, the ¹⁵N σ₁-CSA measurements are as accurate as σ₂-CSA experiments. The encouraging consistency of ¹⁵N CSA parameters extracted from these independent experiments illustrates the accuracy of the current RNCSA approach and that σ₁-CSA recoupling technique is suitable for U-¹⁵N isotope-enriched systems.

As pointed out by us and by others in the case of dipolar recoupling,^{39, 47} R-symmetry based sequences are sensitive to the rf field inhomogeneity. At the same time, we have demonstrated that the sensitivity to the rf field inhomogeneity can be reduced significantly by choosing the appropriate symmetry sequences with symmetry ratio of N/2n > 2.5.³⁹ It is thus important to consider the effect of rf field inhomogeneity on RNCSA line shapes. We have conducted numerical simulations and discovered that the rf inhomogeneity has more pronounced effect on the σ₂-CSA RN symmetry sequences, especially for the sequences with smaller symmetry ratio of N/2n. These findings are summarized in Figure S3 of the supplementary material.⁴⁶ In contrast, σ₁-CSA R-symmetry sequences with relatively large scaling factors exhibit much lower sensitivity to the rf field inhomogeneity. The manifestation of the rf field inhomogeneity is an increase in the intensity of the central peak and a broadening of the RNCSA patterns, which become more pronounced with the increased rf field inhomogeneity. The simulations also reveal the fact that for either σ₁-CSA or σ₂-CSA R-symmetry sequences, the stronger the rf field (Nω_R/2n) is, the weaker the effect from rf field inhomogeneity. Generally, the effect from rf field inhomogeneity of up to 20% can be ignored when the symmetry ratio, N/2n, of the sequence employed is greater than 2.5. In practical terms, the above implies that one has to consider the trade-off between the scaling factor and the rf field inhomogeneity of a particular probe. It should be noted that the rf field inhomogeneity was not taken into account for all the RNCSA fittings in the present work because the 1.8 mm and 1.6 mm MAS probes used have extremely high rf field homogeneity (>90%), and also because the RN sequences used for all the current measurements have the symmetry ratio of N/2n > 2.5.

¹³C CSA recoupling by γ-encoded RN_n^v sequences

We also examined the performance of these γ-encoded RN_n^v symmetry sequences for determining ¹³C CSA interactions in both naturally abundant and isotopically enriched systems. Figure 5 shows the ¹³C experimental and simulated CSA line shapes for all of the carbon sites in an U-¹⁵N-NAV sample spun at the MAS frequency of 10 kHz, recorded with the R10₁⁴ sequence (σ₁-CSA recoupling, right) and R10₁³ sequence (σ₂-CSA recoupling, left). Similar to the ¹⁵N experiments, the fitted ¹³C CSA parameters as well as the uncertainty errors can be easily derived using the SIMPLEX method for each carbon site, as listed in Table 2. The fact that the ¹³C CSA parameters extracted from R10₁⁴σ₁-CSA and R10₁³σ₂-CSA experiments are in excellent agreement indicates that σ₁-CSA recoupling technique is suitable for ¹³C CSA measurements in natural-abundance systems. Moreover, the ¹³C CSA parameters measured from these independent R-based experiments are consistent with the literature values derived on the basis of ROCSA spectra,²⁵ indicating that these γ-encoded symmetry sequences yield highly accurate CSA estimates, even for the sites with small CSA.

Figure 5.

¹³C σ₁- (right) and σ₂- (left) CSA line shapes for Cα (a), Cβ (b), C1 (c), Cγ1 (d), Cγ2 (e), and Co (f) of [¹⁵N]-N-acetyl-valine generated by symmetry sequences R10₁⁴ and R10₁³, respectively. Experimental data are shown as black solid lines, and simulated data – as red dotted lines. The sample was spun at the MAS frequency of 10 kHz. The best-fit ¹³C CSA parameters for all carbon sites are listed in Table 3.

Table 2.

Summary of ¹³C CSA parameters measured for U-¹⁵N-labeled NAV sample.

	R1013		R1014
#	δσ (ppm)	ησ	δσ (ppm)	ησ	δσ (ppm)2	ησ2
Cα	26.3	0.48	24.6	0.51	26.0	0.36
Cβ	10.3	1.0	10.8	1.0	11.0	1.0
C1	21.8	0.69	21.2	0.70	…	…
Cγ1	19.0	0.59	18.9	0.61	18.5	0.58
Cγ2	18.1	0.32	19.0	0.30	17.5	0.65
Co	84.6	0.50	83.6	0.55	85.4	0.49

¹Note: R10₁³ and R10₁⁴ symmetry sequences were employed for σ₂- and σ₁-CSA recoupling. The MAS frequency was 10 kHz. Note that recoupling of ¹³C CSA is efficiently performed with these sequences for the natural abundance carbon sites in this sample.

²Data reported for U-¹³C,¹⁵N-val enriched NAV sample (Reference ²⁵).

The σ₂-CSA symmetry-based recoupling sequences can be applied not only to natural abundance but also to uniformly ¹³C labeled systems due to the inherent capability of these sequences to suppress ¹³C–¹³C homonuclear dipolar couplings. An example of ¹³C CSA measurements in U-¹³C,¹⁵N-alanine using various σ₂-CSA symmetry sequences is given in Figure S4 of the supplementary material.⁴⁶ The best-fit ¹³C CSA parameters for each carbon site are summarized in Table 3. It can be seen that the ¹³C CSA parameters extracted from experiments recorded with different symmetry sequences are in good agreement and consistent with the literature values,²⁵ with the average CSAs for C^α, C^β, and C^′ of 22.0, 13.8, and 68.6 ppm, respectively.

Table 3.

¹³C CSA parameters for U-¹³C,¹⁵N Alanine recorded with various σ₂-CSA RN_n^v symmetry sequences.

			C′		Cα		Cβ
N	n	v	δσ (ppm)	ησ	δσ (ppm)	ησ	δσ (ppm)	ησ
14	2	3	68.5	0.87	21.9	0.60	13.5	0.65
18	2	5	68.4	0.77	22.2	0.58	14.1	0.75
10	1	3	69.6	0.80	21.2	0.72	14.3	0.62
12	1	4	67.7	0.74	22.5	0.52	13.2	0.97

¹Note: The MAS frequency was 10 kHz, and the rf field strength was 5N/n kHz for each RN_n^v symmetry sequence.

For uniformly ¹³C-labeled systems, since the partially recoupled ¹³C–¹³C dipolar interactions would interfere with the ¹³C σ₁-CSA interaction, the σ₁-CSA recoupling technique might not be suitable for dense networks of spins. To examine this hypothesis, we simulated the σ₁-CSA and σ₂-CSA line shapes in the presence of remote homonuclear spins. The results shown in Figure S5 of the supplementary material⁴⁶ indicate that indeed, the σ₁-CSA line shapes are broadened and distorted when dipolar-coupled homonuclear spins are present. Experimental results agree with these simulations, as shown in Figure S6 of the supplementary material:⁴⁶ in a σ₁-CSA recoupling measurements in U-¹³C,¹⁵N-Ala and natural abundance Ala samples, the σ₁-CSA line shapes of the ¹³C^α and ¹³C^β atoms in isotopically labeled Ala is highly distorted when recorded with R12₁⁵ symmetry sequence, as it deviates significantly from that of natural abundance Ala. This is due to the interference from homonuclear ¹³C–¹³C dipolar couplings. It should be noted that the degree of distortion of the CSA patterns is mostly dependent on the ratio of the magnitude of ¹³C–¹³C dipolar interactions to that of CSA interactions, and ¹³C^β with the smallest CSA displays the largest line shape distortion. On the contrary, the recoupled σ₂-CSA line shapes of isotopically labeled Ala are not affected at all by the additional homonuclear dipolar couplings, and we record the same powder patterns as for the natural abundance Ala, as illustrated in Figure S6 in the supplementary material.⁴⁶

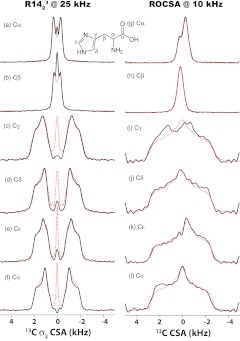
Notably, the fact that a variety of symmetry numbers are suitable for CSA recoupling makes these experiments applicable for a wide range of MAS frequencies, including fast MAS conditions. We have performed ¹³C σ₂-CSA measurements on U-¹³C,¹⁵N-histidine spun at the MAS frequency of 25 kHz. As discussed above, the RN_n^v symmetry sequences for σ₁-CSA recoupling have larger scaling factors, but they cannot suppress the homonuclear ¹³C–¹³C dipole-dipole couplings sufficiently well and give rise to distorted CSA line shapes thus affecting the accuracy of the measurements. The experimental and simulated ¹³C CSA line shapes for all of the carbon sites of histidine recorded by R14₂³ symmetry sequence with an rf field strength of 87.5 kHz, as shown in the left panel of Figure 6. As is clear from the figure, the experimental and the simulated CSA line shapes agree very well attesting to the fact that γ-encoded R-symmetry based sequences are suitable for CSA recoupling under fast MAS conditions. We also performed ¹³C σ₂-CSA measurement with R20₃⁴ symmetry sequence at the MAS frequency of 25 kHz (see Figure S7 in the supplementary material⁴⁶ for the details of NMR experiments and simulations). The CSA parameters extracted from this experiment are consistent with those determined by the R14₂³ symmetry sequence, illustrating that both large and small CSA interactions can be measured with high accuracy.

Figure 6.

Experimental (black solid lines) and simulated (red dotted lines) ¹³C σ₂-CSA line shapes recorded by R14₂³ sequence (left) and ¹³C CSA line shapes recorded by ROCSA sequence (right). Each line shape represents an individual ¹³C site U-[¹³C, ¹⁵N]-histidine: Cα ((a), (g)), Cβ ((b), (h)), Cγ ((c), (i)), Cδ ((d), (j)), Cɛ ((e), (k)) and Co ((f), (l)). The sample was spun at the MAS frequencies of 25 and 10 kHz for RNCSA and ROCSA experiments, respectively. The best-fit ¹³C CSA parameters for all carbon sites are summarized in Table 4.

We have compared the ¹³C CSA line shapes recorded by the above R-symmetry sequences with those extracted from the ROCSA²⁵ experiment at a MAS frequency of 10 kHz. The experimental and simulated ¹³C CSA line shapes for all of the carbon sites are shown on the right panel of Figure 6. As illustrated in Table 4, the best-fit ¹³C reduced anisotropies for all carbon sites are systematically lower in the ROCSA experiments. These lower values are the result of high sensitivity of the ROCSA conditions to the rf field inhomogeneity and rf power settings: even the slightest imperfections in the hardware and experimental conditions (which are often inevitable in biological samples) give rise to inaccurate CSA parameters. Severe distortions are present in the ROCSA ¹³C CSA patterns, especially for carbon groups with larger CSAs. In contrast, the R-symmetry based recoupling sequences are much more robust and tolerant to the hardware and experimental imperfections, especially when the symmetry ratio N/2n is greater than 2.5.

Table 4.

Summary of ¹³C σ₂-CSA parameters for U-[¹³C,¹⁵N]-histidine.

	R1423		R2034,2		ROCSA
#	δσ (ppm)	ησ	δσ (ppm)	ησ	δσ (ppm)	ησ
Cα	16.9 ± 0.6	0.46 ± 0.11	17.6 ± 0.9	0.58 ± 0.16	15.7 ± 1.6	0.55 ± 0.19
Cβ	14.5 ± 2.2	0.93 ± 0.44	…	…	8.1 ± 2.6	0.97 ± 0.85
Cγ	75.8 ± 2.9	0.87 ± 0.15	77.3 ± 0.5	0.80 ± 0.03	69.0 ± 4.3	1.00 ± 0.11
Cδ	71.7 ± 3.4	1.00 ± 0.24	71.0 ± 2.2	0.88 ± 0.06	67.6 ± 0.3	1.00 ± 0.57
Cɛ	71.8 ± 2.1	0.83 ± 0.08	71.0 ± 0.9	0.76 ± 0.11	70.0 ± 3.9	0.76 ± 0.09
Co	66.0 ± 1.1	1.00 ± 0.45	68.1 ± 4.7	0.93 ± 0.17	64.8 ± 3.6	1.00 ± 0.04

¹Note: R20₃⁴ and R14₂³ symmetry sequences were employed for σ₂-CSA recoupling. The rf field strengths were 83.3 and 87.5 kHz, respectively, and the MAS frequency was 25 kHz. TPPM ¹H decoupling with rf field strength of 100 kHz was applied during the RNCSA period. The results of ROCSA recoupling are presented for comparison.

²The experimental and simulated ¹³C CSA line shapes for each carbon site are shown in the supplementary material.⁴⁶

We also note that due to the limitations on the ¹H rf field strength for heteronuclear decoupling in our NMR probe (ω_1H^max ≈ 110 kHz), it is not possible to avoid ¹H–¹³C Hartmann-Hahn matching conditions during the CSA recoupling period especially under fast MAS conditions. Therefore, with our hardware we could not pursue the R-based CSA recoupling experiments at MAS frequencies exceeding 25 kHz. However, with the availability of ultrafast MAS probes capable of delivering high-power ¹H rf field irradiation the R-symmetry based CSA recoupling will be attainable at frequencies higher than 25 kHz.

γ-encoded CSA recoupling: Applications to protein structural and dynamics studies

The γ-encoded symmetry-based σ₁-CSA and σ₂-CSA recoupling methods described here are well suited for structural and dynamics characterization of uniformly and sparsely enriched proteins and protein assemblies. ¹⁵N and ¹³C^′ CSA interactions of the backbone atoms provide quantitative insights into protein structure and dynamics. We have examined the performance of the R-symmetry based recoupling sequences for the determination of ¹⁵N σ₁-CSA and ¹³C^′σ₂-CSA interactions in U-¹³C,¹⁵N-Tyr-enriched C-terminal domain (CTD) of HIV-1 CA capsid protein. The C-terminal domain of HIV-1 CA protein contains three tyrosine residues, Y145, Y164, and Y169. Y164 and Y169 are located in α-helices, while Y145 occupies a pivotal position in the hinge region connecting the C- and N-terminal domains of CA. The hinge region is conformationally flexible on millisecond timescales,^{39, 48, 49, 50, 51} and as we have recently demonstrated, these millisecond motions are related to conformational plasticity of CA, permitting its assembly into different morphologies (i.e., conical, tubular, and spherical).⁵¹

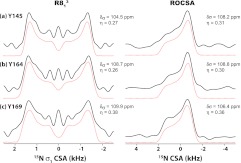
We have recorded the ¹⁵N σ₁-CSA line shapes for all Tyr residues in U-¹³C,¹⁵N-Tyr-CTD by R8₁³ symmetry sequence. The ¹⁵N CSA parameters extracted by numerical simulations of the experimental RNCSA and ROCSA line shapes are shown in Figure 7 and they are in excellent agreement with each other. The ¹⁵N reduced anisotropies, δ_σ, are similar for all tyrosine residues, and close to the rigid limit value (δ_σ = 110 ppm⁵²). The asymmetry parameters, η_σ, are also similar and nearly axially symmetric, between 0.27 and 0.38. This result is fully consistent with our recent studies revealing no significant averaging for the ¹⁵N CSA tensor of Y145 and indicating that the backbone nitrogen is rigid on the timescales faster than ∼10⁻⁶ s.^{39, 51}

Figure 7.

Left: Experimental (black solid lines) and simulated (red dotted lines) ¹⁵N σ₁-CSA line shapes of U-[¹³C, ¹⁵N]-Tyr HIV-1 C-terminal domain (CTD) of CA protein recorded by R8₁³ sequence. Right: Experimental (black solid lines) and simulated (red dotted lines) ¹⁵N CSA line shapes of the same sample recorded by ROCSA sequence. The sample was spun at the MAS frequency of 10 kHz. The best-fit CSA parameters are shown for each Tyr residue.

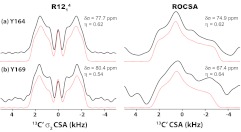
In our prior work, we were limited to the ROCSA-based measurements of ¹⁵N CSA parameters. We have previously attempted to record ¹³C^′ CSA line shapes by the ROCSA sequence. As shown in the right panel of Figure 8, large distortions were observed in these line shapes, which precluded determination of accurate CSA parameters for these carbonyl sites and generally for sites with large CSAs under the experimental conditions attained with our hardware. In contrast, the R-symmetry based sequences discussed here enable the measurements of much larger ¹³C^′ chemical shift anisotropies, with high sensitivity and only half of ROCSA experiment time. For carbonyl CSA measurement, we have employed R12₁⁴ symmetry sequence for σ₂-CSA recoupling, as shown in the left panel of Figure 8. In Figure 8, the experimental (solid lines) and best-fit simulated (dashed lines) ¹³C^′ CSA line shapes for each Tyr residue are presented. The Y145 and Y169 C^′ peaks overlap, and therefore the corresponding line shape is a combination of contributions arising from both residues. Y164 and Y169/Y145 exhibit ¹³C^′δ_σ values of 77.7 and 80.4 ppm, respectively. These values are close to the rigid limit CSA for carbonyl backbone carbons (δ_σ = 80 ppm^{53, 54}), and indicate that no dynamic averaging is taking place on timescales of microseconds and faster, in full agreement with our ¹⁵N CSA and ¹H–¹⁵N dipolar coupling results obtained in this and in recent work.^{39, 51}

Figure 8.

Left: Experimental (black solid lines) and simulated (red dotted lines) ¹³C^′σ₂-CSA line shapes of U-[¹³C^′, ¹⁵N]-Tyr HIV-1 C-terminal domain (CTD) of CA protein recorded by the R12₁⁴ sequence. Right: Experimental (black solid lines) and simulated (red dotted lines) ¹³C^′ CSA line shapes by of the same sample recorded by the ROCSA sequence. The sample was spun at the MAS frequency of 10 kHz. The best-fit CSA parameters are shown for each Tyr residue.

The above results demonstrate that γ-encoded R-type symmetry sequences are well suited for the measurement of large CSA interactions.

Taken together, the results presented in this report demonstrate that RN_n^v symmetry sequences permit recoupling of CSA interactions in a broad regime of experimental conditions, and offer a reliable route to site-specific measurements of chemical shift interactions in a variety of samples, including biological solids.

CONCLUSION

The γ-encoded R-type symmetry sequences are well suited for the measurements of CSA interactions under magic angle spinning. With the appropriately selected γ-encoded RN_n^v symmetry sequences either first-rank (σ₁) or second-rank (σ₂) spatial CSA recoupling can be attained. Both types of γ-encoded RNCSA symmetry schemes are applicable to a wide range of MAS frequencies, including fast MAS conditions. While σ₁-CSA recoupling symmetry sequences exhibit large scaling factors and are advantageous for recoupling of small CSAs, the partial homonuclear dipolar Hamiltonian components being symmetry allowed, in practice make these sequences suitable for CSA measurements only in systems with weak or no homonuclear dipolar interactions. On the other hand, even though γ-encoded σ₂-CSA recoupling symmetry sequences have smaller scaling factors, they efficiently suppress homonuclear dipole-dipole interactions. Therefore, these σ₂-sequences are suitable for CSA measurements in the samples where homonuclear dipolar couplings are present, such as in U-¹³C labeled biological solids. These sequences are also advantageous at high magnetic fields and in systems possessing inherently large CSAs, such as ¹³C carbonyl sites in biological solids and heavy nuclei. We expect that the approach reported here will be widely used for structural and dynamics characterization of a broad range of systems, ranging from macromolecular assemblies to organic solids, and will find many interesting applications in chemistry, biology, materials science, and other disciplines.