Evolving Concepts on Adjusting Human Resting Energy Expenditure Measurements for Body Size

Abstract

Establishing if an adult’s resting energy expenditure (REE) is high or low for their body size is a pervasive question in nutrition research. Early workers applied body mass and height as size measures and formulated the Surface Law and Kleiber’s Law, although each has limitations when adjusting REE. Body composition methods introduced during the mid-twentieth century provided a new opportunity to identify metabolically homogeneous “active” compartments. These compartments all show improved correlations with REE estimates over body mass-height approaches, but collectively share a common limitation: REE-body composition ratios are not “constant” but vary across men and women and with race, age, and body size. The now-accepted alternative to ratio-based norms is to adjust for predictors by applying regression models to calculate “residuals” that establish if a REE is relatively high or low. The distinguishing feature of statistical REE-body composition models is a “non-zero” intercept of unknown origin. The recent introduction of imaging methods has allowed development of physiological tissue-organ based REE prediction models. Herein we apply these imaging methods to provide a mechanistic explanation, supported by experimental data, for the non-zero intercept phenomenon and in that context propose future research directions for establishing between subject differences in relative energy metabolism.

INTRODUCTION

The study of human energy metabolism is central to diverse fields of inquiry ranging from the basic biological sciences to clinical weight control management. A fundamental question in this field is if a subject’s resting energy expenditure (REE) is appropriate for their body size^1–8. High or low REE values can signal underlying metabolic disease⁹, predisposition to weight gain or loss², or metabolic processes that are unrelated to body size. This core question forms the basis of a research thread that extends for well over one century and continues to be debated today^6–8. Herein, we review the evolution of concepts in this field and we supplement our report with new data analyses that reveal underlying current model limitations and that direct future potential research efforts.

REE Measurement

Resting energy expenditure is usually taken as a subject’s endogenous metabolic activity separate from the metabolic effects of food and activity. In this report we use the term REE in this context and recognize similar metrics such as resting, basal, and sleeping metabolic rates¹⁰.

Lavoisier and La Place were the first to measure animal heat production in 1780 using a “direct” ice calorimeter and five years later extended their research to humans¹¹. Today human energy expenditure, the source of endogenous heat production, is typically measured in the laboratory with indirect calorimetry¹ and REE is usually evaluated at thermoneutrality in the supine subject without movement at least 4 hours after the last meal and is reported as a 24 hour value¹². Rigorous adherence to measurement conditions, including ensuring subjects avoid exercise, stressful situations, or stimulants at defined intervals prior to the test will ensure the quality of data collected. Classical indirect calorimetry involves measurement of oxygen consumption and carbon dioxide and urinary urea production rates, although most investigators now use an abbreviated approach that eliminates the need for urinary urea analyses.

REE PREDICTION

Body Size Models

The major REE determinant is body size, an observation first studied systematically in the late nineteenth century⁹. Methods for accurately evaluating body composition did not appear until the middle of the twentieth century¹³ and so early approaches for referencing REE focused on two measurable features of body size, weight and height.

Surface Area Law

Scientific advances during the late eighteenth century provided a physical framework for understanding natural phenomena. Sarrus & Rameaux in an 1838 French Royal Academy presentation¹⁴ and later Rameux’s 1858 publication¹⁵ advanced the concept that food intake varies as a power function of body weight¹⁴. Energy intake, according to the author’s hypothesis, must satisfy the need for energy or heat production, the latter varying as a function of body surface area (SA). Human body volume and thus mass (M) was considered to be a cubic function of height (H), with surface area considered to be proportional (∝) to H². According to this construct, SA∝M^2/3 or M^0.66. Sarrus & Rameaux gave birth to the concept that REE∝SA or M^0.66. Heavy subjects would therefore need to eat less relative to their body weight than do subjects who have a smaller body mass¹⁶.

Newton’s Law of Cooling provides a physical basis for the biological construct of Sarrus & Rameux: the body cools at a rate approximately proportional to the temperature difference between the heated human body at temperature T and the surrounding environment Ts

$$\frac{dQ}{dt}=\alpha A(T_S-T)$$

where A is surface area and α the coefficient of heat transfer¹⁷. According to this construct the amount of heat, or energy, produced must balance surface-area related losses in order to keep core temperature stable.

Rubner in 1883¹⁸ first formally articulated the Surface Area Law based on his observation in fasting dogs that REE depends on surface area and is otherwise independent of body weight. These observations were later expanded to other species in 1901 by Voit¹⁹ and in 1938 by Benedict²⁰. Dubois & Dubois derived the first widely used human surface area equation in 1916²¹ and REE standards based on this and other surface area equations were developed and applied in clinical settings during the first half of the twentieth century. Rubner’s hypothesis was that neural signals in skin, which is proportional to surface area, stimulate cellular metabolic processes and heat production¹⁶.

Von Hoesslin in 1888 was among the first to question the validity of the Surface Area Law by showing that the rate of increase in heat production did not meet predictions when dogs were placed in reduced ambient temperatures²². Others also raised concerns with the Surface Area Law theoretical and empirical basis, but it was not until Kleiber and Brody’s seminal publications^{23, 24} that biologists began to look for alternative explanations for intra- and interspecies differences in REE, or more typically the metabolically similar basal metabolic rate.

Kleiber’s Law

Krogh in 1916 suggested that energy metabolism be expressed as kM^p, with k and p constants²⁵. By applying regression analysis methods to inter-species mammalian data, Kleiber²³ and Brody in 1932²⁴ showed that REE ∝ kM^p where p ranges from 0.70 to instead of p = 0.66 as would be predicted from Sarrus and Rameaux’s Surface Area Law. The inter-species “three-quarters power law” or “Kleiber’s Law” has since been the subject of extensive research and speculation related to mammalian biology²⁶. A consequence of mammalian REE scaling as M^0.75 is that smaller animals have a greater mass-specific REE (i.e., REE/M) than their larger counterparts and this observation is referred to as quarter-power scaling: REE/M∝M^−0.25.

Limitations of Body Surface Area Approach

A logical outgrowth of these collective early observations is that between-subject human REE comparisons should be based on REE/M^p(0.66 ≤ p ≤ 0.75 or REE/SA. This approach assumes that adjusting for the right body mass metric will eliminate the metabolic effects of body size differences that are present between individuals and thus provide the investigator with an unbiased measure of relative REE. A critical analysis of this approach begins with the question how does REE scale to adult human body mass? Importantly, even if interspecies comparisons conform to the Surface Area Law or Kleiber’s Law, a REE model for humans developed solely from these laws may not capture inter-individual variance attributed to age, sex, gender, or race in humans¹⁰. An ideal REE model for humans should include the aforementioned potential covariates with the capacity for scaling by body size to a power.

To examine the question of REE scaling to adult body size, Heusner was among the first¹⁶, and he did so by analyzing data reported on the 238 subjects who participated in the classic 1919 Harris-Benedict REE study⁴. Heusner found that REE scaled to M with powers (X±SE) of 0.61±0.04 and 0.38±0.05 in men and women, respectively. The author then analyzed a cohort of 169 obese men and women reported by White and Alexander²⁷ and respective M powers were 0.64±0.09 and 0.68±0.04.

Livingston and Kohlstadt²⁸ evaluated data from the Harris-Benedict⁴ and Owen et al.^{29, 30} studies along with measurements of their own to develop an allometric REE prediction model and additionally explored the developed model using data published as a supplement to the Institute of Medicine’s (IOM) Macronutrient report³¹. The authors found a small sex difference in how REE scaled to M and their composite equations on 655 adults are: 202xM^0.4722 with an R² of 0.64 and an age (A)-adjusted version, 261M^0.4456-(6.52xA), R²=0.68, both p<0.001.

Heymsfield et al.³² published REE scaling powers based on metabolic data from men and women reported in the IOM Macronutrient report and the New York Obesity Research Center (NYORC). The models with mass scaling powers were 4.92+M^0.69-A^0.14 for 429 IOM men 5.68+M^0.44-A^0.084 for 455 IOM women. The corresponding results for 147 NYORC men were 5.56+M^0.53-A^0.12 and for 197 NYORC women 5.70+M^0.46-A^0.11. These collective human studies reveal that the group mean powers observed when REE is scaled to body mass in adults, even after controlling for age, are highly variable and range widely, much more than the inter-specific Surface Area Law and Kleiber’s Law mass powers of 0.66 and 0.75, respectively. Expressing REE as a ratio to body mass alone raised to a power of 0.66 or 0.75 or to surface area may not appropriately adjust metabolism for between-subject differences in body size. In other words, adjusting energy metabolism as REE/M^0.66–0.75 will create a size-dependent measure if REE actually scales to body size as M^~0.45 as with Livingston-Kohlstadt²⁸ or Heymsfield et al.³². A question that arises is why are the powers observed when REE is scaled to body mass so variable and in some cases far smaller in magnitude than predicted from either the Surface Area Law or Kleiber’s Law? This question is examined in a later section of our review.

Rather than taking a simple ratio to body mass, a pragmatic solution for adjusting REE to body size is to calculate a “predicted” REE from a well-defined reference group. A clinical subject or research group’s REE can then be compared to that of the reference group as a residual, Z, %, or any number of other comparative statistics^{1–3, 8,3, 33, 34}. Many cross-sectional data sets were developed with the aim of referencing REE for surface area (i.e., weight and height), age, and sex³⁵. Numerous statistical prediction formulas are used to reference REE for age, sex, and race, and countless research reports over the past century have used these formulas to see if a subject or group’s REE is high or low relative to body size.

Body Composition Models

Molecular and Cellular Levels

The next period of energy metabolism-body size research had roots in the late 19^th century when animal and fetal chemical composition were first established, eventually leading to the discovery that the body contains tissues of varying metabolic activity. Ludwig Pfeiffer in 1887³⁶ first noted that the variability in animal body water content could be reduced if expressed on a fat-free basis. The concept of fat-free tissue was further elaborated on by Voit in 1901¹⁹ and Rubner in 1902³⁷ who spoke of an “active” protoplasmic mass. Adolf Magnus-Levy reported in 1906³⁸ that ideally tissue composition be reported on a fat-free basis, giving rise to the concept of a fat-free mass (FFM). By 1937 Hastings and Eichelberger³⁹ further refined the FFM concept by demonstrating that water is not bound by neutral fats, nitrogen, or electrolytes. Out of this initial work arose the important division of body mass into two-compartments, fat mass and FFM.

Prior to World War II, however, there were few approaches that could provide reliable estimates of total body fat and FFM in humans. Then, just prior to the war, Talbot in 1938 reported a relationship between skeletal muscle mass and 24-hour urinary excretion of creatinine⁴⁰. Behnke and his colleagues a few years later in 1942 first described the now-classical two-compartment underwater weighing method that partitions body mass into fat and FFM⁴¹. Not long after, Pace and Rathbun in 1945 described the hydration constancy of FFM that provided the basis of the two-compartment hydrometry model⁴². Anderson and his colleagues in 1961 reported a fat estimation method based upon whole-body ⁴⁰K counting⁴³ and Moore and his colleagues in 1963 reported the use of total body potassium and exchangeable potassium for estimation of “body cell mass”⁴⁴. The stage was thus set for moving beyond body weight and height as a means of adjusting REE for between-individual differences in body size.

Miller and Blyth in 1953 were among the first to search for body composition methods that could be used as a “suitable reference standard for the expression of basal oxygen consumption”—in other words, for REE⁴⁵. Good correlations were observed in normal college students between “lean body mass” (i.e., largely FFM) measured by underwater weighing, urinary creatinine excretion, and whole-body basal oxygen consumption. The authors concluded from their findings that “lean body mass” appeared “characterized by a constant basal rate of oxygen consumption”.

During the same year in 1953⁴⁶ Keys and BroŽek advanced the concept of metabolically “active tissue” as the difference between body mass and primarily fat, extracellular fluid, and bone. This concept is similar to that articulated earlier by Voit¹⁹ and Rubner³⁷ of an “active” protoplasmic mass. The most variable of the three “inactive” components, fat, was emphasized by Keys and Brozek as practical to measure and their experimental body composition observations gave impetus to the use of FFM as a means of adjusting REE for differences in body size. Keys and Brozek noted that the lower REE expressed per unit body weight or surface area in women compared to men would likely resolve if REE were to be expressed per unit FFM or ideally active tissue mass⁴⁶. Behnke similarly expressed the view in 1953⁴⁷ that sex differences in the “standard metabolic rate” would resolve if lean body mass replaced body weight or surface area as a means for adjusting metabolic measurements for body size.

Keys and Brozek in their 1953 review lament that “no aspect of basal metabolism is more confused than the problem of the correct method of expressing basal metabolic rate in obesity”⁴⁶. Subnormal values are observed when REE in the obese is referenced to either body weight or surface area and the authors speculated that the “problem would be simpler if the energy metabolism is correctly attributed to the cellular mass of the body”.

Von Dobeln first tested these hypotheses in 1956⁴⁸ by evaluating basal whole body oxygen consumption and FFM by underwater weighing in healthy young adult men and women. The author confirmed that men have a significantly greater VO₂/kg body weight or VO₂/M² surface area compared to women. The women, however, had a greater VO₂/kg FFM compared to the men (p<0.1). Seemingly contradictory observations such as these ushered in the modern era of human metabolic rate assessment.

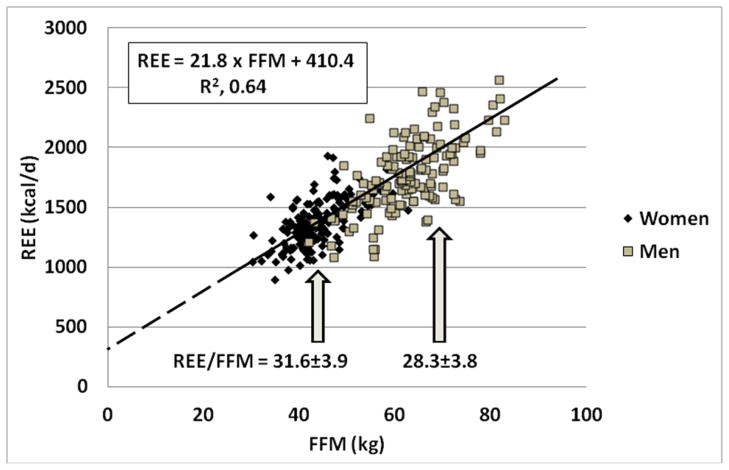
Von Dobeln’s observations six decades ago can be understood in the context of what is now known about the relationship between REE and FFM. As noted, REE should ideally be highly correlated with the body size-composition measure and the adjusted value of REE should be independent of body size. Consider the simple regression model REE = mFFM+b, with m slope and b y-axis (REE) intercept. For the ratio REE/FFM to be independent of FFM, the y-axis intercept must be zero so that REE=mFFM and thus REE/FFM is a stable value (i.e., m) across all healthy adults. In fact, when REE is regressed against FFM the b intercept term is positive and differs significantly in magnitude from zero^1–3. Thus, women who on average have a smaller FFM than men have a larger REE/FFM ratio. This phenomenon is shown in Figure 1 with data taken from a previously published study by our group⁴⁹. Resting energy expenditure for men and women is plotted against FFM and the resulting regression line has a significant intercept term of 410.4 kcal/d. According to this construct and as Von Dobeln showed, women have a larger REE/FFM than do men by about 10% (X±SD, 31.6±3.9 vs. 28.3±3.8 kcal/kg per day). But do women indeed have a relatively “greater” REE than do men after taking more than FFM into account?

Figure 1.

Resting energy expenditure (REE) versus fat-free mass (FFM) in 131 men and 158 women reported in an earlier study⁴⁹. The respective REE/FFM ratios±SD for men and women are also presented in the figure.

One consideration is that adipose tissue, the compartment in which most fat or triglyceride resides, has a substantially lower mass-specific energy expenditure than adipose-tissue free mass (i.e., the tissue-organ level counterpart of FFM)⁵⁰. Women have a higher fraction of their body weight as adipose tissue compared to men and not taking this large compartment into account when interpreting the REE/FFM ratio is one factor that can lead to the impression that women have a “high” metabolic rate for their body size.

Now the standard approach to account for sex differences in REE after adjusting for FFM is to add sex as a prediction model covariate in addition to fat mass, age, and race^{1–3, 51}. The results are typically variable with respect to the significance of these covariates and the reported prediction model will reflect sample size and characteristics along with the methods used to measure REE and body composition. However, even after appropriately adjusting for fat mass, age, and race, women still are often found to have a REE that differs significantly from men².

But fat-free mass has remained the main compartment used by investigators over the past several decades to adjust REE for body size, although Keys and Brozek recognized the need to remove low metabolic rate compartments other than fat from body mass as a means of estimating “metabolically-active” mass⁴⁶. Might these other compartments be ideal measures for adjusting REE for between-individual differences in body size? Information on the relationships between REE and compartments beyond FFM is scant.

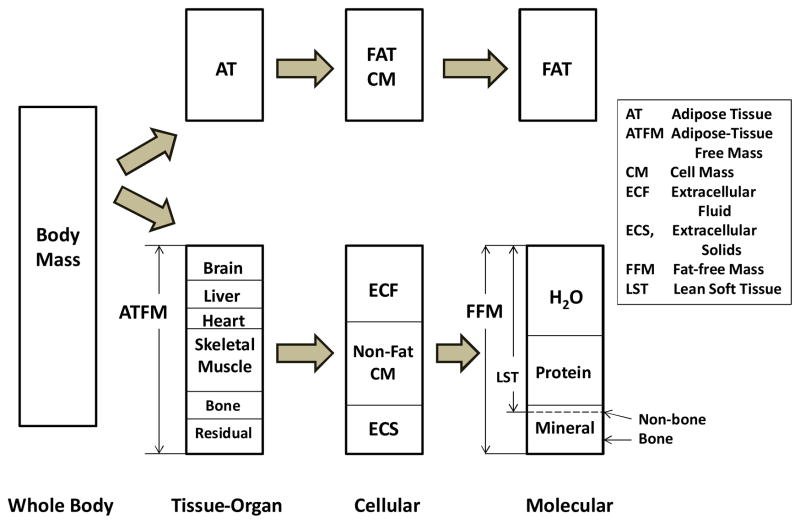
To explore this question the full scope of available body compartments needs to be defined first. Four body composition “levels” are relevant when considering REE: whole-body, tissue-organ, cellular, and molecular (Figure 2). Metabolic and body composition results from two previously published reports from our group^{52, 53} provided data for the descriptive examples that follow. In this work, subjects were healthy weight stable adults ranging widely in age and body mass index who participated in NYORC and Kiel body composition studies. Additional information on these groups and the measurement methods are provided in Supplementary Material.

Figure 2.

Major whole body compartments representing body mass across the tissue-organ, cellular, and molecular body composition levels as cited in this review.

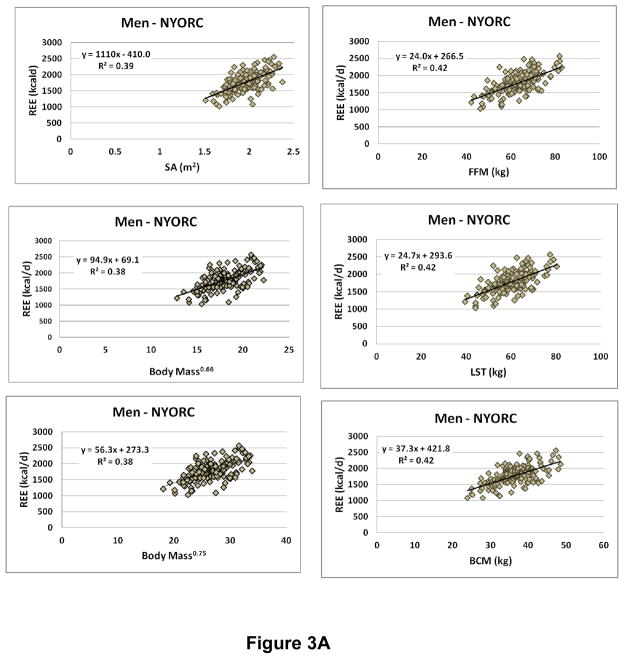
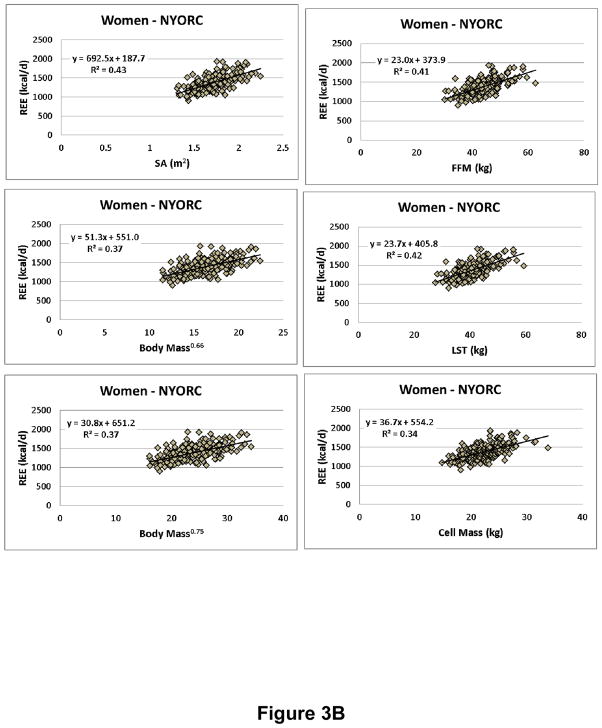
We evaluated the “metabolically active” compartment as suggested by Keys and Brozek at the molecular level as FFM and lean soft tissue (LST) mass, defined as the difference between FFM and the low energy expenditure compartment bone (i.e., bone mineral content, BMC). Both FFM and LST (i.e., FFM-BMC) were estimated with dual-energy x-ray absorptiometry (DXA). Cell mass (CM) at the cellular level was estimated from the whole-body potassium space using the ⁴⁰K method as reported by Moore et al.⁴⁴ and later refined by Wang et al.⁵⁴. Moore considered the body’s cell mass as the actively metabolizing tissue devoid of fat, extracellular fluid, and bone minerals. We thus had three “metabolically-active” compartments for review (i.e., FFM, LST, and CM) in addition to the three provided by body mass and height, surface area, M^0.66, and M^0.75. The results for multiple regression analyses for REE vs. body size-composition are shown in Supplementary Table 1 and scatter plots are shown in Figure 3A (NYORC men) and 3B (NYORC women). Age was added as the only potential covariate to all models.

Figure 3.

Resting energy expenditure (REE) versus body mass, stature, and composition measures in A. men (n=154) and B. women (N=208) from the New York Obesity Research Center (NYORC) study (Supplementary Material). CM, cell mass; FFM, fat-free mass; LST, lean soft tissue; SA, surface area. Data are fit with simple power functions and all are statistically significant at p<0.001.

Within each sex and center (NYORC and Kiel) group the correlations (i.e., R-values) between REE and surface area, weight^0.66, weight^0.75, FFM, LST, and CM were approximately the same. Most of the models included age as a significant covariate and all had significant intercept terms (Supplementary Table 1). Thus, none of these measures meets the criteria for serving as an ideal REE reference since all relate to REE with a significant intercept. Qualitatively, the presence of a significant regression model intercept leads to the concern noted by von Dobeln⁴⁸ and many others since⁵⁵: compared to small subjects, “large” subjects have a lower magnitude REE/FFM. Thus, taking the ratio of REE to FFM, LST, or even CM raises the possibility that subjects who have a large body size have a relatively lower REE⁵⁵.

The presence of a non-zero intercept requires the use of statistical REE adjustment approaches to establish if a subject or group has a “low” or “high” metabolic rate. The question arises, if we indeed can measure the “metabolically active” compartment of the body with great precision, why should there be a non-zero intercept when REE is regressed against FFM, LST, or CM?

Tissue-Organ Level

The resolution to this question may lie in the observation that body composition is more heterogeneous than a division into FM and FFM or even CM; a simple two-component model, even with covariates, does not account for the different metabolic activities of tissues and organs. For example, the brain is known to consume about one-fifth of a person’s REE, whereas bone is essentially metabolically inert⁵⁰ even though both are components of FFM. This implies that to remove the intercept, one should ideally measure energy expenditure at the tissue-organ level.

The first major advance in measuring tissue and organ volumes occurred in 1971 with the introduction of computerized axial tomography (CT) by Hounsfield⁵⁶. Accurate estimates of all major organ and tissue volumes were made possible by combining contiguous high resolution cross-sectional images⁵⁰. The reconstructed volume estimates were then converted to mass with an assumed tissue density (Table 1). Magnetic resonance imaging (MRI) was introduced in the early nineteen seventies by Lauterbur, Mansfield, and Damadian⁵⁶. As with CT, MRI provides high resolution cross sectional images that can be used to reconstruct tissue and organ volumes⁵⁰.

Table 1.

Tissue and organ basal mass-specific metabolic rates (kcal/kg/d) and density^*.

Organ/Tissue	Young non-obese adult	Young obese adult	Older Adult Non-obese+	Density (g/cm3)
Brain	240	232.8	235.2	1.03
Heart	440	426.8	431.2	1.03
Liver	200	194.0	196.0	1.05
Kidneys	440	426.8	431.2	1.05
SM	13	12.6	12.7	1.04
AT	4.5	4.4	4.4	0.92
Residual	12	11.6	11.8	++

^*From^{50, 64–66, 69}

⁺age >50 yrs

⁺⁺Residual mass is not assigned a density but is calculated as body mass minus the sum of other measured mass components.

Abbreviations: AT, adipose tissue; SM, skeletal muscle.

The availability of tissue-organ level (Figure 2) estimates provided a new opportunity to develop physiological REE prediction formulas based upon established heat production rates of major body tissues. The concept underlying these models is simple: tissue and organ mass can be estimated with CT or MRI; the energy expended by each tissue and organ can be calculated as the product of mass and mass-specific metabolic rate, the latter based on values compiled from in vivo and in vitro observations⁵⁰; and REE can then be calculated as the sum of all tissue and organ metabolic rates.

A challenging aspect of these models is derivation of the tissue and organ mass-specific metabolic rates. The relative contributions of tissues and organs to energy expenditure was first studied, largely in intact animals or in isolated preparations, by Barcroft in 1908⁵⁷ and later in 1939 by Field et al.⁵⁸ The 1940s ushered in a new era in measurement of human tissue and organ oxygen consumption as typified by the classic study of Kety and Schmidt in 1945⁵⁹. The authors were the first to estimate brain mass-specific oxygen consumption in unanesthetized healthy young men (3.7 ml/100 g/min) using the nitrous oxide method to measure cerebral blood flow⁵⁹. Assuming that one liter of consumed oxygen translates to 4.9 kcal^{60, 61}, brain mass-specific energy expenditure in these subjects was calculated as 260 kcal/kg/day. Data for other tissues and organs appeared in the literature during this period and by 1950 authors such as Drabkin were tabulating estimated oxygen consumption values for brain, heart, liver, kidneys, and skeletal muscle⁶². Brozek and Grande reported human mass-specific oxygen consumption values for these five compartments with additional refinements in 1955⁶³. Holliday et al. in 1967 extended these efforts by calculating organ mass-specific metabolic rates to produce the first physiological tissue-organ REE model for humans⁶⁰. Elia in 1992 derived mass-specific organ metabolic rates for liver, brain, heart, kidneys, skeletal muscle, adipose tissue, and residual mass, calculated as the difference between body mass and the sum of the measured tissues and organs⁶⁴. Gallagher et al. in 1998⁵⁰ evaluated Elia’s physiological model with tissue and organ volumes measured with MRI in healthy young non-obese adults and found excellent agreement between “calculated” and measured REE⁵⁰. Gallagher’s approach was to calculate the REE of each organ as the product of MRI-measured mass and assumed mass-specific metabolic rate and to then sum the seven estimated whole-body REE components (Table 1). These observations have since been confirmed and expanded upon by Wang et al.^{65, 66}, Later et al.⁶⁷, and Muller et al.⁶⁸ and the mass-specific metabolic rates reported by Elia have been found applicable across men and women⁶⁹ but values are slightly lower in obese⁶⁵ and elderly subjects (Table 1)⁶⁶.

Although the relative contribution of tissues and organs to REE was thus known and appreciated for almost one century, the major breakthrough with respect to physiological REE model development occurred when MRI became available as a means of safely quantifying body composition across the entire human lifespan.

The most striking feature of viewing REE from the tissue-organ perspective is the large contributions of four FFM components (brain, liver, heart, and kidneys) to whole body REE. While <6% of representative body mass, these organs contribute to 60–70% of REE^{50, 63}. Lungs, spleen, and other organs that are relatively small in mass also likely have high mass-specific metabolic rates. Physiological REE model terms for brown fat and the microbiome are not yet available.

In light of this emerging information on human energy metabolism it is worth reconsidering early observations on the relationships between REE and body size and composition. Not only might accounting for organ energy expenditure reduce between-subject variability in REE, but it also might allow REE to form a ratio to body composition that is independent of body size^{55, 70}. Indeed, a growing literature supports the hypothesis that tissue-organ proportions vary with body size and adult age⁷¹, across men and women⁷², and between race groups⁷³. Several representative examples are presented here.

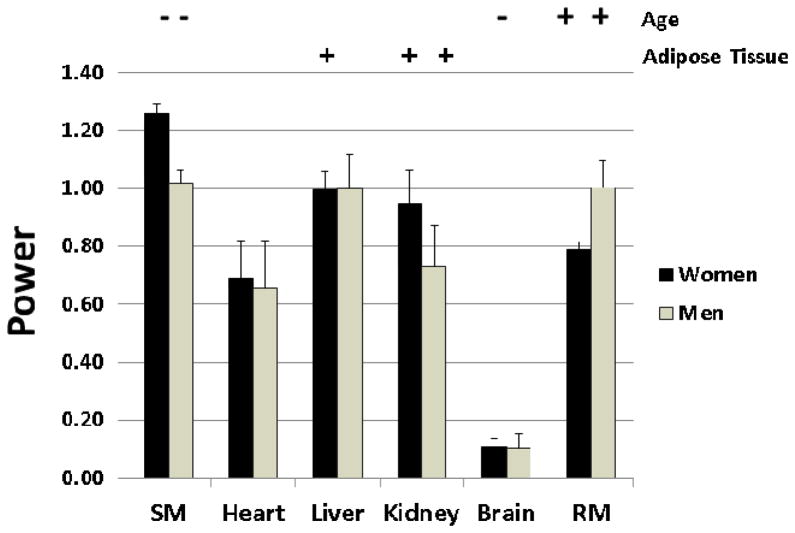
Brain mass, which accounts for about 20% of REE^{50, 71}, is only weakly associated with adult body mass, stature, and FFM⁷⁴. After controlling for FFM and age, tall subjects and women have a relatively smaller brain mass (i.e., as brain/M or FFM) than short subjects and men, respectively⁷⁴. An example of how brain mass differs in relation to other major tissues and organs is shown for the Kiel subjects in Figure 4. Multiple regression analysis was used to establish how skeletal muscle, heart, liver, kidney, brain, and residual mass (weight minus the sum of other tissues, including adipose tissue, and organs) scale to FFM. Tissue-organ mass was set as the dependent variable and FFM, age, and adipose tissue mass as potential predictor variables in multiple regression models. A FFM power of 1.0 (i.e., tissue-organ ∝ FFM¹) generally implies that the tissue and organ change in proportion to FFM. As shown in the figure, all tissues and organs scale to FFM with powers approaching 1.0 except brain, which has powers <0.2 for both men and women. The implication is that the fraction of FFM as brain scales inversely to FFM. In other words, the fraction of FFM as brain is smaller in subjects with a large FFM. Each tissue and organ is additionally associated with age and adipose tissue mass as other FFM predictor variables. This simple descriptive analysis begins to reveal the tissue-organ and thus mass-specific energy expenditure heterogeneity of FFM.

Figure 4.

Powers of Kiel Study (Supplementary Material) tissue-organ level components adjusted for significant age and adipose tissue mass effects observed when scaled to adipose-tissue free mass. The presence of a significant positive (+) or negative (−) age or adipose tissue covariate is noted in the figure. Results are shown ±SE. RM, residual mass; SM, skeletal muscle mass.

The tissue-organ model may also allow us to reduce the impact of or do away with FFM-based REE prediction model covariates such as age and race. For example, old subjects have a smaller fraction of FFM as skeletal muscle compared to young subjects⁷⁵, while the fraction of FFM as skeletal muscle is greater in African Americans than Caucasians⁷³.

Hence, the emerging view is that compartments such as “active protoplasmic mass” and FFM are not metabolically homogeneous but rather vary systematically in tissue-organ proportions with such factors as age, sex, and race.

One approach for establishing the appropriateness of an absolute REE measurement for body size and composition is to calculate a predicted value for REE using measured organ mass and the mass-specific metabolic rates presented in Table 1. The measured values can then be compared in control and active intervention groups to the predicted REE values⁵⁰.

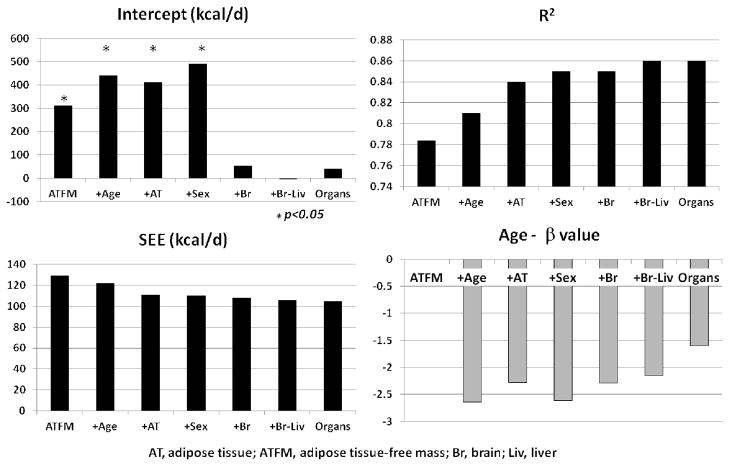
One explanation for the non-zero intercept for the REE-FFM function is that FFM is not a metabolically homogeneous compartment but instead FFM varies systematically in tissue-organ proportions as a function of body size⁷⁰. The availability of tissue-organ and REE measurements from the Kiel Study allows us to test this hypothesis. Here we used the tissue-organ model approach (Figure 2) with adipose tissue and adipose-tissue free mass (ATFM) corresponding to molecular level fat and FFM, respectively. The first step was to derive the traditional REE model with ATFM alone as the predictor variable (model A: R² = 0.78 and SEE = 129.4 kcal/d, Table 2 and Figure 5). Model R² increased and SEE decreased with addition first of age (model B: R², 0.81;SEE, 121.9) and the adipose tissue mass (model C: R², 0.84;SEE, 112.2). Sex added as a borderline significant (model D: p=0.08) covariate to the REE predictor model with ATFM, age, and adipose tissue mass as significant covariates. All four of these models had statistically significant intercepts and they resemble the general form of traditional FFM-based REE prediction models^{1–3, 55}.

Table 2.

Regression models developed for Kiel subjects for REE vs. tissue-organ level body composition.

Model	R (R2)	SEE	P
A. 311.0†+24.4ATFM	0.88 (0.78)	129.4	<0.001
B. 442.2†+24.0ATFM-2.6A	0.90 (0.81)	121.9	<0.001
C. 411.0†+22.1ATFM+4.3AT-2.3A	0.92 (0.84)	112.2	<0.001
D. 491.4†+19.4ATFM+6.2AT+72.7S*-2.6A	0.92 (0.85)	110.0	<0.001
E. 54.4+19.8ATFM+5.3AT+303.7Br-2.3A	0.92 (0.85)	108.0	<0.001
F. −6.1+17.3ATFM+4.5AT+326.9Br+112.8Li-2.1A	0.93 (0.86)	106.4	<0.001
G. 40.6+5.1AT+294.2Br+141.5Li+20.3SM+13.7RM-1.6A	0.93 (0.86)	105.9	<0.001

N= 37 men and 66 women.

^*p=0.08;

^†intercept p<0.05

Abbreviations: A, age; AT, adipose tissue; ATFM, adipose tissue-free mass; Br, brain; Li, liver; S, sex.

Figure 5.

Characteristics of multiple regression models predicting REE in Kiel Study (Table 2 and Supplementary Material) participants. The simplest model predicts REE from adipose-tissue free mass (ATFM) with subsequent addition of age, adipose-tissue (AT), sex, brain mass (Br), and liver mass (Liv) as potential covariates. The final model included brain, liver, kidneys, spleen, heart, skeletal muscle, bone, adipose tissue, and residual mass as potential covariates with brain, liver, skeletal muscle, bone, adipose tissue, residual mass, and age remaining as significant predictor variables. Of the added potential predictor variables, brain, liver, skeletal muscle, bone, adipose tissue, residual mass, and age added as significant covariates. The age panel depicts the β values for age observed across the seven models.

We next added brain mass to this last model, knowing from our earlier example that brain relates substantially differently to FFM than do other tissues and organs. Adding brain mass to the model further decreased the SEE (model E: 108.0) and substantially reduced the intercept from 411.0 to 54.4, which was then non-significant. This observation is consistent with similar findings on an independent database reported by Javed et al.⁷⁶. When high metabolic rate liver mass was then added to the expanded ATFM-centered model, the R² increased further (model F: 0.86), SEE decreased (106.4), and the intercept term remained non significant at −6.1. Sex did not add to either of these organ-supplemented statistical models although age remained a significant covariate. We lastly excluded the composite ATFM compartment and developed a REE prediction model with brain, liver, kidneys, spleen, heart, skeletal muscle, bone (as BMC), adipose tissue, and residual mass along with age and sex as potential predictor variables. Of these, brain, liver, skeletal muscle, bone, adipose tissue, residual mass, and age added as significant covariates. This last model (G) had the highest R² (0.86) and lowest SEE (105.9) of the developed series of REE prediction models with a non-significant intercept of 40.6.

Several new observations emerge from this series of analyses. First, building cross-sectional REE prediction models around compartments such as FFM, and by inference, LST and CM, fails to capture the metabolic heterogeneity that ultimately yields an individual or groups REE. Simply adding brain mass to the “traditional” REE prediction model with ATFM, age, and sex largely eliminated the significant intercept term inherent in these models. Liver, another high metabolic rate organ, also added significantly with brain to the traditional ATFM-based model with elimination of the borderline significant sex term. An opportunity clearly exists to expand these kinds of cross-sectional statistical REE prediction models with larger and more diverse subject groups and to longitudinally monitored cohorts. We can pose questions such as why is liver so variable in mass between individuals such that its effect on REE is significant even after controlling first for ATFM? Does brain mass, which changes little with body size, explain the “non-zero” intercept phenomenon or are other factors involved? Very little is known about how organs change in size with weight gain or loss or with aging and if they remain stable proportions of ATFM.

A second observation is that even though we accounted for all major organs and tissues in our final example model, age remained a significant predictor of REE (Figure 5); older subjects are projected to have a lower REE even after controlling for the mass of all major measured organs and tissues as previously reported by Gonzalez et al.⁷⁷. Herein lays a fundamental limitation of conventional CT or MRI: measured values reflect tissue volume and not composition. Taking liver as an example, we can estimate total liver volume but we cannot account for liver composition in our study. Fat infiltration, collagen deposition, and any number of other components might influence liver composition and thus mass-specific energy expenditure in a manner that cannot be accounted for by measured total liver volume. With the perspective of aging, we ideally would like to have a measure of liver fat-free cell mass. A related effect is that all lean organs and tissue have some lipid (fat), such as in cell membranes, and the fractional amount might vary under different conditions such as noted for liver. Among all organs, brain has the highest fractional lipid content and it is unclear if the reported proportion (Supplementary Table 2) is stable between individuals. Imaging methods, advancing at a rapid pace, might in the near future provide measures of fat-free organ mass.

Returning now to the classical question, why are such variable powers observed when REE is scaled to body mass in adult humans, in some cases far different in magnitude than predicted from either Surface Area of Kleiber’s Laws? Here we can gain insights into these associations through the newly acquired knowledge developed though our analyses of REE links to tissue-organ body composition. Our fundamental model is REE∝kM^p and we can consider adult body mass developing along two planes, one as a function of height and the other related to adiposity. With greater adult height, Quetelet’s rule states that M∝H^{2 53}. Body mass index (W/H²) can serve as a measure of adiposity and we can estimate REE for any given body mass, height, and age using the sex-specific Harris-Benedict equations⁴.

We first examine how REE varies across subjects differing in height. Beginning with an arbitrary fixed BMI (e.g., 24 kg/m²) and age (25 yrs), we can model how REE scales to M by systematically varying H (Supplementary Material). Our model reveals mass powers of 0.81 and 0.51 in men and women, respectively. If we instead lower BMI in our model to 20 kg/m², respective powers increase to 0.83 and 0.54. For perspective, recall that adults differ in relative tissue-organ proportions across height⁵³ and between men and women⁷⁴. These underlying tissue-organ patterns begin to explain the differing empirically observed REE-body mass scaling patterns noted earlier in our review.

We next model REE as a function of adiposity by keeping height constant and systematically varying BMI by changing body mass. Resting energy expenditure now scales to body mass with powers of 0.61 and 0.43 in men and women, respectively. These substantially lower body mass powers presumably reflect a very different mix of low mass-specific adipose tissue⁵⁰ and other higher metabolic rate organs and tissues than observed in our variable height model. If we combine our height and adiposity models across men and women we find that REE ∝ M^0.54. Real populations are obviously far more complex with large variations in height, body mass, age, race, and many other factors. Varying adiposity while keeping height constant thus presents a distinct pattern of changes in tissue and organ proportions that has yet to be fully identified.

An obvious conclusion from this simple modeling exercise is that the scaling relationship between REE and body mass depends on the distribution of body mass across subjects varying in stature, adiposity, or a combination of the two. Stature and adiposity variation each brings differing tissue-organ relationships into play. The notion of a universally applicable scaling relationship between REE and body mass in humans is likely an elusive goal.

EMERGING CONCEPTS

Our historical overview and entry into the current era with technological advances point directly to the next potential wave of research aimed at establishing the basis for individual differences in REE after controlling for body size. We have now shown the complexity of body size-composition relations as defined by adult human energy expenditure. Clearly, these relations negate the likelihood of finding a simple and practical ratio-based means of universally adjusting REE for differences in body size and composition. However, if we return to the key question, if and how subjects differ in REE after controlling for body size and composition, our focus extends beyond the whole body to individual tissues and organs. We might ideally capitalize on emerging non-invasive technologies to measure individual organ mass-specific metabolic rates and cell mass. Rather than focus on the whole body and the associated complexities that come with that process, we might ask instead if brain, liver, or any other organ’s metabolic rate is appropriate for its cell mass. As noted earlier, we can now measure the volume of individual tissues and organs with great accuracy. A new line of research needs to extend this work to organ tissue composition, notably separating the metabolically active portions of cells from other less active or metabolically inactive components. A second line of research needs to focus on existing or new methods of non-invasively quantifying organ mass-specific metabolic rates, of which there are several examples^{78, 79}. Armed with these new methods, studies can focus on how the energy expended by each organ change with perturbations in energy balance, including weight gain and loss brought about by different dietary measures and physical activity regimens.

While our review has focused on REE evaluation in humans, an intense parallel discussion is ongoing among investigators exploring aspects of energy balance components in animal models^6–8. Many of the same critical issues of REE adjustment for body size are at play and the potential advances described in this report are directly applicable to animal research.

CONCLUSIONS

The question of how REE relates to adult human body size and composition has been of interest to workers in diverse research areas for well over one century. A new emphasis is appearing on if and how subtle REE variation can be accounted for by genetic and metabolic processes that are independent of body composition. As shown in our review, the field has evolved in stages driven by new physical theories and measurement technologies. We now stand at the horizon of the next potential advance beyond the whole body to evaluate the REE of individual tissues and organs. Developments in this area are well under way and this tissue-organ focus will likely finally resolve many lingering questions related to biological factors that influence an individual’s energy expenditure.