Faster STORM Using Compressed Sensing

Abstract

In super-resolution microscopy methods based on single-molecule switching, the rate to accumulate single-molecule activation events often limits the time resolution. Here, we developed a sparse-signal recovery technique using compressed sensing to analyze images with highly overlapping fluorescent spots. This method allows an activated fluorophore density an order of magnitude higher than what conventional single-molecule fitting methods can handle. Using this method, we have demonstrated imaging microtubule dynamics in living cells with a time resolution of 3 s.

Despite many achievements in the field of super-resolution microscopy in the past few years^1,2, live cell imaging remains a challenge because of the need for high temporal resolution. Using the same optical system and detector as in conventional light microscopy, super-resolution microscopy naturally requires longer acquisition time to obtain more spatial information, leading to a trade-off between its spatial and temporal resolution. In super-resolution microscopy methods based on single-molecule stochastic switching, also known as Stochastic Optical Reconstruction Microscopy (STORM) or (Fluorescence) Photoactivated Localization Microscopy ((F)PALM)^3,4,5, each camera image samples a random subset of probe molecules in the sample. The temporal resolution is mostly determined by the time to accumulate enough single-molecule switching events so that adjacent localization points can be closer than one half of the desired spatial resolution (Nyquist criterion)⁶. Achieving a 50–70 nm spatial resolution usually requires several thousand frames, or tens of seconds. Increasing the switching rates using stronger excitation can improve the time resolution⁷, but such high excitation intensity could increase photodamage. Moreover, in the case of fluorescent proteins which are often the best labels for live samples, attempting a fast switching rate can cause signal degradation⁷.

An alternative approach is to increase the density of activated fluorophores so that each camera frame samples more molecules. However, this high density of fluorescent spots causes them to overlap, invalidating the widely used single-molecule localization method. Recently, a number of methods have been reported that can efficiently retrieve single-molecule positions even when the single fluorophore signals overlap. These methods are based on fitting clusters of overlapped spots with a variable number of PSFs with either maximum likelihood estimation^{8, 9} (for example, using the DAOSTORM algorithm⁸) or Bayesian statistics¹⁰. The Bayesian method has also been applied to the whole image set¹¹. Here, we present another approach based on global optimization using compressed sensing, which does not involve estimating or assuming the number of molecules in the image. We show that compressed sensing can work with much higher molecule densities compared to DAOSTORM and demonstrate live cell imaging of fluorescent protein labeled microtubules with 3-second temporal resolution.

Compressed sensing has demonstrated great success in many different fields of signal processing^{12, 13}. If the original signal is sparse (i.e. mostly zeros) or can be made sparse after a given transformation, compressed sensing can precisely recover signal from highly noisy or corrupted measurements. Compressed sensing classically deals with a linear measurement b of the original signal x

$$\mathit{b}=\mathit{\text{Ax}}$$ (1)

where the matrix A is a known measurement function. If x is sparse, it can be exactly recovered by minimizing its L1 norm (the sum of the absolute value of each element)

$$\text{minimize}\parallel \mathit{x}{\parallel }_1\text{subject to}\mathit{b}=\mathit{\text{Ax}}$$ (2)

even when b has much fewer elements than x has.

In STORM, the camera image has a linear and shift-invariant relationship with the true molecule distribution to be recovered. To model this relationship as in Eq. 1, we introduce a discrete grid to describe the molecule positions instead of using a list of molecule coordinates as is typically done to represent super-resolution images. The grid spacing is kept much smaller than the camera pixel size (e.g. 1/8 the pixel size) to ensure sufficient accuracy. In this representation, both the molecule distribution in each camera frame, x, and the final super-resolution image summed from all frames are pixelated images. (Supplementary Fig. 1). In each camera frame, every grid point in x represents the brightness of a molecule located at this point. Grid points with no molecules fluorescing will have a value of zero. We then model the camera image as the convolution of the fluorophore distribution, x, with the point spread function (PSF), in a matrix form as shown in Eq. 1. In this case, b corresponds to the camera image, and A corresponds to the PSF. The stochastic switching ensures sparse fluorophore distribution in each frame, that is, most of the elements in x are zeros. Therefore, knowing the PSF, compressed sensing can recover the fluorophore positions even with extensive spot overlap in b. Taken into consideration that the measurement process is inherently noisy primarily due to the photon counting noise, we constrained the L1 norm minimization with:

$$\text{minimize}\parallel \mathit{x}{\parallel }_1\text{subject to}\parallel \mathit{\text{Ax}}-\mathit{b}{\parallel }_2\le \epsilon ·{(\mathrm{\Sigma }{\mathit{b}}_j)}^{1/2}$$ (3)

Due to the Poission distribution of the photon shot noise in b, ε² is exactly equivalent to a target unweighted reduced χ² in the framework of least square fitting. The sum of all x’s from each camera frame gives the final reconstructed image of the structure. More details about our implementation are in the Methods and Supplementary Figures 1 and 2 online.

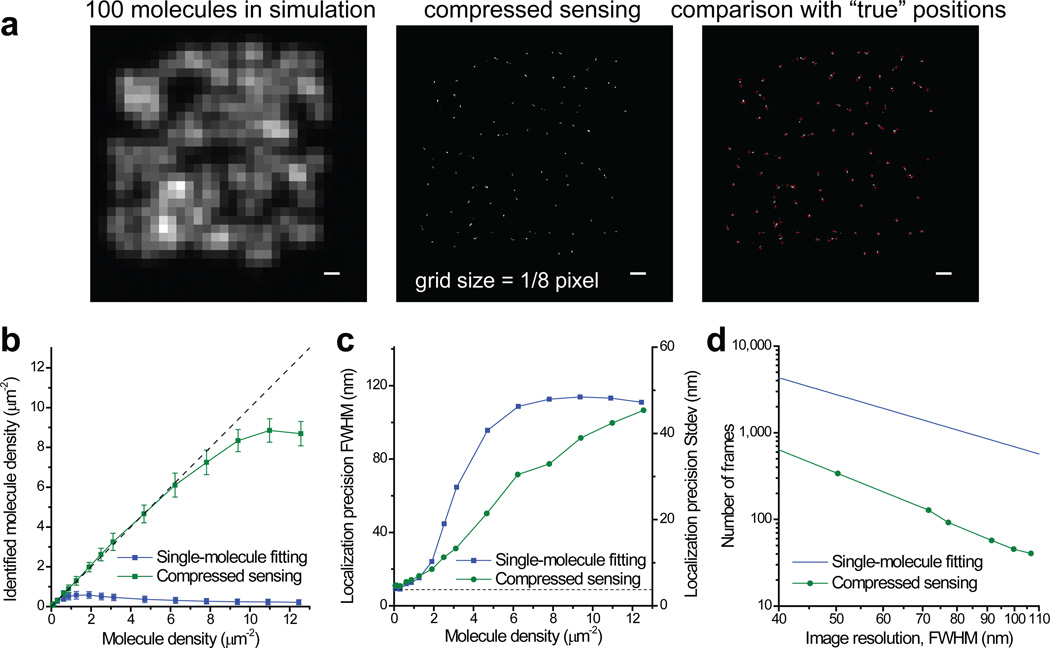
Using compressed sensing, we analyzed a simulated image with 100 molecules randomly distributed in a 4 µm × 4 µm region (Fig. 1a). Although the images of individual molecules completely overlapped, we could identify almost all of the molecules. We have performed further simulations using molecule photon statistics derived from real experiments and with the molecule density ranging from 1 molecule to 200 molecules (12.5 µm⁻²) in the simulation field. To make a fair comparison with other molecule identification methods which return a collection of molecule coordinates, we converted the compressed sensing result from a pixelated image to a molecule list by identifying clusters of non-zero grid points (see Online Methods). Molecules within the 2-pixel border of the simulation region were excluded from the comparison because they experienced lower effective molecular density. In the higher photon number case corresponding to Alexa Fluor 647 (Fig. 1b), compressed sensing identified up to 15 fold as many molecules as compared to our previously used single-molecule fitting method that rejects all overlapping spots¹⁴ (up to 8.8 µm⁻² identified by compressed sensing compared to 0.58 µm⁻² by single-molecule fitting). This improvement is in fact close to the fundamental limit (Supplementary Note and Supplementary Fig. 3). Compressed sensing also out performs DAOSTORM⁸ (Supplementary Note and Supplementary Fig. 4). The localization error of all three methods follows similar increasing trends with increasing molecule density (Fig. 1c and Supplementary Figs. 4–5). At very low densities, compressed sensing has slightly worse (~20%) precision compared to single-molecule fitting, possibly due to it involves an unweighted least square constraint instead of a weighted one. At high densities (> 2 µm⁻²), compressed sensing is substantially better.

Figure 1.

STORM image analysis using compressed sensing. (a) Simulations that demonstrate the capability of compressed sensing to identify molecules efficiently at a high density. Scale bars: 300 nm. Also see Supplementary Figure 7 for a low signal example. (b) Comparison of efficiency of molecule identification using compressed sensing and singe-molecule fitting. The simulation is for an average photon number of 3,000 per molecule and a background of 70 photons per pixel (see online Methods). Error bars stands for standard deviations from repeated simulations. The dashed line marks the case when the number of identified molecules equals to the number of molecule sin the simulation. (c) Comparison of localization precisions. The y axis is labeled in both FWHM and standard deviation (SD). The dashed line marks the Cremer-Rao lower bound (CRLB) of single-molecule localization (8.8 nm FWHM). (d) Minimum number of frames to achieve a given overall image resolution for a continuous 2D sample. The line for the fitting method is calculated using a constant 0.58 µm⁻² identified molecule density, whereas the curves for the compressed sensing are calculated using identified molecule densities that allow the corresponding localization precisions to match the desired image resolution.

We have also simulated two more cases with lower signal levels. In the medium photon number case corresponding to the photoconvertible fluorescent protein mEos2 (Supplementary Fig. 6), the molecule identification efficiency of compressed sensing was only slightly reduced (up to 6.7 µm⁻²). Even in the very low photon number case (200 photons per molecule per frame, Supplementary Figs. 7 and 8), compressed sensing still recovered 3.8 molecules per µm² at a localization precision of 126 nm FWHM.

Next, we examined how compressed sensing can improve the temporal resolution of STORM. At a given camera frame rate, the time to acquire a STORM image with a desired spatial resolution is determined by two factors: the number of frames to accumulate enough single-molecule events for the required sampling density (Nyquist criterion), and the maximum molecular density so that the localization precision is sufficiently high. For single-molecule fitting, the Nyquist resolution is almost always the limiting factor; whereas for compressed sensing, the localization precision becomes the limit. Taking both factors into consideration, by matching the localization-precision-limited resolution and the localization-density-limited resolution, compressed sensing allowed the imaging speed to be increased by 6 to 15 fold compared to the fitting method (Fig. 1d) and 2 to 3 fold compared to DAOSTORM, depending on the desired spatial resolution (see Supplementary Fig. 9).

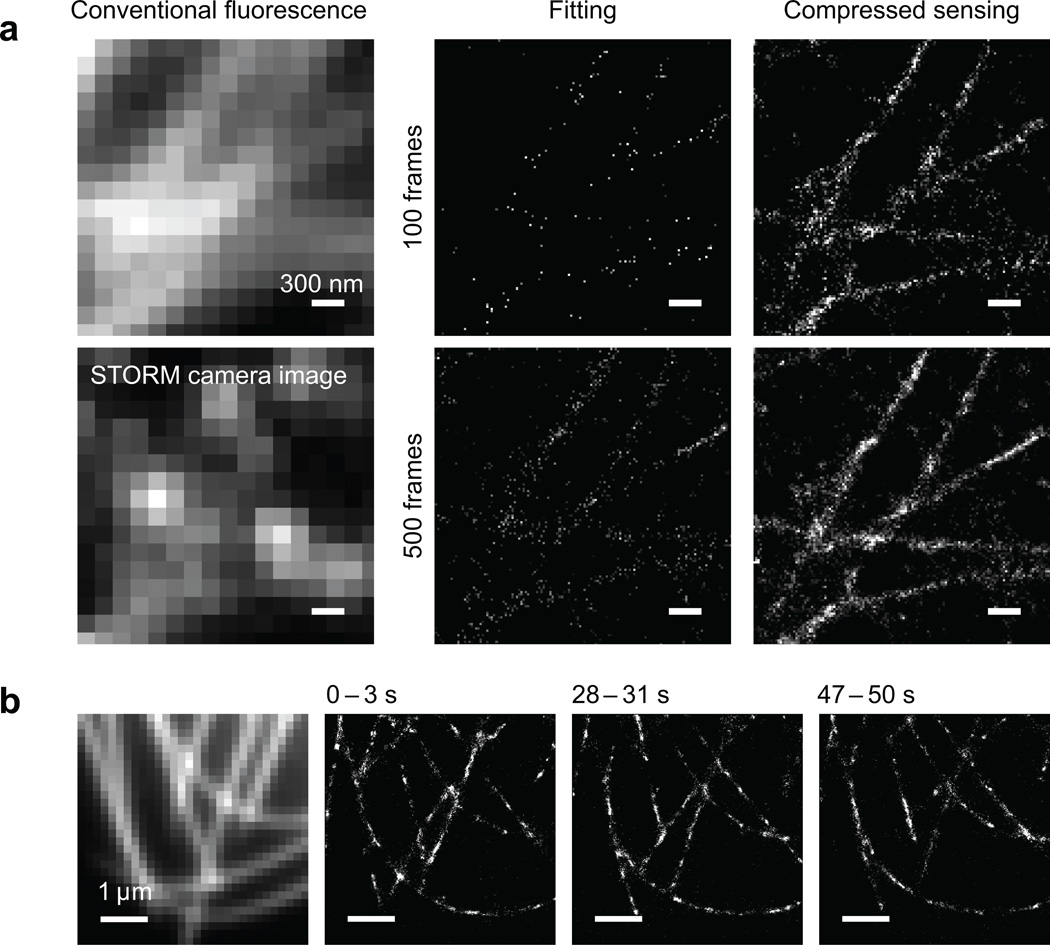
Our STORM experiment with immunostained microtubules in Drosophila melanogaster S2 cells demonstrated that nearby microtubules can be resolved by compressed sensing using as few as 100 camera frames, whereas they were not discernible by the single-molecule fitting method (Fig. 2a). We have also performed live STORM on S2 cells stably expressing tubulin fused to mEos2. At the commonly used camera frame rate of 56.4 Hz, we can reconstruct a super-resolution movie with a time resolution of 3 sec (169 frames) and a Nyquist resolution of 60 nm (Fig. 2b and Supplementary Video), much faster than previously reported⁶. These results have proven that compressed sensing can enable STORM to monitor live cellular processes with second-scale time resolution, or even sub-second-scale if a fast electron multiplying CCD (EMCCD)⁷ or scientific CMOS camera is used. Moreover, although we have only analyzed 2D data, our method in principle applies to 3D super-resolution microscopy, too, when a 3D grid and the 3D PSF are used, e.g. in conjugation with the astigmatic localization method¹⁵.

Figure 2.

Experimental STORM images using compressed sensing. (a) STORM imaging of microtubules in Drosophila S2 cells immunostained with secondary antibody labeled with the Alexa Fluor 647 - Cy3 dye pair. Left column: conventional fluorescence image and one raw image frame during STORM data acquisition, showing high density of activated fluorophores. Middle column: result of single-molecule fitting, reconstructed from 100 and 500 frames of camera images, respectively. Right column: result by compressed sensing using the same set of camera images. Scale bars: 300 nm. (b) STORM imaging of mEos2-tubulin in a living Drosophila S2 cell. The conventional fluorescence image in the leftmost panel is acquired before STORM imaging. Three snapshots from the STORM movie are displayed, each with 3 seconds integration time. The dynamics of the microtubules can be clearly observed. See Supplementary Video online.

Methods

STORM data analysis by compressed sensing

Mathematically, each frame of the measured camera image, b, has a linear relationship with the molecule distribution, x:

$$\mathit{b}=\mathit{\text{Ax}}$$ (4)

where the one dimensional vectors, b and x, consist of row-wise concatenations of the camera and the super-resolution images, respectively. The matrix A is determined by the point spread function (PSF) of the imaging system. The i’th column of A corresponds to the acquired raw image if only one molecule emits fluoroscopic photons at the position index i of x. The goal of the super-resolution image analysis is to obtain x from the measured b, provided that A is exactly known and x is non-negative and sparse (i.e. mostly zeros). Many different mathematical formulations have been proposed in the literature to implement the L1-norm minimization for compressed sensing^{16, 17}. Specifically, we used the following formulation:

$$\begin{array}{l}\hfill \text{Minimize}:{\mathit{c}}^{\mathrm{T}}\mathit{x}\hfill \\ \hfill \text{Subject to}:{\mathit{x}}_i\ge 0\text{and}\parallel \mathit{\text{Ax}}-\mathit{b}{\parallel }_2\le \epsilon ·{(\mathrm{\Sigma }{\mathit{b}}_j)}^{1/2}\hfill \end{array}$$ (5)

where the weight vector, c, is to account for the difference of the total contribution to the camera image from one fluorescent molecule at different locations. The value of the i’th element of c equals the summation of the i’th column of A. The minimization term, c^T x, is equivalent to a weighted L1 norm of x because x is non-negative.

Because (∥Ax – b∥₂)² is the sum of squared deviations of the optimization result from the image value, the constraint on ∥Ax – b∥₂ set an upper limit of χ² on how well the optimization results can match the original image. The Poisson statistics of photon counting implies that the variance of photon counts on pixel j equals to the expectation of the photon counts on that pixel. Therefore, ε² sets the maximum ratio between the sum of squared deviations and the sum of variances (Σb_j), equivalent to the reduced χ² without weighting each pixel with their variances individually.

To account for the background of the image, we introduced one additional element in x. The corresponding element in c is set to zero and all elements in the corresponding column of A are set to 1. In this case, the value of this extra element in x represents a uniform image background, with no sparsity constraint imposed on.

The optimization problem can be solved using standard linear programming with quadratic constraints. A direct implementation of the algorithm, however, requires large memory and computation power, mainly due to the large size of the super-resolution image. Note that the PSF of the imaging system is typically very narrow. We can therefore carry out the optimization separately on small patches of the original image without compromising the overall performance. The detailed procedure of our compressed sensing analysis is described in the Supplementary Note online.

In reality, x describes the fluorescence intensity of molecules on a grid with a spacing much smaller than the camera pixel size. We defined the ratio between the pixel size and the grid spacing as the oversampling factor, R. A larger, R, leads to smaller error in registering molecule positions, but results in longer computation time. The overall performance of compressed sensing, however, is rather insensitive to R (see Supplementary Fig. 1) because it mainly depends on the number of non-zero elements in x, which is independent of the grid size. In all our analyses, we chose R = 8. With a pixel size of 166 nm, the 21 nm grid size should be able to support a final image resolution of 42 nm.

The choice of the size of small image patch will not affect the compressed sensing results as long as it is large enough to cover at least one full PSF. Given that the PSF in our case has a standard deviation of about one pixel, throughout this manuscript, we have used a patch size of 7 by 7 to balance the number of patches to be optimized and the time to optimize each patch.

The choice of the value of ε dictates the balance of sparsity and fidelity in the optimization. An ε value of one demands a perfect fit to the original camera image (a reduced χ² of unity). To accommodate uncertainties in estimating the variances, the value of ε is usually set to be slightly larger than one. In our test, we have found that the recovery of the super-resolution image is not substantially affected with ε value between 1.5 and 2 (Supplementary Fig. 2). Therefore, we have chosen ε = 1.5 as the universal setting for all of our analyses of simulated data.

For experimental data acquired by an EMCCD camera, a factor of √2 must be applied to account for the excess noise introduced by the gain registers in the camera¹⁸. Therefore, an ε value of 2.1 is used when analyzing our experimental data.

We have implemented the algorithm in MATLAB using the CVX optimization package¹⁹. The analysis code as well as a set of example data is included in the Supplementary Software online.

Simulation

To evaluate the performance of our compressed sensing algorithm, we generated simulation images so that the analysis results can be compared to the “known” molecule positions. The simulation randomly places N molecules in a 24 × 24 pixel area in the middle of a 32 × 32 pixel image. The pixel size, 166 nm, matches the pixel size of our experimental setup, and roughly equals to the standard deviation of the PSF of our setup. With the 8 × 8 subdivision, the grid size in the super-resolution image is 21 nm. The simulation program calculates the photon counts in each pixel by taking the following fluctuation sources into consideration:

1. The variation of emitted photons from each molecule. In a STORM experiment, the number of photons detected from each molecule varies greatly due to the stochastic nature of photoswitching. In our simulation, we use a log-normal distribution to approximate the experimentally measured single-molecule photon number distribution. We note that the experimental distribution is close to but not exactly an exponential distribution because it counts the photon number in one frame instead of the entire photoswitching cycle of a fluorophore.

2. The experimentally measured PSF. The PSF of the microscope is measured by acquiring STORM images with low molecule density, aligning single-molecule fluorescent spots according to their centers-of-mass, normalizing and then averaging the aligned single-molecule images. In all of our cases, the radial cross section of the PSF can be nicely fit by the sum of two Gaussian functions, one describing the center peak and the other describing the side-lobe.

3. The background and photon counting noise. The number of detected photons of a pixel follows a Poisson distribution with the mean determined by the fluorescence signal at the pixel and a uniform background. The camera digitization noise is negligible when using an EMCCD camera at proper gain settings. We have not taken into account the excess noise introduced by the EMCCD gain registers.

In our simulations for Figs. 1b–d, Supplementary Figs. 4, 5 and 9, we set the peak of the log-normal photon number distribution at 3,000 photons (with a standard deviation of 1,700 photons) to match that in the experiment of photoswitchable Alexa Fluor 647. The background is 70 photons per pixel. For each N, the simulation is repeated 50 times (1,000 times when N = 1 for better statistics). For the single-molecule fitting method, because of its poor performance in molecule identification at high molecule density, we have run 450 additional simulations for each of the high molecule number conditions (N ≥ 40). The simulated images are analyzed using the compressed sensing algorithm described above, as well as the single-molecule fitting algorithm that we used in our previous publications¹⁴. The single-molecule fitting algorithm uses an elliptical Gaussian function to fit a local maximum in the image, and then applies thresholds in peak height, peak width and ellipticity to reject overlapped molecules. To determine the thresholds, we analyzed the N = 1 simulation with relaxed thresholding, determined the distribution of the corresponding parameters, and set the threshold value.

For the purpose of visualization, in Fig. 1a and Supplementary Figs. 1 and 2, we have fixed the number of photons of all molecules to 3,000, so that the recovered grid points are of similar brightness and thus better discerned by eyes. The background is still 70 photons per pixel. For the same reason, we have fixed the number of photons of all molecules to 200 in Supplementary Fig. 7. The background in this case is 20 photons per pixel.

We have also performed two additional simulations: one with a mean photon number of 750 (standard deviation of 460) and a background of 50 photons per pixel to match that in the experiment of mEos2 (see Supplementary Fig. 6), the other with a mean photon number of 200 (standard deviation of 77) and a background of 10 photons per pixel for a hypothetically low photon count case (see Supplementary Fig. 8).

Method evaluation

The performance of a STORM image analysis algorithm can be characterized by two metrics: the number of molecules that can be identified from an image, and the precision of determining their positions. Unlike the single-molecule fitting method, our compressed sensing algorithm does not directly return a list of molecule coordinates. Instead, it returns a pixelated super-resolution image representing the intensities of molecules on a fixed grid. We note that in the case when a molecule is not located exactly at a grid point, compressed sensing can assign non-zero intensity to the several grid points adjacent to the actual position. Although this effect does not affect the super-resolution image quality because the grid size is much smaller than the desired resolution in high molecule density images, it complicates molecule number counting. To make a fair comparison with the single-molecule fitting method, we convert the compressed sensing results into a list of molecule positions by treating a group of adjacent non-zero grids as one identified molecule and calculating its “position” from the center of mass. To avoid the “edge effect” that molecules at the periphery of the simulation region experiences lower density, those in the 2-pixel border of the simulation region are excluded from the evaluation. The results are shown in Fig. 1b and Supplementary Figs. 4, 6 and 8.

On the other hand, not all the identified molecules may have correct position information. To characterize the localization precision, we match each of the identified molecules in either method to the closest “true position” known from the simulation. Supplementary Figure 5 displays the histograms of the offset in either×or y direction with 1, 14, 50 or 125 molecules in the 16 µm² simulation area. We fit all the histograms with Gaussian peaks and plotted the full-width at half-maximum (FWHM) values as a function of molecule number in Fig. 1c, Supplementary Figs. 4, 6 and 8.

In the end, the overall image resolution is determined by both the density of identified molecules (through the Nyquist sampling criteria) and the precision of determining their positions. The number of camera image frames to accumulate enough identified molecules then links the time resolution to the Nyquist limited spatial resolution. In the case of the single-molecule fitting method with high photon number, the maximum identified molecule density is 0.58 µm⁻² in each frame, with a high localization precision of 20 nm (FWHM). Therefore, when one would like to demand a worse spatial resolution (e.g. 60 nm) in return for a higher temporal resolution, the identified molecule density is always the limiting factor. On the contrary, compressed sensing can identify many more molecules at the price of worse localization precision. In these cases, we determined an “optimal” molecule density so that the localization-limited resolution equals the density-limited resolution. We then calculated the minimum number of frames, at this “optimal” molecule density, to achieve the given Nyquist limited resolution (see Fig. 1d and Supplementary Fig. 9)

Sample preparation

Wildtype S2 cells or S2 cells stably expressing mEos2-tubulin (gift from Eric Griffis in the Ron Vale lab at UCSF) were cultured in Sf-900 II serum free medium (Gibco). Cells were plated onto Lab-Tek II 8 well chambered #1.5 coverglass (Nunc) for fluorescence imaging. Before cell seeding, each chamber was coated with 0.1mg/ml cocanavalin A for at least 0.5 h to allow the cells to acquire a fattened, well-spread morphology. Then cells were seeded into the chambers for 1 h.

For live cell imaging, S2 cells were imaged in the same serum free medium as they were normally cultured. For fixed cell imaging, cells were fixed with 3% paraformaldehyde and 0.1% glutaraldehyde in PBS for 10 min, treated with 0.1% NaBH₄ for 7 min, then permeablized and blocked by 0.5% Triton-X 100 and 3% bovine serum albumin for 10 min. Staining of tubulin was done with mouse monoclonal anti-α-tubulin antibody (1:250, 45min incubation; clone DM1A, T6199, Sigma) and secondary donkey anti-mouse antibody (715-005-151, Jackson Immuno Lab) which we labeled with a mixture of Alexa Fluor 647 and Cy3 dyes (3 µg/mL, 45 min incubation)¹⁴. Fixed cells were imaged in mercaptoethylamine imaging buffer supplemented with an anti-bleaching oxygen scavenger system as previously described²⁰.

Optical setup and imaging

The STORM microscope was constructed with a Nikon Eclipse Ti inverted microscope equipped with a motorized XY stage (Märzhäuser) and Nikon perfect focus system which stabilizes the focusing. Three diode lasers (405 nm from Stradus 405-100, 488 nm from Stradu 488-50, 642 nm from Stradus 642-110, Vortran) were directly shuttered by the computer. The 561 nm solid state laser (Sapphire 561-200, Coherent) light was controlled by an acoustic optical modulator (Crystal Technology). Each laser passed through a filter wheel to control its laser power after the laser output. The four lasers were coupled and collimated into a telescopic optical path and focused to the back focal plane of the oil immersion objective (Nikon Plan Apo VC 100X/1.40) on the microscope.

A quad band beam splitter zt405/488/561/640rpc (Chroma) and a slider equipped with band-pass filters (ET605/70M for mEos2, ET700/70M for Alexa Fluo 647, Chroma) were used to separate the fluorescence signal. The images were recorded with an EMCCD camera (Ixon DV897DCS-BV, Andor) at a frame rate of 56.4 Hz. For excitation, the power of 561 nm (mEos2) and 642 nm (Alexa Fluor 647) lasers were 30 mW and 36 mW, respectively, measured at the back port of the microscope. The activation laser intensity, typically 10 to 30 μW, is adjusted so that a high density of mEos2 or Alexa Fluor 647 molecules is activated in each camera frame. All instrument control and image acquisition were performed with home written software in Python.