Combinatorics of distance-based tree inference

Abstract

Several popular methods for phylogenetic inference (or hierarchical clustering) are based on a matrix of pairwise distances between taxa (or any kind of objects): The objective is to construct a tree with branch lengths so that the distances between the leaves in that tree are as close as possible to the input distances. If we hold the structure (topology) of the tree fixed, in some relevant cases (e.g., ordinary least squares) the optimal values for the branch lengths can be expressed using simple combinatorial formulae. Here we define a general form for these formulae and show that they all have two desirable properties: First, the common tree reconstruction approaches (least squares, minimum evolution), when used in combination with these formulae, are guaranteed to infer the correct tree when given enough data (consistency); second, the branch lengths of all the simple (nearest neighbor interchange) rearrangements of a tree can be calculated, optimally, in quadratic time in the size of the tree, thus allowing the efficient application of hill climbing heuristics. The study presented here is a continuation of that by Mihaescu and Pachter on branch length estimation [Mihaescu R, Pachter L (2008) Proc Natl Acad Sci USA 105:13206–13211]. The focus here is on the inference of the tree itself and on providing a basis for novel algorithms to reconstruct trees from distances.

A task with several relevant applications is the use of a matrix of distances to construct a tree whose leaves’ relative positions somehow reflect the given distances. This is useful both in evolutionary biology, where the tree is intended to represent the evolution of a set of species, populations or genes, and in cluster analysis, where the tree shows the similarities in a collection of objects. In evolutionary biology, the distances are typically estimated from molecular sequences using probabilistic models of sequence evolution (1, 2). The resulting distances can be expected to be approximately additive; that is, there exists a (phylogenetic) tree with branch lengths, so that the lengths of the paths between its leaves (sequences) are approximately equal to the input distances. Finding this tree is the goal of several popular distance-based tree reconstruction methods.

For phylogenetic reconstruction—which this paper concentrates on—the main advantage of distance-based methods is their speed of execution, which is orders of magnitude faster than that of other (potentially more accurate) approaches. As a consequence, distance methods are used whenever computational efficiency is of critical importance: for the reconstruction of very large trees, or—as in the case of bootstrapping—large collections of trees or even to construct initial phylogenies for search heuristics based on more sophisticated approaches. In fact, a general trend in bioinformatics and computational biology is the growing demand for methods that can cope with massive datasets of DNA sequences. Distance-based methods are a possible answer to this demand, not only for phylogenetic inference but also for related tasks such as sequence identification (e.g., in metagenomics) and gene orthology inference (e.g., in functional genomics). A proof of this demand is the continuing success of neighbor-joining (NJ) (3), which to date remains the most cited algorithm in phylogenetics.

The advantage in speed of distance methods is counterbalanced by a lower accuracy than methods that take full sequence information into account (4), such as maximum likelihood (ML), although it has recently been shown that under a certain measure of statistical efficiency, some distance methods are essentially as good as ML (5). A limitation of distance-based methods lies in the fact that if the distances are estimated from pairwise sequence comparisons only, then it may be impossible to infer some parameters common to the evolution of all the sequences (6). However, it is still possible to estimate these parameters from limited sequence samples by ML and then use distance methods for the whole sample.

If we consider the estimation of distances as a separate task, virtually all distance methods are based on two components, corresponding to the two main unknowns in a phylogenetic tree: branch lengths and topology. First, (i) we must define a method to assign lengths to the branches of any tree of fixed topology, so that the distances between leaves are as close as possible to the input distances. Second, (ii) we must choose a criterion to discriminate among the trees with different topologies obtained with the step above. Distance-based algorithms then look for the tree that optimizes this criterion, typically using heuristics such as successive agglomeration [e.g., NJ (3)] and hill climbing [e.g., FastME (7)].

For component i, a weighted least squares (WLS) approach is usually adopted: The lengths of the branches in a tree T are set to the values that minimize

[1]

where the δ_ij are the distance estimates, the 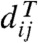are the distances between the leaves of T, determined by the lengths assigned to its branches, and the weights w_ij > 0 are intended to account for the variances of the δ_ij: The higher the variance, the lower the weight and the importance given to the corresponding residual 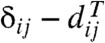. Ideally, w_ij should be proportional to Var[δ_ij]^-1 (see Relationship with WLS and the M&P Formulae below), but in practice setting the weights is a delicate art, because the variances are not known; for example, one trap to avoid is to assume zero variance (and therefore an infinite weight) for the distance between two identical sequences (8). An even more ideal approach would be to also consider the covariances between distances for different pairs of taxa, which leads a generalized least squares (GLS) optimization criterion (9). The optimal branch lengths with respect to 1, and even GLS, can be expressed succinctly in matrix form. However, despite some progress (10), the matrix calculations involved are computationally expensive and remain a limiting factor for the efficiency of the algorithms that use them [such as those implemented in PAUP* (11)].

As for component ii, distance methods fall into two broad categories: (pure) least squares (LS) methods (12, 13) use again a least squares criterion such as 1 to score trees; on the other hand, minimum evolution (ME) methods (14, 15) aim to find the tree with minimum total length [which can be defined in a number of different ways (8, 14, 15); see Statistical Consistency for details], among those whose branch lengths are fitted with component i. The intuition underlying ME is the same as that of maximum parsimony for character-based tree reconstruction: simpler (i.e., shorter) explanations are preferable to more complicated ones.

An important realization has been that in some relevant cases the branch lengths that minimize 1 can be expressed using simple “combinatorial” formulae, which allow to avoid slow matrix calculations. The best-known cases are that with constant weights w_ij (ordinary least squares, OLS) (16, 17) and that with weights proportional to 2^-t_ij, where t_ij is the number of branches in the path between i and j in T (the balanced case) (18). These formulae allow to efficiently calculate branch lengths and to efficiently update the tree length while performing a local search for the optimal tree with respect to ME. For example, the balanced branch length formulae (19) can be used to calculate in O(n²) time, for any tree with n leaves, not only all its branch lengths but also the total lengths of all of its NNI (nearest neighbor interchange) (7) and SPR (subtree pruning and regrafting) rearrangements (20, 21).

A key work on such combinatorial formulae for least squares branch lengths has appeared recently (22). The authors show that all the known formulae are particular cases of a more general framework: Whenever the weights w_ij (or, equivalently, the assumed variances ) have a particular “multiplicative” form (see Relationship with WLS and the M&P Formulae), then the optimal branch lengths with respect to 1 can be calculated using simple formulae—such as those for OLS or the balanced case— which here we refer to as the “M&P formulae” (from the authors Mihaescu and Pachter or the word “multiplicative”). The multiplicative model is biologically and mathematically meaningful, because it can be shown that the variances of the distance estimates are approximately multiplicative for large distances (9, 22, 23).

In the following, we use the seminal work by Mihaescu and Pachter (22) as a starting point. Whereas these authors focused on the problem of branch length estimation, here we switch the focus to tree reconstruction itself—namely, the statistical and algorithmic consequences of the use of combinatorial branch length formulae on tree reconstruction. Our results can be summarized as follows:

1. We define a class of formulae for fitting branch lengths that generalizes the M&P formulae and consequently also all known combinatorial formulae.

2. We prove the statistical consistency of the main distance-based tree reconstruction principles (LS and ME), when combined with our formulae. In other words the optimal tree with respect to any of these principles converges to the correct tree as the input data become more and more abundant and the estimated distances converge to their correct values. Particularly in the case of ME, where it is problematic, this issue has received much attention [e.g., (17, 21, 24–26)]. This addresses the question by Mihaescu and Pachter (ref. 22, p. 13211) of “what classes of semimultiplicative” (a minor generalization of multiplicative) “variance matrices result in consistent tree estimates,” by showing that all multiplicative variance matrices have this property.

3. We investigate the computational efficiency of local search heuristics in combination with our class of formulae. In particular, we describe an algorithm that calculates the branch lengths determined by the adopted formulae not only for a fixed tree T but also for all trees obtained by performing one NNI on T. The entire calculation optimally requires O(n²) time. This algorithm can be used as the basic component for local searches and can be combined with any classic tree reconstruction principle.

Preliminaries: Branch Length Formulae

We employ the standard terminology used in the phylogenetics literature (2, 4, 27) (phylogenetic tree, topology, branch lengths, internal and external branches, etc.). For simplicity, we identify the leaves of a phylogenetic tree with a set of taxa {1,2,…,n}, and we choose to consider only binary trees. We say that two subsets of taxa A and B in a tree are separated by a branch e if any path between an element of A and an element of B passes through e. A and B are k-separated when they are separated by exactly k distinct branches. A proper subset of taxa A⊊{1,2,…,n} is a clade if A and {1,2,…,n} ∖ A are separated by some branch e; in fact, e is unique and is called the root branch of A; the endpoint of e to the side of A is called the root node of A. A branch belongs to clade A if it lies in the path between two elements of A.

We also adopt the following standard conventions for distance-based methods: δ denotes the n × n input distance matrix and δ_ij its element expressing the distance between taxa i and j (in the following, indices i and j are always assumed to be elements of the set of taxa {1,2,…,n}). The distances do not necessarily form a metric, because only δ_ij = δ_ji and δ_ii = 0 are assumed. Given a tree T with branch lengths, d^T denotes the distance matrix where 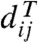coincides with the length of the path between i and j in T. When δ = d^T for some T, we say that δ is additive (with respect to T) (28).

In the rest of this section, we introduce a new class of formulae that express the branch lengths of a generic topology T over {1,2,…,n} as a function of δ. This class is parameterized by some quantities that we present using a probabilistic interpretation (see SI Appendix 1, for more details). Let T be a binary tree topology. Assume that the rules for a random walk on T are defined in the following way: If we enter an internal node from a branch e, we can then exit this node from its two other adjacent branches, f and g, with probabilities γ_ef and γ_eg = 1 - γ_ef, respectively. We require 0 < γ_ef,γ_eg < 1 (note the strict inequalities). These parameters define a (nonzero) probability of reaching any branch of T from any other branch of T.

This also defines a probability distribution over the leaves of any clade A: For any i∈A, let p_i|A = γ_e0e1·γ_e1e2·…·γ_ek-1ek, where e₀ is the root branch of A and e₁,e₂,…,e_k are the branches on the path between the root of A and i. (See Fig. S1) Clearly, the probabilities {p_i|A|i∈A} form a distribution over A. We can then define the average distance δ_AB between any two clades A and B as the expected distance between two taxa chosen at random from A and B according to the distributions defined above:

Note that the δ_AB so defined depend on the γ_ef parameters, as well as on the underlying topology T, but for simplicity we do not indicate this in the chosen formalism. Also note that δ_AB = δ_BA. For simplicity, we write δ_iA (or δ_Ai) instead of δ_{i}A.

In addition to the γ_ef probabilities defined for each pair of adjacent branches (e,f), we introduce a parameter λ_XY for each unordered pair {X,Y} of 3-separated clades in T (recall the definition of k-separated clades above). We constrain these parameters so that, for every internal branch separating clades A = A₁∪A₂ and B = B₁∪B₂ (see Fig. 1B), λ_A1B1 = λ_A2B2 > 0, λ_A1B2 = λ_A2B1 > 0 and λ_A1B1 + λ_A1B2 = 1, meaning that only one parameter among λ_A1B1, λ_A2B2, λ_A1B2 , and λ_A2B1 determines all the others. A possible interpretation for λ_XY is as the probability of drawing T so that X and Y are consecutive in a clockwise ordering of the taxa (which explains why λ_A1B1 = λ_A2B2, λ_A1B2 = λ_A2B1 and λ_A1B1 + λ_A1B2 = 1; see SI Appendix 1, for details).

Fig. 1.

Standard naming of clades and branches when (A) e is external, and (B) e is internal. (C) An NNI-neighbor (around e) of the tree in B.

In summary, we have three free parameters per internal node of T (γ_ef,γ_fg , and γ_ge determine γ_eg,γ_fe , and γ_gf) and one free parameter per internal branch (λ_A1B1 determines λ_A2B2,λ_A1B2 , and λ_A2B1). These parameters determine a set of formulae to estimate the length of any branch in T:

(γ^T,λ^T)-formulae. Let the vectors γ^T = (γ_ef) and λ^T = (λ_XY) be defined for binary topology T, under the constraints described above. Then, for any branch e in T:

where, if e is external, we define A, B, i as in Fig. 1A and, if e is internal, we define A₁, A₂, B₁, B₂ as in Fig. 1B.

Note that because λ_A1B2 = λ_A2B1 = 1 - λ_A1B1 = 1 - λ_A2B2, the formula above for internal branch lengths is (as desired) independent of how we assign names A₁, A₂ to the two subclades of A = A₁∪A₂ and how we assign B₁, B₂ to the two subclades of B = B₁∪B₂. An interpretation of the (γ^T,λ^T)-formulae as averages of simpler formulae is given in SI Appendix 1.

These formulae are a generalization of all the combinatorial formulae proposed in the past to fit the branch lengths of a tree of fixed topology. In particular, the OLS branch lengths (16, 17) can be obtained by setting 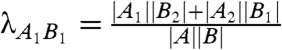(same clade naming as above) and by setting , for every pair of adjacent branches e and f in the configuration of Fig. 1B. Note that the γ_ef parameters thus defined ensure that {p_i|X|i∈X} is uniform for any clade X (in fact the word “unweighted” is often associated to OLS). Similarly, the balanced branch lengths (19) at the basis of the balanced minimum evolution principle (7, 18, 29) are obtained by setting all parameters to 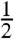. The next section shows that the (γ^T,λ^T)-formulae also generalize the M&P formulae by Mihaescu and Pachter (22). It is easy to see that the (γ^T,λ^T)-formulae still satisfy the independence of irrelevant pairs (IIP) property introduced by those authors (22) as a basic requirement for their formulae.

Finally, we show that the (γ^T,λ^T)-formulae above are correct; that is, they calculate the correct values of the branch lengths of any given tree whenever the distances are additive with respect to that tree (proof in SI Appendix 1). Naturally, because the input distances are only estimates of the real evolutionary distances, they are usually only approximately additive. However, this property is an important prerequisite of any branch length formula, because it ensures the statistical consistency of the branch lengths assigned to the correct topology (see Statistical Consistency below).

Theorem 1.

Let T be a binary topology. For any given branch e in T, assign length ℓ_e to e, and let δ be additive with respect to the resulting tree. Let be the length that is assigned to e by a (γ^T,λ^T)-formula. Then, .

Relationship with WLS and the M&P Formulae

The choice of the weights in 1 is a key factor for the accuracy of least squares tree estimates. The weights w_ij should be proportional to Var[δ_ij]^-1, because this implies that the branch lengths that minimize 1 have minimum variance among all linear unbiased estimators of the branch lengths (under the assumption that the distance estimates are unbiased and uncorrelated for different pairs of taxa) (30). In this section, we consider the case where the weights (and therefore the assumed variances) are “multiplicative”: Given a tree topology T and a collection of weights w = (w_ij) associated to pairs of taxa in T, we say that these weights are multiplicative with respect to T, if we can assign to each branch e of T a weight w_e > 0, so that, for every pair of taxa i and j, where P_ij(T) denotes the set of branches in the path between i and j in T. This condition generalizes several well-known cases: that of constant weights (coinciding with OLS and obtained by setting w_e to 1 for internal branches and to a constant for external ones), that of taxon-specific weights (25) (obtained like for OLS but with w_e free to vary for external branches) and also that of weights exponentially related to the number of branches separating each pair of taxa [which, when the base of the exponent is 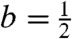, coincide with the balanced weights (19) and are obtained by setting w_e = b for internal branches and to a constant for external ones].

Mihaescu and Pachter (22) have shown that if the assumed weights w are multiplicative with respect to T, then the optimal branch lengths of T with respect to the WLS criterion 1 are given by their M&P formulae. We refer to SI Appendix 2, for a description of these formulae. The following theorem shows that the class of the M&P formulae is contained in that of the (γ^T,λ^T)-formulae, and, conversely, it characterizes the values of γ^T and λ^T corresponding to M&P formulae.

Theorem 2.

Let T be a binary topology. (i) Given any w multiplicative w.r.t. T, the corresponding M&P formulae are also (γ^T,λ^T)-formulae for some choice of γ^T and λ^T satisfying the properties P1 and P2 below. (ii) Given any γ^T and λ^T satisfying the properties P1 and P2 below, the corresponding (γ^T,λ^T)-formulae are also M&P formulae for some choice of w, multiplicative w.r.t. T.

P1. For every internal node of T, if e,f, and g are the three branches incident to it, then γ_efγ_fgγ_ge = (1 - γ_ef)(1 - γ_fg)(1 - γ_ge).

P2. For every pair of clades A and B separated in T by three branches a,e, and b (with a being the root branch of A, and b being the root branch of B), λ_AB = γ_ea + γ_eb - 2γ_eaγ_eb.

Theorem 2, proved in SI Appendix 2, not only shows that the M&P formulae are particular types of (γ^T,λ^T)-formulae but it also provides an alternative set of parameters to represent the M&P formulae: Instead of the branch-associated weights w_e, one can use a set of γ_ef parameters satisfying P1. This condition implies that any of γ_ef,γ_fg and γ_ge can be determined from the other two and P2 implies that all the λ_XY parameters are determined by the γ_ef parameters. This reduces the number of free parameters needed to describe the (γ^T,λ^T)-formulae that are also M&P formulae to 2 per internal node, that is 2n - 4. This is exactly one less than the 2n - 3 branch-associated parameters w_e describing multiplicative weightings, which corresponds to the fact that multiplying all the w_e for external branches by any positive constant results in equivalent weightings with respect to 1.

Theorem 2 establishes that the (γ^T,λ^T)-formulae have enough “expressive power” to optimize the least squares criterion 1, when the weights are multiplicative. It is therefore important to discuss this assumption. First, multiplicative weights generalize the balanced weights, which have been experimentally demonstrated to behave well in combination with ME (18, 31). Second, in the case of distances estimated from molecular sequences, we note that for many models of sequence evolution [for instance Jukes–Cantor (32); see ref. 1 or appendix B in ref. 2 for the general technique], the variance of δ_ij can be approximated by a function of the correct evolutionary distance d_ij that, for small values of d_ij, behaves as a linear function of d_ij, and, for moderate-to-large d_ij, as an exponential of d_ij. This means that, for pairs of taxa separated by small d_ij, the variances of their distance estimates will tend to be additive, whereas for pairs of taxa separated by moderate-to-large d_ij, the variances will tend to be multiplicative. The additive model for the variances (33), or its variant with variances proportional to 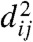(13), are used in practice with δ_ij in place of d_ij, as the latter is unknown. As a result, these approaches need some precautions for very small distance estimates, so as to avoid an overconfidence in these estimates (for δ_ij tending to 0, also the assumed variance tends to 0, and w_ij tends to infinity): For example, one possibility is to add pseudocounts to the numbers of observed differences between sequences (8) (known as “Laplace smoothing”). In this context, the multiplicative model provides a simple and robust alternative for small distances (for δ_ij → 0, the assumed variance tends to a constant) and is mathematically justified for moderate-to-large distances.

The other important assumption here, common to all WLS methods, is that the δ_ij are uncorrelated for different pairs of taxa, which is clearly not true for distances estimated from molecular sequences (9). As mentioned above, covariances between different distance estimates can be accounted for by adopting a GLS criterion. However, setting the covariances and calculating the resulting branch lengths (10) are difficult problems, which explains the lack (to the best of our knowledge) of practical implementations of GLS for phylogenetic reconstruction.

Statistical Consistency

A method for phylogenetic inference is said to be (statistically) consistent if the probability that it reconstructs the correct tree (within any given accuracy) converges to 1 as more and more data are analyzed. For distance-based methods, the consistency of tree inference usually depends in turn on the consistency of the distance estimates; that is, the assumption that δ converges to a matrix d^T containing the distances in the correct phylogenetic tree for the taxa under consideration. Even though in reality the precise consistency of distance estimates cannot be expected to hold—because the models used to obtain these estimates are only approximations of reality—the ability to infer the correct tree in such a best-case scenario is an essential property of any phylogenetic inference method: It is a prerequisite for robust inference of the correct topology with real distance estimates, subject to sampling errors and not perfectly consistent (34–36).

In this section, we state our main results on the statistical consistency of the tree reconstruction methods using the (γ^T,λ^T)-formulae. We leave the proofs to SI Appendix 3. We assume that, for any binary topology T over the taxa of interest {1,2,…,n}, a collection of parameters γ^T = (γ_ef) and λ^T = (λ_XY) is defined, thus defining in turn, for any such T, a set of (γ^T,λ^T)-formulae for estimating the branch lengths of T. We call this a branch length estimation scheme based on (γ,λ)-formulae. (Note the absence of superscript.) We stress that, for the consistency results here, no connection between (γ^T,λ^T) and (γ^T′,λ^T′) for different topologies T and T^′ needs to be assumed; in other words, completely unrelated formulae can be used for any pair of topologies.

Now combine a branch length estimation scheme with an optimization principle, such as LS or ME, that allows us to choose among all the topologically-distinct fitted trees over {1,2,…,n}. We have already described LS (but also see SI Appendix 3). As for ME, three variants of this principle have been proposed, essentially differing for how tree length is defined in the presence of negative branch lengths [which are allowed by many branch length estimation schemes, including those based on (γ,λ)-formulae]. We call them ME_-1 (14), ME₊₁ (15, 37), and ME₀ (8). Assuming that a tree has been assigned the branch lengths , ME_i defines its length as

The three versions of ME then differ in how they deal with negative branch lengths when calculating tree length: ME₊₁ adds together all branch lengths irrespective of their sign, whereas ME₀ ignores negative branch lengths and ME_-1 takes their absolute value. Gascuel et al. (24) previously named ME₊₁, ME₀ and ME_-1, “all-BL,” “positive-BL,” and “absolute-BL,” respectively. The following theorem shows that for these three versions of ME, as well as for LS, tree inference is consistent when (γ^T,λ^T)-formulae are used.

Theorem 3.

Assume that the input distances δ are consistent estimates of the correct evolutionary distances d^T∗, where T^∗ is a binary tree with positive branch lengths. Adopt a branch length estimation scheme based on (γ,λ)-formulae. Then, the optimal trees with respect to LS, ME₊₁, ME₀ and ME_-1 are statistically consistent estimates of T^∗.

Whereas the consistency of LS is a simple consequence of the correctness of the (γ^T,λ^T)-formulae, and is included here for sake of completeness, the result for ME is somewhat surprising, given that ME has been proven to be inconsistent when combined with WLS branch lengths (for some particular values of the weights w_ij) (24). Furthermore, Theorem 3 generalizes all previously known cases of consistency for the ME principle (17, 25, 18). In particular, it demonstrates the statistical consistency of tree reconstruction when using the formulae by Mihaescu and Pachter, thus answering their fundamental question mentioned in the Introduction.

Computational Efficiency

While the statistical consistency results above provide a theoretical basis for the use of (γ^T,λ^T)-formulae, we now consider a more practical advantage of these formulae: the fact that they can be efficiently combined with hill climbing heuristics, a pervasive and successful tool for tree reconstruction. Hill climbing consists of repeatedly applying small changes that improve the score of a candidate tree, until no such change is possible anymore. The behavior of hill climbing is essentially determined by the changes allowed at each step, or in other words by a notion of neighborhood defined over tree space. Here, we consider the simplest such changes, known as nearest neighbor interchanges (NNIs), which consist of swapping the positions of two 3-separated subtrees in a topology: for example, the topology in Fig. 1C can be obtained from that in Fig. 1B by swapping clades A₁ and B₁. When topology T^′ can be obtained from topology T in this way, we say that T and T^′ are NNI neighbors. An NNI transforming T into T^′ is around e, if e is the middle branch among the three branches separating the subtrees being swapped in T. While simple, NNIs can be used to efficiently implement more complex changes (such as SPRs) that can be obtained via a series of NNIs (21, 27).

Clearly, the computational efficiency of a hill-climbing heuristic depends crucially on the ability to efficiently evaluate some/all neighbors of any candidate topology. For all distance-based optimization principles, the evaluation is essentially done on the basis of some function of the assigned branch lengths. It is then important to calculate efficiently the branch lengths of the neighbors that are considered at each iteration. Here, we show that if (γ^T,λ^T)-formulae are used for computing branch lengths, and a natural relation between the γ^T parameters for NNI neighbors is assumed, then the O(n²) branch lengths of all the NNI neighbors of a candidate topology can be calculated in O(n²) time. This is optimal, because these O(n²) branch lengths depend on all the O(n²) input distances.

In order to express the required relation between the γ^T parameters for NNI neighbors, we assume that when performing an NNI around a branch e, all other branches keep their names. (For example, see branches f, g, h, and l in Fig. 1 B and C.) Then, when T^′ is obtained from T with an NNI around branch e, we say that parameter sets γ^T = (γ_e1e2) and 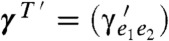, defined for T and T^′, respectively, are almost identical, if 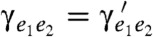, for every pair of adjacent branches (e₁,e₂) in T such that their common endpoint is not also an endpoint of e (in which case e₁ and e₂ are also adjacent in T^′). The intuitive idea is that γ^T and γ^T′ may only differ locally around the location of the NNI. This requirement is a prerequisite for the efficient evaluation of T^′ from that of T. Note the difference here with the approach in the previous section, where we assumed no relationship between parameter sets for different topologies. Our result can now be stated as follows:

Theorem 4.

Let T₀ be a binary topology over taxa {1,2,…,n} and T₁,T₂,…,T_2(n-3) all its NNI neighbors. For all i∈{0,1,…,2(n - 3)}, assume that the branch lengths of T_i are defined by the -formulae, with the constraint that and are almost identical. Then,

1. the branch lengths of T₀ can be calculated in O(n²) time;

2. the branch lengths of all the NNI neighbors of T₀ can be calculated in O(n²) time.

We leave the proof of this result to SI Appendix 4. While point i merely generalizes further a property already known for all M&P formulae (22), the result in ii is novel. It is related to and somehow explains the existence of a number of efficient hill-climbing algorithms for distance-based tree reconstruction. In particular, it predicts the efficiency of hill climbing for balanced minimum evolution (BME), which assumes γ^T parameters always equal to and therefore clearly having the property of being almost identical for NNI neighbors. The existing hill-climbing algorithm for BME (7) directly updates the total tree length, rather than the lengths of each branch, but the worst-case time complexity for each iteration is still O(n²) and results in one of the most accurate and fast distance-based methods (18, 31). Theorem 4 also predicts the efficiency of hill climbing for OLS: The γ_ef parameters for OLS depend in fact on the sizes of the three clades to the sides of e, f, and g (where the latter is the branch adjacent to both e and f), and these do not change when performing an NNI around a branch other than e, f, and g, which implies the almost identity of the γ_ef parameters for NNI neighbors.

Note that Theorem 4 has very wide applicability, not only because of the generality of the formulae it assumes but also because it makes no assumption on the optimization criterion used to score trees (apart from its dependence on the branch lengths). This is unlike the hill-climbing algorithms we mentioned above, which were only applicable to the classic version of ME (the one we call ME₊₁), where all branch lengths are added together, irrespective of their sign.

Discussion

We presented here a framework unifying some of the most successful approaches for distance-based tree reconstruction: For example, ordinary least squares methods for clustering (38) and balanced minimum evolution [BME, the optimization principle behind neighbor-joining (29)] for phylogenetic inference. We have shown that all the methods that fit into this general framework have highly desirable statistical properties (the consistency of the tree estimates) and algorithmic properties (efficiency of hill climbing heuristics).

Our study opens the way for improvements of existing methods and the development of new ones. Novel combinations of branch length formulae and tree optimization principles can be envisaged. For example, our results enable the efficient implementation of hill climbing for the versions of ME discouraging negative branch lengths (or at least not favoring them; see ME_-1 and ME₀ above), in combination with any of the classic branch length estimation schemes (e.g., OLS or that used in BME). Alternatively, our framework enables the use of novel, biologically motivated ways of estimating branch lengths, for example assuming multiplicative variance models based on the current tree estimate.

We conclude by noting that although the class of branch length formulae we consider here is inspired by previous work on multiplicative variance models (22), nothing excludes that it may be applicable to least squares criteria other than WLS with multiplicative weights. In fact, it is easy to construct covariance models with nonzero covariances that result in GLS branch length estimators coinciding with (γ^T,λ^T)-formulae. Future research should aim to elucidate the full potential of our class of formulae.