Cognitive signals for brain–machine interfaces in posterior parietal cortex include continuous 3D trajectory commands

Abstract

Cortical neural prosthetics extract command signals from the brain with the goal to restore function in paralyzed or amputated patients. Continuous control signals can be extracted from the motor cortical areas, whereas neural activity from posterior parietal cortex (PPC) can be used to decode cognitive variables related to the goals of movement. Because typical activities of daily living comprise both continuous control tasks such as reaching, and tasks benefiting from discrete control such as typing on a keyboard, availability of both signals simultaneously would promise significant increases in performance and versatility. Here, we show that PPC can provide 3D hand trajectory information under natural conditions that would be encountered for prosthetic applications, thus allowing simultaneous extraction of continuous and discrete signals without requiring multisite surgical implants. We found that limb movements can be decoded robustly and with high accuracy from a small population of neural units under free gaze in a complex 3D point-to-point reaching task. Both animals’ brain-control performance improved rapidly with practice, resulting in faster target acquisition and increasing accuracy. These findings disprove the notion that the motor cortical areas are the only candidate areas for continuous prosthetic command signals and, rather, suggests that PPC can provide equally useful trajectory signals in addition to discrete, cognitive variables. Hybrid use of continuous and discrete signals from PPC may enable a new generation of neural prostheses providing superior performance and additional flexibility in addressing individual patient needs.

Different cortical areas have been identified as sources for cortical prosthetics to assist subjects with paralysis or amputation (1–13). Motor cortex can provide continuous control of trajectories (3–5, 11–13), which is consistent with its normal function of sending commands directly to the movement generating circuits of the spinal cord. More cognitive variables related to reach goals have been extracted from the parietal reach region (PRR) and area 5d in posterior parietal cortex (PPC) (7, 14, 15). There are several advantages of these cognitive variables for prosthetic applications: (i) decodes of goals are very fast, in the order of 100 ms, and can assist in typing applications (7); (ii) at least two sequential goals can be represented in PRR, and this feature can augment typing and sequential limb movements (16); (iii) goal and trajectory information, when combined, provide better decoding of trajectories than trajectory information alone (17); (iv) bilateral arm movements to a goal are represented and can assist in decoding bimanual behaviors from a single hemisphere (18); and (v) the anterior intraparietal area (AIP) of PPC represents grasp shape, which may reduce the number of cells needed to decode grasping (19).

If PPC also encodes trajectories, then its repertoire of uses for prosthetics control would be further expanded. Deficits in online control of movement trajectories found in clinical studies, for instance, difficulty in trajectory correction during movement (20–22), indicate that PPC is an important site for continuous control of movement, suggesting that movement parameters can be decoded in PPC. Moreover, recent studies show that, under very constrained laboratory conditions of stereotyped movements (2D center-out movements) and with the gaze fixed, trajectory information can be decoded from PPC neurons (17, 23). However, there has been no demonstration that PPC can be used for the more demanding conditions required for neural prosthetic applications that include 3D reaches from varying beginning and end points with gaze free.

The ability to use PPC for everyday prosthetics applications, for both trajectory and goal decoding, is also an open question given the findings that reach targets, particularly in PRR, are coded primarily in eye coordinates (24–26). With gaze free, decoding would, in principle, be much more inaccurate than with gaze fixed. Thus, in the current experiments, we tested whether PPC could provide trajectory information in the presence of natural eye movements and under generally more realistic conditions, including sequences of point-to-point-movements in a 3D workspace.

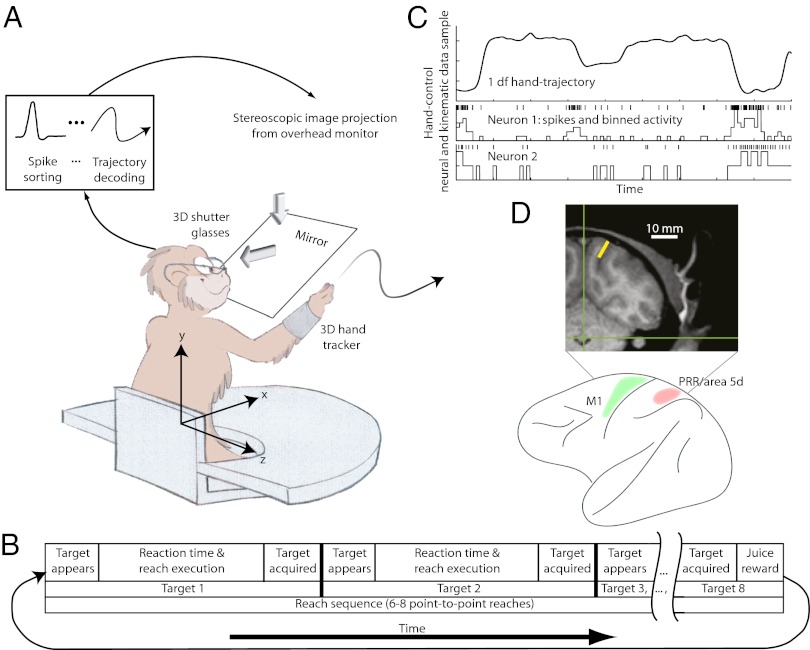
To investigate the feasibility of extracting prosthetic command signals from PPC, we simultaneously recorded ensembles of single- and multiunit spiking activity from area 5d and PRR (Fig. 1D and Fig. S1) in two rhesus monkeys while they performed reaches. First, each monkey used his hand to steer a cursor (reach control) in a 3D virtual reality (VR) environment (Fig. 1 A and B and Movie S1). We constructed and evaluated linear ridge regression (27) and Kalman filter (28) decode models for offline reconstruction of cursor movement from the concurrently recorded neural activity (Fig. 1C). The reach sessions were followed by brain-control sessions where VR-cursor movement was driven by neural activity instead of hand movement to test whether the previously identified decode model would be suitable for direct cortical control of a prosthetic.

Fig. 1.

Behavioral paradigm. (A) In daily recording sessions, each monkey guided a cursor in a 3D VR display to a reach target. The monkey first used his hand to control cursor movement (reach control). Then he steered the cursor using cortical activity (brain control) translated to cursor movement by the decode model identified from the preceding reach-control phase. (B) Timeline of the reach task. Reaches were performed in sequences of six or eight targets. The monkey was rewarded with juice after having completed a sequence of reaches. In brain-control mode, the monkey was rewarded after successful acquisition of single targets. (C) Single df trajectory sample, spike trains, and processed spike bins recorded simultaneously during the reaching task. (D) Unlike previous approaches targeting the motor areas, here, continuous control signals were extracted from PPC. Electrodes were implanted in PRR in the intraparietal sulcus (yellow marker in the coronal MRI slice) and area 5d on the cortical surface.

Results

Offline Reconstruction.

Twenty-nine reach-control sessions were analyzed in monkey R and 33 in monkey G. The offline reconstruction performance was quantified using the coefficient of determination, R², for the best day (Table 1) and the average over all recording days (Table 2). Despite free gaze, the decode model operating in a screen-centered reference frame captured the key features of 3D hand movement (Fig. 2 and Fig. S2) with best-day position reconstruction performance R² = 0.68/0.62 (monkey R/G) and average (over all recording days) position reconstruction performance R² = 0.61/0.52 (monkey R/G.). The Kalman filter provided position estimates significantly more accurate than the ridge filter estimates (P < 10⁻⁸ for monkey R; P < 10⁻⁹ for monkey G; two-sided sign test).

Table 1.

Single best-day offline reconstruction performance (mean ± SD) for ridge and Kalman filter

	Kalman filter, R2				Ridge filter, R2
	x/y/z combined			Single-best df	x/y/z combined
Monkey (no. of neural units)	Position	Velocity	Acceleration	Position	Position
R (70)	0.68 ± 0.03	0.59 ± 0.02	0.33 ± 0.02	0.77 ± 0.02	0.45 ± 0.05
G (55)	0.62 ± 0.04	0.36 ± 0.03	0.11 ± 0.02	0.76 ± 0.01	0.46 ± 0.05

Table 2.

Average (across all sessions) offline reconstruction performance (mean ± SD) for ridge and Kalman filter

	Kalman filter				Ridge filter
	R2 x/y/z combined			OLT (ms)	R2 x/y/z combined
Monkey (no. of neural units)	Position	Velocity	Acceleration	Position	Position
R (65.86 ± 6.89)	0.61 ± 0.06	0.58 ± 0.05	0.34 ± 0.07	82.35 ± 40.18	0.45 ± 0.05
G (64.29 ± 15.02)	0.52 ± 0.06	0.24 ± 0.05	0.07 ± 0.02	79.63 ± 39.43	0.36 ± 0.06

The reported performance was achieved using all neural units (single- and multiunit activity) recorded from area 5d and PRR combined. Because 75% of the implanted electrodes were designed for surface recordings, the neural ensembles reported contained more surface (area 5d) neural units than neural units from the deeper structures (PRR).

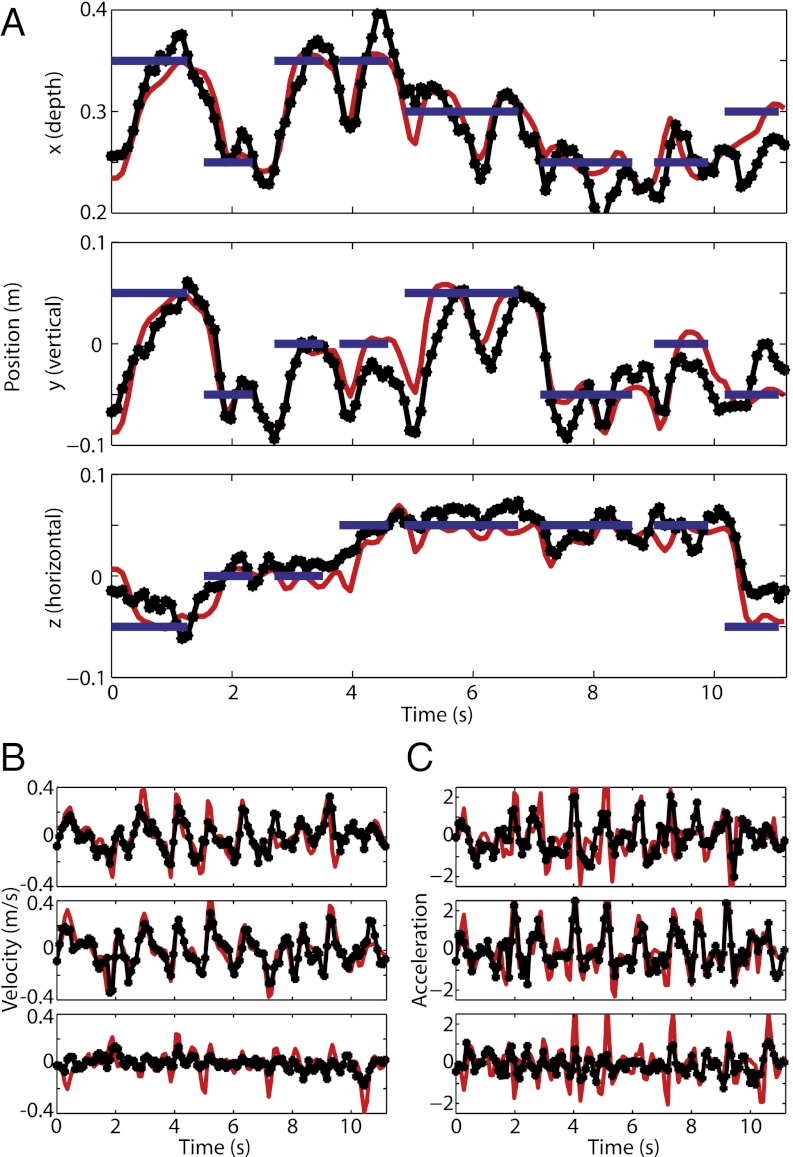
Fig. 2.

Offline Kalman filter 3D-trajectory reconstruction. PPC populations of neurons allow the decoding of position, velocity, and acceleration profiles with high accuracy in a free gaze point-to-point reaching task. (A) Position reconstruction (black) of a previously recorded sequence of reaches (red) to eight targets (blue). ●, discrete reconstruction points resulting from the 90-ms sampling rate used. (B and C) Velocity reconstruction (B) and acceleration reconstruction (C) for the same sequence.

To assess how well trajectories could be reconstructed from PPC neural ensembles of different sizes, we constructed neuron dropping curves (Fig. S3). They show that the position-decoding performance for a neural ensemble of a particular size is very similar between the two animals, although differences in decoding accuracy for velocity and acceleration exist. The neuron-dropping curves also reveal that the reported decoding performance (Tables 1 and 2) is better in monkey R primarily because more neural units were available.

Neural units in PRR are known to respond to visual stimuli (29), which could presumably impair trajectory reconstruction performance, particularly during the onset of high-contrast visual target cues. We, therefore, compared our decoding results with the performance obtained from reconstruction of the same sets of reaches, but after elimination of all visual cue onset phases, and found that the difference in decoding performance was small in both monkeys (SI Results).

Furthermore, the optimal lag time (OLT), representing the temporal offset of movement vs. neural population activity where R² tuning was maximal (Table 2), showed that neural population activity led movement execution on average by ∼80 ms in both monkeys, despite strong known proprioceptive and visual sensory inputs to PPC.

In summary, these offline reconstruction results suggest that (i) PPC populations of neurons allow accurate reconstruction of 3D trajectories under free gaze in a stationary reference frame; (ii) the decoded signal is insensitive to visual perturbations; and (iii) the neural signal leading the movement represents the animals’ intention to move rather than a sensory correlate of movement, thus qualifying it as a potential prosthetic control signal.

Brain Control.

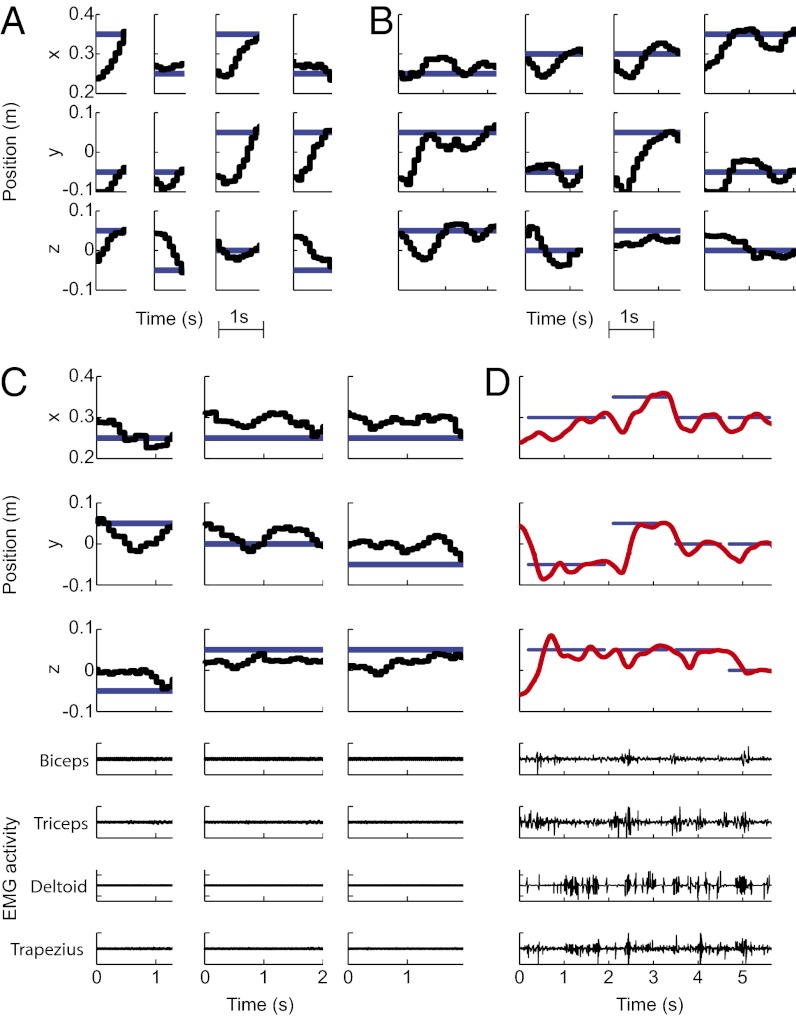
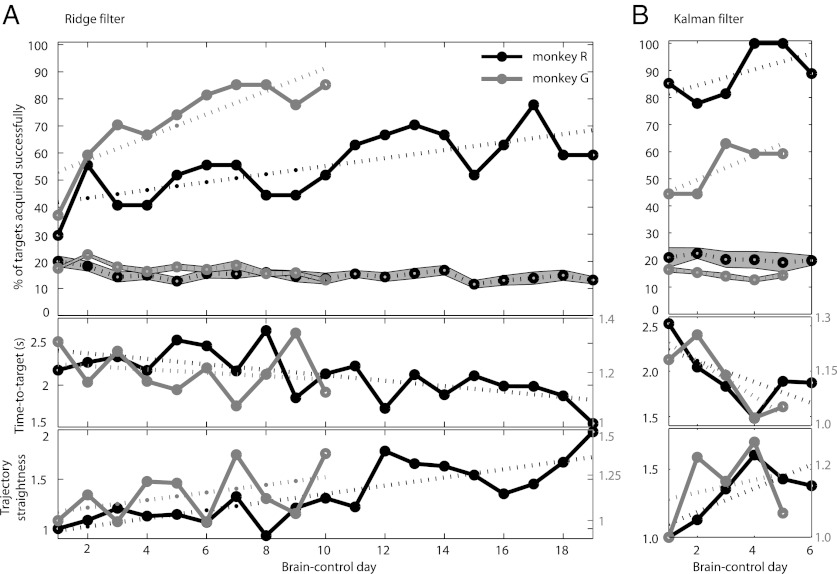
Twenty-five reach sessions were followed by brain-control sessions in monkey R and 15 in monkey G. In the brain-control task, VR-cursor movement was driven by neural activity instead of hand movement to test whether the previously identified decode model would be suitable for direct cortical control of a prosthetic. Both animals performed the brain-control task successfully (Movie S2). They frequently acquired targets rapidly, performing mostly straight reaches directed toward the goal from the initiation of the movement (Fig. 3A), but a number of reaches required adjustments to correct for initially erroneous trajectories (Fig. 3B and Fig. S4). Such visual feedback–driven error correction frequently resulted in successful target acquisition. Over time, behavioral performance improved with practice. During 19/10 (monkey R/G) ridge decode sessions, the success rate increased significantly from 29.63% on the first day to a maximum of 77.78% on day 17 [regression line slope m = 1.48; 95% confidence interval (CI): 0.72/2.23 (lower/upper bounds)] in monkey R and from 37.04% to 85.19% on day 10 (m = 4.24; 95% CI: 2.08/6.40) in monkey G, while always remaining significantly above chance level (Fig. 4). The mean time each monkey required to acquire a target successfully decreased significantly from 2.18 to 1.54 s (m = −0.033; 95% CI: −0.052/−0.014) in monkey R and from 1.31 to 1.13 s (not significant) in monkey G, whereas trajectory straightness, quantifying the goal-directedness of the brain-control trajectories, improved (m = 0.041; 95% CI: 0.026/0.057 in monkey R; not significant in monkey G) (Fig. 4A). To benchmark brain-control task proficiency, we compared time-to-target and trajectory straightness in monkey R (where both variables improved significantly over time) to the same-day performances achieved under hand-control (Fig. S5). The comparison highlights that (i) increasing performance is specific to the brain-control phase of the experiment and therefore cannot be explained by generally improved VR-task proficiency; and (ii) over time, brain-control performance approaches hand-control performance. Success rate, time to target, and trajectory straightness also showed steady improvement during 6/5 (monkey R/G) Kalman filter brain-control sessions. In monkey R, the success rate saturated at 100% after four sessions, and in monkey G, performance recovered from initially 44% to a maximum of 63% success rate despite availability of only a few neural units from aging array implants (Fig. 4B).

Fig. 3.

Online 3D brain-control. (A) Samples of direct brain-control trajectories resulting in target acquisition without requiring correction (reach target: blue; brain-control trajectory: black). (B) Samples of brain-control trajectories resulting in target acquisition after correction for initially wrong direction. (C) Brain-control trajectories in the absence of limb movement verified by the lack of visible EMG activity (lower four graphs) recorded simultaneously from biceps, triceps, deltoid, and trapezius. (D) For comparison: same-session reach-control showing characteristic EMG bursts on all four channels.

Fig. 4.

Learning brain-control. Improving behavioral performance in both monkeys for consecutive brain-control days shows that the monkeys learned to use PPC spike activity driving the decoding algorithm to direct cursor movement. Top graphs show daily success rates and chance performance ± SD (gray band) for ridge (A) and Kalman filter decode (B). Middle graphs show time-to-target for successful reaches. Bottom graphs show trajectory straightness. The trajectory straightness describes the ratio of the shortest (straight) distance from initial cursor location to target location and the actual distance the cursor traveled during the target acquisition, i.e., increasing straightness values indicate more direct trajectories. The trajectory straightness was normalized for first-day performance.

Monkey R was required not to move his limb while controlling cursor movement during a set of nine separate sessions to test brain-control in the absence of proprioceptive feedback modulating PPC activity. The monkey was not accustomed to the electromyographic (EMG) recording equipment attached to his arm to monitor muscle activation; therefore, movements performed while wearing the equipment (Fig. 3D) were less smooth and targets were acquired more slowly than under regular conditions under both hand-control (e.g., Fig. 2A vs. 3D) and brain control (e.g., Fig. 3 A and B vs. 3C). Despite this limitation, monkey R reached up to 66.67% brain-control success rate (chance performance 23.67 ± 1.49%) in the absence of detectable limb movement (Fig. 3 C and D and Movie S3). This result suggests that somatosensory feedback is not necessary to generate control signals in PPC, which will be important for clinical applications in patients who typically have sensory, as well as motor, deficits. The algorithm was trained during actual reaching movements, presumably accompanied by proprioceptive feedback, whereas the brain-control results were obtained in absence of limb movement, thus generating a mismatch between the decoding model and the inputs it expected based on the data on which it was trained. Results may, therefore, be even better when algorithms are trained in the absence of proprioception from the limb, such as in prosthetic patients for whom algorithms will need to be trained using neural activity during imagined movements.

Discussion

The results of this study show that complex, 3D point-to-point movement trajectories can be decoded from PPC under free gaze and that PPC-based brain–machine interfaces (BMIs) for continuous neural control of 3D manipulators are feasible.

Prior PPC studies reported substantially lower performance (R² below 0.3) in two free-gaze 2D decoding studies (2, 5). These low values may reflect the small number of electrodes implanted in the one study (2), whereas in the other study (5), very good grasp-decoding performance was reported, suggesting that the actual targeted site of the PPC was more involved with grasp. R² results comparable to those reported previously by our group in a highly constrained 2D center-out PPC decoding study (17) suggest that the removal of behavioral constraints such as eye fixation and increased task complexity does not impair the usefulness of PPC signals for prosthetic applications. Furthermore, the decoding algorithms operated continuously, requiring neither reinitialization at the beginning of a trial or a sequence nor elimination of visual cue onset responses (29), thus generalizing previous findings (17) to a realistic, unconstrained 3D prosthetic limb control scenario without compromising decoding accuracy.

R² decoding performances reported for M1 have ranged from 0.3 to 0.7 (2, 3, 5), and, thus, the PPC offline decoding results appear to be on par with M1 performance. Brain-control performance, commonly quantified by success rates, appears to be similar to the results reported in a motor cortex–based 3D brain-control study by Taylor et al. (4) (SI Results). Notwithstanding caution in consideration of methodological differences, these results suggest that achievable brain-control performance is comparable to motor cortex.

At first glance, it is surprising to find that PPC encodes a trajectory because it is motor cortex and not PPC that sends movement commands directly to the spinal cord. However, computational models of motor control, as well as lesions to patients and recordings from animals, suggest that PPC signals represent state estimates of ongoing movement whereas M1 signals carry motor commands (20–23, 30–32). Thus, the signals from PPC and M1, although serving different purposes in the brain, are equally suitable for decoding trajectories.

Previous research suggested that neurons in PRR rely primarily on gaze-centered reference frames to represent reach goals (24) and that area 5d neurons use simultaneous gaze- and limb-centered target representations (25). Thus, it appears to be counterintuitive that ongoing movement can be decoded from populations of neurons in a stationary body-centered reference frame, especially in the presence of changing hand–eye coordination patterns. The finding that free gaze does not limit decodability raises the possibility that PPC relies on a limb or body-centered reference frame. Many of the recordings were made from area 5d, and recent results show that a majority of cells in area 5d codes reaches in limb-centered coordinates (33). Another possibility is that trajectories and goals are encoded in different coordinate frames, with hand trajectory representations being affected little by eye movements, whereas reach targets are. This latter possibility is analogous to the medial superior temporal area (MST) encoding visual signals in eye coordinates and vestibular signals in head coordinates (34). A third possibility is that spatial representations depend on the context of the task and, although being more gaze-centered during gaze fixation (23, 24), could be mostly limb-centered during gaze free, thus always being in the coordinate frame that is most pertinent at the current stage of the task (35). Additional studies will be needed to distinguish between these or other explanations.

These findings, strongly suggesting that continuous prosthetic command signals from PPC are on par with continuous signals extracted from the motor areas, have implications for future approaches to BMIs. Their performance may be enhanced by simultaneous extraction of complementary continuous trajectory signals and a variety of high-level goal signals simultaneously, without requiring surgery and implantation of additional recording devices in other brain areas.

This wide array of control signals in PPC is perhaps indicative of its being a bridge between sensory and motor areas and, thereby, providing a broad pallet of sensorimotor variables.

Materials and Methods

General Methods.

Two rhesus monkeys were used in this study. All experiments were performed in compliance with the guidelines of the Caltech Institutional Animal Care and Use Committee and the National Institutes of Health Guide for the Care and Use of Laboratory Animals. Chronic recording electrode arrays (Floating Microelectrode Arrays; MicroProbes) (36) were implanted stereotaxically using magnetic resonance imaging (MRI) to guide the implantation. Four arrays with 32 recording electrodes each were placed in the medial bank of the intraparietal sulcus (IPS), a portion of PRR, and area 5d (Fig. 1D and Fig. S1). The differentially recorded neural signals from all electrically intact electrodes were band-pass filtered (154 Hz to 8.8 kHz), analog to digital converted (40-kHz sampling rate), spike-sorted using window-discriminator spike-sorting (Multichannel Acquisition Processor; Plexon), and stored to hard disk. The neural activity used for offline and online decoding included well-isolated single units and multiunit activity from all electrodes (Fig. S1). All neural units from the cortical surface (area 5d) and from the PRR (medial bank of the intraparietal sulcus) were processed identically and grouped to create the neural ensemble. The spike sorting was adjusted on a daily basis to capture changes in the neural activity available from the recording electrodes. The total number of neural units in the neural ensemble, therefore, fluctuated between days (Tables 1 and 2). All experiments were conducted in a VR environment providing closed-loop, real-time visual feedback (SI Materials and Methods).

The monkey performed reaches by steering his cursor to the target using hand movement during the reach-control phase and using cortical activity during the brain-control phase. The manual reaches were performed in sequences of eight or six, after which the animal received a fluid reward (Fig. 1B), whereas individual reaches were rewarded in brain-control mode. Each sequence started with the presentation of one target chosen pseudorandomly from the pool of 27 possible target locations. The monkey had 10 s to move his cursor to the target in the reach-control task and 4 s (monkey G) or 8 s (monkey R) in the brain-control task. After successful target acquisition, the target extinguished, and the next target appeared at a different location, chosen from the pool of the 26 remaining targets, and so on. A reach was successful if the animal kept the center of the hand cursor within <20 mm of the center of the target for a minimum of 300 ms (reach-control, both monkeys) and <30 mm for 90 ms (brain-control, monkey G) or <30 mm, 180 ms (brain-control, monkey R). Brain-control accuracy requirements were less stringent for animal G than for animal R because an early version of the array implant used in monkey G provided fewer neural channels than the later, revised version of the array implant in monkey R, thus making it harder for monkey G to meet the same accuracy requirements.

General Decoding Methods.

The spike events were collected in 90ms nonoverlapping bins, separately for each neural unit (Fig. 1C). The firing rates were then standardized by first subtracting the neurons’ mean firing rates and then dividing by their SDs. Neural and kinematic data starting from the appearance of the first reach target in a sequence until completion of the last reach in the same sequence were isolated for further processing, whereas recordings from in between sequences (reward and resting phase) were discarded. A total of 216 reaches, i.e., 27 reach sequences consisting of 8 reaches or 36 sequences consisting of 6 reaches, were used for decoding algorithm identification and validation for both ridge and Kalman filter. The sequences recorded during the reach-control segment were shuffled. Eighty percent of the shuffled data were used for training and 20% were used for validation. The shuffling, training, and validation procedure was repeated 100 times to obtain a mean ± SD offline reconstruction performance. Velocity and acceleration signals for Kalman filter algorithm training were obtained through numerical differentiation after convolving the position trajectory with a Gaussian kernel (σ = 12 ms) for smoothing.

Offline Ridge Filter.

The linear regression ridge model (17, 27) reconstructed instantaneous 3D cursor position as a function of the standardized firing rates r(t) of N simultaneously recorded neural units. Each sample of the behavioral state vector, x(t), was modeled as a function of the vector of ensemble firing rates measured for four successive 90-ms bins. Only the four causal bins immediately preceding the movement were used; i.e., the firing rates used in conjunction with the behavioral state x(t) were centered at (t − 315 ms), (t − 225 ms), (t − 135 ms), and (t − 45 ms). An estimate of the 3D cursor position, 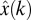, was constructed as a linear combination of the ensemble of firing rates, r, sampled at the four leading binning intervals according to

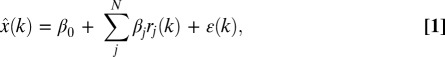where k denotes the discretized 90-ms time steps, ε represents the observational error, and N represents the total number of neural inputs each incorporating four successive bins. β, representing the regression coefficients, was determined using linear ridge regression (SI Materials and Methods).

Offline Kalman Filter.

The discrete Kalman filter implementation (17, 28, 37) estimated the current state of the movement, including velocity and acceleration, in all three degrees of freedom from single causal 90-ms bins of firing rates. Two equations govern the recursive reconstruction of the hand kinematics from the firing rates: an observation equation that modeled the firing rates (observation) as a function of the state of the cursor, x_k, and a process equation that propagated the state of the cursor forward in time as a function of only the most recent state, x_k−1. Both models were assumed to be linear stochastic functions, with additive Gaussian white noise:

The control term, u, was assumed to be unidentified and was, therefore, set to zero in our model, excluding B from the process model.

One simplifying assumption was that the process noise (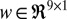), observation noise (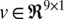), transition matrix (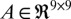), and the observation matrix (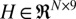) were fixed in time, thus simplifying Eqs. 2 and 3 to

where A and H were identified using least squares regression.

To estimate the state of the cursor, at each time-step k, the process model produced an a priori estimate, 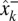, which was then updated with measurement data to form an a posteriori state estimate, 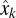. More specifically, the a priori estimate was linearly combined with the difference between the output of the observation model and the actual neural measurement (i.e., the neural innovation) using an optimal scaling factor, the Kalman gain, K_k, to produce an a posteriori estimate of the state of the cursor:

minimizing the a posteriori estimation error.

The entire two-step discrete estimation process of a priori time update and subsequent a posteriori measurement update was iterated recursively to generate an estimate of the state of the cursor at each time step in the trajectory. Both the Kalman gain, K_k, and the estimation error covariance matrix, P_k, have been shown to converge rapidly, decaying exponentially, in <1.5 s (17), and then to remain stable throughout the decoded segment.

Brain Control.

The identified decoding models (ridge filter, Kalman filter) were used to guide cursor movement during the brain-control phase of the experiment, allowing the animal to use cortical signals instead of hand movement to guide the cursor. Cursor position was updated every 90 ms and visualized continuously, without reinitialization, throughout the brain-control session. To assess behavioral performance, daily success rates were computed. Although both animals typically performed brain-control reaches to all 27 targets multiple times, the success rate for the most successful set of 27 reaches was reported in Fig. 2. The average success rate over all trials in a session was typically biased (lower) because it frequently included sets of targets where the monkey chose to rest instead of attempting to perform a brain-control reach, making the best set of 27 brain-control reaches the more appropriate measure to assess success rates.

To calculate the chance levels for success rates, firing rate bin samples for a given neural unit recorded during brain control were shuffled randomly, effectively preserving each neural unit’s mean firing rate but breaking its temporal structure. Chance trajectories were then generated by simulation, iteratively applying the actual decoder to the shuffled ensemble of firing rates to generate a series of pseudocursor positions. The criteria used during actual brain-control trials were applied to these pseudocursor positions to detect successful target acquisition by chance. This procedure was repeated 50 times to obtain a distribution of chance performances for each session, from which a mean and SD were derived.

The time-to-target reported quantifies the average duration of all successful reaches in a session, measured from target cue appearance to successful target acquisition.

The trajectory straightness was assessed by calculating the ratio of trajectory lengths: the shortest possible (straight) trajectory to acquire a target and the actual distance the cursor traveled. Trajectories were analyzed from when the target cue appeared (initial cursor position) until detection of successful target acquisition (final cursor position). The trajectory straightness results, reported as daily averages for all reaches completed successfully, were normalized for first day performance.

Because PPC receives projections from S1 (40, 41) that carry proprioceptive signals, it is unclear whether the movement representation decoded from PPC persists when proprioceptive feedback from the limb is compromised. This was tested by (i) mechanically immobilizing the limb during the brain-control decode session and (ii) monitoring the EMG activity of the muscle groups typically involved in reaching movements in monkey R. EMG recordings were made via small percutaneous hook electrodes (paired hook-wire electrode, 30 mm × 27 gauge; VIASYS Healthcare). Recordings were taken simultaneously from the deltoid, trapezius, biceps, and triceps muscles. To verify proper placement and function of the EMG electrodes, recordings were taken before and after the brain control session during a series of reach sequences where the monkey was required to move his limb to control cursor movement.