Abstract
The amount of information exchanged per unit of time between two nodes in a dynamical network or between two data sets is a powerful concept for analysing complex systems. This quantity, known as the mutual information rate (MIR), is calculated from the mutual information, which is rigorously defined only for random systems. Moreover, the definition of mutual information is based on probabilities of significant events. This work offers a simple alternative way to calculate the MIR in dynamical (deterministic) networks or between two time series (not fully deterministic), and to calculate its upper and lower bounds without having to calculate probabilities, but rather in terms of well known and well defined quantities in dynamical systems. As possible applications of our bounds, we study the relationship between synchronisation and the exchange of information in a system of two coupled maps and in experimental networks of coupled oscillators.
Introduction
Shannon’s entropy quantifies information [1]. It measures how much uncertainty an observer has about an event being produced by a random system. Another important concept in the theory of information is the mutual information [1]. It measures how much uncertainty an observer has about an event in a random system X after observing an event in another random system Y (or vice-versa).
Mutual information (MI) is an important quantity because it quantifies not only linear and non-linear interdependencies between two systems or data sets, but also is a measure of how much information two systems exchange or two data sets share. Due to these characteristics, it became a fundamental quantity to understand the development and function of the brain [2], [3], to characterise [4], [5] and model complex systems [6]–[8] or chaotic systems, and to quantify the information capacity of a communication system [9]. When constructing a model of a complex system, the first step is to understand which are the most relevant variables to describe its behaviour. Mutual information provides a way to identify those variables [10].
However, the calculation of mutual information in dynamical networks or data sets faces three main difficulties[4], [11]–[13]. Mutual information is rigorously defined for random memoryless processes, only. In addition, its calculation involves probabilities of significant events and a suitable space where probability is calculated. The events need to be significant in the sense that they contain as much information about the system as possible. But, defining significant events, for example the fact that a variable has a value within some particular interval, is a difficult task because the interval that provides significant events is not always known. Finally, data sets have finite size. Probabilities computed from finite data sets are subjected to unavoidable sampling errors. As a consequence, mutual information can often be calculated with a bias, only [4], [11]–[13].
In this work, we show how to calculate the amount of information exchanged per unit of time [Eq. (2)], the so called mutual information rate (MIR), between two arbitrary nodes (or group of nodes) in a dynamical network or between two data sets. Each node represents a d-dimensional dynamical system with 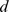 state variables. The trajectory of the network considering all the nodes in the full phase space is denoted by
state variables. The trajectory of the network considering all the nodes in the full phase space is denoted by 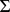 and represents the “attractor”, which in the following calculations is considered to be an asymptotic limiting set. Then, we propose an alternative method, similar to the ones proposed in Refs. [14], [15], to calculate significant upper and lower bounds for the MIR in dynamical networks or between two data sets, in terms of Lyapunov exponents, expansion rates, and capacity dimension. These quantities can be calculated without the use of probabilistic measures. As possible applications of our bounds calculation, we describe the relationship between synchronisation and the exchange of information in small experimental networks of coupled Double-Scroll circuits.
and represents the “attractor”, which in the following calculations is considered to be an asymptotic limiting set. Then, we propose an alternative method, similar to the ones proposed in Refs. [14], [15], to calculate significant upper and lower bounds for the MIR in dynamical networks or between two data sets, in terms of Lyapunov exponents, expansion rates, and capacity dimension. These quantities can be calculated without the use of probabilistic measures. As possible applications of our bounds calculation, we describe the relationship between synchronisation and the exchange of information in small experimental networks of coupled Double-Scroll circuits.
In previous works of Refs. [14], [15], we have proposed an upper bound for the MIR in terms of the positive Lyapunov exponents of the synchronisation manifold. As a consequence, this upper bound could only be calculated in special complex networks that allow the existence of complete synchronisation. In the present work, the proposed upper bound can be calculated to any system (complex networks and data sets) that admits the calculation of Lyapunov exponents.
We assume that an observer can measure only one scalar time series for each one of two chosen nodes. These two time series are denoted by 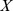 and
and 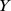 and they form a bidimensional set
and they form a bidimensional set 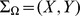 , a projection of the “attractor” into a bidimensional space denoted by
, a projection of the “attractor” into a bidimensional space denoted by  . To calculate the MIR in higher-dimensional projections
. To calculate the MIR in higher-dimensional projections  , see Information S1. To estimate the upper bound of the MIR in terms of Lyapunov exponents obtained from the reconstructed attractor of a scalar time-series see Information S1. Assume that the space
, see Information S1. To estimate the upper bound of the MIR in terms of Lyapunov exponents obtained from the reconstructed attractor of a scalar time-series see Information S1. Assume that the space  is coarse-grained in a square grid of
is coarse-grained in a square grid of 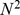 boxes with equal sides
boxes with equal sides  , so
, so 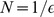 .
.
Mutual information is defined in the following way [1]. Given two discrete random variables, X and Y, each one produces events  and
and 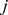 with probabilities
with probabilities 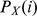 and
and 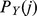 , respectively, the joint probability between these events is represented by
, respectively, the joint probability between these events is represented by 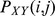 . Then, mutual information is defined as
. Then, mutual information is defined as
| (1) |
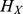 =
=  ,
,  =
=  , and
, and 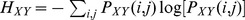 . When using Eq. (1) to calculate the mutual information between the dynamical variables
. When using Eq. (1) to calculate the mutual information between the dynamical variables 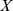 and
and 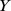 , the probabilities appearing in Eq. (1) are defined such that
, the probabilities appearing in Eq. (1) are defined such that 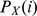 is the probability of finding points in a column
is the probability of finding points in a column  of the grid,
of the grid, 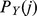 of finding points in the row
of finding points in the row 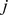 of the grid, and
of the grid, and  the probability of finding points in a box where the column
the probability of finding points in a box where the column  meets the row
meets the row 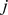 of the grid.
of the grid.
The MIR was firstly introduced by Shannon [1] as a “rate of actual transmission” [16] and later more rigorously redefined in Refs. [17], [18]. It represents the mutual information exchanged between two dynamical variables (correlated) per unit of time. To calculate the MIR, the two continuous dynamical variables are transformed into two discrete symbolic sequences 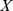 and
and 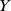 . Then, the MIR is defined by
. Then, the MIR is defined by
| (2) |
where 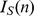 represents the usual mutual information between the two sequences
represents the usual mutual information between the two sequences 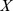 and
and 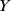 , calculated by considering words of length
, calculated by considering words of length  . If
. If 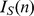 is calculated using
is calculated using 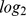 , the MIR in Eq. (2) has units of bits/symbol. If a discrete system is producing the symbols, the units of Eq. (2) are bits/iteration.
, the MIR in Eq. (2) has units of bits/symbol. If a discrete system is producing the symbols, the units of Eq. (2) are bits/iteration.
The MIR is a fundamental quantity in science. Its maximal value gives the information capacity between any two sources of information (no need for stationarity, statistical stability, memoryless) [19]. Therefore, alternative approaches for its calculation or for the calculation of bounds of it are of vital relevance. Due to the limit to infinity in Eq. (2) and because it is defined from probabilities, the MIR is not easy to be calculated especially if one wants to calculate it from (chaotic) trajectories of a large complex network or data sets. The difficulties faced to estimate the MIR from dynamical systems and networks are similar to the ones faced in the calculation of the Kolmogorov-Sinai entropy, 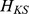 [20], (Shannon’s entropy per unit of time). Because of these difficulties, the upper bound for
[20], (Shannon’s entropy per unit of time). Because of these difficulties, the upper bound for 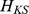 proposed by Ruelle [21] in terms of the Lyapunov exponents and valid for smooth dynamical systems (
proposed by Ruelle [21] in terms of the Lyapunov exponents and valid for smooth dynamical systems (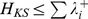 , where
, where 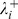 represent all the
represent all the  positive Lyapunov exponents) or Pesin’s equality [22] (
positive Lyapunov exponents) or Pesin’s equality [22] (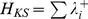 ) proved in Ref. [23] to be valid for the large class of systems that possess a SRB measure, became so important in the theory of dynamical systems. Our upper bound [Eq. (5)] is a result similar to the work of Ruelle, but instead we relate mutual information rate with Lyapunov exponents.
) proved in Ref. [23] to be valid for the large class of systems that possess a SRB measure, became so important in the theory of dynamical systems. Our upper bound [Eq. (5)] is a result similar to the work of Ruelle, but instead we relate mutual information rate with Lyapunov exponents.
Our work is also similar to the work of Wissman-Jones-Binder [24] who have shown that upper and lower bounds for 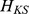 and the sum of the Lyapunov exponents can be calculated in terms of the mutual information, MI, of a trajectory. Their work, like ours, has shown a link between (conditional and joint) probabilities and a dynamical quantity, the Lyapunov exponents. We focus our attention to the relationship between MIR and Lyapunov exponents, Wissman and co-authors focus their attention in the relationship between MI and the Lyapunov exponents.
and the sum of the Lyapunov exponents can be calculated in terms of the mutual information, MI, of a trajectory. Their work, like ours, has shown a link between (conditional and joint) probabilities and a dynamical quantity, the Lyapunov exponents. We focus our attention to the relationship between MIR and Lyapunov exponents, Wissman and co-authors focus their attention in the relationship between MI and the Lyapunov exponents.
Results
One of the main results of this work (whose derivation can be seen in Sec. Methods) is to show that, in dynamical networks or data sets with fast decay of correlation, 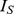 in Eq. (1) represents the amount of mutual information between
in Eq. (1) represents the amount of mutual information between  and
and 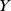 produced within a special time interval
produced within a special time interval 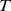 , where
, where 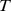 represents the time for the dynamical network (or data sets) to lose its memory from the initial state or the correlation to decay to zero. Correlation in this work is not the usual linear correlation, but a non-linear correlation defined in terms of the evolution of probabilities defined by space integrals, the quantity
represents the time for the dynamical network (or data sets) to lose its memory from the initial state or the correlation to decay to zero. Correlation in this work is not the usual linear correlation, but a non-linear correlation defined in terms of the evolution of probabilities defined by space integrals, the quantity 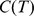 in Eq. (9). Therefore, the mutual information rate (MIR), between the dynamical variables
in Eq. (9). Therefore, the mutual information rate (MIR), between the dynamical variables 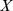 and
and 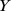 (or two data sets) can be estimated by
(or two data sets) can be estimated by
| (3) |
In systems that exhibit sensitivity to initial conditions, e.g. chaotic systems, predictions are only possible for times smaller than this time  . This time has other meanings. It is the expected time necessary for a set of points belonging to an
. This time has other meanings. It is the expected time necessary for a set of points belonging to an  -square box in
-square box in  to spread over
to spread over 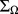 and it is of the order of the shortest Poincaré return time for a point to leave a box and return to it [25], [26]. It can be estimated by
and it is of the order of the shortest Poincaré return time for a point to leave a box and return to it [25], [26]. It can be estimated by
| (4) |
where 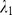 is the largest positive Lyapunov exponent measured in
is the largest positive Lyapunov exponent measured in 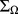 . Chaotic systems can exhibit the mixing property (see Methods), and as a consequence the correlation
. Chaotic systems can exhibit the mixing property (see Methods), and as a consequence the correlation 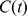 decays to zero, surely after an infinitely long time. The correlation of chaotic systems can also decay to zero for sufficiently large but finite
decays to zero, surely after an infinitely long time. The correlation of chaotic systems can also decay to zero for sufficiently large but finite 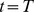 (see Information S1).
(see Information S1).  can be interpreted to be the minimum time required for a system to satisfy the conditions to be considered as mixing. Some examples of physical systems that are proved to be mixing and have exponentially fast decay of correlation are nonequilibrium steady-state [27], Lorentz gases (models of diffusive transport of light particles in a network of heavier particles) [28], and billiards [29]. An example of a “real world” physical complex system that presents exponentially fast decay of correlation is plasma turbulence [30]. We do not expect that data coming from a “real world” complex system is rigorously mixing and has an exponentially fast decay of correlation. But, we expect that the data has a sufficiently fast decay of correlation (e.g. stretched exponential decay or polynomially fast decays), implying that the system has sufficiently high sensitivity to initial conditions and as a consequence
can be interpreted to be the minimum time required for a system to satisfy the conditions to be considered as mixing. Some examples of physical systems that are proved to be mixing and have exponentially fast decay of correlation are nonequilibrium steady-state [27], Lorentz gases (models of diffusive transport of light particles in a network of heavier particles) [28], and billiards [29]. An example of a “real world” physical complex system that presents exponentially fast decay of correlation is plasma turbulence [30]. We do not expect that data coming from a “real world” complex system is rigorously mixing and has an exponentially fast decay of correlation. But, we expect that the data has a sufficiently fast decay of correlation (e.g. stretched exponential decay or polynomially fast decays), implying that the system has sufficiently high sensitivity to initial conditions and as a consequence 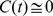 , for a reasonably small and finite time
, for a reasonably small and finite time 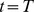
The other two main results of our work are presented in Eqs. (5) and (7), whose derivations are presented in Sec. Methods. An upper bound for the MIR is given by
| (5) |
where 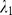 and
and 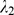 represent the largest and the second largest Lyapunov exponent measured in
represent the largest and the second largest Lyapunov exponent measured in 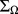 , if both exponents are positive. If the
, if both exponents are positive. If the  -largest exponent is negative, then we set
-largest exponent is negative, then we set 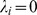 . If the set
. If the set 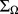 represents a periodic orbit,
represents a periodic orbit, 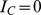 , and therefore there is no information being exchanged. The quantity
, and therefore there is no information being exchanged. The quantity 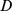 is defined as
is defined as
| (6) |
where 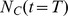 is the number of boxes that would be covered by fictitious points at time
is the number of boxes that would be covered by fictitious points at time 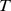 . At time
. At time 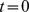 , these fictitious points are confined in an
, these fictitious points are confined in an  -square box. They expand not only exponentially fast in both directions according to the two positive Lyapunov exponents, but expand forming a compact set, a set with no “holes”. At
-square box. They expand not only exponentially fast in both directions according to the two positive Lyapunov exponents, but expand forming a compact set, a set with no “holes”. At 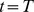 , they spread over
, they spread over 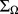 .
.
A lower bound for the MIR is given by
| (7) |
where  represents the capacity dimension of the set
represents the capacity dimension of the set 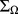
| (8) |
where 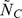 represents the number of boxes in
represents the number of boxes in  that are occupied by points of
that are occupied by points of 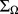 .
.
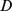 is defined in a way similar to the capacity dimension, though it is not the capacity dimension. In fact,
is defined in a way similar to the capacity dimension, though it is not the capacity dimension. In fact, 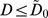 , because
, because 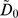 measures the change in the number of occupied boxes in
measures the change in the number of occupied boxes in  as the space resolution varies, whereas
as the space resolution varies, whereas 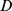 measures the relative number of boxes with a certain fixed resolution
measures the relative number of boxes with a certain fixed resolution  that would be occupied by the fictitious points (in
that would be occupied by the fictitious points (in  ) after being iterated for a time
) after being iterated for a time 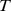 . As a consequence, the empty space in
. As a consequence, the empty space in  that is not occupied by
that is not occupied by 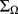 does not contribute to the calculation of
does not contribute to the calculation of 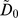 , whereas it contributes to the calculation of the quantity
, whereas it contributes to the calculation of the quantity 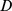 . In addition,
. In addition, 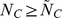 (for any
(for any  ), because while the fictitious points form a compact set expanding with the same ratio as the one for which the real points expand (ratio provided by the Lyapunov exponents), the real set of points
), because while the fictitious points form a compact set expanding with the same ratio as the one for which the real points expand (ratio provided by the Lyapunov exponents), the real set of points 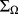 might not occupy many boxes.
might not occupy many boxes.
Methods
Mixing, Correlation Decay and Invariant Measures
Denote by 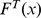 a mixing transformation that represents how a point
a mixing transformation that represents how a point 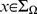 is mapped after a time
is mapped after a time 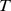 into
into 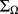 , and let
, and let 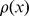 to represent the probability of finding a point of
to represent the probability of finding a point of 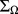 in
in  (natural invariant density). Let
(natural invariant density). Let  represent a region in
represent a region in  . Then,
. Then, 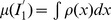 , for
, for 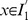 represents the probability measure of the region
represents the probability measure of the region  . Given two square boxes
. Given two square boxes 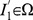 and
and 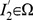 , if
, if 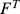 is a mixing transformation, then for a sufficiently large
is a mixing transformation, then for a sufficiently large 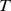 , we have that the correlation defined as
, we have that the correlation defined as
| (9) |
decays to zero, the probability of having a point in 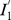 that is mapped to
that is mapped to 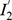 is equal to the probability of being in
is equal to the probability of being in 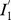 times the probability of being in
times the probability of being in 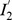 . That is typically what happens in random processes.
. That is typically what happens in random processes.
Notice that 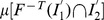 can be interpreted as a joint entropy defined by the probability of being at
can be interpreted as a joint entropy defined by the probability of being at 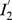 times the conditional probability (that defines elements in a transition matrix) of transferring from the set
times the conditional probability (that defines elements in a transition matrix) of transferring from the set 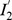 to
to 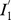 .
.
If the measure 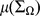 is invariant, then
is invariant, then 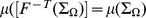 . Mixing and ergodic systems produce measures that are invariant.
. Mixing and ergodic systems produce measures that are invariant.
Derivation of the Mutual Information Rate (MIR) in Dynamical Networks and Data Sets
We consider that the dynamical networks or data sets to be analysed present either the mixing property or have fast decay of correlations, and their probability measure is time invariant. If a system that is mixing for a time interval 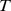 is observed (sampled) once every time interval
is observed (sampled) once every time interval 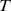 , then the probabilities generated by these snapshot observations behave as if they were independent, and the system behaves as if it were a random process. This is so because if a system is mixing for a time interval
, then the probabilities generated by these snapshot observations behave as if they were independent, and the system behaves as if it were a random process. This is so because if a system is mixing for a time interval 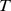 , then the correlation
, then the correlation 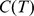 decays to zero for this time interval. For systems that have some decay of correlation, surely the correlation decays to zero after an infinite time interval. But, this time interval can also be finite, as shown in Information S1.
decays to zero for this time interval. For systems that have some decay of correlation, surely the correlation decays to zero after an infinite time interval. But, this time interval can also be finite, as shown in Information S1.
Consider now that we have experimental points and they are sampled once every time interval 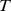 . If the system is mixing, then the probability
. If the system is mixing, then the probability 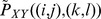 of the sampled trajectory to be in the box with coordinates
of the sampled trajectory to be in the box with coordinates 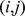 and then be iterated to the box
and then be iterated to the box 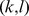 depends exclusively on the probabilities of being at the box
depends exclusively on the probabilities of being at the box 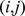 , represented by
, represented by 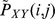 , and being at the box
, and being at the box 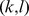 , represented by
, represented by 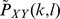 .
.
Therefore, for the sampled trajectory, 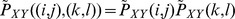 . Analogously, the probability
. Analogously, the probability 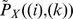 (or
(or 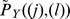 ) of the sampled trajectory to be in the column
) of the sampled trajectory to be in the column  (or row
(or row 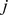 ) of the grid and then be iterated to the column
) of the grid and then be iterated to the column 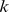 (or row
(or row 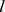 ) is given by
) is given by 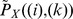 =
= 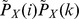 (or
(or 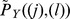 =
= 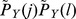 ).
).
The MIR of the experimental non-sampled trajectory points can be calculated from the mutual information of the sampled trajectory points 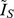 that follow itineraries of length
that follow itineraries of length  :
:
| (10) |
Due to the absence of correlations of the sampled trajectory points, the mutual information for these points following itineraries of length  can be written as
can be written as
| (11) |
where 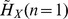 =
= 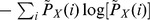 ,
,  =
= 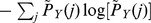 , and
, and 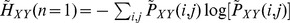 , and
, and 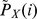 ,
, 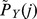 , and
, and 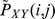 represent the probability of the sampled trajectory points to be in the column
represent the probability of the sampled trajectory points to be in the column  of the grid, in the row
of the grid, in the row 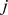 of the grid, and in the box
of the grid, and in the box 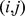 of the grid, respectively.
of the grid, respectively.
Due to the time invariance of the set 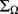 assumed to exist, the probability measure of the non-sampled trajectory is equal to the probability measure of the sampled trajectory. If a system that has a time invariant measure is observed (sampled) once every time interval
assumed to exist, the probability measure of the non-sampled trajectory is equal to the probability measure of the sampled trajectory. If a system that has a time invariant measure is observed (sampled) once every time interval 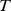 , the observed set has the same natural invariant density and probability measure of the original set. As a consequence, if
, the observed set has the same natural invariant density and probability measure of the original set. As a consequence, if 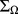 has a time invariant measure, the probabilities
has a time invariant measure, the probabilities 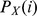 ,
, 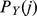 , and
, and 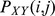 (used to calculate
(used to calculate  ) are equal to
) are equal to 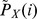 ,
, 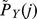 , and
, and 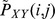 .
.
Consequently, 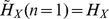 ,
, 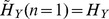 , and
, and 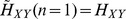 , and therefore
, and therefore 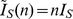 . Substituting into Eq. (10), we finally arrive to
. Substituting into Eq. (10), we finally arrive to 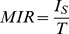 in Eq. (3), where
in Eq. (3), where 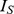 between two nodes is calculated from Eq. (1).
between two nodes is calculated from Eq. (1).
Therefore, in order to calculate the MIR, we need to estimate the time 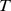 for which the correlation of the system approaches zero and the probabilities
for which the correlation of the system approaches zero and the probabilities 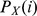 ,
, 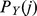 ,
, 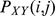 of the experimental non-sampled experimental points to fall in the column
of the experimental non-sampled experimental points to fall in the column  of the grid, in the row
of the grid, in the row 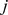 of the grid, and in the box
of the grid, and in the box 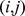 of the grid, respectively.
of the grid, respectively.
We demonstrate the validity of Eqs. (10) and (11) by showing that 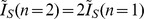 , which leads to Eq. (3). For the following demonstration,
, which leads to Eq. (3). For the following demonstration, 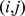 (or (k,l)) represents a box in the subspace
(or (k,l)) represents a box in the subspace  placed at coordinates
placed at coordinates 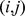 , meaning a square of sides
, meaning a square of sides  whose lower left corner point is located at
whose lower left corner point is located at 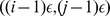 . Then,
. Then,  (or
(or 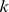 ) represents a column with width
) represents a column with width  in
in  whose left side is located at
whose left side is located at 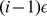 (or
(or 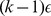 ) and j (or
) and j (or 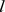 ) represents a row with width
) represents a row with width  in
in  whose bottom side is located at
whose bottom side is located at 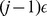 (or
(or 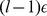 ).
).
If the system is mixing for a time 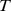 , then the probability of having points in a box
, then the probability of having points in a box 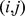 and going to another box
and going to another box 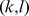 , i.e.,
, i.e., 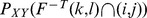 can be calculated by
can be calculated by
| (12) |
Notice that 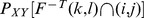 is a joint entropy that is equal to
is a joint entropy that is equal to 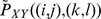 , and could be written as a function of conditional probabilities:
, and could be written as a function of conditional probabilities: 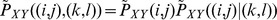 , where
, where 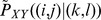 represents the conditional probability of being transferred from the box
represents the conditional probability of being transferred from the box 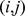 to the box
to the box 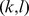 .
.
The same can be done to calculate the probability of having points in a column  that are mapped to another column
that are mapped to another column 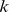 , i.e.
, i.e. 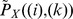 , or of having points in a row
, or of having points in a row 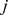 that are mapped to another row
that are mapped to another row 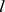 , i.e.
, i.e. 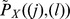 . If the system is mixing for a time
. If the system is mixing for a time 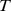 , then
, then
| (13) |
and
| (14) |
for the rows. Notice that 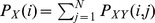 and
and 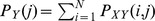 .
.
The order-2 Mutual information of the sampled points can be calculated by.
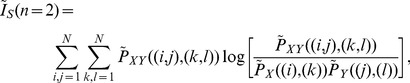 |
(15) |
where 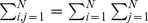 .
. 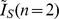 measures the MI of points that follow an itinerary of one iteration, points that are in a box and are iterated to another box. Substituting Eq. (12) in Eq. (15) we arrive at
measures the MI of points that follow an itinerary of one iteration, points that are in a box and are iterated to another box. Substituting Eq. (12) in Eq. (15) we arrive at
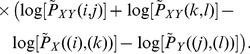 |
(16) |
Then, substituting (13) and (14) in Eq. (16), and using the fact that 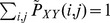 and
and 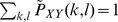 , we arrive at
, we arrive at
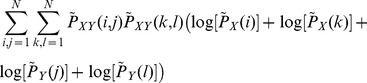 |
(17) |
Re-organizing the terms we arrive at
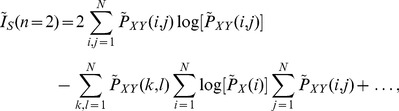 |
(18) |
where  represents other terms that are similar to the term appearing in the last hand-side part of the previous equation. Using the fact that
represents other terms that are similar to the term appearing in the last hand-side part of the previous equation. Using the fact that 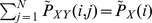 , we arrive at
, we arrive at
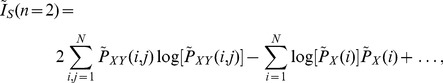 |
(19) |
which can then be written as
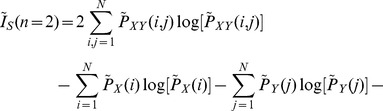 |
| (20) |
Since 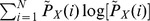 =
= 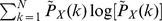 and
and 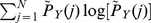 =
= 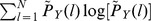 , we finally arrive at that
, we finally arrive at that 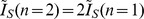 . Similar calculations can be performed to state that
. Similar calculations can be performed to state that 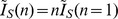 . As previously discussed,
. As previously discussed, 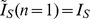 , which lead us to Eq. (3).
, which lead us to Eq. (3).
Derivation of an Upper (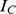 ) and Lower (
) and Lower (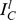 ) Bounds for the MIR
) Bounds for the MIR
Consider that our attractor  is generated by a 2d expanding system with constant Jacobian that possesses two positive Lyapunov exponents
is generated by a 2d expanding system with constant Jacobian that possesses two positive Lyapunov exponents  and
and 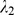 , with
, with 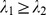 .
.  . Imagine a box whose sides are oriented along the orthogonal basis used to calculate the Lyapunov exponents. Then, points inside the box spread out after a time interval
. Imagine a box whose sides are oriented along the orthogonal basis used to calculate the Lyapunov exponents. Then, points inside the box spread out after a time interval  to
to 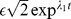 along the direction from which
along the direction from which 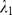 is calculated. At
is calculated. At 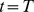 ,
, 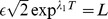 , which provides
, which provides 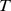 in Eq. (4), since
in Eq. (4), since 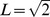 . These points spread after a time interval
. These points spread after a time interval  to
to 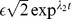 along the direction from which
along the direction from which 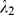 is calculated. After an interval of time
is calculated. After an interval of time 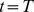 , these points spread out over the set
, these points spread out over the set 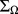 . We require that for
. We require that for 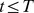 , the distance between these points only increases: the system is expanding.
, the distance between these points only increases: the system is expanding.
Imagine that at 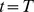 , fictitious points initially in a square box occupy an area of
, fictitious points initially in a square box occupy an area of 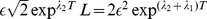 . Then, the number of boxes of sides
. Then, the number of boxes of sides  that contain fictitious points can be calculated by
that contain fictitious points can be calculated by 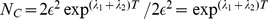 . From Eq. (4),
. From Eq. (4), 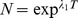 , since
, since 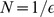 .
.
We denote with a lower-case format, the probabilities 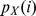 ,
, 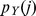 , and
, and 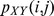 with which fictitious points occupy the grid in
with which fictitious points occupy the grid in  . If these fictitious points spread uniformly forming a compact set whose probabilities of finding points in each fictitious box is equal, then
. If these fictitious points spread uniformly forming a compact set whose probabilities of finding points in each fictitious box is equal, then 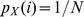 (
(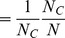 ),
), 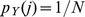 , and
, and 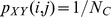 . Let us denote the Shannon entropy of the probabilities
. Let us denote the Shannon entropy of the probabilities 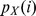 ,
, 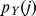 and
and 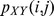 as
as 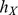 ,
, 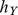 , and
, and 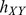 , respectively. The mutual information of the fictitious trajectories after evolving a time interval
, respectively. The mutual information of the fictitious trajectories after evolving a time interval 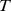 can be calculated by
can be calculated by 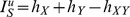 . Since,
. Since, 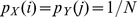 and
and 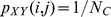 , then
, then 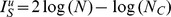 . At
. At 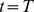 , we have that
, we have that 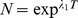 and
and 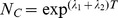 , leading us to
, leading us to 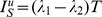 . Therefore, defining,
. Therefore, defining, 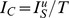 , we arrive at
, we arrive at 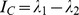 .
.
We define 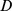 as
as
| (21) |
where 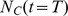 being the number of boxes that would be covered by fictitious points at time
being the number of boxes that would be covered by fictitious points at time 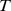 . At time
. At time 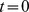 , these fictitious points are confined in an -square box. They expand not only exponentially fast in both directions according to the two positive Lyapunov exponents, but expand forming a compact set, a set with no “holes”. At
, these fictitious points are confined in an -square box. They expand not only exponentially fast in both directions according to the two positive Lyapunov exponents, but expand forming a compact set, a set with no “holes”. At 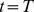 , they spread over
, they spread over 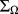 .
.
Using 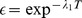 and
and  in Eq. (21), we arrive at
in Eq. (21), we arrive at 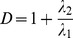 , and therefore, we can write that
, and therefore, we can write that 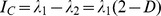 , as in Eq. (5).
, as in Eq. (5).
To calculate the maximal possible MIR, of a random independent process, we assume that the expansion of points is uniform only along the columns and rows of the grid defined in the space  , i.e.,
, i.e., 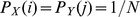 , (which maximises
, (which maximises 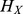 and
and 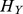 ), and we allow
), and we allow 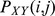 to be not uniform (minimising
to be not uniform (minimising 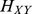 ) for all
) for all  and
and 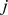 , then
, then
| (22) |
Since 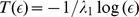 , dividing
, dividing 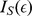 by
by 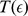 , taking the limit of
, taking the limit of  , and reminding that the information dimension of the set
, and reminding that the information dimension of the set 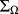 in the space
in the space  is defined as
is defined as 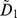 =
= 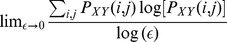 , we obtain that the MIR is given by
, we obtain that the MIR is given by
| (23) |
Since 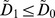 (for any value of
(for any value of  ), then
), then 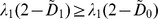 , which means that a lower bound for the maximal MIR [provided by Eq. (23)] is given by
, which means that a lower bound for the maximal MIR [provided by Eq. (23)] is given by 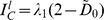 , as in Eq. (7). But
, as in Eq. (7). But 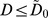 (for any value of
(for any value of  ), and therefore
), and therefore 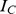 is an upper bound for
is an upper bound for 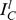 .
.
To show why 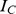 is an upper bound for the maximal possible MIR, assume that the real points
is an upper bound for the maximal possible MIR, assume that the real points 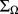 occupy the space
occupy the space  uniformly. If
uniformly. If 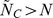 , there are many boxes being occupied. It is to be expected that the probability of finding a point in a column or a row of the grid is
, there are many boxes being occupied. It is to be expected that the probability of finding a point in a column or a row of the grid is  , and
, and 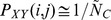 . In such a case,
. In such a case, 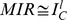 , which implies that
, which implies that 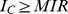 . If
. If 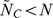 , there are only few boxes being sparsely occupied. The probability of finding a point in a column or a row of the grid is
, there are only few boxes being sparsely occupied. The probability of finding a point in a column or a row of the grid is 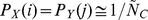 , and
, and 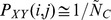 . There are
. There are 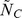 columns and rows being occupied by points in the grid. In such a case,
columns and rows being occupied by points in the grid. In such a case, 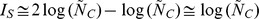 . Comparing with
. Comparing with 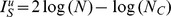 , and since
, and since 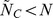 and
and 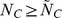 , then we conclude that
, then we conclude that 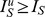 , which implies that
, which implies that 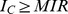 .
.
Notice that if 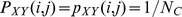 and
and 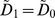 , then
, then 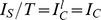 .
.
Expansion Rates
In order to extend our approach for the treatment of data sets coming from networks whose equations of motion are unknown, or for higher-dimensional networks and complex systems which might be neither rigorously chaotic nor fully deterministic, or for experimental data that contains noise and few sampling points, we write our bounds in terms of expansion rates defined in this work by
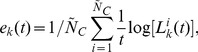 |
(24) |
where we consider 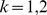 .
. 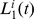 measures the largest growth rate of nearby points. In practice, it is calculated by
measures the largest growth rate of nearby points. In practice, it is calculated by 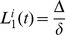 , with
, with  representing the largest distance between pairs of points in an
representing the largest distance between pairs of points in an  -square box
-square box  and
and 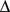 representing the largest distance between pairs of the points that were initially in the
representing the largest distance between pairs of the points that were initially in the  -square box but have spread out for an interval of time
-square box but have spread out for an interval of time  .
. 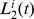 measures how an area enclosing points grows. In practice, it is calculated by
measures how an area enclosing points grows. In practice, it is calculated by 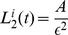 , with
, with 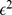 representing the area occupied by points in an
representing the area occupied by points in an  -square box, and
-square box, and 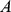 the area occupied by these points after spreading out for a time interval
the area occupied by these points after spreading out for a time interval  . There are
. There are 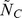 boxes occupied by points which are taken into consideration in the calculation of
boxes occupied by points which are taken into consideration in the calculation of 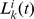 . An order-
. An order-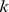 expansion rate,
expansion rate, 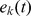 , measures on average how a hypercube of dimension
, measures on average how a hypercube of dimension 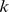 exponentially grows after an interval of time
exponentially grows after an interval of time  . So,
. So, 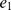 measures the largest growth rate of nearby points, a quantity closely related to the largest finite-time Lyapunov exponent [31]. And
measures the largest growth rate of nearby points, a quantity closely related to the largest finite-time Lyapunov exponent [31]. And 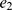 measures how an area enclosing points grows, a quantity closely related to the sum of the two largest positive Lyapunov exponents. In terms of expansion rates, Eqs. (4) and (5) read
measures how an area enclosing points grows, a quantity closely related to the sum of the two largest positive Lyapunov exponents. In terms of expansion rates, Eqs. (4) and (5) read 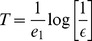 and
and 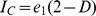 , respectively, and Eqs. (6) and (7) read
, respectively, and Eqs. (6) and (7) read 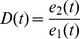 and
and 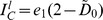 , respectively.
, respectively.
From the way we have defined expansion rates, we expect that 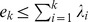 . Because of the finite time interval and the finite size of the regions of points considered, regions of points that present large derivatives, contributing largely to the Lyapunov exponents, contribute less to the expansion rates. If a system has constant Jacobian, is uniformly hyperbolic, and has a constant natural measure, then
. Because of the finite time interval and the finite size of the regions of points considered, regions of points that present large derivatives, contributing largely to the Lyapunov exponents, contribute less to the expansion rates. If a system has constant Jacobian, is uniformly hyperbolic, and has a constant natural measure, then 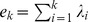 .
.
There are many reasons for using expansion rates in the way we have defined them in order to calculate bounds for the MIR. Firstly, because they can be easily experimentally estimated whereas Lyapunov exponents demand more computational efforts. Secondly, because of the macroscopic nature of the expansion rates, they might be more appropriate to treat data coming from complex systems that contain large amounts of noise, data that have points that are not (arbitrarily) close as formally required for a proper calculation of the Lyapunov exponents. Thirdly, expansion rates can be well defined for data sets containing very few data points: the fewer points a data set contains, the larger the regions of size  need to be and the shorter the time
need to be and the shorter the time  is. Finally, expansion rates are defined in a similar way to finite-time Lyapunov exponents and thus some algorithms used to calculate Lyapunov exponents can be used to calculate our defined expansion rates.
is. Finally, expansion rates are defined in a similar way to finite-time Lyapunov exponents and thus some algorithms used to calculate Lyapunov exponents can be used to calculate our defined expansion rates.
Results and Discussion
MIR and its Bounds in Two Coupled Chaotic Maps
To illustrate the use of our bounds, we consider the following two bidirectionally coupled maps.
| (25) |
where 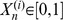 . If
. If 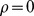 , the map is piecewise-linear and quadratic, otherwise. We are interested in measuring the exchange of information between
, the map is piecewise-linear and quadratic, otherwise. We are interested in measuring the exchange of information between 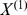 and
and 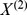 . The space
. The space  is the unit square. The Lyapunov exponents measured in the space
is the unit square. The Lyapunov exponents measured in the space  are the Lyapunov exponents of the set
are the Lyapunov exponents of the set 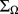 that is the chaotic attractor generated by Eqs. (25).
that is the chaotic attractor generated by Eqs. (25).
The quantities 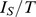 ,
, 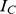 , and
, and 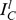 are shown in Fig. 1 as we vary
are shown in Fig. 1 as we vary 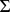 for
for 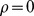 (A) and
(A) and 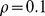 (B). We calculate
(B). We calculate 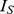 using in Eq. (1) the probabilities
using in Eq. (1) the probabilities 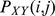 in which points from a trajectory composed of
in which points from a trajectory composed of 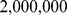 samples fall in boxes of sides
samples fall in boxes of sides  = 1/500 and the probabilities
= 1/500 and the probabilities 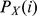 and
and 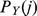 that the points visit the intervals
that the points visit the intervals 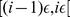 of the variable
of the variable 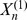 or
or 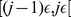 of the variable
of the variable 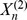 , respectively, for
, respectively, for 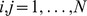 . When computing
. When computing 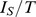 , the quantity
, the quantity 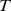 was estimated by Eq. (4). Indeed for most values of
was estimated by Eq. (4). Indeed for most values of 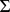 ,
, 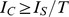 and
and 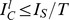 .
.
Figure 1. Results for two coupled maps. 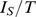 [Eq. (3)] as (green online) filled circles,
[Eq. (3)] as (green online) filled circles, 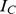 [Eq. (5)] as the (red online) thick line, and
[Eq. (5)] as the (red online) thick line, and 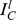 [Eq. (7)] as the (blue online) crosses.
[Eq. (7)] as the (blue online) crosses.
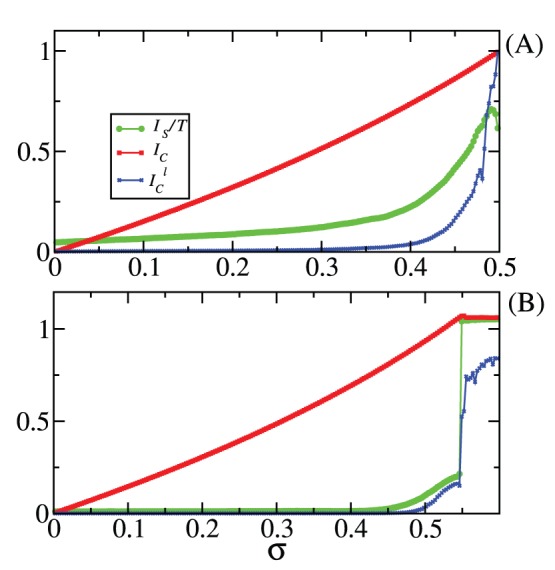
In (A)  and in (B)
and in (B)  . The units of
. The units of  ,
, 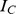 , and
, and 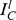 are [bits/iteration].
are [bits/iteration].
For  there is no coupling, and therefore the two maps are independent from each other. There is no information being exchanged. In fact,
there is no coupling, and therefore the two maps are independent from each other. There is no information being exchanged. In fact, 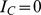 and
and 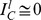 in both figures, since
in both figures, since 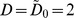 , meaning that the attractor
, meaning that the attractor 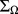 fully occupies the space
fully occupies the space  . This is a remarkable property of our bounds: to identify that there is no information being exchanged when the two maps are independent. Complete synchronisation is achieved and
. This is a remarkable property of our bounds: to identify that there is no information being exchanged when the two maps are independent. Complete synchronisation is achieved and 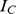 is maximal, for
is maximal, for 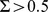 (A) and for
(A) and for 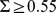 (B). A consequence of the fact that
(B). A consequence of the fact that 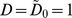 , and therefore,
, and therefore, 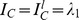 . The reason is because for this situation this coupled system is simply the shift map, a map with constant natural measure; therefore
. The reason is because for this situation this coupled system is simply the shift map, a map with constant natural measure; therefore 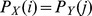 and
and 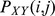 are constant for all
are constant for all  and
and 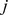 . As usually happens when one estimates the mutual information by partitioning the phase space with a grid having a finite resolution and data sets possessing a finite number of points,
. As usually happens when one estimates the mutual information by partitioning the phase space with a grid having a finite resolution and data sets possessing a finite number of points, 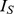 is typically larger than zero, even when there is no information being exchanged (
is typically larger than zero, even when there is no information being exchanged ( ). Even when there is complete synchronisation, we find non-zero off-diagonal terms in the matrix for the joint probabilities causing
). Even when there is complete synchronisation, we find non-zero off-diagonal terms in the matrix for the joint probabilities causing 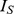 to be smaller than it should be. Due to numerical errors,
to be smaller than it should be. Due to numerical errors, 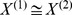 , and points that should be occupying boxes with two corners exactly along a diagonal line in the subspace
, and points that should be occupying boxes with two corners exactly along a diagonal line in the subspace  end up occupying boxes located off-diagonal and that have at least three corners off-diagonal. Due to such problems,
end up occupying boxes located off-diagonal and that have at least three corners off-diagonal. Due to such problems, 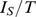 is underestimated by an amount of
is underestimated by an amount of 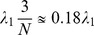 , resulting in a value of approximately
, resulting in a value of approximately 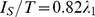 , close to the value of
, close to the value of 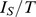 shown in Fig. 1(A), for
shown in Fig. 1(A), for 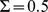 . The estimation of the lower bound
. The estimation of the lower bound 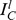 in (B) suffers from the same problems.
in (B) suffers from the same problems.
Our upper bound 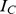 is calculated assuming that there is a fictitious dynamics expanding points (and producing probabilities) not only exponentially fast but also uniformly. The “experimental” numerical points from Eqs. (25) expand exponentially fast, but not uniformly. Most of the time the trajectory remains in 4 points: (0,0), (1,1), (1,0), (0,1). That is the main reason of why
is calculated assuming that there is a fictitious dynamics expanding points (and producing probabilities) not only exponentially fast but also uniformly. The “experimental” numerical points from Eqs. (25) expand exponentially fast, but not uniformly. Most of the time the trajectory remains in 4 points: (0,0), (1,1), (1,0), (0,1). That is the main reason of why 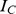 is much larger than the estimated real value of the
is much larger than the estimated real value of the  , for some coupling strengths. If two nodes in a dynamical network behave in the same way the fictitious dynamics does, these nodes would be able to exchange the largest possible amount of information.
, for some coupling strengths. If two nodes in a dynamical network behave in the same way the fictitious dynamics does, these nodes would be able to exchange the largest possible amount of information.
We would like to point out that one of the main advantages of calculating upper bounds for the MIR (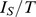 ) using Eq. (5) instead of actually calculating
) using Eq. (5) instead of actually calculating 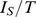 is that we can reproduce the curves for
is that we can reproduce the curves for 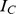 using much less number of points (1000 points) than the ones (
using much less number of points (1000 points) than the ones (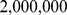 ) used to calculate the curve for
) used to calculate the curve for 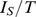 . If
. If 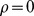 ,
, 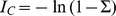 can be calculated since
can be calculated since 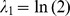 and
and 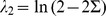 .
.
MIR and its Bounds in Experimental Networks of Double-Scroll Circuits
We illustrate our approach for the treatment of data sets using a network formed by an inductorless version of the Double-Scroll circuit [32]. We consider four networks of bidirectionally diffusively coupled circuits (see Fig. 2). Topology I in (A) represents two bidirectionally coupled circuits, Topology II in (B), three circuits coupled in an open-ended array, Topology III in (C), four circuits coupled in an open-ended array, and Topology IV in (D), coupled in an closed array. We choose two circuits in the different networks (one connection apart) and collect from each circuit a time-series of 79980 points, with a sampling rate of 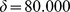 samples/s. The measured variable is the voltage across one of the circuit capacitors, which is normalised in order to make the space
samples/s. The measured variable is the voltage across one of the circuit capacitors, which is normalised in order to make the space  to be a square of sides 1. Such normalisation does not alter the quantities that we calculate. The following results provide the exchange of information between these two chosen circuits. The values of
to be a square of sides 1. Such normalisation does not alter the quantities that we calculate. The following results provide the exchange of information between these two chosen circuits. The values of  and
and  used to course-grain the space
used to course-grain the space  and to calculate
and to calculate 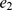 in Eq. (24) are the ones that minimise
in Eq. (24) are the ones that minimise 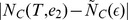 and at the same time satisfy
and at the same time satisfy 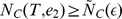 , where
, where 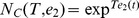 represents the number of fictitious boxes covering the set
represents the number of fictitious boxes covering the set 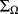 in a compact fashion, when
in a compact fashion, when 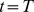 . This optimisation excludes some non-significant points that make the expansion rate of fictitious points to be much larger than it should be. In other words, we require that
. This optimisation excludes some non-significant points that make the expansion rate of fictitious points to be much larger than it should be. In other words, we require that 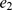 describes well the way most of the points spread. We consider that
describes well the way most of the points spread. We consider that  used to calculate
used to calculate 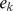 in Eq. (24) is the time points initially in an
in Eq. (24) is the time points initially in an  -side box to become at most apart by 0.8
-side box to become at most apart by 0.8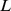 . That guarantees that nearby points in
. That guarantees that nearby points in 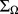 are expanding in both directions within the time interval
are expanding in both directions within the time interval 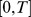 . Assuming that
. Assuming that 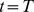 is calculated by measuring the time points initially in an
is calculated by measuring the time points initially in an  -side box to be at most apart by [0.4
-side box to be at most apart by [0.4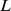 , 0.8
, 0.8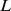 ] produces already similar results. If
] produces already similar results. If 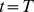 is calculated by measuring the time points become at least apart by
is calculated by measuring the time points become at least apart by 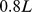 , the set
, the set 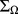 might not be only expanding.
might not be only expanding.  might be overestimated.
might be overestimated.
Figure 2. Black filled circles represent a Chua’s circuit and the numbers identify each circuit in the networks.
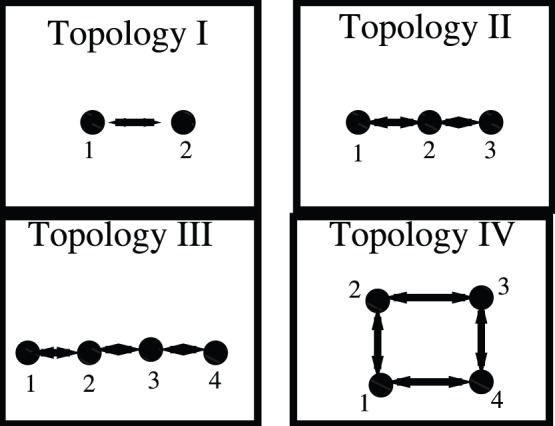
Coupling is diffusive. We consider 4 topologies: 2 coupled Chua’s circuit (A), an array of 3 coupled circuits, an array of 4 coupled circuits, and a ring formed by 4 coupled circuits.
 has been estimated by the method in Ref. [33]. Since we assume that the space
has been estimated by the method in Ref. [33]. Since we assume that the space  where mutual information is being measured is 2D, we will compare our results by considering in the method of Ref. [33] a 2D space formed by the two collected scalar signals. In the method of Ref. [33] the phase space is partitioned in regions that contain 30 points of the continuous trajectory. Since that these regions do not have equal areas (as it is the case for
where mutual information is being measured is 2D, we will compare our results by considering in the method of Ref. [33] a 2D space formed by the two collected scalar signals. In the method of Ref. [33] the phase space is partitioned in regions that contain 30 points of the continuous trajectory. Since that these regions do not have equal areas (as it is the case for  and
and 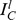 ), in order to estimate
), in order to estimate 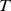 we need to imagine a box of sides
we need to imagine a box of sides 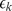 , such that its area
, such that its area 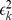 contains in average 30 points. The area occupied by the set
contains in average 30 points. The area occupied by the set 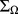 is approximately given by
is approximately given by 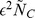 , where
, where 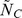 is the number of occupied boxes. Assuming that the 79980 experimental data points occupy the space
is the number of occupied boxes. Assuming that the 79980 experimental data points occupy the space  uniformly, then on average 30 points would occupy an area of
uniformly, then on average 30 points would occupy an area of 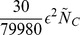 . The square root of this area is the side of the imaginary box that would occupy 30 points. So,
. The square root of this area is the side of the imaginary box that would occupy 30 points. So, 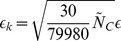 . Then, in the following, the “exact” value of the MIR will be considered to be given by
. Then, in the following, the “exact” value of the MIR will be considered to be given by 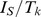 , where
, where 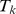 is estimated by
is estimated by 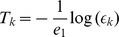 .
.
The three main characteristics of the curves for the quantities 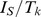 ,
, 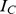 , and
, and 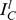 (appearing in Fig. 3) with respect to the coupling strength are that (i) as the coupling resistance becomes smaller, the coupling strength connecting the circuits becomes larger, and the level of synchronisation increases leading to an increase in
(appearing in Fig. 3) with respect to the coupling strength are that (i) as the coupling resistance becomes smaller, the coupling strength connecting the circuits becomes larger, and the level of synchronisation increases leading to an increase in 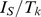 ,
, 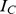 , and
, and 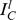 , (ii) all curves are close, (iii) and as expected, for most of the resistance values,
, (ii) all curves are close, (iii) and as expected, for most of the resistance values, 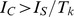 and
and  . The two main synchronous phenomena appearing in these networks are almost synchronisation (AS) [34], when the circuits are almost completely synchronous, and phase synchronisation (PS) [35]. For the circuits considered in Fig. 3, AS appears for the interval
. The two main synchronous phenomena appearing in these networks are almost synchronisation (AS) [34], when the circuits are almost completely synchronous, and phase synchronisation (PS) [35]. For the circuits considered in Fig. 3, AS appears for the interval 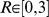 and PS appears for the interval
and PS appears for the interval 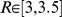 . Within this region of resistance values the exchange of information between the circuits becomes large. PS was detected by using the technique from Refs. [36], [37].
. Within this region of resistance values the exchange of information between the circuits becomes large. PS was detected by using the technique from Refs. [36], [37].
Figure 3. Results for experimental networks of Double-Scroll circuits.
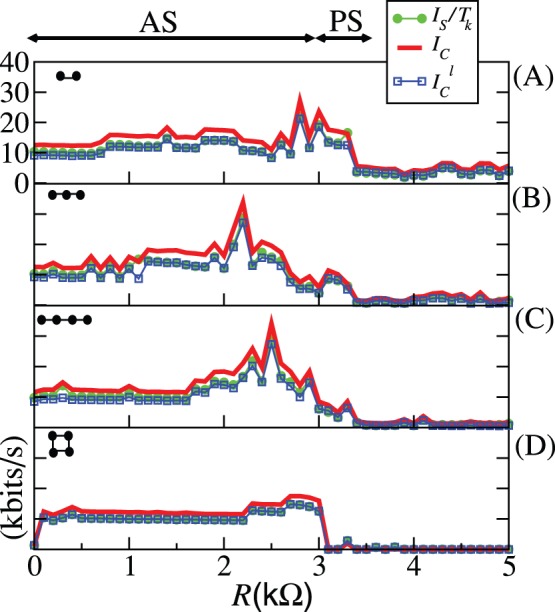
On the left-side upper corner pictograms represent how the circuits (filled circles) are bidirectionally coupled.  as (green online) filled circles,
as (green online) filled circles,  as the (red online) thick line, and
as the (red online) thick line, and 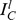 as the (blue online) squares, for a varying coupling resistance
as the (blue online) squares, for a varying coupling resistance 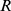 . The unit of these quantities shown in these figures is (kbits/s). (A) Topology I, (B) Topology II, (C) Topology III, and (D) Topology IV. In all figures,
. The unit of these quantities shown in these figures is (kbits/s). (A) Topology I, (B) Topology II, (C) Topology III, and (D) Topology IV. In all figures, 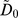 increases smoothly from 1.25 to 1.95 as
increases smoothly from 1.25 to 1.95 as 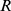 varies from 0.1k
varies from 0.1k to 5k
to 5k . The line on the top of the figure represents the interval of resistance values responsible to induce almost synchronisation (AS) and phase synchronisation (PS).
. The line on the top of the figure represents the interval of resistance values responsible to induce almost synchronisation (AS) and phase synchronisation (PS).
MIR and its Upper Bound in Stochastic Systems
To analytically demonstrate that the quantities 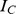 and
and 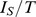 can be well calculated in stochastic systems, we consider the following stochastic dynamical toy model illustrated in Fig. 4. In it points within a small box of sides
can be well calculated in stochastic systems, we consider the following stochastic dynamical toy model illustrated in Fig. 4. In it points within a small box of sides  (represented by the filled square in Fig. 4(A)) located in the centre of the subspace
(represented by the filled square in Fig. 4(A)) located in the centre of the subspace  are mapped after one iteration (
are mapped after one iteration (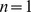 ,
,  ) of the dynamics to 12 other neighbouring boxes. Some points remain in the initial box. The points that leave the initial box go to 4 boxes along the diagonal line and 8 boxes off-diagonal along the transverse direction. Boxes along the diagonal are represented by the filled squares in Fig. 4(B) and off-diagonal boxes by filled circles. At the second iteration (
) of the dynamics to 12 other neighbouring boxes. Some points remain in the initial box. The points that leave the initial box go to 4 boxes along the diagonal line and 8 boxes off-diagonal along the transverse direction. Boxes along the diagonal are represented by the filled squares in Fig. 4(B) and off-diagonal boxes by filled circles. At the second iteration (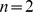 ), the points occupy other neighbouring boxes, as illustrated in Fig. 4(C), and at a time
), the points occupy other neighbouring boxes, as illustrated in Fig. 4(C), and at a time 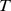 (
(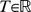 ) the points occupy the attractor
) the points occupy the attractor 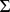 and do not spread any longer. For iterations
and do not spread any longer. For iterations  larger than
larger than 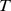 , the points are somehow reinjected inside the region of the attractor. We consider that this system is completely stochastic, in the sense that no one can precisely determine the location of where an initial condition will be mapped. The only information is that points inside a smaller region are mapped to a larger region.
, the points are somehow reinjected inside the region of the attractor. We consider that this system is completely stochastic, in the sense that no one can precisely determine the location of where an initial condition will be mapped. The only information is that points inside a smaller region are mapped to a larger region.
Figure 4. This picture is a hand-made illustration.
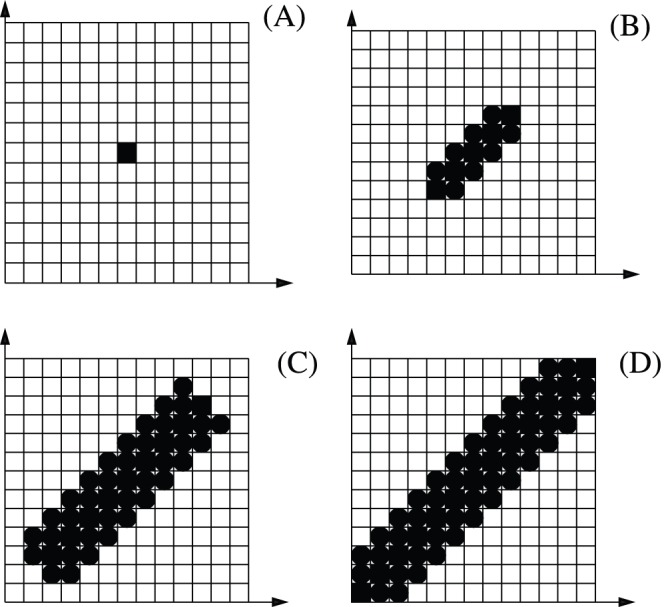
Squares are filled as to create an image of a stochastic process whose points spread according to the given Lyapunov exponents. (A) A small box representing a set of initial conditions. After one iteration of the system, the points that leave the initial box in (A) go to 4 boxes along the diagonal line [filled squares in (B)] and 8 boxes off-diagonal (along the transverse direction) [filled circles in (B)]. At the second iteration, the points occupy other neighbouring boxes as illustrated in (C) and after an interval of time 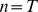 the points do not spread any longer (D).
the points do not spread any longer (D).
At the iteration  , there will be
, there will be 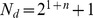 boxes occupied along the diagonal (filled squares in Fig. 4) and
boxes occupied along the diagonal (filled squares in Fig. 4) and 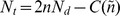 (filled circles in Fig. 4) boxes occupied off-diagonal (along the transverse direction), where
(filled circles in Fig. 4) boxes occupied off-diagonal (along the transverse direction), where 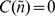 for
for 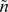 = 0, and
= 0, and 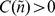 for
for 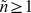 and
and 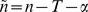 .
.  is a small number of iterations representing the time difference between the time
is a small number of iterations representing the time difference between the time 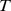 for the points in the diagonal to reach the boundary of the space
for the points in the diagonal to reach the boundary of the space  and the time for the points in the off-diagonal to reach this boundary. The border effect can be ignored when the expansion along the diagonal direction is much faster than along the transverse direction.
and the time for the points in the off-diagonal to reach this boundary. The border effect can be ignored when the expansion along the diagonal direction is much faster than along the transverse direction.
At the iteration  , there will be
, there will be 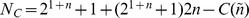 boxes occupied by points. In the following calculations we consider that
boxes occupied by points. In the following calculations we consider that 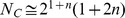 . We assume that the subspace
. We assume that the subspace  is a square whose sides have length 1, and that
is a square whose sides have length 1, and that  , so
, so 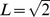 . For
. For 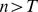 , the attractor does not grow any longer along the off-diagonal direction.
, the attractor does not grow any longer along the off-diagonal direction.
The largest Lyapunov exponent or the order-1 expansion rate of this stochastic toy model can be calculated by 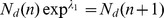 , which takes us to
, which takes us to
| (26) |
Therefore, the time 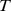 , for the points to spread over the attractor
, for the points to spread over the attractor 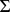 , can be calculated by the time it takes for points to visit all the boxes along the diagonal. It can be calculated by
, can be calculated by the time it takes for points to visit all the boxes along the diagonal. It can be calculated by 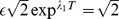 , which take us to
, which take us to
| (27) |
The quantity 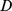 can be calculated by
can be calculated by 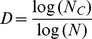 , with
, with 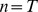 . Neglecting
. Neglecting 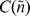 and the 1 appearing in
and the 1 appearing in 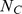 due to the initial box, we have that
due to the initial box, we have that 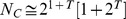 . Substituting in the definition of
. Substituting in the definition of 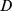 , we obtain
, we obtain 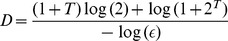 . Using
. Using 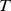 from Eq. (27), we arrive at
from Eq. (27), we arrive at
| (28) |
where
| (29) |
Placing 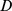 and
and 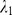 in
in 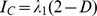 , gives us
, gives us
| (30) |
Let us now calculate 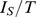 . Ignoring the border effect, and assuming that the expansion of points is uniform, then
. Ignoring the border effect, and assuming that the expansion of points is uniform, then 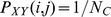 and
and 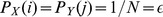 . At the iteration
. At the iteration 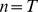 , we have that
, we have that 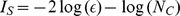 . Since
. Since 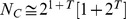 , we can write that
, we can write that 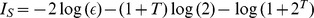 . Placing
. Placing 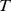 from Eq. (27) into
from Eq. (27) into 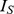 takes us to
takes us to 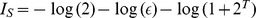 . Finally, dividing
. Finally, dividing 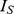 by
by 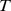 , we arrive that
, we arrive that
| (31) |
As expected from the way we have constructed this model, Eq. (31) and (30) are equal and 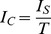 .
.
Had we included the border effect in the calculation of 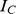 , denote the value by
, denote the value by 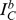 , we would have obtained that
, we would have obtained that 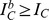 , since
, since 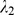 calculated considering a finite space
calculated considering a finite space  would be either smaller or equal than the value obtained by neglecting the border effect. Had we included the border effect in the calculation of
would be either smaller or equal than the value obtained by neglecting the border effect. Had we included the border effect in the calculation of 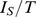 , denote the value by
, denote the value by 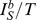 , typically we would expect that the probabilities
, typically we would expect that the probabilities 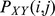 would not be constant. That is because the points that leave the subspace
would not be constant. That is because the points that leave the subspace  would be randomly reinjected back to
would be randomly reinjected back to  . We would conclude that
. We would conclude that 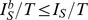 . Therefore, had we included the border effect, we would have obtained that
. Therefore, had we included the border effect, we would have obtained that 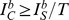 .
.
The way we have constructed this stochastic toy model results in 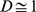 . This is because the spreading of points along the diagonal direction is much faster than the spreading of points along the off-diagonal transverse direction. In other words, the second largest Lyapunov exponent,
. This is because the spreading of points along the diagonal direction is much faster than the spreading of points along the off-diagonal transverse direction. In other words, the second largest Lyapunov exponent, 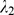 , is close to zero. For stochastic toy models which produce larger
, is close to zero. For stochastic toy models which produce larger 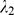 , one could consider that the spreading along the transverse direction is given by
, one could consider that the spreading along the transverse direction is given by 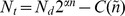 , with
, with 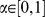 .
.
Expansion Rates for Noisy Data with Few Sampling Points
In terms of the order-1 expansion rate, 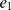 , our quantities read
, our quantities read 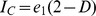 ,
, 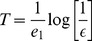 , and
, and 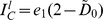 . In order to show that our expansion rate can be used to calculate these quantities, we consider that the experimental system is being observed in a one-dimensional projection and points in this projection have a constant probability measure. Additive noise is assumed to be bounded with maximal amplitude
. In order to show that our expansion rate can be used to calculate these quantities, we consider that the experimental system is being observed in a one-dimensional projection and points in this projection have a constant probability measure. Additive noise is assumed to be bounded with maximal amplitude 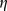 , and having constant density.
, and having constant density.
Our order-1 expansion rate is defined as
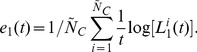 |
(32) |
where 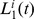 measures the largest growth rate of nearby points. Since all it matters is the largest distance between points, it can be estimated even when the experimental data set has very few data points. Since, in this example, we consider that the experimental noisy points have constant uniform probability distribution,
measures the largest growth rate of nearby points. Since all it matters is the largest distance between points, it can be estimated even when the experimental data set has very few data points. Since, in this example, we consider that the experimental noisy points have constant uniform probability distribution, 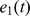 can be calculated by
can be calculated by
| (33) |
where 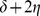 represents the largest distance between pair of experimental noisy points in an
represents the largest distance between pair of experimental noisy points in an  -square box and
-square box and 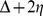 represents the largest distance between pair of the points that were initially in the
represents the largest distance between pair of the points that were initially in the  -square box but have spread out for an interval of time
-square box but have spread out for an interval of time  . The experimental system (without noise) is responsible to make points that are at most
. The experimental system (without noise) is responsible to make points that are at most  apart from each other to spread to at most to
apart from each other to spread to at most to 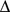 apart from each other. These points spread out exponentially fast according to the largest positive Lyapunov exponent
apart from each other. These points spread out exponentially fast according to the largest positive Lyapunov exponent 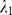 by
by
| (34) |
Substituting Eq. (34) in (33), and expanding 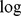 to first order, we obtain that
to first order, we obtain that 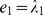 , and therefore, our expansion rate can be used to estimate Lyapunov exponents.
, and therefore, our expansion rate can be used to estimate Lyapunov exponents.
Conclusions
We have shown a procedure to calculate mutual information rate (MIR) between two nodes (or groups of nodes) in dynamical networks and data sets that are either mixing, or exhibit fast decay of correlations, or have sensitivity to initial conditions, and we have proposed significant upper (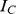 ) and lower (
) and lower (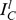 ) bounds for it, in terms of the Lyapunov exponents, the expansion rates, and the capacity dimension.
) bounds for it, in terms of the Lyapunov exponents, the expansion rates, and the capacity dimension.
Since our upper bound is calculated from Lyapunov exponents or expansion rates, it can be used to estimate the MIR between data sets that have different sampling rates or experimental resolution or between systems possessing a different number of events. For example, suppose one wants to understand how much information is exchanged between two time-series, the heart beat and the level of CO in the body. The heart is monitored by an EEG that collects data with a high-frequency, whereas the monitoring of the CO
in the body. The heart is monitored by an EEG that collects data with a high-frequency, whereas the monitoring of the CO level happens in a much lower frequency. For every
level happens in a much lower frequency. For every  points collected from an EEG one could collect
points collected from an EEG one could collect  points in the monitoring of the CO
points in the monitoring of the CO level. Assuming that the higher-frequency variable (the heart beat) is the one that contributes mostly for the sensibility to the initial conditions, then the larger expansion rate (or Lyapunov exponent) can be well estimated only using this variable. The second largest expansion rate (or Lyapunov exponent) can be estimated by the composed subspace formed by these two measurements, but only the measurements taken simultaneously would be considered. Therefore, the estimation of the second largest expansion rate would have to be done using less points than the estimation used to obtain the largest. In the calculation of the second largest expansion rate, it is necessary to know the largest exponent. If the largest is correctly estimated, then the chances we make a good estimation of the second largest increases, even when only a few points are considered. With the two largest expansion rates, one can estimate
level. Assuming that the higher-frequency variable (the heart beat) is the one that contributes mostly for the sensibility to the initial conditions, then the larger expansion rate (or Lyapunov exponent) can be well estimated only using this variable. The second largest expansion rate (or Lyapunov exponent) can be estimated by the composed subspace formed by these two measurements, but only the measurements taken simultaneously would be considered. Therefore, the estimation of the second largest expansion rate would have to be done using less points than the estimation used to obtain the largest. In the calculation of the second largest expansion rate, it is necessary to know the largest exponent. If the largest is correctly estimated, then the chances we make a good estimation of the second largest increases, even when only a few points are considered. With the two largest expansion rates, one can estimate 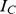 , the upper bound for the MIR.
, the upper bound for the MIR.
Additionally, Lyapunov exponents can be accurately calculated even when data sets are corrupted by noise of large amplitude (observational additive noise) [38], [39] or when the system generating the data suffers from parameter alterations (“experimental drift”) [40]. Our bounds link information (the MIR) and the dynamical behaviour of the system being observed with synchronisation, since the more synchronous two nodes are, the smaller 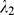 and
and 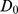 will be. This link can be of great help in establishing whether two nodes in a dynamical network or in a complex system not only exchange information but also have linear or non-linear interdependences, since the approaches to measure the level of synchronisation between two systems are reasonably well known and are been widely used. If variables are synchronous in a time-lag fashion [35], it was shown in Ref. [16] that the MIR is independent of the delay between the two processes. The upper bound for the MIR could be calculated by measuring the Lyapunov exponents of the network (see Information S1), which are also invariant to time-delays between the variables.
will be. This link can be of great help in establishing whether two nodes in a dynamical network or in a complex system not only exchange information but also have linear or non-linear interdependences, since the approaches to measure the level of synchronisation between two systems are reasonably well known and are been widely used. If variables are synchronous in a time-lag fashion [35], it was shown in Ref. [16] that the MIR is independent of the delay between the two processes. The upper bound for the MIR could be calculated by measuring the Lyapunov exponents of the network (see Information S1), which are also invariant to time-delays between the variables.
If the MIR and its upper bounds are calculated from an “attractor” that is not an asymptotic limiting set but rather a transient trajectory, these values should typically differ from the values obtained when the "attractor" is an asymptotic limiting set. The dynamical quantities calculated, e.g., the Lyapunov exponents, expansion rates, and the fractal dimension should be interpreted as finite time quantities.
In our calculations, we have considered that the correlation of the system decays to approximately zero after a finite time 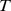 . If after this time interval the correlation does not decay to zero, we expect that
. If after this time interval the correlation does not decay to zero, we expect that 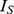 will be overestimated, leading to an overestimated value for the MIR. That is so because the probabilities used to calculate
will be overestimated, leading to an overestimated value for the MIR. That is so because the probabilities used to calculate 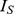 will be considered to have been generated by a random system with uncorrelated variables, which is not true. However, by construction, the upper bound
will be considered to have been generated by a random system with uncorrelated variables, which is not true. However, by construction, the upper bound 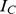 is larger than the overestimated MIR.
is larger than the overestimated MIR.
Supporting Information
(PDF)
Acknowledgments
M. S. Baptista would like to thank A. Politi for discussions concerning Lyapunov exponents and N. R. Obrer for discussions concerning MI and MIR.
Funding Statement
MSB was partially supported by the Northern Research Partnership, Alexander von Humboldt foundation, and the Engineering and Physical Sciences Research Council grant Ref. EP/I032606/1. The research leading to the results has received funding from the European Community? Seventh Framework Programme FP7/2007-2013 under grant agreement No. HEALTH-F2-2009-241526, EUTrigTreat. Furthermore, support by the Bernstein Center for Computational Neuroscience II G\"ottingen (BCCN grant 01GQ1005A, project D1) is acknowledged. RR, EV and JCS thanks the Brazilian agencies Coordenadoria de Aperfeiçoamento de Pessoal de Nível Superior, Conselho Nacional de Desenvolvimento Científico e Tecnológico, Fundação de Amparo à Pesquisa do estado de Minas Gerais and Fundação de Amparo à Pesquisa do Estado de São Paulo. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Shannon CE (1948) A Mathematical Theory of Communication. Bell System Technical Journal 27: 379–423. [Google Scholar]
- 2. Strong SP, Koberle R, de Ruyter van Steveninck RR, Bialek W (1998) Entropy and Information in Neural Spike Trains. Phys. Rev. Lett. 80: 197–200. [Google Scholar]
- 3. Sporns O, Chialvo DR, Kaiser M, Hilgetag CC (2004) Organization, development and function of complex brain networks. Trends in Cognitive Sciences. 8: 418–425. [DOI] [PubMed] [Google Scholar]
- 4.Palus M, Komárek V, Procházka T, Hrncir Z, Sterbova K (2001) Synchronization and information ow in EEGs of epileptic patients. IEEE Engineering in Medicice and Biology Sep/Oct: 65–71. [DOI] [PubMed] [Google Scholar]
- 5. Donges JF, Zou Y, Marwan N, Kurths J (2009) Complex networks in climate dynamics. Eur. Phys. J. 174: 157–179. [Google Scholar]
- 6. Fraser AM, Swinney HL (1986) Independent coordinates for strange attractors from mutual information. Phys. Rev. A 33: 1134–1140. [DOI] [PubMed] [Google Scholar]
- 7.Kantz H, Schreiber T (2004) Nonlinear Time Series Analysis. Cambridge: Cambridge University Press. [Google Scholar]
- 8.Parlitz U (1998) Nonlinear Time-Series Analysis, in Nonlinear Modelling - Advanced Black-Box techniques. The Netherlands: Kluwer Academic Publishers. [Google Scholar]
- 9.Haykin S (2001) Communication Systems. New York: John Wiley & Sons. [Google Scholar]
- 10. Rossi F, Lendasse A, François D, Wertz V, Verleysen M (2006) Mutual information for the selection of relevant variables in spectrometric nonlinear modelling. Chemometrics and Intelligent Laboratory Systems 80: 215–226. [Google Scholar]
- 11. Paninski L (2003) Estimation of entropy and mutual information. Neural Computation 15: 1191–1253. [Google Scholar]
- 12. Steuer R, Kurths J, Daub CO, Weckwerth W (2002) The Mutual Information: Detecting and evaluating dependencies between variables. Bioinformatics 18: S231–S240. [DOI] [PubMed] [Google Scholar]
- 13. Papana A, Kugiumtzis D (2009) Evaluation of Mutual Information Estimators for Time Series. Int. J. Bifurcation and Chaos 19: 4197–4215. [Google Scholar]
- 14. Baptista MS, Kurths J (2008) Information transmission in active channels. Phys. Rev. E 77: 026205–1–026205–13. [DOI] [PubMed] [Google Scholar]
- 15. Baptista MS, de Carvalho JX, Hussein MS (2008) Optimal network topologies for information transmission in active networks. PloS ONE 3: e3479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Blanc JL, Pezard L, Lesne A (2011) Delay independence of mutual-information rate of two symbolic sequences. Phys. Rev. E 84: 036214–1–036214–9. [DOI] [PubMed] [Google Scholar]
- 17. Dobrushin RL (1959) General formulation of Shannon’s main theorem of information theory. Usp. Mat. Nauk. 14: 3–104; transl: Amer. Math. Soc. Translations, series 2 33: 323–438. [Google Scholar]
- 18. Gray RM, Kieffer JC (1980) Asymptotically mean stationary measures. IEEE Transations on Information theory IT-26: 412–421. [Google Scholar]
- 19. Verdú S, Han TS (1994) A general formula for channel capacity. IEEE Trans. Information Theory 40: 1147–1157. [Google Scholar]
- 20. Kolmogorov AN (1958) A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces. Dokl. Akad. Nauk SSSR 119: 861–864; (1959) Entropy per unit time as a metric invariant of automorphisms. Dokl. Akad. Nauk SSSR 124: 754–755. [Google Scholar]
- 21. Ruelle D (1978) An inequality for the entropy of differentiable maps. Bol. Soc. Bras. Mat. 9: 83–87. [Google Scholar]
- 22. Pesin YaB (1977) Characteristic Lyapunov exponents and smooth ergodic theory. Russ. Math. Surveys 32: 55–114. [Google Scholar]
- 23. Ledrappier F, Strelcyn JM (1982) A proof of the estimate from below in Pesin’s entropy formula. Ergod. Theory Dyn. Syst. 2: 203–219. [Google Scholar]
- 24. Wissman BD, McKay-Jones LC, Binder PM (2011) Entropy rate estimates from mutual information. Phys. Rev. E 84: 046204–1–046204–5. [DOI] [PubMed] [Google Scholar]
- 25. Gao JB (1999) Recurrence Time Statistics for Chaotic Systems and Their Applications. Phys. Rev. Lett. 83: 3178–3181. [Google Scholar]
- 26. Baptista MS, Eulalie N, Pinto PRF, Brito M, Kurths J (2010) Density of first Poincaré returns, periodic orbits, and Kolmogorov-Sinai entropy. Phys. Lett. A 374: 1135–1140. [Google Scholar]
- 27.Eckmann JP (2003) Non-equilibrium steady states. arXiv:math-ph/0304043. [Google Scholar]
- 28. Sinai YaG (1970) Dynamical systems with elastic reections. Ergodic properties of dispersing billiards. Russ. Math. Surv. 25: 137–189. [Google Scholar]
- 29. Chernov N, Young LS (2001) Decay of correlations for Lorentz gases and hard balls. Encycl. Of Math. Sc., Math. Phys. II 101: 89–120. [Google Scholar]
- 30. Baptista MS, Caldas IL, Heller MVAP, Ferreira AA (2001) Onset of symmetric plasma turbulence. Physica A 301: 150–162. [Google Scholar]
- 31. Dawson S, Grebogi C, Sauer T, Yorke JA (1994) Obstructions to Shadowing When a Lyapunov Exponent Fluctuates about Zero. Phys. Rev. Lett. 73: 1927–1930. [DOI] [PubMed] [Google Scholar]
- 32. Albuquerque HA, Rubinger RM, Rech PC (2007) Theoretical and experimental time series analysis of an inductorless Chuas circuit. Physics D 233: 66–72. [Google Scholar]
- 33. Kraskov A, Stogbauer H, Grassberger P (2004) Estimating mutual information. Phys. Rev. E 69: 066138–1-066138-16. [DOI] [PubMed] [Google Scholar]
- 34. Femat R, Soís-Perales G (1999) On the chaos synchronization phenomena. Phys. Lett. A 262: 50–60. [Google Scholar]
- 35.Pikovsky A, Rosenblum M, Kurths J (2001) Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge: Cambridge University Press. [Google Scholar]
- 36. Baptista MS, Pereira T, Kurths J (2006) Upper bounds in phase synchronous weak coherent chaotic attractors. Physica D 216: 260–268. [Google Scholar]
- 37. Pereira T, Baptista MS, Kurths J (2007) General framework for phase synchronization through localized sets. Phys. Rev. E 75: 026216–1–026216–12. [DOI] [PubMed] [Google Scholar]
- 38. Mera ME, Morán M (2009) Reduction of noise of large amplitude through adaptive neighborhoods. Phys. Rev E 80: 016207–1–016207–8. [DOI] [PubMed] [Google Scholar]
- 39. Gao JB, Hu J, Tung WW, Cao YH, Distinguishing chaos from noise by scale-dependent Lyapunov exponent. Phys. Rev. E 74: 066204–1–066204–9. [DOI] [PubMed] [Google Scholar]
- 40. Stefański A (2008) Lyapunov exponents of systems with noise and uctuating parameters. Journal of Theoretical and Applied Mechanics 46: 665–678. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)


