Charge hydration asymmetry: the basic principle and how to use it to test and improve water models

Abstract

Charge hydration asymmetry (CHA) manifests itself in the experimentally observed strong dependence of free energy of ion hydration on the sign of the ion charge. This asymmetry is not consistently accounted for by popular models of solvation; its magnitude varies greatly between the models. While it is clear that CHA is somehow related to charge distribution within a water molecule, the exact nature of this relationship is unknown. We propose a simple, yet general and rigorous criterion that relates rotational and charge inversion properties of a water molecule’s charge distribution with its ability to cause CHA. We show which electric multipole components of a water molecule are key to explain its ability for asymmetric charge hydration. We then test several popular water models and explain why specific models show none, little, or strong CHA in simulations. We use the gained insight to derive an analogue of the Born equation that includes the missing physics necessary to account for CHA, and does not rely on re-defining the continuum dielectric boundary. The proposed formula is as simple as the original, does not contain any fitting parameters, and predicts hydration free energies and entropies of spherical cations and anions within experimental uncertainty. Our findings suggest that the gap between the practical continuum electrostatics framework and the more fundamental explicit solvent treatment may be reduced considerably by explicitly introducing CHA into the existing continuum framework.

Introduction

An accurate qualitative and quantitative description of aqueous solvation of molecules is of paramount importance for physical chemistry, biology and biophysics.^1–5 Understanding the detailed microscopic origins of experimentally observed solvation effects is therefore critical for our ability to improve solvation theories and practical water models. Here, the hydration of a single spherical ion is arguably the purest test case for models of solvation as well as for our current level of understanding of the basic physics of charge hydration. And while seemingly simple, ions are critical to the structure and function of biomolecules.^6,7

In the widely used semi-microscopic implicit solvation approach,^1,8–11 water is treated as a structureless, linear response continuum, while the full structure of the molecular solute is retained. Within this formalism, the hydration free energy of a single spherical ion is given exactly by the famous Born equation¹²

$$\mathrm{\Delta }{G}_B(R_i)=-\left(1-\frac{1}{\epsilon }\right)\frac{q^2}{2R_i}$$ (1)

where ε is the dielectric constant of the solvent medium, and R_i is the ion radius. At this conceptual level, however, an important feature of ionic solvation observed in experiment^13,14 – the charge hydration asymmetry^15–22 (CHA) – is completely missing. The phenomenon manifests itself in two ions of the same size but opposite charges, having very different hydration free energies. A good example is K⁺/F⁻ pair, where the CHA is about 50 kcal/mol or 50 % of the ions’ hydration energy.^13,14 For small neutral molecules the size of benzene, the CHA can be as large as 10 kcal/mol,²² resulting in comparable errors in hydration energies predicted by the popular numerical Poisson equation formalism^1,23 which shares the same conceptual basis with the Born model. Hydration asymmetry effects were observed in explicit solvent simulations of ion-ion potentials of mean force (PMF).²⁴

More detailed and complex, microscopic descriptions of hydration,^{17–19,21,22,25–28} often recover various degrees of CHA seen in experiment and provide valuable insights into details of ion hydration. But serious unresolved issues remain: apparently similar, commonly used explicit water models capable of predicting many of bulk water properties reasonably well, may unexpectedly differ amongst themselves substantially²⁸ in their intrinsic ability to predict hydration asymmetries. These differences, up to 14 kcal/mol²⁸ for ions the size of K⁺ and F⁻, are comparable to or larger than many relevant biomolecular energy scales, such as folding free energy of a typical protein. Differences of similar magnitude are found in computational studies of small molecules designed to test CHA.²² Moreover, other seemingly reasonable microscopic models with realistic dipole and quadrupole moments may produce negligible CHA²⁹ in stark disagreement with experiment. The current understanding of the CHA phenomenon is insufficient to consistently explain the differences, and to improve the underlying water models accordingly.

Given the vast number of already available water (solvation) models, and the fact that the search for better ones continues to expand,^30–35 it is critical to identify a clear guiding principle to construct and test these models correctly with respect to strong experimentally observed CHA.

The first goal of this work is to move forward by providing a simple, general and robust quantitative relationship between the charge distribution within a water model and its ability to cause CHA. We will demonstrate how the theory can be used to explain the relative propensities of popular water models to cause CHA. We will then show how our insights can be used to improve the continuum solvent formalism by re-introducing the asymmetry into the basic Born formula through rigorous physics. Identifying and eliminating what appears to be the dominant source of error in the conceptual basis of the continuum electrostatics models is important for the many fields where these models are used.

It should be noted that for isolated ions the experimental hydration energies can be reproduced well by empirical adjustments of the ion radii in the Born formula.^16,36 The idea that hydration asymmetry effects can be subsumed into a re-definition of the dielectric boundary within the fundamentally charge-symmetric linear response continuum framework, e.g., the Poisson equation, is responsible for numerous attempts to develop a universal set of atomic radii for continuum solvent calculations on multiatomic molecules. However, even for very small neutral molecules that approach has been shown to face difficulties.²² A number of different atomic radii sets have been proposed over the years,^37–39 but no single, transferable consensus set has ever emerged.⁴⁰ As a step towards this goal, we will demonstrate how the issues of the dielectric boundary placement and the hydration asymmetry can be clearly decoupled at the conceptual level of the Born model.

Results & Discussion

Origins of ion hydration asymmetry

In general, the free energy of ion hydration is given by

$$\mathrm{\Delta }G\approx \mathrm{\Delta }F=-k_{B}Tln\left(\frac{Z^{II}}{Z^I}\right),$$ (2)

where Z^I and Z^II are the partition functions for a bulk state of water without the ion (pre-hydrated state I with the ion in the gas phase) and for the ion embedded in water (hydrated state II). The charge hydration asymmetry for otherwise identical ions of opposite charge is then ΔΔG = ΔG(+q) − ΔG(−q) = −k_BTln Z^II(+q)/Z^II(−q), where the sum in Z^II(q) = Σ_σ⃗ exp(−βE(q, σ⃗)) extends over all admissible spatial configurations σ⃗ of the ion-water system with the configurational energies E(q, σ⃗).

Since the electrostatic part of E(q, σ⃗) is a quadratic form in charges, Z^II and, hence, ΔG are invariant upon inversion of every charge in the ion-water system. However, Z^II will also be invariant upon inversion of the ion charge alone (q → −q) if the following condition is satisfied: inversion of the charge distribution (ρ_w) within each water molecule, C: = {ρ_w(r⃗) → −ρ_w(r⃗)}, is equivalent to a set of consecutive rotations R of this molecule about its single (often centered on the oxygen) spherically symmetric van der Waals interaction center. Mathematically, this statement can be expressed as C · R = I, where I is the identity operator, and R:= R_n̂1 (ψ₁) × R_n̂2(ψ₂)…, where each rotation R_n̂m (ψ_m) is a rotation through angle ψ_m around some axis n̂_m going through the van der Waals interaction center. If C · R = I, then for each term in the sum Z^II(+q) = Σ_σ⃗ exp(−βE(+q, σ⃗)) there exists a corresponding term in Z^II(−q) with the ion-water configuration Rσ⃗ and the same energy E(−q, Rσ⃗)) = E(+q, σ⃗)). This leads to Z^II(+q) = Z^II(−q) and, hence, to ΔΔG = 0. The equality will hold regardless of the ion size. Conversely,

$$\mathbf{C}·\mathbf{R}\ne \mathbf{I}$$ (3)

is a necessary condition for a water molecule to exhibit CHA. The meaning of the above expression is that the charge inversion can not be mimicked by any set of rotations of the molecule around its single van der Waals interaction center.

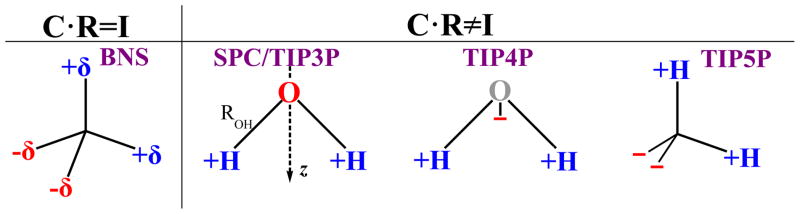
The Ben-Naim and Stillinger (BNS) model,⁴¹ which has two positive and two negative charges of equal magnitude at the vertices of a perfect tetrahedron, Figure 1, satisfies C · R = I, and thus cannot produce CHA. In contrast, a real water molecule, as well as many popular “n-site” water models such as SPC/E,⁴² TIP3P,⁴³ TIP4P⁴³ and TIP5P,^34,35 Figure 1, are not “charge-symmetric” (their charge distributions obey Eq. (3)), and therefore they are expected to exhibit CHA.

Figure 1.

Schematics of several point charge water models and C · R symmetries of their charge distributions.

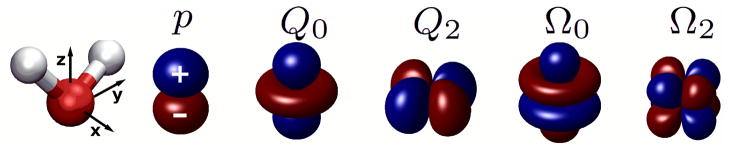
However, water models that satisfy Eq. (3) may still produce very different degrees of CHA, as seen in simulations.^22,28,29 To explain why, we examine individual spherical electric multipole moments (up to the octupole) of real water molecule, Figure 2, in light of our general relationship, Eq. (3).

Figure 2.

Symmetry properties of the lowest non-zero spherical multipole moments of water molecule. Shown are the corresponding charge distributions. From left to right: coordinate system; a dipole, p; a linear quadrupole, Q₀; a square quadrupole, Q₂; a linear octupole, Ω₀, and a cubic octupole, Ω₂. These moments are related to the Cartesian components of the traceless multipole moments of water molecule as Q₀ = Q_zz, Q₂ = 1/2 (Q_yy − Q_xx), Ω₀ = Ω_zzz, Ω₂ = 1/2 (Ω_yyz − Ω_xxz).³¹

For water models consistent with the C_2v symmetry of real water, all individual moments, except linear quadrupole (Q₀), satisfy C · R = I. The same is true for any pair of moments not including linear quadrupole^*. This can be easily seen by comparing rotational transformations that are equivalent to charge inversion for each moment in the pair. For example, charge inversion of the cubic octupole (Ω₂) is equivalent to these rotations: C ≡ R_x̂ (π) = R_ẑ (π/2); for the square quadrupole (Q₂): C ≡ R_x̂ (π) × R_ẑ (π/2) = R_ẑ (π/2); and for the dipole (p) or the linear octupole (Ω₀): C ≡ R_x̂ (π) = R_x̂ (π) ×R_ẑ (π/2). Thus, by itself, only Q₀ appears to be able to cause CHA. However, the magnitude of Q₀ of water molecule is very small, ³¹ and is strictly zero for the SPC/E water model, which presents an apparent paradox – real water as well as the SPC/E model exhibit strong CHA. The paradox is resolved by noticing that while each of the remaining multipoles in Figure 2, or any pair of them is C · R = I symmetric, a combination of p, Q₂ and Ω₂ – all of which significant in a water molecule – is not; the three moments together satisfy C · R ≠ I. Thus, the combination of these three multipole moments causes the ion charge hydration asymmetry. This key observation explains the puzzling results of earlier RISM (the reference interaction site model^17,18,25) calculations of ion hydration where a substantial amount of ion hydration asymmetry was observed only after the octupole moments of water were included.²⁹ While both the dipole and quadrupole moments of commonly used water models vary little amongst each other, the moment Ω₂ is different. For the models shown in Figure 1 this moment (shown in brackets in units of DŲ) varies considerably³¹ between models: 0 = BNS [0.0] < TIP5P/TIP5P-Ew [0.59] < TIP3P [1.68] ≤ SPC/E [1.96] ≤ TIP4P [2.10]. Given that Ω₂ is critical for CHA, we suggest that the above sequence describes the intrinsic propensities of the n-site water models to cause the asymmetry. The relative values of Ω₂ explain the TIP3P < SPC/E < TIP4P sequence of relative hydration asymmetries observed for the F⁺/F⁻ pair in the MD simulations that kept ion parameters constant while probing the water models themselves.²⁸ While we are not aware of an analogous F⁺/F⁻ simulation for TIP5P/TIP5P-Ew, an extrapolation (see “Methods”) to K⁺/F⁻ from the hydration free energies for Na⁺/Cl⁻ previously computed in TIP5P-Ew water⁴⁴ yields a three times smaller CHA than that computed for SPC/E model,²⁸ consistent with the lower Ω₂ of TIP5P-Ew.

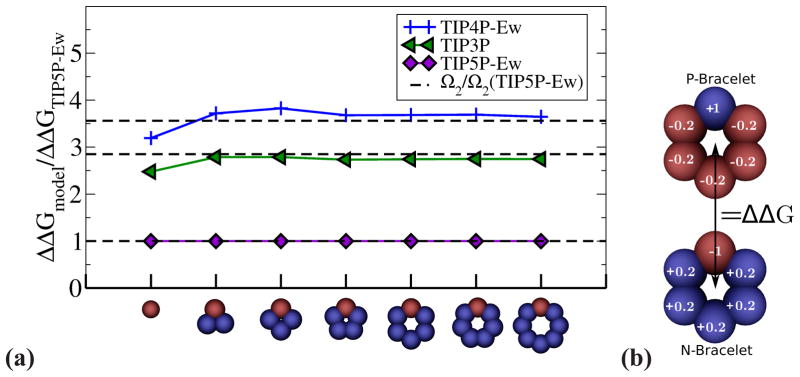
The significant variation between water models in their ability to cause CHA is not limited to ion hydration: the hydration free energy calculations on pairs of “charge-inverted” neutral small molecules show^22,45 that CHA varies as TIP5P-Ew < TIP3P < TIP4P-Ew. In fact, relative CHA correlates well with the CHA prediction based on the relative values of Ω₂, Figure 3.

Figure 3.

(a) Relative ability of several point-charge water models to cause charge hydration asymmetry. ΔΔG is CHA for a pair of charge inverted solutes (ions or neutral molecules, see panel (b)). ΔΔG for TIP5P-Ew water is taken as a reference. The horizontal axis shows various test solutes used (only one molecule of a pair shown). The first structure corresponds to F⁺/F⁻ ion pair (see “Methods”). The rest of the pairs are neutral N/P-bracelets (only N-bracelets shown on the axis) from Ref.^22,45 The horizontal black dashed lines show the relative values of Ω₂ for different water models (relative to Ω₂ for TIP5P model). (b) The example of N- and P-bracelets for the hexagonal charge configuration.²²

In general, not every multipole moment necessarily contributes to the energy of a water molecule in external electric field. Thus, Eq. (3) should be applied selectively to investigate the asymmetry of water response to electric fields other than that produced by a single ion. For example, there will be no asymmetric water response to a constant field since only the dipole moment (obeying C · R = I) contributes to the energy.

Charge-asymmetric ion hydration in continuum solvent

We will now use our understanding of how asymmetric ion hydration works to derive a first-principles “charge-asymmetric” analogue of the Born equation. It is known from explicit solvent simulations^19,46 and analysis of the experimental hydration energies (see Supporting Information) that a purely quadratic dependence of the solvation free energy on the ionic charge for ions of the same sign is remarkably accurate in a wide range of sizes and charge values. This observation suggests the following ansatz for the general case of charge-asymmetric ion hydration:

$$\mathrm{\Delta }G=\mathrm{\Delta }{G}_B(R_{\mathit{eff}})\times \eta$$ (4)

where all of the CHA effects are contained in the yet undetermined function η, while the effective ion radius R_eff is asymmetry-independent and is the same for cations and anions of the same size, R_i. We stress that, without restrictions on η or R_eff, Eq. (4) is not an approximation. In what follows, we will use microscopic water models to infer functional forms of η and R_eff. Specifically, we invert Eq. (4) to define the asymmetry factor η = ΔG/ΔG_B(R_eff). We then estimate ΔG from a realistic, yet analytically tractable microscopic model that contains the key physics responsible for the asymmetric hydration. For ΔG_B(R_eff), we will use a “fully charge-symmetric” microscopic model for which the original Born equation is exact. Note that while direct accurate estimates of ΔG are extremely demanding in terms of the accuracy of the input models and sensitivity to their details,^17,33,47,48 the ratio η = ΔG/ΔG_B(R_eff) may be expected to be much less sensitive to the models used to estimate it. As agreement with experiment will demonstrate, this is indeed the case.

Key derivation steps

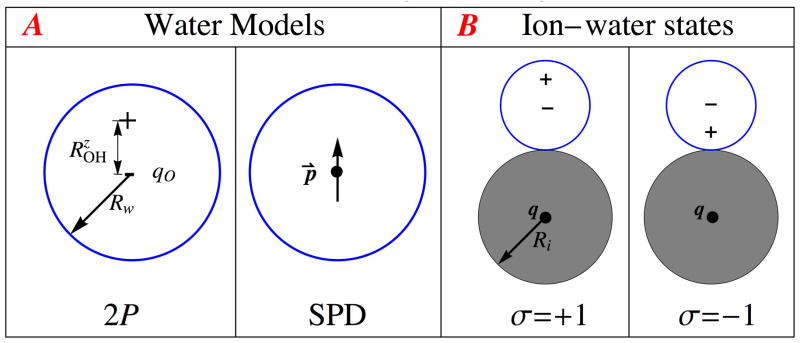
Although most of the detailed water models shown in Figure 1 are charge-asymmetric, these are arguably⁴⁹ not optimal for analytical calculations aimed at elucidating the general principle. Arguably the least complex “charge-asymmetric” C · R ≠ I model is a two-point model, denoted as 2P, with a negative charge at the center of a sphere and a positive charge offset by a certain distance $R_{OH}^z$, Figure 6(A). Our 2P model preserves components of all primitive multipole moments of TIP3P water along its z-axis of symmetry, which are directly related to all components of the traceless moments. Thus, the 2P primitive moments retain the key elements (components) that can cause the hydration asymmetry. Two-point charge models have been used successfully to investigate various hydration phenomena,⁵⁰ including CHA.⁴⁹

Figure 6.

A: The charge-asymmetric 2-point (2P) and the symmetric simple point dipole (SPD) hard sphere water models. Both models have identical dipole moments $\mid \overrightarrow{p}\mid =\mid R_{OH}^z{q}_O\mid$. B: The two orientation states, σ = ±1, of the water dipole in the ion first hydration shell used in Eq. (6). The dipole energy of any other ion-water orientation can be decomposed as a linear combination of these two states.

The simplest reasonable water model that satisfies C · R = I is the simple point dipole (SPD) model, Figure 6. SPD is also unique in that the Born equation Eq. (1), with an effective ion radius, is exact for this model in the mean spherical approximation (MSA) limit.⁵¹

An analysis of the water oxygen radial distributions around model spherical ions³³ reveals that these distributions are not very sensitive to the sign of the ion charge. Thus, the hard sphere model for ion and water with purely electrostatic interactions is a reasonable first-order approximation for estimation of the asymmetry factor η. Using the two simplest water models, 2P that obeys Eq. (3) and SPD that produces an ion solvation free energy in agreement with the Born equation (see Figure 6(A)), in the definition of the asymmetry factor, we obtain via Eq. (2):

$$\eta =\frac{ln\left(\frac{Z_{2P}^{II}}{Z_{2P}^I}\right)}{ln\left(\frac{Z_{\mathit{SPD}}^{II}}{Z_{\mathit{SPD}}^I}\right)}$$ (5)

To make further progress towards a simple analytical model akin to Eq. (1), we restrict the computation in Eq. (5) to the first hydration shell - an approximation that was successfully used in the past to estimate various hydration effects.^15,32,52 Importantly, explicit water simulations show that most of the charge hydration asymmetry effects can be attributed to the first shell.²² With our 2P model, this approximation predicts ion hydration free energies for monovalent ions within ~ 6 % of the experiment, and fully preserves the hydration asymmetry, see Supporting Information.

Within the first-shell approximation, Eq. (5) becomes tractable, see Supporting Information, but still does not lead to a single equation nearly as transparent and insightful as the Born formula. Our next simplifying step is based on the observation that, while the hydration free energy does depend strongly on water-water interactions, the asymmetry factor η is virtually independent of water-water interactions over their entire range of strength when scaled from zero to full, see Supporting Information. Thus, to calculate η, we can set the water-water interactions in Eq. (5) to zero, which drastically simplifies the calculation by decoupling the identical water molecules in the first shell and, thus, making Z factorizable. The focus on ion-water interactions as the cause of the hydration asymmetry is consistent with earlier RISM calculations.⁵³ Denoting ${\zeta }_{1,2P}^{(I,II)}$ and ${\zeta }_{1,\mathit{SPD}}^{(I,II)}$ as the partition functions for ion + single water molecule in the first hydration shell for both models, we have:

$$\eta =\frac{ln\left(\frac{{\zeta }_{1,2P}^{II}}{{\zeta }_{1,2P}^I}\right)}{ln\left(\frac{{\zeta }_{1,\mathit{SPD}}^{II}}{{\zeta }_{1,\mathit{SPD}}^I}\right)}=\frac{ln{\langle e^{-\beta E_{2P}^{\sigma }}\rangle }_{\sigma }}{ln{\langle e^{-\beta E_{\mathit{SPD}}^{\sigma }}\rangle }_{\sigma }},$$ (6)

where E^σ is the electrostatic ion-water interaction energy for the water orientation σ, and 〈〉 _σ denotes averaging over all possible orientations of the water molecule. Additionally, the accuracy of η for realistic ions estimated via Eq. (6) is virtually the same if the number of possible orientations of the water molecule relative to the ion is reduced to just two extreme orientational states (σ = ±1) that span the entire range of possible directions of the water dipole, Figure 6(B). With only two allowed water orientations, we finally obtain from Eq. (6):

$$\eta =\frac{ln\left(\frac{1}{2}{\displaystyle \sum _{\sigma =\pm 1}}{\text{e}}^{-\beta \frac{\sigma {qq}_O{R}_{OH}^z}{R_{iw}(R_{iw}+\sigma R_{OH}^z)}}\right)}{ln\left(cosh\left(\beta \frac{{qq}_O{R}_{OH}^z}{{(R_{iw})}^2}\right)\right)},$$ (7)

where R_iw = R_i + R_w is the distance between ion and water hard sphere centers, and q_O with $R_{OH}^z$ characterize the charge distribution in the model water molecule, Figure 6.

We now turn our attention to R_eff in Eq. (4). As was noted above, in the MSA limit the solvation free energy of an ion of radius R_i in the hard sphere SPD water model ⁵¹ is given by the Born equation with R_eff = R_i + R_s:

$$\mathrm{\Delta }{G}_B=-\left(1-\frac{1}{\epsilon }\right)\frac{q^2}{2(R_i+R_s)},$$ (8)

where R_s could be regarded as a shift of the dielectric boundary from the ion surface (R_s = 0.52 Å at ε = 80 and the standard water radius R_w = 1.4 Å). Recall now that the SPD model is manifestly charge-symmetric, so that R_eff defined above is independent of the sign of the ion charge, as needed by the proposed model. Substituting Eq. (8) and Eq. (7) into our general ansatz Eq. (4) we arrive at

$$\mathrm{\Delta }G=-\left(1-\frac{1}{\epsilon }\right)\frac{q^2}{2(R_i+R_s)}\frac{ln\left(\frac{1}{2}{\displaystyle \sum _{\sigma =\pm 1}}{\text{e}}^{-\beta \frac{\sigma {qq}_O{R}_{OH}^z}{R_{iw}(R_{iw}+\sigma R_{OH}^2)}}\right)}{ln\left(cosh\left(\beta \frac{{qq}_O{R}_{OH}^z}{{(R_{iw})}^2}\right)\right)}$$ (9)

For realistic ions considered here, R_i ≤ 3 Å, |q| ≥ e, the water molecules in the first hydration shell experience a strong enough ion electric field ℰ⃗ such that the energy of the water dipole p⃗ in this field |ℰ⃗p⃗| ≫ k_BT. Under these conditions, Eq. (9) reduces (see Supporting Information for details) to the simpler Eq. (10) below.

Charge-asymmetric “Born” formula

We propose the following “charge-asymmetric” replacement for the Born equation Eq. (1) for the solvation free energy of a spherical ion of radius R_i and charge q in water:

$$\mathrm{\Delta }G=-\left(1-\frac{1}{\epsilon }\right)\frac{q^2}{2(R_i+R_s)}{\left(1+\mathit{Sgn}[q]\frac{R_{OH}^z}{R_i+R_w}\right)}^{-1}.$$ (10)

Just like the original Born formula, the above equation does not have fitting parameters. Un-like the original, Eq. (10) is asymmetric with respect to the sign of the ion charge q through the asymmetry factor

$$\eta (q)={\left(1+\mathit{Sgn}[q]\frac{R_{OH}^z}{R_i+R_w}\right)}^{-1}.$$ (11)

Agreement with experiment

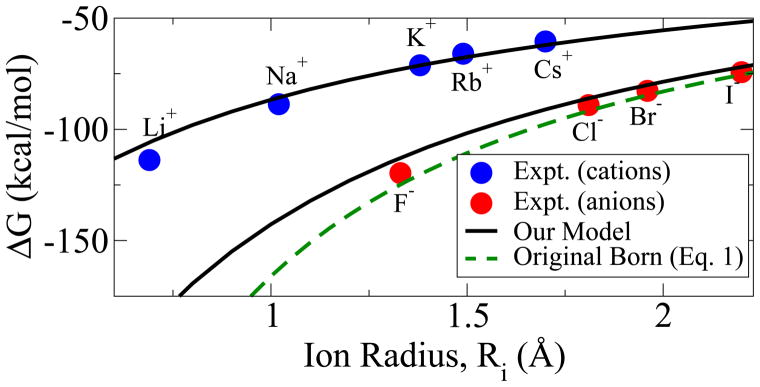
The hydration free energies predicted by Eq. (10) for spherical mono-valent and di-valent ions agree with experiment, Figure 4, essentially within the uncertainty range of the experiments, Table 1. The agreement with experiment is noteworthy given that the proposed model is a very simple-looking equation with no fitting parameters. It is reassuring that the “first principles” MSA value of R_s = 0.52 Å in Eq. (9) is close (= 0.475 Å) to the value that can be obtained by taking R_s as a parameter and fitting Eq. (9) to the experiment. The use of the best fit R_s in Eq. (9) results in an insignificant improvement over the use of the “fist principles” R_s of ~ 1% in agreement between the predicted and experimental hydration energies, see Supporting Information.

Figure 4.

Predicted molar hydration free energies are compared with experiment¹³ for monovalent ions (blue and red dots) at 298 K and 1 mol/L. Solid black lines: our model, Eq. (10). Dashed green line: Born model, Eq. (1). Ion radii are from Ref.¹⁴

Table 1.

Root Mean Square Percent Error (RMSPE) in Hydration Free Energy for different models

Ions	Born*	Latimer†	Our Model‡	Experiment¶
monovalent	60.25%	4.62%	3.94%	6.25%
divalent§	116.86%	3.23%	3.52%	2.14%

^*Born equation, Eq. (1) without any correction in ion radii

^†Empirical correction proposed by Latimer et al. ³⁶

^‡Eq. (10)

^¶RMSPE calculated from two sets of experimental data^13,14

^§RMSPE calculated using cations only; data for spherical simple divalent anions unavailable in¹³

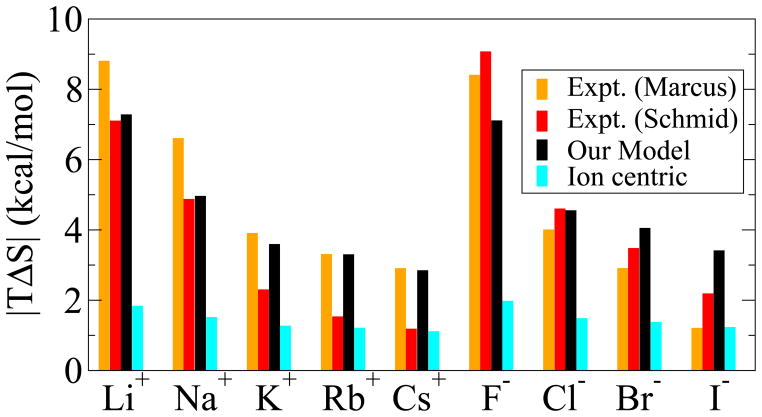
A more subtle test of the model comes from comparing the predicted hydration entropies ΔS = −∂ ΔG/∂T with experiment. The predicted entropy contribution to ΔG of hydration, Eq. (15) in “Methods”, shows an excellent qualitative and a reasonable quantitative agreement with experiments,^13,54 Figure 5. In contrast to this, the “ion-centric” approach, which considers the effective ion radius as a temperature independent, intrinsic property of the ion, cannot properly reproduce ΔS. Within that approach the only contribution to ΔS is due to a temperature dependence of ε (the first term of Eq. (15)) that, for most ions, is not sufficient to account for the experimental values of ΔS. For example, the asymmetry between hydration entropies contributions of K⁺ and F⁻ ions, T |ΔS(K⁺)−ΔS(F⁻)|, predicted by the “ion-centric” approach is only 0.7 kcal/mol, while the experimental values are 4.5 to 6.7 kcal/mol, comparable to our prediction of 3.5 kcal/mol.

Figure 5.

Hydration entropy |TΔS| of monovalent alkali halide ions at 298 K and 1 mol/L. Experimental data: Marcus,⁵⁴ orange bars; Schmid et al.,¹³ red bars. Our model: black bars. The “ion–centric” prescription for empirical correction³⁶ to ion radii: cyan bars.

Microscopic origins of earlier empirical radii corrections

By re-casting Eq. (10) to:

$$\mathrm{\Delta }G=-\left(1-\frac{1}{\epsilon }\right)\frac{q^2}{2\left(R_i+R_s+\mathit{Sgn}[q]\frac{R_{OH}^z(R_i+R_s)}{R_{iw}}\right)}$$ (12)

we recover the form of the Latimer et al. prescription with the radii corrections $C_{+}=R_s+\frac{R_{OH}^z}{R_{iw}}(R_i+R_s)$ and $C_{-}=R_s-\frac{R_{OH}^z}{R_{iw}}(R_i+R_s)$. Our “corrections” range from 0.86 Å (Li⁺) to 0.94 Å (Cs⁺) for monovalent cations and 0.12 Å (F⁻) to 0.08 Å (I⁻) for anions, and are numerically close to the Latimer et al. empirical corrections C₊ = 0.85 Å and C₋ = 0.1 Å. Our model uncovers the microscopic origin of these corrections – specific asymmetry of charge distribution in water molecule that gives rise to CHA in a non-uniform field of the ion.

Propensities of common explicit water models to cause charge hydration asymmetry

For a similar size cation/anion pair (B⁺/A⁻) such as K⁺/F⁻, the dimensionless ratio

$${\eta }^{\ast }(B^{+}/A^{-})=\frac{\mathrm{\Delta }G(B^{+})-\mathrm{\Delta }G(A^{-})}{\frac{1}{2}\mid \mathrm{\Delta }G(B^{+})+\mathrm{\Delta }G(A^{-})\mid }$$ (13)

is a particularly simple and robust measure of CHA. Within our simplified 2P model, the water charge distribution asymmetry is quantified by a single parameter, $R_{OH}^z$, which, by construction, can be related to the ratio of the first two primitive multipole moments of the TIP3P water model, $R_{OH}^z={\stackrel{\sim }{Q}}_{zz}/p$. By identifying ${({\stackrel{\sim }{Q}}_{zz}/p)}^{\mathit{MODEL}}=R_{OH}^z$ we can map commonly used n-site water models onto our simplified 2P model. This allows us to explore their intrinsic hydration asymmetry properties via Eq. (10) and Eq. (13) using η* as a measure of their propensity to cause CHA. Assuming R_i(A⁻) = R_i(B⁺), our ion hydration model predicts for the CHA propensity:

$${\eta }^{\ast }(B^{+}/A^{-})=2\frac{R_{OH}^z}{R_{iw}}.$$ (14)

This result, as well as Eq. (11), suggest that the ion and water sizes affect the CHA propensity only through ion-water distance R_iw, which is experimentally well-defined quantity with a small margin of error. Thus, we can now evaluate (via Eq. (14)) the intrinsic propensity of water models to cause CHA, irrespective of any parametrization of ions. These propensities are shown in Table 2, and are in over-all agreement with our general symmetry arguments presented above. Intrinsic propensities of TIP3P, SPC/E and TIP4P to cause CHA are close to experiment used here as reference,¹³ with TIP4P being the closest, while TIP5P-Ew underestimates CHA by a factor of four.

Table 2.

Predicted relative propensities of several common n–site water models to cause charge hydration asymmetry estimated as η*(K⁺/F⁻), Eq. (14) ( $R_{iw}=2.755Å=\frac{1}{2}(R_i({\text{K}}^{+})+R_i({\text{F}}^{-}))+R_w$). Experimental η* is defined via Eq. (13)

WATER MODEL	BNS	TIP3P	SPC/E	TIP4P	TIP5P-Ew	Experiment
propensity for CHA, η*(K+/F−)	0	0.43	0.42	0.53	0.13	0.51

Note that in neutral solutes, the opposing CHA shifts in ΔG for opposite partial charges may largely cancel out, masking a CHA deficiency of a particular water model. To illustrate the point, consider solvation of a net neutral system of solvent-separated K⁺ and F⁻. According to Eq. (10), its hydration energy can be approximated as $\mathrm{\Delta }G=2\mathrm{\Delta }{G}_B{\left(1-{\left(\frac{R_{OH}^z}{R_{iw}}\right)}^2\right)}^{-1}$ where the correction relative to completely charge-symmetric Born model is of the second order in $\frac{R_{OH}^z}{R_{iw}}$, which is small (about 6 % in this case) compared to the asymmetry correction to individual ion solvation energies. It is therefore possible that while the total computed ΔG appears almost right, the solvation energies of individual groups in the molecule are under- or over-estimated significantly because the CHA is not accounted for correctly. Computed effective charge-charge interactions may contain gross errors in this case, causing distortions in molecule conformation dynamics. Such total solvation energy error cancellations are reminiscent of those that occur in the generalized Born model.⁵⁵

Conclusion

We have used basic statistical mechanics to derive a quantitative connection between the expected CHA and specific symmetry properties of the underlying water model. Mathematically, the principle is expressed as C · R ≠ I, where C and R are the charge inversion and rotation operations applied to the water molecule. It explains why real water exhibits CHA – “charge–inverted water” can not be made from water by any combination of rotations of the molecule about its van der Waals interaction center. When applied to popular water models, the equation shows why some of them cause little to none CHA, while in others this effect is significant. Here, consideration of the symmetry properties of a water model’s electric multipole components was particularly insightful.

Once the key ingredients needed for a water model to exhibit CHA became clear, we used the gained insight to reintroduce the ingredients into the original Born formula, which serves as a conceptual example of the continuum electrostatics. Our approach explicitly separates two problems that are commonly mixed in the development of continuum solvent models: the charge-asymmetry effects and the placement of the dielectric boundary around the ion. The result is an equation that is as simple as the original Born model, free from fitting parameters, and predicts hydration free energies and entropies of spherical ions in good agreement with experiment.

Potential benefits of the proposed replacement for the Born model are at least two-fold. First, due to simplicity of the new formula, it can be used just as the original to describe the basics of aqueous solvation of charges, but now with the hydration asymmetry effects fully taken into account from first principles. Perhaps more importantly, the agreement with experiment we have achieved shows that once the charge asymmetry effects are consistently added to the foundation of the electrostatic continuum formalism, the result can be quite accurate, without the need for empirical parametrization. This result is noteworthy since CHA is obviously not the only real effect currently missing from the continuum solvent framework, compared to e.g. the more fundamental explicit solvent representation. Which suggests that, at least as far as the energetics are concerned, the asymmetry may be the main ingredient still missing from the basis of the existing continuum electrostatics framework. This observation should be particularly useful for future development of implicit solvent models, especially if simplicity, robustness and computational efficiency are key. Over-all, the main potential benefit of the proposed analysis of CHA is that it can be used to test, and ultimately improve, practical water models.

Methods

Water models

Our charge-asymmetric model, Figure 6(A), is a hard sphere, two-point (2P) “charge analogue” of the popular TIP3P.⁴³ The partial charge q_O = −0.834e on the oxygen center is unaltered, but the two hydrogen charges are merged into a single partial charge, +0.834e, offset from the center by $R_{OH}^z=0.586Å$- the projection of the $\overrightarrow{OH}$ vector on the z-axis of symmetry of TIP3P. This transformation preserves all z-components of the primitive (non-traceless) multipole moments of the TIP3P charge distribution about the oxygen center, in particular, the components of the dipole moment, $p_z=\mid \overrightarrow{p}\mid ={\mathrm{\sum }}_i{q}_i{z}_i=\mid q_O{R}_{OH}^Z\mid$, and the quadrupole moment, ${\stackrel{\sim }{Q}}_{zz}={\mathrm{\sum }}_i{q}_i{z_i}^2=\mid q_O{(R_{OH}^z)}^2\mid$. The “charge-symmetric” water molecule is modeled as a hard sphere with a simple point dipole (SPD) in its center; its dipole moment equals that of the 2P model. In both models we use R_w = 1.4Åas a radius of the hard sphere.

Experimental reference

Experimental measurement of hydration energies of individual ions is anything but straightforward. As a result, a variety of different sets of ion hydration energies can be found in literature.^56,57 Comparison between theory and experiment is also not straightforward – one must carefully select experimental reference that corresponds to the type of calculation performed.^44,56 For example, issues such as whether bulk water/vapor interface potential is included need to be considered. Following a discussion of these issues in Ref.,⁵⁶ we have chosen Schmid et al.¹³ as our main experimental reference for free energy ΔG and entropy ΔS of ion hydration. We also use Marcus’ data⁵⁴ to compare with our entropy calculations. Both sets of values are determined for the state conditions T = 298 K and 1 mol/L both in the gas phase and in the solution, and do not include contribution from water/air interface potential consistent with our theoretical approach. The set of ionic radii are obtained from¹⁴ and are shown in Table 3.

Table 3.

Ion Radii used¹⁴ to compute the Hydration Free Energy of monovalent and divalent ions

Alkali ions		Halide ions		Divalent Cations *
Ion	Radius(Å)	Ion	Radius(Å)	Ion	Radius(Å)
Li+	0.69	F−	1.33	Be2+	0.40
Na+	1.02	Cl−	1.81	Mg2+	0.72
K+	1.38	Br−	1.96	Ca2+	1.00
Rb+	1.49	I−	2.20	Sr2+	1.13
Cs+	1.70			Ba2+	1.36

^*Data for spherical simple divalent anions unavailable in¹³ and hence not used in our analyses

Extrapolating absolute hydration free energies

Relative values of the experimental ion hydration free energies are known as the conventional free energies. Provided that at least one value of the absolute hydration free energy is known, it is easy to calculate the other hydration free energies by applying the corresponding differences in the conventional energies.⁵⁸ E.g., ΔG(K⁺) = ΔG(Na⁺) + ΔG_conv(K⁺) −ΔG_conv(Na⁺).

Entropy estimate

The expression for the entropy of ion hydration is obtained from the temperature derivative of ΔG, given by Eq. (10), through its functional dependence on the temperature dependent quantities ε, R_eff and R_iw. To estimate R_eff (T) we assume that the ion/solvent dielectric boundary determined by R_eff expands with temperature at the same rate as the ion-water distance, i.e., ∂R_eff/∂T = ∂R_iw/∂T. The latter quantity is approximated with the rate of a bulk water expansion, ∂R_iw/∂T ≈ ∂R_ww/∂T, where R_ww = 2R_w is a mean distance between neighboring molecules in a bulk water. This rate could be easy expressed via a known value of volumetric thermal expansion coefficient of water, α = 2.57 · 10⁻⁴ K⁻¹ at T = 298 K⁵⁹ (see Supporting Information for details). The experimental value ∂ε/∂T = −0.36 K⁻¹ at T = 298 K is taken from Ref.⁶⁰ The resulting expression for the entropy can be written as

$$\mathrm{\Delta }S=\mathrm{\Delta }G\left(-\frac{1}{\epsilon (\epsilon -1)}\frac{\partial \epsilon }{\partial T}+\frac{\alpha }{3}\left(\frac{R_{ww}}{R_{\mathit{eff}}}+(\eta -1)\frac{R_{ww}}{R_{iw}}\right)\right).$$ (15)