¹H-ENDOR Evidence for a Hydrogen Bonding Interaction that Modulates the Reactivity of a Non-heme Fe^IV=O Unit

Abstract

We report that a novel use of 35 GHz ¹H-ENDOR spectroscopy establishes the presence in 1 of an Fe^IV=O···H–O–Fe^III hydrogen bond predicted by DFT computations to generate a six-membered-ring core for 1. The H-bond rationalizes the difference in C–H bond cleavage reactivity between 1 and 4(OCH₃) (where a CH₃O group has replaced the HO on the Fe^III site). This result substantiates the seemingly paradoxical conclusion that the non-heme Fe^IV=O unit of 1 not only has the electrophilic character required for H-atom abstraction, but nonetheless retains sufficient nucleophilic character to accept a hydrogen bond from the Fe^III-OH unit.

Hydrogen bonding is an essential element in Nature’s toolbox for stabilizing structures and modulating reactivity. The key roles played by hydrogen bonding in the catalytic sites of iron proteins are particularly well illustrated by their contrasting effects on their interaction with O₂. H-bonds to the O₂ as an Fe ligand serve to maintain reversible O₂ binding in hemoglobin and hemerythrin, whereas H-bonds promote O–O bond cleavage in monooxygenases such as cytochromes P450.^1–4 Hydrogen bonding to non-heme metal-oxo units may also be important. Indeed Borovik has elegantly demonstrated the significance of intramolecular hydrogen bonds in stabilizing the first crystallographically characterized, synthetic oxoiron(III) complex.⁵ Oxidizing the oxoiron(III) center to its iron(IV) counterpart significantly weakens H-bonds to the Fe^IV=O center,⁶ but how this affects the reactivity of the Fe^IV=O unit has not been determined.

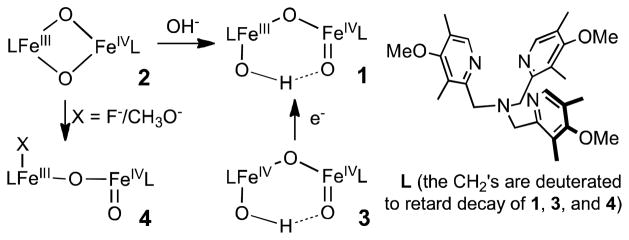
In our efforts to obtain a synthetic model for high-valent intermediate X in the activation cycle of Class 1a ribonucleotide reductases, we generated complex 1 (Scheme 1), which has the Fe^III–O–Fe^IV core found in X and exhibits EPR and Mössbauer spectra very similar to those of X.^7,8–11 Complex 1 can be obtained by nucleophilic attack of hydroxide ion on the [Fe^IIIFe^IV(μ-O)₂] diamond core of 2, generating the open HO–Fe^III–O–Fe^IV=O core of 1. The closely related 4(OCH₃) can be generated by a similar reaction with methoxide, and exhibits similar spectroscopic features.¹² Interestingly, H-atom transfer to 4(OCH₃) from DHA (9,10-dihydroanthracene) occurs 13-fold faster at −80 °C than to 1. It was postulated that this difference occurs because a hydrogen bond in 1 between the proton on the Fe^III–OH and the oxygen atom of the terminal Fe^IV=O (Scheme 1) diminishes the electrophilicity of the Fe^IV=O.¹² Although DFT computations provide support for such an interaction,¹¹ there is no direct experimental evidence for this pivotal H-bond in condensed phase. Given its high reactivity of 1, it is unlikely that it can be crystallized. Therefore, we have employed ¹H-ENDOR spectroscopic studies of 1 to establish the spatial relationship of the O–H proton to the two iron atoms of 1, thereby proving the existence of the six-membered ring whose formation is driven by this hydrogen bond. This H-bond is further discussed as a central element in the interpretation of the C–H bond cleavage reactivity of this unique high-valent complex.

Scheme 1.

Complex 1(OH/OD), like intermediate X, exhibits an S = ½ ground state, as the result of anti-ferromagnetic spin-coupling between the high-spin Fe^III(S = 5/2)/ Fe^IV(S =2) ions. Its 35 GHz EPR spectrum is described by the g-tensor, g = [2.008, 2.003, 1.992], comparable to that of X.^11,13 The spectrum shows a small variability in g_⊥ that is assigned to solvent/freezing effects (Fig S1).^10,14–16

Davies Q-band ¹H-ENDOR spectra^15,16 of 1(OH/OD) collected at g = 2.003 show signals centered at the ¹H Larmor frequency from ¹H with a range of couplings, Fig 1. The most strongly coupled signal, A_max(¹H_A) ~ 35 MHz, is partially lost in the 1(OD) sample ^14,17 (Figs 1 and S2), identifying it with the Fe^III–OH proton, ¹H_A. Protons associated with the supporting organic ligand, hyperfine couplings A ≤ 10 MHz, do not exchange,.¹⁷

Figure 1.

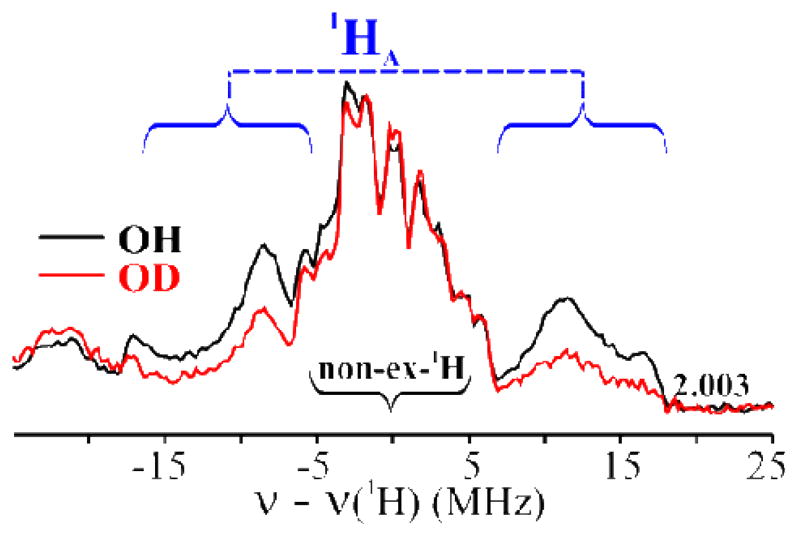
Davies ¹H-ENDOR spectra of 1(OH/OD) at g = 2.003. The blue curly brackets show the ¹H_A signal. Conditions: π-pulse length = 120 ns, τ = 600 ns, repetition time = 40 ms, microwave frequency = 34.698 GHz, T = 2 K.

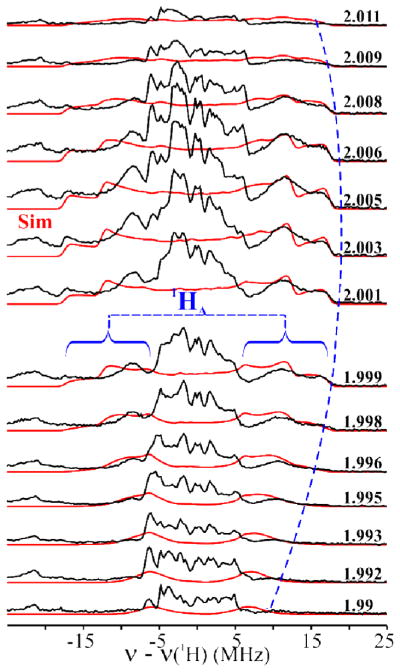
Fig 2 shows the 2-D field-frequency plot of Davies ¹H-ENDOR spectra of 1(OH), collected at numerous fields across the EPR envelope. At g₁ = 2.01 the ¹H_A-doublet exhibits a hyperfine coupling of A(¹H_A) ~ 25 MHz. As the field is increased, the ν⁺ = [ν(¹H) + A(¹H_A)/2] branch of the ¹H_A signal intensifies as a shoulder develops to high-frequency and becomes a peak with maximum hyperfine coupling of A(¹H_A) ~ 35 MHz at g ~ 2.005.¹⁸ Upon further increase in the field the shoulder collapses, and the ν⁺ feature again becomes a single peak at g₃ = 1.992.

Figure 2.

Simulated (red lines; see text for simulation parameters and Table S1) and experimental (black lines) 2-D field-frequency plot of Davies ¹H-ENDOR spectra of 1(OH). Conditions: as in Fig 1.

Previous studies have shown that the anisotropic hyperfine interaction component for a proton in a dinuclear center such as 1(OH) is determined by electron-nuclear point-dipole interactions between the proton and the spin-coupled Fe ions, and that this component can be calculated from the metrical parameters of the Fe^III-H-Fe^IV fragment.^13,19,20 Simulation of the 2-D ENDOR pattern of ¹H_A signals collected at several fields across the EPR envelope of 1 thus began by calculating the dipolar interaction tensor, T_cal, from metrical parameters derived from the DFT optimized structure of 1: Fe^III–Fe^IV distance, d_Fe-Fe = 3.34 Å; parameters defining the –OH proton position relative to the two Fe ions, r₁ = 2.38 Å, β₁ = 56.6° (Fig 3 and Table S1). With the resulting tensor, T_cal = [−9.0, −22.4, +31.4] MHz, taken as the starting point, the isotropic coupling, a_iso, anisotropic tensor components, T_ex,i, i = 1–3, and orientation of the experimental hyperfine tensor, T_ex, relative to the g-tensor were varied until simulations matched the experimental 2-D pattern of ¹H _A ENDOR signals. Overlaid on the experimental spectra (Fig 2) are the excellent simulations computed with the optimized hyperfine tensor, A(¹H_A) = a_iso(¹H_A) + T_ex(¹H_A) = −0.73 + [−11.3, −24.3, +35.6] MHz (orientation relative to g, α = 30.0°, β = 60.0°), which is dominated by the anisotropic term, T_ex(¹H_A).

Figure 3.

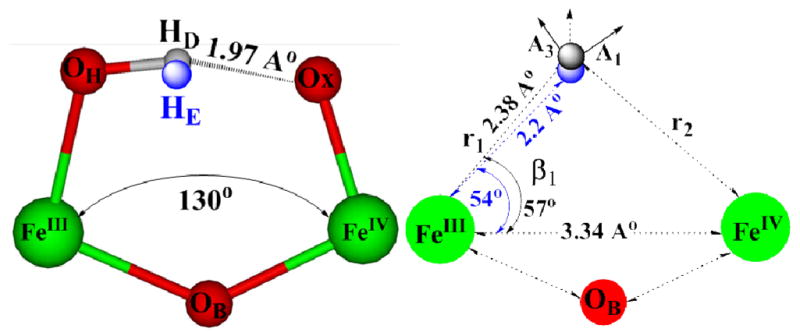
(left) Structural description of ENDOR (H_E) and DFT (H_D) optimized locations of ¹H_A of 1. (right) Definition of metrical parameters used to calculate the cluster dipolar interaction tensor, T.

Through use of the point-dipole equations,^{19,20, 21–22} the experimentally derived T_ex (¹H_A) can in turn be used to infer the actual geometry of the Fe^III-H-Fe^IV fragment. T_ex (¹H_A) differs slightly from T_cal derived from the DFT structure, but the experimental tensor is precisely matched by a proton position that is minimally different from that of the DFT-optimized structure: r₁ = 2.20 Å, β₁ = 54° (Fig 3 and Table S1). Most importantly, simulations with a linear Fe^III–O–Fe^IV, or with ¹H_A rotated about the Fe^III–O_H bond, or even with a bridging hydroxo, completely fail to reproduce the ENDOR results (Figs S5–S8; Tables S1 and S2).

The ENDOR results thus provide strong experimental evidence in support of the DFT-optimized structure of 1, which shows the oxo ligand of the Fe^IV ion and the ¹H_A of the hydroxo ligand on Fe^III ion at a distance indicative of Fe^IV=O···H–O–Fe^III hydrogen bonding. This interaction decreases the Fe^III–O–Fe^IV angle to 130.0°, from the value, 175.0° calculated for 4(F) (and by extension to 4-OCH₃), complexes for which such H-bonding and formation of a closed cycle are precluded.¹¹ Likewise, the hydrogen bonding interaction reduces the dihedral angle in the DFT-optimized structure, O_x=Fe^IV-Fe^III-O_H to 32.0°, whereas it is 180.0° for 4(F).¹¹ The position of the hydroxyl proton, ¹H_A(E), determined by ENDOR measurements of 1 in frozen solution is the same as that of the proton in the DFT-generated structure, ¹H_A(D), within the accuracy of measurements/analysis, and thus the ENDOR measurement confirms the presence in frozen solution of the Fe^IV=O···H–O-Fe^III hydrogen bond predicted by DFT to drive Fe-O-Fe bending in 1 required to generate the cyclic structure.

Additional corroboration of this conclusion derives from the observation that chemical or cryo-reduction of 3 also afforded 1. Precursor 3 has been characterized to be a (μ-oxo)diiron(IV) complex with an EXAFS- determined Fe–Fe distance of 3.32 Å, implicating a bent Fe–O–Fe unit with an Fe–O–Fe angle of ca. 130°.²³ One-electron reduction of 3 thus occurs without an appreciable change in the net Fe–Fe distance.^10,11

This communication reports a novel use of 35 GHz ¹H-ENDOR spectroscopy to precisely probe the solution-phase structure of 1. Metrical parameters derived from ENDOR measurements verify the bending of the Fe–O– Fe linkage predicted by DFT computations, and thus establish the presence of the predicted Fe^IV=O_x…H–O–Fe^III hydrogen bond that drives this bending and generates the cyclic, six-membered-ring core of 1. Indeed the ENDOR results provide the only direct experimental evidence that proves the existence of this hydrogen bond. Its existence in 1 rationalizes the difference in C–H bond cleavage reactivity between 1 and 4(OCH₃).¹² Loss of this hydrogen bond upon replacement of the terminal hydroxide on the Fe^III center of 1 with a methoxide ligand in 4(OCH₃) unmasks the full H-atom abstraction potential of the Fe^IV=O unit. By establishing the postulated hydrogen bond to the oxo group of 1, this study thus substantiates the seemingly paradoxical conclusion that the non-heme Fe^IV=O unit not only has the electrophilic character required for H-atom abstraction, but nonetheless retains the nucleophilic character needed for a H-bond acceptor. Such hydrogen bonding interactions thus are shown to be useful in modulating the reactivity of high-valent iron-oxo species generated in an enzyme active site.