The art of transparency

Abstract

Artists throughout the ages have discovered a number of techniques to depict transparency. With only a few exceptions, these techniques follow closely the properties of physical transparency. The two best known properties are X-junctions and the luminance relations described by Metelli. X-junctions are seen where the contours of a transparent material cross contours of the surface behind; Metelli's constraints on the luminance relations between the direct and filtered portions of the surface specify a range of luminance values that are consistent with transparency. These principles have been used by artists since the time of ancient Egypt. However, artists also discovered that stimuli can be seen as transparent even when these physical constraints are not met. Ancient Greek artists, for example, were able to depict transparent materials in simple black-and-white line drawings. Artists also learned how to represent transparency in cases where neither X-junctions nor Metelli's constraints could apply: for example, where no portions of the objects behind the transparent material extend beyond it. Many painters convincingly portrayed transparency in these cases by depicting the effects the transparent medium would have on material or object properties. Here, we show how artists employed these and other techniques revealing their anticipation of current formalizations of perceived transparency, and we suggest new, as-yet-untested principles.

1. Introduction

In Figure 1a we see a photograph of a paintbrush resting in a glass that is partially filled with water. The perception of the photograph corresponds closely to the perception of the original scene. This correspondence is not very surprising because the physical relations of the light coming from the scene are preserved in the photograph, at least for monocular viewing with no head motion (for the intricacies of picture perception see, eg, Gibson 1971; Hecht et al 2003). However, the photograph in Figure 1b has been altered, removing the break in the brush due to the refraction of light rays by the water. Despite the violation of physical laws, the perception of the scene does not change much, and the water still looks transparent. Moreover, the violation would probably go unnoticed by most observers. Similar violations of physics are frequently found in otherwise realistic paintings where improper perspective, object distortions, or impossible lighting or reflections often have little effect on the perception of space and light in the scene.

Figure 1.

(a) Photograph of a paintbrush in a transparent glass half filled with water. Refraction by the water produces a discontinuity in the brush. (b) The photograph is altered to remove the effect of refraction, but transparency is still perceived.

Whether violations are noticed by observers or not tells us about which violations are checked by an observer's visual system and which are not. In this sense painters have functioned as early vision scientists, discovering techniques of depiction that work for the sets of laws the visual system actually uses and revealing rules that do not. For example, observers are insensitive to impossible reflections in mirrors (eg, Croucher et al 2002; Bertamini et al 2003; Cavanagh et al 2008), physically inconsistent shadows (Casati 2004; Mamassian 2004; Cavanagh 2005) and illumination inconsistencies (Ostrovsky et al 2005). These unnoticed errors reveal the “naive” physics used by the visual brain to interpret scenes—a set of assumptions about the world that is in many cases quite different from real world physics. In this paper we investigate what artists have discovered about transparency, which rules of optics are or are not respected, and whether artists have discovered principles of transparency that scientist have yet to explore.

A transparent material transmits light to some extent so that some of the light arriving on one side of an object can be seen from the other side—the material is not totally opaque. This property, however, is neither necessary nor sufficient for perceptual transparency and, of course, is not typically an option in a painting where the artist mimics the effects of transparency by manipulating the luminance and colors of pigments. So what are the necessary features that trigger transparency percepts in the visual system, and do they exactly model the laws of physical transparency, or are there, again, some violations permitted (as suggested by Figure 1)?

We first survey the scientific work on transparency and then the techniques of artists. We find that in many paintings the basic local properties of transparency are rendered in accordance with transparency—that is, the adjacent luminance values are suitable to trigger the perception of transparency. However, often these luminance relations are not indicative of the depth order of the corresponding surfaces, and hence, observers would be uncertain about which surface is in front and which behind if only the local information was given. Such uncertainty, however, is rarely experienced when looking at an entire painting where the depth order of the different surfaces is usually clearly perceived. Interestingly, contrary to other scene properties like shadow and reflection which were degraded or omitted in the Dark Ages (eg, Gombrich 1995; Casati 2004), the renditions of the luminance properties of transparency seem not to vary strongly over different periods in art history, with similarly accurate depictions occurring in Ancient Egypt, the Middle Ages, and the Renaissance.

However, properties of transparent materials due to refraction index or color filtering are often strongly violated in paintings and do not seem to be verified by the visual system. Finally, artists have also developed other principles of transparency based on longer-range relations and cognitive inference that have received little or no study in the scientific literature.

2. Scientific studies of luminance properties of perceived transparency

The perception of transparency has been a topic of scientific research for almost 150 years (eg, Helmholtz 1867; Koffka 1935; Metelli 1974). The most significant contribution to the study of transparency has been a set of luminance relations described by Fabio Metelli (1970; 1974). These are now called Metelli's Laws, referring to the luminance relations between parts of a surface viewed directly and those parts of the surface that are seen through a transparent layer. In addition to transmitting light, a transparent material may also reflect some light (a material that both reflects and transmits light is sometimes considered translucent; see below). Metelli's Laws yield precise quantitative descriptions of the physical relations between the luminance of a surface and a transparent and reflective layer partly covering the surface (see also Gerbino et al 1990). Reproducing these relations on a 2D depiction reliably yields the perception of transparency (although lightness rather than luminance or reflectance seems to be the appropriate measure; Beck et al 1984; Metelli 1985). Moreover, very good predictions about perceived transparency can also be made based on qualitative or ordinal approximations of Metelli's luminance constraints without taking magnitudes into account (Adelson and Anandan 1990; see also Anderson 1997). As shown in Figure 2a, a transparent square appears in front of the background and in front of a darker second square with both background and dark square visible through the lighter transparent square. The regions where the back and front surfaces cross create X-junctions (one of the two X-junctions is indicated in red in Figure 2a). The luminance relations between the four parts making up the X-junction are closely linked to the perception of transparency and the corresponding depth order (eg, Metelli 1974; Beck et al 1984; Brill 1984; Adelson and Anandan 1990; Gerbino et al 1990; Kersten 1991; Nakayama et al 1990; Plummer and Ramachandran 1993; Anderson 1997; Masin 2006; Singh and Anderson 2002; Koenderink et al 2008; Delogu et al 2010; Koenderink et al 2010). In Figure 2a there is no ambiguity in regard to the depth order of the two squares—ie, the lighter square appears in front of the darker square. In contrast, Figure 2b shows an example where again transparency is perceived, though with an ambiguous depth order: Either of the two light gray squares may be perceived in front of the other. In Figure 2c no transparency is perceived. Instead, the shapes are seen as a light opaque square in front of two dark squares or two L-shapes on a uniform background. (Note that in all three examples talented observers may also perceive one of the surfaces covering the entire image with a hole through which the other is partially seen.)

Figure 2.

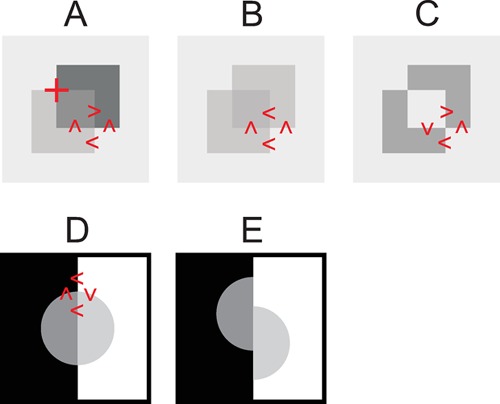
(a) Single-reversing junction where the lower square is normally seen as transparent and in front of the darker square on the farther surface. The red cross indicates an X-junction. (b) Non-reversing junction where either square may be seen as transparent and in front of the other. (c) Double-reversing junction where no transparency is seen. (d) The disc with X-junctions appears transparent. (e) Shifting the halves of the disc removes the X-junctions and eliminates the perception of transparency. Inequality signs in panels (a) through (d) indicate the luminance relations between adjacent surfaces, oriented in accordance with the corresponding boundary.

Each of the three categories—transparent-unambiguous, transparent-ambiguous, and opaque —has characteristic luminance relations across the two edges making up the X-junctions. These ordinal luminance relations are labeled single-, non-, or double-reversing (Adelson and Anandan 1990; see also Beck and Ivry 1988) and completely characterize the perceived transparency. Take, for example, the vertical edge of the X-junction in Figure 2a (marked with the red cross). In the upper as well as in the lower half the part to the left of the vertical edge has higher luminance than the corresponding part to the right. In contrast, along the horizontal edge the top half on the left has higher luminance than the half below, while the top half on the right has lower luminance than below. Hence, the direction of the luminance difference across the border is preserved when comparing the left with the right half but not when comparing the upper with the lower half. Such a junction is called a single-reversing junction (Adelson and Anandan 1990). Correspondingly, an X-junction where the direction of the luminance difference does not change along either edge is called a non-reversing junction (Figure 2b); and an X-junction where it changes at both edges, a double-reversing junction (Figure 2c)—the former yielding ambiguous transparency in regard to the depth order and the latter not yielding transparency perception.

In addition to these qualitative properties, the magnitude of the luminance differences also plays an important role in the perception of transparency (Metelli 1970; 1974). In particular, an intervening transparent layer reduces (or at least does not increase) the luminance differences between the surfaces behind it. This can be seen in Figure 2d where the luminance difference between the black-and-white background is much larger than the luminance difference between the same two background regions appearing behind the gray disc. In particular, the magnitude of luminance differences along a contour can reduce or resolve ambiguity by assigning transparency to the region with the lowest luminance differences (Anderson 1997; 2003). Magnitude constraints are especially efficient in resolving ambiguity when the transparent region is almost opaque, strongly reducing the visible luminance difference compared with the difference between surfaces that are seen directly. Nevertheless, across a broad range of luminance differences, the three qualitative ordinal relationships (non-reversing, single-reversing, and double reversing junctions) are very good predictors for the perception of transparency and the depth order of the corresponding surfaces. Because these three types of ordinal relations are very robust, we were able to classify X-junctions in paintings without access to the original artwork. The effects of displays (photographs of originals, viewed on uncalibrated computer monitors) and measurement scales will shift the relative values but not their ordinal relations (see section 4 below).

The importance of X-junctions for transparency is well established, as can be seen, for example, in Figures 2d and 2e, where removing the X-junctions by shifting the two halves of the circular layer eliminates the transparency percept. (However, explicit X-junctions are not always necessary for the perception of transparency—eg, see Watanabe and Cavanagh 1993). While the role of luminance properties of surfaces making up X-junctions has been extensively studied, there have been few studies of other properties of transparent materials such as refractive index (where errors are not readily apparent, Figure 1). The color constraints for transparency have been examined (eg, D'zmura et al 1997; Faul and Ekroll 2002; see also, Fulvio et al 2006), as have those for superimposed textures (Watanabe and Cavanagh 1996). Beyond this there has been very little work. Artists, on the other hand, have been busy working on transparency for more than 3,500 years. What have they discovered?

3. Transparency in art

Transparency was already depicted in paintings in Ancient Egypt around 1600 BC. The motivation then was probably to capture the precious sheer materials, silk and cotton, worn by the pharaohs and members of their court. Over the centuries, a vast number of paintings have portrayed transparent materials, and these works of art reveal the many principles required for the perception of transparency and those that are not. For example, following Metelli's luminance constraints (1970; 1974; see, also, Beck and Ivry 1988; Adelson and Anandan 1990) is typically sufficient to elicit the perception of transparency. In addition, artists have used two high-level principles to trigger or modulate the perception of transparency: first, material constraints, and second, object constraints. We investigate how these two principles, along with luminance constraints, have been used by artists throughout the centuries and how they effect the perception of transparency.

4. Luminance constraints

We have seen that the luminance relations at X-junctions are predictive of the perception of transparency and the depth order of the corresponding surfaces. Do artists follow these constraints when depicting transparency? Or can they violate the constraints and still evoke the perception of transparency?

We used Photoshop™ to estimate relative order of luminance across the borders of X-junctions in digital versions of artworks from across 3,500 years. There are, of course, many factors that affect the luminance that we measured, including fading of pigments, inaccuracies of photography in the conversion to a digital version, and the use of the often suspect “Value” scaling of Photoshop™. Nevertheless, even this long chain of distortions should preserve ordinal relations, and that is all that we need to classify the luminance relations. Unequal fading of pigments of different colors can affect the ordinal relations, and we tried to avoid artworks where this might be possible. Our analysis of the ordinal relations at X-junctions shows many examples of appropriate luminance relations with very few violations. The deviations lie at the margins of the categories of Figure 2 between the two appropriate cases—no-reversal and single-reversal—and the violation case with a double-reversal. Interestingly, we found no instances of the unambiguous single-reversal case of transparency—perhaps artists did not feel it was necessary, even though it often occurs in nature.

Take, for example, the Ancient Egyptian depiction of a number of dancers and musicians (Figure 3). The second character from the right wears a transparent dress. We can make out X-junctions, for example, between the outlines of the legs, the dress, and the background (see the highlighted circle in Figure 3). Unlike the examples in Figure 2, these X-junctions are not entirely due to luminance differences of the four corresponding quadrants, but on one side established by depicting a contour (the outline of the dress). Measuring the luminance of the four quadrants verified that the luminance of the background and that of those parts of the background that are covered by the dress do not differ, and therefore these X-junctions do not fall readily in any of the three luminance-relation categories, as they all require inequalities. However, if we take a contour as marking little or no difference, then at least the luminance direction does not reverse making this X-junction non-reversing so that it supports transparency with an ambiguous depth order. Looking at the local detail in Figure 3 confirms this classification on a perceptual level: the perceived depth order of the corresponding surfaces is ambiguous. However, the luminance difference between the two regions covered by the dress is markedly smaller than that of the parts in direct view, yielding a magnitude cue for perceiving transparency and thereby reducing ambiguity. Later, we will see that artists do not need to avoid the ambiguous transparency case (non-reversing junction), as the nature of the objects in the scene biases the perception of transparency—observers are much more likely to see a transparent material than a transparent body even though either case is consistent with the luminance relations.

Figure 3.

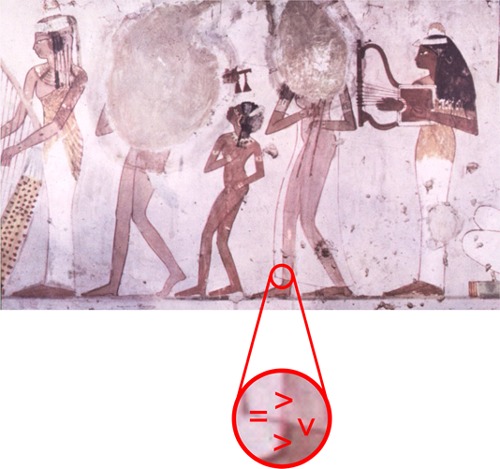
Ancient Egyptian art. Tomb of Jesekaresneb, 18th Dynasty (c. 1550–1292 BC). Logical operators indicate the luminance relations between adjacent surfaces (inequality signs are oriented in accordance with the corresponding boundary).

This early depiction of transparency already mimicked physically correct transparency to a reasonable extent. Did painters in later periods render transparency more appropriately? Indeed, the highly detailed paintings of the Flemish painters of the Early Renaissance (eg, Jan Van Eyck and Rogier van der Weyden) also displayed more realistic renderings of transparency. On the other hand, if some physical violations of transparency are not picked up by the visual system, artists may not have needed to depict transparency so accurately.

In Figure 4, for example, we see a transparent veil covering parts of the body and face of a woman (Portrait of a Lady by Rogier van der Weyden, 1460). We do not see a transparent person in front of a veil background even though it is optically allowed. Specifically, the luminance directions have no reversals and so do not specify which surface is in front.

Figure 4.

Portrait of a Lady (c. 1460) by Rogier van der Weyden. Inequality signs indicate the luminance relations between adjacent surfaces (oriented in accordance with the corresponding boundary).

Moreover, the luminance difference between parts covered by the veil and the difference between the directly seen surfaces is small, hardly helping to reduce ambiguity. This local ambiguity is not reflected on a perceptual level, where it is clear that the veil is in front of the other surfaces.

These two examples do not perfectly reproduce what would be expected when following physical luminance constraints for the depiction of transparency with an unambiguous depth order. While there are other cues for transparency in these artworks (as discussed in section 6), it might be expected that more abstract paintings with little realistic content would have to rely on more accurately rendered luminance constraints when producing perceptual transparency, and artists might in this case chose to depict unequivocal depth order (single-reversal case). In Wassily Kandinsky's Figure 5 in “On White II” (1923), for example, some of the shapes clearly appear transparent, most prominently at the yellow-brownish trapezoid just below the center of the painting. While the preferred depth order of the trapezoid and the large green shape may vary among observers, most observers can see either one in front or behind. As might be expected, ordinal luminance estimates at X-junctions revealed that the local information does not favor a particular depth order; the junctions have no reversals. However, the magnitude constraint favors seeing the green shape as transparent and lying in front of the trapezoid (the smallest luminance difference is found between the green and brown surfaces, ie, between the upper and left quadrant in the highlighted circle). In abstract artworks, there are no cues from familiar objects or layout to resolve ambiguous transparency and so ambiguous depth orders are more frequent here than in more figurative works.

Figure 5.

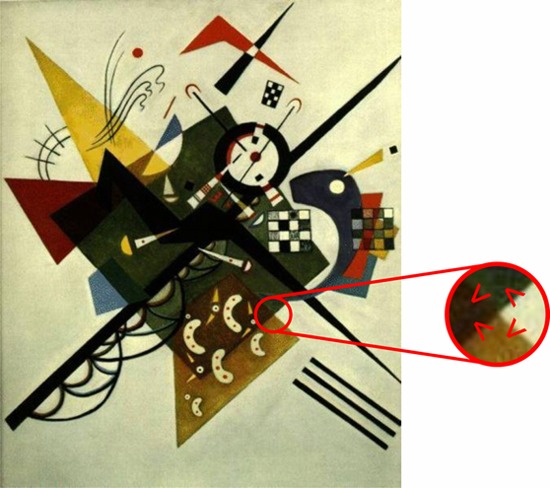
Some of the depicted forms appear transparent. Wassily Kandinsky's On White II (1923). Inequality signs indicate the luminance relations between adjacent surfaces (oriented in accordance with the corresponding boundary).

The example from Egyptian art (Figure 3) with equal luminance on both sides of an X-junction edge shows that the luminance relations do not have to be exactly met to support transparency. However, this does not mean that artists are free from all constraints. When neither local (eg, luminance constraints) nor global (see section 6, object constraints) principles are followed, transparency is less successful. Figure 6 shows an example in which the depiction of transparency failed. (As one can only speculate about the actual intentions of an artist, “failed” transparency only refers to the perception of a particular surface and not to what the artist actually wanted to display.) In Figure 6, although we can easily make out parts of objects that are seen directly and those that should be seen through a transparent surface (water), no transparent medium is perceived. Transparency failed because neither adequate X-junctions nor appropriate luminance and color values are depicted. Mere knowledge that water should be transparent is not sufficient to trigger the corresponding percept.

Figure 6.

An example of failed transparency, Mosaic of Nereis Riding Hippokampus, Imperial Roman period.

All in all, in most of the paintings we measured, the luminance distribution at X-junctions did satisfy the luminance constraints for perceived transparency. However, the local information alone was not sufficient to determine which of the surfaces was in front of the other. As the perception of the depth order is mostly unambiguous, especially in realistic paintings, it is clear that other cues must be used by the visual system to clarify the depth order.

This can be observed in Figure 7 (Greek red-figure pottery, c. 530–560), where transparency is perceived even though the luminance constraints do not apply. The artist successfully rendered transparency using only two distinct luminance values, with the body contours appearing visible through a transparent dress. Note that locally only the X-junctions are informative about the presence of more than one surface (the body and the transparent dress). However, X-junctions consisting of contours alone are not sufficient for triggering any kind of transparency, and this can be easily verified by isolating only a small region around one of the X-junctions in Figure 7. Global features, as will be described in section 6, are essential for the perception of transparency under such highly impoverished conditions, in particular, because any cues from material properties, as those discussed in the next section, are absent in these line drawings.

Figure 7.

Transparency perception achieved without following luminance constraints. Greek red-figure pottery (c. 530–560).

5. Material constraints

Certain materials are more likely to be transparent than others. For example, most rocks are opaque (except some crystals), but water is often transparent. Observers could use such regularities to support perceptual decisions. However, transparency is not a unique feature of any material. In other words, the recognition of a material is not sufficient for making inferences about the presence or absence of transparency. Moreover, transparency may be an important feature for recognizing a certain material in the first place, for example, when distinguishing glass from porcelain, and therefore the recognition of transparency would precede the recognition of the material in this case. Could it, nevertheless, be possible that the recognition of material properties other than transparency supports or counteracts the perception of transparency? Here, we distinguish two types of material properties related to physical transparency that may be depicted in works of art and potentially modulate the perception of transparency: reflectance properties and transmission properties.

5.1. Reflectance properties

Transparent materials often have characteristic surface reflectance properties like highlights (eg, Blake and Bülthoff 1990), pearlescence, and glossiness (eg, Beck and Prazdny 1981; Fleming et al 2003). Also transparent textiles, such as sheer curtains and lace materials, have characteristic reflectance properties (anti-Lambertian reflectance function, see below). These properties are shared with opaque materials but are more noticeable in transparent materials as they are the major source, and sometimes the only source, of light from the material. In other words, the perception of these properties may be a cue for transparent materials; however, since these properties occur in both transparent and opaque materials, they cannot be sufficient to depict transparency in paintings. Nevertheless, the depiction of these properties often supports the perception of transparency. Here, we discuss some of these properties in more detail.

In paintings, artists often depict at least some reflectance properties of the transparent surface (eg, highlights) if they want to depict a highly transparent material and make it visible to the viewer. In Edward Hopper's Nighthawk (1942), for example, it is impossible to see whether the front window contains glass or not (Figure 8). Only the relative opacity of the glass as it curves around the corner on the left physically reveals its presence (of course, the restaurant probably protects its customers from the New York weather so some glass is expected). If Hopper had painted highlights on the window, this would have changed its appearance, leaving no doubt about the presence of glass in the window frame. This effect of highlights can be observed in Figure 9, where the highlights are the main indicator of the transparent material (Fresco, Pompeii). As in Hopper's painting, without these highlights, not much of the material would be visible because of its high level of transparency.

Figure 8.

It is perceptually unclear whether the front window contains glass or not. Nighthawk (1942) by Edward Hopper.

Figure 9.

Highlights are the main indicator for the presence of a transparent material covering the fruit. Roman Fresco, Pompeii.

Along with a number of other features, such as shadows (Casati 2004; Cavanagh 2005) or mirror reflections (Croucher et al 2002), highlights do not have to be accurately depicted to be seen as such (but see Blake and Bülthoff 1990). The white areas indicating reflections on the sphere in Figure 10 are not drawn correctly (eg, they are surrounded by lines), but they still increase the perception of transparency rather than harm it. However, the main indicator of the presence of a transparent sphere is the visibility of its edges.

Figure 10.

The visibility of the edge is the main indicator for the presence of a transparent sphere. Although physically incorrect, the reflections still support the perception of transparency. From The Gardens of Aedena (1988) by Moebius.

One particular surface reflectance property of transparent materials, an “anti-Lambertian reflectance function” is more diagnostic than the others. Transparent materials have a greater interaction with light when it strikes them at higher grazing angles as compared with straight on (the reverse of Lambertian reflectance) because the light passes through and is absorbed or reflected by much more material at these grazing angles. A sheer curtain may be almost invisible seen straight on, as the material blocks little light and its surface weave does not reflect much either. However, when the curtain is angled more steeply relative to the line of sight, it blocks more light from behind and it also reflects more light from the front. This gives the characteristic visibility of the sheer curtain in its folds more than in its flat sections. Figure 11 shows two paintings illustrating this property. Unlike the other material properties, this one property alone may trigger the percept of transparency. In Figure 11a the transparent robe completely covers the undergarment visible through it so there are no uncovered regions to compare with covered ones, and therefore Metelli's luminance constraints cannot apply. However, where the robe is folded, the extra material along the line of sight makes it relatively opaque, creating contours that make X-junctions with the contours of the undergarment, providing evidence for transparency. Admittedly, it is not only the visible folds that determine the transparency percept, but a second principle, object constraints—bodies are normally opaque—contributes as well (see, also, Figure 7 and section 6). Another example is seen in Figure 11b, where the woman holds an apparently transparent material with her left hand. We see the material because of the visibility of its folds, and it appears transparent because the surface seen within the region covered by the material is similar to that around it, suggesting that we see the background through the material even though, in this case, there are no X-junctions, as the background has no sharp contours.

Figure 11.

Characteristic reflection patterns are often found in sheer materials, such as sheer curtains, where folds modulate how much light passes through or is reflected from the material. (a) An underskirt can be seen through the sheer red robe. Hua Qing in Her Bath by Kang Tao (1723–1795). (b) The material the woman holds in her hand appears transparent, although there are no X-junctions. Fresco, Pompeii.

5.2. Transmission properties

Transparent materials have characteristic transmission properties that act on the light arriving from behind the object including diffusion (translucency, eg, Fleming and Bülthoff 2005; Motoyoshi 2010) and refraction. In contrast to the material properties discussed above, these properties have no equivalent in opaque materials. Light traveling through the transparent material undergoes diffusion (point spread function) and refraction (Figure 1). As diffusion and refraction are indicative of many transparent materials, it seems reasonable that artists would make use of these features and paint them when depicting transparency. However, diffusion and refraction are often depicted incorrectly or not at all, even when the physical scene demands them. For example, while the scepter in Figure 12 clearly appears transparent, its refraction is not accurate. As can be seen when looking through the scepter, the visible contours of, for example, the hand do not show any sign of discontinuities. Even when put under scrutiny, this violation of physics does not reduce the perception of transparency. There are countless other examples of paintings in which refraction, especially by water, is not depicted, and these violations are usually not noticed. This insensitivity of observers to violations of refraction in paintings might be one of the reasons why artists do not take great care of rendering refraction that accurately.

Figure 12.

Left panel: Central figure of Ghent Altar (1425) by Jan van Eyck. Right panel: Detail of the transparent scepter.

Although properties of reflectance and transmission contribute to transparency, they are not required (eg, Figures 2, 3, and 7). However, when they are used, reflectance properties are more accurately rendered (eg, Figures 9 and 11) than transmission properties (refraction and diffusion, for example, (Figure 1). This suggests that the visual system is not very sensitive to violations of physical laws when depicting these transmission properties.

6. Object constraints

Luminance constraints and material properties are only two of the principles governing the perception of transparency. We suggest that object-based principles, originating from general knowledge about the properties of the world (“objects of this kind often look like this”) play a significant role for the perception of transparency. Importantly, transparency perception resulting from inferences based on world knowledge does not occur very often without any other principles being at least partly satisfied (but see Figure 7). An example illustrating this principle is shown in Figure 13 (Portrait of an Artist, (Pool with Two Figures) by David Hockney). The diver appears completely covered by water, that is, no parts belonging to the same object are seen directly as well as through the transparent material. Hence, there are no corresponding X-junctions (the light caustics cross the body but do not carry transparency information). However, as “divers usually look like this when under water”, it seems a good inference to make despite the lack of X-junctions and the unrealistic depiction of properties of the water.

Figure 13.

Object-based inference: It looks like a person diving in a swimming pool. He must be seen through transparent water. Portrait of an Artist (Pool with Two Figures) (1972) by David Hockney.

Object-based inferences are a very strong principle for the perception of transparency; however, they are largely neglected in the scientific investigation of transparency. Artists, to the contrary, rely strongly on object-based inferences for depicting transparency in paintings, especially when other principles are not sufficient to trigger a transparency percept. In most of the examples here object-based inferences apply and support the perception of transparency. Usually, objects are perceived in front of or behind other objects and not just in front or behind decontextualized patches of differing luminance. Moreover, object-based inferences also yield very strong cues for the depth order of the comprised objects and surfaces.

In the Ancient Egyptian painting in Figure 3, for example, local information alone does not yield an unambiguous transparency percept. Recognizing the involved parts as belonging to the dress, the person, and the background, however, resolves the ambiguous transparency percept in favor of an unambiguous depth order: Contours surrounding a human body in the depicted fashion are usually not accidental contours of the environment but rather belong to clothes covering the body. As luminance constraints are only partly satisfied and material properties are not apparent, object-based inferences must play a major role in the perception of transparency in this painting. Object-based inferences play an even more important role in the Roman Fresco depicted in Figure 14. The bowl is perceived as transparent, and some of the fruit are seen through the bowl, although neither luminance constraints nor material properties (essentially some highlights) contribute significantly to the effect. The blurred edges of the fruit seen through the glass give an additional cue for transparency. However, this cue is not sufficient, as can be observed by covering the pieces of fruit that are seen directly on top of the bowl. This strongly reduces or even abolishes the transparency percept and lets the fruit seem like a property of the bowl painted on its surface. These examples of Ancient Egyptian and Roman art show that transparency can be depicted by including only some of the essential principles, one of them being object-based inferences.

Figure 14.

Object-based inferences are key for perceiving the bowl as transparent. Fresco in the Villa di Poppea in Oplontis (c. 70 AD).

But even when only the principle of object-based inference is satisfied, and the other principles do not apply, transparency may be perceived. In Figure 7 (Greek red-figure pottery), for example, neither the luminance principle applies nor are any material properties depicted. Nevertheless, contours of a body are clearly seen through a transparent dress. The object-based inference that bodies behind clothes “often look like this” dominates possible alternative ways of seeing the figure. Hence, the perception of transparency may still be achieved without the aforementioned principles as long as other cues, here the contours of the dress and the body, help to segment the scene into different parts and give rise to object-based inferences. However, object knowledge can be overruled by other transparency cues when they strongly indicate conditions that contradict the effective object-based inference. In Figure 15, for example, the man is perceived as transparent contradicting knowledge of the opacity of human bodies (Teatro alla Scala by Liu Bolin). Color and texture cues as well as another object-based inference—namely that the red object seen at the position of the man among all the regularly arranged red seats must also be a seat—yield the perception of a background surface seen through a transparent body.

Figure 15.

Object knowledge can be overruled by other cues. Here, color, texture, and the object-based inference that the red object at the position of the man must be a seat like all the others overrules knowledge of the opaqueness of human bodies. Teatro alla Scala (2010) by Liu Bolin.

Most of the paintings discussed here have in common that object-based inferences support the perception of transparency. But what counts as an object? Is a certain level of realism necessary? A closer look at abstract art gives an opportunity to address this question. In the painting “On White II” (Figure 5), Wassily Kandinsky conveyed depth relations, figure boundaries, surface properties, occlusions, and transparency, all the while evoking uncertainty about which parts of the depicted shapes belonged together. This piece suggests that object-based inferences can also work on a very low level of abstract shapes where jumbled contours and forms are organized into, more or less stable, meaningful wholes.

7. Conclusion

Luminance, material properties, and object properties are all essential aspects of our visual world that have fascinated artists and scientists for many centuries and motivated countless studies on canvas as well as in the laboratory. Here, we investigated how artists used these properties to portray transparency in paintings. In addition to the classic luminance constraints at X-junctions outlined by Metelli, we found that artists make wide use of two other principles—material properties and object-based inferences—that elicit and modulate transparency perception and that have not as yet been a frequent subject of scientific studies. Table 1 shows an overview of the principles and cues that govern the perception of transparency in paintings and the real world, and the perceptual effects of the different cues.

Table 1.

Perceptual effects of transparency cues.

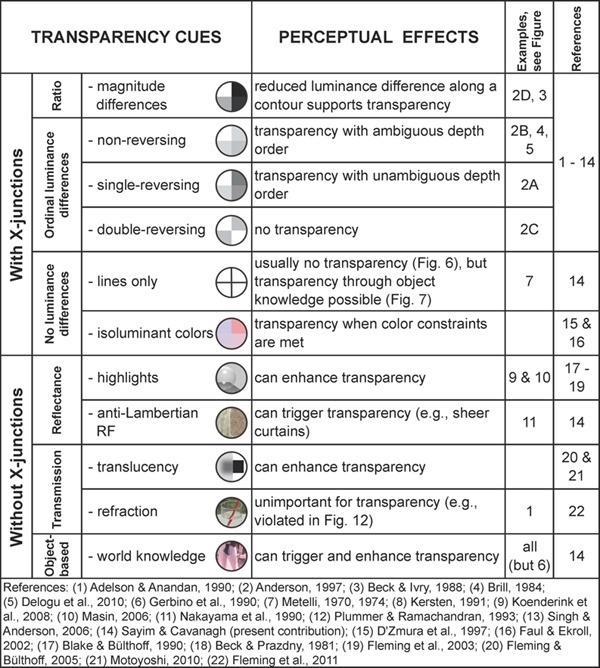
All of these effects have been included in paintings long before they were studied by vision scientists. They are in an important sense discoveries of artists as they explore the ability of pigments to mimic material properties like transparency. The possible exception that have emerged first in the laboratory are the single reversing X-junctions, surprisingly absent from paintings, though often present in natural transparency, and the transparency effects of equiluminous X-junctions, which being physically highly improbable, are virtually never present in natural scenes. Moreover, we saw from artists— work that many transparency cues can be violated as long as a few are present. This gives us a rich source of data to explore the transparency algorithms that must be in place in the visual system.

Biography

Bilge Sayim received a Diploma in Psychology from the Christian-Albrechts-Universität zu Kiel (Germany) in 2005. In 2010, he earned a PhD in Neuroscience at the Ecole Polytechnique Fédérale de Lausanne (EPFL) in Switzerland. Currently, he is a Postdoc at the Centre Attention & Vision in Paris.

Patrick Cavanagh received a Bachelor of Engineering from McGill University in 1968. An interest in artificial intelligence led to a PhD in cognitive psychology from Carnegie-Mellon in 1972. He taught at the Université de Montréal in Psychology until 1989 and at the Department of Psychology at Harvard until 2007. He recently joined the faculty at the Université Paris Descartes.