Abstract
Identifying Ca2+-binding sites in proteins is the first step towards understanding the molecular basis of diseases related to Ca2+-binding proteins. Currently, these sites are identified in structures either through X-ray crystallography or NMR analysis. However, Ca2+-binding sites are not always visible in X-ray structures due to flexibility in the binding region or low occupancy in a Ca2+-binding site. Similarly, both Ca2+ and its ligand oxygens are not directly observed in NMR structures. To improve our ability to predict Ca2+-binding sites in both X-ray and NMR structures, we report a new graph theory algorithm (MUGC) to predict Ca2+-binding sites. Using carbon atoms covalently bonded to the chelating oxygen atoms, and without explicit reference to side-chain oxygen ligand coordinates, MUGC is able to achieve 94% sensitivity with 76% selectivity on a dataset of X-ray structures comprised of 43 Ca2+-binding proteins. Additionally, prediction of Ca2+-binding sites in NMR structures were obtained by MUGC using a different set of parameters determined by analysis of both Ca2+-constrained and unconstrained Ca2+-loaded structures derived from NMR data. MUGC identified 20 out of 21 Ca2+-binding sites in NMR structures inferred without the use of Ca2+ constraints. MUGC predictions are also highly-selective for Ca2+-binding sites as analyses of binding sites for Mg2+, Zn2+, and Pb2+ were not identified as Ca2+-binding sites. These results indicate that the geometric arrangement of the second-shell carbon cluster is sufficient for both accurate identification of Ca2+-binding sites in NMR and X-ray structures, and for selective differentiation between Ca2+ and other relevant divalent cations.
Keywords: Ca2+-binding proteins, graph theory, carbon clusters, side-chain center of mass, NMR
Introduction
Ca2+, a secondary messenger in cellular signal transduction, plays an important role in many biological processes, including the regulation of cell division, differentiation, and apoptosis in the cell life cycle 1–4. Ca2+-binding proteins are significantly related to serious diseases such as Alzheimer’s disease 5,6, heart disease 6, diabetes 6, leukemia 7,8, and cancers 9–12. From a molecular perspective, mutations in close proximity to the Ca2+-binding sites often alter a protein’s ability to bind Ca2+, a malfunction which is sometimes the primary cause of diseases 13–15. Therefore, identifying Ca2+-binding sites in proteins is a crucial step towards understanding the molecular basis of diseases related to Ca2+-binding proteins.
As illustrated in Fig. 1A, the coordination of Ca2+ utilizes various classes of oxygen atoms from carboxyl groups (Asp, Glu), carboxamide groups (Asn, Gln), and hydroxyl groups (Ser, Thr) in side chains, carbonyl oxygen atoms of most residues in the main chain, and from cofactors and water molecules. The majority of all Ca2+-binding ligands originate from turn/loop regions 16–19. Previous studies have revealed that Ca2+ is coordinated by 3–8 oxygen ligand atoms 18,20–22 with an average of 6 ligands for all Ca2+-binding sites, or 7 ligands for only EF-hand sites 17. These hydrophilic oxygen atoms are embedded within multiple, concentric shells of hydrophobic carbon atoms 23. Statistical analysis from us and others revealed that a majority of Ca–O bond lengths fall within the range 2.2–2.9Å and Ca-C bond lengths fall within the range 2.4–4.6Å in Ca2+-loaded X-ray structures 18,20–22,24.
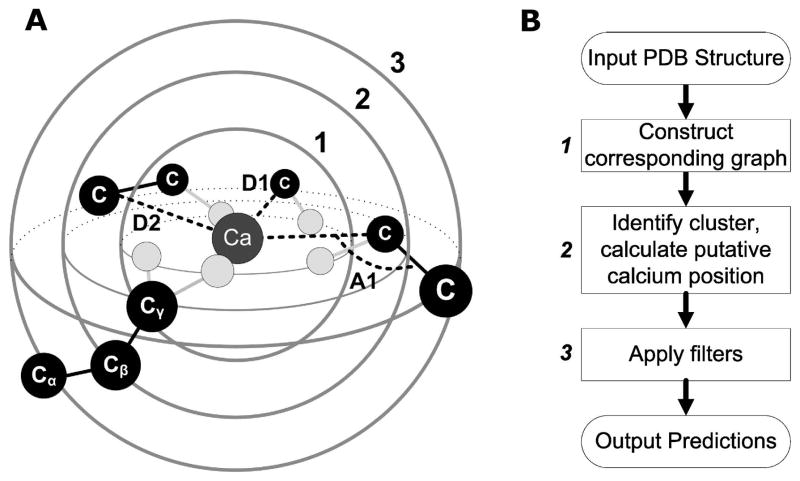
Figure 1. Definition of shells and algorithm workflow.
(A) The central Ca2+ is coordinated by the first shell of oxygen atoms (light gray), which is concentrically embedded into two other shells of carbon atoms (black). Depending on the length of the alkyl side chain, an atom of the second or third shell has a covalent bond with an atom from the first or second shell. D1 represents the distance between Ca2+ and second shell carbon atoms. D2 is the distance between Ca2+ and third shell carbon atoms. A1 stands for the angle formed by Ca2+ and the second and third shell carbon atoms, respectively (Ca-C1-C2). (B) Workflow of MUGC.
Computational methods to predict Ca2+-binding sites have been actively pursued using various approaches 4,25–28. Most of the published structure-based Ca2+-binding site prediction algorithms, including FEATURE 29, Fold-X 30, and the approaches by Nayal et al. 20 and Yamashita et al. 23, rely on the spatial coordinates of ligand oxygen atoms. Our previous work has led to the development of two algorithms, GG31 and MUG 32 for predicting Ca2+-binding sites by constructing a corresponding graph for each protein with a graph theoretic algorithm to identify oxygen atom clusters 31,32. These analyses of binding site geometry have been based mainly on X-ray structures deposited in the Protein Data Bank (PDB), and the prediction approaches derived from them have been tested mostly on X-ray structures with high resolutions. Unfortunately, Ca2+-binding sites with weak affinity (0.05–2mM) often remain unidentifiable or “invisible” in crystal X-ray structures due to low occupancy and conformational ensembles. For example, although extracellular Ca2+ is known to regulate family C of GPCR, Ca2+ was not observed in more than 20 X-ray structures of metabotropic glutamate receptor (mGluR) 33,34. In addition, local or global conformational change almost always occurs upon calcium binding due to alteration of electrostatic interactions. Further prediction of Ca2+ binding sites in X-ray structures of low resolution and homology models requires the capability to overcome large errors and incorrect assignments of the side-chain oxygen atoms 35,36.
As a complementary technique of structural elucidation, NMR offers us additional insights into Ca2+-binding proteins without the requisite of crystallization 37,38. NMR structures differ from X-ray structures in that, typically, a whole ensemble of low energy conformations satisfying the experimental constraints is obtained from the structural calculations. These structures represent the dynamic nature of the protein in solution. However, the Ca2+ ions cannot be directly observed in NMR experiments, but rather are positioned in the structure based on indirect effects exhibited by chemical shifts and constraint-based assumptions. A barrier to identifying Ca2+-binding sites in protein structures derived by NMR is that the geometric coordination of Ca2+-binding sites cannot be determined by direct observation of Ca2+, and this difficulty is compounded by the fact that the positions of the oxygen atom ligands that chelate the Ca2+ are not directly determined either, but extrapolated from templates of their residues, because the isotopically-abundant 16O has an intrinsic zero nuclear spin.
In this paper, we report our progress in predicting Ca2+-binding sites in proteins where the Ca2+ ion may not be directly observable (e.g., low resolution structures, weak affinity binding sites, and NMR structures). We hypothesized that the second, hydrophobic shell of carbon atoms enclosing a Ca2+-binding site could sufficiently determine the site’s location in either X-ray or NMR structures. To test this, we developed a new algorithm, MUGC, which is capable of predicting Ca2+-binding sites by pinpointing the Ca2+ ion position using carbon clusters (i.e., concentric rings of carbon atoms surrounding a ring of oxygen atoms chelating the Ca2+, Fig. 1A), and applying filters based on the centers of mass of side-chain and main-chain oxygen atoms. We have applied MUGC to delineate Ca2+-binding sites in both X-ray and NMR protein structures without reference to explicit side-chain oxygen ligand atoms. The metal selectivity of MUGC has been further evaluated by analyzing three additional protein datasets containing Mg2+, Zn2+, and Pb2+ binding sites. Additionally, MUGC was evaluated with a negative control dataset consisting of protein structures not known to bind Ca2+ or other metal ions.
Our results demonstrate not only that the Ca2+-binding sites in NMR and X-ray structures can be identified based on geometric arrangement of the second-shell carbon cluster, but that this approach with Ca2+-optimized selection parameters, can also selectively differentiate between Ca2+ and other relevant divalent cations. We further anticipate that application of this algorithm will enable us to identify previously-unknown Ca2+-binding sites, deepen our understanding of structural characteristics of Ca2+-binding sites, and improve our ability to design Ca2+-binding proteins with diversified functions.
Materials and Methods
Definition of carbon shells
As seen in Fig. 1A, the Ca2+ ion is bound to oxygen atoms either from side-chain residues (e.g., Glu or Asp) or main-chain carbonyl oxygen, largely via electrostatic interactions. These atoms, in turn, are covalently bound to carbon atoms, which constitute a second shell. A third shell of carbon atoms can be defined as carbon atoms covalently bound to a second shell. The two concentric shells of carbon atoms, in our hypothesis, constitute a scaffold which determines the central binding site. A set of physical parameters describing the spatial relationship of the atoms comprising the binding site can be defined by the angle Ca–C1–C2 and the distance between Ca2+ and C1 (D1 in Fig. 1A) and by the distance between Ca2+ and C2 (D2 in Fig. 1A), where C1 and C2 are carbon atoms within the second and third shells, respectively. The binding site, which includes both the Ca2+ and oxygen atoms, is enclosed in a second shell defined by a particular carbon cluster. The Ca2+ position then can be calculated by geometric parameters related to the second and third shell carbon atoms.
General description of algorithm
In general, execution of this algorithm involves three major steps (Fig. 1B). In step 1, taking a PDB structure as input, we construct the protein topological graph whose vertices are the carbon atoms with associated oxygen atoms. Two vertices share an edge if the distance between them is less than some defined threshold. In step 2, we search for all maximum cliques in the graph to identify carbon clusters, and tentatively position Ca2+ at the geometric center (Ca2+ center) of each cluster. These clusters are required to have at least four carbon atoms, ensuring a minimum of four oxygen atoms in the site available to chelate Ca2+ 18,39. In step 3, we apply three different filters to remove clusters that are not suitable for Ca2+-binding. The remaining clusters, as well as the Ca2+ center of each cluster, are the predicted Ca2+-binding sites. When using dynamic NMR structures for prediction, MUGC screens the best-fit site among all members of the ensembles and uses more inclusive geometric parameters than when using X-ray structures.
The topological graph of protein carbon atoms
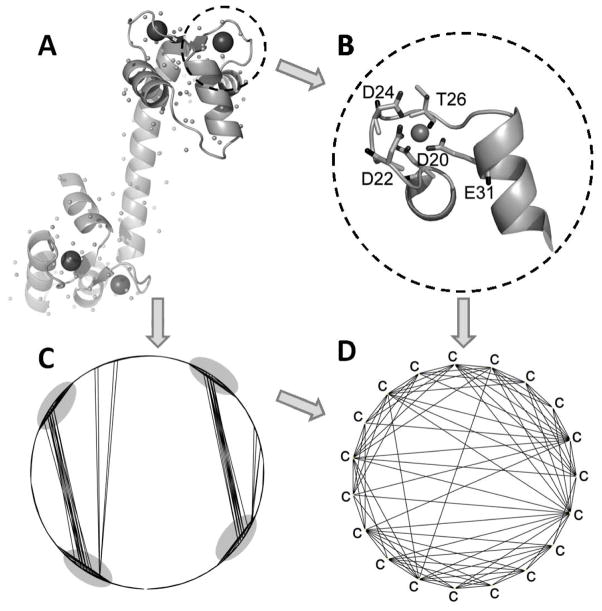
To localize the initial calculation of the Ca2+ position, we construct a graph representation of the protein. First, we extract all Cartesian coordinates of carbon atoms covalently bonded to oxygen atom(s) and calculate the distances between all of these carbon atoms. Then we construct a graph G(V, E) where V is the vertex set and E is the edge set of G. A vertex in V represents one extracted carbon atom. An edge is assigned between two vertices if the distance between these two vertices (C-C distance) is smaller than a predetermined cutoff (7.5 Å for X-ray structures and 8.3 Å for NMR structures). The constructed graph is then recorded in an adjacent matrix (Table S1). For example, calmodulin has four binding sites (Fig. 2A and Fig. 2B). It also has a total of 209 carbon atoms covalently bonded to oxygen atoms. After we construct its topological graph (Fig. 2C and Fig. 2D), the four binding sites are clearly discernible as regions of dense convergence in the graph.
Figure 2. The structure of calmodulin (CaM) and topological graph of carbon atoms.
(A) CaM with center of mass of side chain (the small dots). (B) Ca2+ binding site EF-I of CaM. (C) Topological graph of all carbon atoms in CaM associated with potential oxygen ligands (includes both side-chain and main-chain carbon atoms in putative binding residue). (D) The graph of CaM site EF-I loop.
Center of mass
Proteins in solution, especially their flexible side chains, are in constant motion. To deal with this motion, we use the abstracted side-chain mass center (Fig. 2A) as the reference for predicting Ca2+ position. Side-chain center of mass is beneficial because it reduces sensitivity to errors in the specific locations of side-chain atoms. The mass center of each side chain is calculated using the simple formula, where the ri is the position of each atom and mi is the atom mass.
| (1) |
Ca2+ localization algorithm
After preparation of the topological graph and side-chain center of mass for a given protein, we first search all maximum cliques in a graph constructed from the carbon atoms. Finding all maximal cliques of a general graph is an NP-hard problem,40 requiring more than polynomial computation time to process. Fortunately, in the generated carbon atom graph, the size of any maximal clique never exceeds ten. This ceiling is not a theoretical one, but a pragmatic consequence of our considering only carbon atoms which are covalently bonded with oxygen atoms. These carbon atoms maintain some distance from each other due to the charge repulsion from the attached oxygen atoms. Based on these properties, we apply a well-established algorithm of Bron and Kerbosch 41 to produce all the maximal cliques efficiently. In our case, the maximal cliques are generated within O(n) time, where n is the number of vertices in graph G.
Constraints and filters
We tentatively place Ca2+ in the geometric center of the carbon clusters, and then determine if they qualify based on constraints from various filters including the center of mass of side-chain, elimination of redundant predictions, van der Waals clashes, formal charge and geometric constraints. Initial parameters were selected based on parameters used in previous studies and statistical analyses conducted in our laboratory18,31,39. These parameters, including cutoff distances, were then optimized based on values for selectivity and sensitivity from analysis of the training dataset. These optimized parameters (Table S2) were then applied to the test dataset. For example, the range of distance between Ca2+ and second shell carbon atom (D1 in Fig. 1A) is reported to be between 3.0 – 4.6Å for main-chain carbonyls18. The covalent bond length between second shell carbon atoms and its next-outer shell carbon is 1.54Å. Therefore, we can estimate that the distance between a Ca2+ and the third shell carbon atoms may not exceed 6.14Å and should also be greater than D1. If a predicted Ca2+ position falls outside of this range, this position is not likely a correct prediction.
Performance evaluation on binding sites and binding residues
A Predicted True Site (PTS) is a true Ca2+-binding site for which there is at least one Correct Hit (CH). Sensitivity (SEN) is applied to represent the percentage of PTS in all Documented Sites (DS). Selectivity (SEL) is applied to represent the percentage of Correct Hit (CH) in Total Predictions (TP). Sensitivity measures the proportion of actual binding sites which are correctly identified. Selectivity measures the proportion of predicted binding sites which are correct. Higher selectivity indicates fewer false positive predictions (= over-predicted sites). Higher sensitivity and selectivity are important for reducing the number of predictions and classification errors.
| (2) |
| (3) |
As MUGC predicts both Ca2+ position and binding residues, Correct Hit (CH) could be defined in two ways. In the first definition, a CH is a predicted position falling within a specific distance (here 3.5 Å 31,32,42,43) of the documented Ca2+ position. In the second definition, a CH is a predicted cluster of residues that contains at least two true Ca2+-binding residues 39. In NMR, where Ca2+ is not observable, we measure the prediction performance by comparing the predicted residues to the holo X-ray crystal structures.
Algorithm implementations
The implementation language is mainly Java. The original source codes are available upon request. Matlab, Mathematica and PyMOL were used for graphing and visualization. LPC/CSU online servers were used for identify binding ligand from holo structures 44.
Results
Non-redundant X-ray dataset
To validate our hypothesis, we used two X-ray datasets: a training dataset (Tables S3 and S5), a testing dataset (Tables S4 and S6), and a negative control dataset (Table S13). For the datasets we generated, “non-redundant” applies to sequence identity, and means that we used only sequences with 10% or less similarity. For the published dataset, we made sure that no identical proteins were included within a single dataset. This also applied to the NMR dataset.
The X-ray training dataset (Table S5) was originally from Schymkowitz et al. 30 The X-ray testing dataset (Table S6) was reproduced by incorporating the Ca2+-binding proteins from Pidcock and Moore’s datasets 17 and the validation structures for NMR testing dataset. We eliminated the redundant proteins in the datasets and revised the testing datasets to ensure that at least one binding site in each protein was coordinated by at least four binding ligand atoms. Binding sites with low coordination numbers (three or less) may, due to crystal packing or non-specific binding, imply reduced stability and lower binding affinity at best 39. The X-ray training dataset contained 18 proteins with 45 documented Ca2+. The testing dataset contained 43 proteins with 108 documented protein-coordinated Ca2+. The X-ray training and testing datasets contained continuous (e.g. lactalbumin: 1B9O.pdb and calcineurin: 1AUI.pdb), semi-continuous (e.g. lipase: 1OIL.pdb and proteinase K: 2PRK.pdb), and discontinuous binding sites (e.g. thermitase: 1THM.pdb and penicillin acylase: 1AI4.pdb). The negative control dataset contained 24 proteins selected at random with resolution ≤ 2.0 Å, less than 90% sequence homology, and no indication of metal binding sites in the selected structure or in related structures. All X-ray crystallography structures were obtained from the PDB.
Sensitivity depends on C-C cutoff
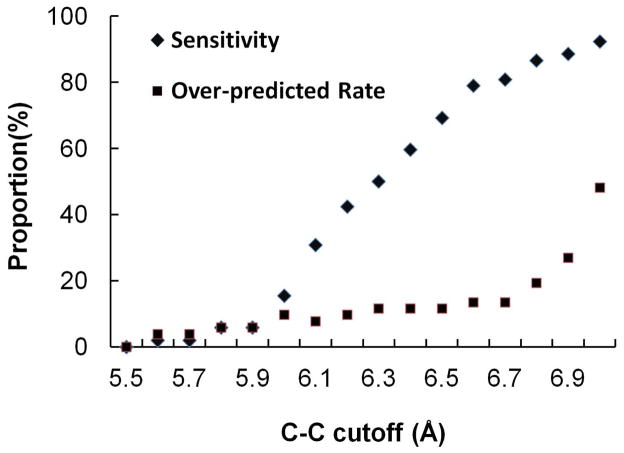
Sensitivity of MUGC was found to increase as the C-C cutoff increases on the X-ray training dataset as well as the over-predicted rate (Fig. 3). The over-prediction rate is calculated by dividing the number of false positive predictions by the total number of documented sites. This is consistent with previous finding that O-O cutoff is positively correlated with sensitivity and false positive predictions31,45. We have used the larger 7.5Å as cutoff, because this accommodates a distance twice the length of the combined Ca2+-O and C-O bond lengths and we have effective methods to eliminate false positives within this range.
Figure 3. Performance in terms of sensitivity on X-ray dataset depending on C-C cutoff.
Sensitivity of MUGC increases as the C-C cutoff increases on the X-ray training dataset as well as the over-predicted rate (the number of false positive predictions divided by the total number of documented sites).
Filters help to eliminate false positive predictions
One of the concerns arising from not directly utilizing coordination atoms to predict Ca2+-binding sites in proteins is the possibility of a large number of false positive predictions. To reduce the number of reported false positive predictions, three types of filters were incorporated into the algorithm: 1). A charge filter, which requires that at least one negatively-charged residue is present within the tentative binding site; 2). Geometric shell filters, which select the putative sites according to geometric relationships between the calculated Ca2+ position and the second and third shell carbon atoms; 3). Filters based on side-chain center of mass and van der Waals clashes. The side-chain center of mass is used in conjunction with main-chain oxygen atoms. If a main-chain oxygen atom is under consideration as the binding ligand, then the distance between the side-chain center of mass and Ca2+ must be greater than that of the Ca-O (carboxylic) distance in the X-ray structure.
We use calmodulin (3CLN.pdb) from the X-ray training dataset to illustrate how these filters work. First, we used vertices representing 209 carbon atoms, using 7.5 Å as C-C cutoff, to construct a topological graph (see Methods). By searching all maximal cliques in the graph, 4626 non-redundant carbon clusters comprising four or more carbon atoms were obtained. Among the 4626 clusters, 4589 are false positive predictions. The charge filter first eliminates 1639 carbon clusters. Next, the geometric shell filters eliminate an additional 2453 clusters, including 1405 clusters where the distance between Ca2+ center and third shell carbon atom is smaller than the distance between Ca2+ center and the second shell carbon atom, and another 1048 are eliminated based on previously-reported geometric parameters.18 The third and final filter eliminates another 497 clusters. For example, we assume that the clash radius between Ca2+-nitrogen is 2.55 Å. If the distance between the Ca2+ center and each nitrogen atom is smaller than this value, we consider that there exists a clash and thus eliminate this cluster. Parameterization details are provided in the supporting information.
In calmodulin, carbon clusters which sequentially passed all filters, are scored as firm predictions; this number is consistent with the documented binding sites. We also have applied the filters separately, to illustrate improved results obtained by sequential combination. The eliminated clusters are summarized in Table I.
Table I.
False positive predictions (calmodulin: 3CLN) remaining following applications of different filters in either consecutive sequencea or individuallyb.
| Filter Type
|
|||
|---|---|---|---|
| Chgc | Geomd | COMe | |
| Sequential | 2950
|
497
|
0
|
| 4589 | 2950 | 497 | |
|
| |||
| Individual | 2950
|
129
|
267
|
| 4589 | 4589 | 4589 | |
Filters were applied consecutively.
Each Filter was applied individually.
Charge filter.
Geometric filter.
Center of mass and clash filter. Numerator represents remaining false positive predictions.
Performance on X-ray testing dataset
MUGC was evaluated with the Ca2+-loaded X-ray testing dataset (Table S6). Out of the 108 documented protein-coordinated Ca2+ ions in the testing dataset, 99 are chelated by more than three binding residues. If we use the predicted Ca2+ position (CP) as a measure, MUGC identified 102/104 sites with coordination numbers greater than three. Five binding sites in this dataset have only three binding residues each. In terms of binding residues (BR), MUGC is able to identify 98/99 binding sites having more than three binding residues and 4/9 binding sites having three or fewer binding residues (Tables II and S6). The only binding site that was not successfully predicted by MUGC was due to the fact that no negatively-charged residues are encountered in this binding site. This is discussed in greater detail in the Discussion section.
Table II.
Prediction based on Ca2+ position.
Prediction based on binding residues.
Total documented sites.
Sensitivity.
Selectivity.
Coordination number.
For the negative control dataset comprising proteins without known Ca2+-binding sites, we define True Negative (TN) as any prediction which does not identify a Ca2+-binding site, and False Negative (FN) as any prediction which does identify a Ca2+-binding site. Based on these criteria, MUGC correctly predicted 16/24 proteins as non-Ca2+-binding proteins, with the remaining 8/24 proteins incorrectly identified as having Ca2+-binding sites. A summary of predictions for this dataset is reported in Supplemental Table S13. The prediction success rate (66%), while lower when compared to values reported for sensitivity and selectivity with the testing dataset, still indicates that the majority of proteins were identified correctly. We can further speculate that one or more of the 8 FN predictions may be Ca2+-binding sites that remain to be identified as such. These results show that our hypothesis is valid on X-ray-derived Ca2+-loaded structures.
Structural differences between X-ray crystallographic sites and NMR solution sites
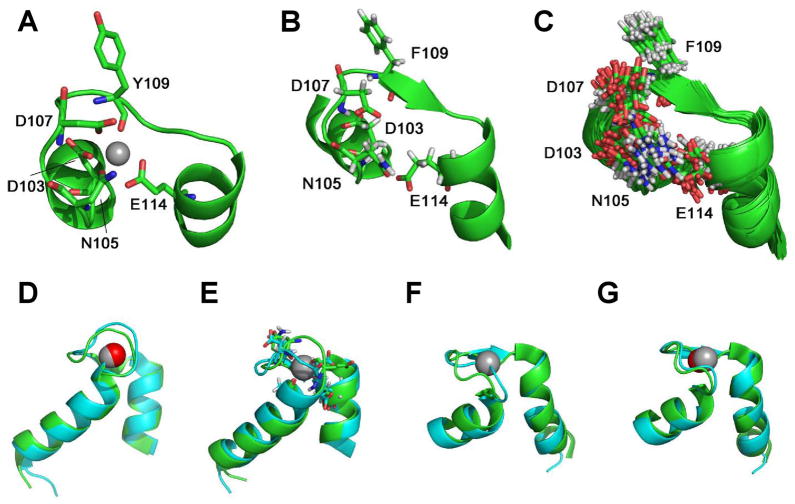
Ca2+ binding sites with high affinity in X-ray structures are well defined due to direct observation of electron density of the metal and its coordinating oxygen atoms. For example, the static features of EF-hand Ca2+-binding sites in proteins such as a troponin C exhibit structurally-similar pentagonal bipyramidal geometries (Fig. 4A). This geometry is well conserved in more than 10 X-ray structures of troponin C 21. In contrast, Ca2+-binding sites in NMR structures usually are not well defined due to lack of directly observable constraints and the dynamic nature of the ensembles. In addition, Ca2+-binding sites are often located on the highly solvent-accessible surface, which reduces the possible connectivity that can be used to define the Ca2+-binding site. For example, the high-resolution structure of troponin C (2TN4.pdb), determined in the presence of 10 mM of Ca2+, has 23 structures in its NMR ensemble. Surprisingly, the third Ca2+-binding site (D103, N105, D107, Y109 and E114) in the least-energy (first) structure of the ensemble cannot be recognized as a Ca2+ site by the criteria developed for static structures.
Figure 4. Structure comparison between X-ray holo and NMR structures.
(A) X-ray structure of troponin C (2TN4.pdb) at a resolution of 2.00 Å. (B) First ensemble of NMR troponin C (1TNW.pdb) determined without Ca2+ constraints. (C) All conformations in the NMR ensemble of troponin C (1TNW.pdb), determined without Ca2+ constraints. Sub-figures (D) through (G) indicate the alignments of the binding site in calbindin D9K NMR structures inferred without Ca2+ constraints (blue) and holo X-ray structure (green). Ca2+ in X-ray is gray and the geometric center of a carbon cluster in the NMR structure is red. (D) Ca2+ can be placed in the binding site formed by the loop A14-E27 in this first member of the ensemble. (E) The binding site formed by the loop D54-E65 of the first member of the ensemble does not appear to accommodate Ca2+, though it is present in the X-ray structure (gray). (F) Similarly, the binding site formed by the loop A14-E27 of the second structure in the ensemble cannot accommodate Ca2+, while (G), that formed by the loop D54-E65, can.
Fig. 4B illustrates this lowest-energy structure, while Fig. 4C shows a composite of all structures in the ensemble. Dynamic motion of the Ca2+-binding sites is implicit in the NMR ensemble, where an ideal binding conformation may exist only temporarily. Such observations motivated us to investigate the performance of algorithms on predictions of NMR structures.
Non-redundant NMR dataset
To validate our hypothesis on NMR structures, we used a published training dataset 39 (Table S7) and constructed a testing dataset (Table S8). The training NMR dataset (Table S7) contains six, EF-hand-type Ca2+-binding proteins with a total of 16 binding sites. In four of these the authors originally deposited structures for which they imposed Ca2+ constraints in determining the structures: calmodulin (2BBM.pdb), parvalbumin (2PAS.pdb), yeast frequenin (1FPW.pdb), and epidermal growth factor receptor pathway substrate 15 (1C07.pdb). It is not possible for us to project the original structures as they might have been constructed without invoking the Ca2+ constraints. In the other two cases (troponin C: 1TNW.pdb and calbindin D9K: 2BCB.pdb) the structures submitted were not modified based on Ca2+ constraints.
We feel it important to include in the testing set only NMR structures which were calculated without use of Ca2+ constraints. The testing dataset (Table S8) contains 11 NMR structures, all of which meet this criterion. Two additional criteria were imposed: i) The data corresponded to the holo forms of the proteins (i.e., all binding sites were occupied by Ca2+ in solution); ii) The NMR structures had corresponding holo structures derived crystalographically, so that prediction results could be validated.
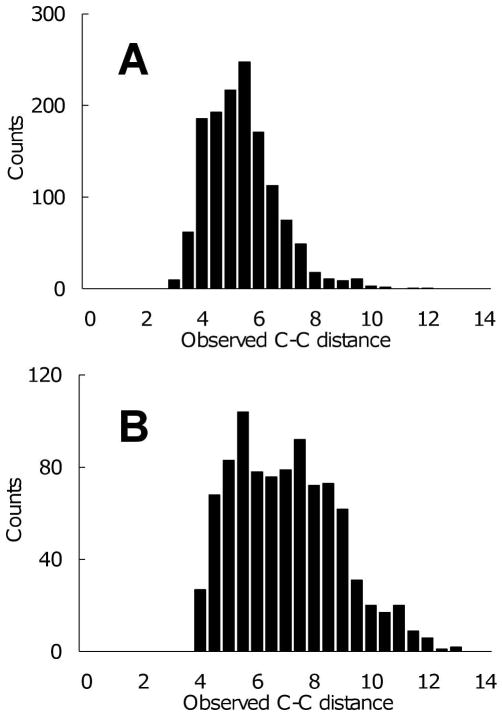
Analysis of C-C distance and geometric centers on a NMR training dataset
We analyzed the C-C distance of binding sites in the NMR structures with and without Ca2+ constraints added to the structural calculations. Each ensemble in the NMR training dataset was evaluated. If the total number of ensembles was greater than 20, we used only the first 20 ensembles in our training NMR dataset. These data show that in the NMR structures with Ca2+ constraints, the second shell C-C distances are clustered between 4 and 7Å, and 90% of the distances fell below 8.3Å, which was used as cutoff for identification of the majority of the carbon atom clusters.
The distribution of C-C distances in NMR binding sites exhibits a lower mean and smaller deviation in the constrained structures (Fig. 5A) as compared with structures lacking Ca2+ constraints (Fig. 5B). This is consistent with our intuition that the addition of Ca2+ to the structures pushes carbon clusters closer to each other in the binding sites, and therefore the NMR structures should be closer to their X-ray holo counterparts.
Figure 5. C-C distances analysis.
(A) four NMR structures from the training dataset with Ca2+ constraints (1C07.pdb, 1FPW.pdb, 2BBM.pdb and 2PAS.pdb). (B) Troponin C NMR structures without Ca2+ constraints (1TNW.pdb).
There exists at least one structure in the ensemble that is similar to the site conformation seen in models derived from X-ray diffraction of holo structures. Naturally, such sites are recognized as having canonical Ca2+-binding geometry. For example, in the NMR structures of calbindin D9K (2BCB.pdb, derived without Ca2+ constraints), we observe that the geometric Ca2+ center determined by the main-chain carbon atoms of residues E17, D19, Q22, together with side-chain carbon of E27, is geometrically similar (within 0.55Å) to the Ca2+ center documented in the holo X-ray-derived structure (4ICB.pdb). Fig. 4D shows this NMR-observed binding loop superimposed on the X-ray structure. Similar congruity is seen between the geometric center fixed by side-chain carbon atoms from D54, N56, D58, E65 and main-chain carbon from E60 as seen in the holo X-ray structure and in the second-ranked structure in the NMR ensemble (Fig. 4G). These observations encouraged us to use more inclusive parameters for the carbon clusters on NMR structures and predict Ca2+-binding positions based on all ensembles.
Performance on NMR training dataset and testing dataset
For the training dataset (Table S7), MUGC identified all binding sites with a selectivity of 88%. For the testing dataset (Table S8), MUGC predicted 20 Ca2+-binding sites out of the (X-ray authenticated) 21 binding sites with 95% sensitivity and 81% selectivity. These results show that using second shell carbon atoms can predict Ca2+ positions in the NMR structures.
MUGC’s capability on modeled structures
Among NMR structures (the testing dataset), the second binding site of the human centrin 2 (in complex with a 17 residue peptide (P1-XPC) from xeroderma pigmentosum group C protein) is missed because the binding site simply deviates too much from the site conformation seen in holo X-ray structures (RMSD of the loop is 2.594 Å) 4. That MUGC misses such distorted sites raises an interesting question: How much distortion from an ideal site can MUGC cope with?
To address this question, we performed an additional experiment. We removed Ca2+ ion from the structure of a bovine intestinal Ca2+-binding protein (PDB: 3ICB; 8.7 kDal, 2 sites) and ran a molecular dynamics (MD) simulation (using AMBER) to generate 199 conformations (refer to Table S9 for the MD protocol). Each conformation has two Ca2+ sites, for a total of 398 binding sites. MD simulation, in the absence of cohesive Ca2+, represents a deliberate attempt to allow the potential ligands to distort a known binding site in a chemically realistic way. Using the simulated structures (in which we “know” site ligands and, roughly, Ca2+ centers), we let MUGC make its predictions. Typical of short-term MD simulations, the individual structures from the trajectory ensemble do not deviate much from the original structure (maximum RMSD is 2.00, Table S9). MUGC predicted 384 out of the 398 Ca2+-binding sites.
Although we have not analyzed binding site integrity in detail across this trajectory, the average RMSD of 1.65 Å is on the order that one might expect for homology modeling or contemporary crystallographic refinement. Perhaps more to the point, it is almost exactly the tolerance our algorithm allows for 3rd-shell-carbon-to-Ca2+ distance (4.54 to 6.14 Å, Δ = 1.60). We presume the 14 missed sites (3.5%) represent the high-end fringe of the average RMSD, and conclude that, though 14 of these “distortions” confounded MUGC (not to mention the apparent outlier in the NMR structures of human centrin 2), this performance testifies to the value of using carbon shell information to track binding sites.
Metal selectivity for Ca2+ over other divalent ions
Many proteins have well-documented binding sites for divalent metal ions other than Ca2+. It becomes particularly relevant to ask whether the criteria we have developed to recognize Ca2+ sites from second-and third- shell carbon coordinates are able to discriminate sites known to bind other divalent metals of similar size. That is, how selective are these criteria for Ca2+ binding as opposed to other divalent metals?
To address this question, we conducted additional research to determine whether the use of carbon shells in MUGC could successfully discriminate between binding sites for Ca2+ as opposed to other divalent metals. Three additional testing datasets (Tables S10–S12) comprising X-ray structures of other metal binding proteins, were evaluated for Mg2+ (52 sites), Zn2+ (51 sites) and Pb2+ (47 sites). Mg2+ and Zn2+ were selected for comparison due to their similar ionic radii (Mg2+ =0.72 Å, Zn2+ =0.75 Å) 46, and because they, along with Ca2+, are the most abundant physiologically-relevant metals involved in biochemical reactions. Pb2+ was selected due to its similar ionic radius with Ca2+ (1.19 vs. 0.99 Å) 46 and a volume of evidence indicating a close relationship between Pb2+ toxicity and Ca2+ metabolism 47–51.
For these analyses, a binding site was considered misclassified if a Ca2+-binding site was predicted within a non-Ca2+ ion (i.e., if it placed a Ca2+ ion within 3 Å of the documented divalent metal 32,39, and if this predicted site is not known to be a true Ca2+-binding site.) Results of our analyses indicate that MUGC does not misidentify, as Ca2+-binding sites, 83%, 96% and 89%, respectively, of documented Mg2+, Zn2+, and Pb2+ binding sites. Moreover, these are under-estimates, since there is no assurance that the “misidentified” sites may not in fact represent sites which can alternatively bind Ca2+, but which have not, as yet, been unidentified experimentally. Indeed, several of the “misidentified” Mg2+ and Zn2+ sites exhibit coordination geometries (and/or utilize ligands) that would be atypical for Mg2+ (e.g., carbonyl oxygen atoms as seen in IKCZ.pdb) but not for Ca2+. Moreover, for some of the documented Mg2+-binding sites, very high concentrations of Mg2+ were added during crystallization (e.g., 250 mM 52 in 1OBW.pdb and 100 mM 53 in 1KCZ.pdb). Thus it would be reasonable to reexamine some of these “misidentified” Ca2+-binding proteins to ascertain if in fact they might be cryptic Ca2+-proteins.
If we discard such questionable cases from our statistics (identified as “Other” in “Misclassified” column of Tables S10–S12), our final results indicate that none of the remaining binding sites for proteins in the Mg2+, Zn2+, or Pb2+ datasets are improperly by MUGC as Ca2+-binding sites, demonstrating excellent metal selectivity.
Discussion
Key factors for metal coordination
Our studies have revealed several key properties that are important for metal coordination. First, a second-shell of carbon clusters encloses the first shell atoms which directly coordinate Ca2+. We hypothesize that the Ca2+ position within a Ca2+-binding protein is determined as much by the positions of carbon atoms in the hydrophobic shells surrounding Ca2+ as by the immediate positions of the oxygen ligands comprising the actual binding site. A practical corollary to this hypothesis is that, in cases where the coordinates of ligand oxygens are poorly defined, the surrounding carbon shells can be relied upon to accurately predict the location of the Ca2+ center. Such cases are observed in crystallographically determined structures, where coordinates of side-chain oxygens may be poorly resolved because of their mobility. Limitations associated with positioning of oxygen atoms in NMR structures are also observed, specifically because the naturally-abundant isotope of oxygen is spectroscopically silent in NMR. In the case of backbone oxygen atoms, these reconstructed positions have higher precision, precisely because the geometry is fixed and no torsion angle is involved. However, for sidechain oxygens, such as from the carboxylic groups of Asp and Glu, which are subject to torsional rotations, there are substantial uncertainties in the positions. The present work represents the first attempt to exploit the relative placement of the carbon atoms to pinpoint Ca2+ centers without reference to the locations of the directly ligated oxygen atoms, particularly those from side-chain.
From the structural perspective of binding sites, the first (hydrophilic) oxygen shell in the binding sites permits the protein’s exposure to water and hydrated Ca2+. This immediate binding scaffold is supported by a second (hydrophobic) shell of carbon atoms, which may restrict flexibility within the site and thereby ameliorate the decrease in binding-associated entropy 54. In order to exercise the regulatory role of Ca2+ in the cell, binding sites in proteins must be able to bind and release Ca2+ within a physiological range of Ca2+ concentrations. This implies not only the existence of a “pre-organized” site, but also restricted structural flexibility within that site 21,23,54, as well as the stable positioning of carbon atoms oriented in such a way to facilitate formation of the hydrophilic oxygen shell which coordinates the Ca2+ directly. Our earlier studies demonstrated that the oxygen shell in the Ca2+-binding site has an identifiable geometry (i.e., four or more oxygen atoms in the site, all separated from each other by an oxygen-oxygen distance ≤ 6Å) 31,32. Our current studies, described here, suggest that this structural regularity must be supported by the associated C-O bonds, implying an appropriately arranged geometry for the surrounding carbon shell – an arrangement which should also be identifiable.
Second, we have shown that the vast majority of Ca2+-binding sites have at least one negatively-charged residue within the tentative binding site. This observation justifies the utility of applying a charge filter, which improves selectivity in predicting various classes of Ca2+-binding sites in the protein data bank 18. In its analysis of X-ray structures, the MUGC algorithm missed only one site in the complex formed between proteolytically-generated lactoferrin fragment and proteinase K (1BJR.pdb) – an exception to the rule, in that there is no negatively-charged binding residue in this binding site which has a coordination number of four. The Ca2+-binding site was composed of residues R12, S15, N257 and A273 55. It is likely that this binding site does not have strong Ca2+-binding affinity.
Third, our analysis of calmodulin has also shown that it is important to ensure that the predicted Ca2+ positions contain neither Van der Waals clashes nor over-lapping side-chain centers of mass. The concept of side-chain center of mass (SC-CoM) has been previously used in protein structural prediction 42. In this work we present a novel application for the use of SC-CoM as an aid to predict Ca2+-binding sites. In a sense, side-chain center of mass is used here as a surrogate for poorly-resolved ligand oxygen coordinates.
Implications for metal selectivity
From Tables S10–S12, we can conclude that, in most cases, MUGC does not mis-classify other metal binding sites as Ca2+-binding sites. There are two key design features in MUGC to help distinguish Ca2+-binding sites from non-Ca2+-binding sites. First, carbon clusters utilized by MUGC are restricted to those with associated oxygen atoms and were required to have at least four carbon atoms. Differences in coordination numbers between Ca2+ and the other metals, as well as variations in ion solvation, result in different ions having different numbers of carbon atoms associated with binding. For example, Mg2+ tends to be more highly-solvated than Ca2+, and the presence of more water molecules results in fewer carbon atoms within the microenvironment of the binding site. Additionally, both Zn2+ and Pb2+ typically utilize fewer binding ligands than Ca2+, and utilize different ligand types 56. As a hard Lewis acid, Ca2+ binds preferentially with oxygen atoms whereas both Zn2+ and Pb2+, considered borderline Lewis acids, may bind with either hard or soft bases, utilizing both nitrogen and sulfur ligands, as well as oxygen. Due to the smaller number of oxygen-based ligands for these metals, MUGC selectively eliminates those sites as potential Ca2+-binding sites.
The second key design feature for identification of Ca2+-binding sites relates to ionic radius, which is another factor by which proteins discriminate between divalent ions 57. For example, Mg2+ is 28% smaller than Ca2+, and this smaller VDW radius alters the geometry of the binding site which then may not accommodate the larger Ca2+ ion. After carefully calibrating the geometric parameters in MUGC with respect to Ca2+ radius and to the spatial relationships of binding ligands in Ca2+-binding sites, MUGC can distinguish Ca2+-binding sites from those of other metals.
Our results indicate that the algorithmic approach of MUGC provides a useful tool for delineating metal binding sites. This differentiation is achieved by carefully tuning the geometric and chemical parameters of MUGC based on analysis of empirical data associated with Ca2+-binding, and parameter optimization.
Comparison of MUGC with other algorithms
Ca2+-binding sites in proteins can be classified into continuous and discontinuous types. Continuous Ca2+-binding sites are formed by the ligand residues from a contiguous stretch of amino acid residues, and include EF-hand Ca2+-binding proteins such as calmodulin and calbindinD9K. Discontinuous Ca2+-binding sites are formed with ligand residues non-adjacent in the primary sequence. Unlike several metal ions such as zinc and iron (with defined coordination geometry and sidechain ligand residues) Ca2+-binding sites in proteins are highly irregular and with diversified coordination number (3–8). Ca2+ ligand atoms can come from side chain carboxyls of Asp and Glu, from amides of Asn and Gln, from hydroxyls of Thr and Ser, and from mainchain carbonyls of all residue types, as well as from solvent such as water 56. Thus, while methods based on sequence-profiles and machine-learning for prediction for some metal ions are reasonably accurate, these prediction algorithms are limited to continuous calcium binding sites, largely canonical EF-hand calcium binding motifs. In our previous paper by Zhou et al, we have designed a Ca2+-binding protein Search Server named CaPS, which extends prediction of Ca2+-binding sites in proteins from canonical EF-hand motifs to pseudo EF-hand and other EF-hand like motifs based on sequence patterns and signatures4. We have successfully applied this method to predict EF-hand-like calcium binding proteins in bacterial and virus systems58,59.
In an effort to compare the prediction capability of MUGC with the sequence-pattern search algorithms, we have submitted the sequences from the training dataset (with 52 calcium binding sites) to the CaPS web-server. CaPS is able to identify all EF-hand-like patterns in 14 calcium-binding sequences on the query proteins without false positive. However, the sensitivity of CaPS (26%) is significantly lower than MUGC (92%) on the whole training dataset, due to its limitation with regards to discontinuous binding sites (data not shown).
We have further compared the capability of MUGC with three structural-based algorithms, including our previous reported MUG, SitePredict, and WebFeature (the web-based implementation of FEATURE) using an NMR testing dataset.
The MUG web-server does not accept NMR ensembles, so we submitted each member of the ensemble one by one; WebFeature and SitePredict do accept ensembles of structures. In these NMR structures there are no documented Ca2+ ions. The prediction results are summarized in Tables III and IV.
Table III.
Identification of Ca2+ positions on NMR structures by MUGC, MUG and FEATURE.
| MUGC | MUG | FEATURE | MUGC+ MUG | |
|---|---|---|---|---|
| PTS a | 20 | 19 | 7 | 21 |
| DS b | 21 | 21 | 21 | 21 |
| CH c | 330 | 284 | 21 | 610 |
| TP d | 403 | 451 | 21 | 859 |
| SEN e | 95% | 90% | 33% | 100% |
| SEL f | 81% | 63% | 100% | 71% |
Predicted True Sites.
Documented Sites.
Correct Hits.
Total Predictions.
Sensitivity.
Selectivity.
Table IV.
MUGC and SitePredict predictions based on binding residues in NMR structures.
Predicted True Sites.
Documented Sites.
Correct Hits.
Total Predictions.
Sensitivity.
Selectivity.
To compare results with FEATURE, whose output is the predicted Ca2+ positions in the structures, we calculated the sensitivity and selectivity by mapping the Ca2+ position into the binding residues. If we observe at least one documented binding residue within 4Å of the predicted position, then we count this position as correct prediction. Failure to meet these criteria results in a false positive. FEATURE predicted 7/21 binding sites with 33% sensitivity and 100% selectivity. Despite this algorithm’s advantage in selectivity, however, it fails to identify a significant proportion of sites in the dataset. This observation illustrates the persistent tradeoff between sensitivity and selectivity.
Most of the published algorithms designed to predict Ca2+-binding sites are based on optimal ligand geometry deduced from high-resolution X-ray static structures, and thus rely heavily on the accuracy of the placement of ligand oxygen atoms. In contrast, MUGC and SitePredict deliberately avoid use of specific side-chain and ligand coordinates in an effort to desensitize the method to vagaries in the location of ligands typical in low-resolution or homology-modeled structures.
To compare our results with SitePredict (whose output is a list of residues involved in binding) we used such residues as a measurement of correctness of the prediction. According to its web-server (dated current as of Dec. 14, 2011) a default cutoff of 4 is used for predictions in binding residues (scores greater than 4 are considered as binding residues). We first compared MUGC with SitePredict in NMR structures. SitePredict predicted 7/21 binding sites. Our data have shown that MUGC exhibits significantly better performance in terms of sensitivity than SitePredict under conditions where both have comparable selectivity. The performance comparison with FEATURE and SitePredict, underscores the inadequacy of site-recognition algorithms, informed by static structures, to recognize sites in dynamic situations 25.
We also compared MUGC with SitePredict for performance with X-ray structures. As for testing on NMR structures, we considered that SitePredict is able to predict a binding site, if it is able to identify at least one binding residue in an authentic site. For our comparative analysis, we applied a more stringent definition for the MUGC’s true-positive prediction sites by requiring that there be at least two binding residues predicted in the authentic site. If the predicted residue is not a binding residue, then it is a false positive residue. In the case that one binding residue appeared in two sites (thermolysin: 1HYT.pdb), we counted it twice for SitePredict’s true positive residue, but once for MUGC’s true positive. The results show that, using these criteria, MUGC has a sensitivity of 94%, while detecting the binding sites at a selectivity rate of 43% (Fig. 6). On the same dataset, SitePredict has a sensitivity of 59% and a selectivity of 20%. These results suggest that the performance of predicting binding residues is improved by using second shell carbon atoms.
Figure 6.
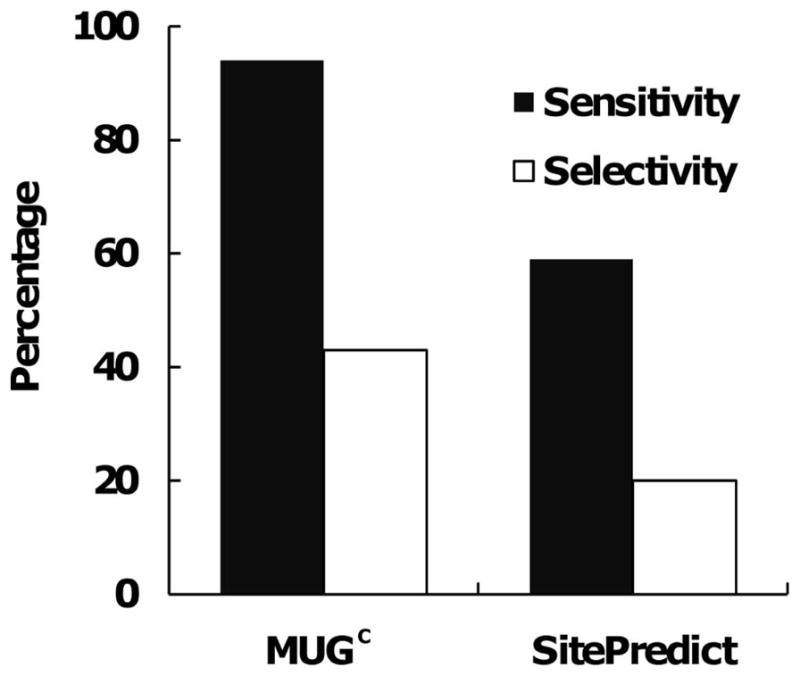
Comparison between MUGC and SitePredict based on residues on testing X-ray dataset.
A comparison between MUGC and our previously-reported MUG algorithm indicated little difference in results when analyzing the static X-ray structure dataset: with MUGC exhibiting 89% sensitivity and 76% selectivity, compared to 91% sensitivity and 73% for MUG. However MUGC results showed improvement compared to MUG with the testing NMR dataset: MUGC has better sensitivity (95%), and fewer false positive predictions, although the selectivity of 81% leaves room for improvement. The comparable results for MUG were a sensitivity of 90% with a selectivity of 61%. MUGC’s superior performance with NMR datasets (Table III), however, is somewhat muted by the fact that these datasets are small. The PDB contains many fewer NMR structures than X-ray structures, and very few Ca2+-binding proteins in NMR structures inferred without Ca2+ constraints. Manually combining the two algorithms yields in 100% sensitivity and 71% selectivity.
Challenges in algorithm evaluations
In this work, several statistical measurements were applied to assess the quality of our predicted results and to estimate errors. First, we evaluated prediction error based on the difference in distance between the predicted and documented Ca2+ centers 29,30. Second, we evaluated a classification error based on ligand residues predicted to be involved in binding versus documented binding ligand residues (See Table II). Third, we evaluated a negative control dataset comprising proteins not currently known to bind Ca2+ or other metal ions.
The challenge for evaluating the accuracy of predicting Ca2+-binding sites stems from the fact that no consensual standard of quality has emerged from previous studies. Earlier works, such as those of Yamashita et al. 23 and Di Cera et al. 20, listed the prediction results but did not include statistical evaluations of the results. Glazer et al. applied sensitivity and selectivity to compare the performance of FEATURE with results reported by Nayal and Di Cera 25, however Schymkowitz et al. have argued that the Fold-X algorithm was better at placing the Ca2+ position than was FEATURE 30. Babor et al. 60 later noted a large number of false positive predictions associated with Fold-X, and also suggested that its force-field optimization step is very sensitive to small changes of position due to the electrostatic nature of the interactions. Quality evaluation is further complicated, as seen in this study, when the “structure” is in fact an ensemble of structures. A concise quality measurement over the ensemble is problematic.
Yet another challenge comes from the definition of a false positive. We take as the most rigorous standard, namely the position of Ca2+ explicitly observed by X-ray diffraction of holo proteins. But X-ray models are not infallible; absence of Ca2+ at a physiologically functional binding site, especially a low affinity one, may simply mean that Ca2+ failed to crystallize at that site. Ironically, one might argue that the most exquisite use of prediction algorithms would be to reveal sites not visualized to contain crystallized Ca2+, but subsequently proved to be bona fide sites.
To predict sites of Ca2+ binding in proteins where the site may be indeterminate because of invisibility in X-ray and NMR structures, we have developed a graph-based, site-recognition algorithm which relies on carbon shell and side-chain center of mass information. This work shows that, using information from carbon atoms, with formal ionic charges and center of mass as additional filters, we can accurately identify Ca2+-binding sites in X-ray holo structures. The binding sites in four holo NMR structures, computed with Ca2+ constraints, could be identified easily by this algorithm. Additionally, by testing 21 NMR binding sites that do not utilize Ca2+ constraints, we have demonstrated improved prediction results with NMR structures using carbon atoms comprising the second and third concentric shells surrounding the binding sites. Finally, our results also demonstrate that the new algorithm is optimized for prediction of Ca2+-binding sites, and able to discriminate Ca2+ from other divalent metal ions such as Mg2+, Zn2+ and Pb2+. The successful identification of Ca2+ positions by using the carbon shell deepens our understanding of the structure of Ca2+-binding sites, thus further enhancing our capability to design Ca2+-binding proteins 61–63. This new algorithm may be applied advantageously to unrefined homology models, low-resolutions models and NMR structures.
Supplementary Material
Acknowledgments
We thank Dr. Jeffrey Skolnick for his introduction to the concept of center of mass, Jingjuan Qiao for formatting help, Yusheng Jiang and You Zhuo for the assistance on sequence-based prediction, anonymous reviewers for critical comments, and Dr. Jiawei Liu for fruitful discussions. This work is partially supported by the following sponsors: GSU MBD fellowship to K.Z., X.W. and M.K., NSF (DMS0070059 to G.C.), and NIH (GM62999, GM081749 to J.J.Y.).
Footnotes
The supporting information contains one file (SupportingInformation.pdf) with thirteen tables. Table S1 provides an example of using an adjacent matrix to represent protein structures. Table S2 summarizes details related to parameterization for cluster cutoff and filters. Tables S3 and S4 provide brief descriptions of the X-ray training and testing sets respectively. Tables S5 and S6 summarize the prediction results for these X-ray datasets, respectively. Tables S7 and S8 detail the prediction results on NMR training and testing datasets. Table S9 details the prediction results on modeled structures. Tables S10–S12 provide results for testing on Mg2+, Zn2+ and Pb2+ datasets. Table S13 provides results for testing on a negative control dataset.
References
- 1.Ermak G, Davies KJ. Calcium and oxidative stress: from cell signaling to cell death. Mol Immunol. 2002;38(10):713–721. doi: 10.1016/s0161-5890(01)00108-0. [DOI] [PubMed] [Google Scholar]
- 2.Berridge MJ, Bootman MD, Lipp P. Calcium - a life and death signal. Nature. 1998;395(6703):645–648. doi: 10.1038/27094. [DOI] [PubMed] [Google Scholar]
- 3.Orrenius S, Zhivotovsky B, Nicotera P. Regulation of cell death: the calcium-apoptosis link. Nat Rev Mol Cell Biol. 2003;4(7):552–565. doi: 10.1038/nrm1150. [DOI] [PubMed] [Google Scholar]
- 4.Zhou Y, Yang W, Kirberger M, Lee HW, Ayalasomayajula G, Yang JJ. Prediction of EF-hand calcium-binding proteins and analysis of bacterial EF-hand proteins. Proteins. 2006;65(3):643–655. doi: 10.1002/prot.21139. [DOI] [PubMed] [Google Scholar]
- 5.Vito P, Lacana E, D’Adamio L. Interfering with apoptosis: Ca(2+)-binding protein ALG-2 and Alzheimer’s disease gene ALG-3. Science. 1996;271(5248):521–525. doi: 10.1126/science.271.5248.521. [DOI] [PubMed] [Google Scholar]
- 6.Berridge MJ, Bootman MD, Roderick HL. Calcium signalling: dynamics, homeostasis and remodelling. Nat Rev Mol Cell Biol. 2003;4(7):517–529. doi: 10.1038/nrm1155. [DOI] [PubMed] [Google Scholar]
- 7.Calabretta B, Kaczmarek L, Mars W, Ochoa D, Gibson CW, Hirschhorn RR, Baserga R. Cell-cycle-specific genes differentially expressed in human leukemias. Proc Natl Acad Sci U S A. 1985;82(13):4463–4467. doi: 10.1073/pnas.82.13.4463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hocker P, Reizenstein P. Calcium and potassium disturbances in acute leukemia. Blut. 1974;29(6):398–406. doi: 10.1007/BF01633675. [DOI] [PubMed] [Google Scholar]
- 9.Slomnicki LP, Nawrot B, Lesniak W. S100A6 binds p53 and affects its activity. Int J Biochem Cell Biol. 2009;41(4):784–790. doi: 10.1016/j.biocel.2008.08.007. [DOI] [PubMed] [Google Scholar]
- 10.Mamillapalli R, VanHouten J, Zawalich W, Wysolmerski J. Switching of G-protein usage by the calcium-sensing receptor reverses its effect on parathyroid hormone-related protein secretion in normal versus malignant breast cells. J Biol Chem. 2008;283(36):24435–24447. doi: 10.1074/jbc.M801738200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang C, Chen T, Zhang N, Yang M, Li B, Lu X, Cao X, Ling C. Melittin, a major component of bee venom, sensitizes human hepatocellular carcinoma cells to tumor necrosis factor-related apoptosis-inducing ligand (TRAIL)-induced apoptosis by activating CaMKII-TAK1-JNK/p38 and inhibiting IkappaBalpha kinase-NFkappaB. J Biol Chem. 2009;284(6):3804–3813. doi: 10.1074/jbc.M807191200. [DOI] [PubMed] [Google Scholar]
- 12.Yang H, Murthy S, Sarkar FH, Sheng S, Reddy GP, Dou QP. Calpain-mediated androgen receptor breakdown in apoptotic prostate cancer cells. J Cell Physiol. 2008;217(3):569–576. doi: 10.1002/jcp.21565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wopfner N, Dissertori O, Ferreira F, Lackner P. Calcium-binding proteins and their role in allergic diseases. Immunol Allergy Clin North Am. 2007;27(1):29–44. doi: 10.1016/j.iac.2006.10.003. [DOI] [PubMed] [Google Scholar]
- 14.Chrysina ED, Brew K, Acharya KR. Crystal structures of apo- and holo-bovine alpha-lactalbumin at 2. 2-A resolution reveal an effect of calcium on inter-lobe interactions. J Biol Chem. 2000;275(47):37021–37029. doi: 10.1074/jbc.M004752200. [DOI] [PubMed] [Google Scholar]
- 15.Pepys MB, Hawkins PN, Booth DR, Vigushin DM, Tennent GA, Soutar AK, Totty N, Nguyen O, Blake CC, Terry CJ, et al. Human lysozyme gene mutations cause hereditary systemic amyloidosis. Nature. 1993;362(6420):553–557. doi: 10.1038/362553a0. [DOI] [PubMed] [Google Scholar]
- 16.Glusker JP. Structural aspects of metal liganding to functional groups in proteins. Adv Protein Chem. 1991;42:1–76. doi: 10.1016/s0065-3233(08)60534-3. [DOI] [PubMed] [Google Scholar]
- 17.Pidcock E, Moore GR. Structural characteristics of protein binding sites for calcium and lanthanide ions. J Biol Inorg Chem. 2001;6:479–489. doi: 10.1007/s007750100214. [DOI] [PubMed] [Google Scholar]
- 18.Kirberger M, Wang X, Deng H, Yang W, Chen G, Yang JJ. Statistical analysis of structural characteristics of protein Ca2+-binding sites. J Biol Inorg Chem. 2008;13(7):1169–1181. doi: 10.1007/s00775-008-0402-7. [DOI] [PubMed] [Google Scholar]
- 19.Davis JA, Handford PA, Redfield C. The N1317H substitution associated with Leber congenital amaurosis results in impaired interdomain packing in human CRB1 epidermal growth factor-like (EGF) domains. J Biol Chem. 2007;282(39):28807–28814. doi: 10.1074/jbc.M704015200. [DOI] [PubMed] [Google Scholar]
- 20.Nayal M, Di Cera E. Predicting Ca2+-binding sites in proteins. Proc Natl Acad Sci U S A. 1994;91:817–821. doi: 10.1073/pnas.91.2.817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.McPhalen CA, Strynadka NC, James MN. Calcium-binding sites in proteins: a structural perspective. Adv Protein Chem. 1991;42:77–144. doi: 10.1016/s0065-3233(08)60535-5. [DOI] [PubMed] [Google Scholar]
- 22.Kretsinger RH. Calcium coordination and the calmodulin fold: divergent versus convergent evolution. Cold Spring Harb Symp Quant Biol. 1987;52:499–510. doi: 10.1101/sqb.1987.052.01.057. [DOI] [PubMed] [Google Scholar]
- 23.Yamashita MM, Wesson L, Eisenman G, Eisenberg D. Where metal ions bind in proteins. Proc Natl Acad Sci U S A. 1990;87:5648–5652. doi: 10.1073/pnas.87.15.5648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dudev T, Lin YL, Dudev M, Lim C. First-second shell interactions in metal binding sites in proteins: a PDB survey and DFT/CDM calculations. J Am Chem Soc. 2003;125(10):3168–3180. doi: 10.1021/ja0209722. [DOI] [PubMed] [Google Scholar]
- 25.Glazer DS, Radmer RJ, Altman RB. Combining molecular dynamics and machine learning to improve protein function recognition. Pac Symp Biocomput. 2008;13:332–343. [PMC free article] [PubMed] [Google Scholar]
- 26.Bordner AJ. Predicting small ligand binding sites in proteins using backbone structure. Bioinformatics. 2008;24(24):2865–2871. doi: 10.1093/bioinformatics/btn543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.de Castro E, Sigrist CJ, Gattiker A, Bulliard V, Langendijk-Genevaux PS, Gasteiger E, Bairoch A, Hulo N. ScanProsite: detection of PROSITE signature matches and ProRule-associated functional and structural residues in proteins. Nucleic Acids Res. 2006;34(Web Server issue):W362–365. doi: 10.1093/nar/gkl124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sodhi JS, Bryson K, McGuffin LJ, Ward JJ, Wernisch L, Jones DT. Predicting metal-binding site residues in low-resolution structural models. J Mol Biol. 2004;342(1):307–320. doi: 10.1016/j.jmb.2004.07.019. [DOI] [PubMed] [Google Scholar]
- 29.Wei L, Altman RB. Pac Symp Biocomput. World Scientific; 1998. Recognizing protein binding sites using statistical descriptions of their 3D environments; pp. 497–508. [PubMed] [Google Scholar]
- 30.Schymkowitz JWH, Rousseau F, Martins IC, Ferkinghoff-Borg J, Stricher F, Serrano L. Prediction of water and metal binding sites and their affinities by using the Fold-X force field. Proc Natl Acad Sci U S A. 2005;102(29):10147–10152. doi: 10.1073/pnas.0501980102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Deng H, Chen G, Yang W, Yang JJ. Predicting calcium-binding sites in proteins - a graph theory and geometry approach. Proteins. 2006;64:34–42. doi: 10.1002/prot.20973. [DOI] [PubMed] [Google Scholar]
- 32.Wang X, Kirberger M, Qiu F, Chen G, Yang JJ. Towards predicting Ca2+-binding sites with different coordination numbers in proteins with atomic resolution. Proteins. 2009;75(4):787–798. doi: 10.1002/prot.22285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Huang Y, Zhou Y, Yang W, Butters R, Lee HW, Li SY, Castiblanco A, Brown EM, Yang JJ. Identification and dissection of Ca2+-binding sites in the extracellular domain of Ca2+-sensing receptor. J Biol Chem. 2007;282(26):19000–19010. doi: 10.1074/jbc.M701096200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kunishima N, Shimada Y, Tsuji Y, Sato T, Yamamoto M, Kumasaka T, Nakanishi S, Jingami H, Morikawa K. Structural basis of glutamate recognition by a dimeric metabotropic glutamate receptor. Nature. 2000;407(6807):971–977. doi: 10.1038/35039564. [DOI] [PubMed] [Google Scholar]
- 35.Babor M, Greenblatt HM, Edelman M, Sobolev V. Flexibility of metal binding sites in proteins on a database scale. Proteins. 2005;59(2):221–230. doi: 10.1002/prot.20431. [DOI] [PubMed] [Google Scholar]
- 36.Betts MJ, Sternberg MJ. An analysis of conformational changes on protein-protein association: implications for predictive docking. Protein Eng. 1999;12(4):271–283. doi: 10.1093/protein/12.4.271. [DOI] [PubMed] [Google Scholar]
- 37.Handford PA, Baron M, Mayhew M, Willis A, Beesley T, Brownlee GG, Campbell ID. The first EGF-like domain from human factor IX contains a high-affinity calcium binding site. EMBO J. 1990;9(2):475–480. doi: 10.1002/j.1460-2075.1990.tb08133.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McClintock KA, Shaw GS. A novel S100 target conformation is revealed by the solution structure of the Ca2+-S100B-TRTK-12 complex. J Biol Chem. 2003;278(8):6251–6257. doi: 10.1074/jbc.M210622200. [DOI] [PubMed] [Google Scholar]
- 39.Wang X, Zhao K, Kirberger M, Wong H, Chen G, Yang JJ. Analysis and prediction of calcium-binding pockets from apo-protein structures exhibiting calcium-induced localized conformational changes. Protein Sci. 2010;19(6):1180–1190. doi: 10.1002/pro.394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tomita E, Tanaka A, Takahashi H, editors. The worst-case time complexity for generating all maximal cliques. Vol. 3106. Heidelberg: Springer Berlin; 2004. pp. 161–170. [Google Scholar]
- 41.Bron C, Kerbosch J. Algorithm 457: finding all cliques of an undirected graph. Communications of the ACM. 1973;16(9):575–579. [Google Scholar]
- 42.Zhang Y, Kolinski A, Skolnick J. TOUCHSTONE II: a new approach to ab initio protein structure prediction. Biophys J. 2003;85(2):1145–1164. doi: 10.1016/S0006-3495(03)74551-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Brylinski M, Skolnick J. FINDSITE-metal: integrating evolutionary information and machine learning for structure-based metal-binding site prediction at the proteome level. Proteins. 2011;79(3):735–751. doi: 10.1002/prot.22913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sobolev V, Sorokine A, Prilusky J, Abola EE, Edelman M. Automated analysis of interatomic contacts in proteins. Bioinformatics. 1999;15(4):327–332. doi: 10.1093/bioinformatics/15.4.327. [DOI] [PubMed] [Google Scholar]
- 45.Glazer DS, Radmer RJ, Altman RB. Improving structure-based function prediction using molecular dynamics. Structure. 2009;17(7):919–929. doi: 10.1016/j.str.2009.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shannon RD. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. 1976;A32:751–767. [Google Scholar]
- 47.Simons TJ, Pocock G. Lead enters bovine adrenal medullary cells through calcium channels. Journal of neurochemistry. 1987;48(2):383–389. doi: 10.1111/j.1471-4159.1987.tb04105.x. [DOI] [PubMed] [Google Scholar]
- 48.Goering PL. Lead-protein interactions as a basis for lead toxicity. Neurotoxicology. 1993;14(2–3):45–60. [PubMed] [Google Scholar]
- 49.Dowd TL, Rosen JF, Gundberg CM, Gupta RK. The displacement of calcium from osteocalcin at submicromolar concentrations of free lead. Biochimica et biophysica acta. 1994;1226(2):131–137. doi: 10.1016/0925-4439(94)90020-5. [DOI] [PubMed] [Google Scholar]
- 50.Godwin HA. The biological chemistry of lead. Current Opinion in Chemical Biology. 2001;5:223–227. doi: 10.1016/s1367-5931(00)00194-0. [DOI] [PubMed] [Google Scholar]
- 51.Atchison WD. Effects of toxic environmental contaminants on voltage-gated calcium channel function: from past to present. J Bioenerg Biomembr. 2003;35(6):507–532. doi: 10.1023/b:jobb.0000008023.11211.13. [DOI] [PubMed] [Google Scholar]
- 52.Harutyunyan EH, Oganessyan VY, Oganessyan NN, Avaeva SM, Nazarova TI, Vorobyeva NN, Kurilova SA, Huber R, Mather T. Crystal structure of holo inorganic pyrophosphatase from Escherichia coli at 1.9 A resolution. Mechanism of hydrolysis Biochemistry. 1997;36(25):7754–7760. doi: 10.1021/bi962637u. [DOI] [PubMed] [Google Scholar]
- 53.Asuncion M, Blankenfeldt W, Barlow JN, Gani D, Naismith JH. The structure of 3-methylaspartase from Clostridium tetanomorphum functions via the common enolase chemical step. J Biol Chem. 2002;277(10):8306–8311. doi: 10.1074/jbc.M111180200. [DOI] [PubMed] [Google Scholar]
- 54.Means AR, editor. Calcium regulation of celluar function. Vol. 30. Academic Press; 1994. [Google Scholar]
- 55.Singh TP, Sharma S, Karthikeyan S, Betzel C, Bhatia KL. Crystal structure of a complex formed between proteolytically-generated lactoferrin fragment and proteinase K. Proteins. 1998;33(1):30–38. [PubMed] [Google Scholar]
- 56.Kirberger M, Yang JJ. Structural differences between Pb(2+)- and Ca(2+)-binding sites in proteins: Implications with respect to toxicity. J Inorg Biochem. 2008 doi: 10.1016/j.jinorgbio.2008.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Falke JJ, Drake SK, Hazard AL, Peersen OB. Molecular tuning of ion binding to calcium signaling proteins. Q Rev Biophys. 1994;27(3):219–290. doi: 10.1017/s0033583500003012. [DOI] [PubMed] [Google Scholar]
- 58.Zhou Y, Frey TK, Yang JJ. Viral calciomics: interplays between Ca2+ and virus. Cell Calcium. 2009;46(1):1–17. doi: 10.1016/j.ceca.2009.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Yanyi C, Shenghui X, Yubin Z, Jie YJ. Calciomics: prediction and analysis of EF-hand calcium binding proteins by protein engineering. Sci China Chem. 2010;53(1):52–60. doi: 10.1007/s11426-010-0011-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Babor M, Gerzon S, Raveh B, Sobolev V, Edelman M. Prediction of transition metal-binding sites from apo protein structures. Proteins. 2008;70(1):208–217. doi: 10.1002/prot.21587. [DOI] [PubMed] [Google Scholar]
- 61.Yang W, Wilkins AL, Ye Y, Liu ZR, Li SY, Urbauer JL, Hellinga HW, Kearney A, van der Merwe PA, Yang JJ. Design of a calcium-binding protein with desired structure in a cell adhesion molecule. J Am Chem Soc. 2005;127(7):2085–2093. doi: 10.1021/ja0431307. [DOI] [PubMed] [Google Scholar]
- 62.Zou J, Hofer AM, Lurtz MM, Gadda G, Ellis AL, Chen N, Huang Y, Holder A, Ye Y, Louis CF, Welshhans K, Rehder V, Yang JJ. Developing sensors for real-time measurement of high Ca2+ concentrations. Biochemistry. 2007;46(43):12275–12288. doi: 10.1021/bi7007307. [DOI] [PubMed] [Google Scholar]
- 63.Tang S, Wong HC, Wang ZM, Huang Y, Zou J, Zhuo Y, Pennati A, Gadda G, Delbono O, Yang JJ. Design and application of a class of sensors to monitor Ca2+ dynamics in high Ca2+ concentration cellular compartments. Proc Natl Acad Sci U S A. 2011;108(39):16265–16270. doi: 10.1073/pnas.1103015108. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.