Incorporation of diffusion weighted magnetic resonance imaging data into a simple mathematical model of tumor growth

Abstract

We build on previous work to show how serial diffusion-weighted MRI (DW-MRI) data can be used to estimate proliferation rates in a rat model of brain cancer. Thirteen rats were inoculated intracranially with 9L tumor cells; eight rats were treated with the chemotherapeutic drug 1,3-bis(2-chloroethyl)-1-nitrosourea and five rats were untreated controls. All animals underwent DW-MRI immediately before, one day and three days after treatment. Values of the apparent diffusion coefficient (ADC) were calculated from the DW-MRI data and then used to estimate the number of cells in each voxel and also for whole tumor regions of interest. The data from the first two imaging time points were then used to estimate the proliferation rate of each tumor. The proliferation rates were used to predict the number of tumor cells at day three and this was correlated to the corresponding experimental data. The voxel-by-voxel analysis yielded Pearson’s correlation coefficients ranging from −0.06 to 0.65, whereas the region of interest analysis provided Pearson’s and concordance correlation coefficients of 0.88 and 0.80, respectively. Additionally, the ratio of positive to negative proliferation values was used to separate the treated and control animals (p < 0.05) at an earlier point than the mean ADC values. These results further illustrate how quantitative measurements of tumor state obtained non-invasively by imaging can be incorporated into mathematical models that predict tumor growth.

1. Introduction

Mathematical models of tumor growth and treatment response are often parameterized by quantities that are difficult to measure in intact organisms with any reasonable spatial resolution. The required inputs to each model are commonly obtained invasively or in isolated, idealized in vitro or ex vivo systems. It is also very difficult to obtain longitudinal measurements of tumor properties if the system under investigation has to be compromised in order to make the measurements. Consequently, there has been limited application of mathematical models to clinical data sets and practically no incorporation into clinical trials. Incorporation of data that can be obtained non-invasively could increase the application and relevance of mathematical modeling of tumors, and one way to accomplish this is through the use of non-invasive imaging.

As imaging data can be obtained noninvasively and in 3D, measurements from individual patients can be incorporated into mathematical models so that the results generated are patient specific. Also, longitudinal studies can be performed and these can be used to verify or modify the models themselves; more specifically, imaging data obtained early during therapy can be used to make predictions which can then be compared to experimental data obtained at a later time point. In this way such models can in practice be assessed for accuracy, and insights can be gained into how a given model should be modified.

The prediction of the response of tumors early in the course of therapy is of fundamental clinical importance. Mathematical modeling based on imaging data may provide a way to predict the state of a tumor at later time points, thereby providing clinicians an ability to modify or change treatments. We and others have previously shown in simulation (Atuegwu et al., 2010; Yankeelov et al., 2010; Konukoglu et al., 2010; Hogea et al., 2007, 2008; Jbabdi et al., 2005) and experiments (Konukoglu et al., 2010; Hogea et al., 2007, 2008; Jbabdi et al., 2005) how imaging data can be incorporated into mathematical models of tumor growth and treatment response. Here we focus on using measurements made with diffusion weighted magnetic resonance imaging (DW-MRI) as initial conditions for a simple mathematical model of tumor growth.

DW-MRI relies on the phenomenon that water molecules in tissues constantly undergo random Brownian motion and diffuse at a rate that is dependent on tissue microstructure. The rate of water diffusion within tissues measured by conventional MR methods are often summarized in terms of an apparent diffusion coefficient (ADC), which is a measure of the effective distance over which water can migrate within tissue within a specified time. Several clinical and animal studies have confirmed the ability of ADC to report on changes in tumor cellularity at some time after treatment. (Galons et al., 1999; Zhao et al., 1996; Chenevert et al., 1997; Hall et al., 2004; Stegman et al., 2000). Furthermore, several investigators have used DW-MRI and its extension, diffusion tensor imaging (DTI), to model how brain tumors grow or respond to treatment.

Konukoglu et al proposed a parameter estimation method for the reaction–diffusion growth model using time series of both synthetic and patient tumors (Konukoglu et al., 2010). The parameters estimated include rate of diffusion of tumor cells in gray and white matter, and the time elapsed since the tumor cells started diffusing. They used synthetic tumors to show the coupling between the parameters of the reaction-diffusion models and were able to estimate tumor cell diffusion in gray and white matter and also the time elapsed since the tumor started diffusing by fixing the proliferation rate of the tumor cells to values found in the literature. For the patient data, they used DTI coupled with prior time series of T₁- or T₂-weighted MR images to estimate the tumor cell diffusion in gray and white matter. They then used the estimated rate of diffusion of tumor cells in gray and white matter to simulate the evolution of the tumor delineation and then compared the simulated results to the observed tumor delineation from a T₁ or T₂ image at a later time point (Konukoglu et al., 2010).

Hogea et al modeled the mechanical effects of gliomas on the surrounding brain tissue using a non-linear reaction-advection–diffusion equation coupled with underlying tissue elasticity equations (Hogea et al., 2007). Using simulations they showed the growth of a synthetic glioma with varying tumor cell diffusivity levels. They also used T₁ images of dogs with implanted brain tumors and T₁ images of a human brain tumor patient to show the improvement of their proposed model over incremental pressure models in predicting the position of selected landmarks in the brain (Hogea et al., 2007). In a separate study, Hogea et al used an adjoint based PDE-constrained optimization to estimate the parameters of a reaction diffusion model of tumor growth and the mechanical impact of the growth on the surrounding tissue in simulation (Hogea et al., 2008). Some of the parameters include tumor cell proliferation rate, variables that control the mechanical deformation of the brain tissue and variables that control the radius, center, and initial number of tumor cells. They used MR images acquired from a human brain cancer patient at two time points to estimate the initial tumor cell density, tumor cell diffusivity in white matter, tumor growth and tumor mass effect. They chose landmarks in the patient’s brain and then used the model to minimize the mismatch between the predicted and the actual landmarks (Hogea et al., 2008).

Jbabdi et al used DTI information in conjunction with a proliferation diffusion model of brain tumor growth to simulate low grade gliomas in a virtual brain provided by a 3D MRI atlas. By fixing tumor cell proliferation to values from the literature, and DTI data from a healthy brain, they estimated the direction of the tumor cell diffusion along fiber tracks and then visually compared the simulated results to the MR images of patients with grade II gliomas (Jbabdi et al., 2005).

These prior studies have focused on predictions of where tumor cells will proliferate based on mechanical constraints and, in general, have not used individual patient data to estimate the rates of growth. The goal of this work is to use only imaging data as input into a simple mathematical model of tumor growth and treatment response. The results from the model will be subject specific. For the mathematical modeling, we build on previous work (Atuegwu et al., 2010; Yankeelov et al., 2010) to show how DW-MRI data can be used to estimate proliferation rates in a 9L model of rat brain cancer for animals treated with the chemotherapeutic drug 1,3-bis(2-chloroethyl)-1-nitrosourea (BCNU or Carmustine) and control animals that were not treated with the drug. Two sets of analyses were performed: voxel based and a region of interest (ROI) based analysis. The DW-MRI data at early time points were used to generate ADC maps that were then used to estimate the proliferation rates of the tumor at both the voxel and ROI level. The proliferation rates were then used to predict the tumor cell density values at a later time point and these were compared to the experimentally measured values at that time point. Also, the proliferation rate was used to calculate a novel proliferation value ratio (PVR) that was used to separate the treated and the control animals after one day of treatment.

2. Materials and Methods

2.1 Animal Model

All procedures in this study were approved by Vanderbilt University’s Institutional Animal Care and Usage Committee. Thirteen male Fischer 344 rats, weighing approximately 250 g, were anesthetized with a 2%/98% isoflurane/oxygen mixture and inoculated intracranially with approximately 10⁵ 9L glioblastoma cells. Eight of the rats were treated with BCNU and five rats were used as untreated, tumor-bearing controls. The tumors were allowed to develop untreated for 11-12 days. All animals were then imaged immediately before (day 0), one day and three days after treatment. The control animals were also imaged on those three days (days 0, 1 and 3).

2.2 Treatment protocol

BCNU is an antineoplastic chemotherapy drug and it has been shown to be effective in the treatment of the 9L tumor model (Chenevert et al., 1997). Treatment solutions were prepared by dissolving a 13.3 mg/kg powdered dose in ethanol, and diluting with saline to achieve a 10/90% ethanol/saline solution totaling approximately 1 mL in total volume. The dose of 13.3 mg/kg has been shown in previous studies to produce an approximate 0.8 log cell kill in 9L tumors (Ross et al., 1998). Control animals received vehicle only (1 mL of 10/90% ethanol/saline). The treatment protocol consisted of a single intraperitoneal injection of BCNU or control injection immediately following the initial imaging session (day 0).

2.3 In vivo imaging

The protocol is described in detail in (Colvin et al., 2011) here we present only the salient features. Approximately eleven days following tumor inoculation, MR images were obtained using a Varian 4.7T Inova imaging system (Palo Alto, CA, USA). Animals were anesthetized with a 2%/98% isoflurane/oxygen mixture, and kept at a constant body temperature of 37° C. The animals were positioned using a rigid bite bar and head restraints. Images were acquired using a quadrature 63 mm radiofrequency coil. On the first day of imaging for each animal, a multi-slice, T₂-weighted fast spin echo scan with 4 echoes (TR = 2000 ms, 16 ms echo spacing, 256×128 matrix, 48×32 mm² FOV, 1 mm slice thickness) was acquired in the coronal plane for locating the tumor region. A 2 mm single axial slice with the same timing parameters, but with a FOV = 32×32 mm² through the central portion of the tumor was acquired. The same slice was then imaged using a pulsed gradient spin echo diffusion-weighted scan with b-values of 0 and 400 s/mm², TR/TE = 2300/75.4 ms, 64×64 matrix size, 2 mm slice thickness, 32×32 mm² FOV, NEX = 10, gradient duration δ = 3 ms, and diffusion interval Δ = 30 ms. An additional pulsed gradient spin echo diffusion-weighted scan at the b = 400 s/mm² value was also obtained with reversed gradient polarity, and averaged with the first to eliminate the presence of gradient cross-terms when the apparent diffusion coefficient (ADC) is computed as described below (Neeman et al., 1991). The diffusion gradients were placed along all three imaging coordinate axes at the same time to maximize the diffusion weighting with the available gradient amplitudes.

As the ADC measurements will be compared at multiple time points in order to facilitate modeling, it is imperative that the selection of the imaging plane is consistent. The co-localization of the central portion of the tumor from the pre- to post-treatment time points was achieved by registering the data obtained at the last two time points to that acquired at the first time point. More specifically, on each day of scanning, a 3D gradient echo image dataset (TR/TE = 25/2.2 ms, FOV = 48×32×32 mm³, matrix = 128×96×96, NEX = 8) encompassing the whole brain was collected. On days 1 and 3 following treatment, these 3D images were co-registered, via a mutual information based rigid registration algorithm (Wells Iii et al., 1996), to the initial 3D image collected on day 0 in order to derive the translation and rotation matrices of the animal’s position with respect to the animal’s pre-treatment position in the laboratory reference frame. That is, on imaging sessions 2 and 3 (days 1 and 3 after treatment, respectively), the 3D data were acquired and exported to Matlab, while the animal was still in the scanner, to determine the translation and rotation transformations needed to register these data to the initial imaging day data. After the transformations were applied, it allowed for the determination of the lab coordinates needed to acquire the DW-MRI data from the same slice of tissue acquired at the initial time point. More details on the registration procedure are provided in (Colvin et al., 2011)

2.4 Image analysis

ADC values were obtained by fitting the attenuated signal in each voxel, S, to Eq. (1):

$$S=S_0{e}^{-b\cdot ADC},$$ (1)

where S₀ is the signal in the absence of diffusion weighting, and b represents the amount of diffusion-weighting imparted to the sample (Stejskal and Tanner, 1965). Whole tumor ROIs were drawn and segmented from the pre-treatment scan and then copied onto the images obtained at subsequent time points. The voxels within the ROI were then used for mathematical modeling.

2.5 Mathematical Modeling

We start with the simple logistic model that describes growth of the number of tumor cells which asymptotically approaches the limiting cellular carrying capacity for a given region of space. This model is explained in detail in (Byrne, 2003) and the relevant equation is

$$N(r,t)=\frac{\theta N(r,0)}{N(r,0)+(\theta -N(r,0))e^{-k\left(r\right)t}},$$ (2)

where N(r,t) is the number of cells per voxel at position r and time t, N(r,0) is the number of cells present at t = 0 and position r, k(r) is the cell proliferative rate at position r, and θ is the cell carrying capacity of the population. The carrying capacity is assumed to be the maximum number of cells that can be contained in a voxel. This was calculated by dividing the voxel volume by the average 9L cell volume which we computed by assuming a spherical shape and a nominal radius of 10 μm.

To estimate the number of cells in each voxel in each day, we assumed a linear relationship between the ADC values of the voxels obtained from Eq. (1). This is a fairly conservative assumption because there is substantial literature evidence supporting it. For example, several studies have shown a strong negative correlation between ADC and cellularity (Sugahara et al., 1999; Chenevert et al., 2000; Hayashida et al., 2006; Anderson et al., 2000; Lyng et al., 2000). In particular, it has been shown that ADC decreases linearly with cell volume fraction (Anderson et al., 2000) and cell density (Lyng et al., 2000; Hayashida et al., 2006; Kono et al., 2001) .We therefore used this relationship to convert ADC values to cell number. To do this conversion, we assumed that the maximum number of cells in a voxel, θ, will occur in the voxel with the minimum ADC value, while the voxel with ADC value of free water ADC_w will contain no tumor cells. This allows us to define the following mapping between ADC and cell number:

$$\frac{ADC(r,t)-AD{C}_w}{AD{C}_{\text{min}}-AD{C}_w}=\frac{N(r,t)}{\theta },$$ (3)

By rearranging Eq. (3), we get Eq. (4):

$$ADC(r,t)-AD{C}_w=N(r,t)\times \frac{(AD{C}_{\text{min}}-AD{C}_w)}{\theta }.$$ (4)

Eq. (4) can be simplified to Eq. (5) by rearranging terms:

$$ADC(r,t)=AD{C}_w-\lambda N(r,t),$$ (5)

where

$$\lambda =\frac{(AD{C}_w-AD{C}_{\text{min}})}{\theta }.$$ (6)

Combining Eqs. (2), (5) and (6) gives Eq. (7) as previously described (Yankeelov et al., 2010):

$$\left(\frac{ADC(r,t)-AD{C}_{min}}{ADC(r,t)-AD{C}_w}\right)=\left(\frac{ADC(r,0)-AD{C}_{min}}{ADC(r,0)-AD{C}_w}\right)e^{-k\left(r\right)t}.$$ (7)

The ADC data from days 0 and 1 were used with Eq. (7) to extract the proliferation rate k(r) of the tumor cells in each voxel position r. Since the half-life of BCNU in vivo is less than 15 minutes (Lee et al., 2005), we assumed that the concentration of the drug was negligible after a few hours and, therefore, the effect on tumor cell proliferation was (essentially) instantaneous. The ADC values from days 1 and 3 were then converted to cell number using Eqs. (5) and (6) to yield an estimate of the number of cells on days 1, N_estimated(r,1) and N_estimated(r,3), respectively. The number of cells within the tumor on day 3 was then calculated, N_calculated(r,3), via Eq. (2) using the calculated proliferation rates and the number of cells in each voxel at day 1 as inputs. The estimated and calculated values were then compared as described below.

In addition to the voxel-by-voxel comparison between the estimated and calculated values, we also performed ROI based comparisons. To do this, the mean ADC values for each tumor ROI for each rat and for each day were calculated. The mean ADC values for days 0 and 1 were then used to calculate the mean proliferation rate k_mean using Eq. (7). N_{estimated_mean}(1) and N_{estimated_mean}(3) (i.e., the mean number of cells on days 1 and 3, respectively) were then calculated using Eqs. (5) and (6). Finally, k_mean was used with N_{estimated_mean}(1) to calculate N_{calculated_mean}(3) using Eq. (2) which was then compared to N_{estimated_mean}(3).

2.6 Effects of smoothing on voxel level analysis

In order to explore the effects of signal-to-noise (SNR) on the results of the modeling, we convolved the voxel level ADC values from days 0, 1 and 3 with a mean filter of varying kernel sizes to reduce the noise in the images. This has the effect of eliminating spurious voxel values which are not representative of their surroundings and increasing the SNR of the image. We hypothesized that an increase in SNR achieved by smoothing the ADC images before modeling would increase the correlation between the calculated and the estimated number of cells at day 3. We used three different kernel sizes [2×2], [4×4], and [8×8] with the degree of smoothing increasing with increasing kernel size. The ADC values obtained after smoothing were used to calculate new k(r), N_estimated(r,3), and N_calculated(r,3) values for all data sets as described in section 2.5.

2.7 Proliferation value ratio (PVR)

We hypothesized that tumors that were treated with BCNU would display a larger number of negative k values than the control group. To test this hypothesis, we constructed a simple measure we term the proliferation value ratio (PVR):

$$PVR=\frac{number(k<0)}{number(k<0)+number(k>0)},$$ (8)

where number(k<0) are the number of proliferation values that are less than zero and number(k>0) are the number of proliferation values that are greater than zero in a particular ROI. The PVR was calculated for both the tumor ROI and an ROI in the healthy appearing contralateral brain. The ROI in the healthy appearing contralateral brain was an identical size as the one used to circumscribe the tumor, and placed symmetrically across from where the tumor was located (an example is seen in Figure 1 below). The PVR was calculated from different combinations of ADC data: days 0 and 1, days 1 and 3, and days 0 and 3. The mean ADC value was also calculated for the tumor ROI and healthy appearing contralateral brain for days 0, 1 and 3.

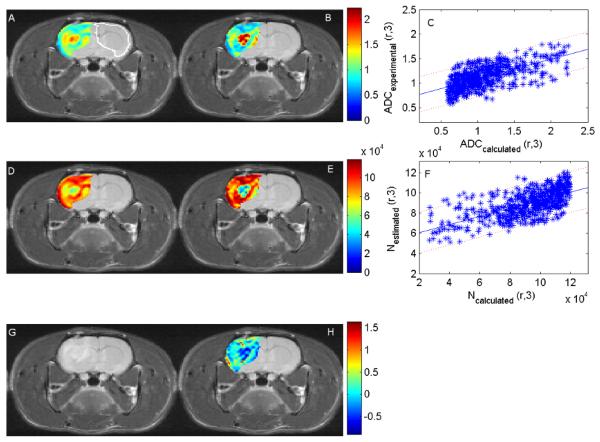
Figure 1.

The panels display an axial cross section through a rat brain with a tumor in the left hemisphere. Panels A and B are the experimental and the calculated ADC values (×10⁻³ mm²/s), respectively. The white outline in panel A was used to calculate the parameters for the contralateral tissue for comparison to the tumor values. Panel C compares these values with the 95% confidence interval indicated by the dotted lines. Similarly, panels D and E present the estimated and calculated number of cells at day 3, respectively, and Panel F compares these values with the 95% confidence interval indicated by the dotted lines. As in the case of the ADC values the Pearson’s correlation coefficient between the calculated and the estimated number of tumor cells is 0.65. Finally, panels G and H depict an anatomical T2 weighted image and the proliferation map calculated from ADC values on days 0 and 1. While the absolute values of the two methods do not quite match, there is general agreement in distribution between the estimated and calculated number of cells at day 3 and between the experimental and the calculated ADC values at day 3.

2.8 Statistical Analysis

Six different statistical analyses were performed on the data sets:1) the Pearson correlation coefficient was used to compare voxel based N_calculated(r,3) and N_estimated(r,3) values for each rat; 2) the concordance correlation coefficient (Lin, 1989) was used to compare voxel based N_calculated(r,3) and N_estimated(r,3) values for each rat; 3) the Pearson correlation coefficient was calculated for the ROI based N_{calculated_mean}(3) and N_{estimated_mean}(3) values for all animals grouped together; 4) the concordance correlation coefficient was calculated for the ROI based N_{calculated_mean}(3) and N_{estimated_mean}(3) values for all animals grouped together; 5) the Wilcoxon test was used to assess the statistical differences between the PVR of the control and treated groups for both the tumor and the contralateral ROIs for each animal; and 6) the Wilcoxon test was used to assess the statistical differences between the ADC of the control and treated groups for both the tumor and the contralateral ROIs for each animal. These tests were then repeated for the smoothed data.

3. Results

Figure 1 shows the experimental and the calculated ADC maps at day 3, N_estimated(r,3) and N_calculated(r,3), and the proliferation parametric maps superimposed on the corresponding T₂-weighted anatomical MR image. Panel A is the experimentally measured ADC value at day 3 obtained from the DW-MRI data, panel B is the calculated ADC value at day 3 obtained by converting the N_calculated(r,3) to ADC values using Eq. (5), and panel C is the experimental versus the calculated ADC values with the 95% confidence interval shown. (Panel A also contains the outline of the ROI used to calculate the contralateral brain tissue parameters.) The correlation coefficient between the experimental and the calculated ADC values is 0.65. Panel D is the experimentally derived estimate of the number of cells at day 3, N_estimated(r,3), panel E is the calculated number of tumor cells at day 3, N_calculated(r,3), and panel F is a plot of the estimated versus the calculated number of cells with the 95% confidence intervals displayed. Panel G is the T₂-weighted MRI at day 3 for anatomical reference, and Panel H is the map of the proliferation rate k(r) obtained using Eq. (7) in conjunction with the ADC values from days 0 and 1. Panels D and E show that although the absolute values for the data do not precisely match, the calculated and the estimated data follow a similar spatial distribution and relative values. For example, trends such as the necrotic core and regions of higher cell values are in similar positions in the calculated and the estimated maps. The individual Pearson’s and concordance correlation coefficients between N_calculated(r,3) and N_experimental(r,3) for all tumor voxels within each rat were calculated and these are shown in Table 1. The Pearson correlation coefficient ranged from −0.06 to 0.65 and the concordance correlation coefficient ranged from −0.06 to 0.58.

Table 1.

The Pearson’s and concordance correlation coefficients between the N_calculated(r,3) and N_experimental(r,3) for both the control and the treated rats.

Rats	Pearson’s correlation coefficient	Concordance correlation coefficient
R1-C	0.08	0.08
R2-C	0.29	0.17
R3-C	0.61	0.58
R4-C	0.14	0.08
R5-C	−0.06	−0.06
R6-T	0.59	0.30
R7-T	0.53	0.36
R8-T	0.17	0.11
R9-T	0.65	0.58
R10-T	0.20	0.09
R11-T	0.62	0.54
R12-T	0.36	0.15
R13-T	0.34	0.19
Mean ± 1.96·SE	0.35 ± 0.13	0.24 ± 0.11

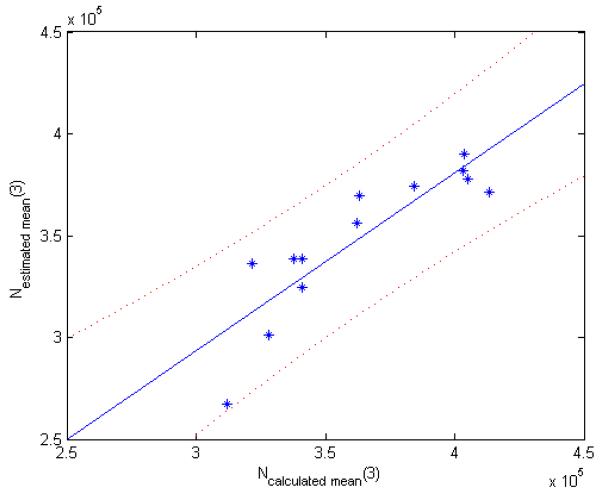
For the ROI analysis, the mean number of cells on day 3 for both the calculated, N_{calculated_mean}(3), and the estimated, N_{estimated_mean}(3), number of cells are shown in Figure 2. The 95% confidence interval is also shown. The Pearson’s correlation coefficient between N_{calculated_mean}(3) and N_{estimated_mean}(3) for all the rats is 0.88 (p = 0.0001) with a 95% confidence interval of (0.63,0.96). This indicates that there is a strong correlation between the calculated and the estimated number of cells on day 3. The concordance correlation coefficient between N_{calculated_mean}(3) and N_{estimated_mean}(3) across all animals is 0.80 with a 95% confidence interval of (0.49,0.93). This also indicates that there is a strong agreement between the N_{calculated_mean}(3) and N_{estimated_mean}(3) and that this relationship nearly falls along the line of unity.

Figure 2.

The figure displays a graph of the ROI average N_{Cakuiated_mean}(3) versus N_{estimated_mean}(3) for each rat with the 95% confidence interval displayed as dotted curves. Each point in the image represents one animal. There is a strong correlation between the mean estimated and the mean calculated number of cells in day 3 with a Pearson’s correlation coefficient of 0.88 (p = 0.0001) with a 95% confidence interval of (0.63, 0.96) for all the rats. The concordance correlation coefficient between N_{calculated_mean}(3) and N_{experimental_mean}(3) for all rats is 0.80 with a 95% confidence interval of (0.49, 0.93).

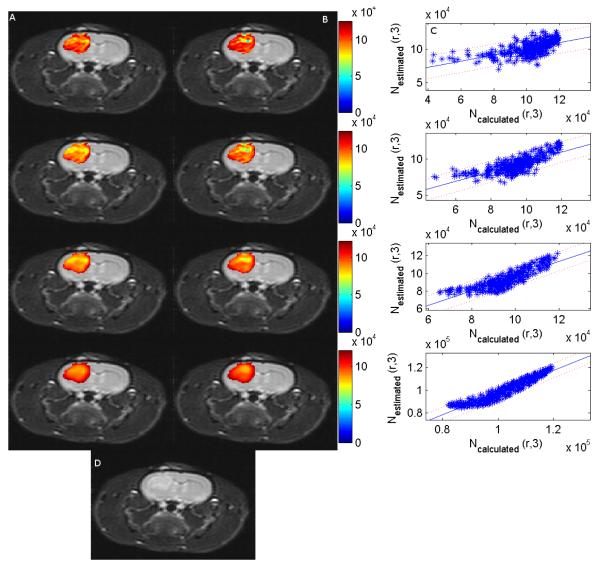
The effect of applying a smoothing filter on the ADC values at days 0, 1 and 3 is shown in figure 3. Column A is the estimated number of cells at day 3, column B is the calculated number of cells at day 3, and column C is a scatter plot of the calculated versus the estimated number of cells at day 3. Panel D is the T₂-weighted image of the rat at day 3. Each row increases the kernel size and therefore the degree of smoothing. The Pearson’s and the concordance correlation coefficients between the estimated and the calculated number of cells increases as the kernel size increases (see tables 2 and 3). The Pearson’s correlation ranged from (−0.06 to 0.65) for no filtering, and then (0.12 to 0.88), (0.18 to 0.94) and (0.60 to 0.99) for kernel sizes of 2×2, 4×4 and 8×8, respectively. The concordance correlation ranged from (−0.06 to 0.58) for no filtering, and then (0.11 to 0.79), (0.14 to 0.88) and (0.36 to 0.95) for kernel sizes of 2×2, 4×4 and 8×8, respectively. This indicates that the weak to moderate correlation found in the voxel level data may be due to the relatively low SNR in the acquired DW-MR images and small errors in coregistration between images. We return to this point in the Discussion section.

Figure 3.

Columns A and B display an axial cross section through a rat brain with the experimentally determined number of cells at day 3 and the calculated number of cells at day 3, respectively. Column C is the corresponding plot of the calculated and the experimental number of cells at day 3 with the 95% confidence interval displayed. Panel D is the T₂ weighted image at time 3.The different rows correspond to different degrees of smoothing with row 1 corresponding to the original image with no smoothing with a Pearson’s correlation of 0.61 between the experimental and the calculated number of cell at day 3; row 2 correspond to a convolution with a 2×2 averaging filter (r = 0.76); row 3 corresponds to a convolution with an 4×4 averaging filter (r = 0.86); and the last row corresponds to a convolution with an 8×8 averaging filter (r = 0.95). As the filter width increases, the correlation between the experimental and the calculated number of cells at day 3 increases which indicates that the weak correlation between the experimental and the calculated number of cells without filtering may be due to the relatively low SNR at which the images were acquired. However, as the smoothing increases, the fine details of the tumor are lost.

Table 2.

The Pearson’s correlation coefficients of the treated and control animals.

	Pearson’s correlation coefficient
Rats	No filtering	2×2	4×4	8×8
R1-C	0.08	0.47	0.65	0.84
R2-C	0.29	0.66	0.83	0.96
R3-C	0.61	0.76	0.86	0.95
R4-C	0.14	0.37	0.58	0.84
R5-C	−0.06	0.12	0.18	0.60
R6-T	0.59	0.71	0.78	0.93
R7-T	0.53	0.73	0.74	0.93
R8-T	0.17	0.50	0.73	0.91
R9-T	0.65	0.75	0.83	0.92
R10-T	0.20	0.78	0.88	0.93
R11-T	0.62	0.88	0.94	0.99
R12-T	0.36	0.82	0.89	0.96
R13-T	0.34	0.60	0.75	0.92
Mean ± 1.96·SE	0.35±0.13	0.63±0.12	0.74±0.11	0.90±0.05

Table 3.

The concordance correlation coefficients of the treated and control animals with different degrees of averaging smoothing.

	Concordance correlation coefficient
Rats	No filtering	2×2	4×4	8×8
R1-C	0.08	0.41	0.51	0.67
R2-C	0.17	0.57	0.73	0.90
R3-C	0.58	0.74	0.84	0.93
R4-C	0.08	0.29	0.47	0.71
R5-C	-0.06	0.11	0.14	0.36
R6-T	0.30	0.36	0.35	0.44
R7-T	0.36	0.71	0.71	0.90
R8-T	0.11	0.44	0.67	0.86
R9-T	0.58	0.71	0.78	0.89
R10-T	0.09	0.70	0.84	0.93
R11-T	0.54	0.75	0.78	0.80
R12-T	0.15	0.79	0.88	0.95
R13-T	0.19	0.41	0.52	0.66
Mean ± 1.96·SE	0.24±0.11	0.54±0.12	0.63±0.12	0.77±0.10

The proliferation value ratio (PVR) and the mean ADC value were calculated for the tumor ROI and the healthy appearing contralateral brain for each rat and are summarized in tables 4 and 5. The PVR was calculated for the control and treated rats using the data from days 0 and 1, 1 and 3, and 0 and 3. Using the data from days 0 and 1, the average tumor PVR for the control and treated rats were 0.33 and 0.55, respectively; this represented a statistically significant difference (p = 0.045) that grew more significant using the day 1 and 3 data (p = 0. 003) or the day 0 and 3 data (p = 0.006). Conversely, the average ADC values (in units of ×10⁻³ mm²/s) for the control and treated rats on day 0 were 0.83 and 0.87, respectively, and 0.78 and 0.88, respectively, for day 1; importantly, neither of these represented a statistically significant difference. It was not until day 3 when the average ADC of the two groups were 0.79 and 1.00, respectively, that a statistically significant difference appeared (p = 0.002).

Table 4.

The tumor PVR and the mean tumor ADC values for both the control and the treated rats.

Tumor (PVR)				Mean Tumor ADC (×10−3 mm2/s)
Rats	Day 0–1	Day 1–3	Day 0–3	Day 0	Day 1	Day 3
R1-C	0.40	0.58	0.52	0.76	0.74	0.82
R2-C	0.45	0.25	0.27	0.79	0.78	0.72
R3-C	0.20	0.36	0.27	0.84	0.78	0.74
R4-C	0.42	0.74	0.60	0.80	0.77	0.86
R5-C	0.18	0.38	0.22	0.95	0.85	0.79
R6-T	0.09	0.82	0.41	0.89	0.78	0.86
R7-T	0.89	0.82	0.96	0.76	0.84	0.99
R8-T	0.62	0.60	0.66	1.01	1.04	1.11
R9-T	0.44	0.74	0.74	1.05	1.05	1.12
R10-T	0.60	0.83	0.83	0.81	0.83	0.90
R11-T	0.49	0.83	0.74	0.76	0.75	0.87
R12-T	0.79	1.00	0.99	0.80	0.87	1.07
R13-T	0.47	0.96	0.94	0.85	0.85	1.11

Table 5.

The contralateral brain PVR and mean ADC values

Contralateral (PVR)				Mean contralateral ADC (×10−3 mm2/s)
Rats	Day 0–1	Day 1–3	Day 0–3	Day 0	Day 1	Day 3
R1-C	0.81	0.41	0.48	0.83	0.92	0.86
R2-C	0.70	0.99	1.00	0.68	0.74	0.93
R3-C	0.02	0.77	0.13	0.91	0.76	0.81
R4-C	0.23	0.97	0.94	0.85	0.81	0.99
R5-C	0.73	0.10	0.17	0.86	0.90	0.77
R6-T	0.89	0.09	0.17	0.84	0.91	0.78
R7-T	0.56	0.19	0.26	0.89	0.91	0.86
R8-T	0.41	0.86	0.87	0.85	0.83	0.95
R9-T	0.04	0.61	0.23	0.93	0.83	0.89
R10-T	0.04	1.00	0.99	0.70	0.57	0.86
R11-T	0.42	0.14	0.10	0.86	0.85	0.78
R12-T	0.18	0.00	0.08	0.94	0.85	0.71
R13-T	0.05	0.73	0.30	0.94	0.79	0.88

Using the data from days 0 an 1, the average PVR for the healthy appearing contralateral brain for the control and treated rats were 0.50 and 0.32, respectively; similar values were found using the day 1 and 3 (0.65 and 0.45, respectively) or day 0 and 3 (0.54 and 0.38, respectively) data. The average ADC values (again, in units of ×10⁻³ mm²/s) for the healthy appearing contralateral brain for both the control and treated rats were 0.83 and 0.87, respectively, for day 0, with very similar values for days 1 and 3. Neither the mean ADC nor the PVR of the contralateral brain could be used to separate the control and treated animals at day 1 (p = 0.354 and 0.524, respectively), or day 3 (p = 0.622 and 0.435, respectively). These data show that the separation of the rats into control and treated rats is due to the characteristics of the tumor and not those of the healthy appearing brain. Table 6 summarizes these results of the Wilcoxon tests.

Table 6.

The p-values of the Wilcoxon tests for the PVR and the mean ADC values

	Day 0–Day 1	Day 1 – Day 3	Day 0 – Day 3
Tumor PVR	0.045	0.003	0.006
Contralateral PVR	0.524	0.435	0.435
	Day 0	Day 1	Day 3
Tumor ADC	0.622	0.127	0.002
Contralateral ADC	0.354	0.833	0.622

Smoothing filters of varying kernel sizes were also applied to the tumor ROI and the contralateral brain. The smoothed data were then used to calculate the PVR and the mean ADC values. A Wilcoxon test was used to separate the PVR and the mean ADC of the rats into control and treated groups. The PVR can separate the control and the treated rats as early as day 1 after treatment for all the kernel sizes except for the 8×8 kernel, while the mean ADC cannot separate the rats until day 3 after treatment for all the kernel sizes except for the 8×8 kernel. The lack of separation of the treated and the control rats when the 8×8 kernel filter is used may be due to the fact that the fine details in the tumor are lost as the kernel size increases. The mean ADC and the PVR of the contralateral brain could not be used to separate the control and the treated animals for all the different degrees of smoothing. Again, this shows that regardless of the increase in SNR due to smoothing, the separation of the rats into the treated and control groups is due to the tumor characteristics and not due to those of the healthy appearing brain. The results are summarized in table 7.

Table 7.

The p-values of the Wilcoxon tests for the PVR and the mean ADC values for the different sizes of the smoothing kernel.

	Day 0–Day 1	Day 1 – Day 3	Day 0 – Day 3
Tumor PVR
No Filter	0.045	0.003	0.006
2×2	0.045	0.006	0.006
4×4	0.030	0.006	0.006
8×8	0.065	0.006	0.006
Contralateral PVR
No Filter	0.524	0.435	0.435
2×2	0.524	0.435	0.555
4×4	0.452	0.376	0.458
8×8	0.331	0.342	0.653
	Day 0	Day 1	Day 3
Tumor ADC
No Filter	0.622	0.127	0.002
2×2	0.833	0.222	0.006
4×4	0.943	0.171	0.030
8×8	1.000	0.524	0.127
Contralateral ADC
No Filter	0.354	0.833	0.622
2×2	0.622	1.000	0.435
4×4	0.724	0.943	0.524
8×8	0.833	0.724	0.354

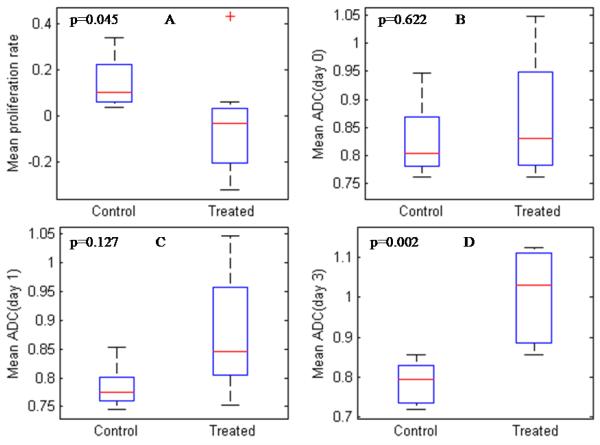
Figure 4 shows a box plot of the mean proliferation rate calculated from days 0 and 1 and the mean ADC values from days 0, 1 and 3. These are represented by panels A, B, C and D, respectively. The box plots show that the mean proliferation rate for the treated and the control animals can be used to separate the rats into their respective groups. This is not unexpected since the PVR can also be used to separate the rats into the two groups. The mean ADC values cannot be used to separate the rats into the two groups until day 3.

Figure 4.

Panel A is a box plot of the mean proliferation rate estimated from days 0 and 1, while panels B, C and D are box plots of the mean ADC from days 0, 1 and 3, respectively. The mean proliferation rate can be used to separate the treated and the control animals (obtained from days 0 and 1; panel A) while the mean ADC cannot separate the treated and the control animals until day 3 (panel D).

4. Discussion

We have shown how ADC values computed from DW-MRI can be used to estimate tumor cell proliferation values via the logistic model of tumor growth. The results of the proliferation rates were then used to predict the tumor cell numbers at a later time point on both the voxel and ROI levels. The proliferation values were also used to separate the treatment and control groups early during the course of therapy. The proliferation value ratio was calculated and used to separate the treated and control tumor cell lines before differences in the mean ADC value could be used to separate the groups and before changes in the tumor volume are observed. In general, the mean PVR was lower for the control animals than the treated animals. This is because the treated animals have a lower proliferation rate and/or a higher cell death due to the application of the drug. It is important to note that the PVR of the contralateral brain with and without the application of a smoothing filter could not be used to separate the rats into the treated and control groups, thereby showing that the separation was due to the tumor and not brain characteristics. This ratio offers the possibility to detect changes in tumor status as early as 24 hours after BCNU treatment and shows the possibility of extending ADC measurements to predict treatment response earlier than mean ADC changes.

The correlations between the calculated and the estimated number of cells on day 3 for the voxel based analysis performed on individual rats show a range from very weak correlation to moderately strong. However, using the mean value of the ADC in the tumor ROI resulted in a strong and significant relationship between the simulated and estimated data. We hypothesized that the combination of the modest relationship at the voxel level and the strong relationship at the ROI level may be due to the relatively low SNR at which the data were collected and, perhaps, subtle registration errors in the slice selection. To test this hypothesis we smoothed the ADC values with a mean filter which resulted in a substantial increase in the strength of correlation between simulated and estimated data, though the process does erode intrinsic spatial heterogeneity within the tumors. Analysis of the data with the mean ADC and the filtered ADC shows a much greater correlation between the estimated and calculated number of cells at day 3. Even though the correlation is greater it is not perfect as shown by the fact that the origin was not included in the 95% confidence interval and also the fact that the line of best fit for the point cloud does not pass through the origin (see Figure 3). Nevertheless, an increase in correlation when the smoothed ADC data were used shows the possibility of using sequential ADC data as a way to model tumor growth and treatment response if sufficient SNR can be achieved.

Some of the limitations in the work include the fact that we assume that the voxels are comprised only of tumor cells thereby ignoring the loose packing of tumor cells in the voxel, and the fact that each voxel contains healthy brain and associated supportive cells and matrix. We also did not incorporate vascular characteristics in the tumor model. This may be accomplished by, for example, adding measurements obtained using dynamic contrast enhanced MRI (DCE-MRI) into the models. We also did not include the effects of cell motility in our model. However, given the length of time over which imaging data were acquired (3 days), and that there were not any substantial changes in tumor volume or shape, the importance of tumor cell motility on bulk tumor shape in our modeling exercise is, perhaps, limited. We also assumed that the proliferation rate can be predicted from comparisons separated by only two days and that this rate remains constant and does not change significantly over the course of the experiment. For experiments of longer duration, this will almost certainly require amendment. Another simplifying assumption is that we assumed the change in ADC from the pre-treatment day to the first post-treatment day was due entirely to the reduction in cellularity. This may be a gross oversimplification as there are certainly other factors that may contribute to the change in ADC. Future improvements to the modeling scheme here may need to incorporate such biologically relevant changes. Of course, the approach presented here must ultimately be validated (or refuted) by direct correlation with histological measurements.

5. Conclusion

Sequential ADC data can be used to predict tumor cell values and treatment response at later time points. Prediction of growth based on early time points agrees with experimental imaging measurements at least for large ROIs. The extension to single studies may require further technical refinements in underlying image quality and coregistration.