Bursting as a source of non-linear determinism in the firing patterns of nigral dopamine neurons

Abstract

Nigral dopamine (DA) neurons in vivo exhibit complex firing patterns consisting of tonic single-spikes and phasic bursts that encode information for certain types of reward-related learning and behavior. Non-linear dynamical analysis has previously demonstrated the presence of a non-linear deterministic structure in complex firing patterns of DA neurons, yet the origin of this non-linear determinism remains unknown. In this study, we hypothesized that bursting activity is the primary source of non-linear determinism in the firing patterns of DA neurons. To test this hypothesis, we investigated the dimension complexity of inter-spike interval data recorded in vivo from bursting and non-bursting DA neurons in the chloral hydrate-anesthetized rat substantia nigra. We found that bursting DA neurons exhibited non-linear determinism in their firing patterns, whereas non-bursting DA neurons showed truly stochastic firing patterns. Determinism was also detected in the isolated burst and inter-burst interval data extracted from firing patterns of bursting neurons. Moreover, less bursting DA neurons in halothane-anesthetized rats exhibited higher dimensional spiking dynamics than do more bursting DA neurons in chloral hydrate-anesthetized rats. These results strongly indicate that bursting activity is the main source of low-dimensional, non-linear determinism in the firing patterns of DA neurons. This finding furthermore suggests that bursts are the likely carriers of meaningful information in the firing activities of DA neurons.

Introduction

The mesolimbic dopamine (DA) system is thought to be centrally involved in subserving reward and goal-directed behavior, and it has been implicated in the etiologies of numerous neuropsychiatric disorders, including schizophrenia, depression and drug addiction (Schultz, 1998, 2002; Chau et al., 2004; Girault & Greengard, 2004). Midbrain DA neurons in vivo produce highly complex firing patterns by switching between single-spiking and bursting modes (Bunney et al., 1973; Grace & Bunney, 1984a,b). DA neurons transmit reward-related signals to the striatum and prefrontal cortex by changing their firing patterns, which encode information for certain types of reward-related learning. Thus, understanding how DA neurons shape their firing patterns is of crucial importance for comprehending how the brain represents the reinforcement of specific behaviors (Cooper, 2002).

Recently, non-linear dynamical methods have demonstrated that the firing patterns of DA neurons, despite their complexity, exhibit a non-linear deterministic structure (Hoffman et al., 1995; Di Mascio et al., 1999; Lovejoy et al., 2001). Non-linear dynamical theory has shown that the irregularity of a time series need not be generated only by a stochastic process. Rather, deterministic systems can also generate highly complex and irregular behaviors because these systems can be exquisitely sensitive even to slight changes in their initial conditions or control parameters. Highly complex but deterministic (i.e. ‘chaotic’) temporal firing patterns have been observed in a variety of neuronal preparations (Chang et al., 1994; Debus & Sandkuhler, 1996; Kayser et al., 2009; Eyherabide & Samengo, 2010), especially in motor neurons (Brochini et al., 2011), suprachiasmatic nucleus (Jeong et al., 2003, 2005) and injured sensory neurons (Wan et al., 2000). However, the origin of non-linear determinism in the firing patterns of DA neurons is poorly understood.

A promising candidate for the origin of non-linear determinism in the firing of DA neurons is bursting activity that is believed to arise from interactions of various neural components of dopaminergic circuits (Overton & Clark, 1997). The degree of determinism in the firing patterning of DA neurons is decreased after experimentally reducing the interactions among individual components of DA circuits (Di Mascio et al., 1999; Hoffman et al., 2001), and bursting as a carrier of neural information has been given considerable support (Gonon, 1988; Schultz et al., 1997; Bayer et al., 2007). However, bursting has not yet been shown explicitly to be a source of non-linear determinism in the inter-spike interval (ISI) firing patterns of DA neurons.

The aim of the present study was therefore to assess whether bursts are a source of this non-linear determinism in the firing of DA neurons. The dimension complexity (DC) of ISIs recorded from bursting DA neurons of the substantia nigra (SN) in rats was compared with the DC of ISIs from non-bursting DA neurons. We also estimated the DC of inter-burst intervals (IBIs) for the ISI records from the bursting DA cells. Finally, we reduced the percentage of bursts in firing patterns of DA neurons using various anesthetics and examined non-linear determinism.

Materials and methods

In vivo single-unit recordings

All procedures were performed in accord with those outlined in the Guide for the Care and Use of Animals US Government Principles, PHS Policy and the Animal Welfare Act, and approved by the Yale Animal Care and Use Committee. Nineteen male Sprague–Dawley rats weighing between 250 and 400 g were anesthetized with chloral hydrate (400 mg/kg, i.p. initial dose, with supplemental doses administered via a lateral tail vein). A heating pad maintained body temperature at 36–38°C. DA neurons in the SN were identified and recorded extracellularly, as described previously (Bunney et al., 1973; Grace & Bunney, 1980, 1983). Glass microelectrodes were made using a Narishige electrode puller, filled with 0.5 M NaCl, and had an impedance between 5 and 15 MΩ. The electrode was lowered into the brain using a hydraulic-microdrive through a small burr hole drilled above the SN (2.8–3.2 mm anterior to the lamboidal suture, 2.0–2.5 mm lateral to the midline). DA neurons were normally found between 6.5 and 8.5 mm below the cortical surface. ISIs were recorded on-line via an interface (Lab-PC+; National Instrument, Austin, Texas, USA) to a PC computer, using in-house software written in LabView for Windows.

ISI firing patterns were recorded from 19 DA neurons for 60–100 min in 19 chloral hydrate-anesthetized rats (one neuron per animal). Eight of the recordings contained both bursts and single-spikes, while the remaining 11 recordings contained only single-spike trains. The mean number of data points was 23 625 ± 3943 (range: 15 039–33 124). For each recording, we discarded the first 2 min of data. We required spontaneous firing rates to vary less than 15% over the period in which the data were collected to help ensure the stationarity of the ISI sequences.

To obtain firing patterns with differing percentages of bursts, ISI sequences of 11 bursting DA neurons were additionally recorded from 11 rats anesthetized with halothane (1%), and were compared with those of eight bursting DA neurons recorded from the chloral hydrate-anesthetized rats (one neuron per animal).

Burst separation analysis

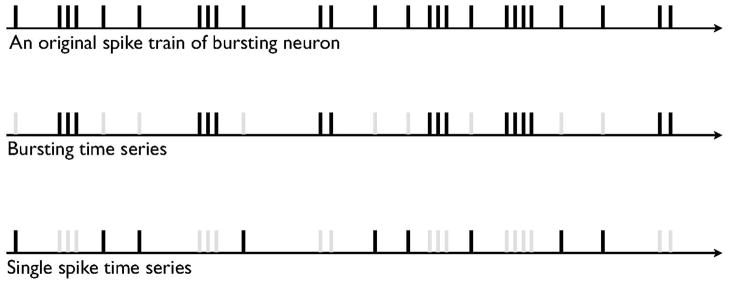
Although the details of the basic firing modes in DA cells depend on modulation of afferent inputs by behavioral stimuli (Hyland et al., 2002), single-spike firing is characterized by slow and irregular spike trains, whereas bursts consist of a series of high-frequency action potentials having a progressively decreasing spike amplitude and a progressively increasing spike duration. The presence of irregularity in firing patterns of the DA neurons was confirmed using coefficient of variation and the local variation (Shinomoto et al., 2009; Fig. 1). To determine whether bursts are a primary source of non-linear determinism in the firing patterns of DA neurons, we separated the ISI data recorded from individual recordings of bursting DA neurons into isolated burst time series and isolated single-spike-extracted time series, as shown in Fig. 1. Isolated single-spikes time series were obtained by eliminating the bursts from the original ISI sequences, and isolated burst time series were obtained by eliminating single-spikes from the original ISI sequences. This burst-elimination method was proposed previously (Prida et al., 1997). We determined ISI criteria to identify bursts on the basis of the valleys of a bimodal ISI histogram and a previously empirically derived criterion (Grace & Bunney, 1984a): the onset of a burst was defined as the concurrence of two spikes with an ISI < 80 ms, and all subsequent spikes were considered to be elements of the bursts unless an ISI exceeded 160 ms, which we took to signal the termination of a burst.

Figure 1.

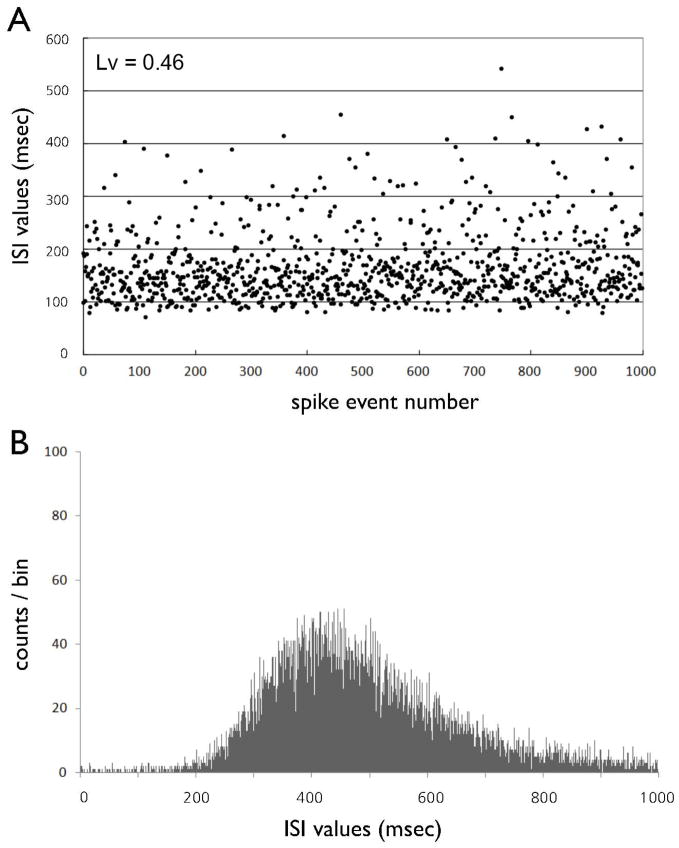
(A) The inter-spike interval (ISI) sequence of a typical non-bursting DA neuron as a function of time. (B) ISI histogram of a non-bursting DA neuron. The ISIs of the spike trains are typically distributed unimodally around an interval of 200–500 ms.

Non-linear dynamical analysis

Non-linear dynamical analyses assess whether a time series is governed by deterministic dynamics that have finite degrees of freedom, i.e. dynamics with finite dimensional complexity, or whether it arises from a random process that cannot be described by a finite number of variables (Jeong, 2002). Non-linear analyses are usually performed in phase-space. In n-dimensional phase-space, each state of the system corresponds to a single point in this space whose n coordinates are the values assumed by the governing variables for this specific state. If the system is observed through time, the sequence of points in phase-space forms a dynamical trajectory. This trajectory fills a subspace of phase-space that defines the system’s attractor.

In most biological systems, however, we are unable to obtain the actual underlying equations that generate complex behaviors, and can observe only temporal sequences of individual states or events {x(t)} that lie on that attractor. In practice, the attractor can be reconstructed in phase-space from the observed sequences {x(t)} by plotting delay coordinates using what is referred to as an embedding procedure (Eckmann & Ruelle, 1985). Here the delay coordinates y(t) = [x(t), x(t + T), …, x(t + (d − 1)T)] are constructed from an observed single time series x(t), where T is the time delay and d is the embedding dimension, to unfold the projection back to a multivariate phase-space that is a valid representation of the original deterministic dynamical system – the attractor thus reconstructed is topologically equivalent to the original dynamical system (Takens, 1981). Recently, a number of studies have shown that the techniques of nonlinear dynamical analysis are applicable to ISI sequences recorded from neurons or neuronal populations (Rapp et al., 1993, 1994; Chang et al., 1994; Sauer, 1994; Schiff et al., 1994; Hegger & Kantz, 1997).

DC is defined as the number of independent variables that are needed to describe fully the temporal dynamics of the system under study (Grassberger & Procaccia, 1983). The DC of a deterministic system is preserved as the embedding dimension increases, whereas the DC of a stochastic system increases without any limit, or saturation, as the embedding dimension increases. Values of the DC in DA ISI time series in this study were estimated using the Grassberger–Procaccia algorithm, and the optimal embedding dimension for this estimation was determined using the false nearest-neighbor method of Kennel et al. (1992; Appendix).

For the value of the time delay T in the embedding procedure, the first local minimum of the average mutual information between the set of measurement x(t) and x(t + T) are often used. Mutual information measures linear and non-linear dependence of two variables (Fraser & Swinney, 1986). However, for most ISI data sets, the average mutual information at one event interval is the first local minimum. Thus, T is set at 1 for ISI data sets.

In this algorithm, the DC calculation is based on determining the relative number of pairs of points in the phase-space data set that are separated by a distance less than r. It is computed as

$$DC=\underset{r\to 0}{lim}\underset{N\to \infty }{lim}\frac{logC(r,N)}{logr},$$ (1)

where the correlation integral C(r, N) is defined by

$$C(r,N)=\frac{2}{(N-W)(N-1-W)}\sum _{i=1}^N\sum _{j=i+1+W}^N\theta (r-\left|{\overrightarrow{x}}_i-{\overrightarrow{x}}_j\right|),$$ (2)

and where x_i and x_j are the points of the trajectory in the phase-space, N is the number of data points in the phase-space, the distance r is a radius around each reference point x_i, and θ is the Heaviside function, defined as 0 if x < 0, and 1 if x ≥ 0. W denotes the Theiler correction (Theiler, 1986) that is used to correct for temporal autocorrelation in the ISI time series.

For small values of r, a scaling property is exhibited: C(r, N) ∝ r^DC. For a self-similar (or fractal) attractor, the local scaling exponent is constant across a long range of r. This region having the constant local scaling exponent is termed a ‘scaling region’. If this plateau is present over a long range of r values, the scaling exponent can be used as an estimate of the DC. Thus, in practice, C(r, N) is plotted against r on a log-log scale to yield the DC as the slope of this curve over a selected range of r. In this study, the slope of the correlation integral curve in the scaling region was estimated using linear regression.

The DCs of the original DA ISI time series were compared statistically with the DCs of surrogate ISI time series, randomized sequences of the original data in which all possible non-linear deterministic components of the original time series are destroyed while preserving other important statistical features of the original time series, such as its mean, variance and autocorrelation (see Appendix; Theilera et al., 1992). Therefore, significant differences in dimensional complexity between the original DA ISI data and these randomly shuffled, surrogate ISI time series indicate the presence of non-linear determinism in the original ISI time series. We compared the DCs for each of the original DA ISI time series with 20 different sets of corresponding surrogate time series data. Pair-wise t-tests of the differences between the DC values of the original ISI time series and the mean of the DC values of their 20 surrogates were applied to test the null hypothesis of no difference between the DCs (i.e. that the original time series were stochastic). With n – 1 (or 19) degrees of freedom and a 0.05 level of significance, the critical value of t was 2.093. Numeric values were expressed as a mean ± SD, and all P-values were of the two-sided type.

Results

Absence of determinism in non-bursting ISI neurons

A typical ISI sequence recorded from the non-bursting DA neuron of a chloral hydrate-anesthetized rat is shown in Fig. 1A. All observed non-bursting DA neurons (n = 11) produced highly irregular ISI sequences, whose distributions for ISI duration were unimodal, having a mean = 240.3 ± 92.6 ms ranging 200–500 ms. Four of 11 (36%) of the DA neurons exhibited ISI histograms that were skewed towards longer ISI values (Fig. 1B).

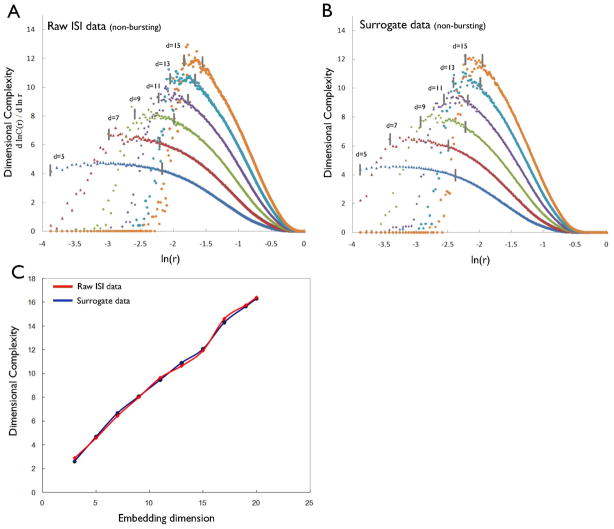
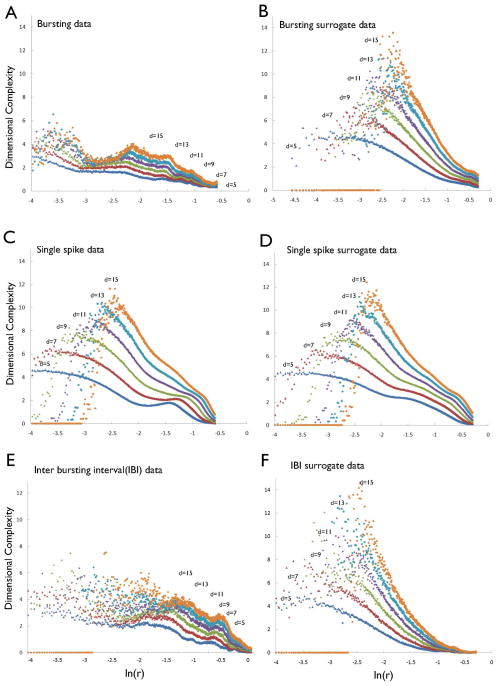
Figure 2A presents the local slopes of the local DC profile (the local scaling exponent) for the ISI sequences from a typical non-bursting neuron as a function of log-scaled r at different embedding dimensions (5, 7, 9, 11, 13 and 15). The average value of the scaling region, the plateau in the local DC profile, at a given embedding dimension approximates the DC value for the data at that embedding dimension. Each ISI sequence under study had long scaling regions over 15% of the attractor size. Figure 2A demonstrates that DC values for ISIs of non-bursting neurons increased without saturation as the embedding dimension increased, i.e. these DC values showed no evidence for the presence of determinism in time series from non-bursting DA neurons. Moreover, the DC profiles of the corresponding surrogate ISI time series were similar to those of the original data (Fig. 2B), further supporting the absence of determinism in non-bursting DA neurons. Figure 2C furthermore depicts the DC values as a function of the embedding dimension for the original ISI time series and for their surrogates, demonstrating that DC values from both the original and their surrogate time series increased similarly without saturation as the embedding dimension increased. The DCs for each of the original ISI time series from these 11 non-bursting DA neurons were compared with the DCs of the 20 corresponding surrogates at a minimum embedding dimension of 12, which was chosen from the false nearest-neighbor method (Appendix). Pair-wise t-tests demonstrated that the differences between the DCs of original and surrogate time series did not differ significantly (t = 0.13, P = 0.56). Furthermore, the mean t-score for the 11 non-bursting ISI time series at an embedding dimension of 12 was 0.25 ± 0.16 (Table 1), confirming that the firing patterns of the non-bursting DA neurons were not deterministic.

Fig. 2.

(A) DC profiles of the inter-spike interval (ISI) data from the non-bursting DA neuron as embedding dimension increases. Vertical line in each dimension denotes the selected range used to generate the average values of DC. (B) DC profiles of its surrogate data. (C) The average values of the DC of the raw ISI data (red line) and its surrogate data (blue line) as the embedding dimension increases.

Table 1.

DCs of real and surrogate data at the embedding dimension of 12, which was chosen from the false nearest-neighbor method

	DC		T-score
	Original ISI data	Surrogate data
Non-bursting neurons (n = 11)	10.74 ± 1.22	10.86 ± 1.31	0.25 ± 0.16
Bursting neurons (n = 8)	5.36 ± 0.59	10.87 ± 0.62	8.42 ± 1.45
Single-spike time series (n = 8)	10.42 ± 0.93	10.68 ± 0.63	0.29 ± 0.13
Bursting time series (n = 8)	3.65 ± 0.41	8.78 ± 0.71	7.14 ± 1.09
IBI time series (n = 8)	6.14 ± 1.14	9.83 ± 0.85	4.31 ± 0.49

Original ISI data from DA neurons recorded from chloral hydrate-anesthetized rats. DC, dimension complexity; IBI, inter-burst interval; ISI, inter-spike interval.

Numerical values represent means ± SD.

Non-linear determinism in bursting ISI neurons

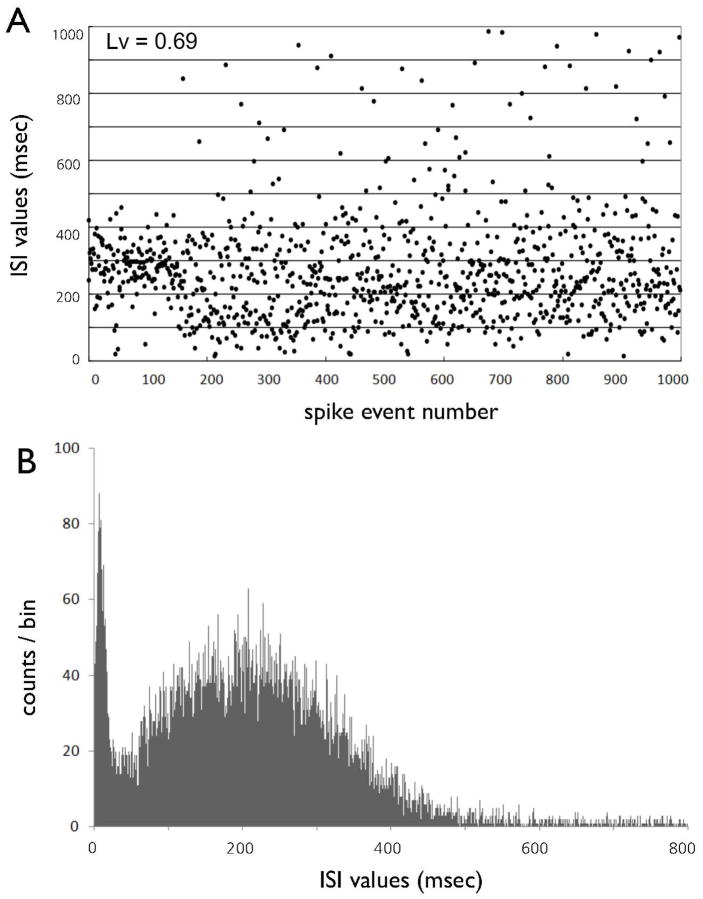
Eight of 19 ISI sequences were recorded from bursting nigral DA neurons in the chloral hydrate-anesthetized rats (Fig. 3A). The ISIs of all bursting DA neurons were bimodally distributed (Fig. 3B). An earlier mode at 10 ms represented ISIs within bursts, and a later mean at 218.7 represented ISIs between bursts, or non-burst-related single-spikes.

Fig. 3.

(A) The inter-spike interval (ISI) sequence of a typical bursting DA neuron as a function of time. (B) ISI histogram of a bursting DA neuron. Bursting DA neurons typically show bimodal ISI distributions.

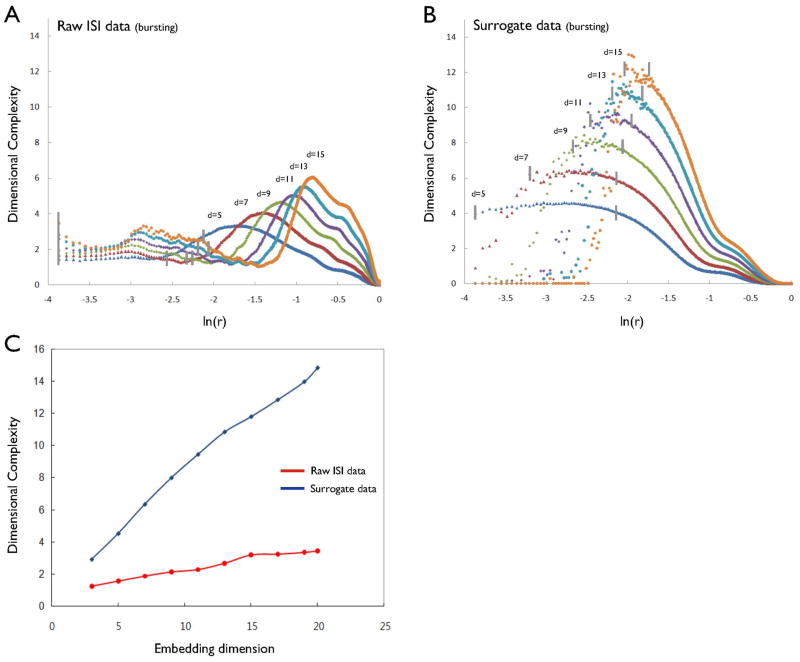
Figure 4A depicts the local DC profiles at embedding dimensions of 5, 7, 9, 11, 13 and 15 for the ISI data from a typical bursting neuron. The scaling region in the local DC profiles is defined as a straight line when the logarithm of the local DC profiles is plotted against the logarithm of the scale r at which it is measured. In the analysis, the scaling region was chosen from the criterion that this slope of the regression straight line was constant over about two orders of magnitude. Figure 4A shows that the local DC profiles had long plateaus, or scaling regions, that ranged from −1.2 to −3.2 (between dashed lines), indicating the presence of low-dimensional, deterministic behavior in these bursting neurons. In contrast, DC values of the surrogate time series increased without saturation as the embedding dimension increased (Fig. 4B). The DC values of the original ISI and the corresponding surrogate time series differed significantly in all embedding dimensions (Fig. 4C). Pair-wise t-tests demonstrated significant differences between DCs for the eight bursting DA neurons (5.36 ± 0.59) and the mean DCs of their surrogates (10.87 ± 0.62) at an embedding dimension of 12 (t = 6.35, P < 0.01). The mean t-score for these eight bursting ISI time series at an embedding dimension of 12 was 8.42 ± 1.45 (Table 1), further indicating that the firing patterns of these bursting DA neurons was deterministic.

Fig. 4.

(A) DC profiles of the inter-spike interval (ISI) data from the bursting DA neuron as embedding dimension increases. Vertical line in each dimension denotes the selected range used to generate the average values of DC. (B) DC profiles of its surrogate data. (C) DC saturation for the ISI data of the bursting DA neuron and the corresponding surrogate data. The average values of the DC of the raw ISI data (red line) and its surrogate data (blue line) as the embedding dimension increases.

To examine further the association between bursting activity and non-linear determinism in the ISI sequences, we generated isolated burst time series by eliminating single-spikes in the ISI sequences of the eight bursting neurons (i.e. using burst separation analysis; Fig. 5). The isolated burst time series exhibited stable DC values that ranged from 2.5 to 5 (mean 3.65 ± 0.41), differing significantly (t = 5.74, P < 0.01) from the DC values of the corresponding surrogate data (mean 8.78 ± 0.71) at a minimum embedding dimension of 12 (Table 1). In contrast, the DCs of isolated single-spike time series (obtained by eliminating bursts in the ISI sequences) from the eight bursting neurons increased as the embedding dimension increased (Fig. 6). The DC values of these single-spike time series did not differ significantly from those of their surrogate data. These results suggest that single-spike activity, even within bursting DA neurons, is generated from stochastic processes.

Fig. 5.

Signal separation. Raw DA time series data into a burst and single-spike time series.

Fig. 6.

DC profiles of isolated burst time series. (A) DC profile of isolated bursting time series. (B) DC profile of its surrogate bursting time series. (C) DC profile of the isolated single-spike time series (eliminating bursts from the raw ISI train). (D) DC profile of surrogate data of isolated single-spike time series. (E) DC profile of inter-burst interval (IBI) train of bursting DA neurons. (F) DC profile of surrogate data from IBI time series.

Furthermore, the IBI time series of bursting DA neurons exhibited non-linear determinism: the mean t-score for the eight IBI time series at the minimum embedding dimension of 9, which was chosen from the false nearest-neighbor method, was 7.14 ± 1.09, indicating the presence of a non-linear deterministic structure in the temporal patterning between bursts themselves in bursting DA neurons. These findings demonstrate the presence of determinism in the bursting behavior of DA neurons, both in the patterning of spike trains within epochs of bursting and in the longer term patterning of the burst epochs themselves.

The effects of differing anesthetic agents on deterministic behavior in DA neurons

Given this compelling evidence that bursting is the primary source of non-linear determinism in the temporal patterning of firing of DA neurons, we assessed the possibility that manipulating the pattern of firing of DA neurons, particularly the pattern of burst firing, would alter the non-linear deterministic structure of DA cell firing. We thus used the anesthetic halothane, which differs from chloral hydrate in its effects on membrane permeability and receptor-mediated activity of DA neurons, to manipulate the patterns of temporal firing in these cells. We compared the non-linear deterministic properties of these DA neurons with those measured in chloral hydrate-anesthetized rats.

The bursting activity of DA neurons in halothane-anesthetized rats differed from that in chloral hydrate-anesthetized rats. In the bimodal ISI distributions of bursting DA neurons in both groups, the earlier mode of DA neurons in chloral hydrate-anesthetized neurons (n = 8) was positioned at 17.2 ± 3.5 ms, and the mode of the later peak was positioned at 193.4 ± 13.5 ms. In contrast, the corresponding modes of the ISIs in halothane-anesthetized DA neurons (n = 8) were positioned at 83.7 ± 13.6 ms and 178.3 ± 17.2 ms. The halothane-anesthetized rats had a significantly smaller mean ISI and mean IBI, as well as a larger percentage of spikes within bursts than in chloral hydrate-anesthetized rats (Table 2), indicating the presence of an overall greater degree of bursting activity in DA neurons associated with use of halothane. The mean number of spikes per burst (burst length), however, was similar across the two groups.

Table 2.

Comparison of bursting activity across different anesthetic groups

	Chloral hydrate	Halothane
Mean ISI*	229.4 ± 81.3	138.3 ± 24.4
% Spikes in bursts*	22.7 ± 12.3	43.6 ± 8.2
Mean burst length	3.1 ± 0.78	3.4 ± 0.65
Mean IBI**	5956.0 ± 1243.4	1661.9 ± 534.5

IBI, inter-burst interval; ISI, inter-spike interval.

^*P < 0.01;

^**P < 0.001.

In both the chloral hydrate and halothane groups, local DC profiles saturated long plateaus, or scaling regions, as the embedding dimension increased; the DC values of their surrogates, however, increased without saturation. Moreover, the DCs of the original ISI sequences differed significantly from those of the surrogates at an embedding dimension of 12 (t = 5.45, P < 0.01). These findings both indicated that firing of DA neurons with use of either anesthesia was deterministic. However, DA neurons in the chloral hydrate group (5.36 ± 0.59) showed lower DCs than did those in the halothane group (8.63 ± 0.83; t = 5.89, P < 0.001), indicating that the deterministic bursting of DA neurons associated with use of chloral hydrate was of relatively lower dimensionality, i.e. it had simpler deterministic structure, than did the bursting associated with the use of halothane.

As before, we separated the original ISIs into ISIs for the component bursts and single-spikes of the bursting DA neurons for both the chloral hydrate- and halothane-treated groups. In both groups, the DCs of isolated burst time series were significantly smaller than those of their surrogates, indicating the presence of non-linear determinism. However, DCs of the isolated burst time series for the chloral hydrate group (3.65 ± 0.41) were significantly lower (t = 5.06, P < 0.01) than those in the halothane group (6.54 ± 0.56), indicating the presence of a simpler deterministic structure to the neural firing in rats anesthetized with chloral hydrate. In contrast, DCs did not differ significantly across groups for the isolated single-spike time series (t = 0.78, P = 0.43) or for their surrogate data (t = 0.66, P = 0.58), indicating that the single-spike activity of bursting DA neurons in both groups is stochastic. Taken together, these findings suggest that the degree of non-linear determinism in bursting DA neurons associated with use of chloral hydrate anesthesia differs from the deterministic bursting associated with use of halothane, and that this difference likely arises specifically from differences that the anesthesia has on the dynamics of the bursting portions of DA neuron spike trains. These results, therefore, support the conclusion that bursts, and not single-spikes, are the likely origin of non-linear determinism in DA neurons.

Discussion

Firing of DA neurons until now has generally been assumed to be random, particularly in anesthetized animals in the absence of overtly rewarding stimuli. This study of the non-linear dynamical properties of in vivo nigral DA neurons, however, has demonstrated that the firing pattern of bursting DA neurons in anesthetized animals is low-dimensional, deterministic, whereas the firing pattern of non-bursting DA neurons is stochastic. Given a burst is a threshold event in which the neuron embarks on a stereotyped excursion through the state space, it is quite reasonable that the firing pattern within a burst is non-linear deterministic (Carelli et al., 2005). In addition to the deterministic firing of spike trains within bursts, the timing of onset of the bursts themselves (i.e. the IBIs) was found to be deterministic. Thus, the transition from single-spiking to bursting behavior is itself regulated by deterministic processes. Together these findings indicate that both the temporal patterning of the onset of bursts and the spiking within bursts is generated and exquisitely regulated by low-dimensional, deterministic rules in DA neurons, despite the highly irregular and complex appearance of cell firing. Finally, the degree of non-linear determinism in the bursting behavior of DA neurons depended on the choice of anesthetic, choral hydrate or halothane, suggesting that experimental manipulation can alter the deterministic complexity and thus the number of parameters that control bursting activity in DA neurons.

Two prior studies support the validity of assessing the deterministic qualities of bursting and single-spike trains independently, as well as our conclusion that single-spikes and bursts in the temporal firing of DA neurons are generated from two separable, independent processes. First, electrosensory pyramidal neurons are known to generate spike trains consisting of two parallel information streams, both single-spikes and bursts; within a given spike train, single-spikes simultaneously code for the entire frequency range of broadband Gaussian sensory stimuli, while bursts selectively encode low-frequency features of the stimuli (Oswald et al., 2004). Second, bursts have been shown to be a likely source of non-linear predictability in the firing patterns of immature hippocampal neurons (Prida et al., 1997).

Bursting in nigral DA neurons is thought to subserve reward-related learning. The switch in the pattern of action potentials from single-spike activity to a bursting mode encodes, integrates and distributes information that is salient to attaining a reward. Approximately 75% of DA neurons, for example, burst in response to the presentation of an unexpected, novel reward (Schultz, 2000). This bursting activity in turn increases DA concentration in the striatum, which in turn mediates synaptic plasticity and reward-related learning (Gonon, 1988; Garris et al., 1994; Garris & Wightman, 1994; Engberg et al., 1997; Schultz et al., 1997; Centonze et al., 2001; Reynolds et al., 2001; Floresco et al., 2003). Bursting activity also enhances the reliability of information transfer across neurons (Miles & Wong, 1986; Lisman, 1997; Snider et al., 1998). Bursts of specific inter-spike frequencies are more likely to induce postsynaptic firing than are bursts at other frequencies (Izhikevich et al., 2003). Bursting boosts the gain of neural signaling of novel events by enhancing DA release and thereby enhancing synaptic potentiation as well (Cooper, 2002). The general conclusion of these prior studies is thus that bursting is the functional encoding unit for the transmission of neural information. Our findings support this view of the functional significance of bursting in DA neurons by demonstrating that bursts are the source of non-linear determinism in the complex firing patterns of midbrain DA neurons.

Single-spikes, in contrast, are generally considered to represent random noise in DA cell firing. Our finding that non-bursting DA cells are non-deterministic confirms the results of prior efforts in the non-linear dynamical modeling of complex firing patterns in non-bursting DA neurons (Canavier et al., 2004). However, the absence of determinism in non-bursting DA neurons does not necessarily imply that single-spikes play no role in information processing. Single-spikes may be involved, for example, in the habituation to rewarding stimuli that have lost their novelty. The transition from bursting to single-spike activity, therefore, may play an important role in adjusting the output gain of individual neurons to boost the signaling of salient events and to dampen interference from non-salient ones (Cooper, 2002). Thus, the ability to dynamically switch the output mode of DA neurons between single-spikes and bursts might provide flexibility within reward circuitry that allows different sets of neurons to preferentially and conditionally encode certain types of reward-related learning over others.

We found that the average DC of bursting time series was approximately 4; this therefore is the number of independent variables necessary to construct a computational model of bursting DA neurons in anesthetized rats. In recent decades, several research groups have developed in vitro models of firing for midbrain DA neurons that invoke a large number of control parameters (Li et al., 1996; Amini et al., 1999; Canavier, 1999; Penney & Britton, 2002; Canavier & Landry, 2006; Kuznetsova et al., 2010; for a review, see Canavier & Shepard, 2009). Although the absolute value of the estimated DC depends on the particular algorithms used to measure it, the demonstration of four-dimensional dynamics in neuronal bursting suggests that a reduced computational model having only four degrees of freedom should capture the essential temporal dynamics of DA cell bursting. These promise to simplify our models for and our understanding of the molecular mechanisms that produce DA cell firing in vivo.

The molecular mechanisms that govern the switch between single-spiking and bursting modes of activity, as well as the timing of spikes within bursts, are currently unknown. Nevertheless, numerous studies suggest that the switch from single-spiking to bursting behavior in DA neurons involves glutamate-mediated neuronal interactions via N-methyl-D-aspartate (NMDA) receptors (Mereu et al., 1983; Johnson et al., 1992; Overton & Clark, 1992; Zhang & Shi, 1999; Floresco et al., 2003; Paladini et al., 2003; Carelli et al., 2005; Szucs et al., 2005; Mrejeru et al., 2011). Bursting in DA neurons is thought to arise from synaptic activation of NMDA receptors, sufficiently depolarizing dendritic membranes to activate high-voltage-activated L-type calcium currents that generate oscillations and bursting activity. There is a hypothesis that calcium entry during bursts activates a calcium-activated potassium current IK_(Ca), which repolarizes the membrane and terminates the burst (Overton & Clark, 1997; Cooper, 2002).

The presence of bursting in DA cell firing under general anesthesia indicates that sensory input is not required for DA neurons to generate bursts. Bursting activity under anesthesia therefore may be determined more by intrinsic membrane properties, or by a preferential inhibition of a γ-aminobutyric acid (GABA)_A influence on DA firing, rather than by strong excitatory sensory inputs (Paladini et al., 1999; Cooper, 2002). Alteration in the degree of non-linear determinism in the bursting activity under differing anesthetics, however, demonstrates the differential influence of anesthetics on the molecular mechanisms that generate bursts in DA neurons. Both anesthetics used in this study, chloral hydrate and halothane, enhance GABA and glycine transmission by inhibiting glutamate-mediated excitation (Weight et al., 1993; Peoples & Weight, 1994; Pistis et al., 1997; Bloms-Funke et al., 1999; Krasowski & Harrison, 2000), and glutamate is thought to be involved in the generation of bursting in DA neurons (Murase et al., 1993). Yet the mechanism through which they alter bursting dynamics may not be via alteration of activity in glutamatergic pathways. Chloral hydrate, the most widely used anesthetic in electrophysiological recording in rats, either directly or via its metabolites, increases GABA and glycine concentrations by suppressing the feedback excitatory inputs to DA neurons following postsynaptic D2-receptor blockade (Mereu et al., 1983; Hamilton et al., 1992; Kitai et al., 1999). Halothane, on the other hand, enhances glutamate uptake and thus rapidly reduces glutamate concentration in the synaptic cleft (Miyazaki et al., 1997). Thus, manipulation of the dynamics of bursting in nigral DA neurons using pharmacological probes may provide an invaluable tool for studying the molecular controls of dynamic functioning in the dopaminergic systems that are undoubtedly of central pathophysiological importance across a wide range of neuropsychiatric illnesses.

Abbreviations

DA

dopamine

DC

dimension complexity

GABA

γ-aminobutyric acid

IBI

inter-burst interval

ISI

inter-spike interval

NMDA

N-methyl-D-aspartate

SN

substantia nigra