Acclimation of Leaf Nitrogen to Vertical Light Gradient at Anthesis in Wheat Is a Whole-Plant Process That Scales with the Size of the Canopy^,,

Abstract

Vertical leaf nitrogen (N) gradient within a canopy is classically considered as a key adaptation to the local light environment that would tend to maximize canopy photosynthesis. We studied the vertical leaf N gradient with respect to the light gradient for wheat (Triticum aestivum) canopies with the aims of quantifying its modulation by crop N status and genetic variability and analyzing its ecophysiological determinants. The vertical distribution of leaf N and light was analyzed at anthesis for 16 cultivars grown in the field in two consecutive seasons under two levels of N. The N extinction coefficient with respect to light (b) varied with N supply and cultivar. Interestingly, a scaling relationship was observed between b and the size of the canopy for all the cultivars in the different environmental conditions. The scaling coefficient of the b-green area index relationship differed among cultivars, suggesting that cultivars could be more or less adapted to low-productivity environments. We conclude that the acclimation of the leaf N gradient to the light gradient is a whole-plant process that depends on canopy size. This study demonstrates that modeling leaf N distribution and canopy expansion based on the assumption that leaf N distribution parallels that of the light is inappropriate. We provide a robust relationship accounting for vertical leaf N gradient with respect to vertical light gradient as a function of canopy size.

In cereals, as in many crop species, nitrogen (N) nutrition is a major determinant in the elaboration of grain yield and quality (Lemaire and Millard, 1999; Lawlor, 2002; Hikosaka, 2005). N is involved in both meristematic and photosynthetic activities, with consequences on plant architecture and carbon acquisition and in fine on grain yield and protein concentration. Beside the total amount of N absorbed by the crop, the allocation of N among plant organs plays a key role in determining crop productivity and quality (Grindlay, 1997; Dreccer et al., 1998; Hikosaka, 2005).

Light interception and leaf N content are the two main factors governing carbon assimilation at the leaf scale (Evans, 1989). For various species, both light and leaf N attenuate with cumulative leaf area index counted from the top of the canopy (Field, 1983; Hirose and Werger, 1987). Leaf N vertical gradients have been regarded as an adaptive response to the local light environment, maximizing canopy photosynthesis and N utilization efficiency (Hirose and Werger, 1987; Hikosaka et al., 1994; Drouet and Bonhomme, 1999), as N is largely contained in the assimilatory enzyme Rubisco. Theoretical studies indicated that leaf N maximizes canopy photosynthesis when it parallels the light gradient (i.e. when the light [K_L] and N [K_N] extinction coefficients are equal), considering that the leaf N gradient is “optimal” in accordance with the “optimization theory” (Field, 1983; Hirose and Werger, 1987; Anten et al., 1995b).

Factors other than the photosynthetic photon flux density (PPFD) might be responsible for the observed leaf N distribution. For instance, the acropetal gradients of leaf age (Hikosaka et al., 1994; Hikosaka, 2005) and light composition (Rousseaux et al., 1999) are known to strengthen the leaf N gradient. However, the impact of each of these factors has been shown to be much less than that of the PPFD gradient (Werger and Hirose, 1991; Pons and de Jong-van Berkel, 2004), although for the grass species Brachypodium pinnatum other factors than light might be involved (Pons et al., 1993). At the molecular level, the process could be driven by the import of compounds such as cytokinins transported in the transpiration stream (Pons et al., 2001; Boonman et al., 2007). Although the actual N distribution usually follows the light gradient, in all studies it is less steep than the calculated optimal N profile maximizing canopy photosynthesis (Pons et al., 1989; Yin et al., 2003). Possible reasons for this discrepancy have been discussed in detail by Kull (2002). Sink-source relations and in particular the demand for N could modulate the light-leaf N relationship (Dreccer et al., 1998), but conflicting results have been reported regarding the effect of N availability on the light-leaf N relationship. While some authors found no effect of N availability (Sinclair and Shiraiwa, 1993; Milroy et al., 2001), others found that the N gradient relative to light (i.e. K_L/K_N) was steeper under low N (Hikosaka et al., 1994; Grindlay et al., 1995; Lötscher et al., 2003) or that the response of the light-leaf N relationship to N availability depended on the developmental stage (Dreccer et al., 2000). Interspecific differences in the light-leaf N relationship have also been reported and were related to differences in phenotypic plasticity (Aerts, 1996) or plant architecture (leaf stature and branching pattern; Anten et al., 1995a; Lötscher et al., 2003).

Since canopy photosynthesis is dependent upon the leaf N gradient, it has been suggested that the pattern of leaf N distribution could be responsible for part of the genetic variability associated with the negative correlation between grain yield and protein concentration reported for various crop species (Dreccer et al., 1998). In wheat (Triticum aestivum), N accumulated before anthesis contributes 30% to 70% of grain N (Mi et al., 2000; Kichey et al., 2007). The efficiency of N translocation from the lower to the upper leaves may increase with the steepness of the N gradient, with only a negligible effect on canopy carbon gain integrated over the whole grain-filling period. This hypothesis is consistent with experimental studies based on a range of genotypes showing that, at a given grain yield level, grain protein concentration is positively related to the efficiency of N translocation either from the lower to the upper leaves (Wang et al., 2005) or from the leaves to the grains (Monaghan et al., 2001; Jukanti and Fischer, 2008). Only a few studies have investigated the intraspecific variability of the light-N relationship at the intraspecific level (Shiraiwa and Sinclair, 1993; Bindraban, 1999; Bertheloot et al., 2008; van Oosterom et al., 2010). For wheat, published analyses of the genetic variability of the light-leaf N relationship were limited to only two to five genotypes, and no genetic differences were found (Bindraban, 1999; Bertheloot et al., 2008).

This paper focuses on the genetic variability of the vertical leaf N gradient with respect to light for wheat. Three main issues were investigated. What is the effect of N supply on the vertical distribution of leaf N? Does the distribution of leaf N with respect to light differ among genotypes? If the adjustment of leaf N to the light gradient varies with both the genotype and N supply, could this genetic and environmental variability have a unique ecophysiological determinant (driving variable)?

These questions were addressed using 16 genotypes (Supplemental Table S1) covering a wide range of variation for N use efficiency (i.e. grain dry mass yield per unit of available mineral N from the soil and fertilizer), for grain protein concentration (Le Gouis et al., 2000; Foulkes et al., 2006; Gaju et al., 2011) and for the deviation from the negative correlation between grain yield and protein concentration (Oury et al., 2003). The 16 genotypes were grown in the field under two conditions of N supply (N− and N+ for low- and high-N treatments, respectively) in order to modulate crop N status at Clermont-Ferrand (CF) in France in two consecutive seasons (experiments CF07 and CF08). In addition, four of the 16 cultivars representing the variability observed for N utilization and N uptake efficiency were grown in the field under two conditions of N supply at Sutton Bonington (SB) in the United Kingdom in one season (experiment SB07). The distribution of leaf N was analyzed at anthesis. The first reason for this is that the distribution of both light and leaf N within the canopy is relatively stable from this phenological stage until almost the end of grain filling (Bertheloot et al., 2008). Whereas the canopy green area index (GAI) decreases dramatically during the grain-filling period, the structure of the canopy affecting light interception does not change significantly during that period. Both the vertical light and N distributions down the canopy are unchanged during most of the grain-filling period; therefore, the K_N-to-K_L ratio is constant during that period (Bertheloot et al., 2008). Similarly, Archontoulis et al. (2011) showed that K_N-to-K_L ratio is not modified during the vegetative and reproductive stages for field-gown sunflower (Helianthus annuus) crops. Therefore, as most of the final grain yield results from carbon assimilated after anthesis (Bidinger et al., 1977; Gebbing and Schnyder, 1999), the N distribution at anthesis is very relevant in terms of carbon assimilation and grain yield in wheat. A second reason is that the number and potential size of grains are determined around anthesis, which therefore appears as a critical stage in the formation of grain yield. A better understanding of the ecophysiological determinants of leaf N gradient at this phenological stage could consequently be crucial for improving wheat productivity and quality (Dreccer et al., 1998).

RESULTS

Canopy Size and N Uptake at Anthesis

All the traits under study were affected by the year of experiment at CF (Table I). That is, lamina N and GAI were higher in 2008 than in 2007. Correspondingly, crops were denser and a larger percentage of the incident PPFD was intercepted by the canopy in 2008 (62% on average) than in 2007 (89% on average; Fig. 1). By contrast, average main shoot leaf lamina N mass per unit leaf area (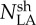) was lower in 2008 than in 2007 (Table I). All traits varied with genotype (Table I). The traits were also greatly influenced by N treatments. For both years, greater N supply increased GAI, main shoot lamina N, and 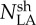. For all the traits under study, the year × genotype and the year × N interactions were significant, indicating that the differences between years were more or less marked according to the cultivar and to the N treatment. Except for GAI, the genotype × N interaction was significant, indicating that the magnitude of the response to N treatment varied across cultivars.

Table I. GAI, main shoot leaf lamina N, and average 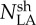for wheat.

Crops were grown in the field at CF during the 2006–2007 (CF07) and 2007–2008 (CF08) growing seasons and at SB during the 2006–2007 growing season (SB07). For each experiment, the minimum, maximum, and average values across the 16 (at CF) or four (at SB) cultivars analyzed are reported. Data are means ± se for two treatments × three independent replicates. P values of the main effects and interactions from split-plot ANOVAs at CF are reported.

Cultivars and Statistical Data	GAI			Lamina N
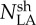	CF07	CF08	SB07	CF07	CF08	SB07	CF07	CF08	SB07
	m2 green tissue m−2 ground			g N m−2 ground			g N m−2 lamina
Alchemy	3.17 ± 0.54	5.14 ± 1.48	–	2.43 ± 0.83	4.18 ± 2.39	–	1.90 ± 0.29	1.57 ± 0.39	–
Beaver	3.05 ± 0.59	5.98 ± 1.88	–	2.22 ± 1.05	4.60 ± 2.32	–	1.94 ± 0.44	1.59 ± 0.41	–
Consort	2.96 ± 0.62	5.78 ± 2.00	–	1.80 ± 0.83	4.64 ± 2.48	–	2.14 ± 0.44	1.59 ± 0.47	–
Paragon	3.62 ± 0.90	5.90 ± 1.59	–	2.03 ± 0.77	3.64 ± 1.68	–	1.71 ± 0.25	1.39 ± 0.45	–
Rialto	2.82 ± 0.51	4.51 ± 1.63	8.30 ± 1.74	1.80 ± 0.83	3.58 ± 1.85	8.62 ± 3.72	1.98 ± 0.35	1.77 ± 0.44	2.02 ± 0.43
Robigus	3.13 ± 0.62	5.90 ± 1.41	–	2.48 ± 0.76	4.10 ± 2.45	–	1.76 ± 0.33	1.39 ± 0.45	–
Savannah	2.96 ± 0.64	5.24 ± 1.50	8.99 ± 1.37	2.43 ± 1.09	4.21 ± 1.84	7.95 ± 2.97	2.16 ± 0.48	1.61 ± 0.31	1.82 ± 0.35
Soissons	3.54 ± 0.76	6.03 ± 1.61	–	2.42 ± 0.69	3.44 ± 1.26	–	1.97 ± 0.40	1.53 ± 0.29	–
Arche	3.51 ± 0.66	7.08 ± 1.45	–	2.24 ± 0.85	4.33 ± 1.80	–	1.48 ± 0.24	1.35 ± 0.31	–
CF9107	3.33 ± 0.66	6.06 ± 1.78	–	2.68 ± 0.90	3.91 ± 1.57	–	1.74 ± 0.20	1.47 ± 0.35	–
CF99102	3.14 ± 0.72	5.46 ± 1.39	9.41 ± 1.94	2.20 ± 0.52	3.47 ± 1.52	8.56 ± 3.40	1.74 ± 0.24	1.47 ± 0.36	1.74 ± 0.33
Perfector	3.23 ± 0.81	6.07 ± 1.89	8.42 ± 1.33	2.27 ± 1.00	4.47 ± 2.11	8.42 ± 2.56	1.71 ± 0.27	1.53 ± 0.33	2.01 ± 0.37
Quebon	2.69 ± 0.71	5.84 ± 1.64	–	1.78 ± 0.72	4.49 ± 2.04	–	1.91 ± 0.39	1.63 ± 0.38	–
Recital	3.01 ± 0.73	5.96 ± 1.28	–	1.96 ± 0.74	3.77 ± 1.39	–	1.49 ± 0.16	1.65 ± 0.37	–
Renan	3.55 ± 0.77	7.09 ± 1.17	–	2.46 ± 0.85	3.66 ± 0.93	–	1.67 ± 0.18	1.61 ± 0.42	–
Toisondor	3.22 ± 0.80	5.33 ± 1.42	–	2.21 ± 1.17	4.30 ± 1.87	–	1.75 ± 0.35	1.56 ± 0.35	–
Minimum	2.82	4.51	8.30	1.78	3.44	7.95	1.48	1.39	1.74
Maximum	3.55	7.08	9.41	2.68	4.60	8.62	2.16	1.77	2.02
Average	3.18	5.85	8.78	2.14	4.07	8.39	1.82	1.54	1.90
P values
N	<0.001			<0.001			<0.001
Year	<0.001			<0.001			<0.001
Genotype	<0.001			0.003			<0.001
N × year	<0.001			<0.001			<0.001
N × genotype	0.470			<0.001			0.004
Year × genotype	<0.001			<0.001			<0.001
N × year × genotype	0.491			0.182			0.004

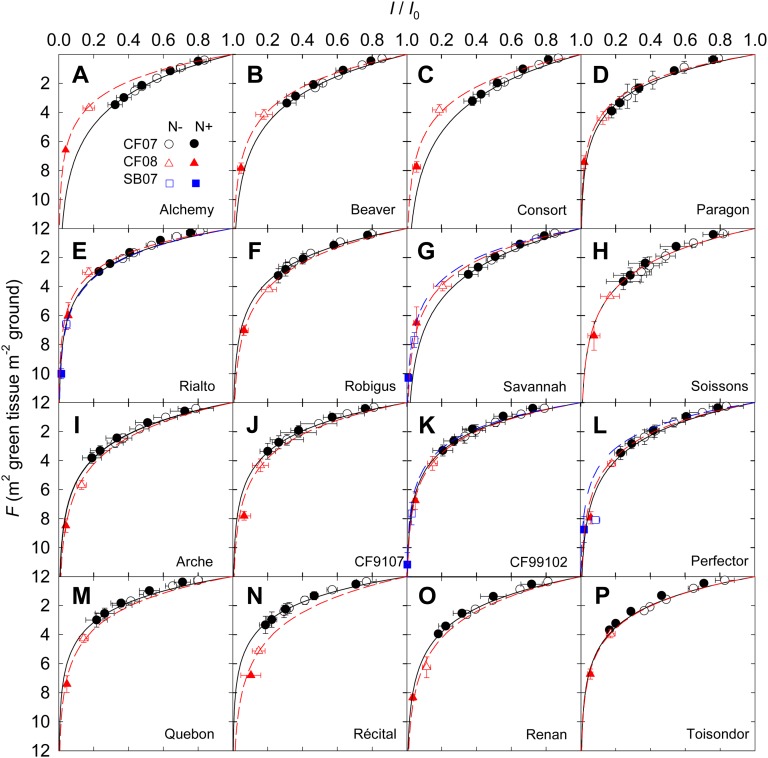
Figure 1.

Cumulative GAI counted from the top of the canopy (F) versus relative PPFD (I/I₀) at anthesis for 16 cultivars of wheat (A–P) grown in the field under N− and N+ at CF during the 2006–2007 (CF07) and 2007–2008 (CF08) growing seasons and for four cultivars grown at SB during the 2006–2007 growing season (SB07). Data are means ± se for three independent replicates. Lines were fitted to the data using the K_L reported in Table II.

Similar conclusions could be drawn from the study of the four cultivars in the three experiments (CF07, CF08, and SB07; Table I). Hence, for the three experiments, the two N treatments strongly modulated crop growth and N economy. Altogether, the different site/year/N treatment/cultivar combinations generated a wide range of variations of canopy structure and total canopy N at anthesis.

Vertical Light Distribution

K_L is commonly estimated from stratified light measurements through the canopy, but this method is very time consuming. Therefore, at CF07, we assessed whether K_L could be estimated without significant bias using a simplified method in which PPFD is measured above the canopy and at ground level only, assuming that light decreases exponentially with cumulative GAI (Shearman et al., 2005). For all the N treatment/cultivar combinations, the decrease of light as a function of cumulative GAI was well described by an exponential function (all r² > 0.982 and P < 0.001; Fig. 1). The average measurement error variance of K_L was similar for the two methods, averaging 0.0041 (n = 12). K_L values estimated using the two methods were tightly correlated (r = 0.949, P < 0.001, degrees of freedom = 31; Supplemental Fig. S1). The slope of the relationship was not different from 1 (P = 0.65, slope = 0.929, 95% confidence interval = 0.828–1.044), and the intercept was not different from 0 (P = 0.21, intercept = 0.048). Since the two methods gave similar results, we used K_L values estimated with the simplified method in the three experiments.

K_L differed neither between years nor between N treatments (Table II). However, K_L differed among cultivars, and the year × genotype interaction was significant. Averaging across the N treatments, K_L ranged from 0.30 (cv Consort) to 0.52 (cv Recital) at CF07 and from 0.37 (cv Recital) to 0.54 (cv Rialto) at CF08 (Table II).

Table II. Canopy K_L and b for 16 cultivars of wheat.

Crops were grown in the field at CF during the 2006–2007 (CF07) and 2007–2008 (CF08) growing seasons and at SB during the 2006–2007 growing season (SB07). Data are means ± se for two treatments × three independent replicates. P values of the main effects and interactions from split-plot ANOVAs for the 16 cultivars at CF are reported.

Cultivars and Statistical Data	KL			b
	CF07	CF08	SB07	CF07	CF08	SB07
	m2 ground m−2 green tissue			dimensionless
Alchemy	0.33 ± 0.04	0.49 ± 0.03	–	1.22 ± 0.09	0.64 ± 0.11	–
Beaver	0.34 ± 0.04	0.41 ± 0.03	–	1.84 ± 0.23	0.68 ± 0.11	–
Consort	0.30 ± 0.04	0.41 ± 0.06	–	1.85 ± 0.20	0.83 ± 0.13	–
Paragon	0.47 ± 0.08	0.51 ± 0.05	–	1.11 ± 0.10	0.70 ± 0.08	–
Rialto	0.48 ± 0.03	0.54 ± 0.07	0.47 ± 0.11	1.15 ± 0.15	0.85 ± 0.07	0.45 ± 0.05
Robigus	0.44 ± 0.06	0.39 ± 0.02	–	1.26 ± 0.12	0.76 ± 0.12	–
Savannah	0.33 ± 0.04	0.41 ± 0.03	0.45 ± 0.05	1.67 ± 0.24	0.75 ± 0.11	0.51 ± 0.08
Soissons	0.39 ± 0.09	0.38 ± 0.06	–	1.72 ± 0.22	0.94 ± 0.17	–
Arche	0.42 ± 0.05	0.38 ± 0.03	–	1.42 ± 0.11	0.76 ± 0.08	–
CF9107	0.47 ± 0.04	0.42 ± 0.10	–	1.29 ± 0.13	0.8 0 ± 0.06	–
CF99102	0.48 ± 0.04	0.46 ± 0.04	0.51 ± 0.07	1.25 ± 0.11	0.69 ± 0.05	0.37 ± 0.04
Perfector	0.43 ± 0.06	0.39 ± 0.04	0.39 ± 0.11	1.33 ± 0.12	0.68 ± 0.09	0.40 ± 0.08
Quebon	0.51 ± 0.07	0.44 ± 0.04	–	1.49 ± 0.16	0.74 ± 0.08	–
Recital	0.52 ± 0.05	0.37 ± 0.02	–	1.41 ± 0.09	0.96 ± 0.05	–
Renan	0.42 ± 0.06	0.38 ± 0.02	–	1.41 ± 0.16	0.84 ± 0.08	–
Toisondor	0.46 ± 0.04	0.45 ± 0.03	–	1.28 ± 0.15	0.82 ± 0.07	–
Minimum	0.30	0.37	0.39	1.11	0.64	0.37
Maximum	0.52	0.54	0.51	1.85	0.96	0.51
Average	0.42	0.43	0.46	1.42	0.78	0.43
P values
N	0.205			<0.001
Year	0. 617			<0.001
Genotype	<0.001			<0.001
N × year	0.603			0.003
N × genotype	0.881			0.174
Year × genotype	<0.001			<0.001
N × year × genotype	0.826			0.465

Vertical Leaf N Distribution with Respect to Vertical Light Distribution

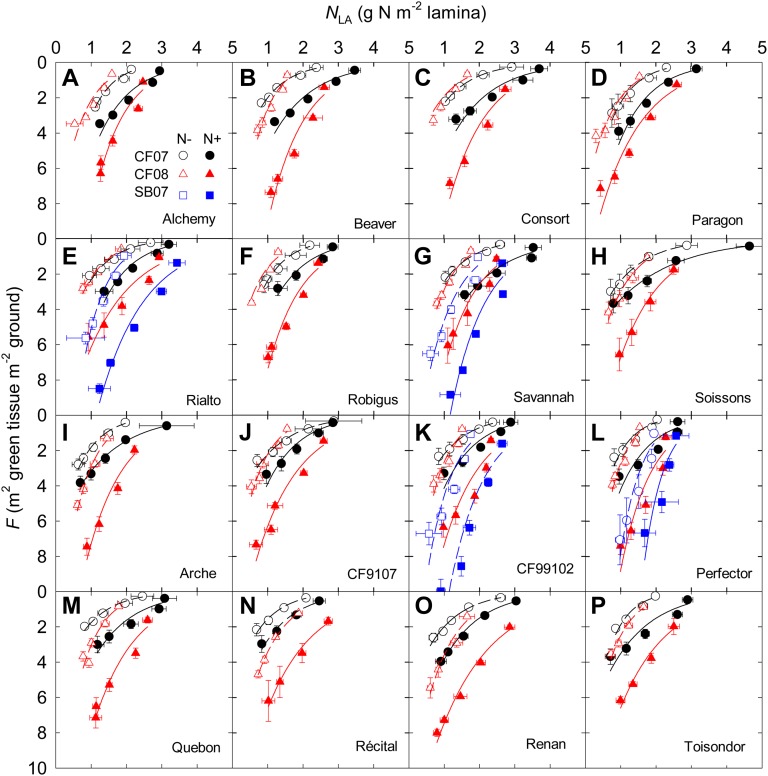
In all cases, the decline of leaf lamina N mass per unit leaf area (N_LA) down the canopy was related to the accumulated GAI, but the relationship depended on the site, year, N treatment, and cultivar (Fig. 2). According to the site/year/N treatment/cultivar combination, N_LA declined from the flag leaf to the lowest leaf in the canopy by 48% to 83%.

Figure 2.

Cumulative GAI counted from the top of the canopy (F) versus N_LA at anthesis for 16 cultivars of wheat (A–P) grown in the field under N− and N+ at CF during the 2006–2007 (CF07) and 2007–2008 (CF08) growing seasons and for four cultivars grown at SB during the 2006–2007 growing season (SB07). Data are means ± se for three independent replicates. Lines were fitted to the data by reduced major axis regression using logarithmic transformation of Equation 4. Symbols and lines are as in Figure 1.

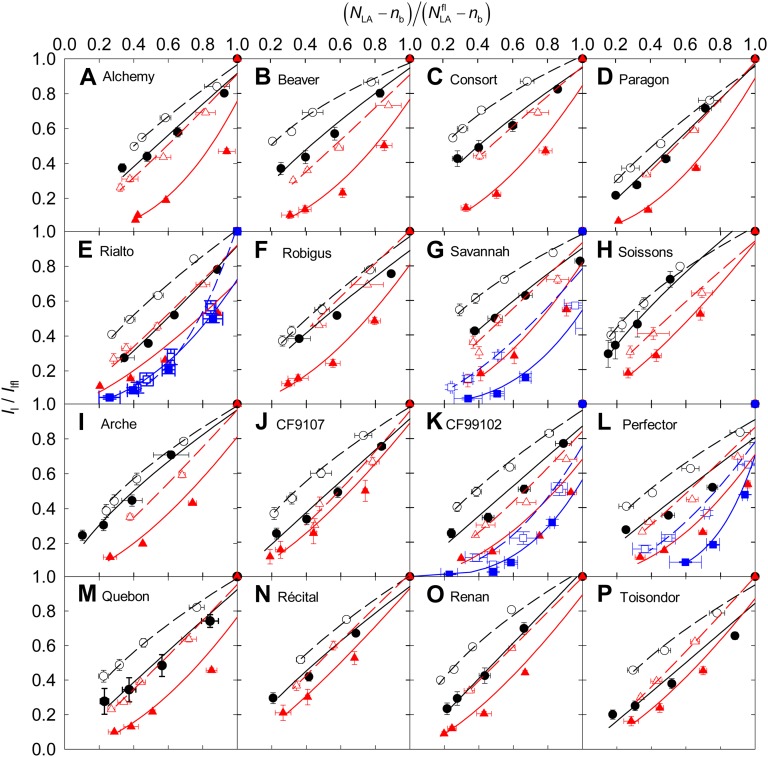
For N−, the relationship between the relative photosynthetic leaf N and the relative incident PPFD could be described satisfactorily by Equation 5 for each site/year/cultivar combination (Fig. 3). The observed N_LA of the flag leaf (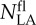) and that estimated using Equation 4 were not different (P = 0.754; Supplemental Fig. S2A). For N+, in most cases, the values obtained by Equation 4 indicated a higher decrease of N_LA at the top of the canopy than observed values, but below the flag leaf it described well the N_LA gradient. 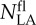estimated using Equation 4 was higher than observed values, as the intercept of the estimated versus observed relation differed from zero (P = 0.023; Supplemental Fig. S2B). This relationship was characterized by the N extinction coefficient with respect to light (b). b was modified by the cultivar, and averaged across the N treatments b varied between 1.23 (cv Paragon) and 2.20 (cv Consort) at CF07 and between 0.66 (cv Alchemy) and 0.98 (cv Recital) at CF08 (Table II). Values were higher for CF07 than for CF08. The year × genotype interaction was significant for b. Whatever the genotype, b was higher for N− (averaging 1.40 across the cultivars and years) than for N+ (averaging 0.96 across the cultivars and years), indicating that the N gradient was systematically steeper under limiting N supply. The differences between N treatments were consistent for all the cultivars (nonsignificant genotype × N treatment interaction). Similar conclusions could be drawn from the study of the four cultivars studied at SB.

Figure 3.

Relative PPFD incident on the leaf (I/I_fl) versus relative photosynthetic N_LA [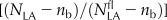] at anthesis for 16 cultivars of wheat (A–P) grown in the field under N− and N+ at CF during the 2006–2007 (CF07) and 2007–2008 (CF08) growing seasons and for four cultivars grown at SB during the 2006–2007 growing season (SB07). For [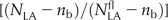], data are means ± se for three independent replicates. For I/I_fl, data at each leaf rank were estimated a posteriori using the fitted curve between I/I_fl and the height in the canopy (data not shown) and the height of each leaf rank. Lines were fitted to the data by reduced major axis regression using logarithmic transformation of Equation 5. Symbols are as in Figure 1.

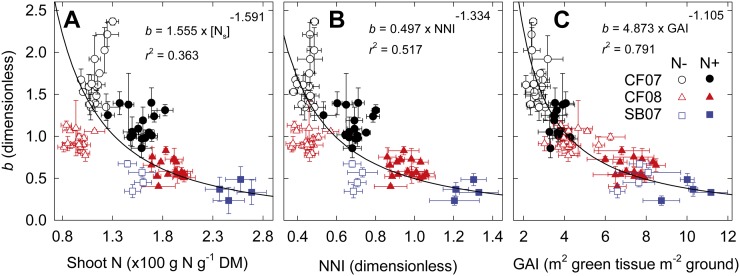
Relationship between Vertical Leaf N Distribution, Crop N Status, and Canopy Size

When all the site/year/N treatment/cultivar combinations were considered, shoot N concentration explained only 36% of b variations (Fig. 4A). A nitrogen nutrition index (NNI) can be determined to quantify crop N status; this index has been shown to be a better indicator of crop N status than shoot N concentration because it is well connected with the physiological regulation of N uptake at the canopy level (Lemaire et al., 2008). The relationship between b and NNI was thus analyzed (Fig. 4B). As expected, NNI explained a larger part (52%) of b variations than shoot N concentration. There was no relationship between b and 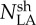(P = 0.15) or 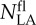(P = 0.86).

Figure 4.

b versus shoot N concentration (A), crop NNI (B), and GAI (C) at anthesis for 16 cultivars of wheat grown in the field under N− and N+ at CF during the 2006–2007 (CF07) and 2007–2008 (CF08) growing seasons and for four cultivars grown at SB during the 2006–2007 growing season (SB07). Data are means ± se for three independent replicates. Solid lines indicate reduced major axis regression fitted to the data after logarithmic transformation. DM, Dry mass.

The relationship between b and GAI was then analyzed in order to assess whether the variability associated with the vertical N distribution, both among cultivars and between N treatments, could be related to differences in canopy size. When the different site/year/N treatment/cultivar combinations were considered, b decreased with increasing GAI according to a unique power function that accounted for 79% of b variations (Fig. 4C):

No correlation was found between K_L and GAI (r = 0.014, P = 0.904); hence, the relationship between b and GAI was due to a correlation between K_N and GAI (r = 0. 92, P > 0.001). As a result of the isometric overall relationship between b and GAI and the exponential decay of the light down the canopy, b was linearly related to the reciprocal of ln of the canopy transmittance (Supplemental Fig. S3).

The allometric relation between b and GAI was statistically significant for 14 of the 16 cultivars (Table III; Supplemental Fig. S4), and the scaling coefficient (β) differed among the cultivars, ranging from 2.16 (cv Rialto) to 5.41 (cv Perfector). No difference was found for the scaling exponent (α) of the b-GAI relationship, and there was no shift along the common slope (Table III), but the parameters α and β were correlated (r = −0.854, P < 0.001).

Table III. Summary statistics of the linear regression analysis of b versus GAI at anthesis for 16 wheat cultivars.

Reduced major axis intercepts (coefficient) and slopes (exponents) and fitted axis means were calculated using the log-log version of the function equation 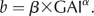. CI, Confidence intervals. Data are plotted in Supplemental Figure S3.

Cultivars and Statistical Data	Exponent		Coefficient		Fitted Axis Mean	GAI at Which b = 1	r2	P Value
	α	95% CI	β	95% CI
	m2 ground m−2 green tissue		dimensionless
Alchemy	−1.28	−1.76 to 0.06	4.59	2.57 to 8.12	0.25	3.30	0.99	0.006
Beaver	−1.17	−1.69 to 0.06	5.36	2.88 to 10.00	0.32	4.22	0.98	0.008
Consort	−0.95	−1.28 to 0.04	3.88	2.63 to 5.75	0.37	4.16	0.99	0.005
Paragon	−0.90	−1.20 to 0.04	3.23	2.19 to 4.68	0.24	3.66	0.99	0.004
Rialto	−0.76	−1.47 to 0.13	2.16	−0.93 to 5.01	0.19	2.74	0.74	0.027
Robigus	−0.86	−1.67 to 0.09	3.27	1.35 to 7.94	0.28	3.98	0.95	0.028
Savannah	−1.01	−1.37 to 0.08	4.14	2.45 to 6.92	0.19	4.05	0.95	0.001
Soissons	−0.95	−1.81 to 0.10	4.89	1.82 to 12.9	0.32	5.28	0.95	0.025
Arche	−0.87	−1.29 to 0.06	4.17	2.34 to 7.41	0.26	5.21	0.98	0.009
CF9107	−0.73	−2.36 to 0.16	2.78	0.57 to 13.5	0.27	4.04	0.77	0.123
CF99102	−0.95	−1.16 to 0.05	3.17	2.29 to 4.36	0.15	3.39	0.98	<0.001
Perfector	−1.25	−2.13 to 0.19	5.42	1.62 to 18.20	0.15	3.85	0.84	0.010
Quebon	−0.76	−1.02 to 0.03	2.62	1.91 to 3.63	0.29	3.57	0.99	0.005
Recital	−0.53	−0.85 to 0.04	2.36	1.62 to 3.47	0.32	5.10	0.97	0.013
Renan	−0.74	−2.09 to 0.15	3.32	0.76 to 14.79	0.25	5.06	0.84	0.086
Toisondor	−0.82	−1.78 to 0.10	2.98	1.12 to 7.94	0.29	3.82	0.92	0.041
P values	0.336		<0.001		0.998
Common parameter	−0.920	−1.017 to −0.847

DISCUSSION

Previous reports based on several species studied under controlled conditions suggested that plant internal N availability could be determinant in the development of the vertical leaf N gradient (Anten et al., 1995b; Lötscher et al., 2003). This suggested that factors other than light could play a key role in the determination of the vertical leaf N gradient with respect to light. Therefore, we analyzed the vertical leaf N gradient in relation to different ecophysiological variables for 16 cultivars of wheat grown under two conditions of N supply in three field experiments. To the best of our knowledge, this is the first study examining the genetic variability related to the vertical leaf N gradient, with respect to the light gradient, at the intraspecific level. Determining whether the genetic variability in this trait can be related to ecophysiological variables had never been tested before. For a staple crop like wheat, such findings could have important implications for plant breeding and modeling.

The Vertical Distribution of Light Varied Among Cultivars

The vertical light gradient is the main environmental factor governing the development of the vertical leaf N gradient in canopies (Werger and Hirose, 1991; Pons and de Jong-van Berkel, 2004). In this study, the distribution of light was described by the K_L. It is broadly acknowledged that the estimation of K_L, which assumes that light attenuates exponentially within the canopy, is a simplification that may not describe the actual light environment, due to sunflecks, diffuse radiations, or variations of leaf angle with depth (Sinclair and Shiraiwa, 1993; Kull and Jarvis, 1995; Johnson et al., 2010). Beyond these concerns, we assessed K_L using a simplified method: instead of performing stratified light measurements at different depths within the canopy, light was measured above the canopy and at ground level only. This methodological choice, motivated by the large number of cultivars under study, was shown to provide reliable estimations of K_L. Several authors have stressed that the development of high-throughput methods for field-based plant phenotyping represents a major bottleneck for analyzing the genetic variability and determinism of plant functional traits (Montes et al., 2007). The method used in this study is well adapted to analyze the genetic variability of K_L, an important canopy-level trait, and therefore represents an important methodological advance.

N treatments did not modify K_L. The stability of K_L for different conditions of N supply reported in this study is consistent with previous studies (Robertson and Giunta, 1994; Muurinen and Peltonen-Sainio, 2006). By contrast, significant differences among cultivars were found. The values of K_L reported here are lower than those reported in some other investigations, where stem and ear surface areas were calculated as their projected surface area (O’Connell et al., 2004; Shearman et al., 2005) or where only leaf surface area was considered to calculate GAI (Muurinen and Peltonen-Sainio, 2006). However, the range of genetic variation for K_L observed in this study is in good agreement with the literature (for review, see Martre et al., 2007). Thus, while increasing N supply increased GAI, the intensity with which light attenuated with increasing cumulative GAI was independent of N supply and canopy size but varied with cultivar. The large year × genotype interaction component nevertheless precludes unambiguous cultivar ranking for this trait.

The Ratio of Vertical Leaf N to Light Gradients at Anthesis Scales with the Size of the Canopy

A power relationship was observed between vertical N and light distributions for each site/year/N treatment/cultivar combination. However, the adjustment of the leaf N gradient to the light gradient (reflected by the value of b) varied according to the cultivar. In addition, it differed with the N treatment: whatever the cultivar, the leaf N gradient relative to the light gradient was steeper at lower N supply. Different descriptors related to crop N status and canopy size were considered. b decreased with increasing shoot N concentration according to a trend that was similar to that reported by Lötscher et al. (2003) for several monocot and dicot species, but most of the variability of b remained unexplained by shoot N concentration. NNI is a better descriptor of crop N status than shoot N concentration (Lemaire et al., 2008) and, as hypothesized by Lötscher et al. (2003), it accounted for a larger part of the variability of b than shoot N concentration. A key result of this study was that b decreased with GAI, indicating that the leaf N gradient to the light gradient became progressively more uniform when canopy size increased. Under N+, most of the cultivars accumulated more N at the top of the canopy (mainly in the flag leaf) than expected by an exponential function of relative light. Nevertheless, this finding did not challenge the observed relationship between b and GAI. Indeed, this relationship remained valid even if we excluded the canopies for which luxury N storage existed at the top of the canopy or the flag leaf for all the canopies (data not shown). In addition, there was no correlation between K_L and GAI. Therefore, the relationship between b and GAI stemmed from the relationship between K_N and GAI.

Whether b should be considered as a function of GAI, or rather GAI as a function of b, is a priori not straightforward. Indeed, if there is a strong vertical attenuation of leaf N, then the crop would not be able to maintain a high GAI, since the leaf at bottom of the canopy would start to senesce due to N shortage. In other words, GAI would decrease as a consequence of increasing b. In our study, the number of leaves per main shoot at anthesis was nearly constant, ranging from four to five leaves. Therefore, the variations of GAI were not caused by differences in leaf number per main shoot but rather by variation in individual leaf size and the number of main shoots per square meter. We can thus conclude that under our experimental conditions, the variations in b were caused by the variation in GAI.

This study is concordant with previous studies (Pons et al., 1989; Kull, 2002) challenging the optimization theory (Hirose and Werger, 1987). In our study, GAI covered a wide range of variation (from approximately 2 to 12 m² m⁻²), but under normal growth conditions, GAI of a mature canopy is generally higher than 4 m² m⁻², and according to our results, b is then lower than 1. These values are in good agreement with all available studies showing that actual leaf N distribution is more uniform (b < 1) than the calculated optimal distribution, which maximizes canopy photosynthesis (b = 1; Chen et al., 1993; Evans, 1993; Hollinger, 1996; Anten et al., 1998). As pointed out by Farquhar (1989), the parallelism between the vertical distributions of light and N (b = 1) was found in models that do not take into account the costs of the construction and maintenance of photosynthesis. It can be assumed that these costs are proportional to GAI and that b scales with GAI so that the N distribution maximizes canopy photosynthesis independently of GAI. Our results strongly suggest that the acclimation of the leaf N gradient to the light gradient is a whole-plant process that depends notably on the size of the canopy, as suggested by Kull (2002).

Both theoretical and experimental results showed that the relative response of canopy photosynthesis to changes in b increases with the size of the canopy (Hirose and Werger 1987; Schieving et al., 1992; Sands, 1995). In our study, different stands covering a wide range of GAI were used to analyze the ecophysiological determinants of b. Under our growing conditions, commercial wheat crops have a maximum GAI ranging between 4 and 6 m² m⁻² (Foulkes et al., 1998); thus, according to Equation 1, b may range from 1.06 to 0.67. According to Hirose and Werger (1987), such variations in b would change canopy photosynthesis up to 10% to 15%. This rough estimation of the potential effect of changes in b on canopy photosynthesis has to be put into perspective using a mechanistic dynamic simulation model of whole-canopy photosynthesis over the whole growing season. A modeling analysis would also allow quantifying the effect of the genetic variability of β of the b-GAI relationship reported in this study on canopy photosynthesis and final grain crop biomass and grain yield.

Anyway, modeling leaf N distribution and canopy expansion based on the assumption that leaf N distribution is always optimal to maximize photosynthesis according to the optimization theory (i.e. b = 1) is definitely inappropriate (Johnson et al., 2010). The relation between b and GAI is robust for a wide range of cultivars. Yet, empirically, it provides a good basis for improving our representation of N distribution within whole-plant models. Our work also puts emphasis on the importance of accurate modeling of GAI, because it determines both the extent of the light-intercepting area and the distribution of N among leaves (through b modulation) and therefore the photosynthesis per leaf area unit.

In summary, the analysis of wheat canopies grown in a wide range of site/year/N treatment/cultivar combinations provided a large variability of the vertical leaf N distribution at anthesis and allowed the three questions framed in the introduction to be answered. Regarding the effect of N supply on the distribution of leaf N, we showed that the distribution of leaf N, with respect to the light distribution, was steeper when N supply decreased. Regarding the second question, when all the cultivars in each site/year/N treatment combination were considered, we found a wide range of b values, but most of these variations reflected a phenotypic plasticity rather than a genetic variability for b, as the genotype × environment interaction was significant. Finally, we found that GAI was a unique ecophysiological determinant of both genetic and environmental variations of b, and we can conclude that the vertical distribution of leaf N scales with the size of the canopy. This finding is in good agreement with previous reports showing that the acclimation of the leaf N gradient to the light gradient is a whole-plant process that depends notably on the size of the canopy (Kull, 2002). The β of this allometric relationship differed among cultivars, suggesting that cultivars could be differently adapted to low-productivity environments.

MATERIALS AND METHODS

Plant Material and Growing Conditions

Sixteen genotypes of wheat (Triticum aestivum) from the United Kingdom and France elite germplasm (Supplemental Table S1) were studied in a 2-year field experiment carried out at CF (45°47' N, 3°10' E, 329 m elevation) during the 2006–2007 (experiment CF07) and 2007–2008 (experiment CF08) growing seasons (named 2007 and 2008, respectively). The genotypes comprised UK- and French-bred cultivars/advanced lines representing feed wheat (Alchemy, Arche, Beaver, Consort, Paragon, Rialto, Robigus, and Savannah) and bread-making wheat (CF9107, CF99102, Perfector, Quebon, Recital, Renan, Soissons, and Toisondor). All cultivars had winter growth habit, except the spring cultivar Paragon. Four of the cultivars (Rialto, Savannah, CF99102, and Perfector), representing the variability observed for N utilization and N uptake efficiency (Gaju et al., 2011), were also grown in 2007 (in experiment SB07) at the University of Nottingham in SB (52°50' N, 1°14' W, 52 m elevation). Soil characteristics for the different experiments are reported in Supplemental Table S2. At CF, crops were sown at a density of 250 seeds m⁻² on November 10, 2006 and November 6, 2007. At SB, crops were sown at a density of 300 seeds m⁻² on October 4, 2006. At both sites, the experimental design was a split plot in which N treatments were randomized on main plots, cultivars were randomized on the subplots, and each treatment combination was replicated three times. Subplot size was 24 × 1.65 m at SB and 7 × 1.5 m at CF. Interrow spacing was 0.17 and 0.125 m at CF and SB, respectively.

Weather conditions during the crop growth seasons are summarized in Supplemental Figure S5. From sowing to anthesis of cv Rialto, which has a rate of development in the middle of the range of the 16 cultivars (Supplemental Table S1), daily mean air temperature averaged 9.7°C and 7.9°C at CF07 and CF08, respectively, and was 9.1°C at SB07. During the same period, accumulated weekly radiation averaged 68 and 74 MJ m⁻² week⁻¹ at CF in 2007 and 2008, respectively, and was 53 MJ m⁻² week⁻¹ at SB. At CF07, the crop received 156 mm of rainfall during the vegetative period, which was lower than the long-term mean. Rainfall was also lower than the long-term mean in January and February 2008. At SB, rainfall was lower than the long-term mean in April and May 2007, during which the crops received 58 mm. At CF, anthesis was recorded between May 4 and 22, 2006, and between May 15 and June 1, 2007, depending on the cultivar (Supplemental Table S1). At SB, it was recorded on June 3 and 4, 2007 depending on the cultivar.

In all experiments, N+ and N− treatments were applied. For N+, the rates of N fertilization were determined using the balance-sheet method to optimize grain yield (Rémy and Hébert, 1977). N was applied as ammonium nitrate granules (34.5% N) in three (SB) to four (CF) splits. At CF, in both years, 4, 8, 8, and 4 g N m⁻² were applied when cv Rialto, reached growth stage 21 (GS21; Zadoks et al., 1974), GS31, GS37, and GS61, respectively. At SB, 6, 9, and 6 g N m⁻² were applied at GS21, GS31, and GS39. The amount of N applied under N− was adjusted in each site-season according to the soil mineral N measured in February (Supplemental Table S2) with the aim of providing approximately 10 g N m⁻² from the combined soil mineral N and fertilizer N, corresponding to a moderate to severe N limitation sufficient to reduce grain yield by approximately 30% compared with N+ conditions. At CF, in both years, 4 g N m⁻² was applied in one split when cv Rialto reached GS31, while at SB, no N was applied in the N− treatment. All other crop inputs, including weed, disease, and pest control and potassium, phosphate, and sulfur fertilizers, were applied at levels to prevent non-N nutrients, weeds, diseases, and pests from limiting yield. At SB, the plant growth regulator chlormequat was applied at GS31. The major growth stages were determined for each cultivar on five to 10 tagged plants per plot every 2 to 3 d according to Tottman (1987).

Plant Sampling

When each cultivar reached GS61, plant material in a 0.5-m² area per subplot was sampled by cutting at ground level. The total fresh mass of the samples was determined, and a 25% subsample (by fresh mass) was randomly selected. The main and secondary shoots were separated and counted. Shoots were classified as main when the top of their ear was in the top 0.15-m layer of the canopy. Thirty main shoots were randomly selected. The distances from the base of the shoot to individual culm leaf ligules and to the base and top of the ear were measured on 10 main shoots. Then, the 30 main shoots were dissected into individual leaf laminae, stem (including leaf sheath), and ear. The fresh mass of the secondary shoots of the subsamples was determined, and subsamples of secondary shoot (approximately 20%) were randomly selected. Their fresh mass was determined before separating them into laminae (pooled), stem (including leaf sheath), and ear. For both main and secondary shoots, green and dead/nonphotosynthetic tissues were analyzed separately as described below.

Green Surface Area Determination

The projected surface areas of green laminae, stems, and ears were determined using a Li-3100 area meter (LI-COR). For the main shoots, the lamina surface area of each phytomer was determined, while for the secondary shoots, the total lamina surface area was determined. Actual stem and ear surface areas were calculated as their projected surface area multiplied by π/2 (Lang, 1991). Canopy GAI (m² green tissue m⁻² ground) was calculated as the sum of lamina, stem, and ear surface area of the main and secondary shoots. GAI between successive main shoot leaf ligules was calculated as the sum of half of the laminae and stem surface area of the main and secondary shoots (plus ear peduncle and ear surface for the upper layer) located below and above each leaf ligule. The laminae and stem surface areas of secondary shoots were distributed to each layer in proportion to the laminae and stem surface areas of primary shoots.

Light Measurements and K_L Calculations

The vertical distribution of PPFD was measured 1 d before plant sampling using a 90-cm-long linear ceptometer (LP-80 AccuPAR; Decagon Devices) equipped with an external PPFD sensor. Simultaneous measurements were taken diagonally across the rows and above the canopy. At CF07, measurements were taken every 10 cm from the top of the canopy to the ground level in three different areas of each subplot (Bertheloot et al., 2008). The attenuation of PPFD down the canopy was described according to the Beer-Lambert’s law (Monsi and Saeki, 2005):

where F (m² green tissue m⁻² ground) is the cumulative GAI from the top of the canopy and I₀ and I (µmol m⁻² s⁻¹) are the PPFD values on a horizontal level above and within the canopy at depth F, respectively. For GAI higher than 0.2 m² m⁻², leaf clumping is very limited in wheat (Demarez et al., 2008); therefore, unbiased estimation of K_L could be done without taking into account the foliage aggregation.

The PPFD at the height of each culm leaf ligule was estimated from an exponential function equation fitted to the PPFD values plotted against the height from the ground level. Then, K_L was estimated by fitting Equation 2 to the estimated log-transformed PPFD values at the ligule heights plotted against log-transformed F. At CF08 and SB07, PPFD was measured above the canopy and at ground level only after confirming the validity of this simplified method of PPFD measurements using CF07 data (Supplemental Fig. S1) and independent data sets including canopies with GAI values ranging from 4.6 to 9.7 m² m⁻² (data not shown).

PPFD was measured at SB07 using a 100-cm-long linear ceptometer (SunScan System SS1; Δ-T Devices). Ten measurements were taken per subplot. K_L was then calculated from Equation 2 (Shearman et al., 2005). All the PPFD measurements were restricted to 10 am to 2 pm (solar time).

The PPFD incident on the leaf surface (I_l; µmol m⁻² s⁻¹) at depth F in the canopy was calculated as follows (Thornley and Johnson, 2000):

where m (dimensionless) is the PPFD transmittance of the leaf laminae, set at 0.08 (Masoni et al., 1996). I_l was calculated after logarithmic transformation of Equation 3. The error due to the use of only the light extinction of the canopy in Equation 3 is most likely negligible (5%–15% at most for genotypes with an erect leaf posture).

Main Shoot Dry Mass, N Concentration, Specific N_LA, Canopy K_N, and NNI

Lamina, stem, and ear dry mass of the main and secondary shoots was determined separately after oven drying at 80°C for 48 h. Samples were then milled, and their total N concentration (N mass per unit dry mass) was determined with the Dumas combustion method (Association of Official Agricultural Chemists method no. 7.024) using a FlashEA 1112 N/Protein Analyzer (Thermo Electron) at CF and a NA-2000 elemental analyzer (Fisons) at SB. Specific N_LA (g N m⁻² lamina) was calculated by dividing the mass of green lamina N by the green lamina surface area. Average N_LA of main shoot leaves was calculated by dividing the total lamina N by the total laminae surface area.

Vertical leaf lamina N distribution through the canopy can be related to F as follows:

where n_b (g N m⁻² leaf lamina) is the N_LA at which light-saturated photosynthesis is nil; K_N (m² ground m⁻² green tissue) is the N extinction coefficient; and 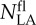approximates the N_LA of the flag leaf. For wheat, after heading, 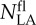may significantly depart from the N_LA at the top of the canopy because of the presence of the ear. Previous works indicated that optimal N distribution can be given by the Lagrange multiplier (Field, 1983; Hirose and Werger, 1987) when maximal photosynthesis is proportional to light availability across leaf layers (Farquhar, 1989). Equation 3 was then derived by Anten et al. (1995b), who showed that N distribution is optimal when convexity and the initial slope of the light-response curve of photosynthesis are constant across leaves.

After eliminating F from Equations 3 and 4, N_LA can be related to PPFD:

where b (dimensionless) is the coefficient of leaf N distribution with respect to relative PPFD incident on a leaf and is equal to the ratio of K_N to K_L and (µmol m⁻² s⁻¹) is the PPFD incident on the leaf at midpoint (in terms of GAI) of the flag leaf lamina. b and 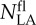were estimated after logarithmic transformation of Equation 5. In wheat, n_b ranges from 0.25 to 0.55 g N m⁻² (Araus and Tapia, 1987; Evans, 1993; Lawlor, 1995; Dreccer et al., 2000; Sudo et al., 2003; Vos et al., 2005; Del Pozo et al., 2007). In a preliminary analysis, we conducted a sensitivity analysis in which n_b was varied from 0.25 to 0.55 g N m⁻² with intervals of 0.05 g N m⁻². This sensitivity analysis showed that b tended to increase linearly with n_b. However, the values of b estimated when either a fixed value of n_b was used or both b and n_b were estimated simultaneously for each cultivar were closely correlated with a slope not significantly different from 1 and n_b was not significantly different among cultivars (data not shown). Therefore, n_b was set at the nominal value of 0.4 g N m⁻². The N_LA of a layer was related to I_l/ at midpoint of that layer (Milroy et al., 2001) estimated using Equation 2 and to K_L estimated from PFFD measurements taken above the canopy and at ground level. According to Anten et al. (1995b), an optimal N_LA distribution maximizing canopy photosynthesis is given when K_L equals K_N and thus b equals 1. b is a key parameter defining the acclimation of leaf photosynthesis to the light environment (Sands, 1995). The value of b increases with the nonuniformity of the N distribution (increasing difference between the N_LA values at the top and bottom of the canopy).

Based on the critical dilution curve of wheat (Justes et al., 1994), a NNI was calculated to quantify crop N status. Although this curve is empirical, it is based on solid theoretical grounds (Lemaire and Gastal, 1997). Climatic conditions can affect growth and N uptake differently, but the NNI incorporates these effects in terms of crop N needs (for a thorough discussion of N dilution in crops, see Lemaire et al., 2008; Gonzalez-Dugo et al., 2010). For a given shoot dry mass (DM; g m⁻²), NNI was calculated as the ratio between the actual and critical shoot N concentrations (N_c; g N g⁻¹ dry mass) defined by the critical dilution curve (Justes et al., 1994):

A NNI value close to 1 indicates an optimal crop N status, and a value lower (or higher) than 1 indicates N deficiency (or N excess).

Statistics

All regression analyses were done in R-2.12.2 for Windows (R Development Core Team, 2007). The two methods for estimating K_L were compared by reduced major axis regression (Warton et al., 2006) with the package SMATR for R (Falster et al., 2006). All ANOVAs were performed with Statgraphics Plus 4.1 for Windows (Statistical Graphics). ANOVA procedures for a split-plot design was used at CF for the 16 cultivars. Replications were regarded as random effects, while N treatment and genotype were fixed effects. For ANOVA across the three experiments and the four cultivars, site and year were regarded as random effects. Statistical differences were judged at α = 0.05.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure S1. Comparison of the two methods used to estimate the canopy K_L.

• Supplemental Figure S2. Estimated versus observed flag leaf lamina N mass per unit leaf area.

• Supplemental Figure S3. Relationship between the ratio of K_N to K_L and the reciprocal of the ln of the canopy transmittance.

• Supplemental Figure S4. Coefficient of leaf N distribution with respect to relative light versus GAI at anthesis for 16 cultivars of wheat.

• Supplemental Figure S5. Weather data for the three growing seasons considered in this study.

• Supplemental Table S1. Cultivar name, country of origin, registration year, height, and anthesis date.

• Supplemental Table S2. Soil characteristics.

Glossary

N

nitrogen

b

nitrogen extinction coefficient with respect to light

K_L

light extinction coefficient

K_L

light extinction coefficient

K_N

nitrogen extinction coefficient

N_LA

leaf lamina N mass per unit leaf area

PPFD

photosynthetic photon flux density

CF

Clermont-Ferrand

SB

Sutton Bonington

GAI

green area index

CF07

experiment at Clermont-Ferrand in 2007

CF08

experiment at Clermont-Ferrand in 2008

SB07

experiment at Sutton Bonington in 2007

NNI

nitrogen nutrition index

β

scaling coefficient

α

scaling exponent