Dead-End Elimination with Perturbations (“DEEPer”): A provable protein design algorithm with continuous sidechain and backbone flexibility

Abstract

Computational protein and drug design generally require accurate modeling of protein conformations. This modeling typically starts with an experimentally-determined protein structure and considers possible conformational changes due to mutations or new ligands. The DEE/A* algorithm provably finds the GMEC (global minimum-energy conformation) of a protein assuming the backbone does not move and the sidechains take on conformations from a set of discrete, experimentally-observed conformations called rotamers. DEE/A* can efficiently find the overall GMEC for exponentially many mutant sequences. Previous improvements to DEE/A* include modeling ensembles of sidechain conformations and either continuous sidechain or backbone flexibility. We present a new algorithm, DEEPer (Dead-End Elimination with Perturbations), that combines these advantages and can also handle much more extensive backbone flexibility and backbone ensembles. DEEPer provably finds the GMEC or, if desired by the user, all conformations and sequences within a specified energy window of the GMEC. It includes the new abilities to handle arbitrarily large backbone perturbations and to generate ensembles of backbone conformations. It also incorporates the shear, an experimentally-observed local backbone motion never before used in design. Additionally, we derive a new method to accelerate DEE/A*-based calculations, indirect pruning, that is particularly useful for DEEPer. In 67 benchmark tests on 64 proteins, DEEPer consistently identified lower-energy conformations than previous methods did, indicating more accurate modeling. Additional tests demonstrated its ability to incorporate larger, experimentally-observed backbone conformational changes and to model realistic conformational ensembles. These capabilities provide significant advantages for modeling protein mutations and protein-ligand interactions.

1 Introduction

Accurate computational protein and drug design requires a biophysically reasonable representation of protein conformations and an efficient method to search protein conformational and sequence space. The full conformational and sequence space available to a protein is too vast to search completely. One approach to this problem is to model the overall fold of a protein on a coarse level, and then to introduce additional detail as needed; this has allowed the de novo design of proteins with a desired overall fold [1, 2, 3]. Alternatively, a protein or protein-ligand complex similar to an experimentally-determined structure can be modeled by searching conformations similar to the empirical structure [4, 5, 6], allowing design of novel proteins or protein-binding drugs [7, 8, 9, 10, 11]. In this case, the conformational search space can be represented by choosing a set of flexible residues, whose conformations are likely to change in response to mutations or new ligands. For protein design, the search can be performed over sequence space as well because multiple amino acid types can be considered for each flexible residue. The conformation and sequence of the entire protein is then represented as a tuple of conformations and amino acid types for the flexible residues. Since the flexibility of protein sidechains is mostly in their dihedral angles and these angles are usually found in discrete clusters called rotamers [12, 13], previous algorithms have typically discretized the conformational space of a residue into sidechain rotamers. Using an energy function, which assigns an energy to each conformation, this scheme casts protein design into a combinatorial optimization problem. Empirical molecular-mechanics energy functions are typically used for this purpose [6, 14].

The sequence and structure of a native or designed protein or complex can be modeled by finding its Global Minimum-Energy Conformation (GMEC): the sequence and conformation of the protein that minimizes the energy function. The GMEC, like any sequence and conformation, can be represented as a tuple of conformations and amino acid types of individual residues. However, consideration of the GMEC alone neglects important entropic effects [15], because proteins in solution populate many conformations. Consequently, considering an ensemble of low-energy conformations results in more accurate predictions of binding and catalysis [5, 16, 8, 10, 14]. This has led to three main types of search methods over protein conformational and sequence space: (a) stochastic, heuristic methods that try to find the GMEC [17, 15, 18, 19, 20, 21, 22], (b) methods to provably find the GMEC [14, 23, 24], and (c) methods to generate conformational ensembles [5, 16, 14, 25]. All these methods require a biophysical model as input. The biophysical model specifies not only the conformations and sequences available to the protein, but also the energy function used to score those conformations and sequences. Often, the space of allowed conformations and sequences is defined using (i) a starting structure, (ii) a set of residues allowed to differ from the starting structure, and (iii) a library of rotamers for those residues to populate. The allowed sequence space to search may be just one sequence, or an astronomical number of combinatorial possibilities. Methods of type (c) may or may not have provable guarantees of accuracy. Our lab has developed methods of types (b) and (c) [5, 16, 26, 27, 28, 8] with provable guarantees of accuracy and successfully tested them in vitro and in vivo, generating mutants and ligands that may aid in synthetic biology [10] and in the treatment of bacterial diseases [7, 10], cystic fibrosis [8], HIV [11], and leukemia [9].

Because finding the GMEC is NP-hard [29, 30], several heuristic algorithms have been developed for this problem [18, 19, 20, 21, 22]. These algorithms can find a relatively low-energy conformation fairly rapidly, albeit without any guarantees of completeness or accuracy. (We will refer to an algorithm as complete if it is guaranteed to consider its entire search space and as accurate if its answers are always correct for the algorithm’s input, at least within a given margin of error). Metropolis Monte Carlo [31]-based methods [32, 33] have been used to search the space of rotamers. These methods can incorporate continuous flexibility by applying the Monte Carlo with minimization method [17], and have also incorporated some backbone flexibility [34]. The GMEC has also been approximated by molecular-dynamics simulation of protein folding [15, 35], offering the added benefit of modeling kinetics. But molecular dynamics is rarely computationally tractable for protein design due to the large sequence space and large number of folding intermediate states that must typically be considered. Unlike DEEPer, the algorithm introduced in this work, molecular dynamics only considers one sequence at a time. Genetic algorithms [36] and numerical global minimization methods [22] have also been used to search for the GMEC, and the heuristic FASTER method [37], which combines deterministic and stochastic steps, has been developed specifically for this search as well.

On the other hand, algorithms to provably find the GMEC are also available [14, 23, 24]. Because they are guaranteed to find the optimal conformation and sequence given a biophysical model, they consider all functionally significant conformational and sequence changes allowed by the model, and thus they will generally produce more empirically accurate results than heuristic algorithms using the same model. Provable algorithms are also useful for evaluating and improving models because they ensure that any discrepancies between experimental results and the predictions of the algorithm are due solely to the inadequacies of the model, and not to the algorithm [14, 8, 28]. Most provable methods for identifying the GMEC start by eliminating rotamers that cannot participate in the GMEC, by using Dead-End Elimination (DEE) [38]. This step is typically followed by the A* search algorithm [39], which finds the GMEC using the unpruned rotamers. If A* is continued after the GMEC is found, it will output the other conformations of the protein gap-free in ascending order of energy. Thus, it can be used to identify all conformations whose energy is within a specified energy interval E_w of the GMEC energy.

This DEE/A* framework has been extended to run more efficiently, to model ensembles, and to include continuous flexibility, enhancements which come with provable guarantees of accuracy and are applicable to the simultaneous search of mutant sequence space and conformational space [14].

First, DEE has been extended to eliminate more rotamers as well as tuples of rotamers at different residues [40]. The related Bounds [41] and conformational-splitting DEE [42] algorithms prune some rotamers that ordinary DEE cannot prune. The HERO algorithm [41] combines these improvements into a single algorithm by applying them successively and iteratively.

Next, DEE/A* has also been extended to allow continuous flexibility within each rotameric state, producing “minimization-aware” algorithms whose pruning is still provable even with this continuous flexibility. In these methods, the conformation is no longer uniquely defined by a tuple of rotamers, but once a rotamer has been assigned to each residue, the GMEC can be found by local minimization. Correspondingly, the “minimization-aware” pruning is followed by a modified A* search that enumerates tuples of rotamers in order of a lower bound on the conformational energy, rather than in order of the conformational energy. The true conformational energies are then obtained by local minimization. The minDEE algorithm [16] allows the sidechain dihedrals to vary continuously within a specified interval about the modal values for a given rotamer, while the BD [26] and brDEE [27] algorithms allow small backbone conformation adjustments while modeling discrete sidechain rotamers. In BD, the backbone is continuously flexible within a voxel. In brDEE, the backbone states are discrete but systematically and closely spaced; the backbone states for each residue are represented using a single parameter. iMinDEE [28], a significantly more efficient version of minDEE, provides a more powerful minimization-aware pruning criterion. i_r denotes a rotamer r at residue position i in the the protein, where r is chosen from a set R, and 1 ≤ i ≤ n, where n is the number of residues in the protein. It prunes a rotamer i_r at a residue i if, for any other rotamer i_t at residue i,

$$E_{⊝}(i_r)-E_{⊝}(i_t)+\sum _{j\ne i}\underset{j_s}{min}(E_{⊝}(i_r,j_s)-E_{⊝}(i_t,j_s))>E_w+I$$ (1)

where E_⊝ is a lower bound on the internal energy of a rotamer or the interaction energy for a pair of rotamers (see [16] and Section 2.4). I, the “pruning interval,” is an upper bound on the energy difference between the GMEC and the lowest lower-bound on a conformational energy, calculated by summing the single-rotamer and pairwise lower-bound energies. This equation will prune rotamers not found in conformations within a user-specified energy interval E_w of the GMEC. If only the GMEC is desired, E_w can be set to 0. In summary, methods based on DEE/A* are now available to provably and efficiently find the GMEC in a search space defined by sidechain rotamers as well as a small amount of continuous flexibility in either the sidechains or the backbone.

Finally, the K^* algorithm [5, 16, 14] compares the conformational ensemble of a protein with a ligand to its ensemble without the ligand. This is done by approximating their partition functions within a provably guaranteed margin of error (given the biophysical model). K^* is an extension for DEE/A* that can be applied to any of the minimization-aware variants of DEE/A*, allowing the modeling of continuous flexibility in computing partition functions. Unlike GMEC-based analysis, this method accounts for entropic effects, allowing substantial improvements in the accuracy of binding predictions. K^* can identify tight-binding sequences from a large sequence space efficiently and with provable accuracy. It has been shown to optimize design for affinity [8, 5, 10, 16, 14].

Further increases in accuracy for modeling mutant or new ligand-bound conformations require including more backbone flexibility, simultaneously with continuous sidechain flexibility (Table I). Three lines of evidence support this need. First, mutations have often been found to induce substantial backbone conformational changes [43, 44, 45]. Second, modeling of continuous sidechain flexibility has been found to substantially enhance the accuracy of rotamer assignments and the identification of low-energy sequences [28]. Third, backbone as well as sidechain degrees of freedom contribute significantly to conformational ensembles [46, 47]. Thus, we present a new algorithm, Dead-End Elimination with Perturbations (DEEPer), that incorporates continuous sidechain and backbone flexibility in a provably complete search. This search always finds the GMEC or a gap-free list of the lowest-energy conformations, depending on the user’s preference, and it interfaces directly with K^* to predict binding affinity using ensembles, maintaining K^*’s provable guarantees on accuracy but giving it the novel ability to account for some backbone conformational entropy. This means that it can estimate binding affinity more accurately. To maintain search efficiency as this additional flexibility is added, increased pruning is necessary. We show that a novel pruning algorithm, indirect pruning, can alleviate the increased computational cost that is incurred with substantial backbone flexibility, while maintaining a provable guarantee of accuracy (Section 2.4). Indirect pruning combines the minimization awareness of iMinDEE [28] with features of Goldstein singles and tuples pruning [40] and Bounds pruning [41].

Table I.

Continuous flexibility in DEE-based protein design algorithms

	Sidechain flexibility
Backbone flexibility	Discrete	Continuous
None	DEE [38]	minDEE [16], iMinDEE [28]
Discrete	BRDEE [27]	DEEPer
Continuous	BD [26]	DEEPer

DEEPer is also well adapted for including backbone perturbations based on information from previous experiments. These can include backbone conformational changes previously observed for the protein of interest, if available, but we also feature two commonly observed forms of backbone flexibility “moves,” the shear [48, 34] and backrub [48]. While the backrub has been incorporated in previous design algorithms [27, 34], the shear has not. Both moves were identified in high-resolution crystal structures by examination of anisotropic electron density and of crystallographic alternates, which are multiple conformations of the same segment of a protein that are each observed in some portion of the molecules in a single crystal. Backrubs also observably accommodate sequence changes in natural proteins [49], thus validating their use for accommodating engineered mutations in protein design. Shears are expected to similarly aid searching of combined conformational and sequence space. Shears and backrubs are relatively small backbone perturbations, so they are suitable for modeling backbone perturbations within helix and sheet secondary structures, where the backbone motion is limited. Together with the five other types of perturbations implemented in DEEPer (Table II), shears and backrubs allow a wide range of backbone flexibility in all types of secondary structure.

Table II.

Types of perturbations

Type	Parameter	Continuous	Residues affected	Where usually found
Shear*	Primary shear angle	Yes	4	Helices
Backrub	Primary backrub angle	Yes	3	β sheets, loops
Loop closure adjustment*	Solution from discrete set	No	3	Loops
Secondary structure adjustment*	Solution from discrete set	No	3–4	Loop-helix or loop-sheet borders
Partial structure switch	Structure from discrete set	No	As desired	Anywhere
Full structure switch	Structure from discrete set	No	All	Entire protein
Proline flip	Boolean: flip or no flip	No	1	Prolines

^*These perturbations cannot, to our knowledge, be performed by any previous protein design algorithm. DEEPer also offers novel combinations of perturbations that have been modeled previously; for example, no previous provable algorithm modeled overlapping backrubs. DEEPer is also novel in combining these perturbations with continuous sidechain flexibility, which is represented as orthogonal to perturbations in conformational space.

Thus, by introducing DEEPer, this paper makes the following contributions:

1. A provable algorithm for searching a continuously-flexible conformational space, including both sidechain and backbone degrees of freedom, as well as simultaneous combinatorial search of mutant sequence space.

2. The extension of iMinDEE [28] to minimize over backbone as well as sidechain degrees of freedom.

3. A general, provable method for introducing backbone perturbations based on previous studies of protein backbone flexibility, such as the shear motion, into protein design calculations.

4. A provable method for modeling ensembles of conformations in which conformations are allowed to vary with respect to sidechain and backbone degrees of freedom, during a search over combined sequence and conformational space.

5. An implementation of DEEPer in our laboratory’s open-source OSPREY protein-design software package [7, 10, 16, 50], available by request as free software.

6. A new minimization-aware conformational pruning algorithm, indirect pruning.

7. Computational tests on 64 proteins to demonstrate that DEEPer identifies lower-energy structures and sequences than previous methods, and tests to demonstrate that it computes biophysically reasonable ensembles of backbone conformations.

2 Methods

DEEPer builds three new components onto iMinDEE [28]. First, we introduce a new representation of backbone flexibility, which we call perturbations (Section 2.1). We introduce seven diverse types of perturbations, some continuous and some discrete (Section 2.2). The second component is the concept of a residue conformation, or RC (Section 2.3). We can represent protein conformations by assigning a residue conformation to each residue. This is analogous to the way that rigid-backbone methods like iMinDEE represent protein conformations by assigning a sidechain conformation to each residue. Taken together, the concepts of perturbations and RCs provide a general method for introducing degrees of freedom affecting multiple residues into the framework of dead-end elimination. The third component, indirect pruning (Section 2.4), is an enhancement of the dead-end elimination algorithm designed to be especially helpful in the presence of perturbations. These topics will be discussed in the following subsections. The general flow of the DEEPer algorithm is illustrated in Fig. 1.

Figure 1.

DEEPer begins with the selection of a set of perturbations to use (this step may be manual or automated). These perturbations define a set of RCs for each residue. RCs that cannot be in low-energy conformations are pruned, using the new indirect pruning algorithm (Section 2.4) as well as previous pruning algorithms. A* with minimization (see Introduction), as in iMinDEE [28], is then used to output low-energy conformations. The result is the GMEC and a gap-free list of all conformations and sequences within a user-specified interval E_w of the GMEC. This list can be used to select mutant sequences to synthesize for experimental testing, either by (i) selection of the sequences with the lowest-energy conformations, or (ii) by a provably-good approximation algorithm to calculate the binding affinities via the K^* software module [5, 16].

2.1 Perturbations

DEEPer searches the space of sidechain dihedrals within a specified interval around the modal dihedral value for each rotamer. This interval is ±9° by default, except for proline, whose dihedrals cannot rotate freely. All other flexibility is represented in the form of perturbations, which can be any conformational adjustments that commute with rotations of the non-proline sidechain dihedrals (Fig. 2). The effect of each perturbation is quantified using a single, scalar perturbation parameter. Some perturbations can feasibly be represented using a continuous range of perturbation parameter values, while other perturbations admit only discrete values of the perturbation parameter (see Section 2.2). These will be referred to as continuous and discrete perturbations, respectively. Each perturbation has a defined set of residues that it can affect. Perturbations should be chosen to keep these sets of residues small whenever possible, since the tractability of DEEPer relies on relatively few perturbations affecting each residue.

Figure 2.

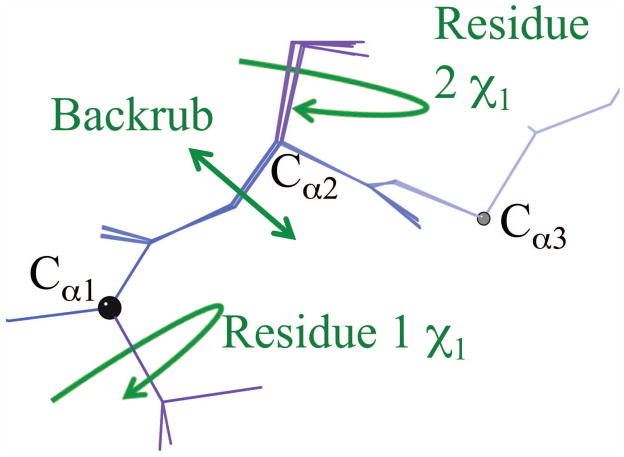
In DEEPer, the conformation of a protein is defined by multiple degrees of freedom. Sidechain dihedrals, such as the χ₁ dihedrals for the residues shown, affect the conformation of only one residue. Perturbations, such as the backrub shown, can affect the conformation of several residues (three in this case; black balls denote the boundaries of the backbone region affected by the backrub).

2.2 Types of perturbations

We implemented DEEPer with seven types of perturbations (Table II, Fig. 3). We will now describe the implementation of each of these perturbations.

Figure 3.

Types of perturbations implemented in DEEPer. Each perturbation is from red backbone and orange sidechains to blue backbone and purple sidechains. Black balls denote the boundaries of the backbone region affected by the perturbation. (a) Backrub. (b) Shear. (c) Loop closure adjustment. (d) Secondary structure adjustment. (e) Partial structure switch. (f) Full structure switch. Two crystal structures of the motor protein Ncd related by a major conformational change are shown (PDB codes 2NCD [67] and 1N6M [43]). (g) Proline flip.

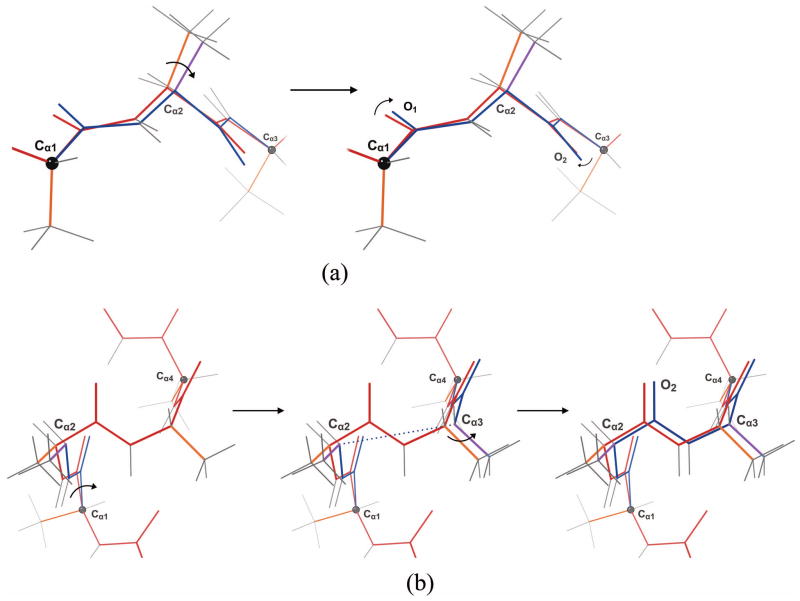
First of all, backrubs (Fig. 3a, Fig. 4a) are applied as in brDEE [27]. Briefly, if the backrub affects residues i through i + 2, the section of protein chain between residue i’s C_α and residue i+2’s C_α is rotated about the axis defined by those two C_αs, and the rotation angle, i.e. the “primary backrub angle,” is the perturbation parameter. Then, in order to reduce bond-angle distortion and maintain any pre-existing hydrogen bonds, a smaller counter-rotation is applied about the peptide plane’s C_α-C_α axis for both of the peptide planes in this section of protein chain. The angle of each counter-rotation is 70% of the angle that minimizes the displacement of the carbonyl oxygen caused by the backrub. In addition to moving the backbone, backrubs reorient the sidechain of residue i + 1 in a direction perpendicular to the local chain direction. Backrubs tend to be found in extended conformations: β sheets or loops in which the mainchain is relatively extended [48].

Figure 4.

Geometry of multi-step perturbations. As in Fig. 3, each perturbation is from red backbone and orange sidechains to blue backbone and purple sidechains. (a) The two steps of a backrub perturbation, starting from an ideal poly-Ala β sheet. First, the dipeptide is rotated by the specified amount (here, +10°) around the C_α1-C_α3 axis (left). Then, each individual peptide is rotated by some fraction (70% by default, here corresponding to −7.0° and −5.6°) of the amount needed to restore the two carbonyl oxygens to their original positions (right). These same rotations, albeit with very different angles, are used for loop closure adjustments and secondary adjustments. (b) The three steps of a shear perturbation, starting from an ideal poly-Ala α helix. First, the N-terminal peptide is rotated by the specified amount (here, +5°) around C_α1 in the C_α1-C_α2-C_α3 plane (left). Then, the C-terminal peptide is rotated around C_α2 in the C_α2-C_α3-C_α4 plane such that the original C_α2-C_α3 distance (dotted line) is maintained (middle). Finally, the original middle peptide is rotated and translated to fit into the gap and to match the original carbonyl orientation (right).

On the other hand, shears (Fig. 3b, Fig. 5, Fig. 4b) move the central peptide of a three-peptide segment parallel to the chain direction; they occur primarily in α helices, particularly at the termini (Jane and David Richardson, personal communication). Shears have previously been proposed by Smith and Kortemme [34]. The shear motion, if affecting residues i through i + 3, rotates the mainchain atoms from residue i’s C_α to residue i + 1’s C_α as well as residue i + 1’s sidechain about residue i’s C_α in the plane defined by residue i’s C_α, residue i + 1’s C_α, and residue i + 2’s C_α. The angle of this rotation, i.e. the “primary shear angle,” is the perturbation parameter. Then residue i + 2’s sidechain and the mainchain segment from residue i + 2’s C_α to residue i + 3’s C_α are rotated as a rigid body about residue i + 3’s C_α in the plane defined by residue i + 1’s C_α, residue i + 2’s C_α, and residue i + 3’s C_α. The angle of rotation is calculated to keep the distance between residue i + 1’s C_α and residue i + 2’s C_α at its unperturbed value. Finally, the mainchain atoms between residue i + 1’s C_α and residue i + 2’s C_α are rotated about the axis defined by those C_αs to make residue i + 1’s carbonyl C–O bond vector as close as possible to its unperturbed direction. As in the case of backrubs, this counter-rotation is intended to maintain hydrogen bonds and reduce bond-angle strain.

Figure 5.

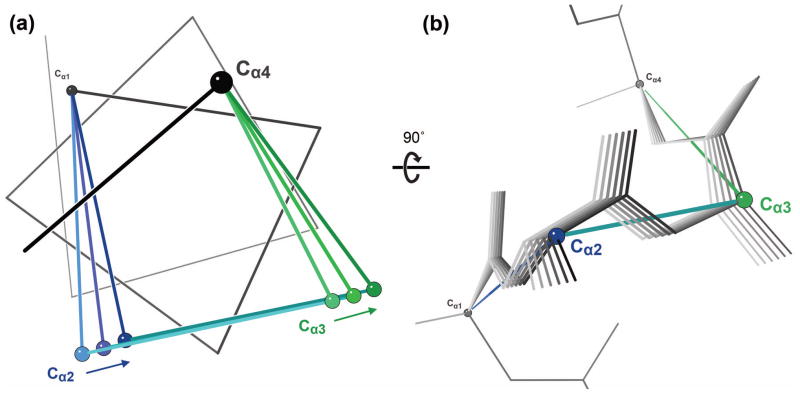
The shear backbone motion. (a) Simple C_α-only representation of shear, viewed down the axis of an ideal α helix (light colors). Shears of 5° (darker) and 10° (darkest) swing the central C_α2-C_α3 peptide (cyan) sideways by coordinated rotations of the C_α1-C_α2 peptide (blue) and C_α3-C_α4 peptide (green). (b) All-atom representation of shear, viewed from the side of the ideal α helix (i.e. rotated 90° from (a)). Shears of 2° over a 10° range are shown. The central carbonyl is notably displaced parallel to the central peptide. One endpoint conformation is marked by balls and line segments colored as in (a).

Thus, although they are local, affecting 3–4 residues each, backrubs and shears together allow a given C_α atom to move in any direction by a small amount. The component rotations of shears and backrubs are illustrated in Fig. 4.

Loop closure adjustments (Fig. 3c) are also perturbations affecting three residues, but unlike backrubs, they do so without changing any bond angles or lengths. The space of such motions is described in [51], and the algorithm from that work is used to implement them. It solves a system of polynomial equations, and each solution is associated with a possible conformation of the tripeptide. Given a residue i, these equations find the different possible segments of protein chain from residue i’s C_α to residue i + 2’s C_α that maintain specified bond angles, lengths, and ω dihedrals without changing the conformation of any other part of the protein at all. For DEEPer, these specified values are taken from the pre-perturbation conformation. The perturbation parameter is a discrete index specifying which solution of the polynomial equations is used to create the perturbed conformation. Loop closure adjustments can be generated using the same component rotations as backrubs (Fig. 4a), though the angles of these rotations and the method by which the angles are determined are completely different (backrubs are biophysically feasible because the distortions in bond angles are small, while loop closure adjustments are biophysically feasible because the rotation angles are computed to avoid any bond angle changes).

Secondary structure adjustments (Fig. 3d) are perturbations that change secondary structure. If one of the residues moved by a loop closure adjustment motion is at the beginning or end of a helix or sheet while the other two are in a loop, then the secondary structure of the helix or sheet residue can effectively be changed to loop structure. Alternatively, a similar motion can be used to convert the first residue in a loop to the secondary structure of the residues preceding it, or to convert the last residue in a loop to the secondary structure of the residues following it. The backbone dihedrals of the residue to be changed are adjusted to be appropriate for the helix or sheet by copying the dihedrals of the adjacent helix or sheet residue. Then, the tripeptide on the other side of the residue from the helix or sheet is placed into the structure using the loop closure equations from [51]. The perturbation parameter is a discrete index identifying a solution to the equations, as for a loop closure adjustment.

Partial structure switches (Fig. 3e) take a section of backbone from another structure and replace the corresponding section of the structure being modeled with it. If needed, the new section of backbone is rotated and translated to fit into the gap. The new and old sections must be very similar in end-to-end length, because otherwise it is impossible to insert the new section without changing its backbone conformation significantly. However, the implementation offers two methods to slightly adjust end-to-end length: scaling coordinates uniformly or using the tripeptide closure method from [51]. Adjusting the length by more than 0.2 Å is set to raise an error in the implementation of DEEPer. Partial structure switches can be used to incorporate different ligand conformations, positions, and orientations as well. This perturbation allows the incorporation of experimentally-observed alternate backbone conformations–e.g. crystallographic alternates, NMR ensembles, or homologous structures–or computational predictions like docking poses or computationally-derived ensembles of loop conformations (e.g. from the POOL algorithm [52]). For a full structure switch (Fig. 3f), the entire system is modeled with a different crystal structure (or other structure) for the perturbed RCs, so this affects all residues of the system.

Proline flips (Fig. 3g) are perturbations that flip the ring pucker of proline from endo to exo or vice versa, thus flipping the signs of all the sidechain dihedrals. Switching the proline peptide conformation from cis to trans, on the other hand, could be accomplished by a partial structure switch.

We also implemented an automatic perturbation selection module, which generates perturbations and residue conformations appropriate to the user’s specified flexible residues. Partial and full structure switches can be included if the user provides alternate-structure information. The module includes a Ramachandran filter and, if chosen by the user, a filter to keep the RMSD (root-mean-square displacement) between the discrete backbone conformations that are considered above a specified value (to ensure conformational diversity). The interested reader will find additional perturbation implementation and selection details in the Supplementary Information (section B.1).

2.3 Residue conformations (RCs)

To use the perturbations described above, we require a new way to represent possible conformational states. To meet this need, DEEPer introduces residue conformations (RCs), which are analogous to rotamers in traditional DEE, but also incorporate the perturbations as additional degrees of freedom. In this section, we first introduce the philosophy and nomenclature behind RCs. We then lay out DEEPer’s strategy for representing RCs in the presence of perturbations affecting multiple residues, performing energy minimization with the correct order of operations even with non-commutative perturbations, and adding special wild-type rotamers to some RCs.

Like rotamers in traditional DEE or iMinDEE [28], RCs are prunable, enumerable states of a residue. Specifically, consider a residue i with s sidechain dihedrals that is affected by c continuous perturbations and d discrete perturbations. Then each RC of i may be represented as a (2s + 2c + d + 1)-tuple whose elements are (1) a maximum and minimum value for each sidechain dihedral angle (following minDEE, we have implemented this as the modal dihedral for the rotamer ±9°), (2) a maximum and minimum parameter value for each continuous perturbation, (3) a single parameter value for each discrete perturbation, and (4) an amino acid type. For a residue with a particular amino acid type whose conformation is described by a set of sidechain dihedral angles and perturbation parameter values, we say that the residue is in a given RC when its amino acid type and discrete perturbation parameters match those of the RC and its sidechain dihedrals and continuous perturbation parameters each fall between the minimum and maximum values for the RC. Let us use the notation i_r for an RC affecting residue i, by analogy to the notation for rotamers [38].

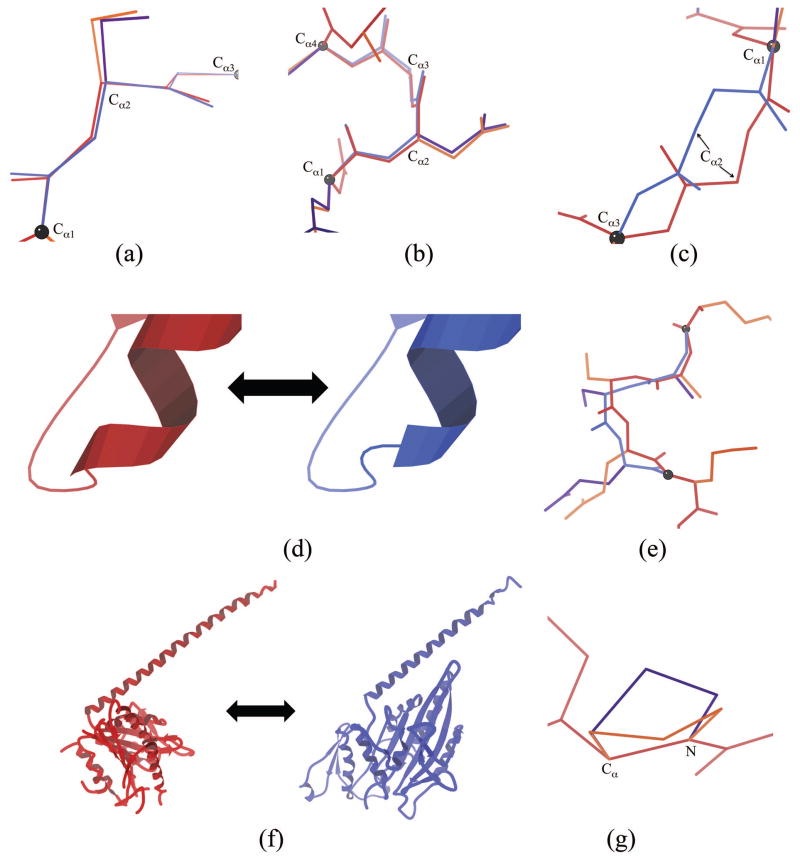
Like a rotamer in minDEE [16, 28], an RC represents a set of closely-related conformations. The sets of conformations are meant to be small enough that the GMEC can be found by local minimization once an RC has been assigned to each residue (Fig. 6). In general, RCs are handled analogously to rotamers in minDEE but can account for backbone as well as sidechain flexibility.

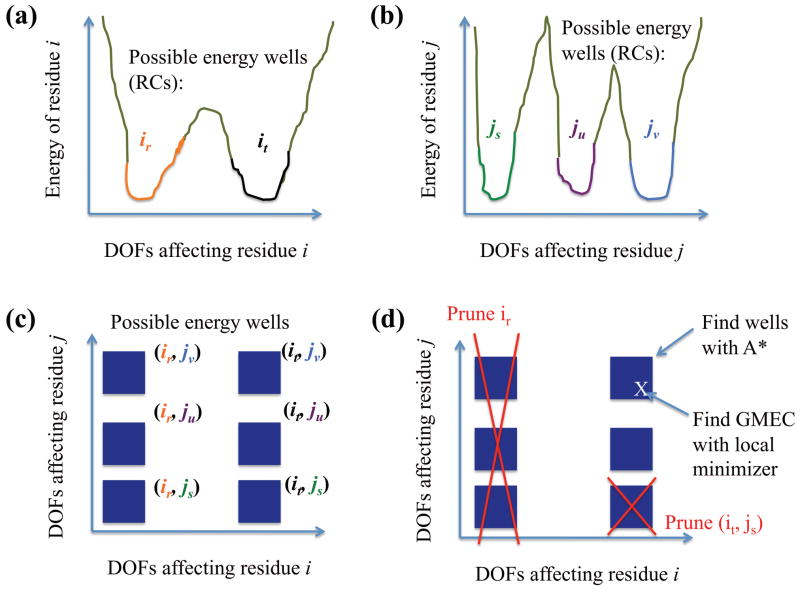
Figure 6.

iMinDEE can be viewed as a global minimization algorithm over many degrees of freedom (DOFs) that searches a set of energy wells. (a, b) RCs represent likely locations for energy wells of particular residues. The notation i_r is used to represent the r^th RC of residue i. (c) This leads to an n-dimensional lattice for the possible energy well locations for n residues. (d) We prune RCs and tuples of RCs using iMinDEE. Then A* is used to identify the energy wells with the lowest lower bounds, and local minimization is used to search these wells for the GMEC.

An important property of perturbations is that if a perturbation is applied to a protein, the perturbation must have the same parameter value for all affected residues. Thus, if a perturbation p affects residue i and j, and two RCs i_r and j_s have different parameter value intervals for p, then the pairwise energy of i_r and j_s can be set to ∞, and the pair should always be pruned. Such a pair is called parametrically incompatible (Fig. 7). For example, if a shear perturbation (Section 2.2) in a protein moves both residues 60 and 61, there can be no conformation in which residue 60 is in an RC with shear parameter 3–5° but residue 61 is in an unsheared RC. RCs at different residues with different but overlapping parameter value intervals for the same perturbation are not allowed, but this restriction does not limit the conformational space available to DEEPer; it only limits the choice of RCs used to represent this conformational space.

Figure 7.

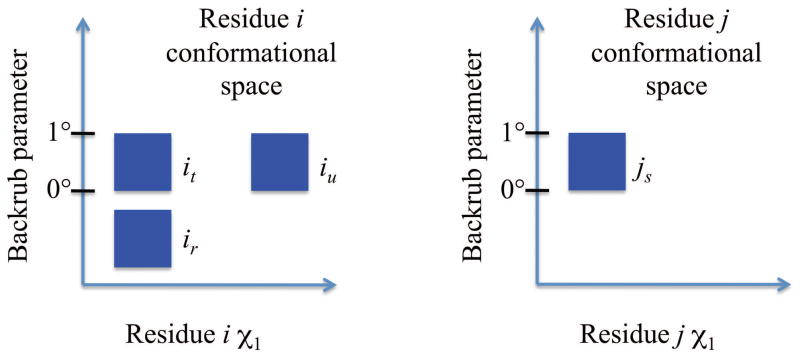
Parametric incompatibility of RCs. Suppose residue i and j are affected by the same backrub. RCs i_t and j_s are parametrically compatible because there exists an overall conformation of the protein in which residue i is in i_t and residue j is in j_s. Similarly, i_u and j_s are parametrically compatible. But i_r and j_s are parametrically incompatible because there is no overall conformation of the protein in which residue i is in i_r and residue j is in j_s.

Pairs of RCs that are not parametrically incompatible will be referred to as parametrically compatible.

Having defined the set of RCs for each residue position and pruned parametrically incompatible pairs, we are ready to search for the GMEC or low-energy ensemble, starting with the same minimization-aware pruning methods as iMinDEE [28], which can be applied without modification if parametrically incompatible pairs are assigned an infinite pairwise energy. This is possible because the derivation of iMinDEE [28] does not assume anything about the geometry of the flexibility. It only assumes that lower bounds for single-rotamer and pairwise interaction energies are available and that there is a method to minimize conformations once rotamers have been assigned. Thus, the iMinDEE algorithm can be applied to RCs with continuous sidechain and backbone flexibility just as it can be applied to rotamers with only sidechain flexibility (see Fig. 6). Pruning is followed by A* search and enumeration of conformations; as in minDEE [16] and iMinDEE [28], the A* search outputs unminimized conformations in order of lower-bound minimized energy, and local minimization is used to identify the GMEC or the desired ensemble. These steps are also part of the iMinDEE protocol [28].

The conformation of the protein is always uniquely defined by the sequence and the values of all perturbation parameters and sidechain dihedrals. This conformation is constructed from the original, wild-type conformation by performing any necessary mutations, rotating sidechains to obtain the correct dihedrals, and then applying all perturbations with the specified parameters. When there are overlapping perturbations, the precise geometry of the RC will typically depend on the order in which the perturbations are applied, so DEEPer must assign an ordering to all the perturbations before beginning calculations. This ordering can be specified by the user, but a default ordering is provided by the automatic perturbation selector (Section 2.2). If the initial conformational state to which a perturbation b is applied depends on the state of a previously applied perturbation a, then any residue affected by b is also considered to be affected by a for purposes of defining RCs and minimization, since a affects the final perturbed conformations of that residue. It is useful to choose an ordering that reduces the number of residues affected by each perturbation and thus the number of RCs. Measures to accomplish this include performing small perturbations after larger ones and applying perturbations in a minimal number of “layers,” where a layer is a set of non-overlapping perturbations applied consecutively.

Like iMinDEE, DEEPer requires minimization of pairwise energies to compute lower-bound energies as well as minimization of the total energy of the protein to obtain final minimized conformations. DEEPer minimizes pairwise energies with respect to all continuous perturbation parameters affecting either of the residues in the pair, in addition to the residues’ sidechain dihedrals. The total energy is minimized with respect to all continuous perturbation parameters and sidechain dihedrals. To change the parameter value for a perturbation p, p can be undone and then reapplied with the correct parameter. To ensure that perturbations are all applied in the correct order, perturbations that were applied after p may have to be undone before p is undone and then reapplied after p is reapplied. As a result, it is best to apply continuous perturbations after discrete ones, so that discrete perturbations do not need to be re-applied during minimization.

At the discretion of the user, the space of RCs in DEEPer can be augmented by introducing wild-type “rotamers” for each residue. These are rotamers generated by taking the sidechain conformation from the starting structure (including the original bond lengths and angles) and then allowing ±9° minimization of sidechain dihedrals. Wild-type rotamers are added to the calculation along with the generic rotamers from the rotamer library (which, in the Penultimate rotamer library [13] we use, correspond to clusters of dihedral angles from high-resolution structures in the PDB).

2.4 Indirect pruning

By construction, DEEPer allows searching a larger conformational space than any previous provable protein design algorithm can search. This additional flexibility can lead to additional computational complexity. In this section, we show that a new algorithm, indirect pruning, can be used to alleviate this complexity. To explain this new algorithm, we first introduce the concept of the pruning zone, and then provide additional machinery that will be needed to describe the algorithm formally. Next, we provide theorems establishing the correctness of indirect pruning and an analysis of its computational complexity. Finally, we provide a simple “toy” example of indirect pruning to illustrate the functioning of the algorithm.

In principle, DEEPer could be implemented using only previous minimization-aware DEE pruning algorithms, such as iMinDEE [28] and minBounds [53]. For these algorithms, RCs are used instead of rotamers, and pairwise energies of parametrically incompatible RC pairs are set to ∞. There is some additional cost due simply to the larger number of RCs than rotamers. However, there is also a source of inefficiency in the DEE pruning step by previous algorithms that arises specifically due to the DEEPer perturbation model (Fig. 8a, b). Let i_r and i_t be any two RCs that include a different parameter value interval for some perturbation p, where p affects both residue i and some other residue k. In such a case, i_r is parametrically incompatible with some RC of k that is parametrically compatible with i_t. But i_t is parametrically incompatible with some other RC of k that is parametrically compatible with i_r. Consequently, the left-hand side of the iMinDEE pruning condition Eq. (1) will necessarily be −∞, since the term in the sum for j = k will be −∞ regardless of whether we are trying to prune i_r using i_t or the other way around. This lack of pruning would require every combination of parameter values for different perturbations to be enumerated in the A* step. The number of such combinations can grow exponentially with the number of perturbations, quickly leading to intractable calculations.

Figure 8.

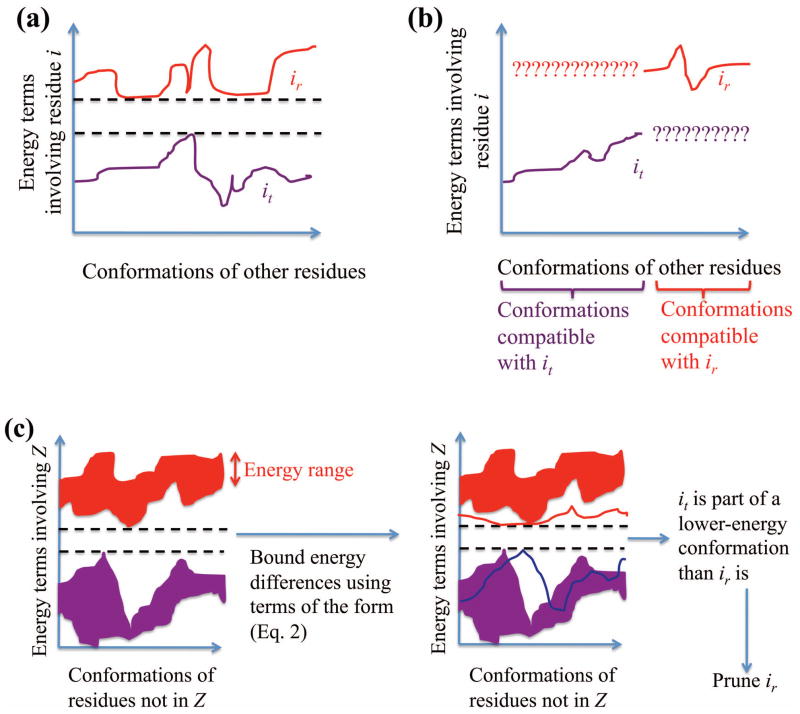
Parametric incompatibility impedes DEE pruning but not indirect pruning. (a) Normally, DEE is able to compare conformations containing a candidate RC i_r to those containing a competitor RC i_t and prune i_r if the conformations containing i_r are always higher in energy. We can determine this by comparing all energy terms involving residue i: its internal energy plus its interaction energies with all other residues. Solid lines denote this summed energy for i_r (red) and for i_t (purple). (b) If i_r and i_t have different parameter intervals for a perturbation, then the conformations of other residues affected by the perturbation cannot be directly compared by the DEE criterion. Thus, pruning using this criterion is impossible, regardless of the energetics of these RCs. (c) This problem is alleviated if we compare all energy terms involving a multi-residue pruning zone rather than just the single residue position i. Indirect pruning works by comparing the sets of all conformations of the pruning zone containing i_r (red) to all conformations of the pruning zone containing i_t (purple). But even for a given set of conformations for all residues outside the pruning zone, each of these sets of conformations will have a range of energies (shown as colored regions). We use bounds (red and blue lines) to avoid the expensive process of considering each conformation of the pruning zone. We seek a lower bound on the energy difference between the best conformation involving i_t (the blue line is an upper bound on this conformation’s energy) and the best conformation involving i_r (the red line is a lower bound on this conformation’s energy, so the difference between the red and blue lines represents a lower bound on the energy difference). Dashed lines indicate the energy gap between conformational states involving i_r and those involving i_t.

To avoid this problem, we derive a new pruning algorithm, indirect pruning, that can prune in such cases. This method is designed to take advantage of already-pruned pairs of RCs. These can be parametrically incompatible pairs, pairs with steric clashes, pairs that have been pruned by other pruning algorithms, and pairs pruned by previous iterations of indirect pruning. Indirect pruning is intended for use in addition to previous techniques, rather than as a replacement for them, in order to obtain optimal pruning.

Pruning zones

We will now introduce the concept of a pruning zone, a key novel feature of our method.

We designate a set of residues as the pruning zone, denoted as Z. In principle, Z may be chosen to be any set of residues in the system (good choices of Z are discussed below). We then attempt to prune RCs for each residue in Z. In DEE pruning, a “candidate” rotamer is said to be pruned using a “competitor” rotamer, with “witness” rotamers at other residues considered in the calculation. Suppose we wish to prune the candidate RC i_r using the competitor RC i_t. Because some RCs elsewhere in the pruning zone may be parametrically incompatible with i_t but not i_r (or vice versa), we may not be able to find witness RCs at those residues. As a result, it is not feasible to prune i_r by considering only the energy terms involving residue i, as DEE does.

Instead, we try to prune all conformations of Z that contain i_r (Fig. 8). Since we represent each conformation of Z as a tuple of RCs, the pruning condition for tuples of RCs (Eq. (4) below) could be used here; this pruning condition considers the energy terms involving all residues in Z. However, pruning each tuple individually would be very time consuming, because the number of conformations of Z grows exponentially with respect to z = |Z|.

To avoid this problem, we use bounds to “indirectly” prune all the tuples containing i_r at once. First, we bound the energy differences that we need to prune conformations of Z containing i_r. Then, we try to identify a conformation of Z that includes i_t and can prune all conformations of Z that include i_r. We still consider the energy terms involving all residues in Z, and we break up the pruning condition into terms of the form Eq. (2) to allow efficient computation of the bounds. This leads to the maximization of a minimum in Algorithm 1 below: we perform a minimization in step 2 to bound the energy associated with Z when residue i is in the RC i_r, and this creates the overall conformation u of Z that will be “hardest” to prune. Then we find the overall conformation v, consisting of i_t and its companions, that will at least approximately maximize the energy difference q (see Algorithm 1) and thus make pruning most feasible. We use a greedy maximization strategy that is not provably optimal to avoid an exponential running time; however, pruning is still provable. Like conformational-splitting DEE [42], this algorithm effectively partitions the search space of “witness” RCs at residues other than that of the RC we are trying to prune. However, by implicitly constructing conformations of the entire pruning zone, it can more comprehensively exclude infeasible conformations from the pruning and thus prune more powerfully than conformational splitting, which only splits conformations based on the RC choice at one or two residue positions.

Unlike previous algorithms, indirect pruning can remove pruned competitor-witness as well as candidate-witness pairs from analysis. Indirect pruning has been implemented first using all flexible residues as the pruning zone, followed by additional pruning zones as described in the Supplementary Information (section B.2).

Notation

Some of the notation presented here is shared with previous work on DEE-based algorithms, such as [16], but some new notation is also required for the explanation of indirect pruning. We define E_⊝(i_r) to be the minimum intra-residue energy that the residue can have while in the RC i_r, and given some other RC j_s (j ≠ i), we define E_⊝(i_r, j_s) as the minimum pairwise interaction energy that residues i and j can have while i is in i_r and j is in j_s. These quantities will be used to calculate lower bounds for conformational energies. Following normal usage, we call an RC or a tuple of RCs at different residues pruned if it has been determined that its residue(s) cannot all be in the specified RC(s) in the GMEC or in any conformation of the desired ensemble. Next, we provide a notation for tuples of RCs. Suppose we have an m-tuple r of RCs, where each RC i_r ∈ r applies to a different residue i; we then define M_r to be the set of residues to which the RCs in r apply. For i ∈ M_r, let i_r denote the RC in r corresponding to i. In other words, we will use the notation i_r to refer to elements in a tuple, indexed by residue. Also, let N denote the set of residues that are not in the pruning zone.

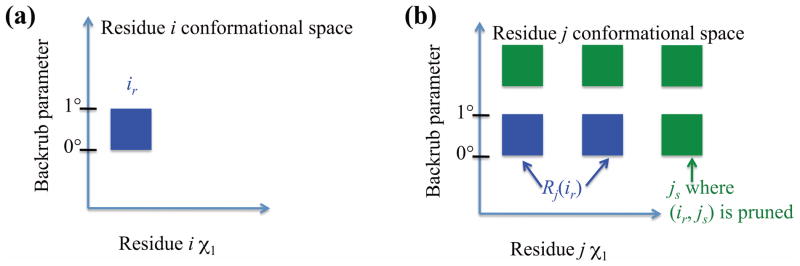
Now, we provide a notation for the RCs that we are searching over. Let R_j be the set of unpruned RCs at residue j. For each pair (i, j) of residues, we can construct a set R_j(i_r) ⊆ R_j containing all RCs of j that may be found in a conformation that also contains i_r (Fig. 9). To do this, for each i ≠ j, we stipulate that an RC j_s ∈ R_j is in R_j(i_r) if and only if j_s has not been pruned and the pair (i_r, j_s) has not been pruned. In other words, R_j(i_r) consists of all the RCs at position j that are compatible with i_r. If the indirect pruning algorithm is to be applied to a given pruning zone multiples times, R_j(i_r) needs to be recomputed each time. This is analogous to the way newly pruned rotamers are excluded from analysis at each iteration in other forms of dead-end elimination. Since i_r is compatible with itself, we also define R_i(i_r) = {i_r}.

Figure 9.

The R_j(i_r) notation. Suppose residues i and j are affected by the same backrub. Then R_j(i_r) (blue voxels on the right) can consist only of RCs with the same parameter range for this backrub as i_r. RCs can also be excluded because of pruned pairs: even though j_s has the same parameter range as i_r, j_s ∉ R_j(i_r), because the pair (i_r, j_s) has been pruned (either by a steric check, a previous round of indirect pairs pruning, or another pruning algorithm). RCs of j that are not in R_j(i_r) (those that cannot be found simultaneously with i_r in a conformation of the protein) are shown in green.

Similarly, let us define R_j(r) to specify the set of RCs of residue j that are compatible with all RCs in r. Unpruned RCs at position j can be excluded from R_j(r) based either on pruned pairs or larger tuples. To make this rigorous, for j ∉ M_r, j_s ∈ R_j is in R_j(r) if and only if no tuple of RCs g specifying the conformation of W ∪ {j} has been pruned, where W ⊆ M_r, j_g = j_s, and h_g = h_r for each residue h ∈ W. If no tuples larger than pairs have been pruned, then this condition can be be simplified: j_s ∈ R_j is in R_j(r) if and only if no pair (i_r, j_s) has been pruned, for i ∈ M_r.

RCs that are part of r are compatible with r, so for j ∈ M_r, R_j(r) = {j_r}.

Formal description of algorithm

Indirect pruning of individual RCs proceeds as follows.

Algorithm 1. Pruning individual RCs

1. For each residue i in Z, and for each ordered pair of RCs (i_r, i_t) at i with i_r ≠ i_t, calculate K(i_r, i_t), where

   $$\begin{array}{c}K(h_a,h_b)=E_{⊝}(h_a)-E_{⊝}(h_b)+\sum _{h^{\prime }\in Z,h^{\prime }<h}\left(\underset{h_{a^{\prime }}^{\prime }\in R_{h^{\prime }}(h_a)}{min}{E}_{⊝}\left(h_a,h_{a^{\prime }}^{\prime }\right)-\underset{h_{b^{\prime }}^{\prime }\in R_{h^{\prime }}(h_b)}{max}{E}_{⊝}\left(h_b,h_{b^{\prime }}^{\prime }\right)\right)\\ +\sum _{j\in N}\underset{j_s\in R_j}{min}(E_{⊝}(h_a,j_s)-E_{⊝}(h_b,j_s)).\end{array}$$ (2)

2. For each pair (i_r, i_t):

   1. Create a variable q and set q = 0.

   2. For each h ∈ Z, iterating in increasing order of h, find the RC h_v that maximizes $\underset{h_a\in R_h(i_r)}{min}K(h_a,h_{\mathbf{v}})$ subject to the conditions h_v ∈ R_h(i_t) and h_v ∈ R_h(j_v) for each j ∈ Z with j < h; add this maximum value to q.

   3. Prune i_r if and only if q > E_w + I, where E_w is the desired energy window and I is the pruning interval (see Introduction).

This pruning condition, unlike the iMinDEE pruning condition Eq. (1), is broken down into the RC pair terms K(h_a, h_b) (see Eq. (2)) first rather than into pairwise and single-residue terms, to facilitate the algorithm. Eq. (2) in turn is broken down into single-residue terms, pairwise terms within the pruning zone, and finally pairwise terms between residues inside and outside the pruning zone.

The indirect pruning strategy can also be applied to pairwise or higher-order pruning (pruning of pairs or larger tuples of RCs). Let r be a tuple of RCs. We will try to prune tuples of residues in the pruning zone, i.e., try to prune some tuples r such that M_r ⊆ Z. To prune tuples, we must first precompute K(i_r, i_t) for each ordered pair of RCs (i_r, i_t) with i_r ≠ i_t at each i in Z. This is the same precomputation as is required for pruning single RCs (Algorithm 1). Our implementation prunes single RCs before pairs and reuses the precomputed K(i_r, i_t) values for the pairs pruning. Then, to attempt pruning of the tuple r using the competitor tuple t, where M_r = M_t (so corresponding elements of r and t are at the same residue), we apply the following algorithm:

Algorithm 2. Pruning a tuple of RCs

1. Set q = 0.

2. For each h ∈ Z − M_r, iterating in increasing order of h, find the RC h_v that maximizes $\underset{h_a\in R_h(\mathbf{r})}{min}K(h_a,h_{\mathbf{v}})$ subject to the conditions h_v ∈ R_h(r) and h_v ∈ R_h(j_v) for each j ∈ Z with j < h; add this maximum value to q.

3. Prune r if and only if q + K(r, t) > E_w + I where

   $$\begin{array}{c}K(\mathbf{r},\mathbf{t})=\sum _{i\in M_{\mathbf{r}}}\left(E_{⊝}(i_{\mathbf{r}})-E_{⊝}(i_{\mathbf{t}})+\sum _{h^{\prime }\in M_{\mathbf{r}},h^{\prime }<i}(E_{⊝}(i_{\mathbf{r}},h_{\mathbf{r}}^{\prime })-E_{⊝}(i_{\mathbf{t}},h_{\mathbf{t}}^{\prime }))\right)\\ +\sum _{h^{\prime }\in Z-M_{\mathbf{r}}}\left(\underset{h_{a^{\prime }}^{\prime }\in R_{h^{\prime }}(\mathbf{r})}{min}\sum _{i\in M_{\mathbf{r}}}({\chi }_{h^{\prime }<i}{E}_{⊝}(i_{\mathbf{r}},h_{a^{\prime }}^{\prime }))-\underset{h_{b^{\prime }}^{\prime }\in R_{h^{\prime }}(\mathbf{t})}{max}\sum _{i\in M_{\mathbf{r}}}({\chi }_{h^{\prime }<i}{E}_{⊝}(i_{\mathbf{t}},h_{b^{\prime }}^{\prime }))\right)\\ +\sum _{j\in N}\underset{j_s\in R_j}{min}\sum _{i\in M_{\mathbf{r}}}(E_{⊝}(i_{\mathbf{r}},j_s)-E_{⊝}(i_{\mathbf{t}},j_s)).\end{array}$$ (3)

The interested reader will find a proof of the following lemma and theorem, showing the correctness of Algorithm 1, in section A.1 of the Supplementary Information:

Lemma 1

Let u be a z-tuple of RCs with Z = M_u. If there exists a z-tuple v of RCs specifying a conformation of Z such that

$$\begin{array}{c}\sum _{h\in Z}\left(E_{⊝}(h_{\mathbf{u}})-E_{⊝}(h_{\mathbf{v}})+\sum _{h^{\prime }\in Z,h^{\prime }<h}\left(E_{⊝}\left(h_{\mathbf{u}},h_{\mathbf{u}}^{\prime }\right)-E_{⊝}\left(h_{\mathbf{v}},h_{\mathbf{v}}^{\prime }\right)\right)\right)\\ +\sum _{j\in N}\underset{j_s\in R_j}{min}\sum _{h\in Z}(E_{⊝}(h_{\mathbf{u}},j_s)-E_{⊝}(h_{\mathbf{v}},j_s))>E_w+I,\end{array}$$ (4)

then u can be pruned, meaning that Z is not found in the conformation u in any overall protein conformation whose energy is within E_w of the GMEC.

Theorem 1

If Algorithm 1 prunes an RC i_r, then no protein conformation whose energy is within E_w of the GMEC will contain i_r.

The correctness of Algorithm 2 is shown by the following theorem, proved in section A.2 of the Supplementary Information:

Theorem 2

If Algorithm 2 prunes a tuple of RCs r, then no protein conformation whose energy is within E_w of the GMEC will contain r.

Complexity

Indirect pruning, like regular DEE, runs in polynomial time. We can characterize the complexity in terms of n, the number of residues in the system; z, the size of the pruning zone, with z ≤ n; and r, the maximum number of RCs at any residue in the pruning zone:

Lemma 2

Indirect pruning of single RCs for a pruning zone Z runs in O(z²r⁴ + znr³ + z³r³) time.

Lemma 3

Indirect pruning of m-tuples of RCs for a pruning zone Z runs in O(z^mr^2m+1(n+z² + zr)) time.

These results are derived in the Supplementary Information (section A.3). Note that pruning all m-tuples takes exponential time with respect to m using any form of DEE simply because the number of possible m-tuples to prune grows exponentially with respect to m. The time cost to prune a single m-tuple is polynomial with indirect pruning or any previous DEE-based algorithm. Unlike the original DEE algorithm, indirect pruning has nontrivial space complexity, because it must calculate the RC-pair terms K(i_r, i_t) for each residue pair (i_r, i_t). However, because there are O(zr²) such pairs, the memory cost is just O(zr²), which is negligible compared to A* or even to the cost of storing a boolean for each tuple indicating whether it is pruned, which is O(n^mr^m).

Because it can prune RCs using RCs in different backbone states, indirect pruning could also be useful in multistate protein design, which designs sequences that prefer one backbone state over another [54].

Toy example of indirect pruning

The indirect pruning condition can be illustrated using the toy example whose energies are listed in Table III. We are using the pruning zone Z = {i, j} and trying to prune i_r using i_t. We will not consider any continuous flexibility, so we can just consider well-defined energies E instead of energy lower-bounds E_⊝ and let I = 0. Suppose residues i and j are affected by a discrete perturbation, which may have parameter value either 0 or 1. The RCs i_r and j_s have parameter value 0 for this perturbation, while i_t and j_s′ have parameter value 1; thus R_j(i_r) = {j_s}, R_j(i_t) = {j_s′}, R_i(j_s) = {i_r}, and R_i(j_s′) = {i_t}. All these RCs have alanine as their amino acid type. Since alanine has no sidechain dihedrals, none of the RCs include bounds for sidechain dihedrals. Furthermore, suppose residue k is not affected by the perturbation but has two rotamers, treated as rigid here: the m rotamer of valine and the t0 rotamer of aspartate (the other rotamers of valine and aspartate having been pruned already). The RCs k_u and k_u′ correspond to the two rotamers of k. They have the amino acid types and dihedral angles of their corresponding rotamers and no perturbation parameters.

Table III.

Pairwise energies for RCs in the toy example. Pruning of RC i_r using i_t will be attempted, with pruning zone Z = {i, j}.

			Pairwise energies
Residue conformation	Perturbation parameter value	Intra-energy	js	js′ ku′	ku
ir	0	2	−2	∞ 5	0
it	1	0	∞	−3 5	−5
js	0	−2	20		3
js′	1	0	2		3
ku	n/a	1
ku′	n/a	1

We first need to calculate K(i_r, i_t) = E(i_r) − E(i_t) + E(i_r, k_u′) − E(i_t, k_u′) = 2, and also we need K(j_s, j_s′) = E(j_s) − E(j_s′) + E(i_r, j_s) − E(i_t, j_s′) + E(j_s, k_u′) − E(j_s′, k_u′) = −1. When we apply our pruning condition, K(i_r, i_t) + K(j_s, j_s′) > E_w, we are pruning all conformations of Z that include i_r (in this case, there is just one such possible conformation of Z, defined by i_r and j_s). Therefore, we prune if 2 − 1 = 1 > E_w. Since we are looking for all conformations within energy E_w of the GMEC, if we want only the GMEC, we set E_w = 0 and thus prune i_r.

2.5 Tests and validation

BD, iMinDEE, and DEEPer were run using OSPREY [50, 55] on 67 test systems to compare their GMECs, thus investigating the advantages of DEEPer in sequence design. The PDB codes of the proteins used were 2ILB (3 tests), 2BGX (2 tests), 1EJG, 1FUS, 1IFC, 1LKK, 1PLC, 1POA, 1RRO, 1WHI, 2GNR, 2RHE, 2TRX, 1L6W, 1L7A, 1L7L, 1L7M, 1L8R, 1L9L, 1L9X, 2OXC, 2OXU, 2OYN, 2OZF, 2OZT, 2P02, 2P0W, 2PK8, 2PL1, 2PLT, 2PSP, 2PTH, 2RMC, 2SGA, 2WEA, 2YGS, 3CAO, 1AHO, 1C75, 1CC8, 1F94, 1FK5, 1I27, 1IQZ, 1JHG, 1M1Q, 1MJ4, 1OAI, 1OK0, 1PSR, 1R6J, 1TUK, 1U07, 1VBW, 1VFY, 1WXC, 1XMK, 1Y6X, 1ZZK, 2AIB, 2BT9, 2CC6, 2CG7, and 2CS7. Structures with hydrogens added were taken from the Richardson lab’s Top4400 database [56] or provided by Pablo Gainza and Kyle Roberts (personal communication). All flexible residues were in chain A except those for 1WXC, which were in chain B. Wild-type rotamers were not used in these tests, in order to provide a fair comparison of DEEPer to previous methods. Also, the tests were run using the automatic perturbation selection mechanism (Section 2.2). The set of flexible residue positions and the set of allowed mutations were selected manually for each system, with a variety of secondary structures and allowed mutations allowed (including some cases with no mutations permitted). Backrub and shear parameters θ were limited to the interval −2.5° ≤ θ ≤ 2.5°, and 5–11 flexible residues were chosen per system, except in a single run without continuous flexibility on a crystal structure of the E. coli amidase AmiD (PDB code 2BGX [57]) where shear and backrub parameters of 0 or ±5° were allowed and 19 flexible residues were chosen. The discrete conformational space of this run allowed visualization of the backbone conformational search space (Fig. 14a). Since this run was performed without continuous flexibility, rigid-rotamer DEE was performed in lieu of iMinDEE and BD, and compared to DEEPer.

Figure 14.

Examples of DEEPer GMEC searches. (a) A sequence-design run on structure 2BGX (AmiD from E. coli). The GMEC backbone moved away from the starting conformation for residues 126–131. The lack of continuous flexibility in this run allows display of all searched backbone conformations. (b) A conformational-search run on structure 2IXT (sphericase). From the starting conformation, a partial structure switch allowed the GMEC to change the backbone to that of a crystallographic alternate conformation for residues 37–42, where its sidechain rotamers also matched. Starting structure, black/gray; complete searched ensemble, purple; GMEC, pink. Green balls demarcate flexible-backbone regions; sidechains outside these regions are omitted for visual clarity.

Additional tests were performed without sequence changes to test the ability of DEEPer to model larger backbone changes, to recover experimentally-observed structures, and to model ensembles. When crystallographic alternates were used as a source of information on backbone conformational changes, wild-type rotamers for the starting alternate only were included in these runs; this inclusion simulates the availability of wild-type rotamers for the starting conformation when DEEPer is applied to a design problem.

3 Results and Discussion

In this section, we present computational tests of DEEPer. The tests show that, given a biophysical model, the additional molecular flexibility in DEEPer leads to more accurate treatment of protein conformations and sequences. These results justify the use of DEEPer in protein design calculations.

Tests of DEEPer using the automatic perturbation selection mechanism on 64 proteins consistently identified lower-energy structures than iMinDEE and BD. Lower-energy structures are more realistic assuming the correctness of the energy function in ranking conformations. (OSPREY’s energy function [7, 10] is based on AMBER [58, 59] and EEF1 [60].) Additional tests on a high-resolution structure of the serine protease sphericase from Lysinibacillus sphaericus (PDB code 2IXT [61]) and on a medium-resolution structure of human ubiquitin (PDB code 1UBQ [62]) demonstrate that DEEPer captures biophysically reasonable backbone motions and couplings of sidechain and backbone motions without introducing unrealistic conformations.

3.1 Comparisons to previous algorithms with less flexibility

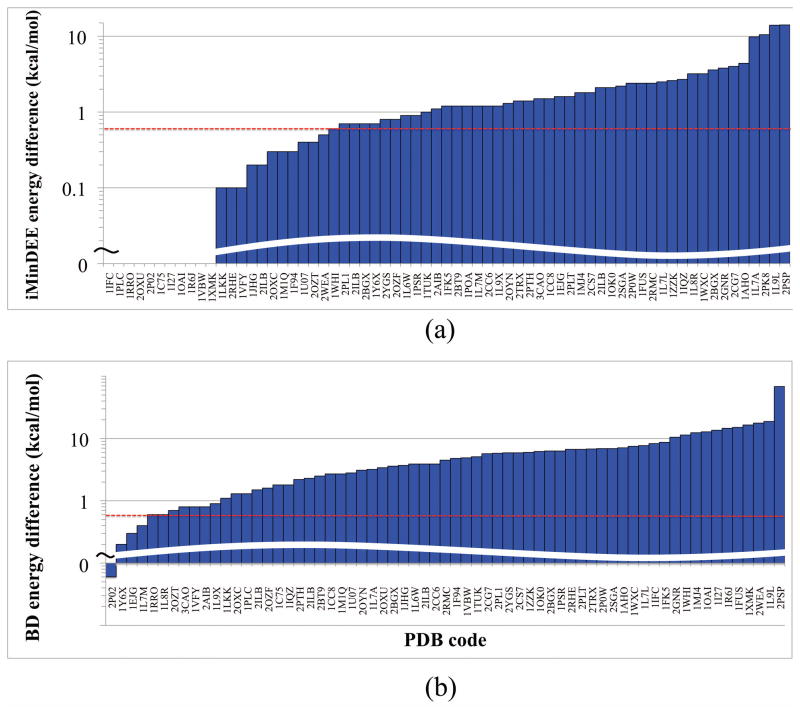
67 sequence-design tests on 64 different proteins, as described in section 2.5, were run to compare the GMECs found by iMinDEE and DEEPer (Fig. 10, 11, 12, 14a). By construction, DEEPer is guaranteed to yield either the same or lower GMEC energy than iMinDEE. Indeed, the GMECs calculated by DEEPer were lower than those calculated by iMinDEE by an average of 1.9 kcal/mol, ranging from 0 to 14.1 kcal/mol (Fig. 10a). 67% of these energy differences exceed the thermal energy at room temperature (0.592 kcal/mol, calculated as the universal gas constant times a room temperature of 298°K), which is a rough measure for functional significance. GMECs were also computed using BD [26], a provable algorithm with more limited backbone flexibility and without continuous sidechain minimization. DEEPer yielded lower GMEC energies in every case but one. In this single case, for the α subunit of human S-adenosylmethionine synthetase 2 (PDB code 2P02), the BD GMEC was only 0.4 kcal/mol lower in energy than the iMinDEE and DEEPer GMECs, which were virtually identical to each other; subtle backbone conformational changes in BD led to the slight energetic advantage of the BD structure, outweighing some larger differences in sidechain dihedrals (which did not include any rotamer changes). On the other hand, the GMECs calculated by DEEPer were lower than those calculated by BD by an average of 6.3 kcal/mol, with the difference ranging up up to 68.4 kcal/mol and exceeding the thermal energy at room temperature in 94% of runs (Fig. 10b).

Figure 10.

DEEPer GMEC designs compared to designs by previous algorithms with less flexibility on 67 test systems. (a) Decrease in energy from the iMinDEE GMEC to the DEEPer GMEC. (b) Decrease in energy from the BD GMEC to the DEEPer GMEC. Two systems are not shown because BD pruned all rotamers, indicating a steric clash for all rigid rotamers that was resolved by continuous minimization in iMinDEE and DEEPer. These systems are Chinese cobra phospholipase A2 (PDB code 1POA) and Pyrococcus furiosus hypothetical protein PF0899 (PDB code 2PK8). One system, the α subunit of human S-adenosylmethionine synthetase 2 (PDB code 2P02) had a higher DEEPer than BD GMEC energy. A dotted red line is shown in both (a) and (b) at the thermal energy at room temperature, 0.592 kcal/mol, as a rough measure of the significance of energy differences.

Figure 11.

DEEPer GMEC designs compared to designs by previous algorithms with less flexibility on 67 test systems, continued. (a) Decrease in energy from the BD to the DEEPer GMEC versus decrease in energy from the iMinDEE to the DEEPer GMEC. (b) Numbers of test systems with given numbers of sidechain rotamer changes between the iMinDEE and DEEPer GMECs.

Figure 12.

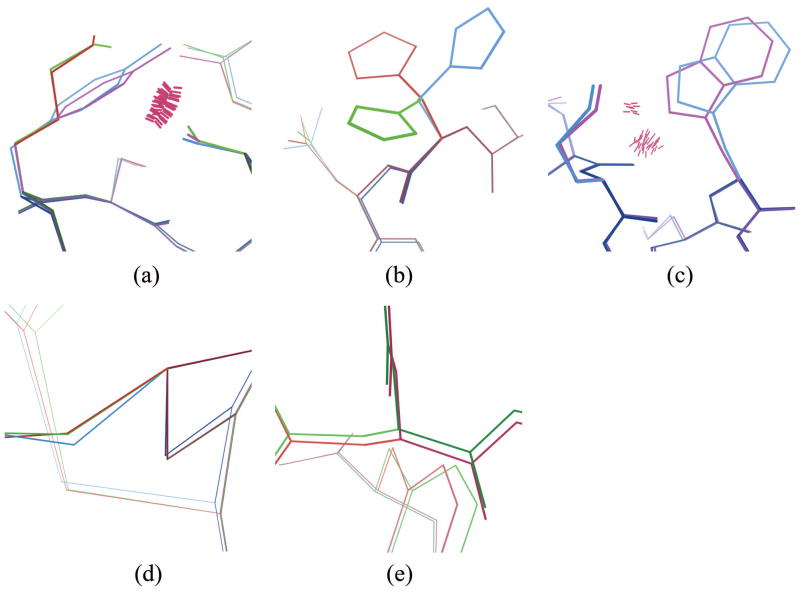
Comparisons of DEEPer GMECs (blue) to iMinDEE GMECs (red) and BD GMECs (green) for four systems. (a) Porcine pancreatic spasmolytic polypeptide (PDB code 2PSP), residues 52–58. Residue 54 is a tyrosine in the DEEPer GMEC but a lysine in the iMinDEE and BD GMECs. A steric clash (pink spikes, generated using Probe [68]) persists after fixed-backbone, flexible-sidechain energy minimization of the rotamers of the DEEPer GMEC (magenta), making a tyrosine at residue 54 infeasible without backbone flexibility. (b–c) Bacillus subtilis cephalosporin D deacetylase (PDB code 1L7A), residues 100–107. The DEEPer, iMinDEE, and BD GMECs all adopt different histidine rotamers at residue 100 (b); the DEEPer rotamer is the only one in the crystal structure. Residue 105 is a tryptophan in the DEEPer GMEC but an alanine in the iMinDEE and BD GMECs (c); a steric clash persists after flexible-backbone, rigid-rotamer energy minimization of the rotamers of the DEEPer GMEC (magenta), making a tryptophan at residue 105 infeasible without continuous sidechain flexibility. (d) The protease penicillopepsin from Penicillium janthinellum (PDB code 2WEA), residues 300–305. The iMinDEE and BD GMEC backbones are very similar; the DEEPer GMEC adopts a different backbone and achieves a lower energy. (e) The Zβ domain of the human RNA editing enzyme ADAR1 (PDB code 1XMK), residues 306–311. The iMinDEE and DEEPer GMECs are virtually identical; the BD GMEC adopts a different backbone but still has a a higher energy due to a lack of sidechain flexibility.

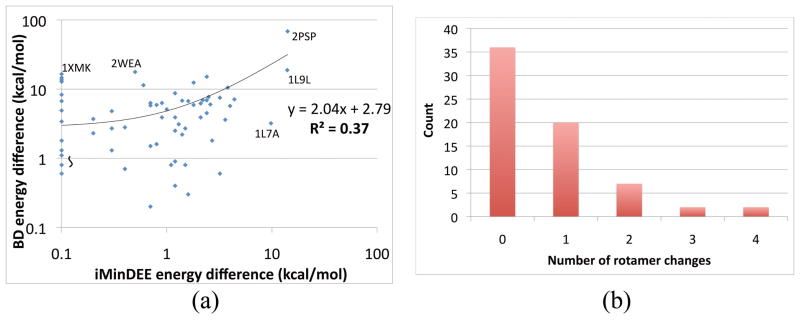
The changes in GMEC energy from iMinDEE to DEEPer and from BD to DEEPer were very weakly correlated (R²=0.37, where R² is the coefficient of determination; see Fig. 11a). This indicates that modeling backbone flexibility is not an effective substitute for modeling continuous sidechain flexibility or vice versa. Part of this weak correlation is explained by a few tests in which DEEPer provided a very large energetic advantage over both iMinDEE and BD, facilitated by a rotamer change or mutation that required both continuous sidechain and backbone flexibility to accommodate. For example, for porcine pancreatic spasmolytic polypeptide (PDB code 2PSP), BD and iMinDEE both had a lysine at position 54 while DEEPer had a tyrosine. A steric clash blocked BD and iMinDEE from having a tyrosine at this position (Fig. 12a). This was associated with the largest GMEC energy difference both between DEEPer and iMinDEE and between DEEPer and BD. For Bacillus subtilis cephalosporin D deacetylase (PDB code 1L7A), DEEPer, iMinDEE, and BD chose different rotamers for histidine 100 (Fig. 12b), although DEEPer identified the native rotamer, likely due to combined backbone and sidechain minimization at adjacent residues asparagine 101 and lysine 104. In the same run, DEEPer chose the wild-type tryptophan at nearby residue 105 instead of the alanine chosen by iMinDEE and BD; steric clashes precluded a tryptophan with either BD backbone minimization alone (Fig. 12c) or iMinDEE sidechain minimization alone. Because of these combined differences, this region was associated with one of the largest DEEPer-iMinDEE energy differences (9.8 kcal/mol), though the DEEPer-BD energy difference was below average (3.2 kcal/mol).

Even the different forms of backbone flexibility modeled by BD and DEEPer were somewhat complementary. In some tests, e.g., for the protease penicillopepsin from Penicillium janthinellum (PDB code 2WEA; Fig. 12d), the BD structure stayed very near the fixed-backbone iMinDEE structure, and DEEPer modeled more backbone motion. In other cases, e.g. for the Zβ domain of the human RNA editing enzyme ADAR1 (PDB code 1XMK; Fig. 12e), the reverse was true: the DEEPer and iMinDEE structures were virtually identical while BD modeled more backbone motion. However, in both cases, continuous sidechain flexibility allowed DEEPer to identify lower-energy sidechain conformations made accessible by its backbone conformational search. For example, for penicillopepsin DEEPer returned a GMEC energy 17.7 kcal/mol lower than BD, and for Zβ the DEEPer and iMinDEE GMEC energies were both 16.5 kcal/mol lower than the BD GMEC energy.

Notably, the perturbations’ effects on the sidechains far exceeded their effects on the backbone; the latter ranged from 0 to 0.39Å all-atom backbone RMSD with an average of 0.06 Å. This is partly due to the “lever effect,” i.e., the greater displacement of sidechain atoms than of backbone atoms during a perturbation because the sidechain atoms are kinematically farther from the axes of the rotations involved in the perturbation (Fig. 13). Thus, despite the small displacements of the backbone atoms, the effects of shears and backrubs on atoms at the end of sidechains can be substantial. For example, a 2.5° backrub centered at an all-trans lysine residue in an ideal β sheet with no other perturbations causes a backbone RMSD for the three affected residues relative to the original structure of just 0.05 Å, and the lysine’s C_α atom moves by just 0.09Å, but the lysine’s terminal N_ζ atom moves by 0.35 Å. Because they induce only small backbone changes, shears and backrubs in the −2.5° to 2.5° parameter range are expected to be biophysically feasible in a wide range of conformations. The backbone motions in DEEPer also induced rotamer changes: one or more rotamer changes were observed in 46% of tests, and up to four rotamer changes per test were observed (Fig. 11b).

Figure 13.

The lever effect for a backrub: the sidechain atoms move the most because they are farthest from the axis of rotation. A 5° backrub is shown. The view on the left looks down the axis of rotation, while the view on the right shows the axis of rotation as a black line.

Energy differences between GMECs found by different algorithms directly measure the effectiveness of the algorithms for their desired function, which is to explore the sequence and conformational space available to a protein and find the lowest-energy sequence and conformation available. Inaccuracy in identifying low-energy conformations and sequences can come from either inaccuracy in the energy function or inaccurate identification of the lowest-energy conformation(s) and sequence(s) given the energy function. DEEPer is intended to reduce inaccuracy of the latter type, and we perform energy comparison tests to separate this task from the also important task of improving energy function accuracy. Because of its provability and its high degree of flexibility, DEEPer is uniquely useful for evaluating and improving energy functions and other modeling assumptions. Errors in the model–i.e., deviations of modeling assumptions from reality–can be identified by running DEEPer and examining deviations of the output from observed structures. Such tests would be much less effective if run using a non-provable algorithm, because errors in the output could be due either to errors in the model or to deviation of the results of the algorithm from the correct answer for the input model. Also, since real proteins exhibit continuous sidechain and backbone flexibility, the most accurate models must have both of these as well, and thus testing these models requires an algorithm with continuous sidechain and backbone flexibility. DEEPer’s provable search of a conformational space with both continuous sidechain and backbone flexibility is thus uniquely suited for testing modeling assumptions.

Both BD and iMinDEE provably find the lowest-energy structure in their chosen conformational spaces, but the significantly lower energies identified with DEEPer indicate that it finds additional significant conformations that involve continuous sidechain and backbone flexibility. Thus, DEEPer is a useful step toward finding better conformations and sequences given an energy function. Together with advances in energy functions, which it will hopefully facilitate, it is a useful step toward finding conformations and sequences more in line with reality.

3.2 Tests of larger backbone conformational changes

To further demonstrate the utility of DEEPer in modeling realistic conformations, tests were performed to show that DEEPer can model larger backbone conformational changes using partial structure switches. The allowed backbone conformations were crystallographic alternates in two segments of the structure of sphericase (2IXT [49]). In each test, the input structural information consisted of the backbones of the two crystallographic alternates as well as the sidechains only of the starting alternate (to be used as wild-type rotamers). The tests maintained the wild-type sequence (see section 2.5).

The first segment was loop residues 36–43, in a fairly surface-exposed region of the protein with some 3₁₀-helical character. Residues 48 and 66 were also allowed sidechain flexibility because of their close contacts with the alternates. Two tests were undertaken. The first test was run without the automatic perturbation selector, meaning the only perturbation available was the partial structure switch that changes the backbone from the starting alternate to the other alternate. The algorithm was being asked to choose a backbone and to pack sidechains onto it, using the wild-type rotamers with the starting alternate or generic rotamers with either the starting or the other alternate. It identified the GMEC as the non-starting alternate, including both its backbone and sidechain rotamers (Fig. 14b). 4 of these 8 rotamers differed from the starting rotamers (counting a proline flip). The second test was run with the automatic perturbation selector, so more perturbations and RCs were available. This test identified the GMEC as a modified version of the non-starting alternate, perturbed by not only the partial structure switch between alternates, but also a loop closure adjustment and some continuous backrub minimization. This GMEC was 3.4 kcal/mol lower in energy than the GMEC from the first test, thus illustrating the value of including additional backbone perturbations.

The second segment was residues 264–270, at a surface-exposed α-helical C-terminus. Two tests were again undertaken; this time both used the automatic perturbation selector, but the second also allowed up to 2.5° in either direction of continuous shear and backrub minimization. Both tests chose the other alternate’s backbone in the GMEC. However, additional backbone perturbations, this time in the form of continuous shear and backrub minimization, reduced the energy by only 0.15 kcal/mol. This is in contrast to the second test on the first segment, where additional backbone perturbations were instrumental in finding a lower-energy conformation.

These results show that partial structure switches alone are sufficient for modeling backbone structure in some cases, but in other cases additional perturbations are important for more fully exploring conformational space. DEEPer is useful for distinguishing between these different types of cases. This capability could be very useful in multistate protein design by revealing small changes in one of the available backbone states that would make that state much more favorable for a given sequence.

3.3 Tests of ensemble generation

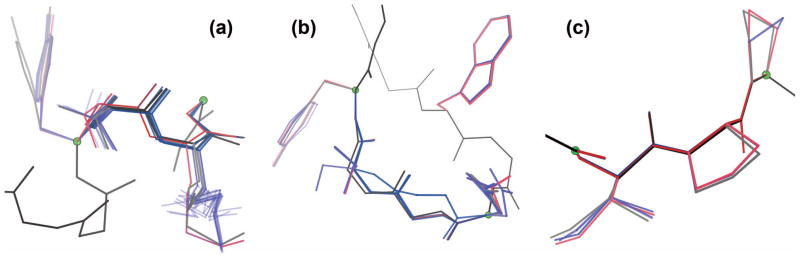
Additional runs were performed to test the ability of DEEPer to generate biophysically reasonable ensembles of low-energy conformations given fixed sequences. In residues 157–160 of 2IXT (the above-mentioned sphericase structure), the crystal structure contains alternate conformations related approximately by a shear motion. This likely indicates increased backbone dynamics compared to other parts of the structure, and indeed the DEEPer ensemble generated using the native sequence showed more diversity of backbone conformations than in tests on other systems, sampling the conformational space around and between the alternates (Fig. 15a). By contrast, in residues 238 and 240–243 of sphericase modeled with a G242S mutation, the DEEPer backbone ensemble was fairly concentrated around the starting-alternate backbone (Fig. 15b). However, DEEPer iden-tified one state in this ensemble significantly different from both alternates, which was generated by a large loop closure adjustment and a subsequent backrub; neither of these perturbations alone yielded a comparably low-energy conformation. Finally, a test on residues 35–38 of ubiquitin, for which only one conformation was crystallographically observable, showed a much more concentrated ensemble (Fig. 15c). These results demonstrate that the combination of different types of flexibility in DEEPer allows it to effectively explore ensembles of realistic conformations, including some with substantial deviation from the starting structure.

Figure 15.

DEEPer ensembles are dependent on structural and sequence contexts. (a) The low-energy ensemble of computed models was fairly wide at residues 157–160 of sphericase (structure 2IXT) and spanned the crystallographic alternates. The GMEC was on the fringe of the ensemble. (b) Residues 238 and 240–243 also have alternates in structure 2IXT, but the low-energy ensemble from DEEPer for the G242S mutant, including the GMEC, was very tight around alternate A. One low-energy model made a significant excursion via a > 90° peptide flip, executed by a loop closure adjustment and backrubs. (c) Residues 35–38 in structure 1UBQ (ubiquitin) have a single well-ordered conformation. Correspondingly, the low-energy ensemble from DEEPer is very compact: the biggest departure is a single proline flip perturbation. Starting structure, black/gray; low-energy ensemble, blue; GMEC, pink. Green balls demarcate flexible-backbone regions; sidechains outside these regions are omitted for visual clarity.

3.4 Modeling entropy

As noted in the Introduction, ensembles generated by DEEPer can be used to estimate binding affinity using the K^* algorithm [5, 16, 14], which compares the partition functions of bound and unbound proteins and ligands. The partition function of a system is defined in K^*’s model as $q_C=\sum _{c\in C}exp(-\frac{E_c}{RT})$, where C is all enumerated conformations (tuples of RCs at all flexible residues), E_c is the minimized conformational energy for conformation c ∈ C, R is the universal gas constant, and T is the temperature. The association constant is then approximated as $K^{\ast }=\frac{q_{PL}}{q_P{q}_L}$, where q_P, q_L, and q_PL are the partition functions of the unbound protein, the unbound ligand, and the protein:ligand complex, respectively [5, 16, 14]. K^* is a provably-good approximation algorithm: it guarantees that the computed binding constant will be within a fraction ε of the theoretical binding constant defined by the model [16, 14]. The value ε is specified by the user, to bound the desired accuracy of the calculation.

The conformations that contribute to K^* partition functions are the result of minimization-aware DEE (iMinDEE, [28, 16]). This means that even if two conformations in the ensemble populate the same torsional well for a given rotamer (or RC), they will in general minimize to different conformational states within that well due to the influences of their different surroundings. K^* computes a large ensemble, so multiple conformational states are indeed likely to be present per torsional well. Furthermore, the same conformation (in terms of rotamers and/or RCs) may minimize differently in the bound vs. unbound states due to the presence vs. absence of the ligand. In practice, we have observed that the bound and unbound rotamer conformations predicted by K^* can have obviously different means and variances, and are statistically significant as different populations. This result suggests that K^* has the potential to correctly model induced motion in torsional wells using its ensembles, particularly in light of other studies showing that population shifts within torsional wells often occur upon binding [63, 64]. The partition functions, and quotients of the bound and unbound states, should reflect such population differences. Hence, K^* can model a measure of conformational entropy and how it changes upon binding.

Nevertheless, K^*, like any finite sum, is a discrete approximation to true continuous entropy. Given this discrete model, K^* guarantees a provably-good approximation, ε-close to the binding constant in the model above (see [16]). Unfortunately, partition functions based on discrete ensembles are imperfect reporters of conformational entropy, since they are computed not over all possible conformational states of the protein but rather over a putatively representative low-energy subset: the discrete set of energy-minimized tuples of RCs at all flexible residues.

Some additional error may be introduced by the choice of shear and backrub parameter ranges for RCs. For example, in principle, one could choose very closely spaced shear and backrub parameters, and then the backbone conformational entropy would be weighted too heavily because of the artificially denser distribution of backbone conformational states (compared to sidechain conformational states). However, the DEEPer/K^* hybrid algorithm avoids the bias toward excessive weighting of backbone conformational entropy in at least two ways. First, such errors will cancel out somewhat when the partition functions in the bound and unbound states are divided. Second, having only a single parameter interval for each shear or backrub will usually make each RC (and thus, each sufficiently low-energy tuple of RCs) correspond to its own energy well.

Finally, the DEEPer/K^* approximation is analogous to the iMinDEE/K^* approximation currently used in OSPREY [50, 55] which computes partition functions over the discrete set of tuples of continuous rotamers at all flexible residues. MinDEE/K^* and iMinDEE/K^* have been to shown to produce improvements in predictions of binding affinity [5, 16, 8, 10, 14]. Notably, K^* provably computes the partition function for its specified flexibility model (DEEPer or rigid-backbone) within a user-specified margin of error ε. Thus, the introduction of approximate backbone conformational entropy through the combination of DEEPer with K^* is also expected to increase the accuracy of predictions.

3.5 Summary

Overall, these results illustrate the important point that sidechain motions are tightly coupled to backbone motions (Fig. 11b, Fig. 14b). In particular, rotamer switches can be enabled either by large discrete backbone motions such as partial structure switches or by small continuous backbone motions such as shears and backrubs. To model this hierarchy of conformational changes, DEEPer includes a broad repertoire of empirically-motivated and biophysically-realistic backbone move types of various magnitudes, and thus is well equipped to study functionally relevant backbone-sidechain couplings in both natural and designed proteins. This coupling is analogous to the utility of small adjustments to structures in multiple structure alignment, which have been found to produce improvements out of proportion to their size [65].

The ability of DEEPer to provably search continuous sidechain and backbone conformational space can be useful for work involving non-provable algorithms as well. Because DEEPer reliably predicts the correct GMEC or ensemble given an energy function and a set of perturbations, tests of DEEPer can be used as tests of modeling assumptions, which can allow generation of more accurate input models for other algorithms (particularly when modeling backbone flexibility). Additionally, the DEEPer GMEC energy is a lower bound on the GMEC energy that any other algorithm can find with the same biophysical model, so DEEPer can provide a benchmark for other highly flexible protein design algorithms.

4 Conclusions

DEEPer provides several advantages over previous algorithms. Due to its continuous, provably complete search over both sidechain and backbone degrees of freedom, it finds GMECs and partition functions that are more accurate with respect to the energy function, resulting in more trustworthy binding predictions and protein or drug designs. DEEPer’s empirically-motivated perturbations help to choose appropriate backbone conformations out of the many possibilities in a way that combines computational tractability with biophysical feasibility. Nevertheless, additional, different perturbations can be easily incorporated in the future due to the accommodating RC framework and indirect pruning method. DEEPer can also use different pairwise energy functions or constraints on the degrees of freedom (e.g., different rotamer definitions or bounds on perturbation parameters) without modification of the algorithm. The energy function and constraints can be derived from either physical or knowledge-based sources. For example, if a more accurate treatment of solvation than that provided by EEF1 is desired, the pairwise Poisson-Boltzmann solvation model of Vizcarra et al. [66] could be used instead. Computational tests exploring both sequence and conformational space for 64 proteins help confirm that DEEPer enables a biophysically realistic search of plausible backbone states and consistently yields lower-energy structures than even a continuously-flexible search of sidechain conformations.

Abbreviations

DEE

Dead-End Elimination

DEEPer

Dead-End Elimination with Perturbations

GMEC

global minimum-energy conformation

RC

residue conformation

DOF

degree of freedom