Modeling the Association Between Particle Constituents of Air Pollution and Health Outcomes

Abstract

There is increasing interest in evaluating the association between specific fine-particle (particles with aerodynamic diameters less than 2.5 µm; PM_2.5) constituents and adverse health outcomes rather than focusing solely on the impact of total PM_2.5. Because PM_2.5 may be related to both constituent concentration and health outcomes, constituents that are more strongly correlated with PM_2.5 may appear more closely related to adverse health outcomes than other constituents even if they are not inherently more toxic. Therefore, it is important to properly account for potential confounding by PM_2.5 in these analyses. Usually, confounding is due to a factor that is distinct from the exposure and outcome. However, because constituents are a component of PM_2.5, standard covariate adjustment is not appropriate. Similar considerations apply to source-apportioned concentrations and studies assessing either short-term or long-term impacts of constituents. Using data on 18 constituents and data from 1,060 patients admitted to a Boston medical center with ischemic stroke in 2003–2008, the authors illustrate several options for modeling the association between constituents and health outcomes that account for the impact of PM_2.5. Although the different methods yield results with different interpretations, the relative rankings of the association between constituents and ischemic stroke were fairly consistent across models.

Several studies have shown that short-term increases in levels of fine ambient particulate matter (particles with aerodynamic diameters less than 2.5 µm; PM_2.5) are associated with an increased risk of cardiovascular morbidity and mortality (1) and exacerbation of respiratory diseases (2). However, PM_2.5 is composed of several constituents that have different physical and chemical properties and different toxicities (3–10).

Studies in which the association between constituents and health outcomes are examined involve additional considerations beyond those that arise in studies of the impact of PM_2.5. First, there are concerns about errors in measurement of both PM_2.5 and constituents. When daily levels of a constituent are very low, measurements may be below the level of detection, leading to unstable estimates of constituent concentrations. Second, PM_2.5 is often associated with both the constituent concentration and the health outcome, potentially confounding the observed association. If a constituent represents a large proportion of PM_2.5 mass or if the exposure pattern of the constituent is highly correlated with that of PM_2.5 (e.g., because it represents a common exposure source), the constituent may seem more strongly associated with adverse health outcomes than other constituents because of its association with PM_2.5 rather than because of its inherent toxicity.

Several strategies have been used to evaluate the relation between specific constituents and health outcomes, such as modeling the association between constituent concentrations and ignoring PM_2.5 or modeling how the constituent modifies the impact of PM_2.5 on a health outcome. However, these techniques may lead to incorrect conclusions. In the present study, we discuss the limitations of these approaches and propose the use of residuals, a method that is commonly used in several fields but that has not been widely adapted in research on constituents and health outcomes. Although the analytic issues discussed below are relevant for studies of individual constituents, multipollutant analyses, studies of source contributions estimated with factor analysis, and studies of the long-term impact of constituents on health outcomes, we illustrate the model options using a straightforward example of the association between 18 constituents and ischemic stroke onset. Because constituents serve as indicators of a combination of species emanating from a particular source, the results pertaining to a certain constituent refer to the impact of that constituent and other species with a similar exposure pattern that likely originate from the same source.

Wellenius et al. (11) reported that an interquartile range (IQR) increase in PM_2.5 levels (6.4 µg/m³) was associated with a 12% increase in the risk of ischemic stroke onset. To illustrate the model options discussed below, we used the subset of this sample for whom we had data on constituents. A priori, we hypothesized that in addition to black carbon, transition metals (e.g., nickel and vanadium), which are tracers of fuel oil combustion and home heating, would be associated with an increased risk of ischemic stroke, whereas chloride, a tracer of sea salt, would not be associated with increased stroke risk.

MATERIALS AND METHODS

Study design

Details of the study design and analysis are described in the Web Appendix (available at http://aje.oxfordjournals.org/). Briefly, we identified consecutive patients 21 years of age or older who were admitted to the Beth Israel Deaconess Medical Center in Boston, Massachusetts, with neurologist-confirmed ischemic stroke and who resided in the Boston metropolitan region. In this study, we restricted our analysis to patients who lived within 40 km of the air pollution monitoring site and had a stroke on dates for which we had data on constituents (January 1, 2003–October 31, 2008). We used the time-stratified case-crossover study design and conditional logistic regression to assess the association between ischemic stroke onset and levels of constituents in the 24 hours preceding each event. This study was approved by the institutional review board at the Beth Israel Deaconess Medical Center.

Model options

The advantages and disadvantages of several model options are summarized in Table 1. The models are represented in the form of a generalized linear model, with the dependent variable for the health outcome (μ) expressed as a function of the independent variables for constituents, total PM_2.5, and a matrix of [γ′X] other covariates. This model can accommodate different functional forms for the regression, such as linear regression, logistic regression, and survival analysis.

Table 1.

Advantages and Disadvantages of Several Options for Modeling the Association Between Particle Constituents and Health Outcomes

Parameter	Question	Modela	Advantages	Disadvantages
Constituent concentration	What is the effect of a particular constituent?	g(μ) = β0 + β1(constituent) + [γ'X]	Easy to interpret	Confounding by total PM2.5
				Confounding by other constituents that covary
Constituent proportion	What is the effect of the percentage of total PM2.5 from a particular constituent?	g(μ) = β0 + β1(constituent/PM2.5) + β2(PM2.5) + β3((constituent/PM2.5) × PM2.5) + [γ'X]	Accounts for total PM2.5 (but may not effectively prevent confounding by PM2.5)	Confounding by total PM2.5
				Confounding by other constituents that covary
				Results do not provide information on absolute magnitude of constituent change associated with outcome.
			Information about PM2.5 composition	Problem of zeros; some constituents contribute little to mass, resulting in unstable estimates.
Interaction between constituent concentration (or constituent proportion) and PM2.5 mass	How does a particular constituent modify the effect of total PM2.5?	g(μ) = β0 + β1(constituent) + β2(PM2.5) + β3(constituent × PM2.5) + [γ'X] or g(μ) = β0 + β1(constituent/PM2.5) + β2(PM2.5) + β3((constituent/PM2.5) × PM2.5) + [γ'X]	Accounts for total PM2.5	Collinearity between constituent and PM2.5
			Easy to interpret	Results do not provide information on absolute magnitude of constituent change responsible for outcome.
			Information about PM2.5 composition
Constituent concentration adjusting for PM2.5 mass	What is the effect of a particular constituent after adjusting for total PM2.5?	g(μ) = β0 + β1(constituent) + β2(PM2.5) + [γ'X]	Accounts for total PM2.5	Confounding by other constituents that covary
				May be over adjusting for constituents highly correlated with total PM2.5
			Easy to interpret	Collinearity between constituent and PM2.5 and extent of this problem depend on relative contribution of constituent to total PM2.5.
				Does not provide indication of variation in constituent while holding total PM2.5 constant.
Constituent residual	What is the effect of a particular constituent holding total PM2.5 constant?	Residual: constituent = total PM2.5	Eliminates confounding by total PM2.5	Hard to interpret: More of one constituent equates to less of another, which is larger problem for constituents with larger contribution to total PM2.5.
		g(μ) = β0 + β1(residual) + [γ'X]	No collinearity between constituent and PM2.5
			Removes extraneous variation due to total PM2.5.	Results do not provide information on absolute magnitude of constituent change associated with outcome.
PM2.5 residual	What is the effect of total PM2.5 holding a particular constituent constant (i.e., effect of PM2.5 with a particular composition)?	Residual: total PM2.5 = constituent	Eliminates confounding by other constituents that covary	Hard to interpret: More of one constituent equates to less of another, which is a larger problem for constituents with larger contribution to total PM2.5.
		g(μ) = β0 + β1(residual) + [γ'X]	No collinearity between constituent and PM2.5	Results do not provide information on absolute magnitude of constituent change associated with outcome.
			Removes extraneous variation due to constituent

Abbreviation: PM_2.5, particles with aerodynamic diameters less than 2.5 µm.

^a The models are represented in the form of a generalized linear model, with the dependent variable for the health outcome (μ) expressed as a function of the independent variables for constituents, total PM_2.5, and a matrix of [γ'X] other covariates. This model can accommodate different functional forms for the regression, such as linear regression, logistic regression, and survival analysis.

Constituent concentration

A common approach is to model constituent concentration alone (5, 8, 12, 13). However, some constituents may be associated with disease based on their correlation with PM_2.5. When PM_2.5 is positively associated with both constituent concentration and adverse health outcomes (1), analyses of individual constituents yield estimates that are biased upward. Additionally, these models are confounded by other constituents that covary with the constituent of interest.

Constituent proportion

One method to account for PM_2.5 is to compute the proportion of PM_2.5 contributed by a particular constituent, which is analogous to calculating the proportion of calories from a macronutrient (nutrient density) (14). Implicitly, the coefficient for the constituent proportion assumes that the impact of the constituent is attributable to the proportion of PM_2.5 mass rather than the absolute constituent level, which seems implausible. Furthermore, a constituent may have a low concentration and yet be highly correlated with PM_2.5 because it represents a common exposure source. Additionally, this approach may incur further errors instead of removing confounding by PM_2.5; for constituents that are weakly correlated with PM_2.5 or that exhibit low variability, dividing by PM_2.5 creates a variable that is highly related to PM_2.5 and may even reverse the direction of the association between the constituent and the health outcome (14). Therefore, one should include in the model a term for PM_2.5, a coefficient that generally represents the impact of PM_2.5 if constituent proportion is not strongly correlated with PM_2.5.

Interaction between constituent concentration (or constituent proportion) and PM_2.5 mass

One option is to include an interaction term for PM_2.5 and the constituent concentration (or constituent proportion). However, constituent concentration and PM_2.5 are often collinear, leading to lower independent variation for both of the terms and an altered interpretation of the results. Additionally, this approach does not quantify the levels of the constituent that pose the increased risk, only the relative importance of different constituents. The greatest drawback of this approach is that the interpretation of an interaction term in this setting is not clear. Usually, interaction terms are used to estimate how an exposure-disease association is modified by an independent third factor, but in this case the interaction involves a component of the exposure itself.

Constituent concentration adjusted for PM_2.5 mass

A simple way to account for PM_2.5 is to include both the constituent concentration and the level of PM_2.5 as terms in a model. The parameter for the constituent represents the impact of higher levels of the constituent (and its correlates), holding the other constituents constant. The parameter for PM_2.5 represents the difference in disease risk associated with all other constituents. Because constituent concentration and PM_2.5 are often strongly correlated, the inclusion of 2 collinear terms may result in unstable coefficients with large variance. This may occur when sulfur and PM_2.5 are simultaneously included in a model. In our data, the sulfur is in the form of (NH₄)₂SO₄. Accordingly, we also constructed a model with sulfur and non-ammonium sulfate mass (defined as PM_2.5 – 4.125 × sulfur mass) and compared the results to a model with sulfur and PM_2.5.

Constituent residual

Invoking the assumptions of linear regression, PM_2.5-adjusted constituent levels can be calculated by constructing a linear regression model with the constituent concentration as the dependent variable and the PM_2.5 level as the independent variable. The residuals from this model are uncorrelated with PM_2.5 levels and represent the variation in constituent levels independent of PM_2.5. The coefficient for constituent residuals in the health outcome model represents the increase in risk associated with higher levels of the constituent while holding PM_2.5 constant, that is, higher levels of the constituent (and other constituents that travel with it) and lower levels of other constituents that make up total PM_2.5 mass.

Assuming the model used to create the residuals was correctly specified, the coefficient for the constituent residual should be identical to the coefficient for constituent concentration in a single-pollutant model. If PM_2.5 is included in the model with the constituent residual, both the coefficient and the standard errors from the residual model should be identical to those from the model adjusted for PM_2.5; however, the interpretation of the PM_2.5 term is slightly different. Because constituent residuals and PM_2.5 are uncorrelated, the coefficient for PM_2.5 in the residual model represents the independent impact of the constituent of interest and the impact of PM_2.5. In the model with PM_2.5 and the constituent, though, the coefficient for PM_2.5 represents the impact of all constituents other than the constituent of interest.

There are several reasons to include a term for PM_2.5 in the model with the constituent residual (14); if PM_2.5 is strongly associated with the health outcome independent of the constituent, including it may improve the precision of the estimate, uncorrelated variables can confound each other in nonlinear models, and this term quantifies the magnitude of the association between PM_2.5 and the health outcome. The main limitation of the residual method is that the interpretation is not as straightforward as other options; a higher level of one constituent (and its correlates) implies lower levels of all others.

PM_2.5 residual

Instead of regressing the constituent concentration on PM_2.5, one could regress PM_2.5 on the constituent concentration, yielding results that answer a different question. As a variable in the health outcomes model, the coefficient for the PM_2.5 residual represents the increase in risk associated with higher levels of PM_2.5 while holding the constituent and its correlates constant, that is, higher levels of PM_2.5 after removing the covariation due to the constituent of interest and all related constituents.

RESULTS

Table 2 presents the clinical characteristics for the participants included in this analysis. Table 3 presents the mean daily levels of PM_2.5 mass and constituent concentrations for the subset of the sample included in this analysis. In this subset of the population, an IQR increase in PM_2.5 levels (6.4 µg/m³) over the past 24 hours is associated with a 14% (95% confidence interval: 2, 28) higher risk of ischemic stroke onset. The correlations between the constituent concentrations are reported in Table 4, the correlations between PM_2.5 and the proportion of PM_2.5 from each constituent are reported in Table 5, and the results of the case-crossover analyses are shown in Figure 1.

Table 2.

Clinical Characteristics of 1,060 Patients Hospitalized for Acute Ischemic Stroke and Residing in the Boston, Massachusetts, Metropolitan Area, 2003–2008^a

	No. of Participants	%
Female	572	54
White	808	76
Past medical history
Stroke or transient ischemic attack	292	28
Atrial fibrillation	275	26
Hypertension	779	74
Coronary artery disease	260	25
Heart failure	143	14
Diabetes mellitus	302	29
Chronic obstructive pulmonary disorder	69	7
Smoking history
Current smoker	155	15
Former smoker	310	29

^a The mean age of the patients was 72.6 years (standard deviation, 15 years).

Table 3.

Mean Daily Levels of Particles With Aerodynamic Diameters Less Than 2.5 µm^a and Constituents^b, Boston, Massachusetts, January 2003–September 2008

					Interquartile Range
Exposure	% Below Detection	Median	Mean (SD)	% of PM	Constituent Concentration	Constituent Residual	PM2.5 Residual
PM2.5		5.2	9.3 (5.9)		6.4
Silicon	1.96	27.9	35.2 (29.7)	0.38	30.3	26.6	5.8
Chlorine	18.97	0.6	17 (79.8)	0.18	5.8	10.8	6.4
Potassium	0	31.6	39.9 (85.2)	0.43	21.4	16.5	6.1
Manganese	5.32	1	2 (1.4)	0.02	1.7	1.6	6
Zinc	0.04	5.9	10.8 (8.6)	0.12	7.2	6.1	5.4
Sodium	4.77	45.3	118 (110.1)	1.27	112.9	80.4	5.3
Copper	3.95	1	2.3 (3.1)	0.02	2.1	1.9	6
Aluminum	2.11	11.1	20.3 (14.3)	0.22	15	11.7
Calcium	1.6	16.3	25.2 (13.4)	0.27	16	15	5.9
Bromine	0.04	0.7	1.6 (1.3)	0.02	1.6	1.4	5.6
Lead	9.82	0.7	2.1 (1.9)	0.02	2.3	2.1	5.4
Selenium	0.04	0	0.6 (0.9)	0.01	0.9	0.8	6
Titanium	1.21	1	2.4 (2.4)	0.03	2.3	2	5.9
Vanadium	4.65	0.8	2.7 (3.1)	0.03	2.7	2.4	5.4
Iron	0	37.6	59.2 (30.6)	0.64	37	31.7	5.2
Sulfur	0.08	456.2	921.6 (746.9)	9.91	650.2	307	2.5
Nickel	1.37	0.8	2.3 (2.1)	0.02	2.2	2	5.7
Black carbon	0	585.3	654.2 (354.1)	7.03	437.6	296.2	4.2

Abbreviations: PM_2.5, particles with aerodynamic diameters less than 2.5 µm; SD, standard deviation.

^a Measured as μm/m³.

^b Measured as ng/m³.

Table 4.

Spearman Correlations Between PM_2.5 and Constituents in Boston, Massachusetts, January 2003–September 2008

	PM2.5	Si	Cl	K	Mn	Zn	Na	Cu	Al	Ca	Br	Pb	Se	Ti	V	Fe	S	Ni	BC
PM2.5	1
Si	0.41	1
Cl	0.07	−0.01	1
K	0.67	0.48	0.29	1
Mn	0.28	0.32	0.13	0.22	1
Zn	0.55	0.31	0.23	0.53	0.43	1
Na	0.53	0.22	0.27	0.42	0.07	0.22	1
Cu	0.35	0.24	0.29	0.36	0.30	0.47	0.17	1
Al	0.55	0.79	−0.01	0.53	0.30	0.32	0.36	0.23	1
Ca	0.39	0.65	0.16	0.42	0.40	0.48	0.19	0.37	0.57	1
Br	0.45	0.26	0.28	0.51	0.12	0.35	0.37	0.25	0.31	0.34	1
Pb	0.43	0.23	0.09	0.44	0.12	0.36	0.23	0.30	0.27	0.19	0.33	1
Se	0.23	0.05	0.02	0.08	0.06	0.13	0.12	0.10	0.10	0.13	0.17	0.07	1
Ti	0.40	0.55	−0.06	0.34	0.28	0.34	−0.02	0.28	0.51	0.66	0.21	0.16	0.20	1
V	0.47	0.14	0.08	0.27	0.13	0.38	0.23	0.11	0.21	0.33	0.25	0.21	0.20	0.34	1
Fe	0.53	0.65	0.10	0.46	0.50	0.59	0.19	0.63	0.57	0.73	0.30	0.31	0.11	0.61	0.31	1
S	0.88	0.30	−0.01	0.48	0.20	0.42	0.58	0.30	0.45	0.31	0.38	0.33	0.26	0.33	0.42	0.42	1
Ni	0.37	0.08	0.15	0.28	0.18	0.50	0.19	0.31	0.14	0.40	0.25	0.20	0.18	0.28	0.75	0.37	0.38	1
BC	0.72	0.29	0.08	0.39	0.32	0.54	0.30	0.51	0.34	0.36	0.28	0.35	0.15	0.36	0.45	0.66	0.58	0.36	1

Abbreviations: Al, Aluminum; BC, black carbon; Br, bromine; Ca, calcium; Cl, chlorine; Cu, copper; Fe, iron; K, potassium; Mn, manganese; Na, sodium; Ni, nickel; Pb, lead; PM_2.5, particles with aerodynamic diameters less than 2.5 µm; S, sulfur; Se, selenium; Si, silicon; Ti, titanium; V, vanadium; Zn, zinc.

Table 5.

Correlation Between Particles With Aerodynamic Diameters Less Than 2.5 µm (PM_2.5) and the Proportion of PM_2.5 From Each Constituent, Boston, Massachusetts, January 2003–September 2008

Constituent	Spearman Correlation Coefficient for PM2.5
Silicon	−0.312
Chlorine	−0.182
Potassium	−0.499
Manganese	−0.443
Zinc	−0.406
Sodium	−0.03
Copper	−0.234
Aluminum	−0.375
Calcium	−0.68
Bromine	−0.25
Lead	−0.149
Selenium	0.0472
Titanium	−0.416
Vanadium	−0.163
Iron	−0.587
Sulfur	0.119
Nickel	−0.333
Black carbon	−0.405

Abbreviation: PM_2.5, particles with aerodynamic diameters less than 2.5 µm.

Figure 1.

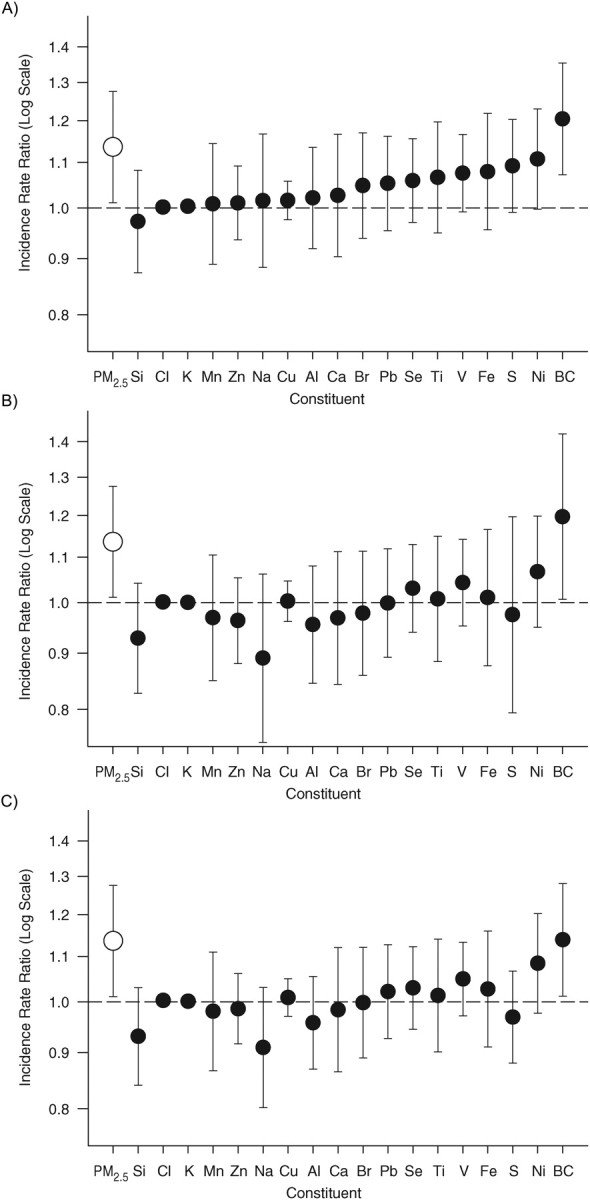
Incidence rate ratios and 95% confidence intervals for the association between an interquartile range increase in particle constituents and ischemic stroke onset in the following 24 hours among 1,060 patients hospitalized for acute ischemic stroke who resided in the Boston, Massachusetts, metropolitan area, 2003–2008. The results are presented for models with parameters for constituent concentration (A), constituent concentration adjusted for total particulate matter (B), and constituent residuals (C). Al, Aluminum; BC, black carbon; Br, bromine; Ca, calcium; Cl, chlorine; Cu, copper; Fe, iron; K, potassium; Mn, manganese; Na, sodium; Ni, nickel; Pb, lead; PM_2.5, particles with aerodynamic diameters less than 2.5 µm; S, sulfur; Se, selenium; Si, silicon; Ti, titanium; V, vanadium; Zn, zinc.

The results were fairly consistent across the different methods that were used to evaluate the association between constituents and ischemic stroke. In all analyses that accounted for PM_2.5, the strongest associations were found for black carbon and nickel, and there was no increased risk associated with sodium or chloride. Although sulfur represents a large proportion of PM_2.5, the greatest harm is seen for constituents that have lower concentrations. Compared with models with constituent residuals, models further adjusted for PM_2.5 did not have improved precision and slightly altered the relative ranking of the different constituents. Compared with models with constituent concentration and PM_2.5, the models with constituent residuals adjusted for PM_2.5 resulted in estimates with a similar relative ranking and smaller variance. When we stratified by warm versus cool season, the results for each constituent were not materially different. Because fireworks may cause a spike in manganese and potassium (15), we conducted a sensitivity analysis excluding data from July 4 and New Year's Eve, and the results for all model options were not materially altered.

Constituent concentration

In models in which PM_2.5 was ignored, several constituents were associated with a higher stroke risk. The strongest associations were seen for black carbon, nickel, and sulfur (Figure 1A).

Constituent proportion

The estimates for constituent proportion were unstable. Consistent with results using other approaches, the estimates for nickel and vanadium were high, but the relative ranking of the coefficients for other constituents differed from other approaches (Web Table 1). One may expect that PM_2.5 will be uncorrelated with constituent proportion and therefore represent the impact of PM_2.5. However, because it is computed as the quotient of constituent concentration and PM_2.5, by definition, there is usually a strong inverse correlation between PM_2.5 and constituent proportion (Table 5). Moreover, it seems implausible that the risk of health outcomes is attributable to the proportion of PM_2.5 mass rather than the absolute level of the constituent. Therefore, this option is not recommended.

Interaction between constituent concentration (or constituent proportion) and PM_2.5 mass

There is no statistical evidence that the association between PM_2.5 and stroke risk is modified by a particular constituent composition (Web Table 2). The estimated association between PM_2.5 and stroke risk differs widely, depending on which constituents and interactions are included in the model.

Constituent concentration adjusting for PM_2.5 mass

Concordant with results from other models, higher levels of black carbon, nickel, and vanadium were associated with higher stroke risk (Figure 1B). In the model with constituent concentration alone, higher levels of sulfur were associated with a higher stroke risk, but this association is much lower after adjustment for PM_2.5. Among the constituents included in this example, sulfur contributed the largest proportion to total mass and was highly correlated with fluctuations in daily PM_2.5 (ρ = 0.88; Table 3). Therefore, it is unclear whether adjustment for PM_2.5 correctly accounted for confounding or whether it inadvertently overadjusted for factors that may be highly correlated with PM_2.5 but that are also inherently toxic. Instead of the model including sulfur and PM_2.5, the estimate for sulfur in a model adjusted for non-ammonium sulfate mass resulted in an estimate that was extremely similar because PM_2.5 and non-ammonium sulfate mass were highly correlated (ρ = 0.94).

Constituent residual

In an analysis using the residuals from the regression of a constituent on PM_2.5, the coefficient represents the impact of higher levels of a specific constituent while holding PM_2.5 constant (Figure 1C). Consider the coefficients for nickel and vanadium, transition metals hypothesized to increase stroke risk, and sodium, a constituent that presumably has no impact on stroke risk. If PM_2.5 is held constant, higher levels of harmful constituents equate to lower levels of harmless ones, so the odds ratios for nickel (odds ratio = 1.09) and vanadium (odds ratio = 1.05) are greater than 1; on the other hand, higher levels of harmless constituents equate to lower levels of toxic ones, so the odds ratio for sodium (odds ratio = 0.90) is less than 1. Further adjustment for PM_2.5 resulted in similar, though slightly weaker, coefficients.

Although the estimates were similar, they were not identical to those from the models adjusted for PM_2.5. Because we found that the association between PM_2.5 and stroke onset was linear on the logit scale, we wanted to account for the linear effect of PM_2.5 in our evaluation of constituents and stroke risk. Therefore, we calculated the residuals using linear regression with 2 continuous terms. This model assumed constant variation in the dependent variable across levels of the independent variable (homoscedasticity), but in this data set, there was greater variation in the constituent residuals at lower levels of PM_2.5 because many of the data were near or below the detection limit when the air is clean (i.e., low levels of PM_2.5). Additionally, diagnostics indicated that there might have been deviations from linearity at the extremes of the distribution, which could explain the slight differences between the coefficients for these models. For instance, it is possible that there are abrupt spikes in some constituents that are not related to the PM_2.5 level on a given day, resulting in a poor fit for the linear model used to create the residuals. Alternatively, in other settings, this may be due to confounding by seasonal variation. We used the time-stratified case crossover approach, which compared exposure levels within month, so the relevant assessment of the fit of the residual model was conducted for each month. However, different assessments may be more appropriate for studies using other regression model specifications.

PM_2.5 residual

In an analysis using the residuals from regressing PM_2.5 on a constituent, the results reflected the increased stroke risk associated with higher levels of PM_2.5 independent of the impact of that specific constituent. For instance, on days with similar levels of vanadium, there was a 10% higher stroke risk associated with an IQR increase in PM_2.5 (vs. 14% when we used PM_2.5, presumably because of less toxic constituents in the PM_2.5); on days with similar sodium levels, there was a 17% increased stroke risk associated with every IQR increase in PM_2.5 (presumably because there were more harmful constituents).

DISCUSSION

In the present article, we illustrated the use of several options for modeling the association between constituents and health outcomes. In our study, we used conditional logistic regression to evaluate the association between constituents and the onset of ischemic stroke, but the considerations for selecting an appropriate parameterization are also relevant for analyses that use linear regression to evaluate the impact of constituents on continuous outcomes and analyses that use source apportionment methods or model the joint impact of several constituents. These considerations are also pertinent in studies of the long-term impact of constituents on health outcomes and apply to Poisson regression and other statistical models.

Although many constituents represent negligible contributions to total PM_2.5, we detected associations between several constituents and stroke risk because constituents with a small mass may still have high toxicity on their own or in combination with other copollutants. Many constituent concentrations are driven by the same meteorological conditions, resulting in a high correlation between daily fluctuations in constituent concentrations. Furthermore, a constituent may serve as a tracer for a prevalent source. For instance, even though the average nickel concentration was only 2.3 ng/m³, representing only 0.02% of PM_2.5 in our region, nickel serves as a tracer of oil combustion, a large contributor to PM_2.5. Therefore, the estimates in the health outcomes model represented the impact of the constituent of interest and the impact of related constituents. Similarly, adjustment for PM_2.5 accounted for potential confounding by PM_2.5 and by other constituents that covary with PM_2.5. For instance, adjustment for PM_2.5 led to a lower estimate for the impact of sulfur because these factors are strongly correlated. The lower estimate from the PM_2.5-adjusted model is due to incorrect overadjustment rather than an accurate portrayal of the impact of sulfur independent of PM_2.5. To mitigate this concern, it may be preferable to adjust for non-ammonium sulfate mass rather than PM_2.5.

This raises an issue that cannot be fully addressed with statistical methods. Because a constituent is emitted from several sources and a single source emits several pollutants, we often cannot distinguish between the independent toxicities of correlated constituents in an observational study. Findings on health risks associated with a given constituent may represent the toxicity of that constituent, it may serve as a marker of other constituents that covary with the constituent of interest (confounding), or it may represent the combination of the constituent's independent toxicity and its interaction with covarying constituents. Therefore, a study of constituents should be guided by a solid theoretical framework and experimental evidence.

Measurement errors for constituents are usually greater than those for PM_2.5. Furthermore, the residuals created on these mismeasured constituents lead to greater variance of the residuals from the linear regression models. These issues may influence point estimates and standard errors for the parameter in a health outcome model. Furthermore, the degree of measurement error may differ by pollutant. Therefore, the coefficients for some constituents may be stronger simply because they are measured with less error than other constituents. During the 7 years of our study, there was a large variation in the number of days on which a constituent could not be detected by the instrument (Table 2).

The association between pollution and health outcomes may display different spatial and seasonal patterns for different constituents (16). Additionally, the mechanism linking ambient pollution and health outcomes may vary by constituent, so the relevant time lags may differ by constituent (5, 8). Stratifying by season and by region and assessing different lag periods may help further characterize the association of interest. Modeling of a potential confounder, such as temperature, will likely have a different lag structure for each pollutant, raising issues about the correct model specification in the presence of temporal misalignment. New methods have been developed to incorporate several distributed lag functions and thereby reduce such errors, although they have not been largely adapted in recent studies (17).

Exposure misclassification in pollution studies involves a combination of 2 types of measurement error (18). Berkson-type errors occur when spatially averaged ambient pollutant levels that reflect the average level of exposure in the population are used as a proxy for each individual's personal exposure and yield no or little bias but decrease statistical power. On the other hand, classical measurement errors are due to differences between average personal exposure and the true ambient level. They tend to bias associations toward the null, with greater attenuation for constituents with higher error variance of the surrogate relative to the variance of the true exposure. In a linear model with 2 correlated pollutants, only one of which has a true harmful effect, the second (harmless) pollutant will generally only appear harmful if there is a strong negative correlation between the measurement errors of the 2 pollutants.

In addition to outdoor concentration levels, personal exposure levels are influenced by time spent indoors, residential characteristics, and indoor sources. For constituents with indoor sources, using fixed monitors as a proxy of personal exposure induces classical error that generally results in an underestimation of the exposure-disease association. A recent report (19) showed that the indoor–outdoor relations among constituents varied substantially across pollutants. Applicable to our illustrative example, the authors compared several measurements in a Boston sample and showed that for pollutants with strong indoor sources (e.g., calcium and silicon), monitor concentrations may be a weaker proxy than for pollutants dominated by outdoor sources (e.g., sulfur, selenium, and vanadium).

It is difficult to anticipate the impact of measurement error due to the lack of empirical evidence on the magnitude of these errors and how the components of error covary across pollutants. Future research is necessary to examine the multivariate error structure across constituents within a city, to examine the implications of such measurement error on studies of health outcomes, and to develop methods for including measurements below the level of detection and incorporating measurement uncertainty into health outcome models.

Several studies used a hierarchical approach to quantify how the association is modified by season- and region-specific particle composition (7, 9, 10). This method could not be carried out in our data set because it requires data from multiple regions with sufficient variation in PM_2.5. Furthermore, this approach as applied to date primarily addresses the impact of season-specific average particle composition and does not capture the biologic relevance of daily variability in PM_2.5 composition.

Others have used factor analysis/source apportionment methods to convert daily levels of constituents into daily source factor scores to identify combinations of pollutants (source contributions) responsible for adverse health outcomes, such as traffic pollutants or pollution from oil combustion (20, 21). These studies modeled the impact of source concentrations (similar to our “constituent concentration” approach) or the impact of sources adjusting for total PM_2.5 (similar to our approach of “constituent concentration adjusting for PM_2.5 mass”). However, the factor loadings for the ostensibly identical source tend to differ across cities. Therefore, similarly labeled sources in different studies do not represent identical exposures. Moreover, this approach still requires consideration of confounding by PM_2.5.

In the present study, we showed several options for accounting for confounding by PM_2.5 in studies in which the impact of constituents on health outcomes are evaluated. Residual methods are particularly useful for isolating the variation in exposure due to a constituent from the variation in PM_2.5. Among the model options that provide valid estimates by accounting for confounding by PM_2.5, each approach involved different considerations and different interpretations but yielded results with similar relative rankings.