R/EBcoexpress: an empirical Bayesian framework for discovering differential co-expression

Abstract

Summary: R/EBcoexpress implements the approach of Dawson and Kendziorski using R, a freely available, open source statistical programming language. The approach identifies differential co-expression (DC) by examining the correlations among gene pairs using an empirical Bayesian approach, producing a false discovery rate controlled list of DC pairs. This interrogation of DC gene pairs complements but is distinct from differential expression analyses, under the general goal of understanding differential regulation across biological conditions.

Availability and implementation: R/EBcoexpress is freely available and hosted on Bioconductor; a source file and vignette may be found at http://www.bioconductor.org/packages/release/bioc/html/EBcoexpress.html

Contact: DrJADawson@hotmail.com or kendzior@wisc.edu

1 INTRODUCTION

The freely available R (R Development Core Team, 2009) package R/EBcoexpress implements the algorithm of Dawson and Kendziorski (2011), an empirical Bayesian approach for identifying differentially co-expressed (DC) gene pairs. Microarray and related high-throughput genomic experiments seek to identify genes that vary across biological conditions. This is often accomplished by identifying genes with changes in mean expression level, so-called differentially expressed (DE) genes [for a review, see Newton et al. (2007)]. Although useful, major biological insights have resulted far less frequently than originally expected (Pollack, 2007; Zilliox and Irizarry, 2007). This is in part because diseases can manifest due to a de- or re-regulation of genes that does not significantly affect each gene's average expression. Thus, identifying other types of differential regulation may increase our ability to distinguish between groups and provide insight into their distinct etiologies (for a discussion, see de la Fuente, 2010). We focus on DC gene pairs, where ‘co-expression’ refers to some measure of correlation.

Early methods for identifying DC gene pairs conduct pair-specific tests for selected pairs within a condition, identify those pairs that are strongly or significantly co-expressed, and declare pairs to be DC if they are co-expressed in one condition but not another (Watson, 2006; Choi et al., 2005). Unfortunately, these approaches sacrifice considerable power by conducting analyses separately within condition and they do not provide probabilistic statements regarding the likelihood that a particular pair is DC. These issues are largely addressed by Lai et al., 2004, but their extension of the traditional F-test to accommodate changes in means and correlations has been shown (Dawson and Kendziorski, 2011) to be overly conservative. Also, since their test statistic simultaneously quantifies DE and DC, selection of a pair provides no information about whether the pair is DE, DC or both.

The approach implemented in EBcoexpress provides a false discovery rate (FDR) controlled list of significant DC gene pairs without sacrificing power. It is applicable within a single study as well as across multiple studies. For more information on the underlying theory, simulations and an application, please see our original paper in Biometrics. For a fully worked example with details at each step of the analysis, please see the vignette that accompanies the R/EBcoexpress package.

2 FEATURES

In our setting, gene pairs are either equivalently co-expressed (EC) or DC. When there are three or more conditions, there are many ways to be DC and hence there will be multiple DC ‘classes’. R/EBcoexpress calculates posterior probabilities for all EC/DC classes by assuming a Bayesian framework for the generation of correlations across conditions for all pairs and estimating the hyperparameters of that framework using an Expectation-Maximization (EM) algorithm. We highlight a few aspects of this process:

Customizable correlation computations: The analysis requires correlations for some set of gene pairs; we outsource the computations to C for efficiency. Although Pearson's correlation can be used, R/EBcoexpress defaults to the biweight midcorrelation, which is similar to Pearson's statistic but is robust to outliers.

Customizable FDR control: R/EBcoexpress outputs a (no. of gene pairs)-by-(no. of classes) matrix of posterior probabilities for all EC/DC classes. The EC posterior probabilities may be used to generate a ‘hard threshold’ version of FDR-control; however, as this approach is somewhat more conservative than necessary and hence less powerful, the package provides a function that provides ‘soft threshold’ FDR-control which controls the posterior expected FDR. In more complex analyses, the availability of posterior probabilities for each DC class allows further assortment and inference among the DC pairs.

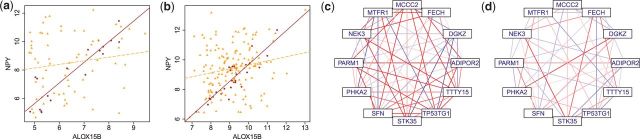
Visualization: R/EBcoexpress provides graphical representations of co-expression exhibited by the data. The user may call up expression data for a given pair and superimpose a ‘robust’ regression line (i.e. one calculated from only those values used in a biweight midcorrelation calculation) for each class. The user may also examine DC at the network level via graph structures. This functionality uses the package R/igraph, but we have simplified the interface so that meaningful DC networks may be generated with ease (Fig. 1).

Fig. 1.

Expression values for a gene pair ALOX15B~NPY deemed to be DC by our paper's meta-analysis are plotted using data from two prostate cancer datasets in (a) and (b). Non-cancerous subjects are in purple (dots) and cancerous subjects are in orange (triangles). A ‘robust’ regression line is superimposed for each condition (cancerous is dashed). In (c) and (d), relationships within and across conditions for a network of 12 genes greedily built up from a seed of PARM1 are shown. Deepness of color indicates strength of evidence of DC, where correlations of magnitude ≥0.5 are given the deepest hue of red (+) or blue (−); magnitudes ≤0.25 have been hidden

3 ANALYSIS INPUTS AND OUTPUTS

A single-study analysis requires a (no. of genes)-by-(no. of samples) matrix of expression values. These values should be normalized in some manner; we suggest background normalization but not quantile normalization, as the latter can produce unpredictable alterations of correlational structure across samples (Qiu et al., 2005). We prefer RMA (Bolstad et al., 2003) for background correction of the intensities contained in the raw (.CEL) files; median correction should follow RMA pre-processing. Lastly, the raw expression data are often returned on the log-scale after normalization. Whether or not this is acceptable depends on the investigator: if associations between raw measurements are of interest, anti-log the data; if associations on the log scale are instead important, remain on the log₂ scale.

After EM computations are complete, as aforementioned every analysis produces a (no. of gene pairs)-by-(no. of classes) matrix of posterior probabilities for all EC/DC classes which may be used for FDR-control and, in analyses where there are three or more biological conditions, the availability of posterior probabilities for each DC class allows further assortment and inference among the DC pairs. This output may inform visualization choices as previously described. Additionally, a function is provided that returns the number of times each gene is included in a DC pair, given a threshold; this information may be used to identify genes that exhibit ‘differential hubbing’ (Hudson et al., 2009).

4 SUMMARY

R/EBcoexpress provides a simple interface inside the R statistical programming language for the identification and exhibition of DC gene pairs.

Funding: This work was funded in part by R01 GM076274.

Conflict of Interest: none declared.