Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Nov 9;2:830. doi: 10.1038/srep00830

High temperatures-related elderly mortality varied greatly from year to year: important information for heat-warning systems

Yuming Guo 1,2,a, Adrian G Barnett 1, Shilu Tong 1
PMCID: PMC3494010  PMID: 23145322

Abstract

We examined the variation in association between high temperatures and elderly mortality (age ≥ 75 years) from year to year in 83 US cities between 1987 and 2000. We used a Poisson regression model and decomposed the mortality risk for high temperatures into: a “main effect” due to high temperatures using lagged non-linear function, and an “added effect” due to consecutive high temperature days. We pooled yearly effects across both regional and national levels. The high temperature effects (both main and added effects) on elderly mortality varied greatly from year to year. In every city there was at least one year where higher temperatures were associated with lower mortality. Years with relatively high heat-related mortality were often followed by years with relatively low mortality. These year to year changes have important consequences for heat-warning systems and for predictions of heat-related mortality due to climate change.

There is increasing public health concern for heat-related mortality worldwide as the global climate is changing1. The Intergovernmental Panel on Climate Change (IPCC) has concluded that without increased investments in countermeasures heat waves will cause increased adverse health impacts, including heat-related mortality2. Urban areas may be particularly vulnerable to heat waves because of high concentrations of susceptible population groups and urban heat islands3,4.

Many studies have shown that high temperatures are related to non-accidental deaths5,6 and cause-specific deaths7,8,9,10,11, and other studies have specifically examined the impacts of heat waves12,13,14. Gasparrini and Armstrong (2011) decomposed the effects of heat into two parts: a “main effect” related to the independent effects of high temperatures, and an “added effect” due to heat waves. Results showed that the “main effect” contributed the most to the excess risk of mortality, while a smaller added effect appeared during heat waves. Rocklöv et al. (2010) found an added effect of heat waves with two or more days above the 98th percentile of temperature. Anderson and Bell (2011) examined the modification of heat wave characteristics (e.g., intensity, duration, and timing in summer) on mortality. They found higher risks for heat waves that were more intense, longer, or occurred in early summer.

Epidemiological studies of heat-related mortality could be used by decision makers to design an early warning system for high temperatures, by establishing a heat threshold and the expected increase in deaths above the threshold. Epidemiological studies are also useful for providing a baseline from which to estimate the potential health effects of climate change. However, these previous epidemiological studies gave estimates for the whole study period, and ignored the potential variability in risks from year to year. Risks may vary from year to year because of differences in the at-risk population (e.g., more elderly people), or because of increased adaptation over time15,16.

Temperature-related deaths are more pronounced in the elderly as they are more sensitive to temperature8,17. The thermal regulation system weakens with age; skin sensory perception may diminish and thermal homeostasis may decline18. This means the elderly are not as physiologically able to get relief from cold and hot temperatures. A higher incidence of pre-existing cardiovascular and respiratory disease in the elderly is another reason why they are vulnerable to temperature extremes19. We therefore restricted our analysis to the elderly as they are a high risk group who will have strong associations between high temperatures and death, which gave us the opportunity to examine how these associations vary over time and space.

Results

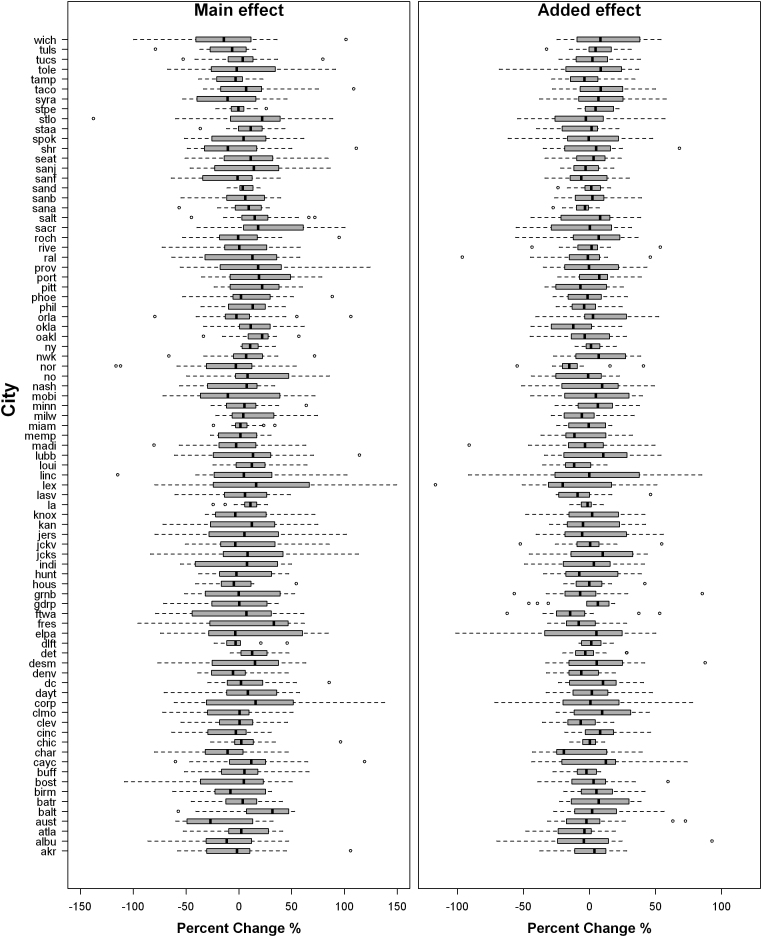
The yearly variability for both the main effect of high temperatures and the added effect is shown for each city in Figure 1. In most cities there was an extremely wide variation in the yearly estimates, and in almost every city both the main and added yearly effects were sometimes negative. The range in the main effects was greatest in Lexington, where the percentage change in yearly elderly mortality ranged from −80% to 150%. The smallest range was in San Diego, where the percentage change in the added effect ranged from −57% to 29%.

Figure 1. Boxplots of the yearly associations between high temperatures and elderly mortality by city between 1987 and 2000.

Figure 1

Open in a new tab

The main effect is the percent change in mortality for an increase in temperature from 75th percentile to the median of high temperature days. The added effect is the percent change in mortality on high temperature days. There are 14 estimates per city. City abbreviations are explained in Supplementary Table S1.

We found a similarly large variation in the associations at the regional level (Table 1). In every region both the ranges in the main and added effects included zero, meaning that in some years high temperatures increased mortality, but in other years high temperatures decreased mortality. The range in estimates at a national level also included zero.

Table 1. Summary statistics for the estimated yearly high temperature effects on elderly mortality by region between 1987 and 2000. The main effect is the percent change in mortality for an increase in temperature from 75th percentile to the median of high temperature days. The added effect is the percent change in mortality on high temperature days. There are 14 estimates for every region. All cells show the percent change in mortality.

  Main effect Added effect
Region Min 25% Median 75% Max Min 25% Median 75% Max
Industrial Midwest –8.1 0.5 6.5 8.9 16.4 –6.9 –5.1 –2.2 –0.4 7.8
North East –16.4 –1.4 5.5 14.2 19.1 –9.8 –5.8 0.0 7.0 20.7
North West –8.5 –1.1 6.6 15.3 32.3 –16.1 –3.5 1.7 3.6 14.2
South East –10.9 –6.4 0.5 7.6 12.9 –11.3 –3.4 0.4 7.0 8.7
South West –12.9 –5.7 0.0 11.7 32.4 –16.6 –8.2 –2.6 5.5 7.9
Southern California –6.9 4.8 7.0 13.1 15.9 –9.8 –4.2 –2.0 0.6 11.1
Upper Midwest –30.2 –1.5 1.4 9.7 38.3 –14.7 –0.7 5.8 15.1 22.8
National –0.3 2.6 4.1 7.7 12.2 –5.3 –1.4 0.1 0.6 2.2
Open in a new tab

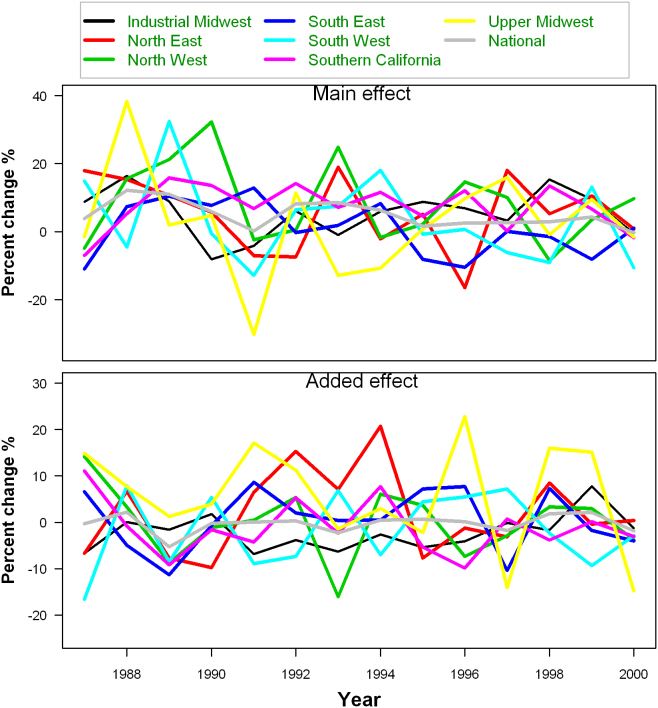
The estimated percent increase in elderly mortality over time by region is in Figure 2. There was a great variation from year to year in both the main and added effects of high temperatures. In general, years with relatively high increases in mortality were often followed by years with relatively low increases, and vice versa.

Figure 2. Mean associations between high temperatures and elderly mortality by region between 1987 and 2000 using a univariate meta-analysis.

Figure 2

Open in a new tab

The main effect is the percent change in mortality for an increase in temperature from 75th percentile to the median of high temperature days. The added effect is the percent change in mortality on high temperature days.

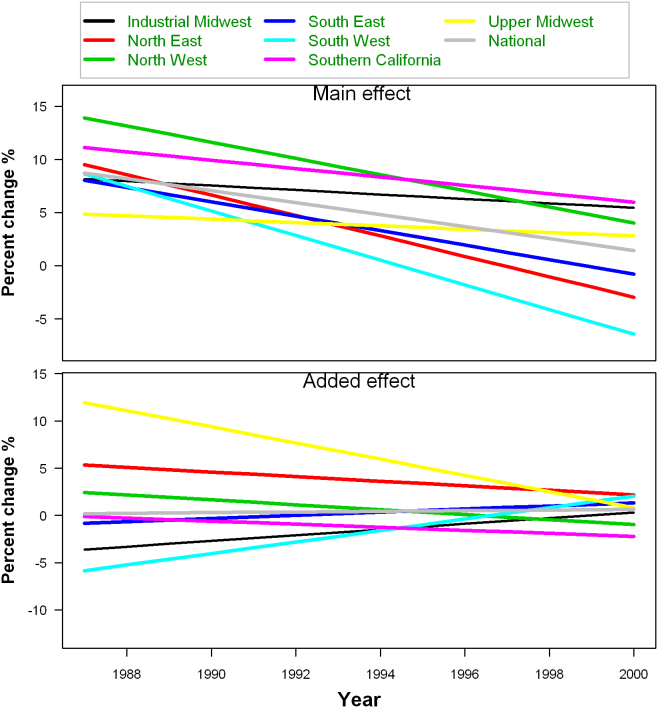
According to the Deviance Information Criteria, the Bayesian hierarchical model fit was not improved by using a non-linear trend over time, so the combined estimates were based on a linear time trend. These linear trends by region are in Figure 3. The main effect declined over time in all of the regions. The added effects moved closer to zero over time in most of the regions.

Figure 3. Trends over time in the associations between high temperatures and elderly mortality by region using a Bayesian hierarchical model.

Figure 3

Open in a new tab

The main effect is the percent change in mortality for an increase in temperature from 75th percentile to the median of high temperature days. The added effect is the percent change in mortality on high temperature days.

Discussion

This study estimated the yearly risks of elderly mortality associated with high temperatures. Both the main and added effects varied greatly from year to year in every city and region. In every city and region there were years where high temperatures were associated with increases in mortality, and other years where high temperatures were associated with decreases in mortality.

Such strong year-to-year variations have important consequences for heat-warning systems, which give advanced warning of dangerous temperatures20,21,22. These systems are designed based on historical observations between temperature and death in a city, and aim to find a temperature threshold above which spikes in deaths occur. They are based on average risks over multiple years and do not account for the year to year variations in risk shown here. This means that these systems are likely to suffer false positives, as in some years the anticipated spike in deaths will not occur. They may also suffer false negatives, as the spike in deaths could be greater than expected or occur at a lower temperature threshold. False positives have financial implications, as much of the preventive actions planned under the current system (such as freeing-up hospital beds) are wasted. False positives may also undermine confidence in the system if the warnings are perceived to be too frequent and without any real need23. We suggest that people who run heat-health warning systems should consider the yearly variability on elderly mortality, and update their systems by each summer.

The great variation in temperature effects shown here also has implications for estimating the future health effects of high temperatures due to climate change24. These projections have been based on associations between temperature and health that ignore the year to year variability in risks. Although the estimated averages from these projections are still valid, any confidence intervals will be too narrow as they missed the uncertainty demonstrated here.

There was some visual evidence that years with relatively high heat-related mortality were followed by years with relatively low mortality (Figure 2). This could be because of changes over time in the susceptible pool (or mortality displacement)15,25,26. A summer with a relatively high level of mortality means less people susceptible to heat-related mortality in the following summer. Studies have also shown that high winter mortality leads to lower mortality (mortality displacement) in the following summer15,25,26, as well as high summer mortality leading to lower winter mortality27.

The main high temperature effect was generally greater than added heat wave effect (Figure 3). The main effect was higher in the Northwest and South California, while the added effect was higher in Northeast and Upper Midwest. These findings are con-sistent with other studies of heat waves and high temperatures28,29. For example, Anderson and Bell (2011) found that heat waves had smaller effects on mortality in the South.

There was a decline in the main effect of high temperature-related death from 1987 to 2000 in all regions (Figure 3). This is consistent with previous US studies7,30. An increased use of air conditioning may be an underlying reason for this reduction in heat-related mortality7,30,31. US studies have shown that associations between high temperatures and mortality were related to the level of air conditioning use28,32,33, and that the use of air conditioning steadily increased in all areas of the United States during 1980 and 20007.

We defined high temperature days as two or more consecutive days with temperatures above the 90th percentile during each warm season (May 1 to September 30). Using a stricter definition (e.g., 2 or more consecutive days with temperatures above the 95th percentile), there were often no high temperature days in some cities. However, the results of our study are consistent with a previous study34, which showed that the main effect of high temperatures is greater than the added heat wave effect.

We did not consider the variability in the effect of temperature according to either cumulative effects or by the timing or intensity of the high temperatures. Previous studies have shown that individual days of extreme heat increased the risk of mortality35,36, and that the added effect of high temperature on mortality was greater for consecutive high temperature days compared with non-consecutive high temperature days34,37. Anderson and Bell (2011) found that a heat wave's effect on mortality varied by its intensity, duration, and timing in the season37.

We did not control for air pollution as a previous study found that the association between heat and mortality in the United States was independent of air pollution29. Other studies have also not controlled for air pollution when assessing the impact of temperature on mortality25,34,37. Exposure to air pollution has very different biological effects compared with exposure to high temperature, and therefore we would expect them to have independent effects.

The model was fitted well for the data as judged by residuals (see Supplementary Fig. S1 online). We changed the degrees of freedom for smoothing for time, and the degrees of freedom of the splines for temperature and lagged temperature. The results were broadly similar (not shown).

We examined the main and added effects using different high temperature definitions (95th with 2 consecutive days of duration). Both the main and added effects of high temperature increased if the 95th percentile was used compared with the 90th percentile (see Supplementary Fig. S2 online).

This study has some strength. The effects of high temperatures on elderly mortality are highly variable from year to year throughout the US. This finding is important from a public health perspective, because it has implications for heat-warning systems and projections of the impact of climate change. We used a flexible non-linear model to capture the main effects of high temperatures, and consider lagged effects up to 10 days. We used a large sample of 83 cities with a wide geographic spread across the United States.

This study has some limitations. We only used 14 years of data. A longer period would be able to better examine the changes over time in temperature-related mortality. To accurately estimate the autocorrelation in the estimates shown in Figure 2 (which we suspect would be negative) would require at least 50 years of data38. We did not have individual exposure data, and so assumed a common exposure to temperature for people in the same city. However, a study reported that temperatures from one monitoring site or averaged temperature from a network of sites are the same as spatial temperatures for assessing city-wide temperature effects on mortality39.

In conclusion, both the effects of high temperatures on elderly mortality varied greatly from year to year, making it difficult to predict the health effects of heat in any one year. There was a gradual reduction in high temperature-related elderly mortality. Cities using heat warning systems need to be aware of both the long-term trends in heat-related mortality and the year to year variations. We recommend that cities evaluate the performance of their warning systems at the end of every summer. Specifically they should check for false positives and false negatives, and verify that the temperature threshold estimated from historical data remains valid.

Methods

Data

We used the data from the publicly available National Morbidity and Mortality Air Pollution Study (NMMAPS) study40,41. This data comprises daily weather, air pollution and mortality for 108 cities in the United States from 1987 to 2000. Data on maximum and minimum temperatures were from the National Climatic Data Center, and daily mortality counts were from the National Center for Health Statistics. Daily non-external deaths counts were for residents, excluding injuries and external causes. More information is available from the NMMAPS web site (http://www.ihapss.jhsph.edu).

We excluded small cities (population under 200,000) and cities with more than 0.5% missing data for air or dew point temperature, which left 83 cities. We stratified the cities into seven regions (Industrial Midwest, North East, North West, South East, South West, Southern California, and Upper Midwest) (see Supplementary Table S1 online). We limited analyses to elderly morality (age ≥ 75 years) in the warm season (1 May–30 September) as we were interested in the effects of heat on a susceptible population. Mean daily temperature, calculated as the average of daily maximum and minimum temperatures, was used as the main exposure variable.

Data analysis

A city-specific Poisson regression model was used to examine each year's high temperature effect on elderly mortality. In the city-specific model, the heat effects were divided into a “main effect” and an “added effect” according to a previous study34. These two estimates were then combined across cities using a univariate meta-analysis to create yearly estimates for each region and for the entire US. The city-level estimates were also combined using a Bayesian meta-analysis in order to estimate trends over time.

To examine the city-specific main effect and added heat wave effect in the warm season, we used the following Poisson regression model in each city and year:

Yt ~ Poisson(μt),

graphic file with name srep00830-m1.jpg

where Yt is the observed daily death count on day t; α is the intercept; Tt,l is a matrix obtained by applying the distributed lag non-linear model (DLNM) to mean temperature, β is vector of coefficients for Tt,l, and l is the lag days; S(t, 3) is natural cubic spline of time, with 3 degrees of freedom for time (1 May–30 September) used to control for trends and seasonal patterns in mortality; HTt is a categorical variable for high temperature days on day t, HTt = 0 if day t was a non-high temperature day, HTt = 1 if day t was a high temperature day (defined below); DOWt is a categorical variable for day of the week, and λ is vector of coefficients.

We modelled the main effect of high temperatures on day t using the term βTt,l which is fitted using a DLNM. A DLNM is a two-dimensional spline which models the main effect of heat along dimensions of temperature and lags. DLNMs overcome the fact that temperatures within a couple of days are strongly correlated by constraining the lagged (delayed) effects of temperatures using a spline42. A cubic spline with 5 degrees of freedom was used to model the lagged (delayed) effect of temperature on mortality up to 10 days34. A cubic spline with 3 degrees of freedom was used to model a non-linear association between temperature and mortality. We used the DLNM to give an estimate of the overall temperature effect by summing over lag days43. This overall estimate was the percent change in mortality between the median temperature among high temperature days against the 75th percentile of temperature in the warm season.

The added effect of high temperatures was modelled by υHTt. We defined high temperatures as two or more than two consecutive days with temperature above the 90th percentile for each city during each warm season in each city (May 1 to September 30).

To examine the variation in the high temperature effects on mortality from year to year, we pooled the yearly national and regional high temperature effects (main effect and added effect separately) across cities using a univariate meta-analysis with a random effect for each city. We plotted the pooled yearly national and regional main effects and added effects from 1987 to 2000.

We used a Bayesian hierarchical model to estimate trends over time for each region and nationally by combin-ing the yearly estimated effects of high temperatures within each city and incorporating the estimates' variance44. Each city was given a random intercept to model its mean heat effect, and a random linear effect of time to model linear trends over time. A sensitivity analysis was conducted to examine random non-linear effects of time. Model fit was assessed using the Deviance Information Criteria45. Bayesian hierarchical models have been used to com-bine estimated effects across communities in air pollution and temperature studies7,37.

Sensitivity analyses were carried out on the parameters for the city-specific model to test the robustness of the results to our assumptions concerning the temperature-mortality relationship. We modified the degrees of freedom for smoothing time from 4 to 8, and the degrees of freedom for the splines for temperature from 4 to 8, and for the lag from 3 to 8.

To test the sensitivity of our results to the definition of high temperatures, an alternative high temperature definition was used: 95th percentile for at least two consecutive days.

The residuals were examined to evaluate the adequacy of the city-specific models. The R software (version 2.11.0, R Development Core Team 2009) was used to fit city specific models. The “dlnm” package of R software was used to create DLNM. The “metafor” package of R software was used to fit univariate meta-analyses. WinBUGS software (version 1.4) was used to fit the Bayesian hierarchical model.

Author Contributions

YG designed the study and directed its implementation, including data analysis, writing the paper, and quality assurance and control. AB helped supervise the study's data analysis and methods, review and edit the paper. ST helped conduct the quality assurance and control, review and edit the paper.

Supplementary Material

Supplementary Information

Supplementary Information

srep00830-s1.pdf (96.5KB, pdf)

Acknowledgments

The authors thank the Department of Biostatistics at the Johns Hopkins Bloomberg School of Public Health and the Health Effects Institute for making the National Morbidity and Mortality Air Pollution Study data publicly available. YG is supported by the QUT Postgraduate Research Award (QUTPRA); ST is supported by a NHMRC Research Fellowship (#553043).

References

  1. Gosling S. N., Lowe J. A., McGregor G. R., Pelling M. & Malamud B. D. Associations between elevated atmospheric temperature and human mortality: a critical review of the literature. Climatic Change 92, 299–341 (2009). [Google Scholar]
  2. IPCC. Climate change 2007: impacts, adaptation and vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. (Cambridge University Press, 2007). [Google Scholar]
  3. Luber G. & McGeehin M. Climate change and extreme heat events. Am J Prev Med 35, 429–435 (2008). [DOI] [PubMed] [Google Scholar]
  4. Kinney P. L., O'Neill M. S., Bell M. L. & Schwartz J. Approaches for estimating effects of climate change on heat-related deaths: challenges and opportunities. Environmental Science & Policy 11, 87–96 (2008). [Google Scholar]
  5. Guo Y., Barnett A. G., Pan X., Yu W. & Tong S. The impact of temperature on mortality in Tianjin, China: a case-crossover design with a distributed lag nonlinear model. Environmental health perspectives 119, 1719–1725 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. McMichael A. J. et al. International study of temperature, heat and urban mortality: the 'ISOTHURM' project. Int J Epidemiol 37, 1121–1131 (2008). [DOI] [PubMed] [Google Scholar]
  7. Barnett A. G. Temperature and cardiovascular deaths in the US elderly: changes over time. Epidemiology 18, 369–372 (2007). [DOI] [PubMed] [Google Scholar]
  8. Guo Y., Punnasiri K. & Tong S. Effects of temperature on mortality in Chiang Mai city, Thailand: a time series study. Environmental health 11 (36) (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Guo Y. et al. A large change in temperature between neighbouring days increases the risk of mortality. PloS one 6, e16511 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Tian Z., Li S., Zhang J., Jaakkola J. J. & Guo Y. Ambient temperature and coronary heart disease mortality in Beijing, China: a time series study. Environmental health 11, (56). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Yu W. et al. Time course of temperature effects on cardiovascular mortality in Brisbane, Australia. Heart 97, 1089–1093 (2011). [DOI] [PubMed] [Google Scholar]
  12. Weisskopf M. G. et al. Heat wave morbidity and mortality, Milwaukee, Wis, 1999 vs 1995: an improved response? Am J Public Health 92, 830–833 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kaiser R. et al. The effect of the 1995 heat wave in Chicago on all-cause and cause-specific mortality. Am J Public Health 97, 158–162 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Vandentorren S. et al. Mortality in 13 French cities during the August 2003 heat wave. Am J Public Health 94, 1518–1520 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Stafoggia M., Forastiere F., Michelozzi P. & Perucci C. A. Summer temperature-related mortality: effect modification by previous winter mortality. Epidemiology 20, 575–583 (2009). [DOI] [PubMed] [Google Scholar]
  16. Sheridan S. C. & Kalkstein A. J. Seasonal variability in heat-related mortality across the United States. Natural Hazards, 1–15 (2010). [Google Scholar]
  17. Yu W. et al. Daily average temperature and mortality among the elderly: a meta-analysis and systematic review of epidemiological evidence. International journal of biometeorology 56, 569–581 (2012). [DOI] [PubMed] [Google Scholar]
  18. Collins K. J. Effects of cold on old people. British Journal Of Hospital Medicine 38, 506 (1987). [PubMed] [Google Scholar]
  19. Wyndham CH F. S. Climate and disease. S Afr Med J 53, 1051–1061 (1978). [PubMed] [Google Scholar]
  20. Hajat S. et al. Heat-health warning systems: a comparison of the predictive capacity of different approaches to identifying dangerously hot days. Am J Public Health 100, 1137–1144 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. O'Neill M. S. et al. Preventing heat-related morbidity and mortality: new approaches in a changing climate. Maturitas 64, 98–103 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hajat S., O'Connor M. & Kosatsky T. Health effects of hot weather: from awareness of risk factors to effective health protection. Lancet 375, 856–863 (2010). [DOI] [PubMed] [Google Scholar]
  23. Kovats R. S. & Kristie L. E. Heatwaves and public health in Europe. The European Journal of Public Health 16, 592 (2006). [DOI] [PubMed] [Google Scholar]
  24. Huang C. et al. Projecting Future Heat-Related Mortality under Climate Change Scenarios: A Systematic Review. Environ Health Perspect 119, 1681–1690 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Ha J., Kim H. & Hajat S. Effect of Previous-Winter Mortality on the Association between Summer Temperature and Mortality in South Korea. Environ Health Perspect 119, 542–546 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Rocklov J., Forsberg B. & Meister K. Winter mortality modifies the heat-mortality association the following summer. Eur Respir J 33, 245–251 (2009). [DOI] [PubMed] [Google Scholar]
  27. Valleron A. J. & Boumendil A. Epidemiology and heat waves: analysis of the 2003 episode in France. C R Biol 327, 1125-1141 (2004). [DOI] [PubMed] [Google Scholar]
  28. Braga A. L., Zanobetti A. & Schwartz J. The time course of weather-related deaths. Epidemiology 12, 662–667 (2001). [DOI] [PubMed] [Google Scholar]
  29. Anderson B. G. & Bell M. L. Weather-related mortality: how heat, cold, and heat waves affect mortality in the United States. Epidemiology 20, 205–213 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Davis R. E., Knappenberger P. C., Michaels P. J. & Novicoff W. M. Changing heat-related mortality in the United States. Environ Health Perspect 111, 1712–1718 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. O'Neill M. Air conditioning and heat-related health effects. Appl Environ Sci Public Health 1, 9–12 (2003). [Google Scholar]
  32. Curriero F. C. et al. Temperature and mortality in 11 cities of the eastern United States. Am J Epidemiol 155, 80–87 (2002). [DOI] [PubMed] [Google Scholar]
  33. Nunes B., Paixao E., Dias C. M., Nogueira P. & Marinho Falcao J. Air conditioning and intrahospital mortality during the 2003 heatwave in Portugal: evidence of a protective effect. Occup Environ Med 68, 218–223 (2011). [DOI] [PubMed] [Google Scholar]
  34. Gasparrini A. & Armstrong B. The impact of heat waves on mortality. Epidemiology 22, 68–73 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Baccini M. et al. Heat effects on mortality in 15 European cities. Epidemiology 19, 711–719 (2008). [DOI] [PubMed] [Google Scholar]
  36. Hajat S. et al. Impact of high temperatures on mortality: is there an added heat wave effect? Epidemiology 17, 632–638 (2006). [DOI] [PubMed] [Google Scholar]
  37. Anderson G. B. & Bell M. L. Heat Waves in the United States: Mortality Risk during Heat Waves and Effect Modification by Heat Wave Characteristics in 43 U.S. Communities. Environ Health Perspect 119, 210–218 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Huitema B. E. & McKean J. W. Autocorrelation estimation and inference with small samples. Psychological Bulletin 110, 291–304 (1991). [Google Scholar]
  39. Guo Y., Barnett A. & Tong S. Spatiotemporal model or time series model for assessing city-wide temperature effects on mortality? Environmental Research, http://dx.doi.org/10.1016/j.envres.2012.1009.1001 (2012). [DOI] [PubMed] [Google Scholar]
  40. Samet J. M., Dominici F., Zeger S. L., Schwartz J. & Dockery D. W. The National Morbidity, Mortality, and Air Pollution Study. Part I: Methods and methodologic issues. Res Rep Health Eff Inst, 5–14 (2000). [PubMed] [Google Scholar]
  41. Samet J. M. et al. The National Morbidity, Mortality, and Air Pollution Study. Part II: Morbidity and mortality from air pollution in the United States. Res Rep Health Eff Inst 94, 5–70 (2000). [PubMed] [Google Scholar]
  42. Armstrong B. Models for the relationship between ambient temperature and daily mortality. Epidemiology 17, 624–631, doi:10.1097/01.ede.0000239732.50999.8f (2006). [DOI] [PubMed] [Google Scholar]
  43. Gasparrini A., Armstrong B. & Kenward M. G. Distributed lag non-linear models. Stat Med 29, 2224–2234, doi:10.1002/sim.3940 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Everson P. J. & Morris C. N. Inference for multivariate normal hierarchical models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 62, 399–412 (2000). [Google Scholar]
  45. Spiegelhalter D. J., Best N. G., Carlin B. P. & Van Der Linde A. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 64, 583–639 (2002). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep00830-s1.pdf (96.5KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES