Skip to main content
PMC home page
Cognitive Neurodynamics logoLink to Cognitive Neurodynamics
. 2012 Jun 14;6(6):485–497. doi: 10.1007/s11571-012-9209-x

Identifying type I excitability using dynamics of stochastic neural firing patterns

Bing Jia 1, Huaguang Gu 1,2,✉
PMCID: PMC3495073  PMID: 24294334

Abstract

The stochastic firing patterns are simulated near saddle-node bifurcation on an invariant cycle corresponding to type I excitability in stochastic Morris–Lecar model. In absence of external periodic signal, the stochastic firing manifests continuous distribution in ISI histogram (ISIH), whose amplitude at first increases sharply and then decreases exponentially. In presence of the external periodic signal, stochastic firing patterns appear as two cases of integer multiple firing with multiple discrete peaks in ISIH. One manifests perfect exponential decay in all peaks and the other imperfect exponential decay except a lower first peak. These stochastic firing patterns simulated with or without external periodic signal can be demonstrated in the experiments on rat hippocampal CA1 pyramidal neurons. The exponential decay laws in the multiple peaks are also acquired using probability analysis method. The perfect decay law is determined by the independent characteristic within the firing while the imperfect decay law is from the inhibitory effect. In addition, the stochastic firing patterns corresponding to type I excitability are compared to those of type II excitability. The results not only reveal the dynamics of stochastic firing patterns with or without external signal corresponding to type I excitability, but also provide practical indicators to availably identify type I excitability.

Keywords: Neural firing pattern, Excitability, Type I excitability, Stochastic process, Integer multiple firing, Saddle-node bifurcation on an invariant cycle

Introduction

Excitability that can induce rest condition to firing is a fundamental characteristic in the nerve system (Hodgkin 1948; Izhikevich 2000). Two classes of neural excitability, type I and type II, were proposed by Hodgkin according to the experimental results (Hodgkin 1948). The firing frequency varied smoothly over a large range as stimulus intensity that could induce firing varied in type I excitability, while the firing frequency were relatively insensitive to stimulus intensity in type II excitability. Two types of excitability were interpreted using concept of nonlinear dynamics. Type I excitability is related to saddle-node bifurcation, while type II is associated to Andronov–Hopf bifurcation (Rinzel and Ermentrout 1989). Except the firing frequency (Hodgkin 1948; Rinzel and Ermentrout 1989; Izhikevich 2000; Tateno et al. 2004), the two types of excitability exhibit different characteristics in many aspects, such as phase response curve (PRC) (Ermentrout 1996; Gutkin et al. 2005; Galán et al. 2005; Tateno and Robinson 2006; Tateno et al. 2007; Tsubo et al. 2007; Prescott et al. 2008b; Stiefel et al. 2009; Phoka et al. 2010), critical amplitude of a sinusoidal stimulus that can induce firing (Xie et al. 2004b), coefficient of variation (CV) in interspike intervals (ISIs) (Gutkin and Ermentrout 1998), synchrony in network (Ermentrout 1996; Galán et al. 2007; Bogaard et al. 2009) and other indicators (Prescott et al. 2008a).

The high CV values such as those observed in cortical spike trains were suggested as an intrinsic characteristic of type I excitability driven by "random" inputs (Gutkin and Ermentrout 1998). In contrast, neural oscillators or neurons exhibiting type II excitability should produce relatively regular spike trains. Regular spiking (RS) pyramidal neurons in layer 2/3 of slices of young rat somatosensory cortex show a continuous firing frequency vs. stimulus current (f − I) relationship, corresponding to type I excitability (Tateno et al. 2004). In fast-spiking (FS) inhibitory interneurons, there is a clear discontinuity in their f − I relationship, corresponding to type II excitability. Type I and II excitability is also examined by f − I relationship in mesencephalic V neurons (Liu et al. 2008). Except the f − I relationship, the PRC, a measure of the spike time shift caused by perturbations of the membrane potential as a function of the phase of the spike cycle of a neuron, is employed to distinguish two types of the excitability (Ermentrout 1996; Gutkin et al. 2005); Galán et al. 2005; Tateno and Robinson 2006; Tateno et al. 2007; Tsubo et al. 2007; Prescott et al. 2008b; Stiefel et al. 2009; Phoka et al. 2010). The PRC can be classified into two categories, type 1 (the spike is always advanced) and type 2 (the spike is advanced or delayed depending on the stimulus phase), corresponding to type I and type II excitability, respectively. The pyramidal neurons in layer 2/3 tend to display type 2 whereas those in layer 5 tend to exhibit type 1. Within each cell type of non-pyramidal regular-spiking (NPRS), low-threshold spiking (LTS), and fast-spiking (FS) cells in rat somatosensory cortex, both types of PRCs were observed, but the proportions and sensitivities to perturbation amplitude were clearly correlated to cell type (Tsubo et al. 2007). In addition, the transition between two types of excitability has also been discovered in the experiment (Stiefel et al. 2009; Prescott et al. 2008b; Liu et al. 2008). For example, in recordings from layer 2/3 pyramidal neurons in visual cortical slices, cholinergic action, consistent with down-regulation of slow voltage-dependent potassium currents such as the M-current, switched the PRC from type II to type I (Prescott et al. 2008b).

Among these studies, to acquire PRC curve or the f − I relationship is very complex because many trials of the experiment should be performed (Tateno and Robinson 2006; Tateno et al. 2007; Tsubo et al. 2007; Prescott et al. 2008b; Stiefel et al. 2009; Phoka et al. 2010). In addition, it is well known that noise can induce stochastic firing patterns near threshold from rest condition to firing via stochastic resonance or coherence resonance (Tateno et al. 2004; Gu et al. 2011a, 2011b; Jia et al. 2011), for both type I and II excitability. When the stochastic firing is evoked, the f − I curve for type II excitability looks like the one for type 1 excitability (Izhikevich 2007), showing that f − I curve may cease to be effectiveness in distinguishing two types of excitability. Therefore, it is necessary to identify the distinction of stochastic firing between type I and type II excitability. Integer multiple firing can be simulated near Hopf bifurcation point in stochastic theoretical model, whether with or without external periodic signal (Gu et al. 2001, 2011a). For example, integer multiple firing pattern can be simulated near Hopf bifurcation point in stochastic Chay model without external periodic signal, employed to interpret the spontaneous ones discovered in the experiments (Braun et al. 1994; Gu et al. 2001, 2011a; Xing et al. 2001; Gong et al. 2002). In the presence of external periodic signal with low frequency, the integer multiple firing pattern with multi-peaks in ISI histogram (ISIH), located at integer multiples of the period of the external signal, were observed in the experiment (Rose et al. 1967; Siegel 1990; Gu et al. 2011a) and simulated in theoretical model (Longtin et al. 1991, 1994; Chialvo and Apkarian 1993; Xie et al. 2004a; Gu et al. 2011a). The exponential decay law and the value of the decay slope were also identified using probability analysis method (Gu et al. 2011a). In these studies, the integer multiple firings were often related to type II excitability, seldom to type I excitability (Xie et al. 2004a).

In this paper, we will study the dynamics of the noise induced stochastic firing patterns corresponding to type I excitability without or with external signal, compared to those for type II excitability. The characteristic of ISIH can be used as a simple and practical indicator to identify type I excitability. A stochastic non-integer multiple firing pattern near saddle-node bifurcation on an invariant cycle is simulated in the stochastic ML model without external signal, manifesting dynamics different to the spontaneous integer multiple firing from type II excitability. Two cases of integer multiple firings similar to those simulated with type II excitability can be simulated near saddle-node bifurcation on an invariant cycle in Morris–Lecar (ML) model stimulated by both external signal and noise. To be consistent with previous study (Gu et al. 2011a), the two cases firings are labeled as case 1 and 3 integer multiple firing, respectively. Case 1 exhibit perfect exponential decay law in all peaks in ISIH, while case 3 manifest exponential decay law with a lower first peak. The integer multiple firing with a higher first peak, generated without external periodic signal, is named as case 2. Firing patterns simulated in ML model with or without external signals were demonstrated in the experiment on the rat hippocampal CA1 neurons. The two cases of integer multiple firing patterns, whether simulated in ML model or observed in the experiment, manifest exponential decay laws identical to those simulated with type II excitability. It shows that the external signal evoked integer multiple firing can also generate when the nervous system is type I excitability.

The rest of the present paper is organized as follows. In Sect. 2, theoretical model, experimental model and time series analysis methods are introduced. Section 3 presents type I excitability in deterministic ML model and firings in stochastic ML model without and with external signal. Section 4 is the firing patterns recorded in rat pyramidal neurons of the hippocampal slice. The spontaneous non-integer multiple firing pattern and two cases of external periodic signal induced integer multiple firing patterns were observed. Exponential decay laws within two cases of integer multiple firings corresponding to type I excitability are tested in Sect. 5. Section 6 is the discussion and conclusion.

Theoretical model, experimental model and time series analysis method

Theoretical model

Deterministic Morris–Lecar model

The Morris–Lecar model (Morris and Lecar 1981; Tateno et al. 2004; Tsumoto et al. 2006; Liu et al. 2010) is considered as a canonical prototype for widely encountered excitability classes of neuronal membranes and is as follows:

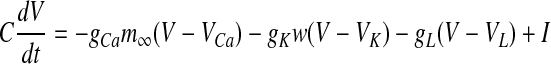graphic file with name M1.gif 1
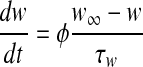graphic file with name M2.gif 2

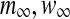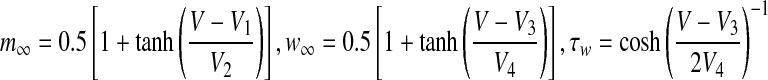where t is the time (the independent variable). Dependent variables are V (the membrane potential) and w (the activation of delayed rectifier K+ current). Parameter I represents the direct current and the background ionic currents. The explicit expressions for Inline graphic and τw are as follows, Inline graphic.

The parameters in this paper are 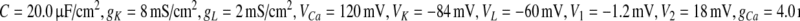Inline graphic (Tateno et al. 2004; Liu et al. 2010). The unit of I is μA/cm2. The unit of time is millisecond.

When 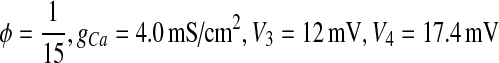Inline graphic, the behavior of ML model is type I excitability (Tateno et al. 2004). When ϕ = 0.04, gCa = 4.4 mS/cm2, V3 = 2 mV, V4 = 30 mV, the behavior is type II excitability (Tateno et al. 2004).

Stochastic ML model without external signal

A Gaussian white noise ξ(t) is introduced to the first equation to form the stochastic ML model without external signal. The noise possesses statistical properties as 〈ξ(t)〉   = 0 and 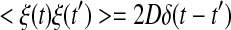Inline graphic, where D is the noise density and δ(•) is the Diract δ-function.

Stochastic ML model with external signal

Both an external periodic signal 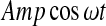Inline graphic and a Gaussian white noise ξ(t) are introduced to the first equation to form the stochastic ML model with external signal. Where Amp is the amplitude and ω is the angle frequency of the external periodic signal.

Deterministic and stochastic ML model are solved by Mannella numerical integrate method (Mannella and Palleschi 1990) with integration time step being 0.1 ms. An action potential is said to occur when the voltage crossed a value of 25.0 mV from below.

Experimental model

Sprague-Dawley (SD) rats (10–19 day-old) were anesthetized with urethane (Gu et al. 2011a; Jia et al. 2011). The brain were rapidly removed and placed in ice-cold dissecting artificial cerebrospinal fluid (ACSF). Then 300 μm-thick coronal slices were prepared using vibratome (NatureGene Corp, USA) and placed in a holding chamber of incubating ACSF and kept at room temperature for at least 1 h before being transferred to an immersion chamber for recordings.

For whole cell patch clamp, slices were transferred to a recording chamber mounted on upright microscope DM-LFSA (Leica, Germany) perfused with ACSF (room temperature). Recordings were made from hippocampal CA1 pyramid neurons visually identified by infrared DIC-video microscopy using a high performance vidicon camera DAGE-MTI (Dage-MTI of Michigan City, Inc., USA). The resistance of microelectrode was 3–5 MInline graphic. All recordings from CA1 pyramidal cells were obtained using a Digidata 1440A interface connected to an AXON700B amplifier (Axon Ins., USA). Data were acquired, processed and analyzed using the Pclamp 10 software (Axon Ins., USA), respectively.

Autocorrelation coefficient

Autocorrelation function, verified to be a practical method to identify dependent or non-renewal characteristic within ISI series (Chacron et al. 2000; Gu et al. 2011a) of neural firing, is employed in this paper.

For a time series (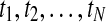Inline graphic) (N is an integer), the mean of the series is

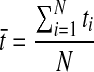graphic file with name M11.gif 3

The autocorrelation coefficient of the time series ρ is defined as

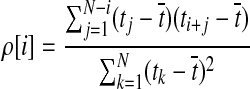graphic file with name M12.gif 4

where the lag 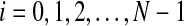Inline graphic.

In general, for a renewal stochastic process, ρ[i] = 0 for all i > 0, implying that the time series is independent. For a non-renewal stochastic process, ρ[i] ≠ 0 for at least one i ≠ 0, implying that there exists some correlation or dependence within the time series.

In this paper, −0.05 ≤ ρ[i] ≤ 0.05 is thought to be nearly zero. Because −0.05 ≤ ρ[i] ≤ 0.05 when i ≥ 2 in this paper, ρ[i] when i < 10 is shown in the corresponding figures.

Analysis to ISI histogram

When a suitable ISI interval is chosen, ISI histogram of integer multiple firing can be acquired, manifesting exponential decay in multiple peaks. Expediently, the peak in ISIH whose sequential number is k is called as kth peak. The maximal amplitude of the kth peak in ISIH, i.e. the ISI height, is labeled as y(k), and the ISI corresponding to y(k) is labeled as x(k). The value of y(k) and x(k) might have a little difference when the ISI interval is chosen as different values. Correspondingly, the value of decay slope also exhibits a little difference. The statistical error in y(k) and x(k) might be induced by the unsuitable choice of the ISI interval.

All number of ISIs in kth peak, i.e. the integrated peaks of the ISI distributions, is labeled as NP(k). Obviously, the y(k) is a partial of NP(k). Different to y(k) that is dependent to the choice of bin, the value of NP(k) is unique and independent. In Ref (Gu et al. 2011a), the exponential decay law existed between NP(k) and k is acquired, proved to be the cause that lead to the exponential relationship appeared between y(k) and x(k).

In this paper, two methods are employed to acquire the linear relationship existed between logy(k) and x(k), and between logNP(k) and k. One is the least square method. The other is the probability analysis method to be introduced in Sect. 5

Firings in stochastic Morris–Lecar model

Saddle-node bifurcation on an invariant cycle in deterministic ML model

In this paper, 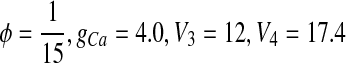Inline graphic. The behaviors of ML model is near a saddle-node bifurcation on an invariant cycle corresponding to type I excitability (Tateno et al. 2004; Liu et al. 2010).

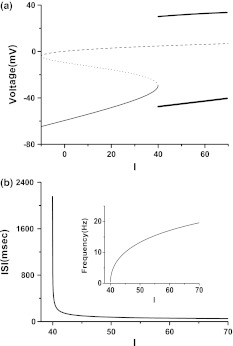
In deterministic ML model, Is≈39.96 is a point of saddle-node bifurcation on an invariant cycle, as shown in Fig. 1a. When I < Is, the behavior of the system is resting with underlying dynamics determined by the coexistence of a stable node, an unstable saddle and an unstable focus. When I > Is, the system’s behavior is period 1 firing. Different from period 1 firing near the Hopf bifurcation point where the period of firing is approximately fixed, the firing period is changed rapidly from 2,148.5 ms when I = 39.97, to 939.7 m when I = 40, to 262.7 ms when I = 40.5, to 194.8 ms when I = 41, as shown in Fig. 1b.

Fig. 1.

Fig. 1

Open in a new tab

a Behaviors of deterministic Morris–Lecar model near the saddle-node bifurcation on an invariant cycle (I≈39.96). Dashed line: unstable focus, dotted line: saddle, thin solid line: stable node, upper (lower) bold solid line: maximal (minimal) amplitude of the stable limit cycle. b Changes of ISI and firing frequency (Insert figure) with respect to I near saddle-node bifurcation on an invariant cycle

Firing in the stochastic ML model without external signal

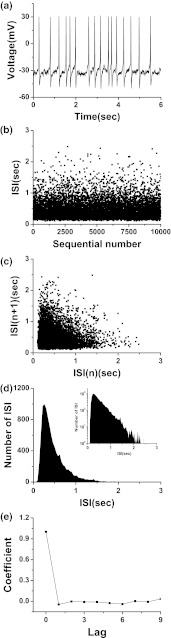
The behavior of the deterministic ML model without external signal (Amp = 0) is rest when I = 39.6. When noise with middle density (D = 0.1) is introduced, stochastic firing pattern is induced. The spike train, ISI series, and fist return map of ISI series are shown in Fig. 2a–c, respectively. In ISIH, the amplitude increases rapidly firstly and then decreases slowly with respect to the increase of ISI, as shown in Fig. 2d. Exponential decay is also exhibited in the decaying part, as shown in the insert figure of Fig. 2d. If the ordinate and abscissa are labeled as y and x, respectively, the relationship between logy and x of the decaying part is logy = 3.370x − 1.442 with correlation coefficient being −0.99, using the least square regression method, as shown in Fig. 2b.

Fig. 2.

Fig. 2

Open in a new tab

The characteristics of spontaneous neural firing induced by noise in the stochastic ML model without external signal I = 39.6 and D = 0.1). a Spike trains. b ISI series. c First return map of ISI series. d ISIH (Insert figure: logarithm scale). e Autocorrelation coefficient of ISI series

ρ[i]≈0 when i ≥ 1, implying that the firing is a renewal process, as shown in Fig. 2e.

Distinction to the case 2 integer multiple firing

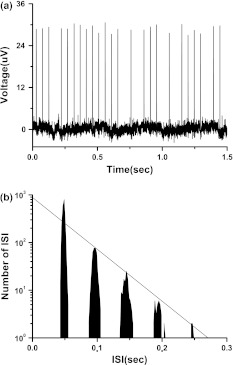
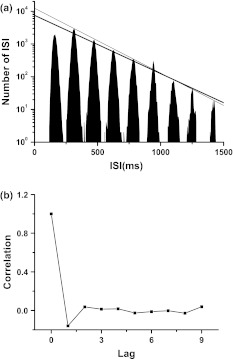
The stochastic firing pattern corresponding to type I excitability is different to case 2 integer multiple firing, a typical neural firing pattern related to Hopf bifurcation point and type II excitability (Gu et al. 2001). Case 2 integer multiple firing pattern (Gu et al. 2001, 2011a; Yang et al. 2009) generated near excitable threshold in the experiments on neural pacemaker, shark multi-modal sensory cell (Braun et al. 1994) and the injured sensory neurons (Xing et al. 2001), and can be simulated near Hopf bifurcation point in the stochastic Chay model (Gu et al. 2001, 2011a; Yang et al. 2009) without external signal. An typical example of case 2 integer multiple firing recorded from the experimental neural pacemaker is shown in Fig. 3, exhibiting exponential decay in other peaks except a higher first peak in ISIH, studied particularly in previous studies (Gu et al. 2001, 2011a; Yang et al. 2009).

Fig. 3.

Fig. 3

Open in a new tab

Spontaneous integer multiple firing pattern generated in the experimental neural pacemaker. a pike trains; b SIH

Case 1 integer multiple neural firing pattern in stochastic ML model with external signal

The integer multiple firing pattern with perfect exponential decay in all peaks in ISIH, i.e. case 1 integer multiple firing, was reported in previous experimental studies (Rose et al. 1967; Siegel 1990; Longtin et al. 1991, 1994).

In this subsection, case 1 integer multiple firing is simulated using the stochastic ML model with type I excitability, a middling noise density and an external signal whose period is longer than 250 ms.

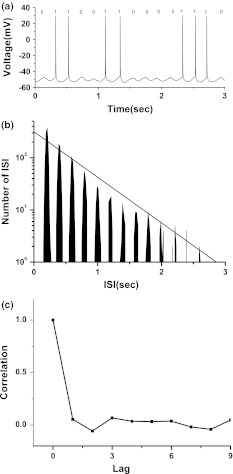
A typical example of case 1 integer multiple firing is simulated when ω = 0.025 (period of external signal is 251 ms), I = 37, Amp = 5 and D = 0.01. The spike trains are shown in Fig. 4a. The ISIs locate at the integer multiples of the period of external signal, as shown in Fig. 4b. Application of least square regression method to y(k) and x(k) yields that logy(k) = 3.349 − 0.00084x(k) with a correlation coefficient being −0.96, as shown in Fig. 4b. ρ[i]≈0 when i ≥ 1, implying that the firing is renewal process, as shown in Fig. 4c.

Fig. 4.

Fig. 4

Open in a new tab

Integer multiple firing pattern simulated in stochastic ML model stimulated by external periodic signal and noise (I = 37, ω = 0.025, Amp = 5, D = 0.01). a Spike trains; b ISI histogram; c autocorrelation coefficient of ISI series

Case 3 integer multiple neural firing pattern in stochastic ML model with external signal

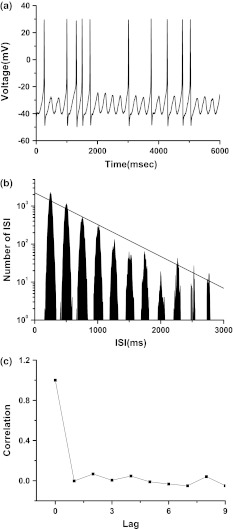
When period of the external signal is decreased, cases 3 integer multiple firing whose first peak in ISIH is lower than that expected by exponential fit while other peaks decay exponentially is simulated. ω = 0.04 is chosen as representative in this subsection.

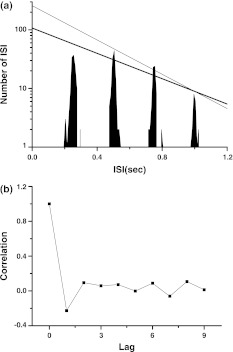
A typical example of case 3 integer multiple firing is simulated in the stochastic ML model when ω = 0.04 (the period of external period is 157 ms), I = 37, Amp = 9 and D = 0.01. The first peak in the ISIH is lower, as shown in Fig. 5a. Application of least square regression method to all peaks yields that logy(k) = 3.876 − 0.00178x(k) with a correlation coefficient being −0.96. Ignoring the first peak, logy(k) = 4.093 − 0.00198x(k) (k > 1) with a correlation coefficient being −0.99, much higher than −0.99. ρ[i] =  − 0.18 when i = 1 and ρ[i]≈0 when i > 1, as shown in Fig. 5b. It shows that the firing pattern exhibits negative correlation and non-renewal characteristic.

Fig. 5.

Fig. 5

Open in a new tab

Integer multiple firing pattern in stochastic Morris–Lecar model stimulated by external periodic signal and noise (I = 37, ω = 0.04, Amp = 9, D = 0.01). a ISI histogram; b autocorrelation coefficient of ISI series

Firing patterns in the experiment on CA1 pyramidal neurons

Spontaneous firing pattern in absence of external periodic signal

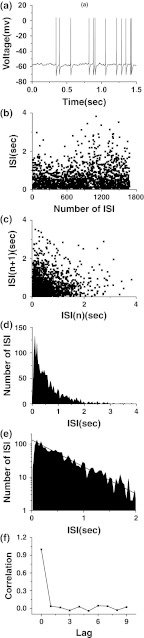
In normal condition without external periodic signal, some CA1 pyramidal neurons in hippocampal slices can generate a kind of stochastic firing pattern different to case 2 integer multiple firing, others can be rest. If suitable polarization current was applied, the spontaneous firings were changed into rest condition. It showed that the spontaneous firing was near the excitable threshold. When suitable depolarization current was applied, some resting CA1 pyramidal neurons in normal condition can generate stochastic firing patterns. A typical example of the firing pattern recorded from a neuron was shown in Fig. 6. The neuron was at resting condition without external current and the membrane voltage was about −60.8 mV. When a depolarization current with strength being as 25 pA was applied, the neuron was changed from resting condition into firing similar to that simulated in stochastic ML in absence of external periodic signal.

Fig. 6.

Fig. 6

Open in a new tab

Spontaneous firing pattern generated in CA1 neuron of hippocampal slice. a Spike trains; b ISI series; c first return map of ISI series; d ISIH; e logarithm of ISIH; f autocorrelation coefficient of ISI series

The spike trains of the firing pattern are irregular, as shown in Fig. 6a. The ISI series and the first return map of ISI series are shown in Fig. 6b and c, respectively. In ISIH, the amplitude increases rapidly firstly and then decreases slowly with respect to the increase of ISI, as shown in Fig. 6d. Similar firing patterns were discovered in previous experimental studies (Gerstein et al. 1960; Rodieck et al. 1962). Exponential decay is also exhibited in the decaying part, as shown in Fig. 6e. If the ordinate and abscissa are labeled as y and x, respectively, the relationship between logy and x of the decaying part is logy =  − 0.80x + 2.12 with correlation coefficient being −0.95, using the least square regression method. ρ[i]≈0 when i ≥ 1, implying the ISI series is independent and is a renewal process, as shown in Fig. 6f.

Case 1 integer multiple firing (perfect exponential decay)

When an external sinusoid current (the period is 200 ms) was applied, a number of resting CA1 pyramidal neurons in hippocampal slice were driven to generate case 1 integer multiple firing. A typical example of case 1 integer multiple firing was shown in Fig. 7a. The ISIs located at integer multiples to the period of external signal and the ISIH exhibited exponential decay in all peaks, as shown in Fig. 7b, similar to that simulated in ML model.

Fig. 7.

Fig. 7

Open in a new tab

Integer multiple firing pattern generated in CA1 neuron of hippocampal slice stimulated by external periodic signal. a Spike train; b ISI histogram; c autocorrelation coefficient of ISI series

Application of the least square regression method to y(k) and x(k) yields that logy(k) = 2.794 − 0.0087x(k) with a correlation coefficient being −0.97, as shown in Fig. 7b. ρ[i]≈0 when i > 0, as shown in Fig. 7c, implying that the ISI series is independent and a renewal process.

Case 3 integer multiple firing pattern (a lower first peak)

When external periodic current (the period is 200 ms) was applied, some resting CA1 pyramidal neurons were driven to generate case 3 integer multiple firing, as shown in Fig. 8. The maximal amplitude of the kth peak in ISIH exhibit exponential decay except the lower first peak, as shown in Fig. 8a, similar to that simulated in ML model.

Fig. 8.

Fig. 8

Open in a new tab

Integer multiple firing pattern generated in CA1 neuron of hippocampal slice stimulated by external periodic signal. a ISI histogram; b autocorrelation coefficient of ISI series

Application of the least square regression method to all peaks yields that logy(k) = 2.03 − 1.08x(k) with a correlation coefficient being −0.93. Ignoring the first peak, logy(k) = 2.412 − 1.463x(k)(k > 1) with a correlation coefficient being −0.99, much higher than −0.93. The similar ISIH were shown in Fig.30 (f) and (g) in previous experimental study (Gammaitoni et al. 1998).

ρ[i]≈ − 0.23 when i = 1 and ρ[i]≈0 when i > 1, implying that there exists negative dependence within the ISI series and the ISI series is a non-renewal process, as shown in Fig. 8b. The negative dependence shows that there exists an inhibitory effect within the firing.

Exponential decay law

In previous study, the exponential decay law of the integer multiple firing related to Hopf bifurcation and type II excitability were analyzed by transforming the ISI series to a binary chain and using probability analysis to the binary chain (Gu et al. 2011a). In this paper, the integer multiple firings related to type I excitability are analyzed through these methods.

Binary chain

Binary chain transformed from the firing pattern

The behavior of external periodic signal induced integer multiple firing pattern is either a spike or a subthreshold oscillation in a period. A binary discrete chain can be acquired according to the rules as follow, a spike in a period of external signal is labeled as 1 and a subthreshold oscillation as 0. For example, an integer multiple firing induced by the external periodic signal, recorded from pyramidal neuron of rat hippocampal slice, whose binary chain is composed of symbols 0 and 1, as shown in Fig. 7a. The binary chain corresponding to Fig. 7a is 011001100001110. The binary chain of the firing pattern can also be acquired from ISI series by transforming each ISI into binary symbols. If an ISI nearly equals k times to the period of the external signal, i.e. locating in the kth peak of ISIH, its binary chain is a string containing k − 1 continual 0, and ended with a 1. The binary chains acquired from two methods are identical (Gu et al. 2011a). Therefore, NP(k) equals the number of strings beginning with 1, followed by k − 1 continual 0 and ended with a 1 in the binary chain.

Probabilities of the binary chain

For the convenience, the definitions or symbols used in the probability analysis are given as follows. The total number of elements in the chain is labeled as N. In practice, N should be large enough to ensure that R1 and R0 is independent to N. The number of symbol 1 and 0 is N1 and N0, respectively. N1 + N0 = N. The probability of 1 and 0 is expressed by the frequence of symbol 1 and 0, respectively. R1 = N1/N and R0 = 1 − R1, respectively. The number of continuous symbols 11, 10, 01 and 00 in the binary chain is labeled as N11, N10, N01 and N00, respectively. N11 + N10 + N01 + N00 = N − 1. R11 = N11/(N − 1), R10 = N10/(N − 1), R01 = N01/(N − 1), and R00 = N00/(N − 1), respectively. Where, R11 + R10 = R1, R01 + R00 = R0, R01 = R10. 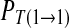The transition probability from 0 to 0, 0 to 1, 1 to 0 and 1 to 1 in the chain is labeled as Inline graphic and Inline graphic, respectively. The corresponding value can be calculated as R00/R0, R01/R0, R10/R1 and R11/R1. 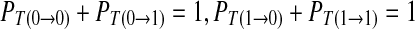In addition, Inline graphic.

Deduction of exponential decay law

NP(k) equals the number of strings beginning with 1, followed by k − 1 continual 0 and ended with a 1 in the chain. Therefore, the relationship between NP(k) and k is:

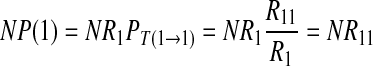graphic file with name M18.gif 5
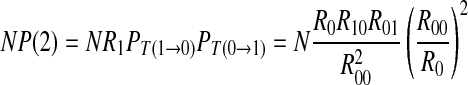graphic file with name M19.gif 6
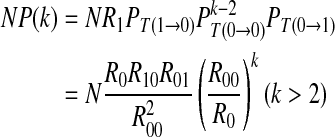graphic file with name M20.gif 7

Equations (5), (6) and (7) can be written as

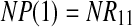graphic file with name M21.gif 8
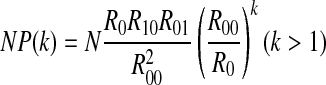graphic file with name M22.gif 9

Therefore, if 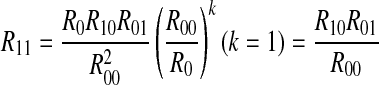Inline graphic, all peaks exhibit perfect exponential decay, corresponding to case 1. If 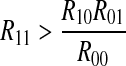Inline graphic, other peaks exhibit exponential decay except a higher first peak, corresponding to case 2. If 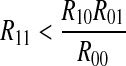Inline graphic, other peaks manifest exponential decay except a lower first peak, corresponding to case 3. The exponential decay law exhibited in case 1, 2 and 3 integer multiple firing are as follows.

Case 1: A spike generated in a period of the external signal imposes no influence to the behavior in the next period. For the corresponding binary chain, a symbol 1 imposes no influence to the next symbol, whether it is 1 or 0. The transition from 0 to 0, 0 to 1, 1 to 0 and 1 to 1 in the binary chain is independent. Therefore, 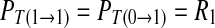Inline graphic, i.e. R11/R1 = R01/R0 = R1.

We can acquire 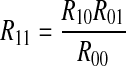Inline graphic because R10 = R01 and R00 = R0R0. The proof procedure is as follows,

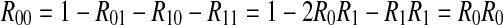graphic file with name M28.gif 10
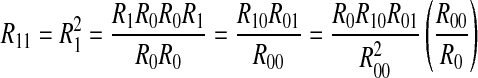graphic file with name M29.gif 11

Therefore, the relationship between NP(k) and k can be reduced to

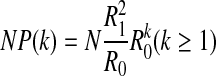graphic file with name M30.gif 12

The result shows that NP(k) decrease exponentially with respect to k for all peaks. The decay slope is related to the probability of symbol 0 R0. Because R0 is less than 1, NP(k) decreases exponentially with respect to the increase of k.

Applying logarithm to Eq. (12),

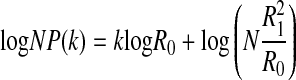graphic file with name M31.gif 13

logNP(k) decays lineally with respect to k. The decay slope is logR0, only related to the probability of symbol 0.

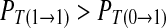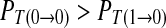Case 2: A spike only imposes excitatory influence to the following spike in the next period. Correspondingly, a symbol 1 imposes excitatory effect to the next symbol 1 in the binary chain. Inline graphic, i.e. R11/R1 > R01/R0. We can acquire Inline graphic.

A proof procedure is as follows,

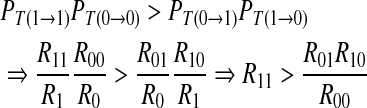graphic file with name M34.gif 14

The result shows that, except a higher value of NP(1), NP(k) (k > 1) decreased exponentially with respect to the increase of k. The decay slope of logNP(k) is log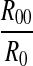Inline graphic when k > 1, related to not only R0, but also the joint probability of continuous symbols 00 R00.

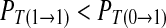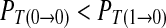Case 3: A spike only imposes inhibitory influence to the following spike in the next period. Correspondingly, a symbol 1 imposes inhibitory effect to the next symbol 1. In this case, Inline graphic, i.e. R11/R1 < R01/R0. We can acquire Inline graphic.

A proof procedure is as follows,

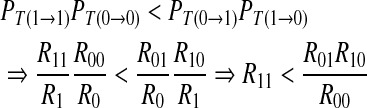graphic file with name M38.gif 15

The result shows that, except a lower NP(1), NP(k) (k > 1) is decreased exponentially with respect to the increase of k. The decay slope of logNP(k) is also log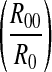Inline graphic when k > 1, related to both R0 and R00.

Test of the exponential decay law

In this subsection, we will test the exponential decay law of the integer multiple firing related to type I excitability in Sects. 3 and 4.

Case 1 integer multiple firing simulated in ML model

In the example shown in Fig. 4, there are 50,001 spikes in 119,087 periods. N = 119,087, N1 = 50,001, N11 = 20,364, N10 = 29,414, N01 = 29,414, N00 = 39,894. The probabilities are R1 = 0.420, R0 = 0.580, R11 = 0.171, R10 = 0.247, R01 = 0.247 and R00 = 0.335, respectively. R11/R1 = 0.407, R01/R0 = 0.426. R11/R1≈ R01/R0 with a relative error 4.66 %, showing that the integer multiple firing is case 1.

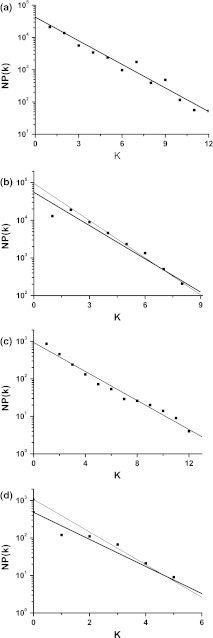
The deducted value of decay slope is log R0 =  −0.237. Applying the least square method to all peaks yields logNP(k) = 4.565 − 0.232k with correlation coefficient being −0.98, as shown in Fig. 9a. The decay slope is −0.232, nearly equaling the deducted value logR0 =  −0.237 with a relative error being 2.11 %.

Fig. 9.

Fig. 9

Open in a new tab

The relationship between NP(k) and k. a Case 1 integer multiple firing simulated in stochastic ML model, shown in Fig. 4; b Case 3 integer multiple firing simulated in stochastic ML model, shown in Fig. 5. The solid line is the regression linear fit for all peaks; the thin line is the regression linear fit for other peaks except the first one; c Case 1 integer multiple firing observed in the experiment, shown in Fig. 7; d Case 3 integer multiple firing observed in the experiment, shown in Fig. 8. The solid line is the regression linear fit for all peaks; the thin line is the regression linear fit for other peaks except the first one

Case 3 integer multiple firing simulated in ML model

In the example shown in Fig. 5, spikes appear in 49,996 out of the total 122,545 periods. N = 122,545, N1 = 49,996, N11 = 12,867, N10 = 37,131, N01 = 37,131 and N00 = 35,415, respectively. The probabilities are R1 = 0.408, R0 = 0.592, R11 = 0.105, R10 = 0.303, R01 = 0.303 and R00 = 0.289, respectively. R11/R1 = 0.257, R01/R0 = 0.512. R11/R1 < R01/R0, showing that the integer multiple firing is case 3.

The deducted values of decay slope are log R0 =  −0.228 and log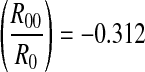Inline graphic, respectively. Application of the least square method to NP(k) and k yields logNP(k) = 4.743 − 0.294k (k ≥ 1) with a correlation coefficient of −0.96, as shown in Fig. 9b (bold line). The decay slope is −0.294, different to the deducted value logR0 =  −0.228. For other peaks except the first one, logNP(k) = 4.985 − 0.321k (k > 1) with a correlation coefficient of −0.99, as shown in Fig. 9b (thin line). The decay slope is −0.321, very close to the deducted value log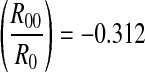Inline graphic. The relative error is 2.88 %.

Case 1 integer multiple firing discovered in the experiment

There were 1,941 spikes generated in 5,000 periods of external signal in the example shown in Fig. 7. N = 5,000, N1 = 1,941, N11 = 799, N10 = 1,201, N01 = 1,201, N00 = 1,798. The probabilities are R1 = 0.388, R0 = 0.612, R11 = 0.160, R10 = 0.240, R01 = 0.240 and R00 = 0.360. R11/R1 = 0.412, R01/R0 = 0.392. R11/R1≈ R01/R0 with a relative error 4.82 %, showing that the integer multiple firing is case 1.

Applying the least square regression method to NP(k) and k, yields logNP(k) = 2.497 − 0.198k with a correlation coefficient −0.983, as shown in Fig. 9c. The decay slope is −0.198, close to the deducted value logR0 =  −0.213 with a relative error 7.05 %.

Case 3 integer multiple firing discovered in the experiment

There were 660 spikes generated in 1,378 periods in the example shown in Fig. 8. N = 1,378, N1 = 660, N11 = 256, N10 = 424, N01 = 424 and N00 = 273, respectively. The probabilities are R1 = 0.479, R0 = 0.521, R11 = 0.186, R10 = 0.308, R01 = 0.308 and R00 = 0.198. R11/R1 = 0.388, R01/R0 = 0.596. R11/R1 < R01/R0, showing that the integer multiple firing is case 3.

Applying the least square regression method to NP(k) and k yields that logNP(k) = 2.686 − 0.362k (k ≥ 1) with a correlation coefficient being −0.96, as shown in Fig. 9d (bold line). The decay slope is −0.362, different to the deducted value logR0 =  −0.287. Ignoring the first peak, logNP(k) = 3.030 − 0.435k (k > 1) with a correlation coefficient being −0.99, as shown in Fig. 9d (thin line). The decay slope is −0.435, nearly equaling the deducted value log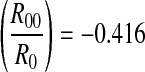Inline graphic with a relative error 4.56 %.

Discussion and conclusion

Identification of the types of excitability is important to the nervous systems. PRC curve and f − I curve are often employed to distinguish type I and II excitability (Ermentrout 1996; Izhikevich 2000; Prescott et al. 2008a), restricted by noise induced firing patterns. For example, PRC curve can be calculated only when the firing is period 1 firing (Tateno et al. 2007). In this paper, the dynamics of noise induced firing patterns corresponding to type I excitability are studied. The ISIH of stochastic firing patterns simulated in ML model and observed in the experiments on rat hippocampal CA1 pyramidal neuron exhibits a continuous distribution, whose amplitude increases sharply firstly and then decreases slowly and exponentially. Similar firing patterns were discovered in many tissues in previous studies (Gerstein et al. 1960; Rodieck et al. 1962; Gu et al 2011b; Jia et al. 2011), suggested that the excitability might be type I. The stochastic firing pattern without external periodic signal corresponding to type I excitability is obviously different to that of the type II excitability being as spontaneous (case 2) integer multiple firing (Gu et al. 2001, 2011a). The ISIH of the spontaneous integer multiple firing pattern exhibits discrete multi-peaks, whose amplitude exhibits exponential decay except the higher first peak. The ISIH of the firing pattern without external signal provides a practical indicator to distinguish type I and type II excitability. The very rapid increasing part in ISIH should be formed by the refractory period with a very little variability, and the exponential decreasing part is formed by an excitation with stochastic dynamics similar to a Poisson process. The essential reason for such an ISIH has not been clear, awaited further study.

In the presence of external signal, case 1 and 3 of integer multiple firing pattern are simulated in ML model with type I excitability and observed in the experiments on rat hippocampal CA1 pyramidal neuron. The case 1 integer multiple firing exhibits perfect exponential decay in all peaks, being as renewal process. No excitatory or inhibitory effect between the behaviors within continual two periods of the external signal. The case 3 integer multiple firing pattern exhibits exponential decay in other peaks except the first lower one, being as non-renewal process. A spike can put inhibitory effect on the behavior in the next period of the external signal. The exponential decay slope of case 1 integer multiple firing is related to the probability of symbol 0 in the corresponding binary chain, acquired by transforming a spike in a period of the external signal to 1 and quiescence to 0, respectively. The exponential decay slope of case 3 is related to both probability of symbol 0 and the joint probability of the continual two symbols 00 in the binary chain. It shows case 1 and case 3 integer multiple firing patterns corresponding to type I excitability exhibit exponential decay laws identical to those of the type II excitability (Gu et al. 2011a), implying that case 1 and 3 integer multiple firing can also be related to type I excitability. It is also known that the case 1 and 3 integer multiple firing patterns are evoked by external signal with low frequency. The dynamics of firing patterns near the threshold evoked by external signal with high frequency should be complex and diversity in ISIH, awaited to be further studied.

Many studies should be done to further identify the dynamics of the type I and II excitability, especially the representation of the two types of excitability in different tissues of the central nerve system (Tateno and Pakdaman 2004; Tsubo et al. 2007; Prescott et al. 2008b; Stiefel et al. 2009). In addition, more practical and simple indictors to distinguish two types of excitability should be explored and provided.

Acknowledgments

This study was supported by National Natural Science Foundation of China under Grant Nos 11072135, 10772101 and 30300107.

References

  1. Bogaard A, Parent J, Zochowski M, Booth V. Interaction of cellular and network mechanisms in spatiotemporal pattern formation in neuronal networks. J Neurosci. 2009;29:1677–1687. doi: 10.1523/JNEUROSCI.5218-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Braun HA, Wissing H, Schäfer K. Oscillation and noise determine signal transduction in shark multimodal sensory cells. Nature. 1994;367:270–273. doi: 10.1038/367270a0. [DOI] [PubMed] [Google Scholar]
  3. Chacron MJ, Longtin A, St-Hilaire M, Maler L. Suprathreshold stochastic resonance firing dynamics with memory in P-type electroreceptors. Phys Rev Lett. 2000;85:1576–1579. doi: 10.1103/PhysRevLett.85.1576. [DOI] [PubMed] [Google Scholar]
  4. Chialvo DR, Apkarian AV. Modulated noisy biological dynamics: three examples. J Stat Phys. 1993;70:375–391. doi: 10.1007/BF01053974. [DOI] [Google Scholar]
  5. Ermentrout GB. Type I membranes, phase resetting curves, and synchrony. Neural Comput. 1996;8:979–1001. doi: 10.1162/neco.1996.8.5.979. [DOI] [PubMed] [Google Scholar]
  6. Ermentrout GB, Galán RF, Urban NN. Reliability, synchrony and noise. Trends Neurosci. 2008;31(8):428–434. doi: 10.1016/j.tins.2008.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Galán RF, Ermentrout GB, Urban NN. Efficient estimation of phase-resetting curves in real neurons and its significance for neural-network modeling. Phys Rev Lett. 2005;94(15):158101. doi: 10.1103/PhysRevLett.94.158101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Galán RF, Ermentrout GB, Urban NN. Reliability and stochastic synchronization in type I vs type II neural oscillators. Neurocomputing. 2007;70:2102–2106. doi: 10.1016/j.neucom.2006.10.075. [DOI] [Google Scholar]
  9. Gammaitoni L, Hanggi P, Jung P, Marchesoni F. Stochastic resonance. Rev Mod Phys. 1998;70:223–287. doi: 10.1103/RevModPhys.70.223. [DOI] [Google Scholar]
  10. Gerstein GL, Kiang NY-S. An approach to the quantitative analysis of electrophysiological data from single neurons. Biophys J. 1960;1:15–28. doi: 10.1016/S0006-3495(60)86872-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gong PL, Xu JX, Hu SJ, Long KP. Chaotic interspike intervals histogram with multipeaked in neurons. Int J Bifurcation Chaos. 2002;12:319–328. doi: 10.1142/S0218127402004346. [DOI] [Google Scholar]
  12. Gutkin BS, Ermentrout GB. Dynamics of membrane excitability determine inter-spike interval variability: a link between spike generation mechanisms and cortical spike train statistics. Neural Comput. 1998;10:1047–1065. doi: 10.1162/089976698300017331. [DOI] [PubMed] [Google Scholar]
  13. Gutkin BS, Ermentrout GB, Reyes A. Phase response curves determine the responses of neurons to transient inputs. J Neurophysiol. 2005;94(2):1623–1635. doi: 10.1152/jn.00359.2004. [DOI] [PubMed] [Google Scholar]
  14. Gu HG, Ren W, Lu QS, Wu SG, Yang MH, Chen WJ. Integer multiple spiking in neural pacemakers without external periodic stimulation. Phys Lett A. 2001;285:63–68. doi: 10.1016/S0375-9601(01)00278-X. [DOI] [Google Scholar]
  15. Gu HG, Jia B, Lu QS. Exponential decay characteristics of the integer multiple neural firing patterns. Cogn Neurodyn. 2011;5:87–101. doi: 10.1007/s11571-010-9145-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gu HG, Zhang HM, Wei CL, Yang MH, Liu ZQ, Ren W. Coherence resonance induced stochastic neural firing at a saddle-node bifurcation. Int J Mod Phys B. 2011;25:3977–3986. doi: 10.1142/S0217979211101673. [DOI] [Google Scholar]
  17. Hodgkin AL. The local electric changes associated with repetitive action in a non-medullated axon. J Physiol. 1948;107:165–181. doi: 10.1113/jphysiol.1948.sp004260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Izhikevich EM. Neural excitability, spiking and bursting. Int J Bifurcation Chaos. 2000;10:1171–1266. doi: 10.1142/S0218127400000840. [DOI] [Google Scholar]
  19. Izhikevich EM (2007) Dynamical systems in neuroscience: the geometry of excitability and bursting. The MIT Press, Cambridge, p 215
  20. Jia B, Gu HG, Li YY. Coherence resonance induced neuronal firing near a saddle node and homoclinic bifurcation corresponding to type I excitability. Chin Phys Lett. 2011;28(9):090507. doi: 10.1088/0256-307X/28/9/090507. [DOI] [Google Scholar]
  21. Liu YH, Yang J, Hu SJ. Transition between two excitabilities in mesencephalic V neurons. J Comput Neurosci. 2008;24(1):95–104. doi: 10.1007/s10827-007-0048-4. [DOI] [PubMed] [Google Scholar]
  22. Liu ZQ, Zhang HM, Li YY, Hua CC, Gu HG, Ren W. Multiple spatial coherence resonance induced by stochastic signal in neuronal networks near a saddle-node bifurcation. Phys A. 2010;389:2642–2653. doi: 10.1016/j.physa.2010.02.029. [DOI] [Google Scholar]
  23. Longtin A, Bulsara A, Moss F. Time interval sequences in bistable system and the noise-induced transmission of information by sensory neurons. Phys Rev Lett. 1991;67:656–659. doi: 10.1103/PhysRevLett.67.656. [DOI] [PubMed] [Google Scholar]
  24. Longtin A, Bulsara A, Pierson D, Moss F. Bistability and the dynamics of periodically forced sensory neurons. Biol Cybern. 1994;70:569–578. doi: 10.1007/BF00198810. [DOI] [PubMed] [Google Scholar]
  25. Mannella R, Palleschi V. Fast and precise algorithm for compute simulation of stochastic differential equations. Phys Rev A. 1990;40:3381–3386. doi: 10.1103/PhysRevA.40.3381. [DOI] [PubMed] [Google Scholar]
  26. Morris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J. 1981;35:193–213. doi: 10.1016/S0006-3495(81)84782-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Phoka E, Cuntz H, Roth A, Häusser M. A new approach for determining phase response curves reveals that Purkinje cells can act as perfect integrators. PLoS Comput Biol. 2010;6(4):e1000768. doi: 10.1371/journal.pcbi.1000768. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Prescott SA, De Koninck Y, Sejnowski TJ. Biophysical basis for three distinct dynamical mechanisms of action potential initiation. PLoS Comput Biol. 2008;4:el000198. doi: 10.1371/journal.pcbi.1000198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Prescott SA, Ratté S, Koninck YD, Sejnowski TJ. Pyramidal neurons switch from integrators in vitro to resonators under in vivo-like condition. J Neurophysiol. 2008;100:3030–3042. doi: 10.1152/jn.90634.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Rinzel J, Ermentrout GB (1997) Analysis of neural excitability and oscillations. In: Koch C, Segev I (eds) Methods in neuronal modeling: from synapses to networks. MIT Press, Cambridge, pp 135–169
  31. Rodieck RW, Kiang NY-S, Gerstein GL. Some quantitative methods for the study of spontaneous activity of single neurons. Biophys J. 1962;2:351–368. doi: 10.1016/S0006-3495(62)86860-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Rose JE, Brugge JF, Anderson DJ, Hind JE. Phase locked response to low-frequency tones in single auditory nerve fibers of the squirrel monkey. J Neurophysiol. 1967;30:769–793. doi: 10.1152/jn.1967.30.4.769. [DOI] [PubMed] [Google Scholar]
  33. Siegel RM. Non-linear dynamical system theory and primary visual cortical processing. Phys D. 1990;42:385–395. doi: 10.1016/0167-2789(90)90090-C. [DOI] [Google Scholar]
  34. Stiefel KM, Gutkin BS, Sejnowski TJ. The effects of cholinergic neuromodulation on neuronal phase-response curves of modeled cortical neurons. J Comput Neurosci. 2009;26:289–301. doi: 10.1007/s10827-008-0111-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Tateno T, Pakdaman K. Random dynamics of the Morris–Lecar neural model. Chaos. 2004;14:511–530. doi: 10.1063/1.1756118. [DOI] [PubMed] [Google Scholar]
  36. Tateno T, Harsch A, Robinson HPC. Threshold firing frequency-current relationships of neurons in rat somatosensory cortex: type 1 and type 2 dynamics. J Neurophysiol. 2004;92:2283–2294. doi: 10.1152/jn.00109.2004. [DOI] [PubMed] [Google Scholar]
  37. Tateno T, Harsch A, Robinson HPC. Phase resetting curves and oscillatory stability in interneurons of rat somatosensory cortex. Biophys J. 2007;92:683–695. doi: 10.1529/biophysj.106.088021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Tateno T, Robinson HPC. Rate coding and spike-time variability in cortical neurons with two types of threshold dynamics. J Neurophysiol. 2006;95:2650–2663. doi: 10.1152/jn.00683.2005. [DOI] [PubMed] [Google Scholar]
  39. Tsubo Y, Takada M, Reyes AD, Fukai T. Layer and frequency dependencies of phase response properties of pyramidal neurons in rat motor cortex. Eur J Neurosci. 2007;25:3429–3441. doi: 10.1111/j.1460-9568.2007.05579.x. [DOI] [PubMed] [Google Scholar]
  40. Tsumoto K, Kitajim H, Yoshinag T, Aihara K, Kawakami H. Bifurcations in Morris–Lecar neuron model. Neurocomputing. 2006;69:293–316. doi: 10.1016/j.neucom.2005.03.006. [DOI] [Google Scholar]
  41. Xie Y, Xu JX, Hu SJ. A novel dynamical mechanism of neural excitability for integer multiple spiking. Chaos, Solitons Fractals. 2004;21:177–184. doi: 10.1016/j.chaos.2003.10.006. [DOI] [Google Scholar]
  42. Xie Y, Xu JX, Kang YM, Hu SJ, Duan YB. Characteristics of critical amplitude of a sinusoidal stimulus in a model neuron. Chin Phys. 2004;13(9):1396–1401. doi: 10.1088/1009-1963/13/9/005. [DOI] [Google Scholar]
  43. Xing JL, Hu SJ, Xu H, Han S, Wan YH. Subthreshold membrane oscillations underlying integer multiples firing from injured sensory neurons. NeuroReport. 2001;12:1311–1313. doi: 10.1097/00001756-200105080-00051. [DOI] [PubMed] [Google Scholar]
  44. Yang MH, Liu ZQ, Li L, Xu YL, Liu HJ, Gu HG, Ren W. Identifying distinct stochastic dynamics from chaos: a study on the multi-mode neural firing patterns. Int J Bifurcation Chaos. 2009;19(2):453–485. doi: 10.1142/S0218127409023135. [DOI] [Google Scholar]

Articles from Cognitive Neurodynamics are provided here courtesy of Springer Science+Business Media B.V.

RESOURCES