Conspectus

This Account describes how attractive interaction of aromatic rings with other groups can influence and control the stereoselectivity of many reactions. Recent developments in theory have led to improved accuracy in the modeling of aromatic interactions. Quantum mechanical modeling can now provide insights into the roles of these interactions at a level of detail not previously accessible, both for ground-state species and for transition states of chemical reactions. In this Account, we show how transition-state modeling led to the discovery of the influence of aryl groups on the stereoselectivities of several types of organic reactions. These reaction types include asymmetric dihydroxylations, transfer hydrogenations, hetero-Diels–Alder reactions, acyl transfers, and Claisen rearrangements.
Our recent studies have led to a novel mechanistic picture for two classes of (4+3) cycloadditions, both of which involve reactions of furans with oxyallyl intermediates. The first class of cycloadditions, developed by Hsung, features neutral oxyallyls containing a chiral oxazolidinone auxiliary. Originally, these cycloadditions were thought rely on differential steric crowding of the two faces of a planar intermediate. Computations reveal a different picture and show that cycloadditions with furan takes place preferentially through the more crowded transition state, with furan adding on the same side as the oxazolidinone’s Ph substituent. The crowded transition state is stabilized by a CH–π interaction between furan and Ph, worth about 2.0 kcal/mol.
Stereocontrol in a second class of (4+3) cycloadditions, involving chiral alkoxy siloxyallyl cations, also is controlled by attractive interactions with aromatic rings. Alkoxy groups derived from chiral α-methylbenzyl alcohols are found to favor crowded transition states, where a CH–π interaction is again present between furan and Ar. The cationic cycloadditions are stepwise, while the Hsung cycloadditions are concerted. Our results suggest that this form of CH–π-directed stereocontrol is quite general and is likely to control the stereoselectivities of other addition reactions in which one face of a planar intermediate bears a pendant aromatic substituent.
1. Introduction
Aromatic interactions (π-stacking, CH–π, cation–π, and anion–π interactions) underpin many important structural phenomena, including conformational equilibria, molecular recognition, self-assembly, and protein–ligand binding.1 Recent developments in quantum mechanical methodology have permitted increasingly accurate modeling of aromatic interactions, not only in ground-state species but also in the transition states of chemical reactions. In this Account, we show how these types of interactions are important in controlling the stereoselectivities of organic reactions.
The synthetic literature contains many examples of asymmetric reactions whose stereoselectivities changed unexpectedly upon replacement of an alkyl substituent by an aromatic group.2 Although “aromatic interactions” are often invoked,3 definitive evidence for their participation generally requires accurate transition-state modeling. This Account summarizes contemporary theoretical approaches that have been applied to modeling of aryl-substituent effects. Quantum mechanical modeling has shown the importance of these types of interactions in transition states and has provided explanations of a number of puzzling phenomena. A number of new modes of stereoinduction controlled by CH–π interactions have been discovered for cycloaddition reactions. Our computations demonstrate that an aryl group can give steric attractions that lead to product distributions opposite from those that would be predicted on the basis of steric crowding.
2. Quantum Mechanical Calculations of Aromatic Interactions
Not all commonly used theoretical methods are well suited to the study of aromatic interactions.4 Modeling of these interactions requires an accurate treatment of dispersion, a quantum mechanical phenomenon that has long posed a challenge to computation. Dispersion involves the interactions between instantaneous dipole moments in the electron distributions of two or more atoms or molecules, and calculations of dispersion-dominated systems require an adequate treatment of dynamical electron correlation.5 The benchmark method for calculations of dispersion binding is coupled-cluster theory at the CCSD(T) level with extrapolation to the complete basis set limit.4,6 This computationally expensive technique is currently practical only for small systems. The less expensive second-order Møller–Plesset perturbation (MP2) theory has a tendency to overestimate dispersion. Grimme’s spin-component scaled MP2 variant (SCS-MP2), however, has shown very good performance.7
Density functional theory (DFT) approaches are commonly used as an alternative to wavefunction-based methods. The literature contains numerous cautionary studies highlighting the fact that many currently popular density functionals, including B3LYP,8 PBE,9 and PBE0,10 yield serious errors for dispersion-dominated systems.4,11 The failures of DFT include the prediction of too-small binding energies or even entirely repulsive interaction potentials for known bound systems. Qualitatively correct trends can sometimes be approximated artificially by use of a small basis set, since a small basis overestimates binding. However, substantial progress has been made in the development of dispersion-inclusive functionals, and a variety of economical methods are now available.
One approach has been to mimic dispersion binding by parameterizing a functional against a dataset that includes non-covalent interactions. The Minnesota meta-GGA functionals developed by Truhlar12 (including M05-2X and M06-2X) have attained prominence as examples of this approach. Although early M0n functionals suffered from grid-related potential energy surface oscillations,13 the methods have achieved substantial popularity in the study of various dispersion-dominated systems.14
A conceptually different approach is dispersion-corrected DFT, a class of procedures often referred to as “DFT-D”.15–18 Here, a conventional DFT energy is corrected by adding a term comprising the sum of individual interatomic dispersion energies, efficiently computed using a set of empirically-derived dispersion coefficients. Increasingly sophisticated versions of this approach include reparameterization of the underlying functional (e.g. B97-D), virtual-orbital-dependent terms in the correlation functional (e.g. B2PLYP-D), higher-order terms, and/or hybridization-specific dispersion coefficients. Grimme’s latest refinements of this approach, termed “DFT-D3”, performed superbly in benchmarking against the standard S22 dataset.15b One advantage of DFT-D of relevance to organic chemists is that one can dissect the total dispersion energy of a system into separate contributions representing the interactions between particular molecular fragments.
Other approaches to the treatment of dispersion are currently being developed and should see widespread use once implemented into software packages.19 The approaches mentioned above are in common use today and are illustrated by the literature examples in the following section.
3. Theoretical Insights into Aromatic Interactions as Stereocontrol Elements
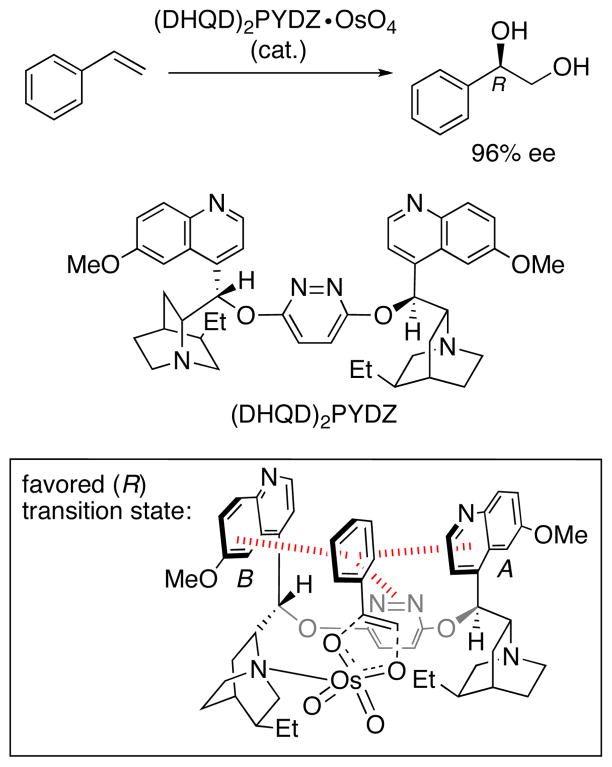
A relatively early example where aromatic interactions were recognized to influence stereoselectivity is the Sharpless asymmetric dihydroxylation. This reaction has been the subject of numerous computational studies, and the enantiocontrol has been explained using several different models.20 In an early computational study, Maseras et al.21 analyzed the asymmetric dihydroxylation of styrene, involving the chiral ligand (DHQD)2PYDZ that coordinates OsO4 and accelerates reaction (Scheme 1). Experimentally, the R enantiomer of the diol is obtained in 96% ee. 22 Hybrid quantum mechanics/molecular mechanics calculations with IMOMM(B3LYP:MM3) suggested that the favored transition state for the stereodetermining (3+2) cycloaddition step has the structure shown in the box in Scheme 1. Face-to-face stacking interactions are present between the styrene Ph group and the quinoline rings of the catalyst, together with an edge-to-face interaction between Ph and the pyridazine ring. These interactions are represented by the hashed red lines. Out of the three interactions, the one involving quinoline ring A was shown to contribute approximately half of the total substrate–catalyst van der Waals interaction energy. By contrast, the corresponding interactions in the transition state leading to the minor (S) enantiomer were only half as stabilizing. The S transition state is 2.7 kcal/mol higher in energy than the R transition state, in good agreement with the experimental enantioselectivity.
Scheme 1.
Sharpless asymmetric dihydroxylation of styrene, catalyzed by (DHQD)2PYDZ.21,22
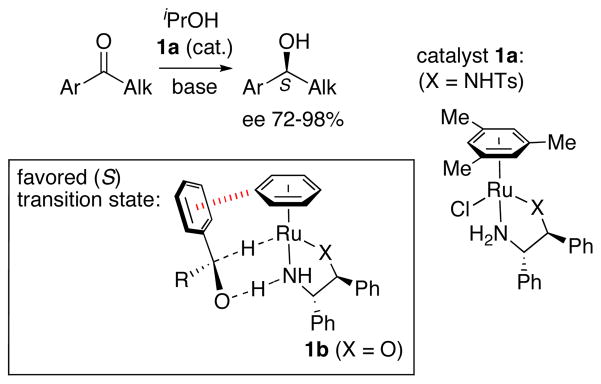
Noyori23–25 uncovered the role of CH–π interactions in transfer hydrogenations of aryl alkyl ketones catalyzed by chiral Ru(η6-arene) complexes (Scheme 2). Complex 1a favored the formation of S alcohols with ees of up to 98%.26 Calculations on model complexes revealed a mechanism involving metal–ligand bifunctional catalysis, where the atoms of H2 are transferred in a concerted fashion from a hydrido complex such as 1b. The enantioselectivity was traced to an edge-to-face interaction between the η6-arene and the aryl group on the ketone (hashed red line). The transition state shown was favored by 2.1 kcal/mol (MP2) over the less crowded enantiomeric transition state, which lacked such an interaction. The same enantiomer of the alcohol was favored if the η6-benzene ligand was replaced by η6-hexamethylbenzene. In this case, the stabilizing CH–π interaction involved one of the hexamethylbenzene methyl groups rather than the arene ring itself.
Scheme 2.
Ruthenium-catalyzed asymmetric transfer hydrogenation of ketones.23–25,26
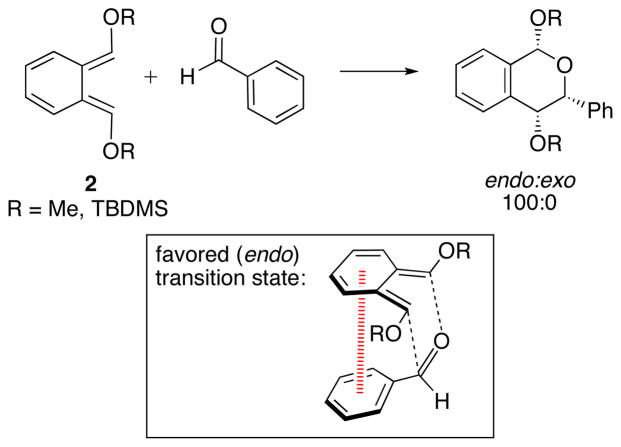
Houk and Danishefsky determined that aryl–aryl stacking interactions are the stereocontrolling element in the hetero-Diels–Alder reactions shown in Scheme 3.27 Experimentally, the cycloadditions of o-xylylenes 2 with benzaldehyde were completely endo selective.27,28 Consistent with experiment, MP2 calculations predicted endo selectivities of ~2 kcal/mol. The endo transition state features a face-to-face arrangement of the two aryl groups, with an Ar–Ar separation of 3.6–3.7 Å, typical for π-stacking. When B3LYP calculations, lacking dispersive interactions, were applied, much smaller endo selectivities were predicted. The reaction of benzaldehyde with an analogous butadiene, where no aryl–aryl interaction can occur, was predicted to favor the exo product.
Scheme 3.
Hetero-Diels–Alder reactions of o-xylylenes with benzaldehyde.27,28
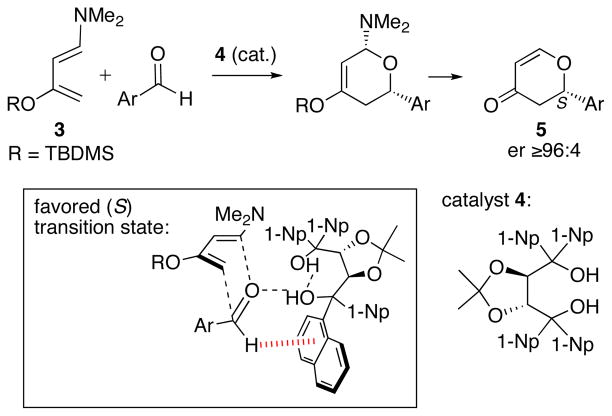
Catalytic asymmetric hetero-Diels–Alder reactions have also been found to involve aryl–aryl interactions. Rawal reported that the TADDOL derivative 4 (Scheme 4) catalyzed the cycloadditions of diene 3 with aromatic aldehydes to afford (after workup) the (S)-dihydropyrones, 5. The enantioselectivities were better than 96:4.29 Computational studies30 using ONIOM multilayer molecular orbital calculations (B3LYP:AM1), in conjunction with Monte Carlo conformational searching, indicated that the reaction occurs preferentially through the transition state shown in the box. The aldehyde is held in position by a combination of cooperative hydrogen bonding to the carbonyl oxygen and a CH–π interaction (3.2 Å) between the CHO proton and proximal naphthyl group. This transition structure was favored over the opposite enantiomer by 1.5 kcal/mol (B3LYP) or 3.4 kcal/mol (M06-2X). It was also favored by ≥3 kcal/mol over transition structures containing alternative modes of aryl–aryl interaction that had been proposed earlier by other workers.31
Scheme 4.
Asymmetric hetero-Diels–Alder reactions of Rawal’s diene with aldehydes, catalyzed by a TADDOL derivative.29,30
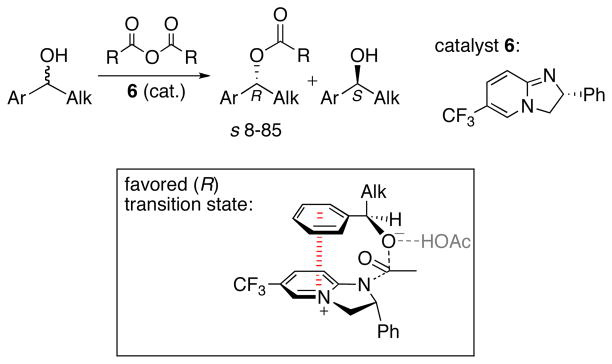
Birman and Houk explained the enantioselectivities of acyl transfer reactions catalyzed by 2,3-dihydroimidazo[1,2-a]pyridines (DHIPs) (Scheme 5).32 These reactions are employed in kinetic resolutions of secondary benzylic alcohols. The DHIP 6 preferentially catalyzed the acylation of R alcohols, with selectivity (s) factors up to 85.33 The preferred acylation transition state was found to have a slipped-stacked geometry. The Ar group of the alcohol is centered roughly over the pyridinium nitrogen atom (Ph–N distance 3.7 Å). This transition structure is more stable than that for acylation of the S alcohol, where no aryl–aryl interaction is present.
Scheme 5.
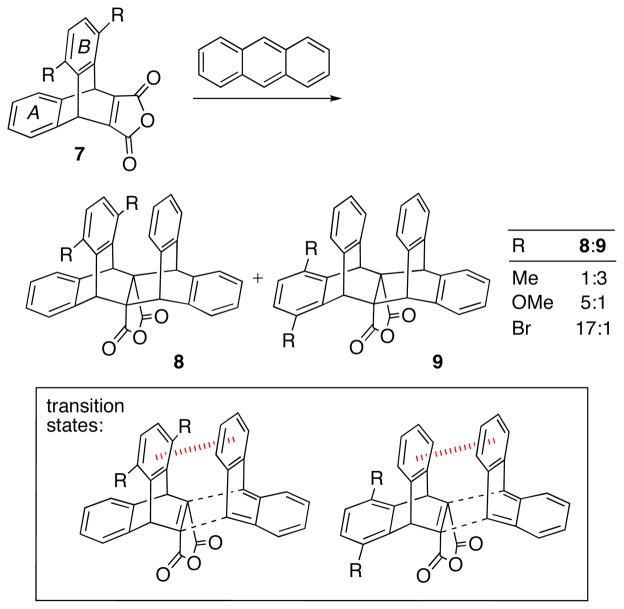
The groups of Swager and Houk34 recently reported Diels–Alder reactions in which the stereoselectivity is controlled by aryl–aryl stacking interactions (Scheme 6). Cycloadditions of anthracene with dienophile 7 (R = Me, OMe, Br) furnished mixtures of the cycloadducts 8 and 9, where the anthracene has added syn or anti, respectively, to the substituted benzene ring (B). The syn/anti ratios ranged from 1:3 (for R = Me) to 17:1 (R = Br). The product distributions were found to correlate with values of ΔΔH‡ computed by several density functionals. Differential aryl–aryl stacking interactions were shown to be the major stereodetermining factor, and intriguingly, the stacking interaction was stronger for OMe than for Me. The substituent effects were suggested not to be due to electron density changes in the aromatic ring but to arise instead from direct through-space dispersion and electrostatic interactions between the R groups and the facing aromatic ring of the anthracene. Extensive studies of such effects by Wheeler et al.35 have shown this conclusion to be quite general.
Scheme 6.
Diastereoselective Diels–Alder reactions of anthracene with aryl-substituted maleic anhydride derivatives.34
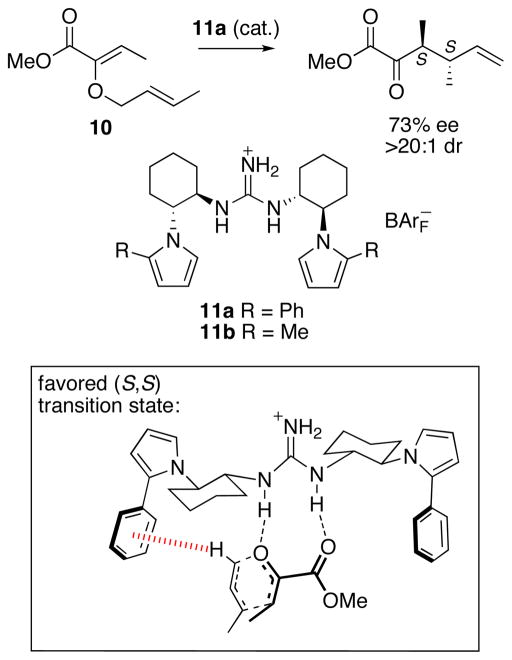
Very recently, Jacobsen36 developed a theoretical model of the factors controlling enantioselectivity in catalytic asymmetric Claisen rearrangements (Scheme 7). The rearrangement of the O-allyl α-ketoester 10, catalyzed by chiral guanidinium salt 11a (R = Ph), furnished the S,S product with 73% ee and >20:1 dr. The analogous Me-substituted catalyst 11b gave only 41% ee. Calculations with DFT and MP2 showed that two NH···O hydrogen bonds determine the orientation of the substrate relative to the catalyst. The S,S configuration is preferred because the transition state is stabilized by a CH–π interaction (3.0 Å) between the positively-charged allyl fragment and the nearby Ph group on the catalyst. This interaction is absent in the R,R transition state.
Scheme 7.
Enantioselective Claisen rearrangements catalyzed by chiral guanidinium salts.36
Although not directly related to stereoselectivity, a recent spectacular example of the role of dispersion is found in the report by Schreiner37 of molecules in which bulky groups stretch CC bonds but stabilize these distorted molecules by dispersive attractive forces. The example shown in Scheme 8 has a C–C bond length of 1.65 Å yet is a crystalline solid, stable up to ≥300 °C. The C–C bond dissociation energy computed with B3LYP-D was 71 kcal/mol.
Scheme 8.
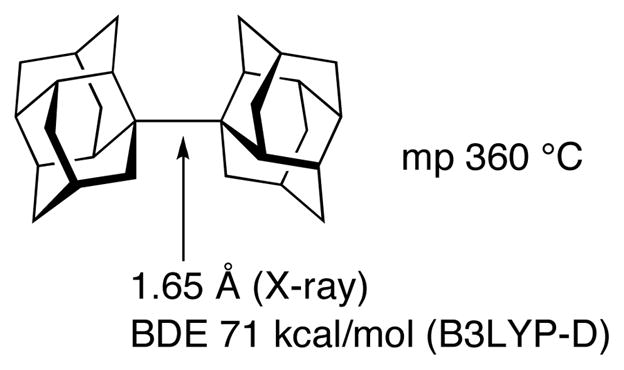
A strained hydrocarbon stabilized by dispersion interactions.
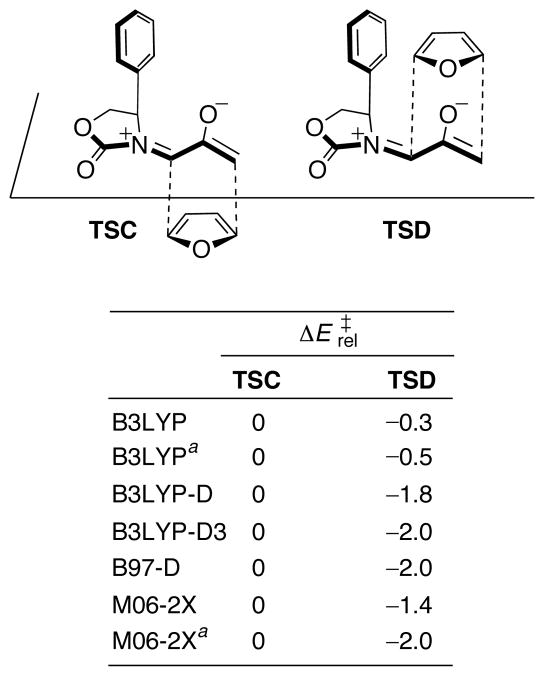
Because many of the above computational studies were performed prior to the advent of dispersion-correcting approaches,38 we have re-evaluated the stereoselectivities with the B3LYP-D3 and M06-2X functionals. The Supporting Information provides a comparison of predicted stereoselectivities for the reactions in Schemes 1–7, as computed by B3LYP, B3LYP-D3, and M06-2X. The D3 correction generally increased the computed stereoselectivities for these reactions by up to 5.3 kcal/mol (ΔΔE‡), while M06-2X/6-311+G(d,p) gave smaller increases of up to 3.0 kcal/mol.
4. Aromatic Interactions as Stereocontrol Elements in Oxyallyl (4+3) Cycloaddition Reactions
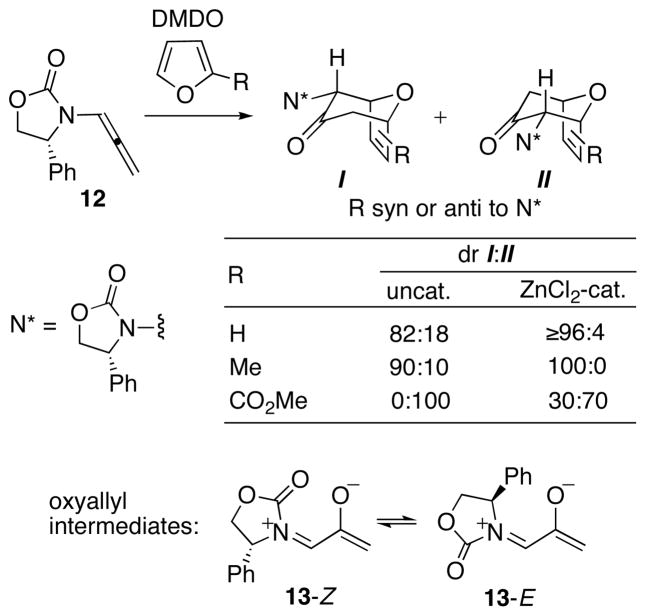
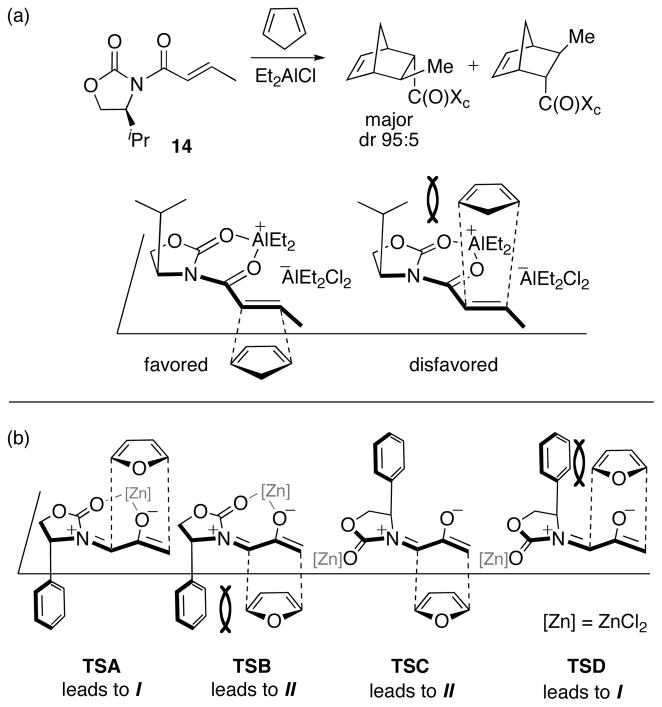
Our work has involved several different types of cycloadditions where stabilizing interactions with aryl groups favor one TS. We discovered a novel form of aryl-induced stereocontrol during collaborative work on (4+3) cycloaddition reactions developed by Richard Hsung.39–41 The Hsung stereoselective route to 7-membered carbocycles is based on (4+3) cycloadditions of oxyallyls containing a chiral oxazolidinone.42 As shown in Scheme 9, the oxyallyl is generated by oxidation of an allenamide and is trapped with a furan (or pyrrole or diene). While I and II may be formed, reactions of 12 with furan and 2-methylfuran favored cycloadduct I. The diastereomer ratios were 82:18 and 90:10, respectively, under thermal conditions and increased to ≥96:4 when ZnCl2 was included in the reaction mixture. Unexpectedly, however, the reaction with methyl 2-furoate favored the opposite diastereomer, II (dr 100:0 under thermal conditions).
Scheme 9.
Hsung’s (4+3) Cycloadditions between Oxazolidinone-Substituted Oxyallyls and Furans.42
Originally, the mechanism of stereoinduction in these (4+3) cycloadditions was thought to resemble that originally proposed by Evans43 for oxazolidinone-directed Diels–Alder reactions (Scheme 10a). Evans proposed that the dienophile 14 combines with Et2AlCl to form a chelate. A diene should add most easily to the face opposite iPr, which is less crowded.44 This type of steric blocking has been invoked in many other oxazolidinone-directed reactions.45 For Hsung’s (4+3) cycloadditions, there are four analogous transition states (Scheme 10b). Cycloadduct I can be formed via either TSA or TSD, and cycloadduct II via TSB or TSC. The I-selectivity obtained with furan and 2-methylfuran was thought to be explained by the less-crowded TSA. This idea appeared to be supported by the increase in I-selectivity brought about by ZnCl2, which forms a chelate with the oxyallyl in TSA. However, this model cannot explain why a 2-CO2R substituent on the furan would lead to reversal of diastereoselectivity.
Scheme 10.
(a) Evans’ Oxazolidinone-Directed Diels–Alder Reaction, showing the Proposed Model for Stereoinduction,43 and (b) Possible Transition Structures for Oxazolidinone-Directed (4+3) Cycloaddition Reactions.
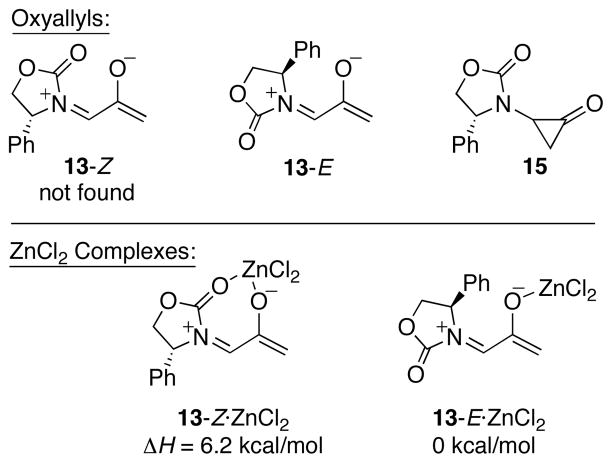
Computations at the B3LYP/6-31G(d) level indicated that only 13-E is an energy minimum (Scheme 11). The Z isomer is destabilized by electrostatic repulsion between the oxygen atoms, and collapses to the isomeric cyclopropanone 15 upon attempted geometry optimization. Significantly, coordination to ZnCl2 does not overcome the electrostatic destabilization of 13-Z; a Z chelate complex does form but it is 6.2 kcal/mol less stable than the E monodentate complex.
Scheme 11.
Possible Oxyallyl Intermediates and ZnCl2 Complexes.
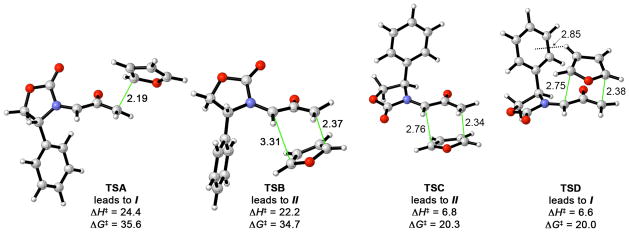
The computed transition structures for the uncatalyzed cycloaddition of 13 with furan are shown in Figure 1. The transition states that contain the E oxyallyl (TSC and TSD) have very low activation energies, while the Z transition states (TSA and TSB) are more than 15 kcal/mol higher in energy (ΔΔH‡). This is true also for the ZnCl2-catalyzed cycloaddition: coordination to ZnCl2 lowers the cycloaddition barriers, but the Z structures remain at least 5.2 kcal/mol above the E structures.
Figure 1.
Transition states for the (4+3) cycloaddition of Hsung’s oxyallyl 13 with furan (B3LYP/6-31G(d), distances in Å, ΔH‡ and ΔG‡ in kcal/mol).
Most interesting is that the addition of furan to the more crowded face of 13 (TSD) is favored by 0.2 kcal/mol (ΔΔH‡) over addition to the less crowded face (TSC). The computed selectivity agrees with experiment, and also persists when modeled in solution by means of continuum calculations with the conductor-like polarizable continuum model (CPCM).46
The 0.2 kcal/mol preference for addition to the more crowded face is traced to an edge-to-face interaction between furan and the oxazolidinone Ph substituent. In TSD, H-3 of the furan lies 2.85 Å from the centre of the Ph ring – within the typical distance range1a for CH–π interactions. The value of ΔΔH‡ increases to 0.6 kcal/mol when the larger 6-311+G(d,p) basis set is used, indicating that the CH–π-directed selectivity is not an artifact of basis set incompleteness. Most importantly, the stereoselectivities computed with several different dispersion-inclusive functionals give larger preferences; these results are shown in Figure 2. B3LYP-D3, B97-D, and M06-2X predict a 1.1–1.7 kcal/mol stronger stabilization of TSD than does B3LYP. A fragment-based analysis using B3LYP-D estimated that the interaction between furan and Ph in TSD is worth 2.6 kcal/mol.
Figure 2.
Relative energies of TSC and TSD, computed with different functionals. B3LYP/6-31G(d) geometries were used, and single-point calculations employed the 6-31G(d) basis set except for the points labeled “a”, which employed the 6-311+G(d,p) basis. ΔE‡rel in kcal/mol.
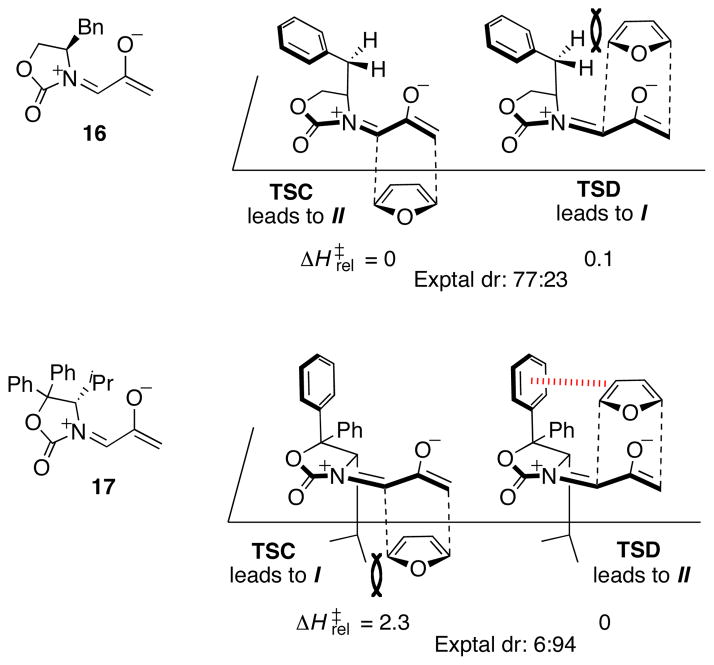
The stereoselectivities involving other oxazolidinone auxiliaries were investigated, and the results are shown in Figure 3. Our predictions led to a definitive determination of the stereoselectivities of these reactions by X-ray crystallography. Several reassignments of stereoselectivity had to be made after it was revealed that different oxazolidinones control stereoselectivity in different ways. Replacement of the Ph group by Bn (16) eliminates the potential for a stabilizing CH–π interaction in TSD, and a repulsive steric interaction is present instead. Accordingly, the predicted selectivity reverts to favor TSC. Experimentally, there is a corresponding selectivity for II (dr 77:23). Seebach’s oxazolidinone (17) elicits a different type of CH–π interaction, since now the Ph group is at C-5 of the oxazolidinone. The stabilizing interaction between furan and the upper Ph group (hashed red line) acts in concert with the steric effect of the iPr group on the lower face of the oxazolidinone, leading to a II-selectivity of 94:6. Of the two stereocontrol elements, the CH-π interaction appears dominant, because when the two C-5 Ph groups are absent, the dr drops to only 55:45.
Figure 3.
Experimental and calculated stereoselectivities for different oxazolidinone auxiliaries (B3LYP/6-31G(d), kcal/mol). Note: the reversed stereochemical designations for the products from 17 arise from the opposite configuration at C-4 of the oxazolidinone.
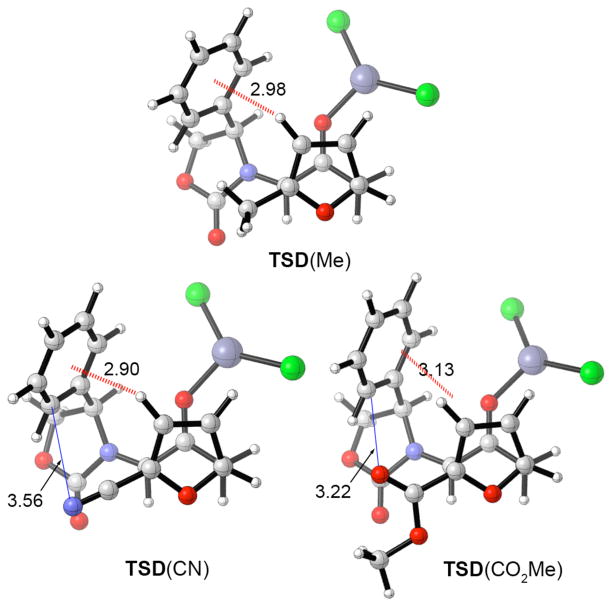
These calculations also rationalized the unexpected reversal of selectivity obtained with methyl 2-furoate (Scheme 9). In Figure 4 are shown transition structures analogous to TSD for ZnCl2-catalyzed cycloadditions of 13 with 2-Me, 2-CN, and 2-CO2Me substituted furans. Each furan favors a cycloadduct in which the furan substituent lies syn to the oxazolidinone, but only for 2-CO2Me is II the major stereoisomer. A CH–π interaction of 2.9–3.1 Å is present in each TS. For 2-CO2Me, however, electrostatic repulsion between the carbonyl oxygen and the Ph π-cloud results in overall destabilization. The uncrowded transition state (TSC) is preferred instead. The fine balance between the stabilizing CH–π interaction and the destabilizing electrostatic repulsion is illustrated by the fact that 2-cyanofuran reacts preferentially via TSD to give I. The cyano nitrogen atom lies 0.3 Å further from the Ph π-cloud than does the carbonyl oxygen atom.
Figure 4.
Top views of the transition states analogous to TSD for 2-Me, 2-CN, and 2-CO2Me substituted furans (B3LYP/6-31G(d)+LANL2DZ, distances in Å).
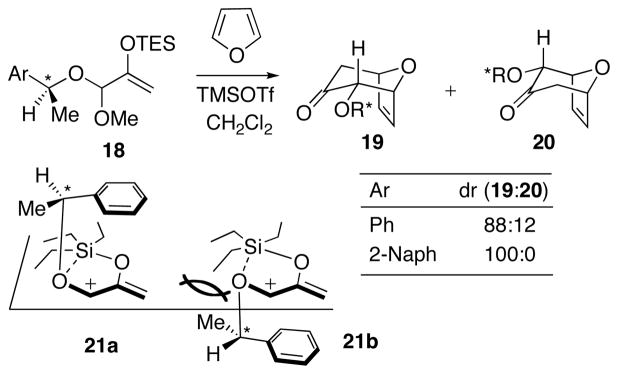
Our discoveries about Hsung’s cycloaddition led to a re-examination of related oxyallyl cycloaddition reactions reported by H. M. R. Hoffmann (Scheme 12).47 The allylic acetals 18 undergo stereoselective, Lewis acid-catalyzed (4+3) cycloadditions with furans to give the diastereomeric cycloadducts 19 and 20. The stereoselectivity is determined by the configuration of the α-methylbenzyl centre in the alkoxy group. Diastereomer ratios ranged from 10% to 100% depending on the Ar substituent and the solvent. The best stereoselectivity was obtained with a 2-naphthyl group in CH2Cl2. Hoffmann suggested that the stereoselectivity was determined by the conformation of the intermediate oxyallyl cation. Two conformers were proposed, 21a and 21b. Both feature a cation–π interaction between the allyl cation and the Ar group, and an intramolecular RO···SiEt3 interaction. Conformer 21b would be disfavored due to steric clashing between Me and TES. Addition of furan to the less-hindered face of conformer 21a (opposite the Ar ring) would furnish the major product.
Scheme 12.
Hoffmann’s Asymmetric (4+3) Cycloaddition, and the Mechanism Originally Proposed to Explain the Stereocontrol.47
In collaboration with Michael Harmata, we performed density functional theory calculations to examine Hoffmann’s cycloaddition reactions.48 B3LYP provided no evidence for the proposed Si···O-bonded intermediates 21a and 21b, and instead indicated that the O–R* bond lay in the same plane as the allyl group (21c).
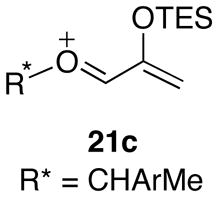
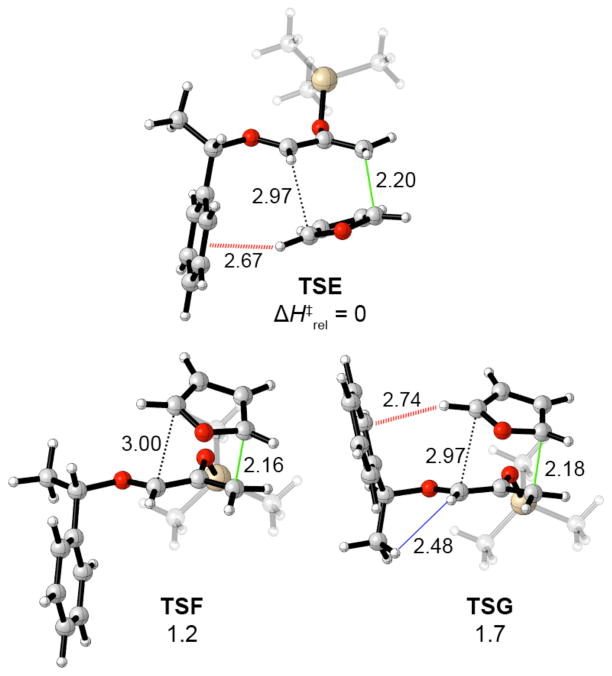
Unlike the cycloadditions of Hsung’s oxazolidinone-substituted oxyallyls, Hoffmann’s cycloadditions are predicted to be stepwise processes. Bond formation occurs first at the CH2 terminus of the oxyallyl cation. The issue of concerted vs. stepwise in this type of (4+3) cycloadditions has been studied previously by Cramer,49 who showed that more electrophilic oxyallyl cations favor stepwise pathways. Three low-lying transition states were located for the initial bond formation (Figure 5). The lowest-energy transition state (TSE) corresponds to the experimental major product, while the other two transition states (TSF and TSG) both lead to the minor diastereomer.
Figure 5.
Transition structures for (4+3) cycloadditions of Hoffmann’s oxyallyl cation 21 (Ar = Ph) with furan (B3LYP/6-31G(d), distances in Å, ΔH‡ in kcal/mol). The TES group was modeled by TMS.
In TSE, furan adds to the crowded face of the oxyallyl cation, with an edge-to-face arrangement (2.7 Å) between furan and Ph. A similar edge-to-face arrangement is present in TSG, but the associated stabilization is outweighed by steric repulsion between the allyl cation and Me group (blue line). TSF lacks any Me–H clash, but also lacks a furan–Ph interaction. When the transition states’ energies are calculated with M06-2X, TSE remains favored overall, but TSG drops below TSF as this functional captures more strongly the stabilization associated with the CH–π interaction.
The calculations also capture the increase in stereoselectivity observed with a 2-naphthyl group. The computed dr in the gas phase for the 2-naphthyl analogue is 95:5 by B3LYP and 99:1 by M06-2X, very close to the experimental value of 100:0. Incorporation of solvent effects by means of CPCM calculations leads to qualitative agreement with the experimental stereoselectivities in CH2Cl2 and THF, and the transition-state modeling correctly predicts the regioselectivities for substituted furans such as 3-Et3Si-furan.
5. Conclusion
Recent advances in theoretical treatments of dispersion have provided the first density functional methods that can reliably model aromatic interactions. For synthetic chemists, these computational methods offer previously inaccessible insights into how aromatic interactions within transition states can influence stereocontrol. Given the large body of aryl-related effects on stereoselectivity that have been reported in the synthetic literature, new mechanisms of stereoinduction remain to be uncovered. Accurate theoretical modeling is also poised to allow design of new applications of aromatic interactions as stereocontrol elements. This area presents important opportunities, since aromatic interactions can enable access to different stereoselectivities from those obtained under simple steric control.
Supplementary Material
Acknowledgments
This research was supported by an NIH grant to KNH (GM-36700) and an Australian Research Council grant to EHK (DP0985623).
Biographies
Elizabeth H. Krenske obtained her PhD from the Australian National University with Professor S. B. Wild in 2005, in the area of organophosphorus and arsenic chemistry. She undertook postdoctoral studies in theoretical organic chemistry as a Fulbright Scholar with Professor Ken Houk at UCLA. Since 2009 she has been an Australian Research Council APD Fellow at the University of Melbourne.
K. N. Houk is the Saul Winstein Chair in Organic Chemistry at UCLA. He has published extensively on pericyclic reactions, stereoselectivity, and molecular recognition and uses the tools of computational chemistry to solve problems in organic and biological chemistry. He is a fellow of the American Academy of Arts and Sciences and Member of the National Academy of Sciences. This is his seventh Account.
Footnotes
Supporting Information Available
Comparison of predicted stereoselectivities for reactions in Schemes 1–7, Figures 2, 3, and 5, as computed with B3LYP, B3LYP-D3, and M06-2X. This information is available free of charge via the Internet at http://pubs.acs.org/.
Contributor Information
Elizabeth H. Krenske, Email: ekrenske@unimelb.edu.au.
K. N. Houk, Email: houk@chem.ucla.edu.
References
- 1.See, for example: Nishio M. The CH/π hydrogen bond in chemistry. Conformation, supramolecules, optical resolution and interactions involving carbohydrates. Phys Chem Chem Phys. 2011;13:13873–13900. doi: 10.1039/c1cp20404a.Lehn J-M. Supramolecular Chemistry: Concepts and Perspectives. VCH; Weinheim: 1995. Gillard RE, Raymo FM, Stoddart JF. Controlling Self-Assembly. Chem Eur J. 1997;3:1933–1940.Meyer EA, Castellano RK, Diederich F. Interactions with Aromatic Rings in Chemical and Biological Recognition. Angew Chem Int Ed. 2003;42:1210–1250. doi: 10.1002/anie.200390319.Burley SK, Petsko GA. Aromatic-Aromatic Interaction: A Mechanism of Protein Structure Stabilization. Science. 1985;229:23–28. doi: 10.1126/science.3892686.Waters ML. Aromatic Interactions in Peptides. Biopolymers, Peptide Science. 2004;76:435–445. doi: 10.1002/bip.20144.
- 2.For reviews, see: Nishio M, Hirota M, Umezawa Y. The CH/π Interaction: Evidence, Nature, and Consequences. Wiley-VCH; New York: 1998. Jones GB. π Shielding in organic synthesis. Tetrahedron. 2001;57:7999–8016.Nishio M. CH/π hydrogen bonds in organic reactions. Tetrahedron. 2005;61:6923–6950.
- 3.For example, see: Corey EJ, Matsumura Y. Evidence for the Importance of π-π-Attractive Interactions in Enantioselective Diels–Alder Reactions Chiral Catalysts of Type (RO)2TiCl2. Tetrahedron Lett. 1991;32:6289–6292.Ishihara K, Kurihara H, Matsumoto M, Yamamoto H. Design of Brønsted Acid-Assisted Chiral Lewis Acid (BLA) Catalysts for Highly Enantioselective Diels–Alder Reactions. J Am Chem Soc. 1998;120:6920–6930.Kürti L, Blewett MM, Corey EJ. Origin of Enantioselectivity in the Jacobsen Epoxidation of Olefins. Org Lett. 2009;11:4592–4595. doi: 10.1021/ol901859d.
- 4.(a) Johnson ER, Mackie ID, DiLabio GA. Dispersion interactions in density-functional theory. J Phys Org Chem. 2009;22:1127–1135. [Google Scholar]; (b) Sherrill CD. Computations of Noncovalent π Interactions. In: Lipkowitz KB, Cundari TR, editors. Reviews in Computational Chemistry. Vol. 26. Wiley; New York: 2009. pp. 1–38. [Google Scholar]; (c) Grimme S. Density functional theory with London dispersion corrections. WIREs Comp Mol Sci. 2011;1:211–228. [Google Scholar]
- 5.Hartree–Fock (HF) theory fails to predict dispersion binding, because it neglects dynamical correlation.
- 6.(a) Jurečka P, Šponer J, Černý J, Hobza P. Benchmark database of accurate (MP2 and CCSD(T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs. Phys Chem Chem Phys. 2006;8:1985–1993. doi: 10.1039/b600027d. [DOI] [PubMed] [Google Scholar]; (b) Takatani T, Hohenstein EG, Malagoli M, Marshall MS, Sherrill CD. Basis set consistent revision of the S22 test set of noncovalent interaction energies. J Chem Phys. 2010;132:144104. doi: 10.1063/1.3378024. [DOI] [PubMed] [Google Scholar]
- 7.Antony J, Grimme S. Is Spin-Component Scaled Second-Order Møller–Plesset Perturbation Theory an Appropriate Method for the Study of Noncovalent Interactions in Molecules? J Phys Chem A. 2007;111:4862–4868. doi: 10.1021/jp070589p. [DOI] [PubMed] [Google Scholar]
- 8.(a) Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]; (b) Becke AD. A new mixing of Hartree–Fock and local density-functional theories. J Chem Phys. 1993;98:1372–1377. [Google Scholar]; (c) Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 9.Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 10.(a) Ernzerhof M, Scuseria GE. Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional. J Chem Phys. 1999;110:5029. doi: 10.1063/1.1634553. [DOI] [PubMed] [Google Scholar]; (b) Adamo C, Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J Chem Phys. 1999;110:6158. [Google Scholar]
- 11.See, for example: Kristyán S, Pulay P. Can (semi)local density functional theory account for the London dispersion forces? Chem Phys Lett. 1994;229:175–180.Hobza P, Šponer J, Reschel T. Density Functional Theory and Molecular Clusters. J Comput Chem. 1995;16:1315–1325.
- 12.(a) Zhao Y, Truhlar DG. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class funtionals and 12 other functionals. Theor Chem Account. 2008;120:215–241. [Google Scholar]; (b) Zhao Y, Truhlar DG. Density Functionals with Broad Applicability in Chemistry. Acc Chem Res. 2008;41:157–167. doi: 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
- 13.Johnson ER, Wolkow RA, DiLabio GA. Application of 25 density functionals to dispersion-bound homomolecular dimers. Chem Phys Lett. 2004;394:334–338. [Google Scholar]
- 14.Zhao Y, Truhlar DG. Applications and validations of the Minnesota density functionals. Chem Phys Lett. 2011;502:1–13. [Google Scholar]
- 15.See, for example: Grimme S. Accurate Description of van der Waals Complexes by Density Functional Theory Including Empirical Corrections. J Comput Chem. 2004;25:1463–1473. doi: 10.1002/jcc.20078.Schwabe T, Grimme S. Double-hybrid density functionals with long-range dispersion corrections: higher accuracy and extended applicability. Phys Chem Chem Phys. 2007;9:3397–3406. doi: 10.1039/b704725h.Grimme S, Antony J, Ehrlich S, Krieg H. A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys. 2010;132:154104. doi: 10.1063/1.3382344.and references cited therein
- 16.Jurečka P, Černý J, Hobza P, Salahub DR. Density Functional Theory Augmented with an Empirical Dispersion Term. Interaction Energies and Geometries of 80 Noncovalent Complexes Compared with Ab Initio Quantum Mechanics Calculations. J Comput Chem. 2007;28:555–569. doi: 10.1002/jcc.20570. [DOI] [PubMed] [Google Scholar]
- 17.Liu Y, Goddard WA., III A Universal Damping Function for Empirical Dispersion Correction on Density Functional Theory. Mat Trans. 2009;50:1664–1670. [Google Scholar]
- 18.Chai J-D, Head-Gordon M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys Chem Chem Phys. 2008;10:6615–6620. doi: 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- 19.(a) Becke AD, Johnson ER. Exchange-hole dipole moment and the dispersion interaction revisited. J Chem Phys. 2007;127:154108. doi: 10.1063/1.2795701. [DOI] [PubMed] [Google Scholar]; (b) Gräfenstein J, Cremer D. An efficient algorithm for the density-functional theory treatment of dispersion interactions. J Chem Phys. 2009;130:124105. doi: 10.1063/1.3079822. [DOI] [PubMed] [Google Scholar]; (c) Kong J, Gan Z, Proynov E, Freindorf M, Furlani TR. Efficient computation of the dispersion interaction with density-functional theory. Phys Rev A. 2009;79:042510. [Google Scholar]; (d) Zhang Y, Xu X, Goddard WA., III Doubly hybrid density functional for accurate descriptions of nonbond interactions, thermochemistry, and thermochemical kinetics. Proc Natl Acad Sci USA. 2009;106:4963–4968. doi: 10.1073/pnas.0901093106. [DOI] [PMC free article] [PubMed] [Google Scholar]; (e) Chai J-D, Head-Gordon M. Long-range corrected double-hybrid density functionals. J Chem Phys. 2009;131:174105. doi: 10.1063/1.3244209. [DOI] [PubMed] [Google Scholar]; (f) Mackie ID, DiLabio GA. Accurate dispersion interactions from standard density-functional theory methods with small basis sets. Phys Chem Chem Phys. 2010;12:6092–6098. doi: 10.1039/b919152f. [DOI] [PubMed] [Google Scholar]; (g) Lee K, Murray ÉD, Kong L, Lundqvist BI, Langreth DC. Higher-accuracy van der Waals density functional. Phys Rev B. 2010;82:081101. [Google Scholar]; (h) Vydrov OA, Van Voorhis T. Implementation and assessment of a simple nonlocal van der Waals density functional. J Chem Phys. 2010;132:164113. doi: 10.1063/1.3398840. [DOI] [PubMed] [Google Scholar]
- 20.For a review: Drudis-Solé G, Ujaque G, Maseras F, Lledós A. Enantioselectivity in the Dihydroxylation of Alkenes by Osmium Complexes. Top Organomet Chem. 2005;12:79–107.
- 21.Ujaque G, Maseras F, Lledós A. Theoretical Study on the Origin of Enantioselectivity in the Bis(dihydroquinidine)-3,6-pyridazine·Osmium Tetroxide-Catalyzed Dihydroxylation of Styrene. J Am Chem Soc. 1999;121:1317–1323. [Google Scholar]
- 22.Corey EJ, Noe MC. A Critical Analysis of the Mechanistic Basis of Enantioselectivity in the Bis-Cinchona Alkaloid Catalyzed Dihydroxylation of Olefins. J Am Chem Soc. 1996;118:11038–11053. [Google Scholar]
- 23.Yamakawa M, Yamada I, Noyori R. CH/π Attraction: The Origin of Enantioselectivity in Transfer Hydrogenation of Aromatic Carbonyl Compounds Catalyzed by Chiral η6-Arene-Ruthenium(II) Complexes. Angew Chem Int Ed. 2001;40:2818–2821. doi: 10.1002/1521-3773(20010803)40:15<2818::AID-ANIE2818>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 24.Noyori R, Yamakawa M, Hashiguchi S. Metal–Ligand Bifunctional Catalysis: A Nonclassical Mechanism for Asymmetric Hydrogen Transfer between Alcohols and Carbonyl Compounds. J Org Chem. 2001;66:7931–7944. doi: 10.1021/jo010721w. [DOI] [PubMed] [Google Scholar]
- 25.Yamakawa M, Ito H, Noyori R. The Metal–Ligand Bifunctional Catalysis: A Theoretical Study on the Ruthenium(II)-Catalyzed Hydrogen Transfer between Alcohols and Carbonyl Compounds. J Am Chem Soc. 2000;122:1466–1478. [Google Scholar]
- 26.(a) Hashiguchi S, Fujii A, Takehara J, Ikariya T, Noyori R. Asymmetric Transfer Hydrogenation of Aromatic Ketones Catalyzed by Chiral Ruthenium(II) Complexes. J Am Chem Soc. 1995;117:7562–7563. [Google Scholar]; (b) Noyori R, Hashiguchi S. Asymmetric Transfer Hydrogenation Catalyzed by Chiral Ruthenium Complexes. Acc Chem Res. 1997;30:97–102. [Google Scholar]
- 27.Ujaque G, Lee PS, Houk KN, Hentemann MF, Danishefsky SJ. The Origin of endo Stereoselectivity in the Hetero-Diels–Alder Reactions of Aldehydes with ortho-Xylylenes: CH–π, π–π, and Steric Effects on Stereoselectivity. Chem Eur J. 2002;8:3423–3430. doi: 10.1002/1521-3765(20020802)8:15<3423::AID-CHEM3423>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 28.Hentemann MF, Allen JG, Danishefsky SJ. Thermal Intermolecular Hetero Diels–Alder Cycloadditions of Aldehydes and Imines via o-Quinone Dimethides. Angew Chem Int Ed. 2000;39:1937–1940. [PubMed] [Google Scholar]
- 29.Huang Y, Unni AK, Thadani AN, Rawal VH. Single enantiomers from a chiral-alcohol catalyst. Nature. 2003;424:146. doi: 10.1038/424146a. [DOI] [PubMed] [Google Scholar]
- 30.Anderson CD, Dudding T, Gordillo R, Houk KN. Origin of Enantioselection in Hetero-Diels–Alder Reactions Catalyzed by Naphthyl-TADDOL. Org Lett. 2008;10:2749–2752. doi: 10.1021/ol800875k. [DOI] [PubMed] [Google Scholar]
- 31.(a) Zhang X, Du H, Wang Z, Wu Y-D, Ding K. Experimental and Theoretical Studies on the Hydrogen-Bond-Promoted Enantioselective Hetero-Diels–Alder Reaction of Danishefsky’s Diene with Benzaldehyde. J Org Chem. 2006;71:2862–2869. doi: 10.1021/jo060129c. [DOI] [PubMed] [Google Scholar]; (b) Harriman DJ, Lambropoulos A, Deslongchamps G. In silico correlation of enantioselectivity for the TADDOL catalyzed asymmetric hetero-Diels–Alder reaction. Tetrahedron Lett. 2007;48:689–692. [Google Scholar]
- 32.Li X, Liu P, Houk KN, Birman VB. Origin of Enantioselectivity in CF3–PIP-Catalyzed Kinetic Resolution of Secondary Benzylic Alcohols. J Am Chem Soc. 2008;130:13836–13837. doi: 10.1021/ja805275s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Birman VB, Uffman EW, Jiang H, Li X, Kilbane CJ. 2,3-Dihydroimidazo[1,2-a]pyridines: A New Class of Enantioselective Acyl Transfer Catalysts and Their Use in Kinetic Resolution of Alcohols. J Am Chem Soc. 2004;126:12226–12227. doi: 10.1021/ja0491477. [DOI] [PubMed] [Google Scholar]
- 34.Wheeler SE, McNeil AJ, Müller P, Swager TM, Houk KN. Probing Substituent Effects in Aryl–Aryl Interactions Using Stereoselective Diels–Alder Cycloadditions. J Am Chem Soc. 2010;132:3304–3311. doi: 10.1021/ja903653j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Raju RK, Bloom JWG, An Y, Wheeler SE. Substituent Effects on Non-Covalent Interactions with Aromatic Rings: Insights from Computational Chemistry. ChemPhysChem. 2011;12:3116–3130. doi: 10.1002/cphc.201100542. and references cited therein. [DOI] [PubMed] [Google Scholar]
- 36.Uyeda C, Jacobsen EN. Transition-State Charge Stabilization through Multiple Non-covalent Interactions in the Guanidinium-Catalyzed Enantioselective Claisen Rearrangement. J Am Chem Soc. 2011;133:5062–5075. doi: 10.1021/ja110842s.For a relevant review, see also: Knowles RR, Jacobsen EN. Attractive noncovalent interactions in asymmetric catalysis: Links between enzymes and small molecule catalysts. Proc Natl Acad Sci USA. 2010;107:20678–20685. doi: 10.1073/pnas.1006402107.
- 37.Schreiner PR, Chernish LV, Gunchenko PA, Tikhonchuk EYu, Hausmann H, Serafin M, Schlecht S, Dahl JEP, Calson RMK, Fokin AA. Overcoming lability of extremely long alkane carbon–carbon bonds through dispersion forces. Nature. 2011;477:308–312. doi: 10.1038/nature10367. [DOI] [PubMed] [Google Scholar]
-
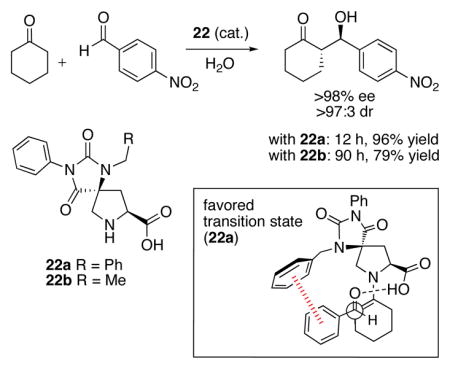
38.A recent paper by Schafmeister et al. reports the asymmetric catalysis of aldol reactions in water by proline derivatives 22. The NBn derivative 22a and the NEt derivative 22b led to similar enantioselectivities and diastereoselectivities, but the rate of reaction for the Bn-substituted catalyst 22a was 44 times faster than that for Et-substituted 22b. M06-2X calculations of the transition states, optimized in water, revealed an edge-to-face interaction between the aldehyde aryl group and the Bn group in 22a. The barrier (ΔG‡) for 22a was 2.6 kcal/mol lower than for 22b, in agreement with the experimental rates. See: Zhao Q, Lam Y, Kheirabadi M, Xu C, Houk KN, Schafmeister CE. J Org Chem. 2012;77:4784–4792. doi: 10.1021/jo300569c.
- 39.Krenske EH, Houk KN, Lohse AG, Antoline JE, Hsung RP. Stereoselectivity in oxyallyl–furan (4 + 3) cycloadditions: control of intermediate conformations and dispersive stabilisation in cycloadditions involving oxazolidinone auxiliaries. Chem Sci. 2010;1:387–392. doi: 10.1039/C0SC00280A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lohse AG, Krenske EH, Antoline JE, Houk KN, Hsung RP. Regioselectivities of (4 + 3) Cycloadditions between Furans and Oxazolidinone-Substituted Oxyallyls. Org Lett. 2010;12:5506–5509. doi: 10.1021/ol1023745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Antoline JE, Krenske EH, Lohse AG, Houk KN, Hsung RP. Stereoselectivities and Regioselectivities of (4 + 3) Cycloadditions Between Allenamide-Derived Chiral Oxazolidinone-Stabilized Oxyallyls and Furans: Experiment and Theory. J Am Chem Soc. 2011;133:14443–14451. doi: 10.1021/ja205700p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.(a) Xiong H, Hsung RP, Berry CR, Rameshkumar C. The First Epoxidations of 1-Amidoallenes. A General Entry to Nitrogen-Substituted Oxyallyl Cations in Highly Stereoselective [4 + 3] Cycloadditions. J Am Chem Soc. 2001;123:7174–7175. doi: 10.1021/ja0108638. [DOI] [PubMed] [Google Scholar]; (b) Antoline JE, Hsung RP. An Unexpected Reversal of Diastereoselectivity in the [4+3]-Cycloaddition Reaction of Nitrogen-Stabilized Oxyallyl Cations with Methyl 2-Furoate. Synlett. 2008:739–744. [Google Scholar]; (c) Lohse AG, Hsung RP. (4+3) Cycloaddition Reactions of Nitrogen-Stabilized Oxyallyl Cations. Chem Eur J. 2011;17:3812–3822. doi: 10.1002/chem.201100260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Evans DA, Chapman KT, Bisaha J. Asymmetric Diels–Alder Cycloaddition Reactions with Chiral α,β-Unsaturated N-Acyloxazolidinones. J Am Chem Soc. 1988;110:1238–1256. [Google Scholar]
- 44.Santos et al. recently reported computational and NMR spectrometric studies suggesting a different mechanism of stereoinduction. They propose that the carbonyl groups of 14 are antiparallel and each binds one AlEt2Cl; steric hindrance from one of the AlEt2Cl groups transmits the chiral information from the oxazolidinone to the incoming diene Bakalova SM, Duarte FJS, Georgieva MK, Cabrita EJ, Santos AG. An Alternative Mechanism for Diels–Alder Reactions of Evans Auxiliary Derivatives. Chem Eur J. 2009;15:7665–7677. doi: 10.1002/chem.200900628.
- 45.Evans DA, Helmchen G, Rüping M. Chiral Auxiliaries in Asymmetric Synthesis. In: Christmann M, Bräse S, editors. Asymmetric Synthesis – The Essentials. 2. Wiley-VCH; Weinheim: 2008. pp. 3–9. completely revised edition. [Google Scholar]
- 46.(a) Barone V, Cossi M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J Phys Chem A. 1998;102:1995–2001. [Google Scholar]; (b) Cossi M, Rega N, Scalmani G, Barone V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J Comput Chem. 2003;24:669–681. doi: 10.1002/jcc.10189. [DOI] [PubMed] [Google Scholar]
- 47.(a) Stark CBW, Eggert U, Hoffmann HMR. Chiral Allyl Cations in Cycloadditions to Furan: Synthesis of 2-(1′-Phenylethoxy)-8-oxabicyclo[3.2.1]oct-6-en-3-one in High Enantiomeric Purity. Angew Chem Int Ed. 1998;37:1266–1268. doi: 10.1002/(SICI)1521-3773(19980518)37:9<1266::AID-ANIE1266>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]; (b) Stark CBW, Pierau S, Wartchow R, Hoffmann HMR. Chrial Allyl Cations Are Captured by Furan with 100% Stereoselectivity: Synthesis of Enantiopure 2-Alkoxy-8-oxabicyclo[3.2.1]oct-6-en-3-ones by Low-Temperature [4+3] Cycloaddition. Chem Eur J. 2000;6:684–691. doi: 10.1002/(sici)1521-3765(20000218)6:4<684::aid-chem684>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 48.Krenske EH, Houk KN, Harmata M. Origin of Stereoselectivity in the (4 + 3) Cycloadditions of Chiral Alkoxy Siloxyallyl Cations with Furan. Org Lett. 2010;12:444–447. doi: 10.1021/ol902591k. [DOI] [PubMed] [Google Scholar]
- 49.Cramer CJ, Barrows SE. Quantum Chemical Characterization of Cycloaddition Reactions between the Hydroxyallyl Cation and Dienes of Varying Nucleophilicity. J Org Chem. 1998;63:5523–5532.Cramer CJ, Barrows SE. Quantum chemical characterization of cycloaddition reactions between 1,3-butadiene and oxyallyl cations of varying electrophilicity. J Phys Org Chem. 2000;13:176–186.See also: Fernández I, Cossío FP, de Cózar A, Lledós A, Mascareñas JL. Concerted and Stepwise Mechanisms in Metal-Free and Metal-Assisted [4+3] Cycloadditions Involving Allyl Cations. Chem Eur J. 2010;16:12147–12157. doi: 10.1002/chem.201001714.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.