PERTURBATION AND SCALED COOK'S DISTANCE

Abstract

Cook's (Cook, 1977) distance is one of the most important diagnostic tools for detecting influential individual or subsets of observations in linear regression for cross-sectional data. However, for many complex data structures (e.g., longitudinal data), no rigorous approach has been developed to address a fundamental issue: deleting subsets with different numbers of observations introduces different degrees of perturbation to the current model fitted to the data and the magnitude of Cook's distance is associated with the degree of the perturbation. The aim of this paper is to address this issue in general parametric models with complex data structures. We propose a new quantity for measuring the degree of the perturbation introduced by deleting a subset. We use stochastic ordering to quantify the stochastic relationship between the degree of the perturbation and the magnitude of Cook's distance. We develop several scaled Cook's distances to resolve the comparison of Cook's distance for different subset deletions. Theoretical and numerical examples are examined to highlight the broad spectrum of applications of these scaled Cook's distances in a formal influence analysis.

1. Introduction

Influence analysis assesses whether a modification of a statistical analysis, called a perturbation (see Section 2.2), seriously affects specific key inferences, such as parameter estimates. Such perturbation schemes include the deletion of an individual or a subset of observations, case weight perturbation, and covariate perturbation among many others [8, 9, 30]. For example, for linear models, a perturbation measures the effect on the model of deleting a subset of the data matrix. In general, perturbation measures do not depend on the data directly, but rather on its structure via the model. If a small perturbation has a small effect on the analysis, our analysis is relatively stable, while if a large perturbation has a small effect on the analysis, we learn that our analysis is robust [11, 16]. If a small perturbation seriously influences key results of the analysis, we want to know the cause [9, 11]. For instance, in influence analysis, a set of observations is flagged as ‘influential’ if its removal from the dataset produces a significant difference in the parameter estimates or equivalently a large value of Cook's distance for the current statistical model [8, 5].

Since the seminal work of Cook [8] on Cook's distance in linear regression for cross-sectional data, considerable research has been devoted to developing Cook's distance for detecting influential observations (or clusters) in more complex data structures under various statistical models [8, 10, 6, 1, 12, 23, 15, 29, 14]. For example, for longitudinal data, Preisser and Qaqish [19] developed Cook's distance for generalized estimating equations, while Christensen, Pearson and Johnson [7], Banerjee and Frees [4], and Banerjee [3] considered case deletion and subject deletion diagnostics for linear mixed models. Furthermore, in the presence of missing data, Zhu et al. [29] developed deletion diagnostics for a large class of statistical models with missing data. Cook's distance has been widely used in statistical practice and can be calculated in popular statistical software, such as SAS and R.

A major research problem regarding Cook's distance that has been largely neglected in the existing literature is the development of Cook's distance for general statistical models with more complex data structures. The fundamental issue that arises here is that the magnitude of Cook's distance is positively associated with the amount of perturbation to the current model introduced by deleting a subset of observations. Specifically, a large value of Cook's distance can be caused by deleting a subset with a larger number of observations and/or other causes such as the presence of influential observations in the deleted subset. To delineate the cause of a large Cook's distance for a specific subset, it is more useful to compute Cook's distance relative to the degree of the perturbation introduced by deleting the subset [11, 30].

The aim of this paper is to address this fundamental issue of Cook's distance for complex data structures in general parametric models. The main contributions of this paper are summarized as follows.

• a.1We propose a quantity to measure the degree of perturbation introduced by deleting a subset in general parametric models. This quantity satisfies several attractive properties including uniqueness, non-negativity, monotonicity, and additivity.
• a.2We use stochastic ordering to quantify the relationship between the degree of the perturbation and the magnitude of Cook's distance. Particularly, in linear regression for cross-sectional data, we first show the stochastic relationship between the Cook's distances for any two subsets with possibly different numbers of observations.
• a.3We develop several scaled Cook's distances and their first-order approximations in order to compare Cook's distance for deleted subsets with different numbers of observations.

The rest of the paper is organized as follows. In Section 2, we quantify the degree of the perturbation for set deletion and delineate the stochastic relationship between Cook's distance and the degree of perturbation. We develop several scaled Cook's distances and derive their first-order approximations. In Section 3, we analyze simulated data and a real dataset using the scaled Cook's distances. We give some final remarks in Section 4.

2. Scaled Cook's Distance

2.1. Cook's distance

Consider the probability function of a random vector ${\mathbf{Y}}^T=(Y_1^T,\dots Y_n^T)$, denoted by p(Y|θ), where θ = (θ₁, . . . , θ_q)^T is a q × 1 vector in an open subset Φ of R^q and Y_i = (y_i,1, . . . , y_i,mi), in which the dimension of Y_i, denoted by m_i, may vary significantly across all i. Cook's distance and many other deletion diagnostics measure the distance between the maximum likelihood estimators of θ with and without Y_i [10, 8]. A subscript ‘[I]’ denotes the relevant quantity with all observations in I deleted. Let Y_[I] be a subsample of Y with Y_I = {Y_(i,j) : (i, j) ∈ I} deleted and p(Y_[I]|θ) be its probability function. We define the maximum likelihood estimators of θ for the full sample Y and a subsample Y_[I] as

$$\widehat{\theta }={\text{argmax}}_{\theta }\text{log}p(\mathbf{Y}\mid \theta )\text{and}{\widehat{\theta }}_{\left[I\right]}={\text{argmax}}_{\theta }\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid \theta ),$$ (2.1)

respectively. Cook's distance for I, denoted by CD(I), can be defined as follows:

$$\mathrm{CD}\left(I\right)={({\widehat{\theta }}_{\left[I\right]}-\widehat{\theta })}^T{G}_{n\theta }({\widehat{\theta }}_{\left[I\right]}-\widehat{\theta }),$$ (2.2)

where G_nθ is chosen to be a positive definite matrix. The matrix G_nθ is not changed or re-estimated when a subset of the data is deleted. Throughout the paper, G_nθ is set as $-{\partial }_{\theta }^2\text{log}p(\mathbf{Y}\mid \widehat{\theta })$ or its expectation, where ${\partial }_{\theta }^2$ represents the second-order derivative with respect to θ. For clustered data, the observations within the same cluster are correlated. A sensible model p(Y|θ) should explicitly model the correlation structure in the clustered data and thus $-{\partial }_{\theta }^2\text{log}p(\mathbf{Y}\mid \widehat{\theta })$ implicitly incorporates such a correlation structure.

More generally, suppose that one is interested in a subset of θ or q₁ linearly independent combinations of θ, say L^Tθ, where L is a q × q₁ matrix with rank(L) = q₁ [4, 10]. The partial inuence of the subset I on ${\mathbf{L}}^T\widehat{\theta }$, denoted by CD(I|L), can be defined as

$$\mathrm{CD}(I\mid \mathbf{L})={({\widehat{\theta }}_{\left[I\right]}-\widehat{\theta })}^T\mathbf{L}{\left\{{\mathbf{L}}^T{G}_{n\theta }^{-1}\mathbf{L}\right\}}^{-1}{\mathbf{L}}^T({\widehat{\theta }}_{\left[I\right]}-\widehat{\theta }).$$ (2.3)

For notational simplicity, even though we may focus on a subset of θ, we do not distinguish between CD(I|L) and CD(I) throughout the paper.

Based on (2.2), we know that Cook's distance CD(I) is explicitly determined by three components including the current model fitted to the data, denoted by $\mathcal{M}$, the dataset Y, and the subset I itself. Cook's distance is also implicitly determined by the goodness of fit of $\mathcal{M}$ to Y for I, denoted by $G(I\mid \mathbf{Y},\mathcal{M})$, and the degree of the perturbation to $\mathcal{M}$ introduced by deleting the subset I, denoted by $\mathcal{P}(I\mid \mathcal{M})$. Thus, we may represent CD(I) as follows:

$$\mathrm{CD}\left(I\right)=F_1(I,\mathcal{M},\mathbf{Y})=F_2(\mathcal{P}(I\mid \mathcal{M}),G(I\mid \mathbf{Y},\mathcal{M})),$$ (2.4)

where F₁(·, ·, ·) and F₂(·,·) represent nonlinear functions.

We may use the value of CD(I) to assess the influential level of the subset I. We may regard a subset I as influential if either the value of CD(I) is relatively large compared with other Cook's distances or the magnitude of CD(I) is greater than the critical points of the χ² distribution [10]. However, for complex data structures, we will show that it is useful to compare Cook's distance relative to its associated degree of perturbation.

2.2. Degree of perturbation

Consider the subset I and the current model $\mathcal{M}$. We are interested in developing a measure to quantify the degree of the perturbation to $\mathcal{M}$ introduced by deleting the subset I regardless of the observed data Y. We emphasize here that the degree of perturbation is a property of the model, unlike Cook's distance which is also a property of Y. Abstractly, $\mathcal{P}(I\mid \mathcal{M})$ should be defined as a mapping from a subset I and $\mathcal{M}$ to a nonnegative number. However, according to the best of our knowledge, no such quantities have ever been developed to define a workable $\mathcal{P}(I\mid \mathcal{M})$ for an arbitrary subset I in general parametric models due to many conceptual difficulties [11]. Specifically, even though [11] placed the Euclidean geometry on the perturbation space for one-sample problems, such a geometrical structure cannot be easily generalizable to general data structures (e.g., correlated data) and related parametric models. For instance, for correlated data, a sensible model $\mathcal{M}$ should model the correlation structure and a good measure $\mathcal{P}(I\mid \mathcal{M})$ should explicitly incorporate the correlation structure specified in $\mathcal{M}$ and the subset I. However, the Euclidean geometry proposed by [11] cannot incorporate the correlation structure in the correlated data.

Our choice of $\mathcal{P}(I\mid \mathcal{M})$ is motivated by five principles as follows.

• (P.a) (non-negativity) For any subset I, $\mathcal{P}(I\mid \mathcal{M})$ is always non-negative.

• (P.b) (uniqueness) $\mathcal{P}(I\mid \mathcal{M})=0$ if and only if I is an empty set.

• (P.c) (monotonicity) If $I_2\subset I_1$, then $\mathcal{P}(I_2\mid \mathcal{M})\le \mathcal{P}(I_1\mid \mathcal{M})$.

• (P.d) (additivity) If $I_2\subset I_1,I_{1\cdot 2}=I_1-I_2$, and p(Y_I1·2|Y_[I1], θ) = p(Y_I1·2|Y_[I1·2], θ) for all θ, then we have $\mathcal{P}(I_1\mid \mathcal{M})=\mathcal{P}(I_2\mid \mathcal{M})+\mathcal{P}(I_{1\cdot 2}\mid \mathcal{M})$.

• (P.e) $\mathcal{P}(I\mid \mathcal{M})$ should naturally arise from the current model $\mathcal{M}$, the data Y, and the subset I.

Principles (P.a) and (P.b) indicate that deleting any nonempty subset always introduces a positive degree of perturbation. Principle (P.c) indicates that deleting a larger subset always introduces a larger degree of perturbation. Principle (P.d) presents the condition for ensuring the additivity property of the perturbation. Since Y_[I1·2] is the union of Y_[I1] and Y_I2, p(Y_I1·2|Y_[I1], θ) = p(Y_I1·2], θ) is equivalent to that of Y_I1·2 being independent of Y_I2 given Y_[I1]. The additivity property has important implications in cross-sectional, longitudinal, and family data. For instance, in longitudinal data, the degree of perturbation introduced by simultaneously deleting two independent clusters equals the sum of their degrees of individual cluster perturbations.

Principle (P.e) requests that $\mathcal{P}(I\mid \mathcal{M})$ should depend on the triple $(\mathcal{M},\mathbf{Y},I)$. We propose $\mathcal{P}(I\mid \mathcal{M})$ based on the Kullback-Leibler divergence between the fitted probability function p(Y|θ) and the probability function of a model for characterizing the deletion of Y_I, denoted by p(Y|θ, I). Note that p(Y|θ) = p(Y_[I]|θ)p(Y_I|Y_[I], θ), where p(Y_I|Y_[I], θ) is the conditional density of YI given Y_[I]. Let θ_* be the true value of θ under $\mathcal{M}$ [24, 25]. We define p(Y|θ, I) as follows:

$$p(\mathbf{Y}\mid \theta ,I)=p({\mathbf{Y}}_{\left[I\right]}\mid \theta )p({\mathbf{Y}}_I\mid {\mathbf{Y}}_{\left[I\right]},{\theta }_{\ast }),$$ (2.5)

in which p(YI|Y_[I], θ_*) is independent of θ. In (2.5), by fixing θ = θ_* in p(Y_I|Y_[I], θ), we essentially drop the information contained in Y_I as we estimate θ. Specifically, ${\widehat{\theta }}_{\left[I\right]}$ is the maximum likelihood estimate of θ under p(Y|θ, I). If $\mathcal{M}$ is correctly specified, then p(Y_I|Y_[I], θ_*) is the true data generator for Y_I given Y_[I]. The Kullback-Leibler distance between p(Y|θ) and p(Y|θ, I), denoted by KL(Y, θ|θ_*, I), is given by

$$\int p(\mathbf{Y}\mid \theta )\text{log}\left(\frac{p(\mathbf{Y}\mid \theta )}{p(\mathbf{Y}\mid \theta ,I)}\right)d\mathbf{Y}=\int p(\mathbf{Y}\mid \theta )\text{log}\left(\frac{p({\mathbf{Y}}_I\mid {\mathbf{Y}}_{\left[I\right]},\theta )}{p({\mathbf{Y}}_I\mid {\mathbf{Y}}_{\left[I\right]},{\theta }_{\ast })}\right)d\mathbf{Y}.$$ (2.6)

We use KL(Y, θ|θ_*, I) to measure the effect of deleting Y_I on estimating θ without knowing that the true value of θ is θ_*. If Y_I is independent of Y_[I], then we have

$$\mathrm{KL}(\mathbf{Y},\theta \mid {\theta }_{\ast },I)=\int p({\mathbf{Y}}_I\mid \theta )\text{log}\left(\frac{p({\mathbf{Y}}_I\mid \theta )}{p({\mathbf{Y}}_I\mid {\theta }_{\ast })}\right)d{\mathbf{Y}}_I,$$

which is independent of Y_[I]. In this case, the effect of deleting Y_I on estimating θ only depends on {p(Y_I|θ) : θ ∊ Θ}.

A conceptual difficulty associated with KL(Y,θ|θ_*, I) is that both θ and θ_* are unknown. Although θ_* is unknown, it can be assumed to be a fixed value from a frequentist viewpoint. For the unknown θ, we can always use the data Y and the current model $\mathcal{M}$ to calculate an estimator $\widehat{\theta }$ in a neighborhood of θ_*. Under some mild conditions [24, 25], one can show that $\sqrt{n}(\widehat{\theta }-{\theta }_{\ast })$ is asymptotically normal and thus $\widehat{\theta }$ should be centered around θ_*. Moreover, since Cook's distance is to quantify the change of parameter estimates after deleting a subset, we need to consider all possible θ around θ_* instead of focusing on a single θ. Specifically, we consider θ in a neighborhood of θ_* by assuming a Gaussian prior for θ with mean θ_* and positive definite covariance matrix Σ_* (e.g., the Fisher information matrix), denoted by p(θ|θ_*, Σ_*). Finally, we define $\mathcal{P}(I\mid \mathcal{M})$ as the weighted Kullback-Leibler distance between p(Y|θ) and p(Y|θ, I) as follows:

$$\mathcal{P}(I\mid \mathcal{M})=\int \mathrm{KL}(\mathbf{Y},\theta \mid {\theta }_{\ast },I)p(\theta \mid {\theta }_{\ast },{\Sigma }_{\ast })d\theta .$$ (2.7)

This quantity $\mathcal{P}(I\mid \mathcal{M})$ can also be interpreted as the average effect of deleting Y_I on estimating θ with the prior information that the estimate of θ is centered around θ_*. Since $\mathcal{P}(I\mid \mathcal{M})$ is directly calculated from the model $\mathcal{M}$ and the subset I, it can naturally account for any structure specified in $\mathcal{M}$. Furthermore, if we are interested in a particular set of components of θ and treat others as nuisance parameters, we may fix these nuisance parameters in their true value.

To compute $\mathcal{P}(I\mid \mathcal{M})$ in a real data analysis, we only need to specify $\mathcal{M}$ and (θ_*, Σ_*). Then, we may use some numerical integration methods to compute $\mathcal{P}(I\mid \mathcal{M})$. Although (θ_*, Σ_*) are unknown, we suggest substituting θ_* by an estimator of θ, denoted by $\tilde{\theta }$, and Σ_* by the covariance matrix of $\tilde{\theta }$. Throughout the paper, since $\widehat{\theta }$ is a consistent estimator of θ_* [24, 25], we set $\tilde{\theta }=\widehat{\theta }$ and Σ_* as the covariance matrix of $\widehat{\theta }$.

We obtain the following theorems, whose detailed assumptions and proofs can be found in the Appendix.

Theorem 1. Suppose that L({Y : p(Y_I|Y_[I], θ) = p(Y_I|Y_[I], θ_*)}) > 0 for any θ = θ_*, where L(A) is the Lebesgue measure of a set A. Then, $\mathcal{P}(I\mid \mathcal{M})$ defined in (2.7) satisfies the four principles (P.a)-(P.d).

As an illustration, we show how to calculate $\mathcal{P}(I\mid \mathcal{M})$ under the standard linear regression model for cross-sectional data as follows.

Example 1. Consider the linear regression model $y_i={\mathbf{x}}_i^T{\beta }_{\ast }+{∊}_i$, where x_i is a p × 1 vector and the ε_i are independently and identically distributed (i.i.d) as $N(0,{\sigma }_{\ast }^2)$. Let Y = (y₁, . . . , y_n)^T and X be an n × p matrix of rank p with i-th row ${\mathbf{x}}_i^T$. In this case, θ = (β^T, σ²)^T . Recall that $\widehat{\beta }={\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}^T\mathbf{y}$, ${\widehat{\sigma }}^2={\mathbf{y}}^T({\mathbf{I}}_n-H_x)\mathbf{y}∕n$, $\text{Cov}\left(\widehat{\beta }\right)={\sigma }_{\ast }^2{\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}$, and $\text{var}\left({\widehat{\sigma }}^2\right)=2{\sigma }_{\ast }^4∕n$, where I_n is an n × n identity matrix and H_x = (h_ij) = X(X^TX)^–1X^T. We first compute the degree of the perturbation for deleting each (y_i; x_i). We consider two scenarios: fixed and random covariates. For the case of fixed covariates, $\mathcal{M}$ assumes $y_i\sim N({\mathbf{x}}_i^T\beta ,{\sigma }^2)$. After some algebraic calculations, it can be shown that $\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$ equals

$$0.5E_{\theta }\left[\text{log}({\sigma }_{\ast }^2∕{\sigma }^2)\right]+0.5\frac{{\mathbf{x}}_i^T{E}_{\theta }\left[(\beta -{\beta }_{\ast }){(\beta -{\beta }_{\ast })}^T\right]{\mathbf{x}}_i}{{\sigma }_{\ast }^2}\approx \frac{1}{2n}+\frac{1}{2}{h}_{ii},$$ (2.8)

where E_θ is taken with respect to $p(\theta \mid {\theta }_{\ast },G_{n\theta }^{-1})$. Moreover, the right hand side of (2.8) contains only terms involving n and X, since perturbation is defined only in terms of the underlying model $\mathcal{M}$. This is also at core why only stochastic ordering is possible for Cooks distance, which is a function of both perturbation and data. See Section 2.3 for detailed discussions. Furthermore, if β is the parameter of interest in θ and σ² is a nuisance parameter, then $0.5E_{\theta }\left[\text{log}({\sigma }_{\ast }^2∕{\sigma }^2)\right]$ and 1/(2n) can be dropped from $\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$ in (2.8).

Furthermore, for the case of random covariates, we assume that the x_i's are independently and identically distributed with mean μ_x and covariance matrix Σ_x. It can be shown that $\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$ equals

$$0.5E_{\theta }\left[\text{log}({\sigma }_{\ast }^2∕{\sigma }^2)\right]+0.5{\sigma }_{\ast }^{-2}\text{tr}\left\{{\Sigma }_x{E}_{\theta }\left[(\beta -{\beta }_{\ast }){(\beta -{\beta }_{\ast })}^T\right]\right\}\approx \frac{1}{2n}+\frac{p}{2n}.$$ (2.9)

If β is the parameter of interest in θ and σ² is a nuisance parameter, then $\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$ reduces to p/(2n). Furthermore, consider deleting a subset of observations {(y_ik, x_ik) : k = 1, · · · , n(I)} and I = {i₁, . . . , i_n(I)}. It follows from Theorem 1 that $\mathcal{P}(\{i_1,\cdots ,i_{n\left(I\right)}\}\mid \mathcal{M})={\sum }_{k=1}^{n\left(I\right)}\mathcal{P}(\left\{i_k\right\}\mid \mathcal{M})$. Furthermore, for the case of random covariates, we have $\mathcal{P}(I\mid \mathcal{M})=n\left(I\right)\mathcal{P}(\left\{1\right\}\mid \mathcal{M})$ for any subset I with n(I) observations. Thus, in this case, deleting any two subsets I₁ and I₂ with the same number of observations, that is n(I₁) = n(I₂), has the same degree of perturbation. An important implication of these calculations in real data analysis is that we can directly compare CD(I₁) and CD(I₂) when n(I₁) = n(I₂).

2.3. Cook's distance and degree of perturbation

To understand the relationship between $\mathcal{P}(I\mid \mathcal{M})$ and CD(I) in (2.4), we temporarily assume that the fitted model $\mathcal{M}$ is the true data generator of Y. To have a better understanding of Cook's distance, we consider the standard linear regression model for cross-sectional data as follows.

Example 1 (continued). We are interested in β and treat σ² as a nuisance parameter. We first consider deleting individual observations in linear regression. Cook's distance [8] for case i, (y_i, x_i), is given by

$$\mathrm{CD}\left(\left\{i\right\}\right)=\frac{{(\widehat{\beta }-{\widehat{\beta }}_{\left[i\right]})}^T{\mathbf{X}}^T\mathbf{X}(\widehat{\beta }-{\widehat{\beta }}_{\left[i\right]})}{{\widehat{\sigma }}^2}=\frac{{\sigma }^2}{{\widehat{\sigma }}^2}{t}_i^2\frac{h_{ii}}{1-h_{ii}},$$ (2.10)

where $\widehat{\beta }$ is the least squares estimate of β, ${\widehat{\sigma }}^2$ is a consistent estimator of σ², $t_i={\widehat{e}}_i∕\left(\sigma \sqrt{1-h_{ii}}\right)$ and ${\widehat{\beta }}_{\left[i\right]}=\widehat{\beta }-{\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{x}}_i{\widehat{e}}_i∕(1-h_{ii})$, in which ${\widehat{e}}_i=y_i-{\mathbf{x}}_i^T\widehat{\beta }$. It should be noted that except for a constant p, CD({i}) is almost the same as the original Cook's distance (Cook, 1977). As shown in (2.8) and (2.9), regardless of the exact value of (y_i, x_i), deleting any (y_i, x_i) has the approximately same degree of perturbation to $\mathcal{M}$. Moreover, the CD({i}) are comparable regardless of i. Specifically, if ε_i N(0, σ²), then $t_i^2$ follows the χ²(1) distribution for all i. For the case of random covariates, if x_i are identically distributed, then all CD({i}) are truly comparable, since they follow the same distribution.

We consider deleting multiple observations in the linear model. Cook's distance for deleting the subset I with n(I) is given by

$$\frac{{(\widehat{\beta }-{\widehat{\beta }}_{\left[I\right]})}^T{\mathbf{X}}^T\mathbf{X}(\widehat{\beta }-{\widehat{\beta }}_{\left[I\right]})}{{\widehat{\sigma }}^2}=\frac{1}{{\widehat{\sigma }}^2}{\widehat{\mathbf{e}}}_I^T{({\mathbf{I}}_{n\left(I\right)}-H_I)}^{-1}{H}_I{({\mathbf{I}}_{n\left(I\right)}-H_I)}^{-1}{\widehat{\mathbf{e}}}_I,$$ (2.11)

where ê_I is an n(I) × 1 vector containing all ê_i for i ∊ I and $H_I={\mathbf{X}}_I{\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}_I^T$, in which X_I is an n(I) × p matrix whose rows are ${\mathbf{x}}_i^T$ for all i ∊ I. Similar to the deletion of a single case, deleting any subset with the same number of observations introduces approximately the same degree of perturbation to $\mathcal{M}$, and the CD(I) are comparable among all subsets with the same n(I). We will make this statement precise in Theorem 2 given below.

Generally, we want to compare CD(I₁) and CD(I₂) for any two subsets with n(I₁) ≠ n(I₂). As shown in Example 1, when n(I₁) > n(I₂), deleting I₁ introduces a larger degree of perturbation to model $\mathcal{M}$ compared to deleting I₂. To compare Cook's distances among arbitrary subsets, we need to understand the relationship between $\mathcal{P}(I\mid \mathcal{M})$ and CD(I) for any subset I. Surprisingly, in linear regression for cross-sectional data, we can show the stochastic relationship between $\mathcal{P}(I\mid \mathcal{M})$ and CD(I) as follows.

Theorem 2. For the standard linear model, where y = Xβ + ε and $∊\sim N(0,{\sigma }^2{I}_n)$, we have the following results:

1. for any $I_2\subset I_1$, CD(₁) is stochastically larger than CD(I₂) for any X, that is, $P(CD\left(I_1\right)>t\mid \mathcal{M})\ge P(CD\left(I_2\right)>t\mid \mathcal{M})$ holds for any t > 0.

2. Suppose that the components of X_I and X_I’ are identically distributed for any two subsets I and I’ with n(I) = n(I’). Thus, CD(I) and CD(I’) follow the same distribution when n(I) = n(I’) and CD(I₁) is stochastically larger than CD(I₂) for any two subsets I₂ and I₁ with n(I₁) > n(I₂).

Theorem 2 (a) shows that the Cook's distances for two nested subsets satisfy the stochastic ordering property. Theorem 2 (b) indicates that for random covariates, the Cook's distances for any two subsets also satisfy the stochastic ordering property under some mild conditions.

According to Theorem 2, for more complex data structures and models, it may be natural to use the stochastic order to stochastically quantify the positive association between the degree of the perturbation and the magnitude of Cook's distance. Specifically, we consider two possibly overlapping subsets I₁ and I₂ with $\mathcal{P}(I_1\mid \mathcal{M})>\mathcal{P}(I_2\mid \mathcal{M})$. Although I₁) may not be greater than CD(I₂) for a fixed dataset Y, CD(I₁), as a random variable, should be stochastically larger than CD(I₂) if $\mathcal{M}$ is the true model for Y. We make the following assumption:

Assumption A1. For any two subsets I₁ and I₂ with $\mathcal{P}(I_1\mid \mathcal{M})>\mathcal{P}(I_2\mid \mathcal{M})$,

$$\mathrm{P}(\mathrm{CD}\left(I_1\right)>t\mid \mathcal{M})\ge \mathrm{P}(\mathrm{CD}\left(I_2\right)>t\mid \mathcal{M})$$ (2.12)

holds for any t > 0, where the probability is taken with respect to $\mathcal{M}$.

Assumption A1 is essentially saying that if $\mathcal{M}$ is the true data generator, then CD(I₁) stochastically dominates CD(I₂) whenever $\mathcal{P}(I_1\mid \mathcal{M})>\mathcal{P}(I_2\mid \mathcal{M})$. According to the definition of stochastic ordering [20], we can now obtain the following proposition.

Proposition 1. Under Assumption A1, for any two subsets I₁ and I₂ with $\mathcal{P}(I_1\mid \mathcal{M})>\mathcal{P}(I_2\mid \mathcal{M})$, Cook's distance satisfies

$$E[h\left(CD\left(I_1\right)\right)\mid \mathcal{M}]\ge E[h\left(CD\left(I_2\right)\right)\mid \mathcal{M}]$$ (2.13)

holds for all increasing functions h(·). In particular, we have $E[CD\left(I_1\right)\mid \mathcal{M}]\ge E[CD\left(I_2\right)\mid \mathcal{M}]$ and $Q_{CD\left(I_1\right)}(\alpha \mid \mathcal{M})$ is greater than the α-quantile of $Q_{CD\left(I_2\right)}(\alpha \mid \mathcal{M})$ for any α ∊ [0, 1], where $Q_{CD\left(I\right)}(\alpha \mid \mathcal{M})$ denotes the α–quantile of the distribution of CD(I) for any subset I.

Proposition 1 formally characterizes the fundamental issue of Cook's distance. Specifically, for any two subsets I₁ and I₂ with $\mathcal{P}(I_1\mid \mathcal{M})>\mathcal{P}(I_2\mid \mathcal{M})$, CD(I₁) has a high probability of being greater than CD(I₂) when $\mathcal{M}$ is the true data generator. Thus, Cook's distance for subsets with different degrees of perturbation are not directly comparable. More importantly, it indicates that CD(I) cannot be simply expressed as a linear function of $\mathcal{P}(I\mid \mathcal{M})$. Thus, the standard solution, which standardizes CD(I) by calculating the ratio of CD(I) over $\mathcal{P}(I\mid \mathcal{M})$, is not desirable for controlling for the effect of $\mathcal{P}(I\mid \mathcal{M})$.

2.4. Scaled Cook's distances

We focus on developing several scaled Cook's distances for I, denoted by SCD(I), to detect relatively influential subsets, while accounting for the degree of perturbation $\mathcal{P}(I\mid \mathcal{M})$. Since we have characterized the stochastic relationship between $\mathcal{P}(I\mid \mathcal{M})$ and CD(I) when $\mathcal{M}$ is the true data generator, we are interested in reducing the effect of the difference among $\mathcal{P}(I\mid \mathcal{M})$ for different subsets I on the magnitude of CD(I). A simple solution is to calculate several features (e.g., mean, median, or quantiles) of CD(I) and match them across different subsets under the assumption that $\mathcal{M}$ is the true data generator. Throughout the paper, we consider two pairs of features including (mean, Std) and (median, Mstd), where Std and Mstd, respectively, denote the standard deviation and the median standard deviation. By matching any of the two pairs, we can at least ensure that the centers and scales of the scaled Cook's distances for different subsets are the same when $\mathcal{M}$ is the true data generator.

We introduce two scaled Cook's distance measures, called scaled Cook's distances, as follows.

Definition 1. The scaled Cook's distances for matching (mean, Std) and (median, Mstd) are, respectively, defined as

$${\mathrm{SCD}}_1\left(I\right)=\frac{\mathrm{CD}\left(I\right)-E[\mathrm{CD}\left(I\right)\mid \mathcal{M}]}{\text{Std}[\mathrm{CD}\left(I\right)\mid \mathcal{M}]}\text{and}{\mathrm{SCD}}_2\left(I\right)=\frac{\mathrm{CD}\left(I\right)-Q_{CD\left(I\right)}(0.5\mid \mathcal{M})}{\text{Mstd}[\mathrm{CD}\left(I\right)\mid \mathcal{M}]},$$

where both the expectation and the quantile are taken with respect to $\mathcal{M}$.

We can use SCD₁(I) and SCD₂(I) to evaluate the relatively influential level for different subsets I. A large value of SCD₁(I) (or SCD₂(I)) indicates that the subset I is relatively influential. Therefore, for any two subsets I₁ and I₂, the probability of observing the event SCD(I₁) > SCD(I₂) and that of the event SCD(I₁) < SCD(I₂) should be reasonably close to each other. Thus, the SCD(I) are roughly comparable. Note that the scaled Cook's distances do not provide a “per unit” effect of removing one observation within the set I, whereas they measure the standardized influential level of the set I when $\mathcal{M}$ is true. Moreover, the standardization in Definition 1 still implies that higher than average values of CD(I) still correspond with high positive values of SCD(I), even though for some deletions, it is possible for SCD(I) to be negative unlike CD(I).

The next task is how to compute $E[\mathrm{CD}\left(I\right)\mid \mathcal{M}]$, $\text{Std}[\mathrm{CD}\left(I\right)\mid \mathcal{M}]$, $\text{Mstd}[\mathrm{CD}\left(I\right)\mid \mathcal{M}]$, and $Q_{CD\left(I\right)}(0.5\mid \mathcal{M})$ for each subset I under the assumption that $\mathcal{M}$ is the true data generator. Computationally, we suggest using the parametric bootstrap to approximate the four quantities of CD(I) as follows.

Step 1. We use $\widehat{\mathcal{M}}=\left\{p(\mathbf{Y}\mid \widehat{\theta })\right\}$ to approximate the model $\mathcal{M}=\left\{p(\mathbf{Y}\mid {\theta }_{\ast })\right\}$, generate a random sample Y^s from $p(\mathbf{Y}\mid \widehat{\theta })$ and then calculate $\mathrm{CD}{\left(I\right)}^{\left(s\right)}=F_1(I,\widehat{\mathcal{M}},{\mathbf{Y}}^s)$ for each s and each subset I.

Step 2. By repeating Step 1 S times, we can obtain a sample {CD(I)^(s) : s = 1, · · ·, S} and then we use its empirical mean $\overline{\mathrm{CD}\left(I\right)}={\sum }_{s=1}^S\mathrm{CD}{\left(I\right)}^{\left(s\right)}∕S$ to approximate E[CD(I)|$\mathcal{M}$].

Step 3. We approximate Std[CD(I)|$\mathcal{M}$], Q_CD(I)(0.5|$\mathcal{M}$), and Mstd[CD(I)|$\mathcal{M}$] by using their corresponding empirical quantities of {CD(I)^(s) : s = 1, · · ·, S}.

In this process, we have used $\widehat{\mathcal{M}}$ to approximate $\mathcal{M}$ [24] and simulated data Y^s from $\widehat{\mathcal{M}}$ in the standard parametric bootstrap method. If Y truly comes from $\mathcal{M}$, then the simulated data Y^s should resemble Y. Since $\widehat{\theta }$ is a consistent estimate of θ_*, $E[F_1(I,\widehat{\mathcal{M}},\mathbf{Y})\mid \widehat{\mathcal{M}}]\approx E[F_1(I,\mathcal{M},\mathbf{Y})\mid \mathcal{M}]$ and thus $\overline{\mathrm{CD}\left(I\right)}$ is a consistent estimate of $E[F_1(I,\mathcal{M},\mathbf{Y})\mid \mathcal{M}]$. Similar arguments hold for the other three quantities of CD(I). In Steps 2 and 3, we can use a moderate S, say S = 100, in order to accurately approximate all four quantities of CD(I). According to our experience, such an approximation is very accurate even for small n. See the simulation studies in Section 3.1 for details. However, for most statistical models with complex data structures, it can be computationally intensive to compute ${\widehat{\theta }}^s$ for each Y^s. We will address this issue in Section 2.6.

As an illustration, we consider how to calculate SCD₁(I) for any subset I in the linear regression model.

Example 1 (continued). In (2.11), since all CD(I) share ${\widehat{\sigma }}^2$, we replace ${\widehat{\sigma }}^2$ by ${\sigma }_{\ast }^2$. Thus, we approximate CD(I) by ${\mathrm{CD}}_{\ast }\left(I\right)={∊}^T{\mathbf{W}}_{\ast }∊∕{\sigma }_{\ast }^2$, where $∊={({∊}_1,\dots ,{∊}_n)}^T\sim N(0,{\sigma }_{\ast }^2{\mathbf{I}}_n)$ and

$${\mathbf{W}}_{\ast }=({\mathbf{I}}_n-H_x)U_I{({\mathbf{I}}_{n\left(I\right)}-H_I)}^{-1}{H}_I{({\mathbf{I}}_{n\left(I\right)}-H_I)}^{-1}{U}_I^T({\mathbf{I}}_n-H_x).$$

To compute SCD₁(I), we just need to calculate the two quantities $E[{\mathrm{CD}}_{\ast }\left(I\right)\mid \mathcal{M}]$ and Std[CD_*(I)|$\mathcal{M}$]. Since CD_*(I) is a quadratic form, it can be shown that

$$\begin{array}{cc}\hfill & E[{\mathrm{CD}}_{\ast }\left(I\right)\mid \mathcal{M}]=E\{\text{tr}\left[{({\mathbf{I}}_{n\left(I\right)}-H_I)}^{-1}\right]\mid {\mathcal{M}}_X\}-n\left(I\right),\hfill \\ \hfill & \text{Var}[{\mathrm{CD}}_{\ast }\left(I\right)\mid \mathcal{M}]=\text{Var}\{\text{tr}\left[{({\mathbf{I}}_{n\left(I\right)}-H_I)}^{-1}\right]\mid {\mathcal{M}}_X\}+2E[\text{tr}\left[{\left\{{({\mathbf{I}}_{n\left(I\right)}-H_I)}^{-1}{H}_I\right\}}^2\right]\mid {\mathcal{M}}_X\},\hfill \end{array}$$

where $E[\cdot \mid {\mathcal{M}}_X]$ denotes the expectation taken with respect to X.

2.5. Conditionally scaled Cook's distances

In certain research settings (e.g., regression), it may be better to perform influence analysis while fixing some covariates of interest, such as measurement time. For instance, in longitudinal data, if different subjects can have different numbers of measurements and measurement times, which are not covariates of interest in an influence analysis, it may be better to eliminate their effect in calculating Cook's distance. We are interested in comparing Cook's distance relative to $\mathcal{P}(I\mid \mathcal{M})$ while fixing some covariates.

To eliminate the effect of some fixed covariates, we introduce two conditionally scaled Cook's distances as follows.

Definition 2. The conditionally scaled Cook's distances (CSCD) for matching (mean, Std) and (median, Mstd) while controlling for Z are, respectively, defined as

$$\begin{array}{cc}\hfill {\mathrm{CSCD}}_1(I,\mathbf{Z})& =\frac{\mathrm{CD}\left(I\right)-E[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]}{\text{Std}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]},\hfill \\ \hfill {\mathrm{CSCD}}_2(I,\mathbf{Z})& =\frac{\mathrm{CD}\left(I\right)-{\mathrm{Q}}_{CD\left(I\right)}(0.5\mid \mathcal{M},\mathbf{Z})}{\text{Mstd}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]},\hfill \end{array}$$

where Z is the set of some fixed covariates in Y and the expectation and quantiles are taken with respect to $\mathcal{M}$ given Z.

According to Definition 2, these conditionally scaled Cook's distances can be used to evaluate the relative influential level of different subsets I given Z. Similar to SCD₁(I) and SCD₂(I), a large value of CSCD₁(I, Z) (or CSCD₂(I, Z)) indicates a large influence of the subset I after controlling for Z. It should be noted that because Z is fixed, the CSCD_k(I, Z) do not reflect the influential level of Z and the CSCD_k(I, Z) may vary across different Z. The conditionally scaled Cook's distances measure the difference of the observed influence level of the set I given Z to the expected influence level of a set with the same data structure when $\mathcal{M}$ is true and Z is fixed.

The next problem is how to compute $E[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$, $\text{Std}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$, $Q_{CD\left(I\right)}(0.5\mid \mathcal{M},\mathbf{Z})$, and $\text{Mstd}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$ for each subset I when $\mathcal{M}$ is the true data generator and Z is fixed. Similar to the computation of the scaled Cook's distances, we can essentially use almost the same approach to approximate the four quantities for CSCD₁(I, Z) and CSCD₂(I, Z). However, a slight difference occurs in the way that we simulate the data. Specifically, let Y_Z be the data Y with Z fixed. We need to simulate random samples ${\mathbf{Y}}_Z^s$ from ${\widehat{\mathcal{M}}}_Z=\left\{p({\mathbf{Y}}_Z\mid \mathbf{Z},\widehat{\theta })\right\}$ and then calculate $\mathrm{CD}{\left(I\right)}^{\left(s\right)}=F_1(I,{\widehat{\mathcal{M}}}_Z,({\mathbf{Y}}_Z^s,\mathbf{Z}))$ for each subset I.

As an illustration, we consider how to calculate CSCD₁(I, Z) for any subset I in the linear regression model.

Example 1 (continued). We set Z = X to calculate CSCD₁(I, Z). We need to compute $E[{\mathrm{CD}}_{\ast }\left(I\right)\mid \mathcal{M},\mathbf{Z}]$ and $\text{Std}[{\mathrm{CD}}_{\ast }\left(I\right)\mid \mathcal{M},\mathbf{Z}]$. Since CD_*(I) is a quadratic form, it is easy to show $E[{\mathrm{CD}}_{\ast }\left(I\right)\mid \mathcal{M}]=\text{tr}\left[{({\mathbf{I}}_{n\left(I\right)}-H_I)}^{-1}\right]-n\left(I\right)$ and $\text{Var}[{\mathrm{CD}}_{\ast }\left(I\right)\mid \mathcal{M}]=2\text{tr}\left[{\left\{{({\mathbf{I}}_{n\left(I\right)}-H_I)}^{-1}{H}_I\right\}}^2\right]$.

2.6. First-order approximations

We have focused on developing the scaled Cook's distances and their approximations for the linear regression model. More generally, we are interested in approximating the scaled Cook's distances for a large class of parametric models for both independent and dependent data.

We obtain the following theorem.

Theorem 3. If Assumptions A2-A5 in the Appendix hold and n(I)/n → γ ∊ [0, 1), where n(I) denotes the number of observations of I, then we have the following results:

1. Let ${\mathbf{F}}_n\left(\theta \right)=-{\partial }_{\theta }^2\text{log}p(\mathbf{Y}\mid \theta ),{\mathbf{f}}_I\left(\theta \right)={\partial }_{\theta }\text{log}p({\mathbf{Y}}_I\mid {\mathbf{Y}}_{\left[I\right]},\widehat{\theta })$ and ${\mathbf{s}}_I\left(\theta \right)=-{\partial }_{\theta }^2\text{log}p({\mathbf{Y}}_I\mid {\mathbf{Y}}_{\left[I\right]},\theta )$, CD(I) can be approximated by

   $$\widetilde{CD}\left(I\right)={\mathbf{f}}_I{\left(\widehat{\theta }\right)}^T{[{\mathbf{F}}_n\left(\widehat{\theta }\right)-{\mathbf{s}}_I\left(\widehat{\theta }\right)]}^{-1}{\mathbf{F}}_n\left(\widehat{\theta }\right){[{\mathbf{F}}_n\left(\widehat{\theta }\right)-{\mathbf{s}}_I\left(\widehat{\theta }\right)]}^{-1}{\mathbf{f}}_I\left(\widehat{\theta }\right);$$ (2.14)

2. $E[\widetilde{CD}\left(I\right)\mid \mathcal{M}]\approx tr\left({\{E[{\mathbf{F}}_n\left(\widehat{\theta }\right)\mid \mathcal{M}]-E[{\mathbf{s}}_I\left(\widehat{\theta }\right)\mid \mathcal{M}]\}}^{-1}E[{\mathbf{s}}_I\left(\widehat{\theta }\right)\mid \mathcal{M}]\right)$;

3. $E[\widetilde{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]\approx tr\left({\{E[{\mathbf{F}}_n\left(\widehat{\theta }\right)\mid \mathcal{M},\mathbf{Z}]-E[{\mathbf{s}}_I\left(\widehat{\theta }\right)\mid \mathcal{M},\mathbf{Z}]\}}^{-1}E[{\mathbf{s}}_I\left(\widehat{\theta }\right)\mid \mathcal{M},\mathbf{Z}]\right)$.

Theorem 3 (a) establishes the first order approximation of Cook's distance for a large class of parametric models for both dependent and independent data. This leads to a substantial savings in computational time, since it is computationally easier to calculate ${\mathbf{f}}_I\left(\widehat{\theta }\right)$, ${\mathbf{F}}_n\left(\widehat{\theta }\right)$, and ${\mathbf{s}}_I\left(\widehat{\theta }\right)$ compared to CD(I). Theorem 3 (b) and (c) give an approximation of $\mathrm{E}[\mathrm{CD}\left(I\right)\mid \mathcal{M}]$ and $\mathrm{E}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$, respectively. Generally, it is difficult to give a simple approximation to $\text{Var}[\mathrm{CD}\left(I\right)\mid \mathcal{M}]$ and $\text{Var}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$, since it involves the fourth moment of ${\mathbf{f}}_I\left(\widehat{\theta }\right)$ which does not have a simple form.

Based on Theorem 3, we can approximate the scaled Cook's distance measures as follows.

Step (i). We generate a random sample Y^s from $p(\mathbf{Y}\mid \mathbf{Z},\widehat{\theta })$ and calculate $\widetilde{\mathrm{CD}}\left(I\right)$ based on the simulated sample Y^s and fixed Z, denoted by $\widetilde{\mathrm{CD}}{\left(I\right)}^s$. Explicitly, to calculate $\widetilde{\mathrm{CD}}{\left(I\right)}^s$, we replace Y in ${\mathbf{f}}_I\left(\widehat{\theta }\right)$, ${\mathbf{F}}_n\left(\widehat{\theta }\right)$, and ${\mathbf{s}}_I\left(\widehat{\theta }\right)$ by Y^s. The computational burden involved in computing $\widetilde{\mathrm{CD}}{\left(I\right)}^s$ is very minor.

Compared to the exact computation of the scaled Cook's distances, we have avoided computing the maximum likelihood estimate of θ based on Y^s, which leads to great computational savings in computing $\widetilde{\mathrm{Cd}}{\left(I\right)}^s$ for large S, say S > 100. Theoretically, since $\widehat{\theta }$ is a consistent estimate of θ_*, $E[\widetilde{\mathrm{CD}}\left(I\right)\mid \mathcal{M}]$ is a consistent estimate of $E[\mathrm{CD}\left(I\right)\mid \mathcal{M}]$. Compared with reestimating ${\widehat{\theta }}^s$ for each Y^s, a drawback of using $\widehat{\theta }$ in calculating $\widetilde{\mathrm{CD}}{\left(I\right)}^s$ is that $\widetilde{\mathrm{CD}}{\left(I\right)}^s$ does not account for the variability in $\widehat{\theta }$. Similar arguments hold for the other three quantities of CD(I).

Step (ii). By repeating Step (i) S times, we can use the empirical quantities of $\{\widetilde{\mathrm{CD}}{\left(I\right)}^s:s=1,\dots ,S\}$ to approximate $E[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$, $\text{Std}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$, $Q_{CD\left(I\right)}(0.5\mid \mathcal{M},\mathbf{Z})$, and $\text{Mstd}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$. Subsequently, we can approximate CSCD₁(I, Z) and CSCD₂(I, Z) and determine their magnitude based on $\widetilde{\mathrm{CD}}{\left(I\right)}^s$.

For instance, let $\widehat{M}\left[\widetilde{\mathrm{CD}}\left(I\right)\right]$ and $\widehat{\text{Std}}\left[\widetilde{\mathrm{CD}}\left(I\right)\right]$ be, respectively, the sample mean and standard deviation of $\{\widetilde{\mathrm{CD}}{\left(I\right)}^s:s=1,\dots ,S\}$. We calculate

$$\begin{array}{cc}\hfill & \mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1(I,\mathbf{Z})=\frac{\{\widetilde{\mathrm{CD}}\left(I\right)-\widehat{M}\left[\widetilde{\mathrm{CD}}\left(I\right)\right]\}}{\widehat{\text{Std}}\left[\widetilde{\mathrm{CD}}\left(I\right)\right]}\hfill \\ \hfill & \mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1{(I,\mathbf{Z})}^s=\frac{\{\widetilde{\mathrm{CD}}{\left(I\right)}^s-\widehat{M}\left[\widetilde{\mathrm{CD}}\left(I\right)\right]\}}{\widehat{\text{Std}}\left[\widetilde{\mathrm{CD}}\left(I\right)\right]}.\hfill \end{array}$$

We use $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1(I,\mathbf{Z})$ to approximate ${\mathrm{CSCD}}_1(I,\mathbf{Z})$ and then compare $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1(I,\mathbf{Z})$ across different I in order to determine whether a specific subset I is relatively influential or not. Moreover, since $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1{(\tilde{I},\mathbf{Z})}^s$ can be regarded as the ‘true’ scaled Cook's distance when $p(\mathbf{Y}\mid \mathbf{Z},\widehat{\theta })$ is true, we can either compare $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1(I,\mathbf{Z})$ with $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1{(\tilde{I},\mathbf{Z})}^s$ for all subsets Ĩ and s or compare $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1(I,\mathbf{Z})$ with $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1{(I,\mathbf{Z})}^s$ for all s. Specifically, we calculate two probabilities as follows:

$$P_A(I,\mathbf{Z})=\sum _{s=1}^{S}1(\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1{(I,\mathbf{Z})}^s\le \mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1(I,\mathbf{Z}))∕S,$$ (2.15)

$$P_B(I,\mathbf{Z})=\sum _{\tilde{I}}\sum _{s=1}^S\frac{1(\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1{(\tilde{I},\mathbf{Z})}^s\le \mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1(I,\mathbf{Z}))}{S\times \#\left(\tilde{I}\right)},$$ (2.16)

where #(Î) is the total number of all possible sets and 1(·) is an indicator function of a set. We regard a subset I as influential if the value of P_A(I, Z) (or P_B(I, Z)) is relatively large. Similarly, we can use the same strategy to quantify the size of CSCD₂(I, Z), SCD₁(I), and SCD₂(I).

Another issue is the accuracy of the first order approximation $\widetilde{\mathrm{CD}}\left(I\right)$ to the exact CD(I). For relatively influential subsets, even though the accuracy of the first-order approximation may be relatively low, $\widetilde{\mathrm{CD}}\left(I\right)$ can easily pick out these influential points. Thus, for diagnostic purposes, the first-order approximation may be more effective at identifying influential subsets compared to the true Cook's distance. We conduct simulation studies to investigate the performance of the first-order approximation $\widetilde{\mathrm{CD}}\left(I\right)$ relative to the exact CD(I). Numerical comparisons are given in Section 3.

We consider cluster deletion in generalized linear mixed models (GLMM). Example 2. Consider a dataset that is composed of a response y_ij, covariate vectors x_ij(p × 1) and c_ij(p₁ × 1), for observations j = 1, . . . , m_i within clusters i = 1, . . . , n. The GLMM assumes that conditional on a p₁ × 1 random variable b_i, y_ij follows an exponential family distribution of the form [18]

$$p(y_{ij}\mid {\mathbf{b}}_i)=\text{exp}\{a{\left(\tau \right)}^{-1}[y_{ij}{\eta }_{ij}-b\left({\eta }_{ij}\right)]+c(y_{ij},\tau )\},$$ (2.17)

where ${\eta }_{ij}=k({\mathbf{x}}_{ij}^T\beta +{\mathbf{c}}_{ij}^T{\mathbf{b}}_i)$ in which β = (β₁, . . . , β_p)^T and k(·) is a known continuously differentiable function. The distribution of b_i is assumed to be N(0, Σ), where Σ = Σ(γ) depends on a p₂ × 1 vector γ of unknown variance components. In this case, we fix all covariates x_ij and c_ij and all m_i and include them in Z. For simplicity, we fix (γ, τ) at an appropriate estimate ($\widehat{\gamma },\widehat{\tau }$) throughout the example.

We focus here on cluster deletion in GLMMs. After some calculations, the first order approximation of CD(I_i) for deleting the i-th cluster is given by

$$\widetilde{\mathrm{CD}}\left(I_i\right)={\partial }_{\beta }{\ell }_i{\left(\widehat{\beta }\right)}^T{[{\mathbf{F}}_n\left(\widehat{\beta }\right)-{\mathbf{f}}_i\left(\widehat{\beta }\right)]}^{-1}{\mathbf{F}}_n\left(\widehat{\beta }\right){[{\mathbf{F}}_n\left(\widehat{\beta }\right)-{\mathbf{f}}_i\left(\widehat{\beta }\right)]}^{-1}{\partial }_{\beta }{\ell }_i\left(\widehat{\beta }\right),$$ (2.18)

where I_i = {(i, 1), . . . ,(i, m_i)}, ${\ell }_i\left(\beta \right)$ is the log-likelihood function for the i–th cluster, ${\mathbf{f}}_i\left(\beta \right)=-{\partial }_{\beta }^2{\ell }_i\left(\beta \right)$ and ${\mathbf{F}}_n\left(\beta \right)={\sum }_{i=1}^n{\mathbf{f}}_i\left(\beta \right)$. Note that

$${\partial }_{\beta }{\ell }_i\left(\widehat{\beta }\right)\approx \{{\mathbf{I}}_p-{\mathbf{f}}_i\left(\widehat{\beta }\right){\left[{\mathbf{F}}_n\left({\beta }_{\ast }\right)\right]}^{-1}\}{\partial }_{\beta }{\ell }_i\left({\beta }_{\ast }\right)+{\mathbf{f}}_i\left(\widehat{\beta }\right){\left[{\mathbf{F}}_n\left({\beta }_{\ast }\right)\right]}^{-1}\sum _{j\ne i}{\partial }_{\beta }{\ell }_j\left({\beta }_{\ast }\right).$$

Then, conditional on all the covariates and {m₁, . . . , m_n} in Z, we can show that $\mathrm{E}[\widetilde{\mathrm{CD}}\left(I_i\right)\mid \mathcal{M},\mathbf{Z}]$ can be approximated by $\text{tr}\left({\{\mathrm{E}[{\mathbf{F}}_n\left(\widehat{\beta }\right)\mid \mathcal{M},\mathbf{Z}]-\mathrm{E}[{\mathbf{f}}_i\left(\widehat{\beta }\right)\mid \mathcal{M},\mathbf{Z}]\}}^{-1}\mathrm{E}[{\mathbf{f}}_i\left(\widehat{\beta }\right)\mid \mathcal{M},\mathbf{Z}]\right)$ when $\mathcal{M}$ is true. Moreover, we may approximate $\text{Var}[\widetilde{\mathrm{CD}}\left(I_i\right)\mid \mathcal{M},\mathbf{Z}]$ by using the fourth moment of ${\partial }_{\beta }{\ell }_i\left({\beta }_{\ast }\right)$. It is not straightforward to approximate $Q_{CD\left(I_i\right)}(0.5\mid \mathcal{M},\mathbf{Z})$ and $\text{Mstd}[\mathrm{CD}\left(I_i\right)\mid \mathcal{M},\mathbf{Z}]$. Computationally, we employ the parametric bootstrap method described above to approximate the conditionally scaled Cook's distances CSCD₁(I_i, Z) and CSCD₂(I_i, Z).

3. Simulation Studies and A Real Data Example

In this section, we illustrate our methodology with simulated data and a real data example. We also include some additional results in the supplement article [27]. The code along with its documentation for implementing our methodology is available on the first author's website at http://www.bios.unc.edu/research/bias/software.html.

3.1. Simulation Studies

The goals of our simulations were to examine the finite sample performance of Cook's distance and the scaled Cook's distances and their first-order approximations for detecting influential clusters in longitudinal data. We generated 100 datasets from a linear mixed model. Specifically, each dataset contains n clusters. For each cluster, the random effect b_i was first independently generated from a $N(0,{\sigma }_b^2)$ distribution and then, given b_i, the observations y_ij (j = 1, . . . , m_i; i = 1, . . . , n) were independently generated as $y_{ij}\sim N({\mathbf{x}}_{ij}^T\beta +b_i,{\sigma }_y^2)$ and the m_i were randomly drawn from {1, . . . 5}. The covariates x_ij were set as (1, u_i, t_ij)^T, among which t_ij represents time and u_i denotes a baseline covariate. Moreover, t_ij = log(j) and the u_i's were independently generated from a N(0, 1) distribution. For all 100 datasets, the responses were repeatedly simulated, whereas we generated the covariates and cluster sizes only once in order to fix the effect of the covariates and cluster sizes on Cook's distance for each cluster. The true value of θ = (β^T, σ_b, σ_y)^T was fixed at (1, 1, 1, 1, 1)^T. The sample size n was set at 12 to represent a small number of clusters.

For each simulated dataset, we considered the detection of influential clusters [4]. We fitted the same linear mixed model and used the expectation-maximization (EM) algorithm to calculate $\widehat{\theta }$ and ${\widehat{\theta }}_{\left[I\right]}$ for each cluster I. We treated (σ_b, σ_y) as nuisance parameters and β as the parameter vector of interest. We calculated the degree of the perturbation $\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$ for deleting each subject {i} while fixing the covariates, and then we calculated the conditionally scaled Cook's distances and associated quantities. Let x_i be an m_i × 3 matrix with the j-th row being ${\mathbf{x}}_{i,j}^T$. It can be shown that for the case of fixed covariates, we have

$$\mathcal{P}(\left\{i\right\}\mid \mathcal{M})=0.5\text{tr}\left\{{\mathbf{x}}_i^T{R}_i{\left(\widehat{\alpha }\right)}^{-1}{\mathbf{x}}_i{E}_{\beta }\left[(\beta -{\beta }_{\ast }){(\beta -{\beta }_{\ast })}^T\right]\right\},$$ (3.1)

where E_β is taken with respect to $p(\beta \mid {\beta }_{\ast },G_{n\beta }^{-1})$ and $R_i\left(\alpha \right)={\sigma }_y^2{\mathbf{I}}_{m_i}+{\sigma }_b^2{1}_{m_i}^{\otimes 2}$, in which $\alpha ={({\sigma }_b^2,{\sigma }_y^2)}^T$ and 1_mi is an m_i × 1 vector with all elements one. We set $G_{n\beta }^{-1}={\left[{\sum }_{i=1}^n{\mathbf{x}}_i^T{R}_i{\left(\widehat{\alpha }\right)}^{-1}{\mathbf{x}}_i\right]}^{-1}$ and substituted β_* by $\widehat{\beta }$.

We carried out three experiments as follows. The first experiment was to evaluate the accuracy of the first-order approximation to CD(I). The explicit expression of $\widetilde{\mathrm{CD}}\left(I\right)$ is given in Example S2 of the supplementary document. We considered two scenarios. In the first scenario, we directly simulated 100 datasets from the above linear mixed model. In the second scenario, for each simulated dataset, we deleted all the observations in clusters n – 1 and n and then reset (m₁, b₁) = (1, 4) and (m_n, b_n) = (5, 3) to generate y_i,j for i = 1, n and all j according to the above linear mixed model. Thus, the new first and n-th clusters can be regarded as influential clusters due to the extreme values of b₁ and b_n. Moreover, the number of observations in these two clusters is unbalanced. We calculated CD(I) and $\widetilde{\mathrm{CD}}\left(I\right)$, the average CD(I), and the biases and standard errors of the differences $\mathrm{CD}\left(I\right)-\widetilde{\mathrm{CD}}\left(I\right)$ for each cluster {i} (Table 1).

Table 1.

Selected results from simulation studies for n = 12 and the two scenarios: m_i, $\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$, M, SD, Mdif (×10^–2), and SDdif (×10^–1) of the three quantities CD(I), $E[CD\left(I\right)\mid \mathcal{M},\mathbf{Z}]$, and $Std[CD\left(I\right)\mid \mathcal{M},\mathbf{Z}]$. m_i; denotes the cluster size of subset {i}; $\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$ denotes the degree of perturbation; M denotes the mean; SD denotes the standard deviation; Mdif and SDdif, respectively, denote the mean and standard deviation of the differences between each quantity and its first-order approximation. In the first scenario, all observations were generated from the linear mixed model, while in the second scenario, two clusters were influential clusters and highlighted in bold. For each case, 100 simulated datasets were used. Results were sorted according to the degree of perturbation for each cluster.

CD (I)
Scenario I						Scenario II
mi	$\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$	M	Mdif	SD	SDdif	mi	$\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$	M	Mdif	SD	SDdif
1	0.10	0.11	0.01	0.09	0.03	1	0.08	0.37	1.01	0.18	0.18
2	0.11	0.12	0.32	0.12	0.15	2	0.11	0.10	0.08	0.09	0.12
2	0.11	0.15	1.24	0.18	0.64	1	0.11	0.08	0.02	0.11	0.02
2	0.13	0.18	0.87	0.19	0.36	2	0.13	0.13	0.08	0.12	0.12
2	0.15	0.17	0.25	0.19	0.20	2	0.16	0.13	-0.13	0.12	0.08
3	0.16	0.23	0.55	0.19	0.50	2	0.20	0.20	0.08	0.19	0.12
2	0.19	0.26	-0.02	0.32	0.25	3	0.23	0.21	-0.06	0.18	0.22
3	0.22	0.34	2.97	0.35	0.99	4	0.25	0.23	0.37	0.23	0.26
4	0.27	0.41	3.35	0.38	1.77	5	0.28	0.78	18.59	0.61	4.71
5	0.40	0.70	5.43	0.60	1.90	5	0.37	0.38	0.90	0.32	0.46
4	0.57	1.15	1.57	1.29	1.73	5	0.54	0.70	1.32	0.68	0.82
5	0.60	1.21	3.62	1.49	1.62	4	0.56	0.65	1.06	0.69	0.54

$E[CD\left(I\right)\mid \mathcal{M},\mathbf{Z}]$
Scenario I						Scenario II
mi	$\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$	M	Mdif	SD	SDdif	mi	$\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$	M	Mdif	SD	SDdif
1	0.10	0.12	0.22	0.02	0.05	1	0.08	0.09	0.43	0.01	0.04
2	0.11	0.12	0.41	0.01	0.03	2	0.11	0.12	0.45	0.02	0.04
2	0.11	0.13	0.46	0.02	0.04	1	0.11	0.13	0.09	0.02	0.03
2	0.12	0.15	0.40	0.02	0.07	2	0.13	0.15	0.38	0.02	0.04
2	0.15	0.17	0.34	0.03	0.08	2	0.16	0.18	0.26	0.02	0.04
3	0.16	0.18	0.77	0.02	0.08	2	0.20	0.23	0.12	0.03	0.05
2	0.19	0.22	0.21	0.04	0.09	3	0.23	0.27	0.46	0.03	0.07
3	0.22	0.26	0.62	0.04	0.09	4	0.25	0.29	1.13	0.03	0.13
4	0.26	0.32	1.63	0.03	0.15	5	0.28	0.36	1.94	0.04	0.18
5	0.40	0.55	2.58	0.07	0.29	5	0.37	0.48	1.86	0.05	0.18
4	0.57	0.97	2.21	0.12	0.21	5	0.53	0.82	4.26	0.10	0.34
5	0.60	1.03	5.87	0.16	0.99	4	0.56	0.93	1.64	0.11	0.17

$Std[CD\left(I\right)\mid \mathcal{M},\mathbf{Z}]$
Scenario I						Scenario II
mi	$\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$	M	Mdif	SD	SDdif	mi	$\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$	M	Mdif	SD	SDdif
1	0.10	0.18	1.48	0.04	0.20	1	0.08	0.13	1.05	0.04	0.22
2	0.11	0.14	1.16	0.03	0.10	2	0.11	0.14	1.18	0.03	0.12
2	0.11	0.15	1.37	0.03	0.16	1	0.11	0.18	0.78	0.04	0.10
2	0.13	0.18	1.72	0.05	0.35	2	0.13	0.18	1.15	0.03	0.13
2	0.15	0.21	2.02	0.05	0.25	2	0.16	0.23	1.28	0.04	0.14
3	0.16	0.19	2.05	0.03	0.25	2	0.20	0.30	1.07	0.06	0.16
2	0.19	0.29	2.36	0.07	0.24	3	0.23	0.31	1.72	0.06	0.22
3	0.22	0.30	2.55	0.07	0.32	4	0.25	0.30	1.96	0.05	0.42
4	0.26	0.35	2.84	0.06	0.39	5	0.28	0.39	4.06	0.09	0.66
5	0.40	0.58	2.13	0.11	0.71	5	0.37	0.50	2.67	0.09	0.52
4	0.57	1.16	1.17	0.18	0.55	5	0.53	0.89	0.60	0.14	0.68
5	0.60	1.14	-4.18	0.25	2.29	4	0.56	1.13	0.94	0.21	0.41

Inspecting Table 1 reveals three findings as follows. First, when no influential cluster is present in the first scenario, the average CD(I) is an increasing function of $\mathcal{P}(I\mid \mathcal{M})$, whereas it is only positively proportional to the cluster size n(I) with a correlation coefficient of 0.83. This result agrees with the results of Proposition 1. Secondly, in the second scenario, the average CD(I) for the true ’good’ clusters is positively proportional to $\mathcal{P}(I\mid \mathcal{M})$ with a correlation coefficient of 0.76, while that for the influential clusters is associated with both $\mathcal{P}(I\mid \mathcal{M})$ and the amount of influence that we introduced. Thirdly, for the true ‘good’ clusters, the first-order approximation is very accurate and leads to small average biases and standard errors. Even for the influential clusters, $\widetilde{\mathrm{CD}}\left(I\right)$ is relatively close to CD(I). For instance, for cluster {n}, the bias of 0.19 is relatively small compared with 0.78, the mean of CD({n}).

In the second experiment, we considered the same two scenarios as the first experiment. Specifically, for each dataset, we approximated $E[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$ and $\text{Std}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$ by setting S = 200 and using their empirical ones, and calculated their first approximations $\widehat{M}\left[\widetilde{\mathrm{CD}}\left(I\right)\right]$ and $\widehat{\text{Std}}\left[\widetilde{\mathrm{CD}}\left(I\right)\right]$. Across all 100 data sets, for each cluster I, we computed the averages of $E[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$ and $\text{Std}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$, and the biases and standard errors of the differences $E[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]-\widehat{M}\left[\widetilde{\mathrm{CD}}\left(I\right)\right]$ and $\text{Std}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]-\widehat{\text{Std}}\left[\widetilde{\mathrm{CD}}\left(I\right)\right]$.

Table 1 shows the results for each scenario. First, in both scenarios, the average $E[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$ is an increasing function of $\mathcal{P}(I\mid \mathcal{M})$, whereas it is only positively proportional to the cluster size n(I) with a correlation coefficient (CC) of 0.80. This is in agreement with the results of Proposition 1. The average of $\text{Std}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$ are positively proportional to m_i (CC=0.76) and $\mathcal{P}(I\mid \mathcal{M})$ (CC=0.99). Secondly, for all clusters, the first-order approximations of $E[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$ and $\text{Std}[\mathrm{CD}\left(I\right)\mid \mathcal{M},\mathbf{Z}]$ are very accurate and lead to small average biases and standard errors.

The third experiment was to examine the finite sample performance of Cook's distance and the scaled Cook's distances for detecting influential clusters in longitudinal data. We considered two scenarios. In the first scenario, for each of the 100 simulated datasets, we deleted all the observations in cluster n and then reset m_n = 1 and varied b_n from 0.6 to 6.0 to generate y_n,j according to the above linear mixed model. The second scenario is almost the same as the first scenario except that we reset m_n = 10. Note that when the value of b_n is relatively large, e.g., b_n = 2:5, the n-th cluster is an influential cluster, whereas the n-th cluster is not influential for small b_n. A good case-deletion measure should detect the n-th cluster as truly influential for large b_n, whereas it does not for small b_n. For each data set, we approximated CSCD₁(I, Z), CSCD₂(I, Z), $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1(I,\mathbf{Z})$, and $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_2(I,\mathbf{Z})$ by setting S = 100. Subsequently, we calculated P_A(I, Z) and P_B(I, Z) in (2.15) and $P_C(I,\mathbf{Z})={\sum }_{I\ne \left\{n\right\}}1(\mathrm{CD}\left(I\right)\le \mathrm{CD}\left(\left\{n\right\}\right))∕(n-1)$. Finally, across all 100 datasets, we calculated the averages and standard errors of all diagnostic measures for the n-th cluster for each scenario.

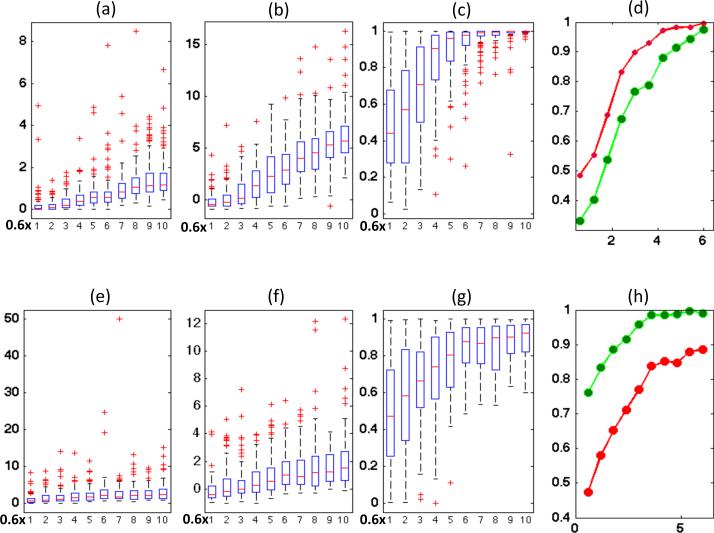
Inspecting Figure 1 reveals some findings as follows. First, deleting the n-th cluster with 10 observations causes a larger effect than that with 1 observation (Fig 1 (a) and (e), (d) and (h)). As expected, the distributions of CD({n}) and $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1(I,\mathbf{Z})$ shift up as b_n increases (Fig 1 (a), (b), (e), and (f)). Secondly, in the first scenario, CD({n}) is stochastically smaller than most other CD(I)s, when the value of b_n is relatively small (Fig. 1 (d)). However, in the second scenario, CD({n}) is stochastically larger than most other CD(I)s (Fig. 1 (h)) even for small values of b_n. Specifically, when m_n = 1, the average P_C({n}, Z) is smaller than 0.4 as b_n = 0.6 and b_n = 1.2, whereas when m_n = 10, the average P_C({n}, Z) is higher than 0.75 even as b_n = 0.6. In contrast, in the two scenarios, the value of P_B({n}, Z) is close to 0.5 as b_n = 0.6 (Fig. 1 (d) and (h)). It indicates that the cluster size does not have a big effect on the distribution of $\mathrm{C}\widetilde{\mathrm{SC}}{\mathrm{D}}_1(I,\mathbf{Z})$ (Fig. 1 (c) and (g)).

Fig 1.

Simulation results from 100 datasets simulated from a linear mixed model in the two scenarios. The first row corresponds to the first scenario, in which m₁₂ = 1 and b₁₂ varies from 0.6 to 6.0. The second row corresponds to the second scenario, in which m₁₂ = 10 and b₁₂ varies from 0.6 to 6.0. Panels (a) and (e) show the box plots of Cook's distances as a function of b₁₂; panels (b) and (f) show the box plots of CSCD₁(I, Z) as a function of b₁₂; panels (c) and (g) show the box plots of P_B(I, Z) as a function of b₁₂; panels (d) and (h) show the mean curve of P_B(I, Z) based on CSCD₁(I, Z) (red line) and the mean curve of P_C(I, Z) based on CD(I) (green line) as functions of b₁₂.

3.2. Yale Infant Growth Data

The Yale infant growth data were collected to study whether cocaine exposure during pregnancy may lead to the maltreatment of infants after birth, such as physical and sexual abuse. A total of 298 children were recruited from two subject groups (cocaine exposed group and unexposed group). One feature of this dataset is that the number of observations per children m_i varies significantly from 2 to 30 [22, 21]. The total number of data points is ${\sum }_{i=1}^n{m}_i=3176$. Following Zhang [26], we considered two linear mixed models given by $y_{i,j}={\mathbf{x}}_{i,j}^T\beta +{∊}_{i,j}$, where y_i,j is the weight (in kilograms) of the j-th visit from the i-th subject, x_i,j = (1, d_i,j, (d_i,j – 120)⁺, (d_i,j – 200)⁺, (g_i – 28)⁺, d_i,j(g_i – 28)⁺, d_i,j(g_i – 28)⁺, (d_i,j – 60)⁺ (g_i – 28)⁺, (d_i,j – 490)⁺(g_i – 28)⁺, s_id_i,j, s_i(d_i,j – 120)⁺)^T, in which d_i,j and g_i (days) are the age of visit and gestational age, respectively, and s_i is the indicator for gender. In addition, we assumed ε_i = (ε_i,1, . . . , ε_i,mi)^T ~ N_mi (0, R_i(α)), where α is a vector of unknown parameters in R_i(α). We first considered $R_i\left(\alpha \right)={\alpha }_0{\mathbf{I}}_{m_i}+{\alpha }_1{1}_{m_i}^{\otimes 2}$. We refer to this model as model M₁. Then, it is assumed that variance and autocorrelation parameters are, respectively, given by V(d) = exp(α₀ + α₁d + α₂d² + α₃d³) and ρ(l) = α₄ + α₅l, where l is the lag between two visits. We refer to this model as model M₂.

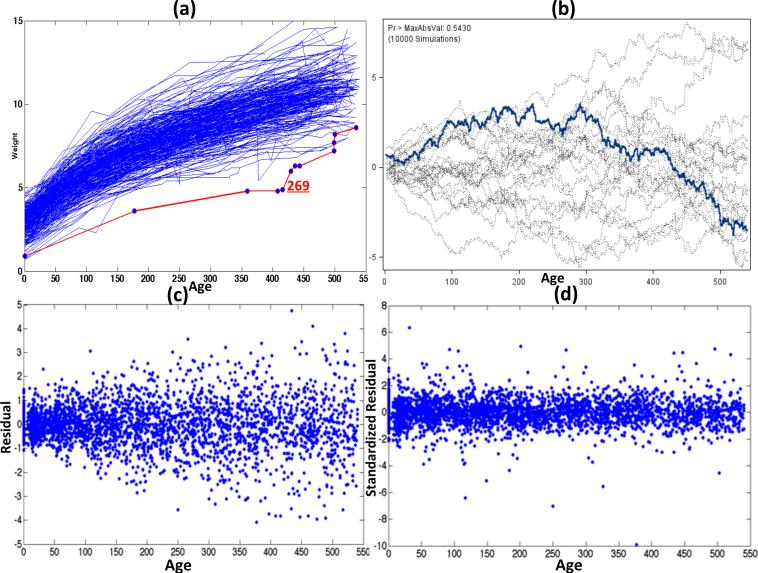
We systematically examined the key assumptions of models M₁ and M₂ as follows. (i) We presented a cumulative residual plot and calculated the cumulative sums of residuals over the age of the visit to test ${\mathbf{x}}_{i,j}^T\beta$ [17], whose p-value is greater than 0.543. It may suggest that the mean structure is reasonable. The cumulative residual plot is given in Figure 2 (b).

Fig 2.

Yale infant growth data. Panel (a) presents the line plot of infant weight against age, in which the observations of subject 269 are highlighted; panel (b) shows the cumulative residual curve versus age, in which the observed cumulative residual curve is highlighted in blue; and panels (c) and (d), respectively, present age versus raw residual and age versus standardized residual for cluster deletion.

(ii) For model M₁, inspecting the plot of raw residuals $r_{i,j}=y_{i,j}-{\mathbf{x}}_{i,j}^T\widehat{\beta }$ against age in Figure 2 (c) reveals that the variance of the raw residuals appears to increase with the age of visit. As pointed by Zhang [26], it may be more sensible to use model M₂. Let ${\tilde{\mathbf{r}}}_i={({\tilde{r}}_{i,1},\dots ,{\tilde{r}}_{i,m_i})}^T=R_i{\left(\widehat{\alpha }\right)}^{-1∕2}{\mathbf{r}}_i$ be the vector of standardized residuals of M₂, where r_i = (r_i,1, . . . , r_i,mi)^T. The standardized residuals under M₂ do not have any apparent structure as age increases (Figure 2 (d)).

(iii) Under each model, we calculated CD(I) for each child [4]. We treated β as parameters of interest and all elements of α as nuisance parameters. For model M₁, we obtained a strong Pearson correlation of 0.363 between Cook's distance and the cluster size. This indicates that the bigger the cluster size, the larger the Cook's distance measure. Figure 4 (b) highlights the top ten influential subjects. Compared with model M₁, we observed similar findings by using CD(I) under model M₂, which were omitted for space limitations.

There are several difficulties in using Cook's distance under both models M₁ and M₂ [19, 7, 4, 3]. First, cluster size varies significantly across children and deleting a larger cluster may have a higher probability of having a larger influence as discussed in Section 2.3. For instance, we observe (m₂₈₅, CD({285})) = (8, 0.738) and (m₂₇₄, CD({274})) = (22, 1.163). A larger CD({274}) can be caused by a larger m₂₇₄ = 22 and/or influential subject 274, among others. Since m₂₇₄ is much larger than m₂₈₅, it is difficult to claim that subject 274 is more influential than subject 285. Secondly, there is no rule for determining whether a specific subject is influential relative to the fitted model. Specifically, it is unclear whether the subjects with larger CD({i}) are truly influential or not. Thirdly, inspecting Cook's distance solely does not seem to delineate the potential misspecification of the covariance structure under model M₁. We will address these three difficulties by using the new case-deletion measures.

(iv) Under each model, we calculated $\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$ for deleting each subject {i} for fixed covariates, and then we calculated the conditionally scaled Cook's distances and associated quantities. We then used 1000 bootstrap samples to approximate CSCD₁(I, Z) and CSCD₂(I, Z). Subsequently, we calculated P_A(I, Z) and P_B(I, Z) in (2.15).

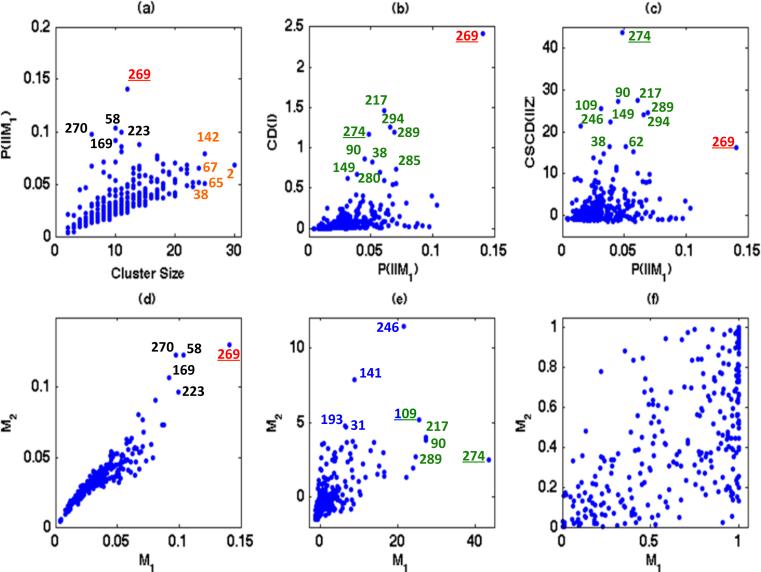
We observed several findings. First, under model M₁, we observed a strong positive correlation between $\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$ and m_i (Fig. 3 (a)). Secondly, even though m₂₆₉ = 12 is moderate, subject 269 has the largest degree of perturbation. Inspecting the raw data in Figure 2 (a) reveals that subject 269 is of older age during visits compared with other subjects. Thirdly, we also observed a strong positive correlation between $\mathcal{P}(\left\{i\right\}\mid \mathcal{M})$ and the Cook's distance (Fig. 3 (b)), which may indicate their stochastic relationship as discussed in Section 2.3. Fourthly, we observed a positive correlation between Cook's distance and the conditionally scaled Cook's distance (Fig. 3(b) and (c)), but their levels of influence for the same subject are quite different. For instance, the magnitude of CSCD₁({269}, Z) is only moderate, whereas CD₁({269}, Z) is the highest one. We observed similar findings under model ${\mathcal{M}}_2$ and presented some findings in Figure 3 (d) and (e).

Fig 3.

Yale infant growth data. Panel (a) shows m_i versus $\mathcal{P}(I\mid {\mathcal{M}}_1)$, in which the ten subjects with the largest values of degree of perturbation or cluster size are highlighted; panel (b) shows $\mathcal{P}(I\mid {\mathcal{M}}_1)$ versus CD(I), in which the top ten influential subjects are highlighted; panel (c) shows $\mathcal{P}(I\mid {\mathcal{M}}_1)$ versus CSCD₁(I, Z), in which the top eleven influential subjects are highlighted; and panels (d), (e), and (f), respectively, show $\mathcal{P}(I\mid \mathcal{M})$, CSCD₁(I, Z), and P_B(I, Z) for models ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$.

We used P_B(I, Z) to quantify whether a specific subject is influential relative to the fitted model ${\mathcal{M}}_1$ (Fig. 3 (f)). For instance, since CD({246}) = 0.253, it is unclear whether subject 246 is influential or not according to CD, whereas we have CSCD₁({246}, Z) = 21.443 and P_B({246}, Z) = 1.0. Thus, subject 246 is really influential after eliminating the effect of the cluster size. Moreover, it is difficult to compare the influential levels of subjects 274 and 285 using CD. All of the conditionally scaled Cook's distances and associated quantities suggest that subject 274 is more influential than subject 285 after eliminating the degree of perturbation difference. We observed similar findings under model ${\mathcal{M}}_2$ and omitted them due to space limitations. See Figure 3 (d) and (e) for details.

We compared the goodness of fit of models ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$ to the data by using the proposed case-deletion measures. First, inspecting Figure 3 (d) reveals a strong similarity between the degrees of perturbation under models ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$ for all subjects. Secondly, by using the conditionally scaled Cook's distance, we observed the different levels of influence for the same subject under ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$. For instance, CSCD₁(I, Z) identifies subjects 246, 141, 109, 193 and 31 as the top five influential subjects under ${\mathcal{M}}_1$, whereas it identifies subjects 274, 217, 90, 109, and 289 as the top ones under ${\mathcal{M}}_2$. Finally, examining P_B(I, Z) reveals a large percentage of influential points for model ${\mathcal{M}}_1$, but a small percentage of influential points for model ${\mathcal{M}}_2$. See Figure 3 (f) for details. This may indicate that model ${\mathcal{M}}_2$ outperforms model ${\mathcal{M}}_1$. Furthermore, although we may develop goodness-of-fit statistics based on the scaled Cook's distances and show that model ${\mathcal{M}}_2$ outperforms model ${\mathcal{M}}_1$, this will be a topic of our future research.

In summary, the use of the new case-deletion measures provides new insights in real data analysis. First, $\mathcal{P}(I\mid \mathcal{M})$ explicitly quantifies the degree of perturbation introduced by deleting each subject. Secondly, CSCD_k(I, Z) for k = 1, 2 explicitly account for the degree of perturbation for each subject. Thirdly, P_B(I, Z) allows us to quantify whether a specific subject is influential relative to the fitted model. Fourthly, inspecting P_B(I, Z) and CSCD_k(I, Z) may delineate the potential misspecification of the covariance structure under model M₁.

4. Discussion

We have introduced a new quantity to quantify the degree of perturbation and examined its properties. We have used stochastic ordering to quantify the relationship between the degree of the perturbation and the magnitude of Cook's distance. We have developed several scaled Cook's distances to address the fundamental issue of deletion diagnostics in general parametric models. We have shown that the scaled Cook's distances provide important information about the relative influential level of each subset. Future work includes developing goodness-of-fit statistics based on the scaled Cook's distances, developing Bayesian analogs to the scaled Cook's distances, and developing user-friendly R code for implementing our proposed measures in various models, such as survival models and models with missing covariate data.

Appendix

The following assumptions are needed to facilitate the technical details, although they are not the weakest possible conditions. Because we develop all results for general parametric models, we only assume several high-level assumptions as follows.

Assumption A2. ${\widehat{\theta }}_{\left[I\right]}$ for any I is a consistent estimate of θ_* ∈ Θ.

Assumption A3. All p(Y_[I]|θ) are three times continuously differentiable on Θ and satisfy

$$\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid \theta )=\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid {\theta }_{\ast })+\Delta {\left(\theta \right)}^T{J}_{n,\left[I\right]}\left({\theta }_{\ast }\right)-0.5\Delta {\left(\theta \right)}^T{\mathbf{F}}_{n,\left[I\right]}\left({\theta }_{\ast }\right)\Delta \left(\theta \right)+R_{\left[I\right]}\left(\theta \right),$$

in which |R_[I](θ)| = o_p(1) uniformly for all $\theta \in B({\theta }_{\ast },{\delta }_0{n}^{-1∕2})=\{\theta :\sqrt{n}\Vert \theta -{\theta }_{\ast }\Vert \le {\delta }_0\}$, where $\Delta \left(\theta \right)=\theta -{\theta }_{\ast },J_{n,\left[I\right]}\left(\theta \right)={\partial }_{\theta }\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid \theta )$ and ${\mathbf{F}}_{n,\left[I\right]}\left({\theta }_{\ast }\right)={\partial }_{\theta }^2\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid \theta )$.

Assumption A4. For any I and Z, ${\text{sup}}_{\theta \in B({\theta }_{\ast },n^{-1∕2}{\delta }_0)}{n}^{-1∕2}{J}_{n,\left[I\right]}\left(\theta \right)=O_p\left(1\right)$,

$$\begin{array}{cc}\hfill & \underset{\theta \in B({\theta }_{\ast },n^{-1∕2}{\delta }_0)}{\text{sup}}\Vert {\mathbf{F}}_{n,\left[I\right]}\left(\theta \right)-E[{\mathbf{F}}_I\left(\theta \right)\mid \mathcal{M},\mathbf{Z}]\Vert =O_p\left(\sqrt{n}\right),\hfill \\ \hfill & \underset{\theta ,{\theta }^{\prime }\in B({\theta }_{\ast },n^{-1∕2}{\delta }_0)}{\text{sup}}{n}^{-1}\Vert {\mathbf{F}}_{n,\left[I\right]}\left(\theta \right)-{\mathbf{F}}_{n,\left[I\right]}\left({\theta }^{\prime }\right)\Vert =o_p\left(1\right),\hfill \end{array}$$

and $0<{\text{inf}}_{\theta \in B({\theta }_{\ast },{\delta }_0{n}^{-1∕2})}{\lambda }_{\text{min}}\left(n^{-1}{\mathbf{F}}_{n,\left[I\right]}\left(\theta \right)\right)\le {\text{sup}}_{\theta \in B({\theta }_{\ast },{\delta }_0{n}^{-1∕2})}{\lambda }_{\text{max}}\left(n^{-1}{\mathbf{F}}_{n,\left[I\right]}\left(\theta \right)\right)<\infty$.

Assumption A5. For any set I and Z,

$$\begin{array}{cc}\hfill & \underset{\theta \in B({\theta }_{\ast },n^{-1∕2}{\delta }_0)}{\text{sup}}{J}_I\left(\theta \right)=O_p\left(\sqrt{n\left(I\right)}\right),\underset{\theta \in B({\theta }_{\ast },n^{-1∕2}{\delta }_0)}{\text{sup}}\Vert {\mathbf{f}}_I\left(\theta \right)\Vert =O_p\left(n\left(I\right)\right),\hfill \\ \hfill & \underset{\theta \in B({\theta }_{\ast },n^{-1∕2}{\delta }_0)}{\text{sup}}\Vert {\mathbf{f}}_I\left(\theta \right)-E[{\mathbf{f}}_I\left(\theta \right)\mid \mathcal{M},\mathbf{Z}]\Vert =O_p\left(\sqrt{n\left(I\right)}\right).\hfill \end{array}$$

Remarks: Assumptions A2-A5 are very general conditions and are generalizations of some higher level conditions for the extremum estimator, such as the maximum likelihood estimate, given in Andrews [2]. Assumption A2 assumes that the parameter estimators with and without deleting the observations in the subset I are consistent. Assumption A3 assumes that the log-likelihood functions for any I and Y_[I] admit a second-order Taylor's series expansion in a small neighborhood of θ_*. Assumptions A4 and A5 are standard assumptions to ensure that the first- and second-order derivatives of p(Y_[I]|θ) and p(Y_I|Y_[I], θ) have appropriate rates of n and n_I [2, 28]. Sufficient conditions of Assumptions A2-A5 have been extensively discussed in the literature [2, 28].

Proof of Theorem 1. (P.a) directly follows from the Jensen inequality, (2.6) and (2.7). For (P.b), if I is an empty set, then KL(Y, θ|I) ≡ 0 and thus $\mathcal{P}(I\mid \mathcal{M})=0$. On the other hand, if $\mathcal{P}(I\mid \mathcal{M})=0$, then KL(Y, θ|I) ≡ 0 for almost every θ. Thus, by using the Jensen inequality, we have p(Y_I|Y_[I], θ) ≡ p(Y_I|Y_[I], θ_*) for all θ ∈ Θ. Based on the identifiability condition, we know that I must be an empty set. Let I_1·2 = I₁ – I₂. It is easy to show that

$$p({\mathbf{Y}}_{I_1}\mid {\mathbf{Y}}_{\left[I_1\right]},\theta )=p({\mathbf{Y}}_{I_2},{\mathbf{Y}}_{I_{1\cdot 2}}\mid {\mathbf{Y}}_{\left[I_1\right]},\theta )=p({\mathbf{Y}}_{I_2}\mid {\mathbf{Y}}_{\left[I_2\right]},\theta )p({\mathbf{Y}}_{\left[I_2\right]}\mid {\mathbf{Y}}_{\left[I_1\right]},\theta ).$$

Thus, by substituting the above equation into (2.6), we have

$$\mathcal{P}(I_1\mid \mathcal{M})=\mathcal{P}(I_2\mid \mathcal{M})+\int p(\theta \mid {\theta }_{\ast },{\Sigma }_{n\ast })p(\mathbf{Y}\mid \theta )\text{log}\left(\frac{p({\mathbf{Y}}_{\left[I_2\right]}\mid {\mathbf{Y}}_{\left[I_1\right]},\theta )}{p({\mathbf{Y}}_{\left[I_2\right]}\mid {\mathbf{Y}}_{\left[I_1\right]},{\theta }_{\ast })}\right)d\theta d\mathbf{Y},$$ (4.1)

in which the second term on the right hand side can be written as

$$\int p(\theta \mid {\theta }_{\ast },{\Sigma }_{n\ast })p({\mathbf{Y}}_{I_2}\mid {\mathbf{Y}}_{\left[I_2\right]},\theta )\left\{\int p({\mathbf{Y}}_{\left[I_2\right]}\mid \theta )\text{log}\left(\frac{p({\mathbf{Y}}_{\left[I_2\right]}\mid {\mathbf{Y}}_{\left[I_1\right]},\theta )}{p({\mathbf{Y}}_{\left[I_2\right]}\mid {\mathbf{Y}}_{\left[I_1\right]},{\theta }_{\ast })}\right)d{\mathbf{Y}}_{\left[I_2\right]}\right\}d\theta d{\mathbf{Y}}_{I_2}\ge 0,$$

which yield (P.c). Based on the assumption of (P.d), we know that

$$p({\mathbf{Y}}_{\left[I_2\right]}\mid {\mathbf{Y}}_{\left[I_1\right]},\theta )=p({\mathbf{Y}}_{I_{1\cdot 2}}\mid {\mathbf{Y}}_{\left[I_1\right]},\theta )=p({\mathbf{Y}}_{I_{1\cdot 2}}\mid {\mathbf{Y}}_{\left[I_{1\cdot 2}\right]},\theta )$$

for all θ. Thus, the second term on the right hand side of (4.1) reduces to $\mathcal{P}(I_{1\cdot 2}\mid \mathcal{M})$, which finishes the proof of (P.d).

Proof of Theorem 2. (a) Let I₃ = I₁ \ I₂, I₁ is a union of two disjoint sets I₃ and I₂. Without loss of generality, H_I1 can be decomposed as

$$H_{I_1}={\mathbf{X}}_{I_1}{\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}_{I_1}^T=\left(\begin{array}{cc}{\mathbf{X}}_{I_2}{\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}_{I_2}^T\hfill & {\mathbf{X}}_{I_2}{\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}_{I_3}^T\hfill \\ {\mathbf{X}}_{I_3}{\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}_{I_2}^T\hfill & {\mathbf{X}}_{I_3}{\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}_{I_3}^T\hfill \end{array}\right).$$

Let λ_1,1 ≥ . . . ≥ λ_1,n(I1) ≥ 0 and λ_2,1 ≥ . . . ≥ λ_2,n(I2) ≥ 0 be ordered eigenvalues of H_I1 and H_I2, respectively, where n(I_k) denotes the number of observations in I_k for k = 1, 2. It follows from Wielandt's eigenvalue inequality [13] that λ_1,l ≥ λ_2,l for all l = 1, . . . , n(I₂). For k = 1, 2, we define ${\Gamma }_k{\Lambda }_k{\Gamma }_k^T$ as the spectral decomposition of H_Ik and ${\mathbf{h}}_k={({\mathbf{I}}_{n\left(I_k\right)}-{\Lambda }_k)}^{-1∕2}{\Gamma }_k^T{\widehat{\mathbf{e}}}_{I_k}={(h_{k,1},\dots ,h_{k,n\left(I_k\right)})}^T$, where Γ_k is an orthnormal matrix and Λ_k = diag(λ_k,1, . . . , λ_k,n(Ik)). It can be shown that for k = 1, 2,

$${\mathbf{h}}_k\sim N(0,{\sigma }^2{\mathbf{I}}_{n\left(I_k\right)})\text{and}\mathrm{CD}\left(I_k\right)=\frac{1}{{\widehat{\sigma }}^2}\sum _{j=1}^{n\left(I_k\right)}\frac{{\lambda }_{k,j}}{1-{\lambda }_{k,j}}{h}_{k,j}^2.$$

Since f(x) = x/(1 – x) is an increasing function of x ∈ (0, 1), this completes the proof of Theorem 2 (a).

Note that $\mathrm{CD}\left(I\right)={\left({\widehat{\sigma }}^2\right)}^{-1}{\sum }_{j=1}^{n\left(I\right)}{\lambda }_j{(1-{\lambda }_j)}^{-1}{h}_j^2$, where λ_j are the eigenvalues of H_I and h = (h₁, . . . , h_n(I))^T ~ N(0, σ²I_n(I)). Moreover, the distribution of λ is uniquely determined by H_I. Combining h ~ N(0, σ²I_n(I)) with the assumptions of Theorem 2 (b) yields that CD(I) and CD(I′) follow the same distribution when n(I) = n(I′). Furthermore, we can always choose an $I_2^{\prime }$ such that $n\left(I_2^{\prime }\right)=n\left(I_2\right)$ and $I_1\subset I_2^{\prime }$. Following arguments in Theorem 2 (a), we can then complete the proof of Theorem 2 (b).

Proof of Theorem 3. (a) It follows from a Taylor's series expansion and assumption A3 that

$${\partial }_{\theta }\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid {\widehat{\theta }}_{\left[I\right]})=0={\partial }_{\theta }\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid \widehat{\theta })+{\partial }_{\theta }^2\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid \tilde{\theta })({\widehat{\theta }}_{\left[I\right]}-\widehat{\theta }),$$

where $\tilde{\theta }=t{\widehat{\theta }}_{\left[I\right]}+(1-t)\widehat{\theta }$ for t ∈ [0, 1]. Combining this with Assumption A4 and the fact that ${\partial }_{\theta }\text{log}p(\mathbf{Y}\mid \widehat{\theta })={\partial }_{\theta }\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid \widehat{\theta })+{\partial }_{\theta }\text{log}p({\mathbf{Y}}_I\mid {\mathbf{Y}}_{\left[I\right]},\widehat{\theta })=0$, we get

$$\begin{array}{cc}\hfill {\widehat{\theta }}_{\left[I\right]}-\widehat{\theta }& ={[-{\partial }_{\theta }^2\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid \widehat{\theta })]}^{-1}{\partial }_{\theta }\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid \widehat{\theta })[1+o_p\left(1\right)]\hfill \\ \hfill & =-{[-{\partial }_{\theta }^2\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid \widehat{\theta })]}^{-1}{\partial }_{\theta }\text{log}p({\mathbf{Y}}_I\mid {\mathbf{Y}}_{\left[I\right]},\widehat{\theta })[1+o_p\left(1\right)].\hfill \end{array}$$ (4.2)

Substituting (4.2) into $\mathrm{CD}\left(I\right)={({\widehat{\theta }}_{\left[I\right]}-\widehat{\theta })}^T{\mathbf{F}}_n\left(\widehat{\theta }\right)({\widehat{\theta }}_{\left[I\right]}-\widehat{\theta })$ completes the proof of Theorem 3 (a).

(b) It follows from Assumptions A2-A4 that

$$\begin{array}{cc}\hfill \widehat{\theta }-{\theta }_{\ast }& ={\mathbf{F}}_n{\left({\theta }_{\ast }\right)}^{-1}{\partial }_{\theta }\text{log}p(\mathbf{Y}\mid {\theta }_{\ast })[1+o_p\left(1\right)]\hfill \\ \hfill & ={\mathbf{F}}_n{\left({\theta }_{\ast }\right)}^{-1}[{\partial }_{\theta }\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid {\theta }_{\ast })+{\partial }_{\theta }\text{log}p({\mathbf{Y}}_I\mid {\mathbf{Y}}_{\left[I\right]},{\theta }_{\ast })][1+o_p\left(1\right)].\hfill \end{array}$$

Let $J_I\left(\theta \right)={\partial }_{\theta }\text{log}p({\mathbf{Y}}_I\mid {\mathbf{Y}}_{\left[I\right]},\theta )$. Using a Taylor's series expansion along with Assumptions A4 and A5, we get

$$\begin{array}{cc}\hfill & J_I\left(\widehat{\theta }\right)=J_I\left({\theta }_{\ast }\right)-{\mathbf{s}}_I\left({\theta }_{\ast }\right)(\widehat{\theta }-{\theta }_{\ast })[1+o_p\left(1\right)]\hfill \\ \hfill & =J_I\left({\theta }_{\ast }\right)-E[{\mathbf{s}}_I\left({\theta }_{\ast }\right)\mid \mathcal{M}](\widehat{\theta }-{\theta }_{\ast })[1+o_p\left(1\right)]\hfill \\ \hfill & =(\{{\mathbf{I}}_p-E[{\mathbf{s}}_I\left(\theta \right)\mid \mathcal{M}]{\mathbf{F}}_n{\left({\theta }_{\ast }\right)}^{-1}\}{J}_I\left({\theta }_{\ast }\right)-E[{\mathbf{s}}_I\left(\theta \right)\mid \mathcal{M}]{\mathbf{F}}_n{\left({\theta }_{\ast }\right)}^{-1}{\partial }_{\theta }\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid {\theta }_{\ast }))[1+o_p\left(1\right)].\hfill \end{array}$$ (4.3)

Since $E[J_1\left({\theta }_{\ast }\right){\partial }_{\theta }\text{log}p({\mathbf{Y}}_{\left[I\right]}\mid {\theta }_{\ast })\mid \mathcal{M}]=0$,

$$E[J_I\left(\widehat{\theta }\right)J_I{\left(\widehat{\theta }\right)}^T\mid \mathcal{M}]=E[{\mathbf{s}}_I\left({\theta }_{\ast }\right)\mid \mathcal{M}]{\mathbf{F}}_n{\left({\theta }_{\ast }\right)}^{-1}\{{\mathbf{F}}_n\left({\theta }_{\ast }\right)-E[{\mathbf{s}}_I\left({\theta }_{\ast }\right)\mid \mathcal{M}]\}[1+o_p\left(1\right)].$$

It follows from Assumption A4 that for θ in a neighborhood of θ_*, F_n(θ) and F_n(θ_*) – f_I(θ) can be replaced by $E[{\mathbf{F}}_n\left(\theta \right)\mid \mathcal{M}]$ and $E[{\mathbf{F}}_n\left({\theta }_{\ast }\right)-{\mathbf{f}}_I\left(\theta \right)\mid \mathcal{M}]$, respectively, which completes the proof of Theorem 3 (b).

(c) Similar to Theorem 3 (b), we can prove Theorem 3 (c).