Bayesian Influence Measures for Joint Models for Longitudinal and Survival Data

Summary

This article develops a variety of influence measures for carrying out perturbation (or sensitivity) analysis to joint models of longitudinal and survival data (JMLS) in Bayesian analysis. A perturbation model is introduced to characterize individual and global perturbations to the three components of a Bayesian model, including the data points, the prior distribution, and the sampling distribution. Local influence measures are proposed to quantify the degree of these perturbations to the JMLS. The proposed methods allow the detection of outliers or influential observations and the assessment of the sensitivity of inferences to various unverifiable assumptions on the Bayesian analysis of JMLS. Simulation studies and a real data set are used to highlight the broad spectrum of applications for our Bayesian influence methods.

1. Introduction

There has been extensive research literature on joint modeling of longitudinal and survival data (JMLS) by using either frequentist or Bayesian methods. For instance, the early development of joint models for longitudinal and survival data was primarily motivated by characterizing the relationship between features of CD4 or viral load profiles and time-to-event in HIV/AIDS clinical trials. JMLS has been further developed in other types of biomedical applications, such as cancer vaccine (immunotherepy) trials and quality of life studies. References include Pawitan and Self (1993); De Gruttola and Tu (1994); Tsiatis, DeGruttola, and Wulfsohn (1995); Faucett and Thomas (1996); Wulfsohn and Tsiatis (1997); Henderson, Diggle, and Dobson (2000); Wang and Taylor (2001); Xu and Zeger (2001); Law, Taylor, and Sandler (2002); Song, Davidian, and Tsiatis (2002); Chen, Ibrahim, and Sinha (2002, 2004a); Brown and Ibrahim (2003a; Brown and Ibrahim (2003b); Brown, Ibrahim, and DeGruttola (2005) and Chi and Ibrahim (2006, 2007) among many others. Nice overviews of JMLS are given in Tsiatis and Davidian (2004) and Yu et al. (2004) from a frequentist perspective, and in Ibrahim, Chen, and Sinha (2001) as well as Hanson, Branscum, and Johnson (2011) from a Bayesian perspective.

Recent advances in computation and prior elicitation have made Bayesian analysis of these “complex” JMLS feasible. For instance, some Bayesian semiparametric approaches for longitudinal profiles include Gaussian processes, and functional Dirichlet processes among others. Nonparametric prior processes for the baseline cumulative hazard function, include the gamma process prior, the correlated gamma process, and the Dirichlet process prior among others. However, very little has been done on developing a general Bayesian influence approach to detect influential points and to assess various unverifiable assumptions underlying the JMLS, which is the focus of this article.

Bayesian local and global influence (or robustness) approaches have been widely used to perturb the data, the prior and the sampling distribution and assess the influence of these perturbations on the posterior distribution and the associated posterior quantities. However, these Bayesian local and global influence approaches are not directly applicable to complex JMLS. Although there are some frequentist diagnostic tools (Dobson and Henderson, 2003; Rizopoulos, Verbeke, and Molenberghs, 2008; Rizopoulos and Ghosh, 2011) developed specifically for some JMLS, they are not sufficient for carrying out sensitivity analysis (e.g., prior) of complex Bayesian analysis of JMLS.

The development of the proposed methodology was primarily motivated by a clinical trial conducted by the International Breast Cancer Study Group (IBCSG) (Chi and Ibrahim, 2006). A subset of the IBCSG data set contains the longitudinal measurements for quality of life (QOL) measured at baseline and at months 3 and 18 after randomization. In addition, we have bivariate failure times, including disease-free survival (DFS) and overall survival (OS), which were collected from n = 832 patients from Switzerland, Sweden, and New Zealand/Australia. The covariates are different therapeutic procedures, age, estrogen receptor (ER) status (negative/positive), and the number of positive nodes of the tumor. Although a Bayesian analysis of joint longitudinal and bivariate survival models have been used to fit this data set (Chi and Ibrahim, 2006), a general diagnostic framework for assessing such a model fit to the IBCSG data is completely lacking. There is a great need to develop various diagnostic measures for the detection of outliers and/or influential observations, and the assessment of the sensitivity of inferences to the prior distributions and other unverifiable assumptions on the JMLS.

The article is organized as follows. In Section 2, we introduce a general model for jointly modeling multivariate longitudinal and survival data. In Section 3, we discuss various perturbation models and then calculate their associated Bayesian influence measures to quantify the effects of perturbing the data, the prior, and the sampling distribution on possible posterior quantities of interest. We present a detailed analysis of the IBCSG data in Section 4.

2. Joint Models of Longitudinal and Survival Data

Consider data from n independent subjects. For each subject, we observe a K × 1 vector of multiple longitudinal responses and an M × 1 vector of multivariate time-to-event outcomes. For the ith subject, let y_ik (t_ijk) be an assessment of the kth longitudinal response measured at time t_ijk and let Y_ik = (y_ik (t_i1k), …, y_ik (t_inikk))^T denote the observed longitudinal process for the kth response for i = 1, …, n, j = 1, …, n_ik, and k = 1, …, K. Moreover, for the ith subject, we observe the event time $T_{im}=min(T_{im}^{\ast },C_{im})$ and the event indicator ${\delta }_{im}=\mathbf{1}(T_{im}^{\ast }\le C_{im})$

for the mth time-to-event outcome for m = 1, …, M, where 1(A) is an indicator function of an event A and $T_{im}^{\ast }$ and C_im denote the true event time and the censoring time, respectively.

We consider a general shared parameter model for jointly modeling the longitudinal and survival data as follows. Let b_i = (b_i1, …, b_iK) be time-independent random effects underlying both the longitudinal and survival processes for the ith subject. Conditional on b_i, all components of the longitudinal outcomes and the time-to-event outcomes are independent. Let Y_i = (Y_i1, …, Y_iK), T_i = (T_i1, …, T_iM)^T, and δ_i = (δ_i1, …, δ_iM)^T. The shared parameter model is defined by

$$p({\mathbf{Y}}_i,{\mathbf{T}}_i,{\delta }_i;\mathit{\theta })=\int p({\mathbf{Y}}_i\mid {\mathit{b}}_i;{\mathit{\theta }}_y)p({\mathbf{T}}_i,{\delta }_i\mid {\mathit{b}}_i;{\mathit{\theta }}_T)p({\mathit{b}}_i;{\mathit{\theta }}_b){d\mathit{b}}_i,$$ (1)

where p(… | …) and p(…) denote the appropriate conditional density and density functions, respectively, and ${\mathit{\theta }}^T=({\mathit{\theta }}_y^T,{\mathit{\theta }}_T^T,{\mathit{\theta }}_b^T)$ is the vector containing all unknown parameters corresponding to each of the submodels. Moreover, corresponding to the partition of ${\mathit{\theta }}^T=({\mathit{\theta }}_y^T,{\mathit{\theta }}_T^T,{\mathit{\theta }}_b^T),{\mathit{\theta }}^T=({\mathit{\theta }}_F^T,{\mathit{\theta }}_I^T)$ can be further decomposed as a finite-dimensional parameter vector ${\mathit{\theta }}_F^T=({\mathit{\theta }}_{y,F}^T,{\mathit{\theta }}_{T,F}^T,{\mathit{\theta }}_{b,F}^T)$ and a vector of infinite-dimensional parameters ${\mathit{\theta }}_I^T=({\mathit{\theta }}_{y,I}^T,{\mathit{\theta }}_{T,I}^T,{\mathit{\theta }}_{b,I}^T)$, such as the baseline hazard function or cumulative baseline hazard function, for each of the submodels. This class of shared parameter models in equation (1) includes most JMLS in the existing literature as a special case (Ibrahim et al., 2001; Tsiatis and Davidian, 2004; Hanson et al., 2011).

We specify each of the submodels in equation (1) as follows. First, we consider a multivariate generalized linear mixed model for the longitudinal process. Specifically, all components of Y_ik conditional on b_ik are independent and the conditional distribution of each y_ik (t_ijk) given b_ik is a member of the exponential family with a nonlinear link function given by

$$g_k(E\{y_{ik}(t_{\mathit{ijk}})\mid {\mathit{b}}_{ik}\})={\eta }_{ik}(t_{\mathit{ijk}},{\mathit{b}}_{ik}),$$ (2)

where g_k (·) is a known monotonic link function and η_ik (t, b_ik) is a parametric or nonparametric function of the random effects and t. Also, η_ik (t, b_ik) may depend on other covariates of interest, such as gender. Furthermore, we consider a general form of η_ik (t, b_ik) given by

$${\eta }_{ik}(t,{\mathit{b}}_{ik})={\mathit{R}}_{ik}(t){\mathit{\beta }}_k+{\mathit{W}}_{ik}(t){\mathit{b}}_{ik},$$ (3)

where R_ik (t) and W_ik (t) are, respectively, the fixed effects and random effects design matrices, and β_k and b_ik are vectors of the corresponding fixed and random effects parameters.

For the specification in equation (3), we may consider a random varying-coefficient model as follows:

$${\eta }_{ik}(t,{\mathit{b}}_{ik})=\sum _{l=1}^p{x}_{il}{\mu }_{\mathit{ikl}}(t)\approx \sum _{l=1}^p\sum _{s=1}^S{\theta }_{\mathit{ikl},s}{x}_{il}{f}_s(t),$$ (4)

where x_i = (x_i1, …, x_ip)^T is a vector of covariates and f_s (t) are known basis functions, such as B-splines. If θ_ikl,s = β_kl,s + b_ikl,s with E(b_ikl,s) = 0, then β_k includes all coefficients β_kl,s and b_ik includes all b_ikl,s for all k, l, and s.

Second, we consider a general multivariate survival model for the survival process as follows. Let S(t₁, …, t_M |z_i, H_i (t, b_i), b_i) be the joint survivor function of (T_i1, …, T_iM) given (z_i, H_i (t, b_i), b_i), where H_i (t, b_i) = {η_ik (t̃, b_ik) : t̃ ∈ [0, t), k = 1, …, K} and z_i is a vector of time-independent covariates. It is assumed that S(t₁, …, t_M |z_i, H_i (t, b_i), b_i) takes the form

$$F(S_1(t_1\mid {\mathbf{z}}_i,H_i(t,{\mathit{b}}_i),{\mathit{b}}_i),\dots ,S_M(t_M\mid {\mathbf{z}}_i,H_i(t,{\mathit{b}}_i),{\mathit{b}}_i);\mathit{\phi }),$$ (5)

where F (…) is a known function, φ is a vector of unknown parameters for characterizing the dependence or association structure, and S_m (t|z_i, H_i (t, b_i), b_i) for m = 1, …, M are the marginal survival functions given (z_i, H_i (t, b_i), b_i). For bivariate time-to-event outcomes, Chi and Ibrahim (2006) have proposed a joint survivor function that is a special case of (5).

For the mth time-to-event outcome, we assume that the marginal hazard function of the ith subject is given by

$${\lambda }_m(t\mid {\mathbf{z}}_i,H_i(t,{\mathit{b}}_i),{\mathbf{b}}_i)={\lambda }_{m0}(t)exp\{{\stackrel{\sim }{g}}_{m0}({\mathbf{z}}_i;{\mathit{\theta }}_{m,T})+\sum _{k=1}^K{\stackrel{\sim }{g}}_{mk}({\eta }_{ik}(t,{\mathit{b}}_{ik}),{\mathbf{b}}_{ik};{\mathit{\theta }}_{m,T})\},$$ (6)

where λ_m0(t) is an unknown baseline hazard function and θ_m,T contains all unknown parameters in λ_m (t|z_i, H_i (t, b_i), b_i) except λ_m0(t). Moreover, g̃_mk (·; ·) for k = 0, …, K are prespecified functions that characterize the effect of the kth longitudinal profile on the mth time-to-event outcome. Then, we calculate $S_m(t\mid {\mathit{z}}_i,H_i(t,{\mathit{b}}_i),{\mathit{b}}_i)=exp(-{\int }_0^t{\lambda }_m(u\mid {\mathit{z}}_i,H_i(t,{\mathit{b}}_i),{\mathit{b}}_i)du)$. In the literature, it is common to assume that

$${\stackrel{\sim }{g}}_{m0}({\mathbf{z}}_i;{\mathit{\theta }}_{m,T})={\mathbf{z}}_i^T{\mathit{\gamma }}_m\text{and}{\stackrel{\sim }{g}}_{mk}({\eta }_{ik}(t,{\mathit{b}}_{ik}),{\mathit{b}}_{ik};{\mathit{\theta }}_{m,T})={\alpha }_{mk}{\eta }_{ik}(t,{\mathit{b}}_{ik})\text{for}k=1,\dots ,K,$$ (7)

where γ_m is a vector of unknown parameters for the time-independent covariates and α_mk are unknown parameters.

Third, we consider a multivariate model for the random effects b_i as follows. Specifically, let p₀(b_i ; θ_b) be a prespecified density function, such as multivariate Gaussian. The density of b_i, denoted by p(b_i ; θ_b), is assumed to take the form p₀(b_i ; θ_b)ψ(b_i ; θ_b), where ψ(·; ·) is a known and nonnegative function such that ∫ p(b_i ; θ_b)db_i = 1. For instance, ψ(b_i ; θ_b) can be the square of a polynomial function of individual components of θ_b and the density of a copula function. We may further consider nonparametric alternatives to the parametric model p(b_i ; θ_b), such as a Dirichlet process.

A formal Bayesian analysis of (θ, b) also involves the specification of a prior distribution p(θ), where b = (b₁, …, b_n). A typical joint prior specification is to assume p(θ) = p(θ_F)p(θ_I), where p(θ_F) and p(θ_I), respectively, denote parametric prior distributions for the components of θ_F and non-parametric prior distributions for the components of θ_I. Let D_o = {(Y_i, T_i, δ_i): i = 1, …, n}. Then, we use Markov chain Monte Carlo (MCMC) methods to obtain samples from the joint posterior distribution of (θ, b), which is given by

$$p(\mathit{\theta },\mathit{b}\mid D_o)\propto p({\mathit{\theta }}_F)p({\mathit{\theta }}_I)\prod _{i=1}^n[p({\mathbf{Y}}_i\mid {\mathit{b}}_i;{\mathit{\theta }}_y)p({\mathbf{T}}_i,{\delta }_i\mid {\mathit{b}}_i;{\mathit{\theta }}_T)p({\mathit{b}}_i;{\mathit{\theta }}_b)].$$ (8)

We focus on nonparametric priors for the nonparametric components in η_ik (t, b_ik) and the baseline hazard or cumulative baseline hazard function. We can take different prior distributions, including a Gaussian prior, zero-inflated priors, and stick-breaking priors among others, for the coefficients {θ_ikl,s} in model (4). For instance, a Dirichlet process for {θ_ikl,s }, denoted by DP(αP₀), usually clusters all the longitudinal profiles into one of k ≤ n clusters, where P₀ is the base probability measure and α is the confidence parameter. See a nice review of Bayesian nonparametric methods for functional data in Dunson (2009).

Different prior distributions for the baseline hazard λ_m0(·) or cumulative baseline hazard Λ_m0(·) include a piecewise constant hazards model, Gamma process model, Beta process model, or a Dirichlet process model. As an illustration, we construct the piecewise constant hazards model for λ_m0(·). We start with a finite partition of the time axis, 0 < c_m,1 < · · · < c_m,L, with c_m,L > T_im for all i and then set λ_m0(t) = h_mℓ for t ∈ I_mℓ = (c_{m, ℓ−1}, c_{m, ℓ}]. Furthermore, a first-order autoregressive prior or an independent gamma prior can be taken for h_m = (h_m1, …, h_mL)^T (Sinha, 1993; Arjas and Gasbarra, 1994; Ibrahim et al., 2001). An important alternative is the gamma process prior for Λ_m0(·), that is, ${\mathrm{\Lambda }}_{m0}~\mathcal{G}P(c_0{\mathrm{\Lambda }}_m^{\ast },c_0)$, where c₀ is a fixed constant and ${\mathrm{\Lambda }}_m^{\ast }(·)$ is a known increasing function with ${\mathrm{\Lambda }}_m^{\ast }(0)=0$.

Our aim is to carry out Bayesian inference about parameters of interest, which requires a reasonably “robust” prior p(θ) and the correct specification of p(Y_i, T_i, δ_i; θ). A nonrobust prior p(θ), the presence of outliers, and the misspecification of the JMLS may introduce serious bias in the estimation and inference on θ. Thus, it is crucial to assess the sensitivity of statistical inference to the prior, the sampling distribution, and outliers. We note that existing frequentist diagnostic tools are not sufficient for this endeavor (Dobson and Henderson, 2003; Rizopoulos et al., 2008; Rizopoulos and Ghosh, 2011).

Example 1

For the purposes of illustration, we consider an example with two longitudinal markers and bivariate survival times. In this case, K = M = 2. Specifically, each longitudinal response is given by

$$\begin{array}{l}{y}_{ik}(t_{\mathit{ijk}})={\eta }_{ik}(t_{\mathit{ijk}},{\mathit{b}}_{ik})+{\epsilon }_{\mathit{ijk}}\\ ={\beta }_{k0}+{\beta }_{k1}{t}_{\mathit{ijk}}+{\beta }_{k2}{r}_i+b_{ik0}+b_{ik1}{t}_{\mathit{ijk}}+{\epsilon }_{\mathit{ijk}},\end{array}$$ (9)

for i = 1, …, 100, k = 1, 2, and j = 1, …, n_i, where the r_i s represent a baseline covariate in the longitudinal model. Moreover, it is assumed that t_ij1 = t_ij2 for all i and j, ε_ij = (ε_ij1, ε_ij2)^T are independently and identically distributed as N₂(0, Σ), and the random effects ${\mathit{b}}_i={({\mathit{b}}_{i1}^T,{\mathit{b}}_{i2}^T)}^T$ are distributed as N₄(0, Φ), where b_ik = (b_ik0, b_ik1)^T for k = 1, 2. Here Σ and Φ for k = 1, 2 are covariance matrices. Conditional on b_i, the two event and censoring times are assumed to be independent and their marginal hazard functions are given by

$${\lambda }_m(t\mid {\mathit{b}}_i,{\mathit{z}}_i)={\lambda }_{m0}(t)exp\{{\alpha }_{m1}{\eta }_{i1}(t,{\mathit{b}}_{i1})+{\alpha }_{m2}{\eta }_{i2}(t,{\mathit{b}}_{i2})+{\mathit{z}}_i^T{\mathit{\gamma }}_m\}$$ (10)

for m = 1, 2, where z_i = (z_i1, z_i2)^T is a vector of time-independent covariates. Let Y_i (t) = (y_i1(t), y_i2(t))^T and η_i (t, b_i) = (η_i1(t, b_i1), η_i2(t, b_i2))^T. The density of (Y_i, T_i, δ_i, b_i) given θ for the ith subject, denoted by p(Y_i, T_i, δ_i, b_i ; θ), is given by

$$\begin{array}{l}{C}_0{\mid \mathbf{\Phi }\mid }^{-1/2}exp\left(-\frac{1}{2}{\mathit{b}}_i^T{\mathbf{\Phi }}^{-1}{\mathit{b}}_i\right)\prod _{m=1}^2{\lambda }_m{(T_{im}\mid {\mathit{b}}_i,{\mathit{z}}_i)}^{{\delta }_{im}}\\ \times exp\left\{-{\int }_0^{T_{im}}{\lambda }_m(u\mid {\mathit{b}}_i,{\mathit{z}}_i)du\right\}\\ \times \prod _{j=1}^{n_i}\left({\mid \mathit{\sum }\mid }^{-1/2}exp\left[-\frac{1}{2}{\{{\mathbf{Y}}_i(t_{ij})-{\mathit{\eta }}_i(t_{ij},{\mathit{b}}_i)\}}^T\times {\mathit{\sum }}^{-1}\{{\mathbf{Y}}_i(t_{ij})-{\mathit{\eta }}_i(t_{ij},b_i)\}\right]\right),\end{array}$$

where C₀ is a constant independent of θ.

To carry out a Bayesian analysis, we take a joint prior distribution for θ as follows:

$$\begin{array}{l}{\mathit{\alpha }}_m={({\alpha }_{m1},{\alpha }_{m2})}^T~N\left({\mathit{\alpha }}_m^0,{\mathit{H}}_{\alpha }^0\right),{\mathit{\gamma }}_m~N\left({\mathit{\gamma }}_m^0,{\mathit{H}}_{\gamma }^0\right),\\ {\mathit{\sum }}^{-1}~{\text{Wishart}}_2({\mathit{R}}^0,{\rho }^0),{\mathbf{\Phi }}^{-1}~{\text{Wishart}}_4\left({\mathit{R}}_{\phi }^0,{\rho }^0\right)\\ {\mathit{\beta }}_k={({\beta }_{k0},{\beta }_{k1},{\beta }_{k2})}^T~N\left({\mathit{\beta }}_k^0,{\mathit{H}}_{\beta }^0\right),\end{array}$$ (11)

for k, m = 1, 2, where ${\mathit{\alpha }}_m^0,{\mathit{H}}_{\alpha }^0,{\mathit{\gamma }}_m^0,{\mathit{H}}_{\gamma }^0$, R⁰, ρ⁰, ${\mathit{R}}_{\phi }^0$, and ρ⁰ are prespecified hyperparameters. For the baseline hazard λ_m0(·), we take a piecewise constant hazards model with 250 subintervals with equal lengths such that ${\lambda }_{m0}(t)={\sum }_{l=1}^L{h}_{ml}\mathbf{1}(t\in (c_{m,l-1},c_{m,l}])$, where the c_{m, l}s are prespecified constants. We take h_{m l} ~ Γ(τ_0l, τ_1l) for l = 1, …, 250 and m = 1, 2. We use MCMC methods to conduct our Bayesian influence analysis on θ and b.

3. Bayesian Influence Analysis

We address three issues related to Bayesian influence analysis of JMLS: perturbation models for perturbing the JMLS, appropriate perturbations, and Bayesian influence measures.

3.1. Perturbation Models and Appropriate Perturbations

We introduce three classes of perturbation models to formally perturb JMLS. Let ω be a perturbation vector in a set Ω ⊂ R^W, which represents a Euclidean space of dimension W, where W is an integer. The perturbed model 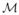= {p(D_o, b; θ, ω): ω ∈ Ω} characterizes various perturbations to the assumed density of p(D_o, b; θ) such that ∫ p(D_o, b; θ, ω)dD_o db = 1 and p(D_o, b; θ, ω⁰) = p(D_o, b; θ) for a unique ω⁰, which represents no perturbation. The first class of perturbations is to individually perturb a subject’s longitudinal profile, repeated measures within each subject, covariates, survival time, and censoring indicator. For instance, we introduce a perturbation vector ω_y,i into p(Y_i |b_i; θ_y) to perturb Y_i such that the perturbed density is given by

$$\prod _{i=1}^n\{p({\mathbf{T}}_i,{\delta }_i\mid {\mathit{b}}_i;{\mathit{\theta }}_T)p({\mathit{b}}_i;{\mathit{\theta }}_b)p({\mathbf{Y}}_i\mid {\mathit{b}}_i;{\mathit{\theta }}_y,{\mathit{\omega }}_{y,i})\},$$ (12)

in which ω = {ω_y,1, …, ω_y,n }. This single-case perturbation equation (12) to the individual’s longitudinal profile is primarily designed to detect one or a few influential subjects, whose longitudinal profiles differ significantly from the other subjects in the evolution process. Furthermore, we may introduce a perturbation vector ω_i into p(T_i, δ_i |b_i; θ_T) to perturb (T_i, δ_i) such that the perturbed density is given by

$$\prod _{i=1}^n\{p({\mathbf{T}}_i,{\delta }_i\mid {\mathit{b}}_i;{\mathit{\theta }}_T,{\mathit{\omega }}_{T,i})p({\mathit{b}}_i;{\mathit{\theta }}_b)p({\mathbf{Y}}_i\mid {\mathit{b}}_i;{\mathit{\theta }}_y)\},$$ (13)

in which $\mathit{\omega }={({\mathit{\omega }}_{T,1}^T,\dots ,{\mathit{\omega }}_{T,n}^T)}^T$. This single-case perturbation equation (13) to the survival data is designed to reveal influential values of survival times relative to other survival times.

The second class is to perturb the shared random effects that underly both the longitudinal measurement and survival processes. For instance, we introduce a perturbation vector ω_b,i to simultaneously perturb (Y_i, T_i, δ_i) with the presence of b_i such that

$$\prod _{i=1}^n\{p({\mathbf{T}}_i,{\delta }_i\mid {\mathit{b}}_i;{\mathit{\theta }}_T,{\mathit{\omega }}_{b,i})p({\mathit{b}}_i;{\mathit{\theta }}_b)p({\mathbf{Y}}_i\mid {\mathit{b}}_i;{\mathit{\theta }}_y,{\mathit{\omega }}_{b,i})\}.$$ (14)

In equation (14), we use the same ω_b,i to simultaneously perturb p(Y_i |b_i ; θ_y) and p(T_i, δ_i |b_i ; θ_T) to delineate large discrepancies between the longitudinal profile and the corresponding survival time, each of which may not be influential by themselves. This single-case perturbation equation (14) is primarily designed to detect influential survival times, whose occurrence is low relative to their subject-specific longitudinal profiles. An alternative perturbation is to introduce a perturbation ω_b,i into p(b_i ; θ_b) such that

$$\prod _{i=1}^n\{p({\mathbf{T}}_i,{\delta }_i\mid {\mathit{b}}_i;{\mathit{\theta }}_T)p({\mathit{b}}_i;{\mathit{\theta }}_b,{\mathit{\omega }}_{b,i})p({\mathbf{Y}}_i\mid {\mathit{b}}_i;{\mathit{\theta }}_y)\}.$$ (15)

Perturbation equation (15) is designed to detect “influential” random effects b_i, whereas their corresponding T_i and Y_i may be not influential. Furthermore, by setting ω_b,i = ω_b, we can formally assess the parametric distributional assumptions of the random effects b_i and the amount of such perturbations to statistical inferences, such as their impact on parameter estimation.

The third class includes perturbations to the prior p(θ) and the simultaneous perturbations to all three components of the Bayesian model. A fundamental issue associated with any Bayesian analysis is how much posterior quantities, such as the Bayes factor, parameter estimates, and credible (or highest posterior density) intervals, are sensitive to changes in the prior distribution. Thus, it is important to assess both Bayesian semiparametric assumptions for the longitudinal profiles and perturbations regarding the nonparametric prior processes for the cumulative baseline hazard function. For instance, we consider a prior perturbation to Λ_m0(t) ~ 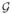P (c₀Λ^*(t), c₀) by assuming Λ_m0(t) ~ 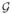P (c₀Λ^*(t, ω_P), c₀) such that ${\mathrm{\Lambda }}^{\ast }(t,{\mathit{\omega }}_P)={\int }_0^t{k}_{\ast }(s,{\mathit{\omega }}_P)h_0(s)ds$ and Λ^*(t, 0) = Λ^*(t). Combining the first two classes with the third class, we can obtain various simultaneous perturbations to the prior, the sampling distribution, and the data, which allows us to assess the simultaneous sensitivity of all components of a Bayesian analysis.

Example 1 (continued)

We consider some simultaneous perturbations as follows:

$$\begin{array}{l}{\mathit{Y}}_i(t_{ij})={\mathit{\eta }}_i(t_{ij},{\mathit{b}}_i)+{\omega }_{y,i}{\mathbf{1}}_2+{\mathit{\epsilon }}_{ij},\\ p({\mathit{b}}_i;{\mathit{\theta }}_b,{\mathit{\omega }}_{b,i})~N_4(\mathbf{0},{\omega }_{b,i}^{-1}\mathbf{\Phi }),\\ p({\mathit{\alpha }}_m\mid {\omega }_{\alpha 1},{\omega }_{\alpha 2})~N({\mathit{\alpha }}_m^0+{\omega }_{\alpha 2}{\mathbf{1}}_2,{\mathit{H}}_{\alpha }^0/{\omega }_{\alpha 1}),\\ p({\mathit{\gamma }}_m\mid {\omega }_{\gamma 1},{\omega }_{\gamma 2})~N({\mathit{\gamma }}_m^0+{\omega }_{\gamma 2}{\mathbf{1}}_2,{\mathit{H}}_{\gamma }^0/{\omega }_{\gamma 1}).\end{array}$$ (16)

Thus, the perturbed (unnormalized) log-posterior is given by

$$\begin{array}{l}-0.5\sum _{i=1}^n\sum _{j=1}^{n_i}{\{{\mathbf{Y}}_i(t_{ij})-{\mathit{\eta }}_i(t_{ij},{\mathit{b}}_i)-{\omega }_{y,i}{\mathbf{1}}_2\}}^T\\ \times {\mathit{\sum }}^{-1}\{{\mathbf{Y}}_i(t_{ij})-{\mathit{\eta }}_i(t_{i,j},{\mathit{b}}_i)-{\omega }_{y,i}{\mathbf{1}}_2\}\\ -0.5\{\sum _{i=1}^n{\omega }_{b,i}{\mathit{b}}_i^T{\mathbf{\Phi }}^{-1}{\mathit{b}}_i^T+\sum _{i=1}^{n}log\mid {\omega }_{b,i}^{-1}\mathbf{\Phi }\mid \\ +{({\mathit{\beta }}_k-{\mathit{\beta }}_k^0)}^T{({\mathit{H}}_{\beta }^0)}^{-1}({\mathit{\beta }}_k-{\mathit{\beta }}_k^0)+log\mid {\mathit{H}}_{\beta }^0\mid \}\\ -0.5\{\sum _{m=1}^2{\omega }_{\alpha 1}{({\mathit{\alpha }}_m-{\mathit{\alpha }}_m^0-{\omega }_{\alpha 2}{\mathbf{1}}_2)}^T\\ \times {\mathit{H}}_{\mathit{\alpha }}^{0-1}({\mathit{\alpha }}_m-{\mathit{\alpha }}_m^0-{\omega }_{\alpha 2}{\mathbf{1}}_2)+2log\mid {\omega }_{\alpha 1}^{-1}{\mathit{H}}_{\alpha }^0\mid \\ +2log\mid {\omega }_{\gamma 1}^{-1}{\mathit{H}}_{\gamma }^0\mid +\sum _{m=1}^2{\omega }_{\gamma 1}{({\mathit{\gamma }}_m-{\mathit{\gamma }}_m^0-{\omega }_{\gamma 2}{\mathbf{1}}_2)}^T\\ \times {\mathit{H}}_{\mathit{\gamma }}^{0-1}({\mathit{\gamma }}_m-{\mathit{\gamma }}_m^0-{\omega }_{\gamma 2}{\mathbf{1}}_2)\}.\end{array}$$ (17)

In this case, ω contains (ω_y,1, …, ω_y,n, ω_b,1, …, ω_b,n, ω_α1, ω_α2, ω_γ1, ω_γ2)^T and ω⁰ = (0, …, 0, 1, …, 1, 1, 0, 1, 0)^T represents no perturbation.

After perturbing the JMLS, we need to quantify the amount of perturbation introduced by each perturbation, the extent to which each component of a perturbation vector contributes to, and the degree of orthogonality for the components of a perturbation vector (Amari, 1990; Zhu, Ibrahim, and Tang, 2011). This is very critical for us to properly pinpoint the cause (e.g., prior) of a large effect. Specifically, we regard the perturbed model p(D_o, b, θ; ω) as the probability density of (D_o, b, θ) for ω and then calculate its score function ∂_ωhℓ(ω), where ∂_ωh = ∂/∂ω_h, ℓ(ω) = log p(D_o, b, θ; ω), and ω_h is the hth component of ω. Thus, the Fisher information matrix with respect to ω, denoted by G(ω) = (g_{h s} (ω)), is a W × W matrix with its (h, s) element given by $g_{hs}(\mathit{\omega })={\text{E}}_{\mathit{\omega }}[{\partial }_{{\omega }_h}\ell (\mathit{\omega }){\partial }_{{\omega }_s}\ell (\mathit{\omega })]=-{\text{E}}_{\mathit{\omega }}[{\partial }_{{\omega }_h{\omega }_s}^2\ell (\mathit{\omega })]$, for h, s = 1, …, W, where Eω denotes the expectation taken with respect to p(D_o, b, θ; ω).

We call p(D_o, b, θ; ω) an appropriate perturbation model if G(ω⁰) equals cI_W, where c is any positive scalar and I_W is a W × W identity matrix (Zhu et al., 2007). Specifically, g_hh (ω) can be regarded as the amount of perturbation introduced by ω_h, whereas the correlation $g_{hs}(\mathit{\omega })/\sqrt{g_{hh}(\mathit{\omega })g_{ss}(\mathit{\omega })}$ indicates an association between ω_h and ω_s. The diagonal structure of G(ω) implies that all components of ω are orthogonal to each other. Orthogonal subcomponents of ω allow for easy detection of the cause of a large effect. If G(ω⁰) is not diagonal, then we choose a new perturbation vector ω̃, defined by

$$\stackrel{\sim }{\mathit{\omega }}(\mathit{\omega })={\mathit{\omega }}^0+\mathit{G}{({\mathit{\omega }}^0)}^{1/2}(\mathit{\omega }-{\mathit{\omega }}^0).$$ (18)

Based on ω̃, we can obtain a new perturbation model p(D_o, b, θ; ω̃) such that G(ω̃) evaluated at ω⁰ equals I_W.

Example 1 (continued)

Let $g_{y,ii}=n_{i}E({\mathbf{1}}_2^T{\mathit{\sum }}^{-1}{\mathbf{1}}_2)=n_i{\rho }^0{\mathbf{1}}_2^T{\mathit{R}}^0{\mathbf{1}}_2$ for i = 1, …, n. It follows from the definition of G(ω⁰) that $\mathit{G}({\mathit{\omega }}^0)=\text{diag}(g_{y,11},\dots ,g_{y,nn},2{\mathbf{1}}_n,M,{\mathbf{1}}_2^T{\mathit{H}}_{\alpha }^{0-1}{\mathbf{1}}_2,M,{\mathbf{1}}_2^T{\mathit{H}}_{\gamma }^{0-1}{\mathbf{1}}_2)$. The diagonal structure of G(ω⁰) indicates that all components of ω are orthogonal to each other. However, because G(ω⁰) does not take the form of cI_W, this indicates that different components of ω introduce different amounts of perturbations. For instance, a large g_y,ii indicates that ω_y,i introduces a large perturbation for a subject with more repeated measures (n_i). In practice, we can always choose the appropriate perturbation scheme in equation (18).

3.2. Local Influence Measures

Let f(p(D_o, b, θ; ω)) = f (ω) be a real objective function (e.g., Bayes factor) of the perturbed model, which defines the aspect of inference of interest for sensitivity analysis. We use f(ω) to measure the effect of a small perturbation ω to a JMLS around ω⁰. Specifically, we consider a smooth curve of the perturbed model p(D_o, b, θ; ω(t)) such that p(D_o, b, θ; ω(0)) = p(D_o, b, θ). Then, the score function of ℓ(ω (t)) with respect to t is equal to ∂_t ℓ(ω(t)) = h^T∂ωℓ(ω(t)), where ∂_t = ∂/∂t, ∂ω = ∂/∂ω, and ∂_t ω(t)|_{t =0} = h ∈ R^W. Then, we quantify the effects of introducing ω(t) to perturb the JMLS by using {f (ω(t)) − f (ω(0))}² relative to the Kullback–Leibler divergence between p(D_o, b, θ; ω(0)) and p(D_o, b, θ; ω(t)), denoted by S(ω(0), ω(t)).

For small t, it follows from a Taylor’s series expansion that S(ω(0), ω(t)) ≈ 0.5t²h^T G(ω⁰)h and f (ω(t)) − f (ω(0)) = ḟ_h(0)t + O(t²), where ${\stackrel{.}{f}}_{\mathbf{h}}(0)={\nabla }_f^T\mathbf{h}$, in which ∇_f = ∂ωf(ω⁰). If ∇_f ≠ 0, we use a quantity FI_f,h called the first-order influence measure (FI) in the direction h ∈ R^W for the objective function f (ω), which is given by

$$\begin{array}{l}{\text{FI}}_{f,\mathbf{h}}={\text{FI}}_{f({\mathit{\omega }}^0),\mathbf{h}}=\underset{t\to 0}{lim}\frac{{\{f(\mathit{\omega }(t))-f(\mathit{\omega }(0))\}}^2}{2S(\mathit{\omega }(0),\mathit{\omega }(t))}\\ ={\text{FI}}_{f({\mathit{\omega }}^0),\mathbf{h}}=\frac{{\mathbf{h}}^T{\nabla }_f{\nabla }_f^T\mathbf{h}}{{\mathbf{h}}^{T}G\mathbf{h}},\end{array}$$ (19)

where G = G(ω⁰). For the appropriate perturbation ω̃(ω) given in equation (18), FI_f,h reduces to ${\mathbf{h}}^T{\mathit{G}}^{-1/2}{\nabla }_f{\nabla }_f^T{\mathit{G}}^{-1/2}\mathbf{h}$ with the constraint h^T h = 1.

We use the maximum value of FI_f,h and its associated eigenvector, denoted by h_max, as influence measures to quantify the largest degree and influential direction of local influence of ω̃ to the JMLS. It can be easily shown that FI_f,hmax equals ${\nabla }_f^T{\mathit{G}}^{-1}{\nabla }_f$ and ${\mathbf{h}}_{max}={\mathit{G}}^{-1/2}{\nabla }_f/\sqrt{{\nabla }_f^T{\mathit{G}}^{-1}{\nabla }_f}$. In particular, h_max can be used to detect robustness of priors or identify influential observations and incorrect sampling distributional assumptions for single-case and global perturbations (Cook, 1986). Following Zhu and Lee (2001) and Zhu et al. (2007), we also suggest inspecting FI_{f, ei} to identify the most significant components of ω̃, where e_i is a W × 1 vector with a 1 for the ith element and 0 otherwise. For instance, we consider the Bayes factor given by f(ω) = log p(D_o; ω) − log p(D_o; ω⁰), where p(D_o; ω) = ∫ p(D_o, b, θ; ω)dbdθ. Thus, under some smoothness conditions, it can be shown that ∇_f = E_ω⁰[∂ωlog p(D_o, b, θ; ω⁰)|D_o ] and ${\mathit{h}}_{max}={\mathit{G}}^{-1/2}{\nabla }_f/\sqrt{{\nabla }_f^T{\mathit{G}}^{-1}{\nabla }_f}$. To calculate the local influence measures associated with f(ω), we just need to compute ∇_f and G. In practice, we can use MCMC methods to draw samples {(θ^(s), b^(s)): s = 1, …, S₀} from p(θ, b; D_o, ω⁰) to approximate ∇_f via ${\nabla }_f\approx S_0^{-1}{\sum }_{s=1}^{S_0}{\partial }_{\mathit{\omega }}logp(D_o,{\mathit{b}}^{(s)},{\mathit{\theta }}^{(s)};{\mathit{\omega }}^0)$.

We can also carry out Bayesian local influence when ∇_f = 0. Because f (ω(t)) = f (ω(0)) + 0.5h^T H_f ht² + O(t³), where ${\mathit{H}}_f={\partial }_{\mathit{\omega }}^{2}f({\mathit{\omega }}^0)$, we introduce a second-order influence measure (SI) in the direction h ∈ R^W, given by

$${\text{SI}}_{f,\mathbf{h}}={\text{SI}}_{f({\mathit{\omega }}^0),\mathbf{h}}=\underset{t\to 0}{lim}\frac{\{f(\mathit{\omega }(t))-f(\mathit{\omega }(0))\}}{S(\mathit{\omega }(0),\mathit{\omega }(t))}=\frac{{\mathbf{h}}^T{\mathit{H}}_f\mathbf{h}}{{\mathbf{h}}^T\mathit{Gh}}.$$ (20)

For ω̃ (ω) in equation (18), SI_f,h reduces to h^TG^−1/2H_fG^−1/2h, where h^T h = 1. Moreover, we also use SI_f,ei and the eigenvalue–eigenvector pairs of G^−1/2H_f G^−1/2 as our influence measures. We use the eigenvector of the largest eigenvalue of G^−1/2H_f G^−1/2, denoted by h_max, as influence measures to quantify the influential direction of local influence of ω̃ to the JMLS.

Finally, we examine the influence measures associated with three common objective functions, these being the φ–divergence, the posterior mean distance, and the Bayes factor, and include the detailed formulas in the supplementary document. Although all three objective functions can assess the local influence of a perturbation vector ω to the JMLS, there is a conceptual difference among these measures. The φ–divergence and the Bayes factor quantify the effects of introducing ω on the overall posterior distribution, whereas the posterior mean distance quantifies the effect of ω on the posterior mean of θ. Because the perturbation vector ω may influence various characteristics of the posterior distribution, such as the shape, mode, and mean, the φ–divergence, and the Bayes factor can be more sensitive to some perturbations of the posterior distribution compared to the posterior mean for certain perturbation schemes ω. In contrast, the posterior mean distance may be more sensitive to perturbations which have a dramatic effect on the posterior mean.

4. Application to the IBCSG Data

We applied our proposed methodology to both simulated data and the IBCSG data discussed in the Introduction Section. For the sake of space, we only present some influence analysis results for the IBCSG data here. We refer the reader to the supplementary document for further details.

For the IBCSG data, we considered a JMLS for jointly investigating the relationship between the multidimensional QOL and the bivariate failure time variables DFS and OS. To satisfy the normality assumption for the four considered longitudinal QOL indicators (appetite, denoted as y₁; perceived coping, denoted as y₂; mood, denoted as y₃; and physical well-being, denoted as y₄), we transformed their corresponding observed values of QOL to $\sqrt{100-\text{QOL}}$ (Chi and Ibrahim, 2006). The transformed QOLs decreased over time and were scaled between 0 and 10 with smaller values reflecting better QOL. There were 832 patients from Switzerland, Sweden, and New Zealand/Australia with a total of 2154 QOL observations being included in this analysis.

Let y_i1(t_ij1), …, y_i4(t_ij4) be the observed values of the transformed QOLs for the ith patient at the jth time point, respectively. We considered the following JMLS:

$$\begin{array}{l}{\lambda }_m(t\mid {\mathit{b}}_i,{\mathit{z}}_i)={\lambda }_{m0}(t)exp\{{\alpha }_{m1}{\eta }_{i1}(t,{\mathit{b}}_{i1})+\cdots +{\alpha }_{m4}{\eta }_{i4}(t,{\mathit{b}}_{i4})+{\mathit{z}}_i^T{\mathit{\gamma }}_m\}\\ y_{ik}(t_{\mathit{ijk}})={\eta }_{ik}(t_{\mathit{ijk}},{\mathit{b}}_{ik})+{\epsilon }_{\mathit{ijk}}={\beta }_{k0}+{\beta }_{k1}{x}_{i1}+\cdots +{\beta }_{k6}{x}_{i6}+{\beta }_{k7}{t}_{\mathit{ijk}}+b_{ik0}+b_{ik1}{t}_{\mathit{ijk}}+{\epsilon }_{\mathit{ijk}},\end{array}$$ (21)

for i = 1, …, 832, j = 1, 2, 3, k = 1, …, 4, and m = 1, 2, where x_i = (x_i1, …, x_i6)^T includes the number of initial cycles, reintroduction, interaction of the number of initial cycles and reintroduction, age, residency for Switzerland, and residency for Sweden. Moreover, z_i includes the number of initial cycles, reintroduction, interaction of the number of initial cycles and reintroduction, age, number of positive nodes, and ER status. We assumed that ε_ij = (ε_ij1, …, ε_ij4)^T are independently and identically distributed as N₄(0, Σ), and the random effects b_ik = (b_ik0, b_ik1)^T are independently and identically distributed as N₂(0, φ_k) for i = 1, …, 832, j = 1, 2, 3, and k = 1, …, 4. For the baseline hazard λ_m0(·), we take the piecewise constant hazards model with 250 subintervals with equal lengths such that ${\lambda }_{m0}(t)={\sum }_{l=1}^L{h}_{ml}\mathbf{1}(t\in (c_{m,l-1},c_{m,l}])$ with L = 250, where the c_m,l s are prespecified constants.

To conduct a Bayesian analysis, we specified the following prior distributions:

$$\begin{array}{l}{\mathit{\alpha }}_m={({\alpha }_{m1},\dots ,{\alpha }_{m4})}^T~N\left({\mathit{\alpha }}_m^0,{\mathit{H}}_{\alpha }^0\right),{\mathit{\gamma }}_m~N\left({\mathit{\gamma }}_m^0,{\mathit{H}}_{\gamma }^0\right),{\mathit{\sum }}^{-1}~{\text{Wishart}}_4({\mathit{R}}^0,{\rho }^0),\\ {\mathit{\beta }}_k={({\beta }_{k0},\dots ,{\beta }_{k7})}^T~N\left({\mathit{\beta }}_k^0,{\mathit{H}}_{\beta }^0\right),h_{ml}~\mathrm{\Gamma }({\tau }_{0l},{\tau }_{1l}),{\mathbf{\Phi }}_k^{-1}~{\text{Wishart}}_2\left({\mathit{R}}_{\phi k}^0,{\rho }_{\phi k}^0\right)\end{array}$$ (22)

for m = 1 and 2, and k = 1, …, 4, where h = {h_ml: m = 1, 2, l = 1, …, L}, ${\mathit{\alpha }}_m^0,{\mathit{H}}_{\alpha }^0,{\mathit{\gamma }}_m^0,{\mathit{H}}_{\gamma }^0$, R⁰, ρ⁰, ${\mathit{\beta }}_k^0,{\mathit{H}}_{\beta }^0$, τ_0l, τ_1l, ${\mathit{R}}_{\phi k}^0$, and ${\rho }_{\phi k}^0$ are prespecified hyperparameters. Moreover, ${\mathit{\alpha }}_m^0,{\mathit{\gamma }}_m^0,{\mathit{\beta }}_k^0$, R⁰, and ${\mathit{R}}_{\phi k}^0$ were set to their Bayesian posterior means obtained from MCMC methods based on noninformative prior distributions for α_m, γ_m, Σ⁻¹, β, and φ_k. We used MCMC methods, whose key steps are described in the supplementary document, to carry out the Bayesian analysis.

To illustrate our influence analysis, we considered five different perturbations to the JMLS and carried out the associated influence analysis. Specifically, for each perturbation ω, we calculated the metric tensor G and then took the new appropriate perturbation ω̃ (ω) given in equation (18). Detailed derivations of influence quantities, such as G(ω⁰), can be found in the supplementary document. We chose the Bayes factor as the objective function and then calculated the local influence measure h_max of the Bayes factor for each perturbation scheme by using the MCMC output. Specifically, a total of 5,000 iterations after 5,000 burn-in samples were used to compute all local influence measures.

The first perturbation is a single-case perturbation, which is obtained by perturbing each subject’s longitudinal profile as follows:

$$y_{ik}(t_{\mathit{ijk}},{\omega }_{\mathit{ijk}})={\beta }_{k0}+{\beta }_{k1}{x}_{i1}+\cdots +{\beta }_{k6}{x}_{i6}+{\beta }_{k7}{t}_{\mathit{ijk}}+b_{ik0}+b_{ik1}{t}_{\mathit{ijk}}+{\epsilon }_{\mathit{ijk}}/{\omega }_{\mathit{ijk}}.$$

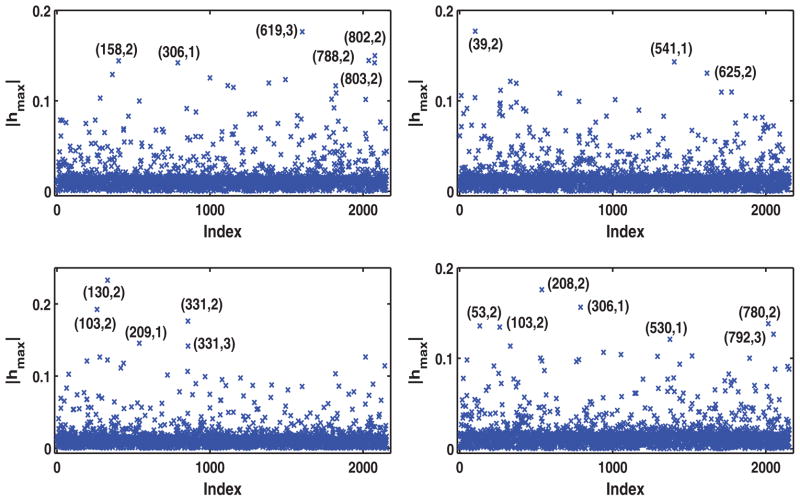
In this case, $\mathit{\omega }={({\mathit{\omega }}_{11}^T,\dots ,{\mathit{\omega }}_{1n_1}^T,\dots ,{\mathit{\omega }}_{n1}^T,\dots ,{\mathit{\omega }}_{nn{}_n}^T)}^T$, in which ω_ij = (ω_ij1, …, ω_ij4)^T for i = 1, …, n = 832, and j = 1, …, 3, and ω⁰ = 0 presents no perturbation. This single-case perturbation is designed to detect influential transformed QOLs of the longitudinal profiles in the evolution process. Figure 1 presents the subcomponents of h_max corresponding to all cases (i, j) for k = 1, 2, 3, and 4, where (i, j) represents the ith patient at the jth time point. Inspecting Figure 1 reveals the most influential cases as (158,2), (306,1), (619,3), (788,2), (802,2), and (803,2) for k = 1; (39,2), (541,1), and (625,2) for k = 2; (103,2), (130,2), (209,1), (331,2), and (331,3) for k = 3; and (53,2), (103,2), (208,2), (306,1), (530,1), (780,2), and (792,3) for k = 4.

Figure 1.

Results of single-case perturbation to longitudinal profiles for the IBCSG data set: Index plots of the local influence measure |h_max| corresponding to k = 1 (left upper panel), k = 2 (right upper panel), k = 3 (left lower panel), and k = 4 (right lower panel).

The second perturbation is also a single-case perturbation, which perturbs each marginal hazard function as follows:

$${\lambda }_m(t\mid {\mathit{b}}_i,{\mathit{z}}_i,{\omega }_{im})={\lambda }_{m0}(t)exp\{{\alpha }_{m1}{\eta }_{i1}(t,{\mathit{b}}_i)+\cdots +{\alpha }_{m4}{\eta }_{i4}(t,{\mathit{b}}_i)+z_i^T{\mathit{\gamma }}_m+{\omega }_{im}\}$$

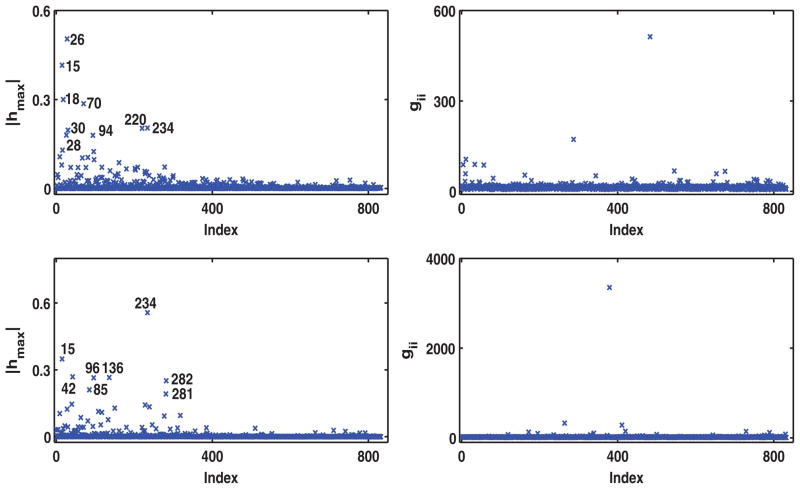
for i = 1, …, n and m = 1, 2. In this case, ω = (ω₁₁, ω₂₁, …, ω_n1, ω_n2) with ω⁰ = 1 representing no perturbation. This single-case perturbation is used to detect influential disease-free survival and overall survival times in the survival process. Inspecting Figure 2 reveals patients 15, 18, and 28 as most influential for m = 1, and patients 15, 42, 85, 96, 136, 234, 281, and 282 for m = 2 by our local influence measure h_max for the Bayes factor.

Figure 2.

Results of single-case perturbation to marginal hazard functions for the IBCSG data set: Index plots of the local influence measure h_max for ω_ins with m = 1 (left upper panel), and for ω_ins with m = 2 (left lower panel), and g_ii with m = 1 (right upper panel), and m = 2 (right lower panel).

The third perturbation is to simultaneously perturb the shared random effects b_i in both the longitudinal profiles and the marginal hazard functions:

$$\begin{array}{l}{y}_{ik}(t_{\mathit{ijk}},{\omega }_{ik})={\beta }_{k0}+{\beta }_{k1}{x}_{i1}+\cdots +{\beta }_{k6}{x}_{i6}+{\beta }_{k7}{t}_{\mathit{ijk}}+{\omega }_{ik}(b_{ik0}+b_{ik1}{t}_{\mathit{ijk}})+{\epsilon }_{\mathit{ijk}}\\ \triangleq {\eta }_{ik}(t_{\mathit{ijk}},{\mathit{b}}_{ik},{\omega }_{ik})+{\epsilon }_{\mathit{ijk}},\end{array}$$

$${\lambda }_m(t\mid {\mathit{b}}_i,{\mathit{z}}_i,{\mathit{\omega }}_i)={\lambda }_{m0}(t)exp\{{\alpha }_{m1}{\eta }_{i1}(t,{\mathit{b}}_{i1},{\omega }_{i1})+\cdots +{\alpha }_{m4}{\eta }_{i4}(t,{\mathit{b}}_{i4},{\omega }_{i4})+{\mathit{z}}_i^T{\mathit{\gamma }}_m\},$$

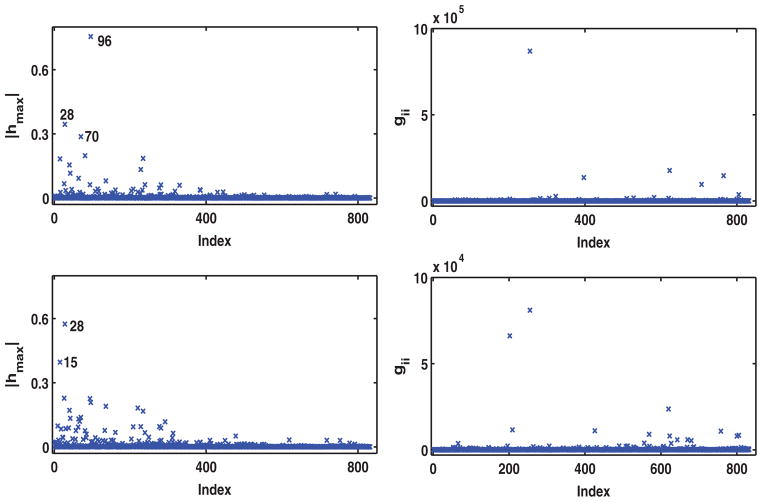
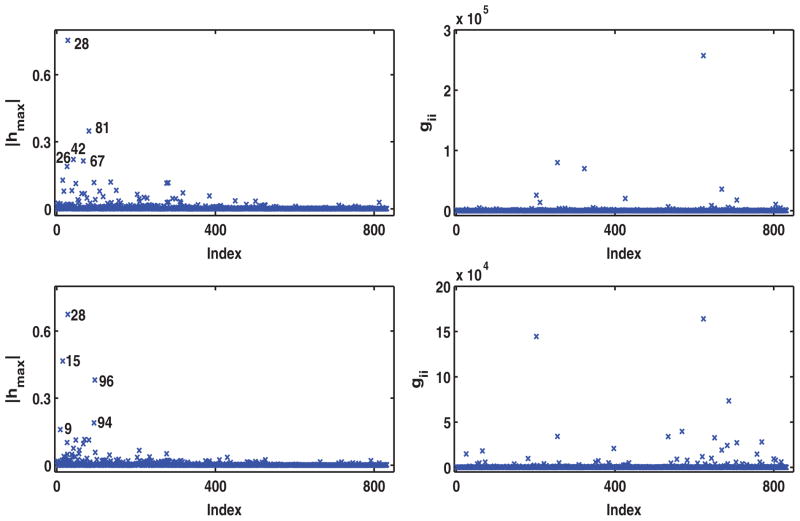
where ω_i = (ω_i1, …, ω_i4). In this case, ω = {ω₁₁, …, ω₁₄, …, ω_n1, …, ω_n4) and ω⁰ = 1 represents no perturbation. This single-case perturbation is used to detect these influential subjects, whose survival times have a low chance of occurrence given their subject-specific longitudinal profiles. Inspecting Figures 3 and 4 reveal the following influential subjects. Specifically, in Figure 3, patients 15, 28, 40, 70, 81, 96, 117, 136, 228, and 282 were detected to be the most influential for k = 1 and patients 15, 28, 30, 40, 70, 94, 136, 220, and 234 were detected to be the most influential for k = 2. Figure 4 shows that patients 15, 28, 70, 81, 136, and 150 were detected to be the most influential for k = 3 and patients 9, 15, 18, 28, 70, 94, 96, and 136 were detected to be the most influential for k = 4.

Figure 3.

Results of perturbing the shared random effects for the IBCSG data set: Index plots of the local influence measure |h_max| for perturbing b_ik with k = 1 (left upper panel), and k = 2 (left lower panel), g_ii with k = 1 (right upper panel) and k = 2 (right lower panel).

Figure 4.

Results of perturbing the shared random effects for the IBCSG data set: Index plots of the local influence measure |h_max| for perturbing b_ik with k = 3 (left upper panel), and k = 4 (left lower panel), g_ii with k = 3 (right upper panel) and k = 4 (right lower panel).

The fourth perturbation involves perturbing the prior distributions as follows:

$$\begin{array}{l}{\mathit{\beta }}_k~N_7({\mathit{\beta }}_k^0+{\omega }_{\beta 0}{\mathbf{1}}_7,{\mathit{H}}_{\beta k}^0/{\omega }_{\beta 1}),\\ {\mathit{\alpha }}_m~N_4({\mathit{\alpha }}_m^0+{\omega }_{\alpha 0}{\mathbf{1}}_4,{\omega }_{\alpha 1}^{-1}{\mathit{H}}_{\alpha m}^0),\\ {\mathit{\sum }}^{-1}~{\text{Wishart}}_4({\rho }_0,{\omega }_{\mathrm{\sum }}^{-1}{\mathit{R}}^0),\\ {\mathbf{\Phi }}_k^{-1}~{\text{Wishart}}_2({\rho }_k^0,{\omega }_{\phi }^{-1}{\mathit{R}}_{\phi k}^0),\\ {\mathit{\gamma }}_m~N_6({\mathit{\gamma }}_m^0+{\omega }_{\gamma 0}{\mathbf{1}}_6,{\omega }_{\gamma 1}^{-1}{\mathit{H}}_{\gamma m}^0),h_{ml}~\mathrm{\Gamma }({\tau }_{\lambda 0},{\omega }_{\lambda }{\tau }_{\lambda 1}).\end{array}$$

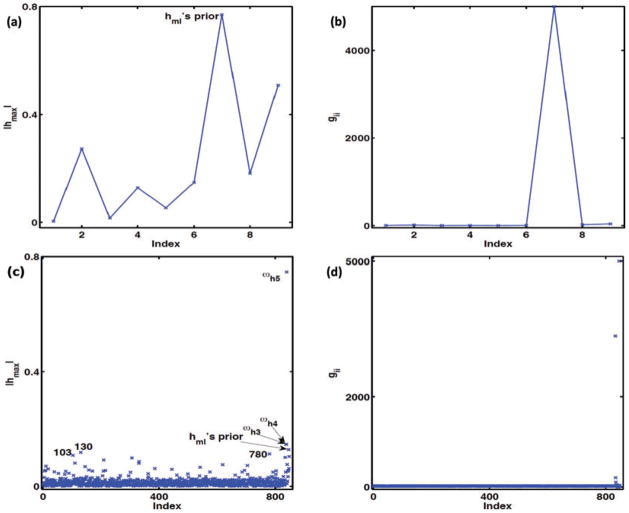
In this case, ω = {ω_β0, ω_β1, ω_α0, ω_α1, ω_γ0, ω_γ1, ω_λ, ω_Σ, ω_φ}, and ω⁰ = {0, 1, 0, 1, 0, 1, 1, 1, 1} represents no perturbation. This perturbation assesses the sensitivity of the Bayes factor to minor changes in the prior distributions. Based on the local influence measures |h_max| for the Bayes factor and the diagonal elements of G(ω⁰), Figures 5(a) and (b) shows that perturbing the prior of h_ml has a large impact on the Bayesian analysis.

Figure 5.

Results of the IBCSG data set. Perturbing the prior distributions: (a) index plot of the local influence measure |h_max| (the left panel); and (b) index plot of g_ii (the right panel) for perturbing priors of the parameters β_k, α_m, γ_m, h_{m l}, Σ and Φ₁, …, Φ₄. The simultaneous perturbation: (c) index plot of the local influence measure |h_max| (the left panel); and (d) index plot of g_ii (the right panel).

The last perturbation is a simultaneous perturbation. Specifically, we consider the following perturbation scheme:

$$\begin{array}{l}{y}_{ik}(t_{\mathit{ijk}},{\omega }_i,{\omega }_b)={\beta }_{k0}+{\beta }_{k1}{x}_{i1}+\cdots +{\beta }_{k6}{x}_{i6}+{\beta }_{k7}{t}_{\mathit{ijk}}+{\omega }_b(b_{ik0}+b_{ik1}{t}_{\mathit{ijk}})+{\epsilon }_{\mathit{ijk}}/{\omega }_i\\ \triangleq {\eta }_{ik}(t_{\mathit{ijk}},{\mathit{b}}_{ik},{\omega }_b)+{\epsilon }_{\mathit{ijk}}/{\omega }_i,\end{array}$$

$${\lambda }_m(t\mid {\mathit{b}}_i,{\mathit{z}}_i,{\omega }_{\lambda },{\omega }_b)={\lambda }_{m0}(t)exp\{{\alpha }_{m1}{\eta }_{i1}(t,{\mathit{b}}_{i1},{\omega }_b)+\cdots +{\alpha }_{m4}{\eta }_{i4}(t,{\mathit{b}}_{i4},{\omega }_b)+{\mathit{z}}_i^T{\mathit{\gamma }}_m+{\omega }_{\lambda }\},$$

and a subset of the $h_{ml}^{\prime }$s and the priors of β_k, α_m, γ_m, h_ml, Σ⁻¹ and ${\mathbf{\Phi }}_k^{-1}$ are pertarbed. In this case, we have

$$\mathit{\omega }=\{{\omega }_1,\dots ,{\omega }_n,{\omega }_b,{\omega }_{\lambda },{\omega }_{h1},\dots ,{\omega }_{hG},{\omega }_{\beta 0},{\omega }_{\beta 1},{\omega }_{\alpha 0},{\omega }_{\alpha 1},{\omega }_{\gamma 0},{\omega }_{\gamma 1},{\omega }_h,{\omega }_{\mathrm{\sum }},{\omega }_{\phi }\}$$

and ω⁰ = {1, …, 1, 1, 0, 1, 1, …, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1} represents no perturbation. We are interested in examining the sensitivity of all components of the Bayesian analysis to such simultaneous perturbations. Based on all the subcomponents of |h_max| and g_ii, Figure 5(c) identifies influential perturbations $b_{ik0}+b_{ik1}t,{\mathit{z}}_i^T{\mathit{\gamma }}_m$, h_ml s and the prior distribution of the h_ml s as well as the three most influential patients 103, 130, and 780. Finally, we deleted the three influential subjects 103, 130, and 780 and recalculated the posterior estimates of the parameters for the IBCSG data (Table 1). Inspecting Table 1 indicates that many subcomponents of β_k and α_m are very sensitive to the deletion of these three subjects.

Table 1.

The IBCSG data set: Posterior means (Mean) of the parameters and their posterior standard deviations (SD) with and without influential patients 103, 130, and 780.

Par.	With		Without		Par.	With		Without
	Mean	SD	Mean	SD		Mean	SD	Mean	SD
α11	0.263	0.055	0.725	0.141	β10	3.481	0.147	4.285	0.052
α12	−0.838	0.042	0.090	0.142	β11	−0.051	0.154	−0.265	0.082
α13	−1.081	0.061	0.077	0.129	β12	−0.090	0.162	−0.106	0.097
α14	1.245	0.076	−1.655	0.215	β13	−0.050	0.222	0.349	0.086
α21	0.642	0.096	1.132	0.146	β14	0.585	0.127	−0.150	0.052
α22	−1.363	0.067	0.062	0.179	β15	0.140	0.182	−0.320	0.059
α23	−1.525	0.056	0.069	0.156	β16	0.174	0.141	−0.154	0.091
α24	1.650	0.121	−2.276	0.334	β17	−0.735	0.056	−0.903	0.019
γ11	0.047	0.240	0.062	0.214	β20	5.177	0.604	5.806	0.140
γ12	−0.437	0.235	−0.398	0.201	β21	0.268	0.124	−0.195	0.154
γ13	−0.149	0.346	0.084	0.399	β22	0.152	0.200	−0.197	0.153
γ14	−1.185	0.243	−0.250	0.164	β23	−0.329	0.219	0.440	0.205
γ15	1.304	0.166	1.058	0.159	β24	0.344	0.246	0.140	0.158
γ16	−0.790	0.212	−0.322	0.154	β25	0.298	0.135	0.204	0.130
γ21	−1.280	0.480	−1.044	0.367	β26	0.377	0.254	0.012	0.122
γ22	−1.851	0.449	−1.685	0.377	β27	−0.863	0.112	−1.014	0.048
γ23	1.525	0.682	1.695	0.723	β30	4.289	0.162	5.048	0.120
γ24	−2.911	0.542	−1.317	0.300	β31	0.347	0.094	0.059	0.118
γ25	2.129	0.245	1.589	0.334	β32	0.213	0.136	0.158	0.125
γ26	−2.929	0.430	−1.726	0.239	β33	−0.428	0.205	−0.089	0.180
σ11	3.941	0.165	4.259	0.205	β34	0.594	0.120	0.148	0.109
σ12	1.588	0.115	1.642	0.120	β35	0.268	0.161	−0.061	0.119
σ13	2.444	0.125	2.524	0.131	β36	0.820	0.104	0.159	0.098
σ14	2.537	0.122	2.533	0.130	β37	−0.823	0.037	−0.855	0.057
σ22	4.163	0.173	3.660	0.164	β40	3.974	0.623	4.560	0.071
σ23	2.716	0.128	2.386	0.129	β41	0.047	0.192	0.017	0.058
σ24	2.112	0.131	2.322	0.129	β42	−0.182	0.241	−0.029	0.065
σ33	4.672	0.171	4.449	0.170	β43	−0.019	0.293	0.130	0.076
σ34	3.129	0.137	3.395	0.142	β44	0.853	0.290	0.215	0.036
σ44	4.695	0.173	5.243	0.177	β45	0.151	0.102	−0.170	0.055
φ1,11	1.516	0.179	1.073	0.207	β46	0.724	0.140	0.158	0.028
φ1,12	−0.567	0.110	−0.356	0.098	β47	−0.655	0.115	−0.661	0.011
φ1,22	0.479	0.078	0.380	0.074	φ3,11	0.685	0.081	1.067	0.117
φ2,11	1.163	0.133	1.539	0.156	φ3,12	−0.267	0.056	−0.376	0.076
φ2,12	−0.241	0.079	−0.289	0.121	φ3,22	0.626	0.079	0.417	0.068
φ2,22	0.654	0.084	0.644	0.139
φ4,11	0.537	0.088	0.328	0.072
φ4,12	−0.144	0.056	−0.090	0.053
φ4,22	0.403	0.057	0.404	0.057