A Health Production Model with Endogenous Retirement

Abstract

We formulate a stylized structural model of health, wealth accumulation and retirement decisions building on the human capital framework of health and derive analytic solutions for the time paths of consumption, health, health investment, savings and retirement. We argue that the literature has been unnecessarily restrictive in assuming that health is always at the “optimal” health level. Exploring the properties of corner solutions we find that advances in population health decrease the retirement age, while at the same time individuals retire when their health has deteriorated. This potentially explains why retirees point to deteriorating health as an important reason for early retirement, while retirement ages have continued to fall in the developed world, despite continued improvements in population health and mortality. In our model, workers with higher human capital invest more in health and because they stay healthier retire later than those with lower human capital whose health deteriorates faster.

1. Introduction

Models of retirement need to be able to reconcile the counterintuitive observations that a) retirees mention deteriorating health as an important reason for early retirement, b) population health and mortality have continued to improve, but c) the age of retirement has declined for nearly a full century in the developed world (though the decline in retirement age has leveled off in the last decade; see, e.g., Blau and Goodstein, 2010). Some of this could be explained by justification bias. Individuals may mention health as a reason to justify the fact that they are retired but in fact retire for other reasons, with health playing a minor role in the decision. For example, French (2005) estimates a life cycle model of labor supply, retirement, and savings behavior using the panel study of income dynamics (PSID). He finds that the structure of the Social Security system and of pensions are key determinants of the high observed job exit rates at ages 62 and 65 while Social Security benefit levels, health, and borrowing constraints are less important determinants of job exit at older ages. In line with this result Lazear (1986) finds that pensions are typically actuarially unfair and that sharp decreases in the actuarial value of retirement with continued work are used as a device by employers to induce earlier retirement of workers. Also Bazzoli (1985) finds that economic variables play a more important role than health in retirement decisions. On the other hand, Dwyer and Mitchell (1998) find the opposite: that health problems influence retirement plans more strongly than do economic variables. Specifically, Dwyer and Mitchell find that men in poor overall health retire between one and two years earlier than others. In other words, while there is agreement that health influences retirement there is disagreement about the importance of health in the retirement decision. Regardless of its current importance, the increased uptake of defined-contribution type pension vehicles such as 401(k)’s, which are actuarially fair, may reduce the importance of pension structure as a key determinant of retirement. This may warrant the inclusion of health as a more prominent determinant of future retirement.

The aim of this paper is to investigate the influence of various conditions, in particular that of an individual’s health, on the decision to retire. To this end, we formulate a stylized structural model of consumption, leisure, health, health investment, wealth accumulation and retirement decisions using the human capital framework of health provided by Grossman (1972a,b, 2000).¹

In this paper we follow the standard assumptions and interpretations employed in the Grossman literature. In particular these include assuming: (i) a constant returns to scale (CRTS) health production process²; and (ii) that the “optimal” health stock is determined by the equilibrium condition for health capital (see, e.g., equation (4a) in Wagstaff [1986], equation (11) in Grossman [2000]). We discuss throughout this paper the implications of these assumptions.

We then find that at the age of retirement the “optimal” level of the health stock is discontinuous.³ This is the result of the standard assumption of a CRTS health production process⁴ and implies that individuals invest an infinite amount (positive or negative) of health investment over an infinitesimally small period of time around the age of retirement.

Two possible solutions have been suggested in the literature to deal with this issue. First, Wolfe (1985) has shown, maintaining the assumption of CRTS, that if initial health is high (well above the equilibrium health stock) the optimal solution is a corner solution where individuals do not invest in medical care for periods of time. Second, Ehrlich and Chuma (1990) have presented a theory with decreasing returns to scale (DRTS). However, theoretical and empirical work on the Grossman model that followed the 1990 publication by Ehrlich and Chuma has continued to rely on the assumption of CRTS.⁵

Following the existing literature, we maintain the standard assumption of a linear health production process, but deal with the bang-bang nature of the Grossman model by incorporating corner solutions. This approach is based on Wolfe (1985) and Galama and Kapteyn (2011). In essence, we offer a solution that is only a small departure from the literature, namely maintaining the standard assumption of a linear health production process, but reaching the logical conclusion that this implies a “bang-bang” solution.

Our model represents, to the best of our knowledge, the first attempt at introducing retirement in the Grossman model in order to arrive at a joint theory of health and retirement. It is an improvement over the model presented by Wolfe (1985). To the best of our knowledge, Wolfe (1985) is the only researcher (with the exception of the more recent work by Galama and Kapteyn, 2011) who has attempted to explore the consequences of corner solutions in some detail. His model and interpretation is however substantially different from ours. Wolfe employs a simplified Grossman model where health does not provide utility. Further, Wolfe interprets the onset of “ … a discontinuous mid-life increase in health investment …” with retirement. We, however, associate the discontinuous increase in health investment with becoming unhealthy (health levels at or below a health threshold leading to health investment) and retirement in our model is a function of the accumulation of pension benefits and the result of life-time utility maximization.

The model can reproduce the observation that the retirement age has continued to fall while retirees point to deteriorating health as an important reason for early retirement at the same time that population health and mortality have continued to improve in the developed world. If advances in population health are largely the result of better nutrition, preventative medicine (through, e.g., vaccination and other means), and better (less taxing) living, working and schooling environments then the overall health endowment H(0) of the population increases and/or the health deterioration rate d(t) decreases. Both effects result in earlier retirement.^6,7 At the same time, workers with higher earnings (say white collar workers) invest more in health and because they stay healthier retire later than those with lower earnings (say blue collar workers) whose health deteriorates faster. Further, we find that higher income (base wage rate w₀(t)) increases the retirement age, while greater wealth (initial assets A(0)) and greater pension wealth (base pension benefit b₀ and fraction α of wages saved) decreases the retirement age. Advances in population wealth levels, but not income, could provide an alternative explanation for decreasing retirement ages.

In section 2 we formulate our model. We first solve the optimal control problem conditional on retirement age, then introduce endogenous retirement. In section 3 we provide simulations. We conclude in section 4 and provide detailed derivations in section 5 (the appendix). Derivations for six specific scenarios are provided separately in a second appendix that is available online on the journal website.

2. Model specification

2.1. General framework: a health production model

A natural framework for our analysis is provided by Grossman (1972a,b). For an excellent review of the basic concepts of this model see Muurinen and Le Grand (1985). Consumers maximize the life time utility function

$${\int }_0^R{U}_w[C(t),H(t)]e^{-\beta t}dt+{\int }_R^T{U}_r[C(t),H(t)]e^{-\beta t}dt,$$ (1)

where utility before retirement U_w[C(t), H(t)], and after retirement U_r[C(t), H(t)], has diminishing marginal returns and is an increasing function in its arguments consumption C(t) and health H(t), T denotes total life time, R is the age of retirement and β is a subjective discount factor. Time t is measured from the time individuals begin employment. The objective function (1) is maximized subject to the following constraints:

$$\begin{array}{l}\begin{array}{lll}\stackrel{.}{H}(t)\hfill & =\mu (t)m(t)-d(t)H(t)\hfill & 0\le t\le T\hfill \\ \stackrel{.}{A}(t)\hfill & =\delta A(t)+Y[H(t)]-C(t)-p(t)m(t)\hfill & 0\le t\le T\hfill \end{array}\\ Y[H(t)]=\{\begin{array}{ll}{w}_0(t)+\varphi (t)H(t)\hfill & 0\le t\le R\hfill \\ b\hfill & R<t\le T\hfill \end{array}\end{array}$$ (2)

Furthermore we have initial and end conditions: H(0), A(0) and A(T) are given.

Ḣ(t) and Ȧ(t) denote time derivatives of health H(t) and assets A(t). The first equation of (2) shows that an individual can invest in the stock of health H(t) by investing m(t) in medical care and/or other health promoting activities (e.g., exercise, diet, etc) with an efficiency μ(t) to improve health and counter the “natural” health deterioration rate d(t).

The second equation is simply the inter-temporal budget constraint, where δ is the interest rate, Y[H(t)] is income, C(t) is consumption and p(t) is the price of health investment m(t).

The third equation in (2) shows how income Y[H(t)] consists of earnings during working life and pension income during retirement. Earnings are a function of health, with w₀(t) a base wage rate that is age dependent (but independent of health) and the marginal production benefit of health ∂Y[H(t)]/∂H(t) = ϕ(t) ≥ 0 determines the extent to which health increases one’s wage. Retirement income b is independent of health.

Thus, we have the following optimal control problem: the objective function (1) is maximized with respect to the control functions C(t) and m(t) and subject to the constraints (2). The Lagrangean or generalized Hamiltonian (see, e.g., Seierstad and Sydsaeter 1987) of this problem is:

$$\mathfrak{J}=U[C(t),H(t)]e^{-\beta t}+p_A(t)\stackrel{.}{A}(t)+p_H(t)\stackrel{.}{H}(t)+q(t)m(t),$$ (3)

where U[C(t), H(t)] = U_w[C(t), H(t)] for t ≤ R; U[C(t), H(t)] = U_r[C(t), H(t)] for t > R; p_A(t) is the adjoint variable associated with the differential equation (2) for assets A(t), p_H(t) is the adjoint variable associated with the differential equation (2) for health H(t), and q(t) a multiplier associated with the condition that health investment m(t) ≥ 0. Despite the simplified nature of our formulation, all essential characteristics of the Grossman model are maintained (see the discussion, section 4, for detail). However, the inclusion of the multiplier q(t) is an essential difference between our formulation and prior formulations of the Grossman model. It allows us to explicitly impose the constraint that medical care is non-negative m(t) ≥ 0 at all times (see also Galama and Kapteyn, 2011).

We proceed as follows. First we solve the optimal control problem conditional on retirement age R (i.e., for fixed exogenous R). We then maximize the indirect utility function with respect to R. Health, savings and retirement thus are jointly determined.

2.2. Exogenous retirement

The first order conditions for maximization of (1) subject to (2) are (for details see the Appendix):

$$\begin{array}{l}\frac{\partial U_w(t)}{\partial C(t)}=p_A(0)e^{(\beta -\delta )t}(t\le R)\\ \frac{\partial U_r(t)}{\partial C(t)}=p_A(0)e^{(\beta -\delta )t}(t>R),\end{array}$$ (4)

and

$$\begin{array}{l}\frac{\partial U_w(t)}{\partial H(t)}=p_A(0)[{\pi }_H(t)-\varphi (t)]e^{(\beta -\delta )t}+\frac{e^{\beta t}}{\mu (t)}\stackrel{.}{q}(t)-\frac{e^{\beta t}}{\mu (t)}\left[\frac{\stackrel{.}{\mu }(t)}{\mu (t)}+d(t)\right]q(t)(t\le R)\\ \frac{\partial U_r(t)}{\partial H(t)}=p_A(0){\pi }_H(t)e^{(\beta -\delta )t}+\frac{e^{\beta t}}{\mu (t)}\stackrel{.}{q}(t)-\frac{e^{\beta t}}{\mu (t)}\left[\frac{\stackrel{.}{\mu }(t)}{\mu (t)}+d(t)\right]q(t)(t>R),\end{array}$$ (5)

where

$${\pi }_H(t)\equiv [p(t)/\mu (t)][d(t)+\delta -\stackrel{.}{p}(t)/p(t)+\stackrel{.}{\mu }(t)/\mu (t)]$$ (6)

is the user cost of health capital at the margin (the interest rate δ represents an opportunity cost).

Equations (4) and (5) represent, apart from simplifications in our formulation (but see section 4), terms in q(t) and the distinction between pre- and post-retirement, standard results for the optimality condition for consumption and the equilibrium condition for the health stock. They are similar to those by Case and Deaton (2005; their equations 5 and 6) for q(t) = 0, i.e., m(t) > 0. Equation (4) requires the marginal benefit of consumption to equal p_A(0) (the shadow price of wealth) times a time varying exponent that either grows or decays with time, depending on the difference between the time preference rate β and the interest rate δ. The marginal benefit of health investment (equation 5) equals the product of the marginal benefit of consumption (equation 4) and the user cost of health capital at the margin π_H(t) (equation 6) minus the marginal production benefits of health ϕ(t) if the individual is working.⁸

From the Mangasarian sufficiency conditions (see Appendix section 5.2) follows that the first-order (necessary) conditions (4) and (5) represent the global maximum of the objective function (1), subject to the constraints (2), under the condition

$$\frac{{\partial }^{2}U(t)}{\partial C{(t)}^2}\frac{{\partial }^{2}U(t)}{\partial H{(t)}^2}\ge {\left(\frac{{\partial }^{2}U(t)}{\partial C(t)\partial H(t)}\right)}^2.$$ (7)

However, because the Lagrangian (3) is concave, but not strictly concave, the solutions for the state and control functions are not necessarily unique.

We can make a number of observations with respect to equations 4 and 5. For now we discuss the case where q(t) = 0, i.e., m(t) > 0 (i.e., no corner solution). First, increasing lifetime resources will lower p_A(0) and hence increase health investment and consequently health. Second, while health continuous to provide a consumption benefit (utility), health does not provide a production benefit (greater income) after retirement (last equation of 2) and retired individuals will reallocate away from health expenditures in the direction of more consumption. Third, a lower price of health investment increases health. Finally, more efficient health investment will lead to more health.

In order to derive analytical solutions for consumption, health, health investment and wealth, we specify the following constant relative risk aversion (CRRA) form for the utility function (1):

$$U_w(C,H)=\frac{{[C^{\zeta }{H}^{1-\zeta }]}^{1-\rho }}{1-\rho };U_r(C,H)={kU}_w(C,H),$$ (8)

where ζ (0 ≤ ζ ≤ 1) is the relative “share” of consumption C(t) versus health H(t) and ρ(ρ > 0) the coefficient of relative risk aversion.

The factor k is the ratio of utility when retired and when working. A simple way to motivate the introduction of the multiplicative factor k is to include leisure in the utility function as follows: U(C, H, L) = C^ζH^1−ζL^τ]^1−ρ, where L is leisure and where we have omitted the multiplicative constant 1/(1 − ρ). Assume that during the working years leisure is equal to L₀ while during retirement leisure is equal to k_rL₀, with k_r > 1. This implies that the ratio of utility before and after retirement is equal to $k\equiv k_r^{\lambda (1-\rho )}$. This specification is consistent with the Stock and Wise (1990) specification in which the utility of consumption in retirement is a multiple of the utility of consumption when working.⁹ Further, this formulation can reproduce the drop in consumption observed at retirement (Banks, Blundell and Tanner 1998; Bernheim, Skinner and Weinberg 2001).

2.2.1. Model solutions: the “optimal” health stock

We begin analyzing the case where q(t) = 0, i.e. m(t) > 0. This case is associated with the “optimal” health stock, as utilized in the literature spawned by Grossman. We denote the solutions for consumption, health investment and health with C_*(t), m_*(t), and H_*(t) for this special case. Solving the first order conditions (4) and (5) and using the Cobb-Douglas utility specification (8), we find the following solutions for the control functions C_*(t) and m_*(t) (for details see the Appendix):

$$C_{\ast }(t)=\zeta \mathrm{\Lambda }{[{\pi }_H(t)-\varphi (t)]}^{1-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}(t\le R)$$ (9)

$$C_{\ast }(t)=k^{\frac{1}{\rho }}\zeta \mathrm{\Lambda }{[{\pi }_H(t)]}^{1-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}(t>R)$$ (10)

$$m_{\ast }(t)=\frac{1}{\mu (t)}{e}^{-\underset{0}{\overset{t}{\int }}d(s)ds}\times \frac{d}{dt}\left\{(1-\zeta )\mathrm{\Lambda }{[{\pi }_H(t)-\varphi (t)]}^{-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}{e}^{\underset{0}{\overset{t}{\int }}d(s)ds}\right\}(t\le R)$$ (11)

$$m_{\ast }(t)=\frac{1}{\mu (t)}{e}^{-\underset{0}{\overset{t}{\int }}d(s)ds}\times \frac{d}{dt}\left\{k^{\frac{1}{\rho }}(1-\zeta )\mathrm{\Lambda }{[{\pi }_H(t)]}^{-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}{e}^{\underset{0}{\overset{t}{\int }}d(s)ds}\right\}(t>R),$$ (12)

where we have used the following definitions:

$$\chi \equiv \frac{1+\rho \zeta -\zeta }{\rho },$$ (13)

and

$$\mathrm{\Lambda }\equiv {\zeta }^{\frac{1-\rho }{\rho }}{\left(\frac{\zeta }{1-\zeta }\right)}^{1-\chi }{p}_A{(0)}^{\frac{-1}{\rho }}.$$ (14)

For the “optimal” health stock H_*(t) we find:

$$H_{\ast }(t)=(1-\zeta )\mathrm{\Lambda }{[{\pi }_H(t)-\varphi (t)]}^{-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}(t\le R)$$ (15)

$$H_{\ast }(t)=k^{\frac{1}{\rho }}(1-\zeta )\mathrm{\Lambda }{[{\pi }_H(t)]}^{-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}(t>R).$$ (16)

Consumption, health investment and health (equations 9 through 16) are functions of various combinations of the user cost of health capital at the margin π_H(t) (see equation 6), minus the marginal production benefit of health ϕ(t).¹⁰

As many authors have found (e.g., Case and Deaton 2005, Grossman 2000), the “optimal” health stock H_*(t) is constant for constant time paths of d(t) = d₀, p(t) = p₀, μ(t) = μ₀, ϕ(t) = ϕ₀ and for β = δ, and decreases for an increasing deterioration rate with age ḋ(t) > 0.

At the age of retirement the solutions (q(t) = 0) for the “optimal” level of consumption (equations 9, 10), “optimal” level of health investment (equations 11, 12) and “optimal” level of health (equations 15, 16) are discontinuous. These jumps represent the change in consumption and health investment as a result of differences in utility from more leisure time during retirement (depending on the value of k, leisure is a substitute or a complement of consumption and health) and because health has no effect on income after retirement (ϕ(t) = 0).

2.2.2. Model solutions: general case

The literature generally assumes that the “optimal” health stock is determined by the equilibrium condition for health capital (e.g., Grossman 1972a,b, 2000; Case and Deaton 2005; Muurinen 1982; Wagstaff 1986; Zweifel and Breyer 1997, Ried 1998). This requires one to assume that individuals are capable of adjusting their health to the “optimal” level instantaneously and without adjustment costs.¹¹

We do not make this assumption and follow Galama and Kapteyn (2011) by explicitly demanding that medical care is non-negative m(t) ≥ 0 by introducing the multiplier q(t) in the Lagrangean (equation 3). We thus allow for the existence of corner solutions where individuals do not invest in medical care m(t) = 0 for certain periods of time. As a result, given initial health H(0), the “optimal” health stock is not the optimal solution.¹² Any situation with “excessive” initial health (initial health H(0) above H_*(0)) is preferable: individuals with excess initial health have higher levels of health and consumption and therefore greater life-time utility.

Individuals with health endowments H(0) below the “optimal” health stock H_*(0) will invest in medical care (an adjustment cost) to reach the “optimal” health level (see for details the Online Appendix). Individuals only invest in health when they are “unhealthy” (health levels below the “optimal” stock) and not when they are “healthy” (health levels above the “optimal” stock). In other words, what is traditionally called the “optimal” solution for health, operates instead as a “health threshold”.

We distinguish six scenarios as shown in figure 1. The health threshold H_*(t) (dotted line) drops at the age of retirement R (for our choice of parameters k < 1 leisure is a substitute of consumption and health, and after retirement ϕ(t) = 0). We show the simplest case in which the health threshold H_*(t) is constant with time (e.g., for constant time paths of d(t) = d₀, p(t) = p₀, μ(t) = μ₀, ϕ(t) = ϕ₀ and for β = δ) but the scenarios are valid for more general cases. Scenarios A, B, C and D begin with initial health H(0) above and scenarios E and F begin with initial health H(0) below the initial health threshold H_*(0). In scenarios A and B health H(t) reaches the health threshold H_*(t) before the age of retirement R (at age t₁). In scenario A the health threshold H_*(t) is once more reached at age t₂ before total life time T, but this is not the case in scenario B. In scenario C health H(t) reaches the threshold H_*(t) after the age of retirement R (at age t₂), and in scenario D health H(t) never reaches the threshold H_*(t) during life. In scenarios E and F individuals begin working life with health levels H(0) below the initial health threshold H_*(0). Individuals will substitute initial assets A(0) for improved initial health H(0) such that initial health equals the initial health threshold H(0) = H_*(0) (see the Online Appendix for a more detailed discussion).

Figure 1.

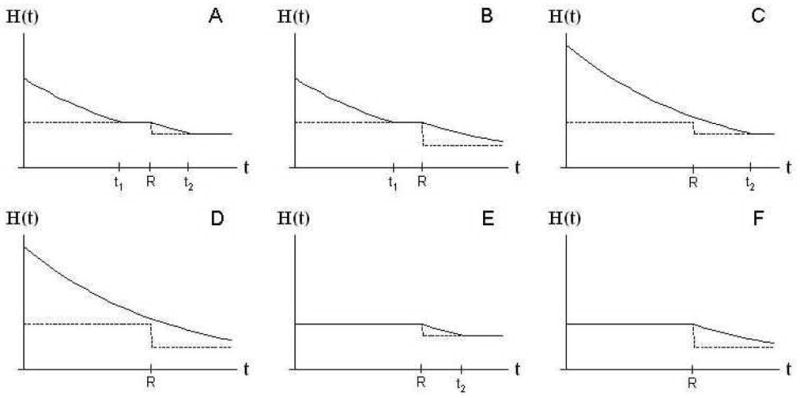
Six scenarios for the evolution of health. t₁ and t₂ denote the ages at which health (solid line) has evolved towards the health threshold (dotted line), and R denotes the age of retirement. The health threshold drops at the age of retirement R as a result of differences in utility due to increased leisure time during retirement (depending on the value of k, leisure is a substitute or a complement of consumption and health) and because health has no effect on income after retirement (ϕ(t) = 0).

The detailed solutions for health H(t), consumption C(t) and health investment m(t) for each of the six scenarios are provided in the Online Appendix. Assets A(t) can be derived from the second equation of (2). Each solution is fully determined, that is, the constant Λ [and hence p_A(0)] can be determined by substituting the solutions for health H(t), consumption C(t) and health investment m(t) into the budget constraint (second equation of 2) and imposing the initial and end conditions for wealth. The result can be written as a fraction Λ ≡ Λ_n/Λ_d, where the numerator Λ_n increases with life-time resources. Hence increasing initial assets A(0), base wages w₀(t), retirement benefits b, production benefits of health ϕ(t) or initial health H(0) increases the constant Λ and thereby consumption C(t), health investment m(t), and health H(t). The denominator Λ_d is a complicated function of the time paths of d(t), p(t), μ(t), ϕ(t) and various model parameters:

$${\mathrm{\Lambda }}_d={\mathrm{\Lambda }}_d[d(t),p(t),\mu (t),\varphi (t),\delta ,\beta ,R,T,k,\rho ,\zeta ].$$ (17)

The full solutions for Λ are provided in the Online Appendix for each of the six scenarios.

2.3. Treatment of benefits

Typically benefits are based on the wages earned during working life. As a stylized representation of this we assume that a fraction of wages αw(t) are saved for retirement. Benefits accumulate with time and are invested with a return on investment of δ (the interest rate) as follows:

$$b(R)=b_0+f(R)\alpha \underset{0}{\overset{R}{\int }}w(t)e^{\delta t}dt,$$ (18)

where the pension accumulation function f(R) describes how benefits accumulate as a function of retirement age R and b₀ represents a base pension benefit.

The base pension benefit b₀ is provided regardless of years worked, e.g., it could represent a first-tier basic pension (OECD 2005) or a statutory poverty line. The remaining term in (18) represents the part of the pension that accumulates with years of work. Pension wealth in retirement thus consists of a base pension b₀ (typically provided by the state), an individual private pension (either defined benefit [DB] and/or defined contribution [DC]) and accumulated assets A(R) that can be drawn down during retirement.

Replacing the assumed flat retirement benefits b by (18) the previously derived equations remain valid with the following transformation

$$\begin{array}{l}{w}_0(t)\to (1-\alpha )w_0(t)\\ b\to b_0+\alpha f(R)\underset{0}{\overset{R}{\int }}{w}_0(t)e^{\delta t}dt\\ \varphi (t)\to \varphi (t)[(1-\alpha )+f(R)\frac{\alpha }{\delta }(e^{-\delta R}-e^{-\delta T})e^{2\delta t}]\end{array}$$ (19)

A derivation of transformation (19) is provided in the Appendix.

2.4. Endogenous retirement

The optimal age of retirement R can be determined by inserting the solutions for C(t), H(t) into the “indirect utility function”, V(R), and differentiating V(R) with respect to R.

$$V(R)\equiv \underset{0}{\overset{R}{\int }}{U}_w(t)e^{-\beta t}dt+\underset{R}{\overset{T}{\int }}{U}_r(t)e^{-\beta t}dt$$ (20)

Unfortunately the resulting expression for V(R) turns out to be unwieldy and we resort to numerically solving for the optimal retirement age R.

3. Simulations

In this section we begin by making some plausible assumptions about the model parameters and initial and terminal conditions. This will provide us with a starting point (our baseline model; section 3.1) from which we will subsequently deviate in order to investigate the impact of the various model levers on the decision to retire. We then briefly explore model simulations of health inequality (section 3.2) and discuss in detail the sensitivity of retirement age (section 3.3) and of other model outcomes (section 3.4) to model parameters.

3.1. Calibration baseline model: white collar worker

Individuals begin work at age 20 (corresponding to t = 0), and, depending on the solution for the optimal retirement age, retire some 45 years later at an age of about 65 years (R ≈ 45). Individuals die with certainty at 85 years of age (T = 65).

For simplicity we assume constant time paths of d(t) = d₀, p(t) = p₀, μ(t) = μ₀, ϕ(t) = ϕ₀, w₀(t) = w₀¹³ and take β = δ. We further assume an annual income of w(t) ≈ $45,000 for healthy “white collar” workers¹⁴ and that healthy workers have a health stock of about 1.5 times that of unhealthy workers (we will discuss “blue collar” workers later). We can then obtain 25% higher earnings for healthy workers¹⁵ for constant marginal production benefits of health ϕ(t) = ϕ₀ ≈ 1.5w₀/H_H (where H_H is health for a healthy worker), and a constant base wage rate w₀(t) = w₀ ≈ $20,000 per year. A roughly 50% decline in wage between first employment (t = 0) and retirement (t = R)⁶ requires that by the age of retirement health has fallen to one-fourth the level of health at first employment H(0). We can simulate such results with an initial health H(0) of $30,000,¹⁶ a constant health deterioration rate d(t) = d₀ of 5%, a contribution rate for retirement α of 15% of wages, zero basic benefits b₀ = 0, a coefficient of relative risk aversion ρ = 1.32, a constant health investment efficiency μ(t) = μ₀ = 0.7% and time preference rate and interest rate β = δ of 3%. We interpret prices p(t) as the co-pay rates, which we take to be constant at p(t) = p₀ = 20%, and m(t) as the total annual medical expenditures – though this could include the cost of other health promoting activities such as exercise, diet, etc.

Hurd and Rohwedder (2003, 2006) find that “on average” consumption drops between 15 and 20% after retirement. We use this observation to determine the value for k by requiring that consumption C(t) drops at retirement to 85% of its value before retirement.¹⁷ Hence we demand that $k^{\frac{1}{\rho \chi }}=0.85$ (see for details the Appendix). For the values chosen, we have k = 0.81.

To ensure that health investment is not too far from the observed mean out-of-pocket medical expenditures of around $3000 per year (corresponding to total medical expenditures of $15,000) we assume ς = 0.85, i.e. that an individual’s preferences are significantly skewed towards consumption and away from health. We assume an actuarially fair benefits accumulation function f(R) = δ/[1 − e^−δ(T−R)], i.e. as approximately in a DC plan. Lastly, we assume that individuals leave no bequests and receive no bequests, i.e. A(0) = A(T) = 0. There are likely many other plausible scenarios and parameter values. The current values are only for illustrative purposes.¹⁸

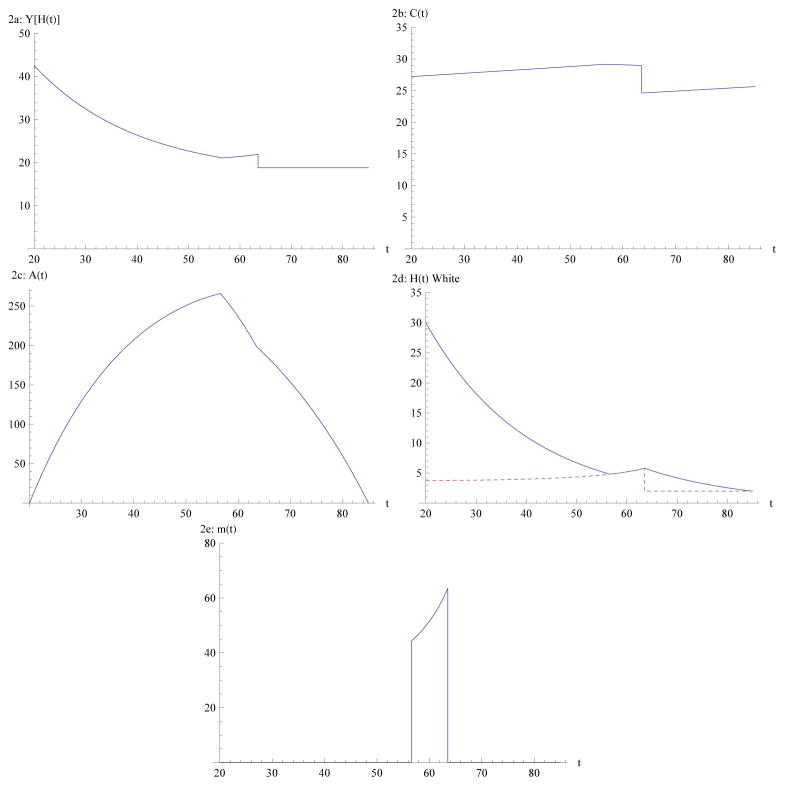
For this set of parameters and assumptions (see Table 1 for a quick overview) we find ourselves in scenario A and determine an optimal age of retirement of 63.52 (corresponding to R = 43.52). Figures 2a–2e describe the evolution of income, consumption, assets, health and health investment for the optimal retirement age of 63.52 years.

Table 1.

Sensitivity (elasticities) of model outcomes to various variables and parameters.

P	P0	$\frac{\partial ln\left[\underset{0}{\overset{T}{\int }}C(t)e^{-\delta t}dt\right]}{\partial ln{P}_0}$	$\frac{\partial ln\left[\underset{0}{\overset{T}{\int }}m(t)e^{-\delta t}dt\right]}{\partial ln{P}_0}$	$\frac{\frac{\partial ln\left[\underset{0}{\overset{T}{\int }}H(t)e^{-\delta t}dt\right]}{\underset{0}{\overset{T}{\int }}{e}^{-\delta t}dt}}{\partial ln{P}_0}$	$\frac{\frac{\partial ln\left[\underset{0}{\overset{T}{\int }}A(t)e^{-\delta t}dt\right]}{\underset{0}{\overset{T}{\int }}{e}^{-\delta t}dt}}{\partial ln{P}_0}$	$\frac{\partial lnR}{\partial ln{P}_0}$
p0	0.20	+0.28	−1.12	+0.07	−1.44	+0.51
μ0	0.7%	−0.25	+2.19	+0.10	+0.96	−0.52
ϕ	1.0	+0.20	+1.70	+0.06	+1.78	−0.52
d0	5%	−0.05	+3.07	−0.54	−1.27	+0.68
β	3%	+0.04	−2.63	−0.01	−0.08	−0.17
δ	3%	+0.03	+0.01	+0.01	−0.16	+0.09
ρ	1.32	+0.01	−0.32	+0.01	+0.04	+0.06
ς	0.85	+0.42	−17.66	−0.42	−0.92	+0.00
k	0.81	+0.06	+0.81	+0.02	+0.23	+0.26
w0	20k$	+0.55	+0.83	+0.04	+0.19	+0.00
α	15%	−0.10	−0.07	+0.01	−0.31	−0.15
H(0)	30k$ [μ]	+0.45	−1.27	+0.96	+0.81	+0.00

Figure 2.

Income (Y[H(t)]; $ thousands), consumption (C(t); $ thousands), assets (A(t) $ thousands), health (H(t); $ thousands; total health [solid line], health threshold [dashed line]) and health investment (m(t); $ thousands per year) versus age for a “white” collar worker.

As Figure 2a shows, earnings Y [H(t)] during working life fall with declining health until the age of retirement when earnings are replaced by an annuity.¹⁹ Consumption C(t) (Figure 2b) is relatively constant over time as individuals smooth consumption through the use of savings A(t)²⁰ (Figure 2c). Consumption shows a sudden drop at retirement to 85% of its level before retirement (this is the direct result of our choice for the value of leisure k) as individuals substitute leisure for consumption. For the parameters chosen, individuals build up assets A(R) of ≈ $198,700 at the age of retirement (Figure 2c) and a pension b of $18,800 per year (representing a present discounted value (b/δ)[1−e^−δ(T−R)] of $222,800). Health H(t) (the solid line in Figure 2d) declines fairly rapidly from a value of $30,000 to about $4,800 by age 56.6 (t₁ = 36.6) after which the individual starts investing in health (see Figure 2e). Health reaches $5,800 by the age of retirement R and declines further to about $2,000 by the end of life T. The dashed line in Figure 2d shows the health threshold. The health threshold increases over time up to the retirement age²¹ after which it suddenly drops due to the substitution of health for leisure and the disappearance of production benefit of health ϕ during retirement.

Because the marginal production benefit of health ϕ(t) is the only term in the transformation (19) that is time dependent, and because the model solutions after retirement are not functions of ϕ(t), the health threshold (Figure 2d) is constant over time during retirement (given our choice of constant health deterioration d(t), prices p(t), efficiency μ(t) and interest rate δ).

3.2. Health inequality

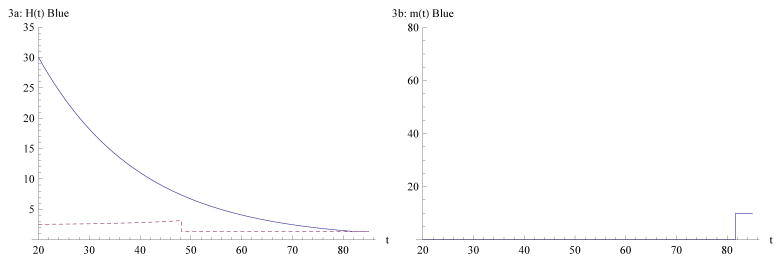
Figure 3a shows the evolution of health for “blue collar” workers with a base wage rate of w₀=$10,000 (half that of “white collar” workers; everything else held constant). The lower earnings of “blue collar” workers reduce their life-time income, their health threshold, and induce earlier retirement at age 53.16 (R = 33.16). As Figure 3b shows, health investment is lower over the life-time. For these specific values workers do not invest in health during working life but only near retirement (scenario C). As a result health declines to about $5,700 by the age of retirement 53.16 (R = 33.16) and to $1,400 by age 81.62 when individuals start investing in health (t₂ = 81.62). Also, earlier retirement extends the retirement phase of life for “blue collar” workers which is characterized by lower levels of health investment and consequently lower health. As a result, at age 82 (t = 62), white collar workers are more than 40 percent healthier than blue collar workers.

Figure 3.

Blue collar health (3a left-hand side; health [solid line] and health threshold [dashed]; $ thousands) and blue collar health investment (3b right-hand side; $ thousands) versus age.

3.3. Retirement

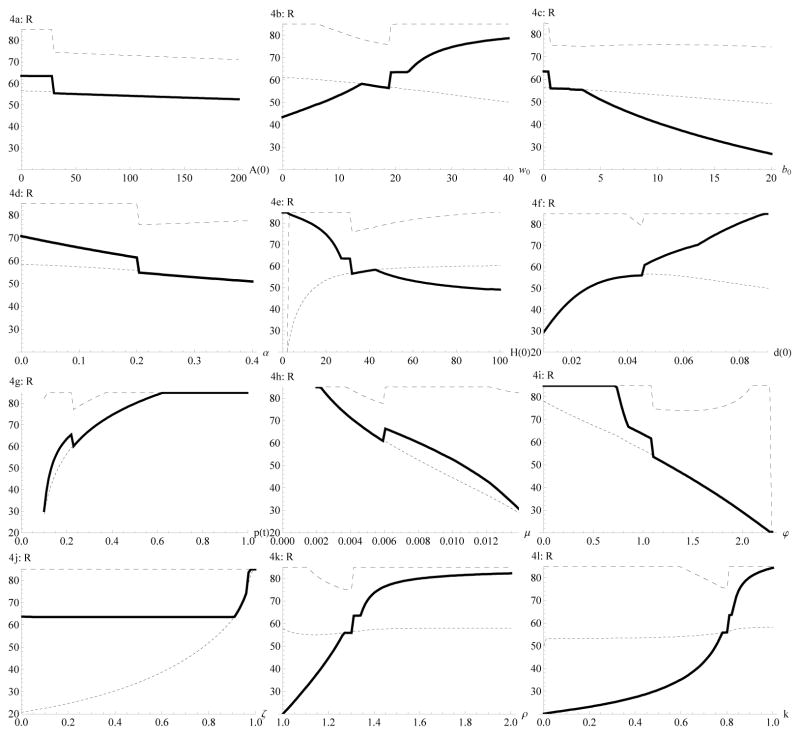
Figures 4a through 4l show the effect of various model parameters on the decision to retire. The solid, dotted and dashed lines show how, respectively, optimal retirement age R, t₁ and t₂ change in response to variation in a number of variables and parameters. As variables and parameters are varied, the solutions cycle through the scenarios A through F (see Figure 1). Transitions between scenarios are often associated with jumps in the optimal retirement age.

Figure 4.

The effect of various variables and parameters on the decision to retire. Initial assets A(0), base wage rate w₀, benefits b₀ are shown in $ thousands, and initial health H(0) in $ thousands. Note: values for health deterioration d(t) < 0.005, prices p(t) < 0.088, health investment efficiency μ > 0.016, and marginal production benefits of health ϕ > 2.29 are not shown as they correspond to a user cost of health capital at the margin [p₀/μ₀] [d₀ + δ] − ϕ₀ that is negative. Values of ρ < 1 and k > 1 are not shown as these require a change in specification; for ρ = 1 the utility function switches from being negative (ρ > 1) to positive (ρ < 1) values. For positive utility, values of k < 1 imply disutility from increased leisure, i.e. we need to also switch to values of k > 1.

Greater initial assets A(0) reduce the retirement age (Figure 4a). Wealthy people have less incentive to work as they can fulfill all or part of their consumption needs through inherited wealth. Unlike a one-off contribution to life-time resources (such as initial assets A(0)), higher wages w₀ provide additional resources for as long as the individual works, thereby increasing the age of retirement (Figure 4b). Indeed Mitchell and Fields (1984) find that higher earnings result in later retirement.

Increasing levels of basic benefits b₀ reduce the retirement age (Figure 4c).²² Indeed, we expect earlier retirement in countries with more generous benefits, as was shown in the cross-country comparison project of Gruber and Wise (1999, 2004, 2012).

The higher the portion α of wages set aside for retirement the earlier an individual retires (Figure 4d). Given that retirement in our formulation is the result of individual choice (benefits are approximately actuarially fair and the timing of retirement is not constrained) the role of pension wealth and of regular savings is essentially the same. Lower pension savings will almost exactly be offset by larger accumulated savings. In case retirement is not a choice variable (or at least restricted in various ways) lower benefits will decrease life time resources, which will lower consumption and thereby also generate more asset accumulation. Indeed Kapteyn and Panis (2003) find a strong negative relation between wealth at retirement and replacement rates when comparing Italy, The Netherlands, and the U.S.

Increasing initial health H(0) reduces the retirement age (Figure 4e). Initial health H(0) provides “health capital” (it generates earnings) and operates qualitatively similar to assets.

The age of retirement increases with increasing rates of health deterioration d(t) = d₀ (Figure 4f). For one, higher health deterioration over one’s life-time reduces the amount of additional life-time earnings resulting from an individual’s inherited health H(0), reducing the “effective” initial health endowment. In addition, the user cost of health capital at the margin [p₀/μ₀] [d₀ + δ]−ϕ₀ is higher, which also leads to delayed retirement.

Similarly increasing prices of health care p(t) = p₀ (Figure 4g), decreasing health investment efficiency μ(t) = μ₀ (Figure 4h) and decreasing marginal productivity benefits of health ϕ(t) = ϕ₀ (Figure 4i) increase the cost of health capital at the margin and raise the retirement age.

The relationships between prices p(t), health investment efficiency μ(t), the marginal production benefits of health ϕ(t), the coefficient of relative risk aversion ρ (Figure 4k), and the factor k (Figure 4l; describing the increased utility from leisure during retirement) and retirement are particularly strong in that individuals never work (R = 0) or never retire (R = T) for certain parameter values. The relative utility weight ς given to consumption versus health has very little impact on the age of retirement (Figure 4j) except near the extreme of ς ≈ 1 (pure consumption model). Model simulations as well as observations of analytical solutions from simplified versions of our model (a ς ≈ 1 pure consumption model as in our simulation and δ = β = 0) show that the parameters ρ (Figure 4k), k (Figure 4l) and retirement R are strongly related.

3.4. Sensitivity analysis

Table 1 displays the baseline model parameter values P₀ and the sensitivity to changes in each of the model parameters of life-time consumption, life-time health investment, life-time health, life-time assets and the age of retirement (endogenous in the model). The sensitivities were estimated by calculating the relative change in the quantity X of interest (e.g., life-time consumption) in response to a one percent change in model parameter values P₀(e.g., ∂ ln X/∂ ln P₀).

Elasticities greater than one indicate that the model is very sensitive to the particular parameter. Most noticeable is the parameter ς describing the relative “share” of consumption versus health in the utility function. A one percent change in ς decreases life-time health investment by nearly 18 percent. It should be noted though that the results in Table 1 are only valid for the particular parameter region close to the model calibration and that sensitivities will be different for different model calibrations.

4. Discussion

We have formulated a stylized structural model of consumption, leisure, health, health investment, wealth accumulation and retirement decisions using the human capital framework of health.

Despite the simplified nature of our model, the essential features of the Grossman model are maintained and differences in formulation are largely immaterial. First, the Grossman model usually contains both goods and services purchased in the market m(t) (e.g., medical care) and own-time inputs τ(t) (e.g., excercise), whereas we only consider goods and services. However, because a standard assumption in the Grossman literature is a Cobb-Douglas relation between the inputs goods/services and own time, and the output, health investment I(t), the Grossman literature also has a linear (CRTS) health production process, and there is no essential difference compared to our formulation in this regard. Further, under Cobb-Douglass the cost of health investment p(t)m(t) + w(t)τ(t) = π(t)I(t), where w(t) is the wage rate (an opportunity cost) and π(t) the marginal cost of investment (a function of p(t) and w(t)). Again there is no loss of generality in that m(t) in our formulation can be thought of as consisting of goods and services and own-time inputs and p(t) can be thought of as the marginal cost of investment, consisting of the price of services and the opportunity cost of time. However, following Case and Deaton (2005), we do make one simplification for analytical convenience, which is the assumption of a linear relation between earnings Y (t) and health H(t). This has relatively modest consequences. For example, it is not the reason for the “bang-bang” nature of the model solutions (which is the result of CRTS in medical care and is common to the Grossman literature). Further, since there is no natural scale to health, one can always apply a continuous and monotonically rising transformation to health, i.e. the assumption of linearity is not as restrictive as it may appear.²³

Specification of a functional form for the utility function and of initial conditions allows us to derive analytic solutions for consumption, health, health investment and wealth, conditional on a given retirement age. We employ the model to investigate the optimal age of retirement by maximizing the implied indirect utility function with respect to the retirement age. In the model individuals find retirement increasingly attractive as they age as a result of three effects: (1) wage declines as a result of gradual health deterioration reducing income from work with age, (2) increased leisure time during retirement and (3) accumulation of pension wealth (which can only be consumed after retirement) with years in the workforce. We find that advances in population health decrease the retirement age, while at the same time individuals retire when their health has deteriorated. This potentially explains why retirees point to deteriorating health as an important reason for early retirement, while retirement ages have continued to fall in the developed world, despite continued improvements in population health and mortality. In our model, workers with higher human capital invest more in health and because they stay healthier retire later than those with lower human capital whose health deteriorates faster.

Our model represents, to the best of our knowledge, the first attempt at introducing retirement in the Grossman model in order to arrive at a joint theory of health and retirement. We have introduced an endogenous retirement decision that depends on health, employment, accumulated pension benefits and preferences. We explicitly recognize that the Grossman model, under the standard assumption of CRTS, produces a bang-bang solution in which the level of health investment is undetermined (e.g., Wolfe, 1985; Ehrlich and Chuma, 1990; Galama and Kapteyn, 2011). One can address the bang-bang nature, modeling such solutions properly, by recognizing that it results in corner solutions for health investment where individuals do not invest in health for certain periods of time.

Our model is nevertheless not without problems. Some model predictions seem caricatures of real life. For example, in the corner solutions that we introduced in this work to address the bang-bang nature of the Grossman model, healthy individuals do not invest in health at all m(t) = 0 for periods of time, while in reality most people see the doctor at least once per year. Also, our regular (“non-corner”) solutions still rely on the standard assumption that health is determined by the equilibrium condition for the health stock. Because of this standard assumption the usual end condition for health H(T) = H_min cannot be guaranteed, and under certain conditions length of life may be infinite (Case and Deaton, 2005). Because we are primarily interested in retirement, we simply break off the program at T.

In keeping with the literature and to allow for comparison with prior work we have adopted standard assumptions in the literature, such as CRTS in health investment and the assumption that health is determined by the health equilibrium condition for non-corner solutions. As we discussed, these assumptions may require rethinking and there seems to be room for further theoretical extensions in the demand for health literature. Introducing diminishing returns to scale in health investment may be one potential avenue to pursue. Another may be the introduction of some form of adjustment costs.

5. Appendix: derivations

5.1. First-order (necessary) conditions

The objective function (1) is maximized subject to the constraints (2). The Langrangian of the problem is given by (3). We have

$${\stackrel{.}{p}}_A(t)=\frac{\partial \mathfrak{J}}{\partial A(t)}=-p_A(t)\delta ,$$ (21)

the solution of which is

$$p_A(t)=p_A(0)e^{-\delta t}.$$ (22)

Further,

$${\stackrel{.}{p}}_H(t)=-\frac{\partial \mathfrak{J}}{\partial H(t)}=\{\begin{array}{ll}-\frac{\partial U_w(t)}{\partial H(t)}{e}^{-\beta t}-p_A(t)\frac{\partial Y(t)}{\partial H(t)}+p_H(t)d(t)\hfill & t\le R\hfill \\ -\frac{\partial U_r(t)}{\partial H(t)}{e}^{-\beta t}+p_H(t)d(t)\hfill & t>R\hfill \end{array}$$ (23)

Maximizing the Langrangian (3) with respect to consumption C(t) provides the first order conditions for consumption (4). Maximizing the Langrangian (3) with respect to medical care m(t) we find

$$\mu (t)p_H(t)=p(t)p_A(t)-q(t),$$ (24)

where q(t) ≥ 0 for m(t) = 0 and q(t) = 0 for m(t) > 0. Differentiating (24) with respect to t, substituting the relations for p_A(t), ṗ _A(t) and ṗ _H(t) from (21), (22) and (23), and substituting the relation (24) to eliminate p_H(t), one obtains the first order conditions for medical care (5).

Using the functional form (8) of the utility function allows us to write the first order conditions for consumption C(t) (4) as follows:

$$\frac{\partial U_w(t)}{\partial C(t)}=\varsigma C{(t)}^{\varsigma -\rho \varsigma -1}H{(t)}^{1-\varsigma -\rho +\rho \varsigma }=p_A(0)e^{(\beta -\delta )t}t\le R$$ (25)

$$\frac{\partial U_r(t)}{\partial C(t)}=k\varsigma C{(t)}^{\varsigma -\rho \varsigma -1}H{(t)}^{1-\varsigma -\rho +\rho \varsigma }=p_A(0)e^{(\beta -\delta )t}t>R.$$ (26)

Similarly, we can write the first order conditions for medical care (5) as:

$$\begin{array}{l}\frac{\partial U_w(t)}{\partial H(t)}=(1-\varsigma )C{(t)}^{\varsigma -\rho \varsigma }H{(t)}^{-\varsigma +\rho \varsigma -\rho }\\ =p_A(0)[{\pi }_H(t)-\varphi (t)]e^{(\beta -\delta )t}-\frac{e^{\beta t}}{\mu (t)}\left[\frac{\stackrel{.}{\mu }(t)}{\mu (t)}+d(t)\right]q(t)+\stackrel{.}{q}(t)\frac{e^{\beta t}}{\mu (t)}\\ =\mathbb{A}{p}_A(0)e^{(\beta -\delta )t}+\mathbb{B}(t\le R)\end{array}$$ (27)

$$\begin{array}{l}\frac{\partial U_r(t)}{\partial H(t)}=k(1-\varsigma )C{(t)}^{\varsigma -\rho \varsigma }H{(t)}^{-\varsigma +\rho \varsigma -\rho }\\ =p_A(0){\pi }_H(t)e^{(\beta -\delta )t}-\frac{e^{\beta t}}{\mu (t)}\left[\frac{\stackrel{.}{\mu }(t)}{\mu (t)}+d(t)\right]q(t)+\stackrel{.}{q}(t)\frac{e^{\beta t}}{\mu (t)}\\ =\mathbb{A}{p}_A(0)e^{(\beta -\delta )t}+\mathbb{B}(t>R),\end{array}$$ (28)

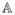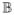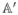where π_H(t) is the user cost of health capital at the margin (equation 6) and the definitions for , , and follow directly from equations (27) and (28).

5.2. Mangasarian sufficiency condition

The Mangasarian sufficient conditions are for the Langrangian (3) to be a concave function of the state (H(t), A(t)) and control (C(t), m(t)) variables. If this is true, and if the first-order conditions (4) and (5) hold, the solutions for the state (H(t), A(t)) and control (C(t), m(t)) variables represent the global maximum. If the Lagrangian (3) is a strictly concave function, the state (H(t), A(t)) and control (C(t), m(t)) variables represent the unique global maximum (e.g., Theorem 6.2 of Caputo, 2005).

The Langrangian (3) is concave if U[C(t), H(t)] e^−βt, p_A(t) Ȧ(t), p_H(t) Ḣ (t) and q(t)m(t) are each concave in the state (H(t), A(t)) and control (C(t), m(t)) variables (e.g., Lemma 6.1 in Caputo, 2005).

A function is concave if its Hessian matrix is negative semidefinite (e.g., Theorem 21.5 in Simon and Blume, 1994). Since p_A(t)Ȧ(t), p_H(t)Ḣ (t) and q(t)m(t) are linear functions of the state and controls, they are negative semidefinite. Theorem 16.2 of Simon and Blume (1994), which states that a matrix is negative semidefinite if and only if every odd principal minor ≤ 0 and every even principal minor ≥ 0, implies that the Hessian matrix of the utility function U[C(t), H(t)] e^−βt is negative semidefinite, if (7) holds.

5.3. Solutions for health, consumption and health investment

Solving the first order conditions (equations 25, 26, 27 and 28) we find

$$C(t)=H(t)\left\{\frac{\zeta }{1-\zeta }\left[\mathbb{A}+\frac{\mathbb{B}{e}^{-(\beta -\delta )t}}{p_A(0)}\right]\right\}t\le R$$ (29)

$$C(t)=H(t)\left\{\frac{\zeta }{1-\zeta }\left[{\mathbb{A}}^{\prime }+\frac{\mathbb{B}{e}^{-(\beta -\delta )t}}{p_A(0)}\right]\right\}t>R,$$ (30)

and the following solutions for C(t) and H(t):

$$C(t)=\zeta \mathrm{\Lambda }{\left[\mathbb{A}+\frac{\mathbb{B}}{p_A(0)}{e}^{-(\beta -\delta )t}\right]}^{1-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}t\le R$$ (31)

$$C(t)=k^{1/\rho }\zeta \mathrm{\Lambda }{\left[{\mathbb{A}}^{\prime }+\frac{\mathbb{B}}{p_A(0)}{e}^{-(\beta -\delta )t}\right]}^{1-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}t>R$$ (32)

$$H(t)=(1-\zeta )\mathrm{\Lambda }{\left[\mathbb{A}+\frac{\mathbb{B}}{p_A(0)}{e}^{-(\beta -\delta )t}\right]}^{-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}t\le R$$ (33)

$$H(t)=k^{1/\rho }(1-\zeta )\mathrm{\Lambda }{\left[{\mathbb{A}}^{\prime }+\frac{\mathbb{B}}{p_A(0)}{e}^{-(\beta -\delta )t}\right]}^{-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}t>R,$$ (34)

where we have used the definitions for χ (equation 13) and for Λ (equation 14).

Using equation (2) one can then solve for health investment m(t):

$$m(t)=\frac{1}{\mu (t)}(1-\zeta )e^{-{\int }_0^{t}d(s)ds}\times \frac{\partial }{\partial t}\left\{\mathrm{\Lambda }{\left[\mathbb{A}+\frac{\mathbb{B}}{p_A(0)}{e}^{-(\beta -\delta )t}\right]}^{-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}{e}^{{\int }_0^{t}d(s)ds}\right\}t\le R$$ (35)

$$m(t)=\frac{1}{\mu (t)}{k}^{1/\rho }(1-\zeta )e^{-{\int }_R^{t}d(s)ds}\times \frac{\partial }{\partial t}\left\{\mathrm{\Lambda }{\left[{\mathbb{A}}^{\prime }+\frac{\mathbb{B}}{p_A(0)}{e}^{-(\beta -\delta )t}\right]}^{-\chi }{e}^{-\left(\frac{\beta -\delta }{\rho }\right)t}{e}^{{\int }_R^{t}d(s)ds}\right\}t>R.$$ (36)

Assets A(t) can be derived by substituting the solutions for health H(t), consumption C(t) and health investment m(t) as follows:

$$A(t)=\left\{\underset{0}{\overset{t}{\int }}[w_0(x)+\varphi (x)H(x)-C(x)-p(x)m(x)]e^{-\delta x}dx\right\}{e}^{\delta t}+A(0)e^{\delta t}(t\le R)$$ (37)

$$A(t)=\left\{\underset{R}{\overset{t}{\int }}[b-C(x)-p(x)m(x)]e^{-\delta x}dx\right\}{e}^{\delta t}+A(R)e^{\delta (t-R)}(t>R).$$ (38)

For positive health investment m(t) > 0 we have q(t) = 0 and H(t) = H_*(t) and therefore 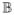= 0. These are the solutions for the health threshold (see equations 9, 10, 11, 12, 15 and 16). On the other hand, for initial conditions H(0) and H(R₊) that are above the health threshold H_*(0) and H_*(R₊) (see Figure 1 scenarios A through F) we have a situation of “excessive” initial health, i.e., the individual is endowed with an initial stock of health that is greater than the level required to be economically productive. In such cases individuals would want to “sell” their health, i.e., chose negative health investment m(t) < 0. Since this is not possible we have a corner solution where m(t) = 0. We can derive the solutions for consumption C(t) and health H(t) by imposing m(t) = 0. We then find a differential equation in q(t) with the following solutions:

$$\begin{array}{l}q(t)=p_A(0){\int }_0^t\mu (x){\left[H(0)e^{\left(\frac{\beta -\delta }{\rho }\right)x}{e}^{-{\int }_0^{x}d(s)ds}\frac{1}{\mathrm{\Lambda }(1-\zeta )}\right]}^{\frac{-1}{\chi }}{e}^{{\int }_x^t[\frac{\stackrel{.}{\mu }(s)}{\mu (s)}+d(s)]ds}{e}^{-\delta x}dx\\ -p_A(0){\int }_0^t\mu (x)[{\pi }_H(x)-\varphi (x)]e^{{\int }_x^t[\frac{\stackrel{.}{\mu }(s)}{\mu (s)}+d(s)]ds}{e}^{-\delta x}dx\\ +q(0)e^{{\int }_0^t[\frac{\stackrel{.}{\mu }(s)}{\mu (s)}+d(s)]ds},(t\le R)\end{array}$$ (39)

$$\begin{array}{l}q(t)=p_A(0){\int }_R^t\mu (x){\left[H(R)e^{\left(\frac{\beta -\delta }{\rho }\right)x}{e}^{-{\int }_0^{x}d(s)ds}\frac{1}{k^{1/\rho }\mathrm{\Lambda }(1-\zeta )}\right]}^{\frac{-1}{\chi }}{e}^{{\int }_x^t[\frac{\stackrel{.}{\mu }(s)}{\mu (s)}+d(s)]ds}{e}^{-\delta x}dx\\ -p_A(0){\int }_R^t\mu (x){\pi }_H(x)e^{{\int }_x^t[\frac{\stackrel{.}{\mu }(s)}{\mu (s)}+d(s)]ds}{e}^{-\delta x}dx\\ +q(R)e^{{\int }_R^t[\frac{\stackrel{.}{\mu }(s)}{\mu (s)}+d(s)]ds}.(t>R)\end{array}$$ (40)

Substituting the above solutions for q(t) into those for consumption C(t) (equations 31 and 32), health H(t) (equations 33 and 34) and health investment m(t) (equations 35 and 36), we find:

$$H(t)=H(0)e^{-{\int }_0^{t}d(s)ds}(t\le R)$$ (41)

$$H(t)=H(R)e^{-{\int }_R^{t}d(s)ds}(t>R)$$ (42)

$$C(t)=\zeta {\mathrm{\Lambda }}^{1/\chi }{(1-\zeta )}^{\frac{1-\chi }{\chi }}H{(0)}^{-\left(\frac{1-\chi }{\chi }\right)}{e}^{\left(\frac{1-\chi }{\chi }\right){\int }_0^{t}d(s)ds}{e}^{-\left(\frac{\beta -\delta }{\rho \chi }\right)t}(t\le R)$$ (43)

$$C(t)=k^{1/\chi \rho }\zeta {\mathrm{\Lambda }}^{1/\chi }{(1-\zeta )}^{\frac{1-\chi }{\chi }}H{(R)}^{-\left(\frac{1-\chi }{\chi }\right)}{e}^{\left(\frac{1-\chi }{\chi }\right){\int }_R^{t}d(s)ds}{e}^{-\left(\frac{\beta -\delta }{\rho \chi }\right)t}(t>R)$$ (44)

$$m(t)=0.$$ (45)

A perhaps more intuitive way of arriving at the same result is by simply substituting m(t) = ξ(t)² and solving the optimization problem for the control variables ξ(t) (instead of m(t)) and consumption C(t) (i.e., one then does not have to resort to using the multiplier q(t) associated with the condition that health investment m(t) ≥ 0 in the Lagrangian 3). One then finds the same first order conditions for maximization with respect to consumption (equations 4). For the first order conditions for maximization with respect to ξ(t) one finds that either ξ(t) = 0 (and hence m(t) = 0) or that the first order conditions (5) are valid for q(t) = 0 ( = 0).

We now have the material to obtain the solutions for each of the scenarios A through F (see Figure 1) in detail. These derivations are provided in the Online Appendix.

5.4. Benefits transformation

Assuming that pension benefits accumulate over time as a fraction α of wages is invested with a return on investment of δ (the interest rate) as in equation (18) life-time income

$$\begin{array}{l}{\int }_0^{T}Y[H(t)]dt={\int }_0^{R}w(t)e^{-\delta t}dt+{\int }_R^T{be}^{-\delta t}dt\\ ={\int }_0^R{w}_0(t)e^{-\delta t}dt+\frac{b}{\delta }(e^{-\delta R}-e^{-\delta T})+{\int }_0^R\varphi (t)H(t)e^{-\delta t}dt,\end{array}$$ (46)

in the new formulation becomes

$$\begin{array}{l}{\int }_0^{T}Y[H(t)]dt=(1-\alpha ){\int }_0^{R}w(t)e^{-\delta t}dt+{\int }_R^T{be}^{-\delta t}dt\\ =(1-\alpha ){\int }_0^R{w}_0(t)e^{-\delta t}dt+\frac{1}{\delta }\left[b_0+f(R)\alpha {\int }_0^R{w}_0(t)e^{\delta t}dt\right](e^{-\delta R}-e^{-\delta T})+{\int }_0^R\varphi (t)\left[(1-\alpha )+f(R)\frac{\alpha }{\delta }(e^{-\delta R}-e^{-\delta T})e^{2\delta t}\right]H(t)e^{-\delta t}dt.\end{array}$$ (47)

Comparing (46) with (47) leads to the identifications made in (19). Note further that the transformations in (19) also preserve the form of the Lagrangean (3) and that the transformations are independent of the control variables C(t) and m(t). Thus the original solutions remain valid with the transformations as long as one includes the derivative of ϕ when calculating health investment (equations 11, 12, 35 and 36),

$$\stackrel{.}{\varphi }=2\varphi f(R)\alpha (e^{-\delta R}-e^{-\delta T})e^{2\delta t}.$$ (48)