Inter-cellular signaling network reveals a mechanistic transition in tumor microenvironment

Abstract

We conducted inter-cellular cytokine correlation and network analysis based upon a stochastic population dynamics model that comprises five cell types and fifteen signaling molecules inter-connected through a large number of cell-cell communication pathways. We observed that the signaling molecules are tightly correlated even at very early stages (e.g. the first month) of human glioma, but such correlation rapidly diminishes when tumor grows to a size that can be clinically detected. Further analysis suggests that paracrine is shown to be the dominant force during tumor initiation and priming, while autocrine supersedes it and supports a robust tumor expansion. In correspondence, the cytokine correlation network evolves through an increasing to decreasing complexity. This study indicates a possible mechanistic transition from the microenvironment-controlled, paracrine-based regulatory mechanism to self-sustained rapid progression to fetal malignancy. It also reveals key nodes that are responsible for such transition and can be potentially harnessed for the design of new anti-cancer therapies.

It has been increasingly recognized that tumor cells do not develop in isolation, but actively interact and co-evolve with stromal cells via a complex inter-cellular signaling network. For example, glioblastoma multiforme (GBM) (1), the most malignant human brain tumor, consists of a highly heterogeneous mixture of cell types including activated astrocytes and microglia. These cells play a crucial role in tumor initiation, progression and invasion (2). They interact with glioma and glioma stem cells through either direct cell-cell contact or soluble protein-mediated signaling pathways. Neglecting the inter-cellular interaction network in tumor microenvironment is inappropriate for comprehensive understanding of tumor development and implicated in the failure of many anti-cancer therapies. A systems biology approach is highly desired to investigate complex tumor microenvironment and recapitulate in vivo dynamical evolution of a tumor. Towards this goal, several approaches have been proposed to model tumor development (3–7), and these mathematical models have significantly advanced our understanding of tumor microenvironment (8, 9). Discrete dynamical systems are employed to describe cell proliferation, differentiation and death (10, 11). Continuous, agent based and hybrid tissue level models have been developed in attempt to assess selected aspects of tumorigenesis such as tumor heterogeneity, selective pressure imposed by physical/chemical conditions of extracellular matrix, phenotypic change triggered by intracellular gene-protein interaction, and growth dynamics (12–19). Probabilistic models are used to examine the mechanism of mutation-driven tumorigenesis (20–23). Although a variety of mathematical modeling strategies have been reported, population dynamics modeling using a set of differential equation best suits the study of tumor development and progression. Ordinary differential equation (ODE) models have been formulated to analyze dynamical evolution of human tumors, such as prostate cancer development with anti-androgen therapy in an intermittent manner (24), stability and bifurcation analysis in tumor gene regulatory network (25), feedback loops in stem cell driven carcinogenesis (14, 26), p53 bistability dynamics (27), Myc-p53 regulation system of cell proliferation and differentiation (28), fitness and selection in a history formulation (29), multistep mutation transformation to cancer (30), and cell cycle transition in cancer cells (31). Partial differential equation (PDE) models have also been well established to study problems involving multiple variables, like spatial dimensions, and thus represent a favorable method to investigate metastatic invasion (32–34), tumor angiogenesis (35), and the dynamics of intra-tumoral convection or diffusion (36, 37). Differential equation-based approaches are also capable of modeling the co-evolution of tumor cell and microenvironment (38–40). For example, tumor-fibroblast crosstalk via two signaling proteins TGF-β and EGF was studied using a partial differential equation model and the result was found to be good agreement with in vitro tumor model created on a semi-permeable membrane (41, 42).

While most studies concern only a few selected signaling pathways in a tumor, we have developed the first model to study the co-evolution of tumor and stromal cells at a large scale and the systems level (43). Herein, based upon this model, we conducted the analysis of cytokine correlation and inter-cellular signaling network in human glioblastoma to assess the collective role of cytokine network in regulating tumor - tumor microenvironment interactions. This model comprises five types of cells, fifteen signaling proteins and 69 signaling pathways (Fig. 1). The in silico results, which are entirely derived from the stochastic simulations without fitting to the experimental data, reflect many emerging patterns and observations that are consistent with human glioma development. Most importantly, we observed the change of cytokine correlation that reveals a rapid transition from the microenvironment-controlled, paracrine-based regulatory mechanism to self-sustained, autocrine-dominant progression to malignant states. We detail the findings and merits of such findings in the following.

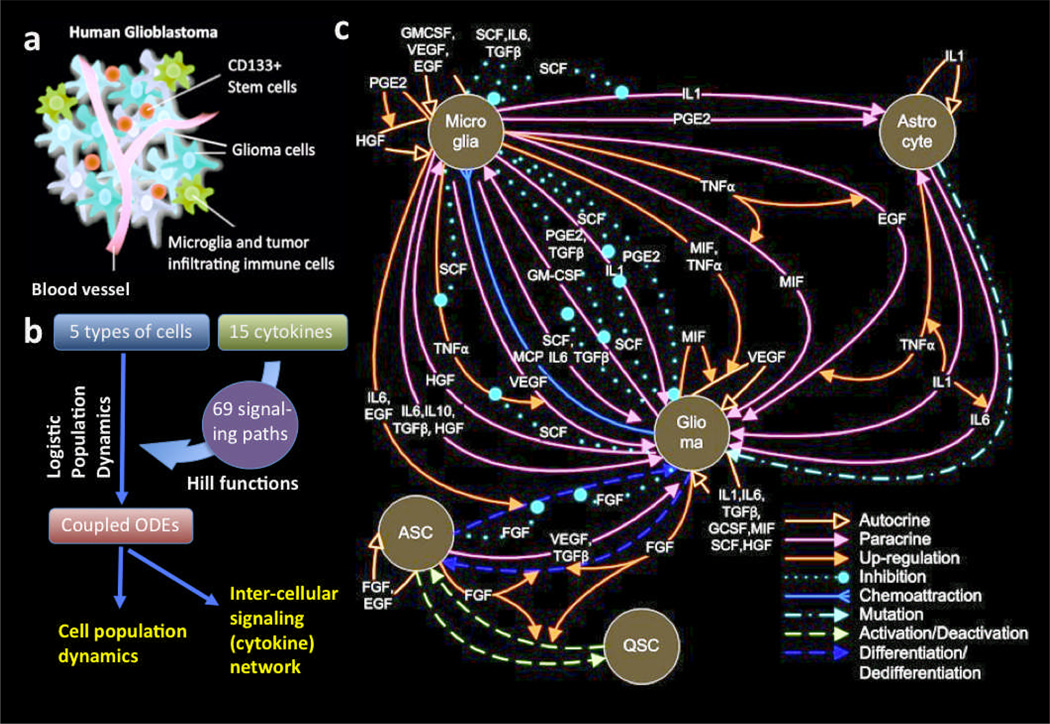
Fig. 1.

Intercellular signaling network in human glioblastoma microenvironment. a. Schematic depiction of human glioblastoma. b. Flow chart showing the construction of a quantitative OED model of intercellular signaling network. c. Detailed depiction of inter-cellular signaling network in human glioma microenvironment. QSC, quiescent glioma stem cell. ASC, activated glioma stem cell.

Results

Construction of a cell-cell communication network in human glioma microenvironment

The population dynamics model of glioblastoma microenvironment has been described previously (43). To help understand the further analysis of inter-cellular cytokine network and the approach toward the discovery of new biological insights, here we briefly re-describe the basic principles and governing equations of this model. The model integrates population dynamics and Hill functions to describe soluble protein-mediated inter-cellular signaling network in tumor microenvironment. This was realized using a coupled stochastic population dynamics model. The evolution of signaling network is interpreted by population dynamics, so the concentration of cells/signaling molecules are controlled by a set of stochastic ordinary differential equations. The details of all ODEs we constructed, their biological implication, and the references from which input values were derived are summarized in full detail in Supporting Information. The general mathematic representation is

$$\stackrel{\begin{array}{l}\text{rate of change of}\\ \text{cell concentration}\end{array}}{\overbrace{\frac{d{x}_i}{dt}}}=\stackrel{\begin{array}{l}\text{immigration},\text{emigration},\\ \text{differentiation from progenitor}\end{array}}{\overbrace{{\displaystyle \sum _{k=1}^{N_i(t)}{Y}_k\mathrm{\delta }(t-{\mathrm{\tau }}_k)}}}+\stackrel{\text{proliferation}}{\overbrace{r_i(t)x_i\left(1-\frac{x_i}{x_{i\text{max}}{\mathrm{\alpha }}_{\text{angiogenesis}}}\right){\displaystyle \prod _{l=1}^{N^{\text{cytokine}}}{\displaystyle \prod _{m=1}^{N^{\text{cytokine}}}\left(1+\frac{u_{il}(t)y_l}{s_l+y_l}\right)\left(1-f_{im}+\frac{f_{im}{s}_m}{s_m+y_m}\right)}}}}-\stackrel{\text{decay}}{\overbrace{d_i{x}_i{\displaystyle \prod _{n=1}^{N^{\text{cytokine}}}\left(1-g_{in}+\frac{g_{in}{s}_n}{s_n+y_n}\right)}}}+\stackrel{\begin{array}{l}\text{mutation},\text{differentiation},\\ \text{dedifferentiation from cell }{x}_k\end{array}}{\overbrace{{\displaystyle \sum _{k=1}^{N^{\text{cell}}}{m}_{ik}(t)x_k{\displaystyle \prod _{p=1}^{N^{\text{cytokine}}}\left(1-h_{ip}+\frac{h_{ip}{y}_p}{s_p+y_p}\right)}}}}$$ (1)

$$\stackrel{\begin{array}{l}\text{rate of change of}\\ \text{cytokine concentration}\end{array}}{\overbrace{\frac{d{y}_j}{dt}}}=\stackrel{\text{production from cell}}{\overbrace{{\displaystyle \sum _{k=1}^{N^{\text{cell}}}{k}_{jk}(t)x_k{\displaystyle \prod _{l=1}^{N^{\text{cytokine}}}{\displaystyle \prod _{m=1}^{N^{\text{cytokine}}}{\displaystyle \prod _{n=1}^{N^{\text{cytokine}}}\left(1+\frac{u_{jl}(t)y_l}{s_l+y_l}\right)\left(1-v_{jm}+\frac{v_{jm}{y}_m}{s_m+y_m}\right)\left(1-w_{jn}+\frac{w_{jn}{s}_n}{s_n+y_n}\right)}}}}}}-\stackrel{\text{decay}}{\overbrace{{\mathrm{\mu }}_j{y}_j{\displaystyle \prod _{p=1}^{N^{\text{cytokine}}}\left(1+\frac{u_{jp}{y}_p}{s_p+y_p}\right)}}}$$ (2)

$$i=1,\dots ,N^{\text{cell}}$$

$$j=1,\dots ,N^{\text{cytokine}}$$

where

$${\mathrm{\alpha }}_{\text{angiogenesis}}(t)=\left(1+\frac{u_{\text{cell\_IL}1}{y}_{\text{IL}1}}{s_{\text{IL}1}+y_{\text{IL}1}}\right)\left(1+\frac{u_{\text{cell\_VEGF}}{y}_{\text{VEGF}}}{s_{\text{VEGF}}+y_{\text{VEGF}}}\right)\left(1+\frac{u_{\text{cell\_HGF}}{y}_{\text{HGF}}}{s_{\text{HGF}}+y_{\text{HGF}}}\right)\left(1+\frac{u_{\text{cell\_MIF}}{y}_{\text{MIF}}}{s_{\text{MIF}}+y_{\text{MIF}}}\right)\left(1+\frac{u_{\text{cell\_SCF}}{y}_{\text{SCF}}}{s_{\text{SCF}}+y_{\text{SCF}}}\right)\left(1+\frac{u_{\text{cell\_FGF}}{y}_{\text{FGF}}}{s_{\text{FGF}}+y_{\text{FGF}}}\right)$$ (3)

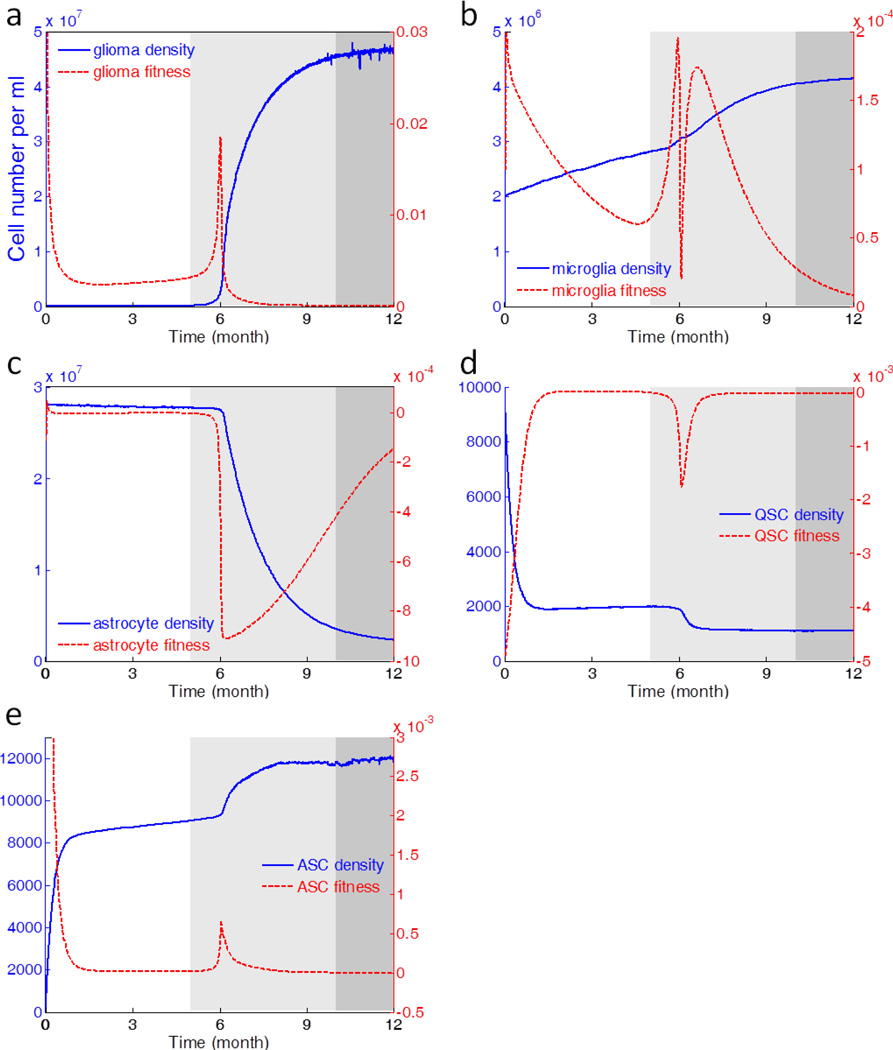
is the angiogenesis factor (Supporting Fig. S1(a)). Monte Carlo simulations of one year evolution under such parameter settings show that glioma cells evolve through three distinct phases, the pre-tumor phase (1–5 months), the rapid expansion phase (6–10 months), and the malignancy phase (11–12 months) (Fig. 2(a)). The three-phase dynamics is demonstrated by our model and consistent with glioblastoma development observed in animal models (44). The longest period is the pre-tumor phase, which is the stage of accumulate genetic and microenvironmental prerequisites to initiate neoplastic transformation. In the context of human glioma, if a tumor microenvironment imposes an evolutionary selection towards astrocytes, the neoplastic process may be halted or even reversed by the increasing apoptotic rates of abnormal/neoplastic cells. The abnormal/neoplastic cells that have survived in the pre-tumor phase gradually gain fitness advantage over astrocytes, and further progress to rapid expansion phase mathematically characterized by a typical exponential growth mode. The tumor cells increase in frequency over time and eventually become the most abundant population. However, the crowded tumor cells compete for resource and, if confined in a given volume, will approach an equilibrium state with a large mass of tumor, which is defined as the malignancy phase.

Fig. 2.

Stochastic dynamics and fitness evolution of glioma, microglia, astrocyte, QSC, and ASC, respectively. The different grayscale zones represent three distinct phases of glioma development revealed by the dynamics modeling; they are pre-tumor phase (white), expansion phase (light gray), and malignancy phase (dark gray). The blue solid curves are the stochastic dynamics of cells, whereas the red dashed lines represent the evolution of fitness, defined as per capita cell growth rate.

Since the tumor cells and microenvironment co-evolve in a gradual and continuous manner, there is no distinct boundary between adjacent phases. In this study, we use the following rules to calculate the length of three phases and the results are rounded to the nearest month. First, the boundary between pre-tumor phase and expansion phase is the time point when the tumor cell proliferation enters the typical exponential growth mode and achieve a moderate density, but still below the theoretical detection limit of MRI (10 labeled cells per 100 µm³ volume (45)) and enhanced CT (40,000 cells/cm² (46)). Second, the boundary between expansion phase and malignancy phase is the time point where tumor cells deviate from the exponential growth trajectory. Afterwards, tumor cells enter a saturated logistic growth mode and the tumor cell population is close to 95% of equilibrium.

Population dynamics of cells and cytokines in glioma microenvironment

Among the five types of cells included in the modeling, glioma, microglia and ASC all show population increase, whereas astrocyte and QSC present a continuous depletion of population (Fig. 2). Glioma has the most drastic sigmoid-shaped growth among all (Fig. 2(a)). Microglia shows comparatively marked increment, reflecting an active role in the development of GBM (Fig. 2(b)). QSC upon stimulation undergoes a reversible process to be activated into ASC conferring self-renewal capability. Under the initial conditions of the model, it favors activation direction, thus QSC continuously decreases in sizes (Fig. 2(d)) to give rise to ASC (Fig. 2(e)). To reveal the underlying cell fate and the switch of tumor phases, we also use “fitness” to represent per capital growth rate:

$$F_i(t)=\frac{d{x}_i/dt}{x_i},i=1,\dots ,N^{\text{cell}}$$ (4)

Glioma, microglia and ASC all show positive fitness, with Glioma maintaining the highest order of fitness (Fig 2(a, b, and e)). Tightly following the initial expansion phase of tumor, all three cells have sharp peaks in fitness. The decline of fitness curves at the end of sixth month is due to the density-dependent effect as the population approaching the carrying capacity. As the cells compete for nutrition, the ones acquire relatively high fitness gain superiority at the price of others, thus QSC and astrocyte score negative fitness values, accompanying the continuously decreasing population (Fig. 2(c and d)). Though being infiltrated by tumor cells, astrocytes strive for keeping abundance until their throne is usurped by glioma due to accumulated tumorigenic agents (Fig. 2(c)).

Autocrine to paracrine transition in tumor development

Glioma cells do not develop in isolation, but co-evolve with stromal cells in tumor microenvironment mediated by autocrine/paracrine signaling network. A specific intercellular signaling could be either autocrine or paracrine depending on their secretion source. To reflect the effect of autocrine and paracrine, we define “autocrine to fitness index” (Eq. 4) and “angiogenesis factor (Eq. 3) with the autocrine indices” as follows:

$$A_i^{\text{fitness}}(t^{*},\mathrm{\Delta }t)={F_i^{\text{autocrine}}-F_i^{\text{zero}}=\frac{d{x}_i/dt}{x_i}|}_{x_j=x_j^{*}+x_j^{\text{autocrine}},y_k=y_k^{*}+y_k^{\text{autocrine}},t=t^{*}+\mathrm{\Delta }t}-{\frac{d{x}_i/dt}{x_i}|}_{x_j=x_j^{*}+x_j^{\text{zero}},y_k=y_k^{*}+y_k^{\text{zero}},t=t^{*}+\mathrm{\Delta }t}$$ (5)

$$A_i^{\text{angio}}(t^{*},\mathrm{\Delta }t)={{\mathrm{\alpha }}_{\text{angiogenesis}}^{\text{autocrine}}(t^{*},\mathrm{\Delta }t)-{\mathrm{\alpha }}_{\text{angiogenesis}}^{\text{zero}}(t^{*},\mathrm{\Delta }t)={\mathrm{\alpha }}_{\text{angiogenesis}}|}_{y_j=y_j^{*}+y_j^{\text{autocrine}},t=t^{*}+\mathrm{\Delta }t}-{{\mathrm{\alpha }}_{\text{angiogenesis}}|}_{y_j=y_j^{*}+y_j^{\text{zero}},t=t^{*}+\mathrm{\Delta }t}$$ (6)

$$i=1,\dots ,N^{\text{cell}}$$

We define “paracrine index” P_i (t^*, Δt) and the “total intercellular signaling index” T_i (t^*, Δt) similarly. The one year simulation of fitness of $A_{\text{glioma}}^{\text{fitness}},A_{\text{glioma}}^{\text{angio}},P_{\text{glioma}}^{\text{fitness}},P_{\text{glioma}}^{\text{angio}},T_{\text{glioma}}^{\text{fitness}},\text{ and }{T}_{\text{glioma}}^{\text{angio}}$ are shown in Supporting Figs. S1(b–d). Paracrine contributes to the major part of glioma fitness and angiogenesis in the pre-tumor phase. However, it is gradually substituted by autocrine since the expansion phase. The breakdown of the driving force facilitates examining the contributions of all the paracrine/autocrine loops associated with tumor development, therefore we calculate the “proportion of autocrine” by the following definition

$$\frac{A_i(t^{*},\mathrm{\Delta }t)}{T_i(t^{*},\mathrm{\Delta }t)}$$ (7)

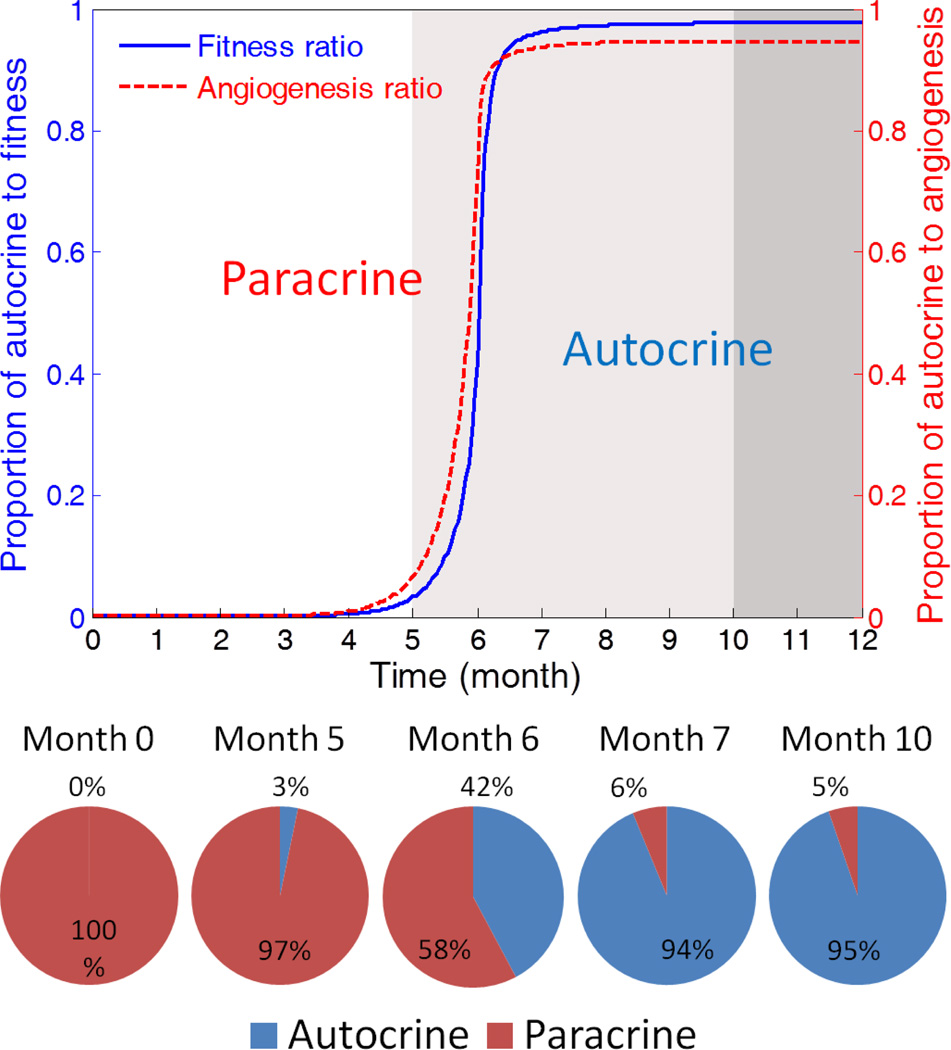
We show the proportional contribution of autocrine and paracrine in Figure 3. The results surprisingly suggest a rapid but smooth transition from paracrine-driven to autocrine-driven tumor progression. Glioma is initiated and primed in a paracrine condition, thus in the pre-tumor and early expansion stage, its fitness is significantly dependent on the microenvironment. However, once the paracrine-triggered tumor progression enters mid-expansion phase, the accumulated autocrine signaling replaces paracrine and the tumor progression will be resistant to interventions from the microenvironment.

Fig. 3.

The evolution of the driving force for glioma progression. The paracrine signaling is the dominant force during the pre-tumor stage, while autocrine signaling becomes the major driving force in the expansion and malignancy phases. The transfer of leadership results in the significant enhancement of the robustness of tumor in a self-sustained manner.

It is of interest to investigate how paracrine loops are established and promotes tumorigenesis. We further breakdown the paracrine driving force and classified them according to their source cell type. The results shown in Supporting Figure S2 demonstrate heterogeneity in paracrine contributors. For example, microglia and astrocyte are the major paracrine donors of glioma fitness at the very beginning. However, their effects turn negative at the end of the sixth month, while the ASC starts to make positive paracrine contribution to glioma fitness. The heterogeneity stems from the fact that autocrine and paracrine do not evolve in isolation, but actually nonlinearly coupled via feedback loops in the complex cell-cell communication network (Fig. 1). This observation suggests that the microenvironment-specific anti-cancer therapy is likely to hit a moving target, and its success requires a careful study of evolution of the intercellular molecular network due to such intervention.

Cytokine correlation map reveals active cell-cell communication and also exhibits an abrupt transition

Signaling molecules are interwoven into complex networks. They work in concert to achieve intercellular communication and regulate cell behaviors. To assess the heterogeneous behavior of signaling molecules and the association with tumor development, we design a correlation matrix analysis – at a given time, the concentration of the signaling molecule, x, is perturbed by ±Δx; the resulting concentration change of another signaling molecule, y, after 72 hours is Δy₊ and Δy₋, corresponding to perturbing +Δx and −Δx, respectively. The correlation factor c_x→y is defined as

$$c_{x\to y}=\frac{\frac{(y+\mathrm{\Delta }{y}_{+})-(y+\mathrm{\Delta }{y}_{-})}{(y+\mathrm{\Delta }{y}_{+})+(y+\mathrm{\Delta }{y}_{-})}}{a}$$ (8)

where a= Δx/x.

The influence of a signaling molecule on the other is quantitatively defined by a correlation factor. Experiments over all these signaling molecules yield a heat map of correlations, also called the correlation matrix (Fig. 4). Each row of the matrix represents the responses of all signaling molecules including itself upon a signal perturbation experiment, at a given simulation time. The snap-shot heat-map results indicate these signals are indeed interlinked and the perturbation of one may significantly influence the production of the other signaling molecules, presumably via cells as the nodes. More importantly, the time course of signaling correlation network (Supporting Fig. S3) exhibits a striking dynamic behavior that cannot be easily revealed by the collective behavior shown in Fig. 3. Substantial correlations between a number of signaling molecules emerge at a very early stage (month 1) and become much greater during the period of rapid glioma expansion (month 6), but quickly diminish when the tumor reaches a steady state (month 7–12). Also the correlation pattern changes drastically along the course of tumor development (Supporting Fig. S4). For example, many factors (such as SCF) negatively regulate TGF-β, EGF and VEGF in the first month, but turns to positively modulate these signaling molecules in the sixth month when glioma cells reach the rapid expansion stage. On the other hand, MCP1, which appears independent of any other signaling molecules in the early and mid stages, is the only cytokine that remains actively interacting with other signaling molecules in the late stage. Such striking pattern switch implies that therapeutic intervention that targets cytokine signaling need to be executed at the early or mid stages when they are inter-linked, whereas such treatment at a slightly late stage may not show efficacy due to the diminishment of cytokine regulatory network. We further analyzed the evolution of signaling correlation pattern (Supporting Fig. S4). The signaling correlations were found to be in cooperation (e.g. IL-6 and EGF at the sixth month (47, 48)), competition (e.g. IL-1 and PGE2 at the sixth month), or equilibrium (e.g. IL-10 and TNF-α at the sixth month) (Supporting Fig S5), reflecting their different regulatory functions in the tumor microenvironment.

Fig. 4.

Signaling correlation matrices. Heat maps show the signaling correlation matrices at selected times. A profound intercellular signaling correlation emerges at the very early stage (month 1), but almost diminishes as soon as the tumor development enters the rapid expansion phase (month 6).

Cytokine network identifies key nodes in dictating tumor development

While heat-maps convey overall impressions of the correlation matrix, reconstructed correlation networks may reveal encoded connections more directly. The fifteen signaling proteins can be classified into five sub-sets according to their cellular function; these subsets are growth factors (EGF, VEGF, HGF, FGF, and SCF), proinflammatory cytokines (IL-1, IL-6, and TNF-α), anti-inflammatory cytokines (IL-10, TGF-β), chemokines (MCP-1, MIF, GCSF, and GMCSF) and Prostaglandin E2. Perturbation on one signaling molecule will exert regulatory effect on the others via intercellular signaling network. We define the impact factor, the capability of one signaling molecule to regulate others and change the network topology, as the sum of the correlation factors:

$$I_i={\displaystyle \sum _{j=1}^{N^{\text{cytokine}}}{c}_{ij}},i=1,\dots ,N^{\text{cytokine}}$$ (9)

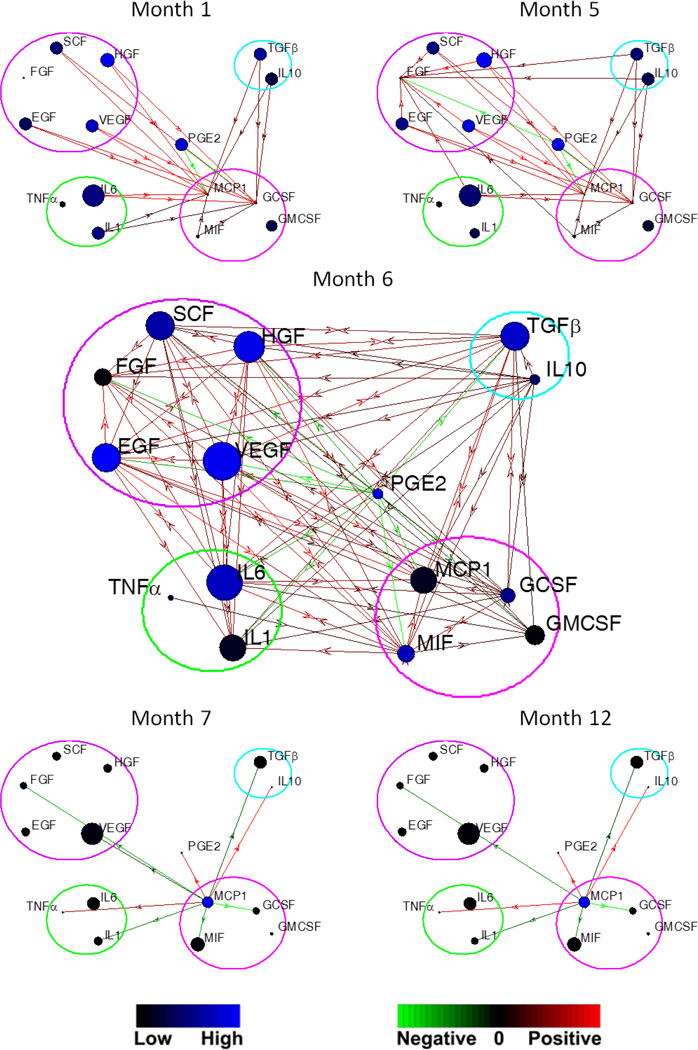
To deliver a global view of the intra- and inter-group signaling regulation, we construct a correlation network (Fig. 5), which integrates concentration, impact factors, and the directional connections of signaling molecules. The time evolution of correlation network reveals several interesting findings (Supporting Fig. S6).

Fig. 5.

Evolution of correlation network of signaling molecules in five functionally classified sub-sets, including growth factors (purple circle), proinflammatory cytokines (yellow), anti-inflammatory cytokines (cyan), chemokines (magenta), and PGE2. Each blue circle (node) represents a signaling molecule. The diameter of the node is proportional to the concentration of the molecule, and the color indicates the impact factor of the cytokine according to the blue color bar. The arrow link between two nodes represents the directional regulation of the two signals. The green-red color bar shows the strength of the up-regulation (red) and down-regulation (green).

Firstly, in the first three months, the growth factor, proinflammatory and anti-inflammatory cytokine groups have unilateral regulation on the chemokine group. There is no mutual effect between the former three groups until the fourth month, exhibited by the growth factor - pro-inflammatory cytokine and the growth factor – anti-inflammatory cytokine connections. The chemokine group gradually strengthens its influence, and becomes the sole dominant inter-group connector in the late expansion phase and malignancy phase. The observation suggests that the signal network is not random, but orderly organized and coordinates with cytokine function. Secondly, there is no necessary link between the impact factor and concentration. The cytokine with high plasma/cerebrospinal fluid concentration may not have significant influence on the intercellular signaling network, suggesting acquiring of expression level at only one time point can not reflect dynamic trend and may lead to misjudgment. Thirdly, the dynamic processes evolve fast in the pre-tumor and expansion phase, and become stable in the malignancy phase. Drastic changes are observed in the fifth to seventh months. This process is in line with the establishment of tumor robustness.

Discussion

We constructed a large-scale, intercellular signaling network in brain tumor microenvironment that includes major cell types and important signaling molecules related to the tumorigenesis events. A stochastic population dynamics model is used to recapitulate the co-evolution of tumor and tumor microenvironment. The model enables the quantification of tumor fitness and unveils the underlying mechanism driving tumor progression. Without fitting to experimental data, this fully predicable model yields emerging patterns that are consistent with experimental observations, demonstrating its merits in physical sciences of cancer.

One of the most important findings is the gradual change of dominant signaling from paracrine to autocrine that starts from the tumor expansion phase to the malignancy phase in which glioma cells become self-sustained and auto-driven. This agrees well with recent studies showing cooperative cell-cell interaction-induced tumorigenesis (48, 49) and epithelial-mesenchymal transition in tumor development (50). More importantly, the model serves as a tool to study the fundamental questions in respect to the role of tumor microenvironment by perturbing this system one molecule at a time and examining the collective responses accordingly. The metrics of correlation matrix was developed to analyze the intercellular signaling network and we observed a striking mechanistic transition: the signaling network emerges at the very early stage, peaks at the mid stage of expansion, but quickly diminishes when the tumor grows to a clinically-detectable size (1×10⁶/ml) (45, 46, 51). Further analysis suggests that paracrine represents a dominant force during tumor initiation and priming, while autocrine supersedes it and supports a robust tumor expansion. Network analysis of all five functional clusters identifies the key nodes responsible for such change. All these studies indicate a possible mechanistic transition from the microenvironment-controlled, paracrine-based regulatory mechanism to self-sustained rapid progression to malignancy stages.

The proposed modeling method and protein correlation analysis provide a mathematic framework to study the dynamics of multi-cellular systems and protein correlation network. Therefore it should be able to be generalized and applied to other disease systems, which involve heterogeneous cellular environment and communication network. The current modeling results also provide new insights into the design of personalized therapy. While most anti-cancer therapeutic strategies focus on direct targeting of cancer cells, this study suggests an alternative approach that targets the microenvironment of a tumor. To utilize the current model to design therapy, there are two major steps. First, evaluate the dynamic protein levels and determine all the potential targets that can maximize the efficacy and minimize the side effects; Second, perturbation analysis to examine the effect of deleting or enhancing these potential targets in a combinatorial fashion. To do so, we have utilized a sensitivity analysis to assess the effect of multiple signals on tumor cell growth rate (43). The most dominant signals can be identified by changing one factor at a time, and the synergistic effect can be revealed by perturbing multiple factors simultaneously to infer the design of combination therapy. It is also worth noting that the sensitivity analysis can be performed over the entire time course to longitudinally assess the changing effect of perturbations on the whole system. As shown in Fig. 3, the one that contributes the most to tumor fitness in pre-tumor phase belongs to paracrine signaling, while in later stages it changes to autocrine signaling. Therefore, this modeling approach not only provides the targets for therapeutic intervention but more importantly the timing of treatment. When the model is applied to monitoring of patient response, the levels of proteins and cell populations can be quantified by measuring clinical tumor specimens. The results can be fed into the model such that it becomes individualized and can predict targets for the specific patient. Once the model is trained with clinical data, it could become a tool to guide the therapy and predict outcomes on the individual patient basis.

Materials and Methods

Assumptions and model construction

A well-mixed species system is considered to capture the time evolution of tumor. We assume that the species included in the model evolve independently of species excluded from the model (oligodendrocyte, etc.). The regulatory effect of cytokines to cell proliferation is expressed by Hill functions (52). The stochastic parameters in Eqs. 1 and 2 are

$$r_i(t)=r_i^0\left[1+\epsilon \text{ sin}\left(\frac{2\pi r_i^0}{\text{ln }2}t+\beta W(t)+\mathrm{\Delta }\right)\right],\epsilon <1$$ (10)

$$m_{ik}(t)=m_{ik}^0\left[1+\epsilon \text{ sin}\left(\frac{2\pi r_k^0}{\text{ln }2}t+\beta W(t)+\mathrm{\Delta }\right)\right],0\le m_{ik}^0\le 1,0\le \epsilon \le \text{min}\left(1,\frac{1}{m_{ik}^0}-1\right)$$ (11)

$$k_{jk}(t)=k_{jk}^0\text{ max}\left(0,1+\mathrm{\sigma }\xi (t)\right)$$ (12)

$$u_{il}(t)=u_{il}^0\text{ max}\left(0,1+\mathrm{\sigma }\xi (t)\right)$$ (13)

$$u_{jl}(t)=u_{jl}^0\text{ max}\left(0,1+\mathrm{\sigma }\xi (t)\right)$$ (14)

$$u_{jp}(t)=u_{jp}^0\text{ max}\left(0,1+\mathrm{\sigma }\xi (t)\right)$$ (15)

where W(t) is a standard Wiener process, and ξ(t) is a zero-mean Gaussian white noise with unit intensity.

Monte Carlo simulation

The stochastic dynamics are studied using Monte Carlo simulations. The Eqs. 1 and 2 have been integrated using both routine ode4 (fixed-step classical fourth-order Runge-Kutta schemes) with Matlab code and solver ode45 (variable-step Dormand-Prince 4–5 pair method) in Simulink modules. The fixed step size for ode4 is 0.01, and the relative error tolerance for ode45 is 1E-6. They gave almost the same results. The generation of Gaussian and Poisson white noise in Eqs. 1 and 2 are involving employing of functions randn and poissrnd, respectively. The Wiener process in Eqs. 10 and 11 is further generated by integrating Gaussian white noise.

Parameter selection

We tried our best to identify all input values or ranges from published experimental data. However some parameters are still unavailable to our best knowledge. We have to make the best estimation based on indirect experimental observations or related studies. Other parameters, for example, the activation/deactivation rates of stem cells, are highly dependent upon the exogenous stimuli, thus could vary in a quite wide range. However we would argue that the initial settings of many parameters only change the quantitative timeline of the dynamics but would not affect the general trends observed in our model that properly reflect the dynamics of human glioma. Thus, without the loss of generality we assigned moderate values to these parameters. We also calibrated our model by adjusting the Hill function parameter s_cytokine and matching the simulation to published in vitro dynamics data.

Insight, innovation and integration.

Tumor cells do not develop in isolation, but actively interact and co-evolve with stromal cells via a complex intercellular signaling network. Although the role of individual stromal cells or soluble mediators has been investigated, a systems-level picture showing the collective effect of cellular and molecular components in tumor microenvironment is yet to be realized. Here we exploit an integrative model that recapitulates the complex cell-cell communication network in human brain tumor microenvironment to assess the collective behavior of inter-cellular signaling pathways. We observed a sharp change of cytokine correlation network during tumor development indicative of a possible mechanistic transition from the microenvironment-controlled, paracrine-based regulatory mechanism to self-sustained rapid progression to fetal malignancy. It also reveals key nodes that are responsible for such transition and can be potentially harnessed for the design of new anti-cancer therapies. Finally, this study can serve as a generic approach to integrate experimental data and reveal underlying mechanisms of tumor microenvironment at the systems level.