Abstract
Measuring complete gene expression profiles for a large number of experiments is costly. We propose an approach in which a small subset of probes is selected based on a preliminary set of full expression profiles. In subsequent experiments, only the subset is measured, and the missing values are imputed. We develop several algorithms to simultaneously select probes and impute missing values, and demonstrate that these probe selection for imputation (PSI) algorithms can successfully reconstruct missing gene expression values in a wide variety of applications, as evaluated using multiple metrics of biological importance. We analyze the performance of PSI methods under varying conditions, provide guidelines for choosing the optimal method based on the experimental setting, and indicate how to estimate imputation accuracy. Finally, we apply our approach to a large-scale study of immune system variation.
Introduction
Gene expression profiling is commonly used to study regulatory mechanisms1 and to obtain a comprehensive view of cellular state2. Both microarrays3 and RNA sequencing offer powerful approaches to profile the transcriptome. However, they become problematic when experimental variables vary along multiple dimensions, such as strains or individuals assayed4–6, cell types7–10, heterogeneous tumor samples11, environmental conditions12, chemical perturbations (e.g. drugs8) at different doses, genetic perturbations13,14, or different time points15–19, since the number of measurements grows combinatorially. The cost of genome-wide assays in experiments varying in even two dimensions is typically prohibitive.
An alternative approach1,8,20,21 exploits redundancy to reduce costs by measuring a small subset of “signature probes” cheaply using technologies such as bead assays22, RT-PCR23,24, direct multiplexed measurement25, microfluidic dynamic arrays26 or hybrid selection27. The information loss is balanced by the ability to perform more experiments. Such signatures can be used to estimate similarity between samples14 or to infer a notion of cellular state1.
Our probe selection for imputation (PSI) approach uses measurements of selected probes to impute a target expression profile (Fig. 1). Broad imputation from a set of single nucleotide polymorphisms is used ubiquitously in genome-wide association studies, but to our knowledge this idea has not been previously used with gene expression data. Limited imputation has been performed previously without probe selection to fill in a few missing measurements (usually up to 20%) interspersed in the gene expression matrix28–30,37. Selection of small probe subsets was also proposed for classifying future samples31 (e.g., as different disease states or outcomes21,32). Our approach couples probe selection and imputation, simultaneously selecting a probe subset, and learning a predictive model of genome-wide expression from measurements of the selected probes. Probes are selected to maximize imputation accuracy using a training set of genome-wide profiles. Like standard genome-wide expression measurements, imputed profiles can be used to infer cellular state, identify differentially expressed genes, compare samples, or identify genes with similar expression profiles.
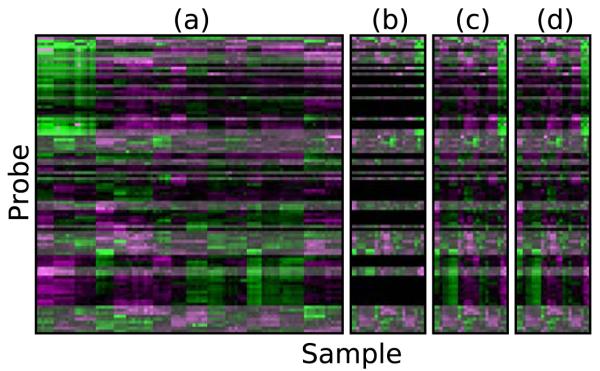
Figure 1.
An integrated approach to probe selection and imputation. (a) A training set of full expression profiles showing 50 selected probes (highlighted) out of 100. (b) The selected probes are measured in new experiments. (c) Expression profiles of the missing probes are imputed based on the 50 selected probes. (d) The true (measured) full expression profile of the additional experiments. The selected probes (highlighted) are identical to (c), while the imputed probes are similar, with small differences due to imputation errors.
Our tests demonstrate that PSI is effective and accurate in a wide variety of settings, using multiple performance metrics of biological importance on relative and absolute scales. Furthermore, we provide guidelines for applying PSI in new experiments, and an analysis of its tradeoffs. The PSI software is freely available at http://ai.stanford.edu/~yonid/psi-1.0.zip.
Results
Methods overview
We designed and implemented 15 PSI methods based on established statistical theory (Supplementary Note). In initial comparisons using five datasets, we identified three methods that dominated performance on all datasets (Supplementary Fig. 1, Supplementary Results). Our in-depth analysis below includes these three leading methods (referred to as “PSI methods”) and two simple methods as baselines for comparison (Table 1a, Online Methods).
Table 1.
Methods and datasets.
| (a) Methods used for comparison | |
|---|---|
| Method | Brief description |
| Locally weighted averaging (LWA) |
Weighted average of entire training set |
| Regularized Gaussian estimation (RGE) |
Model expression of complete probe set as multidimensional Gaussian |
| Structured regression (SR) | Linear regression of target probes using sparse priors |
| Nearest neighbor (NN) | Sample-similarity baseline: use most similar training-set sample |
| Cluster representatives (CR) | Probe-similarity baseline: choose one representative probe from each cluster |
| (b) Datasets used for comparison | ||||
|---|---|---|---|---|
| Dataset | Probes | Samples | Linearity* | SPRL-1* |
| NCI6033 | 1,375 | 60 | 0.0423 | 0.0018 |
| Gasch12 | 788 | 173 | 0.3596 | 0.0789 |
| Full Gasch (fg)12 | 6,152 | 173 | 0.1725 | 0.0049 |
| WormDB (worm)34 | 93 | 363 | 0.0629 | 0.2456 |
| AGEMAP (age)35 | 314 | 40 | 0.5734 | 0.0745 |
| van’t Veer (vv)21 | 4,918 | 78 | 0.0364 | 0.0006 |
| van’t Veer signature (vvsig)21 | 231 | 78 | 0.1460 | 0.0493 |
| Pomeroy (pom)20 | 4,267 | 42 | 0.0634 | 0.0006 |
| ImmGen (imm)36 | 1,771 | 349 | 0.0741 | 0.0146 |
| CMap8 | 1,052 | 1,211 | 0.0673 | 0.0775 |
| TCGAg (http://cancergenome.nih.gov/) | 546 | 386 | 0.0480 | 0.0340 |
| TCGAm (http://cancergenome.nih.gov/) | 534 | 379 | 0.5636 | 0.4 |
Linearity and SPRL are described in the text. SPRL-1 is computed for one selected probe.
Locally weighted averaging (LWA) uses sample similarity to impute probe measurements within new samples as weighted averages of the entire training set. Weights are based on similarities computed using the selected probes, and probes are chosen incrementally to minimize the imputation error using leave-one-out cross validation. The regularized Gaussian estimation (RGE) family of methods models the joint expression of all probes as a multivariate Gaussian, which is then used to impute target probes. Selection is based on minimizing conditional variance, which is equivalent to minimizing imputation error in this model. The chosen RGE variant uses L2-regularization to estimate the inverse covariance matrix. In structured regression (SR), selection and imputation are solved simultaneously using sparse regression models. The chosen variant uses L1,∞ regularization.
We compared these methods to two baselines. Cluster representatives (CR) uses probe similarity. It partitions the training data into clusters of probes with similar expression profiles, and selects one representative probe for each cluster. The expression level of the representative probe in new samples is assigned to all probes in the cluster. Nearest neighbor (NN) is based on sample similarity. It identifies the training set sample most similar to the new sample, and assigns expression values from the training set sample to the new sample.
We evaluated these methods on 12 datasets that vary in many dimensions, including the organism, the number of samples, the number of probes, and the degree of sample heterogeneity (Table 1b, Online Methods). Our experiments and analysis focused on probes showing meaningful variation (referred to as “target probes”), since imputation is trivial for probes whose training set expression level is nearly constant. We evaluated performance using cross-validation, assessing imputation quality for samples not seen in the training set relative to the measured “ground truth” complete expression profiles. The primary evaluation metric consisted of Pearson correlation coefficients (PCC) between imputed and measured levels for each probe over the test set (ground truth PCC, gtPCC). Additional metrics were used to evaluate the identification of differentially-expressed probes for selection, and the clustering of probes and samples.
PSI is effective and accurate
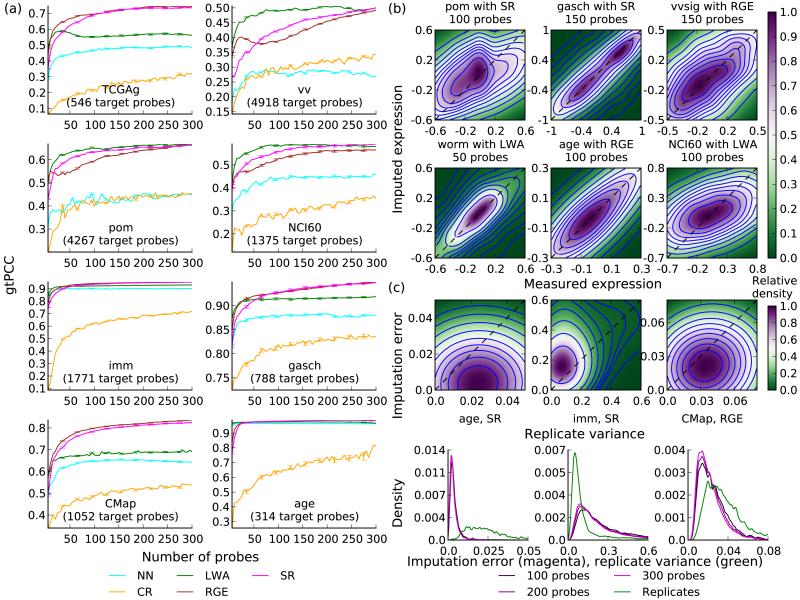
gtPCC values for PSI methods significantly exceeded those for baselines on all datasets, for any number of selected probes between 5 and 300 (Fig. 2a and Supplementary Fig. 2; P < 10−100, t-test). The imputations were accurate throughout the range of values seen in the data (Fig. 2b) and the improvements over baselines were uniform across all PCC values (Supplementary Fig. 3). To evaluate accuracy, we compared imputation error (E) to the underlying noise in the data, estimated by the variance between biological replicates (V) available for three datasets. Imputation errors were computed after averaging K replicates, which reduced their variance by K, allowing separate estimation of the total imputation error (E + V / K) and V. E + V / K was comparable to V on CMap (K = 2, Cohen’s d = 0.7585) and imm (K = 3, Cohen’s d = −0.4974) and notably smaller than V on age (K = 5, Cohen’s d = 1.8926), implying high accuracy relative to the dataset-specific noise (Fig. 2c).
Figure 2.
Relative and absolute imputation accuracy. (a) Median Pearson correlation coefficients between imputed and measured expression levels, using 5 to 300 selected probes, for eight datasets. Error bars, s.e.m; n = number of target probes – number of selected probes. (b) Density heatmaps comparing imputed and measured expression for representative datasets and numbers of selected probes. Colors represent local probe density. Blue contour lines represent regions of equal density. (c) Comparison of imputation error with variance in biological replicates. Top: density heatmaps of probe-specific intra-replicate variance (x axis) vs imputation error (y axis). Bottom: the distribution of intra-replicate variance (green curve) and imputation errors (red curves) for varying numbers of selected probes.
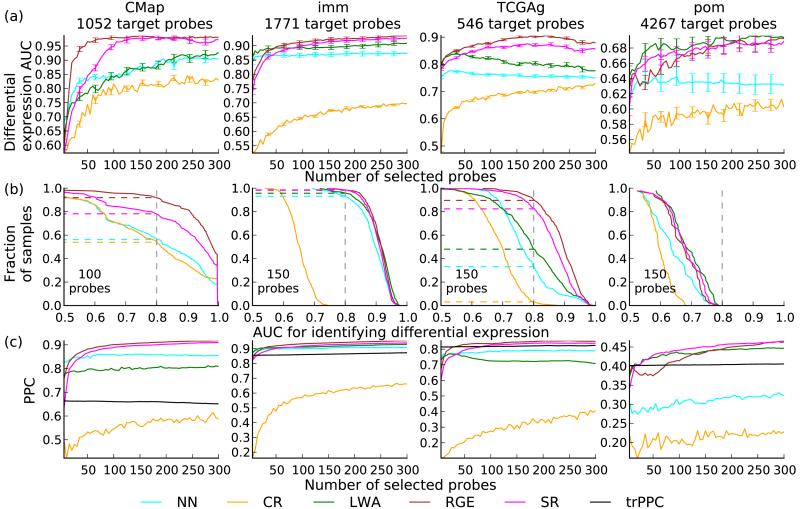
We next analyzed performance using additional metrics of biological importance, starting with identification of differential expression (Online Methods), evaluated on four datasets using 5 to 300 selected probes (Fig. 3a). PSI methods outperformed baselines with overall high accuracy (P < 10−6 for all comparisons except LWA vs NN on CMap, paired t-tests), but between-dataset variability was considerable: on CMap, imm and TCGAg, PSI methods (RGE in particular) achieved good results on absolute scales, with medians above 0.9 and over 80% of sample area-under-curve values above 0.8 (Fig. 3b), while on pom the median was 0.68. This variability emphasizes that imputations are predictions with confidence levels that depend on signal/noise ratios of the training set data.
Figure 3.
Additional evaluation metrics of biological relevance. (a) Area under receiver operating characteristic curve (AUC) values for identifying differentially-expressed probes in a new sample as a function of the number of selected probes. Error bars, s.e.m; n = 1,211 (CMap), 349 (imm), 386 (TCGAg), 42 (pom). (b) CDF plots where for each AUC value (x axis), the corresponding y axis value is the fraction of samples (y axis) with an AUC above that value. (c) Preservation of probe correlation structure is indicated by PPC as a function of the number of selected probes. The black curve corresponds to trPPC, the PPC value with correlations estimated using the training set.
Clustering of gene expression is commonly used to analyze probe correlation structure. We directly evaluated probe-probe correlations (PPC) between the measured and imputed correlation matrices (Online Methods). As a baseline, we computed PCC between training and test set empirical correlation matrices (trPPC), representing dataset-specific variability in correlation structures. The PSI methods RGE and SR were far superior to baselines (Fig. 3c), and also exceeded trPPC with 50 or more selected probes, while CR was significantly below trPPC and NN was inconsistent, suggesting that the imputations accurately preserved similarity structures between probes (P < 10−6 for all comparisons, paired t-tests). The correlations were preserved across all PCC values (Supplementary Fig. 4). Sample-sample correlations (SSC), defined analogously to PPC, were also evaluated. CR performed better and LWA worse relative to other metrics; RGE and SR led on high-performance datasets, with performance above the tagSSC baseline, while on low-performance datasets, CR and tagSSC were better (Supplementary Fig. 5 and Supplementary Results).
Guidelines for applying PSI
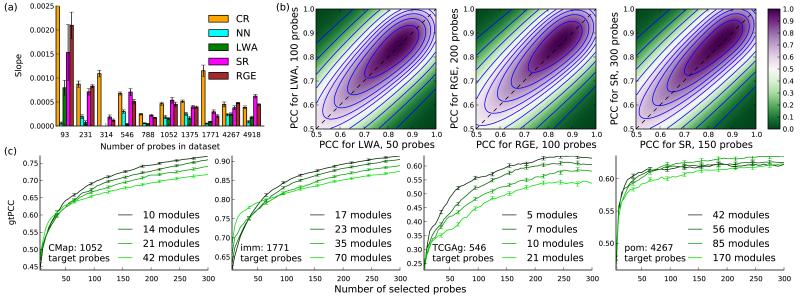
We next established “best use” guidelines for novel applications. The number of selected probes represents a tradeoff between more complex and accurate imputation models and higher costs. A cost-benefit analysis can determine the optimal number. We computed the benefit as mean improvement in overall performance (gtPCC) per additional probe (Fig. 4a, Online Methods), separating baseline performance from the accuracy gains of adding selected probes. SR and RGE showed greater average gains than LWA, and CR showed the largest gain, but due to low baseline performance it was outperformed by the leading methods even at 300 probes. We also examined individual-probe PCC increases from doubling the number of selected probes, across all datasets (Fig. 4b). The gains were uniform across the PCC range, demonstrating the tradeoff between marginal benefits and costs.
Figure 4.
Cost-benefit analysis to determine the optimal number of selected probes and MD modules. (a) Mean improvement in overall performance (gtPCC)with an additional selected probe, measured as the slope of the regression line for gtPCC by number of selected probes. Error bars, standard error of the slope. (b) Density heatmaps of PCC values using 2k vs k selected probes (k = 50, 100, 150) for three PSI methods (n > 60,000 comparisons for each panel). (c) gtPCC vs number of selected probes for various numbers of modules. Lighter greens, more modules. Error bars, s.e.m; n = number of target probes minus number of selected probes.
Another tradeoff exists for RGE methods, where estimating covariance matrices for full expression profiles requires considerable computational resources. We developed a lower-complexity approximation (modular decomposition, MD) by estimating covariance matrices over disjoint subsets (modules) of correlated genes (Supplementary Note). The number of modules trades off accuracy and computational resources, since more modules imply stronger assumptions on the probe covariance structure. Accuracy decreased with increasing modularity on datasets with high overall performance (Fig. 4c) due to information loss across module boundaries, but can improve if overall performance is low by focusing on highly-predictive intra-modular interactions (r = −0.737 between gtPCC changes with increasing modularity and predicted performance; Online Methods). Computational demands typically increase and overall accuracy decreases with increasing numbers of target probes, making MD useful in high-dimensional imputation tasks.
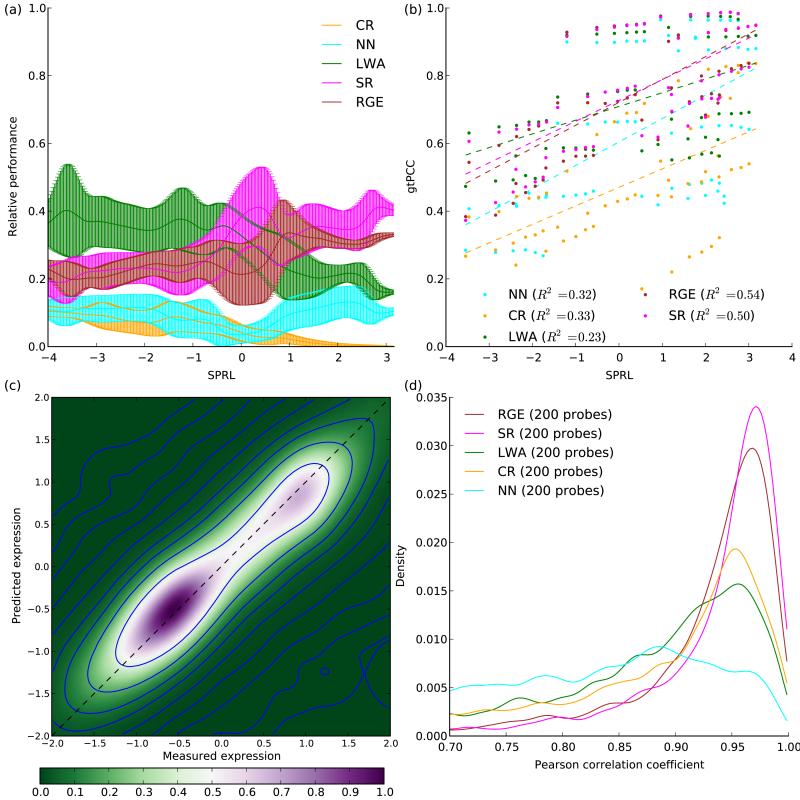
Next, we addressed the choice of PSI method. Among LWA, RGE and SR, the best-performing method depended on the number of selected probes, target probes and training set samples, and data set “linearity”, measured as the fraction of the variance explained by the principal eigenvector of the matrix of inter-probe correlations (Online Methods). To predict PSI performance according to the dataset and number of selected probes, we used the logarithm of the product of the ratio of selected to target probes, the number of training samples, and linearity (samples, probe-ratio, linearity; SPRL). More complex predictors could assign weights to these components, but SPRL is simple, intuitive and requires no parameter fitting.
We evaluated SPRL using a relative performance metric which assigns scores between 0-1 per probe (Online Methods). SPRL predicted the best-performing methods well (Fig. 5a), with LWA leading for SPRL below −1, RGE/SR leading for SPRL above 1, and a transition from LWA to the linear methods between −1 and 1 (Spearman’s rho between SPRL and relative performance, LWA: −0.740, RGE: 0.717, SR: 0.567). Since LWA is nonlinear and nonparametric, it can generate better predictions than parametric methods when very little information is available to estimate parameters (few samples or low probe ratio).
Figure 5.
The samples, probe-ratio, linearity (SPRL) predictor and ImmVar results. (a) Relative performance of methods as a function of SPRL. Data points were computed for each combination of dataset and number of selected probes and interpolated to a smooth curve using a Gaussian kernel (error bars, interpolation s.d.). (b) gtPCC values (y axis) as a function of SPRL (x axis). Each point corresponds to one dataset, a specific number of selected probes and the corresponding gtPCC value. Dashed lines, linear regression fits. Bottom: ImmVar results. (c) Density heatmap comparing measured (x axis) with imputed (y axis) expression levels. (d) Density histogram of Pearson correlation coefficients between measured and imputed expression values for each probe, for 5 methods using 200 selected probes each.
SPRL also predicted overall imputation accuracy (Fig. 5b) without the need to run computationally intensive cross-validation experiments (Spearman’s rho between SPRL and gtPCC, LWA: 0.485, RGE: 0.735, SR: 0.743). The individual components of SPRL were less accurate predictors (Supplementary Table 1).
PSI applied to ImmVar data
We applied PSI to select probes in the ImmVar Project (http://www.immvar.org/), a collaborative study of the impact of human genetic variation on the expression of immune genes in individuals with no known immunologic, inflammatory or infectious disease. Due to the large number of samples (Online Methods), our goal was to define a reduced probe set for signature genes that could be assayed using Nanostring25 and used to give global expression profiles by imputation. We assembled a 58-sample training set from two independent microarray datasets and used the filtering process in PSI to reduce the number of probes to 2,175. Of these, 63 probes of interest were chosen in advance, and PSI was used to select an additional 187 for a total of 250 signature probes (Online Methods).
The high linearity of this dataset (0.35) suggested that linear methods would perform well despite the large number of target probes relative to the number of samples. We selected probes and trained models for LWA, RGE and SR. A test set of 45 new microarray samples that encompassed genetic variation and T-cell activation was then generated (Online Methods).
We compared the imputed expression values to those measured in the test set, across the 2,175 target probes. The linear method accuracies were very high, with PCC modes above 0.95 (Fig. 5c-d), demonstrating that probe selection successfully identified the probes whose expression levels are most informative about the target probes, and imputation reconstructed the target expression profiles with high precision using only those selected probes. Importantly, probes selected in one dataset were used to generate high-accuracy imputations on a different (but related) dataset. The probes selected by RGE are now being used by the ImmVar Project for activated T-cell experiments.
Discussion
PSI can be applied when a training set can be assembled under conditions that are similar for subsequent experiments. The ImmVar results demonstrate that moderate similarity between the training set and subsequent experiments is sufficient to produce highly accurate imputations. Furthermore, imputation from the selected probes predicted the mean of biological replicates with greater accuracy than individual fully measured replicate profiles, implying that information aggregation from multiple probes makes PSI methods robust to noise.
Imputation error is low on average, but researchers may consider certain target probes especially important. Individual probe imputation errors can be weighed accordingly by a straightforward modification to the PSI objective function. Additionally, we analyzed probe characteristics based on imputation error, demonstrating that high imputation errors are strongly associated with measurement errors but not with gene functional classification (Supplementary Fig. 6 and Supplementary Results), supporting the robustness of PSI.
Applying PSI to a new application requires choosing a method and the number of probes to select. SPRL accurately positions applications on an axis that intuitively corresponds to prediction difficulty, making it a valid tool for choosing a PSI method. Computational demands also influence method choice. PSI methods scale well, except RGE, for which we propose using modular decomposition as an approximation. Full time and space complexity analyses are given in the Supplementary Note. Since the number of selected probes trades off cost and accuracy, data alone cannot define an optimal number. SPRL can help estimate overall imputation accuracy and choose a method given the number of selected probes.
Dataset characteristics strongly separate LWA from RGE and SR. LWA can model nonlinear relationships, making it more suitable for low linearity datasets. RGE and SR are parametric, and their accuracy depends on the number of parameters to be estimated (which increases with more target probes) and the amount of training data (which increases with more samples). LWA exploits global similarities in expression patterns, while RGE and SR exploit local relationships between probes. Inferring the global state requires fewer probe measurements than estimating many individual local relationships, explaining why LWA produces better imputations using very few probes, but as additional probes are measured, RGE and SR improve more rapidly using information on finer scales. This also explains why using MD to reduce the number of parameters that need to be estimated is most useful when the learning problem is difficult, as effectively captured by SPRL. Conversely, with sufficient information to estimate a higher-complexity model, reducing the number of parameters decreases performance.
To examine whether SR and RGE are limited by their linear nature, we developed a nonlinear parametric method (RGME) based on estimating a mixture model (Supplementary Results). This method was inferior to the linear methods (Supplementary Fig. 7), suggesting that the disadvantage of the linear methods in the low-performance settings is likely due to the difficulty of estimating a large number of parameters from noisy data with few observations, rather than nonlinear relationships between probes.
Although some of our imputation methods are based on similar statistical foundations to previous work (PCA29,30 and linear regression28,37), the three leading methods were developed here. The PSI paradigm is the first to propose a tight integration between selection and imputation, based on a unified objective. Our proposed solution consists of multiple methods, suitable for a wide range of applications, along with criteria for choosing between them. Imputation uses information from the selected probes to predict target probe expression with accuracy comparable to the similarity between biological replicates. These characteristics make PSI a valuable new tool for understanding cellular networks and their variations.
Online Methods
Software and data
A command-line tool implementing the three leading methods described in our paper (LWA, RGE and SR), with full documentation, is available from the Nature Methods website and at http://ai.stanford.edu/~yonid/psi-1.0.zip. The data sets used in this paper, in the format used by this tool, are included in Supplementary Data.
Datasets and processing
We used the following data sets for evaluation of the methods:
NCI6033, data retrieved from: http://discover.nci.nih.gov/nature2000/data/selected_data/t_matrix1375.txt. 1,375 genes, 60 cell lines.
Yeast stress dataset12. Data retrieved from: http://genome-www.stanford.edu/yeast_stress/data/rawdata/complete_dataset.txt. The full data set contains 6,152 genes and 173 conditions. We also used a “filtered Gasch” data set with only the 788 probes with the highest variance. We refer to the full data set as “fg” and to the filtered one as “gasch”.
WormDB34, data retrieved from: http://www.computationalbio.com/Stanford/KimLab/wormDB/index.php. 93 genes, 363 tissues. We use Supplementary Table 4 (http://download.cell.com/mmcs/journals/0092-8674/PIIS0092867409011180.mmc6.zip) from Liu et al. (PMID 19879847). We refer to this dataset as “worm”.
AGEMAP35, a data set of gene expression in aging mice. AGEMAP covers 8,932 genes in 16 tissues. The data was retrieved from http://cmgm.stanford.edu/~kimlab/aging_mouse/mouse_downloads.htm. We used all 16 tissues, and included only the probes reported by the authors as significantly age-related from Table S5 (http://www.plosgenetics.org/article/fetchSingleRepresentation.action?uri=info:doi/10.13 71/journal.pgen.0030201.st005). There are overall 128 samples (8 mice, 16 tissues) with several biological replicates for each (usually 5). We averaged all the replicates to get the final data set of 314 probes and 128 samples. We refer to this data set as “age”.
Breast cancer data from 78 patients21. The data was retrieved from: http://www.rii.com/publications/2002/vantveer.html. The initial step of processing used originally is the selection of about 5,000 genes that were significantly regulated across the group of samples, defined as: “more than two-fold regulation and significance of regulation p < 0.01 in more than 5 experiments”. We applied these criteria and used the resulting data set, which has 4,918 probes and 78 samples. We refer to this data set as “vv”. The paper also identifies a breast cancer signature using 231 probes. The list of probes is provided in the Supplementary Information (table S2, http://www.nature.com/nature/journal/v415/n6871/extref/415530a-s9.xls). We also included the signature-only data set of 231 probes and 78 samples and refer to it as “vvsig”.
Central Nervous System Embryonal Tumors20. The paper includes several data sets, available from http://www.broadinstitute.org/mpr/CNS/. We used “Data Set A”, which includes 42 samples, and is available from http://www.broadinstitute.org/mpr/publications/projects/CNS/Pomeroy_et_al_0G04850_1 1142001_datasets.zip. We applied the preprocessing steps described there: re-scaling to account for different chip intensities, thresholding, and the variation filters, as described in http://www.broadinstitute.org/mpr/publications/projects/CNS/Pomeroy_et_al_0G04850_1 1142001_suppl_info.doc. This resulted in 4,267 probes and 42 samples. We refer to this dataset as “pom”.
The Immunological Genome36, with gene expression profiles of cells in the immune system of mice. The raw CEL files were downloaded from Gene Expression Omnibus (http://www.ncbi.nlm.nih.gov/geo/), accession number GSE15907, and normalized. The full data has 35,512 probes and 349 samples. A variance filter was applied to select the 1,771 probes with the highest variance. After averaging biological replicates, the data set has 1,771 probes and 126 samples. We refer to this data set as “imm”.
Connectivity Map8, a data set generated at The Broad Institute. We used version 2, which contains 6100 instances overall. We processed the data as follows: we downloaded the raw CEL files from http://www.broadinstitute.org/cmap/ and normalized them. From each drug perturbation sample we subtracted the mean of the control experiments corresponding to that sample (in log2 space). We only used instances for the MCF7 cell type (for which there is the largest number of instances), and the highest concentration available for each drug. We averaged the expression over biological replicates where available. These steps left us with 1,211 samples, each one corresponding to the averaged differential expression of the highest concentration of a single drug relative to its control experiments. Next, we filtered the probes to include only probes whose expression changed at least threefold under at least five drugs. The resulting data set, to which we refer as “CMap”, has 1,052 probes and 1,211 samples.
The Cancer Genome Atlas. We generated two data sets using TCGA data: the first uses microRNA expression from the experiment titled “MicroRNA Analysis of TCGA GBM samples using Agilent MicroRNA array”. Data was retrieved using the TCGA Data Portal at http://tcga.cancer.gov/dataportal/index.asp. This data set, to which we refer as “TCGAm”, includes 534 probes and 379 samples. The second dataset based on TCGA includes all gene expression samples for GBM generated using the HT_HG-U133A chip. The experiment title is “TCGA Analysis of RNA Expression for Glioblastoma Multiforme Using Affymetrix HT_HG-U133A”. The data was also retrieved using the TCGA Data Portal. We used only the 601 genes that were selected for the first round of glioblastoma multiforme (GBM) tumor sequencing. This list is available from http://tcga.cancer.gov/dataportal/data/about/types/sequencing/GBM_PhaseI.xls. Genes were matched to probes by name: exact matches were found for 546 genes, and only those were included. This data set, to which we refer as “TCGAg”, includes 546 probes and 386 samples.
These data sets vary in their sample variance, measurement methods, and numbers of genes and samples, allowing the comparison of the methods under different settings.
PSI methods
Following is a brief description of the selection and imputation processes of the leading and baseline PSI methods. “Greedy selection” means that probes are selected incrementally, with each subsequent probe selected to minimize the imputation error when using cross-validation on the training set with the previously chosen probes together with the newly-added one. Full mathematical and implementation details for all 15 methods are available in the Supplementary Note.
In cluster representatives (CR), the data is clustered using the k-Means algorithm with multiple random restarts to l clusters, and from each cluster, a representative probe is chosen, such that the average distance to all probes in the cluster is minimized. Imputation is done simply by using the value of the representative for the entire cluster.
In k-nearest neighbors (kNN and NN), probes are greedily selected. Imputation is done by finding the k nearest neighbors in the training set (measured by Euclidean distance using only the selected probes), and averaging them. With k = 1, this method is the baseline “Nearest Neighbor” (NN).
In locally weighted averaging (LWA), imputations are weighted averages ∑wiXi of the entire training set, with weights based on the Euclidean distance, measured on the observed probes, between the training sample and the new sample: wi ∞ exp(γ∥Xi-Xnew∥2) with ∑wi = 1. Probes are selected greedily together with the parameter gamma. We also used a variant (Supplementary Note) where each probe has its own kernel width.
Regularized Gaussian estimation (RGE) is a family of methods which consist of learning a generative Gaussian model of the training data using one of several estimation methods described below. Probes are greedily selected to minimize the remaining variance of the target probes (which is equivalent to the expected imputation error), conditioned on the probes already selected: Tr(∑tt-∑ts(∑ss)−1∑st) where ∑tt is the estimated covariance between the target probes, ∑ss is the estimated covariance between the selected probes, and ∑st is the estimated covariance between the selected and the target probes. Imputation is done by computing the expected value of the unobserved probes given the observed ones in the Gaussian model. We used the “L2Cov” variant.
In structured regression (SR), imputations are linear combinations of the selected probes. The regression weights are learned simultaneously with the selection of probes by using a structured prior based on the L1,∞ norm that yields solutions with many zero weights, corresponding to unselected probes.
RGE covariance estimation variants
RGE methods estimate a Gaussian distribution over full expression profiles using the training data. Probe are selected to minimize the prediction error in the model. Imputation is done by computing the conditional expected value of the unobserved probes given the observed ones in the Gaussian model. We developed several variants to estimate the covariance matrix:
PCAC is a probabilistic PCA model estimated on the training data. The number of principal components is chosen by cross-validation. An alternative method based on PCA was also developed, which does not belong in the RGE family. This method, PCAR, uses PCA regression. (Supplementary Note)
In SCESS, the unbiased maximum-likelihood estimate of the covariance matrix is shrunk towards a diagonal covariance matrix, with the shrinkage coefficient determined analytically. In another variant, SCECV, the shrinkage coefficient is chosen using cross-validation (Supplementary Note).
In L1Cov, a sparse precision matrix (the inverse of the covariance matrix) is estimated using L1 regularization. L2Cov is similar, but uses L2 regularization on the precision matrix. L2Cov is the variant that was chosen to represent the entire RGE family (Supplementary Note)
In Soft Modular Gaussian (SMG), the precision matrix is estimated using L2 regularization, where the variance of the Guassian prior for each entry in the precision matrix depends on the Pearson correlation between the corresponding probe pair (Supplementary Note).
Regression variants
RGE methods use Gaussian generative models for the gene expression data and then select probes and impute using the learned models. Regression methods are discriminative and do not model the distribution over the selected probes. They predict the expression of the unobserved probes as linear combinations of the observed ones. Greedy regression (GR) methods use a stepwise procedure to select probes to minimize the imputation error. Structured regression (SR) methods use sparse priors on the regression weights such that only few probes have nonzero weights in the model, corresponding to selected probes. We evaluated several variants, differing mostly in regularization:
L2Reg is the only GR variant, and uses L2 regularization for learning the weights. Selection is done with a greedy algorithm since L2 regularization does not result in sparse weights.
GLL2 and L1Inf are SR variants and yield regression models that are sparse in the number of probes which have nonzero weights. GLL2 uses a block-L1 norm, while L1Inf uses the L1,∞ norm over the regression weights during the selection phase. The L1Inf variant represents the regression family.
ImmVar data
The ImmVar study involves a cohort of 600 blood donors of African American, Asian and Caucasian ancestry. In the expression component of the project, genome-wide expression profiling is being performed on highly purified naïve CD4+ T lymphocytes and CD14+CD16-. In the activation component, CD4+ T cells and monocyte-derived dendritic cells from different individuals are activated in vitro to measure the activation response of these two cell types. The activation component involves a large number of samples, which vary across individual, ligand, cell type, and time point. Since genome-wide expression profiling this many samples would be economically impossible, we elected to use PSI to define a set of 250 signature genes from a limited number of microarrays.
We first assembled a training set from two independent datasets (see below). The first, which provided a component of genetic variability, was generated from resting CD4+ T lymphocytes from peripheral blood of 31 individuals, encompassing both genders and the three ancestries. The second dataset corresponded to transcriptional changes elicited during a time-course analysis of T cell activation. It was generated by activating blood CD4+ T cells (pooled from 4 donors of mixed gender and ethnicity) with anti-CD3/anti-CD28 beads in culture, for different periods of time (0, 45 minutes, 2, 4, 10, 24, 48 and 72 hrs). There were 58 samples in the training set.
The test set was generated by profiling purified CD4+ T cells from 15 different individuals (covering all ethnic and gender groups), activated for 4 and 48 hrs with bead-bound anti-CD3 and anti-CD28, thus encompassing both early and late phases of the T cell response. This test set encompasses simultaneously genetic variation and cell activation.
ImmVar processing
For profiling of purified CD4+ T cells, blood PBMCs were isolated by Ficoll density gradient centrifugation, stained with monoclonal antibodies reactive to CD3/4/8/14/16/19/25/62L, and CD3+CD4+CD62Lhi cells were purified to >99% purity by 2 rounds of flow cytometric sorting on a FACS Aria. 50,000 cells were sorted directly into Trizol for RNA preparation. Isolated RNA was amplified and prepared for hybridization to the Affymetrix HuGene ST1.0 Array using the GeneChip Whole Transcript (WT) Sense Target Labeling Assay. Raw data was normalized using the Robust Multichip Average algorithm in the “Expression File Creator” module in GenePattern.
For profiling of activated cells, CD4+ T cells were isolated from whole blood by negative selection using RosetteSep human CD4+ T cell enrichment cocktail and RosetteSep density medium gradient centrifugation, then stored frozen. On the day of activation, CD4+ T cells from 15 individuals were thawed, resuspended in RPMI supplemented with 10% FCS, and plated at 50,000 cells per well in a 96-well plate. Cells were either left untreated as a baseline control or stimulated with bead-bound anti-CD3 and anti-CD28 at a bead-to-cell ratio of 1:1 for 4 hrs or 48 hrs. At each time point, a second step of purification of CD4+ T cells was performed, with magnetic positive selection using the Invitrogen Dynal CD4 positive isolation kit (96-well format) prior to Trizol extraction of RNA, and microarray profiling as above.
Prior to selection, we filtered the probes using two filters: first, probes must have an expression level above 80 in at least 20% of the samples; second, probes must be differentially expressed (defined as twofold change from the geometric mean) in at least 3 out of the 58 samples.
Identifying differential expression
We ranked the imputed expression profiles, generated receiver operating characteristic (ROC) curves for varying thresholds of classifying a probe as differentially expressed, and summarized the curves using the area under curve (AUC) metric. We evaluated different variants of this metric and demonstrated them to be nearly equivalent in terms of ranking (Supplementary Fig. 8 and Supplementary Results). In our main analysis we focused on the most common case of identifying which probes in a new sample are likely to be differentially expressed, using the common criterion of a twofold change from the mean. By filtering out probes with very low variation, all remaining probes show a minimal degree of differential expression, but not in every sample. This metric evaluates the ability of a method to predict which probes will be differentially expressed in a new sample.
Statistical analysis
All experiments on the 12 main datasets were performed with 5-fold cross validation, using for the analysis only the values of target probes imputed on the 1/5 of the data used as test set within each split. Results were aggregated over splits by averaging or taking the median (for gtPCC). Method-specific parameters were chosen using cross-validation within the training set (4/5 of the data). Expression values were centered by subtracting the training set mean within each training-test split. Metrics used: gtPCC, the median PCC over all target probes; [GS/SS]DE[25]AUC, the area under curve of the ROC curve for identifying differentially expressed probes in a new sample or samples in which a given probe is differentially expressed, 25 indicates the top 25% were used as differentially expressed rather than twofold change from the mean; PPC/SSC, the PCC between the probe-probe/sample-sample correlation matrix computed on the measured expression and the one computed on the imputations, averaged over cross-validation splits; trPPC, the PPC using the training set instead of the imputations; tagSSC, the SSC using selected probes instead of using the imputations.
To compute the average improvement per additional probe we computed the slope of a linear regression line fit to the gtPCC as a function of the number of selected probes, from 50 to 300.
To evaluate the change in imputation accuracy with an increasing number of modules, we first computed Spearman rank-order correlation coefficients between the number of modules used and gtPCC for multiple datasets and numbers of selected probes. The PCC of this measure and a predictor of overall performance (SPRL) was used to assess the relationship between overall accuracy and the accuracy change with increased modularity.
Linearity is computed as the fraction of the variance explained by the first (largest eigenvalue) principal component of the probe-probe covariance matrix. 100 bootstrap iterations were used to compute the mean and variance of the linearity estimator.
Relative performance is based on PCC for each probe, comparing the Fisher transformations of the PCC of each method to the highest-correlated method for that probe by a z-score: let rbest be the PCC of the best method on a specific probe, and r be the PCC of any method, then the relative performance for that method is 2φ((n–3)½(arctanh(r)–arctanh(rbest))), where φ is the CDF of the normal distribution. This relative metric gives a value of 1 to the best-performing method, which continuously decreases to a minimum of 0, as the performance drops farther from that of the best-performing method.
Supplementary Material
ACKNOWLEDGEMENTS
This work was supported by grant RC2 GM093080 from National Institute of Health / National Institute of General Medical Sciences to C.B. and D.K. We thank I. Amit and J. Ye for useful comments on this manuscript.
Footnotes
AUTHOR CONTRIBUTIONS YD and DK designed the methods; YD implemented the methods, wrote the code, performed the experiments and analyzed the data; TF and CB provided data and gave feedback on the results; YD and DK wrote the manuscript; CB reviewed and commented on the manuscript.
COMPETING FINANCIAL INTERESTS The authors declare no competing financial interests.
References
- 1.Amit I, et al. Unbiased reconstruction of a mammalian transcriptional network mediating pathogen responses. Science. 2009;326:257–263. doi: 10.1126/science.1179050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Golub TR, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
- 3.Schena M, Shalon D, Davis RW, Brown PO. Quantitative monitoring of gene expression patterns with a complementary DNA microarray. Science. 1995;270:467–470. doi: 10.1126/science.270.5235.467. [DOI] [PubMed] [Google Scholar]
- 4.Cheung VG, et al. Natural variation in human gene expression assessed in lymphoblastoid cells. Nature Genetics. 2003;33:422–425. doi: 10.1038/ng1094. [DOI] [PubMed] [Google Scholar]
- 5.Schadt EE, et al. Genetics of gene expression surveyed in maize, mouse and man. Nature. 2003;422:297–302. doi: 10.1038/nature01434. [DOI] [PubMed] [Google Scholar]
- 6.Emilsson V, et al. Genetics of gene expression and its effect on disease. Nature. 2008;452:423–428. doi: 10.1038/nature06758. [DOI] [PubMed] [Google Scholar]
- 7.Su AI, et al. Large-scale analysis of the human and mouse transcriptomes. Proc. Natl. Acad. Sci. U.S.A. 2002;99:4465–4470. doi: 10.1073/pnas.012025199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lamb J, et al. The Connectivity Map: using gene-expression signatures to connect small molecules, genes, and disease. Science. 2006;313:1929–1935. doi: 10.1126/science.1132939. [DOI] [PubMed] [Google Scholar]
- 9.Lein ES, et al. Genome-wide atlas of gene expression in the adult mouse brain. Nature. 2007;445:168–176. doi: 10.1038/nature05453. [DOI] [PubMed] [Google Scholar]
- 10.Dimas AS, et al. Common Regulatory Variation Impacts Gene Expression in a Cell Type-Dependent Manner. Science. 2009;325:1246–1250. doi: 10.1126/science.1174148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Alizadeh AA, et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature. 2000;403:503–511. doi: 10.1038/35000501. [DOI] [PubMed] [Google Scholar]
- 12.Gasch AP, et al. Genomic expression programs in the response of yeast cells to environmental changes. Mol. Biol. Cell. 2000;11:4241–4257. doi: 10.1091/mbc.11.12.4241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wagner A. Estimating coarse gene network structure from large-scale gene perturbation data. Genome Res. 2002;12:309–315. doi: 10.1101/gr.193902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hughes TR, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- 15.Whitfield ML, et al. Identification of genes periodically expressed in the human cell cycle and their expression in tumors. Mol. Biol. Cell. 2002;13:1977–2000. doi: 10.1091/mbc.02-02-0030.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chu S, et al. The transcriptional program of sporulation in budding yeast. Science. 1998;282:699–705. doi: 10.1126/science.282.5389.699. [DOI] [PubMed] [Google Scholar]
- 17.Cho RJ, et al. A genome-wide transcriptional analysis of the mitotic cell cycle. Mol. Cell. 1998;2:65–73. doi: 10.1016/s1097-2765(00)80114-8. [DOI] [PubMed] [Google Scholar]
- 18.Spellman PT, et al. Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.DeRisi JL, Iyer VR, Brown PO. Exploring the metabolic and genetic control of gene expression on a genomic scale. Science. 1997;278:680–686. doi: 10.1126/science.278.5338.680. [DOI] [PubMed] [Google Scholar]
- 20.Pomeroy SL, et al. Prediction of central nervous system embryonal tumour outcome based on gene expression. Nature. 2002;415:436–442. doi: 10.1038/415436a. [DOI] [PubMed] [Google Scholar]
- 21.van ’t Veer LJ, et al. Gene expression profiling predicts clinical outcome of breast cancer. Nature. 2002;415:530–536. doi: 10.1038/415530a. [DOI] [PubMed] [Google Scholar]
- 22.Bibikova M, et al. Quantitative gene expression profiling in formalin-fixed, paraffin-embedded tissues using universal bead arrays. Am. J. Pathol. 2004;165:1799–1807. doi: 10.1016/S0002-9440(10)63435-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Paik S, et al. A multigene assay to predict recurrence of tamoxifen-treated, node-negative breast cancer. N. Engl. J. Med. 2004;351:2817–2826. doi: 10.1056/NEJMoa041588. [DOI] [PubMed] [Google Scholar]
- 24.Bustin S. Absolute quantification of mRNA using real-time reverse transcription polymerase chain reaction assays. Journal of Molecular Endocrinology. 2000;25:169–193. doi: 10.1677/jme.0.0250169. [DOI] [PubMed] [Google Scholar]
- 25.Geiss GK, et al. Direct multiplexed measurement of gene expression with color-coded probe pairs. Nat. Biotechnol. 2008;26:317–325. doi: 10.1038/nbt1385. [DOI] [PubMed] [Google Scholar]
- 26.Spurgeon SL, Jones RC, Ramakrishnan R. High Throughput Gene Expression Measurement with Real Time PCR in a Microfluidic Dynamic Array. PLoS ONE. 2008;3:e1662. doi: 10.1371/journal.pone.0001662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gnirke A, et al. Solution hybrid selection with ultra-long oligonucleotides for massively parallel targeted sequencing. Nat. Biotechnol. 2009;27:182–189. doi: 10.1038/nbt.1523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Xing EP, Jordan MI, Karp RM. Feature Selection for High-Dimensional Genomic Microarray Data. Proceedings of the Eighteenth International Conference on Machine Learning.2001. pp. 601–608. [Google Scholar]
- 29.Hedenfalk I, et al. Gene-Expression Profiles in Hereditary Breast Cancer. New England Journal of Medicine. 2001;344:539–548. doi: 10.1056/NEJM200102223440801. [DOI] [PubMed] [Google Scholar]
- 30.Troyanskaya O, et al. Missing value estimation methods for DNA microarrays. Bioinformatics. 2001;17:520–525. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- 31.Oba S, et al. A Bayesian missing value estimation method for gene expression profile data. Bioinformatics. 2003;19:2088–2096. doi: 10.1093/bioinformatics/btg287. [DOI] [PubMed] [Google Scholar]
- 32.Kim H, Golub GH, Park H. Missing value estimation for DNA microarray gene expression data: local least squares imputation. Bioinformatics. 2004;21:187–198. doi: 10.1093/bioinformatics/bth499. [DOI] [PubMed] [Google Scholar]
- 33.Bø TH, Dysvik B, Jonassen I. LSimpute: accurate estimation of missing values in microarray data with least squares methods. Nucleic Acids Res. 2004;32:e34. doi: 10.1093/nar/gnh026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Scherf U, et al. A gene expression database for the molecular pharmacology of cancer. Nat. Genet. 2000;24:236–244. doi: 10.1038/73439. [DOI] [PubMed] [Google Scholar]
- 35.Liu X, et al. Analysis of Cell Fate from Single-Cell Gene Expression Profiles in C. elegans. Cell. 2009;139:623–633. doi: 10.1016/j.cell.2009.08.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zahn JM, et al. AGEMAP: A Gene Expression Database for Aging in Mice. PLoS Genetics. 2007;3:e201. doi: 10.1371/journal.pgen.0030201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Heng TSP, et al. The Immunological Genome Project: networks of gene expression in immune cells. Nature Immunology. 2008;9:1091–1094. doi: 10.1038/ni1008-1091. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.