Spectroscopic and DFT Studies of Second Sphere Variants of the Type 1 Copper Site in Azurin: Covalent and Non-Local Electrostatic Contributions to Reduction Potentials

Abstract

The reduction potentials (E⁰) of type 1 (T1) or blue copper (BC) sites in proteins and enzymes with identical first coordination spheres around the redox active copper ion can vary by ~400 mV. Here, we use a combination of low temperature electronic absorption and magnetic circular dichroism, electron paramagnetic resonance, resonance Raman, and S K-edge X-ray absorption spectroscopies to investigate a series of second sphere variants—F114P, N47S, and F114N in Pseudomonas aeruginosa azurin (Az)—which modulate hydrogen bonding to and protein derived dipoles nearby the Cu-S(Cys) bond. Density functional theory (DFT) calculations correlated to the experimental data allow for the fractionation of the contributions to tuning E⁰ into covalent and non-local electrostatic components. These are found to be significant, comparable in magnitude, and additive for active H-bonds, while passive H-bonds are mostly non-local electrostatic in nature. For dipoles, these terms can be additive to or oppose one another. This study provides a methodology for uncoupling covalency from non-local electrostatics, which, when coupled to X-ray crystallographic data, distinguishes specific local interactions from more long range protein/active interactions, while affording further insight into the second sphere mechanisms available to the protein to tune the E⁰ of electron transfer sites in biology.

1. Introduction

Blue copper (BC), or type one (T1) copper proteins¹ mediate long-range, rapid, and directional electron transfer (ET) in a variety of biological functions.^2–5 The geometric structure of this active site consists of a conserved equatorial trigonal ligand field (LF) made up of a very short Cu-S(Cys) bond and two Cu-N(His) bonds.^6–8 There are two axial ligand positions. The syn (to the C_β-S(Cys) bond) position can be occupied by S(Met) (e.g., plastocyanin (Pc)⁸ and azurin (Az)⁹), O(Gln) (e.g., stellacyanin (St)¹⁰), or nothing (Ile/Phe) (e.g., fungal laccases^11,12). The trans-axial position can be occupied by a carbonyl group provided by the protein backbone (as in Az), which does not covalently bond to Cu but does contribute electrostatically,¹³ or nothing (e.g., Pc and fungal laccases).

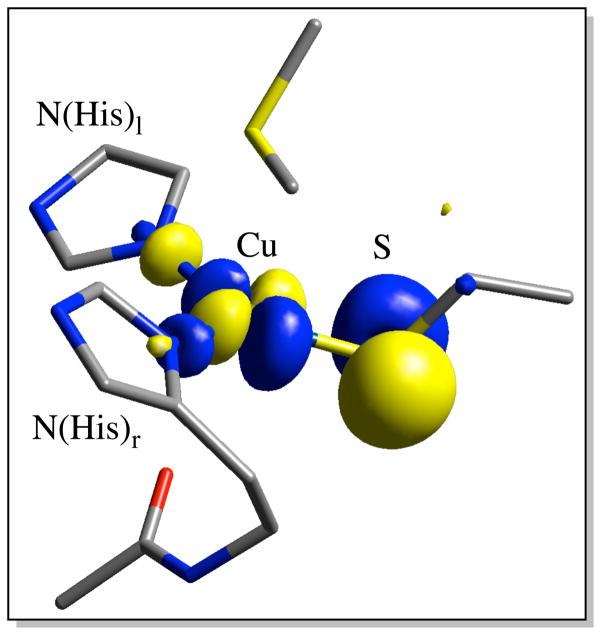
The BC proteins have been studied intensely due to their unique spectral features.^14–16 For the classical BC proteins these consist of an intense S(Cys) → Cu²⁺ ligand-to-metal charge transfer (LMCT) transition at ~600 nm (ε ~ 5000 M⁻¹cm⁻¹),¹⁷ which imparts the characteristic blue color, and a small parallel ^63,65 Cu hyperfine coupling (A_||).^18,19 These unique spectral features reflect the high anisotropic covalency of the T1 site due to the strong π overlap between the Cu(3d_x²−y²) orbital and the out-of-Cu-S-C_β-plane S(3p) orbital. This forms the redox active molecular orbital (RAMO), which is strongly delocalized over both the Cu and the S(thiolate) ligand (Figure 1).

Figure 1.

β-LUMO of the T1 site. Atom coloring: Cu (labeled with text), S(yellow), N (blue), O (red), and C (gray).

For their ET function, a key property of the BC proteins is their reduction potential (E⁰). It has been demonstrated previously that, within the first coordination sphere of the T1 site, the trans-axial ligand plays a major role in tuning E⁰.^20–23 Through analyses of site-directed axial ligand mutants of the T1 site, it was found that E⁰ had a positive linear correlation with the hydrophobicity of the axial ligand.^20,21 Also, through the analyses of the temperature dependence of the absorption and resonance Raman (rR) spectra of the native T1 site in green nitrite reductase (NiR) combined with DFT calculations, it was determined that the S(Met) thioether ligand can tune E⁰ down by ~200 mV due to a stronger interaction energy with the oxidized than the reduced state.²³ The constraint of the Cu-S(Met) distance during redox cycling represents the entatic/rack nature^24–26 of the T1 active site.²³ In addition to the influence of the axial ligand, T1 sites with identical active site ligation can have a wide range of reduction potentials (>400 mV).^15,27 As with other ET proteins, the outer sphere environment is a significant determinant of E⁰ as well, capable of tuning it over this large potential range.

A variety of experimental and computational studies have focused on elucidating the role of outer sphere protein/solvent (defined here as H₂O) interactions with the active site on the E⁰ of BC proteins.^27–34 Parallel studies have also been performed on other redox proteins.^35–40 While the growing body of data has led to the development of concepts for understanding outer sphere mechanisms available to ET proteins to tune E⁰, this is still a difficult endeavor, mostly due to the complexity involved in distinguishing between contributions that can potentially compensate. At least for BC proteins, the mechanism of outer sphere tuning of E⁰ has been considered largely electrostatic in origin, with less focus on contributions from the effects on the covalency of the sulfur-metal bond (defined here as the amount of S(ligand) character present in the redox active metal 3d_x²−y² of the BC site in Figure 1). Experiment^27,41–45 and DFT calculations²⁸ have indicated that H-bonding to the S(Cys) ligand increases E⁰. Likewise, by means of DFT calculations²⁸ and site-directed mutagenesis,^27,46–48 negatively oriented dipoles have been shown to decrease the potential of the T1 site. The effects of hydrophobicity of the axial position on E⁰ have also been extended to the outer sphere environment.³² However, it is important to note that these factors (H-bonds, dipoles, and hydrophobicity) can change the covalency of the ligand-metal bond as well as make electrostatic contributions that do not impact the ligand-metal covalency. Furthermore, H-bonds and protein dipoles have orientations that can have differential effects on the covalency and electrostatics. Thus, to understand outer sphere protein contributions to tuning E⁰, it is important to uncouple and separately estimate the electrostatic contributions and the effects of the protein environment on the covalency of the active site. It is also important to further understand how these are affected by specific H-bond and dipole orientations. This is the focus of the present study.

Recent experimental and computational studies on FeS proteins have been directed toward estimating the covalent contribution^39,49 to E⁰ as well as uncoupling the role of solvent accessibility to the active site.^38,50 Differences in ligand-metal covalency were found to be major contributors to the differences in E⁰. A few computational studies related to understanding the role of the outer sphere environment in BC and FeS proteins have allowed for the protein and solvent to polarize the solute,^30,37,51 which is akin to changes in ligand-metal covalency; however, the contributions from electrostatics and ligand-metal covalency were not uncoupled. The decomposition of covalent and electrostatic contributions thus represents a significant goal in understanding the influence of the outer sphere environment on the E⁰ of ET sites in biology, and, more broadly, for the rational design of redox active components in catalytic architectures.

In the present study, we have used a variety of spectroscopic methods and DFT calculations correlated to experiment in order to investigate the BC sites of the second sphere variants of Az in Table 1. Systematic variations in E⁰ by ~225 mV at the same pH have been measured for this series of second sphere variants,²⁷ which maintain identical first coordination sphere ligand sets. The three variants modulate E⁰ by: (1) F114P Az eliminates an H-bond to the S(Cys) of the BC site;⁴¹ (2) N47S Az deletes a carbonyl dipole that is at a distance of ~3.5 Å for the S(Cys) ligand;²⁷ and (3) F114N Az inserts a carbonyl dipole ~5.0 Å from Cu²⁷ (Figure 2). These studies allow the effect of the environment on E⁰ to be uncoupled by determining that these changes in the environment around the BC center both change the covalency of the Cu-S(Cys) bond as well as make non-local electrostatic contributions (defined here as having no associated change in covalency) to E⁰. The covalent component is obtained directly from experiment (S K-edge X-ray absorption spectroscopy (XAS)) allowing for the independent evaluation of the two contributions. They further have different orientation dependencies for H-bonds and carbonyl dipoles. The experimental quantification and fractionation of these terms provides insight into how the second sphere of the protein tunes the E⁰ of T1 copper proteins and, in general, ET sites in biology.

Table 1.

E⁰ for WT Az and the variants at pH 7.

Protein	E0 (mV)a
WT Az	265 ± 19
F114P Az	171 ± 7
N47S Az	396 ± 26
F114N Az	394 ± 4

^aReference 27.

Figure 2.

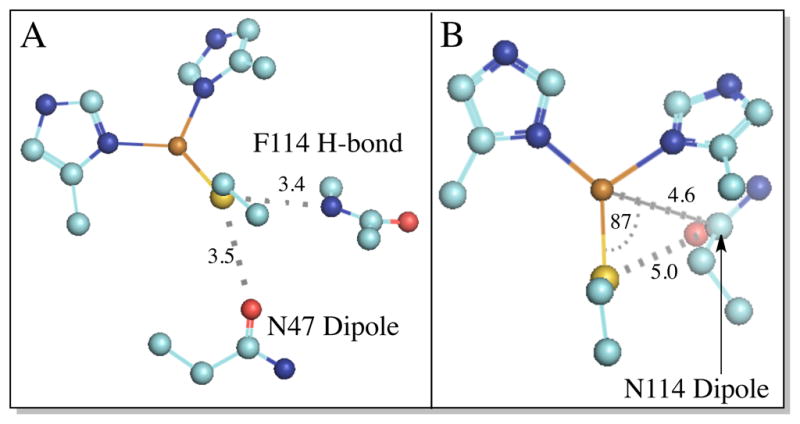
Position of second sphere residue/Cu-S(Cys) interactions. (A) F114 H-bond and N47 dipole; and (B) the N114 dipole (distances are measured to the C atom of the carbonyl group. The angle is measured between S(Cys)-Cu-C(O)). For clarity, the axial S(Met) ligand is not shown. Atom coloring: Cu (brown), S(yellow), N (blue), O (red), and C (teal).

2. Materials and Methods

2.1 Protein Expression and Purification

Expression and purification of WT Pseudomnas aeruginosa azurin (Az) and the variants studied here were performed using previously published protocols.^27,52,53

2.2 Electronic Absorption and Magnetic Circular Dichroism Spectroscopy

Low temperature absorption spectroscopy was performed using a Cary 500 double beam spectrophotometer modified with a Janis Research Super Vari-Temp liquid helium cryostat mounted in the optical path. Low temperature magnetic circular dichroism (MCD) experiments were conducted using two Jasco spectropolarimeters. Each is equipped with a modified sample compartment to accommodate focusing optics and an Oxford Instruments SM4000-7T superconducting magnet/cryostat. This arrangement allows data collection at temperatures from 1.6 to 290 K and fields up to 7 T. A Jasco J810 spectropolarimeter operating with an S-20 photomultiplier tube was used to access the visible and ultraviolet spectral region. A Jasco J730 spectropolarimeter operating with a cooled InSb detector was used for the near-infrared region. MCD samples (50/50 v/v buffer/glycerol mixture) were made in cells fitted with quartz disks and a 0.2 cm rubber gasket spacer. Simultaneous Gaussian fitting of the absorption, and MCD spectra was performed with the Peak-Fit program (Jandel).

2.3 EPR Spectroscopy

X-band electron paramagnetic resonance (EPR) spectra were obtained using a Bruker EMX spectrometer. X-band spectra were obtained at 77 K in a liquid nitrogen finger dewar using an ER 041 XG microwave bridge and an ER 4102ST cavity (parameters for recording the X-band EPR data: 9.39 GHz frequency and 10 G modulation amplitude). Protein concentrations for the EPR spectra were ~1 mM. X-band data were simulated using the XSophe program.

2.4 Resonance Raman Spectroscopy

Resonance Raman (rR) spectra were obtained in an ~135° backscattering configuration with an incident power of ~20 mW using either a Coherent I90C-K Kr⁺ CW ion laser (for WT, N47S, and F114N Az protein samples a the 647.1 nm laser line was used as the excitation source) or a dye laser (Rhodamine 6G, Coherent 599) pumped by a Coherent Innova Sabre 25/7 Ar⁺ CW ion laser (for the F114P Az protein sample a 600.0 nm laser line was used as the excitation source). Scattered light was dispersed through a triple monochromator (Spex 1877 CP, with 1200, 1800, and 2400 groove/mm gratings) and detected with an Andor Newton charge-coupled device (CCD) detector cooled to −80 °C. Samples were contained in NMR tubes immersed in a liquid nitrogen finger dewar. Background spectra were obtained using charcoal at 77 K in an NMR tube. Raman energies were calibrated using Na₂SO₄ and citric acid. Frequencies are accurate to within 2 cm⁻¹.

2.5 S K-edge X-ray Absorption Spectroscopy

S K-edge spectra were measured at the Stanford Synchrotron Radiation Lightsource (SSRL) using the 54-pole wiggler beam line 4-3. Details of the optimization of this beam line for low-energy fluorescence measurements and the experimental setup have been described previously.⁵⁴ S K-edge measurements were performed at ~4 °C. Protein samples were pre-equilibrated in a water-saturated He atmosphere for ~0.5–1 h to minimize bubble formation in the sample cell. Protein solutions were loaded via syringe into a Pt-coated Al block sample holder with a 6.35 μm thick polypropylene window. Prior to beam exposure, all protein samples were fully oxidized using 10-fold excess K₃FeCN₆ ⁵⁵ and were monitored for potential effects of photoreduction throughout the course of data collection. 3–5 scan averages were obtained with no indication of photoreduction. The energy was calibrated from S K-edge spectra of Na₂S₂O₃·5H₂O (first pre-edge feature at 2472.02 eV), run at intervals between sample scans. Data normalization was performed as described in earlier publications.⁵⁶ All samples were spin quantified by EPR using a copper standard to determine the active site loading. The area under the pre-edge peak was quantified by fitting the data using EDG_FIT.⁵⁷ The pre-edge and rising-edge features were modeled with pseudo-Voigt line-shapes with a fixed 1:1 Lorentzian/Gaussian ratio. Normalization procedures introduce ~3% error in the value of the integrated area under the pre-edge peak. The fitted intensities were converted to % S(3p) character using the pre-edge feature of plastocyanin (Pc) as a reference (where 1.02 units of intensity, obtained using EDG_FIT, corresponded to 38% S(3p) character).

2.6 Density Functional Theory Calculations

All calculations were carried out using the Gaussian 09 program.⁵⁸ Properties calculations (i.e., population analyses and ionization energy (IE) calculations) were carried out using solvent corrections (PCM, ε = 4.0).⁵⁹ All IEs are adiabatic (i.e., difference in energy between optimized oxidized and reduced states). All molecular orbital compositions were determined using the QMForge program⁶⁰ (c² and Mulliken population analyses), and all orbital surfaces were generated using the β-LUMO program.⁶¹ Gas phase TDDFT calculations were visualized using the SWizard program revision 4.6^62,63 using Gaussian band-shapes with half-widths of 2500 cm⁻¹. Several different structural models were utilized in the different Results and Analysis Sections.

For Section 3.2.1, all calculations were carried out using the B3LYP⁶⁴ exchange correlation functional (spin unrestricted) with a split-valence basis set (Cu (triple-ζ TZVP⁶⁵) S (6-311G(d)) and all other atoms (6-31G(d)^66–68). Both large and a small models of WT Az have been partially geometry optimized. (L-WT and S-WT, respectively (see Supporting Information Figure S1 for L- and S-type structures.) The starting point for optimization of L-WT was derived from X-ray crystallographic coordinates (PDB ID: 1JZF⁵). Note that crystallographic resolutions are given in Tables 6 – 8). L-WT contains the second sphere protein backbone and side chain R-groups relevant for this study (i.e., F114 and N47; Figure 2). L-WT was partially geometry optimized with protein backbone and R-group constraints (i.e., α- and β-carbons, amide N’s, carbonyl O’s, and terminal methyl C’s). S-WT is a truncated version of L-WT and contains only the side chain R-groups and an ethyl thiolate (S(Et)), which has been used in place of the full S(Cys) of L-WT. The amide H-bonds to the S(Et) ligand in S-WT are modeled with H-F molecules. Note that H-F was chosen due to the similarity of its dipole moment with that of the H-N unit of the amide backbone (e.g., the dipole moment of acetamide is 3.44 D (solvent is benzene), with estimated bond moments for the C=O, N-H, C-N, and C-CH₃ units of 2.4, 0.4, 1.3, and 0.4 D, respectively).⁶⁹ Partial geometry optimization of S-WT involved constraining the α- and β-carbons and the second sphere R-groups in their X-ray crystallographic positions. The S-WT model allows for the systematic perturbation of side chain residues and H-bonds to the S(thiolate) ligand and facilitates further correlation to spectroscopic data with TDDFT and frequency calculations.

Table 6.

Comparison of L- and S-WT bond distances, covalencies, and IEs.

	L-WT	S-WT	1JZF (1.5 Å)	L-WT	S-WT	1JZG (1.4 Å)
	oxidized			reduced
Cu-S(Cys)	2.197	2.205	2.21	2.281	2.288	2.23
Cu-S(Met)	3.317	3.317	3.32	3.317	3.317	3.31
Cu-N(His)l	2.022	2.009	2.08	2.099	2.114	2.12
Cu-N(His)r	2.066	2.038	2.02	2.173	2.130	2.06
S(Cys)-Xla	3.526	3.439	3.44	3.502	3.439	3.44
S(Cys)-Xr	3.585	3.569	3.57	3.473	3.569	3.53
S(Cys)-O(CO(1))	3.576	3.431	3.48	3.459	3.414	3.52
Cu-O(CO(2))	2.548	2.597	2.60	2.554	2.597	2.67
Cu-C(CO(3))	--	--	--	--	--	--
Cudb	38.3	42.0	IE (eV)	4.31	4.15
Spb	32.5	28.7	ΔIE (eV)	--	--
Cudc	43.7	46.9
Spc	39.2	34.0

^aX = N for large models and F for small models.

^bCSPA population analysis.

^cMulliken population analysis.

Table 8.

Comparison of L- and S-N47S and L- and S-F114N bond distances, covalencies, and IEs.

	L-N47S	S-N47S	L-F114N	S-F114N	L-N47S	S-N47S	L-F114N	S-F114N	3JTB (1.8 Å)
	oxidized				reduced
Cu-S(Cys)	2.207	2.217	2.199	2.214	2.301	2.308	2.281	2.297	2.20
Cu-S(Met)	3.317	3.317	3.317	3.317	3.317	3.317	3.317	3.317	3.19
Cu-N(His)l	2.019	2.002	2.026	2.017	2.098	2.113	2.113	2.132	2.26
Cu-N(His)r	2.057	2.047	2.063	2.038	2.156	2.150	2.158	2.115	2.09
S(Cys)-Xla	3.548	3.439	3.529	3.439	3.493	3.439	3.498	3.439	3.49
S(Cys)-Xr	3.533	3.569	3.580	3.569	3.423	3.569	3.480	3.569	3.56
S(Cys)-O(H)(CO(1))	--	--	3.574	3.430	--	--	3.465	3.407	4.13
Cu-O(CO(2))	2.578	2.597	2.549	2.597	2.558	2.597	2.549	2.597	2.82
Cu-C(CO(3))	--	--	4.586	4.672	--	--	4.586	4.650	4.88
Cudb	40.0	44.6	38.4	41.2	4.58	4.47	4.35	4.18	IE (eV)
Spb	29.5	25.6	32.4	30.3	0.27	0.32	0.04	0.03	ΔIE (eV)
Cudc	46.1	49.9	43.8	45.8	−3.0	−3.1	−0.1	1.6	ΔSpb
Spc	35.7	30.2	39.0	35.6	−3.5	−3.8	−0.2	1.6	ΔSpc

^aX = N for large models and F for small models.

^bCSPA population analysis.

^cMulliken population analysis.

Analogous to L-WT, a large model for partial geometry optimization of the F114P Az variant (L-F114P) was created from the X-ray crystallographic coordinates of the oxidized form (PDB ID: 2GHZ⁴¹). The small F114P Az model (S-F114P) was constructed by simply removing one H-F molecule from S-WT followed by a partial reoptimization of the structure with identical constraints.

X-ray crystal structures do not exist for the N47S and F114N Az single mutants; however, an N47S/F114N Az double mutant X-ray crystal structure does exist (PDB ID: 3JTB²⁷). The large model for N47S Az (L-N47S) was obtained by removing the N47 residue from L-WT and re-optimizing the structure, while the large F114N Az model (L-F114N) was created by replacing the F114 R-group with N114 using the N114 X-ray crystallographic coordinates from the N47S/F114N Az double mutant. It should be noted that in an overlay of the WT Az and N47S/F114N Az X-ray crystal structures the F114 and N114 R-groups are nearly congruent; however, the orientation of the Asn carbonyl dipole cannot be determined from X-ray crystallography. Investigation of the H-bonding partners surrounding the R-group as well as partial geometry optimization of an extended F114N Az model, which contained all potential H-bonding donors and acceptors in the vicinity of the N114 residue, resulted in a preferred orientation (by ~3 kcal/mol). This orientation has the positive side of the dipole closest to Cu (see Supporting Information Figure S2). The small N47S Az model (S-N47S) was constructed by deletion of the N47 R-group from S-WT followed by re-optimizing the structure. The small F114N Az model (S-F114N) was created by replacing the Phe114 ring of S-WT with Asn114 in a manner identical to L-F114N.

For Section 3.2.2, all calculations were carried out using the B(38HF)P86^64,70–72 functional (spin unrestricted) with the same split-valence basis set as in Section 3.2.1. For all calculations the T1 geometry is Cu^(2+/+)(S(Et))(S(Me)₂)(N(Im))₂ (where Et = ethyl, Me = methyl, and Im = imidazole). H-bond donors are modeled using an H-F molecule, analogous to the small models discussed above. Geometries are partially re-optimized at each H-bond distance and orientation in both oxidized and reduced states.

For Section 3.2.3, all calculations were carried out in an identical manner to Section 3.2.2; however, due to the large number of calculations geometries were not reoptimized at each dipole distance and orientation. Dipoles are modeled using two equal and oppositely charged point charges (0.66 and −0.66 in the Gaussian 09 program) at a distance of 1.5 Å from one another, which corresponds to a dipole moment similar in magnitude to that of a carbonyl group in the amide unit (calculated at the same level of theory).

3. Results and Analysis

3.1 Spectroscopic

3.1.1 Electronic absorption and magnetic circular dichroism

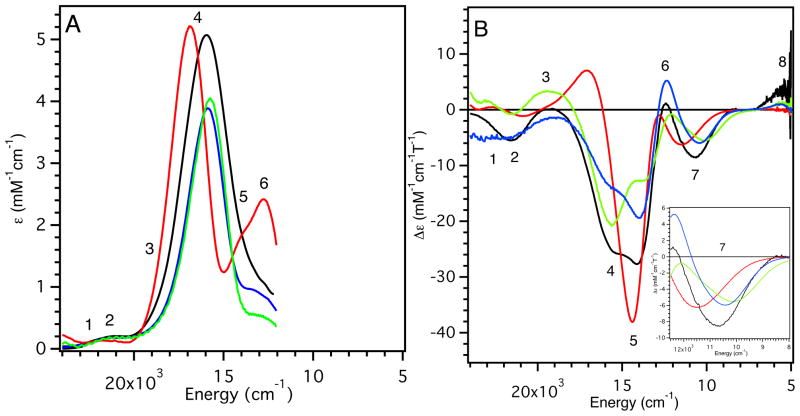
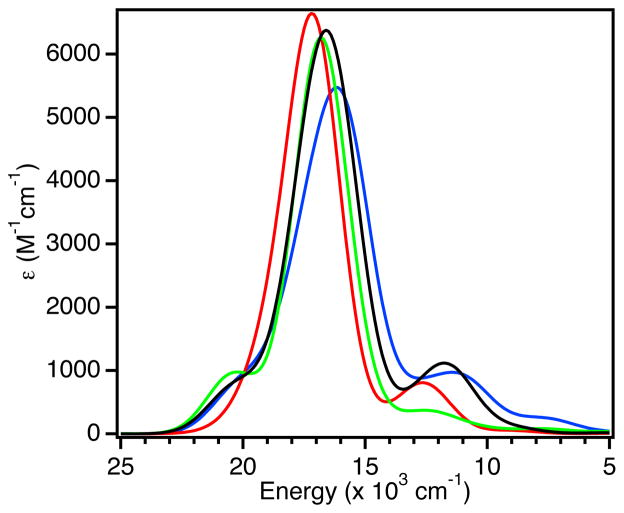
The low-temperature (LT) electronic absorption and MCD spectra of WT, F114P, N47S, and F114N Az are presented in Figure 3 (5000 – 24,000 cm⁻¹ region). Full Gaussian resolutions obtained from simultaneous fits of the absorption and MCD spectra are included in Supporting Information Figure S3 and are summarized in Table 2. For consistency, we adopt the numbering scheme for electronic excited states developed for Pc,¹⁷ which is given in the Gaussian resolutions in Supporting Information Figure S3 and included in Figure 3.

Figure 3.

(A) LT (5 K) electronic absorption and (B) MCD (5 K, 5 T) spectra of WT Az (black line), F114P Az (red line), N47S Az (green line) and F114N Az (blue line). Inset: expanded portion of the MCD spectra in the energy region of band 7.

Table 2.

Experimental electronic absorption and MCD parameters.

Band	assignments in PLC	Wave number				ε (M−1 cm−1)				Δε (M−1 cm−1T−1)				Co/Do
		WT	F114N	F114P	N47S	WT	F114N	F114P	N47S	WT	F114N	F114P	N47S	WT	F114N	F114P	N47S
8	dz2	5430	5750		5500					+3.5	+0.9		+1.1	+	+		+
7	dxy	10700	10600	11800	10200					−8.8	−6.4	−6.7	−6.1	−	−	−	−
6	dxz+yz	12600	12500	13000	12500	730	750	2150	450	+16.9	+10.5	+10.0	+2.0	+0.25	+0.10	+0.03	+0.03
5	dxy−yz	13700	13800	14200	13500	740	650	1400	250	−23.3	−19.0	−39.6	−5.3	−0.34	−0.22	−0.21	−0.16
4	Cys π	15900	15800	16800	15700	5070	3900	5225	4050	−19.2	−12.8	+7.1	−21.1	−0.04	−0.02	+0.01	−0.04
3	Cys σ	18100	17400	20900	16900	510	830	880	1150	+2.9	−1.5	+1.7	−2.7	+0.06	−0.01	+0.01	−0.02
2	His π	20100	19300	22200	18600	160	210	125	350	−0.8	−0.9	−1.2	+2.8	−0.05	−0.03	−0.07	+0.06
1	Met	21900	21200	24600	21200	170	150	125	250	−1.0		+0.5	−1.9	−0.06		+0.03	−0.06

The electronic spectral data can be divided into two regions: LF transitions and ligand-to-metal charge transfer (LMCT) transitions. The nature of the transition was identified by its |C_o/D_o| ratio (i.e., MCD relative to absorption intensity) (Table 2). The ratios were calculated using:⁷³

$$\frac{C_0}{D_0}=\frac{k\text{T}}{{\mu }_B\text{B}}{(\frac{\mathrm{\Delta }\epsilon }{\epsilon })}_{max}$$ eqn 1

where T is the temperature, B is the external magnetic field strength, k is Boltzmann’s constant, μ_B is the Bohr magneton, ε is the absorption maximum in M⁻¹ cm⁻¹, and Δε is the MCD intensity maximum, also measured in M⁻¹ cm⁻¹. k/μ_B is ~1.489 T K^−1.74 For BC sites, the magnitude of the C-term dominantly derives from spin-orbit coupling, which reflects metal d-character and results in intense LF transitions in MCD relative to their respective absorption intensities at the same temperature.¹⁷ This relationship allows the transitions observed in the low energy region (~5000 – 13,000 cm⁻¹) to be assigned as copper-centered LF transitions. They follow the energy order (from assignments for Pc¹⁷): 3d_z² → 3d_x²−y² (band 8) < 3d_xy → 3d_x²−y² (band 7) < 3d_xz+yz → 3d_x²−y² (band 6) < 3d_xz−yz → 3d_x²−y² (band 5). LMCT transitions are at higher energy and assigned as the S(Cys)π (band 4), S(Cys)σ (band 3), N(His) (band 2) and the S(Met) → Cu(3d_x²−y²) (band 1) CT.

Upon removal of an H-bond from the S(Cys) ligand (F114P Az, Figure 3, red lines) the S(Cys)π → Cu(3d_x²−y²) CT band (band 4) is blue-shifted by ~900 cm⁻¹ and the ε increases. Associated with the increase in ε of band 4 there is an increase in the ε of bands 5 and 6 (the 3d_xz,yz combination of LF transitions, which mix with the S(Cys)π → Cu(3d_x²−y²) CT band). From the MCD data, the energy of the 3d_xy → 3d_x²−y² LF transition (band 7) increases by ~900 cm⁻¹ (Figure 3B, Inset). For N47S Az, removing the negatively oriented dipole from within vicinity of the S(Cys) ligand also perturbs the excited state spectral data (green lines). Band 4 shows a small red-shift (~200 cm⁻¹) and a decrease in ε, while bands 5 and 6 also have a decreased ε. Band 7 decreases in energy by ~500 cm⁻¹. For F114N Az (blue lines), the electronic absorption spectrum is almost identical to WT Az, but with a decrease in the ε of band 4 and the LF transitions with which it mixes (bands 5 and 6). The energy of band 7 does not change.

Thus, the major changes observed in Figure 3 associated with the variants are: (1) shifts in energy of the d_xy LF transition, which will be used in the EPR analysis in the next Section, and (2) variations in the energy and intensity of the S(Cys)π → Cu(3d_x²−y²) CT band (band 4) and its intensity mixing into the lower energy LF transitions. Generally, the energy and intensity of band 4 reflect the anti-bonding interaction of the Cu(3d_x²−y²)-based β-LUMO with the S(Cys)π donor orbital: the stronger the interaction, the higher the energy and intensity of this band. Therefore, removing an H-bond to the S(Cys) ligand in F114P Az increases its anti-bonding interaction with the β-LUMO, as the energy and intensity of the S(Cys)π → Cu(3d_x²−y²) CT band (band 4) increases. Conversely, removing the negatively oriented dipole near the S(Cys) in N47S Az decreases the anti-bonding character of the β-LUMO, as the energy and intensity of the (Cys)π → Cu(3d_x²−y²) CT band (band 4) decreases. However, in F114N Az, where a dipole is added near copper, there is a decrease in intensity of band 4 with no change in energy. As shown in Section 3.2.1, this effect reflects a dominant interaction of the dipole with the S(Cys)π donor rather than the acceptor β-LUMO in the CT process. Note also that residue 114 is farther from the BC center (~5 Å from Cu) than residue 47 (~3.5 Å from S) and is solvent exposed, which would lessen its effect.

3.1.2 Electron paramagnetic resonance

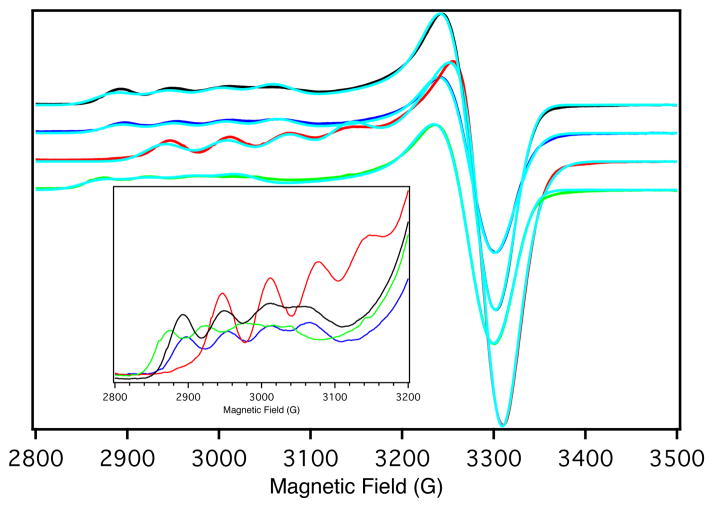
The X-band EPR spectra and their simulations for WT Az and the variants are shown in Figure 4. The resulting spin Hamiltonian parameters are summarized in Table 3. The observation of g_|| > g_⊥ > 2.0023 indicates that the unpaired electron is in the Cu(3d_x²−y²) orbital. Relative to WT Az, the g_⊥ and A_⊥ (g_x,y and A_x,y) of the variants show only small deviations; however, both g_|| and A_|| (g_z and A_z) do exhibit changes. For F114P Az g_|| decreases from 2.262 to 2.211 and the magnitude of A_|| increases from 59 × 10⁻⁴ cm⁻¹ to 68 × 10⁻⁴ cm⁻¹. The opposite behavior is observed for the N47S Az variant. Here, g_|| increases from 2.262 to 2.283, and the magnitude of A_|| decreases from 59 × 10⁻⁴ cm⁻¹ to 51 × 10⁻⁴ cm⁻¹. The spin Hamiltonian parameters of F114N Az are very similar to those of WT Az.

Figure 4.

77 K X-band EPR spectra of WT Az (black line), F114P Az (red line), N47S Az (green line) and F114N Az (blue line) and simulated data (turquoise). Inset: expanded g_|| region.

Table 3.

Spin Hamiltonian parameters from simulations of the X-band EPR spectra.

	WT Az	F114P Az	N47S Az	F114N Az
gx	2.042	2.044	2.040	2.042
gy	2.056	2.046	2.061	2.055
gz	2.262	2.211	2.283	2.258
Axa	11	6	10	11
Aya	11	13	11	11
Aza	59	68	51	58

^a(x 10⁻⁴ cm⁻¹)

The deviation of the g-value from that of the free electron (2.0023) for a Cu(3d_x²−y²) ground state reflects the amount of copper character in the ground state and the LF excited state energies. Ignoring ligand contributions, the deviation of the g_||-value from 2.0023 is given by:

$$g_{\left|\right|}=2.0023-\frac{8\lambda {\alpha }^2{\beta }^2}{E_{xy}}$$ eqn 2

where λ(Cu²⁺) = −830 cm⁻¹, β and α are the metal 3d_x²−y² and 3d_xy orbital coefficients in the LF wave functions, and E_xy is the LF excited state energy. With the assumption that the covalencies of the ground state wave functions for WT Az and the variants are similar (i.e., no change in copper character), the deviation of the g_||-value can be related to the energy of the E_xy LF excited state obtained from MCD data (band 7).

$$\mathrm{\Delta }{g}_{\left|\right|}(\mathit{Variant})=\frac{E_{xy}(WT)}{E_{xy}(\mathit{Variant})}\mathrm{\Delta }{g}_{\left|\right|}(WT)$$ eqn 3

Using the energies of band 7 for E_xy’s (from Section 3.1.1) and the g_|| value of WT Az, eqn 3 predicts a Δg_|| for F114P and N47S Az of 0.238 and 0.275, respectively. These predicted values deviate from the experimental Δg_|| for F114P and N47S Az of 0.211 and 0.283, respectively. Thus, eqn 3 overestimates the magnitude of Δg_|| for F114P Az while it underestimates the magnitude of Δg_|| for N47S Az. This discrepancy requires that the covalency of the ground state wave function increase for F114P Az and decrease for N47S Az. The g_||-value of F114N Az is identical to that of WT Az, indicating that there is little change in copper character between the two.

The copper hyperfine coupling is given by:

$$A_{\left|\right|}=P_d((-\kappa -4/7){\alpha }^2+3/7(g_{\perp }-2.00)+(g_{\left|\right|}-2.00))$$ eqn 4

where P_d = 396×10⁻⁴ cm⁻¹, κ is the Fermi contact term, and α² is the percent metal character in the 3d_x²−y² orbital. Eqn 4 and the experimental changes in g-values allow the hyperfine coupling constants for the variants to be predicted relative to WT Az assuming no change in covalency. For F114P Az, the decrease in experimental g_||-value accounts for a change in A_|| from 59 × 10⁻⁴ cm⁻¹ in WT Az to 78 × 10⁻⁴ cm⁻¹. (Note that A_|| is negative.) Experimentally, however, an A_|| of 68 × 10⁻⁴ cm⁻¹ is observed. For N47S Az, the increase in g_||-value accounts for the observed decrease in A_|| to 51 × 10⁻⁴ cm⁻¹. The A_|| of F114N Az is nearly identical to that of WT Az.

For F114P Az, only including the change in LF excited state energy, E_xy from MCD, overestimates the change in the g_||-value relative to WT Az. Also, the change in g value observed overestimates the change in A_||. For N47S Az, the change in LF excited state energy, E_xy, underestimates the change in the g_||-value relative to WT Az. These data support the analysis in Section 3.1.1 that, in F114P Az, removing an H-bond to the Cu²⁺-S(Cys) bond increases the covalency of the bond. Furthermore, in N47S Az, altering the electrostatic environment near the S(Cys) ligand upon removal of the amino acid side chain carbonyl dipole (negative side toward the S(Cys)) decreases the covalency of the Cu²⁺-S(Cys) bond. In F114N Az, the covalency of the Cu²⁺-S(Cys) bond does not change based on the aforementioned data.

3.1.3 Resonance Raman

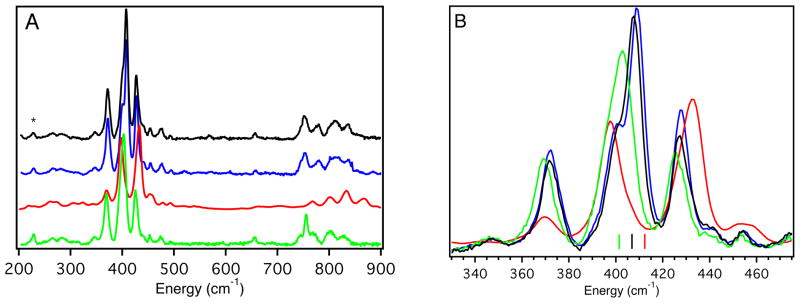
The rR spectra resulting from laser excitation into band 4, the intense S(Cys)π → Cu²⁺(3d_x²−y²) CT band, of WT Az and the variants are presented in Figure 5 (left, 200 – 900 cm⁻¹; right, 330 – 475 cm⁻¹ (normalized to peak M)). Consistent with rR data reported for other BC proteins,^75–86 the 325 – 475 cm⁻¹ region shows several resonance enhanced vibrational features, all of which contain some amount of Cu²⁺-S(Cys) stretching character. The intensity weighted average energy is generally used to determine the relative Cu²⁺-S(Cys) bond strength:⁸⁵

Figure 5.

(A) 77 K rR spectra of WT Az (black line, 647.1 nm), F114P Az (red line, 600.0 nm), N47S Az (green line, 647.1 nm) and F114N Az (blue line, 647.1 nm). (B) Expanded region containing Cu-S vibrations; lines mark the positions of intensity-weighted average, <ν_Cu-S>, of peaks L, M, N, O. <ν_Cu-S> is the same for WT and F114N Az.

$$<\nu \text{Cu}-\text{S}(\text{Cys})>={\sum }_i[(I_{01}^i){({\nu }_i)}^2]/{\sum }_i(I_{01}^i)({\nu }_i)$$ eqn 5

Table 4 summarizes the experimentally determined <νCu-S(Cys)> for WT Az and the variants. WT Az has a <νCu-S(Cys)> of 407 cm⁻¹, which increases to 413 cm⁻¹ for F114P Az, decreases to 402 cm⁻¹ for N47S Az, and does not change for F114N Az. The higher energy region of the rR spectra (700 – 900 cm⁻¹) contains overtones and combination bands of the vibrational features in the 325 – 475 cm⁻¹ region. The sharp feature located at ~756 cm⁻¹ for WT Az has been assigned to the C_β-S(Cys) stretch. The energy of this feature remains the same in F114N Az and shifts to ~753 cm⁻¹ in N47S Az. Resonance enhancement of the C_β-S(Cys) stretch is not observed for F114P Az. (The features at higher energy are too broad and located at energies that allow their assignment as overtone and combination bands). The lack of a resonance enhanced C_β-S(Cys) stretch likely results from the loss of near planarity of the Cu-S(Cys)-C_β-C_α dihedral angle for F114P Az (observed in the X-ray crystal structure, vide infra).

Table 4.

<νCu-S(Cys)> obtained from rR.

	WT Az	F114P Az	N47S Az	F114N Az
<νCu-S(Cys)>a	407	413	402	407

^a(cm⁻¹)

From the increase in the <νCu-S(Cys)>, removing an H-bond to the thiolate in the case of F114P Az increases the strength of the Cu²⁺-S(Cys) bond. Conversely, for N47S Az removing a negatively oriented carbonyl dipole near the S(Cys) decreases the Cu²⁺-S(Cys) bond strength. Replacing the phenyl with the amide dipole in the 114 position (F114N Az) does not perturb the Cu²⁺-S(Cys) bond strength.

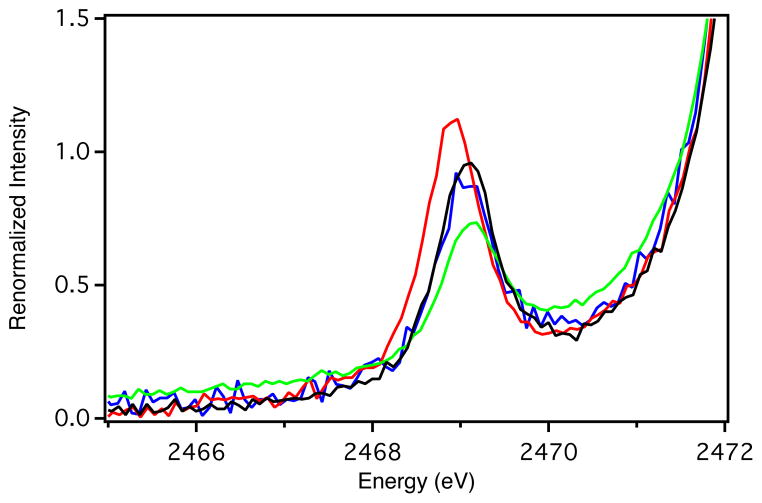
3.1.4 S-K pre-edge X-ray absorption

The S-K pre-edge XAS data are shown in Figure 6. Results from fits to the pre-edge feature are given in Table 5. The pre-edge arises from the excitation of a core S 1s electron on the S(Cys) ligand into the singly unoccupied Cu(3d_x²−y²) molecular orbital (SUMO or β–LUMO in the unrestricted formalism) (a S 1s → Cu(3d_x²−y²) transition). The intensity of this feature is proportional to the total S_p-character in the ground state wave function (β-LUMO). Relative to WT Az, the intensity of the pre-edge increases for F114P Az, decreases for N47S Az, and exhibits little change for F114N Az. Using Pc as a reference (38 ± 3 % S_p-character), the intensity of the S-K pre-edge feature at ~2469 eV amounts to 45 ± 3 % S_p-character in the ground state wave function of WT Az. The intensity increase of the pre-edge feature for F114P Az equates to an increase in S_p-character by ~9 % S_p. The decrease in pre-edge intensity for N47S Az equates to a decrease in S_p-character by ~14 %. F114N Az exhibits a pre-edge intensity very similar to WT Az.

Figure 6.

S-K pre-edge XAS data for WT Az (black line), F114P Az (red line), N47S Az (green line), and F114N Az (blue line) in the pre-edge region. In each case, the spectra have been renormalized to account for total Cu²⁺ loading in the T1 active site.

Table 5.

Results of S-K pre-edge fits.

Protein	pre-edge energy (eV)	Covalency (% Sp)
WT Az	2469.1	45 ± 3
F114P Az	2468.9	54 ± 3
N47S Az	2469.1	31 ± 3
F114N Az	2469.1	43 ± 3

In summary, from Sections 3.1.1 – 3.1.4 it is observed that removing an H-bond to the Cu-S(Cys) bond (F114P Az) increases the covalency (i.e., greater S_p-character) and the Cu-S(Cys) bond strength, while for N47S Az, removing the negatively oriented carbonyl dipole near the S(Cys) decreases the covalency and the bond strength. Interestingly, for F114N Az, the spectral features are essentially identical to WT Az, with the exception that the CT absorption intensity decreases. These spectral changes allow the evaluation of electronic structure calculations, which provide insight into the contributions of the second sphere residues to changes in covalency and electrostatics. How these each contribute to E⁰ is elucidated below.

3.2. Computational

3.2.1 Wild-type and perturbed protein sites: Calibrating calculations to spectroscopic data

As a starting point for calibrating electronic structure calculations to the spectroscopic data presented above, both L- and S-WT models have been partially geometry optimized. The relevant optimized geometric parameters are given in Table 6 and compared to an oxidized X-ray crystal structure of WT Az (PDB ID: 1JZF). The optimized Cu-ligand bond lengths of L- and S-WT are very similar to one another and consistent with experiment. These results are also in agreement with a partial geometry optimization previously reported for WT Az.⁸⁷

The partial geometry optimized structures of L- and S-F114P are given in Table 7. From crystallography, the F114P Az variant has a shorter Cu-S(Cys) bond than WT Az (2.21 to 2.15 Å, although the change is within the resolution of the crystallography). This change in bond length is reproduced by the partially optimized S- and L-F114P structures (2.197 to 2.176 Å (L-WT versus L-F114P) and 2.205 to 2.189 Å (S-WT versus S-F114P)). Besides changes in Cu-ligand bond lengths, the X-ray crystal structure of F114P Az shows a structural distortion of the S(Cys) ligand. When F114 is replaced with P114, three structural changes occur relative to WT Az: (1) the N_l-Cu-S(Cys) angle opens up from ~123° to ~139° (note the notation of N_l (or N_r) refers to the His ligand on the left (or right) side of Cu as viewed along the Cu-S(Cys) bond (see Figure 1)); (2) the N_r-Cu-S-C_β dihedral angle rotates from ~−83° to ~−128°; and (3) the Cu-S-C_β-C_α dihedral rotates from ~−174° to ~−146°. These structural changes are included in L-F114P as this model is derived from crystallography; however, constraints on the α- and β-carbons of the S(Et) ligand in the S-F114P model do not allow for the rotation of the Cu-S(Cys)-C_β-C_α dihedral angle to occur. This structural change is relevant for the interpretation of the TDDFT calculations (vide infra).

Table 7.

Comparison of L- and S-F114P bond distances, covalencies, and IEs.

	L-F114P	S-F114P	2GHZ (1.6 Å)	L-F114P	S-F114P	2GIO 1.7 Å
	oxidized			reduced
Cu-S(Cys)	2.176	2.189	2.15	2.266	2.282	2.25
Cu-S(Met)	2.847	3.317	2.92	2.847	3.317	2.71
Cu-N(His)l	2.000	2.020	1.98	2.066	2.121	2.02
Cu-N(His)r	2.043	2.045	2.08	2.116	2.125	2.09
S(Cys)-Xla	--	--	--	--	--	--
S(Cys)-Xr	3.313	3.569	3.20	3.211	3.569	3.29
S(Cys)-O(CO(1))	3.683	3.579	3.65	3.647	3.523	3.58
Cu-O(CO(2))	3.547	2.597	3.60	3.521	2.597	3.80
Cu-C(CO(3))	--	--	--	--	--	--
Cudb	34.9	40.0	IE (eV)	4.23	3.97
Spb	35.2	34.3	ΔIE (eV)	−0.08	−0.19
Cudc	40.0	44.4	ΔSpb	2.7	5.6
Spc	42.9	40.5	ΔSpc	3.7	6.5

^aX = N for large models and F for small models.

^bCSPA population analysis.

^cMulliken population analysis.

The partial geometry optimized structures of L- and S-N47S and L- and S-F114N are given Table 8. The DFT derived Cu-S(Cys/Et) bond lengths of these models are similar to WT Az, being slightly longer for the N47S Az models. This parallels the changes in Cu-ligand bond lengths between the WT Az and the N47S/F114N Az crystal structures (Table 8).

Frequency calculations were performed on the small models in order to correlate to the <νCu-S(Cys)> from rR spectroscopy. The calculated Cu-S(Et) stretching frequencies are given in Table 9. For S-WT, the calculated Cu-S(Et) frequency is 405 cm⁻¹. This value increases to 412 cm⁻¹ for S-F114P and decreases to 402 cm⁻¹ for S-N47S. The Cu-S(Et) frequency does not change for S-F114N. These calculated changes in Cu-S(Et) frequency are in agreement with the changes in <νCu-S(Cys)> observed from rR spectroscopy.

Table 9.

Calculated Cu-S(Et) stretching frequencies for the small models.

	WT Az	F114P Az	N47S Az	F114N Az
ν (Cu-S(Et)) (cm−1)	405	412	402	405

TDDFT calculations were carried out on the small models. The calculated absorption spectra are shown in Figure 7. These generally reproduce the trends observed in experiment (i.e., little change in the energy and a decreased calculated oscillator strength (f) of the S(Cys)π → Cu(3d_x²−y²) CT band for S-N47S and S-F114N, and a blue-shift and an increase in intensity of S(Cys)π → Cu(3d_x²−y²) CT for S-F114P). The decrease in ε of band 4 in the experimental absorption spectrum of the F114N Az variant derives from a change in the donor orbital in the CT process. While the acceptor β-LUMO is the same in both S-WT and S-F114N (see below), the donor orbital changes from 38 % S_p- and 6 % N(His)-character in S-WT to 33 % S_p- and 9 % N(His)-character in S-F114N. For F114P Az, the increased ε of bands 5 and 6 observed in experiment is not reproduced by the TDDFT calculation on S-F114P. As noted above, however, the thiolate ligand orientation to the T1 site is modified in this variant. Extension of the TDDFT calculations to include the rotation of the N_r-Cu-S-C_β dihedral angle does reproduce the increased intensity of the LF transitions (see Supporting Information Figures S5 and S6 and associated text).

Figure 7.

TDDFT calculated absorption spectra of small oxidized models S-WT (black line); S-F114P (red line); S-N47S (green line); and S-F114N (blue line).

The changes in the calculated S_p-character in the β-LUMO of both large and small models can be compared to the changes in S-K pre-edge intensity between WT Az and the variants. The S_p-characters determined from c² and Mulliken population analyses are given in Tables 6, 7, and 8. As observed for the preceding calculations, experimental trends are reproduced using both the large and small models. For L- and S-F114P, the calculated S_p-character increases relative to L- and S-WT (Table 7). A decrease in S_p-character is calculated for the L- and S-N47S models (Table 8). Both L- and S-F114N have very limited change in S_p-character relative to L- and S-WT models (Table 8).

In order to calculate the adiabatic IEs, the reduced geometries of the large and small models have been optimized in the same way as outlined above for the oxidized sites (Section 2.6). Relevant structural information is given in Tables 6, 7, and 8. For comparison to known structural data, only reduced X-ray crystal structures exist for WT Az and F114P Az; for both, the changes in Cu-ligand bond lengths between the oxidized and reduced X-ray crystal structures are within the resolution. Likewise, for all DFT partially geometry optimized models here only small changes in the Cu-S(Cys/Et) and Cu-N(His) bond lengths were observed (~0.1 Å increase upon reduction). The adiabatic IEs can be calculated by taking the difference in energy between the optimized oxidized and reduced structures (Tables 6, 7, and 8). These values can be compared to changes in E⁰ in Table 1. The IEs for the L- and S-WT models are calculated to be 4.31 and 4.15 eV, respectively. These values serve as reference points for the variant models. The calculated changes in IE for the L- and S-F114P models (relative to L- and S-WT) are −80 and −190 mV, respectively. The IEs of L- and S-N47S both increase by 270 and 320 mV, respectively. Similarly, more positive IEs were calculated for L- and S-F114N (40 and 30 mV, respectively). The calculated IEs for the variants relative to WT Az follow the same trends as the experimental changes in E⁰ (Table 1).

Throughout this Section, we have found that there is a good correlation between the calculated and observed spectroscopic data and for trends in E⁰. It is also interesting to note that, in the case of F114N Az, there are little spectral changes despite a change in E⁰ in both experiment and calculation. We proceed to systematically investigate the effects of H-bonding and carbonyl dipoles on the BC active site and evaluate their contributions to changes in E⁰.

3.2.2 Modeling hydrogen bonds

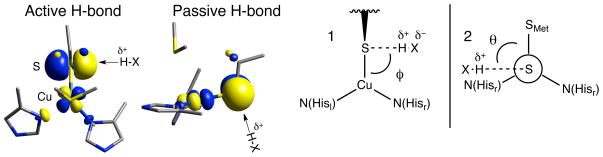
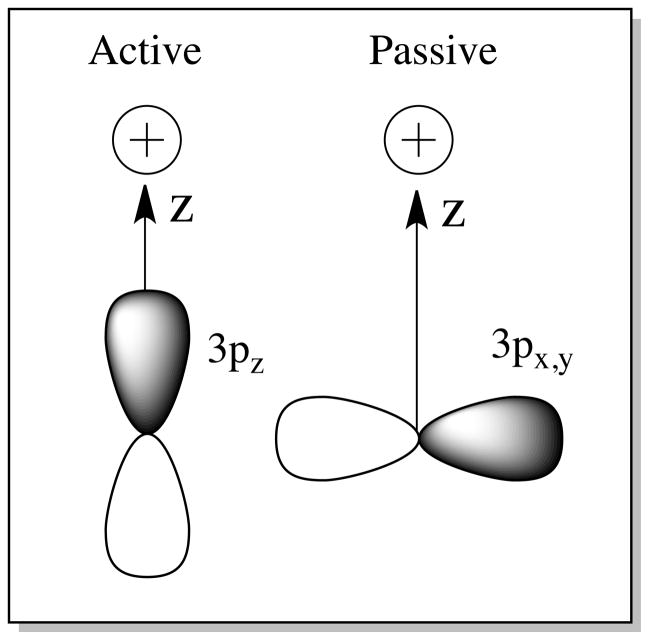
While H-bonding to the Cu-S bond in BC has been considered to some extent computationally,²⁸ it is first important to note that the ground state wave function of the T1 site is highly covalent and anisotropic along the thiolate(π)-Cu²⁺ bond (Figure 8, Left). The relative H-bonding interaction with the S(Et) is therefore dependent on the orientation of the H-bond donor to the β-LUMO. This orientation is characterized by two angles (Figure 8, Right): (1) the Cu-S(Et)-H(δ⁺) angle ϕ (where δ⁺ represents the partial positive charge of the H-bond donor), and (2) the S(Met)-Cu-S(Et)-H(δ⁺) dihedral angle θ. Two limits have been considered; these are termed active and passive H-bonding.⁸⁸ The active orientation for H-bonding is defined as having a Cu-S(Et)-H(δ⁺) angle of 90° and a S(Met)-Cu-S(Et)-H(δ⁺) dihedral angle of ~90° (i.e., the H(δ⁺)-X(δ⁻) unit is in the plane of the Cu-S π-bond). The passive orientation also has a Cu-S(Et)-H(δ⁺) angle of 90°, but the S(Met)-Cu-S(Et)-H(δ⁺) dihedral angle is rotated to 180° (i.e., perpendicular to the S π-bond). The calculated covalency and IE for the active and passive orientations as a function of H-bond (H-F as the H-bond donor) distance from the S of the Cu-S(Et) bond are given in Figure 9 and tabulated in Supporting Information Tables S1 – S3.

Figure 8.

(Left) Active and (Middle) passive orientations for H-bonding to the Cu-S(Cys) bond. (Right, 1) Cu-S(Cys)-H-bond angle and (Right, 2) S(Met)-Cu-S(Cys)-H-bond dihedral angle (Newman projection along Cu-S(Cys) bond).

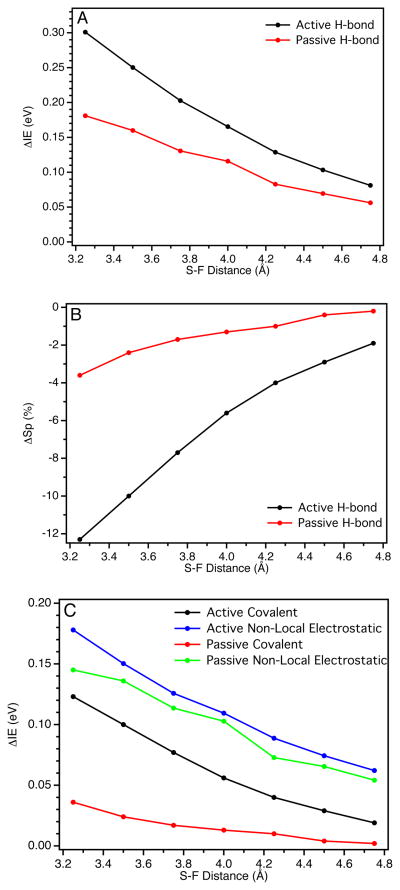
Figure 9.

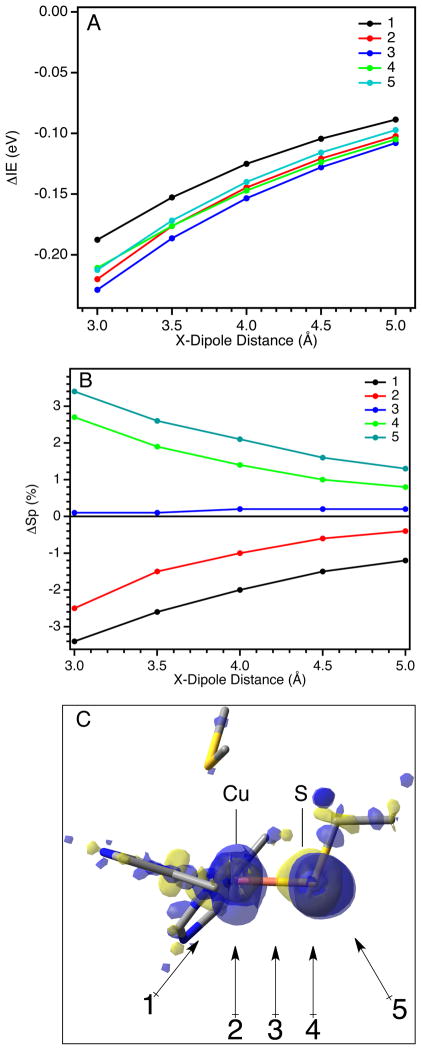
(A) Dependence on the calculated IE of the reduced model and (B) dependence on the calculated S_p-character in the β-LUMO of the oxidized model on the orientation (active versus passive) and distance of an H-bond from the Cu-S(Cys) bond; (C) covalent and non-local electrostatic components to the IE for both active and passive orientations.

For both active (black circles) and passive (red circles) orientations the calculated IE of the reduced site increases as the H-bond distance decreases (Figure 9A; relative to an H-bond at 10 Å). However, as the S^···F distance decreases, the IE increases more sharply for the active orientation than the passive. At 3.5 Å (similar to the crystallographic N-S distance for H-bonds to S(Cys) residues in BC proteins) the ΔΔIE between the active and passive orientations is ~90 mV.

The change in the calculated S_p-character in the β-LUMO as a function of H-bond distance is also orientation dependent (Figure 9B). A decrease in the H-bond distance leads to a significantly larger decrease in the S_p-character in the β-LUMO for the active H-bond orientation relative to the passive orientation. At 3.5 Å, this difference is 7.6 % S_p. Note that there is very little change in covalency for the passive H-bond orientation. We also note that the calculated difference in S_p-character between active and passive orientations (7.6 %) is not sensitive to PCM solvation (despite the Cu-S(Cys) bond itself being quite sensitive, see Supporting Information Table S9 and associated text),^36,89 consistent with the H-bonding interaction being mostly ionic in nature.^{38,88,90–93} Therefore, the difference in the calculated IE between the active and passive orientations can be ascribed to the difference in Cu-S(Et) covalency. Importantly, this allows the total change in the IE of the reduced site to be fractioned into an electrostatic component and a covalent component. The electrostatic component is referred to as non-local electrostatics. Thus, the relative contributions of the non-local electrostatic and covalent components to the IE can be quantified (Figure 9C; also given in Supporting Information Table S3). At 3.5 Å, the IE and S_p-character between active and passive orientations differ by 90 mV and 7.6 % S_p, respectively. An estimate of the covalent component is thus ~−12 mV/% S_p. The negative slope of this correlation indicates that, as the covalency of the Cu-S(Et) bond increases, the IE decreases and thus E⁰ decreases. For comparison, a Mulliken population analysis gives a ΔΔS_p of 9.7 % S_p, which results in a slope of ~−9 mV/% S_p. Therefore, this model predicts a slope for the covalent contribution to the IE of −10 ± 2 mV/% S_p. Importantly, from this analysis, an active H-bond to a S-Mⁿ⁺ bond in an ET protein will have both a non-local electrostatic and a covalent component to E⁰; these contributions to E⁰ are additive and comparable in magnitude.

3.2.3 Modeling carbonyl dipoles

In this Section we investigate the distance and orientation dependence (relative to the Cu-S(Et) bond) of carbonyl dipoles on the calculated IE and S_p-character. In particular, we evaluate the relative contribution of changes in covalency and non-local electrostatics to the IE.

Five dipole orientations relative to the Cu-S(Et) bond have been investigated (Figure 10C). The distance for each orientation is measured from the dipole to: (1) and (2) the Cu; (3) the mid-point of the Cu-S(Et) bond; and (4) and (5) the S (see Supporting Information Figure S4 for geometric parameters for each dipole orientation). The distance dependencies on the calculated ΔIE and ΔS_p-character for these dipole orientations are given in Figures 10A and 10B, respectively (ΔIE and ΔS_p are relative to the calculated value with a dipole at 10 Å). The results of these calculations are also summarized in Supporting Information Tables S4 – S8. For all orientations considered, when the dipole is brought closer to the T1 site on either the Cu or S side of the Cu-S(Et) bond with the negative side of the dipole oriented toward the bond, the calculated ΔIE decreases systematically (Figure 10A). This decrease in IE reflects the electrostatic destabilization of the electron in the RAMO, which lowers E⁰. The result obtained here is consistent with experiment (i.e., the N47S Az variant eliminates a dipole that is negatively oriented toward the S side of the Cu-S(Cys) bond and has a higher E⁰ than WT Az (Table 1)) and previous calculations.²⁸ The ΔIEs for orientations 1 – 5 at a distance of 3.5 Å are −153, −176, −186, −176, and −172 mV, respectively (Table 10). However, it is important to note that, as determined from the analysis in Section 3.2.2, there can be a significant covalent component as well as a non-local electrostatic contribution to these changes in IE. From Figure 10B, both the magnitude and the sign of the calculated ΔS_p-character changes depending on the dipole’s orientation relative to the Cu-S(Et) bond. Bringing a negatively oriented dipole close the Cu side of the Cu-S(Et) bond (orientations 1 and 2) decreases the S_p-character in the β-LUMO. Conversely, bringing the dipole toward the S side of the Cu-S(Et) bond (orientations 4 and 5) increases the S_p-character. Interestingly, when the dipole is in orientation 3 (i.e., oriented at the midpoint of the Cu-S(Et) bond), the S_p-character does not change with distance (Figure 10B, blue circles). Therefore, the calculated ΔIEs in Figure 10A contain covalent contributions that differ in sign and magnitude depending on the dipole orientation being considered. Taking the covalent contribution to be −10 ± 2 mV/% S_p (from Section 3.2.2), the calculated ΔIE’s can be corrected for these differences in covalency (Supporting Information Tables S4 – S8). For orientations 1 – 5 and at a distance of 3.5 Å from the Cu-S(Et) bond, the covalency corrected ΔIE’s are −179, −191, −185, −157, and −146 mV, respectively (Table 10), which represent the non-local electrostatic contribution to the IE of the T1 site due to the presence of the dipole in the orientations given in Figure 10C. The magnitudes follow the order: 2 > 3 > 1 > 4 > 5, which reflects the energetics of the interaction of the dipole with the electron charge distributed over the Cu-S(Et) bond. To consider the energetics in more detail, the negative charge distribution can be estimated from the electron density difference between the reduced and oxidized T1 site (Figure 10C; blue and yellow regions represent the differences in negative and positive charge, respectively). A large fraction of the negative charge density is located on the Cu, but is partially delocalized onto the S. Note that the charge on the Cu extends into the region below the plane due to the asymmetric ligand distribution. The potential energy of interaction between the negatively oriented dipole and the negative charge density is inversely dependent on the square of the distance and the cosine of the angle between the dipole and the negative charge. This consideration reproduces the calculated trend (i.e., 2 > 3 > 1 > 4 > 5). It is interesting to compare the total calculated ΔIE’s to the covalent corrected values (Table 10). The relative magnitudes of the total ΔIE’s calculated for dipoles oriented near the S side of the Cu-S(Et) bond (orientations 4 and 5) are increased due to the covalent component while those on the Cu side (orientations 1 and 2) are decreased.

Figure 10.

(A) The dependence on the calculated IE of the reduced model for different dipole orientations and distances; (B) the dependence on the calculated S_p-character in the β-LUMO of the oxidized model; and (C) orientations (1 – 5) of dipoles from the Cu-S(Cys) bond considered in the text.

Table 10.

Calculated ΔIE, ΔS_p-character, and covalency corrected ΔIE for dipoles in orietations 1 – 5 at a distance of 3.5 Å from the Cu-S(Et) bond.

Orientation	ΔIE (mV)	ΔSp (%)	Cov. IE corr. (mV)	ΔIE corr. (mV)
1	−153	−2.6	26	−179
2	−176	−1.5	15	−191
3	−186	0.1	−1	−185
4	−176	1.9	−19	−157
5	−172	2.6	−26	−146

In summary, from this analysis, a negatively oriented dipole has for all orientations a non-local electrostatic component that lowers the IE and E⁰. However, if the negatively oriented dipole is on the Cu side of the Cu-S bond, the covalency of the bond decreases while if the dipole is on the S side of the Cu-S bond, the covalency increases. Thus, the change in Cu-S covalency can either add to or oppose the change in the IE energy due to non-local electrostatics. When the direction of the dipole is inverted (i.e., positive side toward the Cu-S(Et) bond), a parallel behavior as described above is obtained but with the opposite sign (see Supporting Information Tables S4 – S8). The origin of the difference in S_p-character for dipoles oriented toward either the Cu or S side of the Cu-S bond is addressed in the Discussion Section.

Finally, this analysis can be applied to the N47S and F114N Az variants. When a dipole located at the crystallographic position of N47 (see Figure 2) is removed, the calculated IE increases by ~470 mV, and the S_p-character decreases by 8.4 % S_p. The decrease in covalency contributes additively to the increase in IE. The covalent component can be subtracted to obtain the non-local electrostatic contribution to the IE (~385 mV). Furthermore, when a dipole is inserted at the crystallographic position of N114 (see Figure 2), the IE increases by ~210 mV with little change in S_p-character (0.4 % S_p).

4. Discussion

A large range of reduction potentials has been measured for a series of second sphere variants of Az, including F114P, N47S, and F114N Az.²⁷ In this study, a combination of spectroscopic methods has found changes in the covalencies and strengths of the Cu-S(Cys) bonds in F114P and N47S Az, where an H-bond to S has been eliminated and a negatively facing carbonyl dipole near S was deleted, respectively. Interestingly, in the case of the F114N Az variant, where a positively facing dipole is inserted ~5 Å from the Cu, a change in E⁰ is observed without an associated change in the Cu-S(Cys) covalency and bond strength. This led to the development a method to fractionate the change in E⁰ due to second sphere effects into covalent and non-local electrostatic components. Specifically, the covalent contribution to the IE of the BC site is obtained experimentally from S K-edge XAS and estimated using a computational model involving active and passive H-bonding. In the active H-bond orientation (i.e., oriented along the RAMO in Figure 1), the covalency of the Cu-S(Cys) bond decreased, while in the passive case, the H-bond (at the same distance and angle as in the active case) affected the covalency to a lesser extent. These results allowed for the definition and quantification of the covalent (~−10 mV/% S_p) and non-local electrostatic contributions to the IE and thus E⁰. The nonlocal electrostatic contribution is defined as the interaction energy between an electron distributed across the molecular orbital from which it is ionized and the partial charges and dipoles of the protein environment. The covalent component reflects the modulation of the ligand-metal bond due to a local second sphere effect, which changes the nature of the molecular orbital from which the electron is ionized. The more covalent the ligandmetal bond, the greater the stabilization of the oxidized state over the reduced state (decreasing E⁰). This relates to the greater anti-bonding character of the RAMO, which decreases the IE and thus E⁰. The non-local electrostatic term has been well modeled for ET proteins using QM/MM calculations,^{30,33,37,51,94} with some of these calculations including a contribution from the polarization of the solute by the protein and solvent.^51,95,96 The solute polarization is related to the covalent component. However, the method employed here has the advantage of a direct estimation of each contribution separately as the difference in S covalency is experimentally determined by the S K-edge XAS data.

A comparison of the results for BC presented here with these for FeS clusters is insightful. For FeS clusters, a correlation of E⁰ with % S_p change in covalency (per Fe) was ~−8 mV/% S_p.^38,39 Also, in a series of P450 model complexes, addition of two H-bonds to the Fe-SPh bond increased E⁰ by ~330 mV and decreased the covalency by ~19 % S_p.⁹⁰ From the analysis here, the change in E⁰ due to H-bonding has both a nonlocal electrostatic as well as a covalent contribution. Using the covalent component of ~−8 mV/% S_p from the FeS clusters, the non-local electrostatic contribution associated with two H-bonds to the thiolate is ~180 mV (the covalent component being ~150 mV), which is similar to the non-local electrostatic component obtained here for BC. Therefore, a reasonable estimate for the non-local electrostatic component to E⁰ is ~100 mV/H-bond. It should be noted that the slope estimated for the covalent contribution for the Cu-S(Cys) bond in the T1 site (~−10 mV/% S_p) need not be the same for other sulfur-metal bonds.

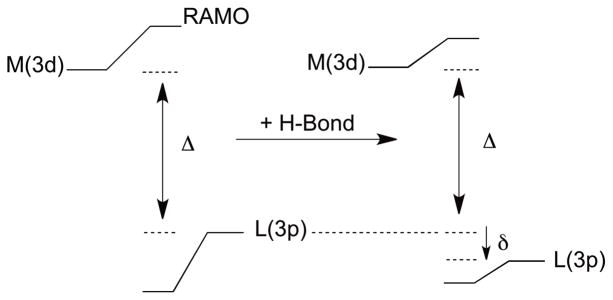
Previous observations of a linear dependence of E⁰ on covalency was understood using a valence bond configuration interaction (VBCI) model.⁹⁰ This VBCI model can be extended to gain insight into the origin of the covalency change and its contribution to E⁰ due to changes in the electrostatic environment around the BC site. If a positive charge (or positively oriented dipole as in the case of H-bonding) is located near the thiolate ligand, it will interact energetically with the ligand-based S(3p) valence orbitals. Of particular importance is the out-of-plane S(3p) orbital, which is π anti-bonding to the Cu(3d_x²−y²) orbital in the SOMO. The energy stabilization of this orbital, defined here as δ, due to a charge or dipole can be thought of in terms of the electrostatic stabilization energy of an electron in the ligand-based S(3p) orbital. δ is negative for attractive and positive for repulsive interactions. The crystal field Hamiltonian for an electron in a p orbital in the presence of one positive charge is

$$H_{xf}=-\frac{{Ze}^2}{a}-\frac{{Ze}^2}{2a^3}(3z^2-r^2)$$ eqn 6

where Z if the effective nuclear charge, e is an electron charge, and a is the distance between the ligand and the positive charge. The contribution to δ for active and passive orientations can be obtained by evaluating H_xf on either a 3p_z or a 3p_x,y atomic orbital, respectively (Figure 11). This gives the following expressions: −(Ze²/a) − (2Ze²/5a³)<r_3p ²> (active) and − (Ze²/a) + (Ze²/5a³)<r_3p ²> (passive). <r_3p ²> is the average distance squared of an electron in a 3p atomic orbital from the nucleus. The values of the two terms were evaluated using DFT calculations.⁹⁷ The first term is approximately three times the value of the second, and the second further stabilizes the electron in the active orientation but destabilizes it in the passive orientation, which results in estimations of δ of −0.30 eV (active) and −0.15 eV (passive). δ can be incorporated into the VBCI model (Figure 12) to increase the energy separation (Δ) between the Cu(3d) and S(3p) orbitals before bonding. The amount of ligand character in the ground state wave function, c_L ² (measured by the S K-edge XAS data), is (H_ML)²/Δ², where H_ML is the resonance integral reflecting ligand-metal overlap. When δ < Δ, which should be the case for H-bonding to a ligand-metal bond, the change in c_L ² upon H-bonding will vary linearly with δ (see Supporting Information). Specifically, a more negative value of δ (greater stabilization energy) will decrease c_L ². Furthermore, the change in δ can be correlated to the change in reduction potential (see Supporting Information). For δ < Δ, ΔE_redox increases linearly with increase in the magnitude of δ (more negative) as this leads to less antibonding character in the RAMO. Thus, the electrostatic interaction with the S(3p_z) orbital in Figure 11 stabilizes (or destabilizes if repulsive) the ligand-based orbital in energy by δ, which decreases c_L ² and increases E⁰. Finally, we note that this VBCI approach can be related to the empirical valence bond (EVB) model of Warshel^98,99 where the environment interacts with the ionic character of the ground state wave function. This will be larger for the reduced than the oxidized state due to the larger covalency of the BC RAMO in Figure 1, therefore affecting the energy more for the reduced site. Here, we use the effect of the environment on the covalency of the oxidized site to evaluate this contribution to E⁰.

Figure 11.

Crystal field model for point charges near the thiolate ligand-based S_3p orbitals.

Figure 12.

VBCI model illustrating the effect of H-bonding and δ on the ligand-metal bonding.

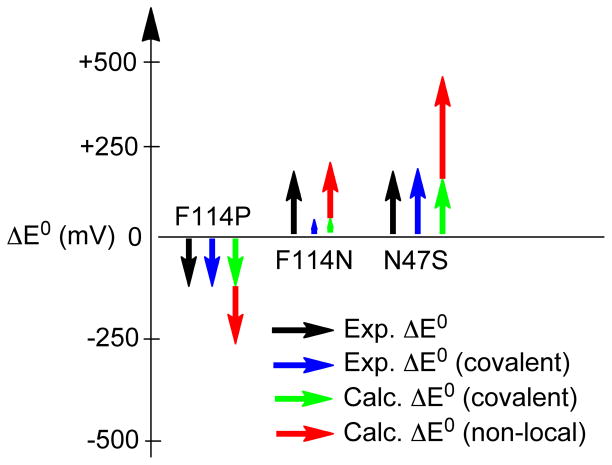
Secondary structural and electronic changes can occur due to point mutations. These can lead to changes in E⁰ either through covalent or non-local electrostatic contributions. This is important to consider for the variants studied here and in general. DFT calculations (vide supra, Section 3.2.2) predicted an ~250 mV increase in the IE of the T1 site due to an active H-bond. This change in IE resulted from both the decrease in covalency (due to a stabilization of the S(3p_z) orbital by δ in Figure 12) as well as the non-local electrostatic term—both of these contributions being additive in increasing E⁰. In the F114P Az variant, a single active H-bond to the Cu-S(Cys) bond has been removed. However, the E⁰ of the F114P Az variant only decreases by ~95 mV relative to WT Az. The spectroscopic data indicate that there is an increase in the covalency as well a strengthening of the Cu-S(Cys) bond in F114P Az. The increase in covalency by ~9 % S_p accounts for an ~90 mV decrease in E⁰. This suggests that the remaining non-local electrostatic component to E⁰ from the H-bond has decreased or been compensated. Insight into this decrease/compensation can be obtained by comparing the X-ray crystal structure of F114P Az to that of WT Az. In WT Az, the phenyl ring of F114 shields the T1 active site from H₂O. As has been observed previously,⁴¹ substituting this residue with Pro in the F114P Az variant opens a H₂O accessible pocket near the T1 site. This allows access of four water molecules (present in both oxidized and reduced crystal structures of F114P Az). One of these water molecules is present with a H₂O – O(C) distance of ~2.9 Å from the trans-axial carbonyl ligand of the T1 site. The Cu-O(C) distance has also increased from ~2.6 Å in WT Az to ~3.6 Å in F114P Az.⁴¹ DFT calculations indicate that considering just the one water dipole and the increase in carbonyl-Cu distance increases the IE of the T1 site by ~50 mV with little change in covalency. Thus, the increased solvation (four H₂Os) adds an additional electrostatic term that opposes the non-local electrostatic change in E⁰ associated with the removal of the H-bond to the Cu-S(Cys) bond. There can also be contributions to E⁰ from changes in the LF environment of F114P Az, but these are expected to be small relative to the other perturbations considered here.

The F114N and the N47S Az variants involve the insertion and deletion of a carbonyl dipole, respectively. In Section 3.2.3, DFT calculations determined that a dipole in the vicinity of the T1 site could significantly alter the IE through both changes in covalency and non-local electrostatics. The change in covalency due to the presence of the dipole could be either additive to or oppose the non-local electrostatic effect on the IE depending on the orientation of the dipole relative to the Cu-S(Cys) bond. With a negatively facing dipole on the S side of the Cu-S(Cys) bond, δ in Figure 12 is positive. This increases the covalency, which further decreases the IE (in parallel with the nonlocal electrostatics). However, with a negative dipole on the Cu side of the Cu-S(Cys) bond, the energy of the Cu(3d) orbital in Figure 12 increases; thus Δ increases and the covalency decreases, which opposes the non-local electrostatic decrease in IE due to the presence of the negative dipole. These results can be used to understand the experimental observations for the F114N and N47S Az variants, which both have an increased E⁰ by ~130 mV relative to WT Az. For F114N Az, DFT calculations reproduce the observation of a change in E⁰ with little change in covalency (ΔIE ~210 mV and Δ% S_p = 0.4) (Section 3.2.3). This suggests that the experimentally observed change in E⁰ for F114N Az is solely accounted for by the non-local electrostatic contribution to the IE due to the presence of the dipole. The lack of a significant change in covalency for this variant reflects its ~5 Å distance from Cu (see Figure 2) as the covalent contribution to the IE falls off more rapidly with distance than the non-local electrostatic term (see Figure 9C). The increase in E⁰ by ~130 mV for N47S Az can be accounted for by the decrease in covalency of the Cu-S(Cys) bond. The experimental decrease in S_p-character is ~14 % S_p, which equates to an ~140 mV increase in E⁰. DFT calculations that involve the removal of the dipole from the N47 position resulted in a decrease in covalency by 8.4 % S_p and an increase in the IE by ~470 mV. Subtraction of the covalent contribution to the IE resulted in a non-local electrostatic component of ~380 mV. This suggests that there is a significant compensation of the non-local electrostatic component. Comparison of crystal structures containing the N47S mutation (i.e., N47S/M121L Az and N47S/F114N Az) with WT Az indicates that this mutation does not result in significant alteration of the secondary protein structure or solvent access near the T1 site. However, the N47 residue is involved in an H-bond network between two T1 ligand-containing loops. BC variants in which this residue is mutated have been found to undergo a large change in the entropic component to E⁰ due to the modification of this H-bond network.⁴⁸ The final results for E⁰ tuning in the Az variants relative to WT Az are summarized in Figure 13. It is observed that the covalent contribution is well estimated from S K-edge XAS, which, when combined with the total change in E⁰, allows the non-local electrostatic contribution to be estimated experimentally. It is further observed that mutations can produce additional changes in the protein environment that can significantly impact the non-local electrostatic component relative to that expected based solely on the point mutation.

Figure 13.

Illustration of the experimentally derived covalent and non-local electrostatic contributions to E⁰ for the variants of Az relative to WT Az and their comparison to calculations.

It is interesting to extend the concepts developed here to other redox-active metalloproteins involved in ET and catalysis. In ET proteins, outer sphere interactions have been demonstrated to strongly modulate reduction potentials and ET flow, while for enzymes they can direct reactivity.¹⁰⁰ The methodology given here is capable of dissecting second sphere interactions into local covalent and non-local electrostatic components. In particular, for two redox active metal ions in proteins that have identical first coordination spheres but very different E⁰’s, the difference in E⁰ due to variations in ligand-metal covalency can be defined experimentally by S K-edge XAS. This is a strong point of emphasis and a powerful tool due to the highly covalent nature of ET active sites in biology. The remaining difference in E⁰ can then be attributed to variations in nonlocal electrostatics. The covalent component will be dominated by second sphere interactions within ~5 Å of the active site; these local interactions include active H-bonds and carbonyl dipoles with specific orientations to the ligand-metal bond. (We note that the sum of the charges and dipoles of the protein and solvent at distances of >5 Å can also contribute to the covalent component, however this is likely small relative to the local contributions.) When the experimental data (i.e., covalent and non-local electrostatics) are combined with structural differences from X-ray crystallography, the origin(s) of the shift in E⁰ between the two active sites can be rigorously defined. This effectively uncouples specific local interactions from more long-range protein/active site interactions—a major goal in understanding outer sphere effects in ET and catalysis. Indeed, using S K-edge XAS, we have already observed protein^39,40 and solvent³⁸ effects on the covalency of Fe-S bonds in the FeS ET proteins and in the heme and non-heme iron enzymes P450⁹² and superoxide reductase (SOR),⁹¹ respectively, that tune redox processes in the former and O₂ and O₂⁻ activation in the latter. A full understanding of these effects now allows their further extension to other systems, be they biological or synthetic.

5. Summary

This study shows that in a series of second sphere variants of the T1 site in Az, the changes in E⁰ can be decomposed into a covalent and a non-local electrostatic component; the covalent component is directly estimated from the experimental S K-edge XAS data. When the change in E⁰ due to a change in covalency of the active site is accounted for, the remaining difference in the enthalpic contribution to E⁰ can be attributed to changes in the non-local electrostatic contribution, thus uncoupling the two terms. Both the covalent and non-local electrostatic contributions can be significant, comparable in magnitude, and additive for active H-bonds, and can be additive or oppose one another for dipoles. The non-local electrostatic term for dipoles is dependent on the distance and angle between the dipole and the charge distribution of the electron being ionized. Furthermore, for point mutations where an H-bond or charge/dipole is added or substituted, additional changes in the vicinity of the active site occur, which can partially compensate the non-local electrostatic effects of the mutation. For BC sites with equivalent first coordination spheres but E⁰’s that vary by >400 mV, as in the T1 centers in the MCOs, this large range of tunability reflects the high covalency and polarizability of the Cu²⁺-S(Cys) bond of the T1 site and its response to the protein environment.