Dual traveling waves in an inner ear model with two degrees of freedom

Abstract

We calculate traveling waves in the mammalian cochlea, which transduces acoustic vibrations into neural signals. We use a WKB-based mechanical model to calculate tectorial membrane (TM) and basilar membrane (BM) motions along the length of the cochlea. This two-degree of freedom approach generates two local modes of motion between the BM and TM that manifest themselves as two traveling waves. The vibration patterns on these masses are very different, producing distinct tuning curves and different characteristic frequencies (CFs) for the TM and the BM. We discuss how the TM stiffness and coupling stiffness influence the characteristics of the waves and tuning curves. We also consider how the differential motions between the masses due to both modes could influence the cochlear amplifier and how mode conversion could take place in the cochlea.

In mammals sound is transduced into neural signals via the organ of Corti (OC), which is contained in the cochlea. It rests on the basilar membrane (BM), which vibrates according to viscoelastic properties that vary lengthwise. Pressure from sound input at the base of the cochlea initiates a traveling wave that is supported by the basilar membrane and peaks at a particular location according to frequency [1]. While the basic principles of this classical model are widely accepted, the precise micromechanics continue to be debated. We find a second traveling wave, which has not been previously demonstrated, by including a second passive structure in a full length model of the cochlea. From this we can reproduce some measured features of BM vibration and infer consequences for amplification. We also discuss how different mechanical properties can affect the predicted responses, and the possibility of mode conversion.

The tectorial membrane (TM) rests on the OC and is capable of vibration in response to acoustic input [2]. Experiments have shown the TM can support a traveling wave in vitro [3] and the absence of the TM affects the BM velocity tuning curve [4]. Data from distortion product otoacoustic emissions (DPOAEs) and neural tuning curves have led to discussion of a second cochlear frequency map due to the coupled vibrations of the TM and BM [5, 6]. Two modes of motion can be found by including the TM as a second mass in models of the cochlear cross section [7–9]. Increasingly detailed models predict how properties of the TM affect cochlear micromechanics, [5, 10–12], but these are often restricted to cross sections, or treat the TM as a local feedback element responding to the BM. Previously, WKB theory was used to explicitly calculate the traveling wave on the BM [13]. In this letter, we show that by modeling the TM and BM each as degrees of freedom in a passive oscillator system, we compute two traveling wave modes.

In this basic model we solve for displacements of the TM and BM. For simplicity, the motions ans springs are depicted strictly vertical (y direction shown in Fig. 1) Also, to simplify the boundary conditions on the fluid problem, the modeled TM extends the full width of the partition. This neglects edge effects, but does not fundamentally change the TM interaction with the fluid. The mass of the OC is included by distributing it such that the vibrating masses are regarded as equal. The smaller stiffness of TM (S_TM) relative to the BM (S_BM) breaks the vertical symmetry. The stiffnesses of the TM and BM decrease exponentially along the length of the cochlea, while the width increases. Other parameters are constant to avoid introducing multiple unknown gradients. Full model parameters, nominally for the mouse, are provided online [14].

FIG. 1.

Illustration of cochlea A) In vivo the cochlea is a long, coiled, tapered duct partitioned by the BM, OC and TM. In this model, the structure is simplified by removing the coiling and height variation, and considering the vertical spatial dimensions symmetric. The stapes excites the fluid motion at z = 0. B) Illustration of the mechanical model. The mass of the OC is divided between the mass of the TM and the BM such that their masses are equal in our model. The gray regions represent fluid C) Illustration of the cross section of the OC.

The equation of motion in terms of location along the cochlea, z, and the excitation frequency, ω (in radians), is

$$\mathbf{\Gamma }(z,\omega )\overrightarrow{A}(z,\omega )=0$$ (1)

where A⃗ is the vector of displacements A⃗ = [A_TM A_BM]^T and Γ is the 2 × 2 matrix

$$\mathbf{\Gamma }(z,\omega )=-{\omega }^2[\mathbf{M}(z)+m_f(z)\mathbf{I}]+i\omega \mathbf{D}(z)+\mathbf{S}(z)$$ (2)

M, D, and S are respectively 2×2 matrices that describe the mass, damping, and stiffness of the cochlear partition depicted in Fig. 1. Off-diagonal terms in D and S couple the two equations. The method is similar to previous applications of WKB theory to cochlear modeling [13, 15] and detailed derivations of the equations are provided online [14]. In this model the fluid in the upper and lower compartments exerts pressure on the TM and BM respectively, adding an effective mass to each. This term, m_f (z), depends on the wavenumber, k(z) and is

$$m_f(z)=\frac{\rho W(z)}{k(z)}\text{coth}[Hk(z)]$$ (3)

where ρ is the fluid density, W(z) is the width of the cochlear partition and H is the height of each fluid compartment. To solve Eq. 1 we set det[Γ(z, ω)] = 0, giving a quadratic equation with two eigenvalues, $m_f^{\pm }(z)$

$$m_f^{\pm }(z)=\frac{1}{2\omega }\{-2{\omega }^2{M}_{11}+2i\omega D_{11}+\text{tr}(S)\pm {[{(\mathrm{\Delta }S)}^2+4{(i\omega D_{12}+S_{12})}^2]}^{\frac{1}{2}}\}$$ (4)

where ΔS = S_BM − S_TM, and assuming the diagonal terms of M and D are equal. Due to the periodic nature of the complex coth term, there are an infinite number of solutions of Eq. 3, most of which have large imaginary parts signifying non-propagating modes. However, when the real part of m_f is positive a single root will be found which has a large real part and small imaginary part of k. As Table I shows, propagating modes are clearly distinguished from evanescent until the wave cuts off. Thus at small z and ω there are two propagating waves, which we denote with + or − superscripts, depending on the sign in front of the square root.

TABLE I.

First three roots of Eq. 3 in descending order of the real components. The value of m_f was determinded for ω = 2π5000 and z = 0.

+ Mode		− Mode
Real	Imag.	Real	Imag.
2.6	−0.0052	3.7	−0.014
0.00031	−89.7	0.0012	−90
0.00015	−180	0.00058	−180

By inserting Eq. 4 into Eq. 2 we can solve for the eigenvectors and obtain the ratio of displacement between the TM and BM,

$${\alpha }^{\pm }(z)=-\frac{2(S_{12}+i\omega D_{12})}{\mathrm{\Delta }S\pm {[{(\mathrm{\Delta }S)}^2+4{(S_{12}+i\omega D_{12})}^2]}^{\frac{1}{2}}}.$$ (5)

Expressing the displacements as a linear combination of the eigenvectors, separating out the scaling and phase components gives

$$\overrightarrow{A}(z,\omega )={\beta }^{+}(z)\left(\begin{array}{c}{\alpha }^{+}(z)\\ 1\end{array}\right)e^{i{\theta }^{+}(z)}+{\beta }^{-}(z)\left(\begin{array}{c}{\alpha }^{-}(z)\\ 1\end{array}\right)e^{i{\theta }^{-}(z)}.$$ (6)

where

$$\theta (z)=\omega t-{\displaystyle {\int }_0^{z}k(\eta )\mathrm{d}\eta ,}$$ (7)

and t is time. To scale the eigenvectors we note that incompressibility of the fluid dictates that the integral of longitudinal fluid flows, V (y), over both fluid compartments is 0 at z = 0. Since the TM bounds the upper compartment and moves independently of the BM, this condition is not automatically satisfied as in previous models. Summing the velocities for each mode, which are proportional to k(z)P(y) [16], and integrating the expression for pressure, P(y), (see online [14]) over the cochlear cross section yields

$$\frac{{\beta }^{+}(0)}{{\beta }^{-}(0)}=-\frac{k^{+}(0)[{\alpha }^{-}(0)-1]}{k^{-}(0)[{\alpha }^{+}(0)-1]}$$ (8)

The partial pressures of the modes in the upper compartment sum to the input stapes pressure, P_s at z = 0, giving

$$P_s=-\frac{\rho {\omega }^2}{H}\left(\frac{{\alpha }^{+}(0)}{k^{{+}^2}(0)}{\beta }^{+}(0)+\frac{{\alpha }^{-}(0)}{k^{{-}^2}(0)}{\beta }^{-}(0)\right)$$ (9)

to determine A⃗(0). Unless the eigenvectors are (−i, 1), energy must be constant within each mode as shown online [14]. It is determined at z = 0, and then used to find A for all z.

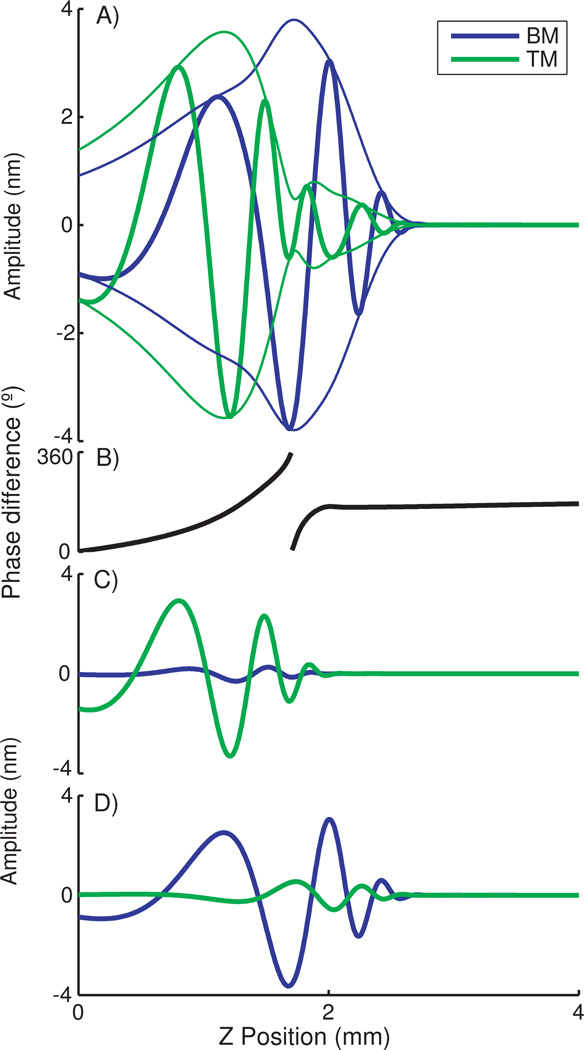
Plotted in Fig. 2 are traveling waves at 31.5 kHz, in a cochlea where the TM is stiffness is less than the BM but of the same order, the coupling stiffness is smaller, and the damping is light. Within modes, the wave from the − mode is larger on the TM than the BM, and vice versa for the + mode, but both waves propagate on both masses. Comparing modes, the amplitudes from both are similar on the TM, while on the BM motions from the + mode dwarf those of the − mode. When combined the waves overlap spatially and form different patterns of vibrations on the TM vs the BM. The modes have different CFs, which given their disproportionate representations leads to a maximum in the TM tuning curve at a lower frequency than the CF of the BM and at nearly the same frequency of a shoulder on the BM tuning curve, as shown in Fig. 3.

FIG. 2.

Traveling waves on the basal end of the BM and TM at 31.5 kHz, the peak of the BM tuning curves. Videos of the traveling waves can be found online [14]. A) Combined mode traveling waves and envelopes. B) Phase differences calculated as TM phase - BM phase. C) Traveling wave for − mode only. D) Traveling wave for + mode only.

FIG. 3.

Tuning curves calculated at z= 1.75 mm (25% the length) from the base of the cochlea. Note frequencies are given here in Hz, not radians. A) Velocity tuning curves for the BM and TM. B) Phase of the BM.

When examining the waves shown in Fig. 2 it is apparent the motions between the TM and BM are nearly in-phase with each other for the − mode and out of phase for the + mode. The total phase difference between these motions varies below the CF of the TM, and is near 180 at the classic BM CF after the − mode cutoff. Shear between the TM and the reticular lamina (RL) is believed to activate the cochlear amplifier. While another dimension needs to be added to the model to elucidate this shear, it is reasonable to expect the phase of BM and TM motion to be a factor. Thus different phases of the traveling wave due to changes between the modes could limit the region of activation.

Mechanical parameters which reproduced a low-frequency shoulder seen in BM tuning curves of either dead [17] or saturated live [18] cochleas were used. A TM stiffness of half that of the BM produces a spacing between BM peak and the shoulder roughly half an octave, which is a resonance interval mentioned in discussions of a second cochlear frequency map [2, 5]. The shoulder is seen at roughly the same frequencies as the TM CF, supporting the idea that TM resonance can be reflected in other measurements. However, one should note that CFs are strongly dependent on coupling, and resonances of either body alone do not directly indicate system resonances in the OC.

By modeling other conditions and considering the analytic expressions for m_f and α we can analyze the effects of different model parameters. Examples of tuning curves with various parameters are available in online Fig. 1 [14]. Changes in the TM or BM stiffness can alter the spacing between the CFs of the two bodies, and the BM peak and shoulder. Different gradients in stiff-nesses could therefore change the peak-shoulder spacings over the length of the cochlea. However, if the stiffnesses change dramatically the two peaks might merge or one of them will not appear at all because the resonant frequency is not excited. Previous work [19] has indicated internal damping of the TM and BM should be small, and we also find that this affects the size and sharpness of the tuning curve peak. However, some damping counters undesired effects of coupling.

The coupling between TM and BM motions increases with larger S₁₂ and D₁₂ and smaller ΔS. For the shoulder to appear on the BM tuning curve some coupling is necessary. Slightly greater coupling can cause a notch to appear in the tuning curves between the shoulder and peak. Greater still, and there can be multiple peaks and valleys in the tuning curve due to an interference effect. Such an effect is seen in other wave phenomena such as the amplitude modulation that can come from playing two similar frequencies. If the coupling is extremely strong, the bodies move together and the + mode has a very small amplitude.

Examining Eq. 3 it is evident the real part of m_f decreases for increasing z and ω, and becomes negative for the − mode first. Because the wave peak and cutoff are closely associated with this, especially for light damping, the − mode will cut off first for most stiffness and damping variations where S_BM > S_TM. The relative amplitude and phase behavior within each mode is determined by α which is plotted in online Fig. 2 [14] for varying S₁₂ and ωD₁₂. Generally |α⁺| > 1 and |α⁻| < 1 unless coupling dominates the mechanical properties. Also, the phase of α reveals that the previously discussed 0° and 180° phases between BM and TM motion are generally true if S₁₂ < ωD₁₂ or ΔS < 2ωD₁₂. Otherwise, the phase between the TM and BM vibration is near −90° in both modes. Near ΔS = 2ωD₁₂ the phase is −90° and the absolute value is 1. At this point we observe the wave numbers k⁺ and k⁻ converge, and there exists the possibility of mode conversion.

Mode conversion is a wave phenomena studied in other fields such as plasma physics, geophysics and optics. It occurs when the wavenumbers of two nonorthogonal modes approach each other, and coincides with a breakdown of the WKB energy conservation equation. In the cochlea, this breakdown occurs when both eigenvectors approach (−i,1). In this limit, the identities of the modes can become confused and they may exchange energy. A transmission coefficient for a two degree of freedom model was work out [20]. Using the deep water approximation for k (i.e. coth(Hk) → 1) this coefficient can be written for the cochlea as

$$T=e^{-\frac{2\pi \rho LW{\omega }^2\left|\mathrm{\Delta }S\right|}{\gamma |tr((S)+2i\omega D_{11}-tr(\mathrm{M}){\omega }^2{|}^2}}$$ (10)

where γ is the exponential decay rate of the stiffness in z. Evaluated near resonance, T can be small and mode conversion or even wave creation can take place. While the conditions for this phenomena are specific, the gradients in TM and BM stiffness are believed to be large to accommodate the large frequency range of mammalian hearing. Thus given wide range ΔS in the cochlea, and the range of ωD₁₂ in a tuning curve this condition could be encountered.

Using a relatively simple passive model we compute vibrations over the length of the cochlea and demonstrate a second cochlear traveling wave. The wave that peaks at lower frequency has a larger vibration on the TM than the BM, and thus could be associated with the TM, but is properly a system resonance. The relative motions of the TM and BM shown here could have important consequences to cochlear activity. Specifically, phase between vibrations of the two membranes is dependent on which mode is dominant and could confine activation of the cochlear amplifier to a narrow region both in space and frequency. In summary, this work unites previous two degree of freedom and WKB models of the inner ear and provides a mechanism using only the passive mechanics of the cochlea to support a second traveling wave. We also discuss the possibility of a mode conversion phenomenon, seen in other areas of wave physics, working in the cochlea.