Summary
Locomotion requires coordinated motor activity throughout an animal’s body. In both vertebrates and invertebrates, chains of coupled Central Pattern Generators (CPGs) are commonly evoked to explain local rhythmic behaviors. In C. elegans, we report that proprioception within the motor circuit is responsible for propagating and coordinating rhythmic undulatory waves from head to tail during forward movement. Proprioceptive coupling between adjacent body regions transduces rhythmic movement initiated near the head into bending waves driven along the body by a chain of reflexes. Using optogenetics and calcium imaging to manipulate and monitor motor circuit activity of moving C. elegans held in microfluidic devices, we found that the B-type cholinergic motor neurons transduce the proprioceptive signal. In C. elegans, a sensorimotor feedback loop operating within a specific type of motor neuron both drives and organizes body movement.
Introduction
All locomotory circuits, from invertebrates to limbed vertebrates, must generate rhythmic activities throughout their motor systems (Delcomyn, 1980; Grillner, 2003; Marder and Calabrese, 1996). To exhibit coherent gaits like crawling, walking, swimming, or running, the rhythmic activities of all body parts must be patterned in specific temporal sequences (Delcomyn, 1980; Grillner, 2003; Marder and Calabrese, 1996; Mullins et al., 2011). Rhythmic motor activities are typically generated by dedicated neural circuits with intrinsic rhythmic activities called the Central Pattern Generators (CPG) (Brown, 1911; Delcomyn, 1980; Grillner, 2003; Kiehn, 2011; Marder and Calabrese, 1996; Mullins et al., 2011). Networks of CPGs can be distributed throughout a locomotory circuit. For example, chains of CPGs have been identified along the nerve cord of the leech and distributed CPG modules have also been found in mammalian lumbar spinal cord to control hindlimb movement (Kiehn, 2006). In isolated nerve cords or spinal cords, even after all muscle and organ tissues have been removed, motor circuits that correspond to different body parts generate spontaneous rhythmic activity, a fictive resemblance of the swimming patterns in behaving animals (Cohen and Wallen, 1980; Kristan and Calabrese, 1976; Mullins et al., 2011; Pearce and Friesen, 1984; Wallen and Williams, 1984).
When a chain of CPGs generates autonomous rhythmic activities, where each CPG corresponds to a different body part, mechanisms to coordinate their activities must be present. Sensory feedback often plays a critical role in this coordination (Grillner and Wallen, 2002; Mullins et al., 2011; Pearson, 1995, 2004). In lamprey and leech, for example, specialized proprioceptive neurons in the spinal cord and body wall modulate the spontaneous activity of CPGs within each body segment (Cang and Friesen, 2000; Cang et al., 2001; Grillner et al., 1984). Activation of these stretch-sensitive neurons, either by current injection or by externally imposed body movements, can entrain CPG activity (McClellan and Jang, 1993; Yu and Friesen, 2004). Similarly, in limbed vertebrates, sensory feedback from mechanoreceptors in the skin and muscle, working through interneuronal circuits that modulate the rhythmic bursting of motor neurons, helps to coordinate limb movements during step cycles (Pearson, 2004).
Here, we study undulatory wave propagation along the body of the nematode Caenorhabditis elegans during forward movement (Figure 1A). The worm offers an opportunity to obtain a complete systems-level understanding of a locomotory circuit. The adult motor circuit has been mapped at synaptic resolution (Chen et al., 2006; White et al., 1986). Recent advances in optical neurophysiology (Chronis et al., 2007; Clark et al., 2007; Faumont et al., 2011; Kawano et al., 2011; Leifer et al., 2011; Liewald et al., 2008; Zhang et al., 2007) now make it possible to explore the physiology of this motor circuit in freely moving animals.
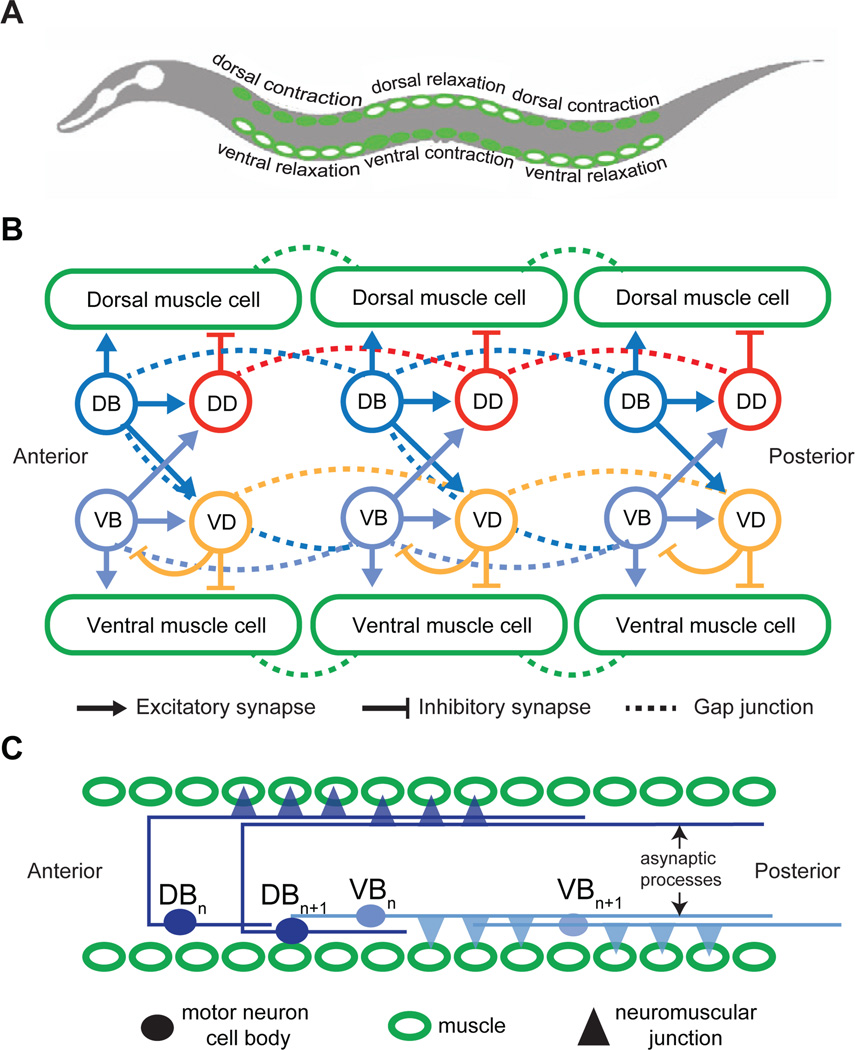
Figure 1. A schematic diagram of the motor circuit in C. elegans.
(A) Worms undulate by alternating contraction and relaxation of dorsal and ventral muscle cells lining the body. Dorsal bending is achieved when dorsal muscle cells contract (filled cells) and ventral muscle cells relax (open cells). Ventral bending is achieved when ventral muscle cells contract and dorsal muscle cells relax.
(B) General patterns of connectivity in the wiring diagram for forward movement. Arrows indicate excitatory chemical synapses from the cholinergic motor neurons (VB and DB). Blunt ended lines indicate inhibitory chemical synapses from GABAergic motor neurons (DD and VD). GABAergic neurons are dispensable for the propagation of the bending wave along the worm body during forward movement. Dashed lines indicate gap junctions between neighboring muscle cells and neighboring neurons of each cell type. Six to twelve neurons of each cell type are distributed along the worm body. The schematic diagram is based on refs. (Chen, 2007; Durbin, 1987; White et al., 1986).
(C) The morphology of DB and VB motor neurons along the circuit. All cell bodies are located in the ventral nerve cord. The axons of VB motor neurons have short anterior axons and long posterior axons. The axons of the DB motor neurons cross to the dorsal nerve cord with long posterior projections.
C. elegans locomotion is controlled by a network of excitatory cholinergic (A and B types) and inhibitory GABAergic (D-type) motor neurons along the nerve cord that innervate the muscle cells lining the worm body (White et al., 1976). Earlier cell ablation studies suggest that B-type cholinergic motor neurons are specifically required for forward locomotion (Chalfie et al., 1985). The 7 VB and 11 DB neurons innervate the ventral and dorsal musculature, respectively (Figure 1). The A-type cholinergic motor neurons, necessary for backward movement (Chalfie et al., 1985), are similarly divided into the D and V subclasses that innervate the dorsal and ventral musculature (not shown in Figure 1).
How the C. elegans motor circuit organizes bending waves along its body during locomotion is poorly understood. Even when all premotor interneurons are ablated (Kawano et al., 2011; Zheng et al., 1999), C. elegans retains the ability to generate local body bending, suggesting that the motor circuit itself (A, B, and D-type neurons and muscle cells) can generate undulatory waves. However, the synaptic connectivity of the motor circuit does not contain motifs that might be easily interpreted as local CPG elements that could spontaneously generate oscillatory activity, e.g., oscillators driven by mutual inhibition between two neuronal classes that can be found in larger animals (Figure 1B). The synaptic connectivity does contain a pattern to avoid simultaneous contraction of both ventral and dorsal muscles; the VB and DB motor neurons that activate the ventral and dorsal muscles also activate the opposing inhibitory GABAergic motor neurons (DD and VD, respectively). However, this contralateral inhibition generated by GABAergic neurons is not essential for rhythmic activity along the body or the propagation of undulatory waves during forward locomotion (McIntire et al., 1993).
In addition, unlike larger animals, the C. elegans motor circuit does not contain specialized proprioceptive or mechanosensory afferents that are positioned to provide information about local movements to each body region through local sensory or interneurons (Figure 1B). The DVA interneuron has been shown to have proprioceptive properties (Hu et al., 2011; Li et al., 2006), but its process spans the whole worm body and is not required for forward locomotion. The lack of specialized sensory neurons within the motor circuit led Russell and Byerly to speculate that individual motor neurons might themselves have proprioceptive properties (White et al., 1986). In particular, electron microscopy showed that the cholinergic motor neurons have long undifferentiated processes that extend along the nerve cord without making synapses. In the B-type motor neurons, for example, these long asynaptic processes extend farther posteriorly than their neuromuscular junctions (Figure 1C) (White et al., 1986). These asynaptic processes were hypothesized to represent specialized proprioceptive sensors. If this is the case, proprioceptive information might be expected to travel from posterior to anterior in the B-type motor neurons. A putative mechanosensory channel UNC-8 is also expressed in motor neurons (Tavernarakis et al., 1997). However, whether any motor neuron is capable of proprioception, or how proprioception is used by the motor circuit, has not been demonstrated.
Biomechanical evidence also implies a role for proprioception in C. elegans locomotion as its gait adapts to the mechanical load imposed by the environment (Berri et al., 2009; Fang-Yen et al., 2010). When worms swim in low load environments like water, the bending wave has a long wavelength (~ 1.5 body length L). When crawling or swimming in high load environments ~10,000-fold more viscous than water, the bending wave has a short wavelength (~ 0.65 L). But whether or how proprioception might be related to gait adaptation has not been determined.
Here, we examined whether the worm motor circuit has proprioceptive properties and how these properties are connected to undulatory dynamics. We apply novel microfluidic devices and in vivo optical neurophysiology to show that proprioceptive coupling between adjacent body segments constitutes the trigger that drives bending wave propagation from head to tail. We found that posterior body regions are compelled to bend in the same direction and shortly after the bending of the neighboring anterior region. We localize this new form of proprioceptive coupling to the B-type cholinergic motor neurons. We quantify the spatial and temporal dynamics of this proprioceptive coupling, and use our biophysical measurements to calculate its role in undulatory dynamics. Proprioception in the C. elegans motor circuit, beyond simply explaining the propagation of an undulatory wave from head to tail, also provides a quantitative explanation for gait adaptation to external load.
Results
The bending of one body region requires the bending of its anterior neighbor
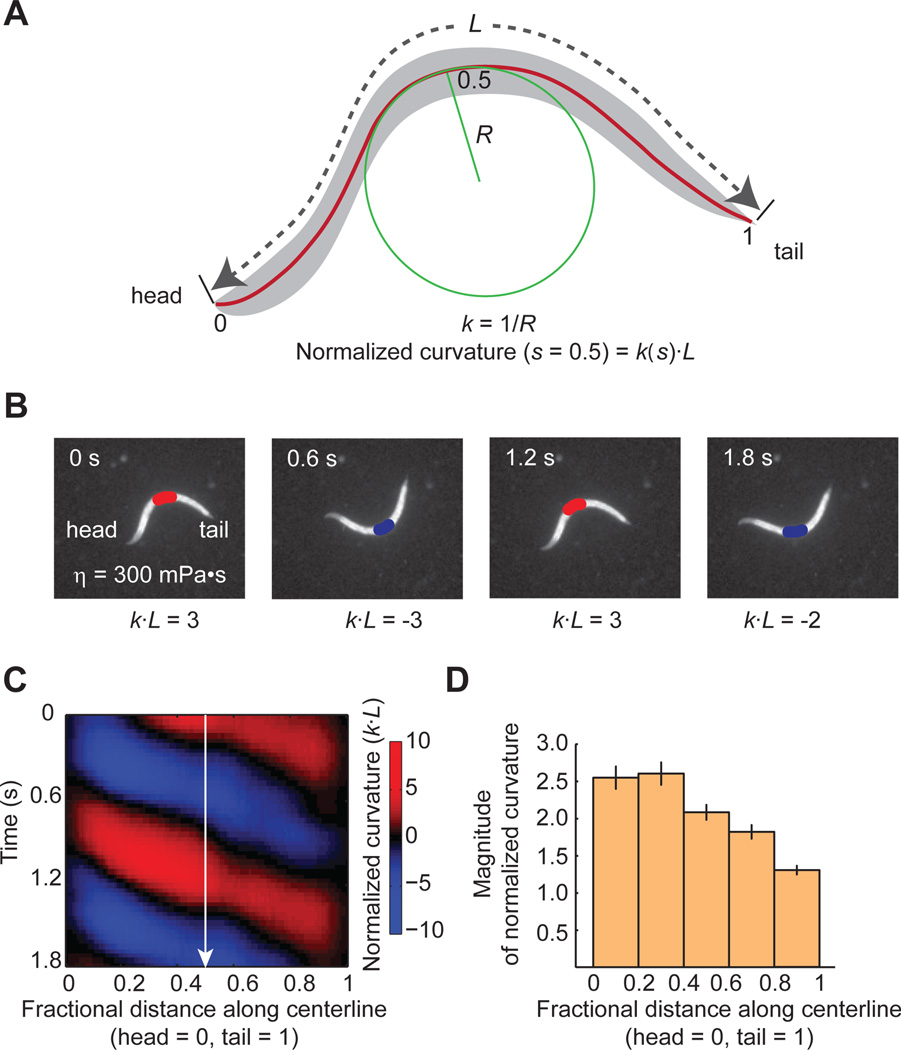
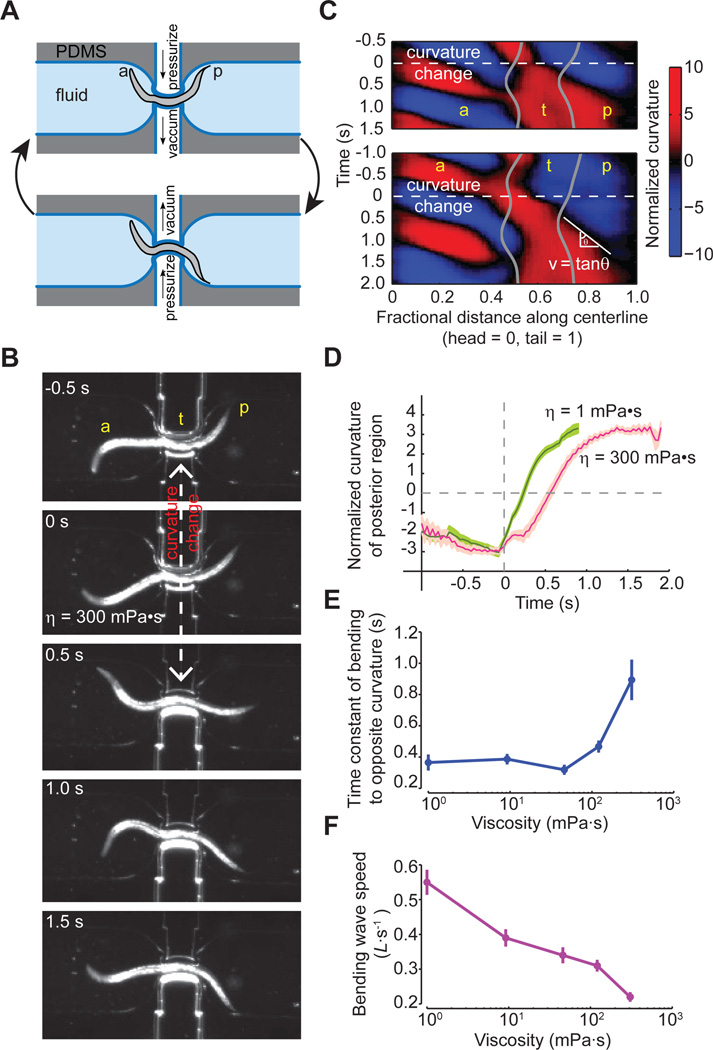
C. elegans moves forward on its side by propagating dorsal-ventral body bending waves from head to tail. The detailed kinematics of bending waves can be quantified by measuring curvature κ at each point along the body centerline over time (Figure 2A). To measure κ, we first calculate R, the radius of curvature at each point along the centerline (κ = 1/R). To compare data from different animals, we measure distance along the worm body as the fractional distance from head to tail (head = 0; tail = 1), and normalize curvature using L, the total length of the body centerline (normalized curvature = κ × L). During sustained forward movement, each body region alternates between positive and negative curvature, and bands of curvature propagate from head to tail as shown in a kymogram (red: positive; blue: negative) (Figure 2B,C). Curvatures measured near the head tend to be larger than curvatures measured near the tail (Figure 2D)
Figure 2. Quantification of undulatory dynamics.
(A) Worm undulatory dynamics is quantified using time-varying curvature along the body. Points along the centerline of length L can be specified in terms of fractional distance from the head (head = 0; tail = 1). The radius of curvature R can be measured at all points along the body. Curvature, κ, is the reciprocal of R. To represent bending in non-dimensional units, we calculate a normalized curvature as κ multiplied by worm length L.
(B) Video images of a worm swimming forward. A red-blue colormap illustrates alternating curvatures at fractional distance = 0.5.
(C) Kymogram of time-varying curvature illustrating retrograde bending waves along the worm represented in non-dimensional units.
(D) Bending magnitude along the body of a wild-type freely swimming worm, measured as the standard deviation of normalized curvature over time. n = 18 worms, mean ± SEM.
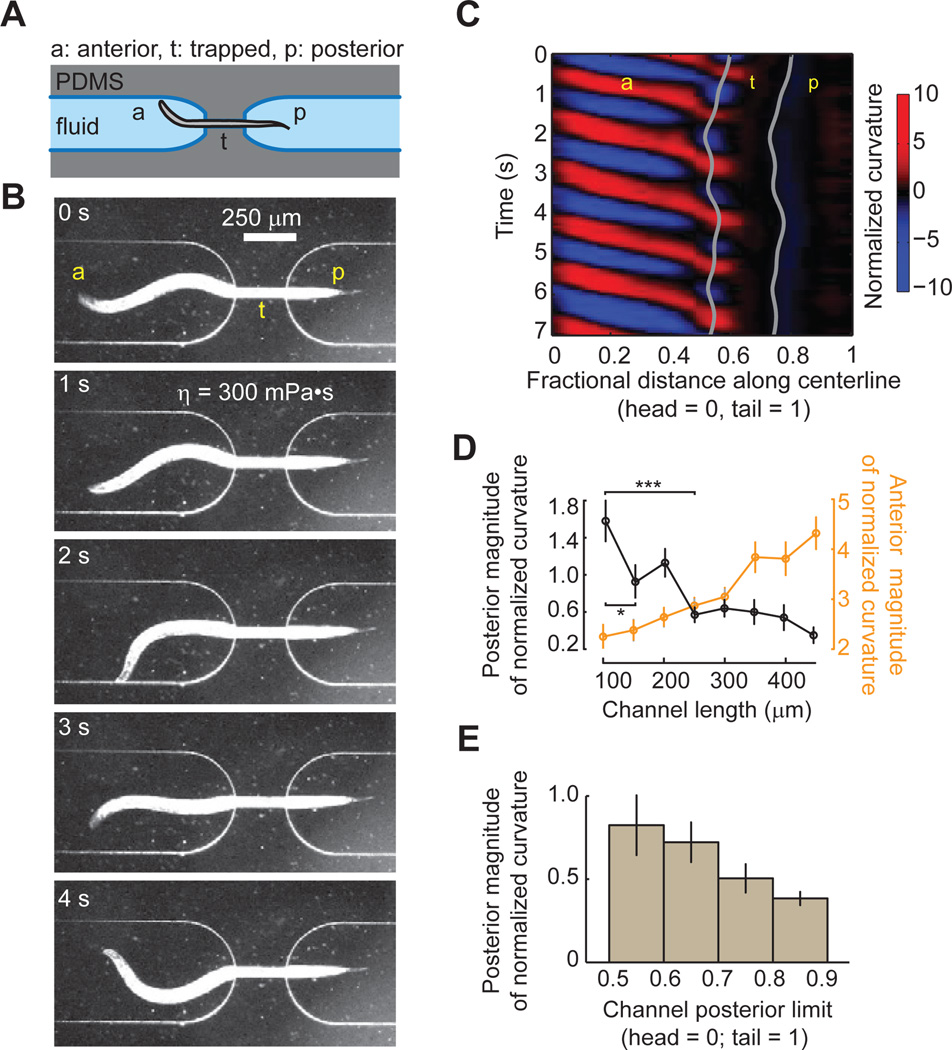
First, we asked how the motor activity in one body region might be affected by the bending of neighboring body regions. To do this, we designed microfluidic devices that immobilized body regions of varying length (Figure 3A,B and Movie S1). Our first device trapped the center of a worm in a narrow straight channel to keep it from bending without impeding worm movement either anterior or posterior to the channel (Figure 3A,B). We used a channel diameter (40 µm) that was sufficient to immobilize the trapped region of a young adult worm (worm diameter is 54 ± 4 µm; mean ± SD) with minimum constriction.
Figure 3. Bending of posterior regions requires anterior bending.
(A) Schematic of microfluidic device. a stands for anterior region, p stands for posterior region, and t stands for trapped region of a worm. PDMS: Polydimethylsiloxane.
(B) Video images of a wild-type young adult worm exhibiting forward undulatory gait inside the microfluidic device (also see Movie S1). The channel divides the worm body into unrestrained anterior, posterior, and trapped middle regions.
(C) Kymogram of time-varying curvature along the body of the worm shown in (B). Gray lines mark the anterior and posterior limits of the straight channel.
(D) Bending magnitude of a posterior and an anterior body region (~ 0.15 worm length) adjacent to the channel, measured as the standard deviation of time-varying normalized curvature, is plotted as a function of the length of the trapped region. n ≥ 10 worms for each condition, mean ± SEM. Position of the posterior limit of the channel is 0.7 ± 0.1 (mean ± standard deviation) for each condition, measured as the fractional distance from head to tail. *P<0.05, ***P < 0.001, Mann-Whitney U test.
(E) Bending magnitude of a posterior body region (mean ± SEM) decreases with the position of the posterior limit of the channel (R = −0.24, p < 0.05, Spearman’s rank correlation test). We measured 64 bouts of forward movement trapped in different channel positions from 20 worms. Channel length is 300 µm.
We consistently recorded bouts of forward movement (> 10 s) when we immobilized a middle portion of the worm (Figure 3A–C). Bending waves would propagate normally to the anterior limit of the channel (orange data points in Figure 3D). Short channels (100 µm long) did not affect wave propagation to the tail; the bending wave that emerged from the posterior limit of the channel (black data points in Figure 3D) exhibited similar amplitude as a freely swimming worm (Figure 2D). However, increasing channel length beyond 200 µm significantly diminished the bending amplitude in the posterior body region (Figure 3D). Increasing channel length also augmented the bending amplitude of the anterior body region, perhaps reflecting an increased effort to escape the channel. Fixing the channel length, but moving it towards the tail also reduced the posterior bending amplitude (Figure 3E).
To determine how immobilization affects muscle activity within and posterior to the channel, we quantified intracellular calcium dynamics in the muscle cells of transgenic animals co-expressing the calcium indicator GCaMP3 (Tian et al., 2009) and RFP in all body wall muscles (Figure S1 and Movie S2). In these animals, intracellular calcium levels can be inferred from the ratio of green to red fluorescence. Whereas muscle cells anterior to the channel exhibited strong rhythmic calcium dynamics during the propagation of bending waves, muscle cells within and posterior to the channel did not (Figure S1). Thus, immobilizing a body region disrupts the propagation of bending waves by lowering motor circuit activity within and posterior to that region. The tail was held rigid and straight in the absence of muscle activity because of the high internal hydrostatic pressure of worms.
Taken together, these results suggest that immobilizing a portion of the worm can directly override rhythmic activity. Motor activity in a posterior region requires the active bending of an anterior region extending ~ 200 µm.
Muscle activity is positively correlated with the curvature of adjacent anterior neighbors
To further explore how the bending of adjacent body regions is coupled, we designed microfluidic devices that trapped the middle region of a worm at defined curvatures (Figure 4A,C). We used channels that were at least 250 µm long to prevent bending waves from propagating into the unrestrained posterior part. We found that the unrestrained posterior region exhibited fixed curvature in the same direction as that imposed on the middle trapped region (e.g., compare the overall shape of the posterior region to the trapped region in Figure 4A and the measured curvature of the posterior region to the trapped region in the kymogram in Figure 4B; also see Movie S3). By using channels with different curvatures, we found that the curvature of the posterior region increased linearly with the imposed curvature on the trapped middle region with slope 0.62 ± 0.03 L (Figure 4C; Figure S2A,B).
Figure 4. Bending of posterior regions is positively correlated with anterior bending.
(A) Video images of a worm exhibiting forward undulatory gait while partially constrained in a curved microfluidic channel (also see Movie S3).
(B) Kymogram of normalized curvature of the worm shown in (A). Gray lines show anterior and posterior limits of the curved channel.
(C) The curvature of the unrestrained posterior body region, measured as a spatial average from the posterior limit of the channel to the tail and a temporal average over bouts of forward movement, is plotted as a function of channel curvature. Each data point (mean ± SEM) represents data from at least 8 animals. Magenta line is the linear least square fit.
(D) Video images of a transgenic worm (Pmyo-3::NpHR) partially constrained in a curved microfluidic channel. The green bar indicates a 2 s interval during which the posterior body wall muscles emerging from the channel was hyperpolarized by green light illumination (also see Movie S4).
(E) Kymogram of normalized curvature of the animal shown in (D). Green shading indicates the body region and duration of green light illumination.
(F) Mean curvature ± SEM of the posterior region emerging from the curved channels as shown in (D) during green light illumination (~ 30 measurements using 6 worms).
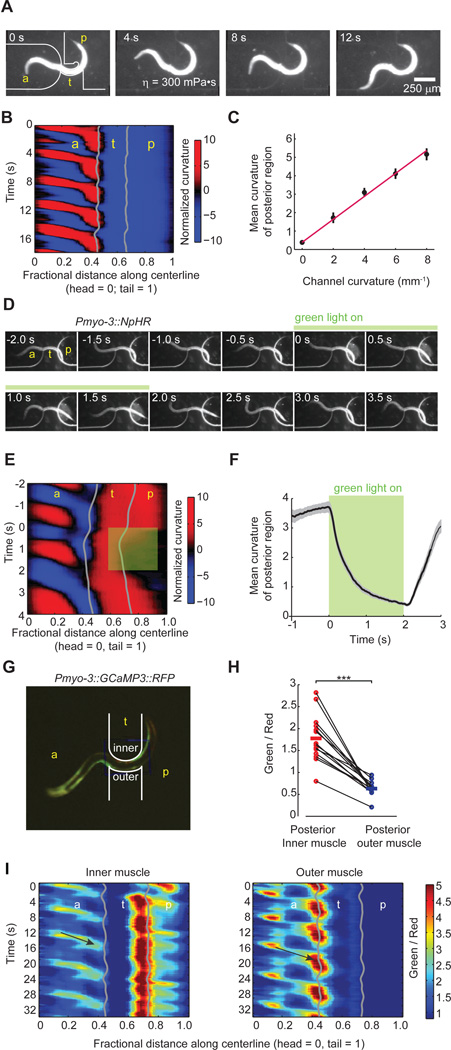
(G) Calcium imaging of body wall muscles in a partially constrained transgenic worm (Pmyo-3::GCaMP3::RFP) in a curved channel. Red fluorescence from RFP constitutes the reference signal. Green fluorescence from GCaMP3 indicates intracellular calcium levels. The contours of the microfluidic channel are drawn in white (also see Movie S5).
(H) Comparison of the ratio of green fluorescence to red fluorescence intensity emitted from inner and outer muscles of the posterior body region. Each data point represents a spatial average of the ratio over a posterior body region (~ 0.2 worm length) adjacent to the channel and a temporal average over a bout of forward movement. Solid lines indicate population mean. Among 14 measurements from 6 worms, six measurements restrict dorsal muscles on the inner side. ***P < 0.001, Wilcoxon signed rank test.
(I) Representative ratiometric kymogram of calcium levels in inner and outer muscle cells of a worm trapped in the device shown in (G). Higher/lower ratios of green fluorescence to red fluorescence in each set of body wall muscles indicate higher/lower intracellular calcium levels. Arrows highlight one calcium wave that propagates from the head to the anterior limit of the curved channel along the inner musculature and outer musculature.
We verified that the fixed curvature of the unrestrained posterior region was due to a fixed pattern of muscle activity. First, by using a transgenic strain that expresses halorhodopsin (Han and Boyden, 2007) in all body wall muscles (Pmyo-3::NpHR), we were able to induce muscle relaxation in the posterior region with green light illumination. The tail reversibly straightened during illumination (Figure 4D–F and Movie S4). Second, we directly monitored muscle activity in the curved posterior region using the muscle calcium reporter GCaMP3 (Figure 4G). In the posterior region emerging from the channel, we consistently measured higher calcium levels in the muscle cells on the inner side than the outer side of the curved body (Figure 4H,I and Movie S5). Third, when the whole animal was paralyzed with sodium azide, the body regions emerging from the curved channel remained straight, instead of following the curvature imposed by the channel (Movie S6).
These results suggest that the bending of anterior body regions dictates the bending of posterior body regions during forward movement. Posterior regions bend in the same direction, and in proportion, to the bend of anterior regions.
Post-channel body curvature follows channel curvature with a viscosity-dependent delay
Next, we measured the time lag between the bending in one body region and the induced bending in the posterior region. To do this, we designed pneumatic microfluidic devices to rapidly change the curvature of a trapped worm (Figure 5A). We flanked both sides of the immobilizing channel with independently controllable inflatable chambers. As with static channels, we found that the curvature of the posterior body was positively correlated with channel curvature. Switching channel curvature towards the dorsal or ventral side induced a corresponding switch in the curvature of the posterior body (Figure 5B–C and Movie S7). This result underscores dorsal/ventral symmetry in the mechanism that couples the curvature of adjacent body regions.
Figure 5. Pneumatic microfluidic device for manipulating body curvature.
(A) Schematic of the pneumatic microfluidic device. The channel is flanked by two chambers. Alternatively pressurizing one chamber while depressurizing the other rapidly switches the curvature the curvature of a region of a trapped worm.
(B) Video images of a partially immobilized wild-type worm. At t = 0 s, the channel starts to change its curvature (also see Movie S7).
(C) Two representative curvature kymograms of a worm trapped in the pneumatic channel. Gray lines mark the anterior and posterior limits of the curved channels. White dashed lines at t = 0 s mark the induced change in channel curvature from negative (color blue) to positive (color red). While the unrestricted anterior body region exhibits opposite bending activities in the two kymograms, this difference did not affect the dynamics of the induced curvature change in the unrestricted posterior body region. The bending wave that shifts the posterior region from negative to positive curvature propagates with a velocity v that is the reciprocal slope of the zero crossing in curvature (color black). A white line is drawn along the zero crossing, and velocity is calculated from its angle with respect to the vertical axis, v = tanθ.
(D) The time course of curvature change in the immediate posterior region (~ 0.1 worm length) emerging from the pneumatic channel after the switch of channel curvature at t = 0 s. The two curves correspond to experiments conducted in two different viscosities. Error bars indicate SEM.
(E) The time constant for relaxation of the posterior region to new curvatures obtained by fitting exponentials to time courses as shown in (D). Each data point represents at least 30 measurements from five worms. Error bars indicate 95% confidence interval to the exponential fits.
(F) The speed of the bending wave following induced changes in channel curvature as a function of fluid viscosity. Error bars indicate SEM.
We found that the switch in curvature of the posterior region propagated with measurable speed from the channel to the tail, consistent with the flow of a retrograde bending signal (Figure 5D–F). To assess whether the delayed bending of the posterior region represented mechanical damping by the external viscous fluid or internal delays within the neuromuscular network, we studied worms in fluids of different viscosity (Figure 5D–F). We found that the bending delay was roughly constant, ~300 ms, in fluids ranging from 1 mPa·s (the viscosity of water) to ~100 mPa·s. In more viscous fluids, the bending delay began to increase, becoming ~ 1 s at 300 mPa·s. These results suggest that ~300 ms represents an upper bound for delays within the neuromuscular network, which are rate-limiting at low viscosities. These neuromuscular delays might reflect delays in synaptic transmission and/or the limiting speed of muscle contraction.
Local proprioceptive coupling is transduced by B-type motor neurons
The C. elegans wiring diagram offers a small number of candidate cell-types within the motor circuit that might play roles in generating or propagating a local proprioceptive signal: the A-type cholinergic motor neurons, B-type cholinergic motor neurons, the D-type GABAergic motor neurons, and muscle cells. One neuron outside the core motor circuit, the DVA interneuron, has also been shown to exhibit proprioceptive properties (Li et al., 2006). We sought to determine which cell-type was responsible for coupling the bending activities of adjacent body regions through proprioception.
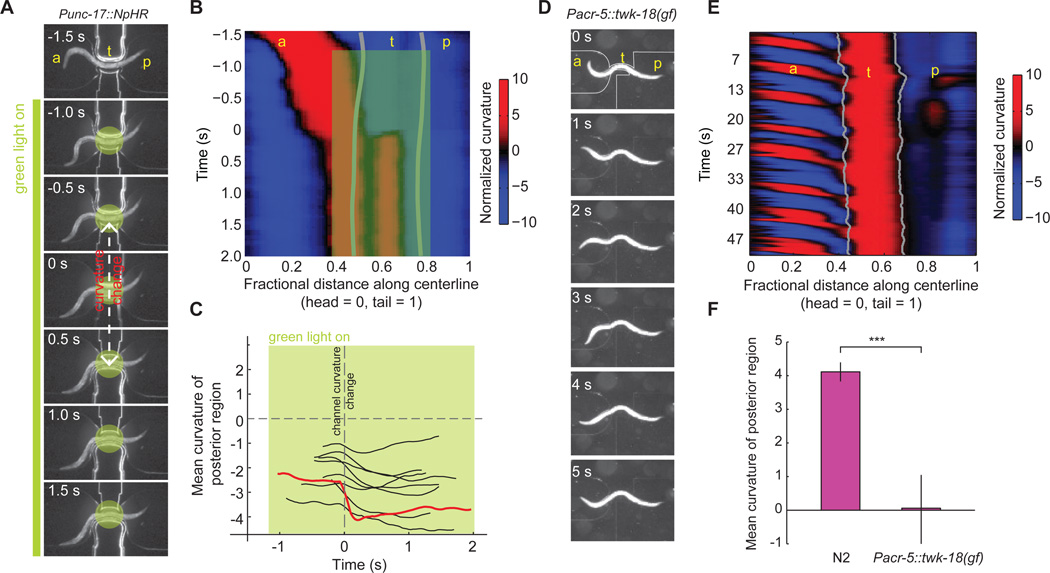
First, we trapped transgenic worms that expressed halorhodopsin in all cholinergic motor neurons (Punc-17::NpHR) in the pneumatic devices, and illuminated them with green light. We found that light-induced hyperpolarization of the cholinergic neurons prevented the posterior body regions from following induced changes in the curvature of the anterior region (Figure 6A–C and Movie S8). Instead, optogenetic inactivation of the cholinergic neurons locked the posterior region in the posture as it was immediately preceding illumination.
Figure 6. B-type cholinergic motor neurons are required for transducing the proprioceptive signal.
(A) Video images of a transgenic worm (Punc-17::NpHR) partially trapped in a pneumatic microfluidic channel. Green bar indicates the duration of green light illumination of the middle portion of the worm before and after induced change in channel curvature at t = 0 s. As a result, the curvature of the tail failed to follow the curvature change of the channel (also see Movie S8).
(B) Curvature kymogram of the transgenic worm trapped in the channel as shown in (A). Green shading indicates the body region and duration of green light illumination.
(C) Curvature of the posterior body region, measured as an average from the posterior limit of the channel to the tail, during onset of illumination (green shading) and the induced change in curvature of the middle region at t = 0 (dashed line). Representative data from five worms were shown. Red curve corresponds to the experiment shown in (A) and (B). A comparison with Figure 5D shows that posterior body region did not switch its curvature after induced curvature change in the trapped middle region during green light illumination.
(D) Video images of a Pacr-5::twk-18(gf)-UrSL-wCherry transgenic worm partially trapped in a static microfluidic channel. B-type cholinergic motor neurons in this strain were specifically deactivated due to the expression of an active K+ channel.
(E) Curvature kymogram of the partially trapped worm shown in (D) during periods of forward movement. A comparison with Figure 3b shows that the posterior body region emerged from the channel no longer follow the curvature of the middle region imposed by the channel.
(F) The mean curvature of the posterior body region emerged from the microfluidic channel in wild type (n = 8) and Pacr-5::twk-18(gf)-UrSL-wCherry transgenic worms (n = 9) during forward movement. All worms were partially trapped in the channel with a curvature 6–8 mm−1. *** p < 0.001, Mann-Whitney U test.
Second, we studied vab-7 mutants, which have specific defects in the morphology of the dorsal B-type cholinergic motor neurons. In these mutants, the DB neurons reverse the orientation of their axons so that they project anteriorly instead of posteriorly (Esmaeili et al., 2002) (Figure S3A) The vab-7 mutation does not affect the ventral B-type motor neurons. During unrestrained forward movement, the bending wave near the head of vab-7 mutants was normal. However, the bending wave that propagates to posterior regions was biased toward the ventral side (Figure S3B, D). When we trapped vab-7 mutants in the pneumatic channels, the posterior region was only able to follow channel bending to the ventral side, not to the dorsal side (Figure S3C, F–G). These results suggest that the dorsal and ventral B-type cholinergic motor neurons are each responsible for propagating dorsal and ventral curvatures to posterior body regions.
Third, we compared the effects of specifically inactivating the A-, B-, and D-type motor neurons. To do this, we examined transgenic animals in which either the A- or B-type cholinergic motor neurons are specifically deactivated by an active K+ channel (Punc-4::twk-18(gf)-UrSL-wCherry and Pacr-5::twk-18(gf)-UrSL-wCherry, respectively) (Kawano et al., 2011; Kunkel et al., 2000), as well as unc-25 mutants that lack the GABA neurotransmitter required by the D-type motor neurons (Jin et al., 1999). During forward locomotion, the bending waves of animals propagated from head to tail when either the A- or D-type motor neurons were inactivated (Figure S4A, C). When trapping the worm in the pneumatic microfluidic device, the posterior region of these worms followed the induced body bending towards either side (Figure S4B, D). In contrast, inactivating the B-type motor neurons prevented an induced bend from anterior regions from propagating to posterior regions (Figure 6D–F and movie S9). When the B-type motor neurons were inactivated, the curvature of the posterior region was not locked to the curvature of the trapped region (Figure 6D,E) as for wild type worms (Figure 4A,B).
The C. elegans motor circuit does not possess local sensory or interneurons that convey local bending information to B-type motor neurons. The DVA interneuron, whose axon spans the whole worm body and connects with most DB motor neurons, has been shown to have proprioceptive properties (Hu et al., 2011; Li et al., 2006). We thus asked whether DVA plays a role in propagating local bending information during forward locomotion. However, we found that laser killing DVA does not disrupt the ability of the posterior region to follow the curvature of the anterior region (Figure S4G–H). Taken together, these results show that neither the A-type, D-type motor neurons, nor the DVA interneuron are needed to propagate the bending signal from anterior to posterior regions. However, the B-type motor neurons are essential.
Gap junctions between muscle cells do not contribute to proprioceptive coupling
We also asked whether the body muscle cells themselves might propagate bending signals from anterior to posterior regions. Adjacent body wall muscle cells are connected by gap junctions mediated specifically by an innexin UNC-9, providing a possible, alternative pathway for transducing the proprioceptive signal (Figure 1B) (Liu et al., 2006). First, we trapped transgenic worms expressing halorhodopsin in their muscle cells (Pmyo-3::NpHR) in the pneumatic channel. We found that specifically relaxing the muscles in the trapped curved region with green light illumination had no effect on the curvature of the free posterior region (Figure S4E–F). We also tested transgenic animals that lacked these gap junctions in their muscle cells. To do this, we used a transgenic unc-9 mutant animal in which unc-9 expression was restored in UNC-9 expressing cells except the body wall muscles. We found that these transgenic animals were fully capable of propagating an imposed bend from anterior to posterior regions (Figure S4H).
As a further test of gap junctions between muscle cells, we optogenetically stimulated body segments in transgenic worms expressing Channelrhodopsin-2 in body wall muscles (Pmyo-3::ChR2) without input from motor neurons. To abolish motor neuron inputs, we treated transgenic worms with ivermectin, which hyperpolarizes the motor circuit by activating glutamate gated chloride channel (Cully et al., 1994), but is not known to affect body wall muscles (Hart (ed.)). Optogenetically inducing ventral or dorsal bending in targeted body segments of paralyzed animals did not induce bending of neighboring regions (n > 10 and Figure S5A–B and Movie S10). We observed similar phenomenon when ivermectin treatment was performed in the unc-13(s69) (n > 10), a loss of function mutation that eliminates synaptic input from motor neurons to muscles (Richmond et al., 1999). These experiments suggest that gap junctions between muscles are insufficient to propagate bending signals between neighboring body regions.
Interestingly, when we optogenetically induced body bending in ivermectin-treated paralyzed worms, the bend would persist long after turning off the illumination (Figure S5A–B and Movie S10). The bend would gradually relax over ~ 40 s, but often in a series of abrupt jumps (Figure S5C). This observation suggests that body wall muscles can exhibit hysteresis: maintaining stable levels of contraction long after stimulation. This observation could also explain why inactivating cholinergic motor neurons in transgenic worms (Punc-17::NpHR) locks them in the posture immediately preceding illumination [Figure 6A–C and (Leifer et al., 2011)].
Bending directly activates B-type motor neurons
Our results thus suggest that the B-type cholinergic motor neurons represent the locus for proprioceptive coupling during forward movement. Next, we sought direct physiological evidence for the proprioceptive properties of the B-type motor neurons. First, we measured the intracellular calcium dynamics of individual DB and VB neurons of unrestrained worms swimming inside microfluidic chambers (Pacr-5-GCaMP3-UrSL-wCherry). Consistent with an earlier study (Kawano et al., 2011), the calcium dynamics of DB6 and VB9, two motor neurons that innervate the opposing dorsal and ventral body wall muscles respectively, are negatively correlated with one another during forward movement (Figure 7A). The cross-correlation between the time-varying calcium signals from DB6 and VB9 are presented in Figure 7B1. Furthermore, we measured the cross-correlation between motor neuron activity and the local curvature of the worm at the position of the motor neurons. We found that the activity of the ventral motor neuron (VB9) is positively correlated with bending towards the ventral side (Figure 7B2), and the activity of the dorsal cholinergic neuron (DB6) is positively correlated with bending towards the dorsal side (Figure 7B3). These results confirm that the sign and amount of local bending is strongly coupled to the activity level in the B-type motor neurons.
Figure 7. Calcium imaging of B-type motor neuron activity induced by bend-sensitive coupling.
(A) Calcium imaging of B motor neuron activity in a forward moving worm. Worms are slightly compressed in the lateral direction (left and right) so that the body movement is confined within a focal plane to allow simultaneous multi-neuron recording. Upper panel: fluorescent video images of two adjacent motor neurons VB9 and DB6 in an unrestrained transgenic worm (Pacr-5::GCaMP3-UrSL-wCherry) swimming within a microfluidic chamber. Middle panel: intracellular calcium dynamics of VB9 and DB6. Lower panel: curvature of the corresponding body region. The intracellular calcium activity can be inferred from the ratio of GCaMP3 fluorescence intensity to wCherry fluorescence intensity. Red fluorescence from wCherry constitutes the reference signal. ΔR/R is the relative deviation of the emission ratio from the baseline.
(B1) Cross correlation between VB9 and DB6 calcium dynamics of forward moving worms. (B2) Cross correlation between VB9 calcium dynamics and the curvature of corresponding body region. (B3) Cross correlation between DB6 calcium dynamics and the curvature of corresponding body region. n = 9 and error bars indicate SEM.
(C1) Representative intracellular calcium dynamics of motor neurons DB6 and VB9 located anterior to the channel. During forward movement, these two neurons exhibited anti-correlated oscillatory calcium activities. (C2) Intracellular calcium dynamics of VB9 and DB6 when the body region containing both neurons was imposed to bend towards the dorsal side. DB6 sustained a higher level of calcium activity. (C3) Calcium dynamics of VB9 and DB6 when the body region containing both neurons was imposed to bend towards the ventral side. VB9 sustained a higher level of calcium activity. In both cases, the calcium dynamics in VB9 and DB6 inactivated during reversal.
(D) Difference of intracellular calcium activity between DB6 and VB9 when the body region containing both neurons were imposed to bend either towards dorsal or ventral side. This quantity is normalized by the total calcium activity of DB6 and VB9 and averaged over a time period (> 20 s) when a worm was moving forward. Each black line represents a different worm and magenta triangles represent the population mean. ** p < 0.005, Wilcoxon signed rank test. n = 10 worms.
To determine whether the bending of anterior regions directly determines the activity of posterior B-type motor neurons, we visualized their calcium dynamics using our curved microfluidic channels. When we imposed a curvature on the middle portion of a worm, bending waves propagated normally from the head to the anterior limit of the channel. When we positioned specific DB and VB motor neurons near the anterior limit of the channel, we observed rhythmic activity correlated with dorsal and ventral bending, respectively (Figure 7C1). When we positioned the same DB and VB motor neurons within or near the posterior limit of the channel, we observed fixed patterns of activity that reflected the curvature imposed by the channel. Bending the worm towards the dorsal side activated the DB motor neuron over the VB motor neuron (Figure 7C2, 7D). Bending the worm towards the ventral side activated the VB motor neuron over the DB motor neuron (Figure 7C3, 7D). These fixed patterns of B-type motor neuron activities relaxed when the worm spontaneously transitioned to backward movement (Figure 7C2, 7C3).
Proprioception is consistent with gait adaptation in response to mechanical load
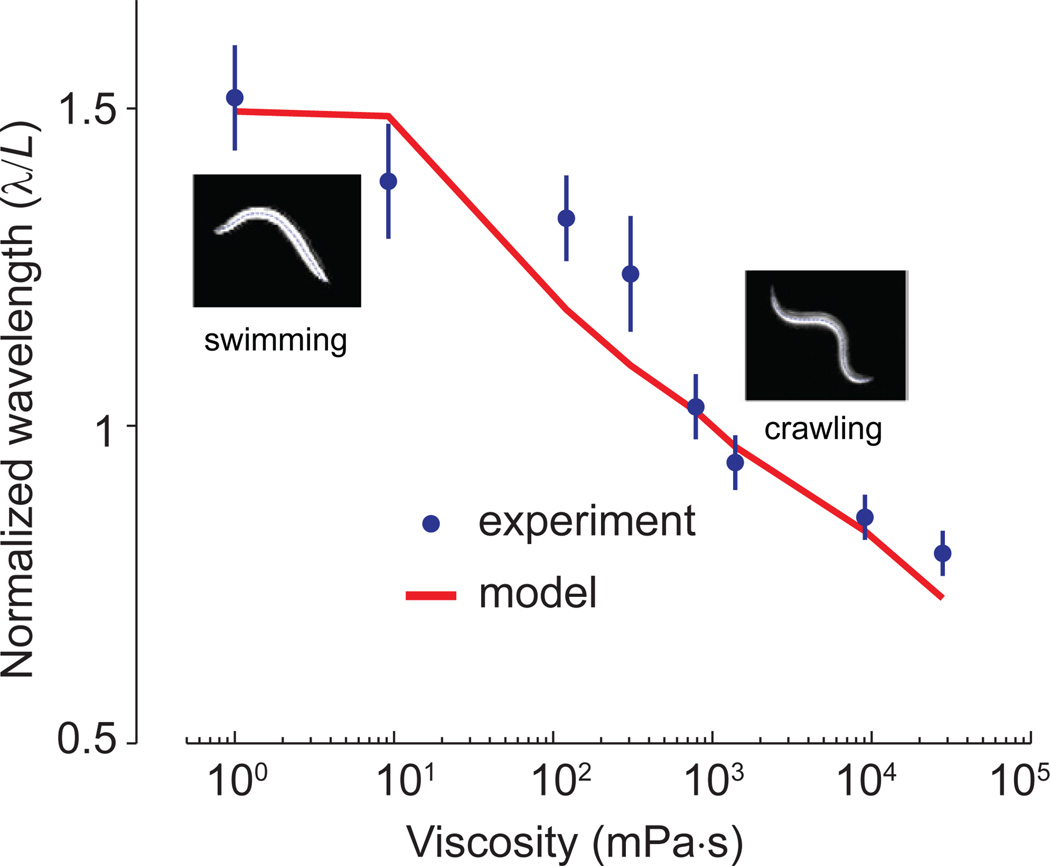
Unlike larger well-studied swimmers like the leech and lamprey, C. elegans is smaller than the capillary length of water (~ 2 mm). At this size, forces due to surface tension that hold the crawling animal to substrates are 10,000-fold larger than forces due to the viscosity of water(Sauvage, 2007). Thus, the motor circuit of C. elegans must adapt to extreme ranges of external load. When worms swim in low load environments like water, the bending wave has a long wavelength (~ 1.5 body length L). When crawling or swimming in high load environments ~10,000-fold more viscous than water, the bending wave has a short wavelength (~ 0.65 L). We asked whether the spatiotemporal dynamics of proprioceptive coupling between body regions plays a role in this gait adaptation.
In our model, we assert that the undulatory wave begins with rhythmic dorsal/ventral bends near the head of a worm. Along the body, however, we assert only the dynamics of proprioceptive coupling measured here and previously measured biomechanics of the worm body. We model the muscles in each body region as being directly activated by bending detected in the neighboring anterior region. We can infer the spatial extent of this coupling l to be ~ 200 µm based on our direct measurements (Figure 3D). For a one millimeter-long worm freely swimming in water, the maximum speed of undulatory wave propagation from head to tail is ~ 2.6 mm/s. Thus, we can estimate the limiting delay τc for transducing a bending signal from region to region to be ~ 80 ms. The simplest linear model for motor circuit activity along the body is fully defined in terms of these parameters, along with biomechanical parameters that were measured in previous work (Fang-Yen et al., 2010): the mechanical drag imposed by the environment and the bending modulus of the worm b. This model can be solved analytically for the wavelength of bending waves, λ:
| (1) |
Here, CN ≈ 30η is the frictional drag coefficient normal to the body centerline, where η is the fluid viscosity. b = 9.5 × 10−14 Nm2 and ω is the angular frequency of undulation in fluid with different viscosities (Fang-Yen et al., 2010). Equation (1) predicts a specific dependence of bending wavelength on fluid viscosity that closely fits experimental observations (Figure 8 and Supplementary Information).
Figure 8. The dynamics of proprioception within the motor circuit are consistent with continuous gait adaptation.
Theoretically predicted dependence of undulation wavelength on external viscosity [red, also see Equation (1)] closely fit the experimental measurements (blue). Error bars are 95% confidence interval.
Proprioception within the motor circuit provides a simple explanation for the propagation of bending waves along the motor circuit. Each body region is compelled to bend shortly after the bending of anterior regions, so that the rhythmic bending activity initiated near the head can generate a wave of rhythmic activity that travels along the whole body. When viewed within the biomechanical framework of the worm body, the spatiotemporal dynamics of proprioception within the motor circuit provides a new explanation for the adaptation of undulatory gait on mechanical load.
Discussion
Prevailing models for rhythmic movements in larger animals involve networks of CPGs that are modulated and entrained by sensory feedback (Marder and Bucher, 2001). For example, the lamprey spinal cord consists of approximately 100 independent CPG units distributed along its length (Cangiano and Grillner, 2003), In most systems, coherent rhythmic movements across the whole body are organized by proprioceptive and mechanosensory feedback to CPG units (McClellan and Jang, 1993; Pearson, 1995; Yu and Friesen, 2004). In the leech, muscle activity between body segments can be coordinated by sensory feedback even after severing the neuronal connectivity between segments (Yu et al., 1999). In Drosophila larvae, specific classes of mechanosensory neurons are required to propagate peristaltic waves during locomotion (Cheng et al., 2010; Hughes and Thomas, 2007; Song et al., 2007).
Here we found a previously undescribed role for proprioception within the motor circuit for propagating rhythmic activities along the body. We show that during forward locomotion, bending waves are driven along the body through a chain of reflexes connecting the activity of neighboring body segments. Unlike larger animals, C. elegans does not have dedicated local sensory or interneurons that might generate or propagate proprioceptive signals within the motor circuit. The cellular economy of the C. elegans wiring diagram implies that individual neurons may have high levels of complexity. Indeed, we have found that the proprioceptive feedback loop that drives forward locomotion is transduced within motor neurons themselves, specifically the B-type cholinergic neurons. The activity of each VB and DB motor neuron is directly activated by ventral and dorsal bending of an anterior region, respectively. Axons of adjacent B-type cholinergic neurons are not anatomically restricted to specific segments, but partially overlap with one another in the ventral and dorsal nerve cords. Thus, going from head to tail, a large posterior portion of each B-type cholinergic neuron runs parallel to the anterior portion of its neighbor in the ventral and dorsal nerve cords. These overlapping portions, along with gap junctions between adjacent neurons, may provide an anatomic platform for propagating a bending signal from neuron to neuron (Figure S6). In vab-7 mutants, the reversed axon projection of DB motor neurons prevents the dorsal posterior bending wave propagation. Disruption of the wiring pattern on the dorsal side, but not the ventral side, of vab-7 mutants might thus explain the specific disruption of dorsal bending waves to the tail.
Both DB and VB motor neurons also have long undifferentiated processes that extend posteriorly beyond their regions of synaptic output to the muscle cells (Figure 1C, S6). We note that this anatomical property of the B-type motor neurons led Russell and Byerly to propose that these processes might have proprioceptive properties. If proprioception were specifically localized to these processes, they would communicate bending signals from posterior to anterior. Because the B-type neurons propagate signals from anterior to posterior, as we have found, the long posterior projections of the B-type motor neurons are unlikely to represent the specialized “proprioceptive antennae”, and we would expect the relevant mechanosensitive elements to be localized near their anterior processes.
One candidate for a potential mechanosensitive channel expressed in the cholinergic motor neurons is the unc-8 gene that encodes a putative mechanically gated ion channel. However, an unc-8(lf) mutation did not disrupt proprioceptive coupling between neighboring body regions (Figure S4H), and the mutant moves like wild type animals. Thus, the molecular mechanism that confers proprioceptive properties to the B-type motor neurons remains to be identified. Identifying genetic lesions that disrupt proprioception in the B-type cholinergic motor neurons would help define the molecular mechanisms. Disruption of these mechanosensitive elements would specifically abolish the propagation of bending waves.
Unlike systems like the leech, lamprey, or vertebrate spinal cord, C. elegans does not appear to depend on a distribution of CPGs along its motor circuit to propagate bending waves. In C. elegans, proprioceptive information is used to directly drive the bending of posterior segments based on the bending of anterior segments, not to entrain the rhythms of separate CPG elements. We propose that a CPG operates near the head of the worm to generate the rhythmic bending of the most anterior segment. Proprioception within the motor circuit, however, suffices to translate the rhythmic activity near the head to sustained undulatory waves along the body.
This form of sensory feedback makes the motor circuit directly responsive to the external environment. We used our biophysical measurements to calculate the effect of proprioception on undulatory waves in surroundings with different viscosities, and uncovered a compelling explanation for the adaptation of undulatory wavelength on external load. At low loads, the worm undulates with a long wavelength. At high loads, the worm undulates with a short wavelength. This dependence has an intuitive biomechanical explanation. As external viscosity increases, it takes longer for a posterior body region to bend in response to any curvature change in its anterior neighbor. Increasing the time scale of the bending response increases the phase difference between the shapes of neighboring body segments, leading to a smaller undulation wavelength.
The small size and experimental accessibility of the C. elegans motor circuit allows the possibility of modeling locomotion that integrates the dynamics of all neuronal and muscular components. Our results suggest that a full model of C. elegans locomotion must integrate the biomechanics of undulatory movement with neuromuscular activity to properly incorporate the role of proprioception within the motor circuit.
Experimental procedures
Worm strains and cultivation
Wild-type, transgenic, and mutant worms were cultivated using standard methods (Brenner, 1974). Detailed strain information can be found in the Supplementary Information. The transgenic worms used in all optogenetic experiments were cultivated in the dark at 20°C on NGM plates with Escherichia coli OP50 and all-trans retinal. We performed all experiments using adult hermaphrodites within a few hours after their final molt.
Microfluidic devices
Custom microfluidic devices were fabricated in PDMS using soft lithography techniques. In the pneumatic microfluidic device, the channel was flanked by two chambers that could be alternatively pressurized and depressurized with a valve system under computer control using custom software written in LabVIEW (National Instruments, Austin, TX). We loaded each microfluidic channel with NGM buffer or dextran solution [~20% dextran in NGM (wt/vol) in most cases]. An individual worm was flowed into the inlet of each microfluidic channel and worm position within each channel was manually controlled by syringes connected to polyethylene tubing.
Measuring undulatory dynamics
Experiments were performed on Nikon microscopes (TE2000 or Eclipse LV150) under 4X magnification with dark field illumination. Image sequences were taken by a CCD camera (Imaging Source) and recorded on a computer at 30 Hz using IC Capture software (Imaging Source). Image analysis was performed using custom software written in MATLAB (MathWorks, Inc. Natick, MA) following methods described in (Fang-Yen et al., 2010).
Calcium imaging of body wall muscle activities
We imaged calcium dynamics within muscle cells of worms partially trapped in microfluidic channels, using similar methods described in (Chen, 2007). GCaMP3 and RFP were excited by LEDs filtered at 448–492nm and 554–572nm respectively using Semrock single-bandpass filters. Fluorescence emission was recorded through an Olympus MVX Plan Apochromat 2X objective (working distance 20mm, numerical aperture 0.5). The fluorescence image was split by a Cairns Optosplit II Image Splitter and the two images (green channel, 499–525 nm; red channel, 581–619 nm) were projected onto two halves of an Andor iXon 885 EMCCD camera. A DinoLite Pro AM413T USB camera was used to track the worm using Worm Tracker 2.0 software developed by the Schafer lab. Zaber T-LSR075A Motorized Linear Slides give automated x-y stage movement. Imaging sequences were recorded on a computer at 10 Hz using Andor Solis software and converted into TIFF files using ImageJ. Images were then analyzed using customwritten MATLAB scripts. Briefly, the two split images were re-aligned and the calcium activities of muscles were calculated as the ratio of green to red fluorescence emission intensities. The true emission intensities from the two channels are calculated using the following formulas: True green = green measured – green background; True red = red measured – red background – 0.153×True green. There is 15.3% bleedthrough from the green to the red channel.
Calcium Imaging of B-type motor neurons
We imaged calcium dynamics in B-type cholinergic motor neurons of worms moving in the microfluidic device using a spinning-disk confocal microscopy (Yokogawa). GCaMP3 and wCherry, which are co-expressed in the B-type motor neurons, were excited by a 488 nm blue laser and a 561 nm yellow laser (Andor Technology) alternatively at every 30 ms. Fluorescence emission was collected through a Nikon Plan Apo 20× objective (working distance 1 mm, numerical aperture 0.75) and projected onto an Andor iXon2 EMCCD camera. Imaging sequences were recorded using the NIS-elements software and converted into TIFF files. Images were then analyzed using custom-written MATLAB scripts. The motor neurons of interest were automatically identified and the calcium dynamics in the cells were calculated as the ratio of GCaMP3 to wCherry fluorescence emission intensities from two sequential images using the following formula:
| (2) |
where Ib is total fluorescence emission intensity excited by the blue laser and Iy is the total fluorescence emission intensity excited by the yellow laser. εr is the ratio of mCherry emission intensity excited by the blue laser to that excited by the yellow laser. εg is the ratio of GCaMP3 emission intensity excited by the yellow laser to that excited by the blue laser. εr = 0.0356 and εg ≈ 0 when the same blue and yellow laser power was used. These ratios were measured using strains expressing only wCherry or GCaMP3 in given neurons.
To measure the correlation between intracellular calcium dynamics in the B-type motor neurons and the bending activity in the corresponding body region, we used canny edge detection method to identify the boundaries of the worm body from the fluorescence images and calculated the curvature of the body segment where the cell body of the motor neurons are located. The cross correlation between calcium activities and curvature was calculated using the following formula:
| (3) |
where Δx(t) and Δy(t) are deviations of x and y from their respective means and 〈·〉 denotes the average over time.
Optogenetic stimulation
We used two optical setups to stimulate transgenic worms expressing Channelrhodopsin or Halorhodopsin. Experiments with the pneumatic microfluidic device (Figure 6A) were conducted on a Nikon microscope (Eclipse LV150) under 10X magnification with dark field illumination. A mercury arc lamp with green filter and field diaphragm was used to illuminate the worm with controlled spot size. Rhodamine in the microfluidic channel (10 µM) allowed us to directly visualize the area and duration of green light illumination. Other optogenetic experiments were performed using a modified version of the CoLBeRT system (Leifer et al., 2011), see Supplementary Information for a more detailed description.
Supplementary Material
Acknowledgements
We are grateful to Christopher Gabel, Cornelia Bargmann, L Mahadevan, and Yun Zhang for useful discussions, Mason Klein for the help with spinning disk confocal microscopy, Zengcai Guo for sharing his strain. This work was supported by NIH Pioneer Award, NSF, and Harvard-MIT Innovation Fund.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Berri S, Boyle JH, Tassieri M, Hope IA, Cohen N. Forward locomotion of the nematode C. elegans is achieved through modulation of a single gait. HFSP Journal. 2009;3:186–193. doi: 10.2976/1.3082260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner S. The genetics of Caenorhabditis elegans. Genetics. 1974;77:71–94. doi: 10.1093/genetics/77.1.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown TG. The Intrinsic Factors in the Act of Progression in the Mammal. P Roy Soc Lond B Bio. 1911;84:308–319. [Google Scholar]
- Cang J, Friesen WO. Sensory modification of leech swimming: rhythmic activity of ventral stretch receptors can change intersegmental phase relationships. Journal of Neuroscience. 2000;20:7822–7829. doi: 10.1523/JNEUROSCI.20-20-07822.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cang J, Yu X, Friesen WO. Sensory modification of leech swimming: interactions between ventral stretch receptors and swim-related neurons. J Comp Physiol A. 2001;187:569–579. doi: 10.1007/s003590100229. [DOI] [PubMed] [Google Scholar]
- Cangiano L, Grillner S. Fast and slow locomotor burst generation in the hemispinal cord of the lamprey. Journal of neurophysiology. 2003;89:2931–2942. doi: 10.1152/jn.01100.2002. [DOI] [PubMed] [Google Scholar]
- Chalfie M, Sulston JE, White JG, Southgate E, Thomson JN, Brenner S. The Neural Circuit for Touch Sensitivity in Caenorhabditis-Elegans. Journal of Neuroscience. 1985;5:956–964. doi: 10.1523/JNEUROSCI.05-04-00956.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen BL. The Watson School of Biological Sciences. Cold Spring Harbor: Cold Spring Harbor Laboratory; 2007. Neuronal Network of C. elegans: from Anatomy to Behavior; p. 96. [Google Scholar]
- Chen BL, Hall DH, Chklovskii DB. Wiring optimization can relate neuronal structure and function. P Natl Acad Sci USA. 2006;103:4723–4728. doi: 10.1073/pnas.0506806103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng LE, Song W, Looger LL, Jan LY, Jan YN. The role of the TRP channel NompC in Drosophila larval and adult locomotion. Neuron. 2010;67:373–380. doi: 10.1016/j.neuron.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chronis N, Zimmer M, Bargmann CI. Microfluidics for in vivo imaging of neuronal and behavioral activity in Caenorhabditis elegans. Nat Methods. 2007;4:727–731. doi: 10.1038/nmeth1075. [DOI] [PubMed] [Google Scholar]
- Clark DA, Gabel CV, Gabel H, Samuel ADT. Temporal activity patterns in thermosensory neurons of freely moving Caenorhabditis elegans encode spatial thermal gradients. J Neurosci. 2007;27:6083–6090. doi: 10.1523/JNEUROSCI.1032-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen AH, Wallen P. The neuronal correlate of locomotion in fish. "Fictive swimming" induced in an in vitro preparation of the lamprey spinal cord. Exp Brain Res. 1980;41:11–18. doi: 10.1007/BF00236674. [DOI] [PubMed] [Google Scholar]
- Cully DF, Vassilatis DK, Liu KK, Paress PS, Van der Ploeg LH, Schaeffer JM, Arena JP. Cloning of an avermectin-sensitive glutamate-gated chloride channel from Caenorhabditis elegans. Nature. 1994;371:707–711. doi: 10.1038/371707a0. [DOI] [PubMed] [Google Scholar]
- Delcomyn F. Neural basis of rhythmic behavior in animals. Science. 1980;210:492–498. doi: 10.1126/science.7423199. [DOI] [PubMed] [Google Scholar]
- Durbin RM. Studies on the development and organisation of the nervous system of Caenorhabditis elegans. University of Cambridge; 1987. p. 121. [Google Scholar]
- Esmaeili B, Ross JM, Neades C, Miller DM, 3rd, Ahringer J. The C. elegans even-skipped homologue, vab-7, specifies DB motoneurone identity and axon trajectory. Development. 2002;129:853–862. doi: 10.1242/dev.129.4.853. [DOI] [PubMed] [Google Scholar]
- Fang-Yen C, Wyart M, Xie J, Kawai R, Kodger T, Chen S, Wen Q, Samuel AD. Biomechanical analysis of gait adaptation in the nematode Caenorhabditis elegans. Proc Natl Acad Sci U S A. 2010;107:20323–20328. doi: 10.1073/pnas.1003016107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faumont S, Rondeau G, Thiele TR, Lawton KJ, McCormick KE, Sottile M, Griesbeck O, Heckscher ES, Roberts WM, Doe CQ, Lockery SR. An image-free optomechanical system for creating virtual environments and imaging neuronal activity in freely moving Caenorhabditis elegans. PLoS One. 2011;6:e24666. doi: 10.1371/journal.pone.0024666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grillner S. The motor infrastructure: from ion channels to neuronal networks. Nat Rev Neurosci. 2003;4:573–586. doi: 10.1038/nrn1137. [DOI] [PubMed] [Google Scholar]
- Grillner S, Wallen P. Cellular bases of a vertebrate locomotor system-steering, intersegmental and segmental co-ordination and sensory control. Brain Res Brain Res Rev. 2002;40:92–106. doi: 10.1016/s0165-0173(02)00193-5. [DOI] [PubMed] [Google Scholar]
- Grillner S, Williams T, Lagerback PA. The edge cell, a possible intraspinal mechanoreceptor. Science. 1984;223:500–503. doi: 10.1126/science.6691161. [DOI] [PubMed] [Google Scholar]
- Han X, Boyden ES. Multiple-color optical activation, silencing, and desynchronization of neural activity, with single-spike temporal resolution. PLoS One. 2007;2:e299. doi: 10.1371/journal.pone.0000299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart, editor. WormBook, T.C.e.R. Community. A.C. Behavior. WormBook; [Google Scholar]
- Hu Z, Pym EC, Babu K, Vashlishan Murray AB, Kaplan JM. A neuropeptide-mediated stretch response links muscle contraction to changes in neurotransmitter release. Neuron. 2011;71:92–102. doi: 10.1016/j.neuron.2011.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes CL, Thomas JB. A sensory feedback circuit coordinates muscle activity in Drosophila. Mol Cell Neurosci. 2007;35:383–396. doi: 10.1016/j.mcn.2007.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin Y, Jorgensen E, Hartwieg E, Horvitz HR. The Caenorhabditis elegans gene unc-25 encodes glutamic acid decarboxylase and is required for synaptic transmission but not synaptic development. Journal of Neuroscience. 1999;19:539–548. doi: 10.1523/JNEUROSCI.19-02-00539.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawano T, Po MD, Gao S, Leung G, Ryu WS, Zhen M. An Imbalancing Act: Gap Junctions Reduce the Backward Motor Circuit Activity to Bias C. elegans for Forward Locomotion. Neuron. 2011;72:572–586. doi: 10.1016/j.neuron.2011.09.005. [DOI] [PubMed] [Google Scholar]
- Kiehn O. Locomotor circuits in the mammalian spinal cord. Annu Rev Neurosci. 2006;29:279–306. doi: 10.1146/annurev.neuro.29.051605.112910. [DOI] [PubMed] [Google Scholar]
- Kiehn O. Development and functional organization of spinal locomotor circuits. Curr Opin Neurobiol. 2011;21:100–109. doi: 10.1016/j.conb.2010.09.004. [DOI] [PubMed] [Google Scholar]
- Kristan WB, Jr, Calabrese RL. Rhythmic swimming activity in neurones of the isolated nerve cord of the leech. J Exp Biol. 1976;65:643–668. doi: 10.1242/jeb.65.3.643. [DOI] [PubMed] [Google Scholar]
- Kunkel MT, Johnstone DB, Thomas JH, Salkoff L. Mutants of a temperature-sensitive two-P domain potassium channel. Journal of Neuroscience. 2000;20:7517–7524. doi: 10.1523/JNEUROSCI.20-20-07517.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leifer AM, Fang-Yen C, Gershow M, Alkema MJ, Samuel AD. Optogenetic manipulation of neural activity in freely moving Caenorhabditis elegans. Nat Methods. 2011;8:147–152. doi: 10.1038/nmeth.1554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Feng Z, Sternberg PW, Xu XZ. A C. elegans stretch receptor neuron revealed by a mechanosensitive TRP channel homologue. Nature. 2006;440:684–687. doi: 10.1038/nature04538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liewald JF, Brauner M, Stephens GJ, Bouhours M, Schultheis C, Zhen M, Gottschalk A. Optogenetic analysis of synaptic function. Nat Methods. 2008;5:895–902. doi: 10.1038/nmeth.1252. [DOI] [PubMed] [Google Scholar]
- Liu Q, Chen B, Gaier E, Joshi J, Wang ZW. Low conductance gap junctions mediate specific electrical coupling in body-wall muscle cells of Caenorhabditis elegans. J Biol Chem. 2006;281:7881–7889. doi: 10.1074/jbc.M512382200. [DOI] [PubMed] [Google Scholar]
- Marder E, Bucher D. Central pattern generators and the control of rhythmic movements. Curr Biol. 2001;11:R986–R996. doi: 10.1016/s0960-9822(01)00581-4. [DOI] [PubMed] [Google Scholar]
- Marder E, Calabrese RL. Principles of rhythmic motor pattern generation. Physiol Rev. 1996;76:687–717. doi: 10.1152/physrev.1996.76.3.687. [DOI] [PubMed] [Google Scholar]
- McClellan AD, Jang W. Mechanosensory inputs to the central pattern generators for locomotion in the lamprey spinal cord: resetting, entrainment, and computer modeling. J Neurophysiol. 1993;70:2442–2454. doi: 10.1152/jn.1993.70.6.2442. [DOI] [PubMed] [Google Scholar]
- McIntire SL, Jorgensen E, Kaplan J, Horvitz HR. The GABAergic nervous system of Caenorhabditis elegans. Nature. 1993;364:337–341. doi: 10.1038/364337a0. [DOI] [PubMed] [Google Scholar]
- Mullins OJ, Hackett JT, Buchanan JT, Friesen WO. Neuronal control of swimming behavior: comparison of vertebrate and invertebrate model systems. Prog Neurobiol. 2011;93:244–269. doi: 10.1016/j.pneurobio.2010.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearce RA, Friesen WO. Intersegmental coordination of leech swimming: comparison of in situ and isolated nerve cord activity with body wall movement. Brain Res. 1984;299:363–366. doi: 10.1016/0006-8993(84)90720-0. [DOI] [PubMed] [Google Scholar]
- Pearson KG. Proprioceptive regulation of locomotion. Curr Opin Neurobiol. 1995;5:786–791. doi: 10.1016/0959-4388(95)80107-3. [DOI] [PubMed] [Google Scholar]
- Pearson KG. Generating the walking gait: role of sensory feedback. Prog Brain Res. 2004;143:123–129. doi: 10.1016/S0079-6123(03)43012-4. [DOI] [PubMed] [Google Scholar]
- Richmond JE, Davis WS, Jorgensen EM. UNC-13 is required for synaptic vesicle fusion in C. elegans. Nat Neurosci. 1999;2:959–964. doi: 10.1038/14755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sauvage P. Laboratoire Matiere et Systemes Compiexes. Paris: Universite Paris Diderot-Paris 7; 2007. Etude de la locomotion chez C. elegans et perturbations mecaniques du mouvement; p. 152. [Google Scholar]
- Song W, Onishi M, Jan LY, Jan YN. Peripheral multidendritic sensory neurons are necessary for rhythmic locomotion behavior in Drosophila larvae. Proc Natl Acad Sci U S A. 2007;104:5199–5204. doi: 10.1073/pnas.0700895104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavernarakis N, Shreffler W, Wang S, Driscoll M. unc-8, a DEG/ENaC family member, encodes a subunit of a candidate mechanically gated channel that modulates C. elegans locomotion. Neuron. 1997;18:107–119. doi: 10.1016/s0896-6273(01)80050-7. [DOI] [PubMed] [Google Scholar]
- Tian L, Hires SA, Mao T, Huber D, Chiappe ME, Chalasani SH, Petreanu L, Akerboom J, McKinney SA, Schreiter ER, et al. Imaging neural activity in worms, flies and mice with improved GCaMP calcium indicators. Nat Methods. 2009;6:875–881. doi: 10.1038/nmeth.1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallen P, Williams TL. Fictive locomotion in the lamprey spinal cord in vitro compared with swimming in the intact and spinal animal. J Physiol. 1984;347:225–239. doi: 10.1113/jphysiol.1984.sp015063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White JG, Southgate E, Thomson JN, Brenner S. The structure of the ventral nerve cord of Caenorhabditis elegans. Philos Trans R Soc Lond B Biol Sci. 1976;275:327–348. doi: 10.1098/rstb.1976.0086. [DOI] [PubMed] [Google Scholar]
- White JG, Southgate E, Thomson JN, Brenner S. The structure of the nervous system of the nematode Caenorhabditis elegans. Philos Trans R Soc Lond B Biol Sci. 1986;314:1–340. doi: 10.1098/rstb.1986.0056. [DOI] [PubMed] [Google Scholar]
- Yu X, Friesen WO. Entrainment of leech swimming activity by the ventral stretch receptor. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2004;190:939–949. doi: 10.1007/s00359-004-0549-9. [DOI] [PubMed] [Google Scholar]
- Yu XT, Nguyen B, Friesen WO. Sensory feedback can coordinate the swimming activity of the leech. J Neurosci. 1999;19:4634–4643. doi: 10.1523/JNEUROSCI.19-11-04634.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang F, Wang LP, Brauner M, Liewald JF, Kay K, Watzke N, Wood PG, Bamberg E, Nagel G, Gottschalk A, Deisseroth K. Multimodal fast optical interrogation of neural circuitry. Nature. 2007;446:633–639. doi: 10.1038/nature05744. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Brockie PJ, Mellem JE, Madsen DM, Maricq AV. Neuronal control of locomotion in C. elegans is modified by a dominant mutation in the GLR-1 ionotropic glutamate receptor. Neuron. 1999;24:347–361. doi: 10.1016/s0896-6273(00)80849-1. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.