Abstract
The self-consistent-charge density-functional tight-binding method (SCC-DFTB) is an approximate quantum chemical method derived from density functional theory (DFT) based on a second-order expansion of the DFT total energy around a reference density. In the present study we combine earlier extensions and improve them consistently with, first, an improved Coulomb interaction between atomic partial charges, and second, the complete third-order expansion of the DFT total energy. These modifications lead us to the next generation of the DFTB methodology called DFTB3, which substantially improves the description of charged systems containing elements C, H, N, O, and P, especially regarding hydrogen binding energies and proton affinities. As a result, DFTB3 is particularly applicable to biomolecular systems. Remaining challenges and possible solutions are also briefly discussed.
1 Introduction
Recent years have shown that approximate quantum chemistry methods form an essential part in the repertoire of computational methods for an atomistic understanding of a broad range of physical, chemical and biological problems. Besides semi-empirical molecular orbital methods such as MNDO,1 AM1,2 PM33 and successive methods,4,5 PDDG/PM3,6 OMx,7,8 the self-consistent-charge density-functional tight-binding (SCC-DFTB) method is an alternative approximate approach derived from density functional theory (DFT) by neglect, approximation and parametrization of interaction integrals.9 Although approximate methods are less accurate than DFT and ab initio methods on average, their main advantage is the increased computational speed, which can be 2-3 orders of magnitude when compared to DFT and Hartree-Fock using mediums sized basis sets. This allows treating large molecules, a large number of conformers and/or sufficiently long sampling for QM or QM/MM molecular dynamics simulations.10
The non-self-consistent version of DFTB11,12 and its basic integral approximations have been proposed in the 1980’s,13,14 still being the center around which all later extensions have been developed. The DFTB energy, similar to other empirical tight-binding models, can be understood as a stationary approximation to the DFT functional15 in the spirit of the Harris functional approach.16 The methodology basically allows to treat systems with small and large17 intramolecular charge transfer, but fails for molecular systems with intermediate charge transfer. SCC-DFTB extends the DFTB method to charge self-consistency and can be derived by a second order expansion of the DFT total energy with respect to charge density fluctuations around a given reference charge density, usually chosen as a superposition of neutral atomic charge densities.9 The SCC-DFTB model now allows also to treat systems with intermediate charge transfer within a molecule and therefore has been a major step forward towards a generally applicable DFT based semi-empirical methodology. Several reviews have appeared concerning the basic formalism and selected applications;18–23 for a recent overview, we would like to point the readers also to a special issue of JPCA.24
In the last years several benchmark studies of SCC-DFTB appeared showing the great success as well as the limitations of this method. Geometries are usually reproduced excellently.9,25–27 Similarly, relative energies of peptide conformers28–30 are nicely reproduced in comparison to higher level methods as well as hydrogen bonding energies.26 While for reaction energies SCC-DFTB performs well on average9,31 heats of formation are overestimated.25,26 Vibrational frequencies are reasonable but severe failures have been noted for certain vibrational modes.26,31–35 A drawback inherited from the derivation of DFT is the missing dispersion interaction. An empirical correction has been suggested and shown to be crucial for the description of nucleic acid base stacking interactions36 and relative stability of α and 310 helices in proteins.37
The SCC-DFTB total energy consists of three terms,
| (1) |
the first one containing the DFTB matrix elements and the third one the DFTB repulsive potential. These two terms correspond to the non-self-consistent DFTB method,11,12 while the second term results from approximations of the second order term of the DFT Taylor series expansion. Several limitations of the current formalism, which result from approximations inherent to those three terms, have been discussed recently,22,38 and current efforts to increase DFTB accuracy try to improve on these approximations. Recently, we have shown that a more sophisticated scheme for fitting the repulsive potential can also increase the overall accuracy to some degree.27
In this work, we concentrate on extensions of the second order SCC term, leaving the other contributions, i.e., the first and the third terms unchanged. As previous work has shown,22,38–40 extensions of the SCC contributions can improve the performance of SCC-DFTB for hydrogen bonded complexes and molecules with localized charges significantly, thereby improving the transferability of DFTB. These activities concern basically two recent developments, an improvement of the effective electron repulsion term in the SCC formalism, the γ-function, and the extension to include third order terms.
The γ-function describes the Coulomb interaction between atomic partial charges Δqa. The functional form chosen for this interaction presupposes an inverse relation of atomic size and chemical hardness,9 which is true for elements within one row of the periodic table22,38 but not for elements of different periods. A particularly large deviation occurs for the hydrogen atom. A newly introduced γh-function corrects this incorrect assumption by an extra term including one additional parameter and as a result, systematically improves hydrogen bonding interactions.39
The inclusion of approximate third order terms leads to a new degree of self-consistency.22,38 In SCC-DFTB, the Coulomb repulsion resulting from the charge density fluctuations as described by the second order SCC terms is computed in a monopole approximation utilizing a newly introduced parameter, the Hubbard parameter (chemical hardness). This parameter is computed from DFT for neutral atoms and is a constant for all charge states of the atom. While this approximation seems to be unproblematic for many covalently bound systems, it is insufficient for molecules that contain large localized net charges. As has been shown, these systems require additional flexibility in the model; i.e., the Hubbard parameters have to become charge dependent, which is achieved by including the approximated third order terms.22,38
The third order terms can be split up into two parts, a diagonal and a off-diagonal one. The diagonal terms lead to a charge dependent on-site self-interaction, the off-diagonal terms modify the SCC Coulomb repulsion between sites. The diagonal contributions significantly improve the proton affinities of CHNO containing molecules, since in these calculations strongly localized net charges occur.39 They also improve the proton affinities of phosphorous containing molecules.40 However, a reasonable accuracy was only achieved by adding an empirical energy contribution in a rather ad hoc fashion, which still did not lead to an acceptable transferability; i.e., different parameter sets had to be developed for different properties. Although these extensions have been shown to be important for describing proton affinities and hydrogen binding energies in various applications,23,41–47 further improvement is required to obtain a more transferrable method for general applications.
In the present study we implement and test the off-diagonal third order contributions. In combination with the γh-function and diagonal third order terms, this establishes a third generation of our DFTB methodology which will be called DFTB3. The off-diagonal terms are shown to overall improve the DFTB performance; most importantly, with this new formalism, a single set of parameters is able to reproduce many properties of CHNO and phosphorous containing complexes with good accuracy. 1
In the next section, we give a short review of DFTB and SCC-DFTB as far as needed to explain the DFTB3 methodology. Next, computational details are discussed, including different ways for calculating proton affinities within the DFTB models. Finally, the performance of DFTB3 is evaluated for several test sets using data collected earlier,39,40 and compared to SCC-DFTB and its previous γh and diagonal third order variants.
2 Theoretical Approach
The efficiency of DFTB is essentially linked to the use of a reference density ρ0, which is calculated from a superposition of neutral atomic densities . This allows to compute Hamilton matrix elements in an atomic orbital (AO) basis in advance, i.e. no integral evaluation is necessary during the runtime of the calculation. The remaining contributions to the total energy are then approximated such that no further computational cost arises beyond the dominant step, which is the diagonalization of the pre-computed Hamilton matrix. Therefore, all required approximations in DFTB are centered around the reference density ρ0 and its deviation with respect to the DFT ground state density ρ, which is denoted by Δρ. The approximations involved have been discussed in detail in previous publications.22,38,49 Essentially, the exchange-correlation energy contribution is expanded in a Taylor series expansion as
| (2) |
where the abbreviations ∫ = ∫d3r, ∫’ = ∫d3r’, ∫” = ∫d3r, ρ = ρ(r), ρ’ = ρ(r’), and ρ” = ρ(r”) are used. The total energy can then be written as
| (3) |
Here ni is the occupation number of the i-th molecular orbital, Vne is the nucleus-electron potential, Vxc is the exchange-correlation potential, and Enn the nucleus-nucleus repulsion.
Approximations of different levels of sophistication can be introduced by truncation of the Talyor series.38 Standard (non-self-consistent) DFTB11,49 neglects second and higher order terms. This leads to a non self-consistent scheme, i.e., the generalized eigenvalue problem has to be diagonalized only once. The SCC-DFTB method approximates the second order terms in the density fluctuations9 while DFTB3 also includes the third order terms in an approximate way. In the following a brief summary of SCC-DFTB and derivations of the third order terms as well as the γh-function are given.
2.1 SCC-DFTB
The SCC-DFTB total energy is an approximation to the first three lines of eq 3. In a simple form the energy can be written as
| (4) |
First, (see eq 1) is the energy contribution from an atomic orbital Hamiltonian depending only on the reference density. The determination of the atomic reference densities and the LCAO basis functions ϕμ needed for the calculation of are discussed elsewhere.11 The Hamilton and overlap matrix elements and Sμv are precomputed and tabulated, i.e. they do not have to be computed during the runtime of the program. This and the use of a minimal valence basis set leads to huge computational savings (2-3 orders of magnitude) compared to full DFT.
Second, the repulsive energy contribution Erep is an approximation of the terms from the second line of eq 3 and consists of the so called DFT double-counting terms, the core repulsion terms and exchange-correlation contribution. In TB theory these terms are usually approximated as a sum of one-center terms and short ranged two-center potentials
| (5) |
where rab is the distance between atoms a and b. The atomic contributions are a constant energy shift which cancel when considering energy differences. For DFTB the atomic contributions are neglected and a repulsive energy Erep is defined as
| (6) |
Third, the energy contribution Eγ is derived from the third line of eq 3 as
| (7) |
where is the net charge of atom a and γ is a function taking account of the electron-electron interaction. The γ-function is given by the integral over a product of two normalized Slater-type spherical charge densities. We want to highlight two main properties of γab which are described in detail in ref 9. For large distances rab, γab basically reduces to 1/rab; i.e., it describes a pure Coulomb interaction of the partial charges Δqa and Δqb. For a=b, γab describes the on-site self-repulsion,
| (8) |
introducing the Hubbard parameter Ua (which is twice the chemical hardness). On the other hand, γab imposes an inverse relationship between the Hubbard parameter and the covalent radius by9
| (9) |
where τa is the exponent of the normalized Slater-type spherical charge density. Therefore, the Hubbard parameter affects two physical properties, the electron-electron interaction within one atom, i.e., the diagonal elements γaa, and the size of the atoms for estimating the two-center terms γab. This estimated atomic size determines the deviation of γab from 1/rab, as shown in Figure 1. The Hubbard parameter Ua is the second derivative of the total energy of a single atom with respect to the occupation number of the highest occupied atomic orbital. In SCC-DFTB it is estimated using Janack’s theorem50 by numerically calculating the first derivative of the energy of the highest occupied atomic orbital with respect to its occupation number for a neutral atom.
Figure 1.
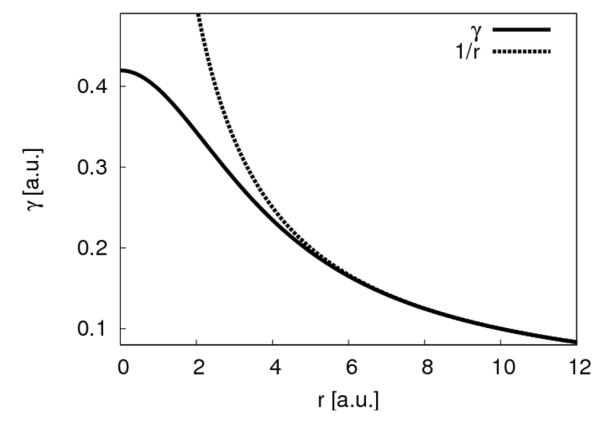
The γ-function (solid line) plotted for the hydrogen-hydrogen interaction deviates from 1/r (dashed line) at short distances and yields the value of the Hubbard parameter UH = 0.4195 a.u. at r = 0 a.u..
2.2 Third order term
An obvious extension of SCC-DFTB is to include also the third order term of the Taylor series expansion of the exchange correlation energy (eq 3). In second order DFTB, the chemical hardness of an atom (Ua) is constant irrespective of its charge state. For example, it does not allow anions to have a different chemical hardness value than the neutral atom or the cation. This is a severe limitation, as discussed in detail previously.22,38 Furthermore, in second order SCC-DFTB the atoms are restricted to have a fixed shape as defined by the initial reference density . In third order, these restrictions are removed, which leads to a significant improvement for highly charged molecules.
The third order term as shown in eq 3 is given by
| (10) |
The same approximations as for the second order integrals can be applied,38,39 (i.e., the description of the charge density fluctuations in terms of superposition of atomic contributions and the restriction of the charge density fluctuations to a monopole term, details see ref 9)
| (11) |
| (12) |
Therefore, in the third order DFTB formalism the derivative of the γ-function with respect to charge introduces the desired chemical behavior for charged systems. For the diagonal terms (first term in eq 12) the derivative of γ implies via eq 8 a charge dependent Hubbard parameter (chemical hardness), i.e. the chemical hardness changes with charge state. Since Ua is also used to approximate the atom size in the damped Coulomb repulsion term γ, a charge dependent Ua will also make the atomic electron-electron repulsion charge dependent. For the off-diagonal terms (second term in eq 12) this effect applies for the electron-electron repulsion between two atoms. Note that γab is dependent on the atomic charges only via the Hubbard parameters Ua and Ub. Introducing
| (13) |
where the latter definition is made to ease the summation, the third order energy contribution becomes
| (14) |
The derivative can be computed analytically, details are given in the Supporting Information. The diagonal term can be computed as the third derivative of the total energy of an atom with respect to charge. Practically, we compute the chemical hardness values for atoms in different charge states (applying Janack’s theorem) and use these values to estimate the third derivative.38
Thus, adding the approximated third-order contribution EΓ to ESCC-DFTB (eq 1) yields the total energy of the third-order formalism
| (15) |
A detailed derivation of the Kohn-Sham equations, the third order Hamilton matrix-elements
| (16) |
| (17) |
and the force equations
| (18) |
is provided in the Supporting Information.
2.3 The γh-function
The γ-function represents the Coulomb repulsion between the density fluctuations within the DFTB approximation, i.e., for spherically constrained atomic densities. In ref 9, an analytical function has been derived, which is:
| (19) |
where S is a short-range function being responsible for the correct convergence of γab at rab = 0. This function imposes a simple rule, which implies that the chemical hardness of an atom is inversely proportional to its size.9 As has been pointed out earlier, traditional semi-empirical methods like MNDO, AM1 or PM3 use a similar approximation for the Coulomb interaction.38 As discussed above, the Hubbard parameter Ua has a dual role: for the SCC on-site contributions, Ua models the effective Coulomb repulsion at site a, while for the off-diagonal terms, the inverse of Ua models the covalent radius of atom a, i.e., it determines the deviation of γab from 1/rab. However, this inverse relation of chemical hardness and atomic size is not strictly valid across the periodic table,38 it basically only holds within one period of the system of elements, as can be seen from Figure 2, which shows the calculated Hubbard parameters for each element in dependence of the covalent radii. Therefore, in principle a different γab should be applied for different rows of the periodic table. Clearly, the deviation is the largest for hydrogen, therefore we proposed to modify γab when hydrogen is involved and introduced a γh-function as38,39
| (20) |
where
| (21) |
In the following we will refer to this function as the γh-function in contrast to the γ-function as was used in standard SCC-DFTB (h = 1 for all cases). Note that different than mentioned in ref 39 the γh-function is also used for the H-H pair. The particular choice of h is to some degree arbitrary. On the other hand, its functional form is quite well physically motivated, correcting the shortcomings of the original function, since the chemical hardness of hydrogen simply cannot be used to represent the hydrogen covalent radius. We note that Clark and coworkers described a similar problem and modification for NDDO-based semi-empirical methods.52
Figure 2.
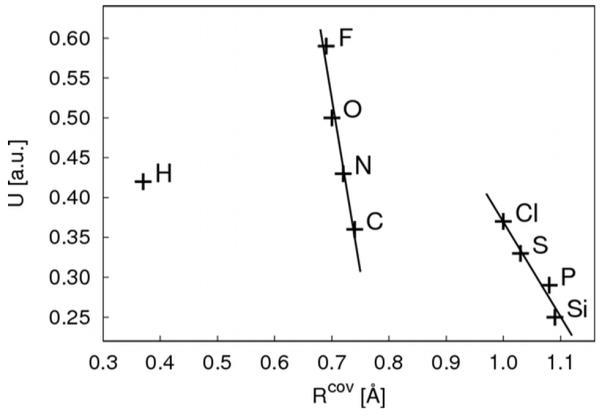
Calculated Hubbard parameters U versus covalent radii Rcov. The covalent radii are taken from the literature.51 For C, H, N, O, F values for Rcov are plotted that are estimated for bonds to second period elements, for Si, P, S, Cl values for Rcov are plotted that are estimated for bonds to third period elements. There is no overall inverse proportional relation as assumed by SCC-DFTB but only for elements within one period.
Up to now, the parameters introduced in the second and third order extensions, in principle, can be calculated based on DFT. Unfortunately, the parameter ζ in eq 21 cannot be computed from DFT but has to be fitted. However, as shown before,22,38 by choosing the parameter ζ such that the binding energy of the water dimer is reproduced correctly, γh becomes more repulsive in the covalent and hydrogen bonding region (see Figure 3), and improves hydrogen bonding systematically. We use the γh-function in combination with the third order terms. Therefore, also the derivative of the γh-function with respect to charge has to be calculated which is shown in detail in the Supporting Information.
Figure 3.
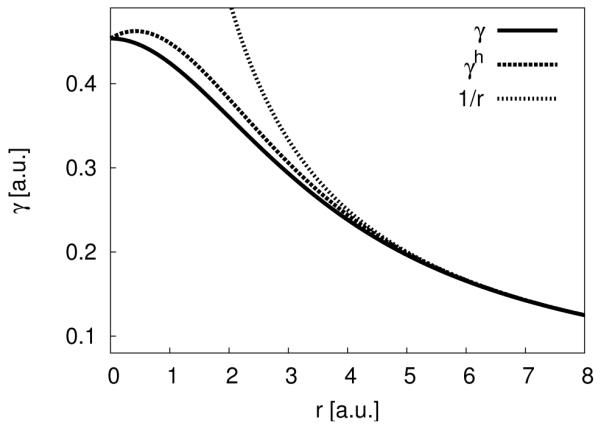
The γh-function plotted for the OH-pair (UO = 0.4954 a.u., UH = 0.4195 a.u.) is more repulsive than the original γ-function but still yields the same limits at r = 0 a.u. and at r → ∞.
3 Computational Details
With DFTB3, one major difference to earlier studies39,40 is the way of calculating proton affinities, which we explain first. We continue with a description of different DFTB variants benchmarked in this work. A short review of the parameters of SCC-DFTB is given and the new parameters of DFTB3 are introduced. Finally we discuss problems that occur for nitrogen containing species.
3.1 Calculation of Proton Affinities using DFTB
The proton affinity is defined as the negative of the enthalpy change for the gas-phase reaction A−(g) + H+(g) → AH(g) at a given temperature. To avoid a large number of vibrational calculations we consider in this work only the potential energy change and do not include zero-point correction, thermal contributions, and the PV-term (difference between energy and enthalpy). This is done consistently for both, reference calculations and DFTB calculations. Due to the neglect of the one-center terms in the repulsive potential eq 5, the energy of a proton is not zero in DFTB53 and can be computed in two ways:
- First, it is given by the SCC-DFTB energy as (see eq 1):
This is a direct result of neglecting the one center terms in the repulsive potential of eq 5, since eq 6 is used for all practical implementation and applications.53 Therefore, the energy of the proton is given by half of the Hubbard parameter of hydrogen, which is 131.62 kcal/mol when computed using the DFT-PBE functional. This value may not be considered an accurate estimate since the Hubbard parameter is computed for the neutral hydrogen atom, however, it is consistent with the SCC-DFTB formalism.(22) - Alternatively, the one center contribution to the repulsive potential can also be computed directly53 as
With the energy of the hydrogen atom EDFT = –0.49772 H (B3LYP/6-311++G(d,p)) and the electronic part of the SCC-DFTB energy, ESCC,el = EH0 + Eγ = –0.27164 H (first and second term in eq 1, here Eγ = 0 a.u.) gives a one-center repulsive energy contribution for the hydrogen atom of kcal/mol.532 For the proton the energy within SCC-DFTB is then given by kcal/mol. Clearly, the electronic energy of a proton should be equal to zero, however, UH is calculated as the derivative of the highest occupied atomic orbital with respect to the occupation number for the neutral hydrogen atom and cannot completely compensate for in the case of H+. For this unique situation where the total charge of the system is removed the pertubative approach of SCC-DFTB fails. Therefore, the energy of the proton was set to +141.87 kcal/mol in earlier studies.39,53(23)
With DFTB3 the direct calculation (i) is slightly modified:
| (24) |
The Hubbard derivative is −0.1857 H using DFT-PBE and the energy of the proton then equals 151.04 kcal/mol now overestimating the value of .
In previous applications, approach (ii) has been used,39,40,53,54 however, this may not be the best choice for general applications. In principle, the energy of the proton is just a constant and not relevant when relative proton affinities are of interest, as, for example, for proton transfer reactions. However, it becomes important when absolute proton affinities and pKa are of interest.55 In the following, we will show that fitting the Hubbard derivatives leads to a drastic improvement of the performance of the method. When Hubbard derivatives are fitted, as in the current work, it is more consistent to use eq 24. Computing the PA’s with
| (25) |
and using a fixed value for the DFTB energy of the proton EH+ means that a change in the Hubbard derivative due to fitting affects only the energy of the molecule AH (EAH) such that the reference proton affinity EPA is obtained irrespective of the potential well depth of the A-H bond. This problem is resolved when calculating EH+ with eq 24, EH+ being different for different hydrogen Hubbard derivatives.
For this reason we decide in the present work to consistently determine the energy of the proton with eq 22 and eq 24 depending on the level of theory.
3.2 DFTB variants
In DFTB a Taylor series expansion is applied for the DFT exchange-correlation energy. While DFTB, the non-selfconsistent variant, includes terms up to first order, SCC-DFTB includes also the second order term and DFTB3 also the third order term. For consistent naming we decided to use the names DFTB, DFTB2, and DFTB3. Note that DFTB2 corresponds to the formally called SCC-DFTB. By default the standard γ-function is used for DFTB2 and the γh-function for DFTB3. In the following benchmark we will compare
DFTB2: formally called SCC-DFTB using the standard γ-function (eq 19) as derived in ref 9 and
DFTB3: full third order extension (eq 15) including the γh-function (eq 20) as derived in present work.
Starting from DFTB2 three major changes have been made to develop DFTB3. First, the γh-function substitutes the standard γ-function, second, diagonal third order terms are included, and third, off-diagonal third order terms are taken into account. To illustrate the effects of each of these extensions separately we also present results for the following intermediate variants:
DFTB2-γh: the standard γ-function of DFTB2 is exchanged by the γh-function
DFTB3-γ: the standard γ-function is used in connection with DFTB3
DFTB3-diag: the γh-function is used and only the diagonal third order terms are included (second term in eq 12 is neglected) as suggested in refs 38,39.
Note that by introducing DFTB3 the intermediate variants become obsolete and are not recommended for practical applications. An overview of all DFTB variants is given in Table 1.
Table 1.
DFTB Variants Compared in Present Study
| name | diagonal third | off-diagonal | |
|---|---|---|---|
| γh-function | order terms | third order terms | |
| DFTB2 | no | no | no |
| DFTB2-γh | yes | no | no |
| DFTB3-γ | no | yes | yes |
| DFTB3-diag | yes | yes | no |
| DFTB3 | yes | yes | yes |
The additional computational costs of the γh-function and the full third order extensions are negligible compared to the diagonalization of the Hamilton matrix, which is the time limiting step in the DFTB methodology. Therefore, the computer time requirements are roughly the same for all variants in Table 1.
3.3 Parameter sets
3.3.1 Electronic and repulsive parameters
The parameters for DFTB2 can be divided into two groups: atomic and diatomic parameters. A short summary of the different parameters is given in the following, for more details see refs 9,11,38,54,56,57.
The atomic parameters are the two confinement radii for wave function and atomic reference density, the Hubbard parameter and the spin-polarization energy. The last two parameters are computed from DFT and are not freely adjustable, the spin-polarization energy is only needed in order to compute heats of formation.27 The two confinement radii are used for a proper choice of LCAO basis functions ϕμ and atomic reference densities . With these atomic parameters one-and two-center integrals of the charge-independent part of the Hamiltonian H0 are calculated in advance and tabulated; for more details see ref 22.
The two-body potentials in Erep (see eq 6) contain the diatomic parameters, which are usually fitted to reproduce reference data such as reaction energies and geometries of small molecules. For adequate fitting with several objectives, different techniques have been described in the literature.11,27,58,59 In this work we use the mio parameters for all atoms and pairs including C, H, N, and O,9,57 which are available from www.dftb.org.
Additionally we use phosphorous parameters as described in ref 40, which have not been released up to now, since the performance was not satisfactory at the second order DFTB2 level of theory. Many of these problems are resolved with DFTB3; however, since the repulsive potentials have been determined for DFTB2, these parameters are still not satisfactory for all purposes, as shown in detail below. Clearly, a new parametrization for DFTB3 has to be developed; nevertheless, current parameters provide reasonable geometries for a wide range of molecules and they will be available soon at www.dftb.org.
Briefly, the confinement radii for phosphorous are chosen as those for sulfur,60 that is 3.8 a0 for the wavefunction of the 3s and 3p valence orbitals, 4.4 a0 for 3d orbitals, and 9.0 a0 for the density compression. While the DFT eigenvalue of the d-orbital is calculated as εd = 0.02 H, it was set to εd = 0.52 H in order to reduce excessive d-orbital involvement in binding situations. The repulsive potentials for six different pairs (P-P, P-C/H/N/O/S) are fitted to a B3LYP/6-31G(d) reference and are truncated to zero in the range of 1.7-3.3 Å using the molecules PH3, PCH, HPCH2, H2PCH3, PN, HPNH, H2PNH2, P2, HPPH, H2PPH2, OPH, H3PO4, H4PO–5, HPS, and H2PSH. Details for the general fitting procedure as has been carried out for the phosphorous parameters can be found in refs 9,57.
3.3.2 New Parameters
The γh-function for the pairs HX (X∈{C, H, N, O, P, S}) describes the dependence between the size of the atom and the electron-electron interaction more correctly; one additional, purely empirical parameter ζ is necessary. It can be determined using only one data point, the binding energy of the water dimer, for which the most accurate theoretical value is 5.0 kcal/mol using CCSD(T).61 Nevertheless, to stay consistent within our fitting procedure as described below we choose the similar value of 4.9 kcal/mol, which is the result from the G3B362,63 method. In Table 2 we denote this way of determining ζ as “calc”. We will also fit this parameter to reproduce an extended data set, in combination with fitting the Hubbard derivatives, then denoted as “fit”.
Table 2.
Parameter Sets for the Different DFTB Variants
| variant | seta | ζ b | c | c | c | c | c | c |
|---|---|---|---|---|---|---|---|---|
| DFTB2 | - | - | - | - | - | - | - | |
| DFTB2-γh | calc | 3.70d | - | - | - | - | - | - |
| DFTB3-γ | calc | - | −0.1492 | −0.1857 | −0.1535 | −0.1575 | −0.0702 | −0.0695 |
| DFTB3-diag | calc | 4.53 | −0.1492 | −0.1857 | −0.1535 | −0.1575 | −0.0702 | −0.0695 |
| DFTB3-diag | fit | 5.0 | −0.04 | −0.14 | −0.11 | −0.17 | −0.07 | - |
| DFTB3 | calc | 4.05 | −0.1492 | −0.1857 | −0.1535 | −0.1575 | −0.0702 | −0.0695 |
| DFTB3 | fit | 4.2 | −0.23 | −0.16 | −0.13 | −0.19 | −0.14 | - |
“calc” stands for calculated Hubbard derivatives Ud and/or ζ fitted to the water dimer; “fit” for a set of parameters fitted to a large set of binding energies and proton affinities. For details see text.
ζ is the unitless parameter as defined in eq 21
is the Hubbard derivative with respect to the occupation number of the highest occupied atomic orbital nX of atom type X in atomic units. In our third order formalism we define
Note that ζ is fitted to yield a binding energy for the water dimer of −4.9 kcal/mol in contrast to ζ = 4.5 as reported in ref39 for DFTB2-γh where ζ was fitted to minimize the error of 22 selected binding energies.
The third order Taylor series expansion of the exchange correlation energy makes use of the Hubbard derivatives , which means one additional parameter per element. These can be determined by taking the numerical derivative of the corresponding Hubbard parameter of a neutral atom with respect to the occupation number of the highest occupied atomic orbital. In Table 2 the Hubbard derivatives are summarized and abbreviated as “calc”; they are calculated with the PBE exchange-correlation functional64 and our in-house program TWOCENT.
Therefore, one parameter set we provide is the “calc” set, where only one parameter (ζ) is fitted to one system (water dimer), and all Hubbard derivatives are calculated. In a different approach, we fit all parameters for a large set of molecules, resulting in the parameter set “fit”. This has been done first for the DFTB3-diag method in ref 39.
It is important to note that fitting of the Hubbard derivatives and ζ basically affects hydrogen bonds and proton affinities, most properties of neutral molecules like equilibrium geometries are not significantly altered. Nevertheless, one has to be careful not to correct at the third order level for errors that result from the second order formalism, i.e., short-comings resulting from the electronic and repulsive parameters of the original DFTB2. Our results indicate that the approximations in the third order terms account very well for the physical effects arising from that level. The remaining errors in the description of H-bonding and proton affinities seem not to result from the third order approximations but from the underlying second order DFTB2. For the moment, we optimize DFTB3 parameters to make it applicable to important chemical and biological problems without refining the DFTB2 approximations.
The idea of DFTB2 is to use as many parameters calculated from DFT as possible. By fitting the Hubbard derivatives we are leaving this spirit and it seems natural to challenge the insistence on DFT calculated Hubbard parameters UX. Surely, a fitting also of these parameters may lead to an improved chemical accuracy, however, at cost of the following benefits; first, a physically robust and transferable method, second, an easy detection of systematic errors, and third, a small space of parameters allowing an easier fitting of the remaining parameters (especially because the Hubbard parameters affect mainly all chemical properties for systems of biological relevance). Please also note that the third order formalism introduces new physics into our method that cannot be compensated just by a new set of fitted Hubbard parameters. In that sense our future work is focused on avoiding empirical fitting of Hubbard parameters and derivatives by improving the electronic (confining radii) and repulsive parameters, that are till now fitted on DFTB2, at the DFTB3 level.
To optimize the parameters for DFTB3-diag, Yang et al. chose a weighted penalty function where the properties of interest included binding energies, proton affinities as well as the root-mean-square gradient of the included molecules calculated at the reference structure.39 Finally they minimized the penalty function using a genetic algorithm optimizing the Hubbard derivatives and the ζ-parameter. In this work we use a “brute force” fitting. A small set of parameters around the calculated values (ζ fitted to the water dimer) is chosen and the performance is evaluated by calculating the mean unsigned error (MUE) of proton affinities and binding energies using geometry optimized molecules for each parameter set. Whenever the parameter set that performs the best reaches a boundary of the current range of parameters, the range is extended. The latter step is repeated until the best set is does not reach any boundaries of the current range.
For the fitting of ζ and the Hubbard derivatives of C, H, N, and O, a set of 22 binding energies and 32 proton affinities as compiled by Yang et al.39 is used to represent important biological properties. The calculations are carried out in the gas phase at 0 K without including the zero-point corrections for both reference and DFTB. Subsequently, the Hubbard derivative of phosphorous is fitted to a set of 18 proton affinities of phosphorous containing molecules (compilation from ref 40) in the same manner but keeping all other parameters fixed. All molecules involved in the fitting procedure are listed in the following subsections.
It is found that the Hubbard derivative of carbon becomes very small during the fitting of DFTB3/fit while all other Hubbard parameters stay close to the calculated values. To avoid getting unphysical values we limit to a lower boundary of −0.23 H. 3 Similarly, becomes quite large during the fit of DFTB3-diag/fit such that we limit it to an upper boundary of −0.04 a.u.. Note that the fitted parameters are different from the ones published by Yang et al.39 since the way of computing proton affinities is different (details see above).
The additional off-diagonal terms within DFTB3 seem to be more repulsive in comparison with DFTB3-diag, therefore ζ becomes smaller to compensate for that as shown in Table 2.
3.3.3 Nitrogen hybridization: a problematic case for a minimal basis set method
Nitrogen hybridization seems to pose a problem for minimal basis set methods like DFTB as well as for NDDO type semi-empirical methods.52 This problem, which may be related to the neglect of d-orbitals in the basis set, is not corrected for by neither γh-function nor the third order terms and leads to dramatic errors when computing deprotonation energies. In previous studies,22,48 consistent errors of about 10 kcal/mol were found specifically for proton affinities of sp3 hybridized nitrogen atoms. Therefore, a modified parameter set “NHmod” was introduced in which the N-H repulsive potential was shifted to correct for these errors. However, since sp2 hybridized nitrogen atoms seem to be described correctly, this correction has only to be applied for a certain electronic configuration of N. Therefore, similar to the situation in force fields, different “atom types” for N have to be introduced at the moment, which clearly limits DFTB’s applicability since these atom types are not allowed to change during a reaction. In this work we present results for a “NHorg” and a “NHmix” parameter set. NHorg denotes the parameters for N-H bonds from the mio set, i.e., in this set no different atom types occur. For the NHmix set the mio potential is only used for compounds containing sp2 or sp1 nitrogen whereas NHmod is applied for sp3 hybridized nitrogen atoms. For reactions where a nitrogen changes its hybridization state from sp2 or sp to sp3 the NHorg repulsive potential is used in order to have consistent energetic contributions for the N-H atom pairs. 4
The fitting procedure for ζ and the Hubbard derivatives is applied separately for NHorg and NHmix; however, both optimized parameters turn out to be equal. This extends the transferability of the “fit” parameter sets (see Table 2) and implies that besides for “calc” also for “fit” the NHorg and NHmix results differ only for test molecules where a sp3 nitrogen is bound to hydrogen.
4 Benchmarks and Discussion
In the following subsections we present benchmark calculations for the different DFTB variants shown in Table 1 regarding geometries, binding energies, proton affinities and proton transfer barriers for CHNO containing molecules and also compare the results with commonly used density functionals. We further show results on proton affinities and hydrolysis reactions of phosphorous containing molecules. Finally some general benchmarks are provided for phosphorous parameters.
The parameters used for the γh-function and third order terms are given in Table 2 and if not explicitly stated, the NHorg repulsive potential is used. Binding energies, proton affinities, proton transfer barriers, and reaction energies are computed using the potential energies at 0 K without including any zero-point energy correction. Deviations are given as the difference to high level ab initio methods (Emethod – Ehigh level), where the high level calculations are performed using the Gaussian03 program.65
The compilation and notation for binding energies and proton affinities are taken from ref 39, proton affinities and hydrolysis reactions of phosphorous containing molecules from ref 40.
4.1 Geometries
The performance of the different DFTB variants is tested for the charge-neutral closed-shell molecules of the G266 set. As shown in Table 3 the geometries do not change significantly for all tested DFTB variants and parameter sets. Similarly, the different NH repulsive potentials NHorg and NHmix cause only very small differences for geometries, for details see Supporting Information.
Table 3.
Mean Unsigned and Maximum Absolute Deviation of Geometrical Propertiesa of the G2 Set for 61 CHNO-Containing Closed Shell Molecules for Different DFTB Variantsb
| Nc | DFTB2 | DFTB3 | PBEd | B3LYPd | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| γ | γ h | γ | diag | full | ||||||
| parameter setb | calc | calc | fit | calc | fit | |||||
| r (Å) | 223 | 0.014 | 0.014 | 0.014 | 0.014 | 0.014 | 0.014 | 0.014 | 0.009 | 0.004 |
| rmax (Å) | 223 | 0.065 | 0.067 | 0.061 | 0.064 | 0.064 | 0.062 | 0.063 | 0.060 | 0.041 |
| a (deg) | 187 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 1.0 | 0.4 | 0.4 |
| amax (deg) | 187 | 4.7 | 6.4 | 4.9 | 6.4 | 6.2 | 6.6 | 6.5 | 1.9 | 1.9 |
bond lengths r, bond angles a, max stands for maximum absolute deviation. Geometric data is compared to the MP2/cc-pVTZ calculations. For details, see Supporting Information.
Number of comparisons
Basis set 6-311G(2d,2p)
Significant differences occur for charged molecules, some of them are summarized in Table 4. For example, the C-C bond length in the acetate anion is overestimated by DFTB2 in comparison to B3LYP67–69/cc-pVTZ;70 that error becomes smaller for the DFTB variants including third order terms. Similar findings are obtained for the O-H bond length of the hydroxide anion, even though in this case also the γh-function has a significant effect. The hydrogen bond length in the water dimer is overestimated using B3LYP/cc-pVTZ71 due to the admixture of HF exchange, it is shorter for a pure GGA functional like PBE/cc-pVTZ, where this bond length is 1.917 Å. DFTB2 under-estimates this bond length (1.889 Å ) indicating that the Pauli repulsion may be underestimated by DFTB. Inclusion of the γh-function even further shortens the hydrogen bond. It is important to note that this is a general trend (also valid for e.g. water clusters), i.e., hydrogen bond lengths are predicted systematically too short by DFTB.
Table 4.
Deviation of DFTB in Comparison to B3LYP/cc-pVTZ for Selected Bond Lengths r in Å
4.2 Binding energies
In a previous study it has been shown that DFTB2 underestimates the strength of hydrogen bonding interactions.39 The performance for hydrogen bonds is drastically improved using the γh-function as shown in Table 5, while the third order corrections alone (3rd) does not seem to have a substantial effect on these properties, however, the errors for the negative charged species are now more consistent with the ones of neutral and positive charged systems. The combination of both extensions in DFTB3-diag and DFTB3 adopts both improvements, the mean unsigned error in comparison to G3B362,63 drops from 8 kcal/mol for DFTB2 to about 3 kcal/mol irrespective of the set of Hubbard derivative parameters (Ud) used. In ref 39 the test of DFTB3-diag have been extended to a larger test set, and we expect similar results for DFTB3.
Table 5.
22 Binding Energies in kcal/mol: Deviation of DFTB in Comparison to G3B3a
| G3B3 | DFTB2 | DFTB3 | ||||||
|---|---|---|---|---|---|---|---|---|
| γ | γ h | γ | diag | full | ||||
| parameter setb | calc | calc | fit | calc | fit | |||
| 2H2O | −4.9 | +1.6 | −0.0 | +1.5 | −0.0 | +0.2 | −0.0 | +0.0 |
| 3H2O | −15.1 | +5.5 | −0.6 | +5.4 | −0.5 | +0.2 | −0.3 | −0.1 |
| 4H2O | −27.4 | +9.7 | +0.6 | +9.4 | +0.8 | +1.8 | +0.8 | +1.1 |
| 5H2O | −36.3 | +13.3 | +1.4 | +12.5 | +1.8 | +3.0 | +1.3 | +1.7 |
| 2H2O(H+) | −33.9 | +4.5 | −2.0 | +5.9 | +2.4 | +3.4 | +0.9 | +2.1 |
| 3H2O(H+) | −57.3 | +10.4 | −0.1 | +11.6 | +5.3 | +6.6 | +3.7 | +5.3 |
| 4H2O(H+) | −77.2 | +13.9 | +1.1 | +15.0 | +6.4 | +7.9 | +5.0 | +6.7 |
| 5H2O(H+) | −91.9 | +18.3 | +1.8 | +19.7 | +7.2 | +9.1 | +6.2 | +8.1 |
| 2H2O(−H+) | −27.4 | −5.1 | −12.8 | +1.5 | −3.4 | −1.5 | −5.9 | −3.2 |
| 3H2O(−H+) | −48.6 | −2.6 | −17.0 | +5.3 | −6.5 | −3.8 | −8.4 | −5.3 |
| 4H2O(−H+) | −66.7 | +0.3 | −17.5 | +9.0 | −5.0 | −1.8 | −7.2 | −3.5 |
| 5H2O(−H+) | −86.3 | +6.1 | −18.2 | +14.2 | −7.7 | −4.1 | −7.8 | −4.7 |
| NH3(H2O) c | −6.6 | +3.2 | +2.1 | +3.1 | +2.0 | +2.2 | +2.1 | +2.1 |
| NH+4(H2O) c | −20.4 | +0.6 | −3.4 | +1.4 | −1.1 | −0.7 | −1.3 | −0.9 |
| 6H2O_book | −45.8 | +16.7 | +1.2 | +16.5 | +1.5 | +3.2 | +1.7 | +2.2 |
| 6H2O_cage | −46.6 | +17.2 | +0.3 | +17.6 | +0.3 | +2.1 | +1.5 | +1.8 |
| 6H2O_prism | −47.2 | +17.6 | −0.0 | +18.0 | +0.1 | +2.0 | +1.3 | +1.7 |
| 6H2O_ring | −44.7 | +16.5 | +1.8 | +15.3 | +2.4 | +3.9 | +1.5 | +2.1 |
| methylimidazole(−H+)(H2O) | −15.9 | +4.1 | +2.0 | +3.2 | +1.4 | +1.5 | +1.2 | +1.1 |
| methylimidazole(H2O)_1 | −6.2 | +2.4 | +1.4 | +2.6 | +1.8 | +1.9 | +1.9 | +2.0 |
| methylimidazole(H2O)_2 | −8.2 | +3.5 | +2.6 | +2.8 | +2.0 | +2.2 | +1.9 | +1.9 |
| methylimidazoleH+(H2O) | −16.0 | +3.3 | +1.2 | +3.9 | +2.2 | +2.3 | +2.3 | +2.5 |
|
| ||||||||
| MUE | 8.0 | 4.0 | 8.9 | 2.8 | 3.0 | 2.9 | 2.7 | |
| MSE | +7.3 | −2.5 | +8.9 | +0.6 | +1.9 | +0.1 | +1.1 | |
| MAX | 18.3 | 18.2 | 19.7 | 7.7 | 9.1 | 8.4 | 8.1 | |
The binding energy is computed as the difference between the complex and the isolated molecules at 0 K, no zero-point energy correction has been included. For the DFTB-methods the deviation is given as the difference to the G3B3 method (Emethod – EG3B3). Compilation of molecules and notation taken from ref 39, Examples of notation: “2H2O”, neutral water dimer; “2H2O(H+)”, protonated water dimer; “2H2O(−H+)”, deprotonated water dimer, “6H2O_book”, neutral water hexamer in the book configuration; “methylimidazole(−H+)(H2O)”, deprotonated methylimidazole comlexed with water; “methylimidazole(H2O)_1”, neutral methylimidazole complexed with water as hydrogen-bond donor; “methylimidazole(H2O)_2”, neutral methylimidazole complexed with water as the hydrogen-bond acceptor; “methylimidazoleH+(H2O)”, protonated methylimidazole complexed with water
When applying NHmix the results are slightly but not significantly different.
In many biological applications, DFT methods with medium sized basis sets are applied. In order to compare DFTB with DFT, we compile also binding energies for the same molecule set (Table 5) using PBE and B3LYP with the 6-31+G(d,p) basis set, which give a mean unsigned error of 7.0 and 3.7 kcal/mol (for details, see Supporting Information). These errors are significantly larger when using basis sets without diffuse function. This of course is due to the basis set super-position error (BSSE) which can be remediated when including the counterpoise correction,72,73 dropping the MUE to 3.7 and 1.3 kcal/mol, respectively. Nevertheless we think it is important to be aware of these large errors, for example, when studying larger bio-molecular systems where the counterpoise correction is rarely done. Therefore, although it is often claimed that certain DFT functionals perform well for hydrogen bonding,74–77 this is only true for converged basis sets, which are often not used in practical applications. In such cases the use of a well calibrated approximate method like DFTB can be even a more appropriate choice. For example, the finding that the active site of bacteriorhodopsin is scrambled using QM/MM-CPMD simulation may be related to an imbalanced description of QM, QM/MM and MM interactions, where one factor contributing to the imbalance may be BSSE.78 The application of empirical dispersion corrections would even worsen the problem, since dispersion further strengthens the interaction, i.e., leads to an even larger over-binding.
4.3 Proton affinities
As shown in earlier studies,39,79 DFTB2 overestimates proton affinities (PA) that implicate acidic oxygen. Yang et al. report an improvement with DFTB3-diag for molecules in which charge is strongly localized, a situation where the third-order term contributes accordingly. In these studies the DFTB2 energy of the proton was assumed to be 141.9 kcal/mol; in the present work we use eq 22 for DFTB2 and eq 24 for DFTB3. Consequently the proton affinities as compiled in Table 6 are shifted by about 10 kcal/mol for DFTB2 in comparison to the earlier studies.
Table 6.
23 Proton Affinities with Acidic Oxygen in kcal/mol: Deviation of DFTB in Comparison to G3B3a
| G3B3 | DFTB2 | DFTB3 | ||||||
|---|---|---|---|---|---|---|---|---|
| γ | γ h | γ | diag | full | ||||
| parameter setb | calc | calc | fit | calc | fit | |||
| H2O | 398.4 | +16.3 | +18.5 | +8.0 | +5.8 | −1.6 | +7.5 | −1.8 |
| 2H2O | 375.9 | +9.6 | +5.7 | +8.0 | +2.3 | −3.2 | +1.7 | −5.1 |
| 3H2O | 365.0 | +8.1 | +1.9 | +7.7 | −0.4 | −5.6 | −0.7 | −7.1 |
| 4H2O | 359.1 | +7.0 | +0.3 | +7.5 | −0.1 | −5.2 | −0.5 | −6.5 |
| 5H2O | 348.4 | +9.2 | −1.1 | +9.6 | −3.7 | −8.7 | −1.6 | −8.3 |
| CH3OH | 392.6 | −5.7 | −2.6 | +3.3 | +5.8 | −0.7 | +5.9 | −0.3 |
| CH3CH2OH | 388.3 | −1.5 | +1.6 | +6.5 | +9.3 | +2.6 | +9.0 | +2.2 |
| CH3CH2CH2OH | 387.6 | −2.2 | +1.0 | +6.0 | +8.7 | +1.9 | +8.6 | +2.0 |
| CH3-CH(OH)-CH3 | 385.6 | +1.4 | +4.7 | +8.2 | +11.7 | +4.6 | +10.7 | +3.3 |
| HCOOH | 351.2 | +1.7 | +3.4 | +8.6 | +14.2 | +7.1 | +10.0 | +2.9 |
| CH3COOH | 355.1 | +1.1 | +3.2 | +6.8 | +12.7 | +5.6 | +8.5 | +0.6 |
| CH3CH2COOH | 354.5 | +1.0 | +3.4 | +7.5 | +13.1 | +6.0 | +9.3 | +1.5 |
| C6H5OH | 356.7 | −4.7 | −2.4 | +8.0 | +11.0 | +5.2 | +9.7 | +4.0 |
| p-CH3-C6H4OH | 357.9 | −5.6 | −3.1 | +7.4 | +10.5 | +4.5 | +9.2 | +3.7 |
| p-NO2-C6H4OH | 334.6 | −9.3 | −7.5 | +2.2 | +5.2 | −0.7 | +3.5 | −1.3 |
| H3O+ | 171.2 | −0.4 | −4.7 | +10.6 | +9.0 | +5.6 | +6.3 | +4.3 |
| 2H2O(H+) | 200.2 | −3.3 | −2.7 | +6.3 | +6.6 | +2.3 | +5.4 | +2.2 |
| 3H2O(H+) | 213.4 | −5.3 | −5.1 | +4.4 | +3.2 | −0.9 | +2.3 | −1.2 |
| 4H2O(H+) | 221.1 | −4.7 | −5.3 | +4.9 | +3.3 | −0.7 | +2.0 | −1.4 |
| 5H2O(H+) | 226.7 | −5.3 | −5.1 | +3.5 | +3.8 | −0.4 | +1.4 | −1.9 |
| CH3OH+2 | 186.8 | −8.3 | −10.3 | +6.5 | +6.1 | +2.0 | +4.6 | +2.2 |
| H2COH+ | 177.1 | −11.8 | −13.8 | +4.3 | +4.3 | +0.5 | +2.6 | −0.2 |
| CH3CHOH+ | 190.2 | −10.1 | −10.8 | +5.8 | +6.5 | +2.4 | +5.1 | +2.0 |
|
| ||||||||
| MUE | 5.8 | 5.1 | 6.6 | 6.8 | 3.4 | 5.5 | 2.9 | |
| MSE | −1.0 | −1.3 | +6.6 | +6.5 | +1.0 | +5.2 | −0.2 | |
| MAX | 16.3 | 18.5 | 16.6 | 14.2 | 8.7 | 10.7 | 8.3 | |
The molecules are given in the protonated form. The proton affinity is computed with the potential energies at 0 K without any zero-point energy correction. For the DFTB methods the deviation is given as the difference to the G3B3 method (Emethod – EG3B3). The compilation of the molecules is taken from ref 39.
While the mean signed error (MSE) for DFTB2 in comparison to G3B3 is quite small, the proton affinities of negatively charged molecules are overestimated and the proton affinities for neutral molecules underestimated. This holds true also when including the γh-function. The situation changes when looking at the third order variants. Even though the MUE is not significantly reduced (or even enlarged) in comparison to DFTB2 the proton affinities for almost all molecules are consistently overestimated and the MSE is (almost) as large as the MUE (+5.2 vs 5.5 kcal/mol in the case of DFTB3/calc). This indicates a consistent overbinding of the O-H bond. This error, however, is not related to the third order formalism but has its roots already in the repulsive potential of DFTB2. As Otte et al26 mentioned, the O-H bond shows an overbinding of about 6-7 kcal/mol. This overbinding can also be roughly estimated by the half of the atomization energy error of H2O, which is 5.8 kcal/mol for DFTB3/calc (using PBE spin-polarization energies, details see ref 27) in comparison to G3B3. This value is very similar to the MSE of DFTB3/calc (5.2 kcal/mol) in Table 6, leading to the conclusion that removing this overbinding remedies the error for the proton affinities. Indeed, once fitting the third order and γh-function parameters (DFTB3/fit) the MSE can be removed to obtain a MUE as small as 2.9 kcal/mol. 5 This would not work for DFTB2, indicating that the third order terms systematically lead to an improvement of DFTB.
Proton affinities with acidic nitrogen are shown in Table 7. Here, DFTB2 shows large errors, which are systematically improved by all third order variants. Large errors remain for the last three molecules in Table 7 with sp3-nitrogen, which show a systematic error of more than 10 kcal/mol, as discussed in detail already in ref.39 The use of NHmod specifically for sp3 hybridized nitrogen, although not satisfactory from a theoretical point of view, remedies this problem (see Table 8). That way the remaining MUE for DFTB3/calc/NHmix is only 2.5 kcal/mol.
Table 7.
9 Proton Affinities with Acidic Nitrogen in kcal/mol: Deviation of DFTB and the NHorg Parameter Set in Comparison to G3B3a
| G3B3 | DFTB2 | DFTB3 | ||||||
|---|---|---|---|---|---|---|---|---|
| γ | γ h | γ | diag | full | ||||
| parameter setb | calc | calc | fit | calc | fit | |||
| HCNH+ | 176.0 | −12.4 | −14.6 | +4.5 | +4.3 | +0.4 | +2.8 | +0.2 |
| CH3CNH+ | 192.3 | −14.3 | −15.4 | +2.9 | +2.6 | −1.2 | +1.9 | −0.9 |
| C5H5NH+ | 229.5 | −17.1 | −18.3 | +1.3 | +0.9 | −3.5 | +0.4 | −2.1 |
| methylimidazoleH+ | 237.3 | −12.7 | −13.4 | +5.3 | +5.1 | +0.8 | +4.7 | +2.1 |
| methylguanidineH+ | 249.3 | −12.0 | −13.4 | +0.8 | +0.4 | −2.2 | −0.8 | −2.9 |
| NH3 | 413.9 | +10.4 | +10.9 | −0.9 | −16.8 | −0.0 | −5.3 | −0.2 |
| NH+4 | 212.3 | −24.4 | −30.5 | −9.2 | −13.0 | −15.0 | −14.4 | −15.8 |
| CH3NH+3 | 223.3 | −26.8 | −30.5 | −10.2 | −11.7 | −15.1 | −13.3 | −15.3 |
| 1-aminobutaneH+ | 228.2 | −26.7 | −29.9 | −9.8 | −11.4 | −14.9 | −12.6 | −14.6 |
|
| ||||||||
| MUE | 17.4 | 19.7 | 5.0 | 7.4 | 5.9 | 6.2 | 6.0 | |
| MSE | −15.1 | −17.2 | −1.7 | −4.4 | −5.6 | −4.1 | −5.5 | |
| MAX | 26.8 | 30.5 | 10.2 | 16.8 | 15.1 | 14.4 | 15.8 | |
The molecules are given in the protonated form. The proton affinity is computed with the potential energies at 0 K without any zero-point energy correction. For the DFTB methods the deviation is given as the difference to the G3B3 method (Emethod – EG3B3). The compilation of the molecules is taken from ref 39.
Table 8.
9 Proton Affinities with Acidic Nitrogen in kcal/mol: Deviation of DFTB and the NHmix Parameter Set in Comparison to G3B3a
| G3B3 | DFTB2 | DFTB3 | ||||||
|---|---|---|---|---|---|---|---|---|
| γ | γ h | γ | diag | full | ||||
| parameter setb | calc | calc | fit | calc | fit | |||
| HCNH+ | 176.0 | −12.4 | −14.6 | +4.5 | +4.3 | +0.4 | +2.8 | +0.2 |
| CH3CNH+ | 192.3 | −14.3 | −15.4 | +2.9 | +2.6 | −1.2 | +1.9 | −0.9 |
| C5H5NH+ | 229.5 | −17.1 | −18.3 | +1.3 | +0.9 | −3.5 | +0.4 | −2.1 |
| methylimidazoleH+ | 237.3 | −12.7 | −13.4 | +5.3 | +5.1 | +0.8 | +4.7 | +2.1 |
| methylguanidineH+ | 249.3 | −12.0 | −13.4 | +0.8 | +0.4 | −2.2 | −0.8 | −2.9 |
| NH3 | 413.9 | +10.4 | +10.9 | −0.9 | −16.8 | −0.0 | −5.3 | −0.2 |
| NH+4 | 212.3 | −13.1 | −19.5 | +2.0 | −2.0 | −3.8 | −3.4 | −4.8 |
| CH3NH+3 | 223.3 | −15.4 | −19.2 | +1.2 | −0.4 | −3.8 | −2.0 | −4.0 |
| 1-aminobutaneH+ | 228.2 | −15.3 | −18.6 | +1.6 | −0.1 | −3.5 | −1.2 | −3.3 |
|
| ||||||||
| MUE | 13.6 | 15.9 | 2.3 | 3.6 | 2.1 | 2.5 | 2.3 | |
| MSE | −11.3 | −13.5 | +2.1 | −0.7 | −1.9 | −0.3 | −1.8 | |
| MAX | 17.1 | 19.5 | 5.3 | 16.8 | 3.8 | 5.3 | 4.8 | |
The molecules are given in the protonated form. The proton affinity is computed with the potential energies at 0 K without any zero-point energy correction. For the DFTB methods the deviation is given as the difference to the G3B3 method (Emethod – EG3B3). The compilation of the molecules is taken from ref 39.
Another encouraging result is the improvement of the proton affinity for NH2−. While for DFTB2 the proton affinity is overestimated, it is underestimated for DFTB3-diag. The error is then substantially reduced using the full third order variants, DFTB3-γ and DFTB3, showing the first example where the third order off-diagonal terms seem to be of importance.
Due to the hybridization problem the error analysis for N-H bond is more involved. Nevertheless, the overbinding of the N-H bond calculated as a third of the error in the atomization energy of NH3 for DFTB3/calc as compared to G3B3 is 2.9 kcal/mol (using PBE spin-polarization energies, details see ref 27), which is comparably small. With the O-H overbinding of 5.8 kcal/mol, we can estimate the error for the relative proton affinity between oxygen and nitrogen containing molecules to be roughly (5.8-2.9) kcal/mol = 2.9 kcal/mol, which is an important measure for the accuracy of proton transfer energetics between different donor and acceptor species.
We also benchmark DFT methods with medium sized basis sets for proton affinities. The MUE of PBE/6-31+G(d,p) and B3LYP/6-31+G(d,p) in comparison to G3B3 is 4.7 kcal/mol and 2.5 kcal/mol, which is comparable to the performance of DFTB3. Note that the use of diffuse functions is essential here, and errors for calculations without diffuse functions are much larger (for details see Supporting Information). For example, the use of HF/4-31G for the description of a proton transfer reaction may not yield a correct description of the dynamics due to errors in the PA’s of donor and acceptor.80
Overall one can find a clear difference in the performance of DFTB2 and DFTB3 due to the inclusion of the third order terms, whereas DFTB3-diag and DFTB3 perform very similar on proton affinities. As for the binding energies, Yang et al.39 compiled larger test sets and showed that DFTB3-diag overall improves the description of proton affinities. This is true for both, using calculated Hubbard derivatives or fitted Hubbard derivatives. With these findings we also expect similar behavior for DFTB3. We have seen that an improved performance for both, hydrogen binding energies and proton affinities of DFTB2 is only found when including both extensions, γh-function and third order terms. Therefore, further benchmark tests are shown in the following for the combination of these extensions and also the improvement of DFTB3 over DFTB3-diag will be discussed.
4.4 Proton transfer barriers
For testing proton transfer barriers, several simple models are considered. For the O…H…O models, we place a proton between two water molecules and between two hydroxide anions. The barriers are calculated for a fixed oxygen-oxygen distance with the shared proton at half the distance between both oxygens. All other hydrogen atoms are geometry optimized. For the relaxed structure, the shared proton is allowed to relax. While for the cationic complex the barriers calculated with MP281/G3large62 are already well reproduced with DFTB2, large errors occur for the anionic model for large O-O distance. These errors are completely removed for both DFTB3-diag and DFTB3. Table 9 summarizes the results, from which we note that the DFTB3 results represent a notable improvement over popular DFT methods with an intermediate basis set.
Table 9.
Proton Transfer Barrier in kcal/mol for a Fixed Distance (rXY) between the Heavy Atoms (X,Y∈{O,N}): Deviation of DFTB and DFT in Comparison to MP2/G3largea
| barrier | rXY | MP2 | DFTB2 | DFTB3-diagb | DFTB3b | PBEc | B3LYPc | ||
|---|---|---|---|---|---|---|---|---|---|
| calc | fit | calc | fit | ||||||
| [H2O-H-H2O]+ | 2.5 | 0.6 | −0.6 | −0.6 | −0.6 | −0.6 | −0.6 | −0.5 | −0.4 |
| 2.6 | 2.4 | −1.4 | −0.2 | +0.0 | −1.1 | −0.8 | −1.9 | −1.0 | |
| 2.7 | 5.2 | −1.1 | +0.5 | +0.8 | −0.7 | −0.3 | −3.2 | −1.5 | |
| 2.8 | 8.9 | −1.3 | +0.5 | +0.9 | −0.9 | −0.4 | −4.4 | −1.9 | |
|
| |||||||||
| [OH-H-OH]− | 2.5 | 0.5 | −0.5 | −0.5 | −0.5 | −0.5 | −0.5 | −0.5 | −0.2 |
| 2.6 | 2.3 | −2.3 | −0.6 | −0.2 | −0.7 | +0.0 | −1.6 | −0.6 | |
| 2.7 | 5.2 | −4.6 | −0.0 | +0.5 | −0.2 | +0.9 | −2.7 | −0.9 | |
| 2.8 | 8.8 | −6.7 | −0.0 | +0.7 | −0.3 | +1.2 | −3.7 | −1.2 | |
|
| |||||||||
| [NH3-H-NH3]+ | 2.6 | 0.4 | −0.4 | −0.4 | −0.4 | −0.4 | −0.4 | −0.4 | −0.3 |
| 2.7 | 1.9 | −1.8 | −1.0 | −1.4 | −1.7 | −1.7 | −1.9 | −1.0 | |
| 2.8 | 4.4 | −2.4 | −0.5 | −1.4 | −2.0 | −2.2 | −3.0 | −1.6 | |
| 2.9 | 7.7 | −2.5 | −0.1 | −1.2 | −2.1 | −2.2 | −4.1 | −2.2 | |
|
| |||||||||
| [NH2-H-NH2]− | 2.5 | 0.1 | −0.0 | +0.3 | −0.1 | −0.1 | −0.1 | +0.0 | +0.0 |
| 2.6 | 1.4 | −1.4 | +5.2 | −1.1 | −0.4 | −1.0 | −1.2 | −0.5 | |
| 2.7 | 3.5 | −3.5 | +5.5 | −0.6 | +1.5 | −0.5 | −2.1 | −0.8 | |
| 2.8 | 6.3 | −4.9 | +6.9 | +0.6 | +2.9 | +0.9 | −3.0 | −1.1 | |
|
| |||||||||
| [NH3-H-H2O]+ d | 2.9 | 25.3 | −8.2 | −5.2 | −4.2 | −5.8 | −5.3 | -e | −2.7 |
| 3.0 | 30.0 | −9.5 | −6.3 | −5.4 | −7.3 | −6.7 | −6.8 | −3.3 | |
| 3.1 | 35.1 | −11.0 | −7.7 | −6.8 | −8.9 | −8.2 | −7.8 | −3.8 | |
| 3.2 | 40.5 | −12.5 | −9.1 | −8.2 | −10.5 | −9.8 | −8.8 | −4.2 | |
|
| |||||||||
| [H2O-H-NH3]+ d | 2.9 | 0.8 | +0.7 | +2.2 | +1.1 | +0.2 | +0.1 | -e | −0.8 |
| 3.0 | 3.3 | +0.9 | +2.9 | +1.5 | +0.2 | +0.1 | −3.0 | −1.6 | |
| 3.1 | 6.7 | +0.3 | +2.3 | +0.9 | −0.6 | −0.7 | −4.5 | −2.3 | |
| 3.2 | 10.7 | −0.8 | +1.3 | −0.2 | −1.9 | −2.0 | −5.9 | −2.9 | |
|
| |||||||||
| [NH2-H-OH]− d | 2.8 | 10.1 | −6.3 | −4.6 | +2.4 | −2.5 | +2.9 | −3.3 | −0.8 |
| 2.9 | 14.2 | −8.6 | −5.2 | +2.1 | −3.1 | +2.7 | −4.2 | −1.1 | |
| 3.0 | 18.6 | −11.1 | −6.0 | +1.4 | −3.9 | +2.1 | −5.1 | −1.4 | |
| 3.1 | 23.3 | −13.4 | −6.7 | +0.7 | −4.7 | +1.5 | −5.9 | −1.6 | |
|
| |||||||||
| [OH-H-NH2]− d | 2.8 | 4.4 | −4.1 | +14.4 | +0.3 | +6.6 | +0.7 | −2.8 | −1.2 |
| 2.9 | 7.8 | −5.2 | +15.8 | +1.1 | +7.9 | +1.6 | −4.0 | −1.7 | |
| 3.0 | 11.6 | −6.6 | +16.5 | +1.2 | +8.4 | +1.7 | −4.9 | −2.0 | |
| 3.1 | 15.8 | −8.8 | +16.2 | +0.1 | +7.8 | +0.7 | −5.8 | −2.3 | |
Barriers are computed as described in the text at 0 K and no zero-point energy correction has been included. For the DFT and DFTB methods the deviation is given as the difference to the MP2 method (Emethod – EMP2). For all models the NHorg parameter set is applied.
Basis set 6-31+G(d,p)
Barrier in comparison to the relaxed structure with the proton binding to the heavy atom that is written on the left hand side of that proton.
a barrier does not exist
Similarly, proton transfer barriers for nitrogen species are tested. DFTB2 underestimates the barriers severely while DFTB3/calc reduces this error and even slightly overestimates the barrier for the negatively charged complex. The DFTB models with fitted parameters show further improved results.
The proton transfer barriers for the models containing one oxygen and one nitrogen atom are computed keeping both heavy atoms fixed and translating the shared proton along the straight line between oxygen and nitrogen. The barrier is then given by the highest energy surrounded by two minima. For the relaxed structure the shared proton is again geometry optimized together with all other hydrogen atoms. Rather large deviations are found for DFTB2 which are reduced with DFTB3-diag/calc and DFTB3/calc. Again, an overall good performance is found for the DFTB3-diag/fit and DFTB3/fit versions; the largest errors appear for [NH3-H-H2O]+, where surprisingly DFT-GGA methods also reveal comparably large errors (see Table 9) in comparison to MP2/G3large.
The use of NHmod has the following consequences on barriers. The N-H bond is energetically shifted by about 10 kcal/mol being more attractive in the binding region. The strength of the bond decreases with larger N-H distances. As a consequence no barrier can be found for the models containing one oxygen and one nitrogen with small N-O distances. Here we see that NHmod is not parametrized and not applicable to proton transfer barriers. Nevertheless, NHmod is a practical solution for correcting errors for proton affinities as has been shown in several applications, e.g. ref 44. For models with two nitrogen atoms, we find very similar results for NHorg and NHmod. Future work will have to be concentrated on solving the hybridization problem and balancing N-H and O-H repulsive potentials such that proton transfer barriers with oxygen and nitrogen participation are described correctly.
To point out this more clearly, we take a look at [NH3-H-H2O]+, a model for a proton transfer between an amino acid with an acidic nitrogen in the side chain (lysine, histidine, arginine) and an oxygen. In the model the nitrogen is sp3 hybridized as would be the case for lysine and we find an error of about 10 kcal/mol; therefore, NHmod should be used. However, when doing so the barrier vanishes, i.e., the energy monotonically rises as the hydrogen moves towards oxygen. Thus, proton affinities and proton transfer barriers can be well described for systems including histidine or arginine (applying NHorg) but special care must be taken for lysine. Using NHmod the proton affinity is described well, but not the barrier height of a proton transfer. The same problem arises for DNA proton transfer reactions, where the MUE is of about 5 kcal/mol for proton affinities of DNA bases as found for DFTB3-diag in ref 39.
4.5 Phosphorous containing molecules
4.5.1 Proton affinity and hydrolysis energetics
For phosphorous containing molecules, we first apply two tests from ref 40. Table 10 shows 18 proton affinities of biological relevance, in Table 11 elementary steps for a representative set of phosphate hydrolysis reactions are listed, which include the hydrolysis of monophosphate ester (MMP) and dimethyl monophosphate ester (DMP) with different protonation states, number of water involved, and dissociative/associative mechanisms.
Table 10.
18 Proton Affinities for Phosphorous Containing Molecules in kcal/mol: Deviation of DFTB in Comparison to G3B3a
| moleculeb | G3B3 | DFTB2 | DFTB3-diagc | DFTB3c | ||
|---|---|---|---|---|---|---|
| calc | fit | calc | fit | |||
| H3PO4 | 334.0 | +17.1 | +23.9 | +18.5 | +18.3 | +5.5 |
| H2PO−2 | 464.5 | +26.2 | +26.6 | +20.0 | +17.2 | −4.3 |
| DMPHd | 336.3 | +9.6 | +20.3 | +14.9 | +15.9 | +4.8 |
| MMPd | 336.7 | +12.0 | +20.9 | +15.4 | +15.8 | +3.8 |
| MMP− d | 460.5 | +21.5 | +26.3 | +19.9 | +18.3 | −1.2 |
| PH3 OH+ | 201.6 | −8.6 | +7.1 | +2.7 | +4.8 | −0.0 |
| PH2 OHOH+ | 201.6 | −2.8 | +10.8 | +6.3 | +8.2 | +2.1 |
| PHOHOHOH+ | 200.8 | +4.5 | +16.3 | +11.7 | +13.6 | +6.2 |
| PH2(OH)=O | 336.6 | +3.0 | +15.7 | +10.4 | +12.2 | +3.3 |
| PH(OH)(OH)=O | 334.7 | +10.7 | +20.4 | +15.0 | +16.0 | +5.3 |
| P(O)(OH)(-O-CH2CH2-O-) | 336.3 | +7.2 | +17.7 | +12.3 | +13.4 | +2.4 |
| P(OH)(OH)(-O-CH2CH2-O-)(OH*) | 359.0 | −3.3 | +18.6 | +12.8 | +12.9 | +0.3 |
| P(OH*)(OH)(-O-CH2CH2-O-)(OH) | 350.4 | +6.7 | +15.9 | +10.6 | +11.0 | −0.4 |
| P(OH*)(OH)(-O-CH2CH2-O-)(OCH3) | 351.2 | +1.8 | +12.8 | +7.4 | +8.9 | −1.4 |
| P(OH)(OCH3)(-O-CH2CH2-O-)(OH*) | 359.6 | −8.3 | +7.9 | +2.1 | +3.3 | −7.2 |
| P(OH*)(OCH3)(-O-CH2CH2-O-)(OH) | 352.9 | +3.6 | +14.5 | +9.2 | +10.1 | −0.5 |
| P(OH)(OH)(OH)(OH*)(OH)_ax | 357.3 | +4.0 | +21.8 | +15.9 | +14.2 | −1.2 |
| P(OH)(OH)(OH)(OH*)(OH)_eq e | 347.0 | +14.0 | - | - | - | −0.0 |
|
| ||||||
| MUE | 9.2 | 17.5 | 12.1 | 12.6 | 2.8 | |
| MSE | +6.6 | +17.5 | +12.1 | +12.6 | +1.0 | |
| MAX | 26.2 | 26.6 | 20.0 | 18.3 | 7.2 | |
The proton affinity is computed with the potential energies at 0 K without any zero-point energy correction. For the DFTB methods the deviation is given as the difference to the G3B3 method (Emethod EG3B3). The compilation of the molecules is taken from ref 40.
The molecules are given in the protonated form.
“DMPH” refers to dimethyl hydrogen phospate, “MMP” to P(O)(OH)(OH)(OCH3), and “MMP−” to P(O)(O)(OH)(OCH3)−
The molecule P(OH)(OH)(OH)(OH*)(OH)_eq dissociates forming H2O for DFTB3-diag and DFTB3/calc. Depending on the basis set this dissociation also occurs for the DFT functionals PBE and B3LYP, e.g. dissociation for basis set 6-311G(2d,2p), no dissociation for basis set cc-pVTZ.
Table 11.
Deviation of Exothermicity and Barrier Height from the DFTB Variants in Comparison to MP2/G3Large Single Point Calculations at B3LYP/6-31+G(d,p) Structures for 37 Elementary Steps in the Hydrolysis of MMP and DMPa
| processb | MP2 | DFTB2 | DFTB3-diag c | DFTB3 c | ||
|---|---|---|---|---|---|---|
| calc | fit | calc | fit | |||
| com1 → ts1 (MMP,B) | 31.0 | −1.0 | −3.9 | −4.2 | −6.7 | −7.2 |
| com1 → int1 (MMP,E) | 30.6 | −2.2 | −2.4 | −2.6 | −6.1 | −7.0 |
| com1 → ts1_2 (MMP,B) | 41.5 | +0.8 | −1.7 | −1.9 | −3.9 | −3.3 |
| com1 → int1_2 (MMP,E) | 31.0 | −4.4 | +0.5 | +0.3 | −4.6 | −5.9 |
| int1_2 → ts2_0 (MMP,B) | 11.9 | −3.0 | −3.0 | −3.0 | −0.2 | +2.7 |
| int1_2 → ts2 (MMP,B) | 3.6 | −5.5 | −4.9 | −4.9 | −2.8 | −1.1 |
| int1_2 → com2 (MMP,E) | −28.8 | +2.1 | +0.0 | +0.1 | +3.3 | +4.4 |
| com1 → diss_tsa (MMP,B) | 36.8 | +4.6 | +2.2 | +2.4 | +3.3 | +4.9 |
| com1 → diss_int (MMP,E) | 19.6 | −7.3 | −7.3 | −6.7 | −3.2 | +0.3 |
| com1_w2 → ts1_2_w2 (MMP,B) | 39.9 | −8.3 | −12.3 | −12.1 | −13.6 | −12.7 |
| com1_w2 → int1_2a_w2 (MMP,E) | 28.0 | −5.0 | −1.5 | −1.8 | −6.6 | −7.9 |
| int1_2a_w2 → int1_2_w2 (MMP,E) | 0.4 | +0.3 | +1.7 | +1.5 | +2.5 | +2.5 |
| int1_2_w2 → ts2_0_w2 (MMP,B) | 11.4 | −4.1 | −10.8 | −10.5 | −7.7 | −5.4 |
| com1_da → ts1_da (MMP,B) | 55.0 | −22.4 | −8.8 | −9.1 | −7.1 | −0.2 |
| com1_da → int_da (MMP,E) | 4.5 | −3.3 | +0.6 | +0.5 | −1.6 | −2.0 |
| com1 → ts1 (DMP,B) | 38.6 | −1.7 | −5.3 | −5.8 | −7.1 | −7.3 |
| com1 → int1 (DMP,E) | 35.4 | −5.7 | −2.2 | −2.4 | −6.4 | −7.6 |
| int1 → int1_2 (DMP,E) | 1.3 | −3.2 | −0.3 | −0.3 | +0.4 | +1.3 |
| int1_2 → ts2 (DMP,B) | 0.6 | +0.2 | −0.5 | −0.6 | +0.4 | +1.2 |
| int1_2 → com2 (DMP,E) | −35.2 | +7.0 | +4.0 | +4.1 | +5.9 | +6.0 |
| n_com1 → n_ts3 (DMP,B) | 33.6 | +4.9 | +3.0 | +2.7 | +0.7 | +0.2 |
| n_com1 → n_int1 (DMP,E) | 13.2 | −3.7 | −0.0 | −0.4 | −3.8 | −4.9 |
| n_int1 → n_ts4 (DMP,B) | 22.9 | +6.4 | +4.1 | +4.0 | +4.8 | +5.1 |
| n_int1 → n_com2 (DMP,E) | −15.8 | +2.2 | −0.1 | +0.0 | +3.2 | +3.7 |
| DMP_P → diss_ts (DMP,B) | 40.9 | +11.6 | +8.3 | +8.1 | +8.8 | +8.8 |
| DMP_P → diss_prod (DMP,E) | 28.2 | +0.6 | −1.7 | −1.8 | −0.0 | −0.9 |
| diss_prod2 → diss_ts2 (DMP,B) | 13.5 | +13.2 | +11.3 | +11.2 | +9.8 | +10.4 |
| diss_prod2 → MMP_P (DMP,E) | −29.8 | +0.8 | +2.9 | +2.8 | +0.3 | +0.6 |
| diss_w_reac → diss_w_ts (DMP,B) | 20.9 | +5.9 | +2.2 | +2.2 | +2.3 | +0.7 |
| diss_w_reac → diss_w_prod (DMP,E) | 18.4 | +4.3 | +0.2 | +0.1 | +1.4 | +0.3 |
| diss_w_prod2 → diss_w_ts2 (DMP,B) | 1.9 | +2.7 | +2.2 | +2.2 | +0.9 | +0.3 |
| diss_w_prod2 → diss_w_reac2 (DMP,E) | −21.0 | −2.5 | +0.4 | +0.4 | −1.4 | −0.7 |
| n_w_com1 → n_w_ts3 (DMP,B) | 28.2 | −2.7 | −4.4 | −4.4 | −7.6 | −8.9 |
| n_w_com1 → n_w_int1 (DMP,E) | 13.1 | −4.1 | −0.7 | −1.0 | −4.5 | −5.8 |
| n_w_int1 → n_w_int2 (DMP,E) | −0.5 | +0.1 | +0.7 | +0.7 | +0.7 | +0.6 |
| n_w_int2 → n_w_ts4 (DMP,B) | 15.1 | +2.0 | −2.2 | −2.0 | −2.3 | −3.1 |
| n_w_int2 → n_w_com2 (DMP,E) | −13.0 | +1.4 | −0.7 | −0.7 | +3.0 | +4.1 |
|
| ||||||
| MUE | 4.4 | 3.2 | 3.2 | 4.0 | 4.1 | |
| MSE | −0.5 | −0.8 | −0.9 | −1.2 | −0.9 | |
| MAX | 22.4 | 12.3 | 12.1 | 13.6 | 12.7 | |
Compilation from 40; No zero-point corrections are included in either exothermicity or barrier heights. All quantities are given in kcal/mol.
The processes are labeled as in ref 40, ‘E’ stands for “Exothermicity”, ‘B’ for “Barrier”, all structures are listed in Supporting Information.
explanations see Table 2
Proton affinities are generally overestimated for DFTB2 and DFTB3/calc. The MUE shows even worse results for DFTB3/calc than for DFTB2; however, similar as for the proton affinities with acidic oxygen, the deviation in comparison to the MP2 results are much more consistent with DFTB3. For DFTB3 all proton affinities are overestimated, the MSE being as large as the MUE (12.6 kcal/mol); additionally, the maximal absolute deviation is smaller than that for DFTB2. As discussed above, about 6 kcal/mol of this error is due to the overbinding of the O-H bond, which can be removed by refitting the O-H repulsive potential. The remaining error may the be reduced by fitting the P Hubbard derivative. For now, the method of choice is DFTB3/fit, for which the MUE is only 2.8 kcal/mol. We want to point out that the Hubbard derivatives for C, H, N, and O are taken from the fit on non-phosphate molecules and only is fitted to the 18 listed proton affinities; this is in contrast to earlier work, where the best performance for DFTB3-diag could only be achieved by fitting all parameters at once.
Table 10 also shows the results for DFTB3-diag/calc which looks similar to DFTB3/calc. However, when using DFTB3-diag/fit the error cannot be reduced as much as is the case for DFTB3/fit. We find that the parameter has very small influence on the proton affinities. The MUE ranges from 10.7 - 12.5 kcal/mol when choosing in the range of −0.40 to −0.04 atomic units, therefore, we keep the calculated parameter . This observation highlights that DFTB3-diag/fit does not properly account for some part of the interactions within these molecules, i.e., the flexibility of the model is not sufficient to yield good results for non-phosphate and phosphate molecules at the same time.
For the hydrolysis reactions the MUE for DFTB2 is 4.4 kcal/mol and is only slightly reduced for DFTB3/fit (Table 11). Note that for the latter the parameter is fitted to the proton affinities only. A special fit also for these reactions does not improve this situation significantly. Surprisingly, DFTB3-diag performs somehow superior with a MUE of 3.2 kcal/mol.
4.5.2 Additional discussion of transferability of parameters
Earlier extensions of DFTB2 have suggested a lack of general transferability, for example, the two phosphorous related parameter sets (see additional discussions in the next subsection), SCC-DFTBPA and SCC-DFTBPR,40 need to be developed for different properties. Both sets are based on DFTB3-diag (without the γh-function) with fitted Hubbard derivatives and an additional empirical Gaussian term (with three additional parameters) to adjust the Hubbard derivatives within the SCC procedure. SCC-DFTBPA is specifically designed for proton affinities of phosphorous containing molecules and yields a MUE for the 18 proton affinities of Table 10 of only 2.6 kcal/mol but performs inferior for proton affinities of non-phosphate molecules. SCC-DFTBPR, on the other hand, is designed for the hydrolysis reactions of Table 11 and shows a MUE for these reactions of only 2.4 kcal/mol but is less accurate for the proton affinities (in particular for non-phosphate molecules).
DFTB3 is a consistent extension of our model and transferable to a wide range of chemical properties. Instead of different methods with a different number of parameters (six or nine parameters additionally to the ones from DFTB2) we now have a method at hand that shows an overall good performance for binding energies and proton affinities of non-phosphate and phosphate molecules using only six additional parameters in comparison to DFTB2 (ζ, , , , , ). A limitation is found, however, for the hydrolysis reactions, for which only a slight improvement is achieved in comparison to DFTB2. DFTB3 is not performing as well as SCC-DFTBPR with that respect, which suggests that further improvements are necessary for the phosphorous parameters and/or for the DFTB formalism.
4.5.3 Geometry and non-isodesmic reactions
In several publications phoshorous parameters (electronic and repulsive parameters) for DFTB2 have been used40,42,45,47,82,83 and the parametrization procedure has been described in ref 40.
Geometrical properties are tested on 35 molecules in the gas phase, including phosphorous containing acids in different protonation states. All DFTB versions perform quite well in comparison to B3LYP/6-31+G(d,p) but there are specific bond types that show a general trend of being too short or too long as summarized in Table 12. For example, bonds for the pairs P-P, P-S and P=S are typically too long. A significant difference between DFTB2 and DFTB3 can be found for the O-P single bond length, which is rather too short for the latter in comparison to B3LYP/6-31+G(d,p). This can be most dramatically seen in the example where an acetate is linked via one oxygen atom to a phosphate group ([CH3COO-PO3]2–). For DFTB2 this molecule almost dissociates with a O-P distance of 2.372 Å, for DFTB3 it is too short (1.818 Å) in comparison to the B3LYP result (1.968 Å). As already shown in ref 40, DFTB2 has too small hydrogen bonding distances for water phosphate bonds. This problem is not resolved for DFTB3 and needs to be addressed with improved description of Pauli repulsion in the DFTB2 framework. The MUE for bond angles is between 2.5 and 3.0 degrees for all DFTB versions. Further details can be found in Supporting Information.
Table 12.
DFTB2 and DFTB3 Errors for the Bond Lengths of 35 Phosphorous Containing Moleculesa in Comparison to B3LYP/6-31+G(d,p)
| bond typeb | n c | DFTB2 | DFTB3/calc | DFTB3/fit d | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAX | MSE | MUE | MAX | MSE | MUE | MAX | MSE | MUE | ||
| rC-P | 6 | 0.042 | +0.022 | 0.022 | 0.041 | +0.018 | 0.018 | 0.041 | +0.021 | 0.021 |
| rC=P | 1 | 0.056 | +0.056 | 0.056 | 0.049 | +0.049 | 0.049 | - | - | - |
| rH-P | 9 | 0.061 | +0.024 | 0.024 | 0.047 | +0.020 | 0.021 | 0.044 | +0.018 | 0.019 |
| rN-P | 1 | 0.001 | +0.001 | 0.001 | 0.001 | +0.001 | 0.001 | 0.001 | +0.001 | 0.001 |
| rO-P | 43 | 0.404 | +0.001 | 0.029 | 0.150 | −0.022 | 0.026 | 0.200 | −0.029 | 0.031 |
| rO=P | 33 | 0.029 | +0.007 | 0.011 | 0.027 | +0.008 | 0.011 | 0.017 | +0.003 | 0.006 |
| rP-P | 4 | 0.109 | +0.077 | 0.077 | 0.118 | +0.081 | 0.081 | 0.148 | +0.098 | 0.098 |
| rP#P | 1 | 0.003 | +0.003 | 0.003 | 0.003 | +0.003 | 0.003 | 0.003 | +0.003 | 0.003 |
| rP-S | 5 | 0.164 | +0.121 | 0.121 | 0.137 | +0.103 | 0.103 | 0.128 | +0.098 | 0.098 |
| rP=S | 3 | 0.070 | +0.062 | 0.062 | 0.064 | +0.059 | 0.059 | 0.061 | +0.059 | 0.059 |
| rOHhb | 3 | 0.141 | −0.138 | 0.138 | 0.225 | −0.222 | 0.222 | 0.192 | −0.186 | 0.186 |
|
| ||||||||||
| overall e | 196 | 0.404 | +0.010 | 0.022 | 0.225 | +0.002 | 0.021 | 0.200 | −0.000 | 0.021 |
Geometries for all molecules are listed in Supporting Information.
bond situations between two atom types, “-” means a single bond, “=” a double bond, rP#P is the bond length of the molecule P2, and rOHhb are hydrogen bonds between a phosphate group and a water, all specifications can be found in Supporting Information
number of comparisons
trimethylmethylenephosphorane does not converge and is excluded from the statistics
Also the bond types rCC, rCH, rCO, rC=O, rHO, rCS, and rHS are included in the overall performance.
For additional test of chemical reactions beyond hydrolysis, 10 reactions has been carried out in which the bonding situation changes, e.g., a O-P bond is exchanged to a H-P bond (9 reactions are hydrogenations). We find large deviations, the MUE being around 50 kcal/mol for all DFTB versions; details can be found in Supporting Information. Among other shortcomings the most important one seems the eminent over-binding of the PO bonds. Thus, while the current phosphorous parameters might well be used for geometries (while special care is necessary for some bond types, see above), proton affinities and hydrolysis reactions, it should not be applied for non-isodesmic reactions.
5 Conclusion
We have presented DFTB3, a new method that extends the standard second order DFTB2 (formally SCC-DFTB) by two conceptually independent improvements. DFTB3 maintains the strengths of DFTB2, such as rapid computation of large scale molecular systems with reliable geometry, but improves transferability and overall accuracy for several properties.
The first concept is the γh-function ameliorating the electron-electron interaction of charge fluctuation. The γh-function corrects the original function, which incorrectly imposes a linear relation between the chemical hardness and the atomic size. This relationship is only valid within one row of the periodic table, and particularly fails when interactions of first row atoms with hydrogen are involved. We therefore introduced one additional, purely empirical parameter (ζ), which can be adjusted to a single reference system like the water dimer. Previous tests have shown that this improves the performance of DFTB2 for hydrogen bonding systematically. Therefore, this correction does not introduce additional terms to total energy in an ad hoc fashion, but establishes a consistent improvement of the electron-electron interaction in the second (and third) order terms of DFTB2 (DFTB3). As a result, the mean unsigned error for hydrogen bonding energies drops from 8.0 kcal/mol for DFTB2 to 4.0 kcal/mol for DFTB2-γh for our fairly broad sets of test systems. A drawback is found for the hydrogen bond lengths which turn out to be too short. 6
The second improvement concerns the extension of DFTB2 to include third order terms of the Taylor series expansion of the DFT exchange-correlation energy. The third order terms cause the chemical hardness (Hubbard parameter) of an atom to be dependent on its charge, which becomes particularly important for the description of systems with localized charges. One additional parameter is introduced for each element, the Hubbard derivative with respect to charge, which can be either computed from DFT for atoms or can be fitted. With the first approach, the DFTB3-γ method does not involve any new empirical parameters. Geometries for charged molecules are slightly improved. Regarding proton affinities the errors become consistently overestimated in contrast to an underestimation for negatively charged systems and an overestimation for positively charged systems with DFTB2.
The combination of both improvements into DFTB3 also combines the effects. The accuracy of DFTB2 for geometries of C, H, N, O containing molecules is maintained. For charged molecules a slight geometrical improvement is found whereas hydrogen bonds are consistently too short. The mean unsigned error for our set of hydrogen binding energies drops below 3.0 kcal/mol. It should be noted that this improved DFTB model outperforms standard DFT functionals using medium sized basis sets without correction for BSSE, a methodology typically used in, for example, QM/MM applications to biological systems. 7 For proton affinities the mean unsigned error is not significantly reduced when using calculated Hubbard derivatives. However, we have shown that the remaining errors arise not due to third order approximations (and neither the γh-function) but result from the repulsive potential terms of second order DFTB2; i.e., the errors could be removed in principle by re-optimizing the DFTB repulsive potentials, with which an empirical fitting of the Hubbard derivative parameters is likely no longer necessary. For the time being, we also present empirically fitted parameters (Hubbard derivatives and ζ), which result in a significant improvement over DFTB2. The mean unsigned deviation for our oxygen containing test systems in comparison to G3B3 results are 5.8, 2.9, and 2.5 kcal/mol for DFTB2, DFTB3 with fitted ζ and Hubbard derivatives, and B3LYP/6-31+G(d,p), respectively.
We have also shown that the energy of a proton is a constant and not equal to zero for DFTB2 (and DFTB3) due to the neglect of atomic contributions within the repulsive energy contribution. There are different eligible ways of how to compute this constant leading to different constants in order to obtain an absolute proton affinity. For reasons of consistency we used the constant as calculated directly from the respective level of theory (DFTB2 or DFTB3). We emphasize that for most applications only relative proton affinities are important, i. e. the value of this constant does not matter at all. Only for specific applications where the absolute proton affinity is needed the value of that constant becomes important, e.g. determining the pKa of a molecule. An empirical but helpful choice different than fitting parameters would then be to use a constant which compensates the consitent over- or underestimation of the respective DFTB variant.
In earlier work, we have already implemented and tested the diagonal part of the third order corrections and provided different parametrizations (Hubbard derivatives, ζ and in some cases also additional parameters).39,40 In our comparison of DFTB3-diag and DFTB3, the newly implemented off-diagonal terms do not seem to lead to a large improvement for molecules consisting of O, N, C and H, except for the NH2 molecule, since the diagonal part is already quite accurate. The most significant advantage of DFTB3 over DFTB3-diag and earlier published extensions of DFTB2 is its consistent performance for hydrogen bonding energies and proton affinities including atoms of type C, H, N, O, and P. While all earlier extensions needed different parameterizations for different properties, DFTB3 with fitted ζ and Hubbard derivatives is more transferable and covers all properties with a single parametrization. One persistent limitation is found for phosphate hydrolysis reactions, where a model based on DFTB3-diag with an empirical Gaussian term and “reaction specific” parametrization of the Hubbard derivatives (SCC-DFTBPR)40 is still needed for better accuracy.
Despite all progress major limitations for DFTB3 remain. First, the error of proton affinities of nitrogen containing molecules seems to correlate with the hybridization state of nitrogen. We discussed the use of different repulsive potentials, NHorg and NHmix, which provides a pragmatic way for calculating accurate proton affinities but is unreliable for studying reactions and proton transfer barriers. Moreover, the scheme is conceptually unsatisfactory. Second, the hydrogen bond lengths are generally too short, and third, large errors are found for non-isodesmic reactions of phosphorous containing species. Addressing these limitations requires developing new electronic and repulsive parameters (or formulations) for DFTB3.
Supplementary Material
Acknowledgement
We thank Dr. Yang Yang and Puja Goyal for providing us compilations and geometries of their earlier works and Dr. Bálint Aradi for implementing the new methodologies into DFTB+ and for helpful discussions. This work was partially supported by NIH grant R01GM084028 (to QC).
Footnotes
Supporting Information Available Detailed derivation of the Kohn-Sham equations, atomic forces and the γh-function within the DFTB3 formalism (Part 1). Excel file for molecular geometries and computed data (Part 2). This information is available free of charge via the Internet at http://pubs.acs.org.
A challenging problem still remains. The proton affinities for sp1 and sp2 hybridized nitrogen species are computed reasonably well; however, this is not the case for sp3 hybidized nitrogen systems, for which proton affinities are underestimated by about 10 kcal/mol. A pragmatic solution was suggested which introduced two nitrogen types shifting the original N-H repulsive energy by these 10 kcal/mol for the second type.22,48 However, it remains unclear if this solution addresses the origin of the problem correctly. Another idea which we are currently exploring is to include d-orbitals to nitrogen.
Within the mio parameter the spin-polarization energies are calculated with LDA, when using PBE values instead the electronic energy contribution for the hydrogen atom is −0.27966 a.u. which gives kcal/mol. For details see ref 27.
For H we find that the self-consistent procedure does not converge for several molecules in our training set.
Note, different than in present work Yang et al.39 defined NHmix that way that NHmod is also used for calculating the proton affinity of NH–2. Since the orbitals calculated on the NH–2 molecule look similar to orbitals on sp2 nitrogen, we apply NHorg for that case.
For water clusters, we note that the PA can be written as the sum of PA for a (neutral or protonated) water molecule and the difference in the binding energies of water clusters of different protonation states. Therefore, the errors in the water cluster PAs can be understood in terms of the errors in the PA of a single (neutral or protonated) water and errors in the binding energies of the relevant water clusters. For example, the fairly large error for the PA of a neutral (H2O)5 is due mainly to the fact that DFTB3/fit overestimates the binding energy of a deprotonated (H2O)5 (−4.7 kcal/mol, see Table 5) but slightly underestimates the binding energy of a neutral (H2O)5 (+1.7 kcal/mol, see Table 5).
In principle, these repulsive energy potentials are intimately coupled to the electronic DFTB terms with which they have been determined. Therefore, they have to be refitted when the DFTB Hamiltonian is modified.
Note that adding empirical dispersion corrections to DFT-GGA would even worsen the situation, since DFT overbinds the H-bonded complexes already due to BSSE.
References
- (1).Dewar MJS, Thiel WJ. Am. Chem. Soc. 1977;99:4899. [Google Scholar]
- (2).Dewar MJS, Zoebisch EG, Healy EF, Stewart JJP. J. Am. Chem. Soc. 1985;107:3902. [Google Scholar]
- (3).Stewart JJP. J. Comput. Chem. 1989;10:209. [Google Scholar]
- (4).Rocha GB, Freire RO, Simas AM, Stewart JJP. J. Comput. Chem. 2006;27:1101. doi: 10.1002/jcc.20425. [DOI] [PubMed] [Google Scholar]
- (5).Stewart JJP. J. Mol. Model. 2007;13:1173. doi: 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Repasky MP, Chandrasekhar J, Jorgensen WL. J. Comput. Chem. 2002;23:1601. doi: 10.1002/jcc.10162. [DOI] [PubMed] [Google Scholar]
- (7).Kolb M, Thiel W. J. Comput. Chem. 1993;14:775. [Google Scholar]
- (8).Weber W, Thiel W. Theor. Chem. Acc. 2000;103:495. [Google Scholar]
- (9).Elstner M, Porezag D, Jungnickel G, Elsner J, Haugk M, Frauenheim T, Suhai S, Seifert G. Phys. Rev. B. 1998;58:7260. [Google Scholar]
- (10).Elstner M, Frauenheim T, McKelvey J, Seifert G. J. Phys. Chem. A. 2007;111:5607. [Google Scholar]
- (11).Porezag D, Frauenheim T, Köhler T, Seifert G, Kaschner R. Phys. Rev. B. 1995;51:12947. doi: 10.1103/physrevb.51.12947. [DOI] [PubMed] [Google Scholar]
- (12).Seifert G, Porezag D, Frauenheim T. Int. J. Quantum Chem. 1996;58:185. [Google Scholar]
- (13).Seifert G, Eschrig H. Phys. Stat. Sol. B. 1985;127:573. [Google Scholar]
- (14).Seifert G, Eschrig H, Bieger WZ. Phys. Chem. (Leipzig) 1986;267:529. [Google Scholar]
- (15).Foulkes WMC, Haydock R. Phys. Rev. B. 1989;39:12520. doi: 10.1103/physrevb.39.12520. [DOI] [PubMed] [Google Scholar]
- (16).Harris J. Phys. Rev. B. 1985;31:1770. doi: 10.1103/physrevb.31.1770. [DOI] [PubMed] [Google Scholar]
- (17).Hazebroucq S, Picard GS, Adamo C, Heine T, Gemming S, Seifert G. J. Chem. Phys. 2005;123:1. doi: 10.1063/1.2038888. [DOI] [PubMed] [Google Scholar]
- (18).Frauenheim T, Seifert G, Elstner M, Hajnal Z, Jungnickel G, Porezag D, Suhai S, Scholz R. Phys. Stat. Sol. B. 2000;217:41. [Google Scholar]
- (19).Elstner M, Frauenheim T, Kaxiras E, Seifert G, Suhai S. Phys. Stat. Sol. B. 2000;217:357. [Google Scholar]
- (20).Frauenheim T, Seifert G, Elstner M, Niehaus T, Köhler C, Amkreutz M, Sternberg M, Hajnal Z, Di Carlo A, Suhai S. J. Phys.: Cond. Matter. 2002;14:3015. [Google Scholar]
- (21).Elstner M, Frauenheim T, Suhai S. J. Mol. Struct.: THEOCHEM. 2003;632:29. [Google Scholar]
- (22).Elstner M. Theor. Chem. Acc. 2006;116:316. [Google Scholar]
- (23).Riccardi D, Schaefer P, Yang Y, Yu H, Ghosh N, Prat-Resina X, König P, Li G, Xu D, Guo H, Elstner M, Cui Q. J. Phys. Chem. B. 2006;110:6458. doi: 10.1021/jp056361o. [DOI] [PubMed] [Google Scholar]
- (24).Density Functional Tight Binding: Contributions from the American Chemical Society Symposium. J. Phys. Chem. A. 2007;111:5607. [Google Scholar]
- (25).Sattelmeyer KW, Tirado-Rives J, Jorgensen WL. J. Phys. Chem. A. 2006;110:13551. doi: 10.1021/jp064544k. [DOI] [PubMed] [Google Scholar]
- (26).Otte N, Scholten M, Thiel W. J. Phys. Chem. A. 2007;111:5751. doi: 10.1021/jp0700130. [DOI] [PubMed] [Google Scholar]
- (27).Gaus M, Chou C, Witek H, Elstner M. J. Phys. Chem. A. 2009;113:11866. doi: 10.1021/jp902973m. [DOI] [PubMed] [Google Scholar]
- (28).Elstner M, Jalkanen KJ, Knapp-Mohammady M, Frauenheim T, Suhai S. Chem. Phys. 2000;256:15. [Google Scholar]
- (29).Elstner M, Jalkanen KJ, Knapp-Mohammady M, Frauenheim T, Suhai S. Chem. Phys. 2001;263:203. [Google Scholar]
- (30).Seabra GDM, Walker RC, Roitberg AE. J. Phys. Chem. A. 2009;113:11938. doi: 10.1021/jp903474v. [DOI] [PubMed] [Google Scholar]
- (31).Krüger T, Elstner M, Schiffels P, Frauenheim T. J. Chem. Phys. 2005;122:1. doi: 10.1063/1.1871913. [DOI] [PubMed] [Google Scholar]
- (32).Witek HA, Morokuma K. J. Comput. Chem. 2004;25:1858. doi: 10.1002/jcc.20112. [DOI] [PubMed] [Google Scholar]
- (33).Witek HA, Morokuma K, Stradomska A. J. Chem. Phys. 2004;121:280318. doi: 10.1063/1.1775787. [DOI] [PubMed] [Google Scholar]
- (34).Witek HA, Morokuma K, Stradomska A. J. Theor. Comput. Chem. 2005;4:639. [Google Scholar]
- (35).Witek HA, Irle S, Zheng G, De Jong WA, Morokuma K. J. Chem. Phys. 2006;125:214706. doi: 10.1063/1.2370877. [DOI] [PubMed] [Google Scholar]
- (36).Elstner M, Hobza P, Frauenheim T, Suhai S, Kaxiras E. J. Chem. Phys. 2001;114:5149. [Google Scholar]
- (37).Liu H, Elstner M, Kaxiras E, Frauenheim T, Hermans J, Yang W. Proteins: Structure, Function and Genetics. 2001;44:484. doi: 10.1002/prot.1114. [DOI] [PubMed] [Google Scholar]
- (38).Elstner M. J. Phys. Chem. A. 2007;111:5614. doi: 10.1021/jp071338j. [DOI] [PubMed] [Google Scholar]
- (39).Yang Y, Yu H, York D, Cui Q, Elstner M. J. Phys. Chem. A. 2007;111:10861. doi: 10.1021/jp074167r. [DOI] [PubMed] [Google Scholar]
- (40).Yang Y, Yu H, York D, Elstner M, Cui Q. J. Chem. Theory Comput. 2008;4:2067. doi: 10.1021/ct800330d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Riccardi D, Yang S, Cui Q. Biochim. Biophys. Acta. 2010;1804:342. doi: 10.1016/j.bbapap.2009.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Yang Y, Cui Q. J. Phys. Chem. A. 2009;113:12439. doi: 10.1021/jp902949f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Phatak P, Frähmcke JS, Wanko M, Hoffmann M, Strodel P, Smith JC, Suhai S, Bondar A, Elstner M. J. Am. Chem. Soc. 2009;131:7064. doi: 10.1021/ja809767v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Phatak P, Ghosh N, Yu H, Cui Q, Elstner M. Proc. Natl. Acad. Sci. USA. 2008;105:19672. doi: 10.1073/pnas.0810712105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Yang Y, Yu H, Cui Q. J. Mol. Biol. 2008;381:1407. doi: 10.1016/j.jmb.2008.06.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Riccardi D, König P, Guo H, Cui Q. Biochemistry. 2008;47:2369. doi: 10.1021/bi701950j. [DOI] [PubMed] [Google Scholar]
- (47).Yang Y, Cui Q. J. Phys. Chem. B. 2009;113:4930. doi: 10.1021/jp810755p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Bondar A, Fischer S, Smith JC, Elstner M, Suhai S. J. Am. Chem. Soc. 2004;126:14668. doi: 10.1021/ja047982i. [DOI] [PubMed] [Google Scholar]
- (49).Seifert G. J. Phys. Chem. A. 2007;111:5609. doi: 10.1021/jp069056r. [DOI] [PubMed] [Google Scholar]
- (50).Janak JF. Phys. Rev. B. 1978;18:7165. [Google Scholar]
- (51).Politzer P, Murray JS, Lane P. J. Comput. Chem. 2003;24:505. doi: 10.1002/jcc.10209. [DOI] [PubMed] [Google Scholar]
- (52).Winget P, Selçuki C, Horn AHC, Martin B, Clark T. Theor. Chem. Acc. 2003;110:254. [Google Scholar]
- (53).Zhou H, Tajkhorshid E, Frauenheim T, Suhai S, Elstner M. Chem. Phys. 2002;277:91. [Google Scholar]
- (54).Elstner M, Cui Q, Munih P, Kaxiras E, Frauenheim T, Karplus M. J. Comput. Chem. 2003;24:565. doi: 10.1002/jcc.10201. [DOI] [PubMed] [Google Scholar]
- (55).Ghosh N, Xavier P-R, Gunner MR, Cui Q. Biochemistry. 2009;48:2468. doi: 10.1021/bi8021284. [DOI] [PubMed] [Google Scholar]
- (56).Witek HA, Köhler C, Frauenheim T, Morokuma K, Elstner M. J. Phys. Chem. A. 2007;111:5712. doi: 10.1021/jp070786o. [DOI] [PubMed] [Google Scholar]
- (57).Elstner M. Ph.D. thesis. Universität-Gesamthochschule Paderborn; 1998. [Google Scholar]
- (58).Witek HA, Irle S, Morokuma K. J. Chem. Phys. 2004;121:5163. doi: 10.1063/1.1775786. [DOI] [PubMed] [Google Scholar]
- (59).Knaup JM, Hourahine B, Frauenheim T. J. Phys. Chem. A. 2007;111:5637. doi: 10.1021/jp0688097. [DOI] [PubMed] [Google Scholar]
- (60).Niehaus TA, Elstner M, Frauenheim T, Suhai S. J. Mol. Struct.: THEOCHEM. 2001;541:185. [Google Scholar]
- (61).Klopper W, Van Duijneveldt-van De Rijdt J, Van Duijneveldt FB. Phys. Chem. Chem. Phys. 2000;2:2227. [Google Scholar]
- (62).Curtiss LA, Raghavachari K, Redfern PC, Rassolov V, Pople JA. J. Chem. Phys. 1998;109:7764. [Google Scholar]
- (63).Baboul AG, Curtiss LA, Redfern PC, Raghavachari K. J. Chem. Phys. 1999;110:7650. [Google Scholar]
- (64).Perdew JP, Burke K, Ernzerhof M. Phys. Rev. Lett. 1996;77:3865. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- (65).Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr., Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian 03. Revision C.02 Gaussian, Inc.; Wallingford, CT: 2004. [Google Scholar]
- (66).Curtiss LA, Raghavachari K, Redfern PC, Pople JA. J. Chem. Phys. 1997;106:1063. [Google Scholar]
- (67).Lee C, Yang W, Parr RG. Phys. Rev. B. 1988;37:785. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- (68).Becke AD. J. Chem. Phys. 1993;98:5648. [Google Scholar]
- (69).Stephens PJ, Devlin FJ, Chabalowski CF, Frisch M. J. Phys. Chem. 1994;98:11623. [Google Scholar]
- (70).Dunning TH., Jr. J. Chem. Phys. 1989;90:1007. [Google Scholar]
- (71).Xu X, Goddard WA., III J. Phys. Chem. A. 2004;108:2305. [Google Scholar]
- (72).Boys SF, Bernardi F. Mol. Phys. 1970;19:553. [Google Scholar]
- (73).Simon S, Duran M, Dannenberg JJ. J. Chem. Phys. 1996;105:11024. [Google Scholar]
- (74).Ireta J, Neugebauer J, Scheffler M. J. Phys. Chem. A. 2004;108:5692. [Google Scholar]
- (75).Zhao Y, Truhlar D. J. Chem. Theory Comput. 2005;1:415. doi: 10.1021/ct049851d. [DOI] [PubMed] [Google Scholar]
- (76).Santra B, Michaelides A, Scheffler M. J. Chem. Phys. 2007;127:184104. doi: 10.1063/1.2790009. [DOI] [PubMed] [Google Scholar]
- (77).Rao L, Ke H, Fu G, Xu X, Yan Y. J. Chem. Theory Comput. 2009;5:86. doi: 10.1021/ct800237n. [DOI] [PubMed] [Google Scholar]
- (78).Baer M, Mathias G, Kuo I-W, Tobias DJ, Mundy CJ, Marx D. ChemPhysChem. 2008;9:2703. doi: 10.1002/cphc.200800473. [DOI] [PubMed] [Google Scholar]
- (79).Range K, Riccardi D, Cui Q, Elstner M, York DM. Phys. Chem. Chem. Phys. 2005;7:3070. doi: 10.1039/b504941e. [DOI] [PubMed] [Google Scholar]
- (80).Lee Y-S, Krauss M. J. Am. Chem. Soc. 2004;126:2225. doi: 10.1021/ja036115v. [DOI] [PubMed] [Google Scholar]
- (81).Møller C, Plesset MS. Phys. Rev. 1934;46:618. [Google Scholar]
- (82).Zhang X, Harrison DHT, Cui Q. J. Am. Chem. Soc. 2002;124:14871. doi: 10.1021/ja027063x. [DOI] [PubMed] [Google Scholar]
- (83).Yang Y, Cui Q. J. Phys. Chem. B. 2007;111:3999. doi: 10.1021/jp070706g. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


