Abstract
Gene regulation is a complicated process. The interaction of many genes and their products forms an intricate biological network. Identification of this dynamic network will help us understand the biological process in a systematic way. However, the construction of such a dynamic network is very challenging for a high-dimensional system. In this article we propose to use a set of ordinary differential equations (ODE), coupled with dimensional reduction by clustering and mixed-effects modeling techniques, to model the dynamic gene regulatory network (GRN). The ODE models allow us to quantify both positive and negative gene regulations as well as feedback effects of one set of genes in a functional module on the dynamic expression changes of the genes in another functional module, which results in a directed graph network. A five-step procedure, Clustering, Smoothing, regulation Identification, parameter Estimates refining and Function enrichment analysis (CSIEF) is developed to identify the ODE-based dynamic GRN. In the proposed CSIEF procedure, a series of cutting-edge statistical methods and techniques are employed, that include non-parametric mixed-effects models with a mixture distribution for clustering, nonparametric mixed-effects smoothing-based methods for ODE models, the smoothly clipped absolute deviation (SCAD)-based variable selection, and stochastic approximation EM (SAEM) approach for mixed-effects ODE model parameter estimation. The key step, the SCAD-based variable selection of the proposed procedure is justified by investigating its asymptotic properties and validated by Monte Carlo simulations. We apply the proposed method to identify the dynamic GRN for yeast cell cycle progression data. We are able to annotate the identified modules through function enrichment analyses. Some interesting biological findings are discussed. The proposed procedure is a promising tool for constructing a general dynamic GRN and more complicated dynamic networks.
Keywords: Differential equations, Network graph, NLME, Nonparametric mixed-effects model, Saccharomyces cerevisiae, SAEM, SCAD, Time course microarray data, Two-stage smoothing-based method, Yeast cell cycles
1. Introduction
Gene regulation plays a fundamental role in biological activities, such as cell growth, division, development, response to environmental stimulus and so on. Genes carry out their functions through DNA transcription and protein synthesis. Reversely, some proteins, like transcription factors, regulate the activity of genes by binding to their promoters or even encoding the proteins themselves. In addition, some noncoding RNAs, the direct transcript replicates of certain DNA segments regulate genes at some important levels of genome function, including chromatin structure, chromosome segregation, transcription, RNA processing, RNA stability, and translation (Carthew and Sontheimer, 2009). The gene regulatory network (GRN) is a complex system, which should be more appropriately modeled in a dynamic way (Hecker et al., 2009).
Owing to the advancement of new high-throughput technologies such as DNA microarray, we are able to observe the dynamic feature of gene expression profiles on a genome scale. This type of data is composed of experimental measurements of all interested genes simultaneously at different time points. Statistical methods for analyzing high-dimensional time course data are subject to active research currently. For example, clustering genes with similar expression profiles based on time course microarray data is particularly useful for identifying co-expressed genes as well as predicting functions of gene products with unknown functions. Several clustering methods have been developed to account for the temporal order of time course data including curve-based nonparametric clustering methods (James and Sugar, 2003; Luan and Li, 2004; Heard et al., 2006) and functional ANOVA methods (Ma et al., 2006; Ma and Zhong, 2008). The identification of differentially expressed genes under different conditions or treatments is another important research topic of time course gene expression data. For example, Yuan and Kendziorski (2006) employed a hidden Markov model, Storey et al. (2005) introduced a curve-based method, Tai and Speed (2009) used a multisample multivariate empirical Bayes method to rank microarray time course data, Chi et al. (2007) applied a Bayesian hierarchical modeling approach and Yao et al. (2005); Hong and Li (2006); Müller et al. (2008); Liu and Yang (2009) proposed functional data analysis approaches to identify temporally differentially expressed genes.
The time course gene expression data also allow investigators to study gene regulatory networks from a dynamic point of view. Currently, several models have been proposed for GRN construction, such as information theory models (Steuer et al., 2002; Stuart et al., 2003); Boolean networks (Kauffman, 1969; Thomas, 1973; Bornholdt, 2008); Bayesian Networks (Heckerman, 1996; Friedman et al., 2000; Hartemink et al., 2001; Imoto et al., 2003; Zou and Conzen, 2005; Needham et al., 2007; Werhli and Husmeier, 2007); vector autoregressive (VAR) and state space models (SSM) (Hirose et al., 2008; Shimamura et al., 2009; Kojima et al., 2009); and differential equation models (Voit, 2000; Holter et al., 2001; DeJong, 2002; Yeung et al., 2002). The information theory model is basically a correlation network and too simple to model a complex network. In addition, it does not accommodate multiple genes with dynamic expressions. The Boolean model is a discrete dynamic model in which the state of a gene is represented by only two states: on or off, so that the time course nature of gene expression profiles is not taken into account efficiently. The Bayesian network makes use of the Bayes’ rule by combining different types of data and prior knowledge. However, the challenge for establishing a Bayesian network comes from the high computational cost to optimize the network from a large number of combinatory candidates. The VAR and SSM models are discrete dynamic models which usually require equally-spaced and intensive time-series data in order to obtain reliable inference results for model parameters. In most cases, only the first-order and linear autoregressive model is used in practice due to the complications in computations and theoretical justifications although it can be theoretically extended to more general cases. Another problem is the identifiability problem embedded in the state space model. Hirose et al. (2008) made the assumption that the covariance matrix of the state equation is fixed as an identity matrix in order to make the model identifiable.
The focus of this paper is on the ordinary differential equation (ODE) modeling approach for the GRN. The ODE approach models the dynamic change of a gene expression (the derivative of the expression) as a function of expression levels of all related genes. So it is a directed network graph model and the dynamic feature of the GRN is automatically and naturally quantified. Both positive and negative as well as the feedback effects of gene regulations can be appropriately captured by the ODE model. A general ODE model for GRN can be written as:
| (1.1) |
where X(t) = (x1(t), …, xn(t))T is a vector representing the gene expression level of gene 1, …, n at time t. F serves as the link function that quantifies the regulatory effects of other genes on the expression change of gene i which depends on parameter θ. In general F can take any linear or non-linear function forms. However, the non-linear specification of F usually needs prior information on biological mechanisms and requires high computational cost, so that the nonlinear ODE model is only feasible for a small-scale network containing only a few to dozens of genes (Weaver et al., 1999; Sakamoto and Iba, 2001; Spieth et al., 2006). Many GRN models are based on linear ODEs due to its simplicity and usefulness in practical applications. However, we also recognize that the dynamics of gene expression may exhibit complex patterns, which may not be completely captured by a linear model. A simple linear ODE model can be written as
| (1.2) |
where parameters θ = {θij}i,j=1,· · ·,n quantify the regulation effects of the genes in the network. For a small-scale ODE-based GRN model (i.e. n is small), some standard statistical methods such as the standard least squares method or likelihood-based method can be used to perform statistical inference for the dynamic parameters θ from time course gene expression data. However, for a large-scale GRN ODE model that involves hundreds or even thousands of genes, the standard statistical methods may fail due to the curse-of-dimensionality.
We employ two methods to deal with the high-dimensional problem. The first one is the dimension reduction by clustering. We notice that many genes usually behave similarly during the experimental period, which makes it difficult to distinguish the expression patterns of these genes based on the time course microarray data. In this case, investigators have proposed clustering methods to group these similarly behaved genes (co-expressed genes) into functional modules (Luan and Li, 2004; Ma et al., 2006; Ma and Zhong, 2008). Consequently, our GRN model can be based on the functional modules instead of individual genes. Thus, the dimension of our ODE model can be significantly reduced. We can write the ODE model for functional modules as
| (1.3) |
where p is the number of functional modules from clustering. In addition, from the sparseness principle (Arnone and Davidson, 1997), each gene or module may be regulated by only a few other genes or modules, i.e., most coefficients βkj, that quantify the regulation effects, are zeros. The model selection approaches for ODE models can be used to determine the significance of parameters so that the dimension of the parameter space can be reduced significantly. We emphasize that the clustering and ODE model selection based on the sparseness principle and regularization are the two key steps for dimension reduction in the proposed GRN construction.
Another important feature of the proposed procedure is the use of mixed-effects modeling approach to deal with the data sparseness in several steps. In the first step, to cluster time course microarray data into functional modules, we adopt the nonparametric mixed-effects smoothing spline model under the framework of a mixture distribution proposed by Ma and Zhong (2008). In the second step, we employ the nonparametric mixed-effects model (NPME) smoothing approach to estimate the mean function and its derivative for each functional module. Then, we use a nonlinear mixed-effects modeling approach to refine the parameter estimates in the ODE models. The mixed-effects modeling approach allows us to borrow information across genes with similar expression patterns, which is more efficient.
In this article, we propose a roadmap to identify dynamic GRNs based on time course microarray data by combining a series of cutting-edge statistical techniques for ODE models and mixed-effects modeling approaches. In Section 2, we provide details of the proposed five-step procedure to identify the dynamic GRN. We applied the proposed method to the cell cycle gene regulatory network identification for yeast in Section 3. In Section 4 we present a simulation study to validate the key steps of the proposed procedure. We conclude the paper with some remarks in Section 5. The theoretical properties and a sketch of the proof for the SCAD estimator of the ODE model are given in the Appendix.
2. A Five-Step Procedure: CSIEF
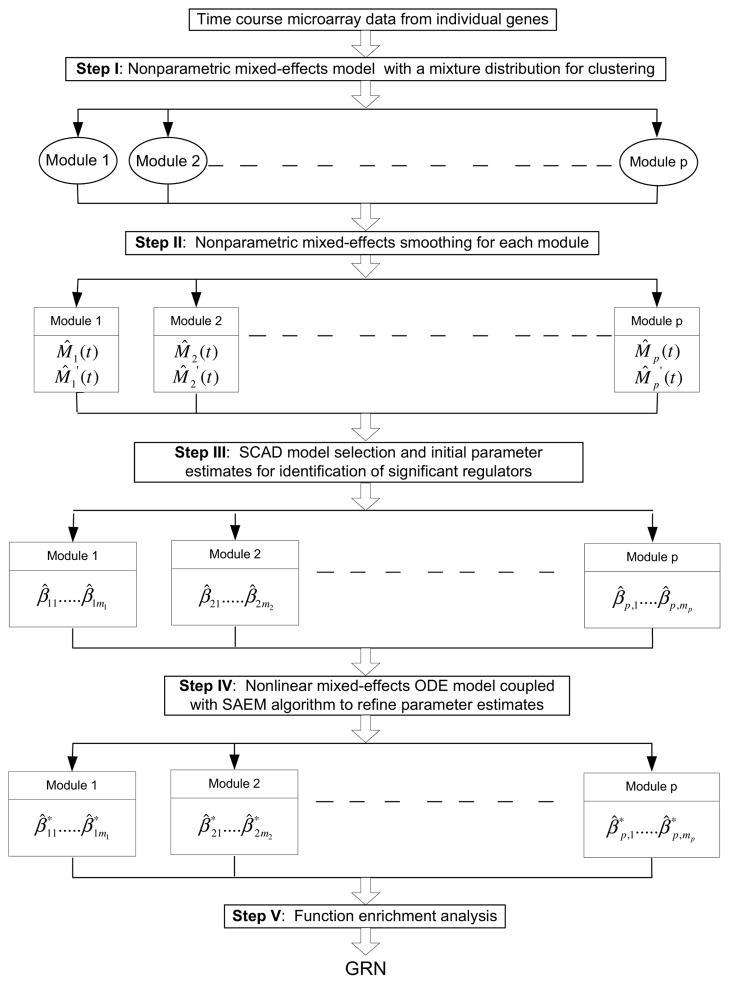
In this section, we propose a roadmap for dynamic GRN identification with five steps. Step I) Clustering individual genes into functional modules: clustering time course microarray data into functional modules using mixed-effects nonparametric models with a mixture distribution (Luan and Li, 2004; Ma et al., 2006; Ma and Zhong, 2008). Step II) Smoothing the time course data to obtain the population (mean) expression pattern and its derivative for each of the functional modules independently. Step III) Identifying significant connections (regulations) among different functional modules: the two-stage estimation method for ODE models (Varah, 1982; Chen and Wu, 2008b,a; Liang and Wu, 2008), coupled with the smoothly clipped absolute deviation (SCAD) technique for high-dimensional variable selection (Fan and Li, 2001; Kim et al., 2008) is employed. Step IV) Refining the parameter estimates for the functional module-based GRN using stochastic approximation EM (SAEM) for mixed-effects ODE models (Delyon et al., 1999; Kuhn and Lavielle, 2005; Samson et al., 2006; Donnet and Samson, 2007). Step V) Performing function enrichment analyses for the identified GRN using Gene Ontology (GO). We coin this five-step procedure as the Clustering-Smoothing-Identification-Estimation-Function enrichment analysis (CSIEF) method. The roadmap for the CSIEF procedure is provided in Figure 1. The details for each step are given below. For convenience, we also provide a list of all notations in Table S1 of the supplementary materials.
Figure 1.
A roadmap for the CSIEF approach of dynamic GRN Construction
2.1. Step I: Clustering
It is important to cluster individual genes into groups or functional modules if the expression patterns of genes are similar during the experimental period. The concept of functional modules is crucial for understanding the proposed GRN construction strategy. It is not only that the expression profiles of the genes in the same module cannot be distinguished from the time course microarray data, but also the genes in the same module may share particular biological functions during the biological process. Thus, clustering individual genes into functional modules based on their expression patterns can help to reduce the dimension of the model, and is also biologically justifiable (Luan and Li, 2004; Ma et al., 2006; Ma and Zhong, 2008).
Several methods have been proposed to cluster time course data which include nonparametric smoothing-based approaches (James and Sugar, 2003; Luan and Li, 2004). Recently Ma et al. (2006) and Ma and Zhong (2008) successfully applied the nonparametric mixed-effects smoothing spline model under the framework of a mixture distribution to cluster time course gene expression data. We adopt this approach for the first step of our proposed procedure. Denote Gi = (gi(t1), · · ·, gi(tni))T as the expression data vector for the ith gene. We assume the following mixture normal distribution with p components (clusters) for Gi,
| (2.4) |
where n is the total number of genes; wk is the proportion of cluster k; μk(.) is the mean curve of cluster k; Ti = (ti1, · · ·, ti,ni)T is the vector of measurement times for gene i and usually all genes share the same measurement times in the same experiment. Since different genes may have different expression patterns and because it is difficult to find a common parametric model for the time course expression profiles for all genes, a mixed-effects nonparametric smoothing splines approach is employed, i.e., a measurement model for Gi for the kth cluster can be written as
| (2.5) |
where the random effect bi quantifies the deviation of gene i from the mean curve μk of the kth cluster and is r × 1 vector following a mean zero normal distribution,
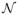 (0, Ωk). Zi is ni × r design matrix for the random effects. Measurement error εi is assumed to follow
(0, Ωk). Zi is ni × r design matrix for the random effects. Measurement error εi is assumed to follow
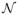 (0, σ2I) and independent of bi. Thus, we have Σk = ZiΩkZiT + σ2I.
(0, σ2I) and independent of bi. Thus, we have Σk = ZiΩkZiT + σ2I.
The maximum penalized likelihood approach can be used to estimate the parameters in models (2.4) and (2.5). Ma et al. (2006) also proposed a variation of the EM algorithm to estimate the cluster proportion parameters wk and assign genes to appropriate clusters. To alleviate the computational cost and to stabilize the algorithm, the rejection-controlled EM algorithm is used to implement the proposed method. The number of clusters is determined by the BIC criterion. See more details for the implementation of this clustering procedure in Ma et al. (2006) and Ma and Zhong (2008).
2.2. Step II: Smoothing
From Step I, we can cluster all genes into functional modules. The expression pattern for all the genes within each module is similar. Thus, we can treat the time course data for all genes within the same module as longitudinal measurements of the expression level for the functional module. To facilitate the identification of significant regulations using the variable selection approach for ODE models in the next step, we need to estimate the mean curve and its derivative for each module independently. The mixed-effects modeling approach for the longitudinal data can be applied for this purpose. In this step, we employ a nonparametric mixed-effects (NPME) model as introduced in Wu and Zhang (2002, 2006) and by others to the data for each functional module to obtain the estimates of the mean expression and its derivative for the module.
Denote tij, i = 1, · · ·, n, j = 1, · · ·, ni as the design time points and gki(tij) is the gene expression level at tij for gene i within the kth functional module, then we can write a nonparametric mixed-effects (NPME) model as
| (2.6) |
where Mk(t) is the mean expression curve for the kth module and its derivative is denoted by , and Vki(t) are random-effects functions that quantify the departure of the ith gene expression level from the mean expression of the module Mk(t).
Over the past decade, many nonparametric smoothing techniques have been proposed to fit the NPME model, which include smoothing spline, regression spline, penalized spline, and local polynomial smoothing (Brumback and Rice, 1998; Wang, 1998; Gu, 2002; Gu and Ma, 2005; Wu and Zhang, 2002). We omit the details of these standard smoothing methods for the NPME model. A good review on these methods can be found in Wu and Zhang (2006). We can apply any of these smoothing techniques to obtain the estimates of Mk(t) and , k = 1, …, p.
2.3. Step III: Identification of Significant Regulations
In this step, we propose a method to identify significant regulations (coefficients) in model (1.3) using a high-dimensional variable selection technique, the smoothly clipped absolute deviation (SCAD) method (Fan and Li, 2001; Kim et al., 2008). First, following the similar idea from Chen and Wu (2008b,a) and Liang and Wu (2008), we plug the estimated mean expression curves and their derivatives, M̂k(t) and , into the ODE model (1.3) to form a regression model,
| (2.7) |
where and xj(t) = M̂j(t). Error term εk(t) is the model approximation error due to the substitutions of the differential equation variables by their estimates from Step II. Since M̂k(t) and in the above model are estimated continuously at any time point t from Step II, we may not need to take t = t1, t2, …, tN as the same time points as the original observation times. In fact, investigators (D’Haeseleer et al., 1999; Wessels et al., 2001; Bansal et al., 2006) have augmented the data for the above ODE-based regression model (2.7) in order to better estimate the ODE coefficients βkj, where N is the number of time points for augmented data. We adopt a similar data augmentation strategy in this step.
If we treat model (2.7) as a standard high-dimensional linear regression model, many model selection methods are available for use, such as, stepwise and subset selection, penalized approaches including bridge selection (Frank and Friedman, 1993), least absolute shrinkage and selection operator (LASSO) (Tibshirani, 1996), smoothly clipped absolute deviation (SCAD) (Fan and Li, 2001) and so on. However, traditional approaches such as stepwise and subset selection methods estimate parameters separately from the model selection stage, which ignore stochastic errors inherited in the stage of model selection and their sampling properties are difficult to derive (Breiman, 1996). On the other hand, the recent work on penalized variable selection approaches such as LASSO and SCAD have demonstrated good properties and advantages to handle high-dimensional models.
The SCAD procedure has been paid great attention because of its desirable properties: unbiasedness, sparsity, and continuity (Fan and Li, 2001). Recently Kim et al. (2008) developed a new computational algorithm, coupled with the concave convex procedure (CCCP) (An and Tao, 1997), to implement the SCAD in an efficient way. This algorithm was confirmed to be less sensitive to the initial value, faster, more stable, and always guaranteed to converge to a minimum, and in addition the oracle property is still ensured in the case where the dimension of covariates is allowed to grow at a certain polynomial rate provided that the true model is sparse. These properties are not attainable for other methods such as LASSO (Meinshausen and Bühlmann, 2006; Zou, 2006). In this paper, we employ Kim et al.’s (2008) idea in our ODE model selection, although it is not trivial to establish the theoretical properties for our ODE model.
Consider the penalized objective function
| (2.8) |
where Jλ(|β|) is the SCAD penalty proposed by Fan and Li (2001), which can be expressed as:
| (2.9) |
where a = 3.7. Note that here β = (β1, β2, …, βp)T and we drop the subscript k for notational simplicity, since we will apply the variable selection technique to each of the p modules separately.
The main idea of the CCCP-SCAD algorithm is to decompose (2.8) as the sum of the convex and concave functions, and then use the CCCP algorithm (An and Tao, 1997) for implementation. The key idea of the CCCP algorithm is to update the solution with the minimizer of the tight convex upper bound of the objective function obtained at the current solution. Thus, even though the objective function given in (2.8) is not convex, it can be decomposed into the sum of a convex function and a concave function, and then the CCCP algorithm can be applied. The most attractive feature of the CCCP-SCAD is that this algorithm is guaranteed to converge to the local minimum and has been shown to have the oracle property for high-dimensional linear models.
Note that Jλ(|β|) = J̃λ(|β|) + λ|β| and |β| is a convex function, where
and J̃λ(|β|) is a differentiable concave function. Thus C(β) in (2.8) can be rewritten as
which is the sum of convex and concave functions. We apply the CCCP algorithm as follows. Given a current solution βc, the tight convex upper bound is given as
| (2.10) |
We then update the current solution of βc with the minimizer of (2.10). We minimize (2.10) by using the algorithm proposed by Rosset and Zhu (2007) as Kim et al. (2008) suggested, because Q(β) is a piecewise quadratic function.
Note that there is a closed-form solution to a linear ODE model, which is a summation of exponential terms (a nonlinear model). However, it will be difficult to estimate the parameters in a high-dimensional nonlinear model and very challenging if not impossible to perform model selection for a high-dimensional nonlinear model. The proposed two-step smoothing-based method transforms this nonlinear regression model into a linear regression model so that standard variable selection approaches for high-dimensional linear regression models can be applied. The computation is easier for the linear model and we can also show that the proposed SCAD estimator has an oracle property under our ODE setting. The theoretical results and the proof are provided in the Appendix.
2.4. Step IV: SAEM for Refining Parameter Estimates
In Step III, we can obtain the estimates of coefficients βkj from model (2.7) while the variable selection is performed using the SCAD approach, which is another advantage of the penalized variable selection methods. However, these estimates are the so-called pseudo-least squares (PsLS) estimates which were investigated by Liang and Wu (2008). As noted by Liang and Wu (2008), the PsLS estimation method is computationally efficient and easy to implement for our variable selection purpose in Step III, but the PsLS estimates are not the most efficient in terms of estimation accuracy. This is because the estimates of the mean expression curves, in particular, their derivatives from Step II may inherit a large error if the data are sparse with a large noise. To overcome this problem, we invoke a nonlinear mixed-effects (NLME) modeling approach to refine the parameter estimates based on the selected model from Step III. The PsLS estimates from the previous step can be used as the initial estimates for the NLME estimates.
The genes in each of the functional module can be treated as “subjects”. Thus, the gene expression data for each module can be considered as a longitudinal data set. The mixed-effects ODE model for module k can be written as
| (2.11) |
where xki is the gene expression level for the ith gene in the kth module, nk is the number of genes in the kth module, M[kj](t) are mean expression levels of the modules that have significant effects (non-zero coefficients determined by the SCAD method in Step III) on the kth module, mk is the number of modules that have significant effect on the kth module. That is, we assume that the ith gene in the kth module is regulated by the mean effects of genes in other modules. To fit model (2.11) and obtain the maximum likelihood estimates of non-zero coefficients βkij, we suggest to use the Stochastic Approximation EM (SAEM) algorithm (Delyon et al., 1999; Kuhn and Lavielle, 2005; Donnet and Samson, 2007).
Denote gki(t) as the expression measurement of gene i at time t in module k; the population parameters βk = (βk1, · · ·, βkmk)T for the kth module and individual parameters βki = (βki1, · · ·, βkimk)T. We have a longitudinal measurement model:
| (2.12) |
where the measurement error εki(t) is assumed to follow an independent normal distribution with mean zero and variance σ2. The between-gene variation can be modeled by random effects of parameters:
| (2.13) |
where random effects bki characterize the deviation of individual genes from the population level of the module. We assume that bki ~
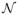 (0, Dk). Note that xki(t) is a solution after integrating ODE (2.11) separately for each module k = 1, · · ·, p, which requires M[kj](t) to be known. We use the nonparametric estimates of M[kj](t) from Step II. Since xki(t) in (2.12) is the solution to ODE (2.11) which is a nonlinear function of βkij and M[kj](t), the response variable gki(t) is nonlinearly related to βkij and M[kj](t). Thus, we are dealing with a nonlinear mixed effects (NLME) model in this step.
(0, Dk). Note that xki(t) is a solution after integrating ODE (2.11) separately for each module k = 1, · · ·, p, which requires M[kj](t) to be known. We use the nonparametric estimates of M[kj](t) from Step II. Since xki(t) in (2.12) is the solution to ODE (2.11) which is a nonlinear function of βkij and M[kj](t), the response variable gki(t) is nonlinearly related to βkij and M[kj](t). Thus, we are dealing with a nonlinear mixed effects (NLME) model in this step.
The SAEM approach is very efficient and generally applicable to obtain the maximum likelihood estimates (MLE) for the unknown parameters in mixed-effects ODE models from longitudinal data. Delyon et al. (1999) has shown that this algorithm converges very well under very general conditions. When the conditional distribution of random effects has no closed-form expression, a Markov chain Monte Carlo (MCMC) method can be used. Kuhn and Lavielle (2005) also established the convergence of the SAEM estimates to the MLE. Donnet and Samson (2007) applied this method to a dynamic ODE model where ODEs are solved by a local linearization scheme. Samson et al. (2006) extended the method to deal with censored data. However, the SAEM approach, similar to other likelihood-based methods for nonlinear models, requires supply of the initial values of the unknown parameters. If these initial values are too far from the true values, the computational algorithm may suffer a convergence problem or may converge to a local maximum, in particular for a high-dimensional parameter space. As aforementioned, the rough estimates of the unknown parameters in the model selection step (Step III) can be served as good starting values for our SAEM algorithm.
2.5. Step V: Function Enrichment Analysis
Based on the variable selection results from Step III and the refined estimates of non-zero coefficients in ODE models from Step IV, we can build the gene regulatory network (GRN) and interpret the results using function enrichment analyses (FEA). The FEA allows us to study what functions of the genes in each module typically perform. Annotating modules appropriately is critical for explaining the constructed GRN. Fortunately, the biological functions of many genes are known and documented in publicly accessible databases such as Gene Ontology Consortium (2000). Genes within a module may perform multiple biological functions. However, a certain function may be over-represented in a module compared to the population of genes in an organism or a biological process which consists of thousands of genes. Therefore, a module can be annotated by enriched function(s).The process of detecting over-represented functions in a module is called function enrichment analysis (Gene Ontology Consortium, 2000). A great deal of genes’ functions have been discovered for many model organisms. Such information provides a platform for measuring the degree of enrichment of certain function(s) in a module. The over-representation of a function in the module can be tested by a hypergeometric distribution (Sokal and Rohlf, 1995),
| (2.14) |
where T is the population size, i.e., the total number of genes in an organism or an interested biological process; S is the number of genes that share the same function in the population; nk is the number of genes clustered in the kth module; and z is the number of genes that share the same function in the module. This formula quantifies the probability of finding the over-represented function in a functional module. In fact, the enrichment test is similar to Fisher’s exact test in a 2 × 2 contingency table where the null hypothesis is that a particular function is not represented in a module more than that in the population. By summing over all the probabilities of the extreme or more extreme than the observed data from (2.14), the p-value can be obtained. Since all categories of gene functions are tested for the same set of genes, a correction is necessary to alleviate the false discovery rate in multiple tests. Bonferroni correction is a conservative way to control the error in this case. The over-represented function is then annotated for each module and the biological interactions of gene functions in a GRN can be interpreted.
3. Identification of Dynamic Gene Regulatory Network for Yeast Cell Cycle
3.1. Time Course Microarray Data for Yeast Cell Cycle-Regulated Genes
The first time course gene expression data set for yeast cell cycle regulated genes were collected by Spellman et al. (1998) and this data set has been analyzed using different approaches by many investigators (Friedman et al., 2000; Holter et al., 2001; DeJong, 2002; Yeung et al., 2002; Yao et al., 2005; Ma et al., 2006; Werhli and Husmeier, 2007). Cell cycle progression in Saccharomyces cerevisiae (yeast) is controlled in part by the sequential transcription of specific gene clusters whose expression peaks at different times during the cell cycle. Such regulation might be required for the proper functioning of mechanisms that maintain orders during cell divisions. Spellman et al. (1998) carried out a series of experiments aimed at objectively identifying all protein-encoding gene transcripts in the genome of Saccharomyces cerevisiae that are cell cycle regulated. They used DNA microarrays to analyze gene expression levels in cell cultures that had been synchronized by three independent methods. They analyzed the data by deriving a numerical score based on a Fourier algorithm (testing periodicity) and using a correlation function, and they found that 800 genes were cell cycle regulated which constitutes > 10% of all protein-coding genes in yeast genome. The gene expression levels were measured at 18 equally spaced time points during two cell cycles. In this paper, we intend to apply differential equation models and the proposed methods in the previous section to establish a dynamic regulatory network among functional modules (instead of individual genes) for the yeast cell cycle.
3.2. Application of the CSIEF Approach
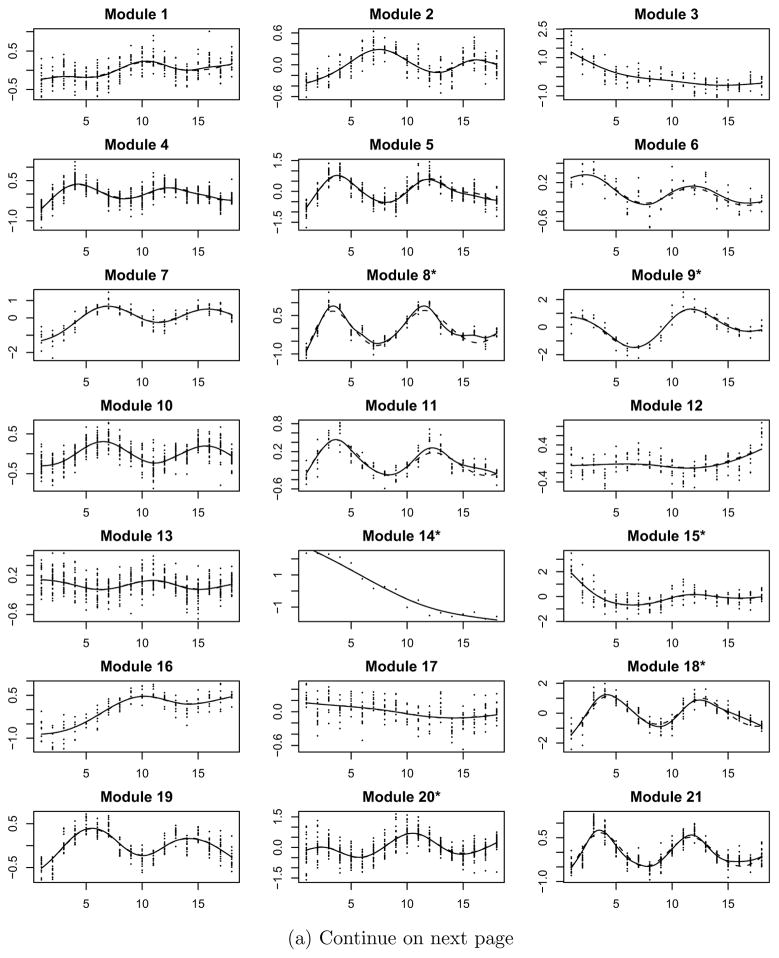
We consider the 800 genes that were identified as cell cycle-regulated by Spellman et al. (1998). Among these 800 genes, many of them showed a similar expression pattern during the two-cell-cycle experiments. It is legitimate to apply the clustering method in Step I of the proposed CSIEF procedure to group these genes into functional modules. The nonparametric mixed-effects smoothing splines method with a mixture distribution (Ma et al., 2006; Ma and Zhong, 2008) was applied to the data and 41 functional modules were identified. The raw data for the 41 modules along with the fitted mean expression curves using the proposed approaches are presented in Figure 2. We can see that these functional modules differ from each other in terms of gene expression patterns, but all genes in the same module behave similarly.
Figure 2.
Yeast cell cycle-regulated gene expression data (dots) for individual modules with nonparametric smoothing estimates of mean expression curves (dashed lines) and the ODE fitted curves (solid lines) by the SAEM approach.
In the second step, we smoothed the data for each of the modules using the nonparametric mixed-effects smoothing splines technique again to obtain the estimates of the mean expression curves and their derivative curves for each module, separately. These estimates were plugged in model (2.7) to formulate a regression-like model in the third step, and then the SCAD approach (Step III of the CSIEF) was used to identify significant regulations (connections) among the 41 functional modules. The SAEM approach was applied to the identified sparse ODE model to refine the parameter estimates for each of the modules in Step IV. We obtained the fitted curves for all modules by integrating 41 ODEs concurrently with parameters estimated from the SAEM approach in Step IV. We overlayed the fitted mean expression curves with the raw data and the smoothed mean curves from Step II in Figure 2 (note that the initial values for the fitted ODE models are taken as M̂k(0) from Step II which are smoothing estimates of Mk(0)). From this figure, we can see that the proposed method fits the data quite well and the fitted mean curves from ODE models (Step IV) for each module also coincide well with the smoothed mean curves from the smoothing splines approach in Step II. We notice that the proposed ODE models not only can fit the simple monotonic curves well, but also can fit complex and periodical curves quite reasonably without invoking any periodical functions explicitly.
Finally we applied the function enrichment analysis (Step V) to each of the 41 functional modules based on Gene Ontology Consortium (2000). The function enrichment analysis is implemented with the whole yeast genome as a population for annotating the modules. These results are reported in Table 1.
Table 1.
Yeast cell cycle gene regulatory network. For a particular module listed in Column 1, Column 4 provides the modules that have a significant effect (inward influence) on this module and Column 5 provides the modules that this particular module has a significant effect on (outward influence).
| Module | # gene | Function Annotation | Inward Influence Modules | Outward Influence Modules |
|---|---|---|---|---|
| 1 | 17 | Nucleotide, nucleic acid transportation | 9−, 15−, 18−, 30− | |
| 2 | 13 | Translational elongation in cellular protein metabolic process | 8−, 25−, 30−, 32, 41 | |
| 3 | 8 | Microtubule cytoskeleton organization | 7, 9−, 14−, 18−, 25 | |
| 4 | 34 | DNA replication, repair, maintenance | 9, 14, 32, 39, 41− | |
| 5 | 22 | Carbohydrate transmembrane transportation | 8, 9, 14, 18−, 32, 41 | |
| 6 | 7 | Ammonia-lyase catalytic activity | 18−, 25, 30, 32−, 41− | |
| 7 | 7 | Cell budding | 18, 25−, 30−, 32, 41 | 3 |
| 8* | 9 | N/A | 18−, 32, 41− | 2−, 5, 18, 19, 24, 25−, 26, 27, 28,32, 34−,39, 40− |
| 9* | 4 | Cell wall organization | 14, 18−, 20, 32−, 41 | 1−, 3−, 4, 5, 10, 11, 13−, 18, 19, 20−, 21, 24, 25−, 26−, 27−, 28−, 31, 32−, 35, 37−, 40−, 41 |
| 10 | 37 | Microtubule based process | 9, 14, 18, 25−, 32, 41 | |
| 11 | 18 | Cell budding neck formation | 9, 14, 18−, 41− | |
| 12 | 19 | N/A | 14−, 15, 41− | |
| 13 | 38 | L-serine ammonia-lyase activity | 9−, 14−, 25, 32, 41− | |
| 14* | 1 | Mating pheromone activity | 14−, 15, 25−, 30−, 38, 41− | 1−, 3−, 4, 5, 9, 10, 11, 12−, 13−, 14−, 15, 16, 17−, 19, 20−, 21−, 22−, 23−, 24, 26−, 29, 30, 31, 32, 33−, 35, 36−, 37−, 38, 39, 40−, 41 |
| 15* | 11 | Conjugation with cell fusion | 14, 15−, 30, 32−, 41 | 1−, 12, 14, 15−, 17, 27, 29, 31−, 33, 34, 35−, 37−, 38− |
| 16 | 8 | Iron ion transmembrane transportation | 14, 30−, 32−, 38−, 41 | |
| 17 | 25 | Intramolecular transferase activity, phosphotransferases | 14−, 15, 25−, 30−, 41− | |
| 18* | 11 | Meiotic mismatch repair | 8, 9, 38, 41− | 1−, 3−, 5−, 6−, 7, 8−, 9−, 10, 11−, 13−, 20−, 21−, 22, 29−, 31−, 32, 33, 34−, 35, 37, 39−, 41 |
| 19 | 18 | Manosyltransferase activity | 8, 9, 14, 25−, 32,41− | |
| 20* | 27 | DNA replication | 9−, 18−, 25, 41− | 9, 22−, 25−, 36, |
| 21 | 31 | Telomere maintenance via DNA recombination; DNA helicase activity | 9, 14−, 18−, 25, 34, 41− | |
| 22 | 24 | Actomyosin contractile ring | 14−, 18, 20−, 32−, 41− | |
| 23 | 6 | Protein amino acid glycosylation | 25−, 30−, 38, 41− | |
| 24 | 23 | ER-associated protein catabolic process; cellular response to heat | 8, 9, 14, 25−, 32, 41− | |
| 25* | 25 | Contract ring contraction involved in cell division | 9−, 20−, 32, 41 | 2−, 3, 6, 7−, 10−, 12−, 13, 14−, 17−, 19−, 20, 21, 23−, 24−, 27−, 38, 40−, 41− |
| 26 | 24 | Chronological cell aging; response to pheromone | 8, 9−, 14−, 30−, 32, 41 | |
| 27 | 25 | Sulfur amino acid biosynthesis, metabolism, transportation | 8, 9−, 15, 25−, 41 | |
| 28 | 39 | Chromosome segregation; sister chromatid cohesion | 8, 9−, 32, 38, 41− | |
| 29 | 19 | Response to abiotic stimulus | 14, 15, 18−, 30, 32 | |
| 30* | 15 | Amino acid myristoylation in protein modification process | 14, 32−, 38− | 1−, 2−, 6, 7−, 12−, 14−, 15, 16−, 17−, 23−, 26−, 29, 31−, 32, 33−, 35, 36−, 37−, 38, 39− |
| 31 | 18 | Fungal-type cell wall biogenesis | 9, 14, 15−, 18−, 30−, 41 | |
| 32* | 3 | N/A | 8, 9−, 14, 18, 30 | 2, 4, 5, 6−, 7, 8, 9−, 10, 13, 15−, 16−, 19, 20, 22−, 24, 25, 26, 28, 29, 30−, 33−, 34, 36, 40− |
| 33 | 23 | N/A | 14−, 15, 18, 30−, 32−, 41 | |
| 34 | 26 | Glycine metabolism | 9−, 15, 18−, 32, 38 | 21 |
| 35 | 29 | Glucanosyltransferase activity | 9, 14, 15−, 18, 30, 41 | |
| 36 | 31 | Methionine metabolism | 14−, 20−, 30−, 32, 38 | |
| 37 | 28 | Nuclear migration along microtubule; chromatin silencing; negative regulation of transcription | 9−, 14−, 15−, 18, 30−, 41 | |
| 38* | 17 | Cell separation during cytokinesis | 14, 15−, 25, 30, 41 | 4, 14, 16−, 18, 23, 28, 30−, 34, 36, 39 |
| 39 | 19 | Response to DNA damage stimulus; DNA repair; DNA strand elongation during DNA replication | 8, 14, 18−, 30−, 38 | |
| 40 | 21 | N/A | 8−, 9−, 14−, 25−, 32−, 41− | |
| 41* | 15 | Nuclear chromatin assembly/disassembly | 9, 14, 18, 25−, 41− | 2, 4−, 5, 6−, 7, 8−, 9, 10, 11−, 12−, 13−, 14−, 15, 16, 17−, 18−, 19−, 20−, 21−, 22−, 23−, 24−, 25, 26, 27, 28−, 31, 33, 35, 37, 38, 40−, 41− |
The superscript ‘−’ on the module numbers indicates the negative (inhibitory) effect (a negative coefficient in the ODE model), otherwise the effect is positive (activatory).
The superscript * indicates the modules that have an effect on multiple other modules.
3.3. Results and Biological Implications
First we notice that 41 functional modules were identified from Step I of the CSIEF procedure (Figure 2 and Table 1). The number of genes in each functional module ranges from 1 to 39 (Column 2 in Table 1). The function annotation results are listed in Column 3 in Table 1. The fourth and fifth columns in Table 1 list all the modules, identified by the SCAD method from Step III, that have significant impact on (inward influence) or are impacted by (outward influence) respectively. If a module effect is negative (inhibitory), we indicate it by a superscript ‘-’ in Columns 4 and 5. A list of the regulation parameter (ODE coefficient) estimates can be found in Table S2 of the supplementary materials.
Figure 2 shows that some of the 41 modules, such as Modules 3 and 14, exhibited a monotonic expression pattern although most of them exhibited a periodical pattern during the two cell cycles. As shown in Table 1, the function annotation suggests that the genes in the identified functional modules may participate in broad activities in a cell cycle such as DNA replication, repair and maintenance, protein synthesis and modification, nucleic acid transportation, nuclear chromatin assembly, cytoskeleton and cell wall organization, cell fusion and division etc..
We also note that the functions of five modules cannot be identified from the function annotation analysis(denoted as ‘N/A’ in ‘Function Annotation’ column in Table 1). But the genes in each of these five modules exhibited similar expression patterns, which indicate that the genes in these modules may share some common functions that have not been discovered to date. We would suggest that experimental biologists explore the genes in these five modules which may lead to new discoveries in cell cycle progression.
The findings from our module-based network modeling are biologically interesting. For instance, the dynamic expression of Module 1 was inhibited (negatively affected) by Modules 9, 15, 18 and 30. We noticed that Module 1’s function is related to nucleic acid transportation, which seems to be inhibited by modules with functions of cell wall organization (the function of Module 9), conjugation with cell fusion (the function of Module 15), meiotic mismatch repair (the function of Module 18), and amino acid myristoylation in protein modification process (the function of Module 30). This seems reasonable since the nucleic acid is transported for DNA synthesis. When a cell is ready to undergo fusion or division, DNA does not participate in such a process. In contrast, the pause of DNA synthesis may help alleviate the burden of accumulating materials and energy for cell fusion or division. In addition, the expression level of Module 1 is almost flat (Figure 2), which seems to be inhibited by some modules such as those identified from Step III of our CSIEF procedure (i.e., Modules 9, 15, 18 and 30). Biological interpretations of function annotations and module interactions for other modules are also interesting, but are omitted here due to space limitation.
One important feature of the identified GRN is that most modules are regulated by only a few other modules (ranging from 3 to 6 modules), which reflects the fact of sparseness of the network connections. However, all the 41 modules are connected via a few important modules that appear to be key players (‘hubs’) in the network. We found that 13 out of 41 modules had the function to regulate other modules. Among them, two modules (Modules 14 and 41) had effects on about 80% of all other modules; five modules (Modules 9, 18, 25, 30, and 32) regulated about 50% of all other modules; and three modules (Modules 8, 15, and 38) regulated about 25% of all other modules. In fact, all 41 modules were regulated and connected by these 10 key modules. In addition, one module (Module 20) regulated 4 other modules and two modules (Modules 7 and 34) regulated one other module by each. We also noticed that very few modules had a feedback loop (the module is regulated by itself). In fact, only two big ‘hubs’, Modules 14 and 41 as well as Module 15 had a negative feedback loop (Table 1).
For the two biggest ‘hubs’, Module 14 only contains one gene with a function of mating pheromone activity and Module 41 contains 15 genes with an annotated function of nuclear chromatin assembly/disassembly. This may suggest that knocking out the gene in Module 14 or some genes in Module 41 may have a significant effect on the yeast cell cycle-regulated gene network, which can be validated via future experiments. Also notice that, among the five modules whose functions were not identified from the GO function annotation (labeled as ‘N/A’ in Column 3 of Table 1), two of them (Modules 32 and 8) are among the second and third largest ‘hubs’ which had an effect on 50% and 25% of all other modules, respectively. This finding provides additional evidence for our suggestion that these 5 modules with unidentified functions are worth more attention from experimental biologists. Recent work published in Nature (Orlando1 et al., 2008) did knock out one gene, cyclin, in a similar yeast cell cycle-regulated gene study. They showed that cells lacking the gene cyclin are blocked at the G1/S border, however, nearly 70% of periodic genes continued to be expressed periodically and on schedule. This suggests that, although the cyclin gene has a function in the regulation of cell-cycle transcription, it is not solely responsible for establishing the global periodic transcription system. This result agrees well with our findings that the gene cyclin was clustered in Module 20 in our analysis and Module 20 is not a big hub although it affects 4 other modules in the network.
Transcription factors(TF) play key roles in regulating yeast gene transcription (Simon et al., 2001). By employing genome-wide binding/location analysis, investigators have already identified the interactions among TFs as well as interactions between TFs and other genes. Lee et al. (2002) identified the binding capability of all 106 TFs of the complete yeast genome which contains 6270 genes. They found that 37% of these genes are bound by one or more of the 106 TFs. We explored the interactions between the 21 cell cycle related TFs and the 800 cell cycle-regulated genes (41 modules). We found, on average, the 21 cell cycle related TFs are more likely to bind to the 13 key modules (‘hubs’) as we have identified, compared to other modules. In particular, among the identified biggest ‘hubs’, Module 41, was affected by >50% of the 21 TFs, followed by Module 14 regulated by more than 40% cell cycle related TFs. This fact suggests that the capability of genes in key modules to regulate other genes is probably due to active transcription binding of cell cycle-related TFs.
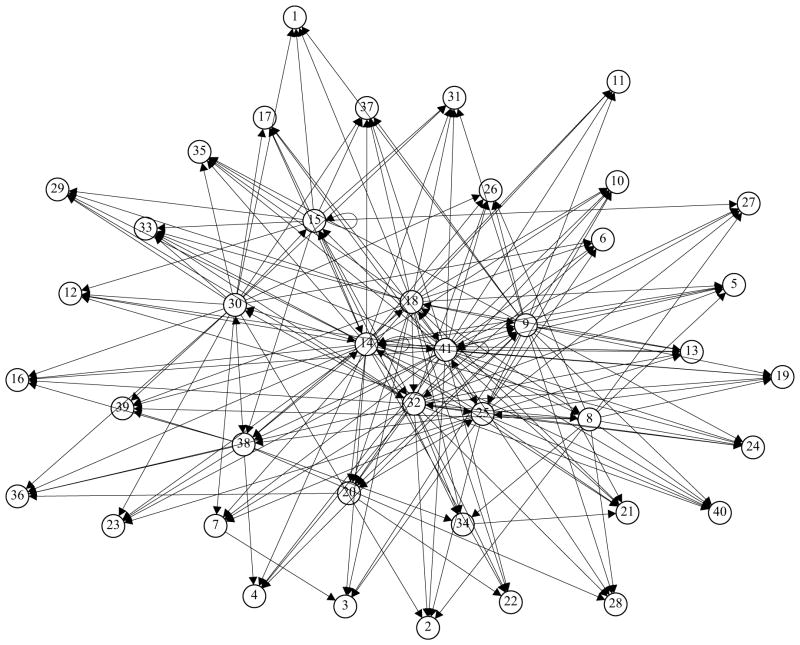
It is helpful to provide an intuitive visualization for the established GRN. We used R function ‘igraph’ to plot the yeast GRN in Figure 3. From this figure, we can clearly see that the large hubs, Modules 9, 14, 18, 25, and 41 are located in the center of the network. Some other important hubs including Modules 30, 8, 15, and 38 can also be easily identified from the graph.
Figure 3.
Graph of yeast cell cycle GRN formed by 41 modules. Each module is represented as a node. Arrow stands for the direction of influence.
4. Simulation Study: Evaluation of ODE Variable Selection and Parameter Estimation
The proposed dynamic GRN construction procedure (CSIEF) is a complicated process involving five steps. In this section, we design simulation experiments to validate some of the key steps such as the ODE variable selection step (Step III) and ODE parameter estimation step (Step IV). The statistical methods in other steps have been well studied in statistical literature and will not be investigated here. We design our simulation study based on the yeast data application in the previous section. We consider a ODE network model with 41 variables (equations) which is the same as the module-based ODE model (1.3). The estimated ODE model parameters (coefficients) are used as the true values in our simulation study (see Table S2 in the supplementary materials). Note that for each of the 41 ODEs, there are 3 to 6 non-zero coefficients and 35 to 38 zero coefficients so that we are mimicking the scenarios of the yeast data application in the previous section. The initial values of the ODE model are taken from the nonparametric smoothing estimates of the mean expression curve Mk(t) at t = 0 for the kth module from Step II in the yeast data analysis. We simulated the experimental data, gki(t) at different time points by solving the ODEs numerically and then adding measurement errors using the following observation model,
| (4.15) |
where nk is the number of genes in the kth module which is set according to Table 1 (Column 2); bki is the random coefficient of gene i in the kth module to quantify the departure of gene i from the mean expression of Module k, which is assumed to follow a standard normal distribution. The measurement error eki(tj) is assumed to follow a normal distribution with mean zero and variance δ2 and we simulated the data for two variance levels, δ2 = 0.05 and 0.5. In order to compare the performance of the proposed method for different sample sizes, we took the number of measurements N = 20, 100 and 300 with equally spaced time points for each gene respectively. The number of simulation runs is taken as Nr = 100.
We applied the SCAD method (Step III) to perform variable selection for the simulated data. Table 2 shows that the SCAD method can correctly select the variables for about 32% of the worst cases (the largest variance and the smallest sample size) and 79% of the best case scenarios (the smallest variance and largest sample size). For other cases, the performance of the SCAD is in between the above two scenarios as we expected. In general, the SCAD approach tends to select more variables (over-fitted). We believe that this problem can be fixed using the adaptive LASSO or other related approaches that penalize more on over-fitted models, but the detailed exploration of this is beyond the scope of this paper.
Table 2.
Simulation results: the SCAD variable selection and comparisons of parameter estimation between the SCAD estimates (Step III) and the SAEM estimates (Step IV), Nr = 100 simulation runs.
| δ2 | N | Under-fitted(%) | Correctly fitted(%) | Over-fitted(%) | SCAD Estimates
|
SAEM Estimates
|
||
|---|---|---|---|---|---|---|---|---|
| ARE(%) | SD | ARE(%) | SD | |||||
|
|
|
|
|
|
|
|
||
| 0.5 | 20 | 13 | 32 | 55 | 27.7 | 9.4 | 15.2 | 10.3 |
| 100 | 20 | 48 | 32 | 16.9 | 8.3 | 11.4 | 8.1 | |
| 300 | 0 | 61 | 39 | 11.4 | 6.2 | 6.9 | 4.5 | |
|
| ||||||||
| 0.05 | 20 | 8 | 44 | 48 | 16.4 | 10.3 | 10.9 | 12.0 |
| 100 | 0 | 57 | 43 | 9.9 | 10.1 | 6.4 | 4.2 | |
| 300 | 0 | 79 | 21 | 6.4 | 5.9 | 3.3 | 2.7 | |
To evaluate the performance of the ODE parameter estimation from Step III and Step IV, we calculated the average relative error (ARE) for all the parameter estimates in model (1.3), which is defined as
| (4.16) |
where is the estimate of parameter βkj in the kth module at the ith simulation run, q is the number of non-zero coefficients in the model, and Nr is the number of simulation replicates (Nr = 100 in our simulation study). We take the average of the AREs for all the parameter estimates in all 41 equations to compare the estimates from Step III and Step IV.
From Step III of the proposed CSIEF method, rough estimates of ODE parameters can be obtained via the smoothing-based estimation method (Liang and Wu, 2008) while the variable selection is performed simultaneously. In Step IV, these estimates are refined using the SAEM method to fit a nonlinear mixed-effects (NLME) model. We applied these methods to the simulated data to evaluate their performance. Table 2 shows the average estimation error for all parameters in model (1.3). The AREs range from 6% to 28% for the smoothing-based SCAD estimates (Step 3) while the AREs are reduced to 3–15% for the SAEM estimates (Step IV). This demonstrates that the SAEM parameter estimation refinement step is necessary. In summary, the SCAD-based variable selection in Step III works quite well for ODE models. The ODE parameter estimates are reasonable and the SAEM estimation refinement in Step IV is necessary.
5. Concluding Remarks
We proposed a roadmap to construct a dynamic gene regulatory network (GRN) based on ordinary differential equation (ODE) models. Statistical inference methods for ODE models and mixed-effects modeling approaches as well as nonparametric smoothing and clustering techniques for repeated measurement data were used to deal with the high-dimensional problem and complex GRN. We successfully applied the proposed method to construct a dynamic GRN for yeast cell cycle-regulated genes. The 800 cell cycle-regulated genes were clustered into 41 functional modules. The functional module-based regulatory network was established. With the help from functional enrichment analysis, we were able to annotate the modules with specific functions. We described the extensive interactions among 41 functional modules and we suggest that some biological implications from our findings are worth further exploration by experimental biologists. We also justified and validated the key methods of the proposed procedure via investigating their theoretical properties and via Monte Carlo simulations.
One limitation of the proposed ODE models for a dynamic GRN is that only linear ODEs are considered here due to the high computational cost and complexity of the variable selection for nonlinear ODEs. The extension of linear ODE models to nonlinear ODE models for dynamic GRN is conceptually straightforward, but the difficulties in computation and variable selection as well as the nonlinear ODE parameter estimation may not be easily overcome. More work in this direction is warranted. Alternative models for dynamic GRN include boolean network, Bayesian network, and hidden Markov models among others. It is interesting to compare these modeling approaches with the proposed ODE model method from both perspectives of computational cost and likelihood to recover the true network. But the computational cost for this comparison is beyond the limit of our current computational power. In Step III, we employed a smoothing-based two-stage estimation method for ODE model parameters (Liang and Wu, 2008) in order to simplify the SCAD-based variable selection for ODE models. Some other more efficient estimation approaches for ODE models such as the nonlinear least squares method (Xue et al., 2010) and generalized profiling approach (Ramsay et al., 2007) are good for ODE parameter estimation, but these methods may not be easily able to handle the variable selection, and thus were not used here. We believe that it is worth future exploration along a similar line.
Gene regulation is a complex dynamic process. In addition, not only genes but also proteins, RNAs, macro or micro molecules play important roles in this process. In theory, the proposed ODE-based network modeling techniques are applicable to the complex network involving more and different biological elements and entities if these data are available, which may help us to reveal more detailed mechanisms of the gene regulatory network in the future.
Supplementary Material
APPENDIX: ASYMPTOTIC RESULTS AND PROOF
For ease of presentation, we consider a local polynomial estimation for M(t) and M′(t) from Step II. It is obvious that the same results apply for splines as well because splines and kernels are asymptotically equivalent in some sense.
Let Tp,t be an n × (p + 1) design matrix, whose (i, j) entry is (ti − t)j−1 for p = 1 or 2, and Wt = diag{Kh(t1 − t), …, Kh(tN − t)} be an N × N diagonal matrix of kernel weights, where Kh(· ) = K(·/h)/h with K(·) being a symmetric kernel function, and h being a proper bandwidth. As a consequence, the estimators M̂(t) and M̂′(t) can be expressed as
respectively, where ξ1 is the 2 × 1 vector having 1 in the first entry and zero in the 2nd entry, while ξ2 is the 3 × 1 vector having 1 in the 2nd entry and zeros in the other entries;
for j = 1, 2, with D and Ri being the covariance matrices of the random-effect and measurement error terms (See Wu and Zhang (2006) for a detailed description), and
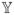 is defined below.
is defined below.
Note that M̂′(t) is actually the slope of the local quadratic fit. Since model (2.7) is not a standard linear regression model, the properties of the SCAD estimator may need to be studied carefully for this ODE-based regression model. Here we study the oracle property of the SCAD estimator for model (2.7).
Let
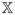 = (x1, …, xN )T for xj = {x1(tj), …, xp(tj)}T,
= (x1, …, xN )T for xj = {x1(tj), …, xp(tj)}T,
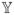 = (Y1, …, YN)T for Yj = {y1(tj), …, yp(tj)}T,
= (Y1, …, YN)T for Yj = {y1(tj), …, yp(tj)}T,
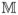 = (M1, …, MN )T for Mj = {M1(tj), …, Mp(tj)}T, j = 1, …, N. For the sparse model, we consider a situation where most of the regression coefficients are exactly 0. Without loss of generality, we assume that the first q regression coefficients are nonzero and the remaining p – q regression coefficients are 0. Let
= (M1, …, MN )T for Mj = {M1(tj), …, Mp(tj)}T, j = 1, …, N. For the sparse model, we consider a situation where most of the regression coefficients are exactly 0. Without loss of generality, we assume that the first q regression coefficients are nonzero and the remaining p – q regression coefficients are 0. Let
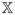 = (
= (
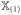 ,
,
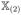 ), where
), where
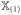 is the first N × q submatrix and
is the first N × q submatrix and
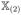 is the last N × (p − q) submatrix of
is the last N × (p − q) submatrix of
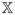 . Similarly, we write β = (β(1), β(2)). Let C
. Similarly, we write β = (β(1), β(2)). Let C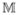 =
=
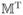
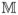 /N, C
/N, C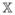 =
=
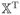
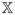 /N,
and
for i, j = 1, 2. In what follows, we denote λmax(A) and λmin(A) as the largest and smallest eigenvalues of matrix A, respectively, and A,j and Aj, the jth column and row of a given matrix A. In addition, in the following theoretical development we express pN = p and qN = q to emphasize that p and q depend on sample size N. We now prove that the oracle estimator is asymptotically a local minimum of C(β). Here the oracle estimator is defined by β̂o = (β̂(1)o, 0(2)), where β̂(1)o is the minimizer of
, 0(2) is (pN – qN )-dimensional 0 vector, and ||·||2 is the standard Euclidean norm on RN. We assume the following regularity conditions:
/N,
and
for i, j = 1, 2. In what follows, we denote λmax(A) and λmin(A) as the largest and smallest eigenvalues of matrix A, respectively, and A,j and Aj, the jth column and row of a given matrix A. In addition, in the following theoretical development we express pN = p and qN = q to emphasize that p and q depend on sample size N. We now prove that the oracle estimator is asymptotically a local minimum of C(β). Here the oracle estimator is defined by β̂o = (β̂(1)o, 0(2)), where β̂(1)o is the minimizer of
, 0(2) is (pN – qN )-dimensional 0 vector, and ||·||2 is the standard Euclidean norm on RN. We assume the following regularity conditions:
Assumption A
The function M(3)(t) is continuous on [0, 1].
The kernel function K is symmetric about zero and is supported on [−1, 1].
The bandwidth h = hN = N−1/7aN is a sequence satisfying h → 0 as N → ∞, where aN is a sequence tending to 0 slower than log−1 N.
ti are iid and have a common compact support and their density function, f (t), is bounded away from zero and has bounded and continuous second derivatives.
Assumption B
-
There exists a positive constant D1 such that for all k = 1, …, pN.
There exists a positive constant D2 such that λmin(C
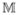 ) ≥ D2.
) ≥ D2.qN = O(Nc1) for some 0 < c1 < 1.
There exist positive constants c2 and D3 such that c1 < c2 ≤ 1 and N(1−c2)/2 min1≤j≤qN|βj| ≥ D3.
The foregoing regularity assumptions (B) were used by Zhao and Yu (2006) to prove the model selection consistency of the LASSO estimator. The following proposition is the main result.
Proposition 1
Assume that E(ei)2κ < ∞ for an integer κ > 0. Let
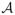 (λN ) be the set of local minima of (2.8) with the SCAD penalty and a regularization parameter λN. Under Assumptions A and B, we have Pr{β̂o ∈
(λN ) be the set of local minima of (2.8) with the SCAD penalty and a regularization parameter λN. Under Assumptions A and B, we have Pr{β̂o ∈
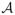 (λN )} → 1 as N → ∞ provided that λN = o(N−(1−c2+c1)/2) and
.
(λN )} → 1 as N → ∞ provided that λN = o(N−(1−c2+c1)/2) and
.
Before we prove the main result, we state the following preliminary fact under Assumptions A and B and its proof can be found in Wu and Zhang (2006):
| (A.17) |
where bN = o(N−1/4aN ) with aN given in Assumption A (iii). Note that (A.17) and Assumption B(ii) indicate that, for large enough N, λmin(C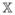 ) ≥ .5D2.
) ≥ .5D2.
Proof of Proposition 1
The proof of Proposition 1 can be completed following the spirit of Theorem 1 of Kim et al. (2008). However, the proof for our case is more complex due to the fact that the SCAD estimator for the ODE model is not based on the observed iid data, instead it is derived from nonparametric smoothing estimates of the functional curves and their derivatives. Here only the key steps that are different from Kim et al.’s (2008) proof are given. Details are omitted due to space limit, but can be obtained from the authors.
Let . Note that ∂Lλ(β)/∂βj is
where . By the second-order sufficiency of the Karush-Kuhn-Tucker condition (see, e.g., Bertsekas, 1999, pp.320), any β to satisfy
| (A.18) |
| (A.19) |
is an element of A(λ). Thus it suffices to show that β̂o satisfies (A.18) and (A.19) with λ = λN.
Note that Sj(β̂o) = 0 for j ≤ qN holds trivially by the definition of the oracle estimator. So for proving (A.18), it suffices to prove that as N → ∞,
| (A.20) |
Let
and
. Note that {M̂′(t1) − M′(t1), · · ·, M̂′(tN ) − M′(tN )}T = Ξ2
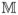 −
−
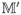 + Ξ2e and
. A direct calculation yields
. It follows that
+ Ξ2e and
. A direct calculation yields
. It follows that
| (A.21) |
We now deal with the three terms on the right-hand side of (A.21) separately. Let and . It follows that
Recall λmin(C ) ≥ .5D2. We know that
. On the other hand, using the arguments similar to the proof of Theorem 1 in Liang and Wu (2008) yields that
. These statements indicate that
) ≥ .5D2. We know that
. On the other hand, using the arguments similar to the proof of Theorem 1 in Liang and Wu (2008) yields that
. These statements indicate that
| (A.22) |
for some positive constant C. Note that
. In addition,
. (A.17) indicates that each element of
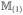 −
−
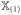 is o(N−1/4). An argument similar to the proof of (A.22) yields that each element of
is of order o(N−1/4). In the same way, we can prove that each element of
is of order o(N−1/4) as well. So the first two terms on the right-hand side of (A.21) are order o(N−1/4). Note that |β̂jo| ≥ |βj| − |β̂jo − βj|. Because minj≤qN|βj | = O(N−(1−c2)/2) and λN = o(N−(1−c2+c1)/2), it suffices to show that max1≤j≤qN|β̂jo − βj| = op(N−(1−c2)/2). Let
. It is equivalent to proving maxj≤qN|zj | = op(Nc2)/2). Using the arguments similar to the proof of Theorem 1 in Kim et al. (2008), we can easily show that, for any η > 0,
is o(N−1/4). An argument similar to the proof of (A.22) yields that each element of
is of order o(N−1/4). In the same way, we can prove that each element of
is of order o(N−1/4) as well. So the first two terms on the right-hand side of (A.21) are order o(N−1/4). Note that |β̂jo| ≥ |βj| − |β̂jo − βj|. Because minj≤qN|βj | = O(N−(1−c2)/2) and λN = o(N−(1−c2+c1)/2), it suffices to show that max1≤j≤qN|β̂jo − βj| = op(N−(1−c2)/2). Let
. It is equivalent to proving maxj≤qN|zj | = op(Nc2)/2). Using the arguments similar to the proof of Theorem 1 in Kim et al. (2008), we can easily show that, for any η > 0,
and we complete the proof of (A.18) for the oracle estimator.
To show (A.19), we have |β̂jo| ≤ λN for j > qN, because β̂jo = 0 by definition. Thus it suffices to show that
| (A.23) |
Note that {Sj(β̂o), for some j = 1 + qN, …, n} can be expressed as
Using the arguments similar to the proof for (A.18) yields that the first two terms are of order o(N−1/4). Thus we are going to deal with
which is denoted by , for some j = 1 + qN, …, N, where h(2)j is the j – qN column vector of H(2) and . Note that , and all eigenvalues of are between 0 and 1, we have that ||h(2)j|| ≤ D1 for all j = qN + 1, …, pN. Recall that . Thus and . As a consequence, we obtain (A.23), and thus complete the proof of Proposition 1.
Contributor Information
Tao LU, Email: tao_lu@urmc.rochester.edu, Department of Biostatistics and Computational Biology, School of Medicine and Dentistry, University of Rochester, Rochester, New York 14642.
Hua LIANG, Email: hliang@bst.rochester.edu, Department of Biostatistics and Computational Biology, School of Medicine and Dentistry, University of Rochester, Rochester, New York 14642.
Hongzhe LI, Email: hongzhe@mail.med.upenn.edu, Department of Biostatistics and Epidemiology, University of Pennsylvania School of Medicine, Philadelphia, PA 19104.
Hulin WU, Email: hwu@bst.rochester.edu, Department of Biostatistics and Computational Biology, School of Medicine and Dentistry, University of Rochester, Rochester, New York 14642.
References
- An LTH, Tao PD. Solving a Class of Linearly Constrained Indefinite Quadratic Problems by DC Algorithms. Journal of Global Optimization. 1997;11:253–285. [Google Scholar]
- Arnone MI, Davidson EH. The Hardwiring of Development: Organization and Function of Genomic Regulatory Systems. Development. 1997;124:1851–1864. doi: 10.1242/dev.124.10.1851. [DOI] [PubMed] [Google Scholar]
- Bansal M, Della Gatta G, di Bernardo D. Inference of Gene Regulatory Networks and Compound Mode of Action from Time Course Gene Expression Profiles. Bioinformatics. 2006;22:815–822. doi: 10.1093/bioinformatics/btl003. [DOI] [PubMed] [Google Scholar]
- Bertsekas DP. Nonlinear Programming. 2 Belmount, MA: Athena Scientific; 1999. [Google Scholar]
- Bornholdt S. Boolean Network Models of Cellular Regulation: Prospects and Limitations. Journal of the Royal Soceity Interface. 2008;5(Suppl 1):S85–94. doi: 10.1098/rsif.2008.0132.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L. Heuristics of Instability and Stabilization in Model Selection. The Annals of Statistics. 1996;24:2350–2383. [Google Scholar]
- Brumback BA, Rice JA. Smoothing Spline Models for the Analysis of Nested and Crossed Samples of Curves (with Discussion) Journal of the American Statistical Association. 1998;93:961–994. [Google Scholar]
- Carthew RW, Sontheimer EJ. Origins and Mechanisms of miRNAs and siRNAs. Cell. 2009;136:642–655. doi: 10.1016/j.cell.2009.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J, Wu H. Efficient Local Estimation for Time-varying Coefficients in Deterministic Dynamic Models with Applications to HIV-1 Dynamics. Journal of the American Statistical Association. 2008a;103:369–384. [Google Scholar]
- Chen J, Wu H. Estimation of Time-varying Parameters in Deterministic Dynamic Models. Statistica Sinica. 2008b;18:987–1006. [Google Scholar]
- Chi YY, Ibrahim JG, Bissahoyo A, Threadgill DW. Bayesian Hierarchical Modleing for Time Course Microarray Experiments. Biometrics. 2007;63:496–504. doi: 10.1111/j.1541-0420.2006.00689.x. [DOI] [PubMed] [Google Scholar]
- DeJong H. Modeling and Simulation of Genetic Regulatory Systems: a Literature Review. Journal of Computational Biology. 2002;9:67–103. doi: 10.1089/10665270252833208. [DOI] [PubMed] [Google Scholar]
- Delyon B, Lavielle M, Moulines E. Convergence of a Stochastic Approximation Version of the EM Algorithm. The Annals of Statistics. 1999;27:94–128. [Google Scholar]
- D’Haeseleer P, Wen X, Fuhrman S, Somogyi R. Linear Modeling of mRNA Expression Levels during CNS Development and Injury. Pacific Symposium on Biocomputing. 1999;4:41–52. doi: 10.1142/9789814447300_0005. [DOI] [PubMed] [Google Scholar]
- Donnet S, Samson A. Estimation of Parameters in Incomplete Data Models Defined by Dynamical Systems. Journal of Statistical Planning and Inference. 2007;137:2815–2831. [Google Scholar]
- Fan J, Li R. Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties. Journal of the American Statistical Association. 2001;96:1348–1360. [Google Scholar]
- Frank I, Friedman J. A Statistical View of Some Chemometrics Regression Tools (with Discussion) Technometrics. 1993;35:109–148. [Google Scholar]
- Friedman N, Linial M, Nachman I, Peer D. Using Bayesian Networks to Analyze Expression Data. Journal of Computational Biology. 2000;7:601–620. doi: 10.1089/106652700750050961. [DOI] [PubMed] [Google Scholar]
- Gene Ontology Consortium. Gene Ontology: Tool for the Unification of Biology. Nature Genetics. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu C. Smoothing Spline ANOVA Models. New York: Springer-Verlag; 2002. [Google Scholar]
- Gu C, Ma P. Optimal Smoothing in Nonparametric Mixed-effect Models. The Annals of Statistics. 2005;33:1357–1379. [Google Scholar]
- Hartemink A, Gifford D, Jaakkola T, Young R. Using Graphical Models and Genomic Expression Data to Statistically Validate Models of Genetic Regulatory Networks. Pacific Symposium on Biocomputing. 2001;6:422–433. doi: 10.1142/9789814447362_0042. [DOI] [PubMed] [Google Scholar]
- Heard NA, Holmes CC, Stephens DA. A Quantitative Study of Gene Regulation Involved in The Immune Response of Anopheline Mosquitoes: an Application of Bayesian Hierarchical Clustering of Curves. Journal of the American Statistical Association. 2006;101:18–29. [Google Scholar]
- Hecker M, Lambeck S, Toepfer S, van Someren E, Guthke R. Gene Regulatory Network Inference: Data Integration in Dynamic Models-a Review. Biosystems. 2009;96:86–103. doi: 10.1016/j.biosystems.2008.12.004. [DOI] [PubMed] [Google Scholar]
- Heckerman D. A Tutorial on Learning with Bayesian Networks. Microsoft Research Tech Report. 1996:MSR-TR–95-06. [Google Scholar]
- Hirose O, Yoshida R, Imoto S, Yamaguchi R, Higuchi T, Charnock-Jones DS, Print C, Miyano S. Statistical Inference of Transcriptional Module-based Gene Networks from Time Course Gene Expression Profiles by Using State Space Models. Bioinformatics. 2008;24:932–942. doi: 10.1093/bioinformatics/btm639. [DOI] [PubMed] [Google Scholar]
- Holter NS, Maritan A, Cieplak M, Fedoroff NV, Banavar JR. Dynamic Modeling of Gene Expression Data. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:1693–1698. doi: 10.1073/pnas.98.4.1693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong F, Li H. Functional Hierarchical Models for Identifying Genes with Different Time-course Expression Profiles. Biometrics. 2006;62:534–544. doi: 10.1111/j.1541-0420.2005.00505.x. [DOI] [PubMed] [Google Scholar]
- Imoto S, Sunyong K, Goto T, Aburatani S, Tashiro K, Kuhara S, Miyano S. Bayesian Network and Nonparametric Heteroscedastic Regression for Nonlinear Modeling of Genetic Network. Journal of Bioinformatics and Computational Biology. 2003;6:231–252. doi: 10.1142/s0219720003000071. [DOI] [PubMed] [Google Scholar]
- James GM, Sugar CA. Clustering for Sparsely Sampled Functional Data. Journal of the American Statistical Association. 2003;98:397–408. [Google Scholar]
- Kauffman SA. Metabolic Stability and Epigenesis in Randomly Constructed Genetic Nets. Journal of Theoretical Biology. 1969;22:437–467. doi: 10.1016/0022-5193(69)90015-0. [DOI] [PubMed] [Google Scholar]
- Kim Y, Choi H, Oh H-S. Smoothly Clipped Absolute Deviation on High Dimensions. Journal of the American Statistical Association. 2008;103:1665–1673. [Google Scholar]
- Kojima K, Yamaguchi R, Imoto S, Yamauchi M, Nagasaki M, Yoshida R, Shimamura T, Ueno K, Higuchi T, Gotoh N, Miyano S. A State Space Representation of VAR Models with Sparse Learning for Dynamic Gene Networks. Genome Informatics. 2009;22:56–68. [PubMed] [Google Scholar]
- Kuhn E, Lavielle M. Coupling a Stochastic Approximation Version of EM with a MCMC Procedure. ESAIM: P & S. 2005;8:115–131. [Google Scholar]
- Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, Zeitlinger J, Jennings EG, Murray HL, Gordon DB, Ren B, Wyrick JJ, Tagne J-B, Volkert TL, Fraenkel E, Gifford DK, Young RA. Transcriptional Regulatory Networks in Saccharomyces Cerevisiae. Science. 2002;298:799–804. doi: 10.1126/science.1075090. [DOI] [PubMed] [Google Scholar]
- Liang H, Wu H. Parameter Estimation for Differential Equation Models Using a Framework of Measurement Error in Regression Models. Journal of the American Statistical Association. 2008;103:1570–1583. doi: 10.1198/016214508000000797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu XL, Yang MCK. Identifying Temporally Differentially Expressed Genes Through Functional Principal Components Analysis. Biostatistics. 2009;10:667–679. doi: 10.1093/biostatistics/kxp022. [DOI] [PubMed] [Google Scholar]
- Luan Y, Li H. Model-Based Methods for Identifying Periodically Expressed Genes Based on Time Course Microarray Gene Expression Data. Bioinformatics. 2004;20:332–339. doi: 10.1093/bioinformatics/btg413. [DOI] [PubMed] [Google Scholar]
- Ma P, Castillo-Davis CI, Zhong W, Liu JS. A Data-driven Clustering Method for Time Course Gene Expression Data. Nucleic Acids Research. 2006;34:1261–1269. doi: 10.1093/nar/gkl013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma P, Zhong W. Penalized Clustering of Large-scale Functional Data with Multiple Covariates. Journal of the American Statistical Association. 2008;103:625–636. [Google Scholar]
- Meinshausen N, Bühlmann P. High-dimensional Graphs and Variable Selection with the Lasso. The Annals of Statistics. 2006;34:1436–1462. [Google Scholar]
- Müller H, Chiou JM, Leng X. Inferring Gene Experssion Dynamics via Functional Regression Analysis. BMC Bioinformatics. 2008;9:60. doi: 10.1186/1471-2105-9-60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Needham CJ, Bradford JR, Bulpitt AJ, Westhead DR. A Primer on Learning in Bayesian Networks for Computational Biology. PLoS Computational Biology. 2007;3:e129. doi: 10.1371/journal.pcbi.0030129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orlando1 DA, Lin CY, Bernard A, Wang JY, Socolar JES, Iversen ES, Hartemink AJ, Haase SB. Global Control of Cell-cycle Transcription by Coupled CDK and Network Oscillators. Nature. 2008;453:944–947. doi: 10.1038/nature06955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay JO, Hooker G, Campbell D, Cao J. Parameter Estimation for Differential Equations: a Generalized Smoothing Approach (with Discussion) Journal of the Royal Statistical Society, Series B. 2007;69:741–796. [Google Scholar]
- Rosset S, Zhu J. Piecewise Linear Regularized Solution Paths. The Annals of Statistics. 2007;35:1012–1030. [Google Scholar]
- Sakamoto E, Iba H. Inferring a Systems of Differential Equations for a Gene Regulatory Network by Using Genetic Programming. Proceedings of the IEEE Congress on Evolutionary Computation. 2001:720–726. [Google Scholar]
- Samson A, Lavielle M, Mentré F. Extension of the SAEM Algorithm to Left-censored Data in Nonlinear Mixed-effects Model: Application to HIV Dynamics Model. Computational Statistics & Data Analysis. 2006;51:1562–1574. [Google Scholar]
- Shimamura T, Imoto S, Yamaguchi R, Fujita A, Nagasaki M, Miyano S. Recursive Regularization for Inferring Gene Networks from Time-course Gene Expression Profiles. BMC Systems Biology. 2009;3:41–54. doi: 10.1186/1752-0509-3-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon I, Barnett J, Hannett N, Harbison CT, Rinaldi NJ, Volkert TL, Wyrick JJ, Zeitlinger J, Gifford DK, Jaakkola TS, Young RA. Serial Regulation of Transcriptional Regulators in the Yeast Cell Cycle. Cell. 2001;106:697–708. doi: 10.1016/s0092-8674(01)00494-9. [DOI] [PubMed] [Google Scholar]
- Sokal R, Rohlf F. Biometry: The Principles and Practice of Statistics in Biological Research, Third edition. New York: Freeman; 1995. [Google Scholar]
- Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, Eisen MB, Brown PO, Botstein D, Futcher B. Comprehensive Identification of Cell Cycle-regulated Genes of the Yeast Saccharomyces Cerevisiae by Microarray Hybridization. Molecular Biology of the Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spieth C, Hassis N, Streichert F. Comparing Mathematical Models on the Problem of Network Inference. Proceedings of 8th Annual Conference on Genetic and Evolutionary Computation. 2006:279–285. [Google Scholar]
- Steuer R, Kurths J, Daub CO, Weise J, Selbig J. The Mutual Information: Detecting and Evaluating Dependencies Between Variables. Bioinformatics. 2002;18:S231–S240. doi: 10.1093/bioinformatics/18.suppl_2.s231. [DOI] [PubMed] [Google Scholar]
- Storey JD, Xiao W, Leek JT, Tompkins RG, Davis RW. Significance Analysis of Time Course Microarray Experiments. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:12837–12842. doi: 10.1073/pnas.0504609102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart JM, Segal E, Koller D, Kim SK. A Gene-Coexpression Network for Global Discovery of Conserved Genetic Modules. Science. 2003;302:249–255. doi: 10.1126/science.1087447. [DOI] [PubMed] [Google Scholar]
- Tai Y, Speed T. On Gene Ranking Using Replicated Microarray Time Course Data. Biometrics. 2009;65:40–51. doi: 10.1111/j.1541-0420.2008.01057.x. [DOI] [PubMed] [Google Scholar]
- Thomas R. Boolean Formalization of Genetic Control Circuits. Journal of Theoretical Biology. 1973;42:563–585. doi: 10.1016/0022-5193(73)90247-6. [DOI] [PubMed] [Google Scholar]
- Tibshirani RJ. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society, Series B. 1996;58:267–288. [Google Scholar]
- Varah JM. A Spline Least Squares Method for Numerical Parameter Estimation in Differential Equations. Society for Industrial and Applied Mathematics Journal on Scientific and Statistical Computing. 1982;3:28–46. [Google Scholar]
- Voit EO. Computational Analysis of Biochemical Systems: a Practical Guide for Biochemists and Molecular Biologists. Cambridge, New York: Cambridge University Press; 2000. [Google Scholar]
- Wang Y. Mixed Effects Smoothing Spline Analysis of Variance. Journal of the Royal Statistical Society, Series B. 1998;60:159–174. [Google Scholar]
- Weaver DC, Workman CT, Stormo GD. Modeling Regulatory Networks with Weight Matrices. Pacific Symposium on Biocomputing. 1999;4:112–123. doi: 10.1142/9789814447300_0011. [DOI] [PubMed] [Google Scholar]
- Werhli AV, Husmeier D. Reconstructing Gene Regulatory Networks with Bayesian Networks by Combining Expression Data with Multiple Sources of Prior Knowledge. Statistical Applications in Genetics and Molecular Biology. 2007;6 doi: 10.2202/1544-6115.1282. Article15. [DOI] [PubMed] [Google Scholar]
- Wessels LF, van Someren EP, Reinders MJ. A Comparison of Genetic Network Models. Pacific Symposium on Biocomputing. 2001;6:508–519. [PubMed] [Google Scholar]
- Wu H, Zhang JT. Local Polynomial Mixed-effects Models for Longitudinal Data. Journal of the American Statistical Association. 2002;97:883–897. [Google Scholar]
- Wu H, Zhang JT. Nonparametric Regression Methods for Longitudinal Data Analysis. Hoboken, NJ: John Wiley & Sons; 2006. (Wiley Series in Probability and Statistics). [Google Scholar]
- Xue H, Miao H, Wu H. Sieve Estimation of Constant and Time-Varying Coefficients in Nonlinear Ordinary Differential Equation Models by Considering Both Numerical Error and Measurement Error. The Annals of Statistics. 2010;38:2351–2387. doi: 10.1214/09-aos784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao F, Müller HG, Wang JL. Functional Data Analysis for Sparse Longitudinal Data. Journal of the American Statistical Association. 2005;100:577–590. [Google Scholar]
- Yeung MKS, Tegner J, Collins JJ. Reverse Engineering Gene Networks Using Singular Value Decomposition and Robust Regression. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:6163–6168. doi: 10.1073/pnas.092576199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M, Kendziorski C. Hidden Markov Models for Microarray Time Course Data in Multiple Biological Conditions. Journal of the American Statistical Association. 2006;101:1323–1332. [Google Scholar]
- Zhao P, Yu B. On Model Selection Consistency of Lasso. Journal of Machine Learning Research. 2006;7:2541–2563. [Google Scholar]
- Zou H. The Adaptive LASSO and Its Oracle Properties. Journal of the American Statistical Association. 2006;101:1418–1429. [Google Scholar]
- Zou M, Conzen SD. A New Dynamic Bayesian Network (DBN) Approach for Identifying Gene Regulatory Networks from Time Course Microarray Data. Bioinformatics. 2005;21:71–79. doi: 10.1093/bioinformatics/bth463. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.