Quantifying transient binding of ISWI chromatin remodelers in living cells by pixel-wise photobleaching profile evolution analysis

Abstract

Interactions between nuclear proteins and chromatin frequently occur on the time scale of seconds and below. These transient binding events are important for the fast identification of target sites as concluded from our previous analysis of the human chromatin remodelers Snf2H and Snf2L from the imitation switch (ISWI) family. Both ATP-driven molecular motor proteins are able to translocate nucleosomes along the DNA and appear to exert this activity only on a small number of nucleosomes to which they bind more tightly. For mechanistic studies, one needs to distinguish such translocation reactions or other long-lived interactions associated with conformational changes and/or ATP hydrolysis from nonproductive chromatin sampling during target search. These processes can be separated by measuring the duration of nucleosome binding with subsecond time resolution. To reach this goal, we have developed a fluorescence bleaching technique termed pixel-wise photobleaching profile evolution analysis (3PEA). It exploits the inherent time structure of confocal microscopy images and yields millisecond resolution. 3PEA represents a generally applicable approach to quantitate transient chromatin interactions in the 2- to 500-ms time regime within only ∼1 s needed for a measurement. The green autofluorescent protein (GFP)-tagged Snf2H and Snf2L and the inactive Snf2L+13 splice variant were studied by 3PEA in comparison to the isolated GFP or red autofluorescent protein and a GFP pentamer. Our results reveal that the residence time for transient chromatin binding of Snf2H and Snf2L is <2 ms, and strongly support the view that ISWI-type remodelers are only rarely active in unperturbed cells during G1 phase.

Many nuclear proteins bind chromatin with surprisingly short residence times on the time scale of seconds and below. This appears to be a general feature required for an efficient search process of factors that need to find specific sites on chromatin as discussed in a number of reviews (1–3). Such a “continuous sampling” type of target location mechanism is characteristic for imitation switch (ISWI) chromatin remodelers as concluded from our previous analysis (3–5). The ISWI family consists of two ATPases, Snf2H and Snf2L, in humans, which assemble into different complexes via association with additional subunits (6, 7). Their ATP-coupled activity repositions nucleosomes on the DNA, which represents an important activity during DNA replication, repair, and transcriptional regulation. Because only a few percent of Snf2H and Snf2L proteins interact with chromatin for more than 500 ms, it appears that in the cell, they translocate only a small subset of nucleosomes to which they bind tightly (4).

As reviewed previously (8), the available repertoire of methods for measuring chromatin interactions either evaluates the redistribution of bleached particles as in fluorescence recovery after photobleaching (FRAP) (9, 10), or uses the correlation between intensity fluctuations. The latter is referred to as fluorescence correlation spectroscopy (FCS) and measures the mobility from fluorescence intensity fluctuations generated by molecules moving in and out of the observation volume (11). Alternatively, in spatiotemporal image correlation spectroscopy (STICS), raster image correlation spectroscopy (RICS), or the pair correlation approach (12–14) intensity fluctuations in different pixels of the fluorescence microscopy image are analyzed. Bleaching and correlation methods provide complementary information on protein mobility and interactions (8).

The current implementation of FRAP analyzes the fluorescence recovery within the postbleach image series to obtain particle mobility. It is well suited to study proteins that have a relatively low mobility or are even immobilized during the time of the measurement. The temporal resolution of FRAP is limited by the acquisition speed of the microscope and the time required for efficient bleaching, which is on the 100-ms time scale for most commercial confocal laser scanning microscopes (CLSMs) like the one used in the present study. In contrast, FCS, STICS, and RICS have better time resolution down to microseconds but can only measure proteins with a relatively high mobility because they are based on evaluating intensity fluctuations that arise from the movement of fluorescent molecules in and out of the observation volume. The application of FCS to quantitate protein binding to chromatin is limited for two reasons. First, in all instances we have studied, chromatin dynamics (and possibly other events that lead to the translocation of nuclear subcompartments) detected via bound fluorescent proteins manifest themselves as additional fluctuations of fluorescence intensity with apparent diffusion times in the range of 10–500 ms (4, 15). This contribution needs to be accounted for in the data analysis and can obscure binding events on the same time scale. Second, FCS cannot be applied when proteins are immobilized for several 100 ms because photobleaching becomes significant. However, nuclear proteins display heterogeneous interactions with chromatin, e.g., both subsecond transient binding and high-affinity interactions during which the protein is typically bound in the range of several 100 ms up to minutes (16). Because the latter type of interaction is frequently considered to reflect a biologically important state, and due to the relatively simple experimental setup, most of the recent studies of nuclear dynamics have relied on FRAP. However, the associated kinetic analysis of transient interactions by FRAP is fraught with difficulties due to comparably low temporal resolution (corresponding to the frame time of the microscope) and noninstantaneous bleaching, as well as uncertainties with respect to the effective bleach spot size and shape (17, 18). Even the intracellular diffusion coefficient of an inert protein, such as red autofluorescent protein (RFP) or green autofluorescent protein (GFP), commonly used as a reference cannot easily be determined in a spatially resolved manner by regular FRAP with many commercial systems. The reason for this is the relatively high mobility of these autofluorescent protein domains with diffusion coefficients above 20 μm²⋅s⁻¹ as derived from FCS measurements in the cytoplasm and the nucleus (19).

Because FRAP and FCS experiments are carried out on different length scales (FCS: ∼0.3 μm, FRAP: >1 μm), scale-dependent phenomena, such as anomalous diffusion or caging effects of the nuclear environment, will affect FRAP and FCS experiments differently. Moreover, reaction-diffusion processes exhibit different properties depending on which time scale is used to study them. This makes the integration of data from the two methods difficult, and the cross-validation of FRAP and FCS experiments is limited to the time regime that is accessible to both techniques (8, 15, 20). Our previous combination of FRAP and FCS measurements of ISWI chromatin remodelers delineated chromatin residence times for transient binding to a relatively large time interval from 1 to 500 ms (4), but no single method was found to be suited to measure both fast and slow processes robustly in the same experiment. Furthermore, the regime between the maximum residence time of 500 ms determined by FRAP and the dwell time of 1–2 ms determined by FCS is hardly accessible by both methods. Nevertheless, the accurate determination of transient binding times is crucial to separate chromatin sampling interactions from productive slower binding events that involve conformational changes of the nucleosome or the remodeler as well as ATP hydrolysis. In in vitro experiments, reaction rates of 0.2–0.5 s⁻¹ for ATP hydrolysis and 0.2–13 bp⋅s⁻¹ for nucleosome translocation were determined for Snf2H and other chromatin remodelers (21–24). Although the upper limit of 500 ms reaction time in living cells could still be compatible with ATP hydrolysis, and possibly also with a translocation step, the dwell time of 1–2 ms measured by FCS can be associated with unproductive binding reactions. Thus, analyzing the 1- to 500-ms regime in a single measurement at high spatial resolution would provide valuable mechanistic information on the mode of interaction between ISWI remodelers and their chromatin substrate.

Here, we address this issue by introducing a fluorescence bleaching method called pixel-wise photobleaching profile evolution analysis (3PEA) that extends the strength of FRAP in identifying slowly moving or immobilized particles to include fast translocations and transient binding events as well. 3PEA exploits the inherent time structure of confocal images caused by the sequential nature of the pixel-by-pixel bleaching and imaging process. Protein mobility parameters are obtained by evaluating particle translocations with millisecond time resolution during the acquisition of a single-image frame within less than 1 s. With this method, we were able to quantify the transient binding of the GFP-tagged chromatin remodelers Snf2H and Snf2L. In addition, the naturally occurring splice variant Snf2L+13 was included in the analysis. In Snf2L+13, the exon 13 disrupts the ATPase cassette of Snf2L, which makes the protein inactive. Because Snf2L+13 was found in the same complexes as Snf2L, it was proposed to function as a dominant-negative variant (25). As a reference for proteins that do not interact with chromatin, the isolated GFP/RFP domain and a GFP pentamer (GFP₅) were used. Our 3PEA analysis of Snf2H and Snf2L revealed that transient binding interactions occur with an average residence time below 2 ms, and are thus well separated from the rare long-lived interactions of several seconds to minutes. These results strongly support the view that Snf2H and Snf2L do not translocate nucleosomes during most of their chromatin interaction events in G1 phase because the <2-ms residence time is too short for repositioning a nucleosome.

Theory

Principle of 3PEA.

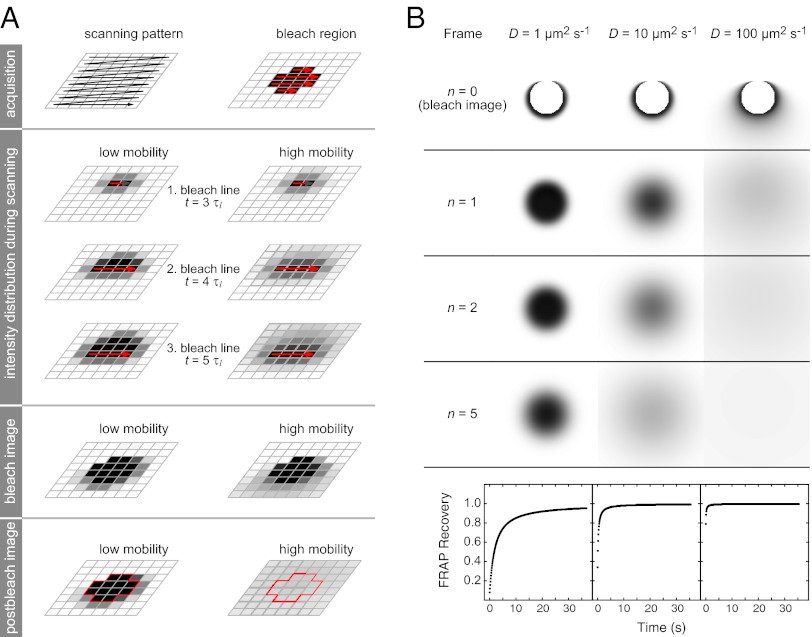
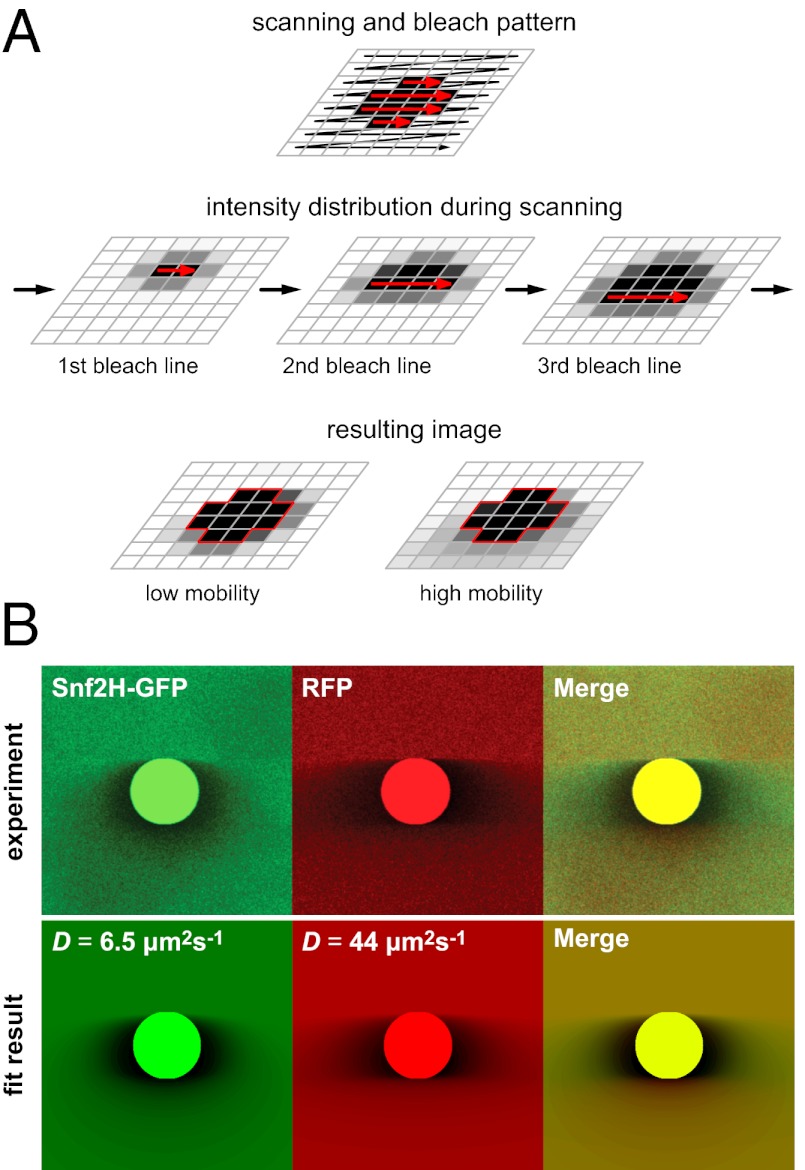
The principle of 3PEA is illustrated in Fig. 1A and Movies S1, S2, and S3. In confocal laser scanning microscopy, the individual volume elements (voxels) of a sample are sequentially illuminated in a raster scan process. Thus, every image pixel is acquired at a unique time point. This applies also for the bleach process in FRAP experiments, which occurs in the same pixel-by-pixel manner as the subsequent image acquisition. The only difference is that the excitation laser intensity is largely increased within the bleach region (Fig. 1A, red arrows). In the current state-of-the-art FRAP analysis, it is ignored that the CLSM acquires and bleaches images in a sequential manner. Instead, the integrated intensity in the bleach spot or the intensity profile is analyzed over time (9, 10, 15, 26), starting with the first postbleach image shown at the bottom of Fig. 1A. Thus, all information on particle mobility during the bleach process is lost. Likewise, translocations that occur during the acquisition time of an image frame, which is around 100 ms per image for the microscope used here, are not resolved. This leads to a relatively low temporal resolution and precludes measurements of faster processes. However, the information on translocations on the millisecond time scale is present in the pixel intensity profile of the bleach frame. This is depicted schematically for particles with high or low mobility in Fig. 1A. The 3PEA approach introduced here explicitly calculates and fits the spatiotemporal intensity distribution generated by the sequential bleach process. It can describe the subsequently acquired postbleach images in the same manner. This is shown in Fig. 1B for the calculated time evolution of intensity profiles for particles with different diffusion coefficients during and after the bleach process. Moreover, effective translocation probability distributions can be derived without assumptions about the underlying microscopic translocation process. In the following, the theory for the 3PEA method is developed to extract the encoded mobility information. The approach is then applied to dissect the transient binding of the ISWI-type chromatin remodelers Snf2H, Snf2L, and Snf2L+13.

Fig. 1.

3PEA concept. (A) A CLSM acquires and bleaches images via a pixel-by-pixel scanning process in a sequential manner. This is not considered in the conventional FRAP analysis. In contrast, 3PEA explicitly calculates and fits the spatiotemporal intensity distribution generated by the sequential bleach process. (B) Time evolution of the intensity profiles for particles with different diffusion coefficients during and after the bleach process. The profiles were calculated for a 128 × 128 image size, a pixel time τ_p of 10 μs, and a line time τ_l of 1 ms. The bleach spot is depicted in white.

3PEA for Diffusion Processes.

The theoretical framework of the 3PEA method is derived here for homogeneous protein distributions. This assumption is valid for all proteins used in this study because they exhibited little spatial variation in their steady-state distribution. For heterogeneous distributions, the intensity profile for the analysis needs to be corrected by subtracting the prebleach distribution. This correction is similar to the well-established procedure for removing immobile protein fractions in RICS (27), and its applicability for 3PEA was confirmed in the analysis of cells exhibiting more heterogeneous chromatin remodeler distributions. The temporal distance between the acquisition of two pixels at (x₀, y₀) and (x₁, y₁) of a CLSM image depends on their spatial coordinates (27) and can be written as

Here, τ_p denotes the time between the acquisition of two adjacent pixels within the same line, τ_l is the time between the acquisition of two adjacent pixels in successive lines, x and y are the pixel coordinates, and s is the pixel size. If a particle is bleached in a volume element around position (x₀, y₀, z₀), the probability 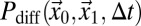that it translocates to position (x₁, y₁, z₁) during the time interval ∆t can be expressed according to a specific model that describes the particle mobility. For pure diffusion, this propagator is given by

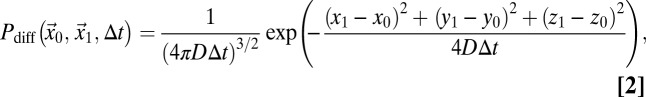with D being the diffusion coefficient of the particle of interest. The point spread function (PSF) of a confocal microscope for detecting a fluorescent particle can be approximated by 3D-Gaussian geometry:

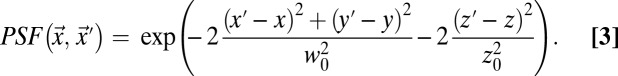Here, 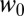and 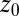are the lateral and axial beam waists, respectively. The PSF is defined in its general form (i.e., as the product of the illumination and detection PSF). The theoretical intensity distribution for a FRAP series acquired with the CLSM (Fig. 1B) is obtained based on the calculation of the amount of particles that were bleached within a volume element around 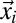and show up in 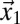when the intensity in the latter position is measured. The loss in fluorescence intensity arising from these bleached particles is proportional to 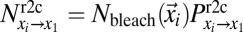and is given by Eq. 4:

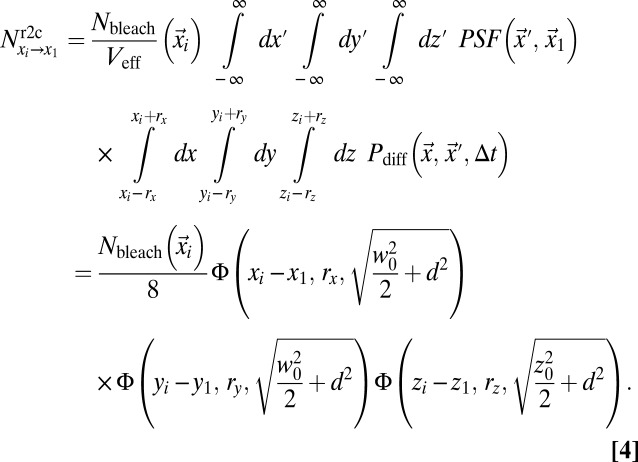Here, 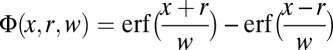; 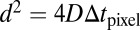is the mean squared displacement (MSD) of the particles; 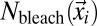is the number of particles bleached in 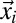(Eq. 5); V_eff = (π/2)^3/2 w₀² z₀ is the effective PSF volume; and r_x, r_y, and r_z are the edge lengths of the volume element considered (Fig. S1A). To obtain the intensity profiles in the bleach and postbleach frames based on Eq. 4, the amount of particles that become bleached in each volume element of the bleach region has to be known. This value depends on the shape of the PSF that extends the bleach process beyond its center position to neighboring areas. In addition, the translocation of bleached particles during the bleach process has to be accounted for. Thus, even before the illumination beam has reached a voxel of interest, this voxel might contain previously bleached particles. Because the initial number of fluorescent particles varies from voxel to voxel, different numbers of particles become newly bleached in each volume element, even in case of identical illumination intensity. The following recursive relation yields the particles that become bleached in a cuboid volume element around 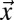at time t when the focus is located at :

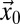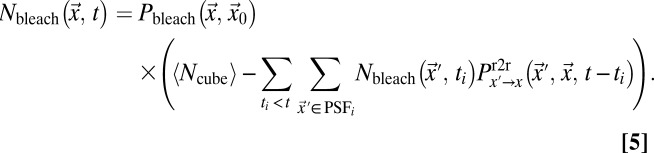In Eq. 5, 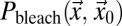denotes the bleach depth at 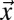, 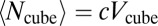is the average particle number within a cuboid volume element, and P^r2r is the translocation probability between two volume elements (SI Text and Fig. S1A). For the first bleach event, the number of bleached particles is determined solely by the bleach depth, which, in turn, depends on the bleach PSF of the microscope (SI Text). For subsequent bleach events, Eq. 5 corrects for the number of bleached particles that are already present in a volume element before the center of the illumination beam has reached it. Accordingly, t_i represents all time points at which bleaching occurred before the center of the illumination beam arrives at position 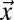, and PSF_i comprises the volume elements that were bleached at time point t_i. If more than one bleach frame is used, the bleach events within previous bleach frames are also included. From Eqs. 4 and 5, the intensity profile for the bleach and postbleach frames is obtained by

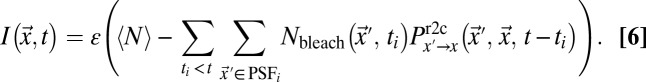Here, 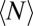is the average particle number within the focal volume, and ε is the visibility of the molecules (i.e., the amount of detected signal per molecule). The maximum signal that can be obtained is I_max = ε〈N〉. This value is reduced if bleaching has already occurred during the preceding raster scan. With the knowledge of the microscope parameters used in the experiment (pixel time τ_p, line time τ_l, frame time τ_f, and beam waists w₀ and w_b), the expression in Eq. 6 can readily be applied to fit intensity profiles and to determine mobility parameters. As outlined in the following section and described in further detail in SI Text, this general theoretical framework can be used to account for anomalous diffusion or to include binding events explicitly.

3PEA for Reaction-Diffusion Processes.

If 3PEA is applied to reaction-diffusion processes, the propagator for pure diffusion given in Eq. 2 is replaced by an expression that also accounts for binding interactions. The probability distribution for a particle’s residence time t_res at a given position in the presence of binding reactions with pseudoassociation rate 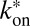(including the concentration of binding sites), and dissociation rate 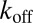is

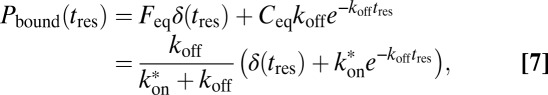with the free and bound fractions 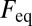and 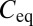in steady state. In Eq. 7, the first term is the probability to find a free particle and the second term is the probability to find a particle bound for t_res. Accordingly, the following propagator for reaction-diffusion processes can be formulated:

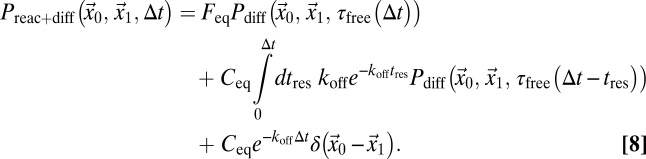Here, 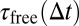is the average time particles have spent in the free state during time ∆t if they were in the free state at t = 0:

In Eq. 9, 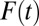is the free fraction after time t, which can be interpreted as the average fraction of particles in the free state or as the fraction of time an individual particle has spent, on average, in the free state. Per definition, particles are initially free; thus, 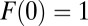. For larger time lags ∆t, the free fraction decreases to 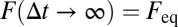because particles become trapped part of the time. The reaction-diffusion propagator in Eq. 8 can be understood intuitively. The first line represents particles that are initially free and subsequently diffuse for 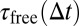. The second line represents particles that are initially bound, dissociate after t_res < ∆t, and diffuse for the rest of the time they spend in the free state [i.e., 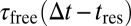]. The third line represents particles that are initially bound and remain bound for t_res > ∆t. In general, the integral in the second line of Eq. 8 has to be solved numerically. For special cases, such as very fast binding [i.e., 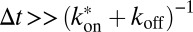] or very slow binding, such as that represented by 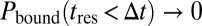, Eq. 8 converges to analytical expressions. The scale-dependent behavior of reaction-diffusion processes is illustrated in Fig. S1 B and C.

The diffusion propagator in Eq. 2 depends only on the product of time and the diffusion coefficient. Thus, if binding events reduce the average time during which a particle is free to diffuse, this can also be accounted for by introducing a time-dependent apparent diffusion coefficient according to Eq. 10:

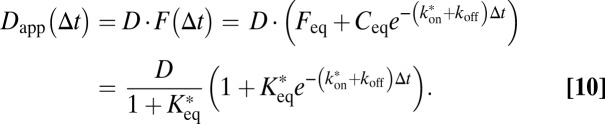Here, 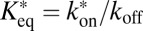is the pseudoequilibrium binding constant that includes the concentration of free binding sites. Eq. 10 yields the weighted average diffusion coefficient for an ensemble with 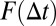free molecules diffusing with 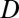and the rest of the molecules being bound to immobile obstacles. For large lag times 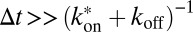, Eq. 10 converges to the time-independent effective diffusion coefficient 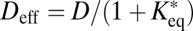introduced previously (28). Further details on the derivation of the above implementation of a reaction-diffusion model into the 3PEA approach are given in SI Text.

3PEA for Arbitrary Translocation Processes.

To obtain information about particle mobility in a model-independent manner, the translocation probability distribution P(Δx, Δt) can be directly calculated from the intensity profile by assigning a characteristic spatial and temporal distance with respect to the set of bleach events to every pixel (SI Text). In this case, ∆x and ∆t are averaged values, and thus not exact. Nevertheless, they reflect that each pixel predominantly contains information about a certain range of length and time scales. Based on these characteristic distances, the effective translocation probability can be directly obtained from the pixel intensity via the relation

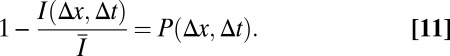Here, 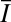is the average prebleach intensity and I(Δx, Δt) is the intensity of the respective pixel. With this approach, typical translocation times can be derived for every spatial distance in the experiment and converted into a plot of the mean squared value of ∆x vs. the weighted average translocation time. This approach is less accurate than fitting the experimental data to theoretical intensity distributions. However, it requires no assumption on the type of the underlying translocation process and provides valuable diagnostic information on the contribution of diffusion, binding, and spatial constraints to the observed particle mobility.

Time Resolution and Accuracy of 3PEA.

The size of the voxels in the calculation of the bleach profiles should be smaller than the PSF and can be chosen according to the desired accuracy and computation speed of the analysis. If the axial extension of the PSF is in the range of the sample thickness, the equations can be simplified because the translocation process is effectively two-dimensional (SI Text and Fig. S2).

To save computational time, diffusion occurring during the bleach of line segments or whole bleach lines can be neglected by using a line-shaped bleach PSF (SI Text). For typical scan speeds and diffusion coefficients, this simplification is justified. The accuracy of 3PEA with this implementation is still below the time τ_l to acquire one line. Thus, in principle, 3PEA can increase the time resolution of bleach experiments by a factor of τ_l/τ_f, which is larger than two orders of magnitude for typical image sizes of 128 × 128 or 512 × 512 pixels. This gain in temporal resolution is due to the modified evaluation scheme and does not depend on the microscope’s maximum frame rate. The 3PEA framework derived here is valid for arbitrary shapes of the bleach region and scan trajectories. The latter feature is particularly important if pixel times differ along the scan line, which can be the case for CLSMs (29). As one special case of the theory derived here, point bleach experiments with a fixed beam like those by Koppel et al. (30) can be treated as well by our theoretical framework. This would involve reducing the scan trajectory to a single position and then subdividing the bleach period into multiple pseudobleach frames. In this manner, particle diffusion during the bleach process could be incorporated into the analysis of such experiments. In the limit of infinitesimal voxel size and infinitely large scan speed, the equations presented here converge to the well-known results obtained previously (28, 31) as shown in the SI Text.

Results

Mobility Differences Between Snf2H, GFP, RFP, and GFP₅ Measured by 3PEA.

The mobility of the chromatin remodeler Snf2H-GFP and free RFP were simultaneously measured in living human U2OS cells (Fig. S3) by analyzing only the bleach frame containing a circular (Fig. 2A) or rectangular (Fig. S4A) bleach region. For comparison, exemplary theoretical intensity profiles for different diffusion coefficients and scan speeds were calculated (Fig. 2B and Fig. S4B). As expected, the bleach corona gets broader with increasing diffusion coefficient and decreasing scan speed. From inspection of Fig. 2 and Fig. S4, it is apparent that the key features of the experimental data are reproduced in the calculated profiles. Snf2H-GFP displayed features of the profiles calculated for both D = 1 and 10 μm²⋅s⁻¹, respectively, whereas the broader corona of free RFP fitted better to the profile for D = 10 μm²⋅s⁻¹. This difference is expected because Snf2H-GFP, as opposed to free RFP, interacts transiently with chromatin, and is thus slowed down (4).

Fig. 2.

Experimental implementation of 3PEA. (A) Mobilities of Snf2H-GFP and RFP in a U2OS cell line measured in a 3PEA experiment with the indicated scan speeds for raster scanning and a circular bleach region with a diameter of 1 μm. In the merge images, the less mobile protein can be readily identified by visual inspection of the predominant color in the area adjacent to the bleach region (Snf2H-GFP in green). (B) Theoretical bleach profiles for different diffusion coefficients calculated for the parameters used in the experiments.

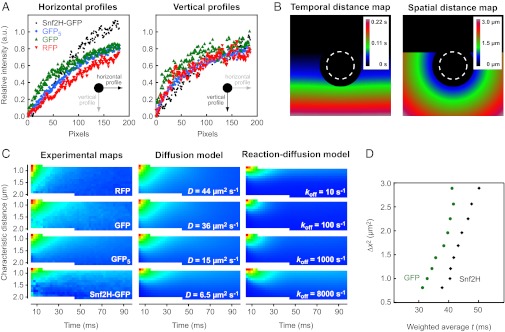
Due to the raster scan process, the bleach coronas are asymmetrical: Along the “fast” horizontal axis, pixels are separated by the short pixel time only, whereas along the “slow” vertical axis, they are separated by the much larger line time, resulting in different shapes of the respective line sections. This is shown in Fig. 3A for experimental bleach profiles from U2OS cells expressing Snf2H-GFP or the GFP, RFP, and GFP₅ references. As described above in the context of Eq. 11, one can assign a characteristic spatial and temporal distance from the bleach region to each image pixel. The corresponding distributions are shown in Fig. 3B, and were used to calculate the effective experimental translocation probability distributions for the different proteins in a model-independent manner (Fig. 3C, experimental maps). The slower Snf2H-GFP displayed a distribution that is elongated along the time axis and shortened along the spatial axis compared with the distributions for GFP and RFP. This reflects that Snf2H-GFP requires more time to translocate a given distance than GFP/RFP or GFP₅, and that fewer molecules reach more distant pixels within the frame time τ_f. The measured translocation probability distributions can readily be evaluated by visual inspection and compared with exemplary theoretical maps for pure diffusion or reaction-diffusion processes with the parameters determined by the profile-fitting analysis described in the next section (diffusion model and reaction-diffusion model in Fig. 3C). It is noted that the reaction-diffusion processes with very small residence times exhibit larger translocation probabilities for short spatial distances (Fig. 3C). A straightforward way to analyze these types of maps is plotting the squared characteristic spatial translocations against the weighted averages along the time axis as shown for GFP and Snf2H (Fig. 3D). The translocation times grow with increasing spatial distance for both GFP and Snf2H. Due to its lower mobility, translocation times for Snf2H are larger than those for GFP. It is noted that both proteins do not show scale-dependent mobility in this type of analysis, which would result in biphasic behavior of the curves.

Fig. 3.

Translocation probabilities for Snf2H-GFP, GFP, RFP, and GFP₅. (A) Horizontal and vertical profiles around the bleach spot differ due to the asymmetry introduced by the raster scan process. Different protein mobility leads to different profiles. a.u., arbitrary units. (B) Each pixel has a defined characteristic spatial and temporal distance from the set of bleach events. Pixels at the bottom are acquired later than pixels in the center of the image. (C) Characteristic spatial and temporal distances can be used to derive the effective translocation probability, P(∆x,∆t). This distribution depends on the protein mobility as shown for the experimental bleach profiles of the different proteins used here. Theoretical profiles show similar probability distributions. (D) Based on the translocation probabilities, the characteristic translocation time can be calculated as the weighted average along the time axis. The resulting diagnostic plots visualize the particle’s mobility on different length scales.

Diffusion Coefficients for Chromatin Remodelers and Reference Proteins.

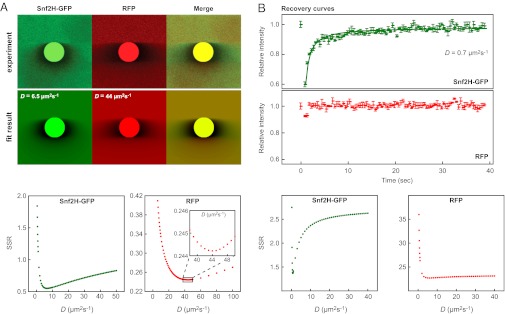
To obtain quantitative mobility information from 3PEA experiments, the intensity distributions of Snf2H-GFP, GFP-Snf2L, GFP-Snf2L+13, GFP, RFP, and GFP₅ were fitted against theoretical profiles (Fig. 4, Fig. S5, and Table 1). The best fit was determined based on the sum of squared residuals (SSR). This value is a measure of the fit quality and has a minimum for the profile with the largest similarity to the experimental data. To determine the diffusion coefficient of the mobile pool, only pixels with a distance of at least 400 nm from the bleach spot were evaluated. Pixels adjacent to the bleach spot that contain information about immobile proteins were ignored for simplicity. 3PEA yielded effective diffusion coefficients of 5–7 μm²⋅s⁻¹ for Snf2H and Snf2L that were clearly lower than that of the similar-sized GFP₅ with D = 15 ± 2 μm²⋅s⁻¹ (Fig. 4A, Fig. S5, and Table 1). Thus, the effective diffusion coefficients measured for the active ISWI ATPases include a contribution from transient binding of the protein to chromatin. It is noted that identical values of D_eff were obtained for Snf2L and the inactive Snf2L+13 variant (Table 1), which demonstrates that the duration of these binding interactions is not affected by the remodeler’s ATP hydrolysis activity. The conventional FRAP analysis conducted using the postbleach images of the same dataset yielded D_eff = 0.7 μm²⋅s⁻¹ (with a confidence interval of D_eff = 0.5–2.0 μm²⋅s⁻¹) for Snf2H-GFP but failed to determine the diffusion coefficient for RFP (Fig. 4B). Because we used a larger image size, and thus a lower frame rate compared with our previous study (4), conventional FRAP yielded a considerably lower value for Snf2H-GFP. This deviation can be corrected by using a broader bleach profile as initial condition for the fit (17, 32). For the inert GFP and RFP reference protein domains, 3PEA yielded averaged values of D = 40 ± 4 μm²⋅s⁻¹ in excellent agreement with previous studies (32, 33).

Fig. 4.

Diffusion coefficients measured by 3PEA and conventional FRAP. (A) Experimental bleach profiles for the scan speed of 1,400 Hz shown in Fig. 2 were fitted to a library of theoretical 3PEA profiles calculated for different diffusion coefficients, yielding D = 6.5 ± 1.0 μm²⋅s⁻¹ for Snf2H-GFP and D = 44 ± 3 μm²⋅s⁻¹ for free RFP. The fit optimum was determined based on the SSR, which has a minimum for the theoretical profile with the largest similarity to the experimental one. The value for Snf2H-GFP was better defined than the result for RFP as evident from the narrower minimum in the SSR plot. (B) Conventional FRAP analysis of the same experiment yielded D = 0.7 μm²⋅s⁻¹ for Snf2H-GFP and failed to determine the diffusion coefficient for RFP.

Table 1.

Mobility and interaction parameters of ISWI remodelers and GFP/RFP references

Protein	Deff, μm2⋅s−1		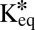koff, s−1	Method
Snf2H-GFP	6.5 ± 1.0	2.1 ± 0.5	>500	3PEA
GFP-Snf2L	5.5 ± 1.5	2.6 ± 1.0	>600
GFP-Snf2L+13	5.5 ± 1.5	2.6 ± 1.0	>600
GFP5	15 ± 2	—	—
RFP	44 ± 3
GFP	36 ± 5
GFP	44 ± 4	—	—	FCS†

^†This value was determined using TetraSpeck beads as a reference for which D = 4.4 μm²⋅s⁻¹ has been determined by dual-focus FCS and dynamic light scattering (47). This is consistent with the theoretical diffusion coefficient for a sphere with a diameter of 100 nm.

Determination of the Dissociation Rate Constant for Snf2H, Snf2L, and Snf2L+13.

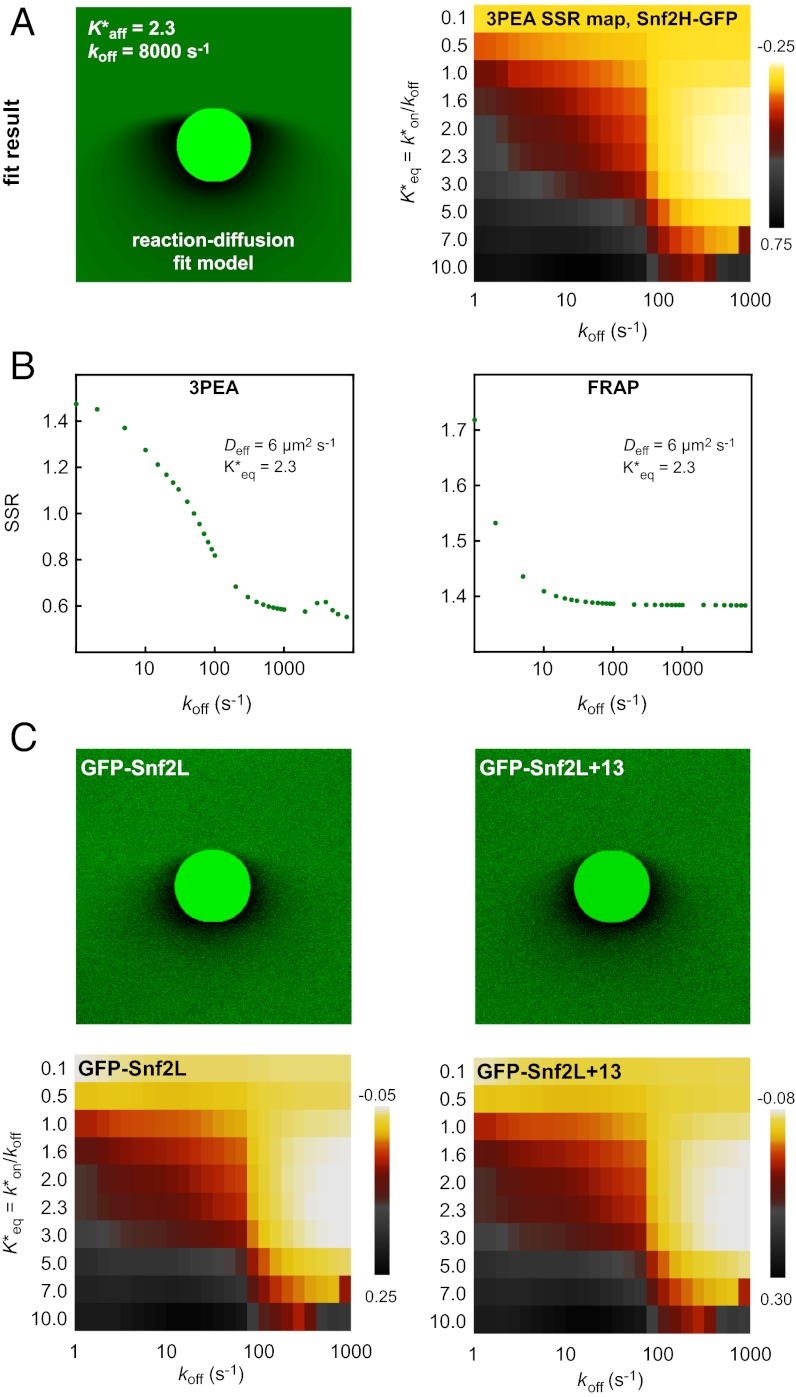
The effective diffusion coefficients determined for Snf2H, Snf2L, and Snf2L+13 in the previous section contain binding contributions from interactions with chromatin. This is apparent from the comparison with the diffusion coefficients obtained for inert proteins of comparable size, such as GFP₅ (Table 1), or from diffusion coefficient measurements of these proteins in the cytosol by FCS (4). Reliable dissection of binding times on chromatin from this reduction of the apparent diffusion coefficient is essential to evaluate if chromatin remodeler activity is present. However, our previously used approach faced technical limitations (4). On the one hand, a relatively short residence time for transient binding needed to be determined more exactly than was possible by conventional FRAP with a time resolution of roughly 100 ms. On the other hand, a protein fraction potentially immobilized on the time scale of more than 10 ms would be hardly accessible to FCS measurements. This is due to contributions to this part of the autocorrelation curve that arise from unintentional photobleaching and the presence of a second component in the correlation function due to chromatin dynamics on the 10- to 500-ms time scale (4, 15). The latter can be directly measured by single-particle tracking of chromatin loci (34, 35). As illustrated in Fig. S6B and consistent with previous findings (36), there is no simple way to retrieve the contribution of chromatin binding from the FCS curves [i.e., to decide if a factor interacts with an immobile (chromatin) substrate or if a bound fraction jiggles around an equilibrium position together with the chromatin fiber]. These problems can be overcome when applying the theoretical 3PEA framework for reaction-diffusion processes derived above. The bleach profiles for Snf2H-GFP, GFP-Snf2L, and GFP-Snf2L+13 were fitted with different values for the dissociation rate constant k_off (Fig. 5). Different pseudoequilibrium binding constants were used, including the values of K*_eq = 2.3 and K*_eq = 1.0 determined previously (4). For Snf2H, good fits to the experimental data were obtained for k_off > 500 s⁻¹ as judged from the resulting SSR plots (Fig. 5 A and B). In contrast, conventional fitting of the FRAP recovery curve could only retrieve a limit of k_off > 10 s⁻¹, which is expected based on the 100-ms frame time (Fig. 5B). Thus, 3PEA is sensitive to a much wider range of dissociation rates than FRAP, which is in line with the theoretical expectations (SI Text), and the finding that fast reaction-diffusion processes can be better studied on small scales (36). For Snf2L and the inactive isoform Snf2L+13, very similar SSR landscapes were obtained with good fits for k_off > 600 s⁻¹ (Fig. 5C). These results indicate that transient chromatin interactions of Snf2H, Snf2L, and Snf2L+13 occur in a very similar manner. Because Snf2L+13 cannot hydrolyze ATP, the transient binding on the <2-ms scale does not depend on chromatin remodeling activity but, instead, reflects the unproductive interaction with potential substrates. This is consistent with the rate constants on the time scale of seconds measured for chromatin remodeling in vitro (21–24). Because the majority of interactions between remodelers and chromatin occur on the millisecond time scale, remodeling events seem to be rare. Taken together, our 3PEA results point to very short residence times for Snf2H, Snf2L, and Snf2L+13 on chromatin of less than 2 ms, in agreement with dwell times of ∼1.4 ms derived from the difference of FCS measurements in the nucleus (τ ∼2.0 ms) and the cytoplasm (τ ∼0.6 ms) (4). Thus, 3PEA was able to resolve the sampling times for transient interactions of the three remodelers in a time regime that previously was only accessible by FCS. Furthermore, the 3PEA results show that there is no significant fraction of Snf2H molecules binding to chromatin for 10–500 ms, which could not be excluded by the previously used combination of FRAP and FCS.

Fig. 5.

Dissociation constants measured by 3PEA. (A) The bleach profile for Snf2H-GFP was fitted against a library with different dissociation rates. The calculated profile that yielded the best fit and the logarithmic SSR map for different dissociation rates and pseudoequilibrium binding constants are shown. (B) The SSR plot for Snf2H-GFP displayed a global minimum at 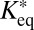= 2.3 and k_off > 500 s⁻¹, corresponding to residence times of less than 2 ms. (C) The same analysis was conducted for GFP-Snf2L and GFP-Snf2L+13, yielding very similar SSR maps and best fits for 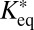= 2.6 and rate constants k_off > 600 s⁻¹.

Discussion

The cell stably maintains its genome and, at the same time, is able to switch reversibly between different functional states. This dichotomy between stability and plasticity is reflected by the dynamic organization of the genome into distinct patterns of chromatin states that can be reorganized in terms of their spatial conformation, protein, and RNA composition as well as by posttranslational modifications of histone and DNA components. Although the vast majority of measurements in living cells were conducted on the time scale of seconds to hours (16), it is emerging that many processes that affect chromatin function occur in the subsecond time regime. This is true for spontaneous chromatin conformation changes in the nucleus (34, 35) as well as for the occurrence of functionally very different interactions of protein factors with chromatin (1–3). The analysis of ISWI-type chromatin remodeler mobility in living cells conducted here clearly revealed transient binding to chromatin as reflected by the value of the effective diffusion coefficient in comparison to that of a GFP pentamer, which has a similar molecular weight (Table 1). Maximum residence times of 2 ms were found for Snf2H, Snf2L, and the inactive splice variant Snf2L+13. In conjunction with the results from our previous FCS and FRAP analysis (4), the following picture emerges: ISWI chromatin remodelers continuously sample nucleosomes via binding interactions that do not involve ATP hydrolysis and, on average, last only for 1–2 ms. Within this time, it can be tested whether a given nucleosome carries additional signals that would mark it to be translocated. Because any subsequent conformational changes and ATP hydrolysis steps would occur only for a fraction of a few percent of binding events during the G1 phase of the cell cycle, these cannot be further dissected. However, when investigating Snf2H or Snf2L at sites of DNA replication and repair, it is clear that the average chromatin interaction time is at least 30 s at these loci with high remodeler activity (4, 5). This is consistent with the catalytical reaction rates from in vitro experiments that yield a similar time needed for ATP hydrolysis and translocation reactions (21–24). In addition, our model fits well to studies with ISWI mutant Drosophila showing that only a small subset of nucleosomes is affected by ISWI activity, arguing for rather rarely occurring translocation events (26).

The additional insight into the dynamics of remodeler–chromatin interactions described above could only be obtained by overcoming various limitations of conventional FRAP with our 3PEA method. 3PEA evaluates the millisecond time information inherent to the pixel-by-pixel bleaching and detection process of a conventional CLSM and the resulting profile of the bleach frame. The power of the method was demonstrated here in a mobility analysis of the transient ISWI chromatin binders in comparison to the inert GFP/RFP using standard CLSM hardware. Diffusion coefficients could be obtained robustly by solely analyzing the bleach frame acquired within less than 1 s of measurement time. Notably, the time scale of 2–500 ms relevant for characterizing the fast transient binding interactions of Snf2H, Snf2L, and Snf2L+13 with chromatin could be characterized. This time scale is not accessible by conventional FRAP because of the roughly two orders of magnitude lower time resolution, and FCS measurements are not suited to quantify chromatin interactions that exceed ∼10 ms of residence time due to slow fluctuations on this time scale arising from chromatin dynamics. It is noted that the time resolution for FRAP can also be improved to reach the 1-ms time regime if a dedicated spot bleach instrument with a fixed beam position is used, as done in the early applications of photobleaching to measurements of diffusion (e.g., 30). Spot bleach experiments can be regarded as a special case of the general 3PEA theory developed here for scanned beams. Interpretation of such experiments within our theoretical framework has the advantage that diffusion of particles during the bleach process can be accounted for, which is relevant for the longer bleach periods that might be required to obtain sufficient bleach depths. However, compared to 3PEA with a CLSM setup as implemented here, spot bleach experiments do not yield mobility information on multiple length scales, which is advantageous for the characterization of scale-dependent processes, such as reaction-diffusion processes or anomalous diffusion (SI Text).

The averaged 3PEA values of D = 40 ± 4 μm²⋅s⁻¹ for the inert GFP/RFP reference protein domains obtained here are in excellent agreement with the values of D = 41 ± 4 μm²⋅s⁻¹ and D = 41 ± 6 μm²⋅s⁻¹ from two other studies (32, 33). This demonstrates that the 3PEA method provides accurate values for the determination of D even for highly mobile particles. In the previous studies, a GFP variant was photoactivated in half of the cell nucleus and traced so that faster particles could be measured more accurately at the expense of a reduced spatial resolution (33) or the bleach corona was accounted for with a Gaussian distribution (32). The small difference between similar-sized GFP and RFP might be due to their different photophysical properties (37, 38). Our GFP/RFP and GFP₅ values were somewhat larger than those from previous FCS measurements for which diffusion coefficients of 20–30 μm²⋅s⁻¹ and 8–10 μm²⋅s⁻¹ were reported (19, 39). This is consistent with the finding that single-focus FCS generally underestimates diffusion coefficients due to deviations of the focal volume from the Gaussian geometry (40), leading to inaccuracies as evident from the comparison of single- and double-focus FCS measurements of small inorganic dyes (40, 41). In our previous study, we used Alexa 488 maleimide with a too small literature value of D = 210 μm²⋅s⁻¹ (42) as a reference. From calibration measurements with well-defined 100-nm size fluorescent latex beads (Fig. S6A and Table 1), we conclude that our previous single-focus FCS analysis of ISWI remodelers (4) underestimated the diffusion coefficients by a factor of roughly 1.5. This leads to a corrected value of D_eff = 20 ± 2 μm²⋅s⁻¹ for Snf2H-GFP in the cytoplasm and of D_eff = 5.9 ± 0.6 μm²⋅s⁻¹ in the nucleus. The latter value is again in good agreement with the 3PEA result of D_eff = 6.5 ± 1.0 μm²⋅s⁻¹. Thus, consistent results are obtained with FCS measurements that use reference values from well-characterized fluorescent particles calibrated by a dual-focus setup and dynamic light scattering (40). The 3PEA method does not require an additional reference with a known diffusion coefficient because it calculates the mobility from the known distance between pixels. This is conceptually similar to correlation methods measuring at spatially separated positions, such as dual-focus FCS, RICS, or pair correlation analysis (14, 27, 41).

A 3PEA measurement can be conducted within 1 s or less, and the method opens up several new approaches for single-cell protein interaction analyses via evaluating protein dynamics in living cells:

• i) Changes in intracellular protein mobility of highly dynamic cellular states that are adopted in response to external stimuli, such as drug treatment, mechanical stress, or DNA damage, can be detected with a time resolution of 1 s.

• ii) Automated high-throughput FRAP experiments will be largely facilitated. This would both improve the reliable detection of differences in intracellular protein mobility and provide a new readout in RNAi screening experiments for systems biology studies of protein networks (43).

• iii) Acquiring protein mobility maps with a resolution on the micrometer scale becomes feasible by sequentially probing multiple locations in the same cell by 3PEA. In such experiments, reversible photoswitching of a suitable fluorophore to a dark state can be used instead of bleaching (44–46), thus enabling hundreds of 3PEA cycles per cell without depleting the pool of fluorescent particles.

• iv) Precise dissection of the binding and diffusion behavior exhibited by a protein of interest can be achieved by applying 3PEA to additional images of the postbleach series to improve the robustness and the resolution of dynamics on different time scales.

• v) Similar to the pair correlation analysis introduced by Gratton and coworkers (14), it would be possible to measure anisotropic diffusion of molecules in living cells by 3PEA. This would involve evaluating the bleach profile at different distances and locations to define areas with increased translocation probabilities and to identify directed transport and/or diffusion barriers.

• vi) By combining 3PEA with conventional FRAP analysis for late time points, it is straightforward to cover a binding time range from ∼2 ms to minutes and to quantify both highly mobile and immobilized fractions in a single bleach experiment.

In summary, the 3PEA method extracts comprehensive protein mobility information over a large dynamic range at an unprecedented accuracy that is particularly valuable to characterize interactions of protein factors with chromatin. It is anticipated that experiments along the lines described here will also yield valuable information on other factors that need to identify their chromosomal target sites efficiently via transient interactions to maintain or change functional chromatin states.

Materials and Methods

Cell Culture and Plasmids.

U2OS cells stably expressing Snf2H-GFP were grown in LabTek chambers (Nalge Nunc) as described previously (4). Transient transfection of pTagRFP-C (Evrogen), pEGFP-N1 (BD Biosciences Clontech), pTagRFP-Snf2H (4), or pEGFP₅ (19) was done using the transfection reagent Effectene (Qiagen) according to the manufacturer’s protocol.

Microscopy.

3PEA experiments were carried out on a Leica SP5 microscope equipped with an HCX PL APO lambda blue 63× oil immersion objective with an N.A. of 1.4 (Leica). Images were acquired with 512 × 512 pixels in size and a scanning speed of 100 Hz or 1,400 Hz, which corresponds to frame times of roughly 6.5 s or 450 ms, respectively. The diameter of the circular bleach spot was chosen to be 1 μm, and the rectangular region had a height of 2 μm and a width of 0.5 μm. To account for the width of the bleach PSF, a circle diameter of 2 μm was used for the conventional FRAP analysis. For bleaching, an argon laser at 488 nm or a diode-pumped solid-state laser at 561 nm was used, both at a power of ∼2 mW in the back aperture of the objective. The experimental profiles for Snf2H-GFP and RFP shown above were averaged over six experiments conducted in three cells. For the other profiles, at least 20 measurements were averaged. FCS experiments were carried out on a Zeiss LSM 710 ConfoCor 3 microscope equipped with a 63× water immersion objective with an N.A. of 1.2 (Zeiss). TetraSpeck 0.1-µm fluorescent microspheres (Invitrogen) were used for calibration of the microscope’s PSF.

Calculations and Software Implementation.

Integrations were carried out using Maple 12 (Maplesoft). Theoretical intensity profiles were generated using a custom-made program written in C++ running on an HP computer cluster (Hewlett Packard) with 128 cores. Bleach profiles used for fitting were calculated with an image size of 512 × 512 pixels, a pixel size of 7.5 nm, a detection beam waist of 300 nm, and a bleach beam waist of 400 nm (the experimental bleach PSF is shown in Fig. S2). A line-shaped bleach PSF was used (see below), and a binning step of eight pixels in scan direction was performed to accelerate the computation. The calculation of one profile of this type required ∼24 h of computation time using one core for the diffusion model, or up to 7 d for the reaction-diffusion model with very large dissociation rates. These calculations need to be made only once for each parameter set and can then be used in tabulated form for the fitting of experimental data to implement the 3PEA approach according to the algorithm depicted in Fig. S7.

Fitting and Error Estimation.

The bleach profile around the circular bleach region was used for determining the fit optimum and for the generation of the SSR profile. To this end, a library with calculated intensity profiles was compared with the experimentally acquired one, which reduced the time required for fitting to below 1 min. A similar strategy was reported previously to compare numerical Monte Carlo simulations with FRAP recovery curves (47). The theoretical profiles were scaled to account for varying bleach depths and gain settings of the microscope, according to the formula I′ = I₀ + sI. Here, I₀ is an offset and s is a scale parameter. Both parameters were adjusted such that the prebleach intensity above the bleach region and the total intensity in the rest of the image corresponded to the experimentally obtained values. The error limits given in the text correspond to the profiles with an SSR that is 0.05% larger than the SSR for the optimum profile. Due to the large number of data points, which correspond to all image pixels outside the bleach region (>200,000 pixels), the statistical confidence within these limits is still higher than 95%. For comparison, the SD between different cells was used, which yielded similar values.