Developmental profile of localized spontaneous Ca²⁺ release events in the dendrites of rat hippocampal pyramidal neurons

Summary

Recent experiments demonstrate that localized spontaneous Ca²⁺ release events can be detected in the dendrites of pyramidal cells in the hippocampus and other neurons (J. Neurosci. 29:7833-7845, 2009). These events have some properties that resemble ryanodine receptor mediated “sparks” in myocytes, and some that resemble IP₃ receptor mediated “puffs” in oocytes. They can be detected in the dendrites of rats of all tested ages between P3 and P80 (with sparser sampling in older rats), suggesting that they serve a general signaling function and are not just important in development. However, in younger rats the amplitudes of the events are larger than the amplitudes in older animals and almost as large as the amplitudes of Ca²⁺ signals from backpropagating action potentials (bAPs). The rise time of the event signal is fast at all ages and is comparable to the rise time of the bAP fluorescence signal at the same dendritic location. The decay time is slower in younger animals, primarily because of weaker Ca²⁺ extrusion mechanisms at that age. Diffusion away from a brief localized source is the major determinant of decay at all ages. A simple computational model closely simulates these events with extrusion rate the only age dependent variable.

1. Introduction

Calcium concentration ([Ca²⁺]_i) changes regulate physiological processes in all cells. In neurons, with the complex arborization and specializations in both dendrites and axons, it is clear that the location of these changes is critical. Ca²⁺ entry through voltage gated Ca²⁺ channels (VGCCs) in the presynaptic terminals and boutons regulates transmitter release. Ca²⁺ entry through postsynaptic ligand-gated receptors, especially NMDA receptors, regulates the induction of some forms of synaptic plasticity and other physiological processes. Widespread Ca²⁺ entry following backpropagating action potentials (bAPs) also contributes to some forms of plasticity. The role of Ca²⁺ release from internal stores in neurons has been less understood, with little data on the underlying mechanisms, spatial distribution, or functions of these changes under physiological conditions.

One form of Ca²⁺ release in pyramidal neurons results from synaptic activation of metabotropic glutamate receptors (mGluRs). This release occurs either as large amplitude propagating waves [1–3] or as smaller Ca²⁺ entry near spines [4]. Localized Ca²⁺ release, mediated either by inositol 1,4,5-trisphosphate (IP₃) receptors (“puffs”) or by ryanodine (RyR) receptors (“sparks”) have been described in a variety of preparations including neurons [5–8]. Two forms of localized Ca²⁺ release have been detected in dendrites. In slice cultures, localized Ca²⁺ release, associated with GABAergic synapses, has been shown to modulate the extension of dendritic processes and may contribute to other aspects of neuronal development [9]. In acute slices recent experiments indicate that faster Ca²⁺ release events occur spontaneously in dendrites [10], presynaptic terminals [11,12], and cell bodies [11]. Spontaneous Ca²⁺ release events in dendrites occur primarily near branch points and their frequency can be modulated by changes in membrane potential and weak mGluR mediated synaptic trains [10]. The specific functions of these Ca²⁺ release events are not clear.

To help understand the significance of the Ca²⁺ release events in dendrites we examined their properties in CA1 pyramidal neurons from animals of different ages. Most properties were similar but two parameters changed with age. The amplitudes were larger and the decay times were slower in younger animals. The increase in decay time with age was primarily due to the stronger combined effect of plasma membrane, Na/Ca exchange, and SERCA pumps in older animals. The small changes in intrinsic properties with age suggest that these Ca²⁺ release events may have a general signaling role in neurons and are not just important during development.

2. Methods

2.1 Whole-cell recording and stimulation

Transverse hippocampal slices (300 μm thick) from Sprague–Dawley rats of different ages (P3–P80) were prepared as previously described [1,12]. Animals were anaesthetized with isoflurane and decapitated using procedures approved by the Institutional Animal Care and Use Committees of New York Medical College and the Marine Biological Laboratory. For older animals just before decapitation the heart was perfused with ice cold solution artificial cerebrospinal fluid (ACSF) composed of (mM): 80 NaCl, 2.5 KCl, 0.29 CaCl₂, 7 MgCl₂, 1.25 NaH₂PO₄, 25 NaHCO₃, 75 sucrose, 10.1 glucose, 1.3 ascorbate and 3 pyruvate. Slices were cut in the same solution. They were incubated for at least 1 h in solution consisting of (mM): 124 NaCl, 2.5 KCl, 2 CaCl₂, 2 MgCl₂, 1.25 NaH₂PO₄, 26 NaHCO₃, and 10.1 glucose, 1.3 ascorbate and 3 pyruvate, bubbled with a mixture of 95% O₂–5% CO₂, making the final pH 7.4. Normal ACSF composed of (mM): 124 NaCl, 2.5 KCl, 2 CaCl₂, 2 MgCl₂, 1.25 NaH₂PO₄, 26 NaHCO₃ and 10.1 glucose, was used for recording.

Submerged slices were placed in a chamber mounted on a stage rigidly bolted to an air table and were viewed with a 60× water-immersion lens in an Olympus BX50WI microscope mounted on an X–Y translation stage. Somatic whole-cell recordings were made using patch pipettes pulled from 1.5 mm outer diameter thick-walled glass tubing (1511-M, Friedrich and Dimmock, Millville, NJ, USA). Tight seals on CA1 pyramidal cell somata were made with the `blow and seal' technique using video-enhanced DIC optics to visualize the cells [13]. For most experiments the pipette solution contained (mM): 145 potassium gluconate, 4 NaCl, 4 Mg-ATP, 0.3 Na-GTP, 14 Na-phosphocreatine, and 10 Hepes, pH adjusted to 7.3 with KOH. Final osmolarity was 297 mOs. This solution was supplemented with either 25 or 50 μM OGB-1 (Oregon Green BAPTA-1, a high affinity calcium indicator; Molecular Probes, Eugene, OR, USA). Except during experiments measuring the buffering capacity (see below) we usually waited at least 15 min after membrane rupture before making measurements. Temperature in the chamber was maintained between 29 and 33°C.

2.2 Dynamic [Ca²⁺]_i measurements

Time-dependent [Ca²⁺]_i measurements from different regions of the pyramidal neuron were made as previously described [10,14]. We used two cameras for our measurements. In earlier experiments we used a high spatial resolution (512×512), Quantix 57 CCD camera (Photometrics, Tucson, AZ), with 5×5 pixel binning to read out at 40 Hz. This camera was adequate to measure Ca²⁺ release event amplitudes and most decay times but was too slow to measure rise times. It was controlled by a custom program (WDI) written in our laboratory. For later experiments we used a RedShirtImaging (Atlanta, GA) NeuroCCD-SMQ CCD camera, controlled by their Neuroplex software. The camera has 80×80 pixels and was read out at 500 Hz. A custom program (SCAN) was used to analyze and display the data from both cameras. After checking that both cameras produced similar results the data were combined to generate the distributions shown in the paper.

We measured fluorescence changes of OGB-1 with excitation at 494 ± 10 nm and emission at 536 ± 20 nm. [Ca²⁺]_i changes are approximated as ΔF/F where F is the fluorescence intensity when the cell is at rest and ΔF is the change in fluorescence during activity. Corrections were made for indicator bleaching during trials with events and spikes by subtracting a linear fit to the signal measured under the same conditions when the cell was not stimulated, after normalizing the unstimulated trace to the same value at the start of the trial, i.e. every point in the unstimulated trace was multiplied by the ratio of the mean of the F values for the first five sampled points (10 ms) of the two traces.

To examine the spatial distribution of postsynaptic [Ca²⁺]_i changes we selected pyramidal neurons that were in the plane of the slice and close to the surface. In these neurons when we used the 60× lens we could examine [Ca²⁺]_i increases over a range of 95 μm with the NeuroCCD-SMQ camera and 140 μm with the Quantix 57 camera. Increases in different parts of the cell are displayed using either selected regions of interest (ROIs) or a pseudo `line scan' display [15].

2.3 Measurement errors

Since the Ca²⁺ release events were highly localized and fast there were several potential sources of measurement error that needed to be considered. The first issue was choosing the location and size of the region of interest (ROI) to measure the Ca²⁺ transients. The smallest pixel size with the NeuroCCD-SMQ camera was 1.2 μm², using the 60× water immersion lens. It is possible that the diameter of the dendrite and the size of the event initiation zone are less than 1.2 μm. Therefore, even without considering light scattering through the slice tissue and the possibility of out of focus elements, each pixel probably detected signals from areas larger than the source of the Ca²⁺ release events. Consequently, it is likely that there were spatial inhomogeneities within the chosen ROIs. Similarly, the time course of the Ca²⁺ release transients probably differed for sites within the ROI, especially at short times before diffusion smoothed the transients. This problem was compounded by the fact that it was often necessary to select ROIs larger than one pixel in order to detect signals with sufficient S/N to make quantitative measurements. If the ROIs extend beyond the dendrite boundaries then background tissue fluorescence affects the measurements of peak transient amplitudes and a correction for this autofluorescence should be applied. Supplementary Fig. S1 illustrates this problem. Choosing a larger ROI resulted in smaller measured peak amplitudes (Fig. S1A). Choosing ROIs with horizontal or vertical binning (Figs. S1B, C) affected the amplitude but not as much as square binning. Since horizontal binning affects the amplitude of bAP transients and Ca²⁺ release events in a similar manner (both require the same autofluorescence correction) we found that the ratio of the measured Ca²⁺ release event amplitude to the measured bAP signal amplitude was relatively insensitive to changes in horizontal binning (Fig. S1D), making this ratio less subject to error. Similarly, we found that binning affected the measured decay times of the event transients (Fig. S2). The best choice was to use horizontal binning (Fig. S2B) since it minimized the effects of spatial inhomogeneities in the event transient. To measure the decay time (FDHM; full duration at half maximum amplitude) of the spike evoked transient we used vertical binning since the decay time was approximately constant along the dendrite.

To improve the S/N of some of the measurements we digitally filtered the event transients with a 3-point or 5-point smoothing algorithm. The 3-point filter replaced each point (sampled at 500 Hz) with a weighted average (1,2,1) of the point and the points before and after. The 5-point filter replaced the point with a weighted average (1,2,3,2,1) of the point and its nearest two neighbors on each side.

Since the S/N of many Ca²⁺ release event signals was not high and the traces were noisy it was not clear if these filters affected event parameters. To examine this issue we applied the filters to averaged Ca²⁺ release events, which had higher S/N. This test (Fig. S2D) showed that these temporal filters had a small effect on the Ca²⁺ release event rise times but almost no effect on the decay times or peak amplitudes. Therefore, to measure rise times we used unfiltered data and occasionally used averaging to improve the S/N of the events when measuring decay times or amplitudes.

Even though we were careful in trying to minimize these sources of measurement error there was significant scatter in the data as shown in the figures. Most of this scatter probably results from biological variation since the patterns looked similar when we reanalyzed the data using ROIs composed of vertical pixel rectangles instead of horizontal rectangles. There still may be some uncorrected errors in the measured parameters for individual events, contributing to scattered results. However, the overall patterns are insensitive to these errors and the general trends are clear. Similar distributions were found with the Quantix and NeuroCCD-SMQ cameras.

2.4 Determination of endogenous Ca²⁺ buffering and other Ca²⁺ signaling parameters

The time course and amplitude of Ca²⁺ signals are affected by both endogenous buffers and added Ca²⁺ indicators. To estimate their effects we followed the protocol for evaluating buffers using single wavelength Ca²⁺ indicators [16], based on previous theoretical considerations [17,18]. Pyramidal neurons were patched with electrodes containing 10–100 μM (most often 50 μM) OGB-1. Starting soon after rupturing the cell membrane the time course and amplitude of single spike evoked Ca²⁺ transients were measured at regular intervals at a dendritic location within 50 μm of the soma. Resting fluorescence and background fluorescence from a nearby location were also determined.

The single wavelength formula for determining [Ca²⁺] is [16]:

$$\frac{\left[C{a}^{2+}\right]}{K_D}=\frac{f∕f_{\max }-1∕R_f}{1-f∕f_{\max }}$$ (1)

where: K_D is the OGB-1 dissociation constant; f = the fluorescence of OGB-1; f_max is the maximum possible f; R_f is the ratio of the maximum to minimum OGB-1 fluorescence (f_max/f_min), determined in solutions of saturating Ca²⁺ and zero Ca²⁺. This formula can be rearranged in terms of more easily measurable parameters:

$$\frac{\Delta \left[C{a}^{2+}\right]}{K_D}=\frac{f_{\max }}{f_0}(1-R_f^{-1})\frac{\delta f}{(\delta f_{\max }-\delta f)\delta f_{\max }}$$ (2)

where: Δ[Ca²⁺] is the change in [Ca²⁺]_i resulting from a stimulus; f_o is the fluorescence at rest; δf≡ΔF/F; δf_max≡ maximum possible ΔF/F. Since we were following the same protocol as Maravall et al. [16], and we were primarily interested in comparing results between young and old animals, we used their calibration values for K_D (206 nM) and Rw_f (8.5). K_D only appears as a scaling factor in these equations.

The endogenous (κ_B) and added (κ_F) buffering capacity were determined from:

$${\kappa }_X=\frac{\Delta \left[XCa\right]}{\Delta \left[C{a}^{2+}\right]}=\frac{K_D^{\left(X\right)}{\left[X\right]}_T}{(K_D^{\left(X\right)}+{\left[C{a}^{2+}\right]}_0)(K_D^{\left(X\right)}+{\left[C{a}^{2+}\right]}_{peak})}$$ (3)

where: X=B (endogenous buffer) or F (added indicator); [Ca²⁺]₀ is the [Ca²⁺]_i at rest; [Ca²⁺]_peak is the [Ca²⁺]_i at the peak of the stimulus. Further details are presented in the Results section.

2.5 Simulation of localized Ca²⁺ release events

We used the NEURON modeling environment [19] to simulate Ca²⁺ release events at different ages. The one dimensional model was an extension of a model previously used to simulate one averaged event [10]. Details are given in the Results section.

Statistical calculation of errors is SEM.

3. Results

3.1 Observation of Ca²⁺ release events in neurons of different ages

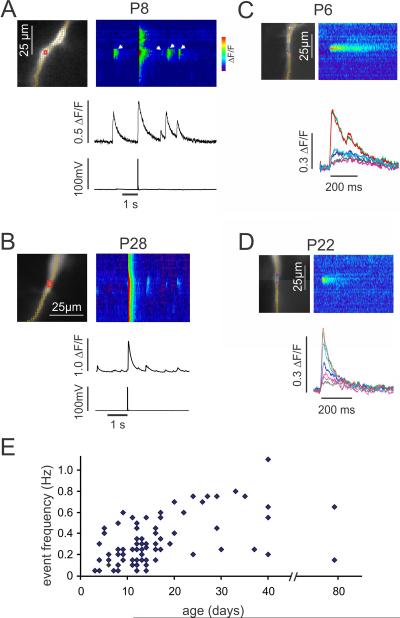
In a typical experiment we recorded changes in [Ca²⁺]_i along a dendritic segment within 100 μm from the soma for a period of 5–20s (Fig. 1A). At a time early in this period an action potential was evoked with a 1 ms intrasomatic pulse, which generated simultaneous [Ca²⁺]_i transients at all locations along the segment. During the remaining time we observed spontaneous localized Ca²⁺ release events at several locations in this dendritic segment. There were no clear membrane potential changes at the times of these events [10]. We detected Ca²⁺ release events in animals of all tested ages (P3–P80). Some properties of these events differed in cells taken from animals of different ages. For example, in a representative trial from a P8 pyramidal neuron the amplitude of the Ca²⁺ release events was almost as large as the Ca²⁺ transient from the bAP at the same dendritic location (Fig. 1A), while in the sample from a P28 neuron the Ca²⁺ release events were much smaller than the bAP signal (Fig. 1B). Also, the decay time (FDHM) of the Ca²⁺ release event from a P6 neuron (92 ms; Fig. 1C) was longer than the decay time of the Ca²⁺ release event from a P22 neuron (63 ms; Fig. 1D). The decay time of the bAP transient from the P8 neuron (340 ms) also was longer than the decay time of the bAP transient from the P28 neuron (130 ms). It was hard to compare the frequency of these events at different ages since many factors (health of slice, time of trial after patching cell, background synaptic activity, and threshold criteria) could affect this rate. However, a simple analysis of event frequency in cells that showed Ca²⁺ release events (Fig. 1E) suggests that there are no strong changes in frequency as a function of age.

Fig.1.

Spontaneous Ca²⁺ release events have different properties in young and old animals, but the frequency of these events does not change dramatically with age. A. CA1 pyramidal neurons were filled with 50 μM OGB-1 from a patch pipette on the soma and the cell was stimulated to fire a single action potential. In a P8 neuron the spike evoked a [Ca²⁺]_i increase that was detected at all dendritic locations as shown in the pseudo `line scan' along the yellow pixels and at the selected region of interest (red ROI). In the time period after the spike several localized event transients (e.g, white arrows) were detected in some dendritic locations. The amplitudes of the events were almost as large as the amplitude of the spike signal at that location. In this and other figures the Y-axis of the pseudocolor image has the same spatial scale as the image to the left and the X-axis of the pseudocolor image has the same time scale as the trace below. B. A similar recording from the dendrite of a P28 pyramidal neuron. The event amplitudes are smaller than the spike signals at the site of the events. C. A Ca²⁺ release event detected in a dendrite of a P6 pyramidal neuron. Four events were averaged, aligning the transients on the rising edge of the signal. The traces show signals from neighboring pixels, each 1.2 μm on a side. The central region of high amplitude was slightly larger than two pixels. D. A similar Ca²⁺ release event from a P22 pyramidal neuron, averaged from six events. The decay time (time to half peak amplitude) of the P22 event (63 ms) is shorter than the event decay time from the P6 neuron (92 ms). E. Event frequency for each cell at a representative site during 20 s trials. In a few cells we measured the frequency at a second location and counted that as another point. We only included events that were clearly above noise level. We did not include trials or cells with no events. We made no measurements on animals between 45–80 days old. The NeuroCCD-SMQ camera was used to generate all signals in A–D. Data from both cameras were used to generate the plot in E.

3.2 Buffering effect of the Ca²⁺ indicator

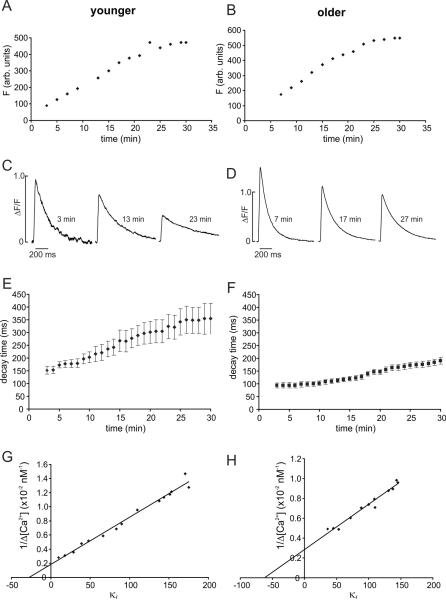
It is well known [20,21] that Ca²⁺ indicators blunt the amplitude of spike evoked Ca²⁺ transients and slow their decay times. Lower concentrations of indicator have less effect. Since buffering by the indicator combines with buffering by intrinsic cytoplasmic molecules, and the concentration and composition of these molecules may vary with age, we tested the buffering effect of OGB-1 at two ages. These were the same experiments used to determine the endogenous buffering power (see below). After breaking into the cell we measured the resting fluorescence as the indicator diffused into the cell over the course of about 15–30 min (Figs. 2A,B). During this period in both young animals and in older animals the increasing OGB-1 concentration lengthened the spike evoked decay time (Figs. 2C,D). Nevertheless, there was a significant difference in decay times measured in neurons from the two age groups at all indicator concentrations even when the measurements were extrapolated to low OGB-1 concentration (Figs. 2E,F; summarized in Table 1). Therefore, indicator buffering was not responsible for the difference in decay times between younger and older animals. We did most of our experiments using 50 μM OGB-1, even though there was some buffering, since the signal-to-noise ratio (S/N) using lower concentrations was inadequate to reliably detect single Ca²⁺ release events. In a few experiments (data not shown) we used 200 μM of the low affinity indicator OGB-5N. Although this indicator, even at this high concentration, has less buffering effect than 50 μM OGB-1, the S/N of the Ca²⁺ release events was too low to reliably detect them, so we abandoned this protocol.

Fig.2.

Exogenous and endogenous Ca²⁺ buffering in animals of different ages. A,B. Fluorescence vs. time at a location in the primary apical dendrites within 50 μm of the soma. Data from two neurons are shown. The “younger” animal was P11 and the “older” animal was P17. Background fluorescence was assayed from a nearby location and was subtracted from the measured values in the dendrites. Zero time was the time of membrane rupture. A steady level was reached in about 25 min in each cell, at which time it was assumed that the OGB-1 concentration was 50 μM (the pipette concentration). C,D. Examples of spike evoked fluorescence signals measured at different times after rupture in these two cells. At later times (higher OGB-1 concentration) the ΔF/F values became smaller and the half decay time became longer. E,F. Half decay times of spike evoked transients measured at different times after membrane rupture. Summary data from 6 younger and 6 older animals are shown. At all times the half recovery times were longer in younger animals. G,H. Plots of 1/Δ [Ca²⁺] (×10⁻² nM⁻¹) vs. κ_F from data from a younger and an older animal. The X axis intercept of the regression line is the endogenous buffering power (κ_B) of the cell [16]. In these examples κ_B=27.4 for the younger neuron and κ_B=61.4 for the older neuron. Summary data are given in Table 1.

Table 1.

Changes in Ca²⁺ release event and bAP parameters between younger (P3–15) and older (P16–40) animals.

	P3–15	N	P16–40	N	p value	Significance
Ca2+ release event ΔF/F	0.23 ± 0.02	57	0.15 ± 0.02	28	0.0017	**
spike ΔF/F	0.71 ± 0.04	57	0.83 ± 0.07	28	0.13
event/spike ΔF/F ratio	0.34 ± 0.02	57	0.18 ± 0.02	28	0.0001	***
event rise time (ms)	12.0 ± 0.5	38	9.3 ± 0.4	20	0.001	***
bAP rise time (ms)	9.8 ± 0.4	38	6.6 ± 0.4	20	0.0001	***
event decay (ms)	99.4 ± 4.0	57	66.5 ± 3.8	30	0.0001	***
bAP decay, 3–5 min (ms)	159 ± 14	6	94 ± 10	6	0.006	**
bAP decay, 15 min (ms)	198.4 ± 10.2	57	112.4 ± 7.8	28	0.0001	***
event/spike decay ratio	0.53 ± 0.02	57	0.62 ± 0.03	30	0.017	*
[Ca2+]i rest (nM)	47 ± 5	6	40 ± 4	6	0.37
Δ[Ca2+]i/spike (nM)	242 ± 42	6	228 ± 28	6	0.81
κ B	40 ± 11	6	89 ± 28	6	0.19
bAP amp (mV)	94.5 ± 2.2	57	97.9 ± 2.7	28	0.36
Vm rest (mV)	−58.4 ± 0.6	57	−59.4 ± 0.6	28	0.33
bAP width (ms)	1.59 ± 0.08	42	1.51 ± 0.11	18	0.59

The top twelve parameters refer to Ca²⁺ signaling measurements. The bottom three parameters refer to electrical measurements. N is the number of cells for each measurement. All errors are SEM. The P value reflects the t-test assessment whether the values for younger and older animals are statistically different

^*0.01<p<0.05;

^**p<0.01;

^***p<0.001

3.3 Ca²⁺ release event parameters

To more quantitatively assess these differences we measured several parameters related to bAPs and Ca²⁺ release events in pyramidal cell dendrites of animals of different ages (P3–P40). We did one set of experiments on a P80 rat (two cells) and detected events similar to the events in the P40 animal. We measured the peak voltage amplitude and width (FDHM) of APs evoked with 1 ms intrasomatic pulses. We measured the signal amplitude (ΔF/F), rise time (10–90%), and decay time of the bAP generated [Ca²⁺]_i changes at the same location as the Ca²⁺ release events. The location was chosen as the site of peak event amplitude using a horizontal ROI of 1×3 pixels (1.2×3.6 μm²). For event amplitude and time course measurements we used the same ROI centered at this location. For the rise times and decay times of bAP signals we used a longer vertical ROI to improve the S/N since the bAP signals did not change significantly over a stretch of the dendrites (see Fig. 5B). The resting fluorescence intensity was corrected for background autofluorescence by subtracting the fluorescence intensity measured from a nearby location in the slice that did not contain OGB-1 filled processes.

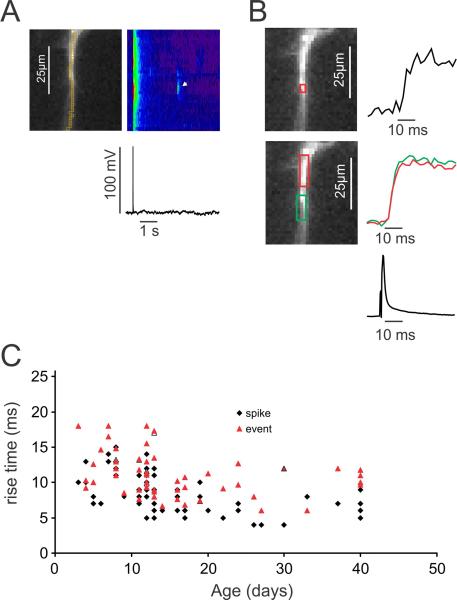
Fig.5.

The rise times of bAP signals and Ca²⁺ release event signals are fast at all ages. A. Typical recording, showing a bAP signal at all dendritic locations and a localized event signal (white arrow). B. The rising edges of the event and bAP signals. The event signal is shown for the red ROI. The bAP signals are shown for two locations, demonstrating that there is no change between the two locations. C. The rise times (10–90%) for many events and bAPs for animals of different ages are shown. While there is some scatter most rise times are between 5–18 ms (see text). Some of the variation may be due to noise in the traces. The NeuroCCD-SMQ camera was used to generate all data in this figure.

3.4 Ca²⁺ release event amplitudes

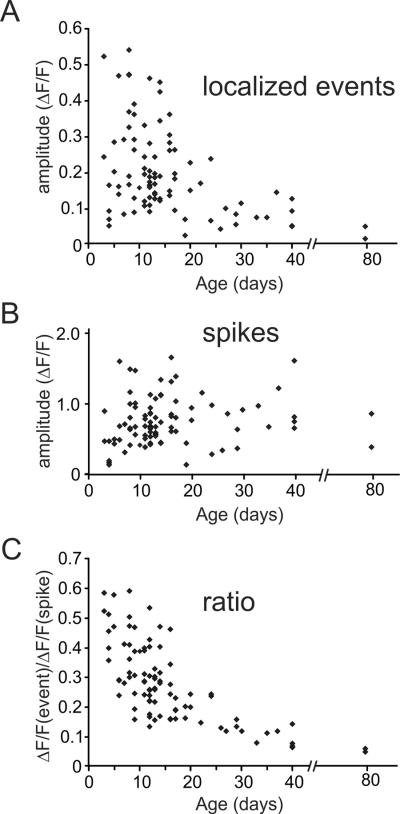
Ca²⁺ release event amplitudes (ΔF/F) ranged from about 0.05–0.55 (Fig. 3A). In this range the corresponding [Ca²⁺]_i changes are almost linearly related to the fluorescence changes of OGB-1 [22]. There was significant variation at each age, but event amplitudes in younger animals (P3–P15: 0.23 ± 0.02, n=57) were clearly bigger than amplitudes in older animals (P16–P40: 0.15 ± 0.02, n=28, p<0.002). Over the same age periods spike evoked fluorescence signals (Fig. 3B) were slightly smaller in younger animals (P3–P15; 0.71 ± 0.04, n=57 versus P16–P40; 0.83 ± 0.07; n=28, p<0.13). The difference between younger and older animals was sharper (Fig. 3C, Table 1) when the amplitudes of Ca²⁺ release events were compared to the amplitudes of bAP [Ca²⁺]_i changes at the same locations in the same trials. Indeed, as illustrated in the example in Fig. 1A, the amplitudes of the events at the youngest ages were almost as large as the bAP signals. The clarity of this trend partly results from the fact that this ratio eliminates most errors due to binning and autofluorescence corrections since the same binning and autofluorescence corrections were applied to both signals.

Fig.3.

The Ca²⁺ release event fluorescence signal amplitude is larger and the spike signal is smaller in younger animals. A. The peak ΔF/F amplitude of many dendritic events in animals of different ages was measured at the event center and was corrected for background fluorescence. When there were several events from the same dendritic location on a trace their amplitudes were averaged. The peak amplitudes were larger in younger animals, although there was a lot of scatter. B. The amplitudes of the signals from bAPs were measured at the same locations. C. The ratio of the event signal to the spike signal, measured at the same location, is plotted for many events. There was a clear decline in the ratio in older animals. There was less scatter in this trend since several kinds of errors cancel in taking the ratio.

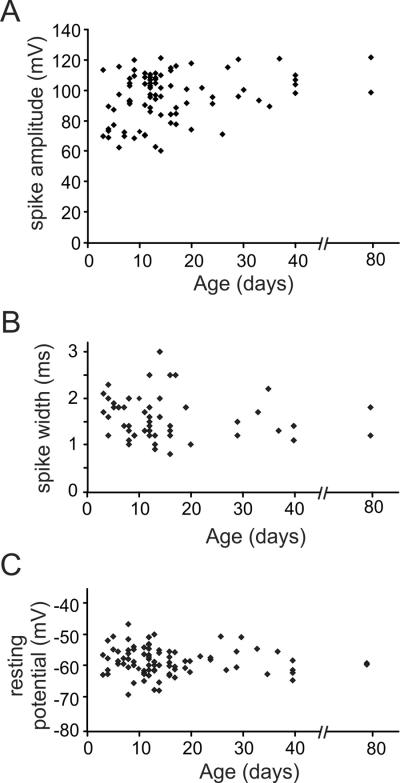
Spike amplitude and width were similar at both ages (amplitude: P3–P15; 94.5 ± 2.2 mV, n=57 versus P16–P40; 97.9 ± 2.7mV, n=28, p<0.36; width: P3–P15; 1.59 ± 0.08 ms, n=42 versus P16–P40; 1.51 ± 0.11 ms, n=18, p<0.59; Figs. 4A, B, Table 1; see also [23,24]. There was no change in resting membrane potential with age (Fig. 4C, Table 1).

Fig.4.

Spike amplitudes, widths, and resting potentials for tested cells at different ages. A. Peak spike voltage amplitudes for events from animals of different ages. Typical amplitudes were 80–120 mV except for animals below P10 where there were more small amplitude action potentials. B. Spike width (FDHM) for the same action potentials. C. Resting membrane potential (uncorrected for junction potential) for the same set of neurons. There was no significant variation with age. See Table 1 for quantitative summary.

3.5 Ca²⁺ release event rise times

The rise time of the events was measured at the center of the events where the rise was fastest. In the cell shown in 5A the event rise time (measured in the small ROI in Fig. 5B) was comparable to or slightly slower than the rise time of the bAP signals in the dendrites (measured in the large boxes in Fig. 5B). The rising phase of the events was noisier than the rising phase of the bAP signals because the event ROI was selected to be as small as possible while the bAP ROI could be chosen over an extended length of dendrite since the backpropagation time was less than a frame interval (2 ms) for this length of dendrite (Fig. 5B). The summary data (Fig. 5C) show that the event rise times (10–90%) were 5–18 ms at all ages, but slightly slower in younger animals (12.0 ± 0.5 ms below 15 days, n=38 and 9.3 ± 0.4 ms older than 15 days, n=20; p<0.001). These times were also slower than the rise times of the bAP signals in the same cells (11.1 ± 0.4 ms, n=58 for events and 8.7 ± 0.4 ms, n=58 for bAPs, averaged over all ages; p<0.0001). Some of the Ca²⁺ release event rise time may result from the fact that the ROI used to measure this time was larger than the source of the event and therefore included a component due to Ca²⁺ or indicator diffusion. The rise time at the initiation site may be faster. There was no correlation between the rise times of bAP signals and event signals in the same cells (not shown), which rules out differences in indicator concentration in the cells as an explanation for the variation in rise times. Tests using square pulses from a light emitting diode (LED) showed that 2–4 ms of these measured rise times were due2 to the frame interval (2 ms) and the random alignment of the start of the fluorescence change and the start of a sampling period.

3.6 Ca²⁺ release event decay times

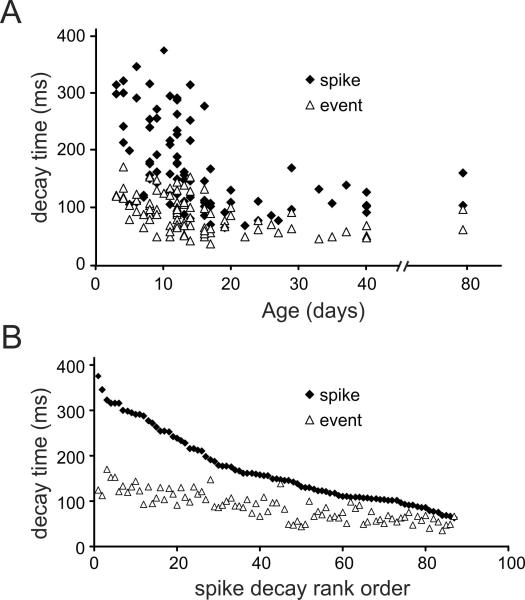
Similarly, we measured the decay times for the events and bAPs at the same locations [10]. Figs. 2E,F and Fig. 6A shows that the bAP evoked fluorescence decay times were shorter in older animals (P16–40: 112 ± 7.8 ms, n=28) than in younger animals (P3–15: 198.4 ± 10.2 ms, n=57; p<0.0001). This difference remained even in measurements with lower indicator concentrations where there is less exogenous buffering (Figs. 2E,F). Event decay times were shorter than bAP decay times at all ages (Fig. 6A) but the difference between younger and older animals was not as great (P3–15; 99.4 ± 4.0 ms, n=57; versus P16–40; 66.5 ± 3.7 ms, n=30; p<0.0001). We could not make this comparison at minimum indicator concentrations because the S/N was too low for quantitative measurements.

Fig.6.

The decay times of Ca²⁺ release event signals are shorter than the decay times of bAP signals at all ages. A. The time for the [Ca²⁺]_i changes to decay to half amplitude (FDHM) was plotted for many events and bAPs at the same dendritic locations in different cells. The decay times of the bAP signals became much shorter in older animals. The decay time for the event signals also became shorter in older animals, but not as dramatically. B. The same data were plotted with the bAP decay time rank ordered. The corresponding event times in each trace are also plotted, showing a similar trend. The difference in decay times is much greater when the spike signals have slow decay times.

Since there was a lot of scatter in these measured decay times we tried to reduce the variation due to indicator buffering and the properties of different cells at the same age. In Fig. 6B the decays times of the events and bAP evoked transients are plotted in rank order of the bAP transients from the longest (~350 ms) to the shortest (~70 ms). This rank order approximately corresponds to the age dependence of the bAP transients. Each event transient was paired with a bAP transient measured at the same dendritic location in the same trial (as in Fig. 1). By plotting the events in this way it is clear that there was a correspondence between the bAP decay times and the event decay times, but there was a smaller range in the event decay times. When we measured the ratio of the decay times we found that event decay times were relatively faster than spike decay times in younger animals (P3–15; 0.53±0.02, n=57; versus P16–40; 0.62±0.03, n=30; p<0.017; table 1).

3.7 Other factors affecting Ca²⁺ release event and spike decay times

In addition to changes in the extrusion rate another factor that could affect the variation in event and spike decay times with age is the endogenous buffer capacity of the cytoplasm. This capacity previously was measured in pyramidal neurons from 14–17 and 24–28 day old animals, where no difference was observed [16], but the buffer capacity is not known for younger animals where we found differences in event parameters. To supply this information we determined the buffering power in younger and older animals by following the protocol of Maravall et al. [16] (see Methods).

We measured the spike evoked Ca²⁺ transients at a site in the proximal apical dendrites soon after breaking into the neuron and at 1–2 min intervals for 30 min. The fluorescence at this ROI was corrected for autofluorescence of the slice by subtracting the fluorescence from a nearby location [18]. We tested the accuracy of this correction by requiring that the fluorescence vs. time curves point toward the origin (Figs. 2A, B). We also required that the corrected ΔF/F values monotonically decrease with time as the indicator concentration increased. These criteria are very sensitive, especially at early times when there is little indicator in the cell. At ~10 min intervals during this protocol we assayed the maximum ΔF/F value by evoking a train of 40 spikes at 63 Hz. This value was multiplied by a factor of 1.18 to correct for failure to reach complete indicator saturation [16]. The maximum ΔF/F value is expected to remain constant during indicator loading even though the ΔF/F per spike is decreasing [16]. If this value began to deviate from constancy at later times we interpreted it as a sign that the cell was becoming unhealthy and we terminated the experiment.

Figs. 2C,D show two series of these measurements from a younger (P11) and an older (P17) animal. It is clear that at both ages the amplitudes (ΔF/F) of the spike evoked transients decreased and the decay times increased over the course of 25 min. At the same time the resting fluorescence intensities (F) were measured. These values reached a steady state (Figs. 2A,B). At this point we assumed that the OGB-1 concentration reached the value in the pipette (50 μM). The concentrations at earlier times were calculated from the relative fluorescence intensity at those times. From these measurements we could calculate the resting [Ca²⁺]_i and the Δ[Ca²⁺]_i per spike using formulas (1) and (2). On average the [Ca²⁺]_i (rest) was 47 ± 5 nM (N=6) for young animals and 40 ± 4 nM (N=6) for older animals. The Δ[Ca²⁺]_i per spike was 242 ± 42 nM (N=6) for young animals and 228 ± 28 nM (N=6) for older animals. The buffering powers were determined from the X axis intercepts of the regression lines in Figs. 2G,H [16]. The parameters on the two axes are rearrangements of equation (2) and (3) to allow a linear fit to the data points [18]. We found that the buffering power was lower in younger animals (κ_B =40 ± 11; N=6) than in older animals (κ_B= 89 ± 28; N=6), but the difference was not statistically significant. The values for the older animals were similar to those determined by Maravall et al. [16] in P14–P28 animals. If we include the data from Maravall et al. [16] then the difference is significant. If the buffering power were smaller or the same in younger animals, as might be hypothesized for developing neurons, then if buffering were the determining factor then the bAP transient decay times would be faster in younger neurons since buffers slow Ca²⁺ transients [25]. This prediction is opposite to our observations.

There are other potential explanations for Ca²⁺ release event amplitude and time course differences between young and old animals. One possibility is that the events do not result from the same mechanism. In our previous paper [10] we showed that the frequency of events from P14–P21 animals was voltage sensitive and was insensitive to TTX and to several ionotropic receptor antagonists (CNQX, APV, picrotoxin). In new experiments (not shown) we tested events in animals from P3–P10 and found the same voltage sensitivity and lack of sensitivity to the blockers (event frequency was 290 ± 30% of control frequency when voltage increased from −63mV to −55mV (n=5) and 30 ± 10% of control frequency when voltage decreased from −63mV to −75mV (n=6); event frequency was 120 ± 20% of control frequency in the presence of 11μM TTX, 100μM APV, 10μM CNQX, and 100μM picrotoxin (n=8)). These results suggest that the event mechanisms in animals of different ages are the same. However, it is possible that there are more subtle differences that were not revealed in this test.

3.8 Computational model

Previously [10], we found that we could simulate the time course and spatial distribution of a Ca²⁺ release event in the dendrite in a simple model by assuming only localized Ca²⁺ release for a brief period and removal by diffusion and a spatially homogeneous extrusion mechanism. This mechanism represented the combined effects of a plasma membrane pump, Na/Ca exchange, and a SERCA pump, since our measurements did not distinguish among these three removal mechanisms. The new measurements in this paper provide an opportunity to further extend and refine these conclusions. In particular, we wanted to see if the model could explain the correlation between the event decay times and the bAP decay times (Fig. 6B). The new useful data are the variation of the decay times of both bAP signals and localized events with age, and the observation that the rise times of the event signals are comparable (or slightly longer) than the rise times of bAP Ca²⁺ transients at the same locations.

We extended the previously developed model [10] to include different extrusion rates at different ages. The revised model still does not consider the effects of Ca²⁺ shuttling by diffusing fluorescent indicator molecules, or Ca²⁺:OGB-1 reaction rates. These factors have been demonstrated to be significant in other situations [26–30], especially for short times and distances, suggesting that our model is only an approximation to the underlying Ca²⁺ dynamics. More accurately, the model represents the rise and decay of the Ca²⁺:OGB-1 complex.

The forward reaction between Ca²⁺ and OGB-1 (k_on = 0.45–0.93 μM⁻¹ms⁻¹; Cornelisse et al, 2007; Bortolozzi et al, 2008) is not instantaneous and slows the fluorescence rise time, especially at low indicator concentrations (see Discussion). However, the main goal of the model was to simulate the decay time, which is much slower than the rise time, and therefore unaffected by this delay. The off-rate for the reaction (0.09–0.19 ms⁻¹ [30,31]) predicts that fluorescence should lag the [Ca²⁺]_i change on the decay phase by 5–11 ms. This is a small correction to the measured decay times and was neglected.

The model assumes that Ca²⁺ is released over a dendritic segment of variable length for a period of 5–15 ms. This temporal range is consistent with the range of observed fluorescence rise times but is probably longer than the underlying conductance change (see Discussion). Changes in this parameter had little effect on the modeled event profile since this time was much shorter than the event decay time. The release spatial profile (1–5 μm) was assumed to be either uniform over this length or greater in the center (Fig. 7B). This variation in spatial extent was an important parameter affecting the shape and time course of the simulated events. Ca²⁺ diffusion was assumed to be one dimensional since radial equilibrium is fast compared to the decay time in a dendrite ~1 μm diameter [30]. We varied the diffusion constant (more precisely the diffusion constant for the Ca²⁺:OGB-1 complex) between 0.02–0.04 μm²/ms, which also affected the decay time. This range of values is based on a measured Ca²⁺ diffusion constant of 0.03 μm²/ms in squid axoplasm [32]. Since there are no data on the variation of the diffusion constant during development we assumed it was constant, which is consistent with the approximate constancy of the endogenous buffer capacity (Table 1; see Discussion). The extrusion rate (combining the membrane pump, Na/Ca exchange, and SERCA pump) was chosen to fit the decay time course of the Ca²⁺ transient evoked by a bAP, which should have no diffusion component since Ca²⁺ entry over the dendritic segment was assumed to be uniform. The extrusion rate was varied to fit bAP Ca²⁺ transients for animals of different ages (P5 and P40; Figs. 7C, D) and these values were used to simulate the event transients for the same locations in the same animals. Variations in event and bAP signal amplitudes do not provide useful information for this model since we assume that Ca²⁺ release, diffusion, and extrusion all scale linearly.

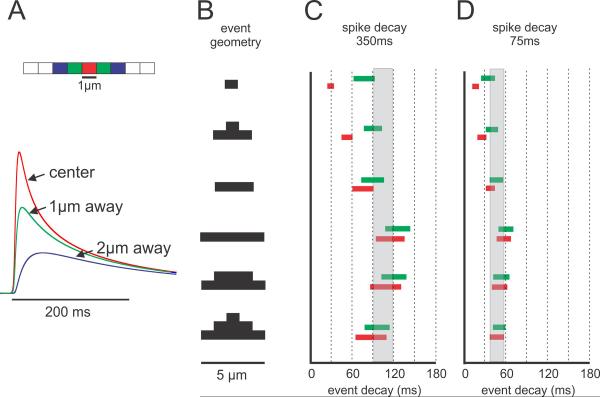
Fig.7.

Model of Ca²⁺ release event decay times showing that the spatial extent of events has the greatest influence on event decay times. A. Model of dendrite divided into 1μm segments. Ca²⁺ removal was controlled by a pump and by diffusion. The extrusion rate constant was adjusted to fit the recovery of the bAP signal where axial homogeneity precludes diffusion. The plots show typical results with traces from the center of each 1μm segment. B. Different event geometries used in the simulations. Release extent was varied from 1–5μm. For the 3μm and 5μm segments release was modeled as either uniform over the segment or peaked (thicker bar) in the center (two versions). C. Different decay times (FDHM) in models where the extrusion rate was forced to give a bAP decay time of 350 ms as measured in some younger animals. For each geometry the Ca²⁺ diffusion constant (D) was varied between 0.02–0.04 μm²/ms and the release duration was varied between 5–15 ms. The red and green bars show the decay time range at the center and 1μm away from the center. They differ most for the model where release extended only over a 1μm segment. The grey bar shows the range of values determined in Fig. 6B. The best fits were for models of about 5μm extent, although 3μm extent could fit if D=0.04 μm²/ms. D. A similar plot except that the extrusion rate was forced to give a bAP signal decay time of 75ms (typical of older animals). Again the models with 5μm spatial extent are closest to the data in Fig. 6B.

Fig. 7A shows an example of model predictions for the time course and relative amplitudes of event Ca²⁺ changes at the center and locations 1 μm and 2 μm to the side, assuming that Ca²⁺ release was twice as large in the center as at locations 1 μm to the side (second example in Fig. 7B). Consistent with the predictions of linear diffusion the transient was largest and fastest in the center, and smaller and slower to the sides. There was a short delay to onset for the blue trace (2 μm to the side) since there was no release at that location and the transient there was entirely the result of diffusion from the release site. Qualitatively, these curves compare well with the transients measured with OGB-1 (Figs. 1C,D; see also Fig. 6D in [10]).

Figs. 7C and D show the predicted decay times at the release center (red bars) and 1 μm away (green bars) for models where the release geometry, diffusion constant, and release duration were varied over the ranges indicated above. We show results for these two locations since the large pixel size in our measurements (1.2 μm) and light scattering in the slice indicate that our measured traces were from dendritic lengths larger than the 1 μm segments in the model. We made models with two values of the membrane pump to generate bAP decay times of 75 ms and 350 ms to correspond with the measured decay times for young and old animals. There is a separate bar for each release geometry and the length of the bar encompasses the range of simulated decay times when the diffusion constant and release duration were varied. As noted above, release duration had almost no effect since it was much shorter than the decay times of the event transients. These predicted event decay times are compared with the range of measured decay times from neurons in young and old animals (gray bars in Figs. 7C and 7D).

The figure shows that the data are consistent with most models where the extent of Ca²⁺ release (as assayed by OGB-1 fluorescence) is at least 3 μm (see Discussion). If Ca²⁺ release extends only 1 μm then the predicted decay time is too fast for events in animals of all ages. This size is consistent with dimensions determined from fluorescence images (Figs. 1C,D). The models suggest that the same set of parameters can be used to model events in young or old animals; it was only necessary to change the extrusion rate according to the requirement to fit the bAP signals at these two ages. In younger animals, where diffusion is the dominant removal mechanism, the modeled decay time was insensitive to small changes in the extrusion rate. In fact, in a model with no extrusion the decay time was only slightly longer (~ 10 ms) than the decay time in P3 animals where extrusion was just developing.

4. Discussion

4.1 Ca²⁺ release events in neurons of different ages

One important result from these experiments is that Ca²⁺ release events occur in pyramidal neurons in animals of all ages (P3–P80). There was no clear change in frequency with age (Fig. 1E), although it was hard to be precise in these measurements. The observation that events can be detected in P80 animals suggests that they serve functions beyond the early developmental period.

The amplitude of the events in the first two weeks (P3–P15) was clearly larger than the amplitude of events in older animals (P16–40), even though there was uncertainty in the measurements because of the spatial gradients near the localized source and difficulty in making accurate background corrections. Since the amplitudes are almost as large as the bAP signals in young animals it is possible that the [Ca²⁺]_i transients from these events could substitute for the bAP evoked [Ca²⁺]_i transients in activating signaling mechanisms (still unclear) at some locations in the dendrites.

The rise time of events was slightly (but significantly) faster in older animals. The reason for this difference is not known. One possibility is that some of the molecular complexes responsible for controlling Ca²⁺ release mature during development. The event decay time was clearly faster in older animals. This difference is probably due to the increase in pump expression in older animals [33]. Since this pump affects the decay time of bAP signals as well as event signals it does not reflect a difference in event properties. The main difference between Ca²⁺ release events in animals from different ages is the peak amplitudes of the measured Ca²⁺ transients.

4.2 Comparison with sparks in cardiac myoctes and frog skeletal muscle

Ca²⁺ sparks were first detected in cardiac myocytes [34]. The localized Ca²⁺ release events in dendrites are similar to those sparks [10]. One difference is that the frequency of dendritic Ca²⁺ events is sensitive to mGluR activation and IP₃ mobilization [10], while sparks in myocytes are much less sensitive since there are fewer IP₃ receptors in myocytes [5]. Sparks in skeletal muscle fibers, which were discovered later [35] also are insensitive to mGluR agonists.

A second difference between cardiac and muscle sparks and the dendritic Ca²⁺ release events is the decay time for the Ca²⁺ transients. For dendritic events the diffusional decay time is over 100 ms, using the data from P3 animals where the pump makes the least contribution (Fig. 6). In cardiac myocytes the decay time is much faster (about 15 ms, increasing to 20 ms if the pump is blocked [36]). In contrast, the decay time for a global Ca²⁺ transient in myocytes (130–150 ms [36,37]) is comparable to the decay time of the bAP evoked transient in pyramidal neurons, suggesting that the combined extrusion rate is similar in the two preparations. In frog skeletal muscle fibers the decay time for sparks is 4.4–5.9 ms [38,39], but the spike evoked transient decays in about 10 ms [40], much faster than in myocytes or dendrites, suggesting that pumps are the dominant removal mechanism in skeletal muscle fibers. One contributor to the slower decay time in dendrites is that these processes are essentially one dimensional, while diffusion is three dimensional in myocytes. But geometry cannot account for all the difference. In our model a sensitive determinant of decay time is the spatial extent of Ca²⁺ release; larger release clusters predicted slower decay times. This result suggests that the release clusters in dendrites are larger than in myocytes and muscles if the only factors determining cluster size are the parameters we included in our model. As noted above the predicted size from the model (3–5 μm) is consistent with dimensions determined from fluorescence images (Figs. 1C,D); the measured size in myocytes is smaller [36]. These considerations only apply to dimensions estimated from the fluorescence signals. Since the indicator shuttles the Ca²⁺ ions the true dimensions of the events in both preparations are likely to be smaller [41].

There are other important differences between dendrites and muscle. One factor is that there are different endogenous Ca²⁺ buffers in muscle fibers [26], which, among other things, could affect the diffusion constant for Ca²⁺. The measured diffusion constant for Ca²⁺ in muscle (0.014 μm²/ms; [42]) is slightly smaller than the measured diffusion constant in squid axoplasm (0.03–0.06 μm²/ms; [32] or the measured diffusion constant in oocytes (0.013–0.065 μm²/ms, depending on the Ca²⁺ load; [43]). Ca²⁺ diffusion in cells is slower than in water because Ca²⁺ binds to intracellular buffers. This binding can be included in the diffusion constant if the binding is rapid and nonsaturating and if the buffer is immobile. These conditions appear to be satisfied in most dendrites [25,44].

A second difference is that our simple model assumes that the extrusion mechanisms are distributed uniformly over the surface of the dendrite or over the surface of the ER within the dendrite. This seems reasonable since the decay time for bAP evoked transients is the same all along the dendrite and the main function of these mechanisms is probably to remove Ca²⁺ that enters through voltage gated channels. In muscle fibers the pumps are concentrated close to the release sites [45]. The significance of this difference is not clear since even in myocytes the decay time course of spark transients is dominated by diffusion [36]. Unfortunately, while there are detailed studies of the Ca²⁺ release complex in myocytes and muscle [46,47] there is little known about the detailed ultrastructural organization of the release channels and associated molecules in dendrites [48].

4.3 Ca²⁺ release event rise times

The measured event fluorescence rise times varied between 5–18 ms (11.1 ± 0.4 ms, averaging over all ages; Fig. 5) of which 2–4 ms are probably due to measurements issues (see Results). These times are comparable to the rise time of sparks in cardiac myocytes [34] but slower than spark rise times in frog muscle fibers (2.7–4.7 ms [38,39]). The times are close to an upper limit on the duration of Ca²⁺ current flowing through ER channels during the release events since removal appears to be much slower. However, it is likely that the mean channel open duration is shorter than the measured fluorescence rise time. One factor is that equilibrium between released or entering Ca²⁺ and OGB-1 takes several ms. The on-rate for the reaction is 0.45–0.93 μM⁻¹ms⁻¹ [30,31], suggesting that the rise time will not be instantaneous for a step increase in [Ca²⁺]_i when low concentrations of indicator are used. Indeed, experiments using 100 μM OGB-1 [30] measured a spike evoked fluorescence rise time of 4.7 ± 0.3 ms, while we measured 8.7 ± 0.3 ms using 50 μM OGB-1. On the other hand, Fig. 5C shows that the event rise times were almost as fast as the bAP rise time at all ages, suggesting that the duration of current flow through the ER membrane during an event is similar to the duration of bAP generated Ca²⁺ current. The duration of spike evoked Ca²⁺ current can be as short as 1 ms in neurons that have similar action potentials, e.g. the presynaptic terminal of the squid giant synapse [49] or the presynaptic terminal of the calyx of Held [50], and have been inferred to be slightly longer in voltage clamped pyramidal neurons [51], all of which are much faster than our measured rise times. However, the Ca²⁺:indicator reaction time may mask a difference between these Ca²⁺ current durations and the Ca²⁺ release event durations in our experiments, allowing for the possibility of slower event rise times.

Supplementary Material

Supplementary Fig. 1

Size of ROI affects the measured peak amplitude of localized Ca²⁺ release events. A series of 9 events from the same dendritic location was averaged by aligning the events at the beginning of their rising phase. The time course of the averaged event was plotted using ROIs of different sizes and geometries. The traces are scaled in units of ΔF/F to compare amplitudes. Scaled amplitudes are shown next to the traces. A. Using square ROIs of different diameter it is clear that the largest amplitude was measured using a box of the smallest size located at the apparent center of the event. B. With ROIs of horizonally aligned rectangular shape the largest amplitude also came from the smallest ROI. C. Similar results with vertically aligned ROIs. D. Ca²⁺ release event and bAP signals were measured using three ROIs of different horizontal dimensions. Their peak amplitudes were smaller when the widest ROI was used.

However, the ratios of the two signals (0.25, 0.22, and 0.21) were similar.

Supplementary Fig. 2

Size of ROI affects the decay time of Ca²⁺ release events and filtering affects the measured rise times. The same averaged event as in Supp. Fig. 1 was analyzed using ROIs of different sizes and geometries. The traces are normalized to compare decay times, which are indicated next to the traces. A. Using square ROIs of different diameter it is clear that the decay time was shortest using the smallest ROI. B. With ROIs of horizontally aligned rectangular shape there was much less difference in the decay times. C. With vertically aligned ROIs there was almost as much difference as with the square ROIs. D. The raw averaged traces were digitally filtered with either a 1-2-1 (2–3) or a 1-2-3-2-1 (3–5) smoothing algorithm (see Methods). The 2–3 filter had no obvious effect on the event trace. However, when the 3–5 filter was used the rise time was slowed.