Homogeneous record of Atlantic hurricane surge threat since 1923

Abstract

Detection and attribution of past changes in cyclone activity are hampered by biased cyclone records due to changes in observational capabilities. Here we construct an independent record of Atlantic tropical cyclone activity on the basis of storm surge statistics from tide gauges. We demonstrate that the major events in our surge index record can be attributed to landfalling tropical cyclones; these events also correspond with the most economically damaging Atlantic cyclones. We find that warm years in general were more active in all cyclone size ranges than cold years. The largest cyclones are most affected by warmer conditions and we detect a statistically significant trend in the frequency of large surge events (roughly corresponding to tropical storm size) since 1923. In particular, we estimate that Katrina-magnitude events have been twice as frequent in warm years compared with cold years (P < 0.02).

The relationship between global warming and Atlantic hurricane activity is a controversial topic (1–3). Some have linked cyclone activity to sea surface temperatures in the cyclogenesis region (2, 4). Other competing hypotheses include teleconnections with El Niño–Southern Oscillation (5), North Atlantic Oscillation (6–8), Atlantic Multidecadal Oscillation (6), tropical temperatures (3, 9), and Sahel drought (10). Whereas others note that bias in the observational record casts doubt on any statistical power from the relationship (11). Estimating and correcting the historical bias hamper assessment of the links between tropical cyclone activity and climate change (1, 2, 11, 12). Hence, any discussion of observational links or causality between global mean temperatures and hurricane impacts relies on an unbiased estimate of hurricanes as a function of time. There is a rising trend over the 20th century in the observed numbers of Atlantic tropical cyclones (1, 12). However, observational methods have improved over time, especially since the satellite era, but also after airborne observations became commonplace; therefore some cyclones were missed in the past.

Most efforts have focused on estimating total Atlantic cyclone activity rather than the number of land-falling storms. This is because relatively few storms make land, and small changes in storm tracks can make a difference between a landfall and a near miss. However, from the economic damage perspective the hurricanes that remain far away from shore in the Atlantic are much less important than those closer to land. Hence in constructing an unbiased record of storms we need to ask what we want to measure. The strong winds and intense low pressure associated with tropical cyclones generate storm surges. These storm surges are the most harmful aspect of tropical cyclones in the current climate (1, 12), and wherever tropical cyclones prevail they are the primary cause of storm surges. A measure of storm surge intensity would therefore be a good candidate measure of cyclone potential impact.

In this paper we construct such a record, using long-term tide-gauge records from stations that have been operational for much longer than the satellite era. These provide a consistent dataset for examining hurricanes affecting the southeastern United States. We also show that the index is actually dominated by land-falling hurricanes rather than winter storms and that the index reflects economic damage. Rather than a simple number count of cyclones, we produce a yearly probability distribution of storm surge intensity. We then apply a robust method of estimating confidence intervals to the frequency of extreme events. Finally we show that there is a difference in frequency of cyclones between cold and warm years and that the effect is strongest for the larger cyclones and hurricanes.

Results

We wish to produce a long-term, homogeneous record of storm surge activity. Tide gauges are very suitable as they are simple devices that have been used for hundreds of years to measure sea level. We define the region of interest to be the western Atlantic between 10°N and 40°N. This leaves us with the six tide gauges from the region of interest (Fig. 1, Inset and Fig. S1) with the main criteria that we wanted to construct a homogeneous record that covered the great 1926 storm surge (13) and the general high cyclone activity of the 1930s. Here, we use data from the Research Quality Data Set (RQDS) (14). The RQDS records are extended to the present using fast delivery data from the global sea level observing system (14) and in a single instance (Mayport, FL) using preliminary water-level data from the National Oceanic and Atmospheric Administration (NOAA) Center for Operational Oceanographic Products and Services (15). We manually screen the data quality of the Mayport preliminary water-level data before down-sampling. We then proceed to filter these records to enhance the storm signal while reducing the signals due to instrument changes, harbor development, and erroneous time shifts in the records.

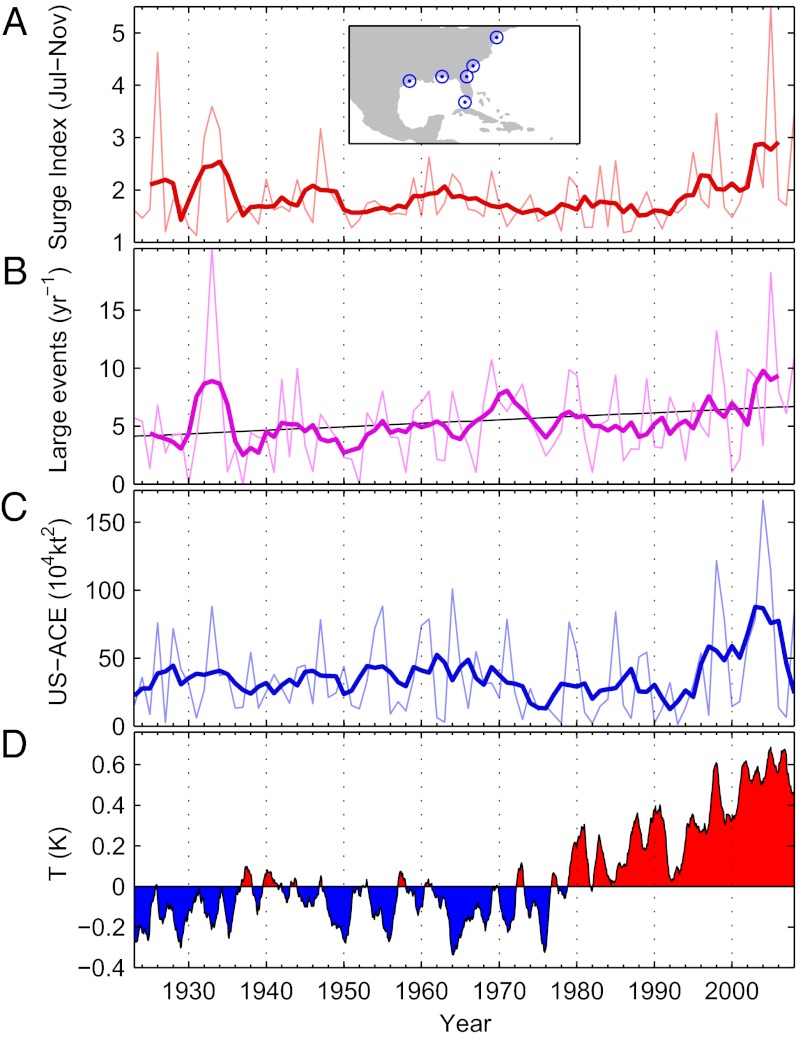
Fig. 1.

(A) Average surge index over the cyclone season. (B) Observed frequency of surge events with surge index greater than 10 units/y (surge index > 10 units) and linear trend (black). (C) Accumulated cyclone energy for US landfalling storms. (D) Annual average global mean surface temperature anomaly from GISTEMP (23), shaded to show warmer and colder than median temperatures. Thick lines in A, B, and C are 5-y moving averages. Inset in A shows locations of the six tide gauges used in the construction of the surge index.

Tropical cyclones are highly localized. However, over time the sea-level disturbance will dissipate. Daily averages increase the storm footprint to hundreds of kilometers, which means that relatively few tide-gauge stations provide adequate coverage. Large storms can also produce extreme sea levels that can be seen in tide-gauge records for several days. The potential energy stored in a sea-level perturbation is related to the square of the vertical displacement of the sea surface (16); hence we use squared day-to-day difference in local sea level. Daily data are insensitive to harbor development and changes in measurement methods, which can strongly affect high-frequency variability such as significant wave height. Day-to-day differencing further minimizes tidal influence and slowly varying trends from, e.g., rising global sea levels (17).

We observe that summer sea level is relatively calm except for the sporadic and obvious influence from cyclones, whereas winters have a higher degree of background variability. We therefore remove the background annual cycle by division. This also brings the records to a common normalized reference that removes local effects due to, e.g., bathymetry (16). We call the multistation daily maximum of deseasonalized squared day-to-day differences the surge index. These processing steps are outlined in more detail in SI Methods, section S1, Fig. S2, and Table S1.

To visualize the surge index and facilitate comparisons to other measures of cyclone activity we have down-sampled the surge index to annual resolution. We do this in two ways (Fig. 1 A and B): The first way is the average value over the hurricane season (which we here define as July–November) and the second way is a measure of the annual frequency of extreme events above a threshold corresponding to five to six events per year.

Discussion

In this section we demonstrate that the surge index primarily records surge threat from tropical cyclones. We compare the new surge index with several common measures of tropical cyclone activity, most of them derived from the Atlantic Hurricane Database (HURDAT; ref. 18) with wind speed corrections as detailed in ref. 2: tropical cyclone counts for various magnitude thresholds on the Saffir–Simpson scale, accumulated cyclone energy (ACE) (19), net tropical cyclone activity (NTC) (20), and power dissipation index (PDI). We also calculate several of these measures restricted to storms making US landfall. These we denote with a US prefix (e.g., US-ACE). Additionally, we compare the surge index with the “PL05” normalized hurricane damage (NHD) from Pielke et al. (21).

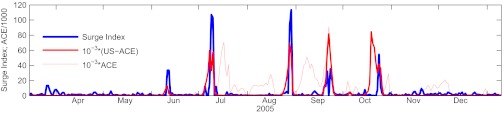
As an example we show the daily surge index compared with ACE and US-ACE for the very active 2005 season (Fig. 2). The ACE is traditionally defined as an annually integrated value. Here, we have made the natural extension of this definition to a daily integrated value. It is clear that the surge index is particularly sensitive to hurricanes making landfall, which supports the interpretation that the surge index is closely related to the actual threat.

Fig. 2.

Comparison of the surge index (blue) with ACE (light red) and US-ACE (red) for the 2005 hurricane season.

Table 1 shows the correlation of the seasonal surge index with other measures. The surge index is positively correlated with all of the comparison measures. The best correlations are found with measures that emphasize intensity (e.g., NTC, ACE, and PDI) and measures that are restricted to US land-falling storms only. Table 1 also shows that low-frequency correlation tends to be at a higher level than the year-to-year correlation. This is to be expected given that there are low-frequency driving agents related to various climate forcings (4, 8). One notable exception is NHD, which shows poor low-frequency correlations. However, NHD has been subjected to extensive corrections for inflation and changes in societal conditions over time (21). These corrections affect primarily low-frequency signals and trends and we interpret the poor low-frequency correlation with surge index to be due to a substantial remaining bias in NHD. We therefore consider the low-frequency variability (i.e., trend) of NHD suspect. We note, however, that the surge index does capture the high-frequency variability in NHD, thus supporting the interpretation that it is truly a proxy for cyclone threat. It is conceivable that the surge index could be used to correct for the remaining bias in NHD.

Table 1.

Correlations between July–November surge index and other measures of cyclone activity

Series	Period of overlap	Correlation full period	Correlation 1950–2005	High-frequency correlation	Low-frequency correlation
Cat 0–5	1923–2008	0.56	0.65	0.51	0.64
Cat 1–5	1923–2008	0.55	0.57	0.54	0.56
Cat 2–5	1923–2008	0.50	0.42	0.51	0.50
Cat 3–5	1923–2008	0.51	0.47	0.42	0.58
Cat 4–5	1923–2008	0.53	0.50	0.46	0.62
Cat 5	1923–2008	0.38	0.61	0.41	0.48
US cat 0–5	1923–2008	0.54	0.55	0.55	0.56
US cat 1–5	1923–2008	0.57	0.57	0.55	0.67
US cat 2–5	1923–2008	0.55	0.56	0.51	0.66
US cat 3–5	1923–2008	0.57	0.60	0.55	0.67
US cat 4–5	1923–2008	0.61	0.70	0.57	0.74
US cat 5	1923–2008	0.38	0.62	0.38	0.46
ACE	1923–2008	0.61	0.58	0.54	0.72
US ACE	1923–2008	0.58	0.58	0.51	0.77
NTC	1923–2006	0.58	0.55	0.48	0.54
PDI	1923–2008	0.60	0.58	0.53	0.73
US PDI	1923–2008	0.58	0.61	0.52	0.75
NHD	1923–2005	0.65	0.66	0.59	0.38

Low-frequency correlation is the correlation of the two series after a 5-y moving average. High-frequency correlation is the correlation of the residuals after subtracting this moving average. A US prefix indicates that the metric has been restricted to US-landfalling storms only. Cat, category.

In Table S2 we show the surge index of the 50 greatest events. The surge index ranking reflects the impact at the specific tide-gauge locations and therefore should not be interpreted as a storm ranking. The purpose of this list is to demonstrate that the surge index truly captures cyclone activity, rather than provide a storm severity ranking. A few events outside the hurricane season cannot be attributed to tropical cyclones. Several of these events, however, show up in other records of extreme weather; e.g., the large March 13, 1993 event is commonly known as the 1993 superstorm (22).

The surge index can be interpreted as a potential threat to infrastructure. A large surge does not necessarily mean that the associated storm caused a lot of damage. It depends on the detailed conditions of when and where the storm hit the coast. We argue that the surge index is a more direct measure of threat than most of the HURDAT-derived measures. Large surge index values are a manifestation of what the storm is able to do exactly at the time of landfall. Other measures, such as integrated kinetic energy (IKE) (24), have been proposed as proxies for the destructive potential. It is beyond the scope of this study to make a detailed comparison with IKE, which relies on high-quality wind data that are not available for all storms. However, the surge index can be used as a method of testing how IKE-type measures reflect actual surge data. For such a comparison it would be possible to include many more additional tide-gauge records as the time frames for high-quality wind data are relatively short.

To estimate the trend in landfalling storm counts, we count the number of large surge events greater than 10 units in 1 y, which is roughly equivalent to hurricane categories 0–5. This threshold was chosen as a compromise between looking at large events and having sufficiently many events to obtain robust statistics. Since 1923 the average number of events crossing this threshold has been 5.4/y, which would increase to 9.5 events/y by 2100 were the best-fitting trend to continue (Fig. 1B). This trend is statistically significant against a null hypothesis with the same power spectrum as the input series (P < 0.02). We do not find a statistically significant trend in the seasonal average surge index (Fig. 1A), which by construction emphasizes the very largest events. This is because the strongest events are rare, and hence a longer time series is needed before a robust trend emerges. The same issues make it more difficult to detect trends in counts of major landfalling hurricanes (or PDI or ACE), compared with counts of all tropical storms.

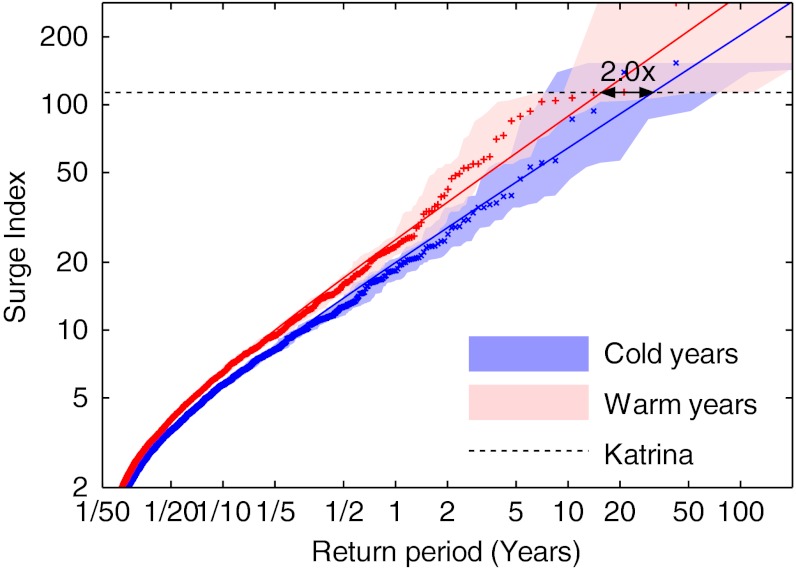
As we are primarily interested in extreme events, it is constructive to examine the changes to the entire surge index probability density function (pdf). We split the surge index into cold and warm years (Fig. 1D) and compare the derived return periods (Methods) for the two subsets (Fig. 3). It is clear that events with annual return periods (reciprocal frequency) are significantly more intense in warm years than in cold years. We can therefore conclude that the surge index distribution is not stationary. For rarer events (with return periods greater than 1 y) the confidence intervals from the warm and cold years overlap, which makes it difficult to visually assess whether the difference is significant. We address this by fitting generalized extreme value (GEV) distributions (Methods) to the cold and warm year data separately in Fig. 3. It is evident that the GEV distribution fits the surge index data, but that there are significant differences between the GEV parameters describing the warm and cold years. Both GEV fits give return periods that are consistent with the 9- to 30-y period for US coastal Katrina-magnitude events estimated from HURDAT (25). We observe that warm years are more active than cold years and that the relative difference in frequency is greatest for the most extreme events. The separate GEV fits suggest that events of Katrina magnitude are approximately two times more frequent in the warm years than in cooler years (Fig. 3). This increase is significant at the 98% confidence level (Methods). The doubling is higher but compatible with earlier estimates from Elsner et al. (25), who reported an 11% increase (with no uncertainty estimate). We emphasize that not all events of Katrina magnitude will have equally devastating impacts. The results are also consistent with the low-resolution 1,500-y overwash sediments from landfalling Atlantic cyclones (6) that showed 40-y smoothed cyclones counts varying by about 50% while global temperatures varied by about 1 °C.

Fig. 3.

Return period plot of surge index distribution for cold (blue) and warm (red) years separately (Fig. 1D). The crosses and shaded bands show return periods and confidence intervals estimated from the empirical cdf (Methods). Solid lines show best-fitting GEV distributions (SI Methods, section S3). The maximal surge index during hurricane Katrina in 2005 is shown as a dotted line.

We have constructed a homogeneous surge index on the basis of instrumental records from six long tide-gauge records. We demonstrate that the surge index correlates with other measures of Atlantic cyclone activity and that it responds in particular to major landfalling cyclones. The surge index can be used to identify and estimate potential remaining biases in other records of cyclone activity.

We detect a statistically significant increasing trend in the number of moderately large surge index events since 1923. We estimate that warm years have been associated with twice as many Katrina-magnitude events compared with cold years in the global average surface temperature record.

Methods: Empirical Return Periods and Confidence Intervals

The return period (R) of events greater than x is related to the cumulative distribution function (cdf) (c) as R(x) = dt/(1 − c(x)), where dt is the sampling frequency. Single storms may be manifested as broad peaks that last several days (Fig. 2), which spoils the intuitive meaning of the return period when we consider daily data. We therefore down-sample the daily surge index series to a series of weekly block maxima before estimating return periods. Weekly resolution was chosen as a trade-off between having high temporal resolution and ensuring that large storms are manifested as single peaks. This resolution proved to be sufficient down-sampling for the GEV distribution to yield high-quality fits and the results are insensitive to further down-sampling.

Because we do not know the true cdf of the underlying process, we have to rely on the observed random sample x₁, x₂, . . . , x_N. That is, we do not know the exact shape of the function c(x). We can estimate c(x_i) empirically from the rank of x_i within the sample (26, 27). The usual method for estimating the uncertainties of the empirical estimate is Greenwood’s formula for the approximate SEs (e.g., ref. 26), which is then inflated to a confidence interval assuming that the errors are normally distributed. However, this approach fails for extreme values and for small sample sizes. For extreme percentiles it is clear that the uncertainties cannot be symmetric, and the uncertainty distribution must be bounded as we know there can be no values outside the 0th- to 100th-percentile range. As we are particularly interested in extreme events, we have developed an alternative robust Monte Carlo approach for determining the confidence interval of the empirical estimates of c and thus R.

We cannot draw surrogate samples according the true distribution of x as we do not know the true distribution function (c). For any random sample (x_i) from c, the corresponding value of c(x_i) will have uniform probability in the interval 0–1 by construction.

So, although we cannot draw samples according to the true process distribution, we can draw samples according to the true distribution of c(x) simply by using a standard uniform random number generator. The goal is to compare this true c(x) with what the empirical estimator of c would give. The difference between the true and estimated percentiles can be used to infer confidence intervals if we ensure that the empirical estimator is equivalent to the one applied to the observed sample. The empirical estimator for c(x_i) is dependent only on the rank of x_i within the sample and on the size of the sample; i.e., it is independent of the distribution, and the rank of c(x_i) will be the same as the rank of x_i. We can therefore apply the empirical estimator directly to a surrogate sample of true percentiles. To summarize, the Monte Carlo procedure for determining the spread in empirical estimates of c is as follows:

• i) Generate a set of N random samples from a uniform distribution between zero and one. Label this c_{surrogate,true}.

• ii) Estimate c empirically from c_{surrogate,true}. Label this c_{surrogate,empirical}.

• iii) Repeat steps i and ii many times.

• iv) The confidence interval of an empirical estimate of the percentile can be determined from the spread of all of the c_{surrogate,true} with the given value c_{surrogate,empirical}.

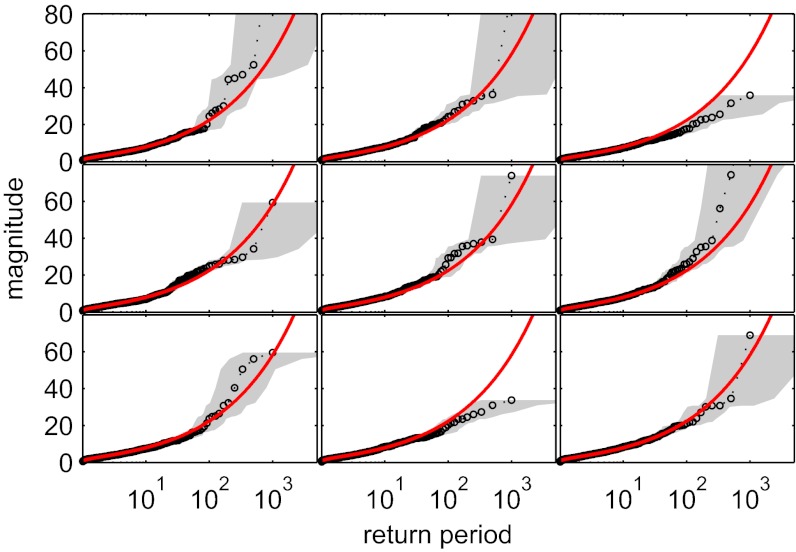
In Fig. 4 we show the viability of the empirical procedure on artificial data with known characteristics.

Fig. 4.

Each subplot shows an example of empirical return periods (circles) and associated 5–95% confidence intervals (horizontal extent of gray band) estimated from 1,000 random samples generated with a prescribed distribution (red). The random samples were drawn from a GEV distribution with parameters k = 0.4, σ = 1.5, and μ = 2.5. Units are arbitrary.

This Monte Carlo approach is more robust, conservative, and flexible than the traditional Greenwood’s equation (26). Further, serial dependence, clustering, and measurement noise can be taken into account in the Monte Carlo approach by designing appropriate noise models. The normalized surge index series show only very weak autocorrelation, so we fit a second-order autoregressive (AR) noise model. The AR noise is then transformed to a uniform distribution. We find that the confidence intervals are not sensitive to the serial correlation for the data used in this study.