Inspection of the Engineered FhuA ΔC/Δ4L Protein Nanopore by Polymer Exclusion

Abstract

Extensive engineering of protein nanopores for biotechnological applications using native scaffolds requires further inspection of their internal geometry and size. Recently, we redesigned ferric hydroxamate uptake component A (FhuA), a 22-β-stranded protein containing an N-terminal 160-residue cork domain (C). The cork domain and four large extracellular loops (4L) were deleted to obtain an unusually stiff engineered FhuA ΔC/Δ4L nanopore. We employed water-soluble poly(ethylene glycols) and dextran polymers to examine the interior of FhuA ΔC/Δ4L. When this nanopore was reconstituted into a synthetic planar lipid bilayer, addition of poly(ethylene glycols) produced modifications in the single-channel conductance, allowing for the evaluation of the nanopore diameter. Here, we report that FhuA ΔC/Δ4L features an approximate conical internal geometry with the cis entrance smaller than the trans entrance, in accord with the asymmetric nature of the crystal structure of the wild-type FhuA protein. Further experiments with impermeable dextran polymers indicated an average internal diameter of ∼2.4 nm, a conclusion we arrived at based upon the polymer-induced alteration of the access resistance contribution to the nanopore’s total resistance. Molecular insights inferred from this work represent a platform for future protein engineering of FhuA that will be employed for specific tasks in biotechnological applications.

Introduction

A persisting challenge in nanobiotechnology is designing robust protein scaffolds that are tractable and versatile under a broad range of experimental circumstances (1–3). Recently, we extensively engineered ferric hydroxamate component A (FhuA) of Escherichia coli by deleting a 160-residue cork domain (C) and four long extracellular loops (4L) (4,5). We named this engineered nanopore FhuA ΔC/Δ4L (Fig. 1). FhuA is a 714-residue, monomeric β-barrel protein composed of 22 antiparallel β-strands, located in the outer membrane of E. coli (6,7). This protein is distinguished from other outer-membrane family members by its numerous functional tasks, including the dual role of transporter and receptor. The major function of FhuA is to mediate the energy-driven, high-affinity Fe³⁺ uptake complexed by the siderophore ferrichrome (6–8). In addition, FhuA transports antibiotics, such as albomycin (9) and rifamycin (10).

Figure 1.

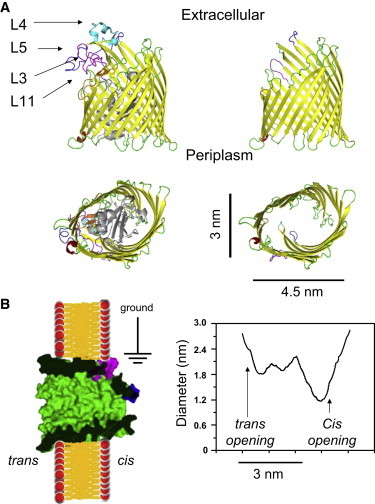
Representation of the modifications to the FhuA protein nanopore. (A) Diagram showing side (upper) and top (lower) views of the crystal structure of the wild-type (FhuA) and modified (FhuA ΔC/Δ4L) proteins with the extracellular loops—L3, L4, L5, and L11—labeled. (B) Surface representation of the engineered FhuA ΔC/Δ4L protein nanopore and its expected orientation in a synthetic planar lipid bilayer. The cartoon was made using the Protein Data Bank structure 1BY5 of the native FhuA protein (7). On the right side, the graph shows the expected internal diameter of the FhuA ΔC/Δ4L protein nanopore along the longitudinal axis, as calculated using the HOLE program (61).

We coupled genetic engineering with a rapid-dilution refolding to obtain a protein nanopore with unusual stability over a broad range of experimental conditions, from highly acidic to very basic pH, as well as from very low to high ionic concentration in the chamber (5). This extensive engineering of the FhuA ΔC/Δ4L protein nanopore encompassed an overall deletion of ∼33% of the wild-type protein. The single-channel conductance of the FhuA ΔC/Δ4L nanopore was ∼4 nS. One immediate question that we asked was how this newly redesigned cork-free β-barrel membrane protein differs from the native FhuA (6,7) (Fig. 1). It is conceivable that the deletion of the cork domain and several long extracellular loops might have an impact not only on the orientation and local conformation of other extracellular loops, but also on the inner dimensions of the β-barrel along the central transversal axis.

To further explore the size and geometry of the engineered FhuA ΔC/Δ4L protein nanopore, we systematically examined the interaction of water-soluble, flexible poly(ethylene glycol)s (PEGs) with its interior by polymer-exclusion experiments. The crystal structure of the native FhuA shows an asymmetric outer-membrane protein with an elliptical cross-sectional area that decreases from the trans to the cis side (Fig. 1) (6,7). Here, the trans side is the periplasmic side and the cis side is the extracellular side of the protein. Interaction of PEGs with transmembrane protein pores and channels has been studied extensively in the last couple of decades. These investigations were primarily targeted at 1), obtaining a mechanistic understanding of polymer partitioning into confined geometries (11–25); 2), obtaining a quantitative approach for the impact of the osmotic effect of polymers on single-channel kinetics (26–28); 3), determining the internal sizes of the transmembrane protein pores using polymer-induced change in their single-channel conductance (29–38) or measuring polymer-induced alteration of the pore’s access resistance (26,39); 4), probing the internal geometry of the transmembrane protein pores using chemical modification, cysteine scanning mutagenesis, and functional polymers (17,40); 5), probing the dynamics of single polymers in confined spaces (13,15,41–43); 6), developing nanopore-based approaches for single-molecule mass spectrometry (44,45); and 7), probing ion-channel structures and opening-closing dynamics (28,41,46).

Here, the extent of the modification to the single-channel conductance in the presence of water-soluble polymers was used to infer the internal diameter of the engineered FhuA ΔC/Δ4L protein nanopore. Examination of this nanopore employing polymer exclusion was motivated by the fact that it remains in the open state for a long period of time (5). PEGs, with molecular mass <2000 Da, which were added symmetrically to both sides of the chamber, reduced the single-channel conductance of FhuA ΔC/Δ4L, confirming its large internal size. Asymmetric addition of PEGs to the chamber produced results that suggest a conical internal geometry of FhuA ΔC/Δ4L with a minimum constriction of ∼1 nm, which is located near the extracellular entrance. This finding is in accord with predictions derived from the crystal structure of the native FhuA protein. Estimates of the nanopore access resistance made using impermeable dextran polymers were employed to infer the average internal diameter of ∼2.4 nm.

Materials and Methods

Preparation of the engineered FhuA ΔC/Δ4L protein nanopores

The construction of the plasmid for the expression of the engineered FhuA ΔC/Δ4L protein nanopores has been reported previously (4). The subsequent modifications of the protocol for obtaining a stiff FhuA ΔC/Δ4L protein nanopore through a rapid-dilution refolding approach have also been described (5). Briefly, the refolding of the FhuA ΔC/Δ4L protein was adopted from a protocol developed by Arora and colleagues (Fig. S1 in the Supporting Material) (47). As a first step, 40 μl of His⁺-tag-purified, denatured FhuA ΔC/Δ4L was diluted 50-fold into a 1.5% n-dodecyl-β-D-maltopyranoside (DDM) in 50 mM Tris-HCl containing 200 mM NaCl and 1 mM EDTA, pH 8.0. The diluted protein samples were left overnight at 23°C to complete the refolding of the FhuA ΔC/Δ4L protein. Aggregated or misfolded proteins were removed by centrifugation. Samples were stored at −80°C in 50-μl aliquots.

Single-channel electrical recordings on planar lipid bilayers

Electrical recordings were performed on synthetic lipid bilayers of 1,2-diphytanoyl-sn-glycero-3-phosphocholine (Avanti Polar Lipids, Alabaster, AL) (48,49). Bilayers were formed across a single 100-μm diameter aperture in a 25-μm thick Teflon film (Goodfellow Corporation, Malvern, PA) separating the cis and trans compartments of an acetal chamber. The cis-half side of the chamber was grounded. Positive polarity was defined such that the potential on the trans side was greater than that on the cis side. The PEG-free initial solution was 1 M KCl and 10 mM potassium phosphate, pH 7.4. To achieve single-channel insertion, FhuA ΔC/Δ4L was added to the cis side of the chamber to a final concentration of ∼0.02 ng/μl. Current recordings were performed using an Axon 200B patch-clamp amplifier (Axon Instruments, Foster City, CA) in the voltage-clamp mode. Data were collected by an Intel Core Duo PC (Dell, Austin, TX) connected to a Digidata 1440A (Axon). Output was filtered using a model 900B 8-pole Bessel filter (Frequency Devices, Ottawa, IL) at 10 kHz. The acquisition rate was 50 kHz. Single-channel insertions were monitored by stepwise changes in the measured current. After insertion, channel conductance was measured at a transmembrane potential of +40 mV. Channels with a single-channel conductance of 4.2 ± 0.2 nS were selected for this study. All experiments were performed at room temperature, 23 ± 1°C. The single-channel acquisition was performed using the Clampex 10.2 (Axon) software. Analysis of the single-channel electrical traces was carried out using the pClamp 10.2 (Axon), Origin 8.1 (Microcal Software, Northampton, MA), and Mathematica 7 (Wolfram Research, Champaign, IL) software.

Polymer reagents

After characterization of the single-channel conductance of each FhuA ΔC/Δ4L nanopore, either a solution containing poly(ethylene glycol)s (PEGs) or dextran replaced the original solution. The following reagents were used in this work: PEG 200, PEG 300, PEG 600, PEG 1000, PEG 1500, PEG 2000, PEG 3000, PEG 4000, PEG 6000, PEG 8000, PEG 10,000, and PEG 12000 (Sigma-Aldrich, St. Louis, MO) (Supporting Material). PEGs were added to 1 M KCl and 10 mM potassium phosphate, pH 7.4, to a final concentration of 15% (w/w). Dextran of molecular mass 40000 Da (Sigma-Aldrich, St. Louis, MO) was added to 1 M KCl and 10 mM potassium phosphate, pH 7.4, to a concentration of 15% (w/w). Solution replacement was performed by perfusion using a Bio-Rad EP-1 Econo Pump (Bio-Rad Laboratories, Hercules, CA). Conductivity of the solutions was measured using an Orion 105A+ conductivity meter (Thermo Electron, Marietta, OH). PEG solutions were perfused either symmetrically, with both sides of the chamber containing the same-molecular-mass PEG, or asymmetrically, where PEG on one side of the chamber was 12000 Da and the examined polymeric species varied on the opposite side of the chamber. Dextran solutions were perfused symmetrically to both sides of the chamber. A detailed perfusion procedure for polymer solutions can be found in the Supporting Material.

Results

Biophysical characteristics of the engineered FhuA ΔC/Δ4L protein nanopore

Recently, we showed that the engineered FhuA ΔC/Δ4L protein nanopore inserts into a synthetic planar lipid bilayer as a monomer in a single orientation (5). Fig. 1 shows the expected orientation and structure of the FhuA ΔC/Δ4L protein, with an open transmembrane β-barrel nanopore. According to this crystal structure, it has an ∼2.8-nm opening on the trans side, close to the bilayer surface, and a constriction of 1.2 nm near the cis end (6,7). These dimensions, which include the contribution of the residue side chains, suggest that it is feasible to use polymers to assess the nanopore diameter along the longitudinal axis. The partitioning properties of PEGs of varying molecular mass were explored by both their symmetric and asymmetric addition to the bilayer chamber.

At 1 M KCl and 10 mM potassium phosphate, pH 7.4, the FhuA ΔC/Δ4L protein nanopore was stable for extended periods at applied transmembrane potentials between −100 mV and +100 mV. FhuA ΔC/Δ4L exhibited a relatively quiet electrical signature (no major large-amplitude current blockades), which was decorated by brief (∼100-μs) and very low-amplitude current deflections at both positive and negative voltages (∼20 pA at +80 mV; Fig. 2 A). The engineered FhuA ΔC/Δ4L nanopore inserted into the bilayer with a range of conductances (5). To facilitate single-channel data analysis, nanopores within a narrow range of conductance were selected (4.2 ± 0.2 nS at +40 mV; Fig. S2). These represent ∼25% of all insertions. Nanopores with this conductance were slightly non-ohmic, with the current response at +100 mV and −100 mV differing by ∼7%.

Figure 2.

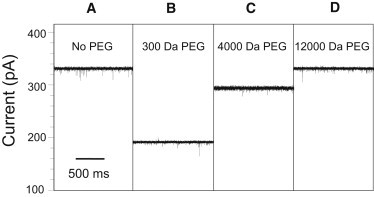
Representative dependence of single-channel electrical current on the PEG molecular mass for the engineered FhuA ΔC/Δ4L protein nanopore. With the addition of small-molecular-mass PEG, the unitary conductance of the nanopore decreases. With addition of larger-molecular-mass PEGs, the conductance nears its PEG-free conductance. All traces show the open-state current through a single FhuA ΔC/Δ4L nanopore. The applied transmembrane voltage was +80 mV. The unitary conductance of these FhuA ΔC/Δ4L nanopores was 4.2 nS in PEG-free solution. All experiments were performed with symmetric solutions containing 15% (w/w) PEG in 1 M KCl and 10 mM potassium phosphate buffer, pH 7.4. All single-channel electrical traces were low-pass Bessel filtered at 1 kHz.

The introduction of PEG into the bath solution changed the single-channel conductance of the nanopore in a manner related to the PEG molecular mass, with lower-mass PEG solution creating a larger decrease in the single-channel conductance and higher-mass PEG solution having a lesser effect. Fig. 2 provides representative single-channel electrical traces of the effect of symmetric addition of 15% (w/w) solutions of PEG on the single-channel conductance of the FhuA ΔC/Δ4L nanopore. In the case of 300-Da PEG, the single-channel conductance dropped to 60% of its PEG-free level (Fig. 2 B), a decrease consonant with the drop in the conductivity of the bulk-solution produced by PEG. The addition of 4000-Da PEG did not dramatically change the single-channel conductance of the nanopore (Fig. 2 C). The presence of 12000-Da PEG in the chamber did not change the unitary conductance of FhuA ΔC/Δ4L (Fig. 2 D), indicating that PEGs of greater molecular size were not able to penetrate into the nanopore interior. A reduced partitioning of the higher-mass PEGs is a result of their increased entropic barrier for the transport from a larger volume, where many polymer configurations are allowed, to a very small volume, where the chain entropy is severely reduced (50).

Voltage dependence of the conductance ratio

We then calculated the conductance ratio as the ratio between the single-channel conductance of FhuA ΔC/Δ4L in PEG-containing solution and the single-channel conductance of FhuA ΔC/Δ4L in PEG-free solution. In this section, the concentration of PEG on each side of the membrane was 15% (w/w). Symmetric additions of 300-Da PEG to the bilayer chamber produced a voltage-independent conductance ratio, in the range ∼0.56–0.58 (Fig. 3). In contrast, asymmetric additions of PEGs, with a molecular mass of 300 Da on the cis side and 12000 Da on the trans side, showed a voltage-dependent conductance ratio, with a lower value of ∼0.65 at a transmembrane potential of −100 mV and a higher value of ∼0.90 at a transmembrane potential of +100 mV. Interestingly, the conductance ratio decreased from ∼0.82 to ∼0.66 when the applied transmembrane potential varied from −100 to +100 mV and the chambers contained 300-Da and 12000-Da PEGs on the trans and cis sides, respectively.

Figure 3.

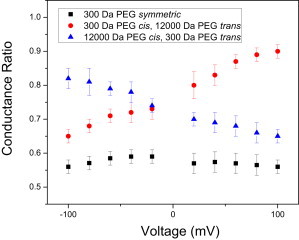
Voltage dependence of the conductance ratio of the FhuA ΔC/Δ4L nanopore, which was induced by the presence of PEGs in the bilayer chambers. Indicated are the currents measured at different voltages for the FhuA ΔC/Δ4L nanopore in 300-Da PEG cis and 12000-Da PEG trans (circles), 12000-Da cis and 300-Da PEG trans (triangles), and 300-Da PEG symmetric (squares). Solutions were 15% (w/w) PEG, in 1 M KCl and 10 mM potassium phosphate, pH 7.4.

A recent study has described PEG motion under the action of an electric field in the α-hemolysin (αHL) protein nanopore (45). That study showed that the transient binding of K⁺ ions to PEG results in a net positive charge. The movement of PEG within the nanopore was then described as due to the resultant electric force and electro-osmotic viscous forces acting on the PEG. Therefore, we judge that the net movement of the low-molecular-mass PEG is from positive to negative transmembrane potential. This process likely explains, at least in part, our experimental observations of the voltage dependence for the low-molecular-mass PEG penetration.

Molecular mass dependence of the conductance ratio

To mitigate the voltage dependence of the conductance ratio produced by PEGs of varying molecular mass, the conductance values were taken at two different applied transmembrane potentials, +100 mV and −100 mV. In addition, we determined the interpolated value of the conductance ratio at a transmembrane potential of 0 mV. Fig. 4 shows a summary of the alterations of the conductance ratio owing to the presence of PEGs of varying molecular mass in the aqueous phase. We define cis experiments as those in which the listed PEG molecular mass was on the cis side of the chamber and impermeable 12000-Da PEG was on the trans side of the chamber. Alternatively, the trans experiments were performed with the listed PEG molecular mass on the trans side of the chamber and impermeable 12000-Da PEG on the cis side.

Figure 4.

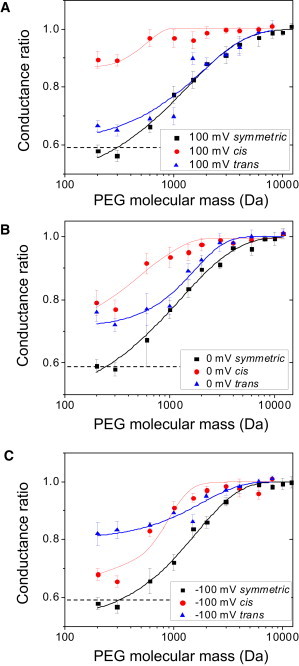
Conductance ratio of the FhuA ΔC/Δ4L nanopore in the presence of PEGs of varying molecular mass. Curves are constructed for transmembrane potentials at +100 mV (A), 0 mV, where conductance values were interpolated (B), and −100 mV (C). Experiments labeled cis were performed with the listed PEG molecular mass on the cis side of the chamber and impermeable 12000-Da PEG on the trans side of the chamber. Alternatively, experiments labeled trans were performed with the listed PEG molecular mass on the trans side of the chamber and impermeable 12000-Da PEG on the cis side. The bottom horizontal dashed line represents the ratio of the conductivity of the bulk solutions containing PEG to the PEG-free solution. The solutions contained 15% (w/w) PEG and 1 M KCl and 10 mM potassium phosphate, pH 7.4.

In Fig. 4, the data points map out different molecular-mass regimes, in which PEG either permeates into the nanopore or does not (see Discussion). For the three transmembrane potentials, +100, 0, and −100 mV, illustrated in Fig. 4, A–C, respectively, low-molecular-mass PEGs (e.g., 200 and 300 Da) induced a substantial decrease in the conductance, suggesting that these PEGs easily enter the nanopore interior. In contrast, in the case of both cis and trans experiments, PEG solutions with PEG molecular mass >6000 Da did not appreciably change the conductance of the FhuA ΔC/Δ4L nanopore. This finding suggests that PEGs of molecular mass >6000 Da do not permeate into the nanopore interior.

Access resistance of the FhuA ΔC/Δ4L protein nanopore

To measure the effect of the change in the access resistance of the nanopore due to the addition of PEG, impermeable dextran was used. Dextran of molecular mass 40000 Da was added to 1 M KCl and 10 mM potassium phosphate, pH 7.4, to a final concentration of 15% (w/w). The decrease in bulk conductivity of the dextran-containing solution was comparable to that of the PEG solution (Table S1). Although PEG increases the activity of potassium ions in the channel, skewing the conductance ratio to a higher value, dextran does not (51). Therefore, the effect of impermeable polymers of PEG and dextran is different. The addition of dextran solution decreased the measured conductivity of the engineered FhuA ΔC/Δ4L protein nanopore by 8.8 ± 2.4% (Fig. S3). This decrease is attributed solely to the change in access resistance associated with the bulk conductivity of the solution surrounding the nanopore. The change in the access resistance with dextran also provides a means of estimating the nanopore diameter (see Discussion) (26).

The power-spectral density of the current noise

Prior examinations of polymer partitioning into large nanopores have employed analysis of fluctuations in the single-channel current noise induced by PEGs using power-spectral analysis (12,18,41). Such studies yielded kinetic information on polymer partitioning into and out of the nanopore. We analyzed the single-channel current of the FhuA ΔC/Δ4L nanopore at an applied transmembrane potential of +100 mV, selecting portions of the single-channel recordings that lacked the rapid downward deflections seen in Fig. 2. The power-spectral density of the current noise of the FhuA ΔC/Δ4L nanopore was taken both with and without symmetric PEG solutions. Fig. 5 A presents the spectral densities of the single-channel current fluctuations of the FhuA ΔC/Δ4L nanopore at a zero transmembrane potential (trace 1), a transmembrane potential of +100 mV in PEG-free solution (trace 2), and a transmembrane potential of +100 mV in the presence of 1000-Da PEG (trace 3). Each analyzed sample was taken from a concatenation of the current recording to a total of 5 s in duration, with the 24-Hz-resolution bandwidth used for spectral analysis. The results for all PEGs employed in this work are illustrated in Fig. 5 B in the form of the low-frequency spectral density, S(0). This value was obtained from the spectra by averaging over the range 100 Hz < f < 1000 Hz and subtracting the background noise at 0 mV applied potential (52). The error bars in Fig. 5 B reflect reproducibility of the PEG-induced noise from three distinct single-channel electrical traces.

Figure 5.

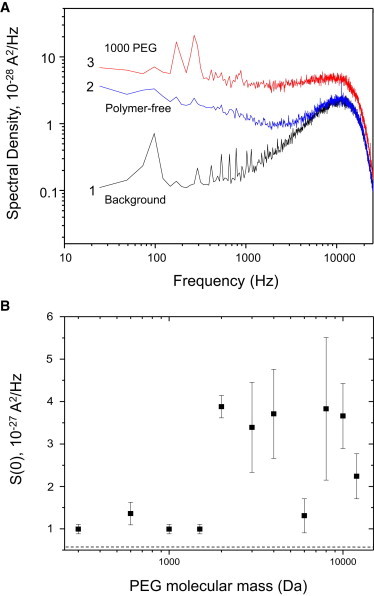
Power-spectrum analysis of noise in the engineered FhuA ΔC/Δ4L protein nanopore. (A) Representative power spectra at +100 mV. Trace 1 represents power spectra taken at 0 mV, trace 2 the power spectrum of a single FhuA ΔC/Δ4L nanopore in PEG-free solution and at +100 mV, and trace 3 the power spectrum of a single FhuA ΔC/Δ4L nanopore in solution containing 1000-Da PEG at +100 mV. Note that the PEG-containing solution has a greater noise level. The sharp cutoff at 10,000 Hz is due to the Bessel filter. (B) Trace indicates the excess S(0) noise in the power spectra of FhuA ΔC/Δ4L with PEG solutions. S(0) values were taken at +100 mV by averaging of the spectral values in the range 100–1000 Hz. Displayed values of each channel are calculated by subtracting the S(0) value at 100 mV from that at 0 mV. The horizontal dashed line represents baseline S(0) noise for PEG-free FhuA ΔC/Δ4L. Results indicate that PEG-induced noise is highest in the impermeable regime.

Discussion

Determining the diameter of the nanopore using an equilibrium partial filling approach

When introduced into solution at an identical concentration of 15% (w/w), different-sized PEGs decreased the conductivity of that solution by the same amount (Table S1). It has also been observed that for many transmembrane protein nanopores, the addition of small, easily penetrating PEGs to solution results in a reduction of their single-channel conductance that is similar to the reduction in the conductivity of the bulk aqueous phase (18). Motivated by these observations, several studies have employed the reduction of single-channel conductance for modeling the partitioning of PEG into the channel interior (12,18,20,23,31,38). In these investigations, the decrease in the single-channel conductance is assumed to be linearly proportional to the monomeric concentration of PEG inside the channel,

$$\frac{g\left(w\right)}{g(\infty )}=1-\gamma p\left(w\right),$$ (1)

where g(w) is the single-channel conductance of the nanopore at a given molecular mass, w. g(∞) indicates the single-channel conductance of the nanopore for a completely excluded polymer, whereas γ is the proportional reduction in the single-channel conductance when PEG lies in its interior. p(w) denotes the partitioning function. Here, we follow the modified scaling model (12,18),

$$p\left(w\right)=\text{exp}\left(-{\left(\frac{w}{w_0}\right)}^{\alpha }\right),$$ (2)

where w is the PEG molecular mass and w₀ is the transition molecular mass of the nanopore that separates the regime of partitioning from that of exclusion. α is the scaling parameter used to sharpen the transition from one regime to the other. When we combine Eqs. 1 and 2, we may fit the symmetric curves shown in Fig. 4. Leaving α, γ, and w₀ as free parameters, the fitting results of these values at +100 mV, 0 mV, and −100 mV are shown in Table 1. The value of w₀ for FhuA ΔC/Δ4L can be compared to that of previously studied nanopores with known diameters to calculate its size by assuming a 3/5 power scaling between the PEG size and mass (53). Using as a reference the outer-membrane protein F (OmpF) of E. coli, which has a known crystal structure (54,55), we can estimate the diameter of the FhuA ΔC/Δ4L nanopore with the formula (23,38)

$$d=d_{\text{OmpF}}{\left(\frac{w_0}{w_{\text{OmpF}}}\right)}^{3/5},$$ (3)

where d_OmpF is 1.4 nm and w_OmpF is 1360 Da (18). The estimated diameter of the FhuA ΔC/Δ4L nanopore is given in Table 1.

Table 1.

Size estimates of the FhuA ΔC/Δ4L nanopore using water-soluble PEGs

Voltage (mV)	PEG addition	γ	w0	α	Diameter (nm)
± 100	Symmetric	0.54 ± 0.06	1330 ± 240	0.8	1.4 ± 0.1
± 100	trans	0.38 ± 0.06	1890 ± 400	1.2	1.7 ± 0.2
0	Symmetric	0.54 ± 0.06	1250 ± 280	0.8	1.3 ± 0.1
0	trans	0.28 ± 0.02	1730 ± 190	1.5	1.6 ± 0.1
−100	Symmetric	0.48 ± 0.03	1610 ± 160	1.0	1.5 ± 0.1
−100	trans	0.2 ± 0.03	1800 ± 430	1.2	1.6 ± 0.2

γ, w₀, and α denote the proportional reduction in single-channel conductance of the nanopore when the PEG polymer lies in its interior, the transition molecular mass of the nanopore, and the scaling parameter used to sharpen the transition from one regime to the other, respectively.

Fig. 1 shows that FhuA ΔC/Δ4L is asymmetric in structure and therefore, asymmetric addition of PEG was performed to probe each opening of the nanopore independently. As is apparent in Fig. 4, the reduction in single-channel conductance for small polymers, such as 200- and 300-Da PEG, in both cis and trans conditions, does not drop the single-channel conductance of the nanopore by the same proportion, γ, seen in the symmetric case. The proportional drop is less than the drop for the conductivity of the bulk aqueous phase. This finding indicates only partial filling of the nanopore with PEGs. The curves in Fig. 4 are fittings of the data made using simple models, in which differently sized PEGs permeate the nanopore in a manner dependent on the nanopore geometry. Symmetric and trans curves were fit using Eqs. 1 and 2 with Origin 8.5. To estimate the size of the cis and trans openings, the fitting procedure must be modified to take into account the noncomplete partitioning. A simple way to do this is to express the proportional reduction in the single-channel conductance when PEG lies in its interior according to the expression

$$\gamma =\frac{g{\left(w\right)}_{\max }-g{\left(w\right)}_{\text{min}}}{g_{\text{noPEG}}},$$ (4)

again allowing γ to be a free parameter when using Eqs. 1 and 2 to fit (23). g(w)_min and g(w)_max are the values of single-channel conductance of FhuA ΔC/Δ4L in the PEG-containing solution in the regimes of full penetration and complete exclusion, respectively. g_noPEG denotes the single-channel conductance of FhuA ΔC/Δ4L in the absence of PEG. Values for α, γ, and w₀ for the trans curve are given in Table 1.

Determining the diameter of the cis opening of the nanopore using a nonequilibrium partial filling assumption

In the above model, equilibrium partitioning of PEG into FhuA ΔC/Δ4L is assumed. A more complex interpretation of partial filling can be found by taking into account that the partitioning is not an equilibrium process for asymmetric partitioning. Also, under asymmetric conditions, PEG will not partition all the way along the longitudinal axis of the nanopore, but instead only partially into its interior. Here, we model the probability of the PEG polymer partitioning at a given distance, x, into the nanopore interior. In this case, the single-channel conductance of the nanopore may be expressed as a function of the integral along its squared cross-sectional radius, R(x), and multiplied by the factor χ(w,x) (36),

$$g\left(w\right)={\left(\underset{0}{\overset{L}{\int }}\frac{dx}{\chi \left(w,x\right)\pi R^2\left(x\right)}\right)}^{-1},$$ (5)

such that χ(w,x) represents the decrease in the conductivity in the presence of the PEG polymer multiplied by the probability of the polymer being there:

$$\chi \left(w,x\right)={\chi }_0-p\left(w,x\right)\left({\chi }_0-\chi \right),$$ (6)

where p(w,x) is the partitioning function for a PEG polymer of a given molecular mass, w, to partition into the nanopore a distance, x. χ₀ and χ denote the conductivity of the solution without and with PEG, respectively. We use the partitioning function (36)

$$p\left(w,x\right)=\text{exp}\left[-{\left(\frac{w}{w_{trans}}\right)}^{\alpha }\right]\frac{\underset{x}{\overset{L}{\int }}{R}^{-2}\left(x\right)dx}{\underset{0}{\overset{L}{\int }}{R}^{-2}\left(x\right)dx},$$ (7)

where α is again the scaling factor and w_trans is the transition molecular mass of PEG at the trans opening. Equation 6 takes into account that the nanopore is not in equilibrium and makes use of the Fick-Jacobs approximation (36). If we assume that the nanopore is conical, with a constant slope, and that the larger trans opening is accurately modeled by using Eqs. 1–4, we may fit the values of $g\left(w\right)/g\left(0\right)$ for the cis data by using Eqs. 5–8. By assuming a trans opening of 1.8 nm and allowing α and χ₀/χ to be free parameters, best fits give estimates of the cis diameter between 0.85 and 1.1 nm for the applied transmembrane potentials used in Fig. 4 (+100 mV, 0 mV, and −100mV). Cis curves were fit using Eqs. 5–7 in Mathematica 7.

Determination of the nanopore diameter using impermeable dextran polymers

To independently assay the nanopore diameter, the contribution of FhuA ΔC/Δ4L’s access resistance to the overall nanopore resistance was measured using impermeable dextran. For a nonselective, cylindrical and ohmic nanopore, the access resistance can be expressed as 1/4χr, where χ is the solution’s conductivity and r is the nanopore radius (39,56). The introduction of impermeable dextran to the bulk aqueous phase decreases the conductivity of the solution surrounding the nanopore to a value of χ^∗, yet the solution in the interior of the nanopore maintains a conductivity of χ. Then the diameter of the nanopore is given by the expression

$$d=\frac{g_{\text{dextran}}}{{\chi }^{\ast }}\frac{1-{\chi }^{\ast }/\chi }{1-g_{\text{dextran}}/g},$$ (8)

where g_dextran is the single-channel conductance of the nanopore when dextran is added symmetrically to chamber, and g is the nanopore conductance in the PEG-free solution (26). This calculation gives an estimated diameter of 2.4 ± 0.6 nm for the FhuA ΔC/Δ4L nanopore. We find that the diameter of the FhuA ΔC/Δ4L nanopore estimated from dextran experiments is significantly larger than that obtained from PEG experiments (Table 2). This is most likely a result of the simplifying assumptions used in the modeling of the access-resistance contribution of dextran (39). Experiments achieved with water-soluble PEGs suggest an asymmetrical and noncylindrical nanopore, whereas a cylindrical nanopore was assumed in the diameter calculation using dextran polymers.

Table 2.

Size estimates of transmembrane protein pores using water-soluble polymers

Protein pore	PEG symmetric (nm)	PEG cis (nm)	PEG trans (nm)	Access-resistance dextran (nm)	Crystal structure (nm)	Reference
FhuA ΔC/Δ4L	1.2–1.6	0.85–1.1	1.4–1.9	2.4 ± 0.6	NA	This work
αHL	4.8	—	—	2.2 ± 0.4	1.4	(12)
Anthrax protective antigen (PA63)	<2.0	—	—	—	NA	(37)
Alamethicin	>1.2	—	—	2.3 ± 1.6	NA	(26)
OmpF	∼1.4	—	—	—	0.7 × 1.1	(18)
OmpU	1.10	—	—	—	NA	(38)
OmpT	0.86	—	—	—	NA	(38)
Epsilon toxin	2.0	0.8	2.0	—	NA	(23)
Syringomycin E channel	—	0.25–0.35	0.5–1.0	—	NA	(36)

Numbers indicate lumen diameters of various protein pores and channels. NA, not available.

The FhuA ΔC/Δ4L nanopore is asymmetric, with a greater opening on the periplasmic (trans) side than on the extracellular (cis) side, as shown by the high-resolution crystal structure of the native FhuA protein (6,7). Fig. 4 and Table 1 reveal that the proportional reduction in the single-channel conductance of the FhuA ΔC/Δ4L nanopore was greater when partitioning PEGs were added symmetrically than when they were added only to the trans or only to the cis side. Similar results have been obtained by other groups who examined various protein nanopores characterized by asymmetric geometries. For example, Nestorovich and co-workers (2010) found that Epsilon toxin (ETX) of Clostridium perfringens exhibits a truncated conical geometry with cis- and trans-opening diameters of 0.8 and 2.0 nm, respectively (23). Indeed, they determined that the proportional reduction in the single-channel conductance of ETX when the PEG polymer lies in its interior was always greater for symmetric than for trans and cis PEG additions. Similar to this work, they also showed that the addition of PEG to the chamber had a strong voltage-dependent impact on the single-channel conductance of ETX. This voltage dependence of the single-channel conductance might result from a combination of sources, such as the asymmetry of the protein nanopore, the voltage dependence of the nanopore structure, large differences in the electro-osmotic effect for small- and large-molecular-mass PEGs, the ion selectivity of the nanopore, and the transient binding of K⁺ ions to PEGs (see Voltage dependence of the conductance ratio).

We noticed that the scaling factor, α, which indicates the steepness of the penetration-to-exclusion transition, depended on the experimental circumstances of the PEG addition. For instance, α was always greater for trans than for symmetric additions (Table 1). What is the interpretation of this finding? We believe that α reflects the mechanism of the interaction of the PEG polymer with the particular entrance at which the polymer was added. In other words, α is a parameter that reflects the way in which the polymer partitions into the specific entrance confinement, depending on its size and geometry, as well as on attractive and repulsive interactions between the polymer and the pore walls.

We also calculated the single-channel conductance of the FhuA ΔC/Δ4L nanopore using either a simple conical or a smooth-walled ellipsoid geometry (Supporting Material). Using a conical geometry, a diameter of 1.6 nm for the trans entrance, a diameter of 1.0 nm for the cis entrance, and a nanopore length of 5.0 nm, we obtained a single-channel conductance of 2.8 nS. On the other hand, using a smooth-walled ellipsoid geometry, with the sides of the large trans opening of 2.6 and 3.9 nm, as derived from the high-resolution crystal structure of the native FhuA protein (6,7), and a nanopore length of 4.5 nm, we obtained a unitary conductance for the cork-free, FhuA ΔC/Δ4L nanopore of 3.4 nS, which is much closer to what we measured in our experiments. It is worth mentioning that this value of the single-channel conductance is highly sensitive to the value of the nanopore length (Supporting Material).

Previous studies have looked at the contribution of polymer interaction with transmembrane channels and pores to the current noise of the system (11,12,14,18,26,27). In the case of αHL and alamethicin, polymer interaction was found to increase the noise when the molecular mass of the polymer was near w₀ (12). However, in the case of OmpF, the attractive interactions of the polymers with the protein interior were negligible (18). We found that no significant noise increase occurred near the transition molecular mass, w₀, suggesting that the nanopore behaves more like OmpF (Fig. 5 B). In contrast, there is excess noise present at a greater PEG molecular mass. Although all visible closures were excluded when analyzing these data, it is still possible that this excess noise occurred as a result of rapid nanopore closures that were not visible as spikes. Increased frequency of brief current spikes of the nanopore was observable when higher-molecular-mass polymers were added (Fig. S3). Given that the polymer-nanopore attractive interactions lead to skewing of the transition molecular mass, w₀, to higher values, we believe that the limited interaction measured near the w₀ regime justifies the use of Eq. 3, and that the comparison with OmpF is apt. It may also explain why estimates with the PEG experiments are smaller than those obtained from the dextran experiments, whereas αHL, which exhibits a large noise response, shows the reverse (12).

Concluding remarks

In summary, we systematically examined the interior of the engineered FhuA ΔC/Δ4L protein nanopore using polymer exclusion. Permeable and impermeable water-soluble polymers were added to the chambers symmetrically or asymmetrically. Results from asymmetric addition of PEG suggest that the nanopore’s extracellular opening is smaller than the periplasmic opening. However, the values obtained in these estimates are smaller than those expected from the crystal structure. A possible explanation for this finding is that the deletion of the cork domain and extracellular loops may modify the inner dimensions of the β-barrel along the central transversal axis. The elliptical nature of the FhuA ΔC/Δ4L nanopore may also contribute to this underestimate, with the minor axes precluding the partitioning of larger-molecular-mass PEGs. This interpretation might explain the discrepancy between the results obtained with PEGs and those with dextran, because the access-resistance calculation assumes a circular nanopore opening. Evaluation of the low-frequency spectral noise density, S(0), provided modest values for PEGs whose molecular mass is comparable to or lower than the transition molecular mass, w₀. This finding suggests that PEGs do not significantly interact with the interior of FhuA ΔC/Δ4L, which is in accord with the hydrophilic nature of the nanopore walls featuring numerous positive and negative charges (6,7). The availability of structural, biochemical, and biophysical information on FhuA will likely ignite future full-atomistic, computational studies for a better mechanistic and quantitative understanding of the major alterations in the size and geometry of the redesigned protein upon dramatic modification of its architecture. These studies might also be employed to obtain precise information pertinent to the stochastic motion and conformation of the large extracellular loops of this outer-membrane protein (57–59). Only some extracellular loop motions of the outer membrane proteins are observed in the single-channel electrical recordings owing to limited time resolution of the employed instrumentation; therefore, a comparison of simulated and measured single-channel current would further contribute to the validation of the molecular structures derived from both experimentation and computation (60).