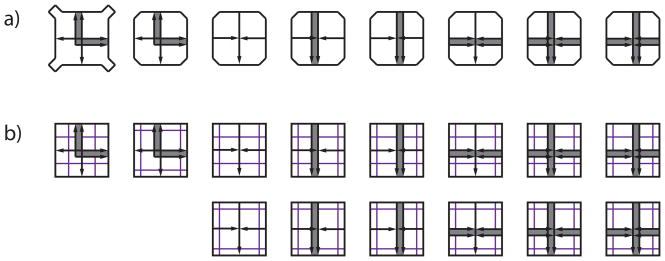Abstract
We introduce a hierarchical self assembly algorithm that produces the quasiperiodic patterns found in the Robinson tilings and suggest a practical implementation of this algorithm using DNA origami tiles. We modify the abstract Tile Assembly Model, (aTAM), to include active signaling and glue activation in response to signals to coordinate the hierarchical assembly of Robinson patterns of arbitrary size from a small set of tiles according to the tile substitution algorithm that generates them. Enabling coordinated hierarchical assembly in the aTAM makes possible the efficient encoding of the recursive process of tile substitution.
Keywords: self assembly, Robinson tiling, recursion, Tile Assembly Model, DNA origami, hierarchical assembly, algorithmic assembly, quasiperiodicity, substitution tiling
Introduction: Self Assembly by Tiles and Molecules
The abstract Tile Assembly Model (aTAM) is a useful mathematical abstraction of molecular self assembly that captures the essence of binding interactions while allowing one to reason about the algorithmic nature of the process (Wang, 1961; Winfree, 1998; Rothemund & Winfree, 2000; Rothemund, 2001; Adleman et al., 2002; Carbone & Seeman, 2003; Soloveichik & Winfree, 2007; Lathrop et al., 2008). In the standard aTAM, square tiles can bind at their edges via identical glues (Wang, 1961), complementary glues, or some other gluing mode (Winfree, 1998; Rothemund, 2001). Complementary glues suit many molecular interactions, in particular DNA binding interactions mediated by Watson-Crick base pairing. Self assembly begins with a nucleus, which might be a single tile or some contiguous finite assembly of tiles. A contiguous set of tiles bound to one another via the given matching rules may be referred to as a supertile, pattern, or assembly (Adleman et al., 2002; Rothemund, 2001; Lafitte & Weiss, 2008a). Tile assembly occurs by random selection of tiles from the tile set followed by comparison to a randomly chosen site at the perimeter of the pattern. In the cooperative model (Winfree, 1998), if the sum of edge glue strengths meets or exceeds the threshold, the tile joins the pattern. This process models macromolecular assembly in aqueous solution where molecular incarnations of tiles move about in three dimensions, bump into one another at random, and bind together if it is energetically favorable to do so. The first molecular scale algorithmic self-assembly using DNA demonstrated clearly that correct tiles compete for their slots with partially-correct tiles, rather than only with incorrect tiles, as they do in periodic self-assembly (Mao et al., 2000). During this random process tiles attach to the growing assembly nondeterministically, however, the emerging pattern may be considered deterministic if there is only one tile that can bind at each position in the pattern (Patitz & Summers, 2008; Soloveichik & Winfree, 2007).
A tile system (Soloveichik & Winfree, 2007), as described above, is capable of universal computation by simulating a Turing Machine (Robinson, 1971) or one-dimensional cellular automata (Winfree, 1998). Tile computation may also be seen as a process that produces a pattern (Rothemund et al., 2004) or a shape (Rothemund & Winfree, 2000; Soloveichik & Winfree, 2007) as the output of a computation. Taking the latter point of view, the input to a tile computation is a tile or supertile and the output, if the computation halts, is a supertile, (that is, a finite pattern or assembly of tiles) or a periodic tiling of the plane (Lafitte & Weiss, 2008a). A non-halting computation produces an infinite tiling of the plane or some infinite subset of the plane (Robinson, 1971). Because a supertile can behave like an individual tile, the supertiles output by a set of tile computations can serve as the input to another computation, or can form another tile system by simulating a tile set and seed tile(s) (Lafitte & Weiss, 2008a; Lafitte & Weiss, 2008b). This view of tile computation makes it clear that if the output of a tile system simulates the original tile computation, then the tile system is carrying out recursion.
One goal of algorithmic self assembly by tile computation is to produce arbitrary desired patterns as efficiently as possible, especially in terms of the number of different tiles needed. The efficiency of an assembly algorithm can be measured in several ways (Rothemund & Winfree, 2000; Rothemund, 2001; Soloveichik & Winfree, 2007; Adleman, 2000; Adleman et al., 2002; Cheng et al., 2004): by the number of different tile types needed, by the number of tile addition events that take place, by the depth of the assembly tree in hierarchical assembly (Chen H-L et al., 2010), and by a combination of the number of tiles, glues, bins, and stages needed for a staged assembly process (Demaine et al., 2008). As a step towards this goal, we target a set of aperiodic patterns from the Robinson tilings that are generated by a simple recursive algorithm of tile substitution, and provide a means for carrying out that algorithm as a tile assembly process in an enhanced aTAM. By adding capabilities to the aTAM that allow for the coordination of hierarchical assembly, the recursive algorithm that produces these patterns may be utilized to effect self assembly from a small tile set. While hierarchical assembly has been considered before (Carbone & Seeman, 2003; Aggarwal et al., 2005; Demaine et al., 2008; Doty et al., 2009; Chen H-L et al., 2010; Doty et al., 2010; Winfree, 2006) along with other variants of staged assembly (Abel et al., 2010; Patitz & Summers 2010; Demaine et al., 2011), we shall see here that it can be an incarnation of recursion, and as such its inclusion enhances the aTAM as a model of algorithmic assembly.
Hierarchical Structure in Robinson and Other Quasiperiodic Patterns
A Wang tile set (Wang, 1961) is called ‘aperiodic’ if every tiling of the plane admitted by the matching rules is aperiodic (Grünbaum & Shephard, 1987). Some experimentation with the Robinson tile set, (Figure 1), should convince the reader that indeed only aperiodic tilings are possible, as described in (Robinson, 1971). The pattern of Figure 2 emerges everywhere in a Robinson tiling, except possibly at dislocations joining the four quadrants of the plane, if they exist. The proof that every tiling enforced by the matching rules of these tiles is aperiodic follows from the necessity of arranging the tiles such that larger and larger squares are defined by the patterns on the tiles, (shown in gray in Figure 2). The emerging patterns may be described as quasiperiodic (Durand, 1999), self-similar (Lafitte & Weiss, 2008a), or hierarchical (Lafitte & Weiss, 2008a; Goodman-Strauss, 1999), and contain squares whose edges are defined by 2n + 1 tiles at the n-th level in the hierarchy. Further experimentation with the tiles of Figure 1 demonstrates that, within the Wang tiling system, it is easy to make errors by adding tiles at random according to the edge matching rules, creating untilable regions. However, arbitrarily large portions of a tiling can be assembled from the tiles by purposefully adding tiles in accordance with the hierarchical pattern of larger and larger squares, a process that coordinates assembly across greater and greater distances as the pattern grows.
Figure 1.
The Robinson aperiodic tiles. a) This set of eight tiles (including reflections), plus all rotations can only tile the plane aperiodically (Robinson, 1971) if shape complementarity and the matching rules of arrow heads meeting arrow tails at the edges of tiles are followed. b) Geometric constraints can be eliminated in favor of parity markings that must line up at the edges between tiles, producing a set of 14 tiles plus their rotations that enforce aperiodic tiling of the plane (Robinson, 1971).
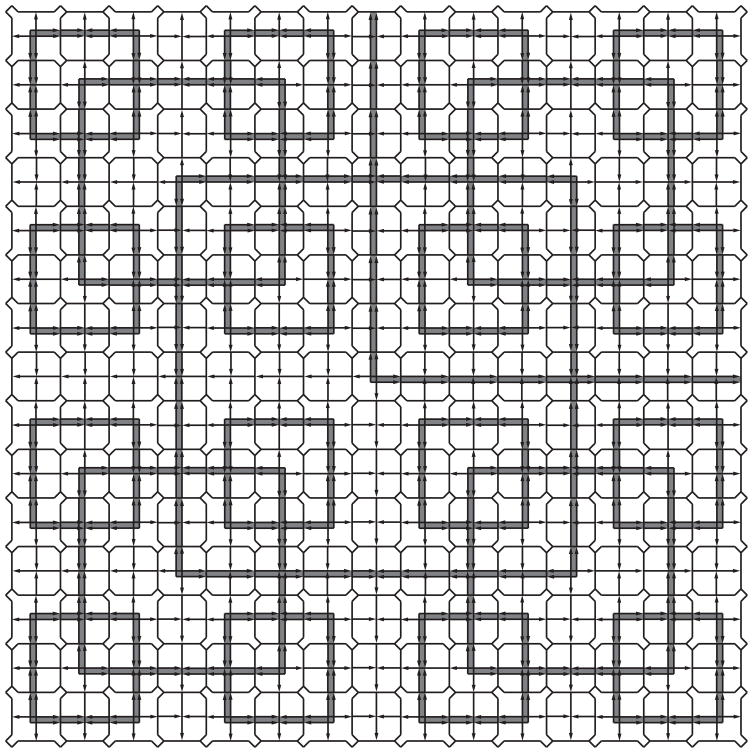
Figure 2.
Robinson 15-square. The Robinson tile set enforces patterns of squares of increasing size emphasized here in gray. The unbounded size of the square patterns in a tiling of the plane by the Robinson tile set proves that the tiling cannot be periodic. The parity tile set of Figure 1b enforces the same patterns (Robinson, 1971).
The matching rules of the original Robinson tiles were not designed with an assembly pathway in mind and they do not readily convert into an aTAM tile set that could direct deterministic assembly of the Robinson patterns. The Penrose tile set, another tile set that enforces aperiodicity (Penrose, 1974) and has hierarchical structure (Penrose, 1979), is also subject to the creation of untileable regions during assembly (Senechal, 1996). This propensity for misassembly has been demonstrated experimentally (Rothemund, 2000). A similar argument for mistiling may be made for any Wang tile set that tiles the plane quasiperiodically, (meaning that finite patterns appear regularly in the plane (Durand, 1999)), and whose matching rules exclude periodic tiling. Many such tiles sets are known (Frank, 2008). The Wang tiling system itself is concerned only with edge matching rules that enforce patterns, and is not formulated to model assembly processes as the aTAM is. While it may be possible to find efficient tile sets (Soloveichik & Winfree, 2007) in the standard aTAM producing Robinson patterns, we suggest enhancements to the aTAM in the next section that allow coordination of hierarchical tile self assembly into arbitrarily large portions of these patterns in accord with their hierarchical structure.
The hierarchical structure of the Robinson and Penrose tilings is due to the substitution rules that generate them. A substitution rule replaces each tile in an assembly by a finite configuration of tiles from the tile set, producing a larger assembly that obeys the matching rules (Frank, 2008; Grünbaum & Shephard, 1987; Senechal, 1996). Substitution rules for the Robinson tiling are shown in Figure 3. Hierarchical assembly can follow some or all of the substitution rules for a given tiling, physically implementing the substitution rules that generate the tilings. Repeating the process with each supertile generates arbitrarily large portions of a tiling. In the next section, we present a hierarchical scheme that only utilizes the first substitution rule shown in Figure 3. Each level of assembly produces a square supertile that behaves at the next level like the supertile it substitutes for. This is what allows hierarchical assembly to embody recursion, and it is also important in the study of tiling as a computational process (Lafitte & Weiss, 2008a).
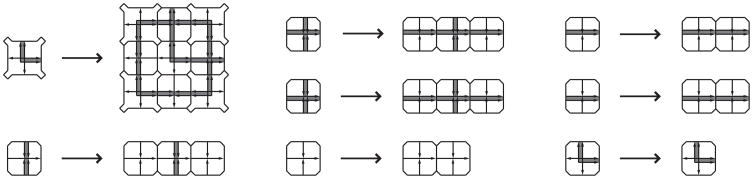
Figure 3.
Robinson substitution rules. These substitution rules provide nonuniform geometric scaling of each tile being substituted for, placing the Robinson tilings in the class of combinatorial substitution tilings (Frank, 2008). By induction, the substitution rules produce the (2m+1)-square from the m-square in one substitution step. For clarity, substitution rules are shown by the arrows on the geometrically constrained Robinson tile set of Figure 1a.
Though it is an algorithmic procedure on tiles, substitution is not directly included in the aTAM or its variants. Hierarchical assembly is a way to incorporate substitution rules into the aTAM in a physically meaningful way. However, hierarchical assembly must be coordinated somehow in the physical world. By comparison, the staged aTAM (Demaine et al., 2008) assumes the intervention of an outside operator who can separate complete assemblies and recombine them in stages. In the next section we present the means to incorporate the coordination of hierarchical assembly into the aTAM without outside intervention via a modest introduction of new capabilities. Modifications that can physically implement the recursive process of substitution enhance the aTAM as a model of algorithmic self assembly.
Hierarchical Self Assembly of Patterns from the Robinson Tilings in an Enhanced Tile Assembly Model
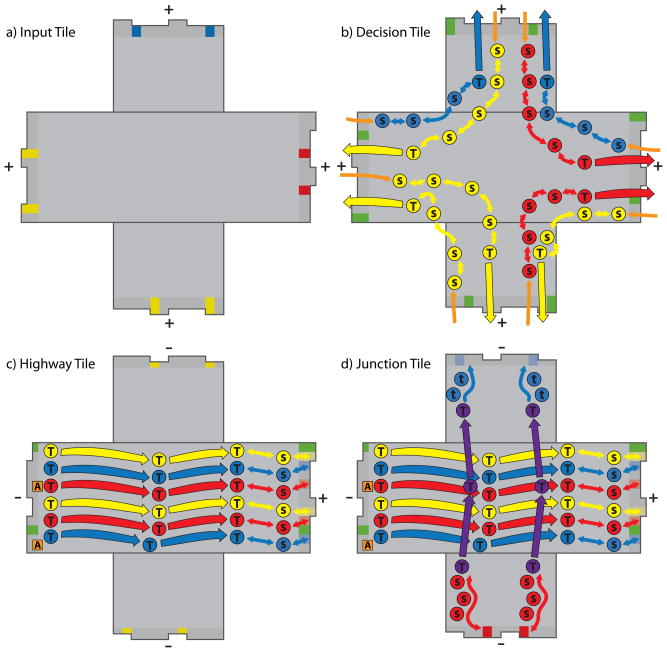
We add two new tile capabilities to the aTAM: signaling and glue activation in response to signals. These modifications enable a hierarchical self assembly process that can implement tile substitution rules, demonstrated here by a tile set of four unique tiles in the modified aTAM that direct the hierarchical self assembly of arbitrarily large patterns from the Robinson tilings. While these modifications are being introduced as a means to coordinate hierarchical assembly, we note that they need not be considered in this context alone, nor are they required in order for hierarchical assembly to occur (Aggarwal et al., 2005). A mathematical formulation of these added capabilities is presented at the end of this section. The hierarchical Robinson tile set, shown in Figure 4, contains fewer tiles than the original Robinson tile sets (compare to the 14 Robinson parity tiles and 8 geometrically constrained tiles in Figure 1), owing to the capability of certain tiles to take on different identities after signals are sent across them.
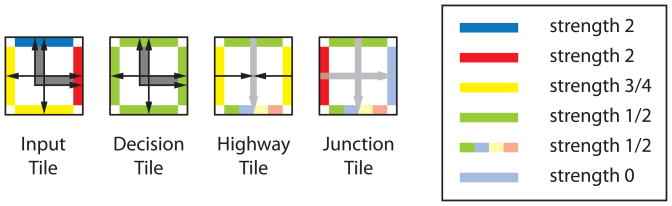
Figure 4.
Hierarchical Robinson tile set. To achieve hierarchical assembly, tiles are endowed with signaling and response to signals by activation of specific glues. The tile set, containing only 4 tiles, is reduced relative to the original Robinson set, (compare to Figure 1), because in this case the two right tiles will gain their identity only after a certain stage of assembly is reached and signals are sent along rows containing these tiles. We shall refer to these four tiles in order as the Input Tile, the Decision Tile, the Highway Tile, and the Junction Tile. Compare to Figure 1 to see the possible identities for the two rightmost tiles; the Highway Tile may become any of the tiles in the 3rd, 4th, or 5th columns in Figure 1, while the Junction Tile may become any tile in the 6th, 7th, or 8th columns. Edge glues are complementary, where an edge with arrow heads binds to an edge of like color with arrow tails that has the strength indicated by the color. We follow the cooperative tile model of computation whereby the overall temperature is 2, and a tile cannot bind a growing assembly unless the sum of its binding interactions meets or exceeds 2 (Winfree, 1998). The binding strengths are: red = 2, blue = 2, yellow = 3/4, green = 1/2. Pale colors, (blue, yellow, and red on the multicolor edges and the blue edge of the Junction Tile), indicate that a binding site is not active yet and thus has strength 0. When activated, the site has the strength indicated by its color. In the multicolor site, only green is active with strength 1/2, and any of the other colors may become active, depending on the signal sent. Light gray arrows indicate signal pathways on which signals have not yet traveled.
The signaling we describe obeys the following rules:
Signals must travel into a tile from a neighboring tile across the mutual interface between the tiles.
Signals must travel into a tile only after it is bound to its neighboring tile. Binding between tiles is mediated by edge glues alone.
Signals may propagate across a tile to any subset of its edges.
Upon reaching the edge of a tile, a signal may activate (or deactivate) an edge glue. That is, the response of any edge of a tile to a signal may be to change the identity and binding strength of the glue at that edge.
Upon reaching an edge of a tile that is already bound to a neighboring tile, the signal may be passed to the neighboring tile.
The idea of glue activation has been explored before (Majumder et al., 2008) in the context of promoting directional growth and error-resilience. Signaling and glue activation are defined here such that signals may propagate through assemblies and alter the binding properties of the exposed edges. After a signaling event, a finite assembly of tiles, (or supertile), can adopt a new identity, whereupon it can take on the role of a single tile in the next level of hierarchical assembly. This makes it possible to coordinate hierarchical assembly and to carry out recursion in the modified aTAM, in particular, to follow substitution rules in tile assembly.
The Hierarchical Self Assembly Process
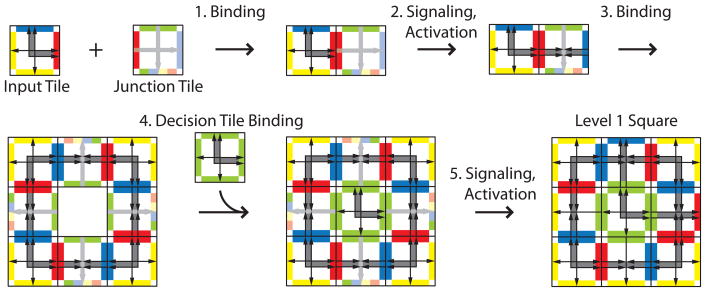
The hierarchy begins at level 0 with individual tiles. Level 1 assembly is detailed in Figure 5. Assembly begins with the Input Tile binding to the Junction Tile and sending a signal that propagates across the Junction Tile to activate its blue glue. Once the blue glue is active, the shell of the level 1 square readily assembles. The Input Tile is meant to be used up completely in level 1 assembly as it is the seed for a tile system where the tile set acting on the seed (or input) consists of the Decision, Junction, and Highway tiles. The square shell, still missing its central Decision Tile, remains symmetric with 4-fold rotational symmetry. In this cooperative assembly process, it is only after the square shape comes together to produce a binding site of overall strength 2 from four sides of strength 1/2 that the central Decision Tile can bind. Due to this step it is necessary for this two-dimensional assembly to occur in a three-dimensional milieu containing the hierarchical tile set. The Decision Tile can bind in one of four orientations, determined randomly by the tile addition process. Thus, the orientation of the binding of this tile ‘decides’ on the orientation of the square. Once bound, the Decision Tile sends signals across all four of its faces that propagate to the edge of the square assembly to activate glues there. The final identity of the Junction Tile is determined by the signal that passes through it, and is indicated in Figures 5, 6, and 7 by single arrows or double arrows to the left or right, (compare to Figure 1). Glue activation in the level 1 square makes this supertile ready to assemble at level 2, taking on the role that the Input Tile played in level 1 assembly.
Figure 5.
Level 1 assembly. Initially only the red glues on the Initiation and Junction Tiles are active and strong enough to bind tiles together (Step 1). The arrow configuration on the blue edge is set up so that it cannot yet bind to itself. Binding sends a signal across the Junction Tile to activate the blue glue on the other side (Step 2). The light gray arrow is replaced by double arrow markings from the original Robinson tile set to indicate that this event has occurred. Once active, four pairs of tiles can come together to form a square shape (Step 3). The central green glue is strong enough to recruit a Decision Tile only after the square has formed (Step 4). Binding of the central green Decision Tile causes signals to be sent in all four directions along the Junction Tiles. The signals sent give these tiles their identity, (indicated by the replacement of all remaining light gray arrows by single or double arrows from the original Robinson tile sets), and activate new binding glues on the perimeter of the level 1 square (Step 5). The strongest active glue becomes the only relevant one in later steps of assembly, therefore we only show the relevant color at the edge of a fixed tile.
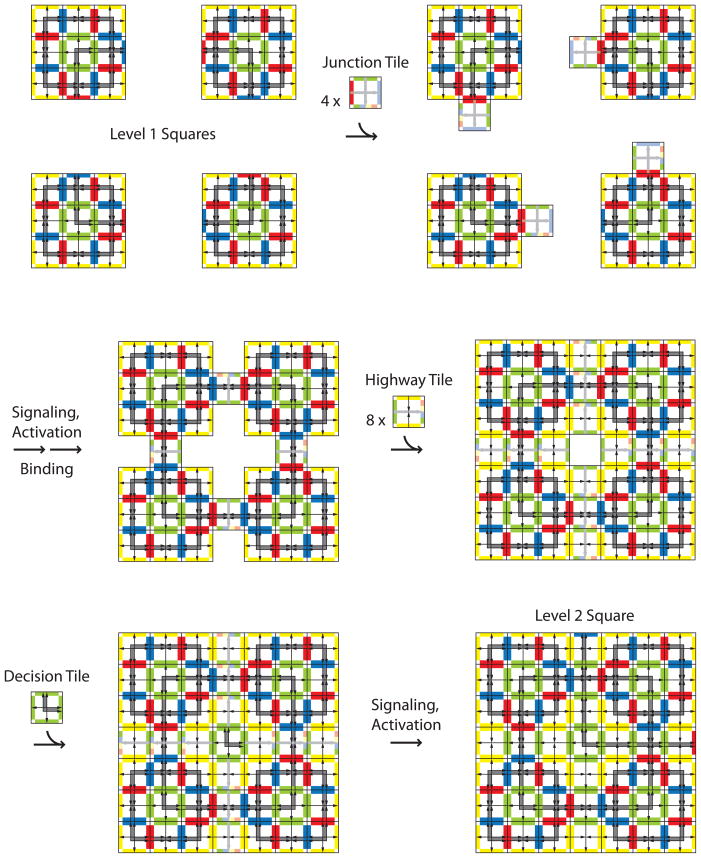
Figure 6.
Level 2 assembly. Assembly follows the same path as level 1, (Figure 5), except that level 1 squares now take the place of individual Input Tiles. At level 2 and beyond, formation of the square is followed by addition of Highway Tiles starting next to the Junction Tiles where the total binding strength is 2. The Highway Tiles must be in place in the interior of the assembly before the central Decision Tile can bind. Further, the rest of the tiles binding via yellow and green edges must be in place for the signal to reach the edge of the assembly and activate a glue. This provides a checkpoint for assembly at each level. The emerging pattern is highlighted in gray, as in Figure 2. In the interior of the square, the green glues at the arrow heads edge of the Highway Tiles are the only relevant glues, but at the edges of the square, the yellow, blue and red glues are the only relevant ones, even though the green glue is still active. Tile edges are colored to reflect the relevant binding sites only.
Figure 7.
Level 3 assembly. Level 2 squares come together as did level 1 and individual tiles in level 2 and level 1 assembly, respectively. Only when four level 2 squares come together will all Highway Tiles plus the Decision Tile bind, allowing the signals to be sent and the level 3 square to be completed. The resulting pattern is the Robinson 15-square, (see Figure 2).
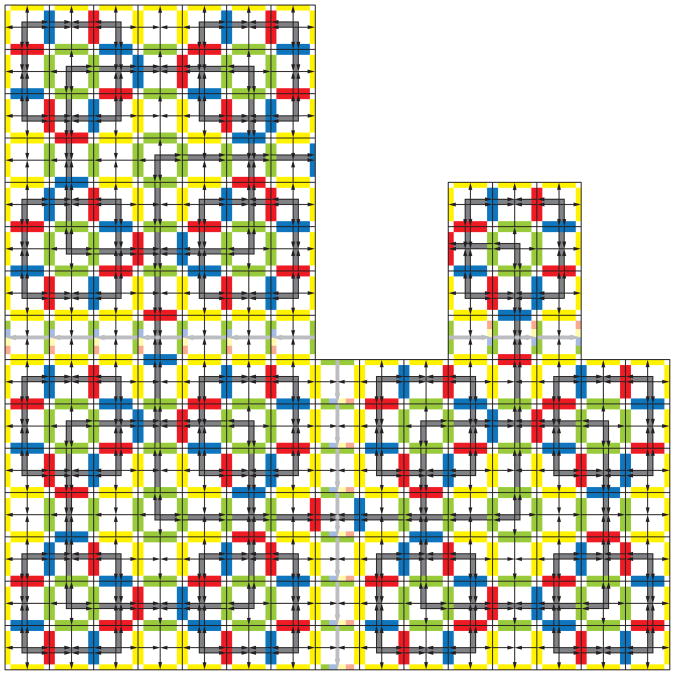
The Highway Tile comes into play at the second level of assembly (Figure 6). While the level 1 square plays the role of the Input Tile, the Junction Tile continues to act individually to bind to the level 1 squares and bring them together. The remaining gaps between level 1 squares are filled by the Highway Tiles. The orientation of the Highway and Junction Tiles is indicated in Figure 1 by the light gray arrows. Cooperativity of binding is needed to orient these tiles to face outward from the center of the assembly. The addition of Highway Tiles begins at the edges of the Junction Tiles where binding strength is sufficient for tile addition and the green glue directs the Highway tiles to bind in the correct orientation. The Decision Tile binds only after the Highway Tiles have created a strength 2 binding site for it in the center of the level 2 assembly. At level 2, the signals from the Decision Tile travel through three tiles to the edge of the assembly. Again, the level 2 square is ready to take the role of the Input Tile in level 3 assembly. At each level of assembly, level n squares are joined together via a single Junction Tile at each interface, then Highway Tiles and the Decision Tile bind individually, so there is no need to scale the interaction strengths or change the temperature as the assemblies get larger. The result of n levels of assembly is a square 2(n+1) – 1 tiles on an edge, thus as a level n square assembles, each signal from the Decision Tile will travel along 2n – 1 tiles. The result of level 3 assembly is shown in Figure 7.
The first potential problem that could occur during assembly is ensuring that an assembly is complete before it can participate in another level of assembly. Since tiles add to the assembly at random, it is possible for a row of Highway Tiles to be one or more tiles short of reaching the edge of the assembly when the Decision Tile binds. The signal could reach the end of the shortened row of Highway Tiles and activate a glue interior to the intended edge of the square assembly (Figure 8). If a red glue is activated in this way it has enough strength to recruit a Junction Tile in a position where a Highway Tile is meant to go. To prevent this problem in the theoretical model, we propose two alternate solutions. In the first, a zero-strength glue marks the outside corner tiles in a square assembly, providing a cue that the edge of the assembly has been reached (Figure 8). This solution also utilizes zero-strength glues to pass the signal from the Decision Tile until it triggers the activation of red, blue or yellow glues at the edge of the assembly. An alternate solution, in a model that allows negative glue interactions, would be to add a negative binding interaction (Doty et al., 2011; Reif et al., 2006) between a green arrow heads edge and a yellow arrow heads edge that would prevent the Junction Tile from binding in the interior of the square assembly. Separate zero-strength signal glues are not needed, as this would make the overall strength of binding the Junction Tile in the wrong place less than 2, so it could not bind. In practice, negative interactions could be the result of steric interference. With the addition of either the outside edge signals or the negative interaction, assembly remains deterministic within each level.
Figure 8.
Edge signals. The Decision Tile may bind and send signals prior to completion of a square assembly. A zero-strength glue may be included on two sides of the Input Tile (shown by an asterisk at the corner) to indicate that it is at the edge of an assembly. This indicator glue is deactivated on both edges after either labeled edge becomes bound to another tile, thus it is maintained only at unbound corners of square assemblies where it serves to inform a Highway Tile that it is positioned at the edge of an assembly. The Highway Tile responds by activating the edge glue that was signaled by the Decision Tile, and signals the Input Tiles to deactivate the indicator glue. A model with negative glue strengths can disallow premature binding of the Junction Tile to and incomplete square assembly providing an alternative to this extra signaling step.
Encoded by just four unique tiles, this assembly process can make mistakes if assemblies from different levels of the hierarchy interact with one another. Misassembly may occur starting at level 2, and is depicted at level 3 in Figure 9. In general, misassembly occurs if a level n assembly incorporates an assembly of level n – 2 or lower. However, an error of this kind does not propagate. If an assembly from a lower level binds, it cannot recruit Highway Tiles all the way to the center of the assembly. This prevents the central position from gaining the strength it needs to recruit the Decision Tile, and without the signals sent by the Decision Tile, the assembly cannot become part of the next level in the hierarchy. This type of misassembly can occur because the process is an approximation of staged assembly lacking the artificial outside intervention that only allows complete assemblies to move on in the staged aTAM (Demaine et al., 2008). Synchronous assembly, in other words perfect staging, whereby each level of assembly is complete and all previous levels have been used up before the next level begins, results in the deterministic production of Robinson patterns of arbitrary size without any of the dead-end products just described. The approximation to perfect staging can be made arbitrarily close in more than one way. One is by including more glues. If, for example a different blue glue is used from one stage to the next, then those stages will not interact with one another. An infinite number of unique glues in place of blue would then separate stages perfectly. However, one can simply choose a finite number, m, of unique glues to use in place of blue, then cycle through their use at each stage of assembly. In that case, misassembly would only be possible if assemblies m stages apart interact, an event that occurs with diminishing probability as m increases. In a different approximation of perfect staging, cycles of assembly during which the blue glue is inactivated temporarily on a global scale can provide time for assemblies at one level to reach completion. By splitting signals from the Decision Tile, it also appears possible to divide the strong interaction between red glues amongst two strength-one edges that are placed further apart at each level of assembly. Alternate solutions to the staging problem appear to alter the balance between the number of tiles and glues needed, the number and variety of signaling events, and the degree of global coordination or outside intervention required.
Figure 9.
Level 3 misassembly. During asynchronous assembly, there could be level 1 squares still present during level 3 assembly. If one binds in place of a level 2 square, it is not possible for the Highway Tiles to bind and reach the center of the growing square, thus the Decision Tile cannot bind and assembly is halted.
The hierarchical assembly process described here reflects the recursive algorithm by which the Robinson tiles may be directed to assemble into an arbitrarily large pattern that obeys the matching rules of the tiles. From a computational point of view, the Input Tile may be seen as the input to a tile system composed of the other three tiles. The output of the computation performed by this tile system is the Robinson 3-square (Figure 5). The 3-square is then fed back into the tile system, still composed of the Highway Tile, Junction Tile, and Decision Tile which outputs the Robinson 7-square (Figure 6), which again serves as the input whose output is the 15-square (Figure 7), and so on. This is recursion in tile computation and theoretically may continue infinitely with this tile set to produce arbitrarily large patterns from the Robinson tilings. Perfectly staged assembly in this tile system is completely deterministic.
Mathematical Formulation of Signaling and Glue Activation
We formalize the addition of signaling and glue activation to the aTAM by adding a signal function, λ, to each tile. We describe the relevant details of the formulation, referring the reader to standard mathematical formalism of the aTAM (Rothemund & Winfree, 2000), as well as formalism of hierarchical assembly (Aggarwal et al., 2005, Chen H-L et al., 2010). A tile type, t, in the aTAM is a 4-tuple (σN, σE, σS, σW) of edge glues (Rothemund & Winfree, 2000) from the set edge glues, Σ. In our enhanced version of the aTAM, a tile type, t = (σN, σE, σS, σW, λ), includes the signal function, λ, in addition to the four edge glues. If tN, tE, tS, tW, are the tile neighbors of bound to the top, right, bottom, and left, respectively, then tN(S), tE(W), tS(N), tW(E), are the edge glues of the neighboring tile edges that are in contact with t. If no tile is bound in a particular direction then it is treated as the empty tile, empty, with null glue, null, whose strength of interaction with all other glues is zero. The domain of the signal function, λ, of tile type includes the glues from the bound edges of the neighboring tiles as well as the glues of itself, and the range is the set of glues at the edges of t, thus we write to express the action of the signal function in activating or changing the glues of the tile t. This formulation is very general and allows one to express signal functions with more capabilities than we use in our construction, such as repeat signaling and tile detachment in response to signals. One may restrict signals to be sent only once by using proto-glues, that is, zero-strength glues that are deactivated by the signal function at the same time that the corresponding glue is activated. If the signal function cannot re-activate the proto-glue, then the signal can only be sent once.
A glue function, γ, determines the strength of the interaction between two edges depending on their edge glues (Aggarwal et al., 2005). Following (Lafitte & Weiss, 2008b), a tile edge may have more than one glue associated with it. This is expressed as a Cartesian product of elements from Σ. The glue function, γ, will give the sum of the pairwise interactions from the Cartesian product of edge glues on neighboring edges as the overall strength of the interaction. We let minus denote arrow tails, plus denote arrow heads, and g, b, y, and r denote green, blue, yellow, and red, respectively to denote the edge glues of the hierarchical Robinson tiles in Figure 4. Further, a subscript 0 is added to indicate that is glue is not active, (that it is a proto-glue), and a subscript b, r, or y indicate that an edge glue is used to pass a signal to a neighboring tile, if that tile contains the appropriate signal function.
The hierarchical Robinson tiles as shown in Figure 4 may be formally expressed as: Input Tile = (b+, r+, y+, y+, λI), , and . Additional signal glues may be present on the Input Tile if the edge-signaling scheme of Figure 8 is used. The binding of the east edge of the Input Tile, tI, as it is oriented in Figure 4 to the west edge of the Junction Tile, tJ, causes a signal to be sent across the Junction Tile to activate the blue color on its east edge, (the first signaling event shown in Figure 5). We write this formally as , where the result is that the east edge of the Junction Tile goes from inactive, , to active, b−. Signals may pass through an assembly as follows. A signal function λ modifies the edge of tile t causing the signal function λ′ of a neighboring tile t′ to modify an edge of t′, causing the signal function λ″ to modify a neighbor t″, and so on through an assembly of connected tiles. This formalution introduces minor modifications to the standard aTAM and satisfies the rules for signaling given above.
DNA Tiles for the Hierarchical Self Assembly of Patterns from the Robinson Tilings
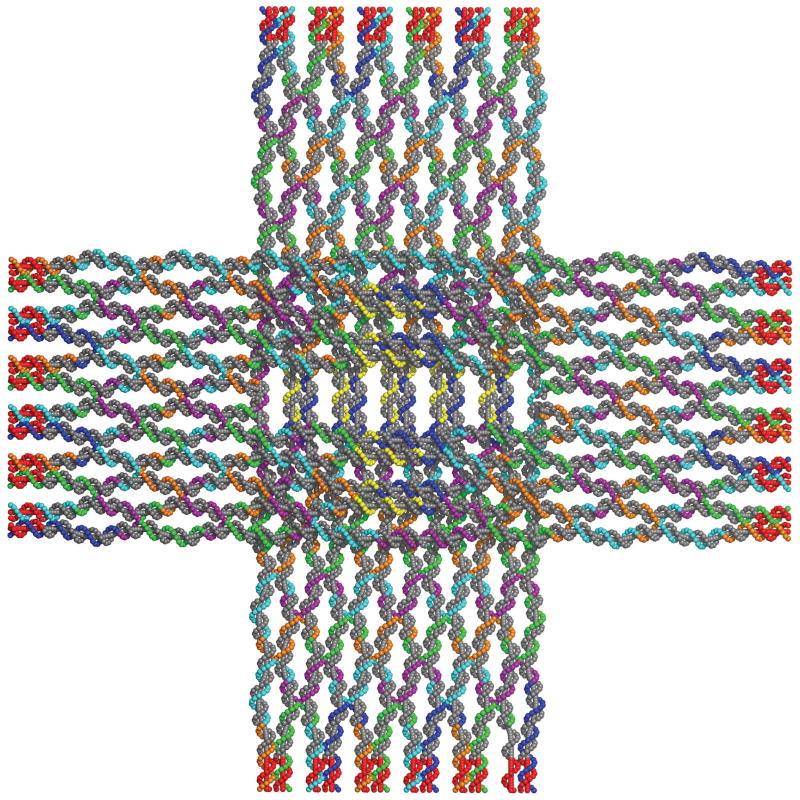
The capabilities of signaling and glue activation, (referred to as “binding site activation” in the practical implementation), that we have added to the aTAM appear to be readily embodied using DNA. Here we present the design of four DNA tiles that can embody the four hierarchical Robinson tiles depicted in Figure 4. DNA origami (Rothemund, 2006) tiles in the shape of a square cross that is about 100 nm on an edge are used as the basic structural unit, (Figure 10). This structure has been shown to produce good quality two dimensional arrays (Liu et al., 2011). Functional DNA strands that can serve as the signaling and binding elements can be incorporated as extensions to the numerous staple strands of the origami. Edge binding between tiles is mediated by 12 DNA helices per edge meeting head on. The sequence space of the edges can be freed from the origami template sequence by moving the template strand back from the edge to create 16 base pair extensions to each edge helix, a modification of the tiles from (Liu et al., 2011), allowing them to be designed as orthogonal binding sequences (sequences having no cross interference) (Choi et al., 2010) using available software (Seeman, 1990; Zadeh et al., 2011; Birac et al., 2006). With square tiles that are about 100 nm on an edge, we expect to obtain assemblies of size 300 nm, 700 nm, 1.5 μm, and 3.1μm on an edge at levels 1, 2, 3, and 4 of the hierarchical assembly process described in the previous section, respectively. Thus, assemblies composed of these tiles have patterns that transition from the nanoscale of the origami tile to the microscale.
Figure 10.
The DNA origami template for the hierarchical Robinson tiles. The DNA origami cross is about 100 nm across and has 12 DNA helices at each edge, grouped in 6 pairs, each ending in a variable number of base pairs whose sequence is independent of the origami template strand sequence. Origami template DNA is shown in iron gray, independent sequences are red, and staple strands are shown in other colors. Staple strands can be extended to provide the functional DNA strands of each tile. Additionally, some helices are lengthened and others shortened to provide shape complementarity to the arrow heads and arrow tails edges, and to provide steric hindrance the to binding between two edges containing arrow heads. These DNA tiles without the edge modifications have been shown to assemble into high quality two-dimensional arrays (Liu et al., 2011). This image was generated using Nanoengineer-1 (Nanorex Inc., 2008) and Pymol (Schrödinger, LLC, 2010).
We have chosen a gain of 16 base pairs at an edge to be equivalent to the strength 2 glue of the model, making the gain of 6 and 4 base pairs equivalent to the strength 3/4, and 1/2 glues respectively. Furthermore, the base pairing interactions along an edge are divided between two separate helices with 3′ or 5′ overhangs of 8, 3, or 2 bases respectively for edges with strength 2, 3/4, or 1/2 glues. Orthogonal sequences should be used for the different colors depicted in Figure 4, and the position and separation between the helices carrying the binding strands can be varied to distinguish further the binding interfaces. The first and fourth nucleotide pairs of DNA helices will be extended by 6 base pairs at edges corresponding to arrow heads, and the 3rd and 6th pairs of DNA helices will be recessed by 6 base pairs at edges corresponding to arrow tails, creating geometric complementarity and creating a steric hindrance that acts as the negative interaction described in the previous section to prevent the binding of a wrongly placed Junction Tile to an incomplete square assembly. We have chosen to implement the negative glue strength solution here, rather than the extra signaling pathway described in the previous section, due to the relative ease of the physically implementing steric hindrance versus adding another signaling pathway. Overlaps of 2 and 3 bases have been shown to be weak enough to allow crystallization to occur (Zheng et al., 2009), demonstrating that cooperative, reversible associations mediated by multiple short DNA strand overlaps may promote proper self assembly. In the absence of any base pairs between adjacent helices on separate tiles, there may nevertheless be a favorable base stacking interaction (Wang et al., 2010).
Binding mechanisms are shown in Figure 11. The basic binding interaction between tile edges is mediated by single-stranded overlaps as shown in Figure 11a. The number of bases in the overlap between tiles is determined by the desired binding strength of the interaction as described above, and could be tuned in a laboratory setting, along with temperature, to optimize proper assembly. Toehold-mediated exchange mechanisms (Yurke et al., 2000; Turberfield et al., 2003; Seelig et al., 2006a; Seelig et al., 2006b; Zhang et al., 2007; Omabegho et al., 2009; Qian & Winfree, 2009) provide the means to suppress globally a specific binding site by altering the concentration of a small single strand of DNA (Figure 11b) that blocks the binding site. The mechanism of Figure 11b utilizes the seesaw gate motif (Qian & Winfree, 2009) to produce a reversible binding site that can be driven towards or away from inter-tile associations by adjusting the concentrations of the two competing strands. With a second strand the edge of a tile can be locked into a non-binding configuration, which might be used to produce cycles of assembly that are controlled globally by adjustments to the concentration of the competing DNA strands in solution. As discussed in the previous section, controlled cycles of assembly could help prevent the misassembly products of Figure 9 from forming by allowing time for assemblies to be completed, thus promoting a close approximation to perfect staging at each level.
Figure 11.
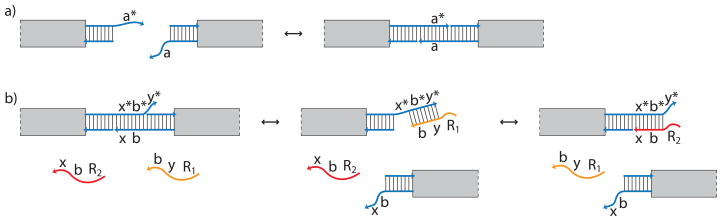
Schematic of DNA-mediated binding between tiles. a) Binding sites consist of complementary single-stranded extensions of 8, 3, or 2 bases at the ends of DNA helices on the edge of a tile. Extensions may be 5′ or 3′, with 3′ extensions shown. Letters identify short DNA sequences and a * denotes the complementary sequence. Arrows indicate the 3′ end of the DNA strand. b) A variant of the seesaw gate (Qian & Winfree, 2009) can be used to modulate the strength of a binding site. One of the two competing strands that is free in solution has a toehold, (y), allowing it to disrupt binding between tiles. The second strand can displace this first one, again using a toehold, (x), to prevent further interaction between the two tiles. By altering concentrations of the two free strands, one could disrupt binding and cycle between the on and off states of a binding site, making binding reversible, as well as synchronizing each level of hierarchical assembly. Strands have toeholds, (R1 and R2), that can be used to regulate their concentrations in solution.
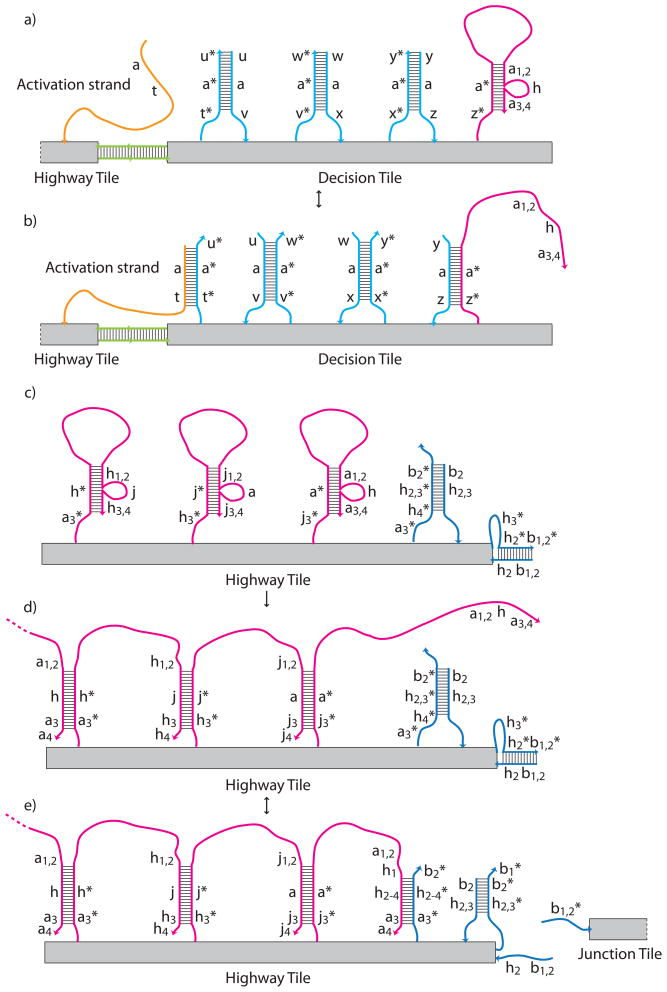
The signaling across and between tiles can be accomplished with a combination of seesaw mechanisms (Qian & Winfree, 2009) and transducers (Seelig et al., 2006a) composed from DNA strands that are tethered to the DNA origami tiles. Elements of the Decision Tile signaling pathways are shown in Figure 12. In any practical implementation, signals must have the following properties and capabilities:
Figure 12.
Decision Tile Signaling pathway. Some labeled sequences are divided into smaller lengths as indicated by subscripts. a) Activation through a neutral signal pathway, (cyan strands), at the beginning prevents the activation strand, (gold), from causing tile binding. b) The last step of the activation pathway opens the first transducer loop (magenta). c) The central downhill transducer cascade, (magenta strands), is made energetically favorable by the gain of four base pairs at each step. Another neutral pathway, (blue strands), transmits the signal to the binding site, (blue strands at the edge of the tile), to activate it by removing a protecting strand. d) After the last transducer loop has opened, the signal may be transmitted to a neighboring tile, allowing the transmission of signals to the edge of an assembly. e) The last transducer strand can instead activate the binding site through a neutral pathway. If the tile is at the edge of an assembly, this makes the edge active and ready for the next level of assembly. Otherwise, the neutral pathway will be able to reverse and release the transducer strand, giving it another chance to pass the signal to a neighboring tile.
-
1
Signals must be robust enough to travel over increasing distances in growing assemblies.
-
2
Signals must in some cases output a sequence different from the input sequence.
-
3
Signaling must not cause binding between tiles, but must instead be transmitted from one tile to an adjacent tile only after binding has occurred.
In our proposed DNA implementation, it is also true that:
-
4
A particular signal may only be sent once across a given tile.
The first property is accomplished by making the transducer cascade across an individual tile energetically favorable and directional by the gain of base pairs at each step of the cascade, lacking toeholds to assist in the reversal of strand binding during the cascade (Dirks & Pierce, 2004). The drawback of this approach is that due to the metastability of the signal pathway, some spurious triggering of the cascade could occur, seen in bulk experiments as a minor component attributed to leakage from the metastable state (Choi et al., 2010), as when a middle domino is accidentally tipped over in the middle of row of dominoes. To offset this possibility, the two separate helices of each binding site are triggered by separate and independent cascades, so that if one is spuriously activated, the binding site will not reach full strength unless the second one is also activated. The second requirement for signaling is achieved automatically by the use of the transducer mechanism. The third item can be accomplished through careful use of seesaw-like pathways. These energetically neutral pathways (Figure 12) can make signal strands available in a reversible fashion. Until an energetically favorable transducer cascade is triggered, the activating strand may be released by a backward swing of the seesaw strand exchanges. Thus, the delay caused by sending the signal through a neutral seesaw pathway prevents the activation strand from causing binding; if a tile is not bound at its edge, the activation strand does not permanently attach a tile to another tile unless the transducer cascade is triggered. A buffer of a few seesaws between the activation strand and the transducer pathway reduces this likelihood.
The important signaling events from the Decision Tile to the edge of an assembly are shown in Figure 12, the signaling across the Junction Tile is shown in Figure 13, and the layout of signaling elements on each of the four hierarchical Robinson tiles is shown schematically in Figure 14. The Input Tile contains fixed, active binding sites only. The assembly process begins as described in Section 3, with the Input Tile binding to the Junction Tile via the red binding site. This binding event displaces a strand that propagates down a neutral seesaw/transducer pathway to the transducer cascade that carries the signal across the tile, where it activates the blue binding site (Figure 13). This signal is activated by the release of an activation strand on the Junction Tile upon binding at the red edge. The signal crosses other signal paths without interference due to the orthogonal sequences of the activation strand and the transducer elements. Once the blue binding site is active on the Junction Tile, assembly will proceed as described in Section 3. The downhill transducer pathways that cross the middle of the Junction Tile and the Highway Tile are composed of tethered elements with DNA tethers long enough to reach the next element in the cascade (Omabegho et al., 2009), but short enough to be expected not to interact with elements on neighboring tiles.
Figure 13.
Junction Tile signal pathway. a) Signal pathway from red binding site through seesaw pathway (red), transducer cascade, (purple and blue), to protected blue arrow tails binding site. b) After a tile binds to the Junction Tile at the red arrow tails site, an activation sequence is freed and the signal is transmitted along a seesaw pathway to the first transducer loop, and continues along the transducer cascade to remove the protection strand from the blue binding site, activating it.
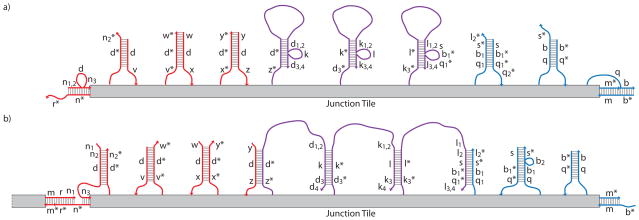
Figure 14.
Schematic representation of the four recursive Robinson tiles made from DNA and their signaling pathways. Binding sites (+,−), neutral seesaws (S), transducers (T,t), and activation strands (A) are indicated on each of the four tiles. Inactive binding sites are indicated with pale colors and two-way arrows between them and seesaw elements (S) on the Highway and Junction Tiles.. The direction of propagation of energetically favorable signal cascades is indicated with arrows. Seesaw pathways that can go in either direction are indicated with arrowheads in both directions. Positions of elements are based on the locations of free staple strand ends. a) The Input Tile contains only binding sites that are already active. b) Activation signals entering the Decision Tile from bound neighbors are indicated in orange. Each neighbor bound to the Decision Tile activates one of the signals on each of the adjacent edges. This arrangement means that two of the three other edges must be bound before a given edge of the Decision Tile can send its signal. This setup is much easier to implement than the 4-way AND gate that the logic of the tile system being implemented would nominally demand. This adjacent neighbor AND gate should suffice for practical purposes. Although there are only two unique activation strands, seesaw pathways (S) on the Decision Tiles are kept orthogonal by using orthogonal toeholds. c) Three different signals can propagate along the Highway Tile, ending in binding site activation as indicate by two-way arrows, or in the propagation of the signal directly from the last transducer (T) to the first transducer of a neighboring tile. d) The Junction Tile contains signaling pathways that cross one another. From left to right this tile has the same pathways as the Highway Tile. From bottom to top is the pathway for an red binding interaction to activate the blue binding site on the top. The orthogonality of this pathway is indicated by coloring the junction signal purple.
The next and final signaling event that completes a given level of assembly occurs after the Decision Tile binds to the center of the assembly. This signaling cascade, some of whose details appear in Figure 12, begins with the Decision Tile binding to four Highway Tiles in the middle of an assembly. Ideally, an AND gate would trigger the release of Decision Tile signals after all its edges are bound, so as to comply with requirement 3 above. In practice, it is easier to have an adjacent Highway Tile trigger the release of one of the two signals that correspond to one color from the adjacent edge. Thus, the Decision Tile must be bound on three sides in order to send one complete signal from the adjacent side. This should suffice for practical purposes. As described above, the activation is accomplished through a neutral seesaw pathway (Figure 12). The signal is sent to an adjacent Highway Tile when the transducer loop is opened and binds to the corresponding transducer loop on the Highway Tile. The transduction continues across the Highway Tile and across the “highway” pathway on the Junction Tile to the Highway Tile at the edge of the assembly where one of the three binding sites, red, blue, or yellow is activated, depending on the signal received. During the propagation of the signal from the Decision Tile to the edge of the assembly, whenever the signal reaches the edge of a Highway Tile, it must continue to propagate if another Highway Tile is bound to the other side, but must activate a binding site if the Highway Tile is at the edge of the assembly (see Figure 12 and discussion in the previous section). These alternative pathways are connected to each other on each Highway Tile by a neutral seesaw path. If there is another Highway Tile adjacent, then the last transducer loop opens and the strand it releases may bind to the first transducer loop on the adjacent tile. However, the released strand (which is still tethered, as are all strands in the signal pathways), may alternatively bind the first helix in the seesaw, displacing strands until the binding site is exposed. If a Highway Tile is adjacent, this path will not be productive and will eventually reverse to release the signal strand again, allowing the signal to continue to the next tile. If the Highway Tile is at the edge of the assembly however, then the binding site may bind to a Junction Tile when it is exposed by the seesaw, and when it is freed from any blocking strands used to synchronize assembly (Figure 11).
As outlined above, DNA origami tiles can be constructed with the necessary structural properties and placement of functional DNA strands to embody the signaling and binding properties needed for the hierarchical self assembly of Robinson patterns described in the previous section. All components and signaling mechanisms suggested here exist in the literature, having been tested experimentally in some form. Other possibilities for signaling, not explored here in detail, would be the use of autonomous DNA walkers and spiders (Omabegho et al., 2009; Lund et al., 2010; Wickham et al., 2011; Yin et al., 2008) to carry a signal strand across a tile, or from one tile edge into a neighboring tile. The need for robust signaling motivates the continued development of reliable signaling mechanisms using DNA strands and structures. The DNA origami tiles have enough space and available staple strands to be decorated with additional DNA extensions that could aid in identifying tile type and orientation using atomic force microscopy (Liu et al., 1999).
Discussion
Hierarchical assembly can be a physical incarnation of the recursive process of tile substitution, and is an algorithm for tile self assembly that enables the efficient production of patterns from the Robinson tilings. Signaling and glue activation in response to signals make coordination of hierarchical self assembly possible in the abstract Tile Assembly Model and can be added by minimal modifications to the formal model. It appears possible to implement these new capabilities using published DNA mechanisms and structures, as demonstrated here by the design of DNA origami tiles that appear capable of self-assembling into arbitrarily large portions of a Robinson tiling through an active assembly process involving signaling and glue activation via DNA strand exchange mechanisms. The process of signaling and of responding to signals by altering binding properties is a familiar one in the realm of molecular biology, hence the properties we have added to the aTAM further enhance its utility in modeling physical assembly processes in addition to making it possible to carry out recursion in the form of hierarchical assembly.
Patterns that are generated by substitution rules include quasicrystalline arrangements such as the Robinson and Penrose tilings. A general hierarchical assembly scheme could implement a different tile substitution rule at each level, rather than the same rule at each level as in the generation of the Robinson patterns. This may aid in the production of arbitrary patterns containing various types of hierarchical structure. Binding site deactivation may enhance other assembly pathways not explored here, such as the process of ‘carving’ described in (Spicher et al., 2006). The extensive hierarchical structure within living organisms suggests the potential utility of this general approach to self assembly.
Many mechanisms for nucleic acid assembly, computation, and function are now known. We have presented here a general scheme and a specific example on how to merge these mechanisms to generate coordinated active self assembly of large patterns that are not periodic. This modification to the aTAM makes it a better model of physical assembly processes carried out by molecules, while at the same time retaining its elegance as a mathematical model and opens the door to the direct inclusion of recursion in self assembly.
Acknowledgments
We thank Natasha Jonoska for helpful discussions and anonymous reviewers for helpful suggestions. This research has been supported by the following grants to NCS: GM-29554 from the National Institute of General Medical Sciences, CTS-0608889 and CCF-0726378 from the National Science Foundation, 48681-EL and W911NF-07-1-0439 from the Army Research Office, N000140910181 and N000140911118 from the Office of Naval Research and a grant from the W.M. Keck Foundation.
Contributor Information
Jennifer E. Padilla, Email: jenpadilla@gmail.com, Monrovia, CA 91016.
Wenyan Liu, Email: wl502@nyu.edu, Department of Chemistry, New York University, New York, New York 10003.
Nadrian C. Seeman, Email: ned.seeman@nyu.edu, Department of Chemistry, New York University, New York, New York 10003.
References
- Abel Z, Benbernou N, Damian M, Demaine E, Demaine M, Flatland R, Kominers S, Schweller R. Shape replication through self-assembly and RNase enzymes. SODA 2010: Proceedings of the Twenty-first Annual ACM-SIAM Symposium on Discrete Algorithms; Austin, Texas. Society for Industrial and Applied Mathematics; 2010. pp. 1045–1064. [Google Scholar]
- Adleman LM. Computer Science Technical Report 00-722. University of Southern California; 2000. Towards a mathematical theory of self-assembly. [Google Scholar]
- Adleman L, Cheng Q, Goel A, Huang M-D, Kempe D, de Espanés PM, Rothemund PWK. Combinatorial optimization problems in self-assembly. Proceedings of the thirty-fourth annual ACM symposium on Theory of computing; 2002. pp. 23–32. [Google Scholar]
- Aggarwal G, Cheng Q, Goldwasser MH, Kao M-Y, de Espanés PM, Schweller RT. Complexities for generalized models of self-assembly. SIAM Journal on Computing. 2005;34:1493–1515. [Google Scholar]
- Birac JJ, Sherman WB, Kopatsch J, Constantinou PE, Seeman NC. Architecture with GIDEON, a program for design in structural DNA nanotechnology. Journal of Molecular Graphics and Modeling. 2006;25(4):470–480. doi: 10.1016/j.jmgm.2006.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carbone A, Seeman NC. Aspects of Molecular Computing, LNCS. Vol. 2950. Springer-Verlag; 2004. Molecular tiling and DNA self-assembly; pp. 61–83. [Google Scholar]
- Chen H-L, Doty D, Seki S, Soloveichik . Parallelism, Program Size, Time, and Temperature in Self-Assembly. 2010. arXiv:1011.3493v1. [Google Scholar]
- Cheng Q, Goel A, de Espanés PM. Optimal self-assembly of counters at temperature two. Proceedings of the First Conference on Foundations of Nanoscience: Self-Assembled Architectures and Devices.2004. [Google Scholar]
- Choi HMT, Chang JY, Trinh LA, Padilla JE, Fraser SE, Pierce NA. Programmable in situ amplification for multiplexed imaging of mRNA expression. Nature Biotechnology. 2010;28(11):1208–1212. doi: 10.1038/nbt.1692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demaine ED, Demaine ML, Fekete SP, Ishaque M, Rafalin E, Schweller RT, Souvaine DL. Staged self-assembly: nanomanufacture of arbitrary shapes with O(1) glues. Natural Computing. 2008;7(3):347–370. [Google Scholar]
- Demaine ED, Patitz M, Schweller R, Summers S. Self-Assembly of Arbitrary Shapes Using RNAse Enzymes: Meeting the Kolmogorov Bound with Small Scale Factor. In: Schwentick, Dürr, editors. STACS 2011: Proceedings of the 28th International Symposium on Theoretical Aspects of Computer Science. 2011. pp. 201–212. [Google Scholar]
- Dirks RM, Pierce NA. Triggered amplification by hybridization chain reaction. Proc Natl Acad Sci USA. 2004;101(43):15275–15278. doi: 10.1073/pnas.0407024101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doty D, Kari L, Masson B. Negative Interactions in Irreversible Self-assembly. In: Sakakibara, Mi, editors. DNA Computing and Molecular Programming, LNCS. Vol. 6518. 2011. pp. 37–48. [Google Scholar]
- Doty D, Lutz JH, Patitz MJ, Summers SM, Woods D. Intrinsic universality in self-assembly. Proceedings of the 27th International Symposium on Theoretical Aspects of Computer Science.2009. [Google Scholar]
- Doty D, Patitz MJ, Reishus Dustin, Schweller Robert T, Summers Scott M. Strong fault-tolerance for self-assembly with fuzzy temperature. FOCS 2010: Proceedings of the 51st Annual IEEE Symposium on Foundations of Computer Science; 2010. pp. 417–426. [Google Scholar]
- Durand B. Tilings and quasiperiodicity. Theoretical Computer Science. 1999;221:61–75. [Google Scholar]
- Frank NP. A primer of substitution tilings of the euclidean plane. Expositiones Mathematicae. 2008;26(4):295–326. [Google Scholar]
- Goodman-Strauss C. Foams, Emulsions, and Cellular Materials (Cargèse, 1997), NATO Adv Sci Inst Ser E Appl Sci. Vol. 354. Kluwer Acad. Publ; Dordrecht: 1999. Aperiodic hierarchical tilings; pp. 481–496. [Google Scholar]
- Grünbaum B, Shephard GC. Tilings and patterns. Freeman; New York, NY: 1987. [Google Scholar]
- Lafitte G, Weiss M. Computability of tilings. Fifth IFIP International Conference on Theoretical Computer Science-TCS 2008: IFIP 20th World Computer Congress, TC 1, Foundations of Computer Science; September 7–10, 2008; Milano, Italy. 2008a. pp. 187–201. [Google Scholar]
- Lafitte G, Weiss M. Logic and Theory of Algorithms. 2008b. Simulations between tilings; p. 264. [Google Scholar]
- Lathrop JI, Lutz JH, Patitz MJ, Summers SM. Logic and Theory of Algorithms. 2008. Computability and complexity in self-assembly; pp. 349–358. [Google Scholar]
- Liu F, Sha R, Seeman NC. Modifying the surface features of two-dimensional DNA crystals. J Am Chem Soc. 1999;121(5):917–922. [Google Scholar]
- Liu W, Zhong H, Wang R, Seeman NC. Crystalline two-dimensional DNA origami arrays. Angew Chemie. 2011;50(1):264–267. doi: 10.1002/anie.201005911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lund K, Manzo AJ, Dabby N, Michelotti N, Johnson-Buck A, Nangreave J, Taylor S, Pei R, Stojanovic MN, Walter NG, Winfree E, Yan H. Molecular robots guided by prescriptive landscapes. Nature. 2010;465(7295):206–210. doi: 10.1038/nature09012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majumder U, LaBean TH, Reif JH. Activatable Tiles: Compact, Robust Programmable Assembly and Other Applications. In: Garzon, Yan, editors. DNA Computing, LNCS. Vol. 4848. 2008. pp. 15–25. [Google Scholar]
- Nanorex Inc. Nanoengineer-1, version 1.1.1 http://www.nanoengineer-1.com/
- Omabegho T, Sha R, Seeman NC. A bipedal DNA brownian motor with coordinated legs. Science. 2009;324(5923):67. doi: 10.1126/science.1170336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patitz MJ, Summers SM. Self-assembly of decidable sets. Proceedings of The Seventh International Conference on Unconventional Computation; Vienna, Austria. 2008. [Google Scholar]
- Patitz MJ, Summers SM. Identifying Shapes Using Self-assembly. In: Cheong, et al., editors. Algorithms and Computation, LNCS. Vol. 6507. 2010. pp. 458–469. [Google Scholar]
- Penrose R. The role of aesthetics in pure and applied mathematical research. Bull Inst Math Appl. 1974;10(7/8):266–71. [Google Scholar]
- Penrose R. Pentaplexity a class of non-periodic tilings of the plane. The mathematical intelligencer. 1979;2(1):32–37. [Google Scholar]
- Qian L, Winfree E. A simple DNA gate motif for synthesizing large-scale circuits. In: Carbone, Pierce, editors. DNA Computing, LNCS. Vol. 5347. 2009. pp. 70–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reif JH, Sahu SE, Yin P. Complexity of Graph Self-assembly in Accretive Systems and Self-destructible Systems. In: Goel, et al., editors. DNA Computing, LNCS. Vol. 3892. 2006. pp. 257–274. [Google Scholar]
- Robinson RM. Undecidability and nonperiodicity for tilings of the plane. Inventiones mathematicae. 1971;12(3):177–209. [Google Scholar]
- Rothemund PWK. Using lateral capillary forces to compute by self-assembly. Proceedings of the National Academy of Sciences of the United States of America. 2000;97(3):984. doi: 10.1073/pnas.97.3.984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothemund PWK. PhD thesis. University of Southern California; 2001. Theory and experiments in algorithmic self-assembly. [Google Scholar]
- Rothemund PWK. Folding DNA to create nanoscale shapes and patterns. Nature. 2006;440(7082):297–302. doi: 10.1038/nature04586. [DOI] [PubMed] [Google Scholar]
- Rothemund PWK, Winfree E. The program-size complexity of self-assembled squares (extended abstract). Proceedings of the thirty-second annual ACM symposium on Theory of computing; 2000. pp. 459–468. [Google Scholar]
- Rothemund PWK, Papadakis N, Winfree E. Algorithmic self-assembly of DNA sierpinski triangles. PLoS Biology. 2004;2(12):e424. doi: 10.1371/journal.pbio.0020424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrödinger, LLC. The PyMOL molecular graphics system, version 1.3r1. 2010. [Google Scholar]
- Seelig G, Soloveichik D, Zhang DY, Winfree E. Enzyme-free nucleic acid logic circuits. Science. 2006a;314(5805):1585. doi: 10.1126/science.1132493. [DOI] [PubMed] [Google Scholar]
- Seelig G, Yurke B, Winfree E. Catalyzed relaxation of a metastable DNA fuel. J Am Chem Soc. 2006b;128(37):12,211–12,220. doi: 10.1021/ja0635635. [DOI] [PubMed] [Google Scholar]
- Senechal M. Quasicrystals and geometry. Cambridge Univ Pr; 1996. [Google Scholar]
- Soloveichik D, Winfree E. Complexity of self-assembled shapes. SIAM Journal on Computing. 2007;36(6):1544–1569. [Google Scholar]
- Spicher A, Michel O, Giavitto J-L. Algorithmic self-assembly by accretion and by carving in mgs. In: Talbi, et al., editors. Artificial Evolution, LNCS. Vol. 3871. 2006. pp. 189–200. [Google Scholar]
- Wickham SFJ, Endo M, Katsuda Y, Hikada K, Bath J, Sugiyama H, Turberfield AJ. Direct observation of stepwise movement of a synthetic molecular transporter. Nature Nanotechnology. 2011;6(3):166–169. doi: 10.1038/nnano.2010.284. [DOI] [PubMed] [Google Scholar]
- Wang H. Proving theorems by pattern recognition II. AT&T Bell Labs Tech J. 1961;40:1–41. [Google Scholar]
- Turberfield AJ, Mitchell JC, Yurke B, Mills AP, Blakey MI, Simmel FC. DNA fuel for free-running nanomachines. Physical review letters. 2003;90(11):118102-1–118102-4. doi: 10.1103/PhysRevLett.90.118102. [DOI] [PubMed] [Google Scholar]
- Winfree E. PhD thesis. California Institute of Technology; 1998. Algorithmic self-assembly of DNA. [Google Scholar]
- Winfree E. Self-healing tile sets. In: Chen J, Jonoska N, Rozenberg G, editors. Nanotechnology: science and computation. Springer-Verlag; Berlin: 2006. pp. 55–78. [Google Scholar]
- Yin P, Choi HMT, Calvert CR, Pierce NA. Programming biomolecular self-assembly pathways. Nature. 2008;451(7176):318–322. doi: 10.1038/nature06451. [DOI] [PubMed] [Google Scholar]
- Yurke B, Turberfield AJ, Mills AP, Simmel FC, Neumann JL. A DNA-fuelled molecular machine made of DNA. Nature. 2000;406(6796):605–608. doi: 10.1038/35020524. [DOI] [PubMed] [Google Scholar]
- Zadeh JN, Steenberg CD, Bois JS, Wolfe BR, Pierce MB, Khan AR, Dirks RM, Pierce NA. NUPACK: Analysis and design of nucleic acid systems. Journal of Computational Chemistry. 2011;32(1):170–173. doi: 10.1002/jcc.21596. [DOI] [PubMed] [Google Scholar]
- Zhang DY, Turberfield AJ, Yurke B, Winfree E. Engineering entropy-driven reactions and networks catalyzed by DNA. Science. 2007;318(5853):1121. doi: 10.1126/science.1148532. [DOI] [PubMed] [Google Scholar]
- Zheng J, Birktoft JJ, Chen Y, Wang T, Sha R, Constantinou PE, Ginell SL, Mao C, Seeman NC. From molecular to macroscopic via the rational design of a self-assembled 3D DNA crystal. Nature. 2009;461(7260):74–77. doi: 10.1038/nature08274. [DOI] [PMC free article] [PubMed] [Google Scholar]